Abstract
The fluctuating nature of power produced by renewable energy sources results in a substantial supply and demand mismatch. To curb the imbalance, energy storage systems comprising batteries and supercapacitors are widely employed. However, due to the variety of operational conditions, the performance prediction of the energy storage systems entails a substantial complexity that leads to capacity utilization issues. The current article attempts to precisely predict the performance of a lithium-ion battery and capacitor/supercapacitor under dynamic conditions to utilize the storage capacity to a fuller extent. The grey box modeling approach involving the chemical and electrical energy transfers/interactions governed by ordinary differential equations was developed in MATLAB. The model parameters were extracted from experimental data employing regression techniques. The state-of-charge (SoC) of the battery was predicted by employing the extended Kalman (EK) estimator and the unscented Kalman (UK) estimator. The model was eventually validated via loading profile tests. As a performance indicator, the extended Kalman estimator indicated the strong competitiveness of the developed model with regard to tracking of the internal states (e.g., SoC) which have first-order nonlinearities.
1. Introduction
Energy storage is a key component of renewable energy systems in terms of ensuring reliable and sustained energy supply. Energy storage is mainly comprised of chemical, electrochemical, and electrical systems. Chemical energy storage involves the conversion of electrical energy into electrochemical energy for intermediate storage, and it is classified as batteries, fuel cells, and electrochemical capacitors [1]. Electrochemical energy storage, consisting of batteries and capacitors/supercapacitors, can be categorized as primary (non-rechargeable), secondary (rechargeable), or thin-film batteries, or supercapacitors. Lithium-ion (Li-ion) batteries are secondary batteries that have dominated market penetration and, in the past decade, have attracted substantial research interest with regard to the prediction of their performance [2,3]. Thin-film Li-ion batteries are miniaturized versions of conventional Li-ion batteries, which have been integrated extensively in modern, smarter, and more compact electronic devices.
Due to the delicate nature of miniaturized smart low-power electrochemical components, the precise estimation of battery attributes such as state-of-charge (SoC), state-of-health (SoH), internal resistance, and temperature dependency is crucial for effective power management [4,5]. SoC is considered to be the most crucial parameter of those that govern the power flow. However, it is not measurable and requires estimation practiced through several methodologies.
Doyle, Fuller, and Newman [6] introduced a white box or electrochemical model for parameter estimation characterized by higher accuracy; however, it was extremely complex to the point of being impracticable. On the contrary, the black box technique affords pragmatic simplification and thus is widely adopted. These models are extremely simplified, involve fewer parameters, and afford ease of handling [7,8,9]. The model, however, has limited ability to predict capacity, power fading, degradation, and the temperature effect [10]. The technique employs fuzzy logic and empirical functions such as Peukert’s law [11,12], as given in Equation (1):
where is the battery capacity, I is the discharge current, k is the Peukert coefficient, and t is the time for discharging the cell. Additionally, Shepherd, Unnewehr, and Nernst introduced a method for estimating the terminal voltage with respect to charge and discharge conditions [13]. Models based on artificial intelligence are currently being employed to effectively predict internal cell dynamics. The limitation lies in a lengthier training process, exhaustive data requirements, and an inability to embrace the physical aging of the cell [14].
The grey box modeling technique emerged as a middle ground between white and black box models, and the equivalent circuit model (ECM) is one example of a grey box technique [15,16]. Grey box models combine prior physical knowledge with experimental data for physical interpretation in order to assign numerical values to model parameters. When modeling a complex system such as an ECM, the model contains some unknown parameters. For instance, when modeling a Li-ion battery, internal impedance is greatly affected by temperature and SoC, but their exact relationship is not well defined. These parametric values are estimated by using the statistical relationship (system identification) from the experimental data, as shown in Figure 1. Some of these models were implemented in [17,18] for the estimation of SoC; these have a simple structure and demonstrate their practicality by replacing complex electrochemical phenomena via the simpler ECM without considerably compromising between battery dynamics and accuracy.
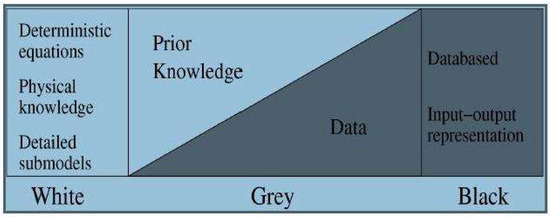
Figure 1.
Grey box modeling [19].
SoC estimation is crucial for power management and control in battery systems. Numerous factors can influence the precise measurement of SoC, such as hysteresis phenomena among charge and discharge cycles, white noise, open circuit voltage characteristics, and current. Inaccurate SoC estimation can lead to shorter calendar life and poor performance due to overcharge and over-discharge of the battery. The techniques available for estimating the SoC of a battery are classified as the direct discharge method, Coulomb counting, impedance-based, and model-based, coupled with estimating algorithms [20,21,22,23] that are governed by parameters that vary with SoC, thus creating an implicit relationship. The available state-of-the-art method for SoC estimation using various estimators is highly developed. However, accurate and precise models are required, especially when dealing with low-power Li-ion batteries and supercapacitors with first- or second-order nonlinearities. This paper attempts to resolve the issues of overly complicated and overly simplified low-power battery modeling through a reasonably accurate, yet simplified, grey box modeling approach. A low-power Li-ion battery and supercapacitor are modeled by employing extended Kalman (EK) and unscented Kalman (UK) estimators for parameter identification to estimate the SoC of the Li-ion battery and capacitor/supercapacitor [24].
2. Modeling Methodology
2.1. Experimental Setup
A test bed consisting of a battery and supercapacitor, Agilent-SMU, a host PC, and control temperature cabin was established indoors, as depicted in Figure 2 [25]. The setup was capable of measuring the current and voltage in the order of µV and pA and could operate in continuous and pulse modes and constant current and constant voltage modes simultaneously. A rechargeable solid-state lithium thin-film battery with a lithium cobalt oxide (LiCoO2) cathode, a lithium phosphorous oxynitride (LiPON) ceramic electrolyte, and a lithium anode with a capacity of 0.7 mAh (EFL700A39) as well as a DMF-series high-performance double-layer supercapacitor were used for the test.

Figure 2.
Test bed for the experiment.
An accurate mathematical relationship between the model input and output was established and categorized as the input/output structure. In conformance with the input/output structure, the experimental data were processed for parameter estimation, identification, and distinction.
The model identification process involved a current signal being fed into the battery/supercapacitor. The respective output voltage was generated, where the discharge current was positive as per the standard test condition, as demonstrated in Figure 3.
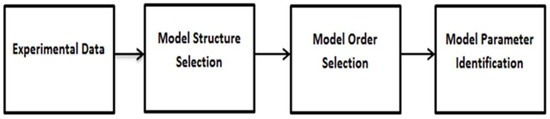
Figure 3.
Identification of the grey box model.
2.2. Data Set
Several experiments including a capacity test, pulse test, open circuit voltage (OCV) (voltage under no load conditions generally depends on the battery design and operating temperature) and state-of-charge test (OCV–SoC), and loading profile test were conducted at various temperatures from 5 °C to 25 °C with an interval of 5 °C. The capacity test revealed information regarding the current capacity to the nominal capacity of different Li-ion batteries (LiMn2O4 LiB cell (C/LMO) which uses carbon as its negative electrode and lithium magnesium oxide for the positive electrode, and the other one is lithium iron phosphate (C/LFP). The capacity differed from the maximum capacity due to the aging process, as presented in Table 1.

Table 1.
Comparison of Li-ion battery specification.
Charge–discharge efficiency tests were used to determine the coulomb efficiency of the cells and, later on, to determine the compensation of the developed model and the accuracy of the SoC estimation and pulse test estimation regarding the model internal parameters. Results of the OCV–SoC test are depicted in Figure 4; the red line represents the current and the blue line indicates the voltage. Figure 4a represents recharging of the battery under constant current and constant voltage conditions (CCCV) and Figure 4c shows that as the voltage approaches its upper cut-off level, the current decreases to a minimum. Figure 4b,d indicates the terminal voltage of the battery in charging and discharging modes.
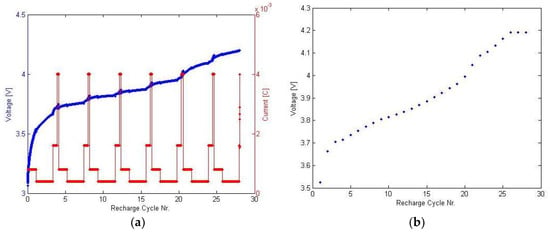
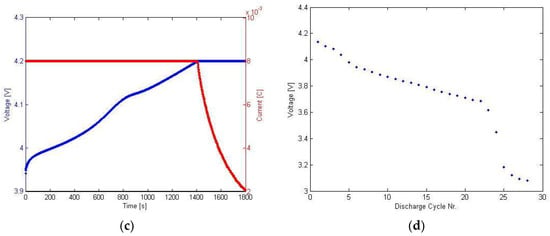
Figure 4.
Open circuit voltage and state-of-charge (OCV–SoC) results: (a) Recharging of the battery under constant current and constant voltage conditions (CCCV); (b) charging terminal voltage; (c) charging of the battery under CCCV; (d) discharging terminal voltages.
2.3. Model Development and State Space Representation
The general representation of the grey box model is represented as [26]:
where t is a time-dependent variable, represents the system state vector, is the input variable, indicates the noises present in the system, and is the vector of unknown parameters. The first term of Equations (2) and (3) is categorized as drift and the second is subsequently characterized as diffusion.
The order of the model is determined by employing the statistical methods (i.e., system identification) through a curve fitting process. The final model involving the ECM and electrochemical model is discretized and represented by the set of differential equations given below:
Li-Ion Battery Model:
Supercapacitor Model:
T indicates sampling interval and T1 is the time constant for RC network. To estimate the state-of-charge (SoC), the basic definition of the coulomb counting method is adopted [20].
and T represent the battery capacity in As and sampling time, respectively. Equations (4), (5), and (9), representing the states and output of the battery model, can be given as:
where are the battery state, output, and input matrix, respectively. They can also be represented in matrix form as:
| . |
The model output and states for the supercapacitor in matrix form are given as:
| . |
2.4. Model Validation
The developed model was validated via the loading profile test in which a load is attached to the battery and supercapacitor, a current is applied under various C-rates, and the outputs are measured. The same current was applied to the model and its output behavior was estimated. Two techniques, namely the unscented and extended Kalman estimators, were applied for the output and state-of-charge (SoC) estimation [27,28]. The input was applied to the model and the terminal voltage was estimated. The measured and estimated terminal voltages were compared and the error was minimized between the two outputs by adjusting the Kalman gain. The new gain value was subsequently applied for the trade-off of the state estimation error. The parameters of the battery were updated by using the new values of the states and the terminal voltage was estimated at a new sampling interval. The measured and estimated output for the battery and supercapacitor is depicted in Figure 5a,b, respectively. It can be seen that overall, the estimated output voltage tracks the measured voltage accurately despite some localized errors caused by adjusting the Kalman gain value.
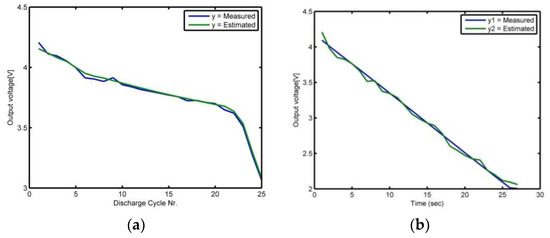
Figure 5.
Measured and estimated terminal voltages: (a) Battery measured and estimated output terminal voltage; (b) the measured and estimated output terminal voltage of the supercapacitor.
The performance of the two estimators for estimating the SoC for the battery is represented in Figure 6. Figure 6a,b depicts the SoC estimation and error in the estimation by employing the EK estimator while Figure 6c,d represents the estimation and its corresponding error by using the UK estimator. As the given model is of the first order, the performance of the EK estimator is much better than the UK estimator. The SoC estimation error in the case of the EK estimator is under 1%, while it approaches 6% for the UK estimator. Based on these findings, for the first-order nonlinear models, the EK estimator shows a noticeably better performance for the SoC estimation compared to the UK estimator.
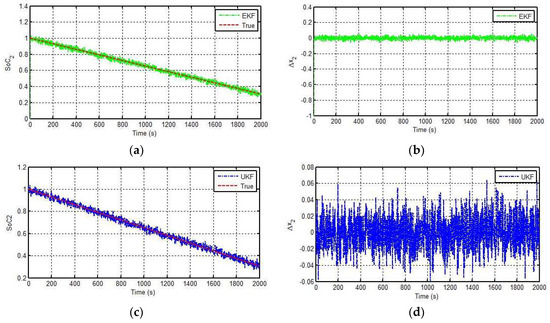
Figure 6.
Battery SoC and error in estimation: (a) SoC estimation with an extended Kalman (EK) estimator; (b) error in EK estimation; (c) SoC estimation with an unscented Kalman (UK) estimator; (d) error in UK estimation.
To establish the robustness of the estimation methods, a wrong initial SoC was set. The performance of the estimation techniques for the supercapacitor can be seen in Figure 7. Figure 7a,c depicts the SoC estimation with the wrong initial values, while Figure 7b,d represents an error in the estimation. At the start, the error value between the measured and estimated SoC was higher because the estimators compensate the error by setting a larger gain value and then adjust the estimation in an effective closed-loop manner. As a result, the estimators converge to the original true value even with the wrong initial estimation.
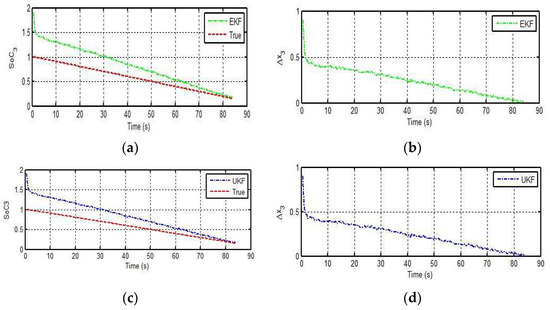
Figure 7.
Supercapacitor SoC and error in estimation: (a) SoC estimation with an EK estimator; (b) error in EK estimation; (c) SoC estimation with a UK estimator; (d) error in UK estimation.
The effectiveness of the developed model is its reduced configurational cost as compared to other models. Furthermore, the developed model can easily be extended to accommodate second-order nonlinearities, e.g., temperature, aging, and capacity fading.
3. Conclusions
A model was implemented and validated in this research paper for a lithium-ion battery and supercapacitor. A grey box technique which includes the partial information of white and black box models was selected for the purpose of modeling. The relationship between the open circuit voltage and state-of-charge was established through the Nernst model. The regression (least squares estimation) technique was selected for its simplicity and the ease of calculation for parameter identification.
The identified model was represented by a set of differential equations and validated through loading profile tests. The model tracked the output effectively; therefore, the model accuracy was established under real conditions. Extended and unscented Kalman estimators were employed to estimate the internal states, such as the state-of-charge. It was concluded that an extended Kalman estimator is well suited to models which have first-order nonlinearities in their dynamic behavior. The robustness of techniques was described by setting the wrong initial estimation of the SoC. The results indicate that even when the wrong initial guess is used, the model tracks the true value of the SoC.
The model suffers from the limitation that it does not model the state-of-health of the battery and supercapacitor. Further study should be conducted in which the aging effect of a miniature-sized Li-ion battery and supercapacitor are investigated. Moreover, the proposed model could be generalized to accommodate different chemistries of Li-ion batteries and supercapacitors.
Author Contributions
Q.N. perceived the idea, conducted the experiment, and composed the results, A.H. provided the critical result analysis and helped in terms of manuscript improvement.
Funding
The research was supported by “United Arab Emirates center-based research under Emirates Centre for Energy and Environmental Research at United Arab Emirates University” with grant “31R106”.
Acknowledgments
The research was supported by United Arab Emirates center-based research under the Emirates Center for Energy and Environment Research with grant 31R106.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Everett, R.; Boyle, G.; Peake, S.; Ramage, J. Energy Systems and Sustainability: Power for a Sustainable Future; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Musardo, C.; Rizzoni, G.; Guezennec, Y.; Staccia, B. A-ECMS: An adaptive algorithm for hybrid electric vehicle energy management. Eur. J. Control 2005, 11, 509–524. [Google Scholar] [CrossRef]
- Howard, W.G.; Schmidt, C.L.; Scott, E.R.; Medtronic Inc. Medical Device Having Lithium-Ion Battery. U.S. Patent 7,337,010, 26 February 2008. [Google Scholar]
- Moreno, J.; Ortúzar, M.E.; Dixon, J.W. Energy-management system for a hybrid electric vehicle, using ultracapacitors and neural networks. IEEE Trans. Ind. Electron. 2006, 53, 614–623. [Google Scholar] [CrossRef]
- Pattipati, B.; Sankavaram, C.; Pattipati, K. System identification and estimation framework for pivotal automotive battery management system characteristics. IEEE Trans. Syst. Man Cybern. Part C 2011, 41, 869–884. [Google Scholar] [CrossRef]
- Fuller, T.F.; Doyle, M.; Newman, J. Simulation and optimization of the dual lithium ion insertion cell. J. Electrochem. Soc. 1994, 141, 1–10. [Google Scholar] [CrossRef]
- Windarko, N.A.; Choi, J.; Chung, G.B. Improvement of electrical modeling of NiMH battery for application of Microgrid System. In Proceedings of the 2010 IEEE Energy Conversion Congress and Exposition, Atlanta, GA, USA, 12–16 September 2010; pp. 4243–4248. [Google Scholar]
- He, H.; Xiong, R.; Guo, H.; Li, S. Comparison study on the battery models used for the energy management of batteries in electric vehicles. Energy Convers. Manag. 2012, 64, 113–121. [Google Scholar] [CrossRef]
- Verbrugge, M.; Tate, E. Adaptive state of charge algorithm for nickel metal hydride batteries including hysteresis phenomena. J. Power Sources 2004, 126, 236–249. [Google Scholar] [CrossRef]
- Perez, H.E.; Siegel, J.B.; Lin, X.; Stefanopoulou, A.G.; Ding, Y.; Castanier, M.P. Parameterization and validation of an integrated electro-thermal cylindrical LFP battery model. In Proceedings of the ASME 2012 5th Annual Dynamic Systems and Control Conference Joint with the JSME 2012 11th Motion and Vibration Conference, Fort Lauderdale, FL, USA, 17–19 October 2012; pp. 41–50. [Google Scholar]
- Van Schalkwijk, W.; Scrosati, B. Advances in lithium ion batteries introduction. In Advances in Lithium-Ion Batteries; Springer: Boston, MA, USA, 2002; pp. 1–5. [Google Scholar]
- Peukert, W. Über die Abhängigkeit der Kapazität von der Entladestromstärke bei Bleiakkumulatoren. Elektrotechnische Z. 1897, 20, 20–21. [Google Scholar]
- Hussein, A.A.; Batarseh, I. An overview of generic battery models. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 24–29 July 2011; pp. 1–6. [Google Scholar]
- Watrin, N.; Blunier, B.; Miraoui, A. Review of adaptive systems for lithium batteries state-of-charge and state-of-health estimation. In Proceedings of the 2012 IEEE Transportation Electrification Conference and Expo (ITEC), Dearborn, MI, USA, 18–20 June 2012; pp. 1–6. [Google Scholar]
- Bohlin, T.P. Practical Grey-Box Process Identification: Theory and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Kroll, A. Grey-box models: Concepts and application. New Front. Comput. Intell. Appl. 2000, 57, 42–51. [Google Scholar]
- Huria, T.; Ceraolo, M.; Gazzarri, J.; Jackey, R. High fidelity electrical model with thermal dependence for characterization and simulation of high power lithium battery cells. In Proceedings of the 2012 IEEE International Electric Vehicle Conference, Greenville, SC, USA, 4–8 March 2012; pp. 1–8. [Google Scholar]
- Hu, X.; Li, S.; Peng, H. A comparative study of equivalent circuit models for Li-ion batteries. J. Power Sources 2012, 198, 359–367. [Google Scholar] [CrossRef]
- Klotz, D. Characterization and Modeling of Electrochemical Energy Conversion Systems by Impedance Techniques; KIT Scientific Publishing: Karlsruhe, Germany, 2014. [Google Scholar]
- Xiong, R.; He, H.; Sun, F.; Liu, X.; Liu, Z. Model-based state of charge and peak power capability joint estimation of lithium-ion battery in plug-in hybrid electric vehicles. J. Power Sources 2013, 229, 159–169. [Google Scholar] [CrossRef]
- Xiong, R.; He, H.; Sun, F.; Zhao, K. Online estimation of peak power capability of Li-ion batteries in electric vehicles by a hardware-in-loop approach. Energies 2015, 5, 1455–1469. [Google Scholar] [CrossRef]
- Salkind, A.J.; Singh, P.; Cannone, A.; Atwater, T.; Wang, X.; Reisner, D. Impedance modeling of intermediate size lead–acid batteries. J. Power Sources 2003, 116, 174–184. [Google Scholar] [CrossRef]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 3. State and parameter estimation. J. Power Sources 2004, 134, 277–292. [Google Scholar] [CrossRef]
- Hu, X.; Murgovski, N.; Johannesson, L.; Egardt, B. Energy efficiency analysis of a series plug-in hybrid electric bus with different energy management strategies and battery sizes. Appl. Energy 2013, 111, 1001–1009. [Google Scholar] [CrossRef]
- Masoudinejad, M.; Emmerich, J.; Kossmann, D.; Riesner, A.; Roidl, M.; ten Hompel, M. Development of a measurement platform for indoor photovoltaic energy harvesting in materials handling applications. In Proceedings of the IREC2015 The Sixth International Renewable Energy Congress, Sousse, Tunisia, 24–26 March 2015. [Google Scholar]
- Smolders, K.; Witters, M.; Swevers, J.; Sas, P. Identification of a Nonlinear State Space Model for Control using a Feature Space Transformation. In Proceedings of the ISMA2006 Conference, Heverlee, Belgium, 18–20 September 2006. [Google Scholar]
- Xiong, R.; Gong, X.; Mi, C.C.; Sun, F. A robust state-of-charge estimator for multiple types of lithium-ion batteries using adaptive extended Kalman filter. J. Power Sources 2013, 243, 805–816. [Google Scholar] [CrossRef]
- Dai, H.; Wei, X.; Sun, Z. Design and implementation of a UKF-based SOC estimator for LiMnO2 batteries used on electric vehicles. Przegląd Elektrotechniczny 2012, 88, 57–63. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).