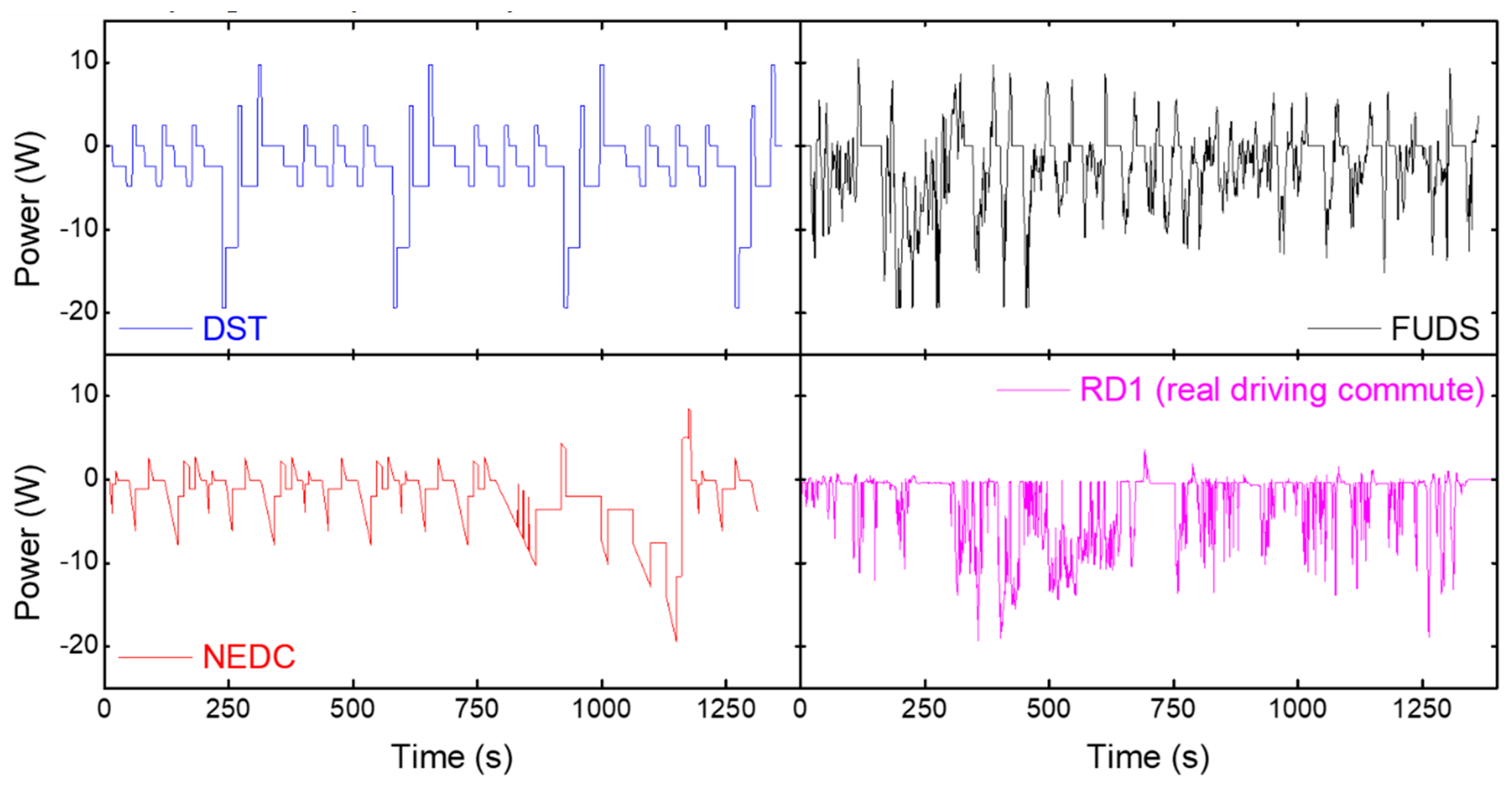
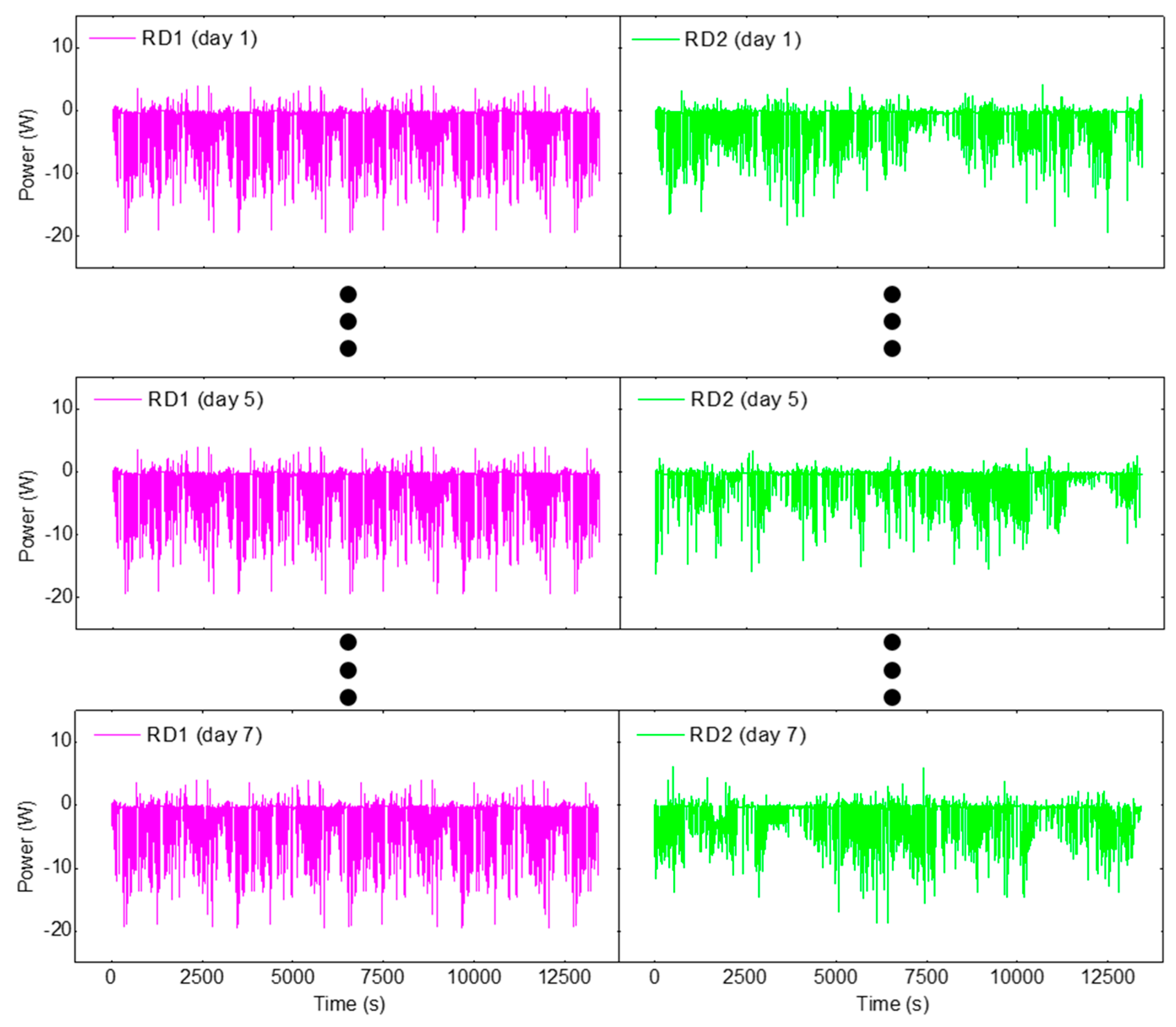
3. Results and Discussion
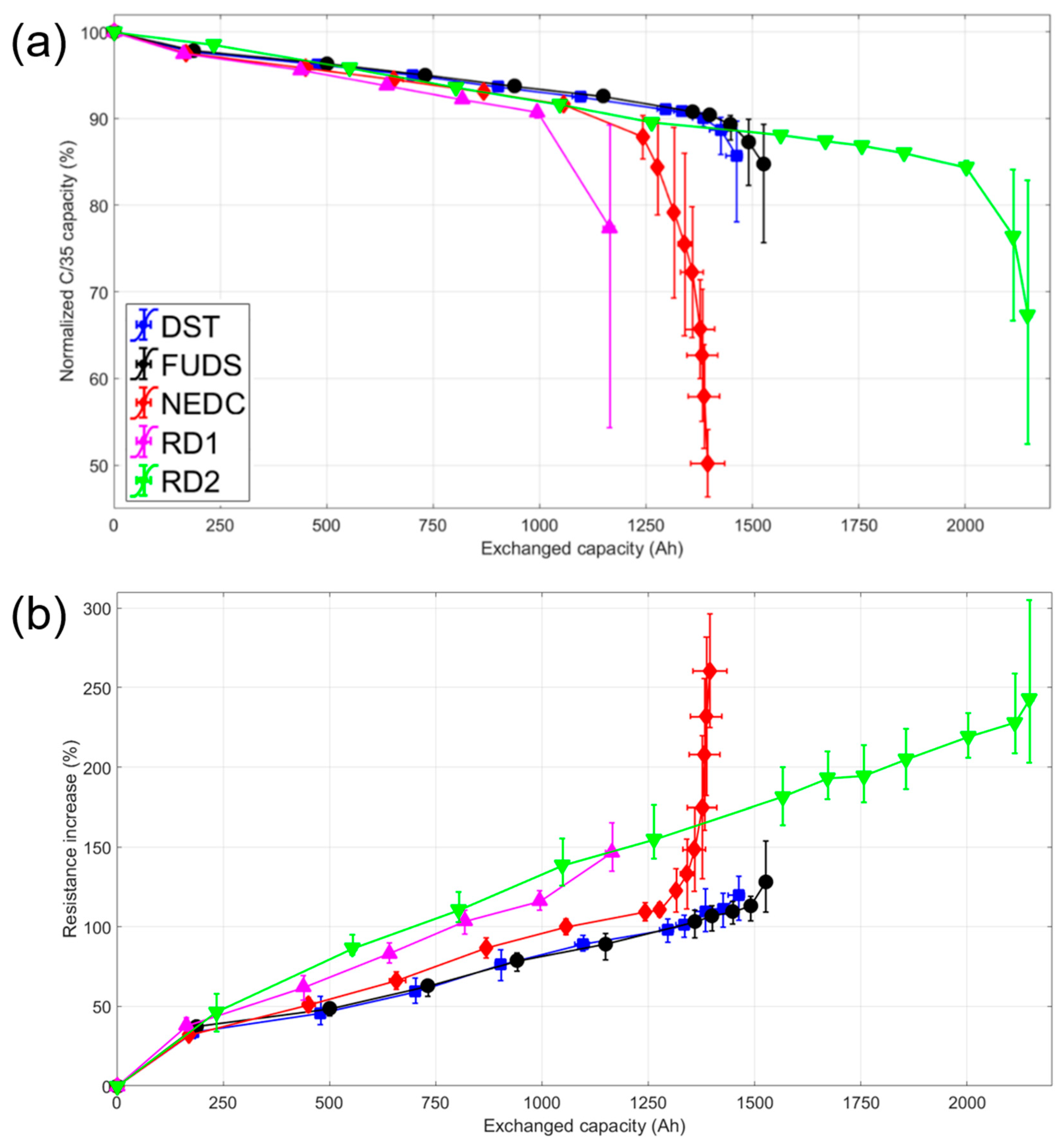
Figure 3 plots the average normalized capacity and resistance increase for the driving conditions versus exchanged capacity. Initially, all cells lost capacity linearly (R
2 > 0.98) at about 0.008% ± 0.001% per Ah of exchanged capacity or 0.023% ± 0.003% per cycle. All 15 cells experienced an accelerated stage of degradation, 0.05% ± 0.02% per Ah of exchanged capacity, after a capacity loss of around 10%. This second stage of aging was predicted in a previous work using the ‘
alawa toolbox [
1]. The cell with the longest lifetime was subjected to the RD2 profile and proceeded to the accelerated aging stage after over 20% capacity loss, but most reached that stage by 11%. The cells subjected to the NEDC and RD1 driving cycles failed on average sooner than the others. Those cells reached the second stage of aging at an average exchanged capacity of 1191 ± 183 and 1216 ± 199 Ah, respectively. These values corresponded to around 350 cycles, in line with what was observed for C/1 charges and discharges [
22]. Those profiles were also the ones that were charged the least during driving (see
Table 1), indicating that regenerative braking could help capacity retention. This result corroborated what was found in literature [
23]. The cells subjected to the DST and FUDS profiles experienced onset of the accelerated aging stage at similar values of capacity exchanged (1438 ± 38 and 1490 ± 78 Ah, respectively, and around 450 cycles). This outcome was unsurprising since DST was derived from FUDS [
2]. The RD2 cells were cycled the longest before succumbing to the second stage (2146 ± 251 Ah, 650 cycles). These cells were subjected to a lower average discharge current (see
Table 1), which might account for their comparatively long cell lifetimes.
In the initial stage, resistance increased more in the cells aged with the real driving profiles than the simulated ones (
Figure 3b). It must be noted that the cells with the highest rates of resistance increase (RD2) were the ones with the longest lives. This highlighted that resistance increase and life expectancy were not correlated. Resistance increased linearly during the first stage of aging, then escalated nonlinearly in the second stage of degradation. Although there was an increase in rate of change of the resistance during the second stage of aging, in general, the disparity between stages was not as pronounced as the one seen in the plot of the capacity fade (
Figure 3a).
Most interestingly, there was a considerable difference (>900 Ah or 275 cycles on average) between the final exchanged capacity of the cells subjected to the RD1 and RD2 profiles revealing a sizeable effect of traffic on property retention. This average difference between driving profiles was the largest in the experiment. From the C-rates of those two profiles (
Table 1), time to complete discharge could vary by 3 h. As a consequence of these observations, it was reasonable to conclude that not one cycling profile with a fixed set of properties could account for the breadth of real driving outcomes. It may be possible to simulate the range of cell lifetimes by adjusting parameters, such as the maximum power, of a single driving cycle. Although, this range of outcomes may indicate unique degradation mechanisms leading to failure. Diagnosis of the cells was performed to illuminate disparities in the degradation induced by the five duty cycles.
To diagnose the cells, IC analysis was employed in conjunction with the features of interest approach [
10,
24] to quantify the different degradation modes and determine path dependency. This analysis was shown to identify metallic lithium deposition [
7] as well as gas evolution in cells [
11]. An extensive discussion on the IC analysis for these cells was previously published [
14] and will not be repeated here.
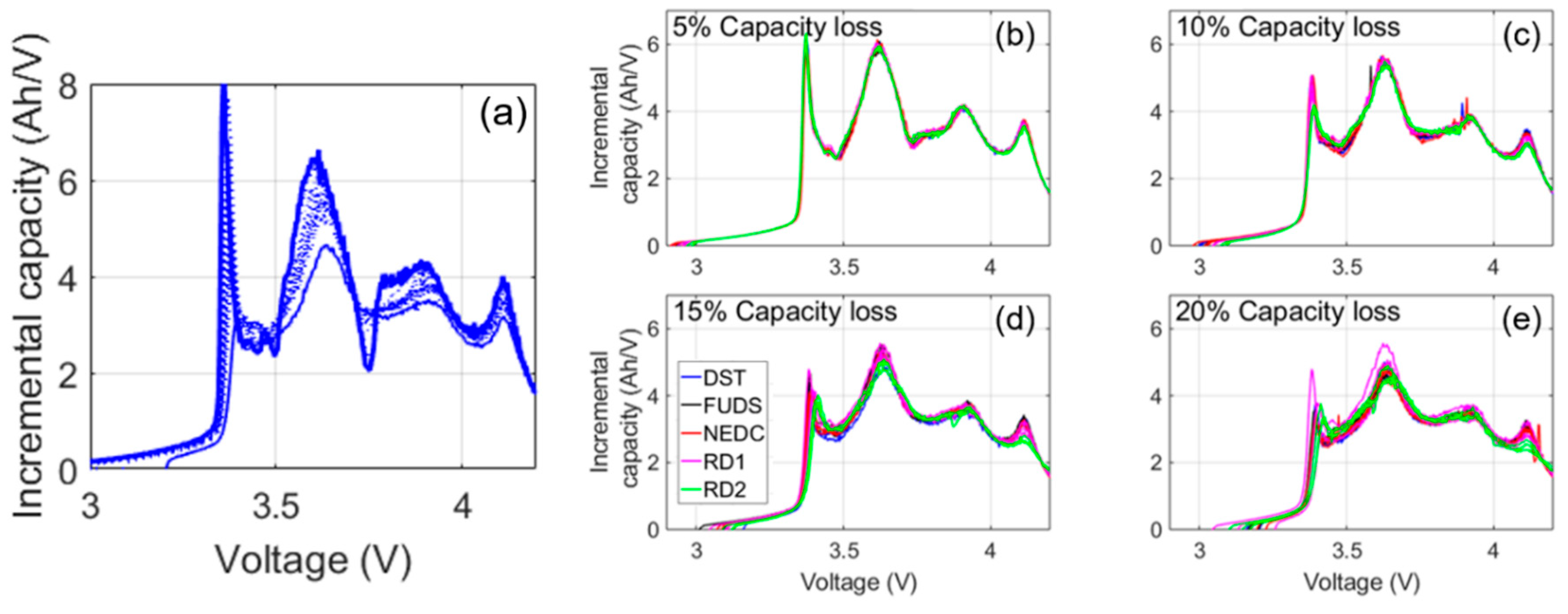
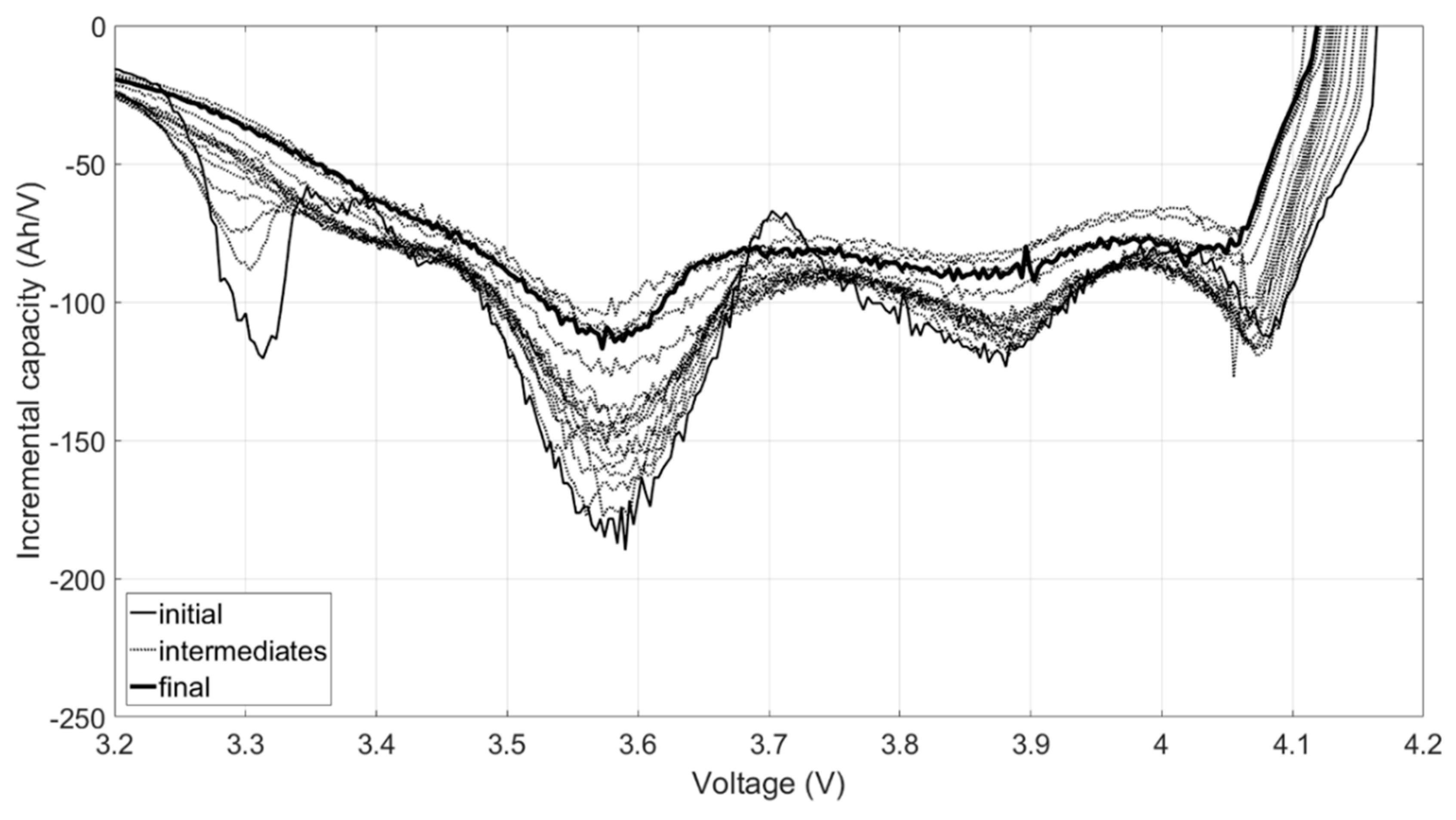
Figure 4a shows the representative IC curve evolution of the C/35 charge. The most noticeable change to the IC signatures during the first few months of cycle aging was the disappearance of a local minimum, or arch, between 3.7 and 3.8 V.
Figure 4b–e compares the IC curves at 5%, 10%, 15%, and 20% capacity loss for all the cells. Overall, the evolution of the curves was similar. At 5% capacity loss, the arch was barely visible (
Figure 4b) and completely gone by 10% loss (
Figure 4c). There was a sharp peak at low voltages that shrank and shifted to higher voltages during aging, but it did not quite disappear, even at 20% loss (
Figure 4e). A slow shift to higher voltages of the beginning of charge was also observed, but there was no shift in the end-of-charge (EOC) voltage. It must be noted, however, that differences between duty cycles were visible in the IC curves at 15% and 20% capacity loss. The highest voltage peak between 4.1 and 4.2 V flattened with age more in the cells exposed to the real driving cycles (RD1 and RD2) than the synthetic ones. In addition, except for one of the RD1 cells, cycle aging with the real driving profiles caused a greater voltage shift and intensity decrease to the peak at 3.4 V. These disparities suggested that real-world battery degradation might not be the same as synthetically induced degradation.
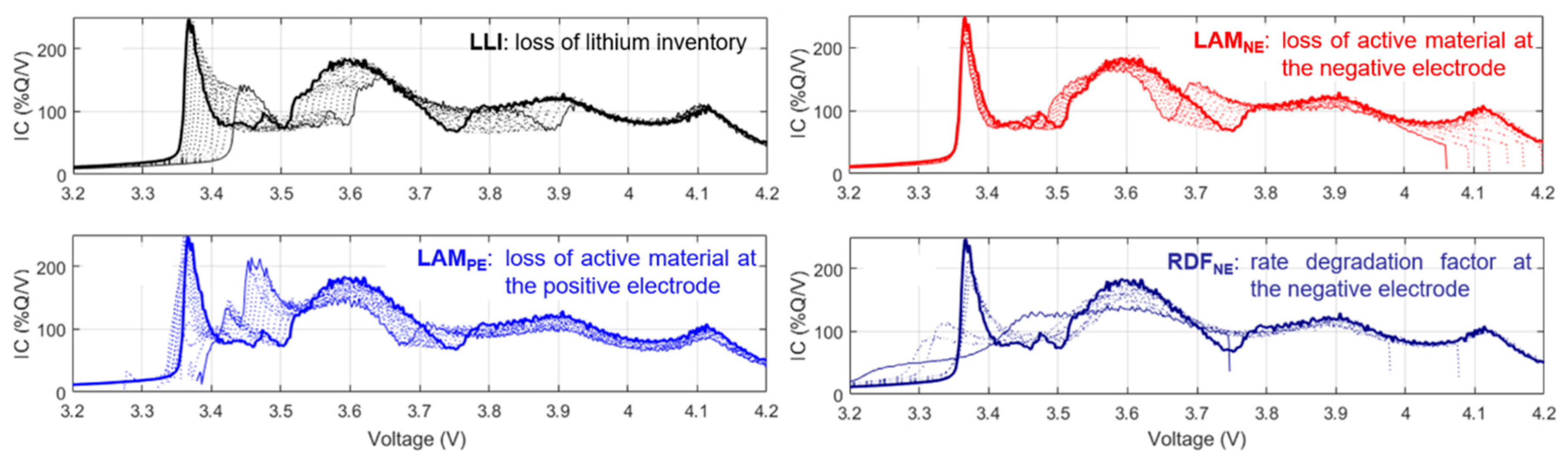
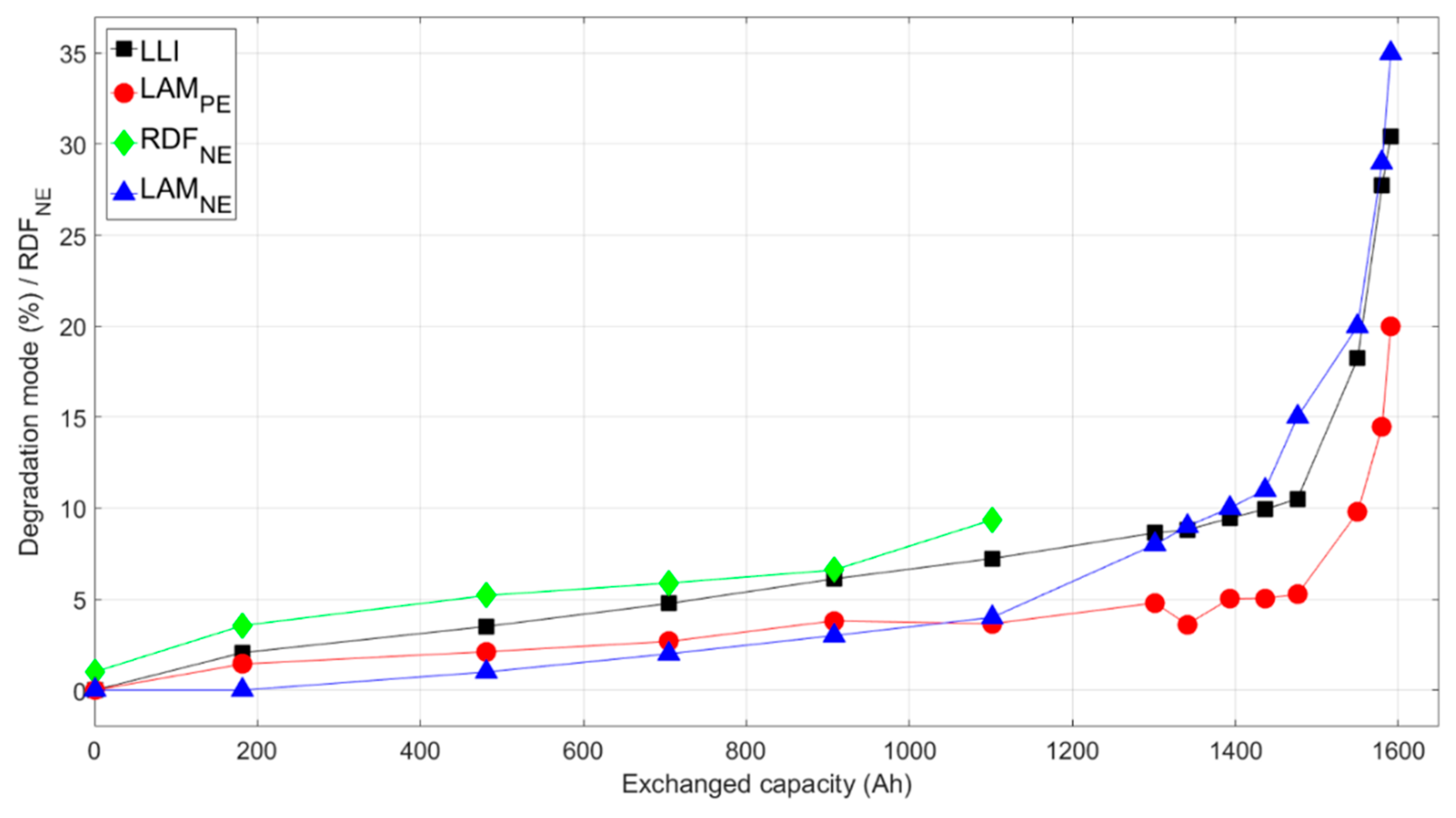
Quantifying changes to the IC curves allowed determination of relative magnitudes of degradation modes occurring during aging, uncovering the differences in the effect of the five driving cycles. Similar to previous work [
1], experimental changes were compared to the emulated IC evolution of a single mode using the
‘alawa toolbox and the degradation table (
Figure 5) [
14]. No single degradation matched the experimental variations; therefore, degradation was induced by a combination of separate modes. This complex combination included the loss of lithium inventory, loss of active material at both electrodes (LAM
PE and LAM
NE for the positive and negative electrodes, respectively), and some kinetic limitations (rate degradation factor, RDF). Scanning all the possible contributions would require an enormous amount of calculation [
10], but a careful observation of
Figure 4a and
Figure 5 reduced the number of cases to consider and allowed direct quantification of LLI, LAM
PE, and the rate degradation factor at the negative electrode (RDF
NE).
First, it can be deduced that capacity fade was not caused by loss of active material. Capacity loss from LAMNE would shift and change the features at the end-of-charge (the peak above 4 V), and capacity fade from LAMPE would make the sharp peak between 3.3 and 3.4 V disappear—none of which were observed experimentally. Therefore, capacity loss was solely induced by LLI. As a result, LLI could be estimated directly from capacity loss. LLI was found to increase linearly during the initial aging stage to about 10% loss for most of the cells, then the value rose dramatically during the second stage.
Second, the decrease in intensity at 4 V could be used as a direct indicator of LAM
PE (
Figure 5) since it was the only degradation that was shown to affect this intensity without receding the highest voltage peak. With exception of the RD2 cells, the LAM
PE remained below 10% during the initial stage. During the initial stage of aging, the real driving cycles induced LAM
PE at a faster rate than the synthetic cycles. At an exchanged capacity of 1000 Ah when all the cells were at the initial stage, the difference was about 2.5%. This degradation mode also accelerated during the secondary stage following the trend in capacity loss, though its value was always less than LLI regardless of the driving cycle.
Third, according to the
‘alawa simulation and
Figure 5, the disappearance of the arch between 3.7 and 3.8 V could only be attributed to decreasing reaction kinetics at the negative electrode, as all the other degradation modes only shifted this feature to lower or higher voltages. Thus, quantifying this change as the cell aged could allow direct estimation of the RDF
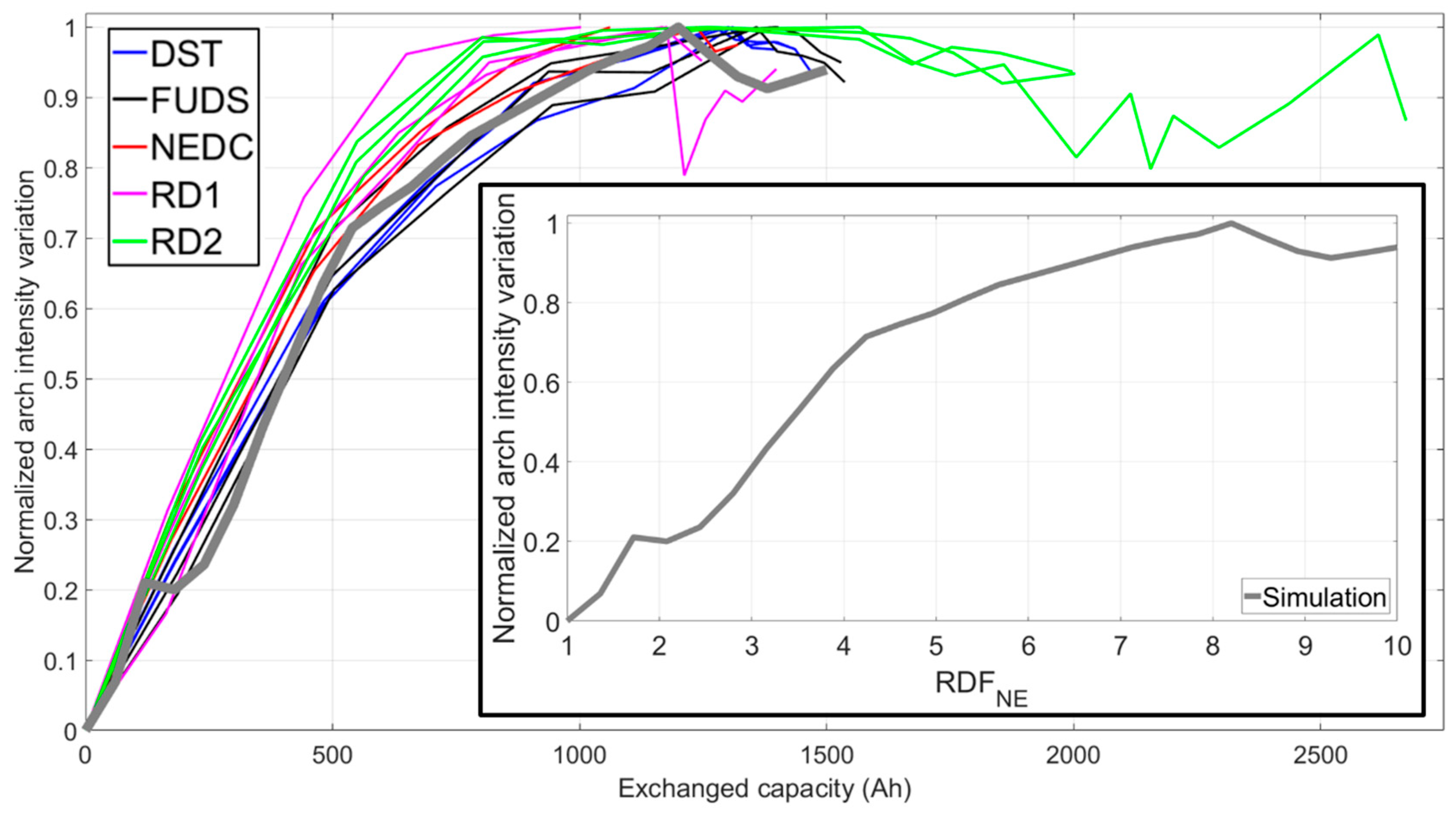
NE. It had to be noted that, according to simulations, the intensity of the arch increased then plateaued with increasing RDF
NE (inset of
Figure 6); therefore, after reaching the plateau beyond a value of 10, the RDF
NE could not be estimated. Experimental data exhibited the plateau, but also a decrease in arch intensity after the second stage of aging started (
Figure 6). This decrease in arch intensity during the second stage was unlikely to be induced by improving reaction kinetics at the negative electrode. Hence, the intensity change within this voltage range during the stage of accelerated capacity fade must be caused by some combination of all the degradation modes. The arch intensity decrease was not observed in previous work [
1] since the cycle-aged cells experienced less than 10% capacity loss and did not undergo this level of degradation. The approach of the RDF
NE towards the plateau value was considered as an indicator of the changes to come, but the RD2 cells were among the first to reach the plateau value (
Figure 6) yet remained at that level for a couple hundred cycles. All cells reached the RDF
NE plateau at different exchanged capacity values, and no distinctions between driving cycles were discerned using this metric.
The last parameter to decipher was LAM
NE. LAM
NE could not be estimated automatically from any single feature on the IC curve because of its combined effect with all other degradation modes. Based on the abovementioned assumptions, the relative values of three of the degradation modes, LLI, LAM
PE, and RDF
NE, were calculated and used to fit the IC curves for all the cells as they aged. Those simulations were performed with various amounts of LAM
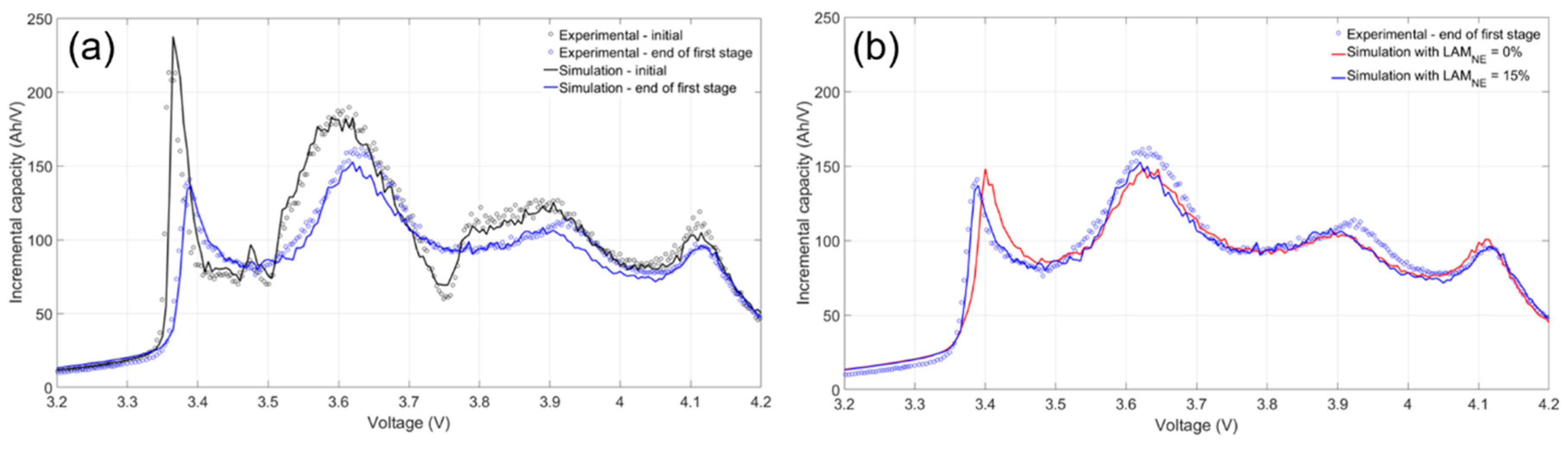
NE, with 1% intervals, until the best fit to experimental data was obtained (
Figure 7a). Since this was the only degradation mode that had to be obtained manually, the estimated values may not have been as reliable as the others, because it accounted for all (or a big part of) fitting errors from the other mechanisms. Initially, little to no LAM
NE was needed to fit the experimental curves. However, as the cell aged, the LAM
NE value became more significant.
Figure 7b compares the experimental and the simulated IC curves with no LAM
NE (solid red curve) and 15% LAM
NE (solid blue curve) at the start of the second aging stage for one of the cells. Adding LAM
NE better simulated the shape and position of the peaks at low and high voltages (at 3.4 and 4.1 V, respectively) without significantly changing the fit of the features between those two peaks. The LAM
NE value shifted the peak around 3.4 V, and this shift was necessary to simulate the experimental IC curves approaching and during the second stage of aging. There were no clear differences in the LAM
NE induced by the five duty cycles during the initial aging stage. All LAM
NE values increased considerably at the onset of the second stage of aging for each cell.
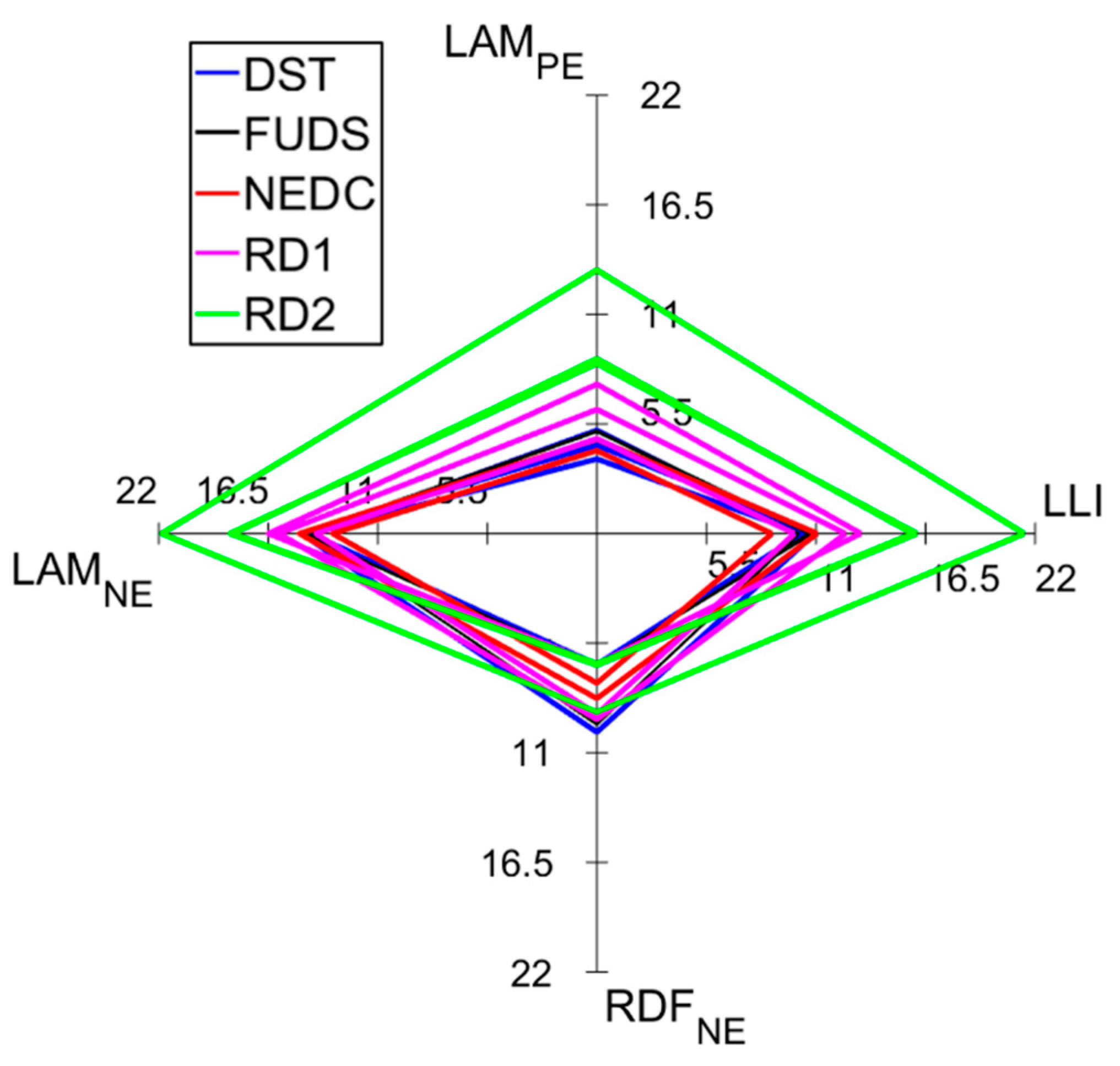
To highlight differences in degradation caused by the five driving profiles, the cells were analyzed at a similar point in their aging process: the transition from the initial to the advanced aging stage. Hence, the degradation modes for all the cells at the onset of the second stage were calculated and summarized in a spider plot, presented in
Figure 8. The plot revealed that the real driving profiles degraded the battery differently than the synthetic ones, with the former on average inducing more LAM
PE and LAM
NE. The RD1 and RD2 profiles induced 6.2% ± 1.4% and 10.2% ± 2.6% LAM
PE, respectively, while the average LAM
PE caused by the synthetic driving cycles at the transition was 4.7% ± 0.5%. In the case of the negative electrode, the RD1 and RD2 profiles induced 15.5% ± 1.3% and 19.5% ± 2.0% LAM
NE, respectively, whereas the synthetic driving cycles induced an average LAM
NE of 14.5% ± 0.5% at the transition. Interestingly, the percent LLI caused by both real driving profiles was higher at the transition (11.9% ± 1.7% for RD1 and 17.8% ± 3.2% for RD2) than the loss of lithium inventory induced by the synthetic ones (10.6% ± 0.3% for DST, 10.5% ± 0.3% for FUDS, and 9.9% ± 1.6% for NEDC) despite, on average, the RD1 cells advancing to the second stage sooner than all the other cells, while the RD2 cells reached the transition the latest. Thus, the magnitude of LLI did not portend the coming of a secondary aging stage, as the average LLI value of the RD2 cells at the onset was much higher than the others. There was a clear difference between degradation induced by the two real driving cycles. Conversely, the distinction between degradation caused by DST and FUDS was negligible. The average LAM
NE caused by both driving cycles was equal (14.6% ± 0.2%), and the average RDF
NE values were very close (7.7% ± 1.9% for DST vs. 7.6% ± 1.7% for FUDS). This comparison proved similar aging paths led to similar degradation.
Although the values varied, there were clear trends for each of the degradation modes irrespective of the driving cycle.
Figure 9 presents the results of the IC curve analysis throughout aging for one of the cells. The plots revealed the representative trend that the degradation modes followed as all the cells aged. LLI, LAM
PE, and LAM
NE all accelerated, seemingly exponentially, during the secondary stage. As the cell aged, the LAM
NE value increased until it equaled or surpassed the LLI. The RDF
NE value tended to reach its plateau value before the acceleration of the other degradation modes. Beyond this point, RDF
NE could not be estimated correctly.
In brief, none of the synthetic driving cycles adequately simulated the effect of either of the real driving profiles in terms of cell lifetime or degradation. There was a range of outcomes from the real driving data made evident by the difference in the capacity loss, resistance, and degradation mode calculations, elucidating the impact of traffic conditions and further complicating the representability of synthetic cycling. In contrast, those same metrics indicated the DST and FUDS cycles aged the cells almost identically. The cells aged with NEDC cycle exhibited similar lifetimes to the RD1 cells but with a different degradation profile. Despite the relative values being dissimilar, the degradation modes followed the same general trend for all cells, suggesting that the range in property retention and degradation can be mimicked by identifying and adjusting certain cycle parameters such as the maximum power.
The quantified degradation modes were then investigated further to determine the cause of the accelerated aging. This battery chemistry has been shown to be susceptible to fast capacity fade instigated by lithium deposition [
25]. In a previous work [
1], it was hypothesized that when the effect of the LAM
NE overcame the influence of the LLI, an accelerated stage of aging would transpire brought on by plating and its repercussions [
26]. Hence, the LAM
NE value in relation to the LLI may be significant as it could, nondestructively, hint at the possible initiation of the secondary stage of degradation observed in the experiment. This hypothesis was developed from the states of charge (SOC) of the electrodes at the full cell’s EOC voltage. The EOC condition was assumed to be attained when the state of charge of the positive electrode (SOC
PE) was 100%. As expected [
27] and confirmed by half-cell testing, the GIC negative electrode (NE) exhibited a higher capacity than the positive electrode (PE). In other words, at full charge, the SOC
PE was 100%, but the state of charge of the NE (SOC
NE) was greater than 0%, and the NE was not fully lithiated [
4]. If lithium plating was to occur during aging, provided that the resistance increase was limited (
Figure 3b) and the cells were kept at ambient temperature, the NE would have to lose enough active material to be unable to store the totality of incoming lithium ions,
Figure S1. As the cell approached full charge, SOC
NE would be 0% before 100% SOC was reached by the PE, necessitating the deposition of lithium onto the NE. Therefore, in battery chemistries with GIC as NE, for Li plating to occur, there must be a threshold value at which the PE attains 100% SOC while SOC
NE equals 0%. This threshold value was dubbed the plating threshold (
LAMNE,PT) and was influenced by the cell characteristics (loading ratio and initial offset), the capacity loss, and the other degradation modes, LLI and LAM
PE. Values above this threshold would lead to deposition of lithium on the NE [
4].
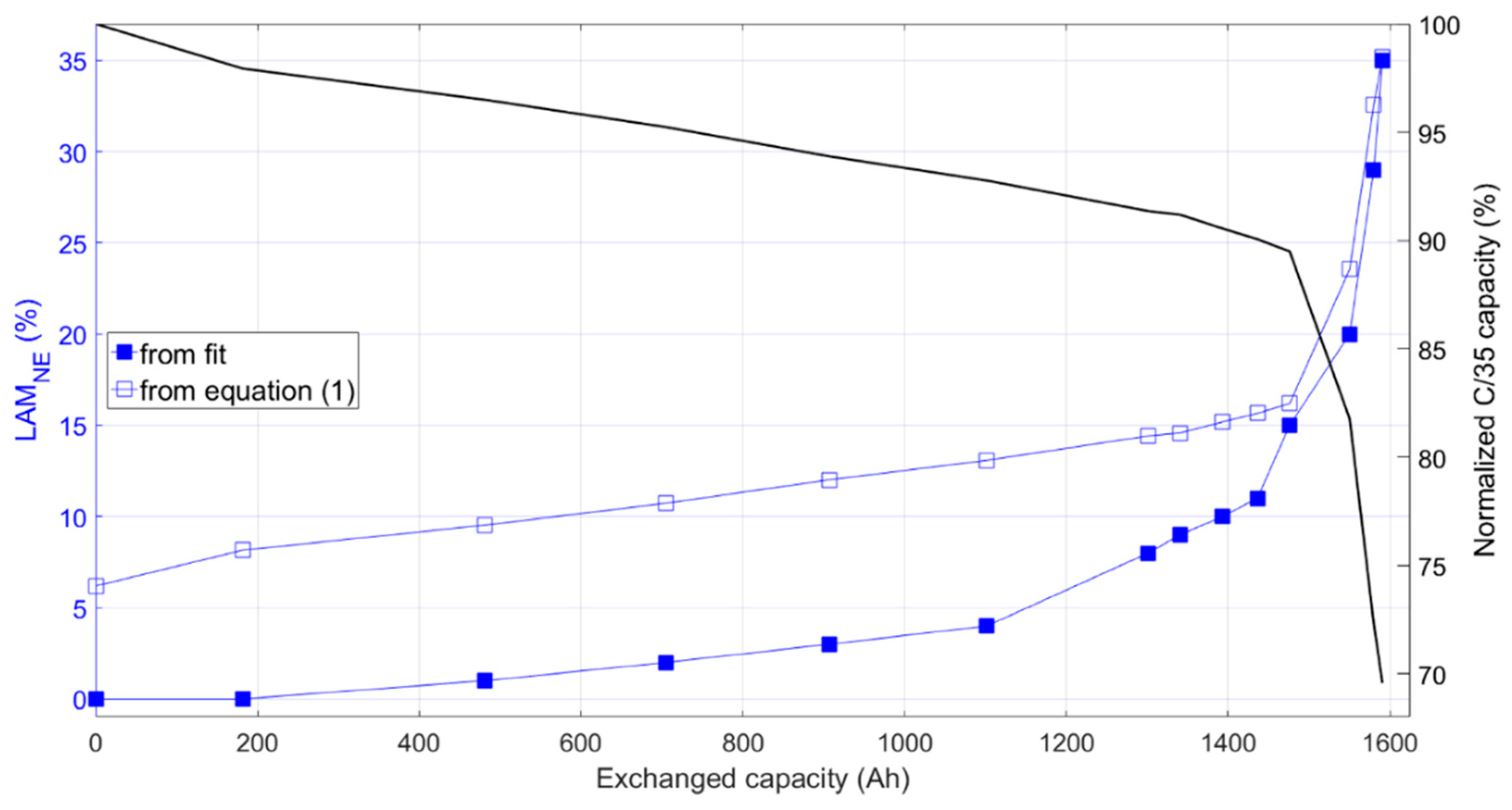
The plating threshold, for LAM
PEs < 10%, was estimated from EOC conditions of the graphite using Equation (1). The derivation of this equation is provided in
Supplementary Materials. It was important to note that the lithium plating was completely irreversible, as evidenced by the absence of additional electrochemical features in the voltage response during discharge [
9,
28,
29,
30] and the shift in the voltage at the beginning of discharge to lower values (
Figure 10). Lithium stripping was not observed in the C/35 IC curves during the accelerated stage or even at failure for all the cells tested. Hence, the plating only added to the rate of the LLI, which accelerated capacity fade. If only irreversible lithium plating were to occur in these cells, the transition to the accelerated aging stage would correspond with the point at which the plating threshold was reached. From this hypothesis, the percent LAM
NE during the second stage could be determined from Equation (1), where
LRini is the initial ratio between the capacities of the negative and positive electrodes or loading ratio, and
OFSini is the SOC
PE offset, relative to the negative electrode, due to the formation of the SEI layer [
4]. The term in parentheses is constant and only depends on initial characteristics. The percentage of LLI,
%LLI, is the value that increases during aging. Using this equation, plating threshold values were estimated throughout aging and compared to the LAM
NE obtained manually from the best fit to the IC curves (
Figure 11). During initial aging, the LAM
NE values estimated from the fit were well under the plating threshold. However, at the onset of the second stage, the fit LAM
NE percentages came within 2% of the equation values, indicating that irreversible plating could lead to accelerating aging. This conclusion will be validated further by postmortem analysis in a subsequent work.
Although diagnosis via IC analysis was achieved, accurate, reliable prognosis of lithium plating was challenging because of the complexity and path dependency involved in cell degradation. Tracking capacity and resistance were simply incapable of anticipating this phenomenon. From the evolution of the IC curve, the disappearance of the arch feature between 3.7 and 3.8 V always occurred before the transition in aging, but it could not be used to detect if the transition was forthcoming. Degradation mode quantification led to a metric,
LAMNE,PT, directly related to Li plating. Though promising, plating threshold analysis needed further investigation for confirmation. Moreover, it was logical to conclude a combination of metrics would be required for such a complicated prognosis. Hence, data at the transition from the initial to the secondary stage were scrutinized further. As suggested by a previous paper [
1], the ratio of the LAM
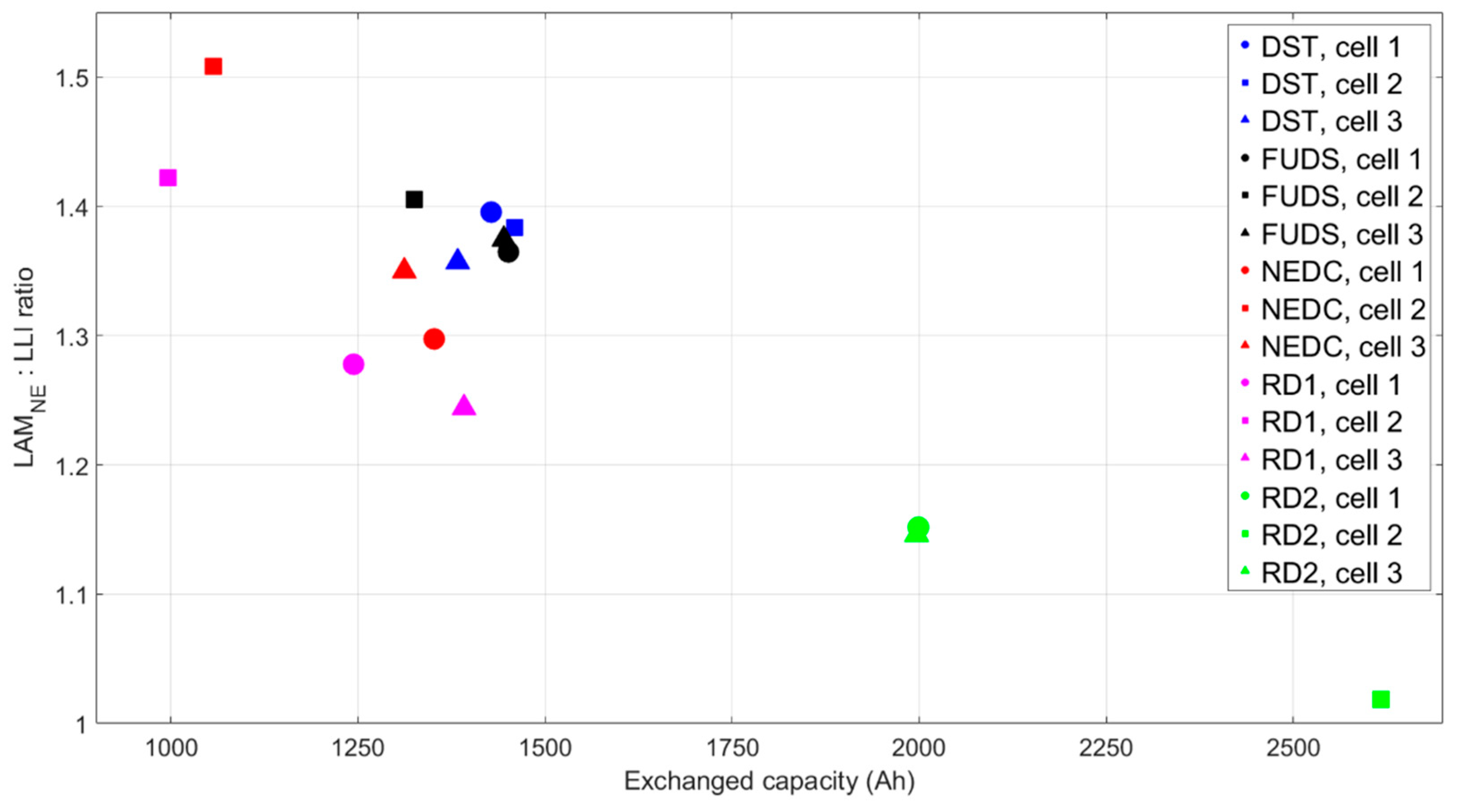
NE to the LLI may be a more decisive parameter in predicting the relative lifetimes of these cells. As shown by
Figure 12, the second stage began sooner for the cells that exhibited a higher LAM
NE: LLI ratio at the transition. The cell with the lowest ratio (RD2, cell 2) exhibited a large decrease in capacity much later in life than the other cells. The LAM
NE: LLI ratio was significant phenomenologically because a value greater than one meant the plating threshold would be reached during aging and prompted a precipitous dip in capacity. Once the cell reached this point, the second stage of aging began, the loss of lithium inventory increased nonlinearly, and complete deterioration of the battery quickly followed. This ratio in conjunction with the RDF
NE value and the plating threshold may lead to a non-heuristic approach to diagnosis and prognosis of batteries.
4. Conclusions
This study addressed three important points for the battery community. First, it determined whether synthetic driving cycles were representative of real driving. Second, it investigated the origin of the second stage of aging. Third, it proposed metrics to forecast the inception of this second stage.
Based on conventional metrics of capacity and resistance, NEDC was the synthetic driving profile that most closely replicated the trend in capacity fade caused by one of the real driving profiles used in this study (RD1). Since the NEDC driving cycle had the lowest charge capacity during discharge, it best simulated the capacity loss in EVs that traveled a regular daily commute. However, any charge-while-driving technology can change this evaluation. Because of the below average discharge current of real driving data from a varied commute (RD2), none of the synthetic driving profiles reproduced the relatively long lifetimes of those cells. Therefore, it was found that the average current and charge capacity during discharge were important parameters, and they should be considered in determining the appropriate synthetic profile for any EV battery lifetime test. More importantly, traffic greatly influenced cell degradation and cycle life. As a result, realistic EV battery testing might also require looping several iterations of the same synthetic cycle at different intensities since none of the synthetic cycles sufficiently imitated the range of lifetimes and degradation profiles caused by real driving.
All cells experienced this second stage of aging, in which the capacity fade accelerated by more than a factor of six. Changes to certain features in the charging IC curves during aging, such as the decrease in the intensity of the arch between 3.7 and 3.8 V and the shifting of the sharp peak at 3.4 V, were found to coincide with this steep increase in cell degradation. The accelerated aging stage was forecasted by the ‘alawa software, which was used to quantify the degradation mechanisms at play in previous studies. Using advanced IC analysis techniques, the cells were diagnosed with presenting symptoms of irreversible lithium plating leading to the accelerated deterioration of properties.
It was found that the LAMNE: LLI ratio was an important parameter in diagnosing the cell. Ratios greater than one were prerequisites to a second stage of aging characterized by lithium plating and accelerated degradation if the plating was irreversible. Values close to or less than one can delay or prevent the appearance of an accelerated aging stage. In addition, the LAMNE value, which is needed to instigate Li plating at any moment of aging, can be calculated using the analysis outlined in this paper.
These findings also expose a critical flaw in conventional state of health (SOH) estimations. SOH is usually defined from capacity loss and/or resistance increase, but this study showed that those measurements were ineffective in predicting the second stage of degradation, consequently leaving the devices vulnerable to unexpected cell failure. A different set of criteria incorporating new parameters (such as the LAMNE: LLI ratio, potentially) might be crucial to accurately define SOH in the future.
The change in arch intensity, the plating threshold, and the ratio of the LAMNE to LLI were identified as possible harbingers of lithium plating and imminent cell death. These metrics can be evaluated in operando without opening the cell. Furthermore, property retention strategies can be proposed based on these metrics. These are capabilities that the conventional examination of capacity loss and resistance increase lack. Parameters based on IC analysis should be monitored and evaluated collectively to determine if intervention, such as applying different rest conditions or preventing complete charging, is required to lengthen cell lifetimes. This promising diagnosis and prognosis technique will be used and refined in future investigations to predict Li-ion battery degradation induced by different grid–EV interactions.