Abstract
Current redox flow battery (RFB) stack models are not particularly conducive to accurate yet high-throughput studies of stack operation and design. To facilitate system-level analysis, we have developed a one-dimensional RFB stack model through the combination of a one-dimensional Newman-type cell model and a resistor-network to evaluate contributions from shunt currents within the stack. Inclusion of hydraulic losses and membrane crossover enables constrained optimization of system performance and allows users to make recommendations for operating flow rate, current densities, and cell design given a subset of electrolyte and electrode properties. Over the range of experimental conditions explored, shunt current losses remain small, but mass-transfer losses quickly become prohibitive at high current densities. Attempting to offset mass-transfer losses with high flow rates reduces system efficiency due to the increase in pressure drop through the porous electrode. The development of this stack model application, along with the availability of the source MATLAB code, allows for facile approximation of the upper limits of performance with limited empiricism. This work primarily presents a readily adaptable tool to enable researchers to perform either front-end performance estimates based on fundamental material properties or to benchmark their experimental results.
Keywords:
flow battery; stack model; vanadium; performance; analysis; model; crossover; shunt current 1. Introduction
Redox flow batteries (RFBs) have been hailed as energy storage solutions that are cost-effective at large (e.g., grid) scales [1,2,3,4]. In contrast to enclosed batteries, RFBs use liquid-phase charge storage materials such that the system power, which scales with reactor area, and energy, which scales with tank volume, can be specified independently. As energy-intensive storage systems can support integration of intermittent renewables, such as solar and wind, into the grid, the scalability of these systems presents an economic opportunity. Presently, RFBs have only seen limited instances of commercial installation, and their cost-competitiveness is curbed by many factors including component cost and energy density [4,5,6]. Although many types of RFBs are being explored, the all-vanadium RFB (VRFB) has been most widely researched and appears to be the closest to broad commercial implementation [7,8]. Key advantages of the VRFB include the low cost of water (ca. 0.001 USD kg−1) and sulfuric acid (ca. 0.09 USD kg−1) and the use of a common redox-active species on both sides of the cell, enabling recovery from crossover-driven capacity fade [4,9,10]. Related RFB research areas that seek to increase energy density and/or employ inexpensive reactants, such as nonaqueous systems [11,12,13], and bromine- [14,15,16], sulfur- [17,18,19], and iron-based chemistries [20,21,22,23], generally focus on development of materials that overcome the undesirable VRFB performance attributes, namely the cell voltage (Eθ = 1.26 V) and the cost of vanadium (ca. 20 USD kg−1) [1,4,24,25]. Many of these emerging storage concepts and novel redox chemistries have demonstrated the potential to surpass the VRFB in the future; however, to date, none has shown sufficient progress to displace the VRFB as the premier RFB for large-scale energy storage [6,17,22,23,25].
The wealth of literature on VRFBs includes systematic component level studies on nearly every performance-driving aspect of their design and operation [8,26,27,28,29]. Perhaps the most-studied VRFB component is the redox-active electrolyte (RAE), as the composition of this solution impacts the hydraulic, kinetic, ohmic, and mass-transfer resistances, as well as the system stability. Past work has demonstrated improved system capacity through RAE engineering including increasing the active species concentration up to 2 M with a mixed-acid electrolyte [30,31] or up to 3 M with a variety of minor additives [32]. Individual contributions to cell losses from acid concentrations [33,34], the low potential (negative) electrolyte [35,36,37,38], and the high potential (positive) electrolyte [39,40] have been studied extensively, and several reviews on VRFB electrolytes describing material properties, composition, and performance have been published [8,26,27]. Broadly stated, typical vanadium-based RAEs have high active species concentrations (ca. 1.5 M), low to moderate viscosities (ca. 2–10 mPa s), high ionic conductivities (200–400 mS cm−1) [8], and poor stability at elevated temperatures due to the precipitation of vanadium as V2O5 [32]. In addition to these RAE-focused activities, several reports have examined membrane properties and their improvement [41,42,43,44,45,46,47,48], the effects of electrodes and their modification [49,50,51,52,53,54,55,56], flow field design [57,58,59,60,61], flow rate [62,63,64], temperature [65,66], and electrolyte rebalancing [10,67]. Although these studies are typically systematic and conclusive for the individual system of interest, the varied experimental configurations between research groups can lead to challenges when trying to combine these individual studies and broadly assess system performance and sensitivity. The field as a whole lacks an accepted control experiment comparing baseline performance of the non-focal components. Thus, attempts to compare, validate, or build upon component advances (e.g., electrode design) reported by different research groups can often be complicated by the differences in operating conditions (e.g., flow rate or electrolyte velocity, potential limitations), in cell design (e.g., flow field type and geometry, reservoir volume, electrode thickness, membrane selection), or in electrolyte conditions (e.g., temperature, composition, sparging conditions). As such, a model with which researchers can readily input their numerous system properties (e.g., electrolyte transport, kinetics, flow field geometry) would aid in the assessment of constituent component contributions and their impact on full system performance. Arguably the most accredited VRFB models have been developed through the complementary work of Shah et al. and You et al. [68,69,70,71], which incorporate numerous physical parameters into a 2D model of the vanadium flow cell. These cell-level models include kinetic (Butler-Volmer), conductivity, and mass-transfer losses in a similar manner to the one used here [72,73]. Each of these models leverage some prior developments from Newman and Tiedemann to describe the porous electrode [74,75]. In addition, modeling efforts have been extended beyond the individual component or cell level to stack systems several times [24,25,76,77,78,79,80,81,82], but each report employs different empirical, inaccessible descriptors of performance-driving parameters (e.g., mass-transfer correlations). Thus, although multiple models exist, they are generally difficult to use, incorporating an overwhelming number of parameters, the selection of which is always subjective even when well-informed.
Just as the myriad of studies on the VRFB have allowed for this special issue, the plethora of system parameters have inspired this particular manuscript. Here, we present first and foremost a user-friendly VRFB model with a graphical-user interface (GUI), coded in MATLAB’s (R2018a) app designer and packaged such that it can be run without MATLAB to broaden accessibility. Perhaps the greatest improvement over prior models is the ease of use and the inclusion of guidance on where additional physical processes, such as secondary reactions, could be integrated as needed. We have also incorporated algorithms for the estimation of crossover of vanadium leading to capacity fade in imperfect membranes. In the interest of preserving simplicity and accessibility of the application algorithm, each modeled component (e.g., porous electrode, membrane, manifold) employs the simplest description that appears sufficient to capture all relevant physics. Practically, this model application presents a tool that, in its most basic form, approximates the upper performance limits of a given VRFB design. From here, second-generation users and developers can include or exclude particular effects of interest or simply examine the system performance as a function of user-specified material parameters. The major modeled components of the single cell include the porous electrodes, the membrane, and the tanks. The porous electrode model estimates cell losses from mass-transfer, kinetics, and distributed conductivity losses within the electrolyte phase using a numerical solution to a previously reported 1D polarization model [72,73]. With the growing interest in the role of mass-transfer in RFBs, we incorporate hydraulic losses through the porous electrode to offset the electrochemical performance benefits of high flow rates [58]. The cell membrane is modeled as a separator with linear concentration profiles from one side to another [83]. In the case of a passive separator (e.g., Daramic), the edge concentration is based on the instantaneous reactor concentrations, and in the case of an active membrane (e.g., Nafion 212), the concentration is based on active site saturation conditions [83,84,85]. The tanks are modeled as reservoirs of a fixed volume with fast homogeneous reactions reducing the solution condition to a combination of two vanadium oxidation states at any given time. To produce a full system model of the VRFB, these component models are coupled to cells with equivalent properties through a circuit network representing shunt current pathways [82,86]. Although the primary objective of this manuscript is the generation of a broadly useful modeling framework for the community, we also explore the sensitivity of predicted system performance to key parameters, such as electrolyte flow rate and the number of cells in a stack, to both illustrate their influence and validate the model results against existing literature.
2. System Models
This section describes the components of the model and their integration into the complete flow battery model, including descriptions of the porous electrodes, membrane, and shunt currents. In brief, the porous electrode model extends upon prior work to accommodate asymmetric kinetics and various states-of-charge (SoCs) [72,73]. The membrane polarization adds linearly to the cell polarization with increases in current, and the model includes a simplistic representation of both concentration- and potential-driven active-species crossover. The shunt currents resistance network is described in detail considering the system manifold geometry, and finally, the model organization within MATLAB is described.
2.1. Electrode Polarization
The electrode polarization model was adapted from past work, where it was used to estimate mass transfer coefficients as a function of operating conditions and material properties [72,73]. In that work, the systems analyzed employed model iron-based RAEs with moderately fast and near-symmetric kinetics. For the purpose of generality, we relax those assumptions enabling extension to the description of an all-vanadium system. Additionally, since the intent of this work is to provide a tool for the community, the description of this model is presented in dimensional form, in contrast to prior work which used a dimensionless form for compactness, to retain physical transparency. The domain and boundary conditions of the electrode model, describing potential as a function of position (x) within the porous electrode from the membrane (x = 0) to the current collector or flow field (x = Le) is shown in Figure 1, where Le is the electrode thickness.
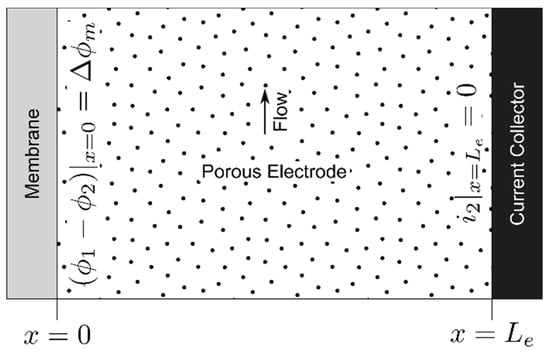
Figure 1.
Porous electrode model domain and boundary conditions. The electrode reaction described by Equation (1) for the high potential electrode or Equation (2) for the low potential electrode occurs throughout this domain.
Within this porous electrode, only the primary electrochemical reactions and the vanadium species concentrations are considered in determining the cell potentials. Neglecting variation of local proton concentrations is reasonable in this case as the concentration is significantly higher than that of the vanadium ions (2.6 M H+ vs. 1.5 M V), and the proton mobility is higher than any of the vanadium ions ( (93) >> DV (3.9) ≈ DIV (3.9) > DIII (2.4) > DII (2.4) × 10−6 cm2 s−1 [87,88]), where Di with i as a roman numerical indicates the diffusion coefficient of the vanadium ion in oxidation state i. Proton diffusivity is denoted as . Additionally, omission of the protons from the kinetic expression enables a simple translation from the VRFB to a generic redox pair. For the high potential (positive) electrode, the primary electrode reaction is described by Equation (1), in which Eθ refers to the standard state reduction potential [1].
Similarly, for the low-potential (negative) electrode, the primary reaction is described by Equation (2) [1].
As with past work, we begin with the Butler-Volmer Equation (3) to describe the faradaic current (in) at the surface of the porous electrode as a function of cathodic (kc) and anodic (ka) rate constants, surface concentrations of the oxidized () and reduced () active species, and the potential of the solid () and liquid () phases [72,89].
where R, T, F, α, and nq are the universal gas constant, the absolute temperature, the Faraday constant, the transfer coefficient, and the number of electrons transferred, respectively. Note that oxidation corresponds to positive current (ik > 0) by this convention. Considering a pseudo-steady state condition within the porous electrode, this faradaic current can be related to the oxidized species mass-transfer coefficient () and bulk concentration () according to Equation (4).
Likewise, we can write a similar expression for the reduced species (5) with a distinct mass transfer coefficient () and bulk concentration ().
Rearrangement of these expressions for the pseudo-steady state flux and substitution into the kinetic expression yields Equation (6), which describes the local current density as a function of kinetic and mass-transfer parameters.
Physically, this equation readily shows that in the limit of infinitely fast mass transfer, the denominator goes to 1, and the expression approaches the original Butler-Volmer Equation (3) with the surface concentration equal to the bulk concentration. For cases in which the mass-transfer coefficient is low, the local current magnitude is reduced as the denominator grows, consistent with the depletion of active material at the electrode surface. This behavior, from a description of coupled mass-transfer and kinetics within a flow-through packed bed reactor, is typical for systems with linear descriptions of mass transfer near the solid (catalyst or electrode) surface and, superficially, mimics Langmuir-Hinshelwood-Hougen-Watson or Michaelis-Menten kinetics. In future work, it may be desirable to consider multiple electrode reactions, such as the effect of parasitic reactions, and/or consider performance as a function of electrode selectivity for a given reaction. In this case, a description for each electrode reaction would be derived, similar to Equation (6), and their sum, weighted by selectivity for each reaction, could be used in place of in in the subsequent analysis. Relating the local reaction current density to the ionic current density (i2) through the liquid-phase RAE requires consideration of the volume-specific electrode surface area, or electrode area per volume, (ae) as described by Equation (7), which is derived from a charge balance on a differential planar control volume within the porous electrode.
The RAE effective conductivity () is estimated according to the Bruggeman relation, , as a function of the RAE conductivity () and the electrode porosity () [72]. The previously established Bruggeman factor of 1.5 originates from a derivation suggesting that tortuosity scales with porosity to the −0.5 [90]. From here, the potential in the liquid phase is related to the ionic current through Equation (8).
For the purpose of solving this problem, we apply Neumann boundary conditions at the current collector and the membrane as there is no ionic current passing through the current collector (), which is an impermeable solid, and we define the current at the membrane-electrode interface to be the total cell current (). For convenience, we also define the overpotential from the electrode () as the difference between the solid and liquid potentials (). Since we neglect the variation in the solid potential within this model, we can combine these expressions to develop our governing differential Equation (9), which we solve numerically (MATLAB, bvp4c) to relate the applied current to the system parameters and the potential drop within the electrode (the mean value of ).
Mass-Transfer Coefficients
This electrode model depends on the value of the mass transfer coefficient for each redox-active species, and estimation of these values is an ongoing area of research [72,73,91]. In light of this, we opted to code in five different correlations from the literature [58,73,91,92,93], as well as to provide the option for a custom mass-transfer correlation of the general form shown in Equation (10), where πi are dimensionless, empirical, user-defined constants, and Sh, Re, and Sc are the Sherwood (), Reynolds (), and Schmidt numbers (). The default fiber diameter (df) is 7 μm [94], and the viscosity (µ) and density (ρ) values for both electrolytes are taken to be 5 mPa s and 1.5 g mL−1, respectively [8]. For simplicity, we assume that electrolyte properties are constant and do not vary as a function of SoC. In our base case for all of the included analysis, we use the correlation in Equation (11) from Barton et al., as it has specifically been demonstrated with the interdigitated flow fields [73].
The average electrolyte velocity (ve) is calculated based on the number of channels (nch), the flow rate through the electrode (Qcell), the channel length (Lch), electrode thickness, and the electrode porosity using Equation (12).
2.2. Membrane Effects
Incorporation of membrane properties into the model enables an analysis of voltaic losses due to the associated resistance as well as of current inefficiency due to active species crossover. The estimate of membrane area specific resistance is based on the membrane conductivity (κmem) and thickness (Lmem), and the membrane voltage drop (ΔVmem) is estimated according to Equation (13).
Since we consider the special case of the VRFB, we couple crossover to our mass balance through three homogeneous redox reactions, Equations (14–16). We assume that each of these reactions occur instantaneously, which is synonymous with having large or well-mixed reservoirs as this would enable the respective solutions to reach a composition with only two oxidation states of vanadium present. Crossover coupled to homogeneous redox reactions contributes to coulombic inefficiencies to different extents based on the ion oxidation states in solution. For example, in the case that V2+ crosses over to the high potential (positive) side, or VO2+ crosses to the low potential (negative) side, the ions will interact with those already present to achieve the intermediate oxidation state, V3+, as described by Equation (14). Similar self-discharge reactions are also listed in Equations (15) and (16), and the combination of these three reactions describe the self-discharge events that are assumed to occur quickly and allow each side of the battery system to maintain mass and charge balances. Additionally, inclusion of these reactions simplifies the system by allowing for the consideration of only one electrochemical reaction for each side of the cell as no more than two oxidation states of vanadium will exist for any significant length of time.
Collectively, these equations allow coupling of the active species crossover flux (NX,i) to Faraday’s law of electrolysis for estimation of active species concentration at each new time step during the simulation according to the Equation set (17) [83]. These equations are derived by simple consideration of the series of events occurring following crossover. For example, we describe the case in which a V2+ ion crosses over from the low potential (negative) side, with a reservoir volume Vlow, to the high potential (positive) side with a reservoir volume Vhigh. Within the high potential (positive) reservoir the ion interacts with a VO2+ ion according to Equation (15) producing a V3+ and a VO2+ ion. From this point, the V3+ ion interacts with another VO2+ ion to form two VO2+ ions according to Equation (16). In total, this crossover of a single V2+ ion produced three VO2+ ions and consumed two VO2+ ions, and this is reflected by the coefficients on the crossover flux of V2+ in Equation set (17). Note that the relative impact of crossover on the composition profile depends on the ratio of the cell area (A) to the reservoir volume (Vi). Also note that if one were to introduce the effect of a side reaction with a rate specified on a volumetric basis, such as vanadium precipitation [32], then that tank reaction could be incorporated within the expressions in Equation set (17).
Active species crossover is accounted for based on literature values of V2+, V3+, VO2+, and VO2+ permeabilities (Κi) through Nafion 117 [41]. The flux through the membrane may be modeled according to Equation (18) whether an active separator/membrane (active sites and surface charge play a role) or passive separator (porous separator without additional chemical functionality or interactions) [83]. Arguably, this treatment is incomplete as we neglect effects from supporting species (e.g., H+, H2O, etc.), but it is practical and provides a qualitative approximation of the crossover flux for each species i (ΝX,i) as a function of the primary system properties, such as ion valence (zi), membrane thickness, ion concentration, and the potential gradient across the membrane, which scales with the current density.
This expression has been solved for the case of linear concentration profiles in the membrane, and the solution for non-zero currents is described by Equation (19), where ci,0 is the concentration of species i at the membrane surface [83]. For open-circuit conditions, Equation (19) is singular, and the simple diffusion problem is solved instead, resulting in Equation (20). These expressions are evaluated for each individual cell and assumed to be uniform over the cell area. Additionally, the flux is taken to be positive for each species as it leaves its native side of the cell, consistent with Equation set (17). Estimation of ci,0 requires a priori knowledge of the membrane behavior. In the case of an active separator/membrane (e.g., Nafion), some condition of active site saturation may be assumed based on the solution conditions, 1.5 M V here [83,84,85]. In the case of a passive separator with a non-specific selectivity (e.g., Daramic), the concentration may be taken as a planar average of the active species concentration using the separator porosity () as its actual liquid-phase concentration is effectively depressed by the inclusion of solid volume.
2.3. Shunt Resistance Network
Shunt currents in multi-cell electrochemical systems are driven by large voltage differences across continuous paths of ionically conductive solutions [77,78,81,86]. Practically, these ion pathways reduce the system efficiency and can even lead to corrosion at the electrode edges [86], a failure mode not considered here. The manifestation of shunt currents within full RFB systems allows cell-to-cell variations in current density and computationally complicates the polarization model as multiple cells must be solved simultaneously with the resistor network depicted in Figure 2.
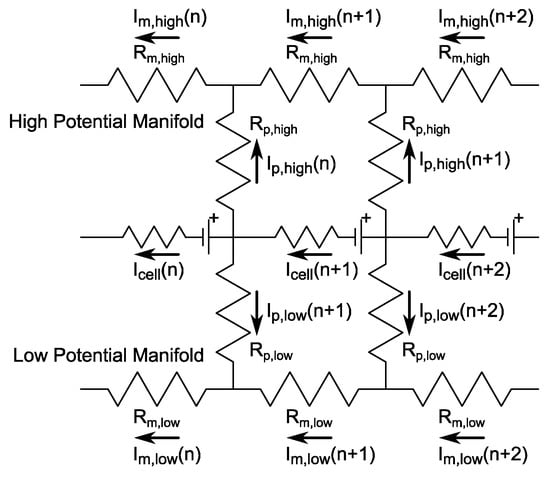
Figure 2.
System resistor network near a generic cell n as used to estimate shunt currents. Arrow directionality indicates positive current flow.
In the case that we consider a stack with N cells and force the inlet and outlet manifolds to be symmetric for each side of the cell, then, in addition to the N cell currents, we must solve for 2N port currents (Ip) and 2(N − 1) manifold currents (Im), which total 5N − 2 currents. Given the system geometry and material properties, we can estimate manifold (Rm) and port (Rp) resistances for each side of the cell. The application of Kirchhoff’s current and voltage laws to this resistor network leads to a set of five repeating equations, Equation set (21) corresponding to the resistor network near cell n based on the cell voltage (Ecell).
Additionally, consideration of the end nodes requires five additional equations, Equation set (22), for a full description of the system, where Itot is the total current applied through the stack.
Although these sets of equations are linear as presented, the cell voltage is a nonlinear function of current density. Past literature has given estimates of these shunt currents, and in all cases, the shunt current magnitudes are small relative to the total system current (< 2%) [77,78,81]. As a result, the variations in cell voltage are minimal. In order to minimize evaluations of the nonlinear cell voltage function and accelerate computation, we linearize the cell voltage about the applied current density using a resistance (rcell) to the incremental change in cell current due to the shunt currents. This approximation is shown in Equation (23), and the value of rcell is evaluated numerically using two function evaluations according to Equation (24), which come from the definition of the derivative and require a model decision in the selection of the current step (ΔI) for the evaluation of this derivative.
If we consider an isolated loop in Figure 2 as current passes from the electrode of a cell through a port, then a single manifold segment, then back through a port to the electrode of the next cell, we can obtain a coarse estimate of the port current magnitude based on Equation (25). Considering that there are two ports (inlet and outlet) connected to each half cell, we take double this value as our current step (ΔI ≅ ±2Iport). For context, in the base case, where we cycle the cell at 100 A, this value is on the order of 3 mA.
2.4. Hydraulic Losses
Electrode permeability (K) is estimated using the Carman-Kozeny Equation (26) similar to past work [95], but the user may opt to input a measured permeability as well. For all the results presented within this manuscript, we use a Carmen-Kozeny constant (kCK) value of 4, which corresponds to randomly aligned fibers [95]. We note here that in a real system, the permeability and mass-transfer resistance are inherently related; however, the mass-transfer model incorporated here does not fully capture this behavior, ignoring the effect of kCK on the mass-transfer losses.
Following front-end evaluation of the permeability, the pressure drop (ΔP) across the porous electrode is estimated using an analytical expression (27) from past work for the interdigitated flow field based on the volumetric flow rate through an individual cell (Qcell) [58,96]. Intermediate steps include the calculation of the channel hydraulic diameter (dh) in Equation (28) based on the channel width (wch) and height (hch), as well as a dimensionless geometry-informed permeability factor (ξ) described in Equation (29) that captures the combined effects of permeability and design parameters, such as the channel length (Lch) and rib width (wrib).
2.5. Model Framework
To increase accessibility, the stack model was written within the MATLAB app designer as this produces a simple graphical user interface (GUI) for visualizing how varying different inputs can impact system performance. Each of the four tabs of the GUI are depicted in Figure 3. Where possible, system inputs were divided between the tabs according to topic: (1) material properties, (2) system properties, (3) simulation, and (4) manifold, membrane saturation, and polarization.
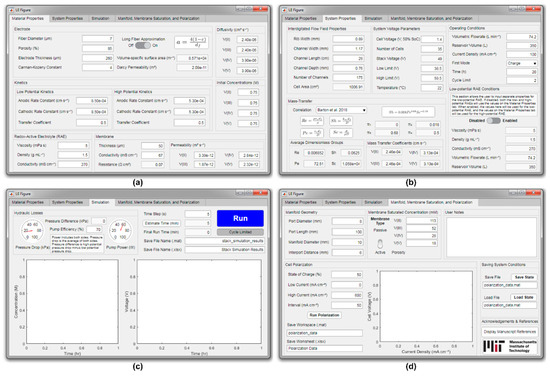
Figure 3.
Model graphical user interface (GUI). (a) Material properties, such as electrode properties, bulk redox-active electrolyte (RAE) properties, and membrane characteristics. (b) System properties, such as flow field geometry and operating conditions. (c) Simulation options, such as time step and output file names, as well as simulation outputs, such as pressure drop and voltage history. (d) Assorted interface components, such as manifold geometry, membrane behavior, a cell polarization tool, and a place for user-input notes.
Here, we note the general overview of system data flow, and the application parameters and functions are classified within Figure 4 to supplement this description. Figure 4 gives a brief list of all the system parameters as well as a short description of all the application functions. The simulation loads in all the user inputs (e.g., electrode porosity) from the GUI, and any changes to these values result in immediate recalculation of the continuously calculated parameters (e.g., mass-transfer coefficients). Toggled options generally affect the interpretation of user inputs (e.g., membrane behavior) or specific options for the conditions of cycling (e.g., limiting the number of cycles simulated). These functions are typically low-complexity; however, the options themselves can have a significant impact on the results of a given simulation. In contrast to this, activated operations may involve lengthier computing time (e.g., simulating cycling) or operations meant to facilitate user experience (e.g., loading references). For example, in order to simulate galvanostatic cycling, the user sets all system properties to appropriate values across all the tabs, then clicks “Run” on the “Simulation” tab to start cycling the VRFB. While running, a popup window will display progress towards the simulation time completed. For the first use, we suggest using the “Estimate Time” button before running, which evaluates the user’s systems speed at solving an ordinary differential equation using MATLAB’s “bench” function and scales this based on the number of time steps needed. After loading the system properties, the application builds the matrix describing the shunt current network and initializes the cell potential. Then, it integrates forward in time from this initial point, evaluating the cell voltages and updating the value of rcell within the shunt current matrix, then solving for the cell, port, and manifold currents at each time step. Additionally, when a half-cycle (charge or discharge) finishes, the element capturing the applied current within the shunt current matrix descriptor must also be updated (as the sign changes). After this solution, the active species concentrations are updated according to Equation set (17). Finally, at each time step, the currents and cell voltages relative to ground are all stored as data accessible by opening the exported Microsoft Excel file or MATLAB workspace. The names of these files are taken from user inputs on the “Simulation” tab of this function. In the case that a single cell is analyzed, this employs a slightly shortened algorithm as shunt currents are not present. After completion of this forward walk through time, a few variables are plotted within the application, specifically, the species concentrations and the system total and cell average voltages are plotted as a function of time. All of the employed code as well as the free-standing application are included in the supporting information (SI) for complete documentation and future implementation. The selected default values of all system parameters are listed in Appendix A in Table A1 along with clarifying illustrations of system geometry in Figure A1.
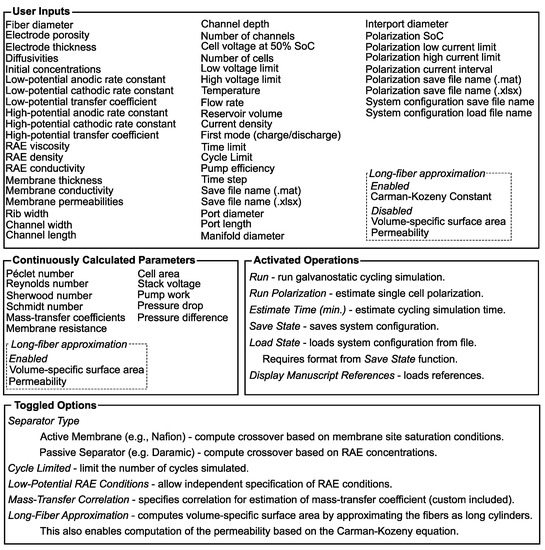
Figure 4.
Categorical listing of application inputs and functions.
3. Results and Discussion
Within this section, a short demonstration of the single-cell model results is shown to validate appropriate behavior from our descriptors of the core physics. Then, we illustrate the impact of active species crossover, which does not inherently produce capacity fade, but does impact the coulombic efficiency and the accessible capacity. Finally, we present a few parametric studies and discuss the implications of these on the overall system performance. The absolute values of the performance metrics presented here are based on the default values selected (listed in Table A1) and will change with differing inputs but the trends described are robust. As the model stands, our results are generally bounded by previous reports of system performance, whether focused on the study of individual components or the overall system, but subject to the user input values.
3.1. Single Cell Performance
The performance of a single cell is examined in the absence of crossover to illustrate the performance of the electrode polarization model and examine sensitivity to some core material parameters, such as the mass-transfer coefficients and kinetic rate constants. To start, Figure 5a shows the impact of mass transfer coefficient on the individual cell performance. The figure itself shows polarization curves at 50% SoC using three different mass transfer coefficient correlations: Schmal et al. [92], Barton et al. [73], and You et al. [91]. While the actual conditions of the cell (1.5 M V, 2.12 L min−1) are the same, there is a large variation in the predicted mass transfer coefficients from these empirical correlations. In recognition of the large variation and its impact on estimates of cell performance, we incorporated several empirical correlations [58,73,91,92,93] directly within the application as well as the option to enter a user-specified correlation in the format of Equation (10). The more recent correlations predict smaller mass-transfer coefficients, and this should be kept in mind throughout the subsequent analysis in which the correlation from Barton et al. [73] is selected as it has been demonstrated specifically with interdigitated flow fields. The frequently cited correlation from Schmal et al. was developed specifically for mass-transfer to an individual fiber, and the experimental setup used in 1985 may not be an accurate representation of the conditions achievable within current-generation VRFBs [92]. In this prior work, the commonly cited correlation was developed for carefully aligned fibers in a flow-through geometry, but comparison of their reactor bed with a modern RFB reveals a few quantifiable differences: typical fiber electrodes are not fully aligned with the direction of flow, interdigitated flow fields have significant flow orthogonal to the electrode plane, carbon paper porosity is typically lower than in the felt employed (ca. 80% vs. 96%), and the fibers are typically smaller than those found in the felt (ca. 7 µm vs. 15 µm) [92]. Perhaps the most interesting aspect of this particular figure is the indication that there is room for improvement in the characterization of mass transfer for RFBs. All three of these prior publications considered df to be the relevant length scale, but it may be important to consider separately the electrolyte path length, electrode thickness, and possibly an independent descriptor for the pore diameter or other details of the electrode microstructure. In particular, the path length within the porous electrode varies significantly with flow field design and experimental setup [73,91,92]. All three of the polarization curves in Figure 5a use literature values for vanadium reaction kinetics [88], which happen to use the same value for the anodic and cathodic reaction directions although different values are used for the high potential and the low potential reactions. As a result, these curves are symmetric about the open-circuit voltage (VOC) as the difference in individual mass transfer coefficients is nearly imperceptible at the cell level. In Figure 5b, we manipulate these rate constants to illustrate the impact that a 10-fold increase or decrease of the kinetic rate constants would have on the cell polarization. This is meant to emphasize that if the kinetic rates previously demonstrated can be achieved within a scaled cell, there is little incentive to catalyze the reactions further as an order-of-magnitude increase produces only marginal improvement in the polarization. Performance-driven research would likely be better served furthering membranes, flow fields, or electrode architecture. Conversely, if those rate constants cannot be achieved, their increase could significantly improve cell performance. Figure 5c shows a single (second cycle) cell discharge for three different current densities at a fixed flow rate. Due to the moderate value of the mass-transfer coefficient estimated, the cell reaches 81% of the theoretical capacity (20.1 Ah L−1) at low current densities, and as this increased to a more moderate value of 300 mA cm−2, this drops sharply to 30% of the theoretical. For comparison, Jiang et al. report accessing 72% of the theoretical capacity at 40 mA cm−2, and decreasing to 25% at 320 mA cm−2 [97]. Figure 5d illustrates the influence of current density and flow rate on the cell voltaic efficiency and accessed capacity. The voltaic efficiency (black, left) decreases from ca. 95% to 88% as the current density is increased with a scaled flow rate from 100 mA cm−2 to 300 mA cm−2 at 2.12 L min−1 and 6.36 L min−1, respectively. This particular area-specific flow rate (2 mL min−1 cm−2) is comparable to reported and optimized values within the field [58,62]. If scaled in this manner for this 1000 cm2 cell, the accessed capacity falls from 88% to 67% of the theoretical in contrast to Figure 5c, where flow rate was held constant. The increase in flow rate increases the accessed capacity as well as the voltaic efficiency due to the increases in the mass-transfer coefficients. Practically, the pumping losses also increase linearly with flow rate from 16 kPa to 48 kPa for 2.12 L min−1 to 6.36 L min−1. Since the pressure drop scales linearly with flow rate, the pump work scales with its square, and in terms of pump power, this corresponds to an increase from 1.6 W to 15 W (32×) with a 70% pump efficiency. Although this may seem a subtle point, it illustrates that the hydraulic losses within a flow battery grow quickly as flow rate is increased in an attempt to overcome mass-transfer resistance. This relationship poses a dynamic problem for the efficient operation of VRFBs as the SoC and system load change. High-power discharge requires some minimum flow rate, which negatively impacts the efficiency.
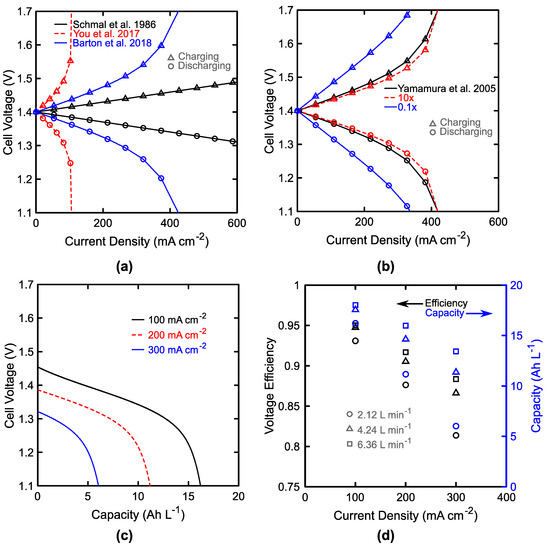
Figure 5.
Single cell performance. Discharge (○) and charge (△) polarization at 50% state-of-charge (SoC) and 1.5 M total active material concentration and a fixed flow rate of 2.12 L min−1 using (a) three different mass-transfer correlations [73,91,92] and (b) three different sets of kinetic parameters, where literature (black) kinetic values are compared to a 10× increase (red) or decrease (blue). (c) Galvanostatic discharge curves for three different current densities at 2.12 L min−1. (d) Single cell voltaic efficiencies (black, left) and discharge capacities (blue, right) as a function of current density and flow rate.
3.2. Membrane Crossover
Figure 6 shows the impact of crossover and separator behavior (active or passive) on the performance and capacity of a single-cell. The accessed capacities on charge and discharge are shown in Figure 6a for cases with and without crossover enabled for a single 1000 cm2 cell operating at 100 mA cm−2 with 2.5 L tanks and flow rate of 2.12 L min−1. The relatively small tank size was selected to keep the simulation time short and approximate common experimental energy-to-power ratios. Permeabilities are listed in Table A1 [41]. Crossover is easily removed by setting the membrane permeability to each active species to 0. The theoretical half-cycle for this configuration is 1 h, and over the 50 cycles shown, the active membranes (Nafion 212 and 117) show low capacity fade. In the case of these cation-exchange membranes, the varied solubilities (listed in Table A1 [84]), or saturation concentrations, of vanadium within the membrane bias crossover in one direction adding to the imbalance of total vanadium on either side. For the conditions shown, the Nafion coulombic efficiency remains high, and the capacity fade is less than many reports of experimental results [97,98,99], likely due to the omission of supporting species crossover. Here, the capacity fade over 50 cycles was 10.7% and 1.9% of the initial accessed capacity for the Nafion 212 and Nafion 117, respectively. For comparison, Jiang et al. show a capacity loss of over 50% and 20% for Nafion 212 and Nafion 117 over 50 cycles [97]. Figure 6b shows the self-discharge from 50% SoC at open-circuit conditions with the same flow rate and tank volume. Practically, this long self-discharge time for a system with an energy-to-power ratio of 1 h is promising for the field. If this low permeability to active species is genuinely achievable, losses due to crossover and self-discharge over the course of a cycle should remain small, and the selectivity of these membranes may be sufficient to satisfy performance metrics for coulombic efficiency. If other losses were included, such as side-reactions, these may present convoluting effects on the system performance, for example, shifting of the average vanadium oxidation state, and may further reduce the system capacity. As it stands, omission of supporting species crossover from the model likely causes the underestimation of capacity fade observed here but the trends are qualitatively correct. We also attempted to include a comparison of a passive separator with a MacMullin number of 4.5 and thickness of 25 μm, similar to Celgard 2500 [100]. The results are not shown here as the capacity fade was rapid enough to prevent meaningful discussion. We expect that the error in the model is greater for the high fluxes experienced with a passive separator due to the omission of supporting species transport.
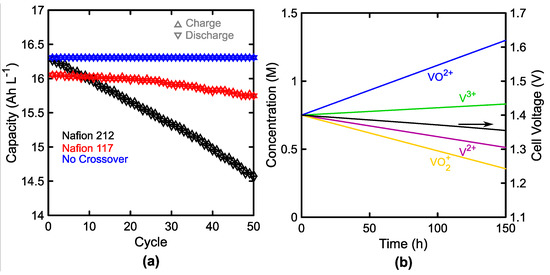
Figure 6.
Single cell crossover impact. (a) Charge (△) and discharge (▽) capacity as a function of cycle number at 100 mA cm−2. Inclusion (black, red) and omission (blue) of crossover clearly indicate its impact on capacity fade with stable current efficiency. (b) Change in active species concentrations as a function of time at open-circuit conditions due to the rate of crossover. Electrolytes contained 1.5 M V initially.
3.3. System Performance
This section demonstrates the impact of some system parameters, such as the number of cells in the stack, on system performance metrics, such as power losses. First, we present resulting shunt currents during discharge for a range of system stack sizes. For the sake of a clear comparison, tank volume and total flow rates are scaled with the number of cells (10 L and 2.12 L min−1 per cell) to maintain a constant energy-to-power ratio (4 h at 100 mA cm−2) and electrolyte velocity. Figure 7a shows the shunt currents within the ports and manifold as a function of position within the stack. These current magnitudes and trends are similar to past work [78,82]. The edge conditions force the manifold current to match the port current, and this is directly observable at cell N for each stack size. At cell 1, the port and manifold currents are equivalent in magnitude and direction, but opposite in sign merely due to the convention chosen in Figure 2. The applied current, 100 A, is much larger than the port and manifold currents, and as a result, the impact of these shunt currents on the cell voltage is minimal as an individual cell voltage is relatively insensitive to a 0.1% change (100 mA vs. 100 A) in the current passing through it. Practically, the port currents may be considered leakage currents from individual cells, and this leakage is summed within the manifold to produce a maximum manifold current near the center of the stack. The port currents are the greatest near the end of the stack and they are minimal near the middle of the stack. Physically, this phenomenon arises due to the fact that each successive cell drives current through the port in the opposite direction of the previous cell. However, at the ends the ports only see one cell thus the leakage (port) currents can grow to a greater value. Figure 7b shows the increase in mean discharge power (left) as a function of stack size alongside the power lost to shunt currents and pump work (right). Across the cases explored, pump work and shunt losses grow significantly with the stack size. However, the relative magnitude of these losses remains small. The shunt current magnitude is consistent with prior reports, both in terms of the relative scale of these currents and the dependence on position within the stack [78,81]. Practically, quantitative comparison of these values is difficult as simple variations in system geometry can significantly affect the results.
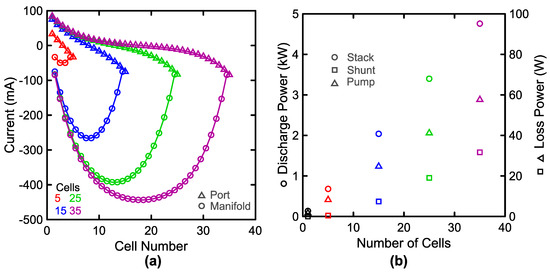
Figure 7.
Stack losses during discharge at as a function of the number of cells when cycled at 100 mA cm−2 with a flow rate of 2.12 L min−1 cell−1 and 1.5 M V. (a) Mean port (△) and manifold (○) currents as a function of position within the stack. (b) Mean stack discharge power (○, left) alongside energy losses due to shunt currents (△, right) and pump work (□, right).
Figure 8 illustrates the impact of flow rate on performance of a 35-cell stack. Figure 8a shows the steady increase in both capacity (left) and energy (right) with increases in flow rate. Increases in flow rate correspond to an increase in the mass-transfer coefficient, thus increasing system energy both by reducing the limiting reactant concentration and by increasing the cell voltage during discharge. Figure 8b shows the impact of flow rate on the average discharge power, pump power, and roundtrip energy efficiency. At low flow rates, increasing the flow rate gives rise to a substantial increase in cell power, but at high flow rates, the pumping losses quickly grow to detract from the overall system efficiency. This loss is emphasized by the difference between the blue markers, which show the roundtrip efficiency with and without accounting for the pumping losses. It is reassuring to see that the heuristically selected flow rate of 2 mL min−1 per cm2 of active area is near the point of maximum efficiency. In this case, the system operates at slightly higher efficiency at 1.5 mL min−2 per cm2 of active area, so if we consider roundtrip energy efficiency to be our primary variable to maximize and constrain the system to an invariant flow rate, then this would be the optimal condition. However, both logic and prior art suggest that to maximize efficiency, a variable flow rate should be employed [101,102]. The system is generally insensitive to mass-transfer coefficient while the reactant is being consumed from an enriched state (i.e., discharging at high SoC or charging at low SoC), thus operation at low or moderate flow rates is optimal here. When the reactant becomes depleted, it then becomes worthwhile to increase the flow rate, enhancing the mass-transfer coefficient and enabling greater accessible capacity. We also note the slope of the efficiency curve to either side of the flow rate corresponding to maximum efficiency. To the left of the maximum, decreases in flow rate produce a sharp decrease in efficiency, whereas to the right, the decrease is slower, suggesting that in the case of uncertainty, erring towards higher flow rates may be favorable. Increasing current density increases the flow rate of maximum efficiency due to the increase in mass-transfer losses (data not shown). Additionally, higher current densities reduce the maximum efficiency due to an increase in all sources of losses. Figure 9 examines the degree to which current density influences the system performance.
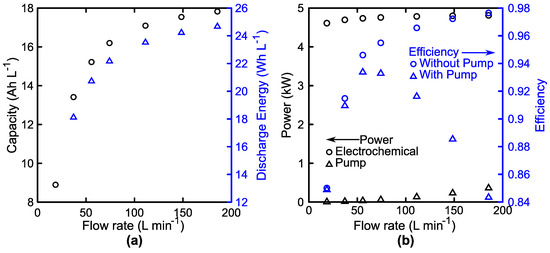
Figure 8.
Influence of flow rate on 35-cell stack performance at 100 mA cm−2. (a) Impact of flow rate on accessible system capacity (black, left) and discharge energy density (blue, right). (b) Impact of flow rate on the average discharge electrochemical power (○, black, left) and the pump power (△, black, left) alongside the roundtrip efficiency with (△, blue, right) and without (○, blue, right) accounting for pumping losses.
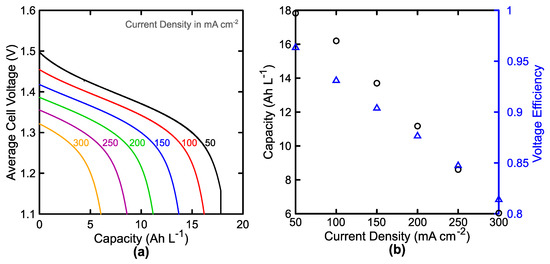
Figure 9.
Performance of the 35-cell stack over a range of current densities at 74.2 L min−1. (a) Discharge curves and (b) accessed capacity (○, black, left) and voltage efficiency (△, blue, right) as a function of applied current density.
Figure 9a shows the impact of current density on the cell-averaged discharge curve at fixed flow rate. As the current increases, the cell voltage and accessed capacity decrease in a near linear fashion as shown in Figure 9b. The accessed capacity decreases from 87% to 30% of the theoretical capacity (20.1 Ah L−1) as the current density increases from 50 mA cm−2 to 300 mA cm−2. The voltage efficiency also decreases from 96% to 81% with this increase in current density. A thorough comparison with the literature reveals that these efficiencies are definitively overestimated at low current densities, but within the range of reported values at high current densities, as results are widely varied in this regime [103,104,105,106,107]. For comparison, Zhou et al. report a voltaic efficiency of 90% and 67% at 80 mA cm−2 and 320 mA cm−2, respectively, but the authors use Nafion 115, which should have a resistance of 2.5× the value used here, representing Nafion 212 [103]. Additionally, this same work reports similar accessed capacities at both low and high current densities (82% and 20% of the theoretical at 80 mA cm−2 and 320 mA cm−2, respectively) [103]. Wang et al. report voltaic efficiencies ranging from 92% to 67% at 40 mA cm−2 and 200 mA cm−2, respectively [104]. Recent demonstration and analysis of controlled-power cycling of a system with multiple vanadium flow battery stacks at 50 kW to 200 kW showed voltage efficiencies of 91% to 80% [105]. In this case, the membrane was not reported, and the estimation of the average current density is unclear. The overestimation of the voltage efficiency at low current density suggests that the kinetic losses may be underestimated and, although these kinetic parameters have been used in past work, their true values likely vary greatly between systems, especially as a function of electrode selection and pretreatment. At high current densities, differences within the literature are more likely explained by variations in the mass-transfer coefficient between systems. For the default conditions employed, this model estimates a limiting current density of a little over 400 mA cm−2 as shown in Figure 5a, but within the literature, one can find limiting current densities for similar electrolyte compositions as low as 60 mA cm−2 or greater than 2600 mA cm−2 [106,107]. These differences arise as a result of the large variations in experimental setup, and serve as motivation for our incorporation of multiple mass transfer correlations as detailed in Section 2.1. As the model stands, these results are generally bound by previous reports of system performance and emphasize the sharp decrease in efficiency and accessed capacity as the limiting current density is approached.
4. Conclusions
We have discussed the development and initial validation of a RFB model packaged as a MATLAB application (see Supplementary Materials), which can be used to assess the upper performance limits of a particular system, here a VRFB. This application advances the field as the model allows for user-selected material properties. Specifically, we chose to emphasize the large variation in predicted mass-transfer coefficients through the incorporation of multiple correlations. Complete, irrefutable descriptions of this parameter as a function of all system parameters remains elusive. Additionally, this model specifically examines performance with an interdigitated flow field and represents the first implementation of this polarization model at the stack scale, by treating the porous electrode as a well-mixed flow-through reactor. Although the default parameters may underestimate the kinetic or ohmic losses, the application allows for user variation of these and any other model parameters, to evaluate performance under conditions of interest. As it stands, this model is a flexible platform, which can be used or modified to address specific questions within the field. For example, this model could be used to estimate short-time-scale performance of other unimolecular redox chemistries (i.e., polarization) by setting the permeabilities to 0, offering a simple side-by-side comparison of a novel chemistry to the VRFB. Some clear steps towards the continued advancement of this model would be the inclusion of economic parameters, additional decay pathways and side reactions, and optimization options. The location within the code to incorporate these additional physical processes has been indicated within the text. This model would also benefit from scientific consensus on the values of different physical parameters, such as the kinetic and mass-transfer coefficients. A potential pathway toward resolving this challenge would be agreement on a common flow cell architecture, preferably small-scale, low cost and easy to manufacture, and the establishment of standardized testing protocols with readily available baseline materials.
Looking forward with respect to the model developed here, we note its limitations in order to present opportunities for improvement in subsequent analysis. First, the model expects and handles the system as if the conversion-per-pass is low. In the case of high conversion, concentration distributions of the bulk active species are significantly altered as the fluid flows along its path through the porous electrode. In such a case, the path should be segmented, and each segment could be solved as if well-mixed, similar to here. Second, the linearization of the cell resistance assumes that the shunt currents are small relative to the applied current. As a result, with low-resistance ports and manifold segments, this model will likely over-predict the system voltage as it underestimates the impact of current leakage on the individual cell potential. Additionally, at very low applied currents, the model may over-predict the impact of leaking current on the cell voltage and will likely underestimate the system voltage. Third, many additional factors affecting performance are not considered, and significant contributions from any of these factors not included within the model can lead to gross errors in performance estimates. Addressing one or all of these aforementioned limitations will further improve model fidelity and we hope the community builds upon this first release.
Supplementary Materials
The following are available online at https://www.mdpi.com/2313-0105/5/1/25/s1, Free standing application installer file: Stack_Simulator_Installer.exe, and the simulator code files for use in MATLAB R2018a: Cell_simulation_gui_v22.mlapp is the main file, and model_electrode_loss_bvp4c.m incorporates the 1D polarization model.
Author Contributions
Conceptualization, J.L.B. and F.R.B.; methodology, J.L.B.; software, J.L.B.; validation, J.L.B.; formal analysis, J.L.B.; investigation, J.L.B.; resources, F.R.B.; data curation, J.L.B.; writing—original draft, J.L.B.; writing—review and editing, J.L.B. and F.R.B.; supervision, F.R.B.; project administration, F.R.B.; funding acquisition, F.R.B.
Funding
This research was funded by the Joint Center for Energy Storage Research (JCESR) managed by Argonne National Laboratory and funded by the Department of Energy (DOE) through the office of Basic Energy Sciences. Argonne National Laboratory, a U.S. DOE Office of Science Laboratory, is operated under contract no. DE-AC02-06CH11357. J. L. B. acknowledges funding from the ExxonMobil-MIT Energy Fellowship (2017–2018).
Acknowledgments
The authors appreciate technical feedback with respect to the explored system space from M. L. Perry (United Technologies Research Center) after development of the initial model.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
Appendix A

Table A1.
Symbol definitions.
Table A1.
Symbol definitions.
| Symbol | Description | Dimensions 1 | Default Value 2 |
|---|---|---|---|
| Le | electrode thickness | L | 260 μm |
| kc | cathodic rate constant | L t−1 | 8.5 × 10−4 cm s−1 [88] |
| ka | anodic rate constant | L t−1 | 5.3 × 10−4 cm s−1 [88] |
| bulk concentration of species i | N L−3 | 0.75 mol L−1 | |
| df | fiber diameter | L | 7 μm [94] |
| km,i | mass-transfer coefficient of species i | L t−1 | m s−1 |
| nq | number of electrons transferred | 1 | |
| n | cell index | - | |
| N | total number of cells | 35 | |
| NX,i | crossover flux of species i | N L−2 t−1 | mol m−2 s−1 |
| x | position within the porous electrode | L | m |
| i | current density | I L−2 | 100 mA cm−2 |
| I | current | I | A |
| ae | volume-specific electrode surface area 3 | L−1 | 85700 m−1 |
| Ri | resistance of element i | M L2 I−2 t−3 | Ω |
| Re | Reynolds number | - | |
| Sh | Sherwood number | - | |
| Ki | membrane permeability of species i | L2 t−1 | m2 s−1 |
| i = V2+ | 3.39 × 10−12 m2 s−1 [41] | ||
| i = V3+ | 1.87 × 10−12 m2 s−1 [41] | ||
| i = VO2+ | 2.84 × 10−12 m2 s−1 [41] | ||
| i = VO2+ | 2.32 × 10−12 m2 s−1 [41] | ||
| ci,sat | membrane solubility of species i | N L−3 | mol m−3 |
| i = V2+ | 113 mM [83] | ||
| i = V3+ | 52 mM [83] | ||
| i = VO2+ | 28 mM [83] | ||
| i = VO2+ | 18 mM [83] | ||
| εmem | membrane porosity | 0.39 [108] | |
| Lmem | membrane thickness | L | 50 μm |
| KCK | Carman-Kozeny constant | 4 [95] | |
| wrib | flow field rib width | L | 0.89 mm [58] |
| wch | flow field channel width | L | 1.17 mm [58] |
| Lch | flow field channel length | L | 28 cm |
| dch | flow field channel depth | L | 0.76 mm [58] |
| nch | number of flow field channels | 175 | |
| dp | port geometric diameter | L | 8 mm [82] |
| dm | manifold geometric diameter | L | 10 mm [82] |
| Lp | port length | L | 100 mm [82] |
| Lm | manifold interport distance | L | 6 mm [82] |
| Vres | reservoir volume | L3 | 350 L |
| VOC | open-circuit voltage | M L2 I−1 t−3 | 1.4 V [109] |
| Elow | lower voltage limit for cycling | M L2 I−1 t−3 | 5.5 |
| Ehigh | upper voltage limit for cycling | M L2 I−1 t−3 | 8.5 |
| T | temperature | T | 22 °C |
| Sc | Schmidt number | - | |
| Pe | Péclet number | - | |
| Di | diffusivity of species i | L2 t−1 | m2 s−1 |
| i = II; species is V2+ | 2.4 × 10−6 cm2 s−1 [88] | ||
| i = III; species is V3+ | 2.4 × 10−6 cm2 s−1 [88] | ||
| i = IV; species is VO2+ | 3.9 × 10−6 cm2 s−1 [88] | ||
| i = V; species is VO2+ | 3.9 × 10−6 cm2 s−1 [88] | ||
| ve | electrolyte average velocity | L t−1 | m s−1 |
| Q | volumetric flow rate of RAE 4 | L3 t−1 | 74.2 L min−1 |
| Subscripts | |||
| ox | oxized redox-active species | ||
| red | reduced redox-active species | ||
| 1 | solid (electrode) phase | ||
| 2 | liquid (electrolyte) phase | ||
| high | high-potential side | ||
| low | low-potential side | ||
| Greek | |||
| α | transfer coefficient | 0.5 | |
| ν | kinematic viscosity | L2 t−1 | m2 s−1 |
| πi | mass transfer correlation parameter | - | |
| κ | RAE conductivity | I2 t3 M−1 L−3 | 270 mS cm−1 [8] |
| κeff | effective RAE conductivity 5 | I2 t3 M−1 L−3 | S m−1 |
| κmem | membrane conductivity | I2 t3 M−1 L−3 | 67 mS cm−1 [110] |
| μ | dynamic viscosity | M t2 L−1 | 5 mPa s [8] |
| ηpump | pump efficiency | 70% | |
| Δt | time step for cycling | t | 20 s |
| ε | electrode porosity | 85% [73] | |
| Δϕm | overpotential at the membrane | M L2 I−1 t−3 | V |
| ΔP | pressure drop | M t−2 L−1 | Pa |
| ρ | RAE density | M L−3 | 1.5 g mL−1 [8] |
| σ | electrode conductivity | I2 t3 M−1 L−3 | S m−1 |
| ϕi | potential in phase i | M L2 I−1 t−3 | V |
1 Dimension key: mass (M), length (L), time (t), temperature (T), current (I), matter (N). 2 In the case of a time-variant variable, the initial value is given. In the case of multiple values being assumed or estimated based on other system parameters, only the default SI units are given. 3 Estimated based on long thin-fiber characteristics based on ae = 4 × (1 − ε)/df [73,91]. 4 This flow rate was selected by scaling the flow rate from a few references [58,62], as well as our own experimental practices. Heuristically, it appears that a flow rate of ~2 milliliters per minute per square centimeter of cell area is fairly standard practice. 5 Estimated using a Bruggeman relation κeff = κε1.5 [72,73,90].
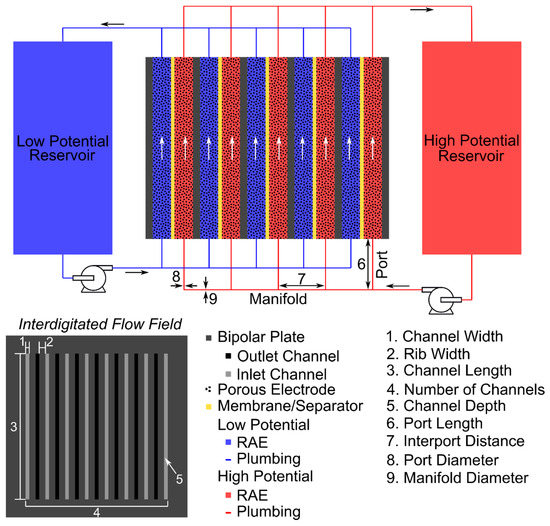
Figure A1.
Clarifying illustration of system geometry parameters that enable extension beyond single-cell analysis.
References
- Weber, A.Z.; Mench, M.M.; Meyers, J.P.; Ross, P.N.; Gostick, J.T.; Liu, Q. Redox flow batteries: A review. J. Appl. Electrochem. 2011, 41, 1137–1164. [Google Scholar] [CrossRef]
- Alotto, P.; Guarnieri, M.; Moro, F. Redox flow batteries for the storage of renewable energy: A review. Renew. Sustain. Energy Rev. 2014, 29, 325–335. [Google Scholar] [CrossRef]
- Leung, P.; Shah, A.A.; Sanz, L.; Flox, C.; Morante, J.R.; Xu, Q.; Mohamed, M.R.; Ponce de León, C.; Walsh, F.C. Recent developments in organic redox flow batteries: A critical review. J. Power Sources 2017, 360, 243–283. [Google Scholar] [CrossRef]
- Darling, R.M.; Gallagher, K.G.; Kowalski, J.A.; Ha, S.; Brushett, F.R. Pathways to low-cost electrochemical energy storage: A comparison of aqueous and nonaqueous fl ow batteries. Energy Environ. Sci. 2014, 7, 3459–3477. [Google Scholar] [CrossRef]
- Leung, P.K.; Li, X.; Ponce de León, C.; Berlouis, L.; Low, C.T.J.; Walsh, F.C. Progress in redox flow batteries, remaining challenges and their applications in energy storage. RSC Adv. 2012, 2, 10125–10156. [Google Scholar] [CrossRef]
- Dmello, R.; Milshtein, J.D.; Brushett, F.R.; Smith, K.C. Cost-driven materials selection criteria for redox flow battery electrolytes. J. Power Sources 2016, 330, 261–272. [Google Scholar] [CrossRef]
- Rychcik, M.; Skyllas-Kazacos, M. Characteristics of a new all-vanadium redox flow battery. J. Power Sources 1988, 22, 59–67. [Google Scholar] [CrossRef]
- Skyllas-Kazacos, M.; Cao, L.; Kazacos, M.; Kausar, N.; Mousa, A. Vanadium Electrolyte Studies for the Vanadium Redox Battery—A Review. ChemSusChem 2016, 9, 1521–1543. [Google Scholar] [CrossRef] [PubMed]
- Turton, R.; Bailie, R.C.; Whiting, W.B.; Shaeiwitz, J.A.; Baille, R.C.; Whiting, W.B.; Shaeiwitz, J.A. Analysis, Synthesis, and Design of Chemical Processes, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2009; ISBN 978-0-13-512966-1. [Google Scholar]
- Rudolph, S.; Schröder, U.; Bayanov, I.M. On-line controlled state of charge rebalancing in vanadium redox flow battery. J. Electroanal. Chem. 2013, 703, 29–37. [Google Scholar] [CrossRef]
- Gong, K.; Fang, Q.; Gu, S.; Li, S.F.Y.; Yan, Y. Nonaqueous redox-flow batteries: organic solvents, supporting electrolytes, and redox pairs. Energy Environ. Sci. 2015, 8, 3515–3530. [Google Scholar] [CrossRef]
- Chen, H.; Cong, G.; Lu, Y.-C. Recent progress in organic redox flow batteries: Active materials, electrolytes and membranes. J. Energy Chem. 2018, 1–22. [Google Scholar] [CrossRef]
- Dieterich, V.; Milshtein, J.D.; Barton, J.L.; Carney, T.J.; Darling, R.M. Estimating the cost of organic battery active materials: A case study on anthraquinone disulfonic acid Estimating the cost of organic battery active materials: A case study on anthraquinone disulfonic acid. Transl. Mater. Res. 2018, 5, 3. [Google Scholar] [CrossRef]
- Singh, N.; McFarland, E.W. Levelized cost of energy and sensitivity analysis for the hydrogen-bromine flow battery. J. Power Sources 2015, 288, 187–198. [Google Scholar] [CrossRef]
- Knehr, K.W.; Biswas, S.; Steingart, D.A. Quantification of the Voltage Losses in the Minimal Architecture Zinc-Bromine Battery Using GITT and EIS. J. Electrochem. Soc. 2017, 164, A3101–A3108. [Google Scholar] [CrossRef]
- Braff, W.A.; Bazant, M.Z.; Buie, C.R. Membrane-less hydrogen bromine flow battery. Nat. Commun. 2013, 4, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Pan, M.S.; Su, L.; Tsai, P.; Badel, A.F.; Valle, J.M.; Eiler, S.L.; Xiang, K.; Brushett, F.R.; Chiang, Y. Air-Breathing Aqueous Sulfur Flow Battery for Ultralow-Cost Long-Duration Electrical Storage. Joule 2017, 1, 306–327. [Google Scholar] [CrossRef]
- Cleaver, T.; Kovacik, P.; Marinescu, M.; Zhang, T.; Offer, G. Perspective—Commercializing Lithium Sulfur Batteries: Are We Doing the Right Research? J. Electrochem. Soc. 2018, 165, A6029–A6033. [Google Scholar] [CrossRef]
- Su, L.; Badel, A.F.; Cao, C.; Hinricher, J.J.; Brushett, F.R. Toward an Inexpensive Aqueous Polysulfide-Polyiodide Redox Flow Battery. Ind. Eng. Chem. Res. 2017, 56, 9783–9792. [Google Scholar] [CrossRef]
- Manohar, A.K.; Kim, K.M.; Plichta, E.; Hendrickson, M.; Rawlings, S.; Narayanan, S.R. A High Efficiency Iron-Chloride Redox Flow Battery for Large-Scale Energy Storage. J. Electrochem. Soc. 2016, 163, A5118–A5125. [Google Scholar] [CrossRef]
- Hawthorne, K.L.; Petek, T.J.; Miller, M.A.; Wainright, J.S.; Savinell, R.F. An Investigation into Factors Affecting the Iron Plating Reaction for an All-Iron Flow Battery. J. Electrochem. Soc. 2014, 162, A108–A113. [Google Scholar] [CrossRef]
- Gong, K.; Ma, X.; Conforti, K.M.; Kuttler, K.J.; Grunewald, J.B.; Yeager, K.L.; Bazant, M.Z.; Gu, S.; Yan, Y. A zinc-iron redox-flow battery under $100 per kW h of system capital cost. Energy Environ. Sci. 2015, 8, 2941–2945. [Google Scholar] [CrossRef]
- Li, B.; Li, L.; Wang, W.; Nie, Z.; Chen, B.; Wei, X.; Luo, Q.; Yang, Z.; Sprenkle, V. Fe/V redox flow battery electrolyte investigation and optimization. J. Power Sources 2013, 229, 1–5. [Google Scholar] [CrossRef]
- Viswanathan, V.; Crawford, A.; Stephenson, D.; Kim, S.; Wang, W.; Li, B.; Coffey, G.; Thomsen, E.; Graff, G.; Balducci, P.; Kintner-meyer, M.; Sprenkle, V. Cost and performance model for redox flow batteries. J. Power Sources 2014, 247, 1040–1051. [Google Scholar] [CrossRef]
- Ma, R.X.; Setzler, B.P.; Gong, K.; Gu, S.; Yan, Y. A General, Analytical Model for Flow Battery Costing and Design. J. Electrochem. Soc. 2018, 165, A2209–A2216. [Google Scholar] [CrossRef]
- Choi, C.; Kim, S.; Kim, R.; Choi, Y.; Kim, S.; Jung, H.Y.; Yang, J.H.; Kim, H.T. A review of vanadium electrolytes for vanadium redox flow batteries. Renew. Sustain. Energy Rev. 2017, 69, 263–274. [Google Scholar] [CrossRef]
- Parasuraman, A.; Lim, T.M.; Menictas, C.; Skyllas-Kazacos, M. Review of material research and development for vanadium redox flow battery applications. Electrochim. Acta 2013, 101, 27–40. [Google Scholar] [CrossRef]
- Kim, K.J.; Park, M.-S.; Kim, Y.-J.; Kim, J.H.; Dou, S.X.; Skyllas-Kazacos, M. A technology review of electrodes and reaction mechanisms in vanadium redox flow batteries. J. Mater. Chem. A 2015, 3, 16913–16933. [Google Scholar] [CrossRef]
- Arenas, L.F.; Ponce de León, C.; Walsh, F.C. Engineering aspects of the design, construction and performance of modular redox flow batteries for energy storage. J. Energy Storage 2017, 11, 119–153. [Google Scholar] [CrossRef]
- Reed, D.; Thomsen, E.; Li, B.; Wang, W.; Nie, Z.; Koeppel, B.; Kizewski, J.; Sprenkle, V. Stack Developments in a kW Class All Vanadium Mixed Acid Redox Flow Battery at the Pacific Northwest National Laboratory. J. Electrochem. Soc. 2016, 163, A5211–A5219. [Google Scholar] [CrossRef]
- Kim, S.; Thomsen, E.; Xia, G.; Nie, Z.; Bao, J.; Recknagle, K.; Wang, W.; Viswanathan, V.; Luo, Q.; Wei, X.; Crawford, A.; Coffey, G.; Maupin, G.; Sprenkle, V. 1 kW/1 kWh advanced vanadium redox flow battery utilizing mixed acid electrolytes. J. Power Sources 2013, 237, 300–309. [Google Scholar] [CrossRef]
- Roe, S.; Menictas, C.; Skyllas-Kazacos, M. A High Energy Density Vanadium Redox Flow Battery with 3 M Vanadium Electrolyte. J. Electrochem. Soc. 2016, 163, A5023–A5028. [Google Scholar] [CrossRef]
- Xi, X.; Li, X.; Wang, C.; Lai, Q.; Cheng, Y.; Zhou, W.; Ding, C.; Zhang, H. Impact of proton concentration on equilibrium potential and polarization of vanadium flow batteries. Chempluschem 2015, 80, 382–389. [Google Scholar] [CrossRef]
- Lawton, J.S.; Tiano, S.M.; Donnelly, D.J.; Flanagan, S.P.; Arruda, T.M. The Effect of Sulfuric Acid Concentration on Physical and Electrochemical Properties of Vanadyl Solutions. Batteries 2018, 4, 40. [Google Scholar] [CrossRef]
- Sum, E.; Skyllas-Kazacos, M. A study of the V(II)/V(III) redox couple for redox flow cell applications. J. Power Sources 1985, 15, 179–190. [Google Scholar] [CrossRef]
- Mousa, A. Chemical and Electrochemical studies of V(III) and V(II) Solutions in Sulfuric Acid Solution for Vanadium Battery Applications. Ph.D. Thesis, University of New South Wales, Sydney, Australia, 2003. [Google Scholar]
- Mousa, A.; Skyllas-kazacos, M. Physical Properties of Negative Half-Cell Electrolytes in the Vanadium Redox Flow Battery. In Electrochemically Enabled Sustainability; CRC Press: Boca Raton, FL, USA, 2014; pp. 395–428. ISBN 9781466575431. [Google Scholar]
- Sun, C.-N.; Delnick, F.M.; Aaron, D.S.; Papandrew, A.B.; Mench, M.M.; Zawodzinski, T.A. Resolving Losses at the Negative Electrode in All-Vanadium Redox Flow Batteries Using Electrochemical Impedance Spectroscopy. J. Electrochem. Soc. 2014, 161, A981–A988. [Google Scholar] [CrossRef]
- Oriji, G.; Katayama, Y.; Miura, T. Investigation on V(IV)/V(V) species in a vanadium redox flow battery. Electrochim. Acta 2004, 49, 3091–3095. [Google Scholar] [CrossRef]
- Rahman, F.; Skyllas-Kazacos, M. Vanadium redox battery: Positive half-cell electrolyte studies. J. Power Sources 2009, 189, 1212–1219. [Google Scholar] [CrossRef]
- Ashraf Gandomi, Y.; Aaron, D.S.; Mench, M.M. Coupled Membrane Transport Parameters for Ionic Species in All-Vanadium Redox Flow Batteries. Electrochim. Acta 2016, 218, 174–190. [Google Scholar] [CrossRef]
- Yu, L.; Lin, F.; Xu, L.; Xi, J. Structure–property relationship study of Nafion XL membrane for high-rate, long-lifespan, and all-climate vanadium flow batteries. RSC Adv. 2017, 7, 31164–31172. [Google Scholar] [CrossRef]
- Schwenzer, B.; Zhang, J.; Kim, S.; Li, L.; Liu, J.; Yang, Z. Membrane development for vanadium redox flow batteries. ChemSusChem 2011, 4, 1388–1406. [Google Scholar] [CrossRef] [PubMed]
- Lawton, J.S.; Jones, A.M.; Tang, Z.; Zawodzinski, T.; National, R.; Tennessee, O.R.; Lindsey, M. Ion Effects on Vanadium Transport in Nafion Membranes for Vanadium Redox Flow Batteries. J. Electrochem. Soc. 2017, 164, A2987–A2991. [Google Scholar] [CrossRef]
- Won, S.; Oh, K.; Ju, H. Numerical analysis of vanadium crossover effects in all-vanadium redox flow batteries. Electrochim. Acta 2015, 177, 310–320. [Google Scholar] [CrossRef]
- Li, X.; Zhang, H.; Mai, Z.; Zhang, H.; Vankelecom, I. Ion exchange membranes for vanadium redox flow battery (VRB) applications. Energy Environ. Sci. 2011, 4, 1147. [Google Scholar] [CrossRef]
- Elgammal, R.A.; Tang, Z.; Sun, C.-N.; Lawton, J.; Zawodzinski, T.A. Species Uptake and Mass Transport in Membranes for Vanadium Redox Flow Batteries. Electrochim. Acta 2017, 237, 1–11. [Google Scholar] [CrossRef]
- Oh, K.; Won, S.; Ju, H. A comparative study of species migration and diffusion mechanisms in all-vanadium redox flow batteries. Electrochim. Acta 2015, 181, 238–247. [Google Scholar] [CrossRef]
- Sun, B.; Skyllas-Kazacos, M. Modification of graphite electrode materials for vanadium redox flow battery application—I. Thermal treatment. Electrochim. Acta 1992, 37, 1253–1260. [Google Scholar] [CrossRef]
- Pezeshki, A.M.; Sacci, R.L.; Delnick, F.M.; Aaron, D.S.; Mench, M.M. Elucidating effects of cell architecture, electrode material, and solution composition on overpotentials in redox flow batteries. Electrochim. Acta 2017, 229, 261–270. [Google Scholar] [CrossRef]
- Fink, H.; Friedl, J.; Stimming, U. Composition of the Electrode Determines Which Half-Cell’s Rate Constant is Higher in a Vanadium Flow Battery. J. Phys. Chem. C 2016, 120, 15893–15901. [Google Scholar] [CrossRef]
- He, Z.; Cheng, G.; Jiang, Y.; Wang, L.; Dai, L. Sulfonated Carbon Nanotubes as Superior Catalysts towards V3+/V2+ Redox Reaction for Vanadium Redox Flow Battery. J. Electrochem. Soc. 2018, 165, A932–A938. [Google Scholar] [CrossRef]
- Liu, S.; Kok, M.; Kim, Y.; Barton, J.L.; Brushett, F.R.; Gostick, J. Evaluation of Electrospun Fibrous Mats Targeted for Use as Flow Battery Electrodes. J. Electrochem. Soc. 2017, 164, A2038–A2048. [Google Scholar] [CrossRef]
- Zhong, S.; Skyllas-Kazacos, M. Electrochemical behaviour of vanadium(V)/vanadium(IV) redox couple at graphite electrodes. J. Power Sources 1992, 39, 1–9. [Google Scholar] [CrossRef]
- Becker, M.; Bredemeyer, N.; Tenhumberg, N.; Turek, T. Kinetic studies at carbon felt electrodes for vanadium redox-flow batteries under controlled transfer current density conditions. Electrochim. Acta 2017. [Google Scholar] [CrossRef]
- Aaron, D.; Yeom, S.; Kihm, K.D.; Gandomi, Y.A.; Ertugrul, T.; Mench, M.M. Kinetic enhancement via passive deposition of carbon-based nanomaterials in vanadium redox flow batteries. J. Power Sources 2017, 366, 241–248. [Google Scholar] [CrossRef]
- Xu, Q.; Zhao, T.S.; Zhang, C. Performance of a vanadium redox flow battery with and without flow fields. Electrochim. Acta 2014, 142, 61–67. [Google Scholar] [CrossRef]
- Darling, R.M.; Perry, M.L. The Influence of Electrode and Channel Configurations on Flow Battery Performance. J. Electrochem. Soc. 2014, 161, A1381–A1387. [Google Scholar] [CrossRef]
- Xu, Q.; Zhao, T.S.; Leung, P.K. Numerical investigations of flow field designs for vanadium redox flow batteries. Appl. Energy 2013, 105, 47–56. [Google Scholar] [CrossRef]
- Zheng, Q.; Xing, F.; Li, X.; Ning, G.; Zhang, H. Flow field design and optimization based on the mass transport polarization regulation in a flow-through type vanadium flow battery. J. Power Sources 2016, 324, 402–411. [Google Scholar] [CrossRef]
- You, X.; Ye, Q.; Cheng, P. Scale-up of high power density redox flow batteries by introducing interdigitated flow fields. Int. Commun. Heat Mass Transf. 2016, 75, 7–12. [Google Scholar] [CrossRef]
- Tang, A.; Bao, J.; Skyllas-Kazacos, M. Studies on pressure losses and flow rate optimization in vanadium redox flow battery. J. Power Sources 2014, 248, 154–162. [Google Scholar] [CrossRef]
- Kim, D.K.; Yoon, S.J.; Lee, J.; Kim, S. Parametric study and flow rate optimization of all-vanadium redox flow batteries. Appl. Energy 2018, 228, 891–901. [Google Scholar] [CrossRef]
- Rudolph, S.; Schröder, U.; Bayanov, R.I.; Blenke, K.; Bayanov, I.M. Optimal electrolyte flow distribution in hydrodynamic circuit of vanadium redox flow battery. J. Electroanal. Chem. 2015, 736, 117–126. [Google Scholar] [CrossRef]
- Zhang, C.; Zhao, T.S.; Xu, Q.; An, L.; Zhao, G. Effects of operating temperature on the performance of vanadium redox flow batteries. Appl. Energy 2015, 349–353. [Google Scholar] [CrossRef]
- Oboroceanu, D.; Quill, N.; Lenihan, C.; Eidhin, D.N.; Albu, S.P.; Lynch, R.P.; Buckley, D.N. Communication—Observation of Arrhenius Behavior of Catholyte Stability in Vanadium Flow Batteries. J. Electrochem. Soc. 2016, 163, A2919–A2921. [Google Scholar] [CrossRef]
- Schafner, K.; Becker, M.; Turek, T. Capacity balancing for vanadium redox flow batteries through electrolyte overflow. J. Appl. Electrochem. 2018. [Google Scholar] [CrossRef]
- Vynnycky, M. Analysis of a model for the operation of a vanadium redox battery. Energy 2011, 36, 2242–2256. [Google Scholar] [CrossRef]
- Chen, C.L.; Yeoh, H.K.; Chakrabarti, M.H. An enhancement to Vynnycky’s model for the all-vanadium redox flow battery. Electrochim. Acta 2014, 120, 167–179. [Google Scholar] [CrossRef]
- Shah, A.A.; Watt-Smith, M.J.; Walsh, F.C. A dynamic performance model for redox-flow batteries involving soluble species. Electrochim. Acta 2008, 53, 8087–8100. [Google Scholar] [CrossRef]
- Shah, A.A.; Walsh, F.C.; Al-Fetlawi, H.; Walsh, F.C. Dynamic modelling of hydrogen evolution effects in the all-vanadium redox flow battery. Electrochim. Acta 2010, 55, 1125–1139. [Google Scholar] [CrossRef]
- Milshtein, J.D.; Tenny, K.M.; Barton, J.L.; Drake, J.; Darling, R.M.; Brushett, F.R. Quantifying mass transfer rates in redox flow batteries. J. Electrochem. Soc. 2017, 164. [Google Scholar] [CrossRef]
- Barton, J.L.; Milshtein, J.D.; Hinricher, J.J.; Brushett, F.R. Quantifying the impact of viscosity on mass-transfer coefficients in redox flow batteries. J. Power Sources 2018, 399, 133–143. [Google Scholar] [CrossRef]
- Newman, J.; Tiedemann, W. Porous-Electrode Theory with Battery Applications. AIChE J. 1975, 21, 25–41. [Google Scholar] [CrossRef]
- Newman, J.; Thomas-Alyea, K.E. Electrochemical Systems, 3rd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2004; ISBN 978-0-471-47756-3. [Google Scholar]
- König, S.; Suriyah, M.R.; Leibfried, T. Validating and improving a zero-dimensional stack voltage model of the Vanadium Redox Flow Battery. J. Power Sources 2018, 378, 10–18. [Google Scholar] [CrossRef]
- Wandschneider, F.T.; Röhm, S.; Fischer, P.; Pinkwart, K.; Tübke, J.; Nirschl, H. A multi-stack simulation of shunt currents in vanadium redox flow batteries. J. Power Sources 2014, 261, 64–74. [Google Scholar] [CrossRef]
- Yin, C.; Guo, S.; Fang, H.; Liu, J.; Li, Y.; Tang, H. Numerical and experimental studies of stack shunt current for vanadium redox flow battery. Appl. Energy 2015, 151, 237–248. [Google Scholar] [CrossRef]
- Wei, Z.; Zhao, J.; Skyllas-Kazacos, M.; Xiong, B. Dynamic thermal-hydraulic modeling and stack flow pattern analysis for all-vanadium redox flow battery. J. Power Sources 2014, 260, 89–99. [Google Scholar] [CrossRef]
- Knehr, K.W.; Agar, E.; Dennison, C.R.; Kalidindi, A.R.; Kumbur, E.C. A Transient Vanadium Flow Battery Model Incorporating Vanadium Crossover and Water Transport through the Membrane. J. Electrochem. Soc. 2012, 159, 1446–1459. [Google Scholar] [CrossRef]
- Xing, F.; Zhang, H.; Ma, X. Shunt current loss of the vanadium redox flow battery. J. Power Sources 2011, 196, 10753–10757. [Google Scholar] [CrossRef]
- Fink, H.; Remy, M. Shunt currents in vanadium flow batteries: Measurement, modelling and implications for efficiency. J. Power Sources 2015, 284, 547–553. [Google Scholar] [CrossRef]
- Darling, R.M.; Weber, A.Z.; Tucker, M.C.; Perry, M.L. The Influence of Electric Field on Crossover in Redox-Flow Batteries. J. Electrochem. Soc. 2015, 163, A5014–A5022. [Google Scholar] [CrossRef]
- Cho, H.S.; Ohashi, M.; Van Zee, J.W. Absorption behavior of vanadium in Nafion®. J. Power Sources 2014, 267, 547–552. [Google Scholar] [CrossRef]
- Sun, C.; Chen, J.; Zhang, H.; Han, X.; Luo, Q. Investigations on transfer of water and vanadium ions across Nafion membrane in an operating vanadium redox flow battery. J. Power Sources 2010, 195, 890–897. [Google Scholar] [CrossRef]
- Darling, R.M.; Shiau, H.-S.; Weber, A.Z.; Perry, M.L. The Relationship between Shunt Currents and Edge Corrosion in Flow Batteries. J. Electrochem. Soc. 2017, 164, E3081–E3091. [Google Scholar] [CrossRef]
- Gandomi, Y.A.; Aaron, D.S.; Zawodzinski, T.A.; Mench, M.M. In Situ Potential Distribution Measurement and Validated Model for All-Vanadium Redox Flow Battery. J. Electrochem. Soc. 2016, 163, A5188–A5201. [Google Scholar] [CrossRef]
- Yamamura, T.; Watanabe, N.; Yano, T.; Shiokawa, Y. Electron-Transfer Kinetics of Np3+/Np4+, NpO2+/NpO22+, V2+/V3+, and VO2+/VO2+ at Carbon Electrodes. J. Electrochem. Soc. 2005, 152, A830. [Google Scholar] [CrossRef]
- Bard, A.J.; Faulkner, L.R. Electrochemical Methods Fundamentals and Applications, 2nd ed.; Harris, D., Swain, E., Aiello, E., Eds.; John Wiley & Sons, Inc.: New York, NY, USA, 2001; ISBN 978-0-471-04372-0. [Google Scholar]
- Tjaden, B.; Cooper, S.J.; Brett, D.J.; Kramer, D.; Shearing, P.R. On the origin and application of the Bruggeman correlation for analysing transport phenomena in electrochemical systems. Curr. Opin. Chem. Eng. 2016, 12, 44–51. [Google Scholar] [CrossRef]
- You, X.; Ye, Q.; Cheng, P. The Dependence of Mass Transfer Coefficient on the Electrolyte Velocity in Carbon Felt Electrodes: Determination and Validation. J. Electrochem. Soc. 2017, 164, E3386–E3394. [Google Scholar] [CrossRef]
- Schmal, D.; Van Erkel, J.; Van Duin, P.J. Mass transfer at carbon fibre electrodes. J. Appl. Electrochem. 1986, 16, 422–430. [Google Scholar] [CrossRef]
- Wilson, E.J.; Geankoplis, C.J. Liquid Mass Transfer at Very Low Reynolds Numbers in Packed Beds. Ind. Eng. Chem. Fundam. 1966, 5, 9–14. [Google Scholar] [CrossRef]
- Zenyuk, I.V.; Parkinson, D.Y.; Connolly, L.G.; Weber, A.Z. Gas-diffusion-layer structural properties under compression via X-ray tomography. J. Power Sources 2016, 328, 364–376. [Google Scholar] [CrossRef]
- Kok, M.D.R.; Khalifa, A.; Gostick, J.T. Multiphysics Simulation of the Flow Battery Cathode: Cell Architecture and Electrode Optimization. J. Electrochem. Soc. 2016, 163, A1408–A1419. [Google Scholar] [CrossRef]
- Darling, R.M.; Badrinarayanan, P. Oxygen Transport in Polymer-Electrolyte Fuel Cells with Interdigitated Air Channels in Porous Bipolar Plates. J. Electrochem. Soc. 2011, 158, B54. [Google Scholar] [CrossRef]
- Jiang, B.; Wu, L.; Yu, L.; Qiu, X.; Xi, J. A comparative study of Nafion series membranes for vanadium redox flow batteries. J. Memb. Sci. 2016, 510, 18–26. [Google Scholar] [CrossRef]
- Li, Z.; Liu, L.; Yu, L.; Wang, L.; Xi, J.; Qiu, X.; Chen, L. Characterization of sulfonated poly(ether ether ketone)/poly(vinylidene fluoride-co-hexafluoropropylene) composite membrane for vanadium redox flow battery application. J. Power Sources 2014, 272, 427–435. [Google Scholar] [CrossRef]
- Luo, Q.; Li, L.; Wang, W.; Nie, Z.; Wei, X.; Li, B.; Chen, B.; Yang, Z.; Sprenkle, V. Capacity decay and remediation of nafion-based all-vanadium redox flow batteries. ChemSusChem 2013, 6, 268–274. [Google Scholar] [CrossRef] [PubMed]
- Landesfeind, J.; Hattendorff, J.; Ehrl, A.; Wall, W.A.; Gasteiger, H.A. Tortuosity Determination of Battery Electrodes and Separators by Impedance Spectroscopy. J. Electrochem. Soc. 2016, 163, A1373–A1387. [Google Scholar] [CrossRef]
- Wang, T.; Fu, J.; Zheng, M.; Yu, Z. Dynamic control strategy for the electrolyte flow rate of vanadium redox flow batteries. Appl. Energy 2017. [Google Scholar] [CrossRef]
- Fu, J.; Wang, T.; Wang, X.; Sun, J.; Zheng, M. Dynamic Flow Rate Control for Vanadium Redox Flow Batteries. Energy Procedia 2017, 105, 4482–4491. [Google Scholar] [CrossRef]
- Zhou, X.L.; Zhao, T.S.; An, L.; Zeng, Y.K.; Zhu, X.B. Performance of a vanadium redox flow battery with a VANADion membrane. Appl. Energy 2016, 180, 353–359. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, Y.; Liu, L.; Xi, J.; Wu, Z.; Qiu, X. Broad temperature adaptability of vanadium redox flow battery-Part 3: The effects of total vanadium concentration and sulfuric acid concentration. Electrochim. Acta 2018, 259, 11–19. [Google Scholar] [CrossRef]
- Bryans, D.; Amstutz, V.; Girault, H.; Berlouis, L. Characterisation of a 200 kW/400 kWh Vanadium Redox Flow Battery. Batteries 2018, 4, 54. [Google Scholar] [CrossRef]
- Bhattarai, A.; Wai, N.; Schweiss, R.; Whitehead, A.; Lim, T.M.; Hng, H.H. Advanced porous electrodes with flow channels for vanadium redox flow battery. J. Power Sources 2017, 341, 83–90. [Google Scholar] [CrossRef]
- Sun, C.-N.; Mench, M.M.; Zawodzinski, T.A. High Performance Redox Flow Batteries: An Analysis of the Upper Performance Limits of Flow Batteries Using Non-aqueous Solvents. Electrochim. Acta 2017, 237, 199–206. [Google Scholar] [CrossRef]
- Joseph, D.; Büsselmann, J.; Harms, C.; Henkensmeier, D.; Larsen, M.J.; Dyck, A.; Jang, J.H.; Kim, H.J.; Nam, S.W. Porous Nafion membranes. J. Memb. Sci. 2016, 520, 723–730. [Google Scholar] [CrossRef]
- Hudak, N.S. Practical thermodynamic quantities for aqueous vanadium- and iron-based flow batteries. J. Power Sources 2014, 269, 962–974. [Google Scholar] [CrossRef]
- Xie, W.; Darling, R.M.; Perry, M.L. Processing and Pretreatment Effects on Vanadium Transport in Nafion Membranes. J. Electrochem. Soc. 2016, 163, A5084–A5089. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).