Discharge by Short Circuit Currents of Parallel-Connected Lithium-Ion Cells in Thermal Propagation
Abstract
1. Introduction
2. Influence of SoC on TR Behaviour
3. Experiment
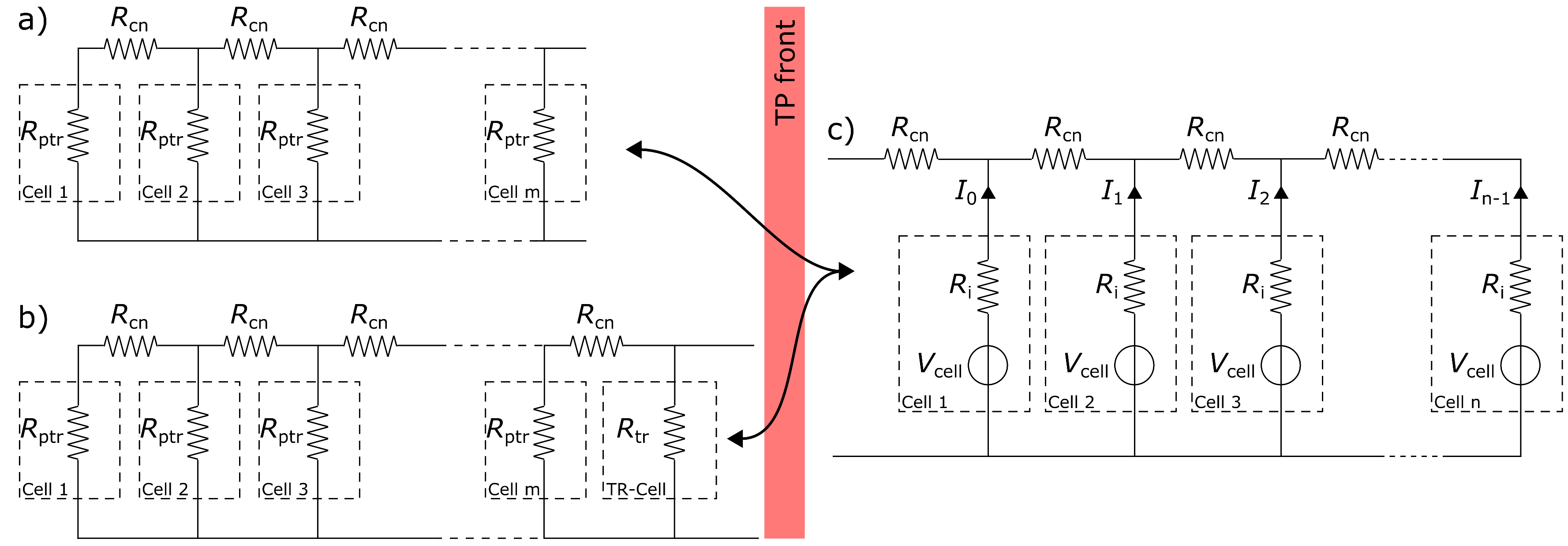
4. Modelling
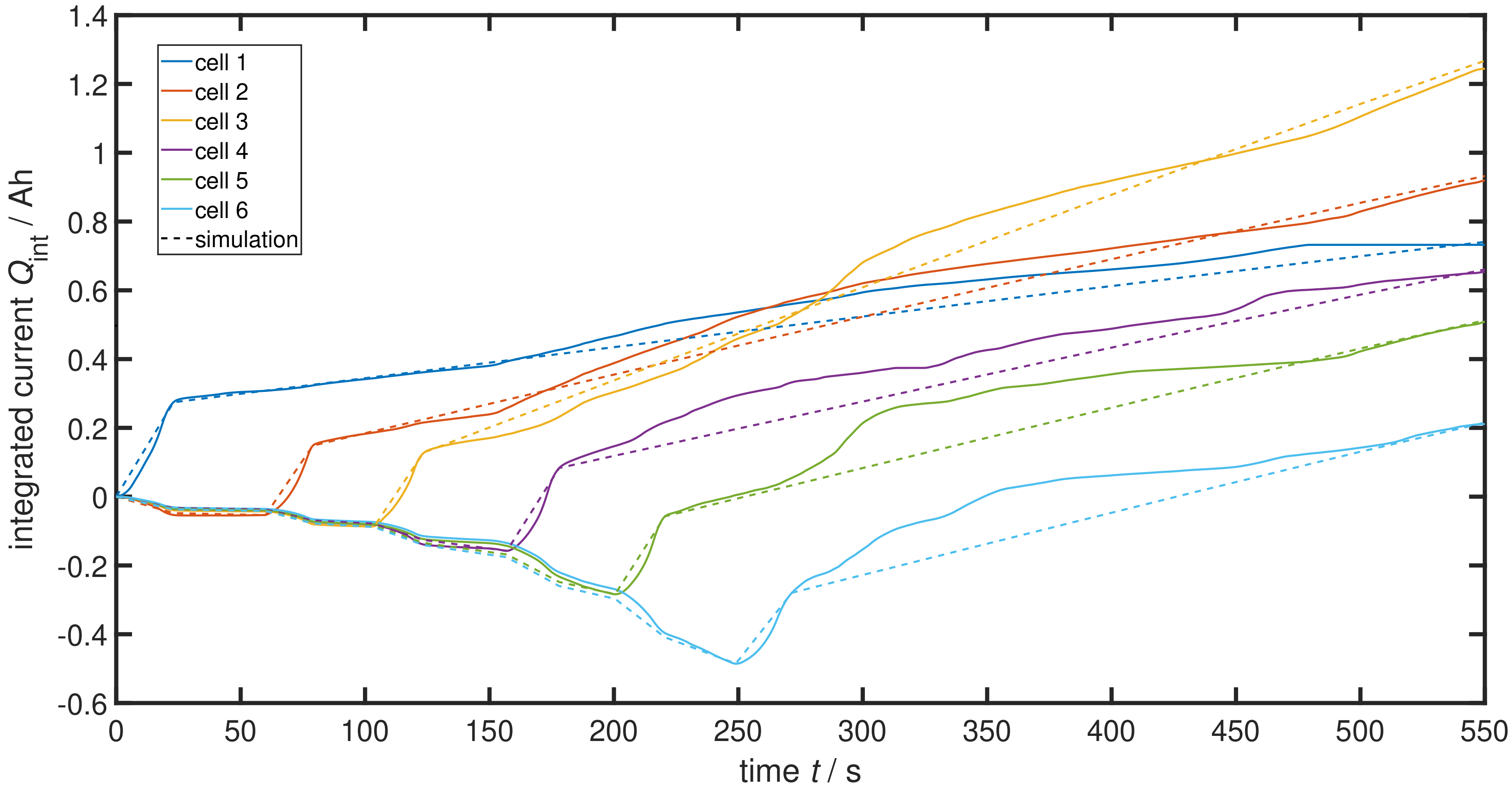
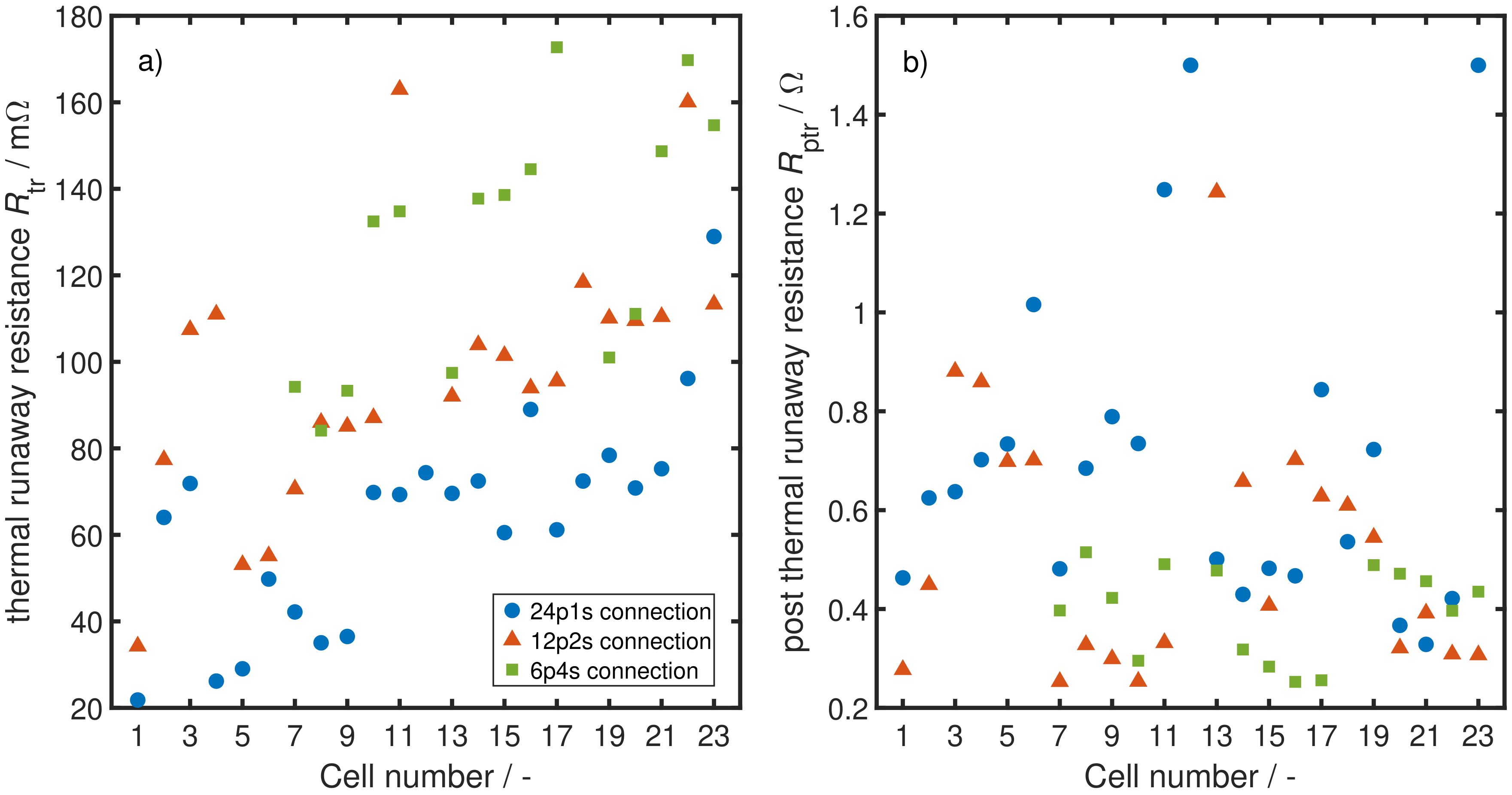
4.1. Parameter Estimation
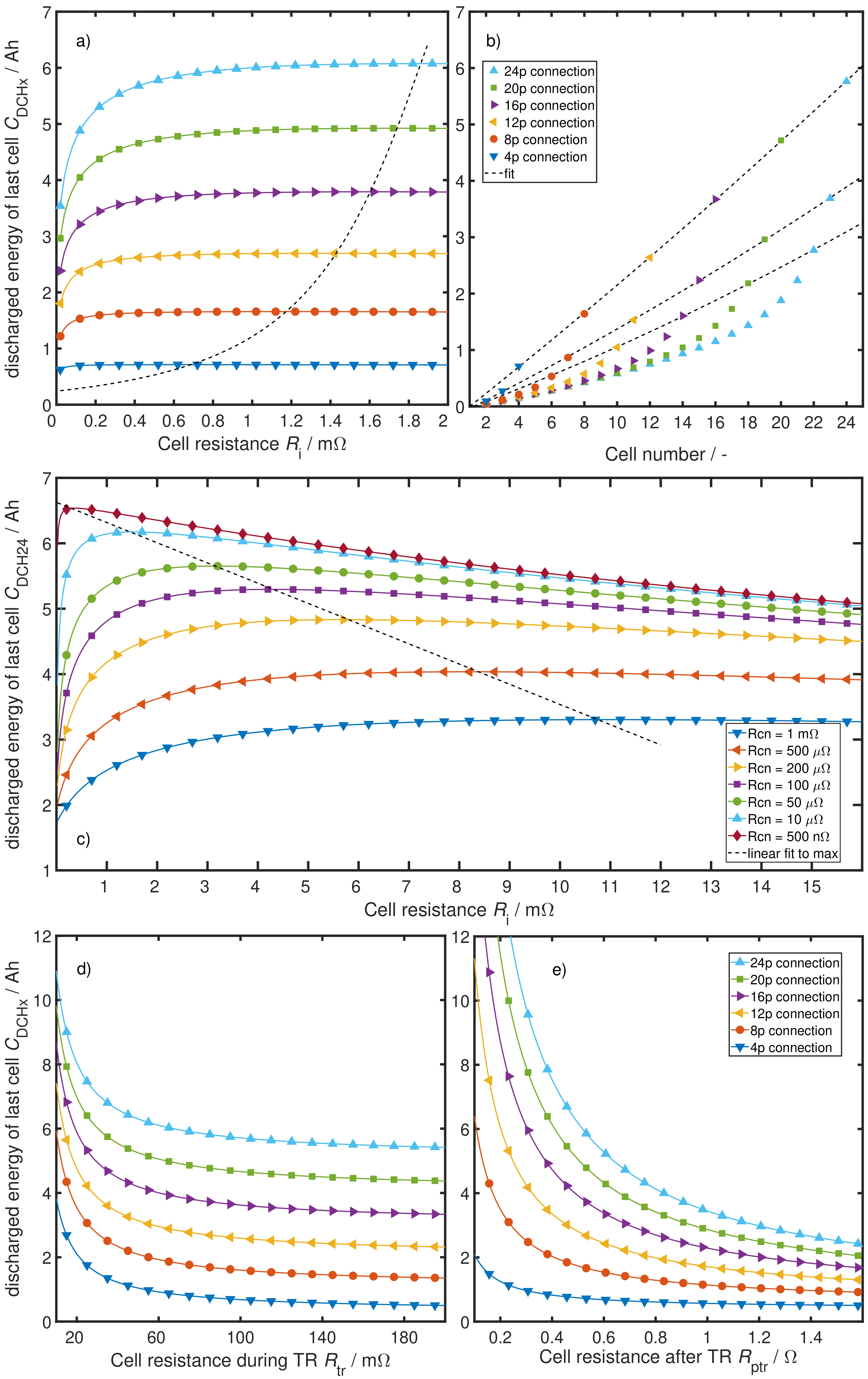
4.2. System Analysis
5. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| EV | all-electric vehicle |
| TR | thermal runaway |
| TP | thermal propagation |
| SoC | state of charge |
| ECM | equivalent circuit model |
| NMC | Li[NiMnCo]O |
References
- Nykvist, B.; Nilsson, M. Rapidly falling costs of battery packs for electric vehicles. Nat. Clim. Chang. 2015, 5, 329–332. [Google Scholar] [CrossRef]
- Yuan, Q.; Hao, W.; Su, H.; Bing, G.; Gui, X.; Sadikhani, A. Investigation on Range Anxiety and Safety Buffer of Battery Electric Vehicle Drivers. J. Adv. Transp. 2018, 2018. [Google Scholar] [CrossRef]
- Esmaili, M.; Shafiee, H.; Aghaei, J. Range anxiety of electric vehicles in energy management of microgrids with controllable loads. J. Energy Storage 2018, 20, 57–66. [Google Scholar] [CrossRef]
- Rothgang, S.; Baumhöfer, T.; Sauer, D. Necessity and Methods to improve Battery Lifetime on System Leve. In Proceedings of the Electric Vehicle Symposium EVS28, Goyang, Korea, 3–6 May 2015. [Google Scholar]
- Brand, M.; Hofmann, M.; Steinhardt, M.; Schuster, S. Current distribution within parallel-connected battery cells. J. Power Sources 2016, 334, 202–212. [Google Scholar] [CrossRef]
- Dubarry, M.; Devie, A.; Liaw, B. Cell-balancing currents in parallel strings of a battery system. J. Power Sources 2016, 321, 36–46. [Google Scholar] [CrossRef]
- Fill, A.; Koch, S.; Pott, A.; Birke, K. Current distribution of parallel-connected cells in dependence of cell resistance, capacity and number of parallel cells. J. Power Sources 2018, 407, 147–152. [Google Scholar] [CrossRef]
- Orcioni, S.; Buccolini, L.; Ricci, A.; Conti, M. Lithium-ion Battery Electrothermal Model, Parameter Estimation, and Simulation Environment. Energies 2017, 10, 375. [Google Scholar] [CrossRef]
- Pastor-Fernández, C.; Bruen, T.; Widanage, W.; Gama-Valdez, M.; Marco, J. A Study of Cell-to-Cell Interactions and Degradation in Parallel Strings: Implications for the Battery Management System. J. Power Sources 2016, 329, 574–585. [Google Scholar] [CrossRef]
- Roscher, M.; Kuhn, R.; Döring, H. Error detection for PHEV, BEV and stationary battery systems. Control Eng. Pract. 2013, 21, 1481–1487. [Google Scholar] [CrossRef]
- Lopez, C.; Jeevarajan, J.; Mukherjee, P. Experimental Analysis of Thermal Runaway and Propagation in Lithium-Ion Battery Moduls. J. Electrochem. Soc. 2015, 162, A1905–A1915. [Google Scholar] [CrossRef]
- Koch, S.; Fill, A.; Birke, K. Comprehensive gas analysis on large scale automotive lithium-ion cells in thermal runaway. J. Power Sources 2018, 398, 106–112. [Google Scholar] [CrossRef]
- Lamb, J.; Orendorff, C.; Steele, L.; Spangler, S. Failure propagation in multi-cell lithium ion batteries. J. Power Sources 2015, 283, 517–523. [Google Scholar] [CrossRef]
- Feng, X.; Sun, J.; Ouyang, M.; Wang, F.; He, X.; Lu, L.; Peng, H. Characterization of penetration induced thermal runaway propagation process within a large format lithium ion battery module. J. Power Sources 2015, 275, 261–273. [Google Scholar] [CrossRef]
- Balakrishnan, P.; Ramesh, R.; Kumar, T.P. Safety mechanisms in lithium-ion batteries. J. Power Sources 2006, 155, 401–414. [Google Scholar] [CrossRef]
- Wang, Q.; Ping, P.; Zhao, X.; Chu, G.; Sun, J.; Chen, C. Thermal runaway caused fire and explosion of lithium ion battery. J. Power Sources 2012, 208, 210–224. [Google Scholar] [CrossRef]
- Liu, X.; Stoliarv, S.; Denlinger, M.; Masias, A.; Snyder, K. Comprehensive calorimetry of the thermally-induced failure of a lithium ion battery. J. Power Sources 2015, 280, 516–525. [Google Scholar] [CrossRef]
- Mendoza-Hernandez, O.; Ishikawa, H.; Nishikawa, Y.; Maruyama, Y.; Umeda, M. Cathode material comparison of thermal runaway behavior of Li-ion cells at different state of charges including over charge. J. Power Sources 2015, 280, 499–504. [Google Scholar] [CrossRef]
- Doughty, D.; Roth, E. A General Discussion of Li Ion Battery Safety. Electrochem. Soc. Interface 2012, 21, 37–44. [Google Scholar] [CrossRef]
- Golubkov, A.; Scheikl, S.; Planteu, R.; Voitic, G.; Wiltsche, H.; Stangl, C.; Fauler, G.; Thaler, A.; Hacker, V. Thermal runaway of commerial 18650 Li-ion batteries with LFP and NCA cathodes - impact of state of charge and overcharge. RSC Adv. 2015, 5, 57171–57186. [Google Scholar] [CrossRef]
- Ma, L.; Nie, M.; Xia, J.; Dahn, J. A systematic study on the reactivity of different grades of charged Li[NixMnyCoz]O2 with electrolyte at elevated temperatures using accelerating rate calorimetry. J. Power Sources 2016, 327, 145–150. [Google Scholar] [CrossRef]
- Ribière, P.; Grugeon, S.; Morcrette, M.; Boyanov, S.; Laruelle, S.; Marlair, G. Investigation on the fire-induced hazards pf Li-ion battery cells by fire calorimetry. Energy Environ. Sci. 2012, 5, 5271–5280. [Google Scholar] [CrossRef]
- Coleman, B.; Ostanek, J.; Heinzel, J. Reducing cell-to-cell spacing for large-format lithium ion battery modules with aluminum or PCM heat sinks under failure conditions. Appl. Energy 2016, 180, 14–26. [Google Scholar] [CrossRef]
- Wilke, S.; Schweitzer, B.; Khateeb, S.; Al-Hallaj, S. Preventing thermal runaway propagation in lithium ion battery packs using phase change composite material: An experimental study. J. Power Sources 2017, 340, 51–59. [Google Scholar] [CrossRef]
- Koch, S.; Birke, K.; Kuhn, R. Fast Thermal Runaway Detection for Lithium-Ion Cells in LArge Scale Traction Batteries. Batteries 2018, 4, 16. [Google Scholar] [CrossRef]
- Feng, X.; Ouyang, M.; Liu, X.; Lu, L.; Xia, Y.; He, X. Thermal runaway mechanism of lithium ion battery for electric vehicles: A review. Energy Storage Mater. 2018, 10, 246–267. [Google Scholar] [CrossRef]
- Santhanagopalan, S.; Ramadass, P.; Zhang, J. Analysis of internal short-circuit in a lithium ion cell. J. Power Sources 2009, 194, 550–557. [Google Scholar] [CrossRef]
- Fu, Y.; Lu, S.; Li, K.; Liu, C.; Cheng, X.; Zhang, H. An experimental study on burning behaviors of 18650 lithium ion batteries using a cone calorimeter. J. Power Sources 2015, 273, 216–222. [Google Scholar] [CrossRef]
- Richard, M.; Dahn, J. Accelerating Rate Calorimetry Study on the Thermal Stability of Lithium Intercalated Graphite in Electrolyte I. Experimental. J. Electrochem. Soc. 1999, 146, 2068–2077. [Google Scholar] [CrossRef]
- Maleki, H.; Howard, J.N. Role of the cathode and anode in heat generation of Li-ion cells as a function of state of charge. J. Power Sources 2004, 137, 117–127. [Google Scholar] [CrossRef]
- Röder, P.; Baba, N.; Wiemhöfer, H.D. A detailed thermal study of a Li[Ni0.33Co0.33Mn0.33]O2/LiMn2O4-based lithium ion cell by accelerating rate and differential scanning calorimetry. J. Power Sources 2014, 248, 978–987. [Google Scholar] [CrossRef]
- Biensan, P.; Simon, B.; Pérès, J.; de Guibert, A.; Broussely, M.; Bodet, J.; Perton, F. On safety of lithium-ion cells. J. Power Sources 1999, 81–82, 906–912. [Google Scholar] [CrossRef]
- Kirchhoff, G. Ueber den Durchgang eines elektrischen Stromes durch eine Ebene, insbesondere durch eine kreisförmige. Ann. Phys. 1845, 140, 497–514. [Google Scholar] [CrossRef]
- Holbrook, J. Specialized Applications of the Laplace Transform. In Laplace Transforms for Electronic Engineers, 2nd (revised) ed.; Pergamon Press Ltd.: Oxford, UK, 1966; Chapter IX; p. 269. [Google Scholar]
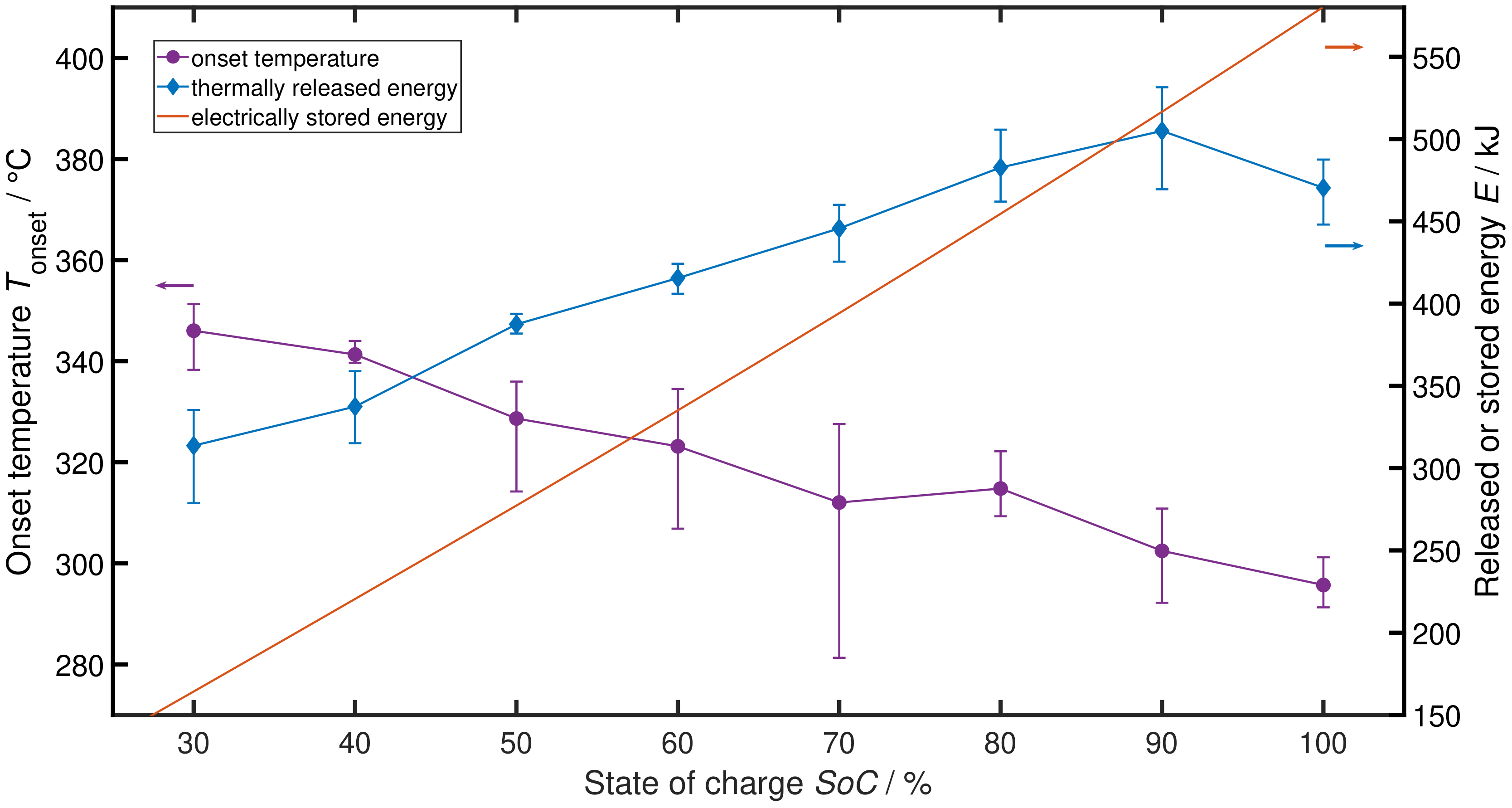
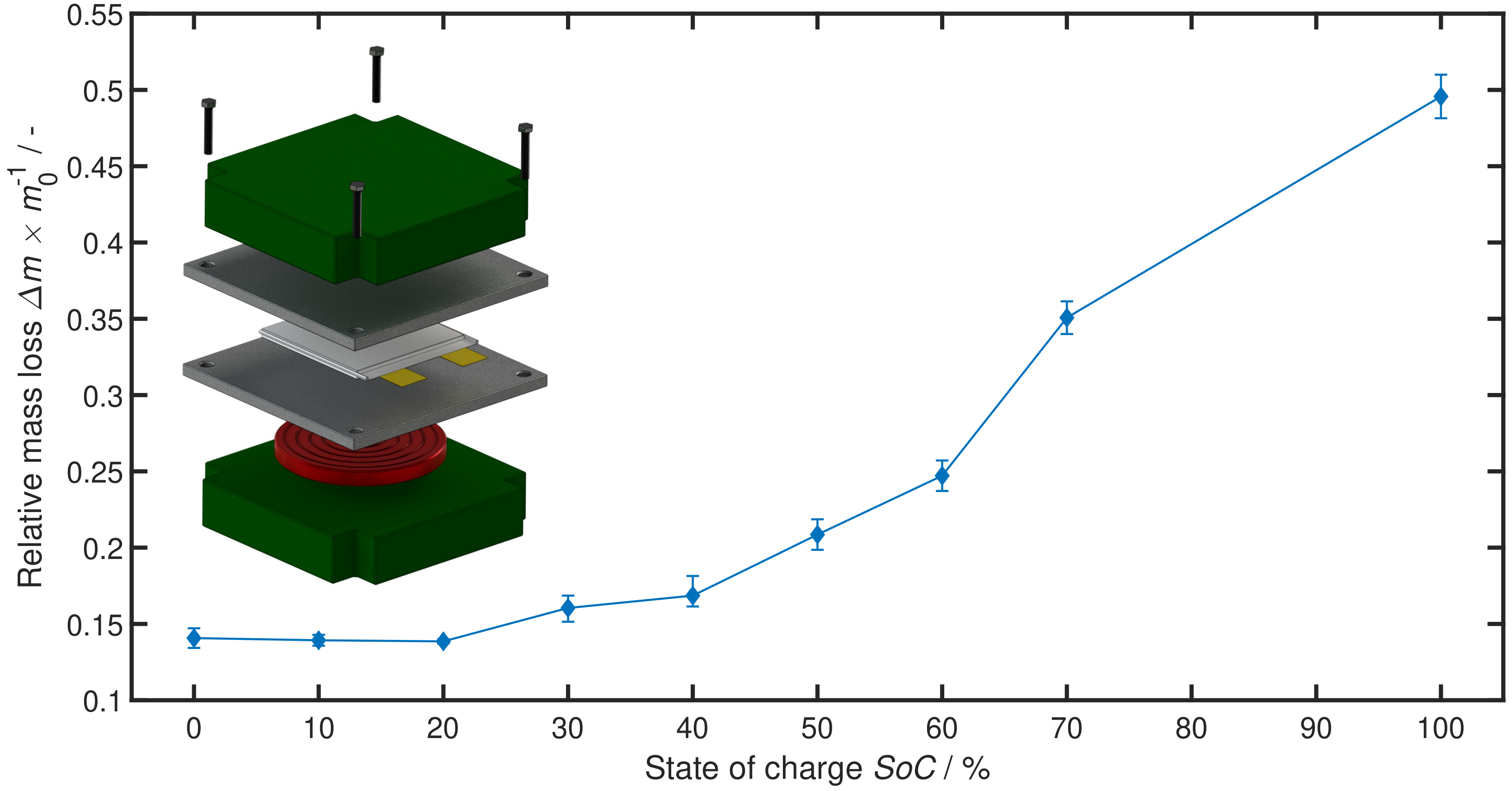

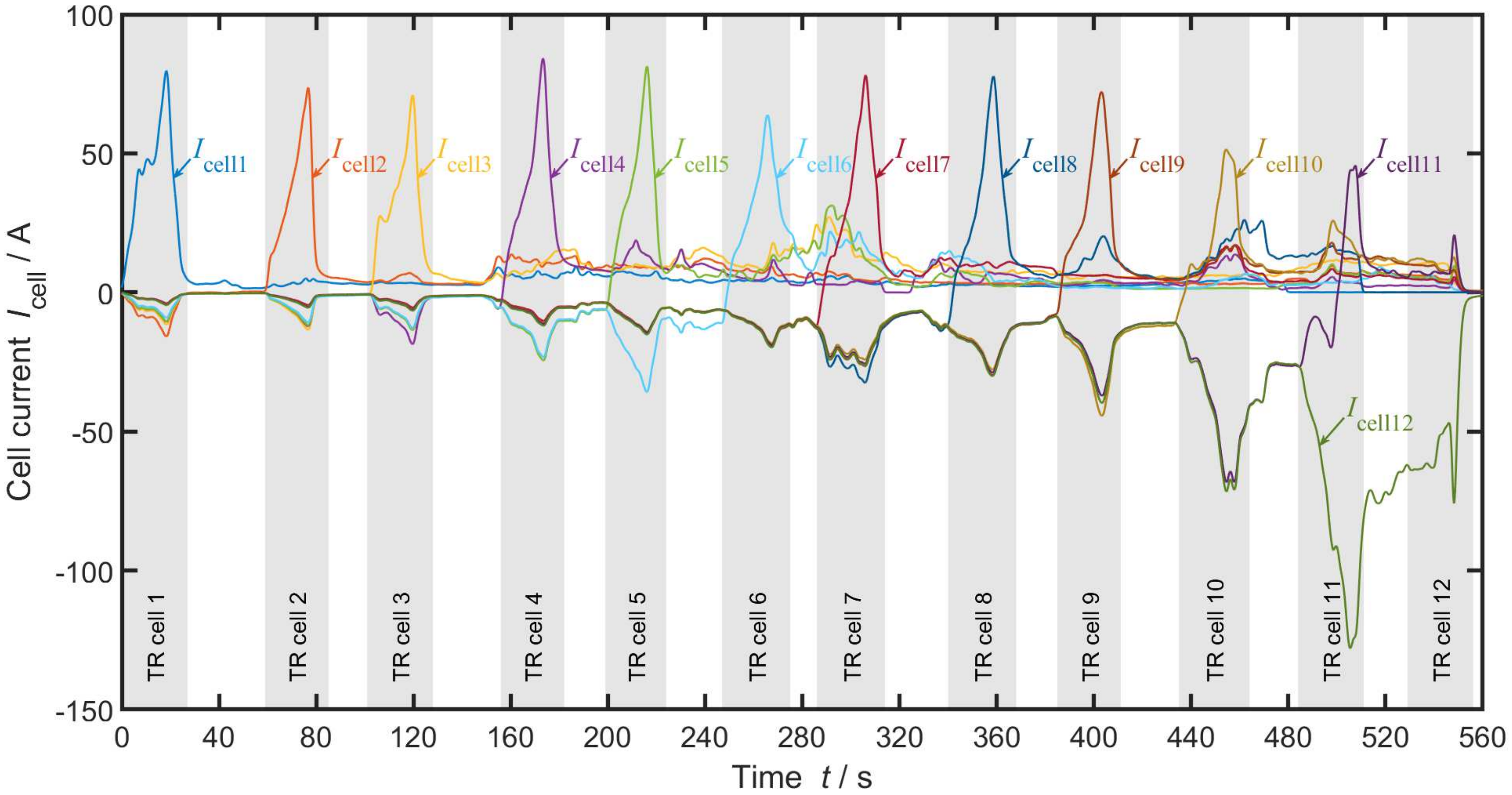
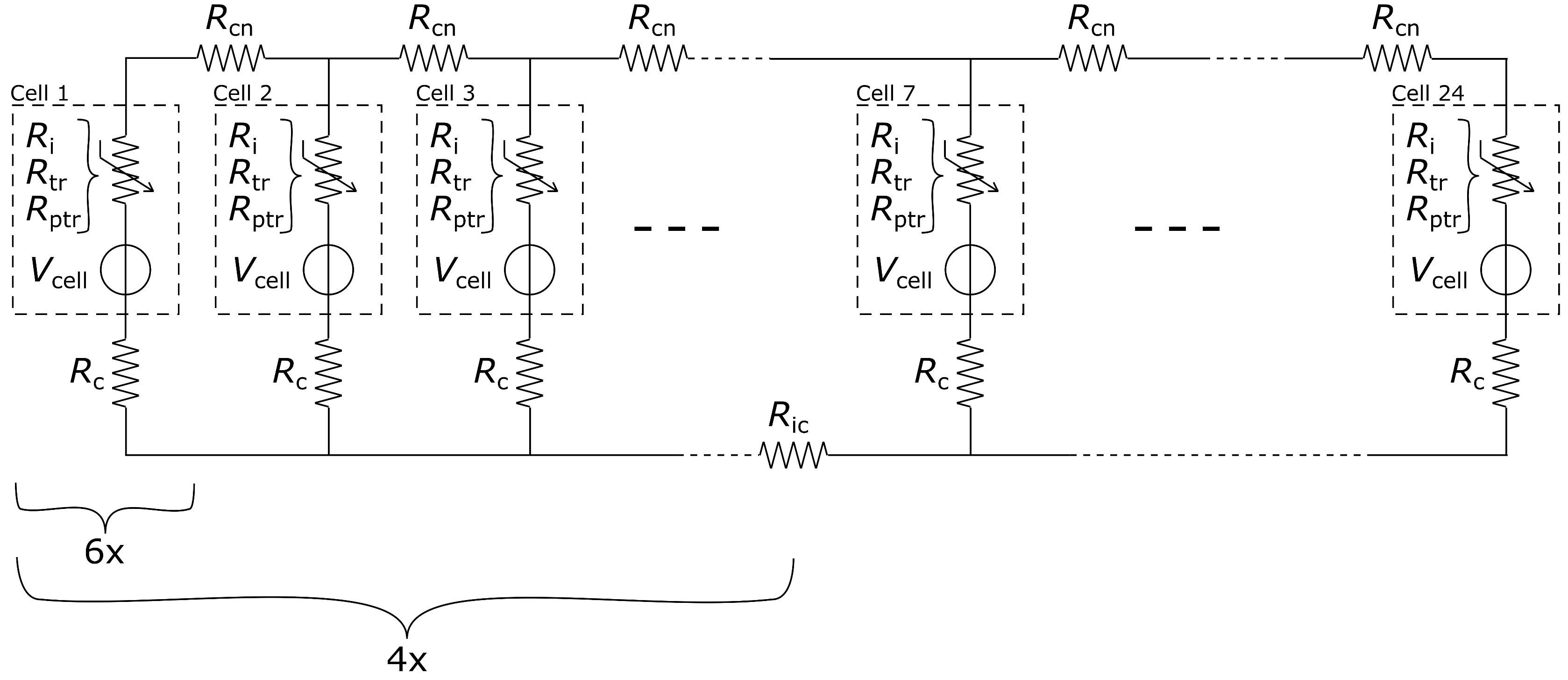
| Parameter | Symbol | Range or Value |
|---|---|---|
| cell voltage | 4.15 V | |
| cell internal resistance | 0.5 m | |
| parallel connection resistance | 15 | |
| cell resistance during TR | 1–300 m | |
| cell resistance after TR | 0.1–2 | |
| wire resistance | 0.5–3 m | |
| bridge resistance | 0.5–3 m |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koch, S.; Fill, A.; Kelesiadou, K.; Birke, K.P. Discharge by Short Circuit Currents of Parallel-Connected Lithium-Ion Cells in Thermal Propagation. Batteries 2019, 5, 18. https://doi.org/10.3390/batteries5010018
Koch S, Fill A, Kelesiadou K, Birke KP. Discharge by Short Circuit Currents of Parallel-Connected Lithium-Ion Cells in Thermal Propagation. Batteries. 2019; 5(1):18. https://doi.org/10.3390/batteries5010018
Chicago/Turabian StyleKoch, Sascha, Alexander Fill, Katerina Kelesiadou, and Kai Peter Birke. 2019. "Discharge by Short Circuit Currents of Parallel-Connected Lithium-Ion Cells in Thermal Propagation" Batteries 5, no. 1: 18. https://doi.org/10.3390/batteries5010018
APA StyleKoch, S., Fill, A., Kelesiadou, K., & Birke, K. P. (2019). Discharge by Short Circuit Currents of Parallel-Connected Lithium-Ion Cells in Thermal Propagation. Batteries, 5(1), 18. https://doi.org/10.3390/batteries5010018






