Coefficients of Thermal Expansion of Al- and Y-Substituted NaSICON Solid Solution Na_3+2xAl_xY_xZr_2−2xSi₂PO₁₂

Abstract

Because of an increasing interest in NaSICON materials as electrolyte materials in all-solid state sodium batteries, their thermal expansion was investigated in this study. The thermal expansion coefficient (CTE) of the Al and Y-substituted NaSICON compositions Na_3+2xAl_xY_xZr_2−2xSi₂PO₁₂ with 0 ≤ x ≤ 0.3 was obtained by dilatometry and compared to the CTE derived from the lattice parameters using high-temperature X-ray diffraction. The difference in CTE obtained from techniques, the influence of sodium content and central metal cation on CTE, as well as other observations such as phase changes are described and rationalized.

1. Introduction

The increasing interest in solid-state sodium batteries has made deeper understanding of the involved materials a necessary requirement. Due to a wide range of structural stability and excellent electrical performance, NaSICONs have the potential to be used as electrolytes in solid-state batteries [1,2,3,4,5]. However, for successful application in batteries, their mechanical properties and the thermal expansion behavior must also be studied in order to avoid thermal stresses and assure thermally stable cathode-electrolyte contact to avoid micro-cracking at the interface.

Thermal expansion is represented by its coefficient (CTE), and it can be obtained using different experimental techniques. High-temperature X-ray diffraction (HT-XRD) is the most reliable technique to measure the CTE at the crystallographic unit cell level where the lattice expansion is determined as a function of temperature. Typically, the lattice of NaSICON expands anisotropically [6,7,8]. As an example, the NaSICON material Na_3.4Sc₂(SiO₄)_0.4(PO₄)_2.6 shows nearly no expansion of the a lattice parameter (<0.1%), but a substantial expansion of the c lattice parameter of 2.15% between room temperature and 600 °C [9,10]. The resulting CTEs are 1.34 × 10⁻⁶ K⁻¹ and 37.3 × 10⁻⁶ K⁻¹, respectively, leading to a mean CTE of 13.3 × 10⁻⁶ K⁻¹. The anisotropy is a crucial material property, as it results in residual stresses during cooling after sintering and thus induces micro-cracks, reduces the electrical conductivity, and increases safety risks [8,11]. This is particularly true for materials with crystal anisotropy and depends also on the microstructure (e.g., grain orientation). In addition, the formation of micro-cracks also erases the results of CTE measurements by dilatometry. In this case, the dimensional change of samples is measured mechanically using a pressure-sensitive push-rod or optically with a laser system. The length change is recorded as a function of temperature from which the CTE can be determined. Since CTE determination from dilatometry uses the macroscopic dimensional change, it therefore also includes changes in microstructure [12].

A careful sample preparation combined with sensitive and well-calibrated measurements may result in accurate CTEs from dilatometry similar to HT-XRD even for polycrystalline materials. For example, the CTE of dense 8 mol % yttria-stabilized zirconia is 10.5 × 10⁻⁶ K⁻¹ and 9.7 × 10⁻⁶ K⁻¹ when measured with dilatometry [13] and HT-XRD [14], respectively. In NaSICON materials, often the CTEs from dilatometry are much smaller than the values obtained from HT-XRD, which results from the creation of cracks [11], particularly during the cooling step after sintering. These cracks become narrower and disappear during dilatometry measurements, because of volume expansion while heating. This often leads to CTE values smaller than the data derived from crystallographic measurements and, even worse, the sometimes negative slope of the dilatometry curves [15,16,17,18,19] triggered an intense research activity and led to the misinterpretation that NaSICON materials might be “zero-expansion” ceramics [15].

As shown in Figure 1, the CTE measurements on Na_1+xZr₂Si_xP_3−xO₁₂ only show an acceptable agreement between HT-XRD and dilatometry for x ≥ 1.5 [8]. Typically, a hysteresis in the cooling and heating curves of dilatometry indicates the influence of micro-cracks [17,20]. Only a careful sample preparation results in a crack-free material to achieve CTE values that are in good agreement with XRD data.

Recently, we have reported the crystallographic and electrical properties of the series Na_3+2xAl_xY_xZr_2−2x(SiO₄)₂(PO₄)₃ (hereafter: NAYZSiP_x) with 0 ≤ x ≤ 0.3 [21]. NAYZSiP_x has a monoclinic structure for 0 ≤ x < 0.2, and transforms into a rhombohedral R$\overline{3}$c phase when x ≥ 0.2. For x < 0.2, the monoclinic to rhombohedral transition occurs at temperatures between 100 and 200 °C, and their stoichiometries, crystal structure and lattice parameters are given in

Table 1. Composition and crystal structure of NAYZSiP_x compounds.

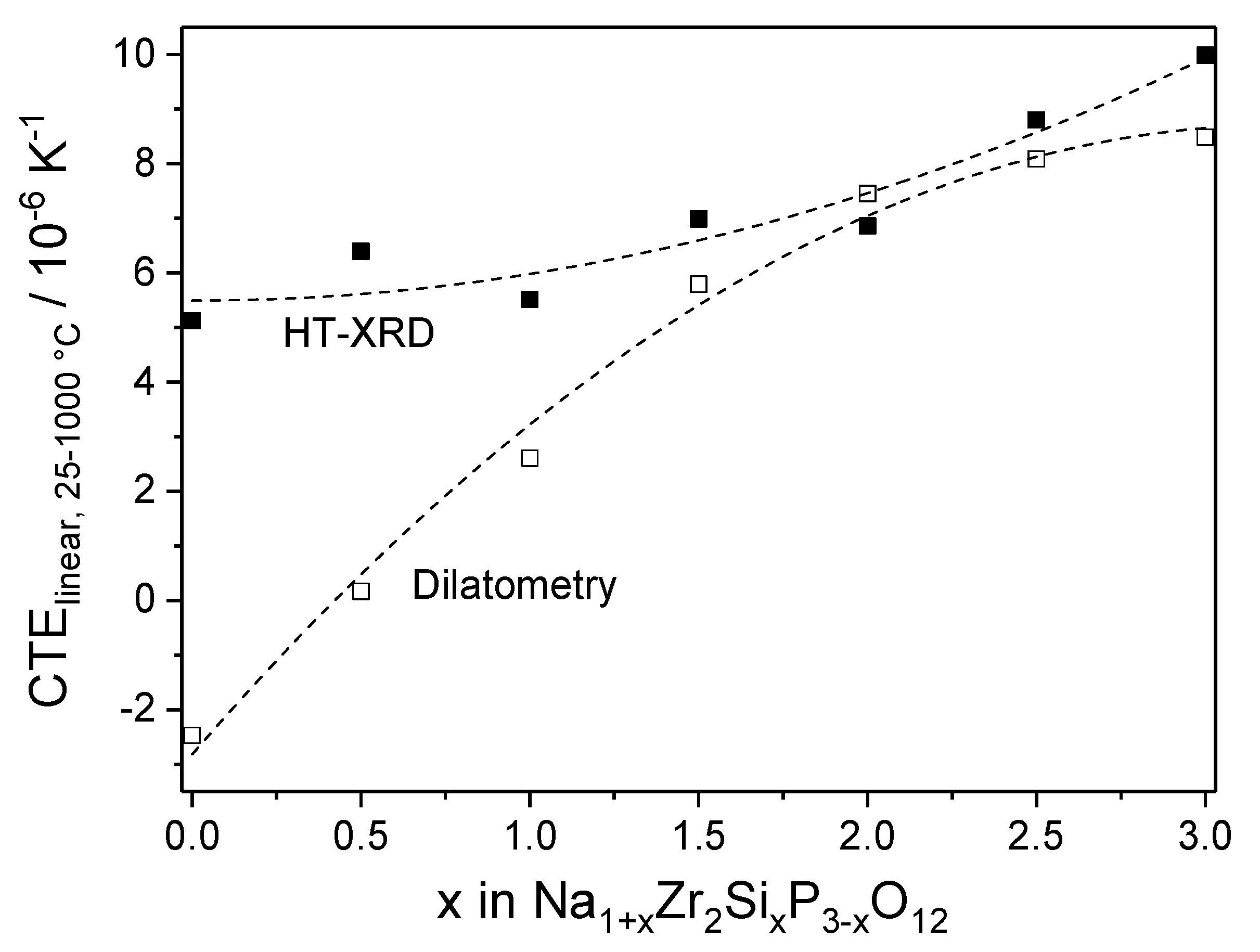
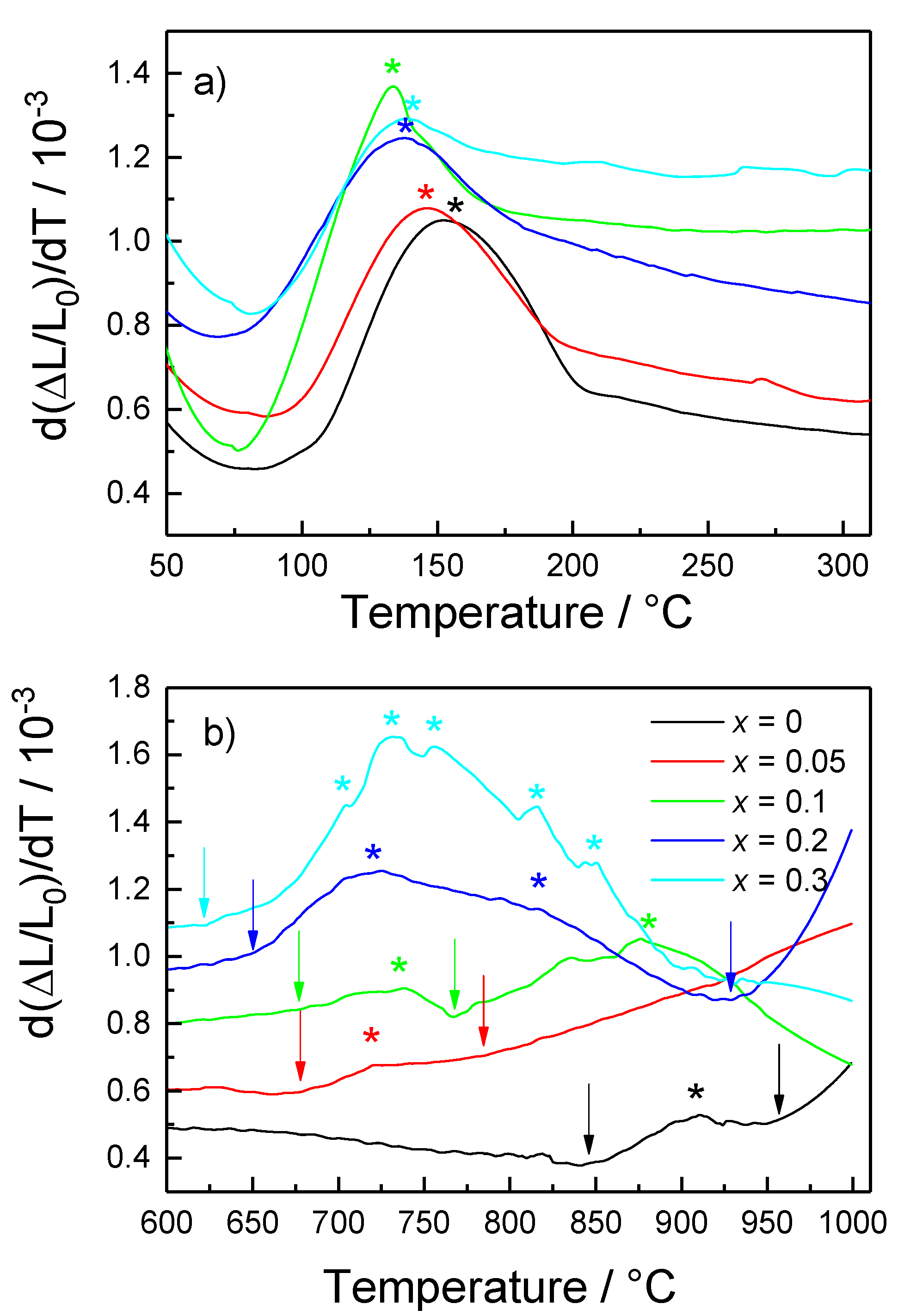
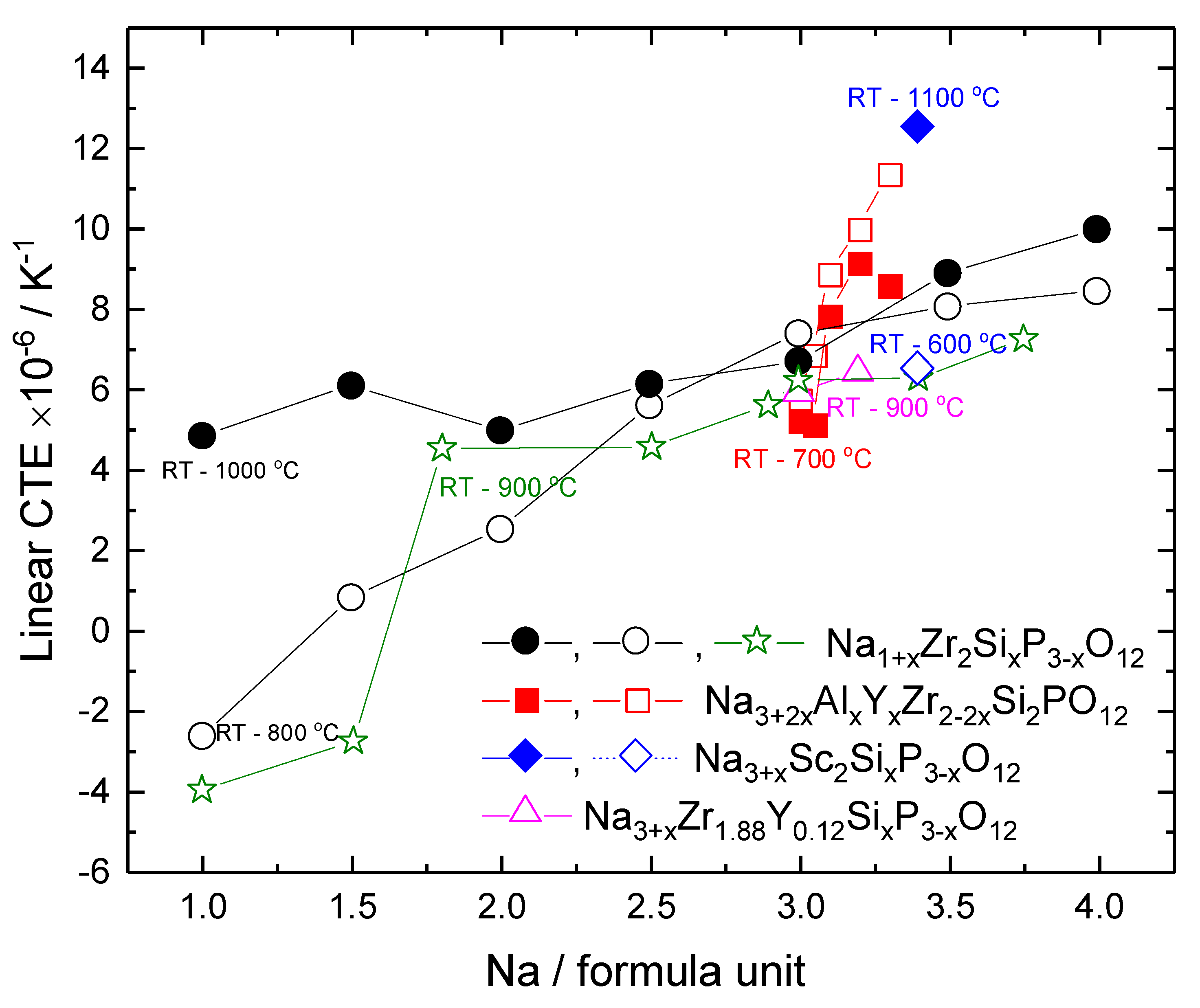
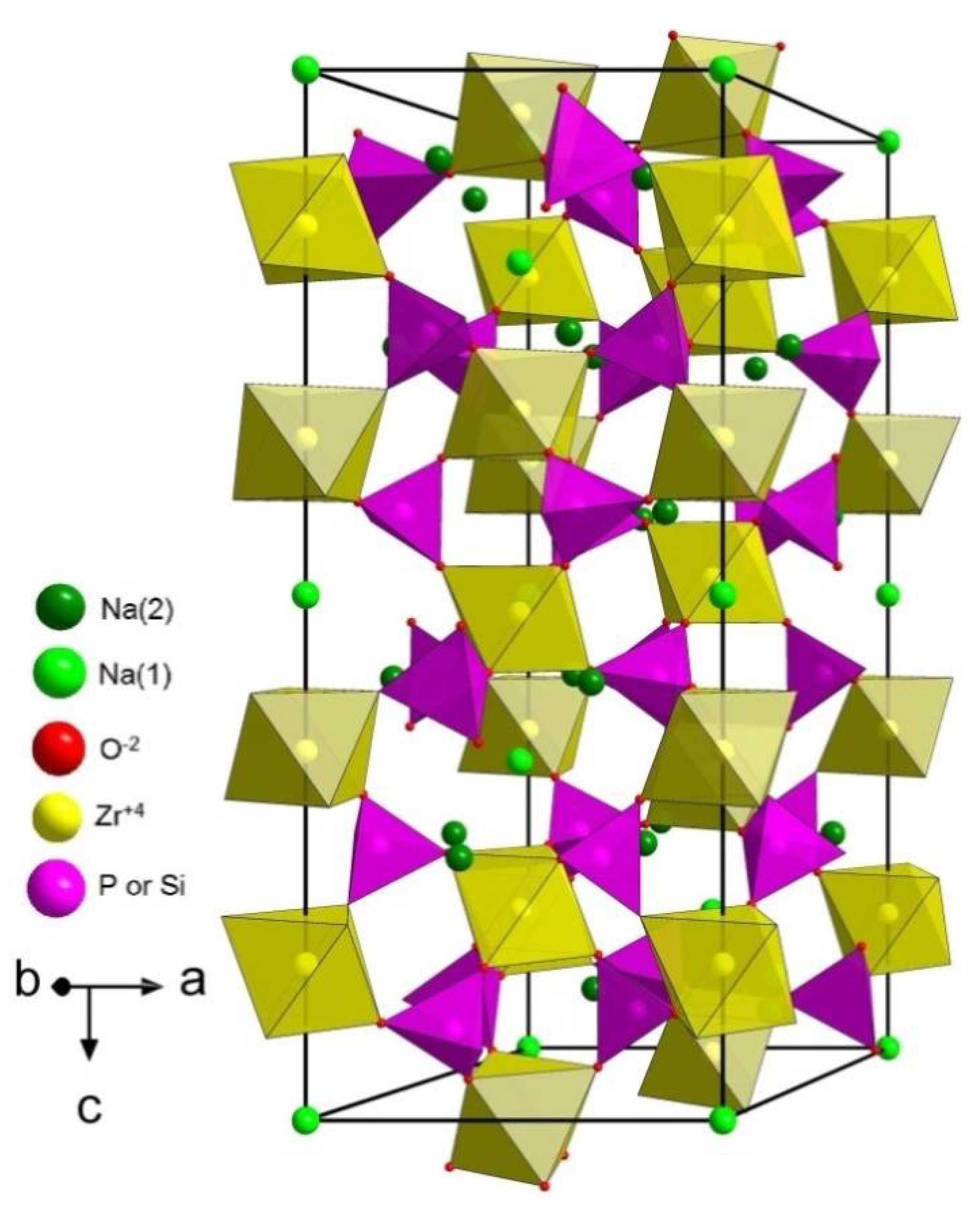
Material	Lattice Parameters and Space Groups
	25 °C	Space Group	700 °C	Space Group
NAYZSiP0	a: 15.637(1), b: 9.045(1), c: 9.225(1), β: 123.64(1)°	c2/c	a = b = 9.058(2), c: 23.173 (4)	R$\overline{3}$c
NAYZSiP0.05	a: 15.665(1) b: 9.058(1), c: 9.233(1), β: 123.79(1)°	c2/c	a = b = 9.070(1), c: 23.161(1)	R$\overline{3}$c
NAYZSiP0.1	a: 15.671(1) b: 9.065(1), c: 9.221(1), β: 123.95(1)°	c2/c	a = b = 9.090(9), c: 23.133(3)	R$\overline{3}$c
NAYZSiP0.2	a = b = 9.096(1), c: 22.741(2)	R$\overline{3}$c	a = b = 9.120(9), c: 23.034(6)	R$\overline{3}$c
NAYZSiP0.3	a = b = 9.110(3), c: 22.671(1)	R$\overline{3}$c	a = b = 9.139(6), c: 23.938(8)	R$\overline{3}$c

[21]. In this study, we further determined the CTEs by dilatometry and compared them with the CTEs obtained from HT-XRD reported earlier.

2. Experimental

All specimens were prepared from powder precursors by uniaxial pressing 150 MPa into a rectangular shape (40 × 5 × 3–5 mm) and subsequent sintering at 1000–1250 °C. The terminal faces were cut and polished to give samples 25 mm in length. The synthesis of the powders and more details on sample preparation and sintering conditions are given elsewhere [21]. Sintered samples with density in the range of 85–93% were used to measure the length changes as a function of temperature to determine the CTE. In a temperature range ΔT, a sample with a reference length L₀ has a length change ΔL, and its CTE is calculated according to:

$$CTE=\frac{\mathrm{\Delta }L}{\mathrm{\Delta }T L_0}$$

(1)

The dilatometry experiments were carried out with a push-rod dilatometer 402C from Netzsch, Germany, calibrated with a sapphire single crystal. Temperature was calibrated using an interpolation routine with five standard metals after determination of their melting points. Each sample was heated with 180 K/h to 1000 °C, and then the temperature was kept constant for 0.5 h to control the dimensional stability of the specimens. Finally, the samples were cooled with −180 K/h to 30 °C.

For comparison with HT-XRD results, the crystallographic unit cell parameters (i.e., volume, V) can be related to the linear CTE:

$$\frac{\mathrm{\Delta }L}{\mathrm{\Delta }T{L}_0} = \frac{1}{3}\frac{\mathrm{\Delta }V}{\mathrm{\Delta }T V_0}$$

(2)

Hence, the CTE calculations using Equations (1) and (2) assume that the macroscopic body behaves like a single crystal. Using the hexagonal lattice parameters of the rhombohedral structure of investigated NaSICON materials, the linear CTE can be expressed as

$$\frac{\mathrm{\Delta }L}{\mathrm{\Delta }T L_0} = \frac{1}{3 \mathrm{\Delta }T}\left(2\frac{\mathrm{\Delta }a}{a_0}+\frac{\mathrm{\Delta }c}{c_0}\right)$$

(3)

3. Results and Discussions

The dilatometry measurements of the series NAYZSiP_x during heating is shown in Figure 2. The dilatometry curves indicate a small change in slope between 120 and 160 °C, which corresponds to a monoclinic to rhombohedral phase transition [21,22]. The transition temperature decreases with increasing the substitution content until x = 0.2. As shown in Figure 3a, the transition temperatures can be easily obtained from the first derivative of the dilatometry curves, better showing the slope changes. Additional slope changes at higher temperatures are also visible in Figure 2. The straight dashed lines indicate the deviation from a linear thermal expansion and show, on the one hand, that the additional expansion increases with increasing x, and, on the other hand, that the onset temperature of the additional expansion decreases with increasing x. The slope changes at high temperatures are summarized in Figure 3b and consist of two contributions which both tend to decrease in temperature with increasing x. The onset temperatures and maxima of slope changes are listed in

Table 2. Onset temperatures and maxima of slope changes deduced from Figure 3a,b. The values of the high-temperature processes have an error of about ± 20 °C.

x	Tmon-rhom/°C	Tonset1/°C	Tmax1/°C	Tonset2/°C	Tmax2/°C
0	152	850	910	955	>1000
0.05	146	675	720	780	>1000
0.1	138	670	735	770	880
0.2	136	650	720	935	815
0.3	138	625	740	-	830

. In addition, in this temperature region, secondary phase formation is observed by HT-XRD measurements.

Therefore this change in slope at high temperatures could be due to secondary phase segregation processes, and, especially for the samples with x ≥ 0.1, the formation of new phases as observed in HT-XRD measurements. Starting at about 700 °C, the substituting cations Al³⁺ and Y³⁺ leave the NaSICON structure, form ternary compounds like Y₄Al₂O₉ and AlPO₄ (as observed from HT-XRD [21]) and consequently reduce the unit cell volume of NaSICON. It is, therefore, interesting to note that the substituting elements show a low solubility in the NaSICON structure at 1000 °C and below, whereas they are widely incorporated in the host lattice at sintering temperatures of 1150–1200 °C. The leaching of Al³⁺ and Y³⁺ at 1000 °C can be monitored during the short dwell time of 0.5 h during the dilatometer measurements. In this period, the samples elongate very systematically with an individual constant rate which is proportional to the substitution level. After 0.5 h, they have accumulated a length increase by (0.126 ± 0.008)x (in %). Therefore, the dilatometer measurements are composed of two contributions: (a) a static contribution from the existing phases at room temperature, i.e., NaSICON and small amounts of monoclinic ZrO₂ and AlPO₄ [21], determining the linear steady increase with increasing temperature (dotted lines in Figure 2), and (b) a dynamic contribution resulting from the changing phase contents above 700 °C and determining the deviation from the constant expansion rate.

The existence of small amounts of secondary phases (ZrO₂ and AlPO₄) is the reason why the CTE obtained from dilatometry curves is higher than the values derived from HT-XRD (Table 2) due to the larger thermal expansion of both compounds. Assuming the rule of mixtures, the CTEs of the pure materials between room temperature and 700 °C, i.e., 8.65 × 10⁻⁶ K⁻¹ for monoclinic ZrO₂ [23] and 36 × 10⁻⁶ K⁻¹ for AlPO₄ [24], as well as the corresponding amounts derived from the XRD measurements, the CTE of the phase mixture can be calculated according to

$$CT{E}_{composite} = {\displaystyle \sum }_{i}CT{E}_i v_i$$

(4)

in which v_i is the volume fraction of phase i. The used parameters and resulting CTEs are also listed in

Table 3. CTEs between room temperature and 700 °C of NAYZSiP_x and the used volume fractions of AlPO₄ and ZrO₂ for calculating the CTE according to Equation (4).

x	CTEHT-XRD/K−1 10−6	CTEdil./K−1 10−6	CTEcalc./K−1 10−6	${\mathit{v}}_{\mathit{A}\mathit{l}\mathit{P}{\mathit{O}}_4}$/%	${\mathit{v}}_{\mathit{Z}\mathit{r}{\mathit{O}}_2}$/%
0	5.22	5.72	5.69	1.4	1.1
0.05	5.11	6.84	6.83	5.3	2.2
0.1	7.81	8.85	8.83	3.3	3.4
0.2	9.13	9.97	9.99	3.2	2.8
0.3	8.57	11.34	11.33	10.0	5.6

and show that especially small amounts of AlPO₄ may have a significant impact on the thermal expansion of a polycrystalline NaSICON material. Therefore, the small impurities easily explain the larger CTEs obtained from dilatometry although the opposite trend might be expected.

Apart from the shift in length during the dwell time, the cooling curves do not show any unusual phenomena like hysteresis, abrupt length changes, or smooth minima which were frequently observed in former investigations [8,15,16,17,18].

In the case of NaSICON materials, often the CTEs obtained from dilatometry are much smaller than the ones from HT-XRD. This is because the particles expand anisotropically, leading to creation of cracks during cooling after sintering originating from large grain sizes [8,11]. Subsequently, during the dilatometry measurements, these cracks are reversibly filled up by the surrounding expanding material, and consequently, the detected length changes of the sample are smaller than a crack-free material. However, a careful sample preparation can result in similar CTE values obtained from dilatometry and HT-XRD. As shown in this study, the difference is in the range of only 0.5–2.5 × 10⁻⁶ K⁻¹ (Table 2).

In Figure 4, the CTEs of the NAYZSiP_x system are compared to those of Na_3+xSc₂Si_xP_3−xO₁₂ [10], Na_1+xZr₂Si_xP_3−xO₁₂ [8,19], and Na_3+xY_0.12Zr_1.88Si_xP_3−xO₁₂ [25]. Among these materials, a general observation is evident: materials containing only Zr⁴⁺ as transition metal in the polyanionic lattice show a much smoother slope with increasing sodium content than those materials with mixture of tetra- and trivalent cations (Sc³⁺, Al³⁺, and Y³⁺) or materials containing only trivalent cations. Obviously, the two different bond strengths, i.e., Zr⁴⁺-O²⁻ and M³⁺-O²⁻ given in

Table 4. Bond dissociation energies at 298 K of Zr⁴⁺-O and M³⁺-O taken from [26].

A-B	D°/kJ mol−1
Zr-O	766.1 ± 10.6
Al-O	501.9 ± 10.6
Y-O	714.1 ± 10.2
Sc-O	671.4 ± 1.0

(with M = Sc, Y, Al), cause a different dependence of the thermal expansion and vibrational amplitudes on the composition of the NaSICON materials.

On the one hand, the CTEs of NaSICON materials increase with Na content per formula unit when Zr⁴⁺ is used as transition metal cation in the polyanionic lattice. This is because at higher temperature, sodium ions become highly mobile, induce increased repulsive forces, and therefore increase the vibrational magnitude within the lattice. On the other hand, the substitution with trivalent transition metal cations (e.g., Al³⁺, Sc³⁺, Y³⁺) also influences the CTE of the NaSICON material. Since the trivalent cations are replacing Zr⁴⁺ in the crystal lattice (Figure 5), the octahedra become larger due to less charge polarization of oxygen atoms, or in other words, reduced bond strength between trivalent cation and oxygen in the octahedra. This is validated by the calculations of the volume of ZrO₆ [27] and ScO₆ [28] octahedra, i.e., 11.69 ų and 13.49 ų, respectively. As a consequence of enlarged octahedra with central trivalent cations, the lattice vibrations become more pronounced, especially at elevated temperatures. This explains why the CTE of NAYZSiP_x and other NaSICON compounds substituted with trivalent cations are increasing much more in dependence of x than NaSICON materials with tetravalent cations (Figure 4).

4. Conclusions

The coefficients of thermal expansion coefficient (CTE) of the NaSICON series NAYZSiP_x were measured by dilatometry. The CTE values were similar to those obtained by HT-XRD. The prerequisite for accurate dilatometry measurements is a careful sample preparation for achieving crack-free specimens. The CTEs of NaSICON materials increase with Na content per formula unit when Zr⁴⁺ is used as transition metal cation in the polyanionic lattice. This is because sodium influences the charge polarization and therefore induces stronger lattice vibrations due to increased repulsive forces within the lattice. In addition, the substitution of trivalent transition metal cations influences the CTE because they have weaker attractive forces towards oxygen atoms of the octahedra as compared to tetravalent cations, which also leads to higher lattice vibrations.