Abstract
Conventional grid-forming (GFM) inverter control strategies often rely on fixed parameters and overlook the dynamic variation in energy stored in the DC link capacitor. This limitation can degrade transient performance and stability, particularly under power fluctuations and grid disturbances in renewable energy systems. To address this issue, this paper proposes an adaptive GFM control method that integrates real-time estimation of the DC link capacitor energy into the control loop. A Kalman filter-based observer is designed to estimate the capacitor energy state accurately and robustly using only local voltage and current measurements. The estimated energy deviation is then used to dynamically adjust key control parameters, including the virtual inertia and droop coefficients in the virtual synchronous generator (VSG) framework. These adaptive adjustments enhance the inverter’s damping and inertial behavior according to the internal energy buffer, improving performance under variable operating conditions. Simulation results in MATLAB/Simulink R2023b demonstrate that the proposed method significantly reduces power and voltage overshoots, shortens settling time, and improves DC link voltage regulation compared to conventional fixed-parameter control.
1. Introduction
In recent decades, the rapid proliferation of renewable energy sources (RESs)—notably photovoltaic (PV) generation and battery energy storage systems (BESS)—has accelerated the transition toward converter-dominated grids. While this shift offers sustainability and flexibility benefits, it simultaneously reduces synchronous inertia and complicates frequency and voltage regulation, particularly in weak grid and islanded microgrids [1,2,3,4,5]. In parallel, updated interconnection and ride-through requirements (e.g., at distribution and transmission levels) increasingly expect inverter-based resources to contribute to stability support rather than merely follow the grid, further motivating advanced control strategies for converter-interfaced generation [6,7,8].
Within this context, grid-forming (GFM) control has emerged as a cornerstone for establishing and regulating local voltage/frequency and enabling robust power sharing using only local measurements. Representative approaches include power-synchronization control (PSC), virtual synchronous machine/virtual synchronous generator (VSM/VSG) control, and oscillator-based methods such as virtual oscillator control (VOC) and its complex/dispatchable variants; recent surveys and benchmarks have clarified their relationships, implementation choices, and stability trade-offs [9,10,11,12,13,14,15]. Compared with phase-locked loop-based grid-following (GFL) controls that can be sensitive to short-circuit ratio (SCR), reactive set-points, and bandwidth choices, GFM schemes target intrinsic stability across a wider operating envelope [16,17,18].
Practical deployment, however, demands more than nominal regulation. Field-relevant capabilities—current limiting under faults/overloads, fault ride-through (FRT), unbalanced and sequence-domain operation, black start and resynchronization—must be coordinated with the outer regulation loops to avoid adverse interactions and loss of stability margins. A growing body of work documents protection-aware limiter designs, multi-phase operation, and restoration procedures, including experimental and hardware-in-the-loop demonstrations [19,20,21,22,23,24]. These results underscore that GFM controllers must remain effective not only near nominal conditions but also during severe network events and device constraints.
Another active line of research revisits parameter selection for droop- and VSG-type GFM controllers. Traditionally, virtual inertia, active-power damping, and reactive droop gains are fixed around nominal or worst-case assumptions; yet under intermittent generation, fluctuating demand, and weak grid conditions, such fixed parameters become suboptimal, causing inadequate damping, excessive overshoot, or sluggish response [25,26]. To address this, adaptive strategies have been proposed—ranging from inertia/droop scheduling driven by frequency or voltage deviations to feed-forward decoupling and optimization-guided gain updates—demonstrating improved transient performance and power sharing across varying conditions while preserving compatibility with inner loops and protection layers [27,28,29,30].
Despite these advances, many adaptive GFM implementations primarily rely on external grid-side signals to drive parameter changes while paying comparatively less attention to the converter’s internal energy buffer—the DC link. In practical PV–BESS architectures, the DC link couples the source with the AC output and acts as a finite energy reservoir whose availability and dynamics constrain admissible transients, especially under weak grids, current limits, or rapid PV/BESS power swings. Recent studies quantify how much “virtual inertia” can be effectively extracted from the DC link capacitor at the voltage-control timescale and how DC-side dynamics influence AC-side stability, unbalanced performance, and interactions with protection layers [31,32,33,34,35]. Building on these insights, several works advocate energy-aware GFM designs that sense or estimate the DC-side energy and shape outer-loop behavior accordingly, yielding improved damping when internal energy is abundant and conservative actuation when energy is scarce [36,37,38,39,40,41].
The main contributions of this paper can be summarized as follows:
- Real-Time DC link Energy State Observation: A Kalman filter-based estimator is developed to accurately reconstruct the capacitor’s internal energy state from noisy DC-side measurements, providing a reliable internal energy status for real-time control.
- Adaptive VSG Control Framework: A systematic adaptive strategy is proposed to dynamically tune virtual inertia and droop parameters based on the real-time capacitor energy deviation, significantly enhancing system transient stability and dynamic responsiveness.
- Enhanced System Resilience and Performance: Comprehensive simulation studies under various operating conditions validate the effectiveness of the proposed method, showing substantial improvements in frequency stability, voltage regulation, current quality, and transient response when compared to conventional fixed-parameter control methods.
The remainder of this paper is structured as follows. Section 2 presents the system configuration and basic control strategy of the system. Section 3 details the proposed adaptive control approach, including capacitor energy state estimation and parameter adaptation mechanisms. Simulation results and performance analyses are discussed in Section 4. Finally, Section 5 provides concluding remarks.
2. System Description and Basic Control
This section introduces the overall PV–BES grid-forming inverter system used throughout the paper. We summarize the hardware architecture, define the main signals and parameters, and outline the baseline control structure that serves as a reference for later comparisons. The goal is to establish consistent notation and assumptions before detailing each subsystem and its control loops. The following subsection describes the physical configuration of the PV unit, the battery energy storage interface, and their connection to the shared DC link and the grid-forming inverter. It also clarifies the role of passive components and measurement points that will be referenced by the control diagrams and simulations.
2.1. PV-BES System Description
Figure 1 illustrates the architecture of the PV-BES GFM system. It consists of three subsystems: the PV unit, the BES unit, and the GFM inverter. The PV subsystem includes a PV panel and a DC-DC converter. The PV array generates a voltage vpv and current ipv, which are filtered by the capacitor Cpv. The PV panel connects to the shared DC bus through the DC link capacitor Cdc. The BES subsystem provides active power balancing and dynamic support to the DC link. It consists of a battery stack providing the voltage vbat and current ibat, via a bidirectional DC-DC converter. The bidirectional converter allows the battery to either charge or discharge, depending on the control command and system operating conditions, enabling energy exchange with the DC link to stabilize voltage vdc.
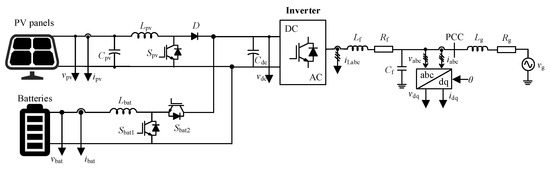
Figure 1.
Configuration of the PV-BES system.
The inverter interfaces the DC link with the AC grid and operates under a GFM control scheme. It converts the DC voltage into three-phase AC currents iLabc, which are injected into an LC filter comprising an inductance Lf and a capacitor Cf. The voltage at the point of common coupling (PCC), denoted as vabc, along with the output current iabc, is measured and transformed into the synchronous rotating reference frame using a phase-locked loop (PLL). This yields the voltage and current components vdq and idq, respectively, which are subsequently used for implementing dq-axis control strategies. Furthermore, vg denotes the utility grid voltage, while the inductance Lg and resistance Rg represent the grid-side impedance. The DC link capacitor Cdc serves as an energy buffer between the PV/BES front ends and the inverter.
2.2. Basic Control of the PV-BES GFM System
As shown in Figure 2a, the PV subsystem utilizes a maximum power point tracking (MPPT) algorithm to ensure efficient energy harvesting. Among various MPPT techniques, the perturb and observe (P&O) method remains popular due to its straightforward implementation. This method determines the PV voltage reference , which is regulated by a proportional–integral (PI) controller. The resulting control signal is applied to a pulse-width modulation (PWM) module to generate the switching duty ratio for the boost converter.

Figure 2.
PV and BES systems control block diagram: (a) MPPT control and (b) BES dual-loop control (PI: proportional–integral controller; PWM: pulse-width modulation).
In the BES system, the control structure comprising an outer voltage loop and an inner current loop is adopted, as depicted in Figure 2b. The voltage loop ensures tracking of the DC link voltage reference and provides the reference current, which is then regulated by the inner control loop. This configuration enables stable energy exchange at the DC bus.
The GFM inverter is regulated by a virtual synchronous generator (VSG) control strategy, enabling it to mimic the dynamic behavior of a synchronous machine and provide inertia and damping support to the system. As presented in Figure 3, the VSG controller is composed of two parts: the active power control (APC) loop and the reactive power control (RPC) loop, which can be described as follows:
where Pref and Pe denote the reference and the output active power, while ωn and Dp correspond to the nominal angular frequency and active damping factor, respectively. Similarly, Qref, Qe, Dq, K, Vn, and Vo represent the reactive power reference, output reactive power, reactive droop coefficient, virtual inertia associated with reactive dynamics, nominal voltage, and measured PCC voltage, respectively.

Figure 3.
Virtual synchronous generator control block diagram: (a) active power control and (b) reactive power control.
3. Proposed Control Strategy
This section presents the energy-aware adaptive control framework that augments the baseline VSG scheme. We develop a Kalman filter-based observer to estimate the DC link capacitor energy in real time, then use this estimate to schedule the virtual inertia and droop coefficients within bounded ranges.
3.1. Capacitor Energy State Estimation
In conventional GFM inverter control schemes, the DC link capacitor is often assumed to maintain a constant voltage, and its energy dynamics are typically overlooked. However, under transient disturbances such as power imbalance or load variation, the stored energy in the DC capacitor can fluctuate significantly, thereby affecting the system’s frequency and voltage stability. To address this limitation, this work introduces a capacitor energy-aware control strategy based on real-time estimation of the DC link energy state.
The DC link capacitor energy at any time t can be expressed as follows:
where Cdc is the capacitance value and vdc(t) is the instantaneous DC link voltage. The energy deviation from its nominal value is defined as follows:
To improve the accuracy and robustness of the energy estimation, a Kalman filter-based observer is developed. This estimator utilizes the measured DC link voltage and current to reconstruct the real-time energy state while mitigating the impact of sensor noise and modeling uncertainties. The discrete-time state-space model of the capacitor energy is derived from the power balance across the DC link:
where Ts is the sampling period, and idc, vdc,k are the measured current and voltage at the kth sampling instant. The measurement equation is expressed as follows:
with zk denoting the noisy observation and vk representing the measurement noise. The Kalman filter is implemented using the standard recursive prediction and update steps, which includes prediction and update procedure:
Here, is the updated energy estimate, and Kk is the Kalman gain calculated based on the prediction error covariance and measurement noise covariance.
As shown in Figure 4, this real-time energy estimate is used as a feedback signal in the adaptive control layer to dynamically modify the inverter’s virtual inertia and droop coefficients. By incorporating capacitor energy variation into the control law, the proposed strategy improves the system’s ability to maintain frequency and voltage stability during dynamic events, such as load changes or renewable generation fluctuations.
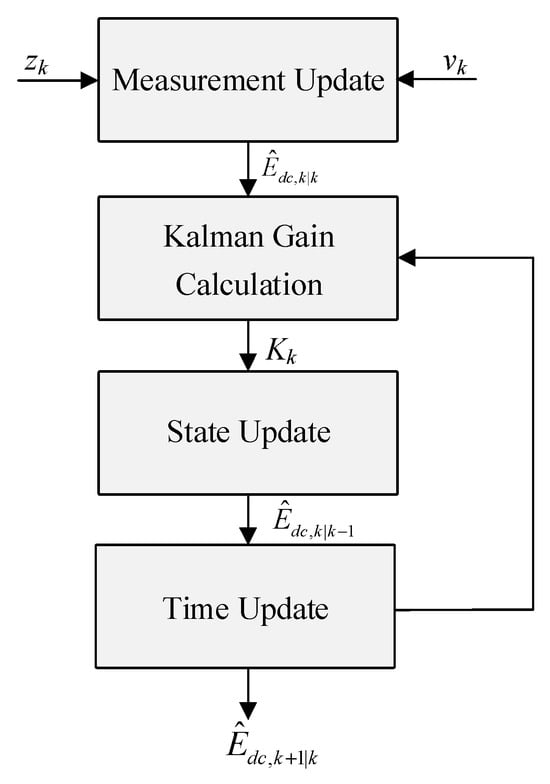
Figure 4.
Block diagram of the Kalman filter-based capacitor energy state observer.
3.2. Proposed Adaptive Grid-Forming Control Strategy
Based on the real-time estimation of the DC link capacitor energy state described in Section 3.1, this section presents the proposed adaptive GFM control strategy. The central idea is to exploit the observed energy deviation ΔEdc(t) as a dynamic indicator of the system internal power balance and use it to modulate key control parameters in the virtual synchronous generator (VSG) framework, thereby enhancing the inverter adaptability and grid-supporting capabilities under varying operating conditions.
The VSG control emulates the inertial and damping behavior of a conventional synchronous machine by using the swing equation to generate the reference angle for voltage synthesis. Conventionally, the virtual inertia J and damping coefficients Dp, Dq are fixed, which may result in suboptimal performance during large disturbances or capacitor energy depletion. To overcome this limitation, we introduce an adaptive mechanism that continuously adjusts these parameters as follows.
The virtual moment of inertia is dynamically modified based on the estimated energy deviation, which is shown as follows:
where J0 is the nominal virtual inertia and kj is the adaptive gain. When the capacitor energy increases, higher inertia is emulated to enhance frequency support; when energy is low, the inertia is reduced to preserve system stability and avoid overreaction. The active power–frequency relationship is enhanced by adjusting the damping coefficient:
Here, ωn is the nominal frequency, Dp0 is the base droop gain, and kp governs the strength of the adaptation. This adjustment enables better frequency regulation under high capacitor energy while preventing excessive response when energy is scarce.
Similarly, the voltage–reactive power droop behavior is tuned using the estimated energy state, which can be expressed as follows:
In this expression, Vn is the nominal voltage, and Dq, kq denote the static and adaptive reactive power droop gains, respectively. By adapting these coefficients, the inverter improves voltage support under dynamic load changes without compromising capacitor stability.
Figure 5 summarizes the proposed adaptive GFM control architecture. The Kalman filter-based observer monitors the energy state of the DC link capacitor in real time. The resulting ΔEdc(t) is then fed into the parameter adjustment module, which dynamically tunes the VSG parameters. This control framework allows the inverter to flexibly adjust virtual dynamics in accordance with its internal energy availability, enhancing both transient and steady-state performance. This proposed strategy effectively couples the physical energy constraints of the DC-side with the inverter AC-side dynamics, establishing a cyber-physical feedback loop.
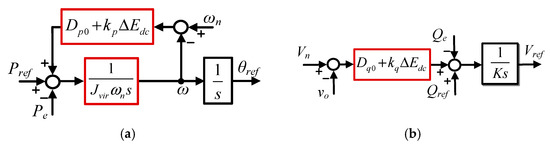
Figure 5.
The VSG power control loop: (a) the active power control loop, and (b) the reactive power control loop.
3.3. Adaptive Parameter Adjustement
Building on the estimated capacitor energy state obtained from the Kalman filter observer, this section presents the mechanism for adaptively adjusting the key control parameters in the VSG control framework. The aim is to enhance the system flexibility and dynamic performance by modulating virtual inertia and droop coefficients in real-time in response to internal energy variations.
In conventional GFM control, parameters such as virtual inertia J, active power droop coefficient Dp, and reactive power droop coefficient Dq are statically tuned based on worst-case scenarios or nominal conditions. However, these parameters directly affect the transient response and stability margin of the inverter. Under significant power fluctuations or during transitions in the photovoltaic or battery output, static control parameters may no longer yield optimal performance.
Therefore, adaptively tuning these parameters according to the energy stored in the DC link capacitor enables more responsive and robust control, especially under weak grid conditions or high renewable penetration scenarios. The saturation limits can be imposed on adaptive parameters to prevent excessive parameter drift:
The overall adaptive adjustment process is summarized as follows:
1. Real-time energy estimation
The DC link capacitor energy is continuously estimated using the Kalman filter-based observer, which utilizes measurements of the DC voltage vdc and current idc. The estimator compensates for measurement noise and model uncertainty, ensuring reliable energy state information.
2. Deviation computation
The estimated energy is compared with a predefined nominal reference to calculate the deviation:
This deviation serves as the key indicator of the system’s energy surplus or deficiency, directly influencing the control strategy.
3. Parameter adaptation
Based on , the virtual inertia , and the droop coefficients , , are adaptively adjusted according to the predefined linear laws:
These relationships ensure that more stored energy leads to stronger inertia and damping effects, improving transient stability and power-sharing performance, while lower energy leads to a conservative control response to preserve system integrity.
4. Control law update
The newly computed adaptive parameters are fed into the virtual synchronous generator (VSG) control framework. Specifically, they affect the swing equation and voltage-reactive power dynamics.
This real-time update ensures that the inverter continuously adapts its response to grid and load fluctuations based on internal energy availability.
This adaptive mechanism enables the GFM inverter to operate with energy-aware intelligence, maintaining optimal damping and inertial behavior across diverse grid and load conditions. Compared to traditional fixed-parameter designs, the proposed method improves both dynamic performance and robustness, particularly in weak grid scenarios or systems with fluctuating PV/BES power.
3.4. Practical Smoothing and Bounded Adaptation of Parameters
To avoid aggressive or discontinuous updates of the adaptive parameters and to ensure robust behavior in highly dynamic conditions, the proposed controller employs lightweight smoothing and bounding mechanisms on top of the existing energy-driven laws for J, Dp, and Dq introduced in Section 3.2 and Section 3.3. The goal is to suppress high-frequency noise and prevent excessive parameter excursions while preserving responsiveness to genuine disturbances.
1. Low-pass smoothing and rate limiting:
The raw scheduled value is first passed through a first-order low-pass filter with time constant , and then rate-limited to cap the maximum per-period change:
where denotes the smoothed parameter used by the VSG loops, Ts is the control period, and is the maximum allowed rate. In our studies we used and of the corresponding baseline per control period, which balances disturbance responsiveness (<100 ms) with adequate filtering of DC link sensor ripple and avoids abrupt shifts during load rejection or PV/BES transients.
2. Hard bounds (projection) for safe operating ranges:
To prevent extreme values and guarantee grid code-compliant behavior, each adjusted parameter is projected onto a compact interval
with limits chosen from hardware and stability considerations. Using the baselines in (12), the representative ranges are as follows:
These envelopes were verified not to violate current/voltage limits and to preserve small-signal margins across the scenarios considered.
3. Rationale and long-horizon behavior:
The combination of smoothing, rate limiting, and projection makes the closed loop a gain-scheduled system with bounded, slowly varying parameters. In practice, this prevents chattering near the bounds, mitigates the effect of high-frequency measurement noise from the DC link, and avoids “bang-bang” responses.
3.5. Tuning Methodology for Adaptive Gains
This subsection provides a practical, implementation-oriented recipe to tune the adaptive gains kj, kp, and kq without changing the published control law. The goal is to obtain consistent transient performance and stability across operating conditions while keeping the scheduling bounded and grid code compliant.
The baseline and admissible spans are as follows:
First, select a code-compliant baseline and define admissible envelopes for the scheduled parameters based on hardware and stability limits (e.g., ). These envelopes act as hard guards together with the rate-limit and smoothing mechanisms described earlier.
Normalized driver and first-shot gains:
Let the driver be the normalized DC link energy deviation with expected range ; the scheduling laws are linear with saturation:
Choose target parameter excursions at , and back-solve the initial gains:
Typical starting ranges that worked well in our studies are ; the exact values are then clipped by and subjected to the rate limiter, which prevents overly aggressive actions.
We assess the influence of via a compact sweep (or Latin-hypercube sample) over their admissible box and evaluate a composite index combining overshoot, settling time, ITAE of the DC link/voltage errors, and PCC current peak. Trends are generally intuitive: increasing kj strengthens inertia and improves RoCoF but may slow power settling if oversized; increasing kp reduces active-power overshoot at the expense of slightly larger steady-state droop; increasing kq enhances voltage support but can amplify reactive-power variation if too large. The selected triplet however minimizes the index while respecting current/voltage limits.
Robust tuning (uncertainty set):
To ensure stability and consistency across configurations, we repeat the evaluation over an uncertainty set (e.g., SCR and line-impedance variation, Cdc tolerance/aging, sensor noise, and digital delay) and check small-signal margins around operating points. The final gains are those achieving the best performance–robustness trade-off within the envelopes.
3.6. Real-Time Computational Footprint and Resource Usage
This section quantifies the incremental cost introduced by the estimator and the adaptive scheduling. The added workload consists of the following: (i) a low-order (scalar or 2–3 state) discrete Kalman filter that estimates the DC link energy; and (ii) three linear, rate-limited adaptive laws for the virtual inertia and droop gains. Both components have constant per-sample complexity, i.e., O(1) operations independent of system size. For the commonly used scalar Kalman filter, each control interrupt executes one prediction and one update comprising tens of additions/multiplications and a single division; at a 10 kHz control rate, this corresponds to roughly 0.3–0.6 MFLOPs/s. The three adaptive updates add only a few dozen arithmetic operations, keeping the total below 0.8 MFLOPs/s. If a slightly higher-order filter (e.g., 3 × 3) is chosen, the cost remains modest—about 2–4 MFLOPs/s at 10 kHz—because the matrices are fixed-size and admit efficient implementations (e.g., precomputed steady-state gains or Cholesky-based scalar inversions). The memory footprint is likewise small: state vectors, covariances, noise/gain parameters, and saturation/rate-limit buffers together require well under 1 kB in floating point (a few hundred bytes for a scalar filter). On representative industrial controllers—e.g., TI C2000 F2837xD (200 MHz, FPU) or ARM Cortex-M7 (≥400 MHz, FPU)—the incremental ISR time measured/estimated for the scalar filter plus adaptive laws is <5–10 μs at 10 kHz, leaving ample headroom for PWM, current loops, and housekeeping. When desired, the filter and/or adaptation can run in a slower supervisory loop (e.g., 1–2 kHz) without affecting closed-loop stability; fixed-point implementation is straightforward given the small dynamic range.
4. Simulation Results
To validate the effectiveness of the proposed energy-aware adaptive GFM control strategy, time domain simulations were conducted using MATLAB/Simulink R2023b. The control parameter is shown Table 1. The test system includes a PV-BES GFM system under both conventional fixed-parameter VSG control and the proposed adaptive control method.

Table 1.
Control parameters of the system referring to Figure 1.
A step change in the active power reference was introduced at t = 2 s to emulate a disturbance scenario such as a sudden load variation or generation ramp event. The performance of both control strategies was compared in terms of active and reactive power dynamics, current response, and DC link voltage regulation.
As illustrated in Figure 6, under the conventional VSG control (left), the active power Pe exhibits an overshoot of approximately 0.35 kW, and the settling time exceeds to 0.4 s. In contrast, the proposed adaptive control (right) significantly reduces the overshoot and enables faster recovery to steady-state conditions. The reactive power Qe remains stable in both cases, demonstrating proper decoupling in the control structure.
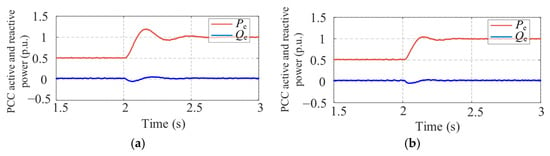
Figure 6.
Transient responses of active and reactive power at the PCC. (a) Conventional fixed-parameter VSG control. (b) Proposed adaptive energy-aware VSG control.
The phase-a current ia at the PCC is shown in Figure 7. The conventional method leads to an evident overshoot and oscillation immediately following the disturbance. The adaptive method, by contrast, effectively damps these oscillations and reduces peak current amplitude, thereby enhancing current quality and alleviating stress on power components.
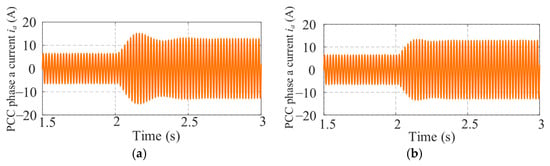
Figure 7.
PCC phase-a current responses during active power disturbance. (a) Conventional method. (b) Proposed adaptive energy-aware VSG control.
The DC link voltage vdc dynamics are presented in Figure 8. With conventional control, a noticeable voltage sag occurs after the disturbance, followed by underdamped oscillations. The proposed adaptive control improves voltage recovery by adjusting virtual damping and inertia based on real-time capacitor energy state, yielding a faster regulation process.
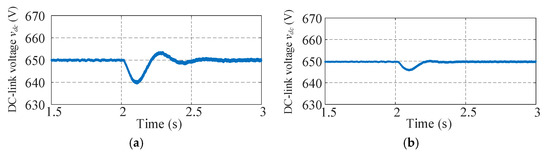
Figure 8.
DC link voltage vdc under disturbance. (a) Conventional control. (b) Proposed adaptive energy-aware VSG control.
In addition, to evaluate the dynamic performance of the proposed adaptive GFM control under grid frequency disturbances, a test scenario involving a step frequency drop of 0.1 Hz was introduced at 2 s. Figure 9a,b illustrate the active and reactive power responses at the PCC under conventional and adaptive control, respectively. Under conventional fixed-parameter VSG control, the active power response exhibits a clear overshoot and long regulation time, indicating insufficient damping and fixed inertia tuning. In contrast, the adaptive method significantly reduces the overshoot and enables quicker restoration to steady-state values due to the energy-dependent adjustment of virtual inertia and damping coefficients.
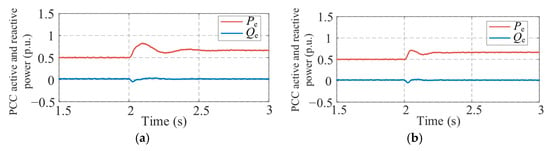
Figure 9.
Transient responses of the PV-BES GFM system during the frequency disturbance. (a) Conventional fixed-parameter VSG control. (b) Proposed adaptive energy-aware VSG control.
As the parameter shown in Table 2, Figure 10a,b show the PCC phase-a current responses under both control strategies. The conventional method results in noticeable oscillations and peak current during the disturbance period, which can stress the power components and degrade current quality. By contrast, the proposed adaptive strategy effectively suppresses these oscillations and maintains a more stable current profile, demonstrating enhanced transient damping and improved electromagnetic compatibility. These results confirm the benefit of real-time capacitor energy awareness in enhancing GFM inverter performance during grid disturbances.

Table 2.
Control parameters of the system.
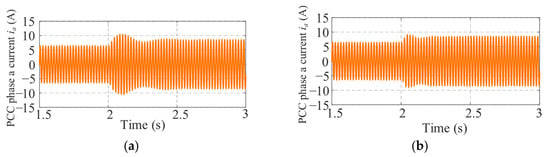
Figure 10.
PCC phase-a current responses during the frequency disturbance. (a) Conventional method. (b) Proposed adaptive energy-aware VSG control.
As shown in Figure 11, under a commanded DC link voltage step from 650 V to 700 V at t = 2 s, the conventional fixed-parameter VSG exhibits a pronounced excursion in PCC active power and a small reactive-power swing before damping out. By contrast, when the energy-aware scheduling is enabled, the active and reactive power remain essentially undisturbed and return to steady state without visible overshoots. This behavior indicates that modulating the virtual inertia and droop within bounded ranges, driven by the estimated capacitor energy deviation, provides additional transient damping without altering the steady-state setpoints.
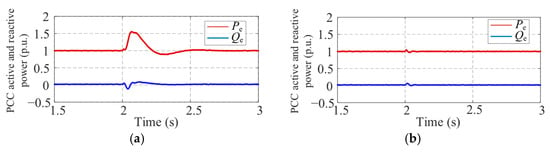
Figure 11.
Transient responses of the PV-BES GFM system during the DC link voltage disturbance. (a) Conventional fixed-parameter VSG control. (b) Proposed adaptive energy-aware VSG control.
The DC link voltage response further highlights the difference between the two strategies, as shown Figure 12. With fixed parameters, the step in the reference produces overshoot followed by damped oscillations. With the proposed energy-aware control, the DC link voltage tracks the new reference nearly monotonically, with minimal overshoot and short settling. The improvement is consistent with the additional effective damping introduced by the adaptive scheduling while respecting the predefined saturation and rate-limit constraints.
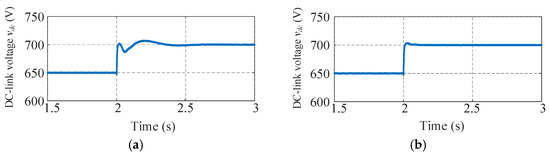
Figure 12.
DC link voltage vdc during the DC link voltage disturbance. (a) Conventional fixed-parameter VSG control. (b) Proposed adaptive energy-aware VSG control.
5. Analysis of Adjustable Parameters and Limits
This section analyzes how the adjustable parameters affect performance and stability and documents the limits used in practice. We consider four groups: (i) baseline controller parameters , (ii) adaptive gains , (iii) scheduling safeguards (saturation bounds and rate limits), and (iv) observer-related settings (process/measurement noise covariances and the prefilter bandwidth). The analysis is tied to the representative scenarios used in the results.
5.1. Baseline Parameters:
The baselines set the nominal dynamic character of the virtual synchronous generator (VSG) and should satisfy grid code envelopes. Increasing J0 reduces the initial rate of change in frequency and active-power swing but can slow settling if excessive. Increasing Dp0 reduces active-power overshoot and oscillation, at the cost of a slightly larger steady-state droop. Increasing Dq0 improves voltage support and reactive-power sharing but may raise reactive oscillation if oversized. In all cases, the baselines remain within the hardware and grid code limits documented below.
5.2. Adaptive Gains:
The energy-aware scheduling uses the normalized DC link energy deviation to modulate inertia and droop. The laws are linear with saturation:
Larger kj strengthens the inertial response and improves RoCoF resilience under weak grid disturbances, but overly large values can prolong active-power settling. Larger kp adds active-power damping and suppresses overshoot; if too large, it may increase steady-state droop. Larger kq raises voltage stiffness and mitigates excursions via reactive support; excessive values can amplify reactive-power swings.
Comparative illustration (two typical settings): To make the influence concrete, we report two gain triplets built from the baseline in Table 1 and an expected range :
Set A (balanced):
Set B (weak grid-oriented):
Set A offers fast settling with moderate damping; Set B prioritizes weak grid robustness and overshoot suppression. The side-by-side time domain results for these sets are included in the scenario figures; small-signal trends follow the qualitative descriptions above.
5.3. Scheduling Safeguards: Bounds and Rate Limits
To avoid aggressive updates and parameter drift, the scheduled parameters are smoothed and rate-limited, then projected onto compact intervals:
5.4. Observer and Prefilter Settings
The estimator uses a low-order discrete Kalman filter driven by a power-balance model. The process and measurement noise covariances Q and R are chosen from expected DC link power mismatch during fast transients and sensor noise levels, respectively. The prefilter bandwidth for is set by above to reject high-frequency ripple in while keeping responsiveness to genuine disturbances. The values used in each scenario are reported alongside the controller settings for reproducibility.
5.5. Practical Limits and Recommendations
Recommended envelopes and rates are those in Section 5.3; they prevent saturation chattering, ensure bounded parameter motion, and maintain compliance with current/voltage limits. For tuning, Set A provides a balanced default, while Set B is preferable in weak grid tests or when current peaks must be minimized. Final choices are scenario-dependent and are documented per case together with the corresponding metrics to support reproducibility.
6. Conclusions
This work presented an energy-aware grid-forming control in which a low-order Kalman observer estimates the DC link capacitor energy and the resulting deviation schedules the virtual inertia and droop within predefined bounds. Using the same MATLAB/Simulink plant and solver settings for all cases, the method reproducibly improved transient behavior in the tested scenarios—active-power steps, small frequency deviations in a weak grid setting, and commanded DC link voltage steps—relative to a fixed-parameter VSG baseline. In particular, the adaptive scheduling reduced overshoot, shortened settling, and mitigated DC link excursions while preserving the steady-state set-points. These findings are limited to the simulated operating envelope, parameter ranges, and disturbance magnitudes reported here; broader grids, multi-inverter interactions, and hardware effects remain to be assessed. Future work will extend validation to PHIL/experimental platforms, examine coordination with current-limiting, and formalize robustness to component drift and measurement noise.
7. Future Works
This study focused on a simulation-based assessment of an energy-aware grid-forming strategy that schedules virtual inertia and droop using a DC link energy estimate. Several research avenues remain. We will extend the framework from a single inverter to multi-inverter operation in microgrids, studying cluster-level power sharing, weak grid interactions, unbalanced/harmonic conditions, and black-start/resynchronization procedures. In addition, we plan to integrate the energy-aware scheduling with fault-ride-through and current-limit coordination, assessing compliance with grid code envelopes (frequency/voltage droop, RoCoF limits) during grid faults and severe transients.
Another direction is robust tuning and long-term stability. We will formalize gain-scheduling guarantees with bounded parameter rates and envelopes, conduct long-horizon stochastic tests (irradiance/load profiles, SCR/impedance variation, digital delay), and automate gain selection via sensitivity-guided searches over uncertainty sets. We also plan to study capacitor aging and parameter drift, including adaptive/noise-aware observer covariances and health-monitoring hooks for Cdc. Finally, to facilitate reproducibility and comparison, we will release parameter tables, test scripts, and minimal models (where permitted by policy), enabling independent replication of all scenarios and metrics.
Author Contributions
Conceptualization, X.L. and Y.F.; methodology, X.L.; software, X.L.; validation, X.L., Y.C. and Y.F.; formal analysis, X.L.; investigation, X.L.; resources, Y.C.; data curation, X.L.; writing—original draft preparation, X.L.; writing—review and editing, Y.F.; visualization, X.L.; supervision, Y.F.; project administration, Y.F.; funding acquisition, Y.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| Abbreviation | Meaning |
| AC | Alternating Current |
| APC | Active Power Control |
| BES | Battery Energy Storage |
| BESS | Battery Energy Storage System |
| CV | Constant Voltage |
| DC | Direct Current |
| FRT | Fault Ride Through |
| GFM | Grid-Forming |
| GFL | Grid-Following |
| MPPT | Maximum Power Point Tracking |
| PCC | Point of Common Coupling |
| PI | Proportional–Integral |
| PLL | Phase-Locked Loop |
| PWM | Pulse-Width Modulation |
| PV | Photovoltaic |
| RES | Renewable Energy Sources |
| RoCoF | Rate of Change of Frequency |
| SCR | Short-Circuit Ratio |
| SOC | State of Charge |
References
- Blaabjerg, F.; Teodorescu, R.; Liserre, M.; Timbus, A.V. Overview of control and grid synchronization for distributed power generation systems. IEEE Trans. Ind. Electron. 2006, 53, 1398–1409. [Google Scholar] [CrossRef]
- Rocabert, J.; Luna, A.; Blaabjerg, F.; Rodríguez, P. Control of power converters in AC microgrids. IEEE Trans. Power Electron. 2012, 27, 4734–4749. [Google Scholar] [CrossRef]
- Milano, F.; Dörfler, F.; Hug, G.; Hill, D.J.; Verbič, G. Foundations and challenges of low-inertia systems. In Proceedings of the 2018 Power Systems Computation Conference (PSCC), Dublin, Ireland, 11–15 June 2018; pp. 1–21. [Google Scholar]
- Huang, L.; Xin, H.; Li, Z.; Ju, P.; Yuan, H.; Lan, Z. Grid-synchronization stability analysis and loop shaping for PLL-based power converters with different reactive power control. IEEE Trans. Smart Grid 2020, 11, 501–516. [Google Scholar] [CrossRef]
- Wen, B.; Boroyevich, D.; Burgos, R.; Mattavelli, P.; Shen, Z. Analysis of d-q small-signal impedance of grid-tied inverters. IEEE Trans. Power Electron. 2016, 31, 675–687. [Google Scholar] [CrossRef]
- IEEE Standard 1547-2018; IEEE Standard for Interconnection and Interoperability of Distributed Energy Resources with Associated Electric Power Systems Interfaces. The Institute of Electrical and Electronics Engineers, Inc. (IEEE): New York, NY, USA, 2018.
- IEEE Standard 2800-2022; IEEE Standard for Interconnection and Operation of Inverter-Based Resources (IBRs) Interconnecting with Associated Transmission Electric Power Systems. The Institute of Electrical and Electronics Engineers, Inc. (IEEE): New York, NY, USA, 2022.
- North American Electric Reliability Corporation (NERC). Reliability Guideline: BPS-Connected Inverter-Based Resource Performance; North American Electric Reliability Corporation (NERC): Atlanta, GA, USA, 2021. [Google Scholar]
- Zhang, L.; Harnefors, L.; Nee, H.-P. Power-synchronization control of grid-connected voltage-source converters. IEEE Trans. Power Syst. 2010, 25, 809–820. [Google Scholar] [CrossRef]
- Zhong, Q.-C.; Weiss, G. Synchronverters: Inverters that mimic synchronous generators. IEEE Trans. Ind. Electron. 2011, 58, 1259–1267. [Google Scholar] [CrossRef]
- D’Arco, S.; Suul, J.A.; Fosso, O.B. Control system tuning and stability analysis of virtual synchronous machines. In Proceedings of the IEEE ECCE, Denver, CO, USA, 15–19 September 2013; pp. 2664–2671. [Google Scholar]
- D’Arco, S.; Suul, J.A. Virtual synchronous machines—Classification of implementations and analysis of equivalence to droop controllers. In Proceedings of the 2013 IEEE Grenoble Conference PowerTech, Grenoble, France, 16–20 June 2013; pp. 1–7. [Google Scholar]
- Lu, X.; Dhople, S.V.; Johnson, B.B. Benchmarking nonlinear oscillators for grid-forming power converters. IEEE Trans. Power Electron. 2022, 37, 9293–9308. [Google Scholar] [CrossRef]
- Poolla, B.K.; Mallada, E.; Groß, D. Frequency-shaping control for weakly coupled inverter-based resources. IEEE Control Syst. Lett. 2023, 7, 879–884. [Google Scholar] [CrossRef]
- Bahrani, B.; Ravanji, M.H.; Kroposki, B.; Ramasubramanian, D.; Guillaud, X.; Prevost, T. Grid-forming inverter-based resource research landscape: Understanding the key assets for renewable-rich power systems. IEEE Power Energy Mag. 2024, 22, 18–32. [Google Scholar] [CrossRef]
- Sun, J. Impedance-based stability criterion for grid-connected inverters. IEEE Trans. Power Electron. 2011, 26, 3075–3078. [Google Scholar] [CrossRef]
- Cespedes, M.; Sun, J. Impedance modeling and analysis of grid-connected voltage-source converters. IEEE Trans. Power Electron. 2014, 29, 1254–1261. [Google Scholar] [CrossRef]
- Wang, X.; Blaabjerg, F.; Wu, W. Modeling and analysis of harmonic stability in an AC power-electronics-based power system. IEEE Trans. Power Electron. 2014, 29, 6421–6432. [Google Scholar] [CrossRef]
- Baeckeland, N.; Chatterjee, D.; Lu, M.; Johnson, B.; Seo, G.-S. Overcurrent limiting in grid-forming inverters: A comprehensive review and discussion. IEEE Trans. Power Electron. 2024, 39, 14493–14511. [Google Scholar] [CrossRef]
- Qoria, T.; Benchaib, A.; Lebey, T.; Rault, P. Grid-forming control VSC-based including current limitation under balanced and unbalanced faults. Electr. Power Syst. Res. 2023, 222, 109436. [Google Scholar]
- Zhao, X.; Lu, M.; Seo, G.-S. Grid-forming converter current-limiting design to enhance transient stability. IFAC-Pap. 2022, 55, 163–168. [Google Scholar]
- Kroposki, B. Introduction to Grid-Forming Inverters; (NREL Report NREL/TP-5D00-90256); National Renewable Energy Laboratory: Golden, CO, USA, 2024. [Google Scholar]
- Du, W.; Nguyen, Q.H.; Wang, S.; Kim, J.; Liu, Y.; Zhu, S.; Tuffner, F.K.; Huang, Z. Positive-sequence modeling of droop-controlled grid-forming inverters for transient stability simulation of transmission systems. IEEE Trans. Power Del. 2024, 39, 1736–1748. [Google Scholar] [CrossRef]
- Seo, G.-S.; Sawant, J.; Ding, F. Black Start of Unbalanced Microgrids: Harmonizing Single- and Three-Phase Grid-Forming Inverters; (No. NREL/CP-5D00-86971); National Renewable Energy Laboratory: Golden, CO, USA, 2023. [Google Scholar]
- Simpson-Porco, J.W.; Dörfler, F.; Bullo, F. Voltage stabilization in microgrids via quadratic droop control. IEEE Trans. Autom. Control 2017, 62, 1239–1253. [Google Scholar] [CrossRef]
- Eberlein, S.; Tushar, W.; Yuen, C.; Dragicevic, T. Optimisation, benchmark testing and comparison of droop control approaches. IET Smart Grid 2021, 4, 546–559. [Google Scholar] [CrossRef]
- Li, L.; Wang, R.; Li, X. A Communication-free adaptive virtual inertia control of cascaded virtual synchronous generators. Int. J. Electr. Power Energy Syst. 2023, 145, 108570. [Google Scholar]
- Wang, J.; Liu, Z.; Feng, K.; Liu, J. An adaptive droop and feedforward control-based transient power sharing and decoupling method for grid-forming inverters in islanded microgrids. IEEE Trans. Ind. Electron. 2025, 72, 4800–4810. [Google Scholar] [CrossRef]
- Shi, R.; Zhang, X.; Hu, C.; Xu, H.; Gu, J.; Cao, W. Self-tuning virtual synchronous generator control for improving frequency stability in autonomous photovoltaic–diesel microgrids. J. Mod. Power Syst. Clean Energy 2018, 6, 482–494. [Google Scholar] [CrossRef]
- Karimi, A.; Radan, A.; Mokhtari, H.; Parniani, M. Inertia response improvement in AC microgrids: A fuzzy-based virtual synchronous generator control. IEEE Trans. Power Electron. 2020, 35, 4321–4331. [Google Scholar] [CrossRef]
- Peng, Q.; Fang, J.; Yang, Y.; Liu, T.; Wang, H.; Blaabjerg, F. Maximum virtual inertia from DC-link capacitors considering system stability at voltage-control timescale. IEEE J. Emerg. Sel. Top. Circuits Syst. 2021, 11, 79–89. [Google Scholar] [CrossRef]
- Al-Khayyat, A.S.; Tammineedi, M.; Blaabjerg, F. Virtual inertia extraction from a DC bus capacitor in a three-phase inverter. E-Prime—Adv. Electr. Eng. 2024, 5, 100227. [Google Scholar]
- Yu, J.; Hu, J.; Ding, T.; Ma, Y. Small-signal stability of multi-converter infeed power systems within the DC-link voltage timescale. Symmetry 2021, 13, 157. [Google Scholar] [CrossRef]
- Tayyebi, A.; Groß, D.; Anta, A.; Kupzog, F.; Dörfler, F. Frequency stability of synchronous machines and grid-forming power converters. arXiv 2020, arXiv:2003.04715. [Google Scholar]
- Zhu, N.; Papathanassiou, S.A.; Strbac, G. Comparative analysis and optimal allocation of virtual inertia for grid-forming and grid-following devices. IET Renew. Power Gener. 2024, 18, 2086–2099. [Google Scholar] [CrossRef]
- Tian, A.; Yang, X.; Chen, X.; Ma, S. Two-stage PV grid-connected control strategy based on DC-link capacitor dynamic self-synchronization unit. Sustain. Energy Grids Netw. 2023, 33, 100926. [Google Scholar]
- Qin, Y.; He, J.; Wu, J.; Li, W.; Guerrero, J.M. A DC-link voltage synchronous control with enhanced performance for grid-forming wind turbines. IET Renew. Power Gener. 2024, 18, 635–648. [Google Scholar] [CrossRef]
- Ray, I.; Kushwaha, A.K.; Shukla, A.K. Grid-forming inverter control for PV sources considering DC-link stability and limits. IET Renew. Power Gener. 2025, 19, 401–414. [Google Scholar] [CrossRef]
- Dörfler, F.; Groß, D. Control of low-inertia power systems. Annu. Rev. Control Robot. Auton. Syst. 2023, 6, 415–445. [Google Scholar] [CrossRef]
- Lin, Y.; Eto, J.H.; Johnson, B.B.; Flicker, J.D.; Lasseter, R.H.; Pico, H.N.V.; Seo, G.-S.; Pierre, B.J.; Ellis, A. Research Roadmap on Grid-Forming Inverters; (No. NREL/TP-5D00-73476); National Renewable Energy Laboratory: Golden, CO, USA, 2020. [Google Scholar]
- Bozalakov, D.; Qazi, S.; De Kooning, J.D.M.; Vandevelde, L. Power quality improvement by grid-connected inverters driven by the three-phase damping control strategy operated in different modes. Int. J. Electr. Power Energy Syst. 2025, 169, 110689. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).