Abstract
Fault diagnosis accuracy in lithium-ion battery-based energy storage systems is significantly constrained by the limited availability of fault-specific datasets. This study addresses this critical issue by proposing a diffusion-based data augmentation methodology tailored explicitly for battery fault diagnosis scenarios. The proposed conditional diffusion model leverages transfer learning and attention-enhanced fine-tuning strategies to generate high-quality synthetic fault data, ensuring targeted representation of rare fault conditions. By integrating condition-aware sampling strategies, the approach effectively mitigates mode collapse issues frequently encountered in adversarial generative methods, thus substantially enriching the diversity and quality of fault representations. Comprehensive evaluation using statistical similarity measures and downstream classification tasks demonstrates notable improvements. After the integration of attention mechanisms, the Pearson correlation coefficient between the synthetic and real samples increases from 0.29 to 0.91. In downstream diagnostic tasks, models trained on augmented datasets exhibit substantial gains in regards to the recall and F1-score, which increase from near-zero levels to values exceeding 0.91 for subtle overcharge and overdischarge faults. These results confirm the effectiveness and practical utility of the proposed augmentation approach in enhancing diagnostic performance under data-scarce conditions.
1. Introduction
Modern power systems are increasingly dependent on lithium-ion battery-based electrochemical energy storage systems (ESSs) to maintain stability and operational efficiency. As this dependence deepens, ensuring the safety, reliability, and efficiency of ESSs has become a critical concern. Consequently, advanced fault detection mechanisms have become essential components in contemporary battery management systems (BMSs) [1,2]. Recent research has extensively leveraged machine learning models to diagnose anomalous battery behaviors and effectively predict failures [3]. Nonetheless, the performance of these data-driven diagnostic methods fundamentally depends on the quality and comprehensiveness of their training datasets. Currently, there exists a significant imbalance between the abundant availability of normal operational data and the severe scarcity of fault-related samples, considerably limiting the efficacy of fault diagnosis algorithms. This data scarcity arises primarily due to three factors: (1) the inherently rare occurrence of battery faults, making data collection subsequently sparse; (2) safety concerns and associated risks that preclude the deliberate induction of battery failures for experimental data acquisition; and (3) confidentiality regulations imposed by industrial manufacturers, which frequently restrict researchers’ access to proprietary fault databases, thereby exacerbating dataset limitations [4,5,6].
Battery faults typically manifest in two distinct patterns: failures resulting from improper or prolonged extreme usage and sudden catastrophic events. The gradual deterioration process, represented by continuous capacity fade and increasing internal resistance, is usually latent during early phases but potentially escalates into severe safety hazards without timely detection and intervention [7]. To effectively diagnose these diverse and complex fault patterns, extensive and high-quality fault datasets are essential yet currently scarce. Therefore, addressing this dataset insufficiency is crucial to improving the robustness, reliability, and safety of machine learning-driven battery fault diagnostics.
In response to the data imbalance challenge, researchers have increasingly explored generative modeling techniques as a means to synthesize fault data. Among these, generative adversarial networks (GANs) have been prominently introduced to address data scarcity by learning underlying data distributions through adversarial training between generator and discriminator networks. Recent research has reported the successful implementations of GANs in battery diagnostic contexts. For instance, Qiu et al. [8] developed a Wasserstein GAN incorporating gradient penalty techniques (WGAN-GP) to augment training datasets for accurate state of charge (SOC) estimation. Liu et al. [9] combined TimeGAN and Pyraformer architectures for battery state of health (SOH) predictions, significantly enhancing predictive modeling. Similarly, Hu et al. [10] employed conditional WGAN-GP (CWGAN-GP) incorporating residual networks for lithium-ion battery thermal fault image synthesis, achieving improved diagnostic accuracy. Additionally, Falak Naaz et al. [11] augmented battery data (e.g., voltage and temperature) via GANs to facilitate neural network learning for battery SOC/SOH estimation tasks. Advanced architectures have also integrated GAN-based frameworks with emerging methods, including federated learning, self-supervised learning, and noise-injection strategies, to further enhance data quality and minimize dependence on labeled samples.
Despite demonstrable potential and promising preliminary successes, GAN-based models encounter notable limitations hindering widespread practical adoption. First, GAN methods frequently suffer from mode collapse, in which generators produce repetitive, low-diversity samples that inadequately represent the complex and diverse fault scenarios encountered in real-world applications [12,13]. Secondly, GAN training typically necessitates substantial amounts of data, resulting in impaired performance under the limited-data conditions characteristic of battery fault datasets. These inherent drawbacks significantly restrict the practical applicability of GAN approaches for battery fault diagnosis.
Diffusion models have emerged as a transformative advancement in generative modeling, offering unprecedented performance in synthesizing high-fidelity and diverse data while ensuring robust and stable training dynamics [14]. Their success spans a wide range of application domains, from time-series augmentation [15,16] to natural image synthesis [17] and dynamic video generation [18], for which maintaining temporal coherence and realistic variability is critical. Moreover, diffusion models excel at capturing complex data distributions and preserving physical plausibility, making them particularly well-suited for scientific and engineering applications. They have been successfully applied in fields with stringent structural and temporal requirements, such as medical imaging, climate simulation, and financial forecasting [19,20,21]. However, despite their promise, current implementations still face unresolved challenges—such as long inference times and the need for domain adaptation when applied to highly specialized data regimes. Notably, their potential remains underutilized in the context of lithium-ion battery fault data synthesis, where the need for both temporal accuracy and data scarcity mitigation is especially pronounced.
Although diffusion models show immense potential to transform data augmentation in battery diagnostics, their integration into fault data synthesis remains limited. Existing applications in other domains highlight their strength in generating temporally coherent and physically plausible data, even under constraints posed by small or imbalanced datasets. These capabilities make them particularly well-suited to address the shortcomings of GAN-based methods in battery fault modeling. Yet, practical deployment in this domain requires overcoming domain-specific challenges, such as adapting pretrained diffusion models to sparse fault data and validating the realism of the generated sequences under real-world diagnostic constraints.
To bridge this research gap, this paper presents a dedicated diffusion-based data augmentation methodology tailored for lithium-ion battery fault scenarios. The proposed framework not only leverages the architectural strengths of diffusion models but also integrates domain adaptation techniques and targeted sampling mechanisms to ensure high-fidelity and diverse fault data synthesis. The main contributions of this study are as follows:
- (1)
- A novel condition-aware diffusion sampling strategy, enabling controllable data synthesis based on specific fault types and severity conditions. This technique mitigates mode collapse issues commonly observed in GAN approaches and significantly broadens the representation of rare fault scenarios.
- (2)
- An attention-integrated, layer-wise fine-tuning strategy to optimize diffusion models for ESS data, effectively addressing long-range temporal dependencies while controlling architectural complexity. This approach enhances generation fidelity and promotes practical deployment in real-world applications.
- (3)
- A comprehensive validation approach, comparing generated samples against original data using multiple quantitative metrics, thereby ensuring the synthesized data’s fidelity and diagnostic utility for realistic battery fault diagnosis.
The remainder of this paper is organized as follows: Section 2 describes the experimental setup, detailing data collection procedures and dataset characteristics. Section 3 presents the theoretical background and implementation details of the proposed diffusion-based generative model. Section 4 evaluates extensive experiments and compares the proposed method with existing state-of-the-art methods, considering both statistical rigor and diagnostic applicability. Finally, Section 5 summarizes key findings, outlines limitations, and suggests clear directions for future research endeavors.
2. Experiments
2.1. Experimental Setup
The experimental workflow of this study is illustrated in Figure 1, comprising two main parts: aging data acquisition and fault data collection. The fault data represent both overcharge and overdischarge conditions. All experiments were conducted using a custom-built battery testing platform previously developed and validated by the research team. Details of this platform and the associated dataset were reported in our earlier publications [22,23].
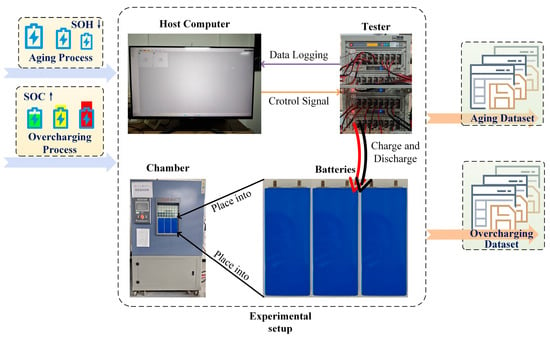
Figure 1.
Schematic of the test bench.
The dataset was generated through in-house testing of 25 prismatic LiFePO4 cells (model TB-027070180D-Fe-25 Ah, TOPBAND, Shenzhen, China), each with dimensions of 27 mm × 70 mm × 180 mm (width × depth × height). These cells comprise a graphite anode and a lithium iron phosphate cathode. Key specifications include a nominal voltage of 3.2 V, a rated capacity of 25 Ah, cut-off voltages of 3.6 V (charge) and 2.3 V (discharge), and a maximum continuous discharge rate of 1 C. The design cycle life is 2000 cycles, and the operational temperature range spans −20 °C to 55 °C.
Battery voltage and capacity data were recorded using a battery testing system (CT-4016, NEWARE, Shenzhen, China), with the ambient temperature maintained at approximately 25 °C throughout the experiments.
2.2. Data Acquisition
2.2.1. Aging Test
To emulate load-shifting operations commonly encountered in stationary energy storage systems, the cells were subjected to continuous charge–discharge cycling under a constant current (CC) regime. Cycling continued until the SOH of each cell declined below 90%, which typically occurred after approximately 700 cycles. Two representative cells were selected for further analysis, with final SOH values of 88.93% and 88.66%, respectively.
Each charging cycle yielded a voltage profile that was treated as a distinct data instance. All profiles were resampled to a fixed length of 991 data points to ensure uniformity.
2.2.2. Fault Test
To maintain consistency across all fault conditions, a unified preconditioning protocol was adopted. Each cell was initially charged to the standard cut-off voltage of 3.65 V under a CC regime. If applicable, charging then continued under the same regime until the designated overcharge voltage was reached, followed by a constant voltage (CV) hold for a specified duration. The evolution of voltage during the fault test is depicted in Figure 2.
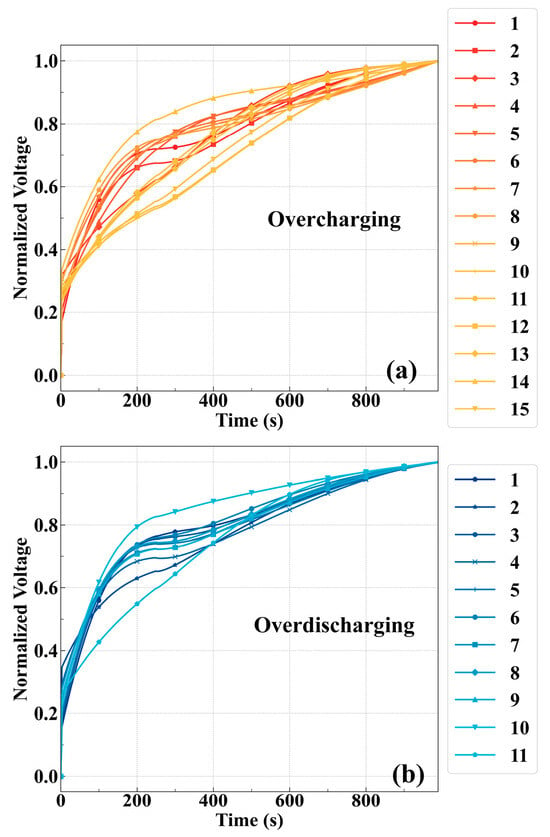
Figure 2.
Voltage curves of the charging process: (a) overcharge; (b) overdischarge.
For overdischarge testing, the cells were discharged to 2.8 V under CC and subsequently discharged further to the target undervoltage level. The overdischarge threshold was set based on empirical observations showing that nearly the entire nominal capacity of the cell is exhausted by this point. Although the data sheet indicates a minimum discharge voltage of 2.0 V, operation near this limit is typically avoided in practice. The 2.8 V threshold aligns with standard BMS settings and ensures sufficient representation of overdischarge cases in the dataset.
In the first group, Cells 1–4 were charged to 3.8 V and then held at this voltage for varying durations. Specifically, Cell 1 was held for 5 min, Cell 2 for 10 min, Cell 3 for 15 min, and Cell 4 underwent two consecutive holds of 5 min each. The second group, consisting of Cells 5–7, was charged to higher voltages: 4.0 V, 4.2 V, and 4.5 V, respectively. Each cell in this group was held at the target voltage for 10 min. The third group (Cells 8–13) underwent a stepwise voltage-increase protocol. Cell 8 was charged to 4.8 V and held for 10 min. Cells 9–13 were charged to 5.0 V and held for progressively longer durations: 10 min for Cell 9, 20 min for Cell 10, 30 min for Cell 11, 40 min for Cell 12, and 60 min for Cell 13.
For the overdischarge experiments, Cells 14–16 were discharged to target voltages of 2.0 V, 1.5 V, and 1.0 V, respectively, with each cell held at constant current for 5 min at the target voltage. Cells 17–19 were discharged to 1.5 V and held for durations of 10, 20, and 30 min, respectively. Cells 20 and 21 were discharged to 1.0 V, with holding durations of 10 min and 30 min, respectively. To examine the cumulative effects of repeated undervoltage conditions, Cells 22 and 23 were subjected to 5 and 10 repeated deep-discharge cycles to 1.5 V.
These comprehensive test protocols yielded a diverse dataset encompassing a wide range of voltage deviations, which serve as the basis for subsequent diffusion model training and evaluation.
3. Methodology
The diffusion model generates fault data under specific conditions, incorporating structured auxiliary information to guide the generation process. Additionally, transfer learning is employed to transfer knowledge from aging dataset, thereby improving the training of models for fault-specific data. The workflow and research framework at this stage of this study are illustrated in Figure 3, providing a clear overview of the method.
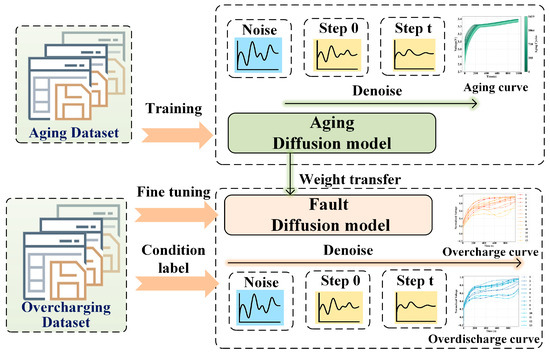
Figure 3.
The proposed diffusion models.
3.1. Transfer Learning Diffusion Models
3.1.1. Diffusion Models
Diffusion models are a class of probabilistic generative methods that synthesize data by gradually reversing a predefined stochastic noising process. Starting from pure Gaussian noise, they iteratively recover structured outputs through a learned denoising trajectory. This reformulation avoids common pitfalls associated with GANs, such as mode collapse and training instability, by casting the generation task as a sequence of denoising steps [24,25].
In the forward process, real data is progressively perturbed by Gaussian noise across T discrete steps. At each timestep t, the corrupted data xt is sampled according to a Markov process:
Here, βt is a predefined variance schedule controlling the noise magnitude, and I is the identity matrix. As the process progresses, the data structure is gradually destroyed, ultimately converging to an isotropic Gaussian distribution.
To generate data, the model learns to reverse this process by approximating the posterior distribution . Instead of reconstructing the original sample directly, the model is trained to predict the added noise ϵ using the following denoising objective:
where ϵ is the sampled Gaussian noise, and denotes the noise predicted by the denoising network at time step t. This mean squared error (MSE) loss drives the model to progressively remove noise and reconstruct coherent data structures.
This denoising formulation is particularly well-suited for generating time series data such as battery voltage signals, which exhibit smooth and structured temporal variations. Unlike static image data, battery degradation signals demand the preservation of both temporal consistency and physically consistent temporal behavior. The progressive refinement in diffusion models aligns well with these requirements, enabling the model to capture subtle dynamic trends while maintaining continuity across time steps.
3.1.2. Diffusion with Transfer Learning
To alleviate the training challenges caused by the limited availability of fault data—particularly for overcharge and overdischarge scenarios—we propose a conditional diffusion framework enhanced by transfer learning. This approach first learns generalized representations from a source domain containing abundant normal battery aging data and subsequently transfers this knowledge to generate synthetic samples in a target domain characterized by scarce fault data. By leveraging shared structural patterns across domains, the model is able to synthesize realistic and diverse time series sequences corresponding to various fault types, despite the presence of significant data imbalance [26].
Accordingly, the source domain is represented as and the target domain as , where x denotes battery voltage time series sequences and y is the corresponding condition label (e.g., normal aging, overcharge, or overdischarge).
To incorporate label information into the generative process, the reverse denoising step is reformulated as a conditional distribution:
where and are noisy data at adjacent time steps, c is the fault condition label, and , represent the predicted mean and variance. This conditional formulation enables the model to generate fault-specific trajectories by conditioning on the desired class.
The training objective is similarly extended to incorporate conditional information. The noise prediction loss is defined as
where ϵ is the true noise added at time step t, and is the model’s prediction conditioned on fault label c.
To promote effective knowledge transfer from the source to the target domain, we introduce domain-specific loss terms that account for distributional differences:
where and are the losses evaluated over the source and target distributions and , respectively. The function denotes a general task-specific loss, such as mean squared error (MSE).
The total objective for training the conditional diffusion model with transfer learning is defined as
Here, is a hyperparameter that balances the generalization capacity learned from the source domain with the adaptability to the target fault domain.
By leveraging abundant normal aging data to guide learning in the low-data fault domain, this conditional transfer learning framework significantly enhances the diversity and realism of the generated fault samples. As a result, the proposed model effectively addresses the data scarcity issue inherent in battery fault diagnosis and prognosis tasks.
3.1.3. Conditional Label Design
To enable the targeted synthesis of fault-specific battery data, the conditional label vector y is designed to incorporate categorical and physically interpretable continuous attributes. Specifically, the conditional vector comprises two key components: categorical fault types and fault-severity-related continuous features.
The categorical component is defined as a one-hot encoded vector indicating mutually exclusive fault modes, represented as
where denote overcharge and overdischarge fault scenarios, respectively. At any given time, exactly one component is set to 1, ensuring mutual exclusivity and clear semantic boundaries among fault modes.
The continuous attributes quantitatively encode fault severity based on physically measurable variables closely related to battery degradation mechanisms. For overcharge conditions, these variables include normalized peak voltage deviation , fault occurrence repetition count , and cumulative duration . Correspondingly, for overdischarge scenarios, the labels consist of minimum voltage deviation , discharge repetition count , and undervoltage exposure duration . The complete continuous label set can be expressed as
Hence, the integrated conditional label vector is structured as
These continuous features are selected based on their strong physical correlations to underlying battery degradation processes, such as lithium dendrite formation during sustained overcharge and SEI layer degradation during prolonged overdischarge. The selection and relevance of these continuous attributes are empirically validated by Pearson correlation analysis, highlighting consistent, interpretable linear relationships with observed voltage waveforms under respective fault scenarios.
To reinforce semantic clarity and prevent cross-contamination between different fault scenarios, continuous attributes corresponding to the inactive fault type are explicitly set to zero during training and data synthesis. Accordingly, when the overcharge condition is active, the conditional vector is structured as
Conversely, under overdischarge conditions,
This structured sparsity ensures meaningful and interpretable conditioning, facilitates disentangled representation learning, and thus effectively enhances the conditional generative model’s capability to synthesize realistic and physically consistent battery fault data.
3.1.4. Attention Method
While conditional diffusion with transfer learning enables fault-specific generation, it remains challenging to capture long-range temporal dependencies inherent in battery voltage time series. To address this limitation, we integrate a self-attention mechanism into the diffusion framework. Attention modules allow the model to dynamically weigh the importance of different temporal segments, facilitating the modeling of subtle yet critical variations across extended time horizons, which is particularly relevant for characterizing battery degradation and fault progression [27].
Thus, given an input feature tensor , where B denotes the batch size, C the number of feature channels, and L the sequence length, the self-attention mechanism computes weighted feature representations based on pairwise correlations across time. The operation is defined as
where Q, K, and V represent the query, key, and value matrices derived from linear projections of input features, and is a scaling factor corresponding to the dimensionality of the keys. The resulting attention outputs are projected back into the original feature space through a residual connection to stabilize training and preserve contextual continuity.
To explicitly incorporate fault condition information, we extend this mechanism into a conditional attention formulation by introducing learned bias terms associated with each fault type:
where is a bias matrix parameterized by the condition label c. This conditional attention enables the model to emphasize temporal patterns distinctive to specific fault types, such as overcharge or overdischarge, thereby enhancing the fidelity of fault-specific sequence generation.
In implementation, attention modules are embedded at multiple abstraction levels within the diffusion model, including intermediate encoder blocks and bottleneck layers. This hierarchical design empowers the model to jointly learn both global contextual dependencies and fine-grained temporal dynamics—capabilities that are essential for accurately synthesizing realistic fault behavior. The scheme of the attention method is shown in Figure 4.
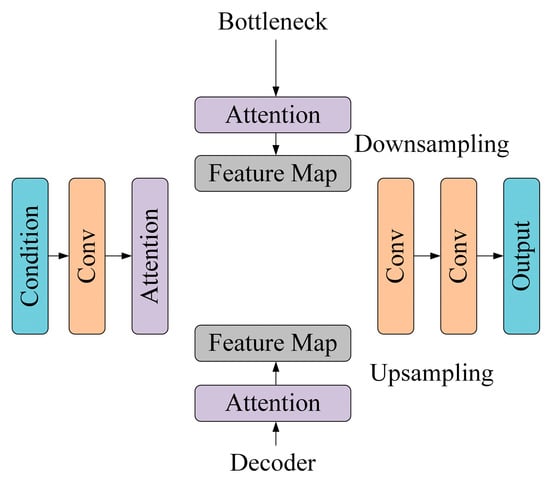
Figure 4.
Schematic overview of transferable conditional diffusion model with multi-level attention integration.
3.2. Validation Framework
To evaluate the fidelity of synthetic fault data generated by the proposed diffusion model, a multi-perspective validation framework is adopted. This framework assesses both statistical consistency and temporal alignment between real and generated sequences. The evaluation considers three key aspects: distributional divergence, pointwise error, and trend correlation.
Kullback–Leibler (KL) divergence is employed to quantify the difference between the probability distributions of real and synthetic datasets, serving as a measure of global statistical alignment. A lower KL divergence indicates a closer match between the underlying data distributions, reflecting improved consistency in the global structure of the signals [28,29].
To evaluate pointwise accuracy, MSE and mean absolute error (MAE) are calculated as
where and represent the real and generated values at each timestep. These metrics capture the average magnitude of deviation, with lower values indicating higher numerical similarity between real and generated signals.
To assess the similarity between the temporal patterns, the Pearson correlation coefficient (PCC) is computed to measure linear alignment between real and synthetic trends:
A higher PCC value indicates stronger consistency in trend dynamics between the real and generated sequences, validating the preservation of key temporal characteristics.
Although these metrics are computed from the same data, they capture different aspects of alignment and can yield different values. Specifically, KL divergence assesses how well the generated data replicates the global statistical structure of the real data, while MSE and MAE quantify pointwise numerical deviations, which are more sensitive to amplitude noise or slight temporal shifts. In contrast, PCC focuses solely on the similarity of trends, but is invariant to scaling and translation.
In this study, the diffusion-based generator is designed to prioritize distributional fidelity and temporal dynamics, which explains the observed low KL divergence and high PCC, despite the presence of moderate pointwise errors in MSE/MAE. These variations across metrics reflect their complementary roles in evaluating different fidelity dimensions and collectively offer a robust validation of the generated data’s utility.
Together, these complementary metrics ensure that the generated data not only reproduces the statistical structure of real fault signals but also retains the temporal dynamics critical for downstream diagnostic and prognostic tasks in battery health monitoring.
4. Results and Discussion
This section presents key experimental results and an analysis of the diffusion-based fault data augmentation framework for lithium-ion battery systems. First, the generative fidelity of the diffusion model is qualitatively and quantitatively assessed, using a GAN as a baseline for comparison. Next, the efficiency and effectiveness of model optimization strategies, including attention mechanisms and progressive layer unfreezing, are evaluated for their impact on data quality under limited fault data conditions. Finally, the validity of the augmented datasets is confirmed through fault classification tasks using various deep learning architectures.
4.1. Feasibility of Diffusion Model
Based on the training protocol detailed in Section 3, this subsection evaluates the fundamental generative fidelity and computational efficiency of diffusion models for fault data augmentation. Visual inspections of the generated samples across the training epochs illustrate the convergence and qualitative resemblance to real fault patterns. These visual results, depicted in Figure 5, confirm that the synthetic voltage profiles generated by the conditional diffusion model accurately capture real charge dynamics, such as rapid voltage rise, mid-range nonlinearity, and saturation behavior, even with limited training data.
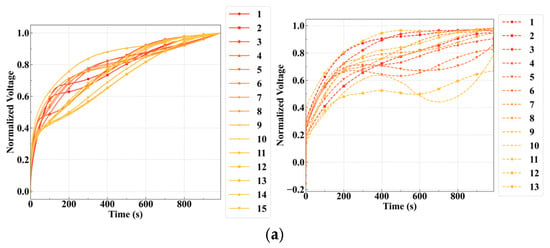
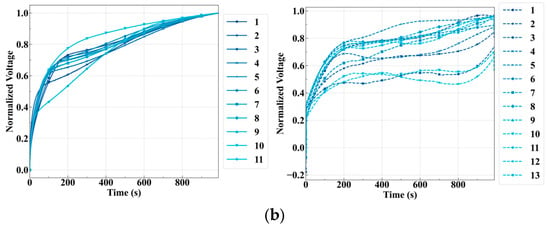
Figure 5.
Synthetic voltage profiles under fault conditions. Original and generated voltage curves for mild overcharge (a) and overdischarge (b) using the conditional diffusion model. The samples show high similarity to real fault profiles.
Since most battery fault diagnosis problems are inherently formulated as classification tasks, evaluating downstream classification performance is essential. This allows us to assess whether the generated fault data effectively enhance the model’s ability to identify and differentiate fault types, especially under data-scarce conditions.
Table 1 summarizes the computational costs associated with each generative framework. Compared with the GAN baseline, which required up to 3000 epochs of pre-training and an additional 1200 epochs of fine-tuning for fault-specific training, the diffusion model converged significantly faster, requiring only 200 epochs of pre-training and 150–200 epochs of fine-tuning. This reduction in computational demand highlights the diffusion model’s efficiency, largely attributable to its training mechanism, which does not rely on adversarial dynamics.

Table 1.
Computational costs of data augment framework for training and tuning.
Generative fidelity is quantitatively evaluated using KL divergence, MSE, MAE, and PCC, as summarized graphically in Figure 6. Under the mild overcharge condition (label “C”), the diffusion model yielded a KL divergence of 0.00995, an MSE of 0.01257, an MAE of 0.08035, and a PCC of 0.91425. Although the GAN achieved slightly better metrics in this scenario—such as an MAE of 0.05088 and a PCC of 0.97553—the performance differences remained minor. Similarly, under mild overdischarge conditions (label “D”), the diffusion model achieved a KL divergence of 0.01533 and a PCC of 0.93535, again closely approaching GAN performance (PCC 0.98937), despite operating under data-scarce conditions and fewer training epochs.
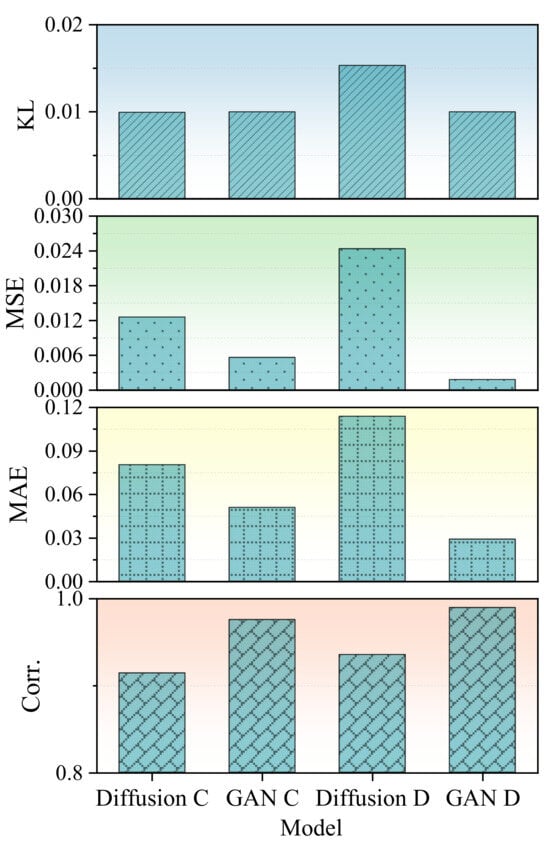
Figure 6.
Quantitative comparison of generative models. Performance of diffusion and GAN models regarding four metrics (KL, MSE, MAE, PCC) for fault types C and D. Diffusion achieves comparable results with lower training costs.
These empirical findings are consistent with several of the theoretical strengths of diffusion models. First, diffusion models employ denoising score matching, a likelihood-based objective that promotes stable gradient flows and helps avoid mode collapse, which is a common issue in GANs [30,31]. This property is particularly advantageous in rare fault scenarios, where data scarcity often leads to overfitting. In addition, the iterative generation process supports progressive sample refinement, which helps preserve both global structure and local variations—an important requirement for time-series data. Moreover, the conditional structure of diffusion models allows for targeted sample generation based on fault labels, supporting class-consistent synthesis, even when data is sparse.
The conditional diffusion model demonstrates comparable generative performance to that of GANs, while significantly reducing computational resources. Its theoretical stability, precise temporal reconstruction capabilities, and robust class-conditional consistency make it particularly suitable for fault data augmentation tasks in battery diagnostics, where annotated fault data is inherently limited.
4.2. Model Optimization
4.2.1. Attention Mechanisms
To enhance the diffusion model’s ability to refine informative patterns from limited fault datasets, attention mechanisms were integrated into the network architecture. This design enables the model to focus selectively on salient temporal and structural features, thereby improving the quality of conditional generation. Such refinement is particularly advantageous in low-data regimes, where maximizing the utility of the available information is essential. The integration retains the original diffusion framework, while introducing minimal additional complexity, ensuring scalability and compatibility with downstream diagnostic tasks.
Figure 7 compares the performance of diffusion models with and without attention under mild overcharge (C) and overdischarge (D) conditions. Models equipped with attention consistently outperform their non-attention counterparts across all four metrics. For instance, under condition C, the PCC improves from 0.29 to 0.91, and the MAE drops from 0.24 to 0.08. Similar improvements are observed under condition D, where attention substantially reduces generative variability and improves output fidelity.
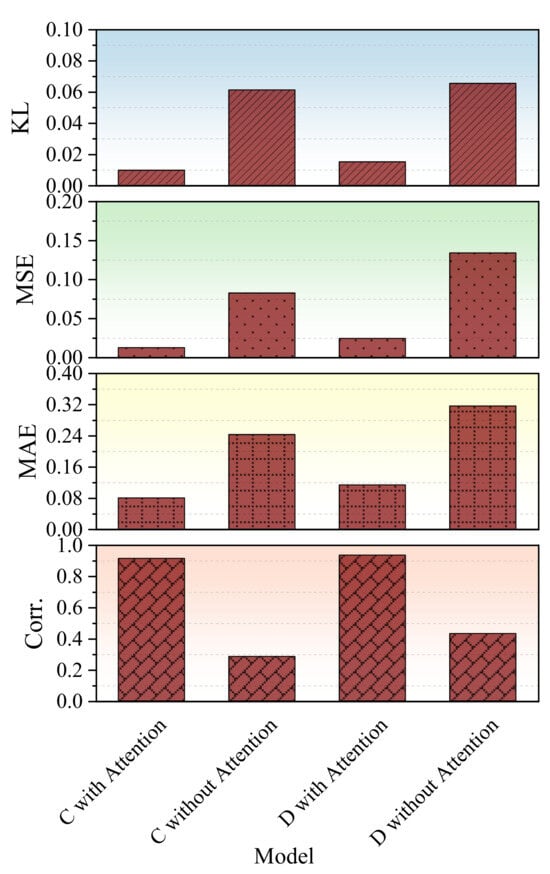
Figure 7.
Effect of attention mechanisms on generative performance. Comparison of diffusion models with and without attention under overcharge (C) and overdischarge (D) conditions. Models with attention show lower error metrics (KL, MSE, MAE) and higher PCC, demonstrating improved fidelity and stability for synthetic fault data generation.
These performance gains stem from the attention mechanism’s ability to dynamically prioritize fault-relevant features during sample generation. In the diffusion process, attention guides each denoising step toward critical time-localized or structurally significant cues, which is especially important for capturing subtle deviations indicative of faults. By adaptively allocating computational focus, the model better preserves fine-grained temporal features that might otherwise be overlooked.
Beyond empirical improvements, attention also improves interpretability and consistency. It introduces a soft alignment between the conditioning signal (i.e., the fault label) and the model’s internal states, facilitating class-specific fidelity, even in data-scarce scenarios. These results indicate that attention is not merely an auxiliary addition, but a valuable component that enhances both representational precision and robustness in conditional diffusion-based fault data augmentation.
4.2.2. Progressive Layer Unfreezing
To adapt the pretrained diffusion model to a fault domain with limited data, a progressive layer unfreezing strategy was adopted during transfer learning. Instead of updating all model parameters simultaneously, this approach incrementally unfreezes deeper layers over time. Such staged fine-tuning allows early layers to retain transferable low-level features, while later layers gradually specialize in fault-specific patterns. This process helps reduce overfitting, stabilizes convergence, and improves generalization in small-sample scenarios.
Notably, this hierarchical adaptation also reflects the invariance-of-representation principle discussed in representation theory and information geometry, where lower layers preserve stable, transformation-invariant features, while higher layers adapt to task-specific manifolds [32,33].
Figure 8 illustrates the impact of three unfreezing configurations: (i) unfreezing only the final layer, (ii) unfreezing the last three layers, and (iii) fully unfreezing the entire model. Among these, the three-layer unfreezing strategy achieves the best balance between adaptability and stability. It consistently outperforms the other settings across key evaluation metrics.
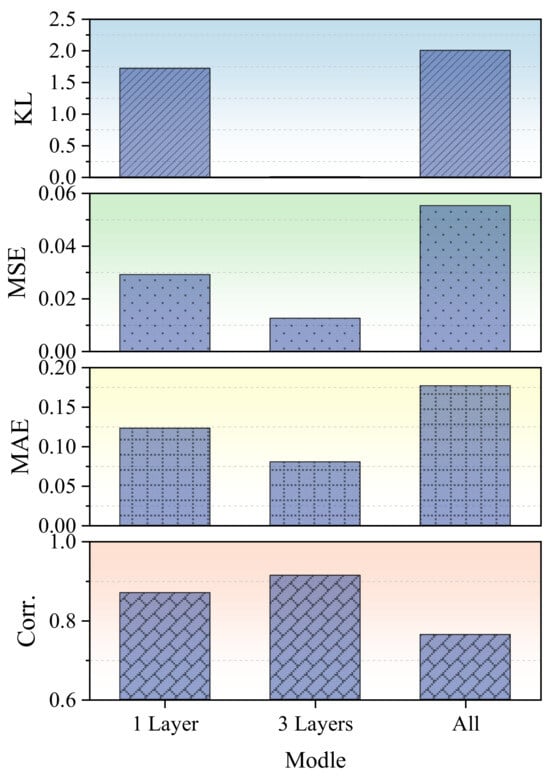
Figure 8.
Impact of layer unfreezing strategies on fine-tuning performance. Evaluation of three transfer learning strategies for the diffusion model: unfreezing the last layer, the last three layers, and all layers. The three-layer unfreezing configuration achieves optimal results across all scenarios.
Specifically, unfreezing only a single layer results in limited representational flexibility and moderate accuracy. In contrast, fully unfreezing the entire network leads to unstable optimization, reflected by a high MAE of 0.177 and a reduced PCC of 0.764, likely due to overfitting and loss of pretrained knowledge. The three-layer strategy achieves the lowest KL divergence and the highest PCC (0.914), indicating effective adaptation without compromising generalizability.
These findings align with established principles in transfer learning. Gradually increasing the number of trainable layers enables the model to refine higher-level features while preserving useful base representations. This prevents abrupt shifts in internal feature space and supports smoother optimization, which is particularly critical when training data is sparse.
4.3. Practical Test
Having optimized the diffusion-based generative model in Section 4.2, we now evaluate the practical utility of the augmented fault datasets in regards to downstream fault diagnosis performance. As most fault diagnosis frameworks in lithium-ion battery systems rely on classification models, this evaluation serves as a direct and application-aligned validation of the augmented data. Unlike statistical similarity measures, classification tasks test whether the synthetic data contain informative and discriminative features that contribute to real-world diagnostic improvement.
Specifically, several widely used deep learning classifiers—including convolutional neural network–long short-term memory (CNN–LSTM), bidirectional LSTM (Bi-LSTM), LSTM, gated recurrent unit (GRU), one-dimensional CNN (1D-CNN), and multi-layer perceptron (MLP)—were trained and tested on both original and diffusion-augmented datasets for overcharge and overdischarge scenarios. The evaluation focused on classification accuracy, precision, recall, F1-score, and ROC–AUC, providing a comprehensive measure of augmentation effectiveness. This setup allowed for direct comparisons of classifier robustness before and after data augmentation.
Results for the overcharge scenario are summarized first. Figure 9a,b shows the classification performance of the six models before and after augmentation. Prior to augmentation, despite achieving high accuracy (approximately 0.99), most models displayed poor recall and F1 scores, with values close to zero (≤0.05). This indicated significant difficulties in correctly identifying fault instances due to limited training data. After augmentation, substantial improvements were observed across all models. For instance, CNN–LSTM, GRU, and LSTM exhibited consistent increases in recall and F1 scores, reaching values around 0.92 (recall) and 0.96 (F1-score). Models such as Bi-LSTM and 1D-CNN achieved perfect performance across all metrics, including an ROC–AUC of 1.0.
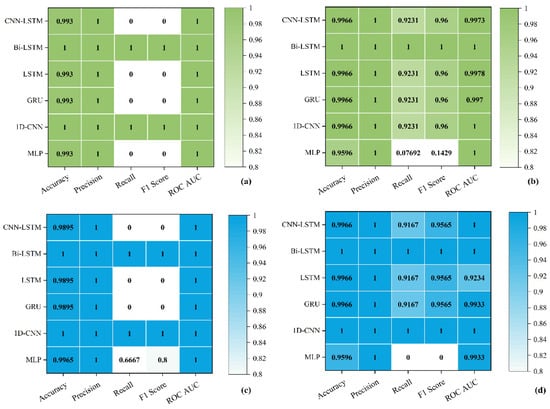
Figure 9.
Performance comparison of diagnostic models under overcharge and overdischarge conditions, before and after data augmentation. (a,c) Without augmentation, performance varies across models, with some models showing relatively low recall and F1 scores. (b,d) After applying data augmentation, all models demonstrate improved performance, especially in recall and F1 metrics, indicating enhanced fault classification capability and better generalization across fault types.
The overdischarge scenario results are presented in Figure 9c,d. This fault condition is more challenging due to its subtle characteristics. Before augmentation, temporal models again showed low recall and F1 scores (≤0.05), despite maintaining high accuracy (>0.98), indicating class imbalance and inadequate fault representation. The MLP model performed slightly better, achieving a recall of 0.67 and an F1-score of 0.80, although still underperforming compared to more complex architectures. After augmentation, all temporal models substantially improved, achieving recall, F1, and ROC–AUC scores above 0.91. Notably, Bi-LSTM and 1D-CNN again achieved perfect metrics. These improvements confirm that diffusion-generated synthetic samples effectively capture and reinforce discriminative fault features, even for subtle fault types like mild overdischarge.
The quantitative enhancements demonstrate that the proposed diffusion-based augmentation framework significantly improves model sensitivity to rare fault conditions. By enriching the training dataset with realistic synthetic samples, the approach enhances fault detection capability across both relatively evident and more subtle scenarios. Temporal models, dependent on sequential features, particularly benefit from augmented data due to its improved temporal diversity and feature consistency.
5. Conclusions
This study presents a conditional diffusion-based data augmentation framework specifically developed to address fault data scarcity in lithium-ion battery diagnostics. The proposed methodology incorporates a conditional sampling strategy that allows for targeted generation of synthetic samples corresponding to specific fault types and severity levels. Unlike adversarial approaches susceptible to mode collapse, the diffusion-based method provides improved diversity and broader representation of rare fault scenarios, thereby effectively enriching the training dataset.
To enhance generation fidelity and adapt to temporal characteristics inherent in battery data, the diffusion model is optimized by integrating attention mechanisms along with a progressive layer unfreezing strategy. These enhancements enable the model to effectively capture long-range temporal dependencies and maintain stable performance during fine-tuning. Experimental validation confirms that the optimized diffusion model generates synthetic sequences exhibiting strong statistical consistency and temporal alignment with real fault data, underscoring its suitability for practical deployment.
The efficacy of the proposed framework is validated through comprehensive statistical assessments and diagnostic evaluations utilizing multiple deep learning classifiers. Classifiers trained on augmented datasets exhibit notable improvements in recall and F1 scores, particularly for subtle or underrepresented faults.
Future research will extend this framework to encompass additional fault conditions, such as thermal abuse and internal short circuits. Efforts will also focus on improving model robustness under varying operational and environmental scenarios. Incorporating physics-informed constraints and uncertainty quantification into the diffusion-based framework represents another promising direction, aimed at further ensuring physical consistency and enhancing the reliability and safety of synthesized battery data in practical applications. Finally, comparative analyses with traditional model-based diagnostic methods will be pursued to further evaluate diagnostic accuracy, computational efficiency, and potential deployment on embedded hardware platforms in energy storage systems. In addition, the integration of lightweight GAN components into the diffusion pipeline—potentially through collaborative or distillation-based strategies—will be explored to assess whether hybrid generative architectures can provide further benefits under data-scarce and resource-constrained conditions.
Author Contributions
Conceptualization, Z.Y.; methodology, Z.Y.; software, Z.Y. and W.L.; validation, Z.Y. and Y.P.; formal analysis, Z.Y. and W.L.; investigation, Z.Y.; resources, Z.Y.; data curation, Z.Y., Y.P. and W.L.; writing—original draft preparation, Z.Y.; writing—review and editing, J.M. and Z.S.; visualization, Z.Y.; supervision, J.M. and Z.S.; project administration, Z.Y.; funding acquisition, Z.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by [National Key Research and Development Program of China] grant number [2023YFB2408201].
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Li, C.; Zeng, K.; Li, G.; Chen, P.; Li, B. A novel fault diagnosis method for battery energy storage station based on differential current. Appl. Energy 2023, 352, 121970. [Google Scholar] [CrossRef]
- Han, X.; Li, Y.; Nie, L.; Huang, X.; Deng, Y.; Yan, J.; Kourkoumpas, D.-S.; Karellas, S. Comparative life cycle greenhouse gas emissions assessment of battery energy storage technologies for grid applications. J. Clean Prod. 2023, 392, 136251. [Google Scholar] [CrossRef]
- Zhao, J.; Feng, X.; Tran, M.; Fowler, M.; Ouyang, M.; Burke, A.F. Battery safety: Fault diagnosis from laboratory to real world. J. Power Sources 2024, 598, 234111. [Google Scholar] [CrossRef]
- Bamati, S.; Chaoui, H. Developing an online data-driven state of health estimation of lithium-ion batteries under random sensor measurement unavailability. IEEE T. Transp. Electr. 2022, 9, 1128–1141. [Google Scholar] [CrossRef]
- Johnson, J.M.; Khoshgoftaar, T.M. Survey on deep learning with class imbalance. J. Big Data 2019, 6, 1–54. [Google Scholar] [CrossRef]
- Abowd, J.M.; Schmutte, I.M.; Vilhuber, L. Disclosure Limitation and Confidentiality Protection in Linked Data. In Administrative Records for Survey Methodology; Wiley: Hoboken, NJ, USA, 2021; pp. 25–59. [Google Scholar]
- Zhao, J.; Qu, X.; Wu, Y.; Fowler, M.; Burke, A.F. Artificial intelligence-driven real-world battery diagnostics. Energy AI 2024, 18, 100419. [Google Scholar] [CrossRef]
- Qiu, X.; Wang, S.; Chen, K. A conditional generative adversarial network-based synthetic data augmentation technique for battery state-of-charge estimation. Appl. Soft. Comput. 2023, 142, 110281. [Google Scholar] [CrossRef]
- Liu, X.; Yang, K.; Zou, B.; Zhang, X.; Bao, G.; Ma, B.; Zhang, L.; Tan, R. Accurate estimation of state of health for lithium-ion batteries based on Pyraformer and TimeGAN data augmentation. J. Power Sources 2025, 640, 236722. [Google Scholar] [CrossRef]
- Hu, F.; Dong, C.; Tian, L.; Mu, Y.; Yu, X.; Jia, H. CWGAN-GP with residual network model for lithium-ion battery thermal image data expansion with quantitative metrics. Energy AI 2024, 16, 100321. [Google Scholar] [CrossRef]
- Naaz, F.; Herle, A.; Channegowda, J.; Raj, A.; Lakshminarayanan, M. A generative adversarial network-based synthetic data augmentation technique for battery condition evaluation. Int. J. Energ. Res. 2021, 45, 19120–19135. [Google Scholar] [CrossRef]
- Ren, Z.; Zhu, Y.; Liu, Z.; Feng, K. Few-shot GAN: Improving the performance of intelligent fault diagnosis in severe data imbalance. IEEE T. Instrum. Meas. 2023, 72, 1–14. [Google Scholar] [CrossRef]
- Dubiński, J.; Deja, K.; Wenzel, S.; Rokita, P.; Trzcinski, T. Selectively increasing the diversity of gan-generated samples. In Proceedings of the International Conference on Neural Information Processing, New Delhi, India, 22–26 November 2022; Springer: Berlin/Heidelberg, Germany; pp. 260–270. [Google Scholar]
- Yang, L.; Zhang, Z.; Song, Y.; Hong, S.; Xu, R.; Zhao, Y.; Zhang, W.; Cui, B.; Yang, M.-H. Diffusion models: A comprehensive survey of methods and applications. ACM Comput. Surv. 2023, 56, 1–39. [Google Scholar] [CrossRef]
- Cao, H.; Tan, C.; Gao, Z.; Xu, Y.; Chen, G.; Heng, P.-A.; Li, S.Z. A Survey on Generative Diffusion Models. IEEE Trans. Knowl. Data Eng. 2024, 36, 2814–2830. [Google Scholar] [CrossRef]
- Wen, H.; Lin, Y.; Xia, Y.; Wan, H.; Wen, Q.; Zimmermann, R.; Liang, Y. DiffSTG: Probabilistic Spatio-Temporal Graph Forecasting with Denoising Diffusion Models. In Proceedings of the 31st ACM International Conference on Advances in Geographic Information Systems (SIGSPATIAL), Hamburg, Germany, 13–16 November 2023; Association for Computing Machinery: New York, NY, USA; pp. 1–12. [Google Scholar]
- Kazerouni, A.; Aghdam, E.K.; Heidari, M.; Azad, R.; Fayyaz, M.; Hacihaliloglu, I.; Merhof, D. Diffusion models in medical imaging: A comprehensive survey. Med. Image. Anal. 2023, 88, 102846. [Google Scholar] [CrossRef]
- Ho, J.; Salimans, T.; Gritsenko, A.; Chan, W.; Norouzi, M.; Fleet, D.J. Video diffusion models. Adv. Neural Inf. Process. Syst. 2022, 35, 8633–8646. [Google Scholar]
- Nguyen, V.C.; Quang, D.T. Estimation of SoH and internal resistances of Lithium ion battery based on LSTM network. Int. J. Electrochem. SC. 2023, 18, 100166. [Google Scholar] [CrossRef]
- Huang, S.; Li, J.; Wu, L.; Zhang, W. Data quality augmentation and parallel network modeling for residual life prediction of lithium-ion batteries. J. Power Electron. 2024, 24, 955–963. [Google Scholar] [CrossRef]
- Park, J.; Ko, H.; Lee, J. Modeling asset price process: An approach for imaging price chart with generative diffusion models. Comput. Econ. 2024, 1–27. [Google Scholar] [CrossRef]
- Yang, Z.; Pan, Y.; Liu, W.; Meng, J.; Song, Z. Enhanced fault detection in lithium-ion battery energy storage systems via transfer learning-based conditional GAN under limited data. J. Power Sources 2025, 645, 237192. [Google Scholar] [CrossRef]
- Yang, Z.; Zheng, K.; Zheng, H.; Zhou, F.; Meng, J.; Song, Z. Multi-task learning framework for fault detection in energy storage system lithium-ion batteries: From degradation to slight overcharge. J. Energy Storage 2025, 127, 117164. [Google Scholar] [CrossRef]
- Ahsan, M.M.; Raman, S.; Liu, Y.; Siddique, Z. A comprehensive survey on diffusion models and their applications. Preprints 2024. [Google Scholar] [CrossRef]
- Wang, G.; Cai, Y.; Liu, P.; Xia, J.; Su, S. Principles of Diffusion Models and Their Applications on Medicine. In Proceedings of the 2023 13th International Conference on Information Technology in Medicine and Education (ITME), Wuyishan, China, 24–26 November 2023; IEEE: Piscataway, NJ, USA; pp. 724–729. [Google Scholar]
- Zhou, Y.; Zhang, X.; Wang, Y.; Zhang, B. Transfer learning and its application research. J. Phys. Conf. Ser. 2021, 1920, 12058. [Google Scholar] [CrossRef]
- Soydaner, D. Attention mechanism in neural networks: Where it comes and where it goes. Neural Comput. Appl. 2022, 34, 13371–13385. [Google Scholar] [CrossRef]
- Apellániz, P.A.; Jiménez, A.; Galende, B.A.; Parras, J.; Zazo, S. Synthetic tabular data validation: A divergence-based approach. IEEE Access 2024, 12, 103895–103907. [Google Scholar] [CrossRef]
- Kosun, C. Examining vehicular speed characteristics through divergences from prior distributions. Sn. Appl Sci. 2021, 3, 199. [Google Scholar] [CrossRef]
- Ho, J.; Jain, A.; Abbeel, P. Denoising diffusion probabilistic models. In Proceedings of the 34th Conference on Neural Information Processing Systems (NeurIPS 2020), Online, 6–12 December 2020; Curran Associates, Inc.: Red Hook, NY, USA; Volume 33, pp. 6840–6851. [Google Scholar]
- Song, Y.; Sohl-Dickstein, J.; Kingma, D.P.; Kumar, A.; Ermon, S.; Poole, B. Score-based generative modeling through stochastic differential equations. arXiv 2011, arXiv:2011.13456. [Google Scholar]
- Wood, J.; Shawe-Taylor, J. Representation theory and invariant neural networks. Discret. Appl. Math. 1996, 69, 33–60. [Google Scholar] [CrossRef]
- Nielsen, F. An elementary introduction to information geometry. Entropy 2020, 22, 1100. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).