Early Remaining Useful Life Prediction for Lithium-Ion Batteries Using a Gaussian Process Regression Model Based on Degradation Pattern Recognition †
Abstract
1. Introduction
- (1)
- The insufficiently comprehensive feature extraction. Battery degradation influences the dynamic trajectories of various battery states, such as voltage, current, capacity, and others. This inspires researchers to perform lifetime predictions based on the variation in the above states. Existing battery early-life prediction methods tend to extract health features only from a direct or indirect aging physical quantity [34], which makes it difficult to characterize early decline comprehensively. For example, Yin et al. [35] focus on a single discharge-derived feature, i.e., average power, without considering charging-phase information or a broader set of health indicators, which may limit the richness of the feature space used for life prediction.
- (2)
- The empirically determined machine learning hyperparameters. The data-driven model’s parameters are also directly assigned by experience without optimization, which may lead to the degradation of battery early life prediction capability. This approach is highly dependent on trial and error and expert intuition, which can be both time-consuming and inconsistent across datasets or tasks. Moreover, without systematic optimization, models are less likely to reach their full predictive potential, and the reproducibility of results may suffer due to the lack of standardized tuning procedures.
- (3)
- The interference between batteries with different degradation modes. Many existing studies apply machine learning models directly to the full dataset without performing degradation mode classification or clustering [36,37]. However, such an approach overlooks the inherent heterogeneity in battery aging behaviors arising from variations in usage conditions, manufacturing inconsistencies, or operational environments. Without separating different degradation patterns, the learned model tends to average across distinct behaviors, potentially masking important trends and leading to degraded predictive accuracy and generalization performance. Batteries with large differences in lifespan may have differences in degradation mechanisms and interfere with each other in machine learning.
- The early aging of batteries in different life intervals may behave differently. To make the life prediction more targeted towards similar types, degradation pattern recognition was considered in advance. This prevents short-life batteries from being influenced by long-life batteries.
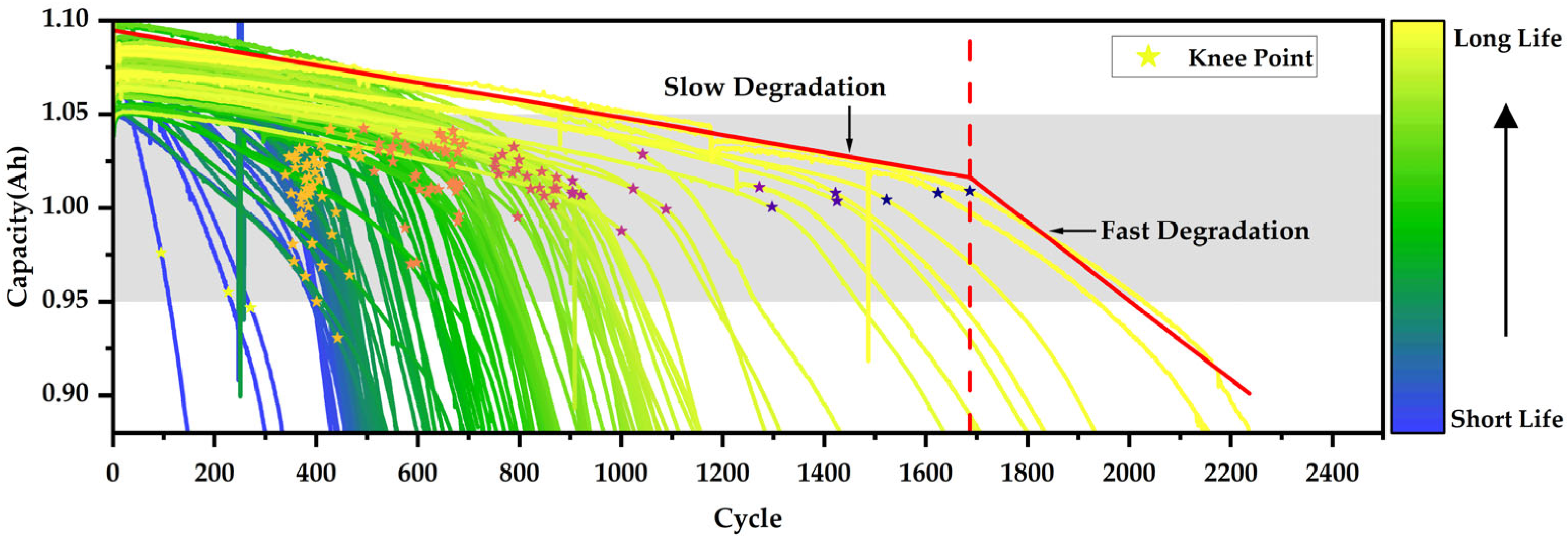
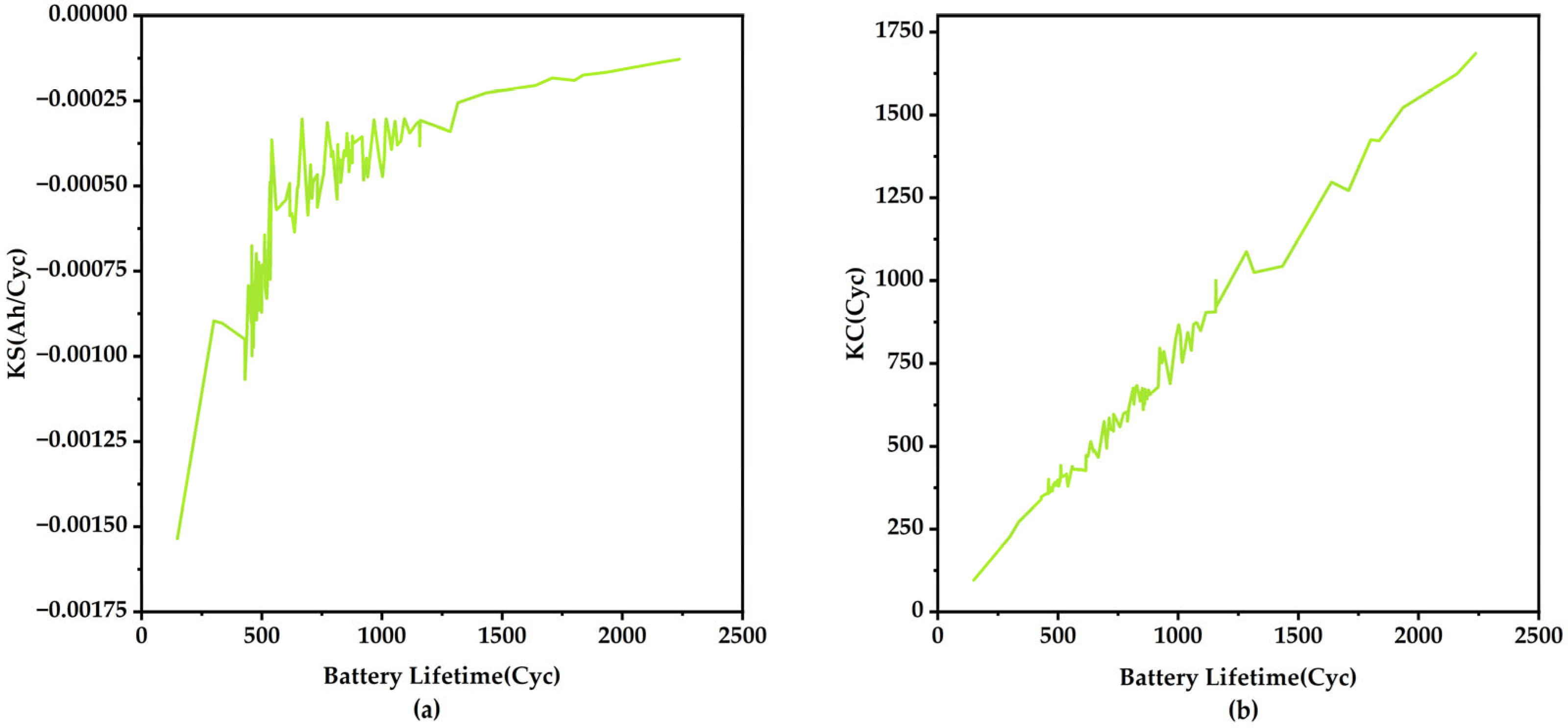
- Considering the influence of nonlinear aging on the lifetime, based on the correlation between the knee point and the EOL cycle, the predicted knee point and knee slope are innovatively used as supplementary features for the lifetime prediction, which improves the prediction accuracy of RUL.
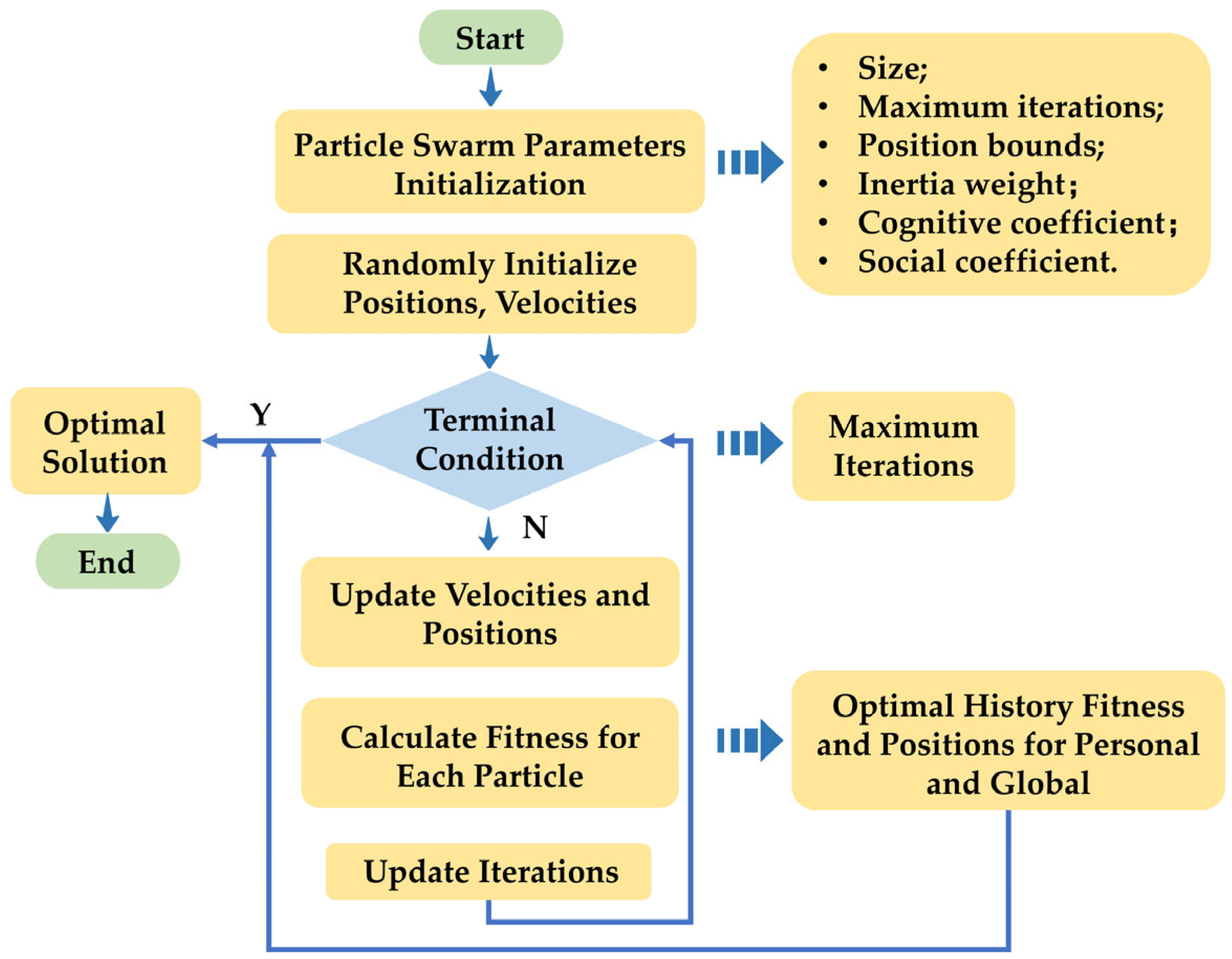
- To determine the hyperparameters of the composite kernel function in the GPR model, the particle swarm optimization algorithm was employed to achieve parameter self-tuning and enhance the adaptability of the prediction model.
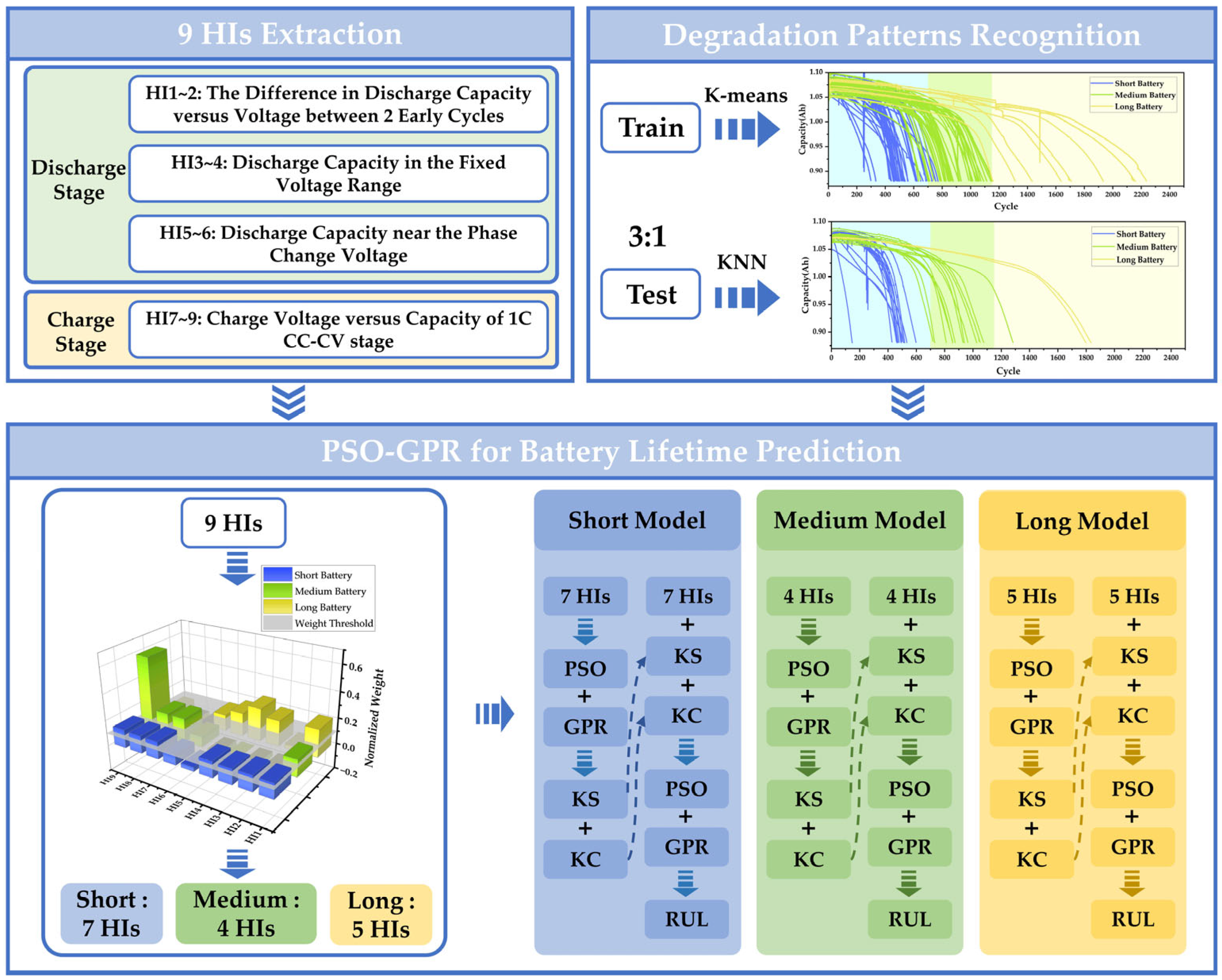
2. Battery Dataset, Feature Extraction, and Degradation Pattern Recognition
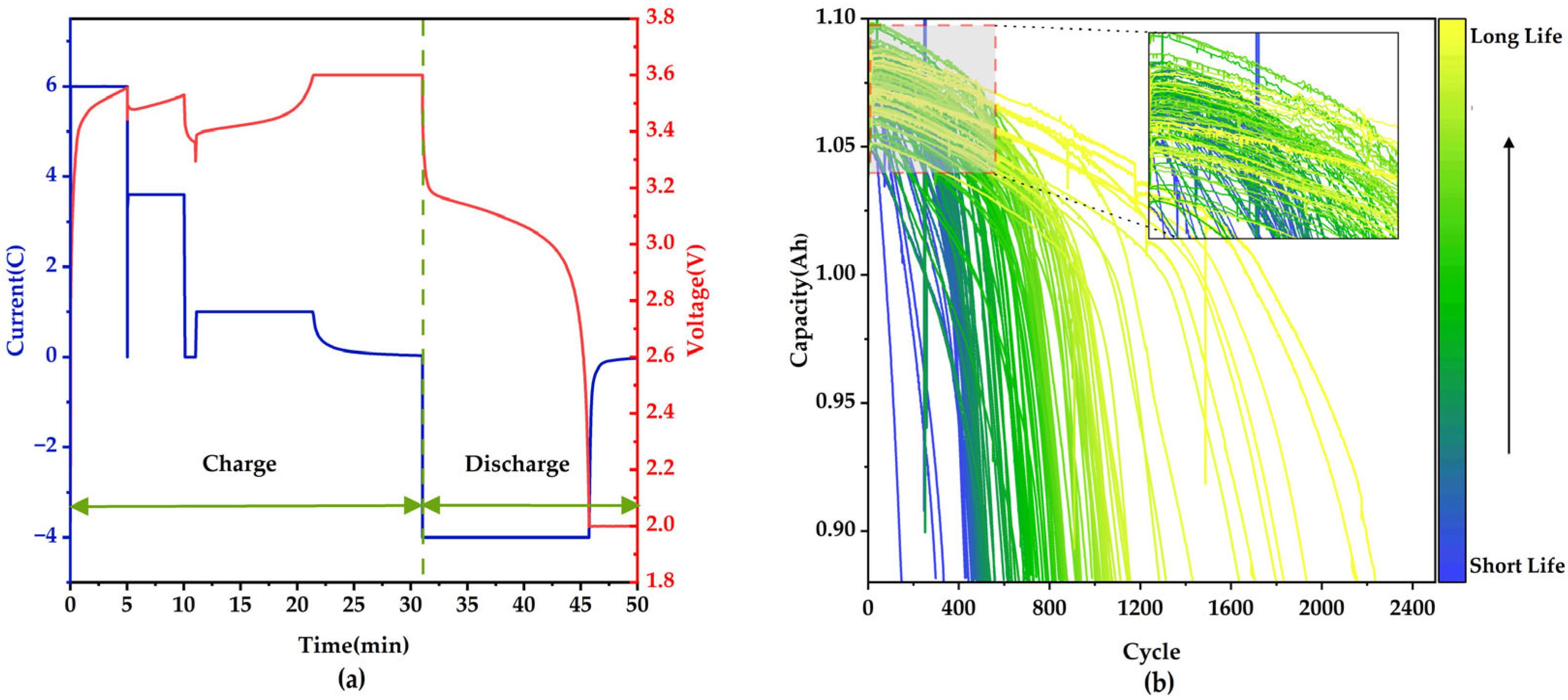
2.1. The Battery Aging Dataset
2.2. The Battery Health Indicator Extraction
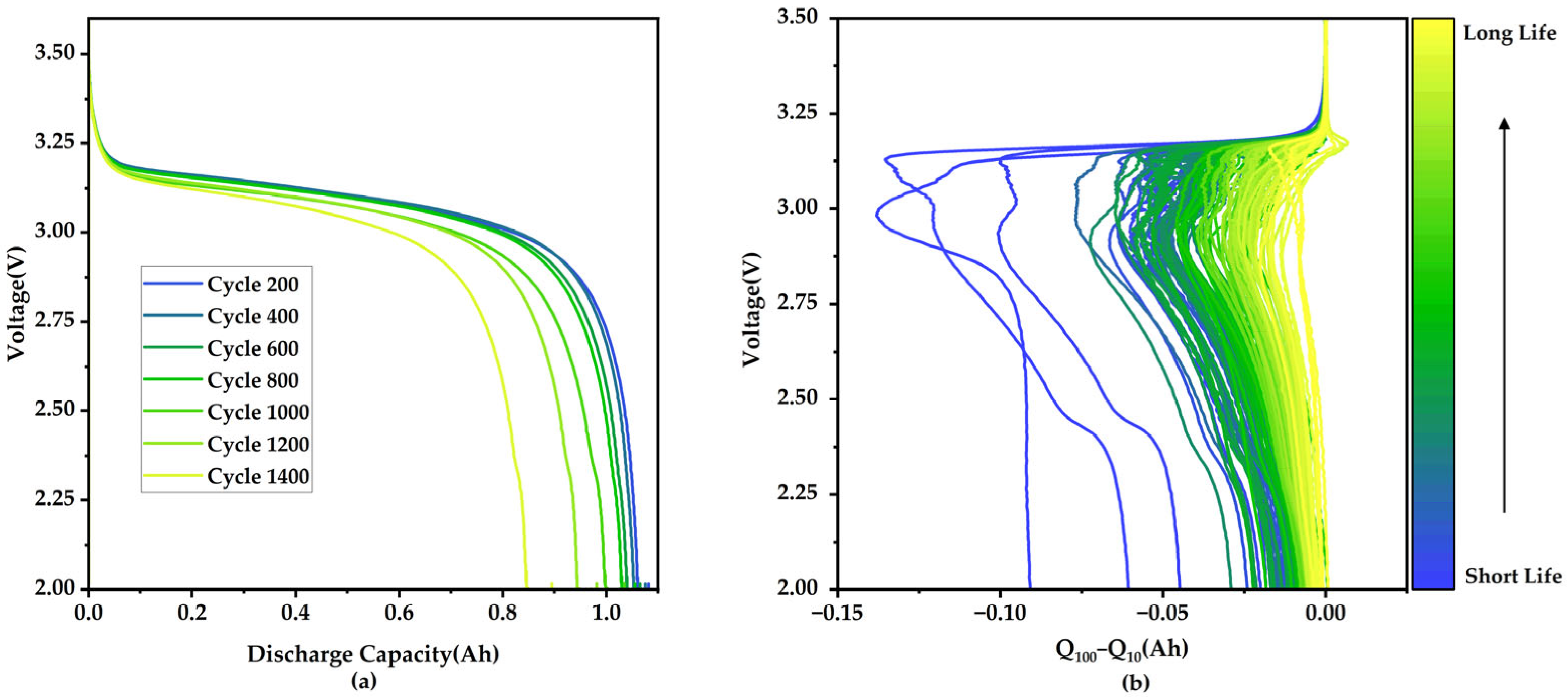
2.2.1. The Difference in Discharge Capacity Versus Voltage Between Two Early Cycles
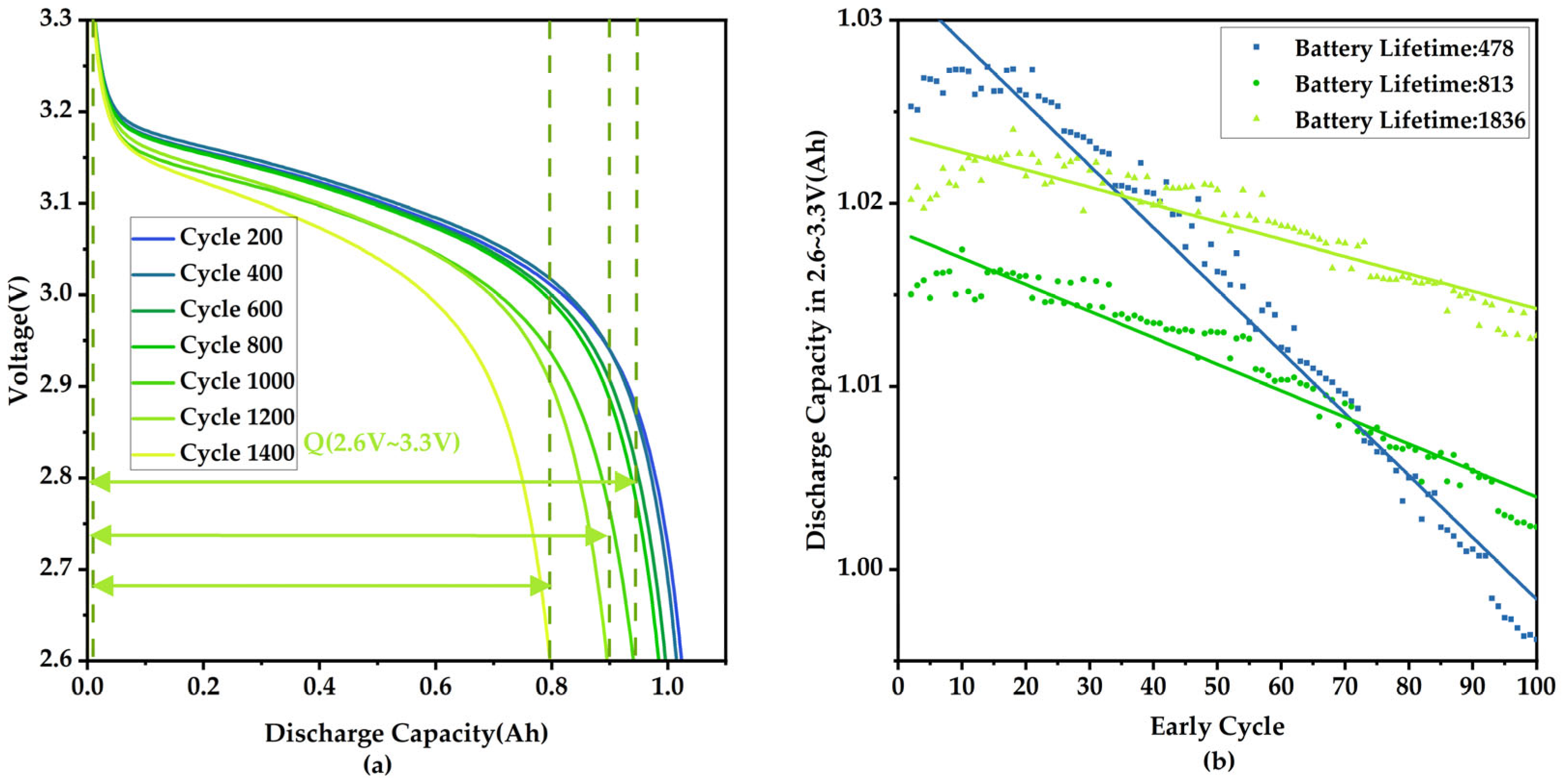
2.2.2. Discharge Capacity in the Fixed Voltage Range
2.2.3. Discharge Capacity near the Phase Change Voltage
2.2.4. Charge Capacity of 1C CC-CV Stage
2.2.5. The Correlation Analysis Between Battery Lifetime and HIs
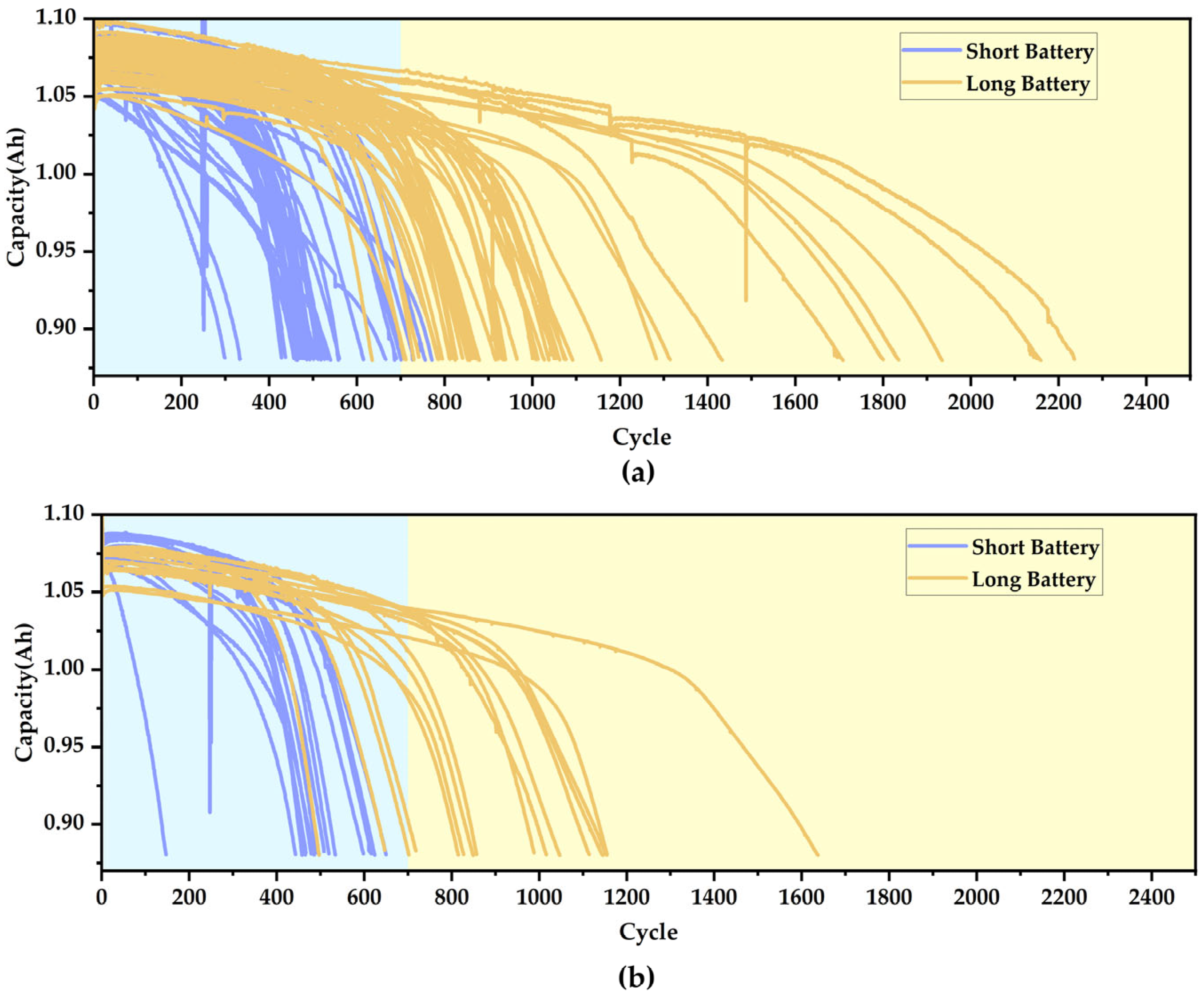
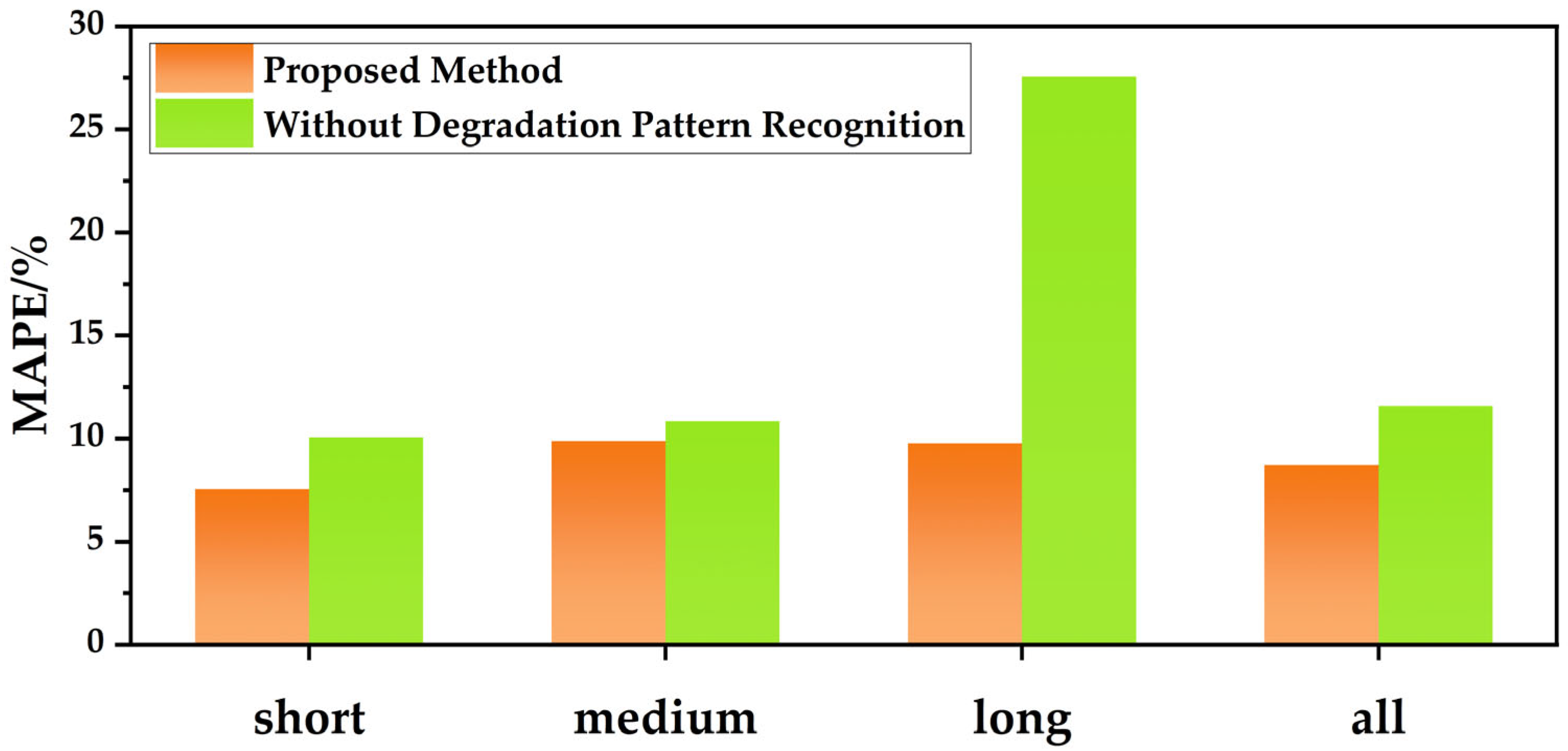
2.3. The Battery Early Degradation Pattern Recognition
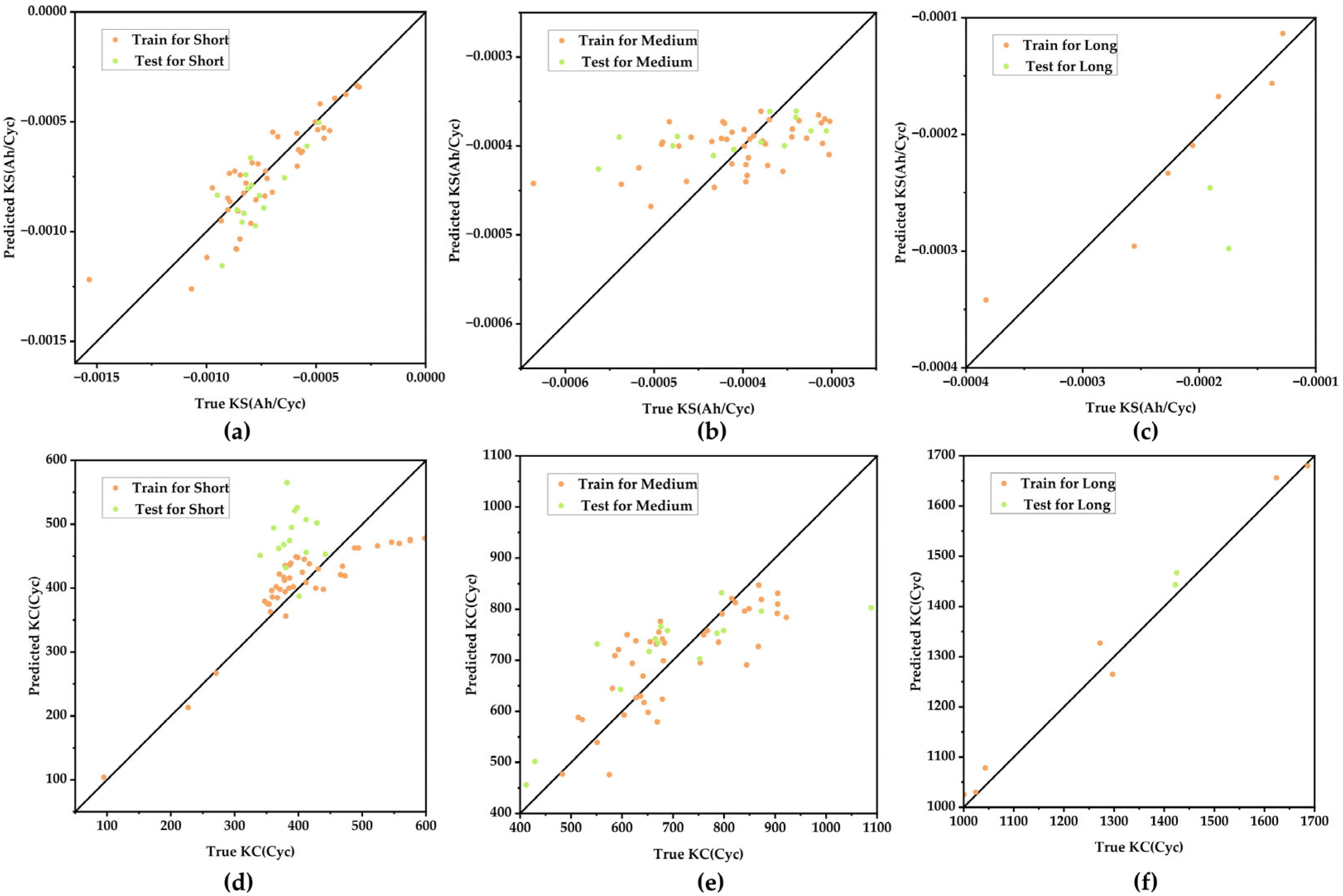
3. Feature Engineering and Supplementary Features Related to Knee
3.1. Feature Engineering
3.2. Identification of Supplementary Features Related to Knee Point
4. RUL Prediction Method
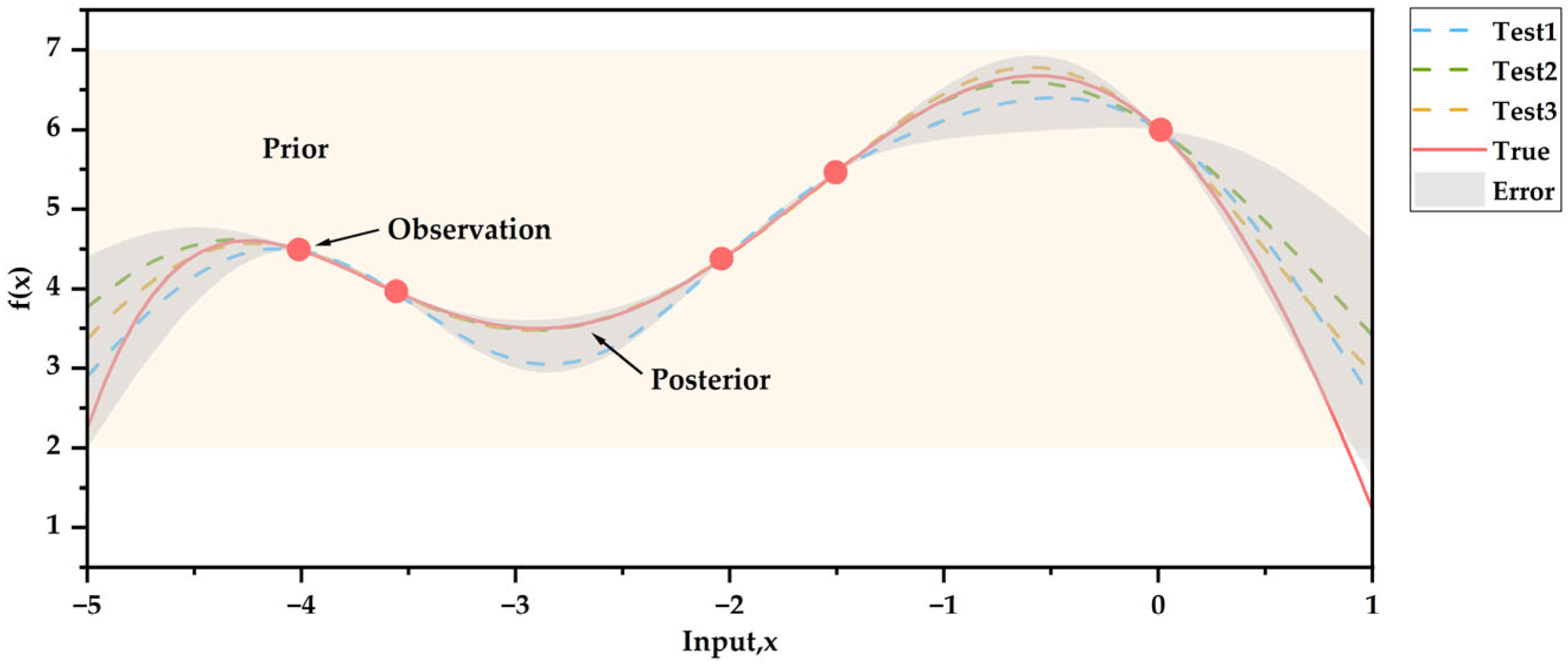
4.1. GPR-Based Prediction Model
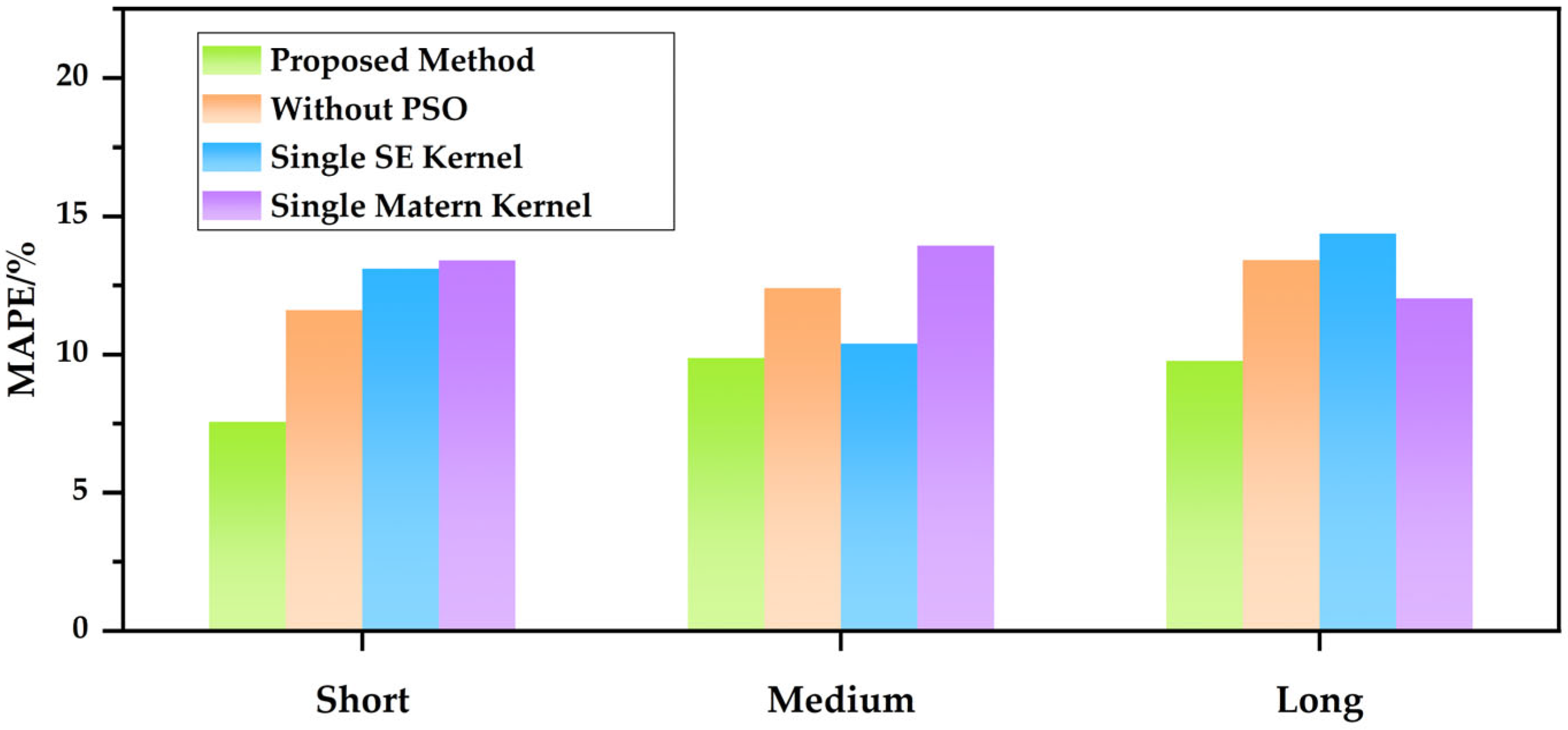
4.2. PSO-Based Hyperparameter Optimization
4.3. The General Framework of the RUL Prediction Method
5. Results and Discussion
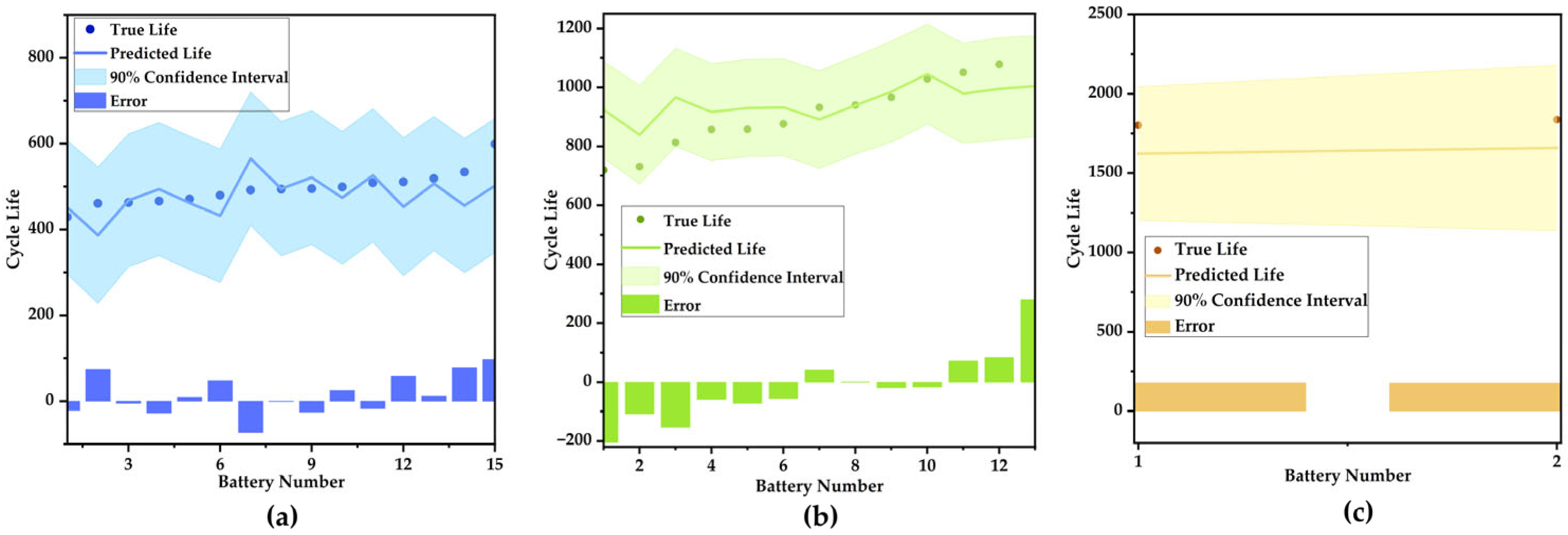
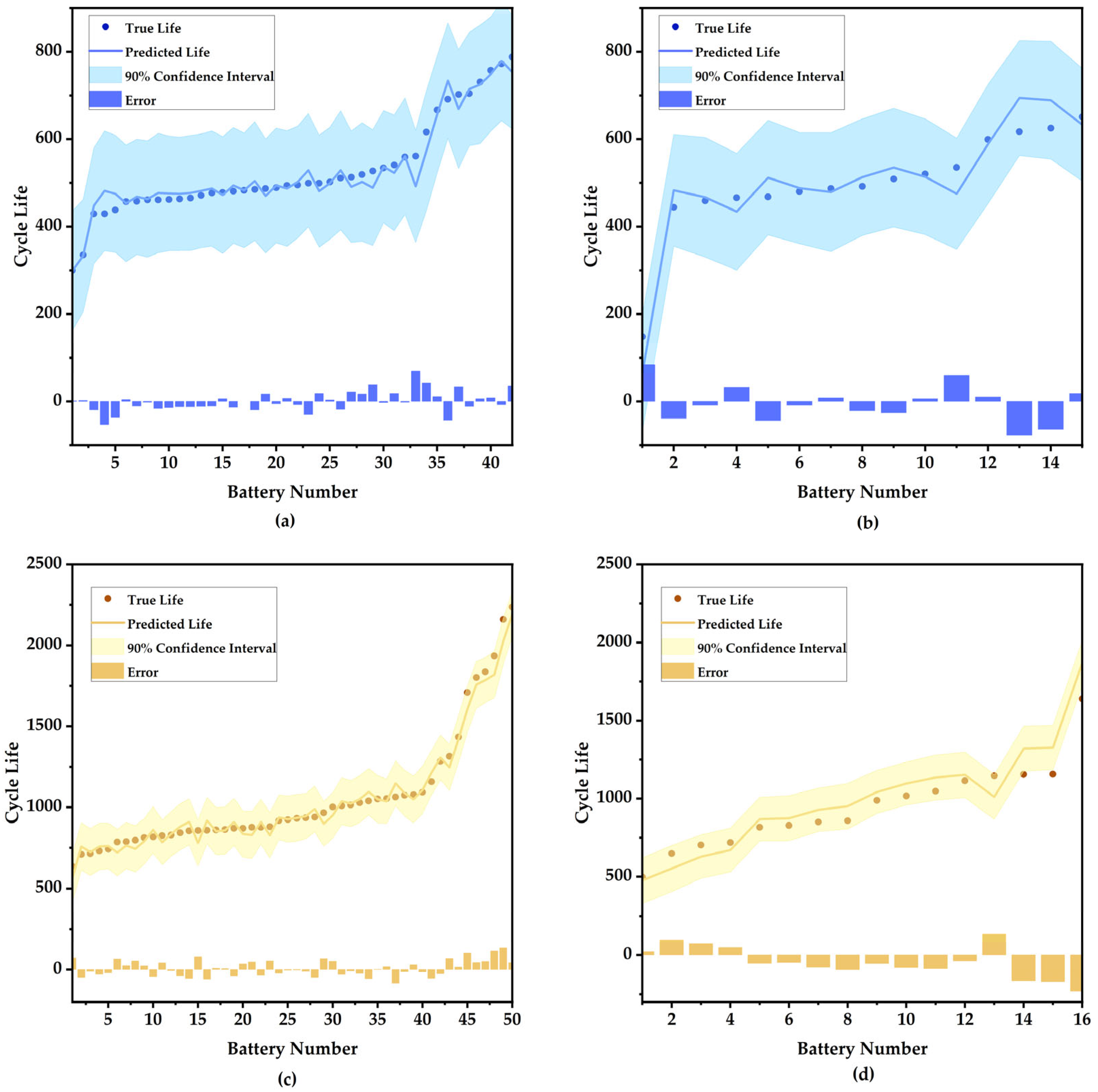
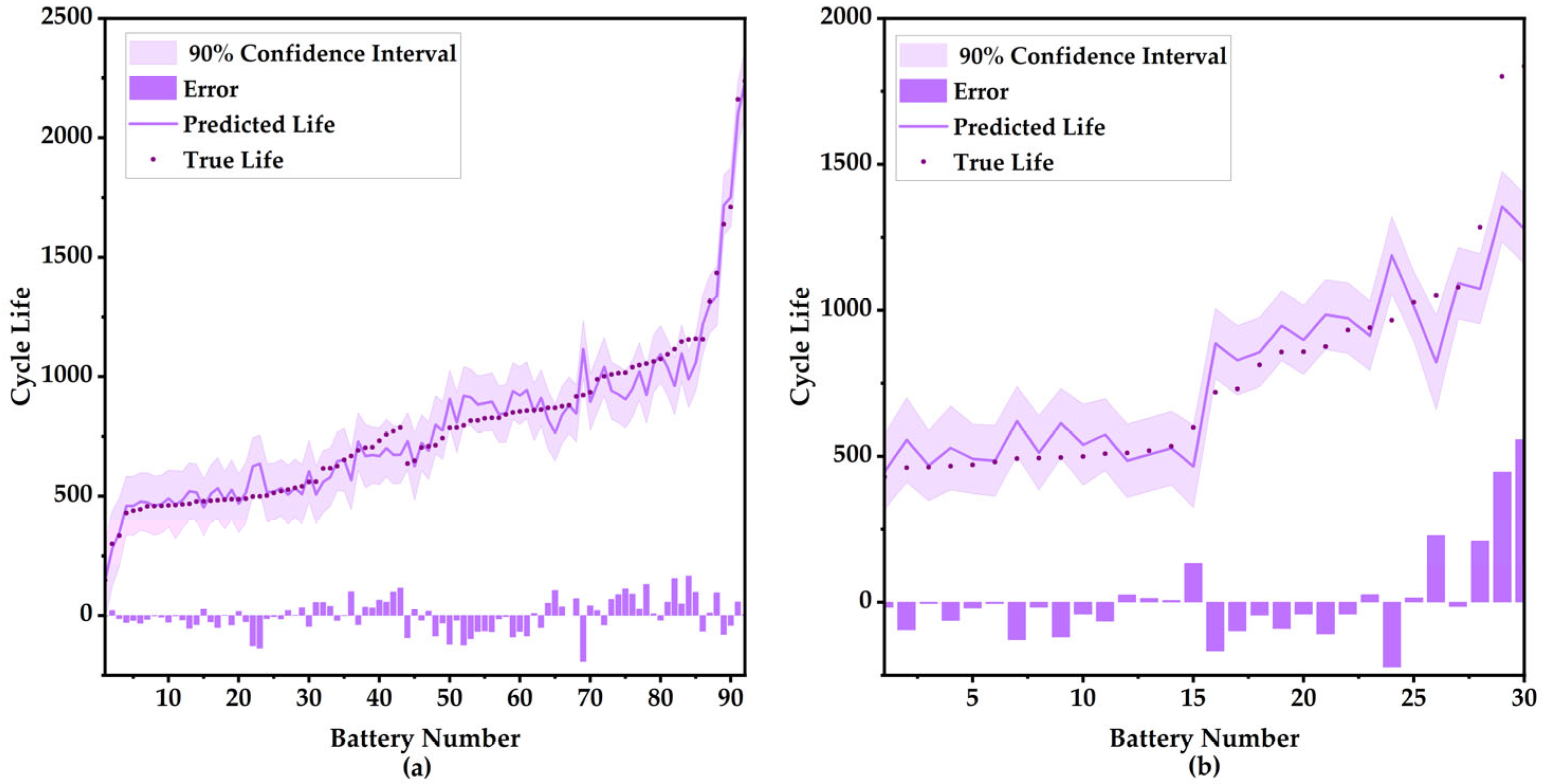
5.1. The Verification of RUL Prediction
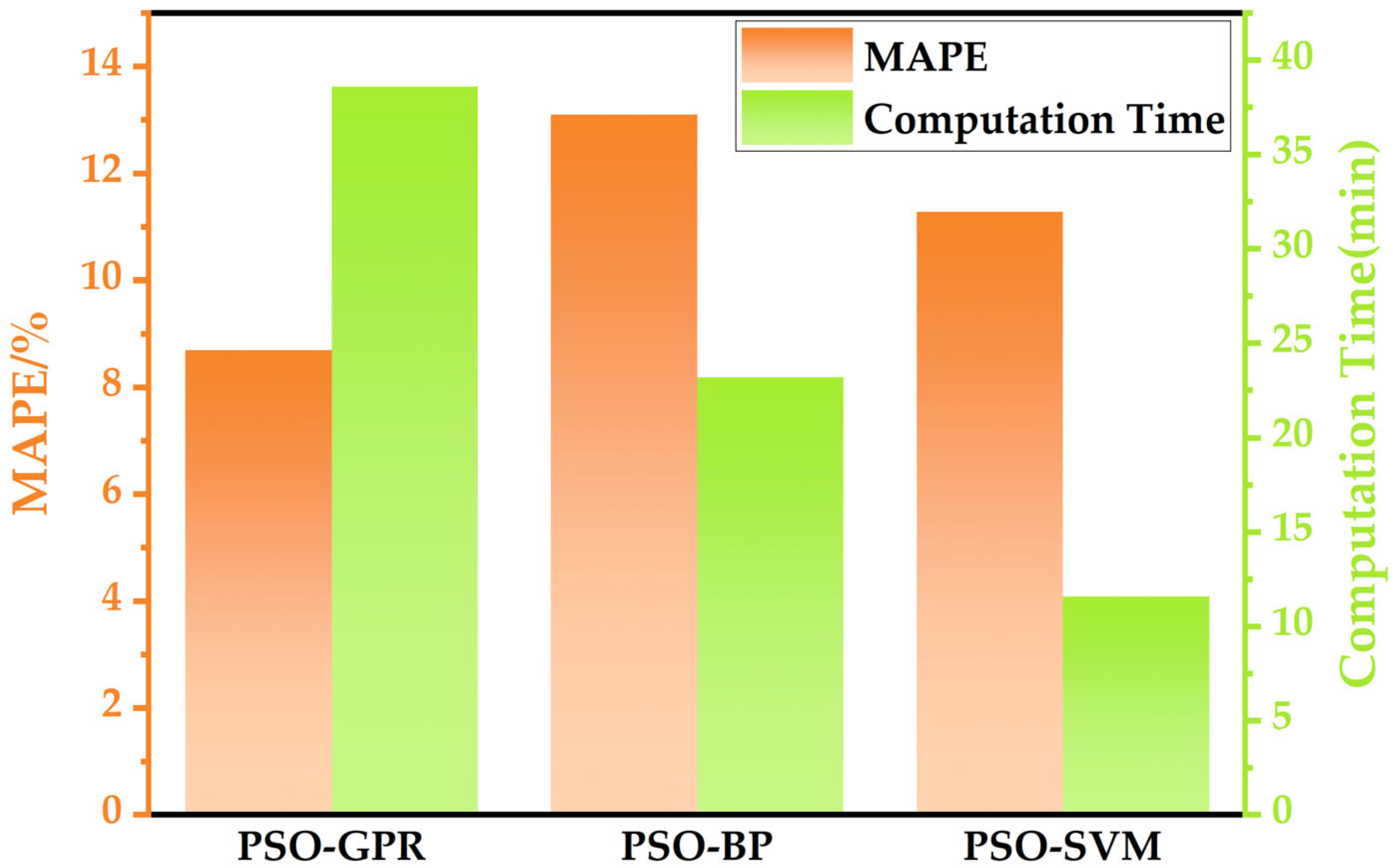
5.2. The Comparison with Other Models
5.2.1. Validation Result with Different Cluster Number
5.2.2. Validation Result with Different GPR Kernels
5.2.3. Validation Result with Other Algorithms
6. Limitations and Outlook
- This paper is actually a single-point estimation of battery life based on early feature extraction, which is only based on early (first 100 cycles) data to roughly predict how many cycles the battery can live. But in practical applications, it may be necessary to obtain the specific decline trajectory of the battery, i.e., the capacity at a certain point in time. Therefore, further attempts should be made to see if giving early degradation data can enable the prediction of battery decline trajectories.
- The dataset used in this paper is the publicly available MIT–Stanford dataset, which only includes LFP/C LIB with altered charge conditions. However, in practical applications, other LIB materials exist and may have different degradation patterns under the same cycling conditions. Therefore, to enhance generalization, prediction models should be developed for more battery types (e.g., NCA, NMC) and cycling conditions (e.g., temperature, discharge rates, depth of discharge). It is also necessary to verify if the degradation patterns recognized in this paper are suitable for other batteries with different systems.
- The health features extracted in this paper come from the full charge/discharge curves of batteries. But when electric vehicles are used, batteries are not always fully charged and discharged. There may be a distinct difference between the features extracted from the full charge/discharge aging and the partial ones. Consequently, relevant experiments should be conducted to explore the feasibility of the method in this paper. Also, extracting features from temperature and current can also be considered.
- In this study, the extraction of HIs, as well as model optimization and training, are performed offline. However, offline RUL prediction methods are difficult to implement in electric vehicles in practical applications. Therefore, future research should focus on online prediction methods to achieve higher practicality. For different electrochemical systems, a battery cloud data platform can be built. Early battery aging data from users is extracted and encrypted for upload to this platform, and then allocated to a suitable battery pattern. On one hand, machine learning models are deployed on the cloud to analyze the data and send back details to the vehicle about battery degradation trajectories, knee points, and EOL points. On the other hand, the size of cloud samples is expanded to ensure the accuracy of future vehicle predictions.
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xie, J.; Lu, Y.C. A retrospective on lithium-ion batteries. Nat. Commun. 2020, 11, 2499. [Google Scholar] [CrossRef] [PubMed]
- Huang, R.; Wei, G.; Wang, X.; Jiang, B.; Zhu, J.; Chen, J.; Wei, X.; Dai, H. Revealing the low-temperature aging mechanisms of the whole life cycle for lithium-ion batteries (nickel-cobalt-aluminum vs. graphite). J. Energy Chem. 2025, 106, 31–43. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, X.Y.; Yuan, Y.J.; Dai, H.F.; Wei, X.Z. Fast Capacity Estimation for Lithium-Ion Batteries Based on XGBoost and Electrochemical Impedance Spectroscopy at Various State of Charge and Temperature. Automot. Innov. 2024, 7, 473–491. [Google Scholar] [CrossRef]
- Han, X.B.; Lu, L.G.; Zheng, Y.J.; Feng, X.N.; Li, Z.; Li, J.Q.; Ouyang, M.G. A review on the key issues of the lithium ion battery degradation among the whole life cycle. eTransportation 2019, 1, 100005. [Google Scholar] [CrossRef]
- Huang, R.J.; Wei, G.; Wang, X.Y.; Jiang, B.; Zhu, J.G.; Ji, C.Z.; Chen, J.A.; Wei, X.Z.; Dai, H.F. A novel framework for low-temperature fast charging of lithium-ion batteries without lithium plating. Chem. Eng. J. 2024, 497, 154729. [Google Scholar] [CrossRef]
- Diao, W.P.; Saxena, S.; Han, B.; Pecht, M. Algorithm to Determine the Knee Point on Capacity Fade Curves of Lithium-Ion Cells. Energies 2019, 12, 2910. [Google Scholar] [CrossRef]
- Li, Y.; Liu, K.L.; Foley, A.M.; Zülke, A.; Berecibar, M.; Nanini-Maury, E.; Van Mierlo, J.; Hoster, H.E. Data-driven health estimation and lifetime prediction of lithium-ion batteries: A review. Renew. Sustain. Energy Rev. 2019, 113, 109254. [Google Scholar] [CrossRef]
- Deng, Z.W.; Lin, X.K.; Cai, J.W.; Hu, X.S. Battery health estimation with degradation pattern recognition and transfer learning. J. Power Sources 2022, 525, 231027. [Google Scholar] [CrossRef]
- Fan, W.J.; Jiang, B.; Wang, X.Y.; Yuan, Y.J.; Zhu, J.G.; Wei, X.Z.; Dai, H.F. Enhancing capacity estimation of retired electric vehicle lithium-ion batteries through transfer learning from electrochemical impedance spectroscopy. eTransportation 2024, 22, 100362. [Google Scholar] [CrossRef]
- Jiang, M.; Li, D.; Li, Z.; Chen, Z.; Yan, Q.; Lin, F.; Yu, C.; Jiang, B.; Wei, X.; Yan, W.; et al. Advances in battery state estimation of battery management system in electric vehicles. J. Power Sources 2024, 612, 234781. [Google Scholar] [CrossRef]
- Ma, R.; Tao, S.; Sun, X.; Ren, Y.; Sun, C.; Ji, G.; Xu, J.; Wang, X.; Zhang, X.; Wu, Q.; et al. Pathway decisions for reuse and recycling of retired lithium-ion batteries considering economic and environmental functions. Nat. Commun. 2024, 15, 7641. [Google Scholar] [CrossRef] [PubMed]
- Jiang, B.; Zhu, Y.L.; Zhu, J.G.; Wei, X.Z.; Dai, H.F. An adaptive capacity estimation approach for lithium-ion battery using 10-min relaxation voltage within high state of charge range. Energy 2023, 263, 125802. [Google Scholar] [CrossRef]
- Hu, X.S.; Xu, L.; Lin, X.K.; Pecht, M. Battery Lifetime Prognostics. Joule 2020, 4, 310–346. [Google Scholar] [CrossRef]
- Liu, Q.Q.; Zhang, J.Y.; Li, K.; Lv, C. The Remaining Useful Life Prediction by Using Electrochemical Model in the Particle Filter Framework for Lithium-Ion Batteries. IEEE Access 2020, 8, 126661–126670. [Google Scholar] [CrossRef]
- Wang, A.Y.; Chen, H.T.; Jin, P.; Huang, J.; Feng, D.; Zheng, M.X. RUL Estimation of Lithium-Ion Power Battery Based on DEKF Algorithm. In Proceedings of the 14th IEEE Conference on Industrial Electronics and Applications (ICIEA), Xi’an, China, 19–21 June 2019; pp. 1851–1856. [Google Scholar]
- Lian, Y.; Wang, J.V.; Deng, X.; Kang, J.; Zhu, G.; Xiang, K. Remaining Useful Life Prediction of Lithium-Ion Batteries using Semi-Empirical Model and Bat-Based Particle Filter. In Proceedings of the 2020 IEEE International Symposium on Circuits and Systems (ISCAS), Seville, Spain, 12–14 October 2020; pp. 1–5. [Google Scholar]
- Ramadesigan, V.; Chen, K.J.; Burns, N.A.; Boovaragavan, V.; Braatz, R.D.; Subramanian, V.R. Parameter Estimation and Capacity Fade Analysis of Lithium-Ion Batteries Using Reformulated Models. J. Electrochem. Soc. 2011, 158, A1048–A1054. [Google Scholar] [CrossRef]
- Guha, A.; Patra, A. Online Estimation of the Electrochemical Impedance Spectrum and Remaining Useful Life of Lithium-Ion Batteries. IEEE Trans. Instrum. Meas. 2018, 67, 1836–1849. [Google Scholar] [CrossRef]
- Micea, M.V.; Ungurean, L.; Cârstoiu, G.N.; Groza, V. Online State-of-Health Assessment for Battery Management Systems. IEEE Trans. Instrum. Meas. 2011, 60, 1997–2006. [Google Scholar] [CrossRef]
- Yang, Z.S.; Wang, Y.H.; Kong, C.Z. Remaining Useful Life Prediction of Lithium-Ion Batteries Based on a Mixture of Ensemble Empirical Mode Decomposition and GWO-SVR Model. IEEE Trans. Instrum. Meas. 2021, 70, 1–11. [Google Scholar] [CrossRef]
- Guo, W.; He, M. An optimal relevance vector machine with a modified degradation model for remaining useful lifetime prediction of lithium-ion batteries. Appl. Soft Comput. 2022, 124, 108967. [Google Scholar] [CrossRef]
- Liu, D.T.; Zhou, J.B.; Pan, D.W.; Peng, Y.; Peng, X.Y. Lithium-ion battery remaining useful life estimation with an optimized Relevance Vector Machine algorithm with incremental learning. Measurement 2015, 63, 143–151. [Google Scholar] [CrossRef]
- Wang, S.; Zhao, L.L.; Su, X.H.; Ma, P.J. Prognostics of Lithium-Ion Batteries Based on Battery Performance Analysis and Flexible Support Vector Regression. Energies 2014, 7, 6492–6508. [Google Scholar] [CrossRef]
- Huang, H.Z.; Wang, H.K.; Li, Y.F.; Zhang, L.L.; Liu, Z.L. Support vector machine based estimation of remaining useful life: Current research status and future trends. J. Mech. Sci. Technol. 2015, 29, 151–163. [Google Scholar] [CrossRef]
- Jia, J.F.; Liang, J.Y.; Shi, Y.H.; Wen, J.; Pang, X.Q.; Zeng, J.C. SOH and RUL Prediction of Lithium-Ion Batteries Based on Gaussian Process Regression with Indirect Health Indicators. Energies 2020, 13, 375. [Google Scholar] [CrossRef]
- Wei, Z.Y.; Liu, C.Y.; Sun, X.W.; Li, Y.D.; Lu, H.Y. Two-phase early prediction method for remaining useful life of lithium-ion batteries based on a neural network and Gaussian process regression. Front. Energy 2024, 18, 447–462. [Google Scholar] [CrossRef]
- Zhou, Y.T.; Huang, Y.N.; Pang, J.B.; Wang, K. Remaining useful life prediction for supercapacitor based on long short-term memory neural network. J. Power Sources 2019, 440, 227149. [Google Scholar] [CrossRef]
- Zhu, Y.H.; Shang, Y.L.; Duan, B.; Gu, X.; Li, S.P.; Chen, G.C. A Data-Driven Method for Lithium-Ion Batteries Remaining Useful Life Prediction Based on Optimal Hyperparameters. In Proceedings of the 41st Chinese Control Conference (CCC), Hefei, China, 25–27 July 2022; pp. 7388–7392. [Google Scholar]
- Ren, L.; Zhao, L.; Hong, S.; Zhao, S.Q.; Wang, H.; Zhang, L. Remaining Useful Life Prediction for Lithium-Ion Battery: A Deep Learning Approach. IEEE Access 2018, 6, 50587–50598. [Google Scholar] [CrossRef]
- Li, S.; Fang, H.J.; Shi, B. Remaining useful life estimation of Lithium-ion battery based on interacting multiple model particle filter and support vector regression. Reliab. Eng. Syst. Saf. 2021, 210, 107542. [Google Scholar] [CrossRef]
- Tong, Z.M.; Miao, J.Z.; Tong, S.G.; Lu, Y.Y. Early prediction of remaining useful life for Lithium-ion batteries based on a hybrid machine learning method. J. Clean. Prod. 2021, 317, 128265. [Google Scholar] [CrossRef]
- Severson, K.A.; Attia, P.M.; Jin, N.; Perkins, N.; Jiang, B.; Yang, Z.; Chen, M.H.; Aykol, M.; Herring, P.K.; Fraggedakis, D.; et al. Data-driven prediction of battery cycle life before capacity degradation. Nat. Energy 2019, 4, 383–391. [Google Scholar] [CrossRef]
- Tang, Y.G.; Yang, K.; Zheng, H.R.; Zhang, S.J.; Zhang, Z. Early prediction of lithium-ion battery lifetime via a hybrid deep learning model. Measurement 2022, 199, 111530. [Google Scholar] [CrossRef]
- Xu, L.; Deng, Z.W.; Xie, Y.; Lin, X.K.; Hu, X.S. A Novel Hybrid Physics-Based and Data-Driven Approach for Degradation Trajectory Prediction in Li-Ion Batteries. IEEE Trans. Transp. Electrif. 2023, 9, 2628–2644. [Google Scholar] [CrossRef]
- Yin, A.J.; Tan, Z.B.; Tan, J. Life Prediction of Battery Using a Neural Gaussian Process with Early Discharge Characteristics. Sensors 2021, 21, 1087. [Google Scholar] [CrossRef]
- Cai, N.; Que, X.P.; Zhang, X.; Feng, W.G.; Zhou, Y.H. A deep learning framework for the joint prediction of the SOH and RUL of lithium-ion batteries based on bimodal images. Energy 2024, 302, 131700. [Google Scholar] [CrossRef]
- Ansari, S.; Ayob, A.; Lipu, M.S.H.; Hussain, A.; Abdolrasol, M.G.M.; Zainuri, M.; Saad, M.H.M. Optimized data-driven approach for remaining useful life prediction of Lithium-ion batteries based on sliding window and systematic sampling. J. Energy Storage 2023, 73, 109198. [Google Scholar] [CrossRef]
- Fu, L.; Jiang, B.; Zhu, J.; Dai, H. An Early Remaining Useful Life Prediction Method for Lithium-ion Batteries using Optimization Algorithm-Assisted Gaussian Process Regression. In Proceedings of the 2024 IEEE Transportation Electrification Conference and Expo, Asia-Pacific (ITEC Asia-Pacific), Xi’an, China, 10–13 October 2024; pp. 109–114. [Google Scholar]
- He, J.; Wei, Z.; Bian, X.; Yan, F. State-of-Health Estimation of Lithium-Ion Batteries Using Incremental Capacity Analysis Based on Voltage–Capacity Model. IEEE Trans. Transp. Electrif. 2020, 6, 417–426. [Google Scholar] [CrossRef]
- Stuart, A.L.; Conover, W.J. Practical Nonparametric Statistics; Wiley: Hoboken, NJ, USA, 1972. [Google Scholar]
- Miraftabzadeh, S.M.; Colombo, C.G.; Longo, M.; Foiadelli, F. K-Means and Alternative Clustering Methods in Modern Power Systems. IEEE Access 2023, 11, 119596–119633. [Google Scholar] [CrossRef]
- Kira, K.; Rendell, L.A. The Feature Selection Problem: Traditional Methods and a New Algorithm. In Proceedings of the AAAI Conference on Artificial Intelligence, San Jose, CA, USA, 12–16 July 1992. [Google Scholar]
- Robnik-Šikonja, M.; Kononenko, I. Theoretical and Empirical Analysis of ReliefF and RReliefF. Mach. Learn. 2003, 53, 23–69. [Google Scholar] [CrossRef]
- Fan, W.J.; Zhu, J.G.; Qiao, D.D.; Jiang, B.; Wang, X.Y.; Wei, X.Z.; Dai, H.F. Prediction of nonlinear degradation knee-point and remaining useful life for lithium-ion batteries using relaxation voltage. Energy 2024, 294, 130900. [Google Scholar] [CrossRef]
- Williard, N.D. Degradation Analysis and Health Monitoring of Lithium Ion Batteries. Master’s Thesis, University of Maryland, College Park, MD, USA, 2011. [Google Scholar]
- Neubauer, J.; Pesaran, A. The ability of battery second use strategies to impact plug-in electric vehicle prices and serve utility energy storage applications. J. Power Sources 2011, 196, 10351–10358. [Google Scholar] [CrossRef]
- He, W.; Williard, N.; Osterman, M.; Pecht, M. Prognostics of lithium-ion batteries based on Dempster-Shafer theory and the Bayesian Monte Carlo method. J. Power Sources 2011, 196, 10314–10321. [Google Scholar] [CrossRef]
- Yang, F.F.; Wang, D.; Xing, Y.J.; Tsui, K.L. Prognostics of Li(NiMnCo)O2-based lithium-ion batteries using a novel battery degradation model. Microelectron. Reliab. 2017, 70, 70–78. [Google Scholar] [CrossRef]
- IEEE 485-2020; IEEE Recommended Practice for Sizing Lead-Acid Batteries for Stationary Applications. IEEE: New York, NY, USA, 2020; p. 1.
- Satopaa, V.; Albrecht, J.; Irwin, D.; Raghavan, B. Finding a “Kneedle” in a Haystack: Detecting Knee Points in System Behavior. In Proceedings of the 2011 31st International Conference on Distributed Computing Systems Workshops, Minneapolis, MN, USA, 20–24 June 2011; pp. 166–171. [Google Scholar]
- Fermín-Cueto, P.; McTurk, E.; Allerhand, M.; Medina-Lopez, E.; Anjos, M.F.; Sylvester, J.; dos Reis, G. Identification and machine learning prediction of knee-point and knee-onset in capacity degradation curves of lithium-ion cells. Energy AI 2020, 1, 100006. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, Y.; Gao, Y.; Wang, F.; Mu, B.; Zhang, W. Accelerated fading recognition for lithium-ion batteries with Nickel-Cobalt-Manganese cathode using quantile regression method. Appl. Energy 2019, 256, 113841. [Google Scholar] [CrossRef]
- Bacon, D.W.; Watts, D.G. Estimating the transition between two intersecting straight lines. Biometrika 1971, 58, 525–534. [Google Scholar] [CrossRef]
- Wei, M.; Ye, M.; Wang, Q.; Xu, X.X.; Twajamahoro, J.P. Remaining useful life prediction of lithium-ion batteries based on stacked autoencoder and gaussian mixture regression. J. Energy Storage 2022, 47, 103558. [Google Scholar] [CrossRef]
- Deng, Z.W.; Hu, X.S.; Lin, X.K.; Xu, L.; Che, Y.H.; Hu, L. General Discharge Voltage Information Enabled Health Evaluation for Lithium-Ion Batteries. IEEE-ASME Trans. Mechatron. 2021, 26, 1295–1306. [Google Scholar] [CrossRef]
- Hu, X.S.; Che, Y.H.; Lin, X.K.; Deng, Z.W. Health Prognosis for Electric Vehicle Battery Packs: A Data-Driven Approach. IEEE-ASME Trans. Mechatron. 2020, 25, 2622–2632. [Google Scholar] [CrossRef]
- Shi, J.Q.; Wang, B.; Murray-Smith, R.; Titterington, D.M. Gaussian process functional regression Modeling for batch data. Biometrics 2007, 63, 714–723. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; The MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Aye, S.A.; Heyns, P.S. An integrated Gaussian process regression for prediction of remaining useful life of slow speed bearings based on acoustic emission. Mech. Syst. Signal Process. 2017, 84, 485–498. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Nickisch, H. Gaussian Processes for Machine Learning (GPML) Toolbox. J. Mach. Learn. Res. 2010, 11, 3011–3015. [Google Scholar]
- Probst, P.; Boulesteix, A.L.; Bischl, B. Tunability: Importance of Hyperparameters of Machine Learning Algorithms. J. Mach. Learn. Res. 2019, 20, 1–32. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 1944, pp. 1942–1948. [Google Scholar]
- Long, B.; Xian, W.M.; Jiang, L.; Liu, Z. An improved autoregressive model by particle swarm optimization for prognostics of lithium-ion batteries. Microelectron. Reliab. 2013, 53, 821–831. [Google Scholar] [CrossRef]
- Duvenaud, D.; Lloyd, J.; Grosse, R.; Tenenbaum, J.; Ghahramani, Z. Structure Discovery in Nonparametric Regression through Compositional Kernel Search. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GE, USA, 16–21 June 2013. [Google Scholar]
- Yao, J.; Powell, K.; Gao, T. A two-stage deep learning framework for early-stage lifetime prediction for lithium-ion batteries with consideration of features from multiple cycles. Front. Energy Res. 2022, 10, 1059126. [Google Scholar] [CrossRef]
- Paradis, S.; Whitmeyer, M. Pay Attention: Leveraging Sequence Models to Predict the Useful Life of Batteries. arXiv 2019, arXiv:1910.01347. [Google Scholar] [CrossRef]
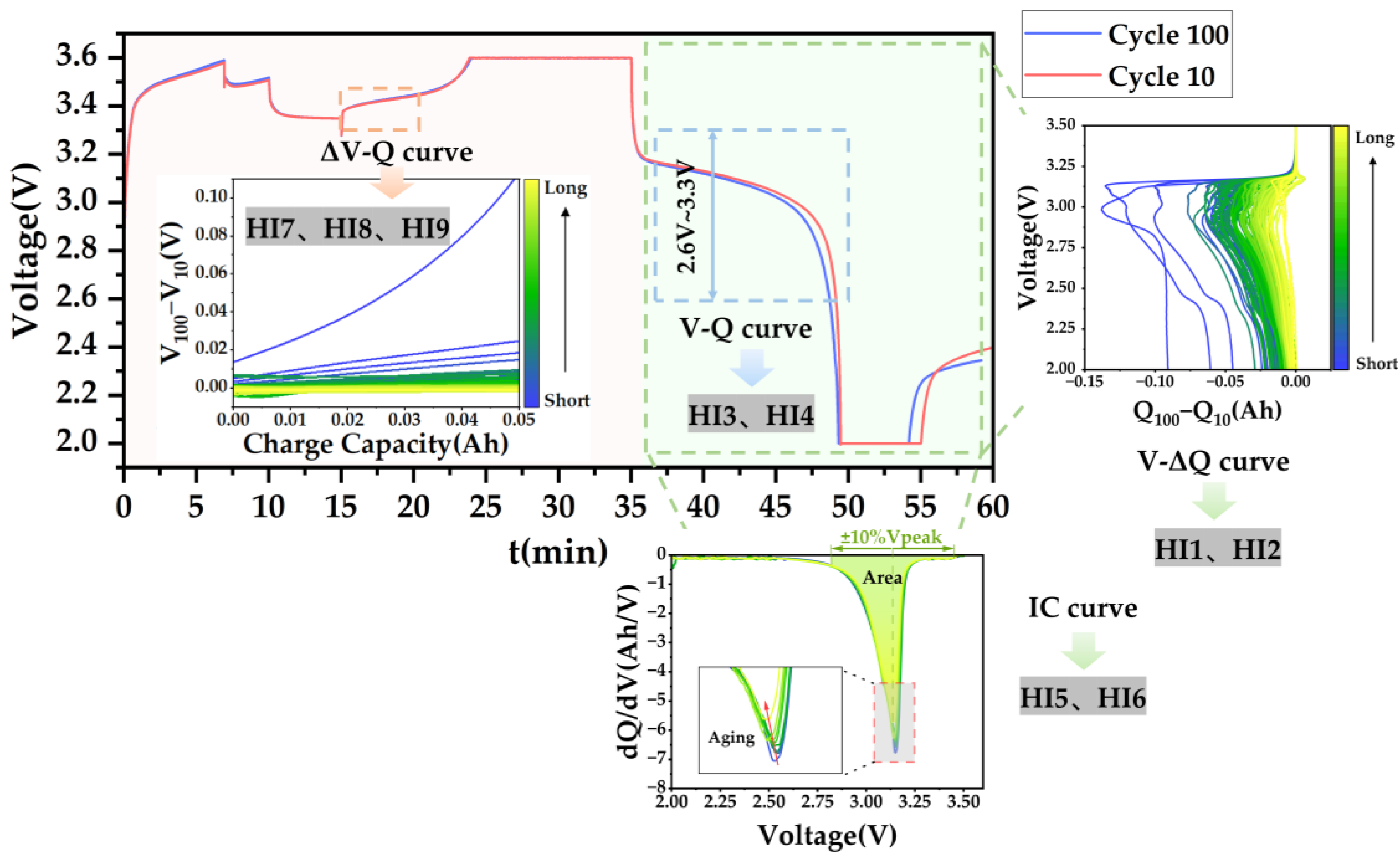
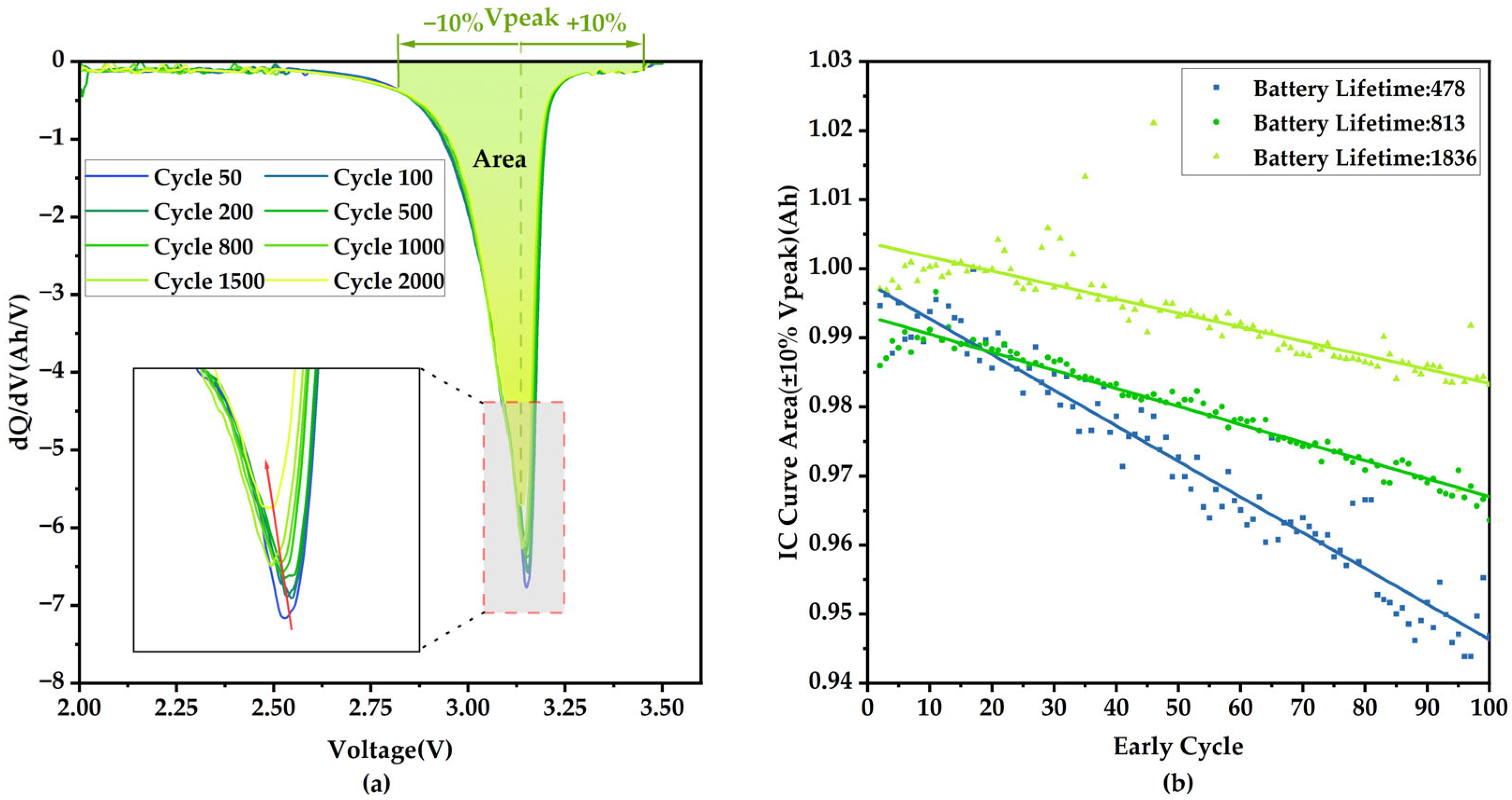
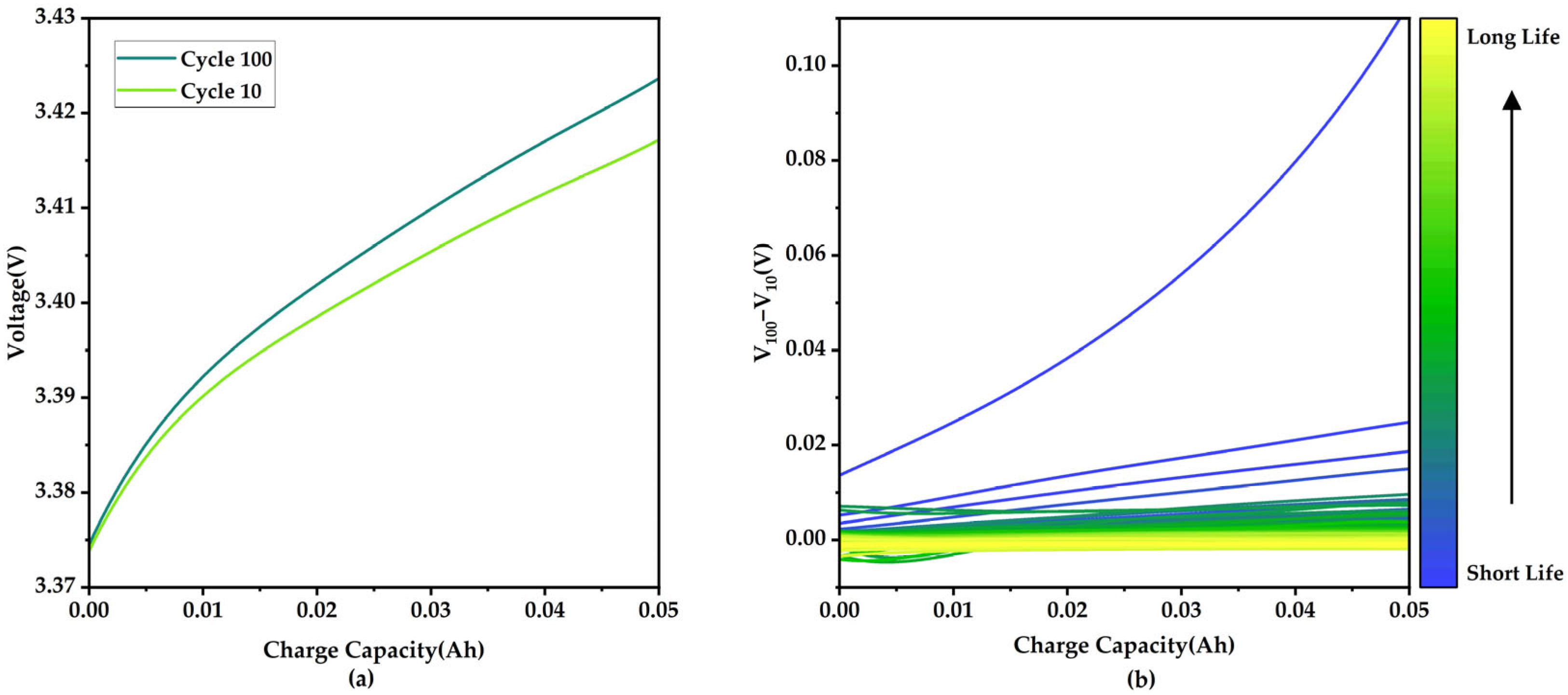
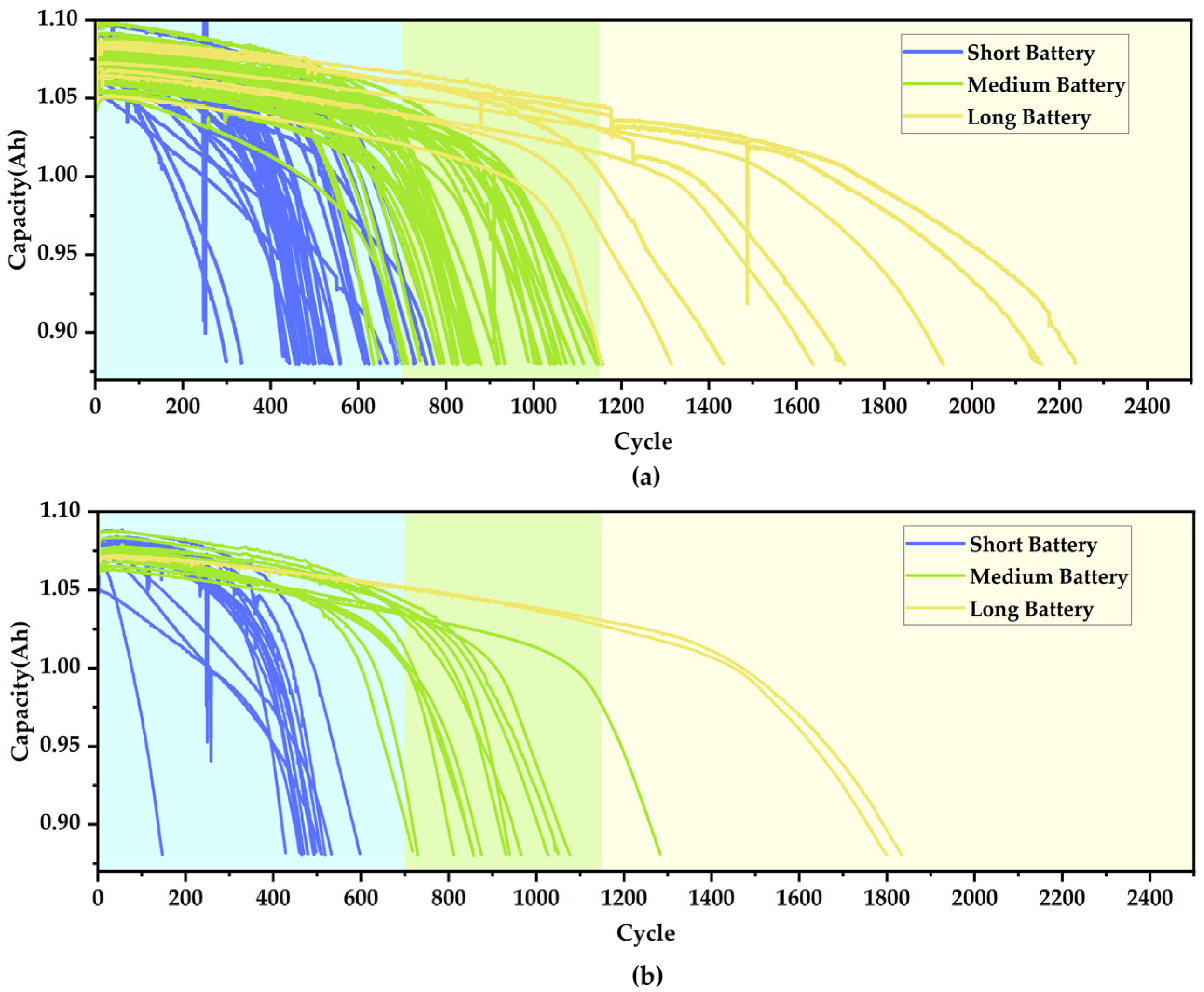
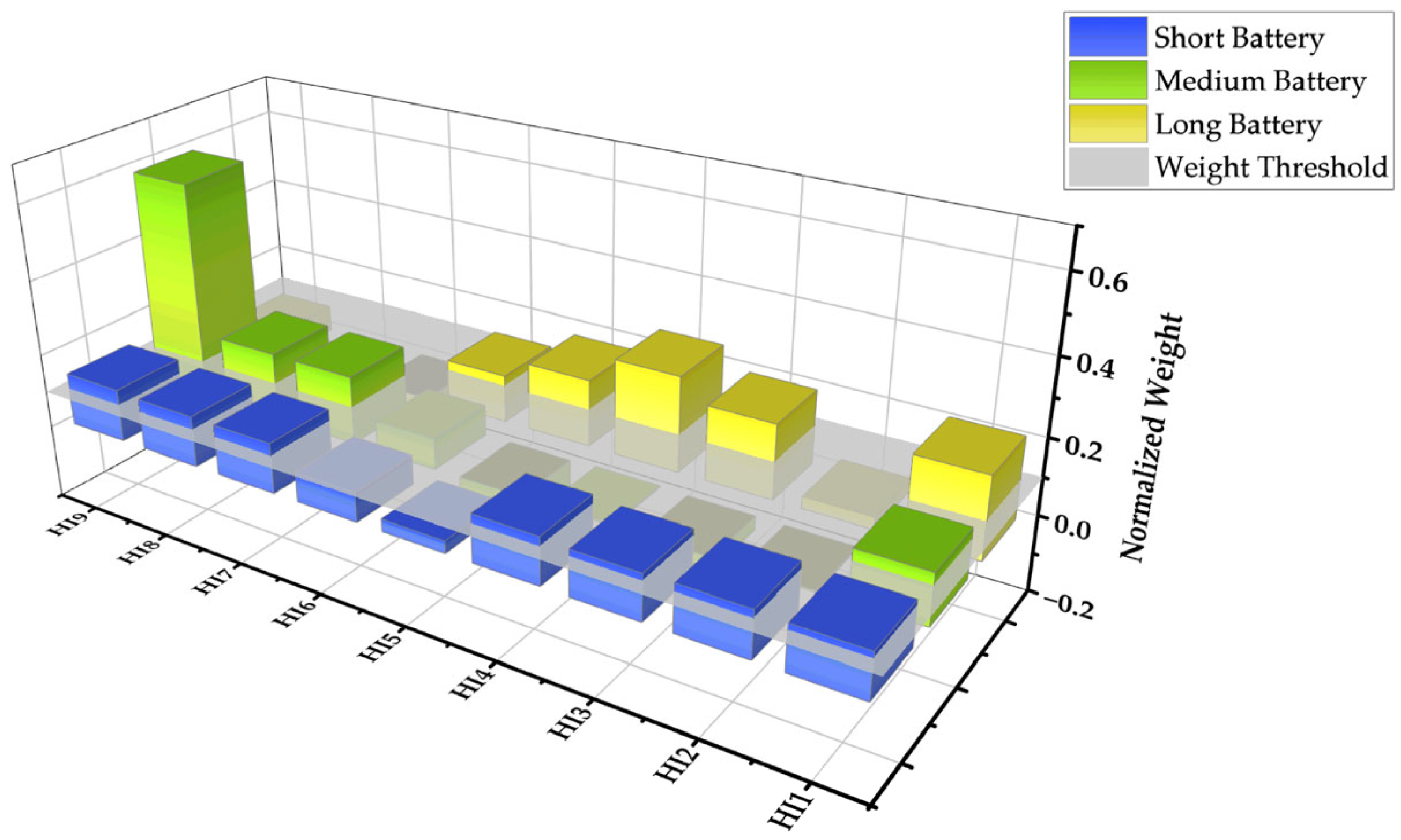
| Notation | Details of Extracted Features | Spearman |
|---|---|---|
| HI1 | The standard deviation of the difference in discharge capacity curves between Cycle 100 and Cycle 10 versus voltage. | −0.9001 |
| HI2 | The peak of the difference in discharge capacity curves between Cycle 100 and Cycle 10 versus voltage. | 0.8940 |
| HI3 | The difference in discharge capacity in the fixed voltage range (2.6~3.3 V) between Cycle 100 and Cycle 10. | 0.8793 |
| HI4 | The linear slope of discharge capacity in the fixed voltage range (2.6~3.3 V) with Cycle 2 to Cycle 100. | 0.8865 |
| HI5 | The difference in the area near the peak voltage of the IC curve (±10%) between Cycle 100 and Cycle 10. | 0.8221 |
| HI6 | The linear slope of the area near the peak voltage of the IC curve (±10%) with Cycle 2 to Cycle 100. | 0.8739 |
| HI7 | The mean value of the difference in voltage curves between Cycle 100 and Cycle 10 versus charge capacity (0~0.05 Ah) in 1C CC-CV stage. | −0.8543 |
| HI8 | The maximum value of the difference in voltage curves between Cycle 100 and Cycle 10 versus charge capacity (0~0.05 Ah) in 1C CC-CV stage. | −0.8704 |
| HI9 | The variance of the difference in voltage curves between Cycle 100 and Cycle 10 versus charge capacity (0~0.05 Ah) in 1C CC-CV stage. | −0.8411 |
| Kernel | Formula | Parameter |
|---|---|---|
| Squared Exponential | ||
| Matérn | ||
| Exponential | ||
| γ-Exponential | ||
| Rational Quadratic | ||
| Polynomial |
| Short | Medium | Long | |
|---|---|---|---|
| PSO-GPR | 7.55% | 9.87% | 9.76% |
| BP | 17.32% | 12.53% | 24.58% |
| SVM | 10.80% | 10.53% | 30.61% |
| RF | 9.04% | 15.14% | 10.25% |
| CNN | 12.90% | 15.67% | 29.75% |
| LSTM | 14.18% | 11.35% | 28.68% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, L.; Jiang, B.; Zhu, J.; Wei, X.; Dai, H. Early Remaining Useful Life Prediction for Lithium-Ion Batteries Using a Gaussian Process Regression Model Based on Degradation Pattern Recognition. Batteries 2025, 11, 221. https://doi.org/10.3390/batteries11060221
Fu L, Jiang B, Zhu J, Wei X, Dai H. Early Remaining Useful Life Prediction for Lithium-Ion Batteries Using a Gaussian Process Regression Model Based on Degradation Pattern Recognition. Batteries. 2025; 11(6):221. https://doi.org/10.3390/batteries11060221
Chicago/Turabian StyleFu, Linlin, Bo Jiang, Jiangong Zhu, Xuezhe Wei, and Haifeng Dai. 2025. "Early Remaining Useful Life Prediction for Lithium-Ion Batteries Using a Gaussian Process Regression Model Based on Degradation Pattern Recognition" Batteries 11, no. 6: 221. https://doi.org/10.3390/batteries11060221
APA StyleFu, L., Jiang, B., Zhu, J., Wei, X., & Dai, H. (2025). Early Remaining Useful Life Prediction for Lithium-Ion Batteries Using a Gaussian Process Regression Model Based on Degradation Pattern Recognition. Batteries, 11(6), 221. https://doi.org/10.3390/batteries11060221












