Attention Mechanism-Based Neural Network for Prediction of Battery Cycle Life in the Presence of Missing Data
Abstract
1. Introduction
2. Methods
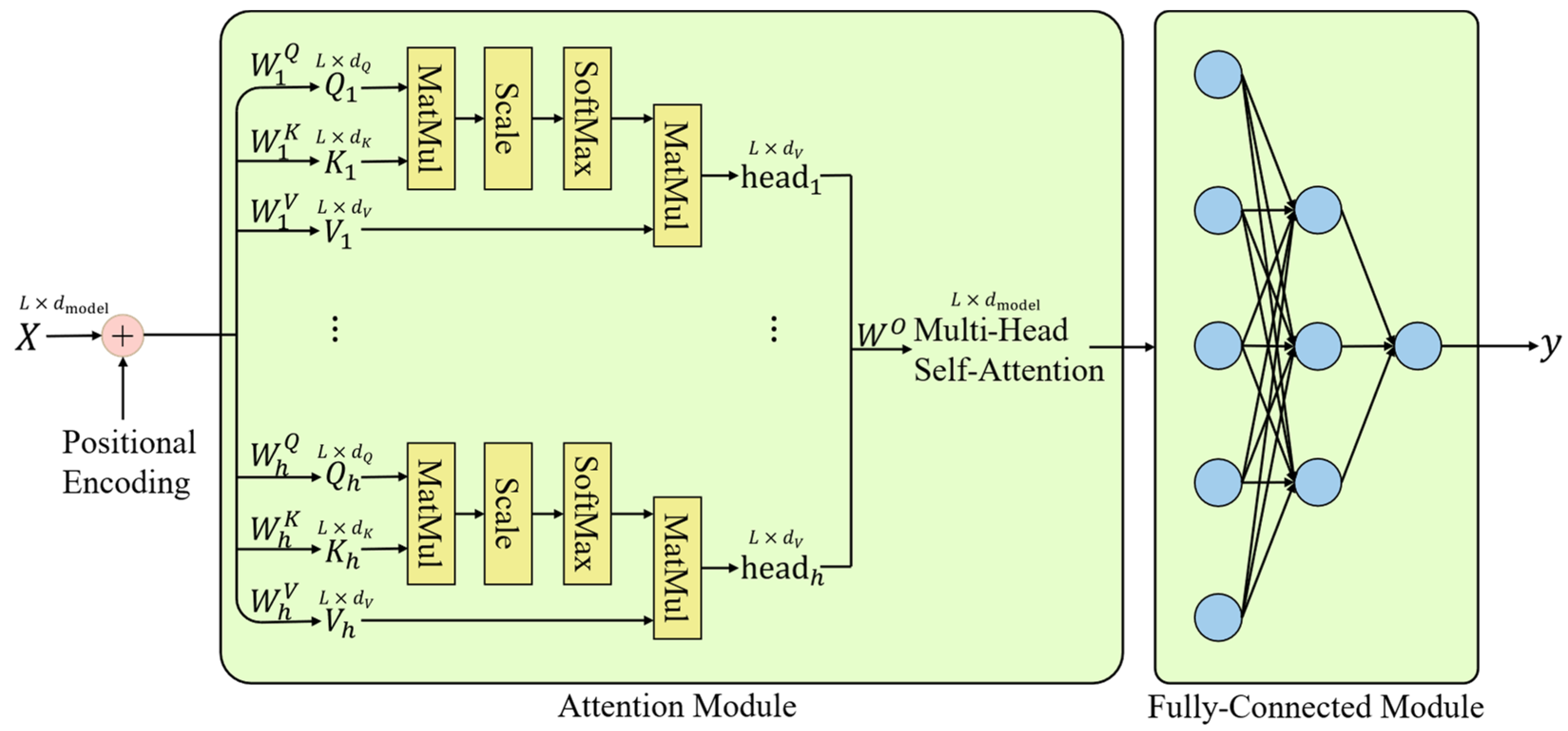
2.1. The Self-Attention Mechanism
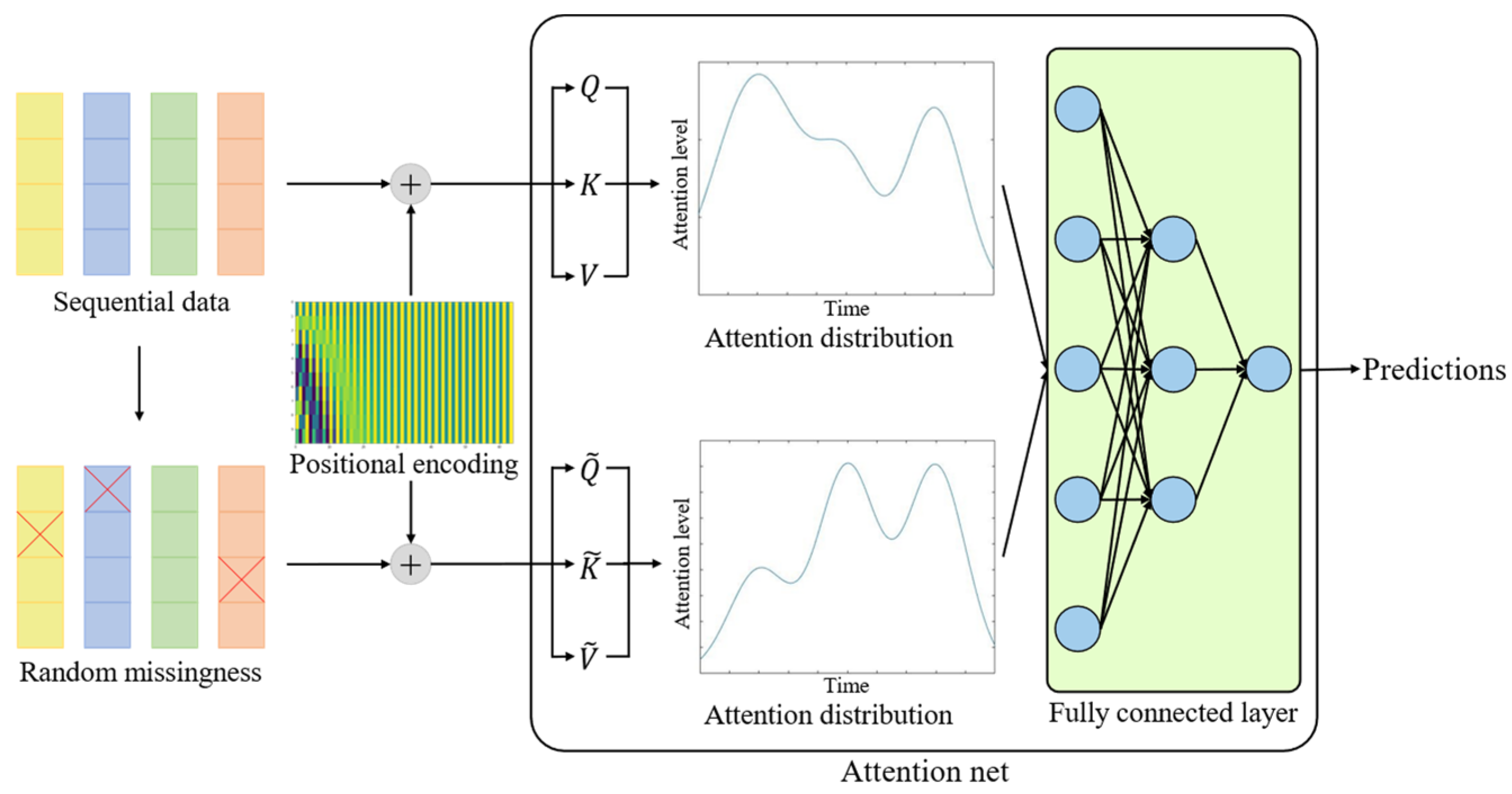
2.2. Handling Missing Data with the Self-Attention Mechanism
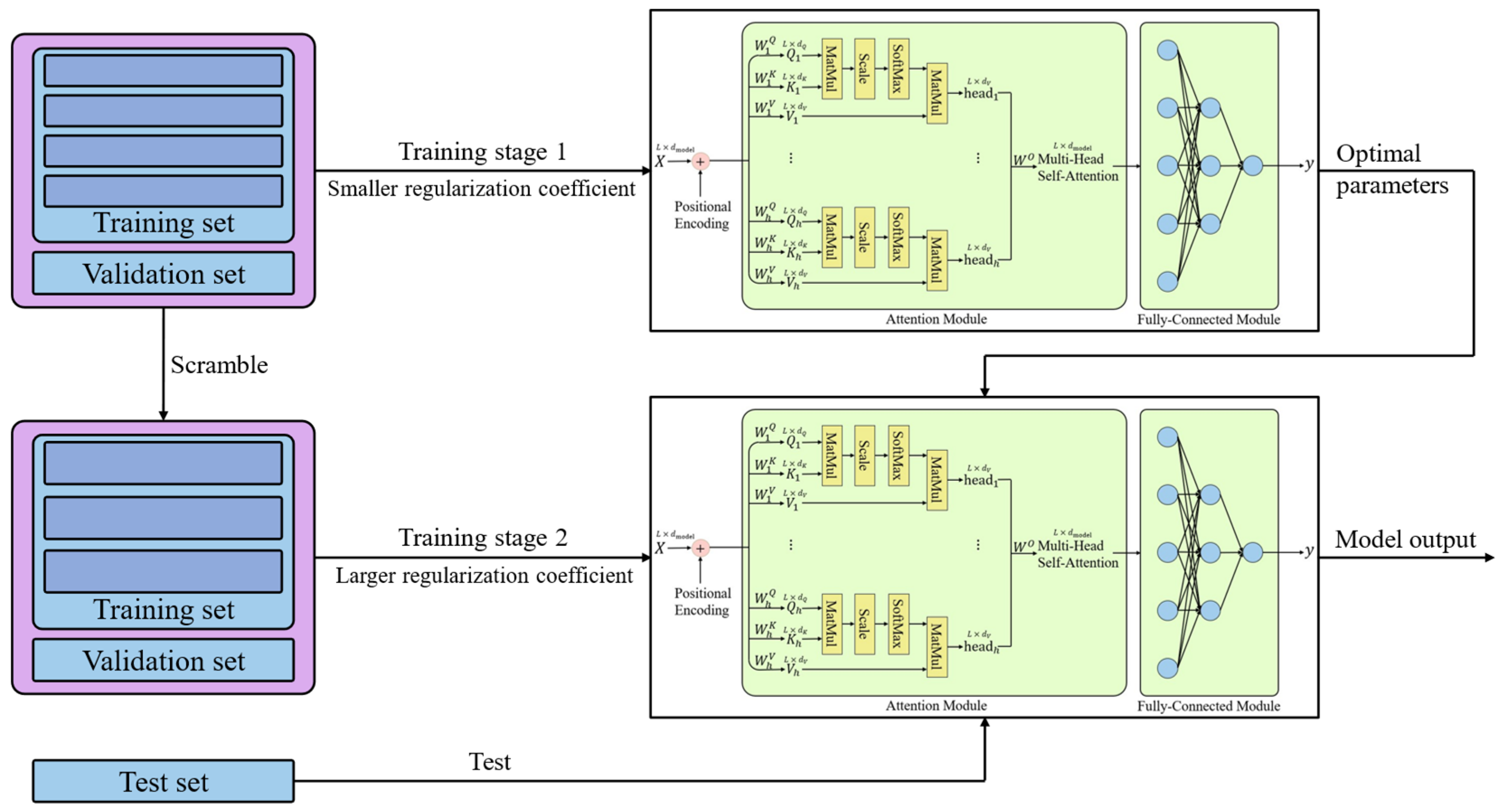
2.3. Training Process
3. Description of Dataset and Data-Missing Patterns
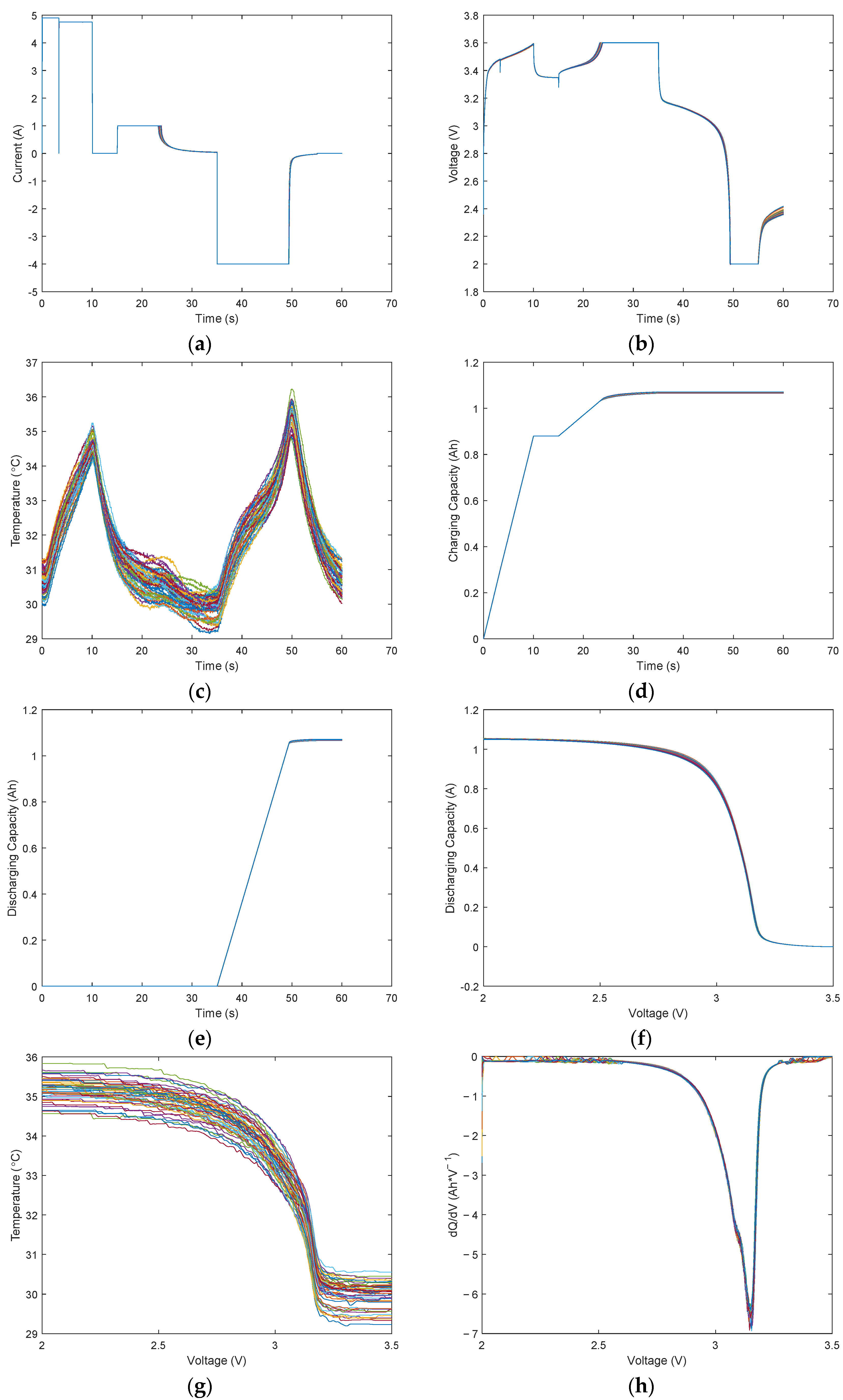
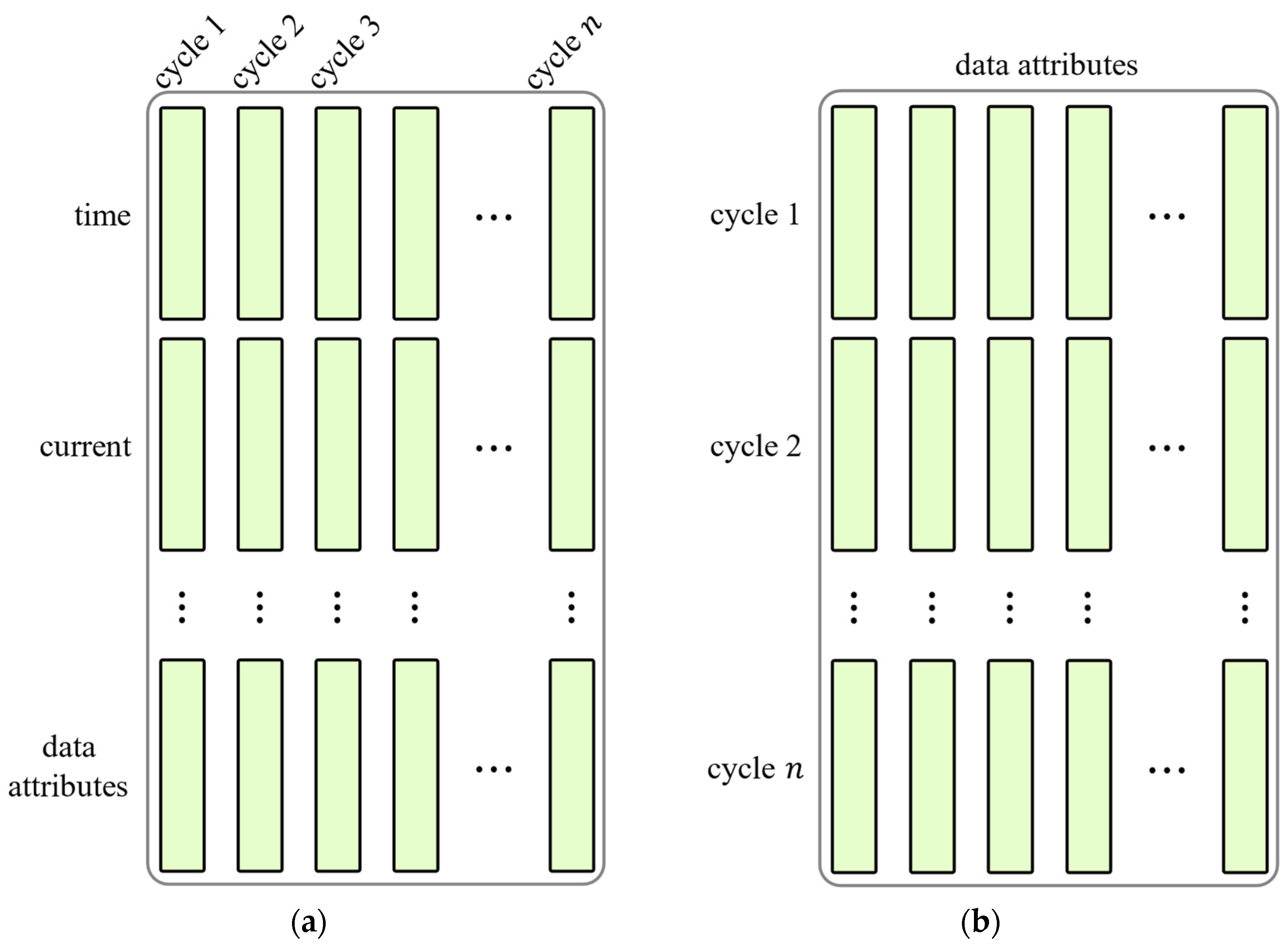
3.1. Dataset and Input Data Construction
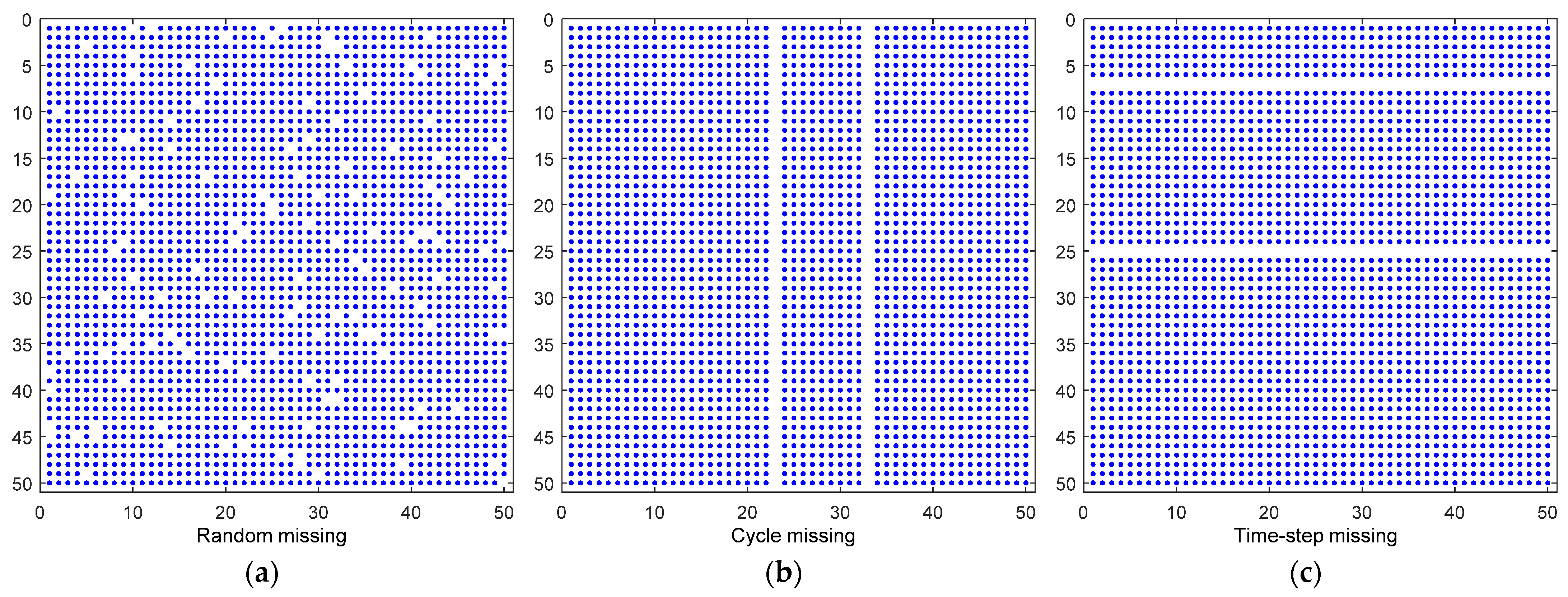
3.2. Addition of Missing Data
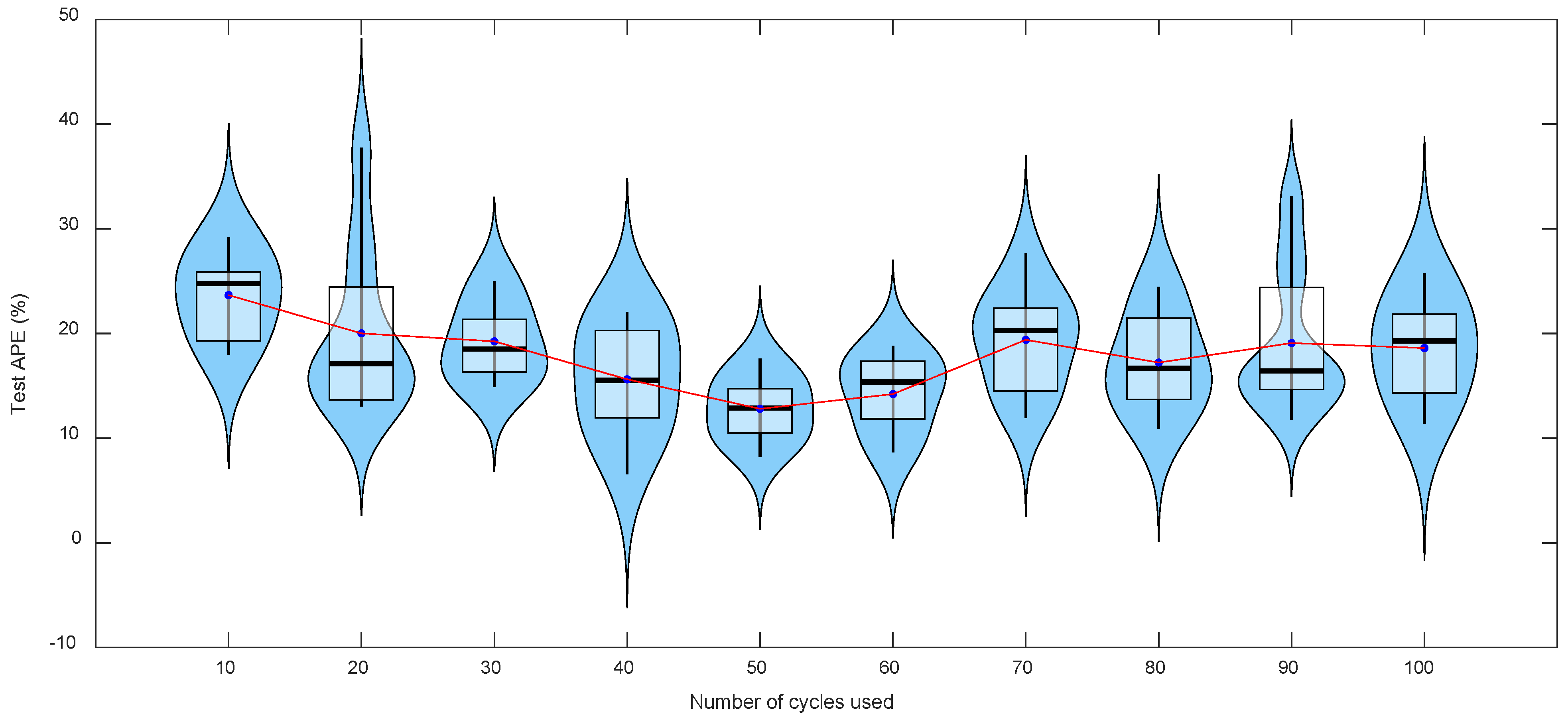
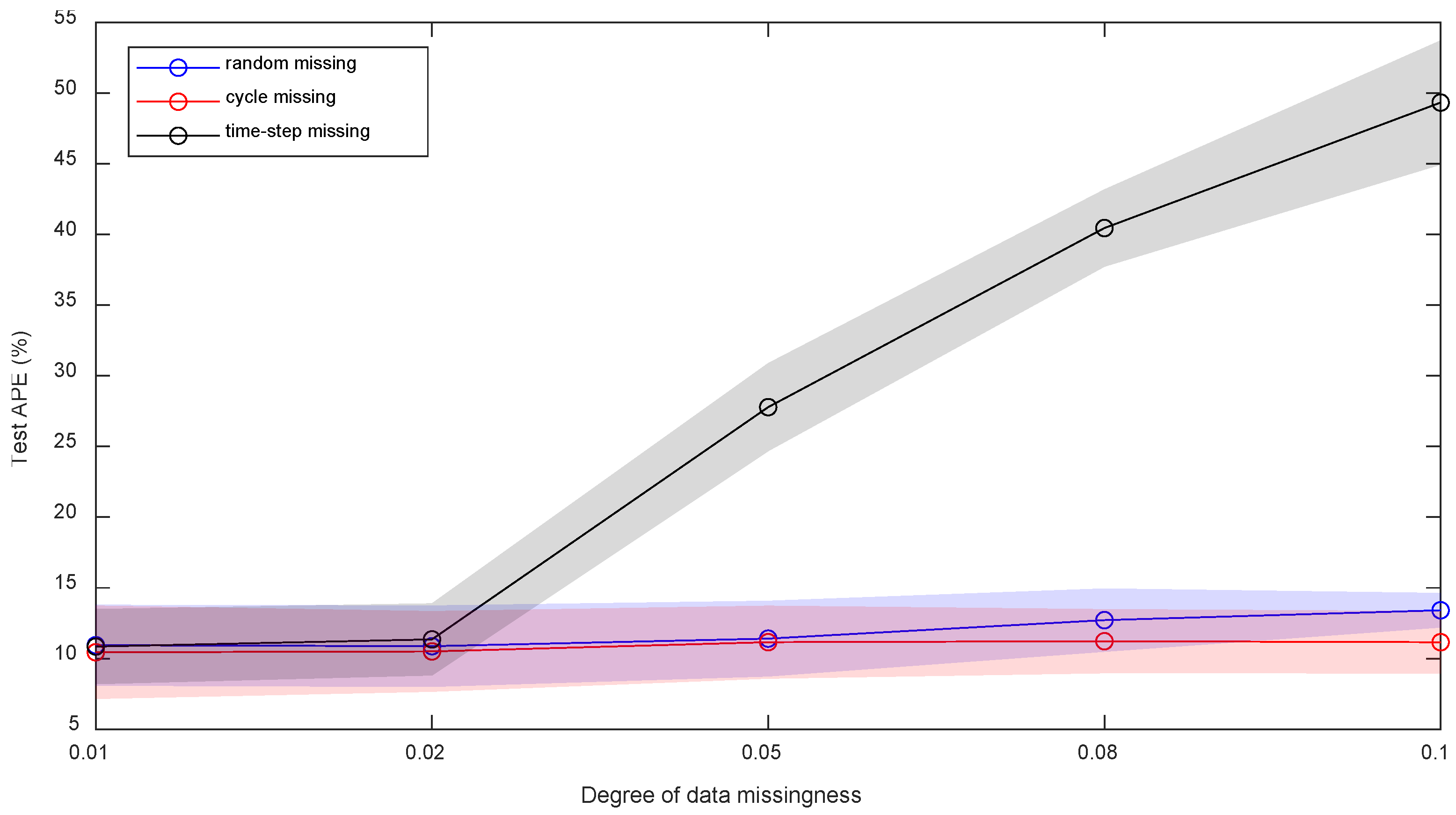
4. Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liang, Y.; Zhao, C.Z.; Yuan, H.; Chen, Y.; Zhang, W.; Huang, J.Q.; Yu, D.; Liu, Y.; Titirici, M.M.; Chueh, Y.L.; et al. A Review of Rechargeable Batteries for Portable Electronic Devices. InfoMat 2019, 1, 6–32. [Google Scholar] [CrossRef]
- Olabi, A.G.; Abbas, Q.; Shinde, P.A.; Abdelkareem, M.A. Rechargeable Batteries: Technological Advancement, Challenges, Current and Emerging Applications. Energy 2023, 266, 126408. [Google Scholar] [CrossRef]
- König, A.; Nicoletti, L.; Schröder, D.; Wolff, S.; Waclaw, A.; Lienkamp, M. An Overview of Parameter and Cost for Battery Electric Vehicles. World Electr. Veh. J. 2021, 12, 21. [Google Scholar] [CrossRef]
- Lebrouhi, B.E.; Khattari, Y.; Lamrani, B.; Maaroufi, M.; Zeraouli, Y.; Kousksou, T. Key Challenges for a Large-Scale Development of Battery Electric Vehicles: A Comprehensive Review. J. Energy Storage 2021, 44, 103273. [Google Scholar] [CrossRef]
- Tran, M.K.; Bhatti, A.; Vrolyk, R.; Wong, D.; Panchal, S.; Fowler, M.; Fraser, R. A Review of Range Extenders in Battery Electric Vehicles: Current Progress and Future Perspectives. World Electr. Veh. J. 2021, 12, 54. [Google Scholar] [CrossRef]
- Cheng, X.; Liu, H.; Yuan, H.; Peng, H.; Tang, C.; Huang, J.; Zhang, Q. A Perspective on Sustainable Energy Materials for Lithium Batteries. SusMat 2021, 1, 38–50. [Google Scholar] [CrossRef]
- Hannan, M.A.; Wali, S.B.; Ker, P.J.; Rahman, M.S.A.; Mansor, M.; Ramachandaramurthy, V.K.; Muttaqi, K.M.; Mahlia, T.M.I.; Dong, Z.Y. Battery Energy-Storage System: A Review of Technologies, Optimization Objectives, Constraints, Approaches, and Outstanding Issues. J. Energy Storage 2021, 42, 103023. [Google Scholar] [CrossRef]
- Weiss, M.; Ruess, R.; Kasnatscheew, J.; Levartovsky, Y.; Levy, N.R.; Minnmann, P.; Stolz, L.; Waldmann, T.; Wohlfahrt-Mehrens, M.; Aurbach, D.; et al. Fast Charging of Lithium-Ion Batteries: A Review of Materials Aspects. Adv. Energy Mater. 2021, 11, 2101126. [Google Scholar] [CrossRef]
- Kebede, A.A.; Kalogiannis, T.; Van Mierlo, J.; Berecibar, M. A Comprehensive Review of Stationary Energy Storage Devices for Large Scale Renewable Energy Sources Grid Integration. Renew. Sustain. Energy Rev. 2022, 159, 112213. [Google Scholar] [CrossRef]
- Chen, T.; Jin, Y.; Lv, H.; Yang, A.; Liu, M.; Chen, B.; Xie, Y.; Chen, Q. Applications of Lithium-Ion Batteries in Grid-Scale Energy Storage Systems. Trans. Tianjin Univ. 2020, 26, 208–217. [Google Scholar] [CrossRef]
- Park, S.; Pozzi, A.; Whitmeyer, M.; Perez, H.; Kandel, A.; Kim, G.; Choi, Y.; Joe, W.T.; Raimondo, D.M.; Moura, S. A Deep Reinforcement Learning Framework for Fast Charging of Li-Ion Batteries. IEEE Trans. Transp. Electrif. 2022, 8, 2770–2784. [Google Scholar] [CrossRef]
- Newman, J.; Tiedemann, W. Porous-electrode Theory with Battery Applications. AIChE J. 1975, 21, 25–41. [Google Scholar] [CrossRef]
- Elmahallawy, M.; Elfouly, T.; Alouani, A.; Massoud, A.M. A Comprehensive Review of Lithium-Ion Batteries Modeling, and State of Health and Remaining Useful Lifetime Prediction. IEEE Access 2022, 10, 119040–119070. [Google Scholar] [CrossRef]
- Khodadadi Sadabadi, K.; Jin, X.; Rizzoni, G. Prediction of Remaining Useful Life for a Composite Electrode Lithium Ion Battery Cell Using an Electrochemical Model to Estimate the State of Health. J. Power Sources 2021, 481, 228861. [Google Scholar] [CrossRef]
- Lam, F.; Allam, A.; Joe, W.T.; Choi, Y.; Onori, S. Offline Multiobjective Optimization for Fast Charging and Reduced Degradation in Lithium Ion Battery Cells. In Proceedings of the 2021 American Control Conference (ACC), New Orleans, LA, USA, 25–28 May 2021; pp. 4441–4446. [Google Scholar] [CrossRef]
- O’Kane, S.E.J.; Ai, W.; Madabattula, G.; Alonso-Alvarez, D.; Timms, R.; Sulzer, V.; Edge, J.S.; Wu, B.; Offer, G.J.; Marinescu, M. Lithium-Ion Battery Degradation: How to Model It. Phys. Chem. Chem. Phys. 2022, 24, 7909–7922. [Google Scholar] [CrossRef] [PubMed]
- Jokar, A.; Rajabloo, B.; Désilets, M.; Lacroix, M. Review of Simplified Pseudo-Two-Dimensional Models of Lithium-Ion Batteries. J. Power Sources 2016, 327, 44–55. [Google Scholar] [CrossRef]
- Kong, X.; Plett, G.L.; Scott Trimboli, M.; Zhang, Z.; Qiao, D.; Zhao, T.; Zheng, Y. Pseudo-Two-Dimensional Model and Impedance Diagnosis of Micro Internal Short Circuit in Lithium-Ion Cells. J. Energy Storage 2020, 27, 101085. [Google Scholar] [CrossRef]
- Liu, B.; Tang, X.; Gao, F. Joint Estimation of Battery State-of-Charge and State-of-Health Based on a Simplified Pseudo-Two-Dimensional Model. Electrochim. Acta 2020, 344, 136098. [Google Scholar] [CrossRef]
- Ashwin, T.R.; Chung, Y.M.; Wang, J. Capacity Fade Modelling of Lithium-Ion Battery under Cyclic Loading Conditions. J. Power Sources 2016, 328, 586–598. [Google Scholar] [CrossRef]
- Han, X.; Ouyang, M.; Lu, L.; Li, J. Simplification of Physics-Based Electrochemical Model for Lithium Ion Battery on Electric Vehicle. Part I: Diffusion Simplification and Single Particle Model. J. Power Sources 2015, 278, 802–813. [Google Scholar] [CrossRef]
- Han, X.; Ouyang, M.; Lu, L.; Li, J. Simplification of Physics-Based Electrochemical Model for Lithium Ion Battery on Electric Vehicle. Part II: Pseudo-Two-Dimensional Model Simplification and State of Charge Estimation. J. Power Sources 2015, 278, 814–825. [Google Scholar] [CrossRef]
- Lee, J.L.; Chemistruck, A.; Plett, G.L. Discrete-Time Realization of Transcendental Impedance Models, with Application to Modeling Spherical Solid Diffusion. J. Power Sources 2012, 206, 367–377. [Google Scholar] [CrossRef]
- Stetzel, K.D.; Aldrich, L.L.; Trimboli, M.S.; Plett, G.L. Electrochemical State and Internal Variables Estimation Using a Reduced-Order Physics-Based Model of a Lithium-Ion Cell and an Extended Kalman Filter. J. Power Sources 2015, 278, 490–505. [Google Scholar] [CrossRef]
- Deng, Z.; Hu, X.; Lin, X.; Xu, L.; Li, J.; Guo, W. A Reduced-Order Electrochemical Model for All-Solid-State Batteries. IEEE Trans. Transp. Electrif. 2021, 7, 464–473. [Google Scholar] [CrossRef]
- Lai, X.; He, L.; Wang, S.; Zhou, L.; Zhang, Y.; Sun, T.; Zheng, Y. Co-Estimation of State of Charge and State of Power for Lithium-Ion Batteries Based on Fractional Variable-Order Model. J. Clean. Prod. 2020, 255, 120203. [Google Scholar] [CrossRef]
- Parhizi, M.; Pathak, M.; Ostanek, J.K.; Jain, A. An Iterative Analytical Model for Aging Analysis of Li-Ion Cells. J. Power Sources 2022, 517, 230667. [Google Scholar] [CrossRef]
- Ng, M.F.; Zhao, J.; Yan, Q.; Conduit, G.J.; Seh, Z.W. Predicting the State of Charge and Health of Batteries Using Data-Driven Machine Learning. Nat. Mach. Intell. 2020, 2, 161–170. [Google Scholar] [CrossRef]
- Severson, K.A.; Attia, P.M.; Jin, N.; Perkins, N.; Jiang, B.; Yang, Z.; Chen, M.H.; Aykol, M.; Herring, P.K.; Fraggedakis, D.; et al. Data-Driven Prediction of Battery Cycle Life before Capacity Degradation. Nat. Energy 2019, 4, 383–391. [Google Scholar] [CrossRef]
- Zhang, Y.; Feng, X.; Zhao, M.; Xiong, R. In-Situ Battery Life Prognostics amid Mixed Operation Conditions Using Physics-Driven Machine Learning. J. Power Sources 2023, 577, 233246. [Google Scholar] [CrossRef]
- Hong, J.; Lee, D.; Jeong, E.R.; Yi, Y. Towards the Swift Prediction of the Remaining Useful Life of Lithium-Ion Batteries with End-to-End Deep Learning. Appl. Energy 2020, 278, 115646. [Google Scholar] [CrossRef]
- Thelen, A.; Li, M.; Hu, C.; Bekyarova, E.; Kalinin, S.; Sanghadasa, M. Augmented Model-Based Framework for Battery Remaining Useful Life Prediction. Appl. Energy 2022, 324, 119624. [Google Scholar] [CrossRef]
- Nuhic, A.; Terzimehic, T.; Soczka-Guth, T.; Buchholz, M.; Dietmayer, K. Health Diagnosis and Remaining Useful Life Prognostics of Lithium-Ion Batteries Using Data-Driven Methods. J. Power Sources 2013, 239, 680–688. [Google Scholar] [CrossRef]
- Tseng, K.H.; Liang, J.W.; Chang, W.; Huang, S.C. Regression Models Using Fully Discharged Voltage and Internal Resistance for State of Health Estimation of Lithium-Ion Batteries. Energies 2015, 8, 2889–2907. [Google Scholar] [CrossRef]
- Mansouri, S.S.; Karvelis, P.; Georgoulas, G.; Nikolakopoulos, G. Remaining Useful Battery Life Prediction for UAVs Based on Machine Learning. IFAC-PapersOnLine 2017, 50, 4727–4732. [Google Scholar] [CrossRef]
- Guo, J.; Li, Z.; Pecht, M. A Bayesian Approach for Li-Ion Battery Capacity Fade Modeling and Cycles to Failure Prognostics. J. Power Sources 2015, 281, 173–184. [Google Scholar] [CrossRef]
- Khumprom, P.; Yodo, N. A Data-Driven Predictive Prognostic Model for Lithium-Ion Batteries Based on a Deep Learning Algorithm. Energies 2019, 12, 660. [Google Scholar] [CrossRef]
- Ren, L.; Zhao, L.; Hong, S.; Zhao, S.; Wang, H.; Zhang, L. Remaining Useful Life Prediction for Lithium-Ion Battery: A Deep Learning Approach. IEEE Access 2018, 6, 50587–50598. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiong, R.; He, H.; Liu, Z. A LSTM-RNN Method for the Lithuim-Ion Battery Remaining Useful Life Prediction. In Proceedings of the 2017 Prognostics and System Health Management Conference, PHM-Harbin 2017—Proceedings, Harbin, China, 9–12 July 2017; pp. 1–4. [Google Scholar]
- Guo, W.; Sun, Z.; Vilsen, S.B.; Meng, J.; Stroe, D.I. Review of “Grey Box” Lifetime Modeling for Lithium-Ion Battery: Combining Physics and Data-Driven Methods. J. Energy Storage 2022, 56, 105992. [Google Scholar] [CrossRef]
- Liao, L.; Köttig, F. A Hybrid Framework Combining Data-Driven and Model-Based Methods for System Remaining Useful Life Prediction. Appl. Soft Comput. J. 2016, 44, 191–199. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar] [CrossRef]
- Severson, K.A.; Monian, B.; Love, J.C.; Braatz, R.D. A Method for Learning a Sparse Classifier in the Presence of Missing Data for High-Dimensional Biological Datasets. Bioinformatics 2017, 33, 2897–2905. [Google Scholar] [CrossRef] [PubMed]
- Severson, K.A.; Molaro, M.C.; Braatz, R.D. Principal Component Analysis of Process Datasets with Missing Values. Processes 2017, 5, 38. [Google Scholar] [CrossRef]
- Jeong, H.; Wang, H.; Calmon, F.P. Fairness without Imputation: A Decision Tree Approach for Fair Prediction with Missing Values. In Proceedings of the 36th AAAI Conference on Artificial Intelligence, Virtual, 22 February–1 March 2022. [Google Scholar]
- Twala, B.E.T.H.; Jones, M.C.; Hand, D.J. Good Methods for Coping with Missing Data in Decision Trees. Pattern Recognit. Lett. 2008, 29, 950–956. [Google Scholar] [CrossRef]
- Chen, L.; Xu, Y.; Zhu, Q.X.; He, Y.L. Adaptive Multi-Head Self-Attention Based Supervised VAE for Industrial Soft Sensing with Missing Data. IEEE Trans. Autom. Sci. Eng. 2023, 1–12. [Google Scholar] [CrossRef]
- Wu, R.; Zhang, A.; Ilyas, I.F.; Rekatsinas, T. Attention-Based Learning for Missing Data Imputation in HoloClean. In Proceedings of the 3rd MLSys Conference, Austin, TX, USA, 15 March 2020. [Google Scholar]
- Yu, J.; Wu, B. Attention and Hybrid Loss Guided Deep Learning for Consecutively Missing Seismic Data Reconstruction. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5902108. [Google Scholar] [CrossRef]
- Ansari, S.; Ayob, A.; Hossain Lipu, M.S.; Hussain, A.; Saad, M.H.M. Remaining Useful Life Prediction for Lithium-Ion Battery Storage System: A Comprehensive Review of Methods, Key Factors, Issues and Future Outlook. Energy Rep. 2022, 8, 12153–12185. [Google Scholar] [CrossRef]
- Ma, G.; Zhang, Y.; Cheng, C.; Zhou, B.; Hu, P.; Yuan, Y. Remaining Useful Life Prediction of Lithium-Ion Batteries Based on False Nearest Neighbors and a Hybrid Neural Network. Appl. Energy 2019, 253, 113626. [Google Scholar] [CrossRef]

| APE (%) | RMSE (Cycles) | |||||
|---|---|---|---|---|---|---|
| Train | Validation | Test | Train | Validation | Test | |
| Random missing | 9.4 | 10.8 | 11.3 | 82 | 119 | 104 |
| Cycle missing | 8.8 | 9.3 | 10.3 | 77 | 102 | 100 |
| Time-step missing | 9.8 | 9.8 | 11.1 | 80 | 108 | 99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Jiang, B. Attention Mechanism-Based Neural Network for Prediction of Battery Cycle Life in the Presence of Missing Data. Batteries 2024, 10, 229. https://doi.org/10.3390/batteries10070229
Wang Y, Jiang B. Attention Mechanism-Based Neural Network for Prediction of Battery Cycle Life in the Presence of Missing Data. Batteries. 2024; 10(7):229. https://doi.org/10.3390/batteries10070229
Chicago/Turabian StyleWang, Yixing, and Benben Jiang. 2024. "Attention Mechanism-Based Neural Network for Prediction of Battery Cycle Life in the Presence of Missing Data" Batteries 10, no. 7: 229. https://doi.org/10.3390/batteries10070229
APA StyleWang, Y., & Jiang, B. (2024). Attention Mechanism-Based Neural Network for Prediction of Battery Cycle Life in the Presence of Missing Data. Batteries, 10(7), 229. https://doi.org/10.3390/batteries10070229







