Battery Scheduling Optimization and Potential Revenue for Residential Storage Price Arbitrage
Abstract
1. Introduction
2. Materials and Methods
2.1. Energy Price Data
2.2. Battery Scheduling Optimisation Model
2.2.1. Objective Function
2.2.2. Constraints
3. Results
- Capacity: 10 kWh;
- Charging/Discharging power: 5 kW (for Case 1) and 10 kW (for Case 2);
- Charging/Discharging efficiency: 95%;
- SOC upper limit: 90%;
- SOC lower limit: 10%;
- Optimization scenario: max revenue.
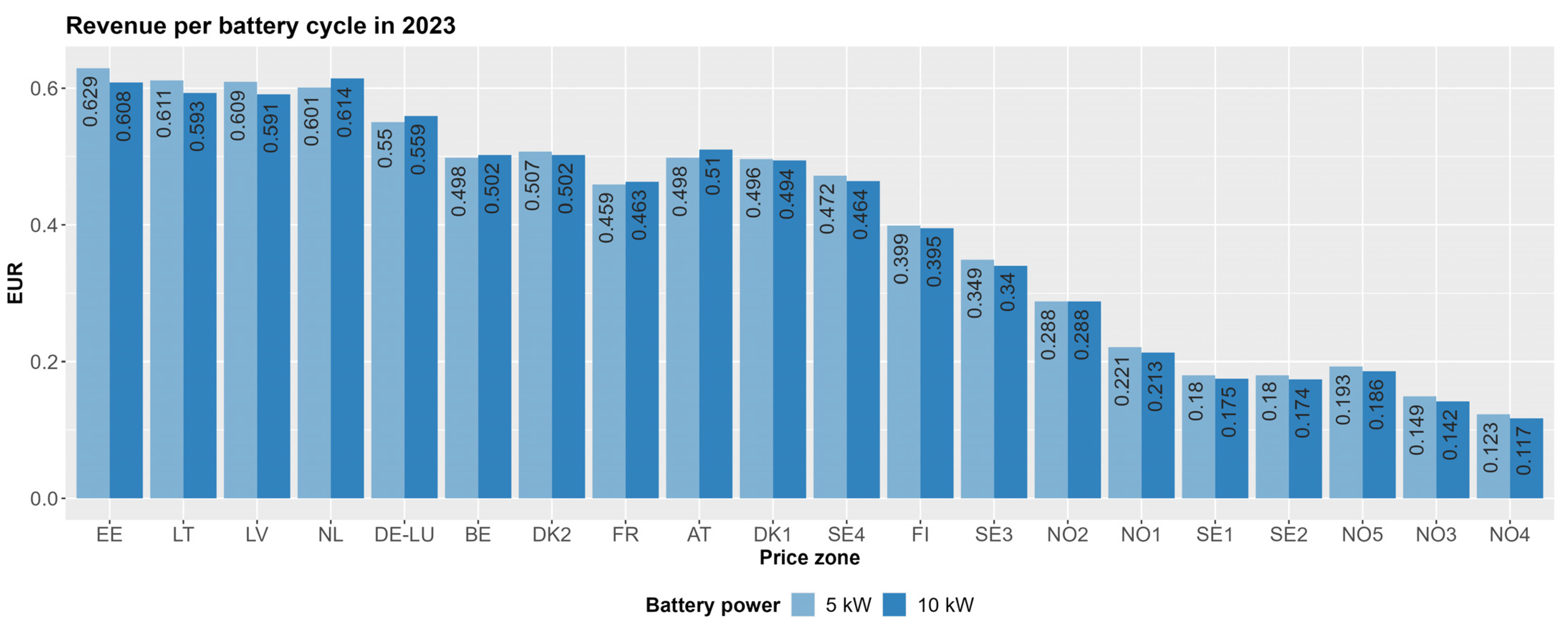
3.1. Case Study with a 5 kW/10 kWh Battery
3.2. Case Study with 10 kW/10 kWh Battery
4. Conclusions
- A 5 kW/10 kWh battery gives the highest revenue in the Baltic region with the top 1 of 409.78 EUR in the Estonian price zone and the top 2–3 with almost identical revenue in Lithuania and Latvia;
- The lowest possible revue is in Norway zone 4 (NO4);
- The mean number of cycles per year in all price zones is 1.4 cycles per day;
- The 10 kW battery results on an average 7.98% increase in total revenue across various regions. The average monetary increase in all price zones is 20.68 EUR;
- The findings indicate that while 10 kW batteries can generate higher total revenue, 5 kW batteries are more efficient in terms of revenue per cycle.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Zone Definitions | Description |
| AT | Austria |
| BE | Belgium |
| DK1 | Denmark |
| DK2 | Denmark |
| EE | Estonia |
| FI | Finland |
| FR | France |
| DE-LU | Germany–Luxembourg |
| LV | Latvia |
| LT | Lithuania |
| NL | Netherlands |
| NO1 | Norway |
| NO2 | Norway |
| NO3 | Norway |
| NO4 | Norway |
| NO5 | Norway |
| SE1 | Sweden |
| SE2 | Sweden |
| SE3 | Sweden |
| SE4 | Sweden |
| Symbols | Description |
| t | Steps of time |
| Δt | Duration of time period t, 1 h |
| T | Day-ahead optimization period, 24 h |
| C(t) | Energy price at time period t, EUR/kWh |
| Echg(t) | Charge energy at each time period t, kWh |
| Edis(t) | Discharge energy at each time period t, kWh |
| Pchg(t) | Charge power at each time period t, kW |
| Pdis(t) | Discharge power at each time period t, kW |
| Rchg_max | Maximum charging rate |
| Rdis_max | Maximum discharging rate |
| Bcap | Battery capacity, kWh |
| Ichg(t) | Binary variable indicating that battery is charging |
| Idis(t) | Binary variable indicating that battery is discharging |
| SOC(t) | State of charge of the battery at the time t, kWh |
| ηchg | Battery charge efficiency, % |
| ηdis | Battery discharge efficiency, % |
References
- Sioshansi, F.P. California’s ‘Duck Curve’ Arrives Well Ahead of Schedule. Electr. J. 2016, 29, 71–72. [Google Scholar] [CrossRef]
- Sheha, M.; Powell, K. Using Real-Time Electricity Prices to Leverage Electrical Energy Storage and Flexible Loads in a Smart Grid Environment Utilizing Machine Learning Techniques. Processes 2019, 7, 870. [Google Scholar] [CrossRef]
- BloombergNEF. Scaling the Residential Energy Storage Market. November 2023. Available online: https://assets.bbhub.io/professional/sites/24/Scaling-the-Residential-Energy-Storage-Market.pdf (accessed on 16 April 2024).
- BloombergNEF. Lithium-Ion Battery Pack Prices Hit Record Low of $139/kWh. November 2023. Available online: https://about.bnef.com/blog/lithium-ion-battery-pack-prices-hit-record-low-of-139-kwh/ (accessed on 16 April 2024).
- Shabani, M.; Shabani, M.; Wallin, F.; Dahlquist, E.; Yan, J. Smart and optimization-based operation scheduling strategies for maximizing battery profitability and longevity in grid-connected application. Energy Convers. Manag. X 2024, 21, 100519. [Google Scholar] [CrossRef]
- Peñaranda, A.F.; Romero-Quete, D.; Cortés, C.A. Grid-Scale Battery Energy Storage for Arbitrage Purposes: A Colombian Case. Batteries 2021, 7, 59. [Google Scholar] [CrossRef]
- Komorowska, A.; Olczak, P.; Hanc, E.; Kamiński, J. An analysis of the competitiveness of hydrogen storage and Li-ion batteries based on price arbitrage in the day-ahead market. Int. J. Hydrogen Energy 2022, 47, 28556–28572. [Google Scholar] [CrossRef]
- Krishnamurthy, D.; Uckun, C.; Zhou, Z.; Thimmapuram, P.R.; Botterud, A. Energy Storage Arbitrage Under Day-Ahead and Real-Time Price Uncertainty. IEEE Trans. Power Syst. 2018, 33, 84–93. [Google Scholar] [CrossRef]
- Salles, M.B.C.; Huang, J.; Aziz, M.J.; Hogan, W.W. Potential Arbitrage Revenue of Energy Storage Systems in PJM. Energies 2017, 10, 1100. [Google Scholar] [CrossRef]
- Kataray, T.; Nitesh, B.; Yarram, B.; Sinha, S.; Cuce, E.; Shaik, S.; Vigneshwaran, P.; Roy, A. Integration of smart grid with renewable energy sources: Opportunities and challenges—A comprehensive review. Sustain. Energy Technol. Assess. 2023, 58, 103363. [Google Scholar] [CrossRef]
- Soudagar, M.E.M.; Ramesh, S.; Khan, T.M.Y.; Almakayeel, N.; Ramesh, R.; Ghazali, N.N.N.; Cuce, E.; Shelare, S. An overview of the existing and future state of the art advancement of hybrid energy systems based on PV-solar and wind. Int. J. Low-Carbon Technol. 2024, 19, 207–216. [Google Scholar] [CrossRef]
- Lew, D.; Bartlett, D.; Groom, A.; Jorgensen, P.; O’Sullivan, J.; Quint, R.; Rew, B.; Rockwell, B.; Sharma, S. Getting to 100% renewables: Operating experiences with very high penetrations of variable energy resources. IET Renew. Power Gener. 2020, 14, 3899–3907. [Google Scholar] [CrossRef]
- Belmonte, B.B.; Mouratidis, P.; Franke, G.; Rinderknecht, S. Developments in the cost of grid balancing services and the design of the European balancing market. Energy Rep. 2023, 10, 910–931. [Google Scholar] [CrossRef]
- Wang, Z.; Kirschen, D.S. Two-stage optimal scheduling for aggregators of batteries owned by commercial consumers. Transm. Distrib. IET Gener. 2019, 13, 4880–4887. [Google Scholar] [CrossRef]
- Brogan, P.V.; Best, R.; Morrow, J.; Duncan, R.; Kubik, M. Stacking battery energy storage revenues with enhanced service provision. IET Smart Grid 2020, 3, 520–529. [Google Scholar] [CrossRef]
- Nord Pool|Day-Ahead Prices. Available online: https://data.nordpoolgroup.com/auction/day-ahead/prices (accessed on 28 May 2024).
- European Clean Power Pathways Explorer. Ember. Available online: https://ember-climate.org/data/data-tools/european-clean-power-pathways-explorer/ (accessed on 30 June 2024).
- Barbour, E.; González, M.C. Projecting battery adoption in the prosumer era. Appl. Energy 2018, 215, 356–370. [Google Scholar] [CrossRef]
- Wankmüller, F.; Thimmapuram, P.R.; Gallagher, K.G.; Botterud, A. Impact of battery degradation on energy arbitrage revenue of grid-level energy storage. J. Energy Storage 2017, 10, 56–66. [Google Scholar] [CrossRef]
- Pena-Bello, A.; Burer, M.; Patel, M.K.; Parra, D. Optimizing PV and grid charging in combined applications to improve the profitability of residential batteries. J. Energy Storage 2017, 13, 58–72. [Google Scholar] [CrossRef]
- Hassan, A.S.; Cipcigan, L.; Jenkins, N. Optimal battery storage operation for PV systems with tariff incentives. Appl. Energy 2017, 203, 422–441. [Google Scholar] [CrossRef]






| Zone | Country | EUR/MWh | ||||
|---|---|---|---|---|---|---|
| Mean | Max | Min | SD | Sum, Thousand | ||
| AT | Austria | 102.14 | 437.47 | −500.00 | 44.38 | 894.76 |
| BE | Belgium | 97.27 | 330.36 | −120.00 | 45.87 | 852.08 |
| DK1 | Denmark | 86.83 | 524.27 | −440.10 | 48.82 | 760.60 |
| DK2 | 81.25 | 524.27 | −60.04 | 50.12 | 711.78 | |
| EE | Estonia | 90.79 | 777.18 | −60.04 | 55.79 | 795.31 |
| FI | Finland | 56.47 | 777.18 | −500.00 | 56.71 | 494.65 |
| FR | France | 96.86 | 276.12 | −134.94 | 45.53 | 848.46 |
| DE-LU | Germany–Luxembourg | 95.18 | 524.27 | −500.00 | 47.58 | 833.74 |
| LV | Latvia | 93.89 | 777.18 | −56.55 | 54.55 | 822.51 |
| LT | Lithuania | 94.44 | 777.18 | −56.55 | 54.87 | 827.31 |
| NL | Netherlands | 95.82 | 463.77 | −500.00 | 49.05 | 839.36 |
| NO1 | Norway | 66.95 | 332.00 | −61.84 | 44.68 | 586.49 |
| NO2 | 79.45 | 261.85 | −61.84 | 36.29 | 695.95 | |
| NO3 | 38.55 | 332.00 | −10.06 | 32.79 | 337.74 | |
| NO4 | 29.95 | 332.00 | −10.06 | 26.21 | 262.34 | |
| NO5 | 67.05 | 261.85 | −6.62 | 43.40 | 587.32 | |
| SE1 | Sweden | 39.97 | 332.00 | −60.04 | 34.17 | 350.15 |
| SE2 | 39.98 | 332.00 | −60.04 | 34.16 | 350.20 | |
| SE3 | 51.70 | 332.00 | −60.04 | 45.33 | 452.90 | |
| SE4 | 64.88 | 332.00 | −60.04 | 50.64 | 568.34 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paulauskas, N.; Kapustin, V. Battery Scheduling Optimization and Potential Revenue for Residential Storage Price Arbitrage. Batteries 2024, 10, 251. https://doi.org/10.3390/batteries10070251
Paulauskas N, Kapustin V. Battery Scheduling Optimization and Potential Revenue for Residential Storage Price Arbitrage. Batteries. 2024; 10(7):251. https://doi.org/10.3390/batteries10070251
Chicago/Turabian StylePaulauskas, Nerijus, and Vsevolod Kapustin. 2024. "Battery Scheduling Optimization and Potential Revenue for Residential Storage Price Arbitrage" Batteries 10, no. 7: 251. https://doi.org/10.3390/batteries10070251
APA StylePaulauskas, N., & Kapustin, V. (2024). Battery Scheduling Optimization and Potential Revenue for Residential Storage Price Arbitrage. Batteries, 10(7), 251. https://doi.org/10.3390/batteries10070251






