Abstract
Cathode formulation, which describes the amount of cathode active material (CAM), conductive additives (CAs), and binder within a cathode compound, is decisive for the performance metrics of lithium-ion battery (LIB) cells. The direct measurement of electronic resistance can be an enabler for more time- and cost-efficient cathode formulation improvements. Within this work, we correlate the electronic resistance with the electrochemical performance of cathodes. Two different high Nickel NCM cathode materials and numerous CAs are used to validate the findings. A detailed look into the resistance reduction potential of carbon black (CB) and single-walled carbon nanotubes (SWCNT) and their mixtures is made. Finally, an impact estimation of cathode formulation changes on LIB key performance factors, such as energy density and cost, is shown.
1. Introduction
Lithium-ion batteries (LIBs) are of great importance for the decarbonization of a series of industries. Typical requirements for a LIB for automotive use are high volumetric energy density (VED), fast-charging, long cycle life, safety, and low cost. Effective cathode design plays a crucial role in achieving the specified targets for a LIB. Cathodes usually consist of cathode active materials (CAMs), conductive additives (CAs), and binder. From these components, only CAM is active in storing lithium; CAs are added to enhance the electronic conductivity of the cathode; and a binder is added for cohesion within the compound and adhesion to the current collector (CC). Many researchers use formulations that are rich in inactive components, such as 80:10:10 (CAM:CA:binder, by %) [1]. To increase VED, it is essential to maximize the amount of active materials and minimize the amount of inactive materials in the cathode compound. The ratio has been optimized by application-oriented researchers, with current industrial cells containing 95–98% CAM [2]. A promising way to increase the CAM content of a formulation is by applying advanced CAs showing improved properties and morphology. Typically, carbon black (CB) is used as the main CA in compound cathodes. However, in recent years, multi-walled carbon nano tubes (MWCNTs), single-walled carbon nano tubes (SWCNTs) [3], carbon nanofibers (CNF), and graphene [2] have also found their way into cathode formulations. Entwistle et al. [4] published an extensive review of electronic conductivity and different CAs in battery electrodes. By using advanced Cas, researchers have already shown the possibility of reaching >99% CAM content within a LIB cathode without sacrificing cycling stability [2].
Although we screened a lot of articles on the topic of cathode formulation optimization, we did not find a clear engineering tool guiding the way. Commonly, a trial-and-error approach is taken, often based on pre-testing of various formulations in half cells followed by a validation of results for the most promising candidates in full cell formats. An alternative, more systematic approach for effective engineering of cathode formulations is to separate and investigate the functions of each inactive component. The binder is mainly responsible for adhesion, which can be tested with 90°-peel tests. The main function of CAs is to enable the unhindered transport of electrons from the current collector to each CAM particle inside the cathode compound without inhomogeneities in the current distribution. This capability can be described as the electronic conductivity, or, in its reciprocal, the electronic resistance. The electronic resistance of a cathode can be subdivided into the electronic compound resistance (RCompound) and the electronic contact resistance (RContact). RCompound describes the electronic resistance within the electrode compound, whereas RContact describes the electronic resistance at the interface between the cathode compound and the current collector.
In our recent work, we summarized and critically analyzed the numerous methods used to determine and separate both of these resistance types [5]. Methods that can be applied to a dry electrode coating are of special interest in this regard as they avoid building cells to measure electronic resistance, a time-consuming action that also blocks test channels. The company HIOKI recently commercialized a device that allows the probing of a dry electrode to extract the specific resistance types RContact and RCompound from a single measurement [6]. By using this electronic resistance measurement (ERM), much faster and easier optimization of electrode formulations should be possible. However, until now, very limited experimental studies have been published on the actual threshold for electronic resistance to foster the high C-rate capability of a cathode. It is also unknown to what extent the type of CA is impacting the electronic resistance. Tian et al. [7] attempted an electronic resistance quantification of CAs for cathodes by using a 2-point ERM approach. It was concluded that an electronic conductivity of 1 S∙m−1 linked to a high amount of ~12% of CB is necessary. However, some obvious limitations of the study are: (A) non-calendered cathodes were measured, although this is irrelevant for the final application in commercial LIB cells and the performance of non-calendered ones is largely different from calendered ones; (B) the test was only conducted for one CAM type (NCM811).
To improve our understanding of the impact of electronic resistance on cell performance, we investigated the correlations between ERM results and electrochemical results. For an extensive study, we looked at single-crystalline (SC) and poly-crystalline (PC) NCM811 CAMs under variation of CA type and CA share. Specific characteristics of CA types with altering morphology and properties are examined in detail, as well as potential synergies of CA-mixtures. Finally, a more general view of electrode design parameters, including cost, was taken. The findings in this work guide the way to a faster and more efficient approach for cathode formulation optimization, saving precious time and resources for research labs. It also allows for a faster adoption of new CA grades in the LIB market.
2. Materials and Methods
2.1. Cathode Preparation
For the preparation of cathode slurries, CAM was homogenized with CA and polyvinylidene fluoride binder (PVDF) in battery grade N-Methyl-2-pyrrolidon (NMP, water ≤ 300 ppm) using a thinky mixer. The CAMs used in this work were poly-crystalline NCM with ~85% Nickel content (PC-NCM811; D50 = 12.55 µm) and single-crystalline NCM with ~85% Nickel content (SC-NCM811, D50 = 3.52 µm) sourced from commercial suppliers. The CAs used in this work are carbon black (CB) (LITx HP, CABOT, Boston, MA, USA) and single-walled carbon-nanotubes (SWCNTs) (TUBALL, OCSiAl, Luxembourg). Cathode slurries were coated with a doctor blade (BYK, 12 cm width) on 20 µm battery grade Al-current collector. Coating thickness was adjusted to obtain mass loadings corresponding to an areal capacity of 3 mAh∙cm−2 (half-cell vs. Li/Li+ at C/3 and 25 °C, max. ± 1.5% loading variance was accepted), if not stated otherwise. The coated electrodes were dried at 80 °C under vacuum overnight. Cathodes were then calendered at room temperature with a lab calender to a porosity of 30% (press density of 3.2 to 3.4 g∙cm−3) if not stated otherwise.
2.2. Measurements
All ERMs within this work were carried out with HIOKI RM2610. All measurements were performed on dry cathode electrodes. Three coins (ø15 mm) were punched from the calendered cathode sheet, and each coin was measured twice, resulting in a total of six measurements per coating. Further information on the measurement device and measurement principle can be found in the technote provided by the device manufacturer [6] or in our previous work [5]. ERM with HIOKI RM2610 yields electronic resistance data for the cathode compound (RCompound) and the contact interface between CC and compound (RContact). The sum of both resistances is designated in this work as total electronic resistance (TER). Further details on the interpretation, data quality, and convertibility of these values are explained in our previous work [5].
For measurements in half-coin cells (HCC), ø15 mm electrode coins were punched and dried overnight at 80 °C under vacuum. Coin cells (CR2016) were assembled in an argon-filled glovebox (<3 ppm H2O, <3 ppm O2). Li-metal coins ø16 mm (China Energy Lithium Co, Ltd., Tianjin, China) were used as a counter and reference electrode (2-electrode setup). As electrolyte, 100 µL of 1.2 M LiPF6 in a mixture of ethylene carbonate (EC), dimethyl carbonate (DMC) and ethyl methyl carbonate (EMC) (EC:DMC:EMC = 30:35:35 by volume) +1.5 wt.% vinylene carbonate was used in the coin cells. Tests were performed on Basytec CTS battery cyclers at a constant temperature of 25 °C. The voltage range was 3.0–4.3 V vs. Li/Li+. The test protocol used a constant current—constant voltage (CC-CV) charge with charge rates limited to a maximum of C/3 to avoid Li dendrites. Current limit for CV phase was kept constant at C/20 for every cycle. The discharge C-rates varied from C/10 up to 6C as indicated in the graphs.
3. Results
3.1. Correlation of ERM Results with HCC Results
In this chapter, we will investigate the correlation of ERM results with HCC measurements. This is of high importance as HCC is a setup widely used for screening and optimizing cathode formulations. To prove that ERM is a suitable method for cathode formulation optimization, we must first determine if a reliable correlation exists between ERM results and electrochemical performance in HCC.
As explained in the introduction, ERM and HCC have fundamental differences. In ERM, the electronic resistance of the electrode in a dry state is measured. In contrast, in HCC, the total resistance of the cell is acquired, including not only electronic resistances but also a variety of other ionic resistances as explained in more detail in [5]. While ionic resistances are negligibly influenced by small changes in the cathode formulation, electronic resistances, show a much stronger dependency. In fact, the main reason for adding CA to the cathode formulation is to improve its electronic conductivity. At low CA contents, the electronic resistance is high and, thus, a main contributor to the cell resistance. However, at high CA contents, the electronic resistance becomes negligibly small in comparison to ionic resistances. A scheme of this relation is shown in the Supporting Information in Figure S1.
To find the amount of CA for which the electronic resistance starts dominating the electrochemical performance, we prepared electrodes containing different CA amounts and benchmarked them in ERM versus HCC discharge rate tests. The PVDF content in all samples was held constant at 1.38%. All electrodes had the same electrode loading of 3 mAh∙cm−2 and were calendered to the same porosity of 30%.
In Figure 1a, the discharge capacities of cathodes manufactured from PC-NCM811 under variation of CB amount are shown. Cathodes with 0% CB and 0.25% CB show deteriorating capacities at C-rates much lower than comparable cathodes with ≥0.5% CB. All cathode samples containing ≥0.5% CB show equal performance within the experimental error. At C-rates ≥ 5C all of the samples show strongly decreasing discharge capacities, which we attribute to ionic diffusion limitations [5].
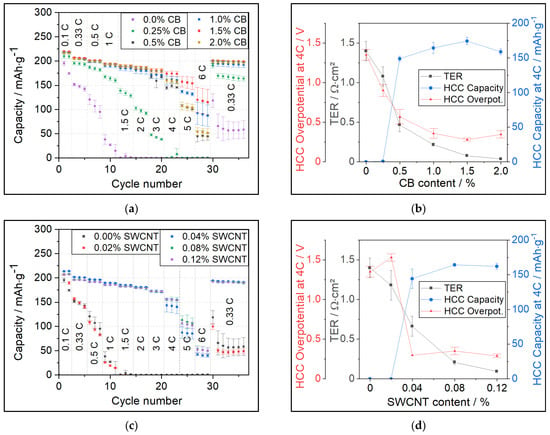
Figure 1.
(a) C-rate test of PC-NCM811 cathodes with different CB contents in HCC; (b) Comparison of TER vs. overpotential (Overpot.) and discharge capacity measured at 4C in HCC for PC-NCM811 cathodes with different CB contents; (c,d) same tests for PC-NCM811 cathodes with SWCNT as replacement for CB under variation of SWCNT contents.
The HCC test running from low C-rate to high C-rate delivers two types of key information when it comes to formulation optimization:
- (i).
- Discharge capacity at low C-rate gives an indication if all CAM particles are well electronically connected within the cathode compound.
- (ii).
- Discharge capacities at higher C-rates provide valuable information on how large the electronic resistance in the cathode is. (If the same CAM is used, the ionic resistances can be assumed as constant).
To some extent, points (i) and (ii) are connected. For example, it can be the case that in HCC tests, cathode formulations A and B perform similar at low C-rates (i.e., all CAM particles connected) but show significant differences at higher C-rates (i.e., insufficient conductive network established).
To evaluate the influence of cathode formulation on C-rate capability, analyzing the correct C-rate area in the HCC tests is mandatory. At very low C-rates the experimental error of HCC (standard deviation between cells of ~5 mV or ~2 mAh∙g−1) is often large compared to the signal observed for formulation changes. With higher C-rates, the voltage drop (overpotential) caused by electronic resistance is growing according to Ohms law. Due to the growing overpotential, the cut-off voltage is reached earlier, leading to a lower amount of charge (capacity) exchanged. Obviously, the differences in electronic conductivity become more pronounced with a higher C-rate. However, at very high C-rates, the electrodes will become diffusion-limited, and for currents above the diffusion-limiting C-rate [8], very large experimental errors will be observed. Therefore, the sweet spot for formulation evaluation is the C-rate range close but still below the diffusion-limiting C-rate. We recommend the scheme shown in Figure S2 to follow above explanation. In our study on cathodes with a loading of 3 mAh∙cm−2 and a discharge C-rate of 4C, this provides a reasonable basis for performance comparison.
Figure 1b shows the comparison of ERM results with HCC results for PC-NCM811 cathodes with different CB contents. The red triangles show the mean overpotential in HCC at 4C discharge, calculated by subtracting the average discharge voltage of the cathode in HCC from the open-circuit voltage (OCV) of the cathode material of 3.78 V vs. Li/Li+ obtained via quasi-OCV measurement. The measurement results of the average discharge voltage for the example of PC-NCM811 are shown in Figure S3. More information on the calculation of the mean overpotential is given in Supplementary Materials Section S2. Gray squares indicate the ERM in TER and blue dots give the specific discharge capacity at 4C. At 0.0% and 0.25% CB, the TER and overpotential are high; thus, measured capacities are close to zero. The step to 0.5% CB shows a strong decline in TER and overpotential, leading to a steep increase in measured capacity. With 1.0% CB, the TER and overpotential decrease even more, which is accompanied by a further increase in capacity. Up to 1.0% CB, the HCC overpotential correlates quite well with the TER, which is a strong indication that the main contribution to the resistance in these samples is caused by the electronic resistance. This is also the reason the reduction in TER is directly translated into higher capacity.
Although the TER still decreases for samples with 1.5% CB and 2.0% CB, no significant influence on the HCC overpotential or capacity can be observed. This indicates that the TER in these samples is not decisive anymore for cell performance, as other resistance contributions such as charge-transfer and electrolyte become dominant instead [5,9,10]. The measurement also allows us to define the TER of 0.22 Ω∙cm2 (at 1% CB) as a target value since a further TER decrease does not influence the improvement of electrochemical performance in a positive way.
Interestingly, when using Ohm’s law to calculate overpotentials based on the TER, the obtained values are insignificantly smaller and far below the measured overpotentials. For example, the 0.25% CB sample showed a TER of 1.08 Ω∙cm2. Considering the loading of 3 mAh∙cm−2, the calculated overpotential would be as little as ~13 mV at a C-rate of 4C. Instead, the measured overpotential was 280 mV for the 1.5% CB and 900 mV for the 0.25% CB sample. It can be assumed that overpotentials from the Li-anode, charge-transfer, and electrolyte are constant and almost the same for all samples. Therefore, the difference of 620 mV should, in theory, arise from the change in electronic resistance. However, this value is far from the 13 mV calculated from ERM. In our previous work, ref. [5] it was shown that swelling of the electrode causes a significant increase in electronic resistance. For the contact resistance, roughly a 5-fold increase was measured. But even with this “correction calculation”, the TER-based assessment only yields 65 mV (from TER (13 mV∙5) as swelling factor) which is far below the overpotential measured in HCC.
The shape of the TER curve also supports the percolation theory [4], saying that at a specific amount of CA, a percolation network is formed, and a drastic decrease in electronic resistance can be found for CA contents above this “percolation threshold”.
To further investigate and validate the correlation between TER and HCC results, another set of cathode formulations now containing SWCNT as a single CA were tested. HCC results are shown in Figure 1c, and the correlation with TER is shown in Figure 1d. In a similar manner as for the CB variation, samples with minimal CA amounts of 0.0% and 0.02% SWCNT show very low discharge capacities in HCC. This effect is already visible at C-rates ≥ 0.33C. For the 0.04% SWCNT sample, we observed a steep decrease in TER and HCC overpotential as well as a strong increase in capacity retention at higher C-rates. In the next formulation containing 0.08% SWCNT, the TER is decreasing to 0.21 Ω∙cm2, which is accompanied by another significant increase in HCC discharge capacity by ~15 mAh∙g−1 at 4C. For a higher SWCNT share, the TER continues to fall; however, without any positive impact on HCC overpotential or capacity.
In the same manner as discussed for CB, the cathodes containing SWCNT should follow the percolation theory. The percolation threshold for SWCNT seems to be around 0.04% and is therefore much lower than for CB (~0.5%). This is in alignment with the other literature, which has already shown the potential of SWCNT as an outstanding CA [7].
As shown by Itou et al. [11], the amount of CA in a cathode compound may also influence tortuosity and, therefore, resistance types such as electrolyte resistance. However, even though the CA content within the electrode in [11] was changed from 4% to 14%, the tortuosity just increased slightly from around 3 to 4, in some cases, with tortuosity measurement errors of 0.5. Therefore, it was assumed in this work that the change in CA does not significantly impact tortuosity and its corresponding resistances.
As shown before, for the PC-NCM811 samples containing either CB or SWCNT, the critical TER value is ~0.25 Ω∙cm2. Below this threshold, no further positive impact on HCC performance was observed. Tian et al. [7] did electronic resistance experiments by using dry cathode measurement in coin cells and concluded that an electronic out-of-plane conductivity of 1 S∙m−1 is high enough to optimize cathode rate performance. Based on our sample geometry (~45 µm coating thickness), this value translates to 0.45 Ω∙cm2 areal-specific resistance (ASR), a value quite close to the herein found prediction. However, in [7], it was also suggested that >12% CB would be required to achieve this value. We attribute the significant difference to the herein found amount (1% CB), mainly to the non-calendering of cathodes in [7]. The tremendous impact of calendering on electronic resistance was already shown in [5].
In the next step, it is necessary to validate if the TER threshold derived from PC-NCM811 measurement (0.25 Ω∙cm2) also holds true for other CAM morphologies. A SC-NCM811 was used, and CB contents were varied. As for the PC-NCM811 samples, the loading was kept at 3 mAh∙cm−2 and porosity was set to 30%. The results of the C-rate tests in HCC and comparison with TER data are shown in Figure 2. The samples with ≤0.5% CB show very high TER and, thus, exhibit poor discharge capacity at C-rates over 1C. At 1% CB, the HCC capacity at 4C is already considerably higher. Still, the saturation point is not reached before 1.5% CB, and a higher CB content of 2.0% does not support the increase in HCC capacity anymore. The TER for the 1.5% CB sample is 0.25 Ω∙cm2, which is again very close to the TER limit value measured for the PC-NCM811 samples. However, whereas the CB amount to reach this TER threshold is 1.5% for SC-NCM811, only 1.0% CB is required for PC-NCM811. This can mainly be attributed to the low intrinsic electronic conductivity of SC-NCM811 particles. To assess this intrinsic electronic conductivity, the TER of 0.0% CA samples was checked. The TER for PC-NCM811 and SC-NCM811 is 1.4 and 8.4 Ω∙cm2, respectively. An in-depth comparison of the TER for PC-NCM811 vs. SC-NCM811 under variation of CA can be found in Figure S4. For comparable formulations (same CA-type and CA-content), the resistance of the SC-NCM811 samples is between 3 and 6 times higher than for the PC samples. One of the reasons for the higher electronic resistance of SC NCMs is the morphology, which allows less “anchoring” of the particles into the CC-foil [5]. Anchoring the CAM in the CC is a key factor in reducing contact resistance. Furthermore, the D50 of SC-NCM (3.52 µm) is significantly smaller than the D50 of PC-NCM (12.55 µm). This difference causes significantly more SC-NCM particles at the same electrode thickness compared to PC-NCM. Which is in turn also causing more particle-particle contact areas at which electron transfer must occur. The electron transfer at these particle-particle interfaces may be slowed down by sluggish contact or by the presence of a non-conducting binder. It can be assumed that these higher numbers of particle–particle contacts cause higher electronic resistance and a higher need for CAs.
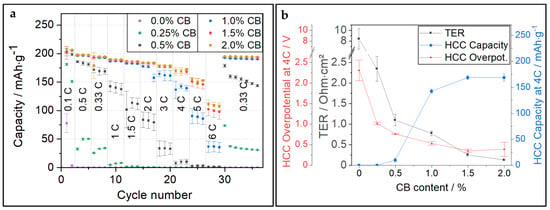
Figure 2.
(a) C-rate test of SC-NCM811 cathodes with different CB contents in HCC; (b) Comparison of TER vs. overpotential and discharge capacity measured at 4C in HCC for SC-NCM811 cathodes with different CB contents.
We found that ERM results can be well correlated with data obtained from HCC tests. Also, there is a TER threshold of about 0.25 Ω∙cm2, for which a further improvement in conductivity does not support the HCC performance. To save money, weight, and volume, the electrode running significantly below this TER threshold due to the addition of high amounts of CA is to be avoided. It should be mentioned here that this threshold was determined for HCC tests at 25 °C. As the ionic resistance is decreasing strongly with increasing temperature, the TER threshold is expected to be significantly lower at higher measurement temperatures (and consequently higher at lower temperatures).
3.2. Similarities and Differences in Various Types of CA
After correlating HCC results with ERM and defining the TER threshold value, we want to focus in more detail on the similarities and differences of different CA types. As shown in [5], the electronic resistance of an electrode consists of the resistance in the coating compound (RCompound) and the resistance at the interface between the coating and CC, often designated as contact resistance (RContact). For better comparability of resistance contributions, we harmonized the resistance dimensions by normalizing the RCompound to the electrode area (ASR). Figure 3a,b show RContact and RCompound from the ERM of PC-NCM811 cathodes with different amounts of CB and SWCNT.
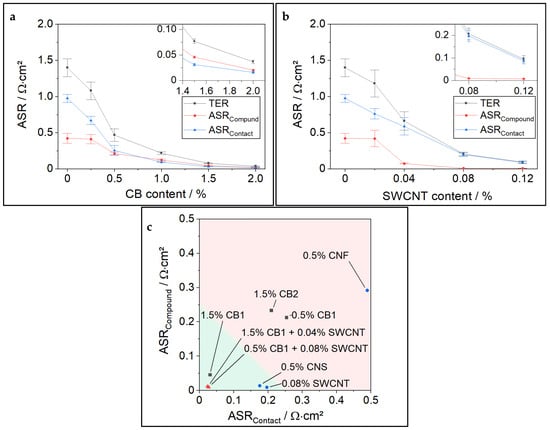
Figure 3.
(a) Detailed ERM results of PC-NCM811 with different CB contents; (b) Detailed ERM results of PC-NCM811 with different SWCNT contents; (c) Comparison of various CAs in combination with PC-NCM811. All cathodes have a constant PVDF content of 1.38%, similar loading of 3.0 mAh∙cm−2, and porosity of 30%.
As soon as the percolation threshold of ~0.5% CB is reached for the cathode samples with variable CB contents, both resistance types, RCompound and RContact, contribute equally to the total resistance. This is significantly different for the SWCNT samples, for which RContact makes up almost the complete TER after approaching the percolation threshold at around 0.04% SWCNT. SWCNTs demonstrate outstanding capability in reducing RCompound, a characteristic attributed to their high aspect ratio (L/D) [4]. The distribution for SC-NCM811 with different CB amounts is shown in Figure S5. It shows a higher TER than PC-NCM samples at very low CB contents but shows a similar trend in the ratios of RCompound and RContact as was found in PC-NCM CB variation samples.
Figure 3c compares the electronic resistance components for a broad variety of CAs tested in PC-NCM811 cathodes. Gray squares show CBs, blue dots show “advanced CAs” with a high aspect ratio, such as CNT, and red triangles show binary mixtures. The green area designates the target TER value ≤0.25 Ω∙cm2.
It is notable that different types of CB showed a very different ability to reduce electronic resistance. CB1, which is used throughout this paper, yields a TER of 0.076 Ω∙cm2 when 1.5% is applied. In contrast, 1.5% CB2 yields a much higher TER of 0.43 Ω∙cm2, which is rather comparable to the TER value of 0.5% CB1. This emphasizes that designing high-performance cathodes is a challenge considering not only the types of CA (e.g., CB, SWCNT, MWCNT, CNF) but also the great variation within each class of CAs depending on their morphology (particle size, branching, surface, aspect ratio), functionalities, purity, and so on, making, e.g., some CB more suitable than others. Figure 3c also highlights that SWCNTs and CNS are highly capable of reducing the RCompound. Interestingly, mixtures of CB and SWCNT show exceptionally low TER, a phenomenon worth studying in very detail in the next chapter.
3.3. Investigation of Synergy Effects in Electronic Conductivity for CA Blends
As shown above, SWCNTs are very capable of reducing RCompound, whereas CB shows a clear strength in improving RContact. Therefore, it is obvious that combining both CAs will bring synergetic benefits.
To save experimental time, it is desirable to predict the TER of CA-mixtures based on an in-depth understanding of dominant conduction effects. For this reason, we applied a simple resistance scheme, as shown in Figure 4a.
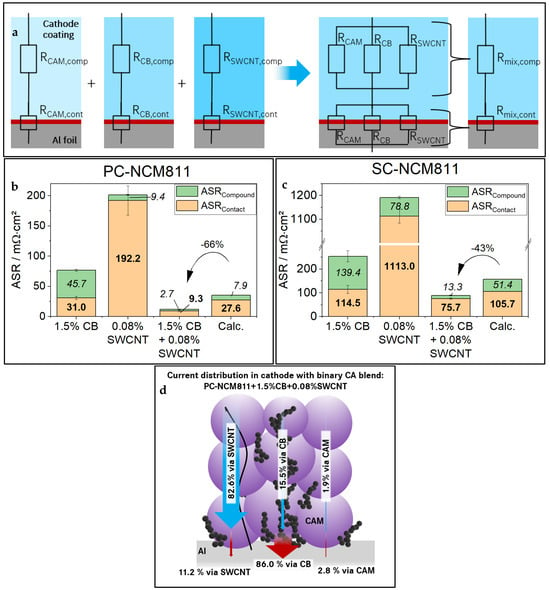
Figure 4.
(a) Schematic model for calculation of expected resistances of cathodes with CA-mixtures; ERM results of (b) PC-NCM811and (c) SC-NCM811 samples containing single type CAs, one exemplary CA-mix as well as the estimated resistance for this CA-mix. For better distinguishability ASRCompound values are given in italic font, ASRContact values are given in bold. (d) Schematic presentation showing the distribution of electronic current transport through the cathode network according to the presented resistance model.
As discussed earlier, it is rational to split TER into RCompound and RContact. Now we add the assumption that within the compound as well as the contact plane to CC, the resistance contributions of CAM, CB, and SWCNT can be separated into parallel resistances. The influence of PVDF was neglected in this model. Still, to obtain a fair comparison, the PVDF content was held constant at 1.38% in the investigated samples. From measurements performed for cathodes without CA (CAM sample) and at different CA contents (CAM + CB and CAM + SWCNT samples), it was possible to calculate the contribution of each component by using this simple resistance model. The detailed formulas are shown in Supplementary Materials, Section S3. The resistance model also allows each component to attribute its individual share of the total current transported in the compound and through the contact plane. A scheme of this current distribution is given in Figure 4d for a PC-NCM811 cathode with a binary mix of CA (1.5% CB + 0.08% SWCNT), which enables a better understanding of the impact and function of each component. The CA-mix cathodes were also manufactured and measured in ERM and HCC. The ERM results of cathodes containing single-type CA vs. one exemplary CA-mixture are shown in Figure 4, together with the estimated TER for PC-NCM811 (b) and SC-NCM811 (c). The calculation tables are given in Supplementary Materials, Section S3. As expected, the binary mixture of CAs profits from the benefits of each of its components. ASRCompound as well as ASRContact are lower in the mixture than in each of the single CA cathodes. In fact, we can even observe 66% and 43% lower electronic resistances in the experiment for PC-NCM811 and SC-NCM811, respectively, than expected from the theoretical model. The exact reason for the lower-than-expected electronic resistance is not well understood and needs further research. The authors assume a synergic effect between the two Cas; therefore, this deviation will be further designated as a “synergy effect”.
There are several points to be considered when using the above-shown resistance model:
- The RContact is strongly influenced by electrode porosity, which is not accounted for in the model. As the porosity was held constant at 30% for all samples in this work, this simplification is acceptable.
- The influence of binder on TER was neglected. This holds true as long as the binder content is kept constant, which was the case here (1.38% PVDF).
By applying the resistance model, it is possible to calculate the expected TER for each CA-mix within the studied CA matrix. The results of these calculations for our PC-NCM811 samples are given in Figure 5a. Gray contour lines are shown to indicate the TER, with a thicker contour line for the TER threshold of 0.25 Ω∙cm2. The violet dots, including specific TER values, indicate CA-mixtures that were experimentally tested. As discussed previously, for all these mixtures, a lower experimental TER value was found than expected from the calculation highlighting the synergy effect (the percentages in brackets show the extent of TER synergy). A more detailed evaluation of the ERM of these CA-mixtures is given in Figure S8.
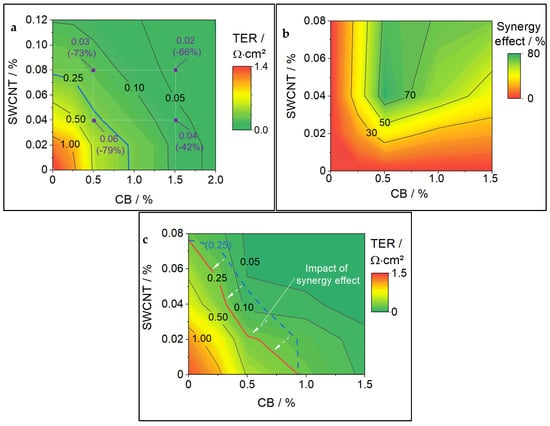
Figure 5.
(a) TER calculated based on the measurement of single CA cathodes. Violet dots indicate the TER of CA-mixtures also tested experimentally to assess the synergy effect (in brackets); (b) plot of estimated synergy effects for a variety of CA compositions; (c) TER corrected by synergy effects. The red line indicates the TER with synergy effect. The blue dotted line gives the TER without synergy effect as a reference. The white error are a guide to the eye to indicate the movement of the TER caused by synergy effect.
The contour plot of TER synergies for the tested CA-mixture matrix is shown in Figure 5b. Samples containing only one type of CA were assumed to have zero synergy (which is a trivial assumption). The points between single-type CA cathodes and the tested CA-mixes were linearly interpolated. The synergy effects determined for CA-mixtures ranged from 42% to 79%. The highest synergy effect was found for the mixture of 0.5% CB with 0.04% SWCNT.
There is no clear reason why the highest synergy effect was found for this mixture. It can be presumed that the synergy effect is generally bigger at CA contents closely above the respective percolation thresholds. For example, mixing SWCNTs into a CB amount close to the percolation threshold could help to improve the conductive network and enable full percolation. This would then cause a fast decrease in electronic resistance, which would show a synergy effect in our calculation.
The calculated values for TER (shown as contour in Figure 5a) have then been reduced by the experimentally found synergy effect (shown as contour in Figure 5b) to enable the closest possible TER forecast for the full matrix of possible CA-mixtures. The results of these correction calculations are given in the contour plot in Figure 5c. The synergy effect values were only interpolated (towards 0% CA) and not extrapolated; therefore, Figure 5b,c are only given for the experimentally tested matrix up to 0.08% SWCNT + 1.5% CB.
As a reference, the blue dotted contour line shows the 0.25 Ω∙cm2 TER from the uncorrected plot. In contrast, the red 0.25 Ω∙cm2 TER line can now be considered the target for tailoring CA. TERs above this line (going into the red area) can be assumed to show worse electrochemical performance. However, TERs below the line will show similar electrochemical performance but will contain more CA than needed, which degrades the volumetric and gravimetric energy density. The TER threshold contour line is taken over into the next chapter for a comparison of cost and volume distribution.
3.4. Tailoring of Cathode Formulations for Cost and Energy Density Optimization
In this chapter, we want to go beyond the discussion of electronic conductivity and take a deeper look into the potential of TER considerations for the minimization of inactive materials (CA and binder) in the cell for VED increase and cost reduction. Figure 6 shows the distribution of cost and energy density metrics for three different cathode formulations.
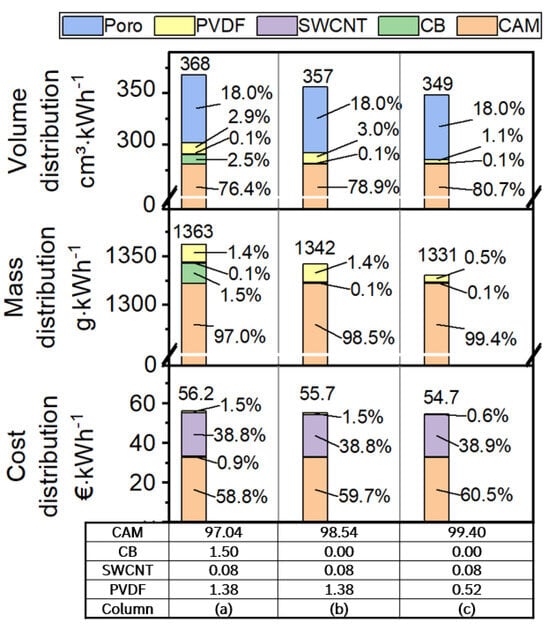
Figure 6.
Impact of cathode formulation on the fraction of CAM, CA, and PVDF per volume in the cathode compound (volume distribution), per weight in the cathode compound (weight distribution), per cost of cathode compound (cost distribution). More detailed information is given in the Supplementary Materials.
The first row compares the volume demand of each component for 1 kWh of cathode compound. This metric is the reciprocal value of volumetric energy density and enables a good comparison of the space required by different components in the electrode. The porosity was set constant at 18% in this calculation example. Column (a) shows a formulation with 97.04% CAM, 1.5% CB, 0.08% SWCNT, and 1.38% PVDF. When looking into the electrode volume distribution, only 76.4 vol% are used for active materials, and 5.5 vol% are used for inactive materials. The difference in mass ratios is caused by the fact that inactive materials have much lower densities than typical LIB active materials. In column (b), the CB is omitted. It was shown in the above chapters that the electronic conductivity is still sufficient since 0.08% SWCNT is applied. Omitting the CB reduces the volume used for 1 kWh by 3 vol%, from 368 cm3∙kWh−1 to 357 cm3∙kWh−1. Given the fixed porosity and recipe change, the electrode density is rising from 3.70 g∙cm−3 (CB + SWCNT, column (a)) to 3.76 g∙cm−3 (SWCNT, column (b)). With a decrease in CB, the BET in the electrode is decreased as well, which allows for a reduction in PVDF [12,13]. Therefore, in column (c), the PVDF content was decreased to the amount needed to still reach sufficient adhesion, with test results given in Supplementary Materials Section S5. Compared to the formulation in column (a), the space used up by this highly optimized formulation is 5 vol% less for 1 kWh of coating, accompanied by a high electrode density of 3.82 g∙cm−3.
The second row shows the mass of electrode compound needed for 1 kWh of battery cell. The weight distribution is already known as the formulation is by default given in %, and it clearly shows that a reduction in both CB and PVDF saves about 2.35% of the compound weight per 1 kWh of cell from 1363 g∙kWh−1 (column (a)) to 1331 g∙kWh−1 (column (c)).
The third row gives a cost distribution. Of course, these results are highly dependent on the prices assumed for each material, and the values used for this calculation are given in Table S4. In Supplementary Materials Section S7, it is also described in more detail why the price assumptions should be taken cautiously. However, in any case, SWCNTs are currently a very high-cost CA. Therefore, it is evident that SWCNTs contribute a significant part to the cost of the cathode electrode compound. If cheaper cathode materials (e.g., LFP, LFMP) are taken into consideration, the cost share of SWCNT would grow even further.
As CAM is by far the biggest part in mass within the cathode compound, it is not surprising that, also with the price assumptions taken in this work, the CAM still makes up for the biggest part of cost with percentages from 58.8% (column (a)) to 60.5% (column (c)). The total cost of the cathode compound is decreased by decreasing the inactive parts in the electrode from 56.2 €∙kWh (column (a)) to 54.7 €∙kWh (column (c)). Omitting the CB (column (b)) reduced the cost by about 0.5 €∙kWh (~0.9%), and the reduction in PVDF reduced the cost by a further 1 €∙kWh (~1.7%). As mentioned, the SWCNTs have a high specific cost and are therefore making up for ~38.8% of the cathode compound cost, even though just 0.08wt% are included.
Figure 7 shows additional cathode design examples that were processed using the same base parameters as in Figure 6. All formulations shown in (a) have been measured with ERM and are below the TER threshold of 0.25 Ω∙cm2. The labeling of data points indicates each formulation as the CAM:CB:SWCNT:PVDF ratio (by %). Gray squares indicate formulations without SWCNTs. The absence of SWCNTs is the reason for the good performance of these formulations on the cost parameter. The blue dot indicates a formulation without CB, making this cathode composition very efficient in volume usage (highest VED). Red triangles indicate CA-mixtures. The cost and VED calculated for the samples were normalized to the reference formulation 99.40:0.00:0.08:0.52 (VED and cost = 100%) and given in percentages on the respective opposite axis. Especially as the price assumed for SWCNTs (20 k€∙kg−1) is extremely high, the most notable outcome of this plot is the strong cost-dependence of SWCNT and the high cost-reduction potential of avoiding this CA. On the other hand, the usage of SWCNT allows for a significant reduction in CB and PVDF contents, from which VED and cost can profit. As all formulations in this plot are below the TER threshold and, therefore, show the same electrochemical performance in HCC, we can note here that there will be several recipes containing an excess of CA and binder. This drives costs up and VED down without a clear advantage for electrochemistry, at least for non-aged cathodes in HCC tests.
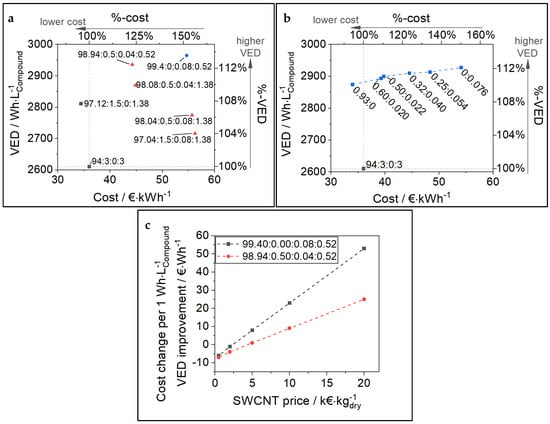
Figure 7.
(a) Trade-off between VED and cost for various cathode formulations. The inlayed description can be read as CAM:CB:SWCNT:PVDF (by %). (b) Different cathode formulations along the synergy-corrected TER threshold from Figure 5. For (a,b) the porosity was assumed to be 18%. (c) Cost sensitivity analysis for changes in the recipe and SWCNT cost. Formulations with SWCNT can often reduce CB and binder leading to higher VED. However, costs per VED increase (in €∙kWh) can be high depending on the actual SWCNT price. For better comparability the formulation 94:3:0:3 was chosen as reference and for normalization (%-scales) in all plots.
For the calculations in Figure 7b, the formulations along the TER threshold (red bold line in Figure 5c) were used and labeled as the CB:SWCNT ratio (by %). As explained in the previous chapter, the formulations along this threshold contain exactly the CA amount needed to observe no negative impact on the electrochemical performance in the HCC experiment. Once again, the data points reflect the tradeoff between cost and volume usage, and no clear optimum (no superior cathode composition) can be found. However, the samples with a balanced mixture of CB and SWCNT (e.g., 0.5% CB + 0.022% SWCNT) show slight advantages, which can be attributed to the synergy effect of the CA-mix. Cost and VED are normalized to the reference formulation of 0.93% CB + 0.0% SWCNT (0.93:0, VED and cost = 100%) and given in percentages on the respective opposite axis.
It is possible and of industrial interest to quantify the costs that arise with the VED improvement through the use of SWCNTs. For example, as shown in Figure 7a, the change in formulation from 94:3:0:3 to 99.4:0:0.08:0.5 can increase VED by 354 Wh∙L−1Compound (+13.5%). However, at the same time, the cost parameter is increasing considerably by 18.7 €∙kWh (+52%). In other words, 1 Wh∙L−1Compound of VED improvement comes at a high cost of 53 €∙Wh−1. Of course, this cost change per VED improvement strongly depends on the price of SWCNT used in the cathode formulation. Therefore, a sensitive analysis of the impact of SWCNT price on cost per VED improvement over a baseline composition (94:3:0:3) is shown in Figure 7c for two exemplary formulations. More details on the calculation are given in Supplementary Materials, Section S7. The VED improvement over the baseline is 354 Wh∙L−1Compound (+13.5%) and 325 Wh∙L−1Compound (+12.4%) for 99.40:0.00:0.08:0.52 and 98.94:0.50:0.04:0.52, respectively. With the decreasing price of SWCNT, the cost per 1 Wh∙L−1Compound of VED improvement declines linearly, and, as expected, the slope is lower for the sample containing less SWCNT. Interestingly, as soon as the SWCNT price falls below about 2 k€∙kg−1, the cost change per VED improvement becomes negative. This means that while VED is increasing, the cost for 1 kWh of cathode compound is falling below the baseline formulation (94:3:0:3). This is caused by the reduction in inactive materials CB and PVDF in the formulations, exploiting the synergy effect observed for SWCNT, which leads not only to improved VED but also reduced cost.
4. Conclusions
This study investigated in detail the possibilities and limitations of ERM. It was shown that, to some degree, the ERM results can be correlated with electrochemical HCC results. By testing different CAMs and Cas, the correlation of ERM with HCC results was further validated. Different CAs, especially CB and SWCNT, were investigated in detail, linking their properties and morphology to their impact on cathode structure and performance. Mixtures of CA were tested, and synergetic effects were benchmarked against a simple physics-based calculation model. Finally, our findings were integrated into the holistic consideration of electrode formulation, also considering the high relevance the choice of CA has on volumetric energy density and estimated LIB cost.
The main conclusions from this study are:
- The results obtained from ERM can be correlated to HCC C-rate results. If the electronic resistance measured for dry cathode is too high, the HCC C-rate performance deteriorates.
- By testing different CAMs, CA-types, and CA-amounts, we found a TER of 0.25 Ω∙cm2 is the threshold for a measurable impact on HCC capacity at 25 °C. When staying below this value, HCC performance was not influenced (neither negatively nor positively) by changes in CA.
- TER reduction follows the percolation theory. In the herein tested PC-NCM811 samples, the percolation threshold is reached with either 0.04% SWCNT or 0.5% CB. Instead, for samples of SC-NCM811, a higher CB threshold (~1% CB) was measured. It must be noted that CBs of different structures and specific surface areas will yield different threshold values.
- The electronic resistance values gathered from HIOKI RM2610 ERM cannot be applied to directly predict the overpotential of a LIB cell. Total resistances in the real cell are expected to be significantly higher than the electronic resistance alone.
- A simple resistance theory is introduced, which enables a fast and easy estimation of TER for CA-mixtures. However, CB+SWCNT mixes consistently yield lower TERs than calculated, an observation we ascribe to a synergetic effect.
- The application of SWCNT allows for a significant reduction in CB and binder content, guiding the way towards higher gravimetric and volumetric energy density. However, challenges towards mass production and very high prices are a hindrance to the widespread application of SWCNT.
With the findings of this work, the optimization of cathode formulations becomes more time- and cost-efficient. ERM can be used for the pre-screening of suitable formulations without the need for an accurate adjustment of electrode loading, the assembly of HCC, or the extensive usage of test channels. Thus, not only tailoring the minimum amount of inactive components (CA, binder) for fulfillment of cathode performance requirements but also the implementation of CAs with advanced design or cost structure becomes straight forward.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/batteries10070227/s1.
Author Contributions
Conceptualization, C.S. and S.T.; methodology, C.S.; investigation, C.S.; data curation, C.S.; writing—original draft preparation, C.S.; writing—review and editing, S.T., K.N. and A.M.; visualization, C.S.; supervision, S.T., M.F. and K.N.; project administration, M.F. and A.M.; funding acquisition, M.F. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the German Federal Ministry for Economic Affairs and Climate Action within the NEWBIE project (grant no. 01MV21013A).
Data Availability Statement
Data are contained within the article or Supplementary Material.
Conflicts of Interest
Authors Christoph Seidl, Sören Thieme and Martin Frey are employed by the Mercedes-Benz AG. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
| ASR | Areal specific resistance |
| CA | Conductive additive |
| CAM | Cathode active material |
| CB | Carbon black |
| CC | Current collector |
| CNF | Carbon nanofiber |
| DMC | Dimethyl carbonate |
| EC | Ethylene carbonate |
| EMC | Ethyl methyl carbonate |
| ERM | Electronic resistance measurement |
| HCC | Half coin cell |
| LIB | Lithium-ion battery |
| MWCNT | Multi-walled carbon nanotube |
| NCM | Lithium nickel cobalt manganese oxide |
| NMP | N-Methyl-2-pyrrolidone |
| OCV | Open circuit voltage |
| PC | Poly crystalline |
| PVDF | Polyvinylidene difluoride |
| RCompound | Electronic compound resistance |
| RContact | Electronic contact resistance |
| SC | Single crystalline |
| SI | Supplementary information |
| SWCNT | Single-walled carbon nanotube |
| TER | Total electronic resistance |
| VED | Volumetric energy density |
References
- Gören, A.; Costa, C.M.; Silva, M.M.; Lanceros-Méndez, S. State of the art and open questions on cathode preparation based on carbon coated lithium iron phosphate. Compos. Part B Eng. 2015, 83, 333–345. [Google Scholar] [CrossRef]
- Park, C.W.; Lee, J.-H.; Seo, J.K.; Ran, W.T.A.; Whang, D.; Hwang, S.M.; Kim, Y.-J. Graphene/PVDF Composites for Ni-rich Oxide Cathodes Toward High-Energy Density Li-ion Batteries. Materials 2021, 14, 2271. [Google Scholar] [CrossRef]
- Tian, R.; Park, S.-H.; King, P.J.; Cunningham, G.; Coelho, J.; Nicolosi, V.; Coleman, J.N. Quantifying the factors limiting rate performance in battery electrodes. Nat. Commun. 2019, 10, 1933. [Google Scholar] [CrossRef] [PubMed]
- Entwistle, J.; Ge, R.; Pardikar, K.; Smith, R.; Cumming, D. Carbon binder domain networks and electrical conductivity in lithium-ion battery electrodes: A critical review. Renew. Sustain. Energy Rev. 2022, 166, 112624. [Google Scholar] [CrossRef]
- Seidl, C.; Thieme, S.; Frey, M.; Nikolowski, K.; Michaelis, A. Comparison of Electronic Resistance Measurement Methods and Influencing Parameters for LMFP and High-Nickel NCM Cathodes. Batteries 2024, 10, 105. [Google Scholar] [CrossRef]
- Hioki, E.E. Corporation. Electrode Resistance Measurement System RM2610. Available online: https://www.hioki.com/euro-en/products/resistance-meters/resistance/id_6740 (accessed on 16 December 2022).
- Tian, R.; Alcala, N.; O’Neill, S.J.K.; Horvath, D.V.; Coelho, J.; Griffin, A.J.; Zhang, Y.; Nicolosi, V.; O’Dwyer, C.; Coleman, J.N. Quantifying the Effect of Electronic Conductivity on the Rate Performance of Nanocomposite Battery Electrodes. ACS Appl. Energy Mater. 2020, 3, 2966–2974. [Google Scholar] [CrossRef]
- Heubner, C.; Nickol, A.; Seeba, J.; Reuber, S.; Junker, N.; Wolter, M.; Schneider, M.; Michaelis, A. Understanding thickness and porosity effects on the electrochemical performance of LiNi0.6Co0.2Mn0.2O2-based cathodes for high energy Li-ion batteries. J. Power Sources 2019, 419, 119–126. [Google Scholar] [CrossRef]
- Pritzl, D.; Bumberger, A.E.; Wetjen, M.; Landesfeind, J.; Solchenbach, S.; Gasteiger, H.A. Identifying Contact Resistances in High-Voltage Cathodes by Impedance Spectroscopy. J. Electrochem. Soc. 2019, 166, A582–A590. [Google Scholar] [CrossRef]
- Landesfeind, J.; Pritzl, D.; Gasteiger, H.A. An Analysis Protocol for Three-Electrode Li-Ion Battery Impedance Spectra: Part I. Analysis of a High-Voltage Positive Electrode. J. Electrochem. Soc. 2017, 164, A1773–A1783. [Google Scholar] [CrossRef]
- Itou, Y.; Ogihara, N.; Kawauchi, S. Role of Conductive Carbon in Porous Li-Ion Battery Electrodes Revealed by Electrochemical Impedance Spectroscopy Using a Symmetric Cell. J. Phys. Chem. C 2020, 124, 5559–5564. [Google Scholar] [CrossRef]
- Landesfeind, J.; Eldiven, A.; Gasteiger, H.A. Influence of the Binder on Lithium Ion Battery Electrode Tortuosity and Performance. J. Electrochem. Soc. 2018, 165, A1122–A1128. [Google Scholar] [CrossRef]
- Marks, T.; Trussler, S.; Smith, A.J.; Xiong, D.; Dahn, J.R. A Guide to Li-Ion Coin-Cell Electrode Making for Academic Researchers. J. Electrochem. Soc. 2011, 158, A51. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).