Evaluation of Advances in Battery Health Prediction for Electric Vehicles from Traditional Linear Filters to Latest Machine Learning Approaches

Abstract

In recent years, there has been growing interest in Li-ion battery State-of-Health (SOH) estimation due to its critical role in ensuring the safe and reliable operation of Electric Vehicles (EVs). Effective energy management and accurate SOH prediction are essential for the reliability and sustainability of EVs. This paper presents an in-depth review of SOH estimation techniques, starting with an overview of seminal methods that lay the theoretical groundwork for battery modeling and SOH prediction. The review then evaluates recent advancements in Machine Learning (ML) and Artificial Intelligence (AI) techniques, emphasizing their contributions to improving SOH estimation. Through a rigorous screening process, the paper systematically assesses the evolution of these advanced methods, addressing specific research questions to evaluate their effectiveness and practical implications. Key findings highlight the potential of hybrid models that integrate Equivalent Circuit Models (ECMs) with Deep Learning approaches, offering enhanced accuracy and real-time performance. Additionally, the paper discusses limitations of current methods, such as challenges in translating laboratory-based models to real-world conditions and the computational complexity of some prospective methods. In conclusion, this paper identifies promising future research directions aimed at optimizing hybrid models and overcoming existing constraints to advance SOH estimation and battery management in Electric Vehicles.

1. Introduction

Lithium-ion batteries are critical for the operation of Electric Vehicles (EVs), with their performance being significantly affected by various degradation processes. Accurate estimation of a battery’s State-of-Health (SOH) is essential to ensure the safety, reliability, and cost-effectiveness of EVs, especially as the demand for these vehicles continues to grow [1].

Battery Management Systems (BMSs) monitor key parameters such as current, voltage, temperature, State-of-Charge (SOC), SOH, and State-of-Power (SOP) [2]. SOH, which represents the ratio of a battery’s current maximum capacity to its rated capacity [3], serves as a critical indicator of battery degradation. The precision of SOH models and predictive algorithms within BMSs directly impacts system performance, making accurate modeling particularly crucial. As the adoption of EVs and portable electronics increases, there is a growing demand for more advanced BMS technology [4]. Lithium-ion batteries typically degrade to 80% of their original capacity before reaching the end of their useful life, highlighting the importance of SOH monitoring to ensure reliable operation [5,6,7,8,9,10].

The SOC, which reflects the battery’s current energy state, is also a key parameter, because changes in the SOC provide insights into the aging and degradation of battery capacity. Accurate SOC prediction thus aids in SOH estimation, which in turn determines the remaining lifespan of the battery [11,12].

Various methods for SOH estimation have been developed, with SOC-based approaches playing a significant role. By integrating real-time data such as current, voltage, and temperature over multiple charge/discharge cycles, these approaches enable more accurate SOH predictions. This real-time integration not only optimizes battery performance but also prevents failures and extends battery life.

Recent advancements in Machine Learning (ML) methods have further enhanced SOH estimation. Heinrich et al. [13] provide a comprehensive evaluation of ML techniques in battery modeling, demonstrating how these models have replaced traditional physical models by leveraging in-vehicle sensor data, significantly reducing the need for expensive laboratory experiments. The study also emphasizes that the performance of data-driven methods varies depending on the specific application and dataset used, making it essential to compare different approaches to identify the most effective solution. In their analysis, they compare conventional regression methods with neural networks, which had been trained on diverse automotive driving profiles. Their findings show that neural networks, particularly Feedforward and Convolutional Neural Networks, outperform conventional methods in both complexity and accuracy. With an average error deviation of approximately 0.16% and a Root Mean Square Error (RMSE) of 5.57 mV at the battery cell level, these models provide the precision required for practical battery management.

Despite these advancements, several challenges remain. The varying performance rates of ML-based approaches across different datasets and applications underscore the need for more robust and generalized models. Additionally, traditional analytical and model-based methods, while reliable, struggle with real-time adaptability, particularly under diverse driving conditions and environmental factors. As a result, further research into hybrid models that combine the strengths of both traditional and ML approaches could address these limitations and provide more reliable SOH predictions. To better understand these challenges, it is essential to explore the primary modeling approaches that follow.

Analytical methods, such as current integration and open-circuit voltage (OCV) techniques, offer clear SOH estimates but face limitations due to accumulated noise and the requirement for long rest periods to ensure accuracy [14].

Model-based approaches can be classified further into white-box, gray-box, and black-box models, each offering various trade-offs between accuracy, computational complexity, and real-time applicability.

White-box models are based on detailed electrochemical principles, simulating battery behavior through fundamental parameters like charge transfer rates and diffusion processes. While these models provide high precision, their computational demands and simplified assumptions about real-world dynamics can reduce accuracy under dynamic conditions [15]. Factors such as charge rates, temperature effects [16], and aging processes [17] significantly impact the accuracy of these models, making them less suitable for real-time applications [18].

The widely employed and popular gray-box models, including Equivalent Circuit Models (ECMs), combine physical insights with empirical adjustments. ECMs approximate battery behavior using circuit analogies and can estimate the State-of-Charge with high accuracy, typically within a 3% margin of error according to the reference [19]. These models are particularly useful for real-time SOH estimation and Remaining Useful Life (RUL) predictions, though challenges remain in terms of data quality and computational demands [20]. Simple Equivalent Circuit Models of Li-ion batteries, consisting of a series resistance and up to two RC elements, are already suitable for performing reliable simulations. ECMs with up to five RC branches, or an additional Constant Phase Element (CPE) that models the double-layer effect, are suitable for modeling highly dynamic processes such as EV operation [21]. By using Resistance Constant Phase Element (RCPE), the impedance spectrum can be modeled with the highest accuracy, making these types of models suitable for diagnostic purposes as well according to [21]. However, this results in an increase in computational demand, which can pose challenges in real-time applications. This, among other factors, drives the need for more advanced SOH development.

Black-box models, or data-driven approaches, aim to approximate an unknown system by building a model based solely on input and output data, without requiring detailed knowledge of the internal workings of the system. In the case of systems based on lithium-ion technology, ML techniques are employed to predict battery states based on large measurement datasets, without relying on detailed physical modeling. Machine Learning excels at recognizing patterns within complex datasets, for instance, with models such as multi-channel Neural Networks (NNs) showing high accuracy in capacity estimation [22]. However, since many internal variables are not directly measurable in real-world vehicle applications, the role of such data-driven, approximative models is becoming increasingly important. These models, though powerful, are highly dependent on the quality and variety of training data, which reflect real-world conditions, which may be hard to be acquired outside of a laboratory environment [23]. Moreover, data sparsity and the lack of interpretability make ML models harder to understand and maintain [24].

Battery degradation is influenced by various operational conditions, such as fluctuating currents and extreme temperatures [25,26]. Although traditional methods, such as the Wiener process, have often been used for degradation modeling [27,28,29,30], data-driven approaches have emerged as effective alternatives, enabling adaptive learning from large datasets to capture intricate degradation patterns. Additionally, the specific chemistry of lithium-ion batteries significantly impacts State-of-Health predictions, as highlighted in the paper [31], particularly for Nickel Manganese Cobalt (NMC) and its degradation modes. The variety in battery chemistry presents a significant challenge for accurate modeling and predictions.

In the past decade, there has been notable evolution in model-based methods, including Kalman Filters (KFs) [32,33] (widely known as linear quadratic estimation filters), Extended Kalman Filters (EKFs), which apply first-order Taylor expansions to linearize nonlinear systems and Unscented Kalman Filters (UKFs) [34,35]. These methods provide high accuracy in battery state estimation but require precise dynamic models and can be complex to implement [16,17]. Hybrid models, which integrate both model-based and data-driven approaches, have been developed to address the limitations of real-world data while enhancing computational efficiency through detailed simulations used to train machine learning models.

Significant advancements have occurred in Machine Learning techniques, especially over the last five years, including probabilistic methods, meta-learning, adversarial learning, semi-supervised learning, etc., which push the boundaries of traditional approaches. For instance, probabilistic models that manage uncertainty and incorporate prior knowledge are crucial for optimizing the battery life cycle, as highlighted in [36]. Moreover, Deep Learning—a subset of ML—excels at processing both structured and unstructured data, enabling the extraction of complex features essential for accurate battery state estimation [37]. Notably, physics-informed Neural Networks (PINNs) have been proposed to combine empirical degradation models with Neural Networks for improved SOH estimation [38]. Furthermore, the enhanced methodologies by Hofmann et al. [39] have demonstrated adaptability across various battery types and conditions.

As the automotive industry evolves, these advancements play a crucial role in optimizing battery performance, preventing failures and supporting electric mobility [10,40].

This review offers an in-depth exploration of recent advancements in battery health estimation, focusing on the growing role of Machine Learning (ML) and Artificial Intelligence (AI). By examining the evolution from classical methodologies to more sophisticated modern approaches, the ongoing need for accurate and robust State-of-Health estimation is emphasized, particularly to meet the increasing requirements of advanced Battery Management Systems.

Section 2 details the methodology employed for screening and selecting the reviewed papers, ensuring a thorough and structured approach to the topic.

Section 3 presents an in-depth analysis of State-of-Charge estimation techniques, exploring the impact of battery degradation mechanisms and the various modeling approaches applied to Electric Vehicle batteries. Representative methods such as Kalman Filters and their adaptations are discussed, followed by more recent developments that integrate aging models.

Section 4 shifts focus to SOH estimation techniques, contrasting traditional methods with newer, more advanced models that address the limitations of classical approaches. Special emphasis is placed on methods applicable to EVs, where enhanced accuracy and predictive power are crucial.

In Section 5, the review highlights the growing role of Deep Learning in SOH estimation, showcasing techniques such as Long Short-Term Memory (LSTM) networks and hybrid models. These advanced methods, along with Convolutional Neural Networks (CNNs), significantly improve the precision of health assessments by considering real-world factors such as temperature and current variations.

Section 6 provides a brief outlook on secondary applications, particularly the evolving research into battery second-life applications. It explores the challenges associated with battery heterogeneity and unknown first-life conditions, and it discusses emerging techniques that seek to address these complexities.

Finally, Section 7 concludes the review by offering perspectives on future research directions, emphasizing the critical need for continued innovation in battery health management systems to support the rapidly expanding EV market and other energy storage applications.

2. Materials and Methods

This literature review addresses several key questions regarding the application of machine learning techniques for SOC (and related SOC) estimation in Li-ion batteries used in Electric Vehicles (EVs). The following Research Questions have been defined to guide this review:

• What are the primary Machine Learning (ML) techniques currently used for State-of-Health (SOH) estimation in Li-ion batteries for Electric Vehicles?
  • It will guide the exploration of the specific algorithms and models that researchers have developed and utilized.
• How do different data sources (laboratory, in-vehicle, field data) impact the accuracy and robustness of machine learning models for SOH estimation?
  • This question addresses the variability and reliability of the data used to train ML models. It aims to explore how the source of data influences model performance and what type of data is most conducive to accurate SOH prediction.
• What are the key challenges in applying machine learning techniques for SOH estimation in Li-ion batteries, and how do these challenges vary across different environmental conditions and application scenarios?
  • This question seeks to identify the limitations and difficulties encountered when applying ML models in real-world settings, such as the effects of temperature fluctuations, aging, and varying usage patterns on the accuracy of SOH estimation.
• What are the differences between analytical, traditional approaches in SOH estimation, how do they evolve, and how do Machine Learning methods integrate with these traditional approaches?
  • This question will help compare traditional SOH estimation techniques with ML-based methods, identifying strengths, weaknesses, and potential synergies between the two, as well as also demonstrate the progess of the methods.
• What are the future research directions for improving the accuracy, adaptability, and computational efficiency of ML-based SOH estimation models for Li-ion batteries in EVs?
  • This question is forward-looking, aiming to identify research gaps, technological needs, and innovative approaches that could enhance ML techniques’ effectiveness for SOH estimation.

The methodology design for this literature review is structured to systematically analyze and synthesize existing studies on Machine Learning (ML) techniques for State-of-Health (SOH) estimation in Li-ion batteries specifically used in Electric Vehicles (EVs). This review adopts a systematic approach, emphasizing transparency and reproducibility. A comprehensive search of the relevant literature was conducted using the Scopus database, which is a reputable and extensive source of peer-reviewed research papers, patents, and other academic documents. The search aimed to capture a broad range of studies from various domains at the first step. The search strategy was guided by the key terms identified from the research questions. 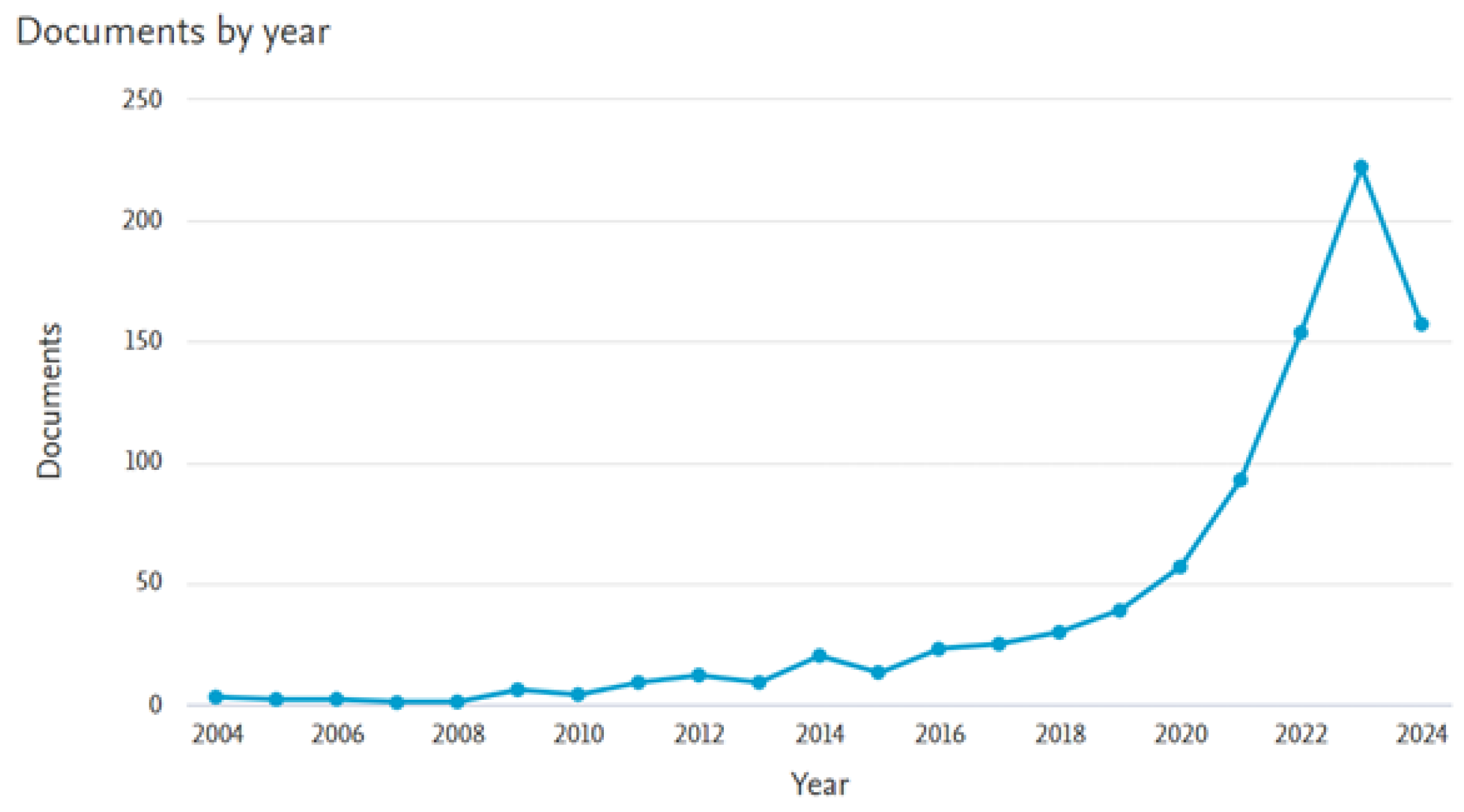The following Boolean search string was used: TITLE-ABS-KEY (electric AND vehicle) AND KEY (battery AND state AND of AND health) AND TITLE-ABS-KEY (lithium AND ion) AND PUBYEAR > 2003 AND PUBYEAR < 2025. This search string was designed to include papers and patents published after 2003, up until 2024, to ensure that the review covers both foundational and the most recent advancements in the field. The keywords used in the search strategy for this literature review were carefully chosen to maximize the relevance and comprehensiveness of the retrieved documents. They reflect the key components of the research focus, ensuring that the literature review captures the most pertinent studies. The search with the above-mentioned keywords resulted in 882 documents and 16,286 patents. Nearly half of these have been published in the past five years (2020–2024), indicating strong industrial need and progress, with 8754 patents found during this period. Figure 1 shows the distribution of the number of documents published by year. In Figure 2 the distribution of the resulting papers according to the leading journals can be observed. Figure 3 illustrates the number of papers published by researchers from different countries, highlighting the geographic diversity and concentration of research efforts in this field. In Figure 4, the distribution of patents published by leading patent offices are displayed. Recent patents indicate that industry development priorities are increasingly centered on advancing battery management systems, optimizing modular battery architectures, enhancing vehicle control systems, and developing advanced low-resistance materials, highlighting a focus on innovation in energy management and Electric Vehicle infrastructure (see, e.g., [41,42,43,44,45,46,47,48,49,50]).

The 882 documents retrieved in this study are distributed across various subject areas, with the share of subject area on Engineering (730), followed by Energy (504), Computer Science (209), and Mathematics (189). Other disciplines such as Chemistry (120), Materials Science (75), and Environmental Science (71) also contributed significantly, highlighting the interdisciplinary nature of battery research and its relevance across a wide range of scientific fields, according to Scopus Analytics. After narrowing down the search to the field of computer science, where most AI-driven and Machine Learning-based solutions appear, 209 documents were identified. From these documents, 183 range between 2019 and 2024, which indicates the relevance of the collected material. These documents are categorized by document type, including 132 conference papers, 72 articles, four reviews, and one book chapter. The 72 articles published between 2009 and 2024 form the main basis of this review, with the aim of revealing how artificial intelligence is being leveraged to advance battery management systems. Narrowing the focus to computer science captures the most innovative and technical advancements in battery management systems, particularly those leveraging machine learning. This approach allows for a deeper exploration of the most cutting-edge solutions and methodologies, offering insights into how computational techniques are transforming battery health monitoring. In addition to the primary 72 articles, other selected papers and book chapters have been included based on a manual review from the field of engineering within the retrieved database.

The organization of the reviewed papers follows a structured approach designed to highlight the evolution of SOH estimation techniques and their advancements through Machine Learning and AI. It categorizes the development according to key modeling directions, also addressing the modeling of State-of-Charge prediction. This review begins by establishing a foundational understanding through the exploration of traditional SOH estimation methods and seminal works, providing readers with the historical context and highlighting the limitations of early approaches. This is followed by a discussion of recent methods that have replaced classical SOH estimation techniques with more accurate aging models tailored specifically for Electric Vehicles (EVs), showcasing how advancements have improved the applicability of these models. The following then transitions to more advanced deep learning approaches. This includes detailed discussions on the implementation of the most popular deep learning techniques, feature extraction, etc., as well as the integration of Machine Learning with traditional modeling approaches in hybrid techniques. Notable advancements such as AI-driven techniques, Long Short-Term Memory networks (LSTMs), and Convolutional Neural Networks (CNNs) are examined, focusing on their capabilities for real-time predictions and adaptability to varying operational conditions (see, e.g., [51,52,53,54,55,56]). Lastly, the review briefly explores the latest research on secondary applications, particularly in scenarios where early usage data have been unavailable. This section highlights how batteries, once unsuitable for use in EVs, can be effectively repurposed for use in renewable energy systems and other applications, demonstrating the versatility and extended utility of battery technologies.

The primary aim of this review is to synthesize the existing literature on Machine Learning techniques for SOH estimation in Li-ion batteries used in electric vehicles without collecting or analyzing primary data, as recommended by [57]. To ensure comprehensive coverage of the field, inclusion screening was conducted based on predefined criteria, following the methodology outlined by [58] and the guidelines from [57]. This approach ensured transparency and rigor in the selection process.

The structured approach to systematic reviews proposed by [59] was adopted to screen the 209 documents for inclusion in this study. To assess the quality of the sources, a 5-point quality scoring system was implemented. This scoring system, based on domain-specific evaluations, was employed to address potential biases and enhance the validity of the findings. Following [59], this approach involved formulating specific assessment questions to guide the screening process, evaluating the relevance and robustness of the studies and synthesizing findings in a comprehensive manner.

To explore various aspects of SOH (and related SOC) estimation, the review is guided by five key assessment questions, as detailed in

Table 1. Assessment questions for evaluating ML techniques for SOH estimation, designed based on the recommendations of Kitchenham et al. [59].

Assessment Question	Description	Evaluation Metric
1	Coverage of ML techniques for SOH estimation in Li-ion batteries	1: Narrow; 2: Some; 3: Broad; 4: Comprehensive; 5: Thorough
2	Analysis of data sources’ impact on ML model performance	1: Minimal; 2: Some; 3: General; 4: Thorough; 5: Comprehensive
3	Identification and discussion of challenges in different conditions	1: Few; 2: Minimal; 3: Key challenges; 4: Detailed; 5: Extensive
4	Comparison of ML methods with traditional approaches	1: Little; 2: Basic; 3: General; 4: Detailed; 5: Comprehensive
5	Proposal of future research directions for improving ML models	1: None; 2: Some; 3: General; 4: Well-defined; 5: Innovative

. These questions aim to identify the primary machine learning techniques employed, evaluate the impact of different data sources on model performance, and investigate the challenges encountered in real-world applications, among other critical aspects. This targeted approach allows for a thorough examination of the field and the identification of the most pertinent sources.

The following Table 1 presents the assessment questions used in this review. Each question is designed to evaluate specific aspects of the included studies, focusing on their relevance and robustness.

3. State-of-Charge Estimation Techniques

3.1. Battery Degradation Mechanisms and Impact on Performance

Understanding the underlying physics of battery degradation and leveraging advanced estimation techniques are key to optimizing battery performance and extending its lifespan. Lithium-ion batteries degrade primarily through two mechanisms: the loss of lithium inventory (LLI) and the loss of active material (LAM). Both mechanisms involve complex electrochemical and mechanical processes that alter the battery’s performance over time [60].

The formation of the solid electrolyte interphase (SEI) layer on the anode is a key factor in the loss of lithium inventory. This SEI layer forms as a result of side reactions between lithium ions and the electrolyte [61]:

$${\mathrm{Li}}^{+}+e^{-}+\mathrm{EC}\to \mathrm{SEI}+{\mathrm{Li}}_2{\mathrm{CO}}_3$$

where ${\mathrm{Li}}_2{\mathrm{CO}}_3$ represents a common decomposed product of the electrolyte, as a specific example shows in [60].

The loss of active material (LAM) occurs due to mechanical stresses within the battery, particularly in the electrodes during cycling. Repeated expansion and contraction of the electrode materials during lithiation and delithiation can cause micro-cracks and the detachment of electrode particles, leading to a reduction in the active surface area available for electrochemical reactions [61], which can be represented as follows:

$$\mathrm{LAM}\stackrel{\mathrm{leads}\mathrm{to}}{\to }\mathrm{Reduced}\mathrm{Active}\mathrm{Surface}\mathrm{Area}\stackrel{\mathrm{results}\mathrm{in}}{\to }\left\{\begin{array}{c}\mathrm{Lower}\mathrm{Capacity}\hfill \\ \mathrm{Higher}\mathrm{Internal}\mathrm{Resistance}\hfill \end{array}\right.$$

More details about the aging mechanisms (e.g., thermal, electrochemical, etc.) of lithium cells can be found in [62], and modeling details can be found in [60]. These degradation mechanisms are accelerated by factors such as high states of charge, elevated temperatures, and aggressive cycling conditions. The cumulative effect is a reduction in the battery’s capacity, an increase in internal resistance, and ultimately, a decline in performance [61].

3.2. State-of-Charge Estimation and Modeling Techniques for Electric Vehicle Batteries

In everyday Electric Vehicle usage, batteries are typically not recharged after they are fully depleted; instead, they are usually recharged when the State-of-Charge falls between 20% and 40%. This practice helps to maintain battery health and performance. However, due to the nonlinear nature of battery capacity and degradation, SOC readings may become inaccurate, affecting the estimation of the battery’s full capacity. The performance and maintenance of lithium-ion batteries are also climate-dependent [63]. According to recent research, the efficiency and longevity of the cells can vary significantly with temperature, and the freshness of the electrolyte—determined by the battery’s production and electrolyte filling dates—can influence performance. In particular, the study indicates that lithium-ion batteries with newer electrolytes might exhibit different characteristics across various climates. It also reviews thermal management strategies designed to address temperature-related performance issues and enhance battery durability in both cold and hot conditions [64].

Traditional methods for estimating the SOC of batteries, such as the Equivalent Circuit Model (ECM), often necessitate frequent recalibration due to the evolving characteristics of the battery over time. The Equivalent Electric Circuit (EEC) model is a prevalent approach for simulating the behavior of high-power lithium-ion battery cells, especially for estimating the SOC. This model offers a detailed representation of the battery’s electrical response, as demonstrated by the second-order model detailed in [65].

The following equations describe how SOC and terminal voltage are computed both continuously and discretely. The system’s behavior is governed by the following state-space equations:

$$\left[\begin{array}{c}{\dot{V}}_1\\ {\dot{V}}_2\\ \dot{S}\end{array}\right]=\left[\begin{array}{ccc}-{\displaystyle \frac{1}{R_1{C}_1}}& 0& 0\\ 0& -{\displaystyle \frac{1}{R_2{C}_2}}& 0\\ 0& 0& 0\end{array}\right]\left[\begin{array}{c}{V}_1\\ V_2\\ S\end{array}\right]+\left[\begin{array}{c}{\displaystyle \frac{1}{C_1}}\\ {\displaystyle \frac{1}{C_2}}\\ -{\displaystyle \frac{1}{Q}}\end{array}\right]I$$

(1)

where ${\dot{V}}_1$ and ${\dot{V}}_2$ are the rates of change of the voltages across two resistors—$V_1$ and $V_2$—and $\dot{S}$ is the rate of change of the SOC—$R_1$ and $R_2$—and $C_1$ and $C_2$ are the resistances and capacitances of the circuit elements, respectively. Q represents the total charge capacity of the battery, and I is the input current.

The terminal voltage V is computed as follows:

$$V=V_{OC}\left(S\right)-V_1-V_2-I{R}_0$$

(2)

where $V_{OC}\left(S\right)$ denotes the open-circuit voltage as a function of SOC, and $R_0$ is the internal resistance. $V_1$ and $V_2$ represent the voltage drops across the resistive components of the model, and $I{R}_0$ accounts for the voltage drop due to the internal resistance.

The open-circuit voltage $V_{OC}$ as a function of SOC k is given by

$$V_{OC}={\alpha }_0+{\alpha }_{1}k+{\displaystyle \frac{{\alpha }_2}{k}}+{\alpha }_{3}lnk+{\alpha }_{4}ln(1-k)$$

(3)

Here, the ${\alpha }_i$ values are constant coefficients derived from polynomial fitting of the open-circuit voltage model to SOC–OCV data. The parameter k represents the SOC of the battery, and the equation describes the relationship between SOC and the open-circuit voltage.

In the discrete time domain, the SOC is calculated iteratively based on a sampling interval $\Delta t$. The SOC update equation is given by

$${\mathrm{SOC}}_n={\mathrm{SOC}}_{n-1}-{\displaystyle \frac{\eta I_l\Delta t}{C_i}}$$

(4)

where ${\mathrm{SOC}}_n$ represents the battery’s State-of-Charge at the nth sampling instant, ${\mathrm{SOC}}_{n-1}$ is the State-of-Charge at the previous sampling instant, $\eta$ is the coulombic efficiency indicating the battery’s charge and discharge efficiency, $I_l$ is the load current, $\Delta t$ is the sampling interval, and $C_i$ is the battery’s nominal capacity.

At the nth sampling instant, the voltages are updated using the following equations:

$$\begin{array}{cc}\hfill V_{1,n}& =V_{1,n-1}{e}^{\left(-{\displaystyle \frac{\Delta t}{R_1{C}_1}}\right)}+I_{l,n-1}{R}_1\left(1-e^{\left(-{\displaystyle \frac{\Delta t}{R_1{C}_1}}\right)}\right),\hfill \\ \hfill V_{2,n}& =V_{2,n-1}{e}^{\left(-{\displaystyle \frac{\Delta t}{R_2{C}_2}}\right)}+I_{l,n-1}{R}_2\left(1-e^{\left(-{\displaystyle \frac{\Delta t}{R_2{C}_2}}\right)}\right),\hfill \\ \hfill V_n& =V_{OC}-V_{1,n}-V_{2,n}-I_{l,n}{R}_0.\hfill \end{array}$$

(5)

Here, $V_{1,n}$ and $V_{2,n}$ are the voltages measured by two voltage responses across the RC networks at the nth sampling instant, while $V_{1,n-1}$ and $V_{2,n-1}$ are the voltages measured at the previous sampling instant. The terms $R_1$ and $R_2$ represent the resistances of the dividers, and $C_1$ and $C_2$ denote their capacitances. $V_{OC}$ is the open-circuit voltage of the battery, $R_0$ is the internal resistance of the battery, and $I_{l,n}$ is the load current at the nth sampling instant.

The sampling interval $\Delta t$ is the time elapsed between two consecutive sampling points.

For discrete-time modeling, the state-space representation is given by

$${\mathbf{x}}_{n+1}=\Phi {\mathbf{x}}_n+\Gamma u_n+{\zeta }_n$$

(6)

$$y_{n+1}=C{\mathbf{x}}_{n+1}+D{u}_n+{\xi }_n$$

(7)

where ${\mathbf{x}}_n={\left[V_{1,n}{V}_{2,n}{k}_n\right]}^T$ is the state vector, $y_n=V_{t,n}$ is the observation, and $u_n=I_{l,n}$ is the input. The matrices are defined as follows:

$$\Phi =\left[\begin{array}{ccc}{e}^{\left(-{\displaystyle \frac{\Delta t}{R_1{C}_1}}\right)}& 0& 0\\ 0& e^{\left(-{\displaystyle \frac{\Delta t}{R_2{C}_2}}\right)}& 0\\ 0& 0& 1\end{array}\right],\Gamma =\left[\begin{array}{c}{R}_1\left(1-e^{\left(-{\displaystyle \frac{\Delta t}{R_1{C}_1}}\right)}\right)\\ R_2\left(1-e^{\left(-{\displaystyle \frac{\Delta t}{R_2{C}_2}}\right)}\right)\\ {\displaystyle \frac{\eta \Delta t}{C_i}}\end{array}\right]$$

(8)

$$C=\left[\begin{array}{ccc}-1& -1& {\displaystyle \frac{d{V}_{OC}\left(k\right)}{dk}}\end{array}\right],D=-R_0$$

(9)

where ${\zeta }_n$ and ${\xi }_n$ represent external disturbances and measurement noise, respectively. The parameter vector to be estimated is $\theta ={[R_1,R_2,C_1,C_2,R_0]}^T$. Standard laboratory tests, such as hybrid pulse power characterization (HPPC) tests at various temperatures, are commonly employed for parameter identification of the cell model. However, due to model inaccuracies and measurement noise, the cell model may slightly differ from the actual cell behavior, leading to small errors in SOC estimation. To enhance SOC estimation accuracy, various techniques such as Kalman Filters, extended Kalman Filters, Unscented Kalman Filters, PI-based observers, sliding mode observers, and others have been utilized to compensate for these effects and have achieved satisfactory results according to the literature (see, e.g., [66]). Further approaches, such as integral correction methods and advancements to address initial model uncertainties and measurement noise, have also been developed.

On the other hand, tradtional techniques such as Electrochemical Impedance Spectroscopy (EIS) have been employed for evaluating battery characteristics, including the State-of-Charge and State-of-Health. However, EIS is often time-consuming and may be impractical for large-scale applications [67], such as Electric Vehicle fleets. Moreover, EIS methods can struggle to capture the dynamic and varied operating conditions of EV batteries, highlighting the need for more adaptive and efficient approaches.

3.3. Improved Techniques

A widely adopted approach for SOC estimation involves the use of the Kalman Filter (KF) and its various adaptations [68,69]. The KF provides optimal SOC estimates by minimizing mean squared errors, effectively addressing issues related to cumulative errors and uncertain initial SOC values. However, the KF is inherently suited to linear time-varying systems [70,71,72]. Since the dynamics of battery cells are nonlinear, it is necessary to approximate the system using a linear time-varying model through the process of linearization. To accommodate this nonlinearity, the Extended Kalman Filter (EKF) is often employed, extending the KF framework to handle nonlinear models [34]. Over the years, several significant methods have been developed to enhance SOC estimation under these conditions, as demonstrated in studies such as [73,74,75,76]. Despite its advantages, the process of linearization can sometimes compromise accuracy, potentially leading to estimator divergence.

To address these limitations, newer techniques such as the Unscented Kalman Filter (UKF) [34,35] and the Cubature Kalman Filter (CKF) have been introduced as more robust alternatives [77,78]. These methods, instead of relying on linearization, employ sigma points to estimate the statistics of a Gaussian random variable undergoing nonlinear transformations. Specifically, the CKF improves upon these approximations by utilizing a spherical–radial cubature rule to compute multivariate moment integrals, providing higher accuracy in nonlinear Bayesian filtering [79].

However, these filters typically assume that process and measurement noise covariances are known and constant. In real-world applications, noise characteristics often vary over time or deviate from Gaussian distributions. For example, external disturbances can cause non-Gaussian noise with heavy-tailed or skewed distributions [80,81,82]. Furthermore, outliers or abrupt changes can degrade the filter’s performance, leading to estimation errors or divergence. To address these challenges, robust and adaptive filtering strategies have been developed for non-Gaussian environments and uncertain noise statistics (see e.g., [83]). Applications of discrete-time nonlinear systems with non-Gaussian noise models are prevalent in various fields, including sensor networks for data fusion, maritime navigation and tracking, and industrial process control and monitoring [83]. The non-Gaussian noise in a nonlinear system can be mathematically described by combining discrete-time nonlinear state transition and measurement equations, where noise components are modeled using Gaussian Mixture Models (GMMs) [83]. GMMs provide a flexible framework to represent complex noise characteristics that deviate from Gaussian distributions, enabling more accurate modeling of real-world systems where such noise is common. This approach improves the filter’s ability to handle multimodal distributions, outliers, or skewed noise, thus enhancing estimation accuracy.

Mathematically, the process noise $w_k$ and measurement noise $v_k$ can be modeled using GMMs [84] as follows:

$$p\left(w_k\right)=\sum _{j=1}^{G_1}{\alpha }_j·N(w_k\mid {\mu }_j,{\Sigma }_j)$$

(10)

$$p\left(v_k\right)=\sum _{m=1}^{G_2}{\beta }_m·N(v_k\mid {\nu }_m,{\Theta }_m),$$

(11)

in which $p\left(x\right)$ represents the probability density of the noise component, $G_1$ and $G_2$ are the number of Gaussian components for process noise and measurement noise, respectively, ${\alpha }_j$ and ${\beta }_m$ denote the weights of the Gaussian components, with

$$\sum _{j=1}^{G_1}{\alpha }_j=1\mathrm{and}\sum _{m=1}^{G_2}{\beta }_m=1,$$

(12)

while $N(w_k\mid {\mu }_j,{\Sigma }_j)$ and $N(v_k\mid {\nu }_m,{\Theta }_m)$ denote Gaussian distributions with mean ${\mu }_j$, ${\nu }_m$ and covariance matrices ${\Sigma }_j$, ${\Theta }_m$, respectively.

Thus, the noise component $v_k$ is modeled as

$$v_k\sim p\left(v_k\right)$$

(13)

where $p\left(v_k\right)$ approximates any complex, non-Gaussian noise distribution using a mixture of Gaussians.

The modeling of non-Gaussian noise presents significant challenges for traditional filters, which are primarily designed for Gaussian noise. Consequently, newer methodologies, such as the Robust Kalman Filter, have emerged to consider the non-Gaussian nature of the noise during filtering processes. By incorporating these advanced techniques, it becomes possible to enhance state estimation accuracy and reliability in systems characterized by complex noise environments, particularly in applications where the dynamics of battery systems involve intricate electrochemical processes, as highlighted in [85]. A summary of the taxonomy of key Kalman Filter methods is presented in Table 2.

In addition to robust filtering techniques, decentralized and distributed filters, such as the the Decentralized Kalman Filter (DKF) [86] and Distributed Kalman Filter with Covariance Intersection (DKF-CI) [87], are designed to optimize state estimation in large-scale, interconnected systems, particularly when sensor networks are involved and noise characteristics are not Gaussian [88,89,90]. These methods aim to improve accuracy by addressing cumulative errors and noise variations across different sensors or subsystems. Additionally, Robust and Nonlinear Filters—such as the Robust Kalman Filter [91]—offer superior performance in scenarios where traditional linearization techniques like the EKF fall short, especially in handling the nonlinearities of battery systems where electrochemical processes are complex, as was pointed out in [85].

Building upon these advancements, Adaptive techniques—such as those explored in recent studies on Adaptive EKF [92] and adaptive UKF algorithms [93]—dynamically adjust filter parameters to account for variations in the statistical properties of process and measurement noise. These methods have shown significant promise in improving SOC estimation accuracy in Battery Management Systems (BMS) and battery SOH prediction applications, even under uncertain or varying conditions.

Fu et al. [87] introduced a tightly coupled Distributed Kalman Filter (DKF) that integrates a Gaussian Mixture Model (GMM) [94] to address non-Gaussian noise and uses covariance intersection to reduce cumulative errors from Local Kalman Filters (LKFs). To further enhance robustness, an index Huber function was developed to mitigate the effects of large covariance values from LKFs. Simulations and real-world experiments confirmed the method’s effectiveness, outperforming other DKF algorithms in terms of RMSE and cumulative error. A multi-sensor state estimation experiment on a hexapod robot further validated this approach. More detailed information on the various versions and taxonomy of KFs can be found in a comprehensive study by [95].

Table 2. Taxonomy of Key Kalman Filter Methods (1960–2022).

Method Name (Year)	Problem Solved	Strengths	Limitations
Kalman Filters
Kalman Filter (KF) (1960) [32]	Estimates the state of linear dynamic systems from noisy observations.	Minimizes estimation errors. Efficient with low computational demands. Navigation and control systems.	Limited to linear systems. Assumes known model parameters and noise.
Extended Kalman Filter (EKF)	Addresses nonlinear systems by linearizing state-space equations.	Applicable to a wider array of nonlinear systems. Widely used in robotics. Maneuvering scenarios.	Requires local linearization, introducing potential errors. Computationally demanding.
Decentralized and Distributed Filters
Decentralized Kalman Filter (DKF) (1978) [86]	Optimally estimates states in large-scale interconnected dynamical systems.	Reduces computation time with a hierarchical structure. Stable in high-order systems. Suitable for large-scale industrial applications.	Limited to linear systems. May face communication challenges.
Distributed Kalman Filter with Covariance Intersection (DKF-CI) (2022) [87]	Enhances state estimation in multi-sensor systems under non-Gaussian noise.	Reduces the impact of non-Gaussian noise. Enhances accuracy. Effective in multi-sensor networks for surveillance and monitoring.	Increased complexity in implementation. Dependent on network reliability.
Robust and Nonlinear Filters
Robust Kalman Filter (RKF) (1994) [91]	Designed for environments with uncertainties in model parameters.	Accommodates uncertainties. Provides reliable estimates. Useful in aerospace and autonomous vehicles.	Complexity in high-dimensional systems. Limited use in continuous-time systems.
Unscented Kalman Filter (UKF) (1997) [34]	An accurate alternative to EKF for nonlinear systems.	Eliminates the need for explicit linearization. Better accuracy than EKF. Useful in tracking and navigation.	Higher computational burden. Can diverge under severe system noise.
Adaptive and Multiple Model Filters
Interacting Multiple Model (IMM) (1988) [96]	Efficiently tracks systems with multiple switching modes.	Adapts to changing system dynamics. Reduces computational load. Useful in aerospace and defense applications.	Complexity increases with more models. Needs careful handling of nonlinear systems.
Multiple Model Adaptive Estimation (MMAE) 2000 [97]	Manages systems exhibiting multiple models or switching behaviors.	Parallel bank of KF. Deals with model uncertainty. Applicable in target tracking and dynamic system monitoring.	High computational load. Sensitive to the density of models.
Advanced Tracking Methods
IMM with CKF (IMM-CKF) (2010) [98]	Improves tracking for maneuvering targets using nonlinear models.	Combines strengths of IMM and CKF. Robust in angle-only measurement scenarios. Suitable for military and surveillance applications.	Computational demands increase with system size. Requires well-defined models.
IMM with Adaptive Robust UKF (IMM-ARUKF) (2017) [99]	Integrates adaptive fading UKF and robust UKF to manage model uncertainties using a Markov chain for state estimation.	Provides flexibility and improved accuracy through dual filtering.	More complex implementation. Requires careful tuning of transition probabilities.
Window-based Multiple Model Adaptive Estimation (WMMAE) (2017) [100]	Enhances MMAE by incorporating window size as an additional tuning parameter.	Adapts window size for optimal filtering. Incorporates simplicity. Applicable in real-time data analysis.	Complexity in determining optimal window size. Performance sensitive to window selection.

Table 2. Taxonomy of Key Kalman Filter Methods (1960–2022).

Method Name (Year)	Problem Solved	Strengths	Limitations
Kalman Filters
Kalman Filter (KF) (1960) [32]	Estimates the state of linear dynamic systems from noisy observations.	Minimizes estimation errors. Efficient with low computational demands. Navigation and control systems.	Limited to linear systems. Assumes known model parameters and noise.
Extended Kalman Filter (EKF)	Addresses nonlinear systems by linearizing state-space equations.	Applicable to a wider array of nonlinear systems. Widely used in robotics. Maneuvering scenarios.	Requires local linearization, introducing potential errors. Computationally demanding.
Decentralized and Distributed Filters
Decentralized Kalman Filter (DKF) (1978) [86]	Optimally estimates states in large-scale interconnected dynamical systems.	Reduces computation time with a hierarchical structure. Stable in high-order systems. Suitable for large-scale industrial applications.	Limited to linear systems. May face communication challenges.
Distributed Kalman Filter with Covariance Intersection (DKF-CI) (2022) [87]	Enhances state estimation in multi-sensor systems under non-Gaussian noise.	Reduces the impact of non-Gaussian noise. Enhances accuracy. Effective in multi-sensor networks for surveillance and monitoring.	Increased complexity in implementation. Dependent on network reliability.
Robust and Nonlinear Filters
Robust Kalman Filter (RKF) (1994) [91]	Designed for environments with uncertainties in model parameters.	Accommodates uncertainties. Provides reliable estimates. Useful in aerospace and autonomous vehicles.	Complexity in high-dimensional systems. Limited use in continuous-time systems.
Unscented Kalman Filter (UKF) (1997) [34]	An accurate alternative to EKF for nonlinear systems.	Eliminates the need for explicit linearization. Better accuracy than EKF. Useful in tracking and navigation.	Higher computational burden. Can diverge under severe system noise.
Adaptive and Multiple Model Filters
Interacting Multiple Model (IMM) (1988) [96]	Efficiently tracks systems with multiple switching modes.	Adapts to changing system dynamics. Reduces computational load. Useful in aerospace and defense applications.	Complexity increases with more models. Needs careful handling of nonlinear systems.
Multiple Model Adaptive Estimation (MMAE) 2000 [97]	Manages systems exhibiting multiple models or switching behaviors.	Parallel bank of KF. Deals with model uncertainty. Applicable in target tracking and dynamic system monitoring.	High computational load. Sensitive to the density of models.
Advanced Tracking Methods
IMM with CKF (IMM-CKF) (2010) [98]	Improves tracking for maneuvering targets using nonlinear models.	Combines strengths of IMM and CKF. Robust in angle-only measurement scenarios. Suitable for military and surveillance applications.	Computational demands increase with system size. Requires well-defined models.
IMM with Adaptive Robust UKF (IMM-ARUKF) (2017) [99]	Integrates adaptive fading UKF and robust UKF to manage model uncertainties using a Markov chain for state estimation.	Provides flexibility and improved accuracy through dual filtering.	More complex implementation. Requires careful tuning of transition probabilities.
Window-based Multiple Model Adaptive Estimation (WMMAE) (2017) [100]	Enhances MMAE by incorporating window size as an additional tuning parameter.	Adapts window size for optimal filtering. Incorporates simplicity. Applicable in real-time data analysis.	Complexity in determining optimal window size. Performance sensitive to window selection.

As demonstrated above, the charging and discharging processes of batteries are inherently complex, with electrochemical reactions strongly influenced by external environmental factors. Developing precise and reliable real-time SOC and SOH estimation algorithms remains a significant challenge. Accurate SOC estimation is critical, as it directly impacts SOH prediction accuracy. Therefore, SOC-based SOH estimation remains a major research focus, with ongoing efforts aimed at improving both the accuracy and robustness of these methods [101,102].

Table 3. Advantages and Disadvantages of Common SOC Estimation Approaches.

Procedure	Advantage	Disadvantage
Electrochemical-based, e.g., [17]	Accuracy	In situ implementation is too complex
Coulomb count, e.g., [3,103]	Simple implementation	Depends on initial charge level; not applicable under dynamic loads
Open-circuit voltage-based, e.g., [3,104]	No need for an algorithm	Requires long rest periods
Extended Kalman Filter, e.g., [105]	Accurate, robust against noise	High computational demand (online application cumbersome); complex
Sliding Mode Observer, e.g., [106]	Accurate, handles system and model inaccuracies well	Nonlinear; complex

provides a brief comparaison of the advantages and disadvantages of some of the traditional and seminal approaches to SOC estimation, highlighting how more recent techniques offer promising solutions for real-time Battery Management Systems.

3.4. Integration with Aging Models

This subsection explores recent advancements in both SOC estimation and battery aging models, as these areas are closely interconnected with the overall health assessment of batteries.

Recent research has introduced innovative methods that not only improve the accuracy of SOC estimation but also has addressed the impact of battery aging and degradation. This subsection presents in chronological order some of the most promising techniques introduced between 2022 and 2024, focusing on their novel approaches and improvements over traditional methods. By examining these recent advancements, it is aimed to illustrate how the field is evolving to present methods that show significant promise for enhancing battery management systems.

Belonging to the gray-box modeling category, the inherently ECM-based method known as the Adaptive Integral Correction-Based State-of-Charge Estimation (AIC-SE) was introduced in 2022 to enhance the accuracy of SOC estimation [107] in 2022. This technique builds upon traditional estimation frameworks by integrating real-time correction mechanisms, thereby improving robustness and reliability under dynamic operating conditions [107]. This method builds on a third-order RC equivalent circuit model and incorporates two additional correction loops—resistance correction and cell capacity correction—to handle model inaccuracies caused by aging. The AIC-SE method demonstrated notable improvements in SOC estimation accuracy, achieving a maximum error of ±0.8% and a Root Mean Square (RMS) error of less than 0.3%, compared to the Unscented Kalman Filter (UKF), which showed an RMS error of 11%.

In terms of computational efficiency, the AIC-SE method is significantly more efficient than the UKF. The AIC-SE method primarily involves integral calculations for the correction factors: the integral correction factor $Z_c$ is computed using the formula $Z_c=K_Z\int (V_{t\mathrm{Measured}}-V_t)dt$, the resistance correction factor $M_R$ is calculated as $M_R=K_R\int (T_{S\mathrm{Measured}}-T_S)dt$, and the cell capacity correction factor $M_Q$ is determined by $M_Q=K_Q\int (Z_c-Z_{M\mathrm{Ref}})dt$. Each of these integrals involves summation over n time steps, resulting in approximately $3n$ operations. Additionally, basic arithmetic operations for updating the SOC and model parameters add about $2n$ operations. Thus, the total number of operations for the AIC-SE method is roughly $5n$.

Conversely, the UKF involves more complex computations. The sigma point generation step requires matrix square roots and multiplications, which involves about $n^2$ operations. This significant difference in computational burden highlights the AIC-SE method’s practicality for real-time applications. Moreover, the AIC-SE method achieved superior accuracy in SOC estimation, making it an effective solution for managing the challenges posed by Li-ion battery aging and degradation with fewer computational resources.

There is a further notable improved method proposed in the paper [108] in 2023, which presents the Variational Bayesian Maximum Correntropy Cubature Kalman Filter (VBMCCKF) for accurate State-of-Charge (SOC) estimation in lithium-ion batteries. This method enhances SOC estimation by combining advanced filtering and statistical techniques. Cubature Kalman Filter (CKF) provides high-accuracy SOC estimation through nonlinear state space modeling. The Variational Bayesian Approach is used to improve measurement error covariance estimation by using Bayesian inference. This approach enables the algorithm to adaptively estimate the covariance matrix of measurement errors, addressing the uncertainty and variability in noise that simpler methods might not fully capture. The Variational Bayesian method refines the accuracy of the covariance estimates, leading to more reliable SOC predictions. The Maximum Correntropy Criterion’s main advantage is that it robustly suppresses measurement outliers by optimizing the filter performance against non-Gaussian noise. This criterion enhances the filter’s ability to handle irregularities in the measurement data, which can degrade the performance of traditional filters. The VBMCCKF method showed significant improvements in SOC estimation accuracy, with a reduction in the Mean Absolute Error (MAE) of 77% compared to the Extended Kalman Filter (EKF), 68% compared to the Cubature Kalman Filter (CKF), and 49% compared to the Variational Bayesian Cubature Kalman Filter (VBCKF). By combining Variational Bayesian error estimation with robust outlier handling, the VBMCCKF maintained high performance even in the presence of noisy and irregular data [108]. This advanced approach not only boosts estimation accuracy but also enhances the robustness of Battery Management Systems, contributing to extended battery life and a more reliable operation.

As demonstrated by the substantial volume of research, significant advancements have been made in enhancing classical Kalman Filter-based approaches. However, it is also crucial to acknowledge other notable methodologies that have emerged, offering substantial practical significance in the field.

A particularly important area of recent study is the development of battery aging models designed to take into account the impact of user charging practices on battery degradation in electric vehicles.

The study presented in 2024 by [109] introduces a comprehensive battery aging model that investigates the impact of user charging behaviors on the degradation of batteries in Electric Vehicles. This model systematically incorporates critical aging parameters, including the SOC, battery temperature ($T_{\mathrm{Bat}}$), time, and the number of full equivalent cycles (NFECs), to provide a nuanced understanding of how these factors collectively influence battery longevity.

The model is composed of two main components. The first part focuses on aging related to SOC and temperature. The capacity loss is expressed by as follows:

$$d{\mathrm{Closs}}_{t\to t+dt}=d\left((A+B·\mathrm{SOC})e^{-{\displaystyle \frac{E_a}{k_B{T}_{\mathrm{Bat}}·t^z}}}\right)$$

(14)

where $E_a$ is the activation energy; $k_B$ is the Boltzmann constant; and A, B, and z are parameters associated with SOC, temperature, and time. The second part of the model accounts for the impact of NFEC on aging, which is given by:

$$d\mathrm{Closs}(t\to t+dt)=k_{FEC}·\mathrm{NFEC}$$

(15)

The novelty of the model proposed by [109] lies in its integration of the battery model with aging as a subsystem of the Electric Vehicle (EV), encompassing all operational modes—parking, driving, and charging. This comprehensive approach allows for a detailed simulation of battery degradation by considering the interactions between different subsystems.

A key feature of this model is its use of the Energetic Macroscopic Representation (EMR) [110] formalism. The EMR formalism, developed in 2000, is a graphical tool that organizes the interconnections between subsystems systematically, representing power flows and causal relationships between different components. This unified framework enhances the accuracy of the simulations by ensuring that all subsystems interact correctly.

By incorporating the EMR formalism, the model provides a structured and integrated approach to understanding how various charging practices and operational scenarios affect battery aging. The simulations reveal that strategies such as reducing the frequency of charging can significantly extend battery lifespan. Specifically, charging every four days instead of daily increases the time required to reach 80% of the battery’s State-of-Health by 36%.

The use of the EMR formalism is crucial for achieving this level of integration and accuracy, as it facilitates the systematic modeling of complex interactions within the battery system and between subsystems. The proposed approach [109] represents a significant advancement in optimizing battery management and understanding the impact of different charging practices on battery aging.

3.5. Summary

To conclude, the three modeling techniques highlighted in this subsection represent main approaches that reflect successful advancements in both SOC estimation and battery aging models. These developments indicate that researchers are increasingly focused on enhancing complexity and accuracy, taking into account the demands of real-time applications and the impacts of environmental factors.

New methods, such as AIC-SE and VBMCCKF, offer significant advantages in the accuracy of SOC estimation and computational efficiency. For instance, the AIC-SE method improves SOC estimation accuracy to ±0.8% compared to the traditional Unscented Kalman Filter (UKF), with an RMS error of less than 0.3%. In contrast, the VBMCCKF, which combines the Variational Bayesian method with the maximum correntropy criterion, reduced the Mean Absolute Error (MAE) by 77% compared to the Extended Kalman Filter (EKF), marking a significant advancement in SOC estimation.

The VBMCCKF effectively handles the dynamic estimation of measurement error and performs well in noisy environments due to its combination of Variational Bayes and the maximum correntropy criteria. Additionally, the AIC-SE provides a robust and computationally efficient solution but may not achieve the same high level of accuracy as the VBMCCKF.

Therefore, if accuracy and noise handling are the primary concerns, techniques utilizing the combination of Variational Bayes and maximum correntropy criteria may be favored and considered the best among current approaches. However, if computational efficiency and real-time applications are prioritized, the AIC-SE could also be a good choice, indicating that ECM modeling approaches still hold great advantages in this respect.

Additionally, the battery aging model presented in the 2024 study integrates the effects of SOC, temperature, and the number of full cycles on degradation, which is indeed a good approach if optimizing battery lifespan with respect to charging practices is essential.

Overall, these developments not only enhance the accuracy of SOC estimation but also contribute to longer battery life and more reliable operation.

4. State-of-Health (SOH) Estimation Techniques

This subsection examines traditional SOH estimation methods that are widely employed in both academic and industrial settings, as summarized in

Table 4. Traditional Approaches for State of Health Estimation.

Aspect	Formula	Parameters	Notes
Capacity Degradation [111]	$\mathrm{Capacity}\mathrm{Degradation}(\%)=\left(1-{\displaystyle \frac{\mathrm{Current}\mathrm{Capacity}}{\mathrm{Original}\mathrm{Capacity}}}\right)\times 100$	Current Capacity, Original Capacity	Measures the percentage decrease in battery capacity.
Internal Resistance [112]	$R_{int}={\displaystyle \frac{V_{oc}-V_{load}}{I}}$	$V_{oc}$ (open-circuit voltage), $V_{load}$ (voltage under load), I (current)	Measures resistance by comparing voltage drop under load.
Cycle Life, e.g., [113]	Number of cycles before capacity drops below a specified percentage of original capacity	Capacity Threshold	Empirically measured; indicates the number of cycles until capacity falls below a threshold.
Self-Discharge Rate [114]	Self-Discharge $\mathrm{Rate}(\%)=\left({\displaystyle \frac{\mathrm{Capacity}\mathrm{Loss}}{\mathrm{Initial}\mathrm{Capacity}}}\right)\times 100$	Capacity Loss, Initial Capacity	Measures the percentage of capacity lost over time when the battery is not in use.
Voltage Deviation [111]	$\mathrm{Voltage}\mathrm{Deviation}(\%)={\displaystyle \frac{\mathrm{Nominal}\mathrm{Voltage}-\mathrm{Measured}\mathrm{Voltage}}{\mathrm{Nominal}\mathrm{Voltage}}}\times 100$	Nominal Voltage, Measured Voltage	Measures the deviation of actual voltage from nominal.
State-of-Health (SOH), e.g., [111]	$\mathrm{SOH}(\%)={\displaystyle \frac{\mathrm{Current}\mathrm{Capacity}}{\mathrm{Original}\mathrm{Capacity}}}\times 100$	Current Capacity, Original Capacity	General health measure, reflecting capacity relative to original.
Temperature-Adjusted Capacity Degradation, e.g., [111]	$\mathrm{Capacity}\mathrm{Degradation}(\%)=\left(1-{\displaystyle \frac{\mathrm{Current}\mathrm{Capacity}}{\mathrm{Original}\mathrm{Capacity}}}\right)\times \left(1+\alpha (T-T_{ref})\right)\times 100$	Current Capacity, Original Capacity, $\alpha$ (temperature coefficient), T (current temperature), $T_{ref}$ (reference temperature)	Adjusts capacity degradation based on temperature variation.
Temperature-Adjusted Internal Resistance, e.g., [115]	$R_{int}=R_{int,ref}\times \left(1+\beta (T-T_{ref})\right)$	$R_{int,ref}$ (reference internal resistance), $\beta$ (temperature coefficient), T (current temperature), $T_{ref}$ (reference temperature)	Adjusts internal resistance based on temperature.
SOH Calculation Using Model, e.g., [102]	$\mathrm{SOH}(\%)={\displaystyle \frac{1}{\mathrm{K}}}\times \left({\mathrm{SOC}}_{\mathrm{estimated}}-{\mathrm{SOC}}_{\mathrm{measured}}\right)\times 100$	K (constant), ${\mathrm{SOC}}_{\mathrm{estimated}}$, ${\mathrm{SOC}}_{\mathrm{measured}}$	SOH can be estimated by comparing the estimated SOC to the measured SOC, adjusted by model parameters.

. These methods focus on fundamental parameters, such as capacity degradation, internal resistance, and cycle life, providing essential insights into battery performance.

The inclusion of the brief collection of the these traditional techniques serves to highlight the foundational approaches that have historically underpinned battery health assessments. By understanding these established methodologies, we can better appreciate the advancements introduced in the subsequent chapter. Newer estimation methods often leverage more sophisticated data analysis and predictive modeling techniques, addressing the limitations inherent in traditional approaches. Thus, the juxtaposition of these two categories of methods will elucidate the evolution of SOH estimation, illustrating how contemporary practices enhance accuracy and adaptability in battery management systems.

4.1. Recent Methods for Replacing Classical SOH Estimation Methods, Improved Aging Models Applicable in EVs

Recent developments in SOH estimation have focused on replacing classical methods with more sophisticated models that incorporate improved aging mechanisms, particularly those applicable in EVs.

An effective strategy for enhancing the accuracy of SOH predictions involves the development of novel health indicators used in combination with traditional Machine Learning techniques. In this context, ref. [116] introduces a new health indicator, the Degradation Speed Ratio, as an innovative alternative to the traditional SOH metrics for assessing battery performance. The DSR is derived from directly measured parameters—specifically voltage and time—thereby obviating the need for a full charging cycle, which leads to a reduction in battery resting times by approximately 84%. This indicator demonstrates a robust correlation with battery capacity and serves as a critical marker for determining battery end-of-life (EOL). Accordingly, the DSR is derived from the voltage curves during charging cycles. As batteries age, the time required to reach a target voltage decreases, reflecting a degradation in the battery’s health. The slope of the voltage curves during charging is calculated using the formula:

$$m={\displaystyle \frac{V_{4.1}-V_{4.0}}{t_2-t_1}},$$

(16)

where $V_{4.1}$ and $V_{4.0}$ are voltages at two points, and $t_2$ and $t_1$ are the corresponding times. For end-of-life cycles, the slope is denoted as

$$m_0={\displaystyle \frac{V_{4.1}-V_{4.0}}{t_0^2-t_0^1}}.$$

(17)

As demonstrated by the study in [116], the Degradation Speed Ratio (DSR) is determined by comparing the slopes across multiple charging cycles, specifically indicating the rate of degradation within a defined voltage range, such as [3.8–3.9 V], and is measured in mV/s. This ratio effectively reflects the degradation speed of the battery, where a higher DSR value signifies a more pronounced capacity fade. The study demonstrates that utilizing the DSR in combination with a Gaussian Process Regression (GPR) [117] model and a Multilayer Perceptron Neural Network (MLPNN) model yields highly accurate estimates of capacity loss and degradation. This novel approach exhibits improved sensitivity and precision when compared to existing models. The limitations of conventional models in detecting the early stages of degradation have been noted by [116], who argue that these traditional approaches often lack the sensitivity necessary for accurate early detection. In contrast, the method proposed in the same study has demonstrated a significant enhancement in predictive accuracy. Meanwhile, ref. [118] also highlighted the limitations associated with relying solely on traditional SOH metrics, which tend to be less responsive to subtle changes in battery health. The incorporation of the DSR, as proposed by [116], effectively addresses these issues by offering a more robust measure of degradation.

Significant early efforts have been made to advance the traditional equivalent circuit model (ECM) approach, particularly for applications in electric transportation. For instance, a method from 2015 for estimating the SOH of lithium-ion batteries in electric vehicles, utilizing the conventional ECM approach, is presented in [119]. This method involves analyzing the bulk capacitance of the equivalent RC circuit model. It introduces an innovative algorithm designed to compute the attenuation factor of the bulk capacitance across various cycles, as well as a discrete nonlinear observer tailored for precise identification of this capacitance. The system is discretized at sampling intervals to improve both accuracy and reliability. Experimental results validate the method’s efficiency in accurately estimating SOH [119].

In contrast, a more recent paper from 2024 [120] applies an improved strategy to the basic equivalent circuit model (ECM) by incorporating a second-order hybrid equivalent circuit model and an adaptive update rate to account for temperature effects. This approach utilizes a nonlinear observer with integrated filters to accurately estimate the SOH, demonstrating a mean absolute error of less than 0.5% and a Root Mean Square Error of less than 0.2% in SOH estimation.

Furthermore, the latest cloud solutions [52] published in 2023 continue to utilize traditional equivalent circuit-based gray-box modeling approach, yet they reveal that eight months of monitoring data can achieve a level of precision previously unattainable in the past by model parameter estimation using standard laboratory tests. This study presents also a tuning procedure for a moving window least squares algorithm designed to estimate the parameters of a 2-RC equivalent circuit battery model, leveraging real-time data collected from a test vehicle and uploaded to the Stellantis-CRF cloud. The application of this cloud-based approach to extensive road tests demonstrated minimal estimation errors, rivaling those typically found in controlled laboratory environments. By consistently tracking the estimated model parameters over time, the authors reported accurate SOH evaluation, which effectively identifies the early signs of battery aging with unprecedented accuracy.

In light of previous advancements, the paper [121] introduces a new framework for predicting the SOH of lithium-ion batteries, addressing the limitations inherent in traditional measurement approaches. The framework represents a significant shift from conventional methods by integrating three sophisticated techniques: linear statistical k-nearest neighbors (LSKNNs) for data interpolation and noise reduction, maximal information entropy search (MIES) for feature selection, and collective sparse variational Gaussian process regression (CSVGPR) for SOH forecasting.

Turning now to the specific components of the framework, LSKNNs is initially employed to estimate missing data points and to filter out noise from incomplete charging measurements. Subsequently, MIES is used to refine the feature set by removing features that exhibit minimal correlation with SOH. This selective approach ensures that only the most pertinent features are utilized. Finally, CSVGPR addresses uncertainties in the data, thereby enhancing the accuracy of SOH predictions. In terms of evaluation, the framework was tested using NASA’s battery dataset, comparing its performance against other statistical learning methods. Quantitatively, the framework demonstrated superior performance in SOH estimation. For instance, compared to methods such as ElasticNet, Support Vector Regression (SVR), Random Forest, and Gradient Boosting, the proposed framework reduced the Root Mean Square Error (RMSE) by 77.8%, from the lowest RMSE value of 0.0510 (ElasticNet) to 0.0113. Furthermore, when compared to Gaussian Process models with different kernels (e.g., Matern 32, Matern 52, Squared Exponential, etc.), the RMSE was reduced by 55.5% from 0.0254 to 0.0113, confirming the robustness and superior accuracy of the proposed framework.

4.2. Summary

Recent advancements in SOH estimation emphasize the shift from classical methods to more sophisticated models tailored for Electric Vehicles. Selected papers are presented in this subsection representing the leading modeling approaches: the degradation model in combination with classical Machine Learning [116], ECM-based methods, and a hybrid approach.

A notable innovation is the Degradation Speed Ratio (DSR), which improves prediction efficiency by eliminating the need for full charging cycles, reducing waiting times by approximately 84%. The DSR has shown a strong correlation with battery capacity, making it a crucial metric for determining battery end-of-life (EOL). Combining the DSR with Machine Learning techniques like a Multilayer Perceptron Neural Networks (MLPNNs) has yielded highly accurate estimates of capacity loss, surpassing traditional models that struggle with early degradation detection. For instance, these combined methods demonstrate significant improvements in sensitivity and precision.

Innovations in the equivalent circuit modeling approach have also contributed to enhanced SOH estimation. Recent approaches incorporating second-order hybrid ECM models have achieved mean absolute errors of less than 0.5% and Root Mean Square Errors under 0.2% [120]. Cloud-based solutions utilizing extensive road test data have shown that real-time monitoring can lead to highly accurate SOH evaluations by using ECM model [52]. This also suggest the potential of the improved ECM-based approaches. This trend, which can be drawn form the above, is in accordance with the above conclusion about the SOC-based techniques, where the ECM-based approaches with various improvements still are in the main line.

It can be seen that, next to the ECM-based approaches, hybrid techniques [121] provide outstanding precision, which notably outperform earlier techniques. Despite the complexity of the hybrid method, which makes the realtime application challenging, this framework presents a significant advancement over traditional SOH estimation approaches by effectively addressing the key challenges of data interpolation, feature selection, and uncertainty management.

Overall, these developments indicate a strong focus on real-time applications and data-driven approaches, significantly advancing the reliability of battery management systems in EVs.

The latest deep learning approaches, particularly LSTM, CNNs, and hybrid techniques, have emerged as the most popular methods for SOH estimation. The following chapter presents selected works that represent the key trends identified during the screening process, offering snapshots of how these techniques have contributed to successful outcomes.

5. Deep Learning Applications in SOH Estimation

5.1. LSTM and Hybrid Models

In this review, several of the selected works employ techniques that align with one of the key approaches, utilizing improved aging models similar to those discussed in previous sections to enhance estimation accuracy. However, for Remaining Useful Life prediction, the integration of deep learning techniques becomes indispensable, as it has been demonstrated by [122].

A new comprehensive SOH degradation model, which integrates deep learning with an enhanced SOH degradation model that incorporates additional factors beyond the basic capacity ratio is suggested by [122]. The proposed technique put the emphasis on that the battery health degradation is influenced by various operational conditions, including charging and discharging currents, as well as temperature effects. Specifically, the model integrates the following elements: battery operating state defined by the charging current during charging and the discharging current during operation; operating time represented by the duration of charging and discharging cycles; temperature effects by including environmental temperature data during discharging and charging temperature data, which are crucial for reflecting real-world conditions and the battery’s thermal management system.

The approximate SOH degradation model under the real operating environment of the battery model proposed by [122] is as follows:

$$\Delta \mathrm{SOH}\left(i\right)={\displaystyle \frac{\left[(I_c\left(i\right)\times d_1+T_c\left(i\right)\times d_2)\times t_c\left(i\right)\right]+\left[(I_d\left(i\right)\times d_3+T_d\left(i\right)\times d_4)\times t_d\left(i\right)\right]}{\sum \left[(I_c\left(i\right)\times d_1+T_c\left(i\right)\times d_2)\times t_c\left(i\right)\right]+\sum \left[(I_d\left(i\right)\times d_3+T_d\left(i\right)\times d_4)\times t_d\left(i\right)\right]}}\times \Delta \mathrm{SOH},$$

(18)

in which $I_c$ and $I_d$ represent the the normalized average charging and discharging currents, $T_c$ and $T_d$ denote the normalized battery and environmental temperatures, $t_c$ and $t_d$ stand for the charging and discharging times, while $d_1$, $d_2$, $d_3$, and $d_4$ are the weights assigned to different influencing factors.

This comprehensive model offers a more accurate representation of battery degradation by incorporating multiple operational factors and temperature effects. Unlike the simple capacity ratio model, it considers how varying conditions during charging and discharging, as well as thermal management, influence the overall health of the battery. This results in a more precise estimation of SOH under real-world conditions. Furthermore, the paper introduces a Remaining Useful Life (RUL) prediction model based on Long Short-Term Memory (LSTM) networks. This model enhances the prediction accuracy over a four-month period by capturing temporal dependencies through the integration with LSTM. While this approach improves prediction accuracy, it also introduces increased computational complexity, which poses challenges for real-time implementation on in-vehicle processors. This complexity indicates a need for optimization in future work to facilitate practical applications.

Additionally, the study points out that neural networks are particularly adept at handling time-dependent battery processes, with their ability to continuously learn proving highly beneficial. This feature allows the models to maintain accuracy and relevance with minimal computational cost, addressing the evolving electrical behavior of batteries over time. Such adaptability ensures that battery models remain reliable throughout the battery’s operational lifespan, offering substantial advantages in real-world automotive applications.

While the previous study focused on integrating deep learning techniques for precise Remaining Useful Life (RUL) prediction and battery degradation modeling under real-world conditions, the subsequent work in [123] shifts attention to Machine Learning approaches for efficient SOH estimation. Although both studies employ different techniques, they belong to the family of hybrid approaches aimed at achieving more accurate state assessment and prediction. In the first case, the model combines deep learning to enhance SOH degradation estimation, while [123] integrates machine learning and feature extraction techniques to achieve high-accuracy SOH estimation while minimizing computational load for online applicability.

In [123], the authors emphasize the critical role of feature extraction in accurately assessing the State-of-Health (SOH) of batteries, particularly in adapting laboratory data to operational fleet-level data. By extracting six key features from partial ranges, their proposed data processing pipeline effectively captures the battery’s aging state. Three Machine Learning (ML) algorithms were utilized for easy online deployment, demonstrating that the hybrid feature set achieved high SOH estimation accuracy, with a minimum Root Mean square error (RMSE) of 0.36%. Importantly, the inclusion of voltage-based features significantly enhanced the accuracy of battery state evaluation, improving it by up to 20%.

Next, the work by Anas et al. in [124] expands on these hybrid approaches by reviewing advanced deep learning methods for predicting the Remaining Useful Life (RUL) of batteries. Their principal innovation is the synthesis of various deep learning models—including Convolutional Neural Networks (CNNs), Long Short-Term Memory (LSTM), Gated Recurrent Units (GRUs), and their bidirectional variants—into hybrid frameworks like CNN-LSTM-DNN, and CNN-GRU-DNN. These models utilize a wide range of features, such as voltage, current, temperature, and their time-series averages, to enhance the accuracy of RUL predictions.

The study includes a comprehensive benchmark analysis comparing the performance of these new hybrid models against existing methodologies using NASA datasets, revealing a notable improvement up to a 90.5% reduction in the Root Mean Square Error (RMSE) compared to previous models. Their research demonstrates that integrating diverse neural network architectures in these hybrid models effectively manages the complexities of battery datasets. However, the computational intensity and complexity of these models may limit their practical application in real-time scenarios. While they show significant value in controlled laboratory environments with ample data and computational resources, further refinement may be needed for real-world implementation to optimize efficiency and scalability.

Multi-model approaches are also popular hybrids, such as a bank of LSTMs. The method described in [53] employs a sophisticated framework consisting of four neural network models: one dedicated to estimating the SOH and three forming a “neural network model bank”—designated as normal, caution, and fault models—for SOC estimation. This method integrates a range of parameters, including time, voltage, current, temperature, and previous SOC values, to enhance the accuracy of predictions. Experimental results indicate that the Long Short-Term Memory model significantly surpasses other models in performance, delivering more reliable estimates of SOC and SOH, thereby improving the overall efficiency of the battery management systems.

Moreover, the Gated Recurrent Unit combined with the soft-sensing method has demonstrated significant potential for accurate long-term Remaining Useful Life predictions of Li-ion batteries, as discussed in [125]. Although effective in controlled environments with historical data, the practical implementation of this method may encounter challenges due to varying real-world charging conditions. Therefore, while the method is well-suited for laboratory settings, further adaptation and validation are necessary to ensure reliable deployment in real-world scenarios where battery usage conditions fluctuate.

In [54], the focus shifts to addressing battery degradation through the estimation of SOH using data-driven methodologies. The study utilizes extensive datasets, encompassing voltage, current, and temperature information obtained from the NASA Prognostics Center of Excellence. The data underwent Fourier Resampling before being analyzed using three machine learning techniques: Long Short-Term Memory, Deep Neural Networks (DNNs), and GRUs. Hyperparameter tuning was applied to optimize these algorithms, aiming to improve accuracy while mitigating computational complexity. Among the evaluated techniques, GRUs achieved strong performance, with a Root Mean Square Error (RMSE) of 0.003, a Mean Absolute Error (MAE) of 0.003, and an R-squared error of 0.004. These results affirm the effectiveness of GRUs for SOH estimation across various battery samples and provide significant insights for precise battery performance evaluation and maintenance planning. While GRUs has shown remarkable results, methods that combine GRUs with LSTM networks generally offer enhanced performance, particularly in scenarios requiring the modeling of long-term dependencies.

LSTM networks have gained considerable attention and demonstrated significant effectiveness in recent advancements, particularly in the method for SOH estimation of lithium-ion batteries presented in [55]. This method employs an LSTM network that excels in managing time-series data. The approach begins with a comprehensive analysis of the battery’s charge–discharge voltage curve and incremental capacity (IC) curve to derive meaningful handcrafted features (HFs) designed to capture essential patterns associated with battery degradation. To enhance the relevance of these features, the authors utilizes Grey Relational Analysis (GRA) and the Entropy Weight Method (EWM), refining the selection process to ensure that the most pertinent features are incorporated into the model. The selected five HFs are subsequently fed into the LSTM network for SOH prediction. The Adam optimization algorithm is employed to optimize the parameters of the LSTM model, thereby improving training efficiency and predictive accuracy. Experimental results demonstrate that this method achieved a maximum estimation error of 4.55% when trained on 60% of the cycle data for a single battery. Even when utilizing training data from only one battery, the SOH estimation error for other cells remained below 5.99%. These results indicate that the proposed method surpasses traditional models such as Elman Neural Networks [126], Support Vector Machines (SVMs) [127], and Gaussian Process Regression (GPR) [117], offering enhanced accuracy and robustness in SOH prediction.

In [128], a novel neural network model is introduced for estimating the RUL of energy storage batteries, named the Multi-Feature Fusion and Dual-Attention Long Short-Term Memory (MDA-LSTM) network. This model diverges from conventional approaches that rely solely on battery capacity by incorporating multiple features and temporal information. The MDA-LSTM network integrates a Multi-Feature Fusion (MFF) module to strengthen the model’s capacity to exploit various feature dependencies and employs a Dual-Attention Module (DAM), which includes both local and global attention mechanisms to capture short-term and long-term temporal dependencies. The effectiveness of the proposed model was validated through experiments conducted on multiple datasets, including those from NASA and the CALCE datasets. The results demonstrate that the Multi-Feature Fusion and Dual Attention Long Short-Term Memory (MDA-LSTM) network surpasses existing baseline methods, achieving superior prediction accuracy. Comprehensive testing and feature selection experiments affirm the model’s robustness and generalizability across diverse datasets.

Further approaches using LSTM include a novel method for predicting the SOH of Li-ion batteries, employing a stacked BiLSTM deep neural network with data exclusively from constant current charging [129]. This method leverages parameters such as charging current, voltage, measured current, voltage, and temperature to forecast SOH accurately. It is particularly effective during the constant current phase of charging, with prediction errors reducing to 5.5% Root Mean Square Error and a capacity RMSE of 0.033 Ampere-hours as more data were included. The stacked BiLSTM model, benefiting from its bidirectional structure, integrates both forward and backward data during training, resulting in more reliable SOH predictions compared to traditional recurrent networks or unidirectional LSTMs. This model is thus well suited for real-time SOH estimation during quick charging operations.

To advance the field further, the study presented by [130] addresses the ongoing challenges of optimizing algorithms for Battery Management Systems in electric and hybrid Electric Vehicles, with a particular focus on accurately estimating the SOC, SOH, and RUL of lithium-ion batteries, which are characterized by their nonlinear and complex behavior. The authors introduce a novel approach by integrating a Long Short-Term Memory network into an AI-based BMS framework. Given that LSTM networks are particularly effective for sequence problems, their application in dynamic battery state estimation is well justified, as evidenced by previous studies.

The main innovation of the work by Nagarale et al. [130] lies in the implementation of the LSTM model on a Field-Programmable Gate Array (FPGA), specifically using the Xilinx Zynq System-on-Chip (SOC) PYNQ Z2 board. While the use of GPUs and ASICs is prevalent in AI applications, this study underscores the advantages of FPGAs, such as lower power consumption and higher-speed processing, which are essential for real-time BMS applications in EVs. The design employs Python for model training and validation and Xilinx Vitis High-Level Synthesis (HLS) tools for synthesis. However, a key issue that needs to be raised is the practicality of deploying FPGAs in commercial EVs. The implementation of the LSTM network on an FPGA, as presented in [130], appears to be more of a proof-of-concept rather than a fully developed solution ready for commercial deployment. The cost and practicality of integrating FPGAs into a vehicle’s BMS may pose significant challenges, limiting its widespread application. Although the results demonstrating low Root Mean Square Error (RMSE) values—0.3438 during training and 0.3681 during validation—are promising and suggest high model accuracy, transitioning to a commercially viable solution will require addressing these cost and scalability concerns associated with FPGA usage. While the experimental results are promising and demonstrate the accuracy and robustness of the proposed BMS, this raises many questions regarding whether the FPGA-based approach can be scaled efficiently and economically for real-world applications. The study’s focus on technical feasibility rather than commercial applicability highlights a common pitfall in the literature, where the emphasis on innovation can sometimes overshadow considerations of practicality.

To highlight again the problem of available only partial operation history data, the fresh study of [39] addresses the issue of partial data by developing a TCN-LSTM model for accurate OCV reconstruction. The model uses synthetic data from an automotive NCA cell and is refined with Bayesian optimization. It excels in reconstructing the OCV, with an MAE below 22 mV, and in estimating the SOH, with a MAPE below 2.2%, even when trained with limited experimental data. The advanced use of transfer learning allows the model to effectively generalize across different battery chemistries, although limitations in extrapolation were noted when data were insufficient.

In addition to the existing techniques, deep fusion, a hybrid approach also, proves effective for battery SOH estimation, especially in real-world conditions where traditional methods often struggle. The paper [131] presents a framework for estimating battery SOH in on-road EVs by extracting labeled capacities from historical data of 707 EVs over three years. This approach achieves a Mean Absolute Percentage Error (MAPE) of less than 2.97% through full charge and discharge tests. It leverages 22 health indicators (HIs) and 4 HI sequences derived from partial charging data. Two models were developed: a global SOH estimation framework utilizing Gaussian Process Regression (GPR) [117], similar to the approach in paper [132], which yielded an MAPE of 2.07% in repeated validations, and a Deep Fusion Transfer Learning Network (DFTN) for individual EVs, achieving an average MAPE of 1.42%, with the best vehicle reaching an MAPE of 0.23%.

5.2. CNN and CNN-LSTM-Integrated Models

In the paper by Yao et al. (2024) [51], an innovative method, CNN–WNN–WLSTM, is introduced, integrating Convolutional Neural Networks (CNNs), Wavelet Neural Networks (WNNs), and Wavelet Long Short-Term Memory (WLSTM) networks. The CNN component automatically extracts features from raw battery data, while the WNN and WLSTM modules process these features and estimate the SOH, leveraging the rapid convergence of WNN and the time series analysis capabilities of WLSTM. The RMSprop optimizer is employed to enhance performance compared to the Adagrad optimizer. Experimental results using data from the NASA Ames Prognostics Center demonstrate that CNN–WNN–WLSTM outperforms other machine learning methods, including traditional backpropagation neural networks and Gaussian Process Regression, in both accuracy and robustness. This positions CNN–WNN–WLSTM as a promising approach for advanced battery health management.

Turning to more advanced techniques, the recent study by Wang et al. (2022) [56] presents a novel approach to lithium battery capacity prediction through a combined Convolutional Neural Network–Long Short-Term Memory–Conditional Random Field (CNN-LSTM-CRF) model. Inspired by methods from natural language processing (NLP), this model represents a significant application of a CRF layer in predicting battery remaining useful life. The incorporation of CRFs facilitates a more intuitive representation of capacity decline over time by effectively capturing dependencies between output variables—a crucial aspect for tasks involving structured outputs such as sequences or grids.

In this model, the CNN component efficiently extracts feature data, while the LSTM module excels at identifying temporal trends, thereby enhancing the accuracy of battery capacity predictions. Ablation experiments confirm the CRF layer’s contribution to improved prediction performance. Overall, the CNN-LSTM-CRF model surpasses previous approaches in battery capacity prediction, with the innovative use of CRFs representing a significant advancement, particularly in terms of interpretability regarding capacity decline.

However, the model’s computational demands must be considered. The CRF layer, especially when integrated with deep learning architectures like CNNs and LSTMs, requires substantial computational resources for both training and inference. The extensive parameter computation, complex dynamic programming, and management of large datasets may exceed the capabilities of standard in-vehicle processors, which are typically optimized for simpler, low-latency tasks. Future research should address these challenges, potentially through techniques such as transfer learning, to enhance the model’s practicality for real-time applications in battery management systems. This proposed direction for future work underscores the model’s potential as a valuable tool in the industry.

Another study [133] also utilizes LSTM for battery capacity forecasting by introducing an advanced LSTNet model. This approach first segments discharged battery data into long-term and short-term sequences, integrating a Convolutional LSTM (ConvLSTM) to capture complex capacity features and incorporating an autoregressive (AR) component to improve robustness while using a shortcut connection structure to accelerate convergence. The model combines outputs from both linear and nonlinear components to enhance predictive performance. Testing on two datasets, including data from four batteries in the NASA dataset [134], reveals that the model effectively tracks capacity degradation curves, achieving a maximum Root Mean Square Error (RMSE) of 0.65%, a Mean Absolute Error (MAE) of 0.58%, and a Mean Absolute Percentage Error (MAPE) of 0.435% with 40% of the data allocated for training, validating the model’s accuracy and practicality.

In a significant development, the paper by Yan et al. (2024) [135] introduces a novel methodology for predicting the Remaining Useful Life (RUL) of solid-state lithium-ion batteries (SSLIBs). This study integrated an enhanced Convolutional Neural Network (CNN) with a newly proposed optimization algorithm, the Energy Circle Sparrow Search Algorithm (ECSSA). This approach leverages the advanced feature extraction capabilities of the improved CNN while optimizing model parameters using the ECSSA, demonstrating improved accuracy in RUL predictions. This methodological advancement highlights the trend of combining sophisticated neural network architectures with innovative optimization techniques to tackle complex battery management challenges. The CNN’s enhancements focus on optimizing hyperparameters and adjusting its structure to improve feature extraction and predictive accuracy.

The CNN employs advanced convolutional layers characterized by kernel sizes $k\times k$ and varying stride lengths s. The convolution operation is mathematically defined as

$$\mathrm{Conv}\left(x\right)=f(W\ast x+b)$$

(19)

where W represents the kernel weights, ∗ denotes the convolution operation, and b is the bias term. This formulation illustrates how the network processes input data to extract meaningful features, which is essential for overall performance.

To model nonlinear relationships effectively, activation functions such as the Exponential Linear Unit (ELU) are utilized:

$$\mathrm{ELU}\left(x\right)=\left\{\begin{array}{cc}x\hfill & \mathrm{if}x>0,\hfill \\ \alpha (e^x-1)\hfill & \mathrm{if}x\le 0\hfill \end{array}\right.$$

(20)

The ELU activation function mitigates the vanishing gradient problem, enabling more efficient learning.

Another commonly used activation function is the Swish function:

$$\mathrm{Swish}\left(x\right)=x·\sigma \left(x\right)$$

(21)

where

$$\sigma \left(x\right)={\displaystyle \frac{1}{1+e^{-x}}}$$

(22)

is the sigmoid function. These activation functions enhance the model’s ability to capture complex patterns in the data.

Residual connections are mathematically expressed as

$$\mathrm{Output}=\mathrm{F}\left(x\right)+x$$

(23)

This formulation preserves information across layers, effectively addressing the vanishing gradient issue and facilitating the training of deeper networks.

To refine the selection of health indicators (HIs), the method employs Mutual Information, which is mathematically defined as

$$I(X;Y)=\sum _{x\in X}\sum _{y\in Y}p(x,y)log{\displaystyle \frac{p(x,y)}{p\left(x\right)p\left(y\right)}}$$

(24)

This metric quantifies the dependency between HIs and Remaining Useful Life (RUL), providing insight into their relevance in the predictive model. Additionally, the k-nearest neighbor algorithm computes distances:

$$d(x_i,x_j)$$

(25)

between data points, further assessing HI relevance and improving the CNN’s generalization capability.

The mathematical novelty of the ECSSA encompasses several key innovations. Circle Chaotic Mapping enhances diversity in the initial hyperparameter space through chaotic sequences, which are represented by

$$\mathrm{CM}\left(t\right)=\mathrm{mod}(\varphi ·t,1)$$

(26)

where $\varphi$ is a chaotic parameter, increasing the exploration of potential solutions. The Nonlinear Attenuation Coefficient is defined as

$$\eta \left(t\right)={\displaystyle \frac{1}{1+\gamma t}}$$

(27)

with $\gamma$ as a scaling factor and t representing iterations. This coefficient dynamically adjusts the balance between exploration and exploitation during optimization.

Cauchy Mutation is mathematically expressed as

$$x^{\prime }=x+\Delta x$$

(28)

where $\Delta x\sim \mathrm{Cauchy}\left(\gamma \right)$, indicating that $\Delta x$ follows a Cauchy distribution. Unlike the more commonly used Gaussian (normal) distribution, which tends to generate smaller, more incremental changes, the Cauchy distribution introduces larger, more frequent perturbations. This is due to the “heavy tails” of the Cauchy distribution, which allow for occasional large deviations. As a result, this mutation technique is particularly effective in helping the model escape local optima by encouraging exploration of more diverse regions of the solution space, whereas Gaussian mutations might result in smaller, more gradual adjustments, potentially limiting the model’s ability to explore beyond local minima.

Together, these mathematical advancements in CNN architecture and optimization techniques significantly enhance the accuracy and robustness of RUL predictions, effectively addressing the complex dynamics of SSLIBs. The combined use of PCA and CNN with feature optimization and dimensionality reduction techniques presents a robust solution for more accurate and efficient SOH estimation in lithium-ion batteries, as shown in the paper by Lin et al. (2024) [136]. This novel method integrates feature optimization with a Convolutional Neural Network (CNN) to reduce redundancy in multiple features and enhance prediction accuracy. The proposed method reduces information redundancy by optimizing the combination of features derived from electrical, thermodynamic, and electrochemical data. This is achieved through Principal Component Analysis (PCA) followed by CNN, leading to a more efficient representation of battery aging characteristics. The CNN model is enhanced with feature dimensionality reduction techniques, employing smaller kernel sizes (2 × 1) and including 64 kernels in the first block and 16 in the second block to capture detailed feature variations while minimizing model complexity. Activation functions like ReLU and Sigmoid are used to improve computational efficiency and ensure that outputs are constrained within the appropriate range. The feature dimension is then optimized using a simulated annealing algorithm (SA) with a mean-variance objective function, improving the CNN’s performance by efficiently finding the optimal feature set, reducing computational resources, and enhancing estimation accuracy. The proposed method showed a significant improvement in SOH estimation performance compared to traditional CNN approaches and fixed-dimension PCA-CNN models, achieving more than a 20% increase in the Mean Absolute Error (MAE) and a 30% increase in the Root Mean Square Error (RMSE) metrics, validating its effectiveness through comparative experiments on the Oxford dataset [137].

In recent advancements in battery management, innovative methodologies have emerged to address the challenges of real-time SOH estimation, particularly in handling incomplete and partially observed data. The paper by Mazzi et al. (2024) [138] contributes to this area by introducing a sophisticated real-time SOH estimation model that employs a deep learning (DL) framework. This framework integrates a One-Dimensional Convolutional Network (1D-CNN) with a Bidirectional Gated Recurrent Unit (BiGRU), offering a robust approach to improving estimation accuracy under conditions of data incompleteness and partial observations. The hybrid CNN-BiGRU model extracts key features from input data through the 1D-CNN layers, while the BiGRU layers perform sequence learning in both directions. By using current, voltage, and temperature measurements from the electric vehicle’s Battery Management System (BMS), this approach avoids complex and time-consuming feature extraction. The model’s hyperparameters were optimized using Bayesian Optimization (BO) based on a Gaussian Process (GP), achieving a low Mean Squared Error (MSE) of $1.2\times {10}^{-5}$ in just 19 iterations. The accuracy of the optimized model was validated using a NASA-provided lithium-ion battery dataset with multiple discharge profiles, showing a Mean Absolute Error (MAE) of 2.080% and a Root Mean Square Error (RMSE) of 2.516% for the investigated battery set, which had 70 cycles at 24 °C. Additionally, it achieved an end-of-life (EOL) indicator error of zero cycles for the same data.

5.3. Optimization Strategies for Deep Learning Models

The study by Zhi et al. [139] represents a significant advancement in SOH estimation for lithium-ion batteries. Initially, the Random Forest algorithm is employed to identify key health factors using data from NASA. Following this, a Support Vector Regression (SVR) [140] model is developed for estimating the battery’s SOH. To enhance the accuracy and convergence speed of the SVR model, the Genetic Algorithm (GA) [141]–Particle Swarm Optimization [142] (PSO) technique was utilized to optimize its parameters. This approach, which has been validated on four batteries, achieved a Root Mean Square Error (RMSE) of 0.40% and an average Absolute Percentage Error (MAPE) of 0.56%. Compared to the Genetic Algorithm–Support Vector Regression (GA-SVR) and Particle Swarm Optimization–Support Vector Regression (PSO-SVR) methods, the proposed approach demonstrated a reduction in the average RMSE by 0.10% and average MAPE by 0.17%, and it decreased the number of iterations by seven generations relative to GA-SVR. These findings indicate that the proposed method offers improved accuracy and efficiency in SOH estimation.

Building on this foundation, Waseem et al. [143] introduce a novel method for estimating the SOH of lithium-ion batteries through a hybrid approach that integrates Grey Wolf Optimization (GWO) [144] with Bayesian-Regularized Neural Networks (BRNNs) [145]. This innovative method utilizes health features (HFs) derived from battery charging and discharging processes, with critical voltage and current characteristics identified through correlation analysis. GWO was employed to optimize and select hyperparameters for the BRNN, thereby enhancing the model’s global search capabilities and accuracy.

The promising results of the GWO-BRNN approach are noteworthy; it has been tested using the NASA battery dataset and has demonstrated superior performance, achieving SOH estimation errors of less than 1%. This significant improvement over existing methods underscores the potential of this approach in advancing effective prognostics and health management for electric vehicle batteries, contributing to the development of eco-friendly and reliable electric transportation solutions.

However, it is essential to consider the challenges associated with this method. Despite its high accuracy in SOH estimation and effective hyperparameter optimization, the GWO-BRNN method presents challenges related to computational complexity. The intricate nature of GWO and BRNN, combined with the opaque nature of neural networks, poses difficulties for practical implementation. Although this method excels in controlled laboratory settings where computational resources are abundant, its complexity may limit its feasibility for real-time applications where resources are constrained and interpretability is crucial. Thus, for practical applications in Battery Management Systems, simpler or more interpretable methods may be preferable.

In a complementary approach, another significant contribution presented in [146] is the development of a novel method for evaluating the SOH and predicting the Remaining Useful Life (RUL) of Electric Vehicle (EV) batteries using raw data collected directly from these vehicles. Unlike data obtained from controlled battery experiments, which tend to be more consistent, EV data frequently encounters challenges such as inconsistent usage patterns, data errors, extended sampling intervals, and varying environmental conditions. To address these issues, the authors have introduced several new evaluation features and employed an interpolation correction method based on data clustering at 1-second intervals. This approach has led to a notable improvement in accuracy, reducing the relative error in current integration to 0.94%.

Moreover, the study has incorporated the D-NSGA-II [147] optimization method, which dynamically selects the optimal voltage interval based on temperature variations. This dynamic approach has further refined SOH estimation and minimized model computation time. The results of this optimization demonstrate the advantages of the dynamic method, providing greater flexibility in designing SOH estimators tailored to specific applications.

Nevertheless, accurately estimating the SOH for lithium-ion batteries remains a critical challenge, especially given that electric vehicles often operate under conditions where complete charge and discharge cycles are not achieved. This limitation complicates the direct monitoring of battery capacity and internal resistance, which are traditional indicators of SOH, as was pointed out in [148]. To address this issue, the method in [148] proposed an indirect SOH estimation method for online EV lithium-ion batteries, utilizing an arctangent function adaptive Genetic Algorithm combined with a backpropagation (BP) neural network (ATAGA-BP). The proposed method leverages constant current drop time (CCDT), constant current drop capacity (CCDC), and maximum constant current drop rate (MCCDR) during the constant voltage charging stage as health indicators to indirectly assess battery degradation. The ATAGA-BP algorithm establishes the relationship between these indicators and the available battery capacity. Simulation results with NASA data show that this method correlates over 85% with battery capacity, has a 3.7% error in SOH estimation, and improves the iteration efficiency by 17.8%. This advancement represents a significant step toward overcoming the limitations of traditional SOH estimation methods and contributes to the technological readiness of battery monitoring systems.

5.4. Summary

Deep learning applications demonstrate significant advancements in estimating the SOH of lithium-ion batteries. A notable example is the comprehensive SOH degradation model introduced by [122], which incorporates various operational factors like charging currents and temperature effects. This model provides a more nuanced understanding of battery degradation, moving beyond simplistic capacity ratio metrics.

The use of Long Short-Term Memory (LSTM) networks is particularly significant, as they excel at capturing temporal dependencies, which are crucial for predicting Remaining Useful Life (RUL). This integration improves prediction accuracy over time, though it also increases computational complexity, posing challenges for real-time application in vehicles.

Moreover, feature extraction methods are gaining importance, as demonstrated in [123], where six key features were identified to optimize SOH estimation while minimizing computational load. This approach shows how Machine Learning can complement deep learning techniques, achieving high accuracy in state assessment.

Hybrid models that combine different neural network architectures, such as Convolutional Neural Networks (CNNs) with LSTMs, have shown promising results in managing the complexities of battery datasets. However, practical implementation remains a challenge due to the high computational demands of these models. Addressing these issues will be crucial for developing efficient, real-time battery management systems that can reliably operate in varying real-world conditions.

Optimization strategies, including GA-PSO, GWO-BRNN, and D-NSGA-II, significantly improve the accuracy and efficiency of SOH estimation for lithium-ion batteries. These approaches not only enhance predictive performance but also reduce computational time, facilitating real-time applications. However, more complex algorithms like GWO-BRNN pose challenges for practical implementation, highlighting the need to balance accuracy with execution simplicity. Research also indicates that advanced AI techniques are crucial for secondary battery applications, where detailed usage data is often lacking.

The subsequent subsection will provide a brief overview of several recently published studies to illustrate the current state of research in secondary applications, particularly focusing on the repurposing of batteries.

6. Latest Research on Secondary Applications—Brief Outlook to Future Research Directions

An increasing body of literature is focusing on critical aspects of battery second life, with [149] offering valuable insights for developing robust qualification algorithms and reliable health monitoring systems, while [150] highlights the limitations of conventional SOH assessment methods due to battery heterogeneity and unknown first-life conditions, advocating for a novel partial coulometric counter technique to enhance capacity aging evaluation.

Accurate estimation of battery SOC and SOH is essential for extending the lifespan and optimizing the usage of lithium-ion battery packs in electric vehicles is proposed in [151]. This paper presents a comprehensive co-estimation approach using an Adaptive Extended Kalman Filter (AEKF) for second-use lithium-ion batteries under various cycling conditions. The method involves analyzing battery test data to build a cycle-dependent equivalent circuit model (cECM) and estimating its parameters with a Recursive Least Squares (RLS) algorithm. The AEKF then simultaneously estimates SOC and SOH based on this enhanced model. The approach was validated with a LiCoO2 cell under constant current conditions, demonstrating high accuracy with SOC errors below 2.2% and SOH errors (capacity and internal resistance) under 1.7% and 2.2%, respectively. This scheme is significant for improving the reuse and efficiency of lithium-ion batteries.

The paper [152] introduces an SOH estimation algorithm for lithium-ion batteries using a Temporal Convolutional Network (TCN). The TCN’s self-learning capability allows it to model the complex, nonlinear behavior of batteries under varying environmental and operational conditions throughout their lifespan. The method demonstrated achieves high accuracy, with a Mean Squared Error (MSE) of less than 1%, even for dynamic load profiles. Trained on the NASA data as well, this approach has the potential to significantly reduce the uncertainty associated with the performance of retired electric vehicle batteries used in second-life applications. The results suggest that the TCN provides a robust and efficient solution for accurately predicting battery health.

In transitioning from the use of retired Electric Vehicle (EV) battery cells for secondary applications, it is essential to consider how these batteries can also be effectively integrated into Battery Energy Storage Systems (BESSs). As EV batteries reach the end of their automotive life, their residual capacity can be harnessed in stationary storage applications, contributing to grid stability and peak load management. However, effective integration of these second-life batteries into BESSs requires careful consideration of both operational costs and the health of the battery cells.

To address these challenges, the study presented in [153] develops a comprehensive BESS operation cost model that accounts for the increased costs associated with battery aging. This model aims to minimize operational costs at each time step using a Particle Swarm Optimization (PSO) method, which is particularly effective in optimizing complex, multi-dimensional systems. The results demonstrate that this approach not only optimizes BESS scheduling costs during peak load shifting but also improves the SOH variation between battery systems compared to traditional power allocation methods. This finding is crucial for applications where both new and retired battery systems are used together, highlighting the potential for second-life batteries to contribute economically to energy storage solutions.

Additionally, the proposed economic optimization method can be seamlessly integrated into existing BESS scheduling systems to minimize costs in applications such as EV charging stations and energy trading in the electricity market. This integration underscores the dual utility of second-life batteries in both transportation and stationary storage contexts, making a strong case for their continued development and use.

Further, recent research by [154] examines key degradation factors, such as the formation of solid electrolyte interphase (SEI) and lithium plating, which contribute to reduced battery capacity over time. The study emphasizes the importance of accurately estimating the remaining useful capacity for potential secondary applications or recycling. By focusing on the incremental capacity analysis method, which tracks battery degradation through detailed data extraction and model training, the study provides precise insights into battery health. This level of analysis is critical for ensuring the reliability and efficiency of second-life battery systems, whether in EVs or stationary storage applications.

However, despite these advances, the research [154] points to a critical gap: the lack of clear standards for regrouping batteries, particularly in relation to cell-to-cell variation. Understanding how these variations affect overall pack performance is crucial for the reliability and safety of second-life battery applications. Establishing standardized quantitative approaches that consider self-balancing mechanisms among cells is essential for achieving consistent performance. While certain cooling structures can mitigate cell-to-cell variation, they present a trade-off with cost, indicating that a balance must be found.

Regulatory frameworks, such as UL 1974 [155], which address safety and performance evaluation for used batteries, are early steps in the right direction, which was also emphasized in [154]. However, standards like IEC 62933-5-3 [156], which focus on the safety of second-life battery systems, require further adaptation to encompass the unique challenges posed by components sourced from used batteries. Consequently, the variability in the quality of used batteries underscores the current inadequacies of existing testing standards in accurately reflecting the performance and safety of these systems.

Furthermore, the book chapter published by [152], several critical challenges limiting the application of retired Electric Vehicle (EV) batteries in second-life applications are delineated.

First, the competitiveness of second-life batteries presents a significant challenge. The introduction of newer generations of batteries, which offer enhanced quality, performance, and lower costs, exacerbates the difficulty of economically exploiting second-life batteries. This situation could diminish the economic attractiveness of repurposed batteries and potentially exacerbate the environmental impact of battery manufacturing over its entire lifecycle [157,158]. In addition, regulatory issues pose a substantial barrier. The current regulatory frameworks in many countries do not adequately address the specifics of second-life batteries. These batteries are classified as hazardous goods, leading to higher transportation costs due to special handling requirements. Furthermore, the lack of clear and transparent regulations for battery storage in the energy market complicates the implementation of second-life applications [152]. In addtion, the design of battery packs is a notable challenge. Battery packs are initially optimized for use in vehicles, which often does not align with the needs of stationary storage applications. This misalignment results in increased repurposing costs when the packs are used outside their original intended application. Integrating second-life repurposing considerations into the initial design could mitigate these costs, though it may introduce additional expenses during the primary application phase.

Lastly, there is uncertainty in remaining battery lifetime and performance degradation. The performance and degradation rates of second-life batteries are highly variable and depend on numerous factors, such as temperature, depth of discharge, and current rates. This variability is further compounded by differences in battery chemistry and historical usage, making it challenging to predict the batteries’ performance reliably in their second life [159].

Addressing these challenges is crucial for ensuring the safe, economically viable, and efficient utilization of retired EV batteries in secondary applications.

This situation reveals that the field is still in its formative stages and underscores the urgent need for extensive research and development to advance standards and practices in this evolving area.

7. Perspectives

The papers reviewed in this study collectively advance the field of State-of-Health and State-of-Charge estimation for lithium-ion batteries in EVs through innovative methodologies and models. The methodologies employed range from traditional machine learning techniques like Multi-LAyer Perceptrons to advanced deep learning models incorporating LSTM and CNN. Each approach has its own strengths and limitations, making it challenging to determine a universally superior method. The most interesting results are collected in

Table 5. Snapshots of State-of-Health (SOH) estimation methods (2019–2024), highlighting the most successful models from main modeling approaches. Ordered by accuracy.

Method	Accuracy Metrics	Model Details
Wu et al. (2024) [120]	MAE < 0.5%, RMSE < 0.2%	Second-order hybrid equivalent circuit model with adaptive update rate, Nonlinear observer
Wang et al. (2024) [123]	RMSE = 0.36%	Feature extraction with ML algorithms, Hybrid feature set
Rao et al. (2024) [54]	RMSE = 0.003, MAE = 0.003, R-squared error = 0.004	GRU, LSTM, DNN, NASA data
Heinrich et al. (2021) [13]	Average error deviation = 0.16%, RMSE = 5.57 mV	Feedforward and Convolutional Neural Networks, In-vehicle sensor data
Zhi et al. (2022) [139]	RMSE = 0.40%, MAPE = 0.56%	SVR optimized with GA-PSO, NASA data
Anas et al. (2024) [124]	90.5% reduction in RMSE	Hybrid deep learning methods, NASA datasets
Mazzi et al. (2024) [138]	MAE = 2.080%, RMSE = 2.516%, EOL indicator error = 0 cycles	1D-CNN combined with BiGRU, Laboratory data
Yao et al. (2024) [51]	Superior performance compared to traditional methods	CNN–WNN–WLSTM, NASA Ames Prognostics Center data
Ping et al. (2023) [133]	RMSE = 0.65%, MAE = 0.58%, MAPE = 0.435%	LSTNet with ConvLSTM and AR component, NASA data
Yayan (2021) [129]	RMSE = 5.5%, Capacity RMSE = 0.033 Ah	Stacked BiLSTM, Constant current charging data
Waseem et al. (2023) [143]	SOH estimation errors < 1%	GWO-BRNN, NASA dataset
Hell et al. (2022) [125]	Effective in controlled environments	GRU with soft-sensing method
Lee et al. (2022) [53]	LSTM model significantly surpasses others	Neural network model bank for SOC and SOH
Wang et al. (2022) [56]	Significant improvement over traditional models	CNN-LSTM-CRF model
Zhou et al. (2019) [160]	SOH estimation error = 8%	GPR-EKF with fragment charge data, Partial data
Li et al. (2022) [148]	SOH estimation error = 3.7%	ATAGA-BP, Partial data
Wu et al. (2020) [55]	Maximum estimation error = 4.55%, Estimation error < 5.99% for other cells	LSTM network, Handcrafted features (HFs), Grey Relational Analysis (GRA), Entropy Weight Method (EWM), Adam optimization, NASA data
Hafez et al. (2023) [108]	77% MAE reduction compared to EKF	VBMCCKF method, even in the presence of noisy and irregular data
FadeCapacity (2022) [116]	High accuracy	Degradation Speed Ratio (DSR), reduced waiting time
DataDriven (2022) [122]	Accurate RUL prediction over 4 months	LSTM with CRF
entropy (2022) [121]	Effective SOH prognosis	LSKNN + MIES + CSVGPR
2015SOH (2015) [119]	High accuracy	Bulk Capacitance Method with discrete nonlinear observer

and

Table 6. Comparison of SOC estimation methods (2019–2024). Snapshots of selected recent successful solutions with accuracy, representing key examples of different modeling approaches.

Reference	Method Name	Accuracy
[107]	AIC-SE	±0.3% RMS error
[108]	VBMCCKF	77% MAE reduction compared to EKF, even in the presence of noisy and irregular data
[109]	Aging Model	Significant improvement in capacity loss prediction

, which present the methods for SOH and SOC estimation in increasing order of accuracy.

However, the accuracy metrics reported in these studies vary, including the MAE, RMSE, and MAPE. Direct comparisons are complicated by these differences. For instance, Wu et al. (2024)’s [120] RMSE of 0.2% is significantly lower than Wu et al. (2020)’s [55] maximum error of 4.55%, indicating that Wu’s (2024) model may be more precise under the conditions tested. Differences in data handling, such as the proportion of data used for training and testing, impact the reported accuracy metrics. For example, Ping’s model [133] uses 40% of the data for training, which may affect its accuracy compared to Wu’s [120] approach with a different data allocation strategy.

The practical deployment of these models in real-world scenarios requires further validation. For instance, methods achieving lower error rates in controlled environments may face challenges when applied to varied real-world conditions. While each approach has demonstrated its strengths, such as Wu’s [120] high precision and Ping’s [133] integration of convolutional layers with LSTM, the variability in metrics and data handling underscores the need for standardized evaluation practices. Note that the Tables above pertains solely to the selected works; however, it effectively illustrates the trends observed in the examined period.

This review addresses several key questions related to the application of Machine Learning (ML) techniques for SOH (and related SOC) estimation in lithium-ion batteries used in EVs, thus formulated in Section 2 Materials and Methods. Initially, the review identifies the primary ML techniques currently employed, including traditional methods like SVR and advanced models such as LSTM-CNN hybrids. These techniques are highlighted as significant developments in the field, guiding the exploration of algorithms and models utilized by researchers (Research Question 1).

A noteworthy observation from the sources is that a significant number of research papers in recent years have focused on advanced machine learning approaches for performance evaluation under conditions of data incompleteness and partial observation. This review demonstrates that incomplete data still leads to lower accuracy even in more advanced machine learning models, as highlighted in studies such as [160]. However, recent studies have shifted towards using more comprehensive datasets, like the NASA dataset, which significantly improves accuracy and comparability. This transition addresses the impact of data sources on model performance, emphasizing the need for thorough data to achieve reliable outcomes (Research Question 2).

Despite these advancements, challenges persist. As shown in Table 5 (e.g., by [148]) and discussed in the review, even the most advanced techniques struggle with the variability and complexity of real-world data. Field data, in particular, presents issues such as inconsistent usage patterns and environmental factors, which continue to affect model performance. Thus, while comprehensive datasets enhance accuracy, the ongoing difficulties highlight the need for further improvements in handling diverse data environments (Research Question 2 and Research Question 3).

In addition, real-time operation continues to present challenges despite advancements in data evaluation methodologies. The review supports the idea that cloud solutions can enhance data processing capabilities. As demonstrated by [52], the continued use of traditional equivalent circuit-based models in conjunction with cloud technologies has proven that a greater volume of monitoring data can achieve outstanding precision. This underscores the value of big data utilization in improving accuracy through model parameter estimation, addressing challenges in applying ML techniques in varying environmental conditions and application scenarios (Research Question 3).

The recent study by Wang et al. (2022) [56] introduces an innovative approach to lithium battery capacity prediction through a combined Convolutional Neural Network–Long Short-Term Memory–Conditional Random Field (CNN-LSTM-CRF) model. It is critical to note that while this model demonstrates impressive predictive capabilities, its computational demands warrant consideration. The CRF layer, particularly when integrated with deep learning architectures like CNNs and LSTMs, requires substantial computational resources for both training and inference. This observation highlights an important aspect of future research directions for improving the accuracy and computational efficiency of ML-based SOH estimation models, such as adaptability and computational efficiency (Research Question 5). Future research should address these challenges, potentially through techniques like transfer learning, to enhance the model’s practicality for real-time applications in battery management systems.

A significant contribution from Mazzi et al. (2024) [138] introduces a sophisticated real-time SOH estimation model that employs a deep learning (DL) framework, highlighting the importance of feature extraction as a crucial task in Machine Learning for battery SOH estimation. Their study demonstrates that the CNN-BiGRU model, when tested on data extracted from a vehicle’s Battery Management System (BMS), can avoid complex and time-consuming feature extraction processes. Interestingly, the study also highlights that despite the critical impact of temperature on aging, the deep learning model effectively handles SOH estimation without the need for extensive feature engineering, showcasing its practicality in real-world applications (Research Question 3).

The correlation between electrical circuit Modeling and advanced Machine Learning techniques is noteworthy. Combining these traditional methods with deep learning approaches still offers competitive results, even when compared to the latest deep learning models. This finding addresses how traditional approaches in SOH estimation evolve and integrate with ML methods (Research Question 4). The reviewed papers also indicate that recent studies have extensively explored a variety of Machine Learning (ML) techniques for SOH estimation in lithium-ion batteries. Techniques such as Adaptive Integral Correction-Based State of Charge Estimation (AIC-SE) and Variational Bayesian Maximum Correntropy Cubature Kalman Filter (VBMCCKF) have been developed to improve the accuracy and robustness of SOH estimation. The AIC-SE method enhances SOC estimation by integrating real-time correction mechanisms, while the VBMCCKF combines advanced filtering with statistical techniques for superior accuracy in SOC estimation.

Recent advancements include Convolutional Neural Networks (CNNs), Long Short-Term Memory (LSTM) networks, and their hybrids (e.g., CNN-LSTM-CRF and CNN-WNN-WLSTM). These models excel in capturing complex patterns and dependencies in battery data, achieving significant improvements in accuracy and reliability. New methods, such as the Degradation Speed Ratio (DSR) and advanced hybrid frameworks like the Multi-Feature Fusion and Dual Attention Long Short-Term Memory (MDA-LSTM) network, offer enhanced predictive performance by combining novel health indicators with sophisticated neural network architectures. Key challenges in applying ML techniques across different scenarios are identified in this review. Factors such as temperature fluctuations and different charging practices continue to pose challenges not only for traditional methods but for deep learning models as well. Models like the AIC-SE and advanced ECM methods address these issues by incorporating temperature effects and dynamic updates. Techniques such as LSTM and hybrid models (e.g., CNN-WNN-WLSTM) show improved adaptability to various usage scenarios, addressing the complexity of real-world battery operations (Research Question 3). The study effectively compares and integrates ML methods with traditional SOH estimation approaches. Traditional methods like equivalent circuit models (ECMs) and Kalman Filters are compared with advanced ML techniques. For example, the VBMCCKF and hybrid LSTM models demonstrate improvements over traditional methods such as the Unscented Kalman Filter (UKF) and Extended Kalman Filter (EKF) in terms of accuracy and noise handling. The integration of ML with traditional approaches, such as combining ECMs with ML techniques, enhances overall estimation accuracy and robustness (Research Question 4).

Overall, this review concludes several future research directions to advance ML-based SOH estimation. Future work may focus on improving feature selection, outlier detection, and adaptation to diverse environmental conditions. Techniques such as the Degradation Speed Ratio (DSR), a new health indicator, combined with advanced neural network models (e.g., MDA-LSTM), offer promising pathways for improving accuracy. Research should aim to optimize algorithms for better computational efficiency, making them suitable for real-time applications. Innovations such as CNN with feature optimization and dimensionality reduction techniques are examples of efforts to address computational demands. Additionally, further research should explore methods to integrate multiple data sources more effectively, leveraging the strengths of both laboratory and field data to improve SOH estimation models (Research Question 5).

Regarding future work, a brief outlook on battery second usage is provided. This area is crucial for future research and presents challenges that require more exploration regarding the application of advanced machine learning techniques. A growing body of literature emphasizes critical aspects of battery second life, with studies such as [149] offering valuable insights into developing robust qualification algorithms and reliable health monitoring systems. This work highlights the limitations of conventional SOH assessment methods, particularly due to battery heterogeneity and unknown first-life conditions, as noted by [150]. Crucially, this research advocates for novel techniques like partial coulometric counters to enhance capacity aging evaluation, addressing gaps left by traditional methods. Furthermore, accurate estimation of SOC and SOH is vital for extending the lifespan of lithium-ion batteries, as demonstrated by [151] through a comprehensive co-estimation approach using Adaptive Extended Kalman Filters (AEKFs).

Despite these advances, current research points to several limitations that remain key challenges. The challenge of battery heterogeneity and varying operational conditions in second-life applications remains a significant hurdle. Additionally, the absence of standardized quantitative approaches for assessing battery performance under partial data conditions, where data is often inconsistent due to usage patterns, errors, and environmental factors, remains a critical issue. Addressing these limitations will be crucial for advancing the reliability and efficiency of second-life battery applications and enhancing the safety and performance of Battery Energy Storage Systems (BESSs).