The Influence of Magnetic Fields on Electrophoretic Processes in Magnetic Colloids with Different Stabilization Mechanisms

Abstract

Electrophoretic nanostructuring is a promising approach for the creation of functional surfaces and active layers. The potency of this approach may be further enhanced by additional factors of various natures, such as magnetic fields. In this work, we have studied the process of electrophoresis in thin layers of water- and kerosene-based magnetic liquids and the effect of additional magnetic fields on the occurring processes. It was found that the electrophoresis process can be significantly affected by inhomogeneous magnetic fields. The possibility of compensating electrophoresis processes in such systems by means of inhomogeneous magnetic field influence was shown. Structural changes in magnetic colloids on hydrocarbon bases under the influence of an electric field have been studied. The role of electrohydrodynamic flows arising in this process is considered, and the influence of the magnetic field on the configuration of the formed labyrinth structure is studied. The dependence of the threshold value of the electric field strength corresponding to the emergence of the structure on the temperature and additionally applied magnetic field has been established. The obtained results could contribute to the development of an original method for determining the charge and magnetic moment of a single nanoparticle.

1. Introduction

Magnetic fluids are ultra-disperse colloidal solutions of ferri- and ferromagnetics in liquid media. These systems attract the intense attention of researchers both from a fundamental point of view and for their practical applications in engineering and medicine [1,2,3,4,5,6,7,8]. The interest in magnetic fluids is dictated by their magnetic properties, which are unique to liquid systems. In this connection, an overwhelming number of works are devoted to investigations of their magnetic, magnetohydrodynamic, and magneto-optical properties [4,9,10,11,12]. At the same time, the electrical properties of magnetic fluids and their dependence on a magnetic field are also of undeniable interest. These properties are determined by electrokinetic phenomena that are characteristic of colloidal systems. For instance, electrohydrodynamic (EHD) flows of dielectric liquids are used to intensify heat transfer, for fine spraying in various installations, and in cryogenic technology. Since there is a direct conversion of the energy of a direct electric current into the translational motion of a liquid, they can be used to create EHD transducers [13,14]. The most common are magnetic fluids based on hydrocarbon dispersion media. Since they are more stable and retain aggregative stability for a long time, they are widely applied in engineering and instrumentation [15,16,17,18]. In recent years, interest has shifted to the electrophoretic properties of water-based colloidal systems and their possible applications for magnetic drug delivery methods or medical diagnostics [19,20,21,22,23]. Electrophoretic systems are used for the creation of magnetic coatings for microelectronics [24], the deposition of protective coatings [25], heat transfer systems [26], electronic-paper displays [27], microfluidic devices [28,29], and bioanalytical assays [30,31,32].

The electrical properties of magnetic colloids based on hydrocarbon and aqueous media have significant differences due to the different stabilization mechanisms. In the first case, stabilization is achieved by the steric repulsion of amphiphilic molecules adsorbed on the surface of presumably uncharged magnetite particles, while in the second case, stability is maintained mainly due to the electrostatic repulsion of double electrical layers formed on the boundary of the colloidal particles. The latter factor determined that the majority of charge transfer processes and electrokinetic phenomena studies were conducted in water-based systems [33,34,35,36], but still, much attention was also paid to the study of the electrical properties of magnetic fluids based on hydrocarbon media. The use of hydrocarbon-based magnetic fluids as a dielectric medium can facilitate the use of EHD flows, so in this case it becomes possible to control the process through the additional action of a magnetic field. At the same time, we have no information about specific, already-existing applications of EHD flows in magnetic fluids. It was demonstrated that in magnetic fluids based on non-polar solvents, charge transfer can be carried out either by free ions formed during the synthesis of the system or by colloidal particles themselves [37,38]. The origin of charged particles in non-polar solvents remains unclear. In some works, it is speculated that such systems contain a small fraction of both negatively and positively charged particles [39,40,41], while other researchers assume that initially the particles are not charged but can acquire a charge when they are near the electrodes [42,43,44].

Another problem in electrophoretic studies of magnetic fluids originates from structural and phase transitions that occur in the presence of electric fields [45,46,47]. It was demonstrated that under a constant electric field, magnetic fluids can form structured lattices or autowaves in thin layers [48,49]. These processes are associated with a local concentration of nanoparticles and can be associated with a change in color, but the mechanisms of such structural changes remain unclear [50].

Previously, a significant effect of combined magnetic and electric fields on the processes of deposit formation during the evaporation of flat drops was shown for water-based magnetic fluid [51]. The observed effects originated from the balance between thermodynamic processes in the drying drops and the influence of electric and magnetic fields on dispersed magnetic nanoparticles. It should be noted that with the simultaneous action of magnetic and electric fields on an evaporating drop, either an increase in external influence or compensation of electric forces by magnetic ones can occur. Thus, it follows from the above that one of the possible approaches to studying the electrophoretic mobility of magnetic fluids can be based on the interplay of electrophoresis and magnetophoresis.

In the present work, studies of the process of electrophoresis in thin layers of water- or oil-based magnetic fluids and the effect of additional exposure to a magnetic field were undertaken. It has been shown for the first time that the process of electrophoresis in magnetic colloids can be significantly affected by an inhomogeneous magnetic field. The features of the electrophoresis process under the simultaneous action of electric and inhomogeneous magnetic fields have been studied. Based on the results of such studies, an attempt was made to develop a new method for determining the magnetic moment and size of colloidal particles.

In addition, studies of structural changes in thin layers of magnetic colloids on hydrocarbon bases under the influence of an electric field were continued. The role of the EHD flows that rise in this case is considered, and the influence of the magnetic field on these processes is studied. The dependence of the threshold value of the electric field intensity corresponding to the appearance of a labyrinth structure on temperature and an additionally applied magnetic field was demonstrated, as was their dependence on the thickness of the sample, the temperature, and the applied field strength. Additionally, for the first time, we demonstrate the structuring of the colloidal particles not only near the electrode surface but in the entire interelectrode space.

2. Materials and Methods

Chemicals: Iron (II) chloride tetrahydrate, iron (III) chloride hexahydrate, and oleic acid were obtained from Sigma Aldrich (St. Louis, MO, USA). Ammonia, ethanol, sodium hydroxide, and toluene were obtained from Chimmed (Saint Petersburg, Russia) and used without further purification. Kerosene was obtained from Arikon (Moscow, Russia).

Water-based magnetic fluid (Sample No. 1): The material was synthesized by the modified co-precipitation protocol described earlier [52,53]. Briefly, 2.5 g of iron chloride (II) tetrahydrate and 5 g of iron chloride (III) hexahydrate were dissolved in deionized water, and 11 mL of ammonia was added under constant stirring. The formed iron oxide was magnetically separated, washed until neutral pH with deionized water, and ultrasonically dispersed in 100 mL of deionized water for two hours. The resulting stable hydrosol consisted of 10 ± 3 nm magnetite nanoparticles according to TEM measurements (see Supplementary Figures S1 and S2), the mean hydrodynamic radius was 32 nm according to DLS (Supplementary Figure S3), and the mass fraction of magnetite nanoparticles was 1 wt%. The sample showed superparamagnetic behavior and magnetization up to 63 emu/g (Supplementary Figure S4). For the experiments, the sample was diluted with deionized water to the desired concentration.

Kerosene-based magnetic fluid (Sample No. 2): The material was synthesized following the protocol described in ref. [51]: 4.32 g of iron chloride (III) hexahydrate, 1.6 g of iron chloride (II) tetrahydrate, and 19 g of oleic acid were soluted in 160 mL of an ethanol/water/toluene mixture with a fraction of 1:1:2 under reflux. A total of 2.4 g of sodium hydroxide dissolved in 5 mL of an ethanol/water/toluene mixture was quickly added. Reflux was continued for a further 2 h. Once cooled, an excess of ethanol was added, and the precipitate was collected by centrifugation at 4000× g. The precipitate was washed 4 times with ethanol and dispersed in 10 mL of kerosene with 0.1 mL of oleic acid. The sol consisted of 11 ± 3 nm magnetite nanoparticles according to TEM measurements (see Supplementary Figures S5 and S6), the mean hydrodynamic radius was 27 nm according to DLS (Supplementary Figure S7), and the mass fraction of magnetite nanoparticles was 12 wt%. The sample showed superparamagnetic behavior and magnetization up to 78 emu/g (Supplementary Figure S8). For the experiments, the sample was diluted with kerosene to the desired concentration.

Characterization of materials: Hydrosols and nanoparticles were characterized using the dynamic light scattering (DLS) device Photocor Compact Z (Moscow, Russia), transmission electron microscopy (TEM) on a FEI Tecnai G2 F20 S-Twin (Hillsboro, OR, USA) microscope, and a LakeShore Cryotronics 7410 (Westfield, OG, USA) vibrating sample magnetometer. For the DLS measurements, samples were diluted with the proper solvent (water or toluene for samples No. 1 and No. 2, respectively) to a concentration of 1 µg/mL and measured in a sample cuvette using a 633 nm laser. For TEM measurements, the samples were diluted in ethanol, applied dropwise onto carbon grids, and studied at ×97,000 magnification. An array of particles > 2000 was surveyed for each sample. Measurements and statistical processing of the measurement results were carried out using ImageScope software created by SMA LLC (Moscow, Russia). A more detailed description of the materials may be found in previously published works [8,54,55,56,57].

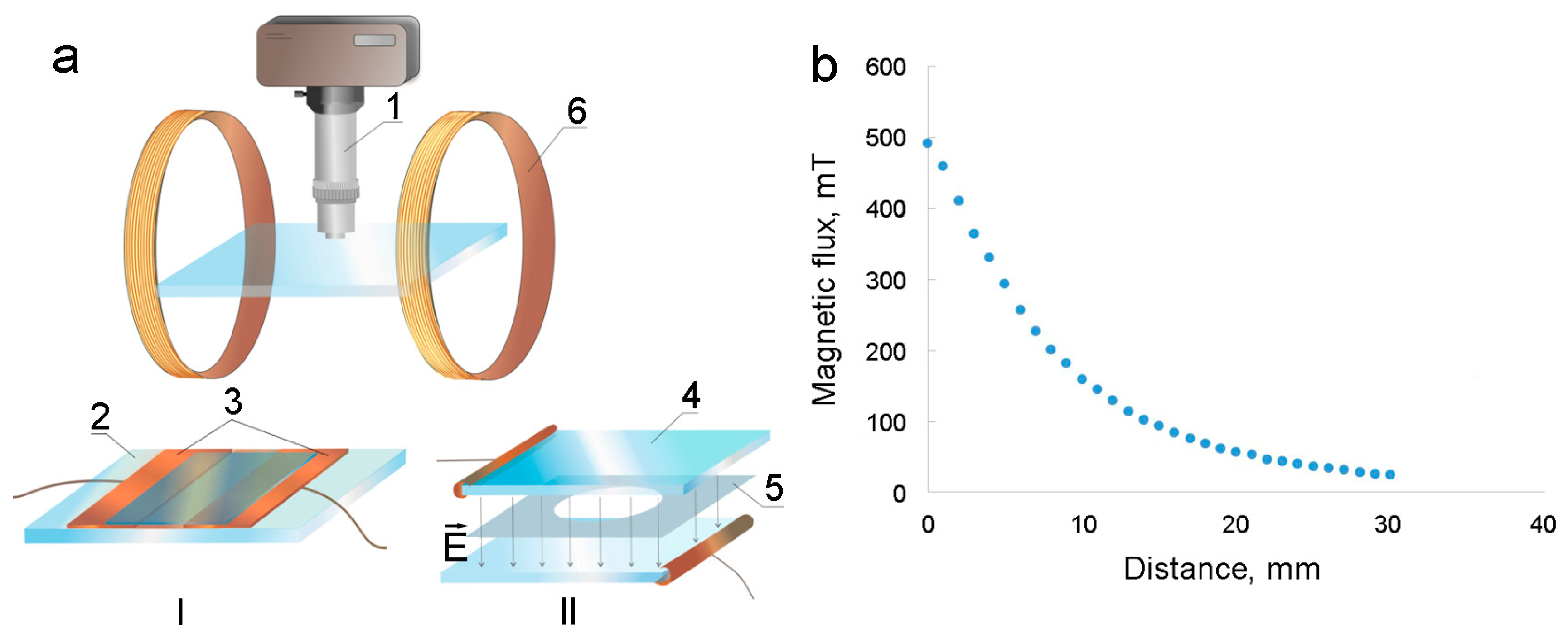
Electrophoretic investigations: The electrophoresis experimental studies were performed on an installation shown in Figure 1a.

The main part of the device was the measuring cell (1). The cell consisted of two electrodes, between which a layer of the studied magnetic fluid was placed. One of the electrodes (ring type) was a thin rectangular metal plate (3) made of copper or aluminum foil with a circle-shaped hole cut in the center. This electrode was glued onto a horizontally located flat glass substrate (4). The second electrode was a thin rod (5), which was installed in the geometric center of the first electrode, perpendicular to the plane of the substrate. The thickness of the outer electrode was 0.2 mm, the inner diameter was 20 mm, and the diameter of the needle electrode was 0.05 mm. The inner space of the annular electrode was completely filled with the studied magnetic fluid, so that its free surface was at the same level as the upper side of the plate. For experiments with a near-uniform electric field cell, a modified electrode geometry (2) was used. In this assembly, the rod electrode was replaced by a flat one, which was a round plate of metal foil with a diameter of 18 mm glued to the substrate in the center of the internal space of the first electrode. The sample was placed into the annular gap between the electrodes, whose width was 2 mm. After the cell was filled, a voltage was applied to its electrodes from a DC source of the MATRIX MPS–3003L-1 (Shenzhen, China), and changes in the concentration of dispersed particles near both electrodes were observed. To study the effect of magnetic fields on the electrophoresis, the cell was placed over a conical ferromagnetic core (6) with an annular permanent magnet or magnetizing coil to form an inhomogeneous magnetic field with a circular symmetry. For these purposes, a ring ceramic ferrite permanent magnet was used, the outer and inner diameters of which were 110 mm and 25 mm, respectively, and the thickness of which was 20 mm. A core made of soft magnetic iron of the ARMCO type was placed inside the ring magnet, the length of the protruding conical part of which was 43 mm. As can be seen in Figure 1b, the maximum achievable induction value in the geometric center of the cell was 190 mT, and the value of its average change per unit length at the location of the sample was $\frac{\partial B}{\partial r}=328 \mathrm{m}\mathrm{T}/\mathrm{m}$.

Electrohydrodynamic flows study: To study the formed structures and development of electrohydrodynamic flows in thin layers of the studied magnetic fluids, optical microscopy was used. This was performed on two types of cells with perpendicular or parallel applications of electric fields on the assembly shown in Figure 2a.

The first type of cell had the shape of a rectangle and was made of a glass slide (2), on the surface of which two rectangular metal plates (3) (copper foil, 0.2 mm thick) were glued, and the distance between electrodes was 2 mm (Figure 2a, cell I). The space between electrodes was filled with the tested sample, and the cell was topped with a cover glass. To create an electric field, a voltage was applied to the electrodes from a direct current source. The field strength E was estimated from the voltage U and the distance between the electrodes (E = U/Δr). The second cell was round-shaped and consisted of two transparent rectangular glass plates (4) with a conductive coating (Figure 2a, cell II). A Teflon film (5) with a round hole in the middle was placed between the conductive glass surfaces, and the cell was filled with the tested magnetic fluid. The thickness of the liquid layer was 18–70 μm and was controlled by using polymer films of different thicknesses.

During the observations, the cells were placed on the object stage of a Biolam-type optical microscope (1) without magnetizable parts. The microscope was equipped with a video camera connected to a computer. To carry out additional exposure to a magnetic field with a small intensity, the cell was equipped with a Helmholtz coil magnetizing system (6). The diameter of the Helmholtz coils was 27 cm; they created a uniform magnetic field at the location of the measuring cell, the intensity of which is proportional to the current. With a current strength in the coils of I = 1 A, it was 1.83 kA/m. For exposure to stronger magnetic fields, permanent cylindrical neodymium magnets were used. The magnet was 25 mm in diameter and 15 mm high. Figure 2b shows the dependence of the magnetic induction of such magnets as a function of the distance from their ends. The combination of two such magnets allowed us to reduce the inhomogeneity of the field in the area of the experiments.

For temperature control, the samples were placed on a thermostatic system shown in Figure 3. The cuvette (1) with the test liquid was pressed with a mechanical clamp (2) to a thermosetting system, which was a massive copper parallelepiped (3) with a flow-through tube (4). The dimensions of the system were 70 mm × 50 mm × 12 mm. The water at the desired temperature was pumped through the system with a thermostat from the TERMEX M12M-X232B (Tomsk, Russia). The temperature was controlled by a copper–constantan thermocouple located in a slot under the sample wall and pressed against the thermostatic system.

3. Results

As was mentioned above, we previously studied the features of deposit formation during the evaporation of flat drops of a magnetic fluid located on a solid conducting substrate [36]. It was found that the impact of an electric field created by applying a voltage between the substrate and a needle electrode placed in the center region of the drop significantly changes the architecture of the deposit. Figure 4 illustrates the difference in the structure of the deposit formed with a positive needle electrode and negative substrate potentials (Figure 4a) and vice versa (Figure 4b) for water-based magnetic fluid. The experiment was carried out during the time of complete evaporation of the drop (about 2 h) and the formation of a dry deposit at a potential difference between the electrodes of 5 V. This difference originates from the process of electrophoresis that occurs in such a medium under the influence of an electric field.

Initial assessments were performed on Sample No. 1 using the round-shaped electrode (see Materials and Methods for details). The experiments were conducted at a temperature of 14 °C and 100% humidity to prevent the droplet from evaporation; the volume of the sample in the cell was 2.5 µL. With this setup, the localization of the fluid in the region adjacent to the inner boundary of the negatively charged ring electrode was observed (Figure 5a). A change in polarity resulted in the opposite behavior of the fluid, so it was located in the area surrounding the needle electrode (Figure 5b). In these experiments, the potential difference between electrodes was 30 V. When the process of electrophoresis was interrupted by switching off the applied voltage, the homogeneity of the layer was slowly restored.

Additionally, studies were carried out using ring-shaped electrode assemblies. As can be seen in Figure 6, the fluid behaved similarly and demonstrated a time-dependent process of nanoparticle localization in the annular gap between the electrodes near the inner boundary of the outer electrode at its negative potential (the initial sample concentration was 0.63 wt%, the potential difference between the electrodes was 15 V, and the temperature was 14 °C). As can be seen, the near-electrode layer reached increased concentration stops, while the remaining part of the interelectrode space became transparent over time. It can be assumed that in this case there was a complete stratification of the magnetic fluid so that the entire dispersed phase was concentrated at the electrode surface. Electrodes polarity exchange led to a similar formation of a concentrated layer at the boundary of the inner electrode. This, together with the results presented in Figure 6, indicates that the colloidal particles of the sample have a positive charge.

As can be seen from Figure 6, a layer of increased concentration with a clear boundary is formed near the electrode. This indicates that in this region, an increase in the concentration of particles, due to their strong magnetic dipole interaction, leads to the aggregation of the magnetic fluid at the electrode—the formation of a new, more concentrated phase. After some time, the entire sample of magnetic fluid in the interelectrode space is divided into two phases: a thin layer of the dispersed phase at the electrode and a dispersion medium that fills the rest of the interelectrode space. Using this fact, one can estimate the approximate speed of the electrophoretic motion of particles as a function of the width of the interelectrode space and the time of complete separation of the colloidal system. To make these evaluations, a sample of a magnetic colloid with a lower concentration of the dispersed phase (0.3 wt%) was used. The determination of the time of complete separation of the colloid in the interelectrode space was carried out at various values of the voltage on the electrodes. In this case, measurements at the same voltage were carried out three times, and the cell was filled anew before each measurement. The results obtained are presented in Figure 7.

The next steps were aimed at determining the influence of non-homogenous magnetic fields on electrophoresis processes. The idea behind these experiments was based on the conception that during the simultaneous application of electric and non-uniform magnetic fields, magnetic forces can either enhance or counter the action of electric forces. The latter case was realized when the external electrode was negatively charged, so the electrophoretic forces were directed toward the outer surface of the cell. In this setup, the alternation of the magnetic field parameters may be adjusted to compensate for the electrophoretic strength of the applied electric field. To test this possibility, we studied the zones with increased concentrations of nanoparticle formation processes under the combined action of a constant inhomogeneous magnetic field and an electric field. A visualization of the result is shown in Figure 8.

As can be seen from the figure, the influence of a constant inhomogeneous magnetic field on electrophoresis processes becomes more pronounced with a decrease in electrode potential. Under the experimental conditions, the highest apparent homogeneity of the sample layer corresponded to the voltage on the electrodes, U = 0.1 V. It can be assumed that under these conditions, the effects of magnetic and electric forces on a charged magnetic colloidal particle are compensated. All the obtained results can be used for calculations of the zeta potential and charge of a single nanoparticle, as described in the Discussion section.

Another set of evaluations of the magnetic field influence on electrophysical processes of magnetic nanoparticles was carried out on kerosene-based magnetic fluid (Sample No. 2). However, the impact of an electric field with the same field strength as in the study of a water-based sample did not lead to a visible redistribution of the concentration of colloidal particles in Sample No. 2. Reducing the concentration of the original sample also did not change the situation. This may indicate the absence of a charge on the colloid particles based on kerosene stabilized by adsorption layers of oleic acid molecules. Note that this conclusion is inconsistent with the results of [39,40,41], in which it was concluded that colloidal particles may have a charge. It can be assumed that particles can acquire a charge when exposed to an electric field, as suggested in ref. [42]. In this case, this requires stronger fields than those used in the experiments. It is also possible that, as indicated in [44], only a small part of the particles is charged. This complicates the detection of changes in the colloid concentration at the electrode with sufficient clarity.

It turned out that with an increase in the electric field strength to sufficiently high values (above ~10⁵ V/m), electrohydrodynamic flows developed in the interelectrode space, the intensity and configuration of which depended on the geometry of the electrodes. Additionally, it was found that these flows can change with increasing field strength. When the fields reached a strength of about 250 kV/m, the flows became sufficiently developed, and regions with a higher concentration of the dispersed phase in the colloidal system were formed. Figure 8a shows photographs of the flows observed in an optical microscope and the resulting inhomogeneity of the colloid between the electrodes with a distance of 2 mm between them at a voltage of 1 kV (in cell I, shown in Figure 2a).

With the additional action of the magnetic field, the shape of the areas of increased concentration undergoes some changes (Figure 9b). Obviously, the latter is associated with the effect of a magnetic field on the interfaces between highly concentrated and ordinary phases. When the magnetic field was turned off, the contours of local regions with an increased concentration of particles were restored. The subsequent shutdown of the electric field led to the cessation of currents; however, areas of increased concentration persisted for some time (45–60 min). After sufficient time had elapsed, the concentration was equalized throughout the volume (Figure 9c).

Additional observations of structural changes during electrohydrodynamic flows were made in the same cell without the coverslip. It turned out that in the case where the surface of the layer was below the upper edges of the electrodes, the nature of the structural changes was the same as in the layer limited from above by a glass plate. However, when the volume of the interelectrode space was completely filled with the sample so that its free surface was at the level of the edges of the electrodes, the process changed significantly (Figure 10).

When the applied voltage reached 600 V/m, the flows developed right near the surface of the electrodes, which led to enlightenment in the space adjacent to them. At the same time, a more concentrated layer in the form of a dark band formed in the rest of the interelectrode space. A further increase in voltage to 350 kV/m led to the visible appearance of flows and the destruction of the dark layer into separate shapeless agglomerates (Figure 10b). The additional action of the magnetic field directed in the plane of the cell perpendicular to the electrodes led to the formation of structures elongated along the field from shapeless agglomerates within seconds (Figure 10c). Note that in the absence of an electric field, the formation of such a structure under the action of the same magnetic field did not occur.

Experiments on thin layers of Sample No. 2 enclosed between two glass plates with a conductive coating (cell II in Figure 2a) gave a much more pronounced visualization of the processes of formation of structural formations in magnetic fluid. In this case, the development of electrohydrodynamic flows led to the formation of a labyrinth structure near the glass surfaces. Figure 11a shows a labyrinth structure arising under the action of an electric field (195 kV/m) and its transformation after the additional application of a magnetic field (900 A/m) directed along the plane of the cell (Figure 11b, Supplementary Video S1). The transformation of the labyrinth structures into elongated forms under the influence of an in-plane magnetic field proved that the nature of the observed effects originated from the local concentration of colloidal nanoparticles in magnetic fluid as a result of electrohydrodynamic flows.

The morphology of the formed labyrinth structures was dependent on the thickness of the sample. As can be seen in Figure 12, thin samples formed more detailed structures, while thicker colloid layers showed a lower degree of order under the same conditions.

The formed labyrinth structures were dynamic objects, with their parameters dependent on the experimental temperature. Thus, an increase in temperature led to an elongation of the labyrinth stripes, as can be seen in Figure 13 and Supplementary Videos S2–S4.

As mentioned above, the formation of such a structure has been observed in several works [45,46,47], while the mechanism for the formation of highly concentrated labyrinth-type regions remains unclear to date. It is known from the literature that such structures appear when a certain threshold value of the electric field strength is reached, which depends on the conductivity of the medium.

To test this conception, additional experiments were carried out by increasing the electrical conductivity of Sample No. 2 from the original test. To do this, 5 mg of iodine per 10 mL of the sample was added to the system according to protocols published earlier [43,58]. This operation led to an increase in the electrical conductivity value from γ = 1.2 × 10⁻⁶ S/m to γ = 1.4 × 10⁻⁶ S/m. This manipulation shifted the threshold value of the field strength corresponding to the appearance of a labyrinth structure from E = 378 kV/m to E = 167 kV/m. This parameter was also inversely dependent on the temperature of the experiment due to an increase in the electrical conductivity of the dispersion medium (Figure 14). Indeed, as the temperature rises, the electrical conductivity of the dispersion medium increases according to the Frenkel formula [42]:

$$\gamma =\frac{1}{T}\exp \left(-\frac{T_0}{T}\right),$$

(1)

which contributes to the development of flows at lower values of the electric field strength.

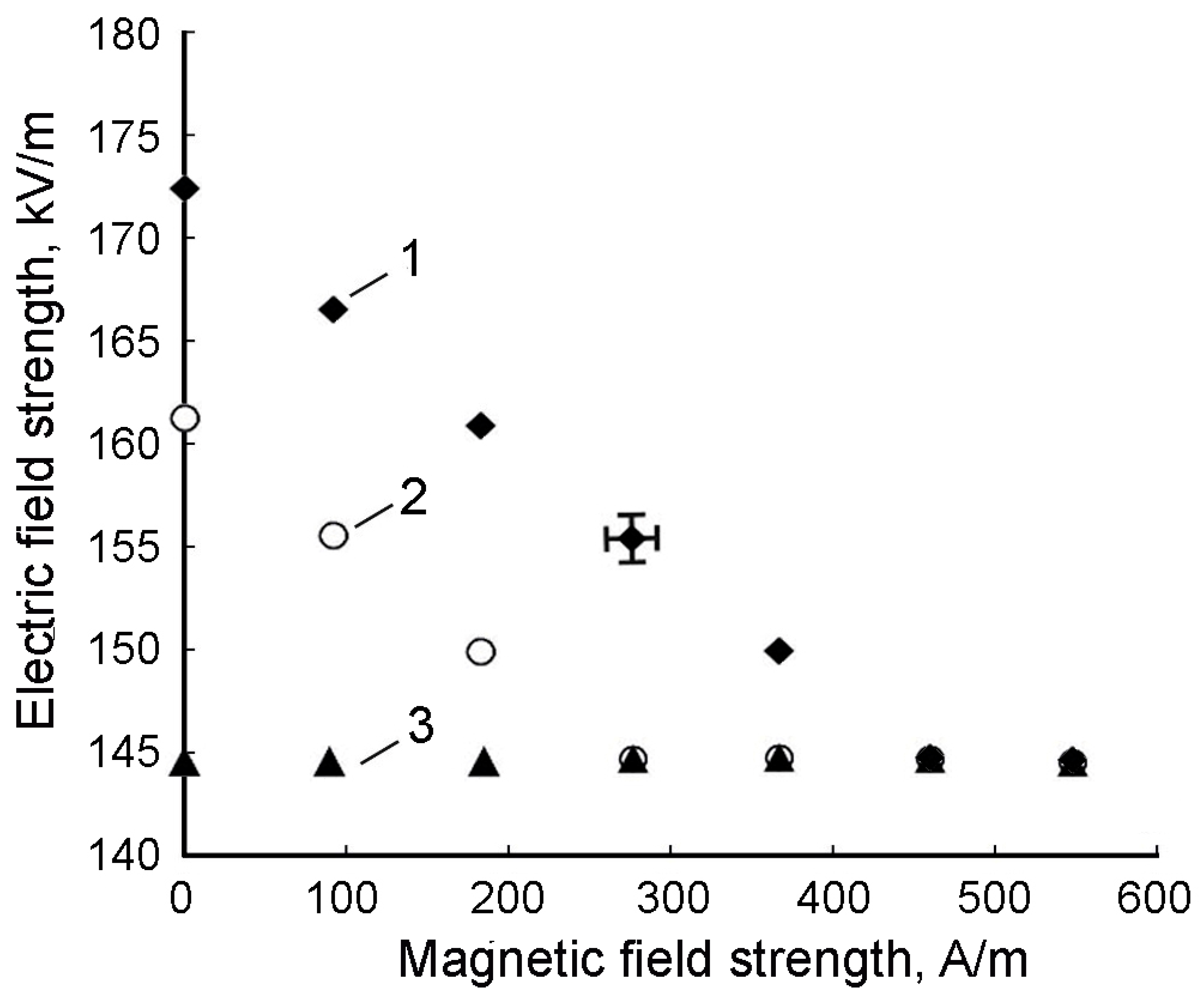
It was also found that a magnetic field previously applied to the cell led to a decrease in the value of the threshold voltage at which a labyrinthine structural lattice appeared. Figure 15 shows the dependences of the threshold value of the electric field strength on the magnetic field strength at different temperatures (the magnetic field was directed perpendicular to the electric field, and the thickness of the sample layer was 18 μm).

As can be seen from Figure 15, when the temperature reached 50–60 °C, the threshold value of the electric field strength corresponding to the appearance of a labyrinth structure practically ceased to depend on the additional effect of the magnetic field. It should be noted that the dependencies shown in Figure 15 are in conflict with similar dependencies given in ref. [47]. It turned out that their agreement in the studied range of magnetic field strengths is observed only with an increase in the thickness of the studied sample layer above 35 μm. In the course of the research, it was also found that the formation of a labyrinth structure occurs over a period of time, the value of which also depends on temperature and on the intensity of an additionally applied magnetic field. Graphs of these dependencies are shown in Figure 16a,b, respectively.

4. Discussion

As is known, the phenomenon of electrophoresis can be considered from two different points of view, which ultimately lead to the same results for electrophoresis rate estimation [59]. Thus, the first approach is connected with the direct analysis of the motion of a charged particle with the action of a force on it from the electric field. The particle motion equation in this case can be written as:

$$m\frac{dv}{dt}=qE-6\pi \eta va,$$

(2)

where m is electrophoretic mobility, v is velocity, a is the radius of the particle, and η is the viscosity of the medium around the particle. The influence of resistance forces leads to the establishment of a constant value of the velocity of the particle $\frac{dv}{dt}=0$, the value of which can be expressed as follows [59]:

$$v=\frac{qE}{6\pi a\eta },$$

(3)

where q is the charge of the particle and E is the electric field strength.

Another way to describe the process of electrophoresis is related to the direct consideration of the double electric layer, while the phenomenon of electrophoresis is considered the opposite of electroosmosis. In this case, the rate of the electrophoresis can be described as [59]:

$$v=\frac{{\epsilon }_0\epsilon \zeta E}{\pi \eta },$$

(4)

where ε is medium permittivity and ζ is the zeta potential. This expression was further improved by Hückel, taking into account the correction for electrophoretic braking [59]:

$$v=\frac{2{\epsilon }_0\epsilon \zeta E}{3\pi \eta },$$

(5)

A comparison of Equations (3) and (5) allows us to find an expression for calculating the electric charge of a colloidal particle [1]:

$$q=4{\epsilon }_0\epsilon \zeta a,$$

(6)

It should be noted that the process of electrophoresis in magnetic fluids, in contrast to other colloidal systems, may have features associated with a stronger interaction of particles due to the forces of magnetic interaction of single-domain nanoparticles. Previously, the study of electrophoresis in magnetic fluids was carried out using a colloid based on kerosene [44]. In this work, the dependence of the concentration of particles at the electrode on time was obtained by taking into account the diffusion of particles using the equation for the particle flux caused by electrophoresis. At the same time, the distribution of the concentration of nanoparticles in colloids between the electrodes is not continuous, as follows from the results of our studies for the water-based magnetic fluid.

Experimental measurements of the electrophoretic mobility of water-based magnetic fluid (Figure 7) demonstrated that the electrophoretic velocity of nanoparticles had a linear dependence on the applied force, which is in good agreement with Equations (3) and (5). These results indicated the legitimacy of the proposed method for the determination of the electrophoresis parameters in magnetic colloids. Using Equation (4) and transforming it into the form of:

$$\zeta =\frac{3\pi \eta v}{2{\epsilon }_0\epsilon E},$$

(7)

gave a zeta potential value of ~+15 mV, and the charge of a single colloidal nanoparticle calculated by Equation (6) was valued at q = 2.5 × 10⁻¹⁸ C. These values were two times lower than the experimental data of the zeta potential obtained by the DLS technique and the calculated single nanoparticle charge, which were +30 mV and q = 5 × 10⁻¹⁸ C, respectively. This difference originated from several factors: firstly, electrokinetic methods are known to have lower accuracy for determining the electrical parameters of colloidal particles compared to DLS [60], and secondly, since electrokinetic studies were performed in thin colloid layers, the motion of particles may be affected by the influence of surface phenomena. Additionally, strong magnetic interactions between nanoparticles resulting in particle aggregation under experimental conditions may appear.

When the electrophoresis experiments were conducted in the presence of an inhomogeneous magnetic field, the electrophoretic mobility of the magnetic fluid was suppressed and compensated by the oppositely directed magnetic drag force. The compensation condition is determined by Equation (8):

$$q\overrightarrow{E}=\left(\overrightarrow{m}\nabla \right)\overrightarrow{B},$$

(8)

where m is the magnetic moment of the colloidal particle and q is the charge. Equation (9) can be used for a rough estimation of the magnetic moment of a colloidal particle under compensation conditions. If magnetic and electric forces are projected in the direction of the cell radius, Equation (9) is transformed into the next form:

$$q\frac{U}{\mathsf{\Delta }r}=m\frac{\partial B}{\partial r}\cos a,$$

(9)

where Δr is the distance between the electrodes, m is the magnetic moment of the particle, q is its charge, and a is the angle between the directions of the magnetic moment and the magnetic field. The presence of an angle between the direction of the field and the moment of the particle is associated with the disorienting effect of thermal motion. As is known, the average value of $〈\cos a〉$ depends on the ratio of the energy of a particle in a magnetic field to its thermal energy and can be determined by the Langevin function: $〈\cos a〉=L\left(\frac{mB}{kT}\right)$. In sufficiently strong magnetic fields, this value is close to unity. To facilitate calculations, this condition can be considered acceptable, the use of which will not lead to an error greater than the measurement error. In calculations, we used the value of the charge found from the results of the study of dynamic light scattering, and the value $\frac{\partial B}{\partial r}$ was determined experimentally; its value along the distance between the electrodes remained constant at 328 mT/m. The value of the magnetic moment calculated in this way turned out to be m = 6.4 × 10⁻¹⁶ A/m². Assuming that m = M_sV, where M_s is the magnetization of the material, the volume of the particle and its diameter were estimated. According to calculations, the particle diameter was about 61 nm, which exceeds the diameter of the nanocrystallite determined by electron microscopy but correlates with the diameter measured by the DLS technique (Supplementary Figure S3). As follows from the above, one of the reasons for the error may be the difficulty of establishing homogeneity in the sample layer when determining the voltage on the electrodes, corresponding to the compensation of magnetic and electrical forces.

In this regard, the determination of the magnetic moment of a colloidal particle based on the results of the simultaneous action of an electric and magnetic field was carried out in a different way, without compensating for their combined effect. For this, the particle velocity was determined at a voltage on the electrodes of 2.5 V, with and without additional exposure to a non-uniform magnetic field. In this case, the equations of particle motion can be represented as:

$$m\frac{d{v}_1}{dt}=qE-6\pi \eta v_{1}a,$$

(10)

$$m\frac{d{v}_2}{dt}=qE-m\frac{\partial B}{\partial r}\cos a-6\pi \eta v_{2}a,$$

(11)

Taking into account speed constancy, these equations can be transformed into:

$$m=\frac{6\pi \eta a\left(v_1{-v}_2\right)}{\frac{\partial B}{\partial r}\cos a},$$

(12)

Similar to Equation (9), it was assumed that the angle between the directions of the magnetic moment and the magnetic field was very small, so the value of cos a was assumed to be close to unity. The obtained value of the particle velocity under the influence of only an electric field was calculated as v₁ = 2.4 × 10⁻⁶ m/s, and with the simultaneous action of a magnetic and electric field, v₂ = 2 × 10⁻⁶ m/s. These data, as well as the value of the hydrodynamic radius a obtained by DLS, were used to calculate the magnetic moment of the particle using Equation (12). Its value turned out to be equal to 7.26 × 10⁻¹⁷ Am². Using this value to calculate the particle diameter gave d = 28.6 nm, which also, as in the previous calculations, exceeds the particle diameter determined using electron microscopy. This may be due to the formation of aggregates of colloidal magnetic particles under the influence of a sufficiently strong magnetic field, which was not taken into account in the calculations. In addition, a thin layer of highly concentrated colloid formed near the electrode surface can be affected by body forces. Thus, we can conclude that the effect of a magnetic field on the electrokinetic processes of magnetic colloids is associated not only with the effect of an inhomogeneous field on individual particles but also with a change in the structural state of the system. Note that a similar conclusion was reached earlier in ref. [61] when studying magnetophoresis in magnetic colloids based on kerosene.

An analysis of the above results allows us to conclude that the use of the simultaneous action of magnetic and electric forces on a colloidal particle has not yet made it possible to create more accurate results than the existing method for determining the moment of a particle and its size. It can be assumed that this is due to the insufficient accuracy of the electrokinetic method underlying the research. However, the use of this idea when using other methods for determining the speed of colloidal motion (for example, the method of dynamic light scattering) can be more productive.

Similar experiments with a kerosene-based magnetic fluid (Sample No. 2) had a large effect on the electrophoretic mobility of the dispersed nanoparticles due to the low conductivity of the medium. Visible flows appeared only with the application of electric potentials that were 10⁶ fold higher than those for deionized water, which are 250 kV/m and 0.1 V/m, respectively. This ratio is in correlation with the difference in electric conductivity of the dispersion media, which are 10 pS and 1 mS for kerosene and deionized water, respectively. The appearance of structural transformations in Sample No. 2 in an electric field was associated with the developing electrohydrodynamic instability. The development of electrohydrodynamic flows in the colloids is facilitated by an increase in the conductivity of the dispersion medium and an increase in the electric field. This can be associated with the process of ion formation due to the near-electrode reaction (injection) at the cathode. It was concluded in ref. [43] that the increase in the conductivity of a kerosene-based magnetic fluid stabilized with oleic acid is due to the formation of conductive ions from oleic acid molecules in dissociation and electrochemical processes.

It should be noted that earlier, the formation of similar structures as a result of the action of electrohydrodynamic flows was observed in a number of works [62,63,64,65]. At the same time, more attention was paid to colloids on aqueous bases. The emergence of electrohydrodynamic flows in such systems was associated with injection processes near the electrodes, and the formation of a structure was associated with electrokinetic and hydrodynamic interactions between micron particles [65,66]. Structural formations of particles in these works, as a rule, were observed near the surface of the electrodes; it was assumed that this was due to the deposition of charged particles on the electrodes. However, later, similar phenomena were discovered in colloidal systems with uncharged particles, which did not allow us to draw final conclusions regarding the mechanisms of these phenomena.

It should be noted that the colloids studied by us are weakly conducting media, and no electrokinetic processes are observed in them when exposed to an electric field. This was the basis, as mentioned above, for concluding that the particles of such colloids have no charge. However, in contrast to the previously studied colloidal systems in the works referred to above, the particles of magnetic colloids have a magnetic moment, which significantly enhances their interaction. Such systems are stabilized by shells of long-chain oleic acid molecules adsorbed on the particle surface. The energy of the repulsive forces of such shells in fractions can be represented as Equation (13) [1]:

$$U_1=2\pi d^2\varphi \left(2-\frac{r+d}{\varsigma }ln\left(\frac{d+2\varsigma }{r+d}\right)-\frac{r}{\varsigma }\right),$$

(13)

where d is the diameter of the magnetite particle, ϕ is the concentration of polymer molecules on the surface of the magnetite particle, and ς is the length of the polymer molecule.

The attraction of dispersed particles is carried out due to van der Waals forces and magnetic dipole interaction forces. The attraction energy due to van der Waals forces in kT units varies inversely with the square of the distance between particles [67]:

$$U_2=\frac{A}{12kT}\left[\frac{d^2}{{(d+r)}^2}+\frac{d^2}{{(d+r)}^2-d^2}+2ln\left(1-\frac{d^2}{{(d+r)}^2}\right)\right],$$

(14)

where A is Hamaker’s constant and k is Boltzmann’s constant.

For the dipole-dipole interaction energy, the expression given in ref. [68] can be used:

$$U_3=-\frac{1}{3}{\left(\frac{{\mu }_0{m}^2}{4\pi kT{d}^3}\right)}^2{\left(\frac{d}{r+d}\right)}^6+\frac{7}{450}{\left(\frac{{\mu }_0{m}^2}{4\pi kT{d}^3}\right)}^4{\left(\frac{d}{r+d}\right)}^{12},$$

(15)

where m is the magnetic moment of the particle.

The calculation of the potential curve of the interaction of colloidal particles, taking into account these expressions for a magnetic fluid based on kerosene, was previously carried out in ref. [69]. It has two minima and a potential barrier that are characteristic of the interaction of colloidal particles (Figure 17). It should be noted that the depth of the secondary minimum, which corresponds to a reversible aggregation, does not exceed the thermal motion energy.

The attraction energy of particles in an electric field can increase due to the induction of electric moments in them, which should be taken into account when analyzing the total interaction energy. At the same time, the calculation of the interaction energy of such dipoles, carried out in ref. [69], gave a value an order of magnitude lower than the energy of the magnetic dipole interaction. As a result, taking it into account practically does not affect the shape of the presented potential curve of the interaction of colloidal particles. It is obvious that the causes of the detected occurrence of regions with an increased concentration of particles are associated with the occurrence of flows and their hydrodynamic effect on the behavior of particles. Thus, colloidal particles can be forced out of the developing flows and form areas of increased concentration between two closely spaced flows of the dispersion medium. In this case, under certain conditions associated with the design of the measuring cell, due to a decrease in the distance between the particles due to such a hydrodynamic effect, their interaction energy increases, sufficient to deepen the secondary minimum of the potential interaction curve to its commensurability with the thermal motion energy kT. As a result, the reversible formation of a new, more concentrated phase occurs, presumably at the surface of the cell electrodes. However, more specific mechanisms for the formation of such structures in a magnetic colloid subjected to electrohydrodynamic flows still remain unclear.

5. Conclusions

Thus, in the present work, the process of electrophoresis in thin layers of water- and kerosene-based magnetic fluids was studied. It was found that during the deposition of single-domain particles on the electrode, due to the significant value of their magnetic dipole interaction, an interlayer of a highly concentrated colloid phase is formed. The discovered phenomenon was identified as a phase transition in a system of magnetic dipole particles. It has been established that after a certain period of time, the growth of the near-electrode layer of increased concentration stops while the remaining part of the interelectrode space becomes transparent. This served as the basis for the proposal of an original method for estimating the electrophoretic velocity of colloidal particles. It was shown that the process of electrophoresis in magnetic colloids can be significantly affected by an inhomogeneous magnetic field. The features of the electrophoresis process under the simultaneous action of electric and inhomogeneous magnetic fields have been studied. Based on the results of such studies, an attempt was made to develop a new method for determining the magnetic moment and size of colloidal particles.

In addition, studies of structural changes in magnetic colloids on hydrocarbon bases under the influence of an electric field were continued. The effect of temperature and magnetic field on the dimensional parameter of the labyrinth structure that appears in thin layers (20–70 μm) of such colloids bounded by plate electrodes has been studied. It was demonstrated that the threshold value of the electric field strength corresponding to the appearance of a labyrinth structure and the time of such structuring was dependent on the temperature and strength of the preliminarily applied magnetic field. The dependence of the time of appearance of the labyrinth structure on the temperature and strength of the additionally applied magnetic field has been studied. It was shown that such structures are forming not only in the near-electrode space and thin films but in the entire volume of the cell with a thickness of several millimeters. The features of the appearance and transformation of such structures in a magnetic field in the presence of a free surface of the colloid layer are established. The fundamental role of electrohydrodynamic flows in the formation of structural formations in an electric field is pointed out, and the influence of a magnetic field on these processes is studied.