Influence of Mn Doping on Local Spin Moments and Stacking Fault Energies in Co(Mn) Alloys
Abstract
1. Introduction
1.1. Cobalt Phases
1.2. Density Functional Theory and Stacking Faults
1.3. Experimental Determination of Stacking Faults
2. Methodology
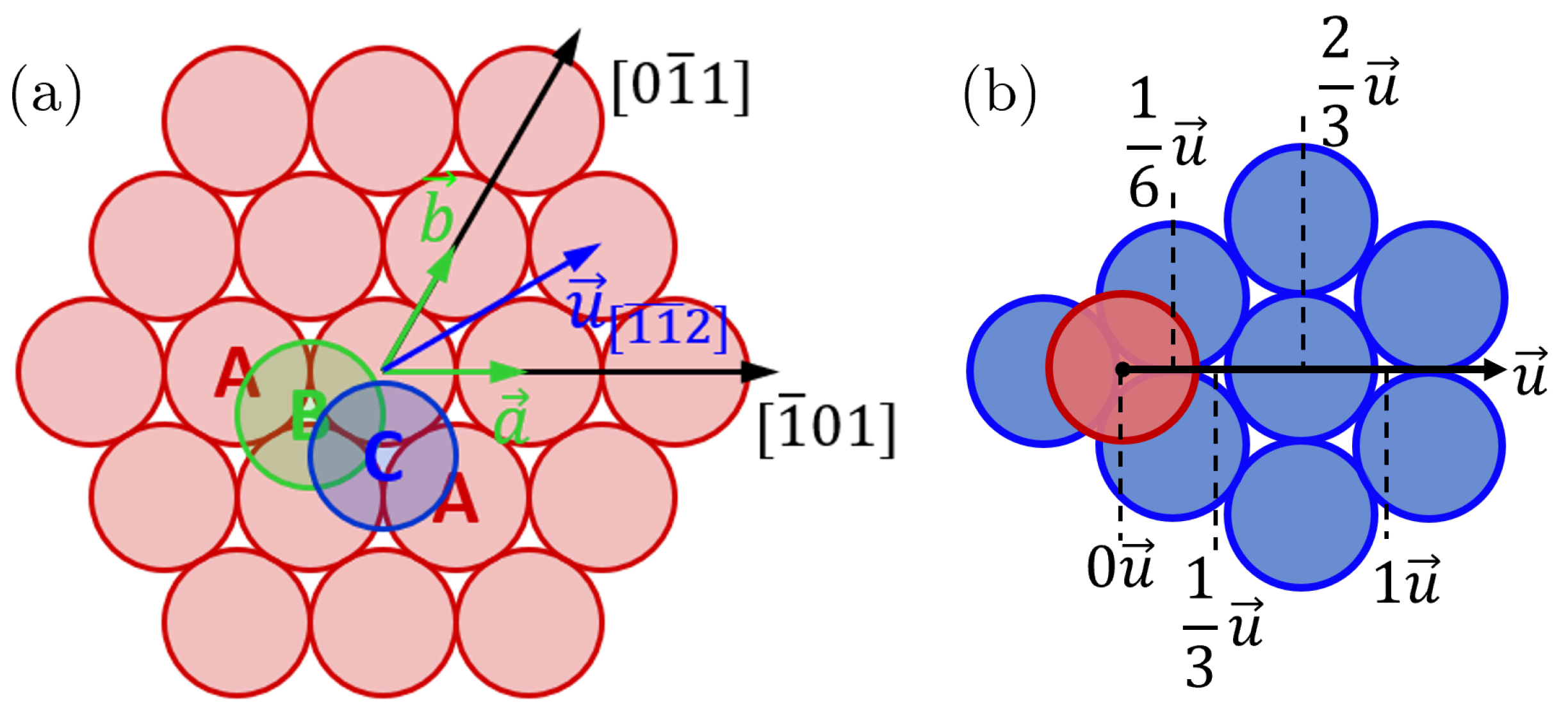
2.1. Supercell Design
2.2. DFT Parameters
2.3. Calculating SFE
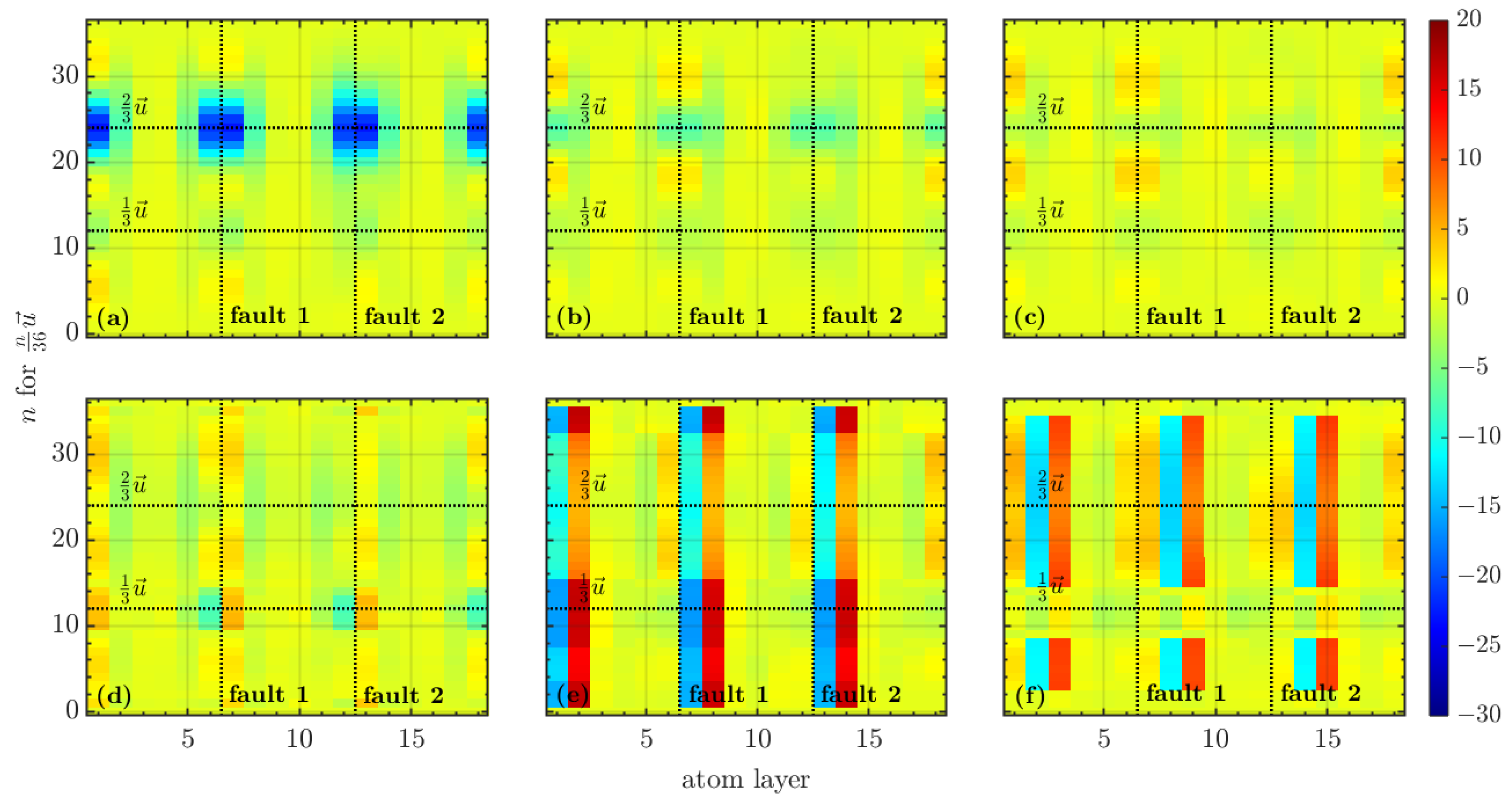
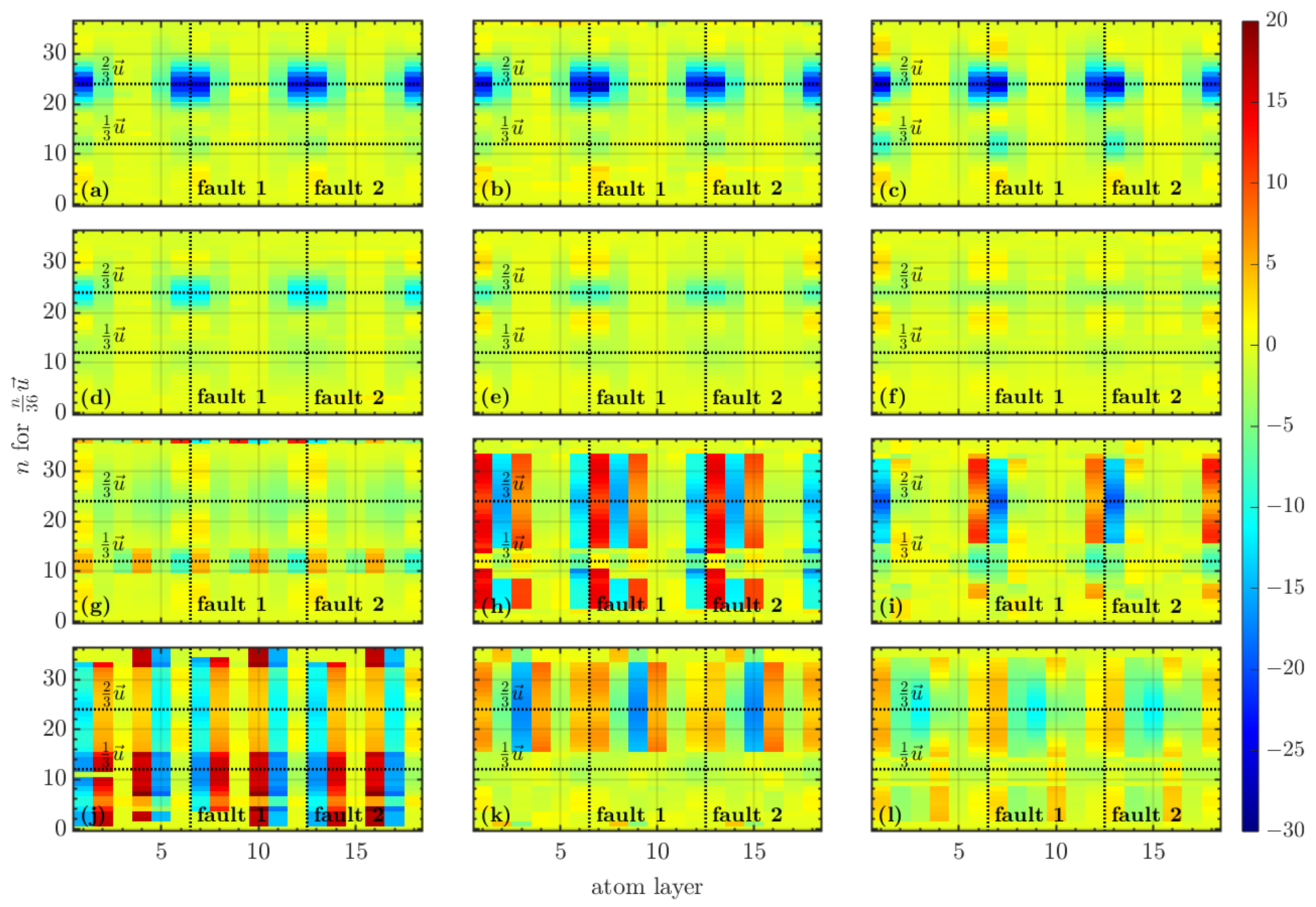
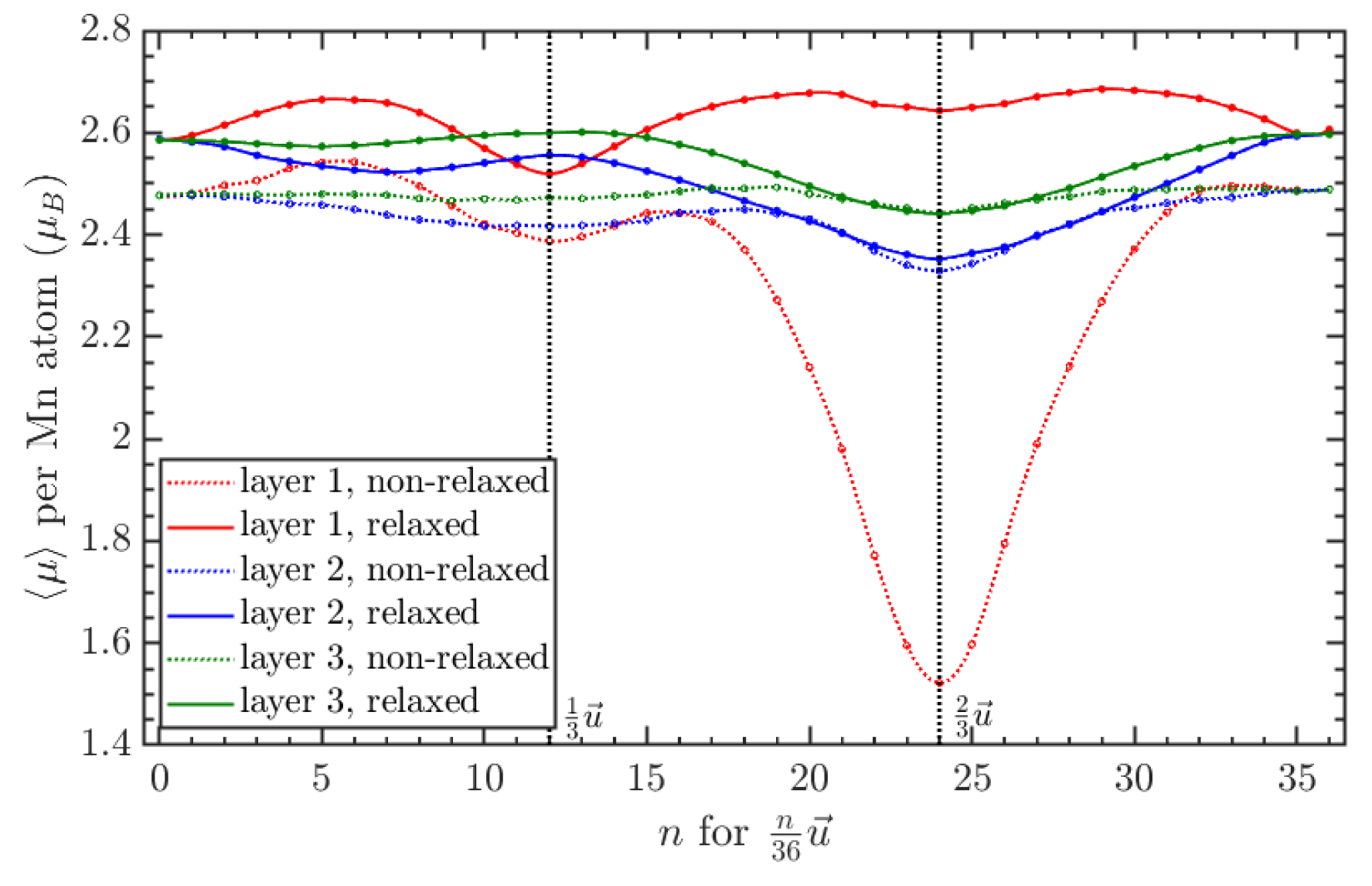
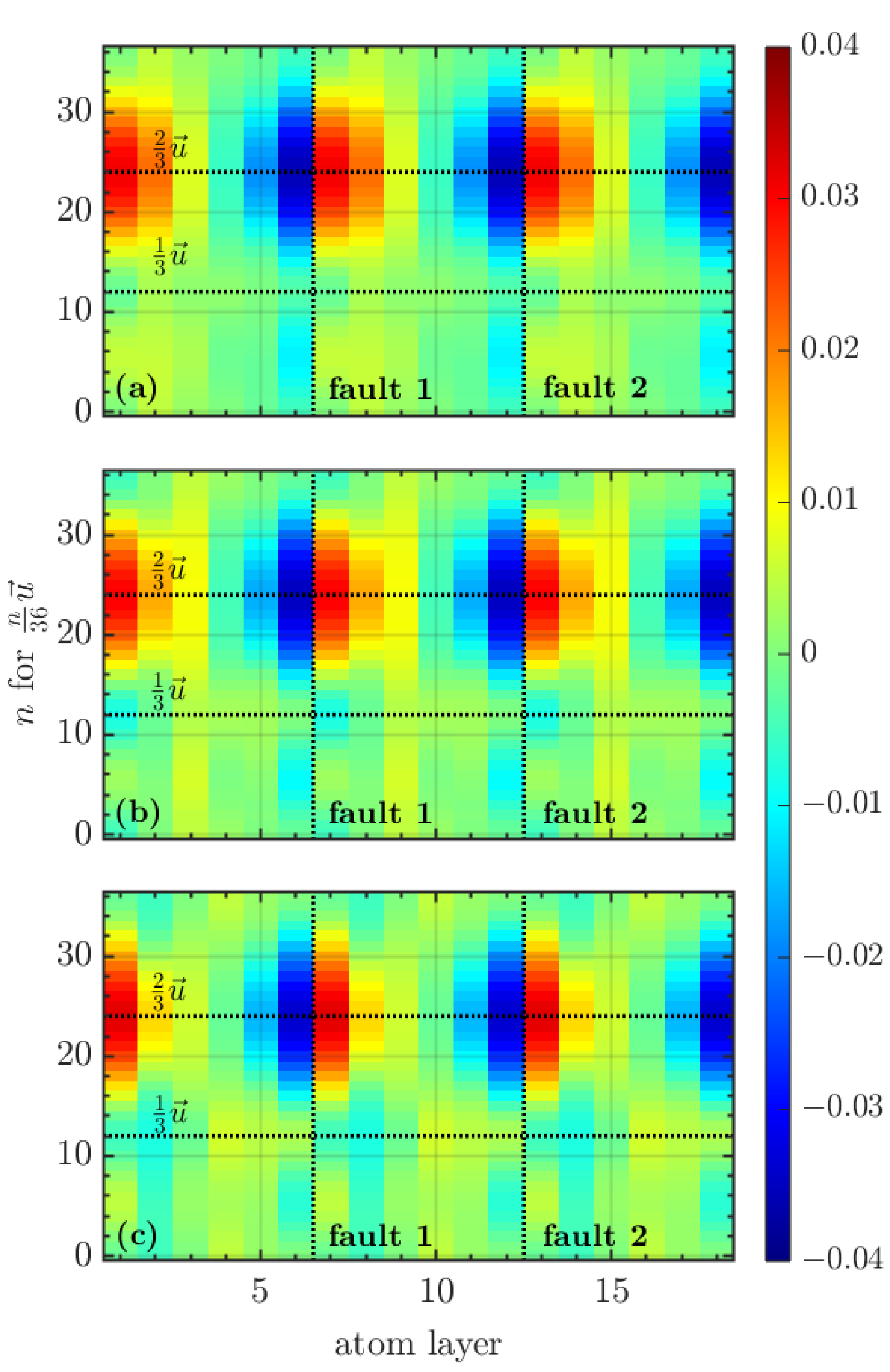
3. Results and Discussion
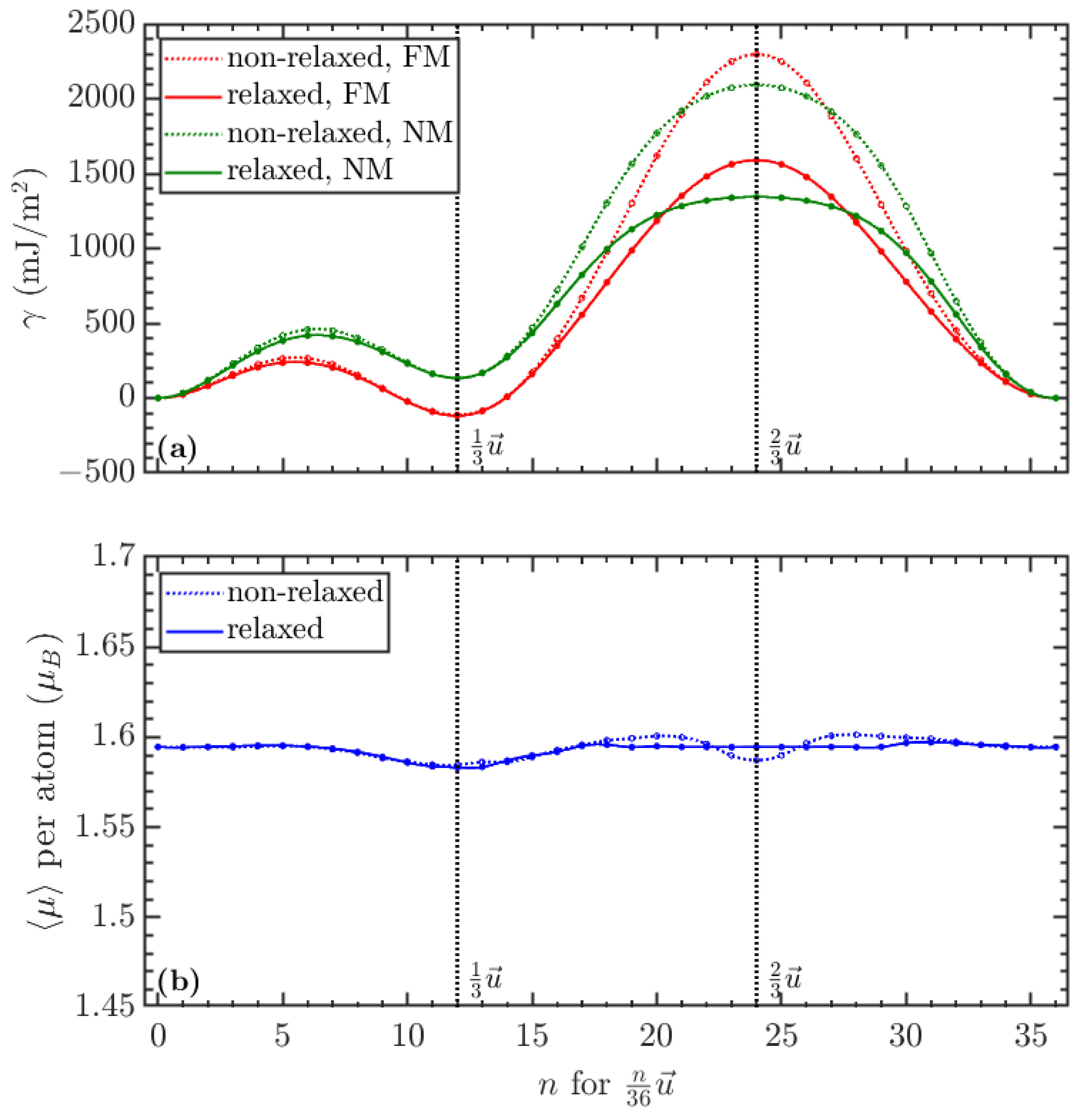
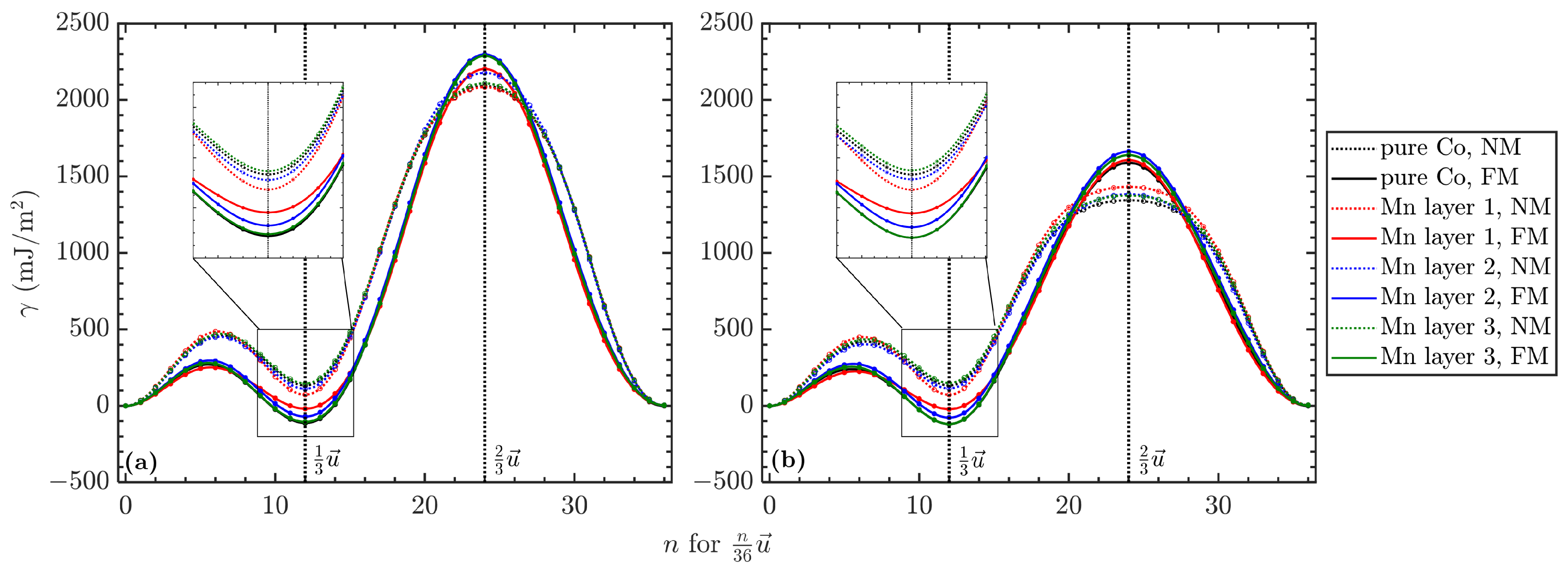
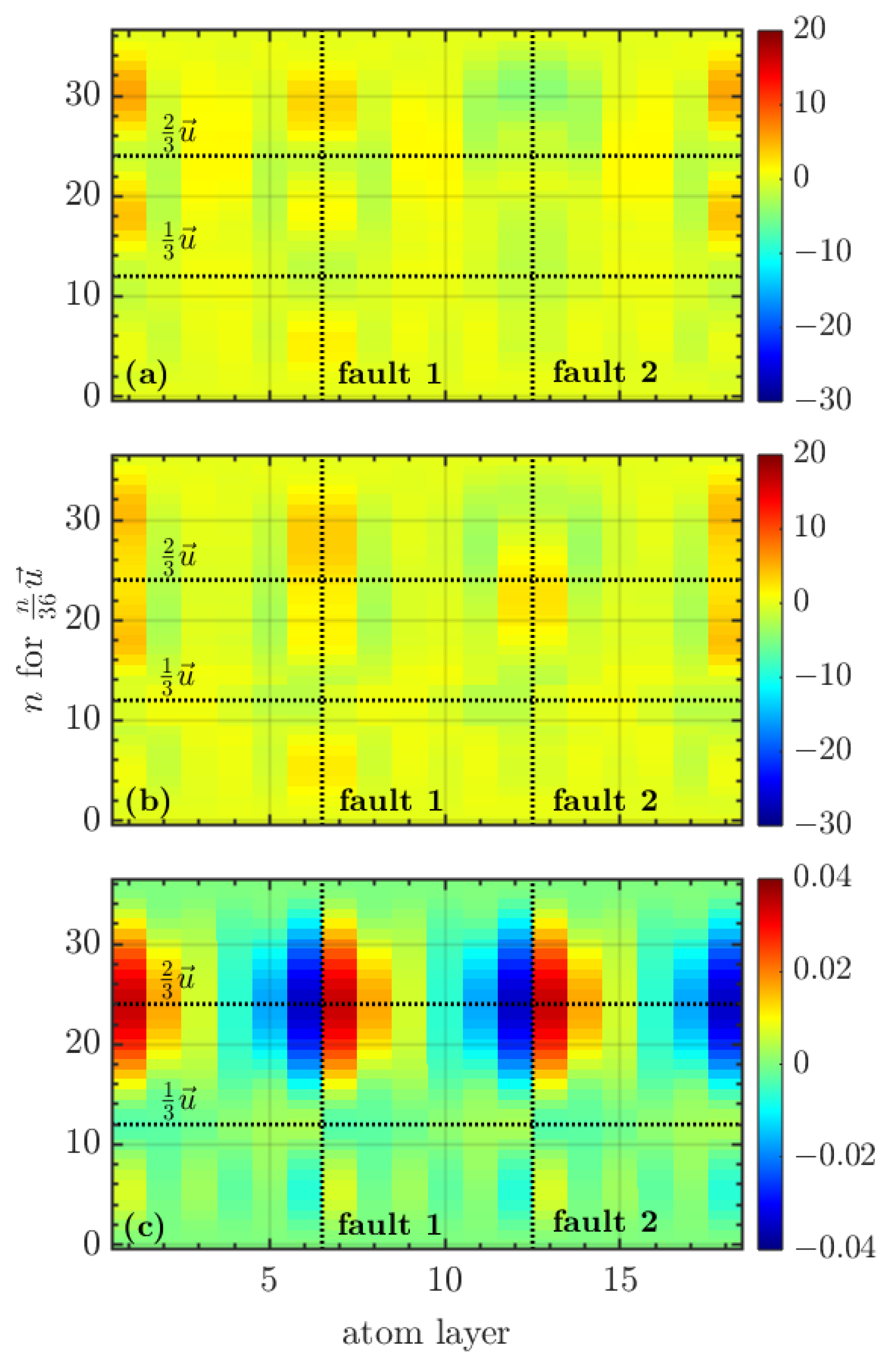
3.1. SFE Behavior
3.2. Magnetic Behavior
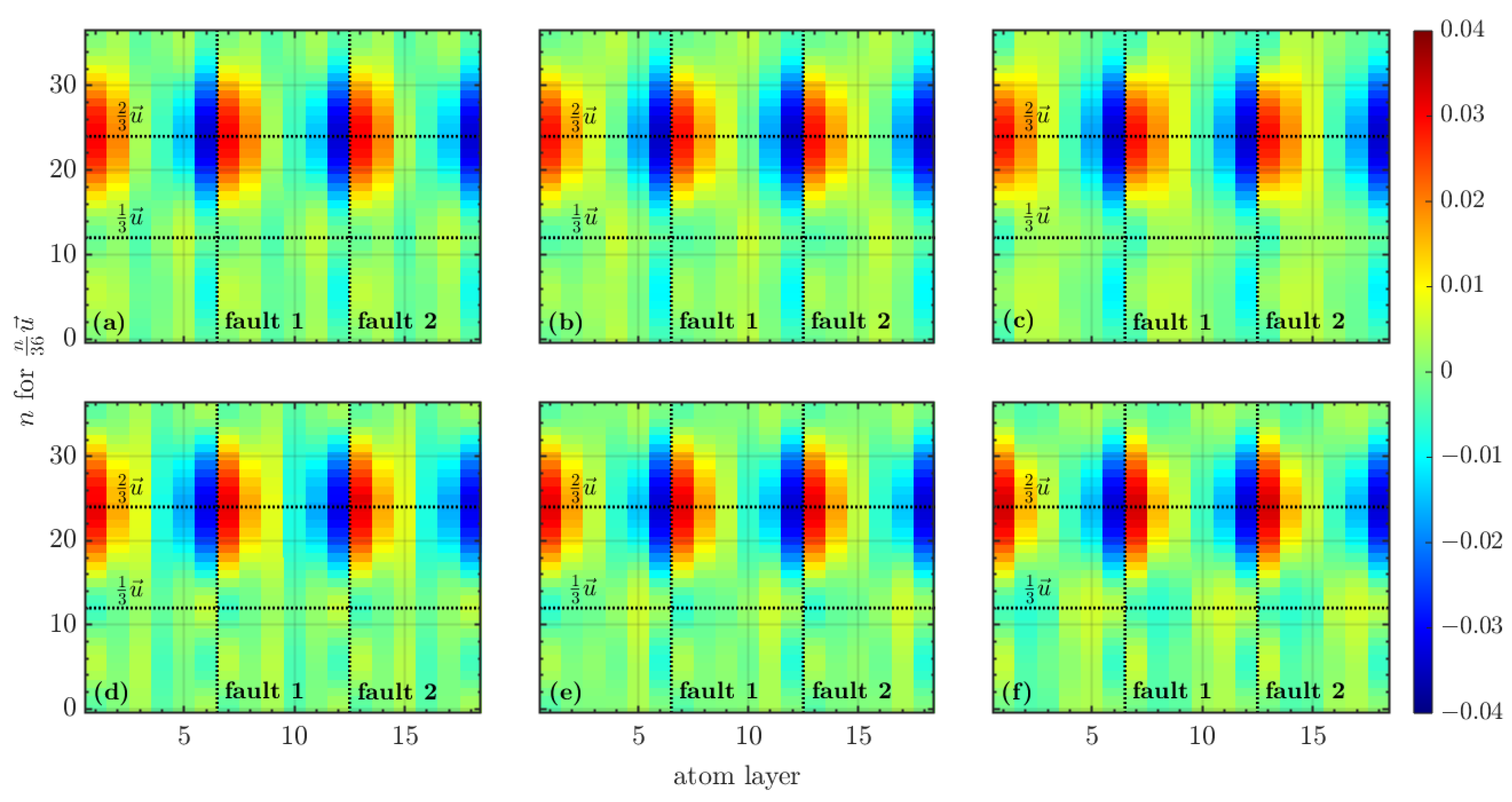
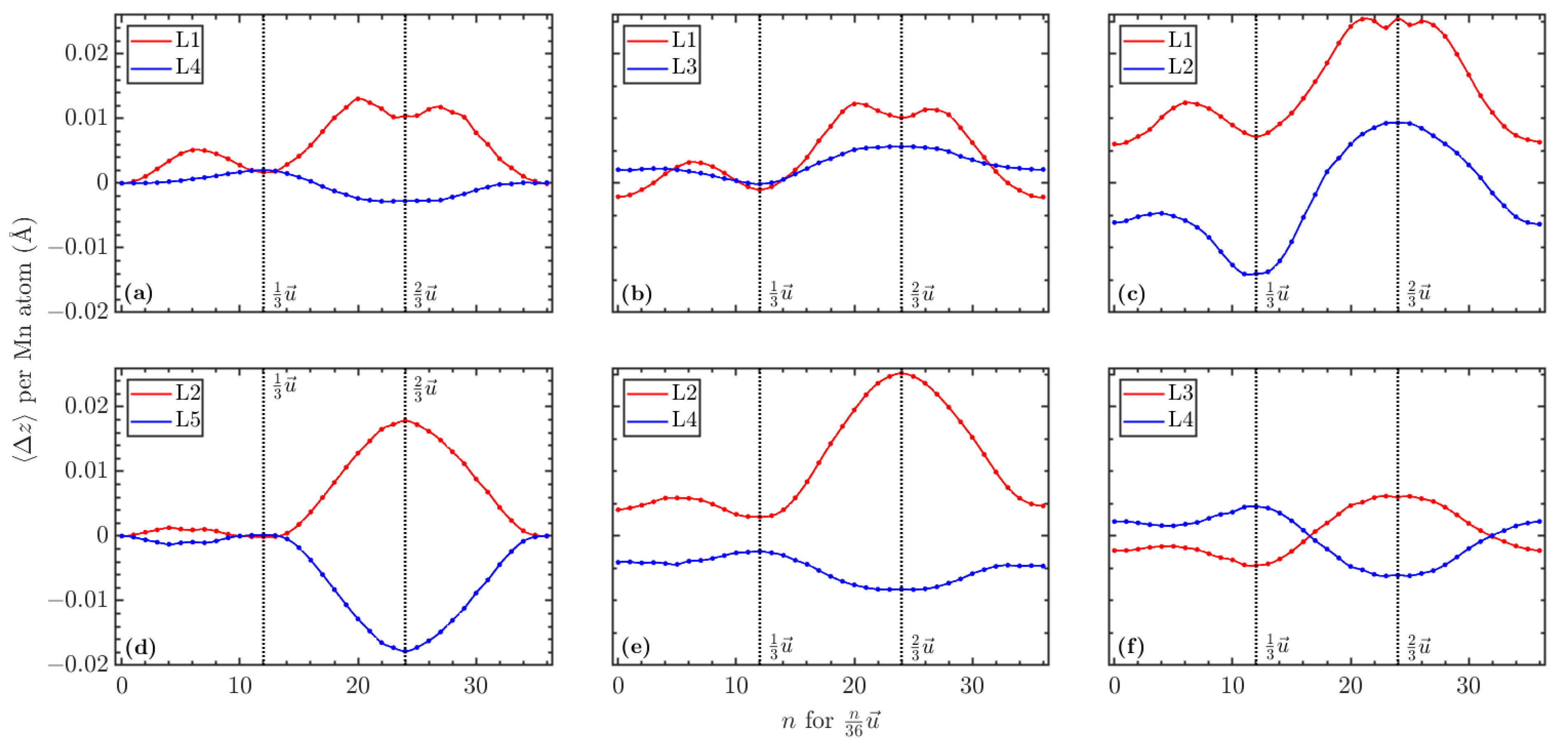
3.3. Relaxation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FM | Ferromagnetic |
| HCP | Hexagonal close-packed |
| FCC | Face-centered cubic |
| SFE | Stacking fault energy |
| NM | Nonmagnetic |
| DFT | Density functional theory |
| A(N)NNI | Axial (next-)nearest neighbor Ising |
| ISF | Intrinsic stacking fault |
| VASP | Vienna ab initio simulation package |
References
- Welstead, J.; Felder, J.L. Conceptual design of a single-aisle turboelectric commercial transport with fuselage boundary layer ingestion. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016; p. 1027. [Google Scholar] [CrossRef]
- Gutfleisch, O.; Willard, M.A.; Brück, E.; Chen, C.H.; Sankar, S.; Liu, J.P. Magnetic materials and devices for the 21st century: Stronger, lighter, and more energy efficient. Adv. Mater. 2011, 23, 821–842. [Google Scholar] [CrossRef] [PubMed]
- McHenry, M.; Laughlin, D. Nano-scale materials development for future magnetic applications. Acta Mater. 2000, 48, 223–238. [Google Scholar] [CrossRef]
- Herzer, G. Nanocrystalline soft magnetic alloys. Handb. Magn. Mater. 1997, 10, 415–462. [Google Scholar] [CrossRef]
- Leary, A.M.; Ohodnicki, P.R.; McHenry, M.E. Soft magnetic materials in high-frequency, high-power conversion applications. JOM 2012, 64, 772–781. [Google Scholar] [CrossRef]
- Srivastava, A.; Cole, K.; Wadsworth, A.; Burton, T.; Mewes, C.; Mewes, T.; Thompson, G.B.; Noebe, R.D.; Leary, A.M. Broadband characterization of stress induced anisotropy in nanocomposite Co74.6Fe2.7Mn2.7Nb4Si2B14. J. Magn. Magn. Mater. 2020, 500, 166307. [Google Scholar] [CrossRef]
- Koenig, A.G.; Tweddle, D.; Leary, A.; Noebe, R.; Mewes, C.; Mewes, T.; Thompson, G.B. Evaluating the effect of Mn composition on chemical partitioning in Co(78−x)Fe2MnxB14Si2Nb4 magnetic amorphous nanocomposites. J. Alloys Compd. 2021, 875, 159976. [Google Scholar] [CrossRef]
- Nakarmi, P.; Koenig, A.; Tweddle, D.; Cole-Piepke, K.; Leary, A.; Noebe, R.; Thompson, G.; Mewes, C.; Mewes, T. Magnetization dynamics of amorphous and nanocomposite CoFeMnNbSiB films with the addition of excess cobalt and boron. J. Magn. Magn. Mater. 2022, 564, 170029. [Google Scholar] [CrossRef]
- Byerly, K.; Ohodnicki, P.; Moon, S.; Leary, A.; Keylin, V.; McHenry, M.; Simizu, S.; Beddingfield, R.; Yu, Y.; Feichter, G.; et al. Metal Amorphous Nanocomposite (MANC) Alloy Cores with Spatially Tuned Permeability for Advanced Power Magnetics Applications. JOM 2018, 70, 879–891. [Google Scholar] [CrossRef]
- Owen, E.A.; Jones, D.M. Effect of Grain Size on the Crystal Structure of Cobalt. Proc. Phys. Soc. Sect. B 1954, 67, 456–466. [Google Scholar] [CrossRef]
- Stepanyuk, V.; Zeller, R.; Dederichs, P.; Mertig, I. Electronic structure and magnetic properties of dilute Co alloys with transition-metal impurities. Phys. Rev. B 1994, 49, 5157–5164. [Google Scholar] [CrossRef]
- Achmad, T.L.; Fu, W.; Chen, H.; Zhang, C.; Yang, Z.G. Effect of strain on the intrinsic stacking fault energy of fcc Co: A first-principles study. J. Mater. Sci. 2018, 53, 10217–10230. [Google Scholar] [CrossRef]
- Tian, L.Y.; Lizárraga, R.; Larsson, H.; Holmström, E.; Vitos, L. A first principles study of the stacking fault energies for fcc Co-based binary alloys. Acta Mater. 2017, 136, 215–223. [Google Scholar] [CrossRef]
- Iskounen, N.; Dubos, P.A.; Fajoui, J.; Coret, M.; Moya, M.J.; Girault, B.; Barrier, N.; Bruzy, N.; Hug, E.; Gloaguen, D. Experimental Investigation of Allotropic Transformation of Cobalt: Influence of Temperature Cycle, Mechanical Loading and Starting Microstructure. Metall. Mater. Trans. A 2021, 52, 1477–1491. [Google Scholar] [CrossRef]
- Zheng, G. Molecular dynamics and first-principles studies on the deformation mechanisms of nanostructured cobalt. J. Alloys Compd. 2010, 504S, S467–S471. [Google Scholar] [CrossRef]
- Limmer, K.; Medvedeva, J.; Van Aken, D.; Medvedeva, N. Ab initio simulation of alloying effect on stacking fault energy in fcc Fe. Comput. Mater. Sci. 2015, 99, 253–255. [Google Scholar] [CrossRef]
- de la Peña O’Shea, V.A.; Moreira, I.d.P.R.; Roldán, A.; Illas, F. Electronic and magnetic structure of bulk cobalt: The α, β, and ϵ-phases from density functional theory calculations. J. Chem. Phys. 2010, 133, 024701. [Google Scholar] [CrossRef]
- Moruzzi, V.; Marcus, P.; Schwarz, K.; Mohn, P. Ferromagnetic phases of bcc and fcc Fe, Co, and Ni. Phys. Rev. B 1986, 34, 1784–1791. [Google Scholar] [CrossRef]
- Men’shikov, A.; Takzeĭ, G.; Dorofeev, Y.; Kazantsev, V.; Kostyshin, A.; Sych, I. The magnetic phase diagram of cobalt-manganese alloys. J. Exp. Theor. Phys. 1985, 89, 1269–1279. [Google Scholar]
- Zhao, S.; Osetsky, Y.; Stocks, G.; Zhang, Y. Local-environment dependence of stacking fault energies in concentrated solid-solution alloys. NPJ Comput. Mater. 2019, 5, 13. [Google Scholar] [CrossRef]
- Hu, Q.M.; Yang, R. Basal-plane stacking fault energy of hexagonal close-packed metals based on the Ising model. Acta Mater. 2013, 61, 1136–1145. [Google Scholar] [CrossRef]
- Lu, G.; Kioussis, N.; Bulatov, V.V.; Kaxiras, E. Generalized-stacking-fault energy surface and dislocation properties of aluminum. Phys. Rev. B 2000, 62, 3099–3108. [Google Scholar] [CrossRef]
- Yan, J.; Zhang, Z.; Yu, H.; Li, K.; Hu, Q.; Yang, J.; Zhang, Z. Effects of pressure on the generalized stacking fault energy and twinning propensity of face-centered cubic metals. J. Alloys Compd. 2021, 866, 158869. [Google Scholar] [CrossRef]
- Achmad, T.L.; Fu, W.; Chen, H.; Zhang, C.; Yang, Z.G. Effect of solute segregation on the intrinsic stacking fault energy of Co-based binary alloys: A first-principles study. J. Alloys Compd. 2018, 748, 328–337. [Google Scholar] [CrossRef]
- Achmad, T.L.; Fu, W.; Chen, H.; Zhang, C.; Yang, Z.G. Effects of alloying elements concentrations and temperatures on the stacking fault energies of Co-based alloys by computational thermodynamic approach and first-principles calculations. J. Alloys Compd. 2017, 694, 1265–1279. [Google Scholar] [CrossRef]
- Achmad, T.L.; Fu, W.; Chen, H.; Zhang, C.; Yang, Z.G. First-principles calculations of generalized-stacking-fault-energy of Co-based alloys. Comput. Mater. Sci. 2016, 121, 86–96. [Google Scholar] [CrossRef]
- Dodaran, M.S.; Guo, S.; Khonsari, M.M.; Shamsaei, N.; Shao, S. A theoretical calculation of stacking fault energy of Ni alloys: The effects of temperature and composition. Comput. Mater. Sci. 2021, 191, 110326. [Google Scholar] [CrossRef]
- Muzyk, M.; Pakiela, Z.; Kurzydlowski, K. Generalized stacking fault energy in magnesium alloys: Density functional theory calculations. Scr. Mater. 2012, 66, 219–222. [Google Scholar] [CrossRef]
- Bleskov, I.; Hickel, T.; Neugebauer, J.; Ruban, A. Impact of local magnetism on stacking fault energies: A first-principles investigation for fcc iron. Phys. Rev. B 2016, 93, 214115. [Google Scholar] [CrossRef]
- Wu, X.; Wang, R.; Wang, S. Generalized-stacking-fault energy and surface properties for HCP metals: A first-principles study. Appl. Surf. Sci. 2010, 256, 3409–3412. [Google Scholar] [CrossRef]
- Su, Y.; Xu, S.; Beyerlein, I.J. Density functional theory calculations of generalized stacking fault energy surfaces for eight face-centered cubic transition metals. J. Appl. Phys. 2019, 126, 105112. [Google Scholar] [CrossRef]
- Denteneer, P.J.H.; van Haeringen, W. Stacking-fault energies in semiconductors from first-principles calculations. J. Phys. C Solid State Phys. 1987, 20, L883. [Google Scholar] [CrossRef]
- Cheng, C.; Needs, R.J.; Heine, V.; Churcher, N. Confirmation of an ANNNI-Like Model for Polytypism in SiC. Europhys. Lett. 1987, 3, 475. [Google Scholar] [CrossRef]
- Ning, X.; Ye, H. Experimental determination of the intrinsic stacking-fault energy of SiC crystals. J. Phys. Condens. Matter 1990, 2, 10223. [Google Scholar] [CrossRef]
- Aerts, E.; Delavignette, P.; Siems, R.; Amelinckx, S. Stacking Fault Energy in Silicon. J. Appl. Phys. 1962, 33, 3078. [Google Scholar] [CrossRef]
- Reed, R.; Schramm, R. Relationship between stacking-fault energy and x-ray measurements of stacking-fault probability and microstrain. J. Appl. Phys. 1974, 45, 4705. [Google Scholar] [CrossRef]
- Gallagher, P. The Influence of Alloying, Temperature, and Related Effects on the Stacking Fault Energy. Metall. Trans. 1970, 1, 2429–2461. [Google Scholar] [CrossRef]
- Liu, S.; Wu, Y.; Wang, H.; He, J.; Liu, J.; Chen, C.; Liu, X.; Wang, H.; Lu, Z. Stacking fault energy of face-centered-cubic high entropy alloys. Intermetallics 2018, 93, 269–273. [Google Scholar] [CrossRef]
- Murnaghan, F.D. Finite Deformations of an Elastic Solid. Am. J. Math. 1937, 59, 235–260. [Google Scholar] [CrossRef]
- Gholizadeh, H.; Draxl, C.; Puschnig, P. The influence of interstitial carbon on the γ-surface in austenite. Acta Mater. 2013, 61, 341–349. [Google Scholar] [CrossRef]
- Hirth, J.; Lothe, J. Theory of Dislocations, Reprint Edition. 1992. Available online: https://www.researchgate.net/publication/249656382_The_Theory_of_Dislocations (accessed on 4 May 2023).
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for Ab Initio Total-Energy Calc. Using a Plane-Wave Basis Set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1997, 77, 3685–3688. [Google Scholar] [CrossRef] [PubMed]
- Pulay, P. Convergence acceleration of iterative sequences. the case of scf iteration. Chem. Phys. Lett. 1980, 73, 393–398. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Chandran, M.; Sondhi, S. First-principle calculation of stacking fault energies in Ni and Ni-Co alloy. J. Appl. Phys. 2011, 109, 103525. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhu, Y.; Liao, X.; Horita, Z.; Langdon, T. Tailoring stacking fault energy for high ductility and high strength in ultrafine grained Cu and its alloy. Appl. Phys. Lett. 2006, 89, 121906. [Google Scholar] [CrossRef]







| (mJ/m) at ISF | ||||
|---|---|---|---|---|
| System | FM, Non-Rel. | FM, Rel. | NM, Non-Rel. | NM, Rel. |
| Co | −112.23 | −118.77 | 133.25 | 132.90 |
| 1Mn, layer 1 | −18.38 | −21.66 | 72.96 | 72.38 |
| 1Mn, layer 2 | −70.45 | −77.17 | 111.02 | 113.61 |
| 1Mn, layer 3 | −104.79 | −118.25 | 146.53 | 149.36 |
| 2Mn, layers 1,4 | −16.40 | −18.93 | 79.54 | 82.09 |
| 2Mn, layers 1,3 | −21.73 | −26.94 | 75.75 | 82.19 |
| 2Mn, layers 1,2 | 1.89 | −1.62 | 40.40 | 47.08 |
| 2Mn, layers 2,5 | −26.28 | −27.04 | 85.94 | 92.93 |
| 2Mn, layers 2,4 | −75.91 | −87.27 | 108.93 | 102.26 |
| 2Mn, layers 3,4 | −116.62 | −129.67 | 145.51 | 147.27 |
| Co [13] | – | −106.2 | – | – |
| Co [26] | – | 0.15 | – | – |
| Co (hcp) [15] | – | ≈75 | – | – |
| Co-9 at.% Mn [26] | – | 4.57 | – | – |
| Co-9 at.% Cr [13] | – | ≈−150 | – | – |
| Co-9 at.% Cr [26] | – | −25.78 | – | – |
| () per Atom at ISF | ||
|---|---|---|
| System | Non-Relaxed | Relaxed |
| Co | 1.585 | 1.583 |
| 1Mn, layer 1 | 1.605 | 1.608 |
| 1Mn, layer 2 | 1.608 | 1.614 |
| 1Mn, layer 3 | 1.611 | 1.614 |
| 2Mn, layers 1,4 | 1.633 | 1.641 |
| 2Mn, layers 1,3 | 1.639 | 1.630 |
| 2Mn, layers 1,2 | 1.544 | 1.560 |
| 2Mn, layers 2,5 | 1.635 | 1.642 |
| 2Mn, layers 2,4 | 1.602 | 1.604 |
| 2Mn, layers 3,4 | 1.561 | 1.579 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cole-Piepke, K.; Nakarmi, P.; Koenig, A.; Thompson, G.B.; Mewes, T.; Mewes, C.; Noebe, R.; Leary, A. Influence of Mn Doping on Local Spin Moments and Stacking Fault Energies in Co(Mn) Alloys. Magnetochemistry 2023, 9, 138. https://doi.org/10.3390/magnetochemistry9060138
Cole-Piepke K, Nakarmi P, Koenig A, Thompson GB, Mewes T, Mewes C, Noebe R, Leary A. Influence of Mn Doping on Local Spin Moments and Stacking Fault Energies in Co(Mn) Alloys. Magnetochemistry. 2023; 9(6):138. https://doi.org/10.3390/magnetochemistry9060138
Chicago/Turabian StyleCole-Piepke, Kayla, Prabandha Nakarmi, Alicia Koenig, Gregory B. Thompson, Tim Mewes, Claudia Mewes, Ronald Noebe, and Alex Leary. 2023. "Influence of Mn Doping on Local Spin Moments and Stacking Fault Energies in Co(Mn) Alloys" Magnetochemistry 9, no. 6: 138. https://doi.org/10.3390/magnetochemistry9060138
APA StyleCole-Piepke, K., Nakarmi, P., Koenig, A., Thompson, G. B., Mewes, T., Mewes, C., Noebe, R., & Leary, A. (2023). Influence of Mn Doping on Local Spin Moments and Stacking Fault Energies in Co(Mn) Alloys. Magnetochemistry, 9(6), 138. https://doi.org/10.3390/magnetochemistry9060138






