Exploring Crystal Structure, Hyperfine Parameters, and Magnetocaloric Effect in Iron-Rich Intermetallic Alloy with ThMn12-Type Structure: A Comprehensive Investigation Using Experimental and DFT Calculation
Abstract
:1. Introduction
2. Experimental Techniques
3. Results and Discussion
3.1. Crystal Structure
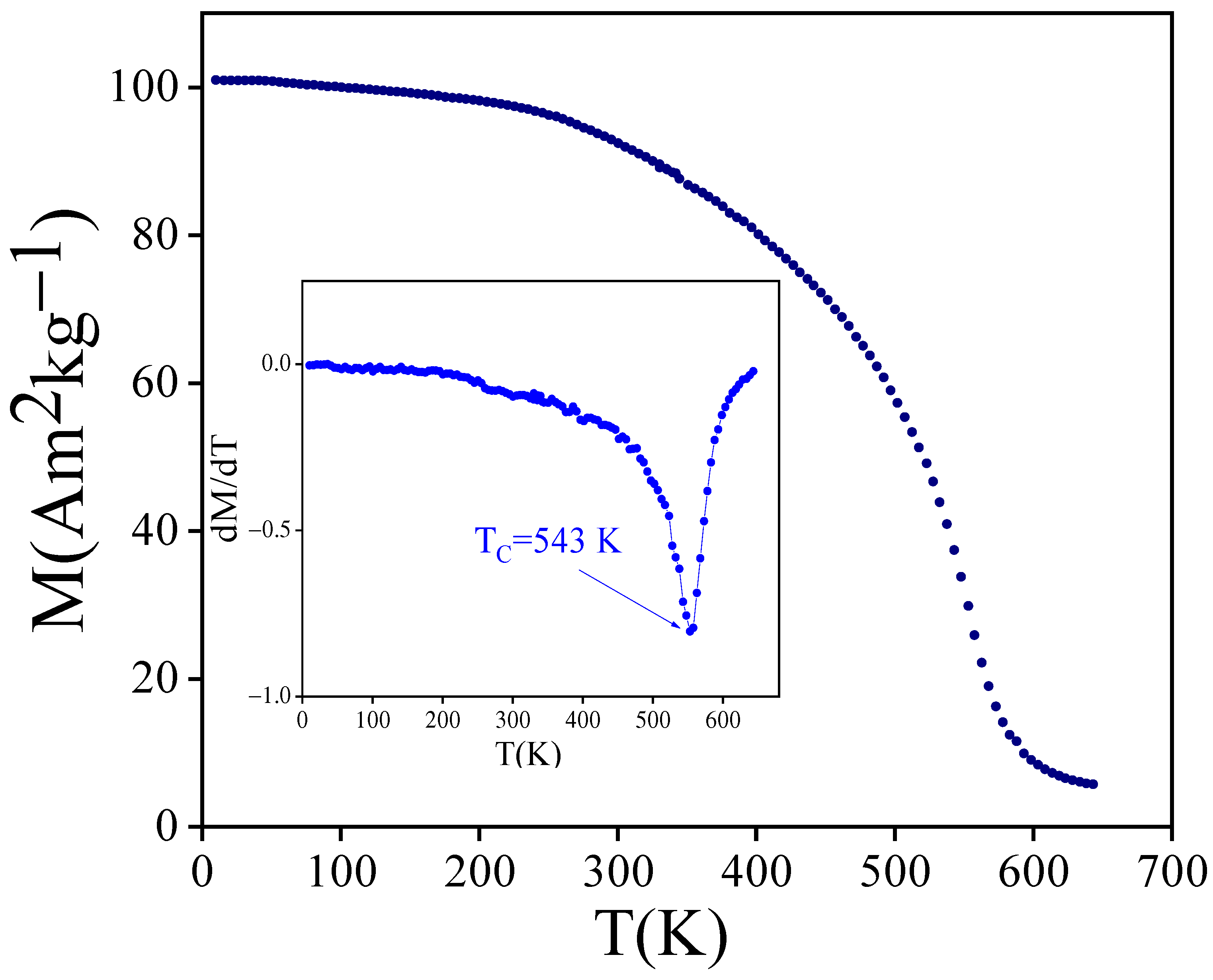
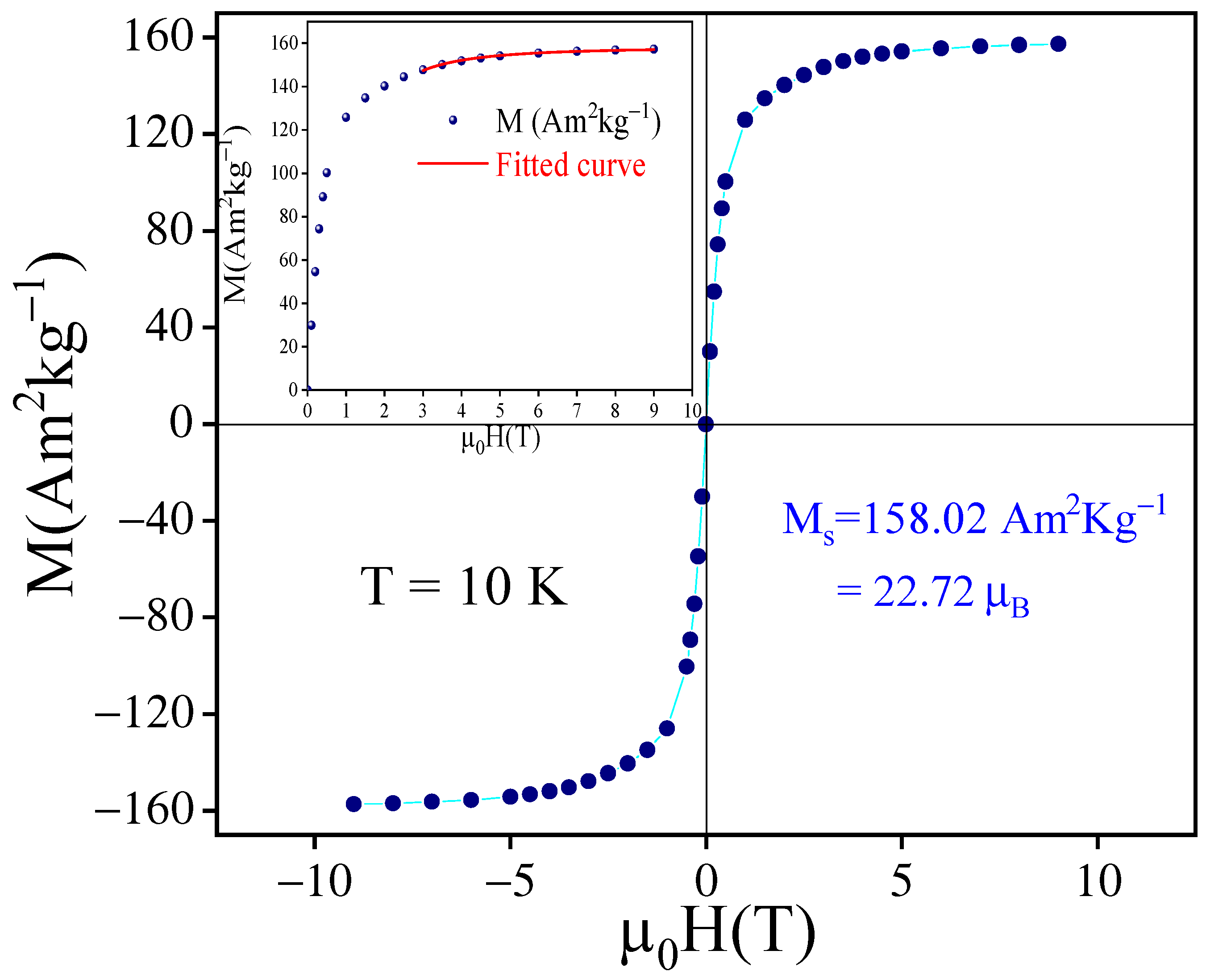
3.2. Intrinsic Magnetic Properties
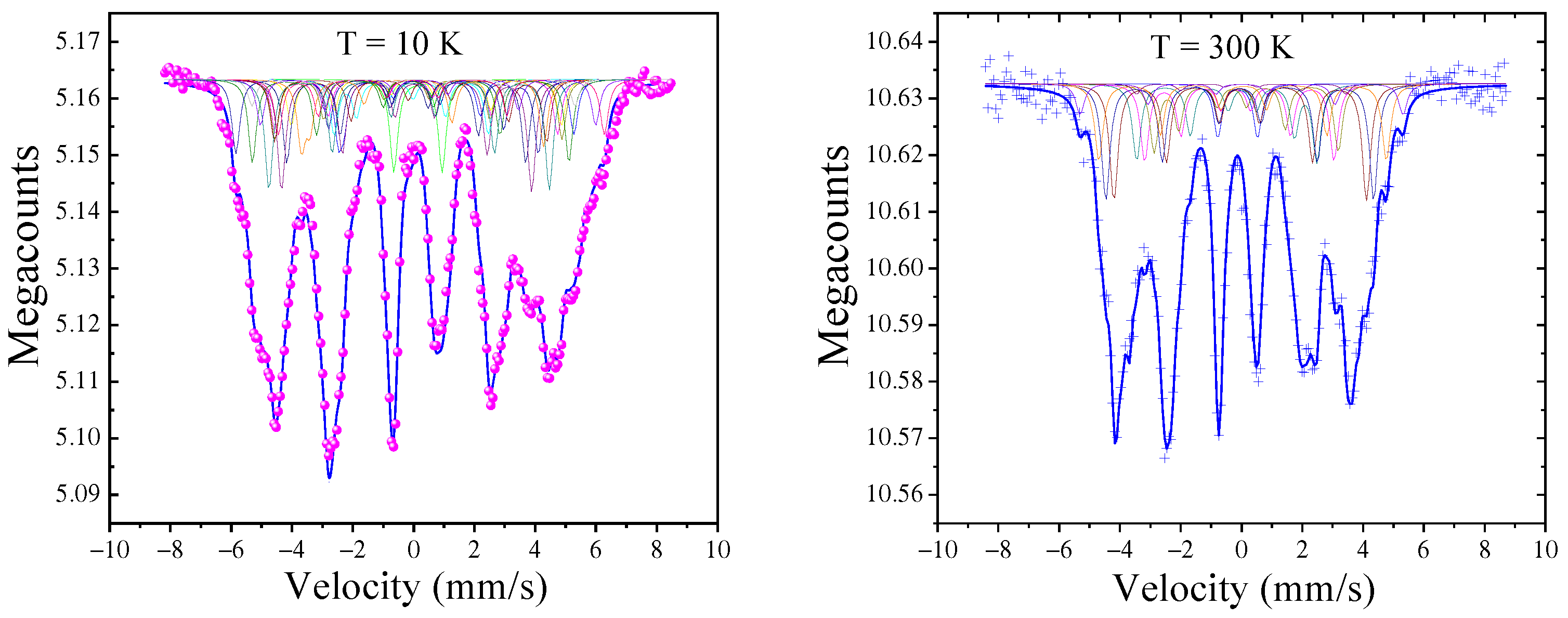
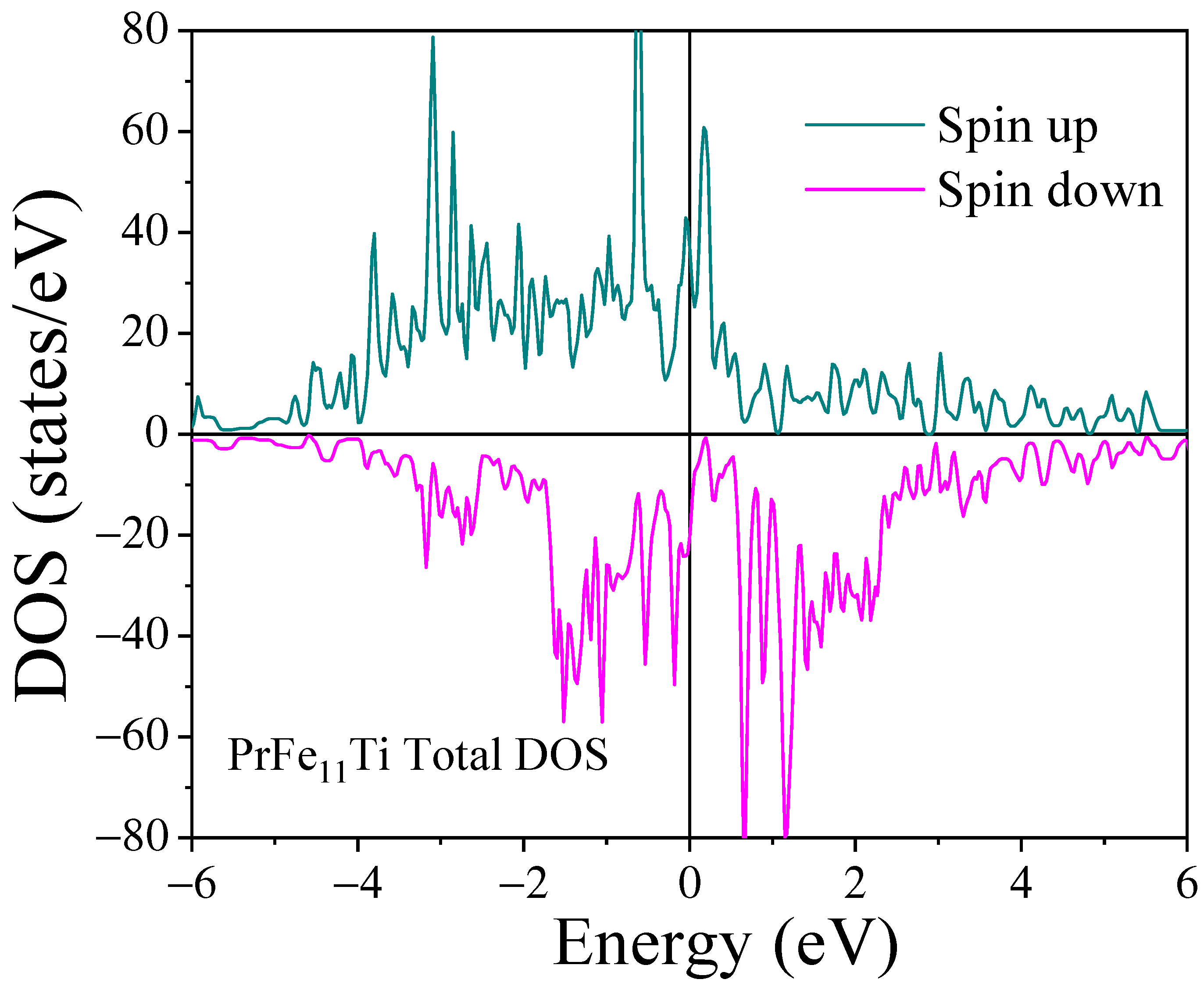
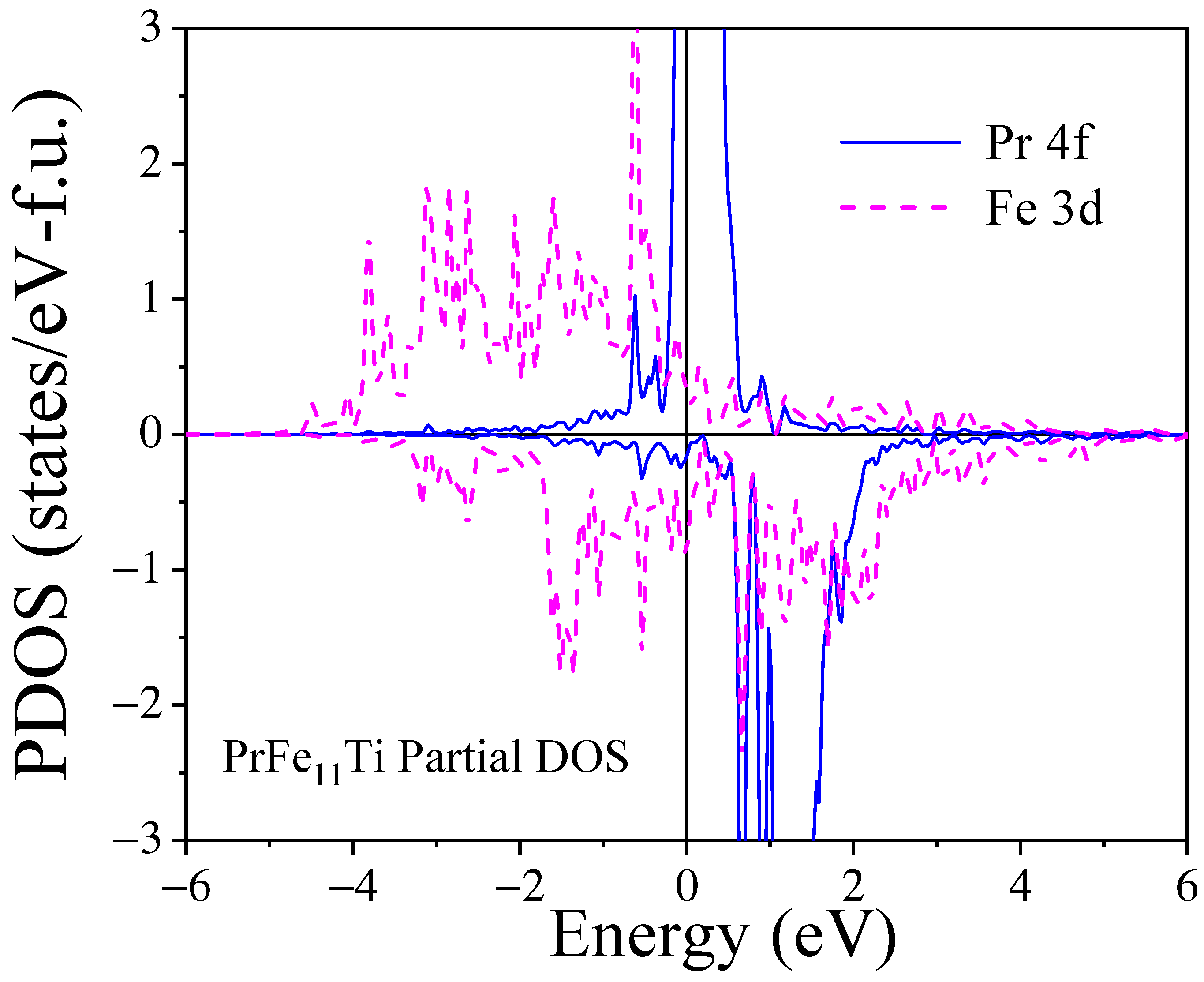
3.3. Mössbauer Spectrometry and DFT Calculations
- The cut-off parameter was established as 7, where denotes the magnitude of the largest K vector.
- We implemented = 12 Ry for Fourier potential expansion.
- 1200 k-points in the Brillouin zone.
- The muffin-tin radii were set at 2.50, 2.14, and 2.17 Bohr for Pr, Fe, and Ti atoms, respectively.
- To distinguish between valence and core states, we adopted a cut-off energy of 7 Ry
- Convergence was deemed achieved when the total energy difference was less than Ry and the charge was below electron charges.
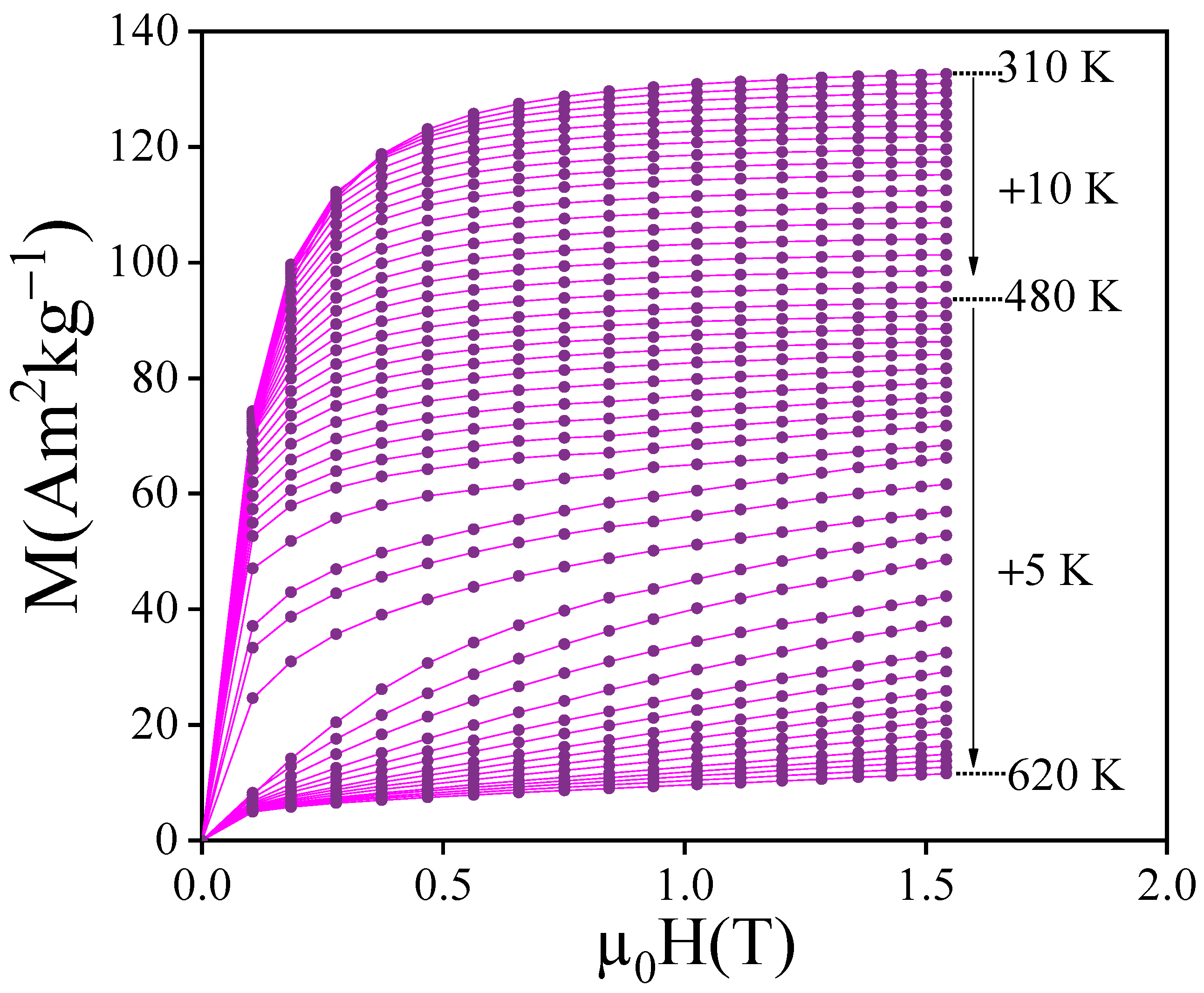
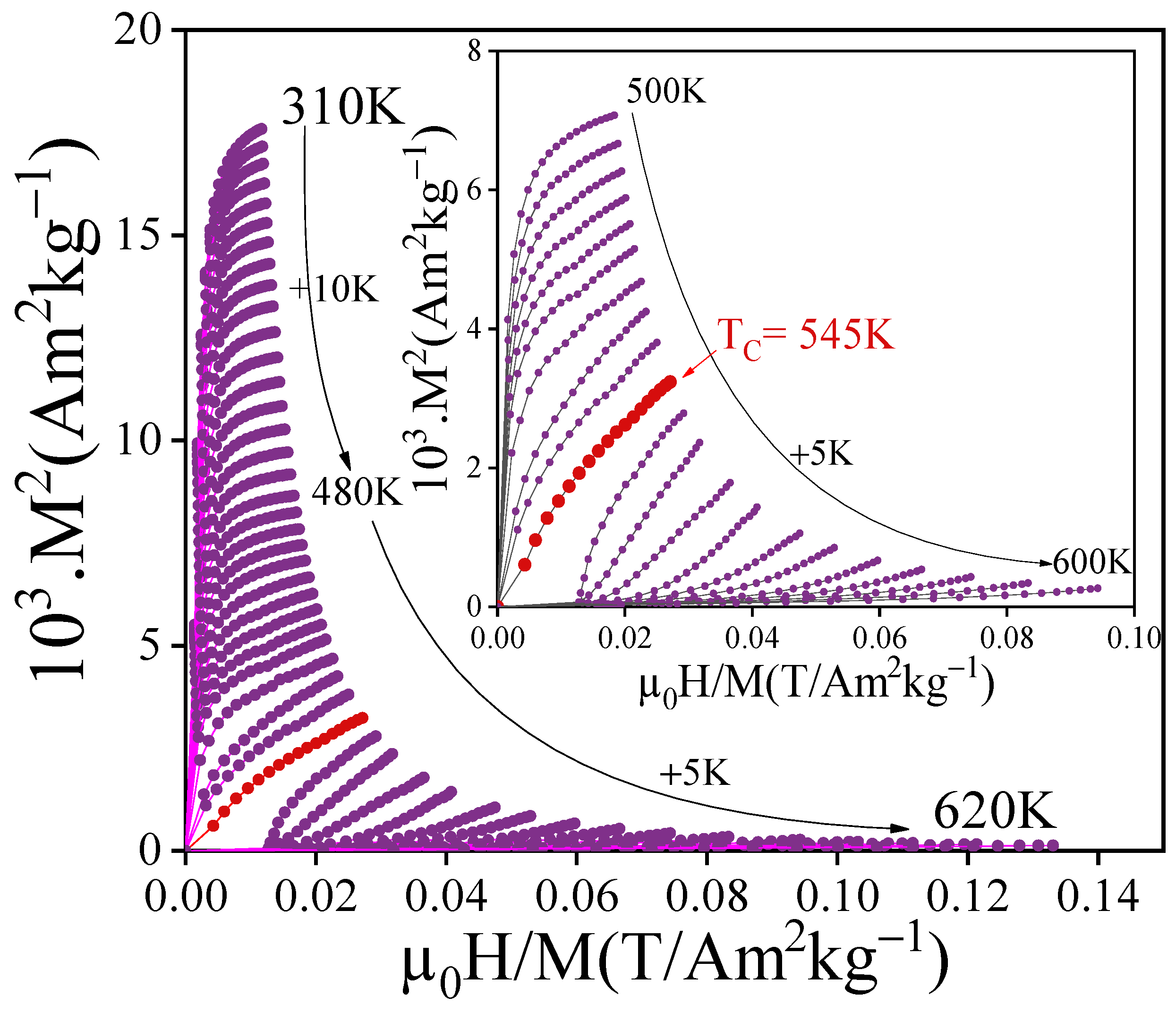
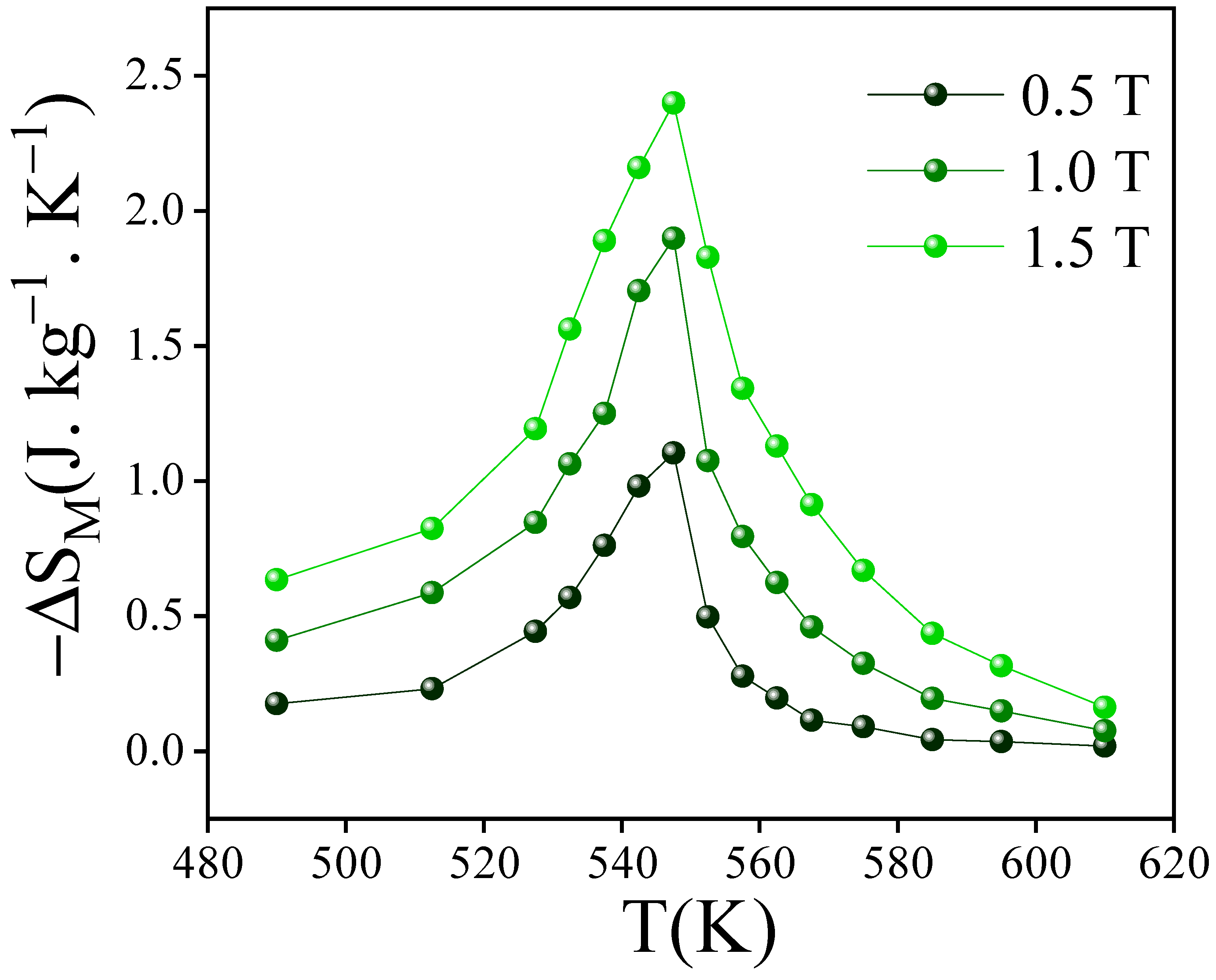
3.4. Magnetocaloric Performance
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- De Mooij, D.; Buschow, K. Some novel ternary ThMn12-type compounds. J. Less-Common Met. 1988, 136, 207–215. [Google Scholar] [CrossRef]
- Buschow, K. Permanent magnet materials based on tetragonal rare earth compounds of the type RFe12-xMx. J. Magn. Magn. Mater. 1991, 100, 79–89. [Google Scholar] [CrossRef]
- Bhandari, C.; Paudyal, D. Enhancing stability and magnetism of ThMn12-type cerium-iron intermetallics by site substitution. Phys. Rev. Res. 2022, 4, 023012. [Google Scholar] [CrossRef]
- Oboz, M.; Talik, E. Properties of the GdTX (T = Mn, Fe, Ni, Pd, X = Al, In) and GdFe6Al6 intermetallics. J. Alloys Compd. 2011, 509, 5441–5446. [Google Scholar] [CrossRef]
- Gabay, A.; Cabassi, R.; Fabbrici, S.; Albertini, F.; Hadjipanayis, G. Structure and permanent magnet properties of Zr1-xRxFe10Si2 alloys with R = Y, La, Ce, Pr and Sm. J. Alloys Compd. 2016, 683, 271–275. [Google Scholar] [CrossRef]
- Hadjipanayis, G.; Gabay, A.; Schönhöbel, A.; Martín-Cid, A.; Barandiaran, J.; Niarchos, D. ThMn12-Type Alloys for Permanent Magnets. Engineering 2020, 6, 141–147. [Google Scholar] [CrossRef]
- Makurenkova, A.; Ogawa, D.; Tozman, P.; Okamoto, S.; Nikitin, S.; Hirosawa, S.; Hono, K.; Takahashi, Y. Intrinsic hard magnetic properties of Sm(Fe, Co)12-xTix compound with ThMn12 structure. J. Alloys Compd. 2021, 861, 158477. [Google Scholar] [CrossRef]
- Zhang, J.; Tang, X.; Sepehri-Amin, H.; Srinithi, A.; Ohkubo, T.; Hono, K. Origin of coercivity in an anisotropic Sm (Fe, Ti, V)12-based sintered magnet. Acta Mater. 2021, 217, 117161. [Google Scholar] [CrossRef]
- Gschneidner, K.A.; Pecharsky, V.K.; Tsokol, A.O. Recent developments in magnetocaloric materials. Rep. Prog. Phys. 2005, 68, 1479. [Google Scholar] [CrossRef]
- Pecharsky, V.K.; Gschneidner, K.A. Magnetocaloric effect from indirect measurements: Magnetization and heat capacity. J. Appl. Phys. 1999, 86, 565–575. [Google Scholar] [CrossRef]
- Wada, H.; Tanabe, Y. Giant magnetocaloric effect of MnAs1-xSbx. Appl. Phys. Lett. 2001, 79, 3302–3304. [Google Scholar] [CrossRef]
- Chen, Y.F.; Wang, F.; Shen, B.G.; Hu, F.X.; Sun, J.R.; Wang, G.J.; Cheng, Z.H. Magnetic properties and magnetic entropy change of LaFe11.5Si1.5Hy interstitial compounds. J. Phys. Condens. Matter 2003, 15, L161. [Google Scholar] [CrossRef]
- Manekar, M.; Roy, S.B. Reproducible room temperature giant magnetocaloric effect in Fe–Rh. J. Phys. D Appl. Phys. 2008, 41, 192004. [Google Scholar] [CrossRef]
- Phan, M.H.; Yu, S.C. Review of the magnetocaloric effect in manganite materials. J. Magn. Magn. Mater. 2007, 308, 325–340. [Google Scholar] [CrossRef]
- Guo, Z.B.; Du, Y.W.; Zhu, J.S.; Huang, H.; Ding, W.P.; Feng, D. Large magnetic entropy change in perovskite-type manganese oxides. Phys. Rev. Lett. 1997, 78, 1142–1145. [Google Scholar] [CrossRef]
- Gharbi, S.; Marouani, Y.; Issaoui, F.; Dhahri, E.; Hlil, E.K.; Barille, R.; Costa, B.F.O. Assessment of structural, optical, magnetic, magnetocaloric properties and critical phenomena of La0.57Nd0.1Sr0.18Ag0.15MnO3 system at room temperature. J. Mater. Sci. Mater. Electron. 2020, 31, 11983–11996. [Google Scholar] [CrossRef]
- Mandal, K.; Yan, A.; Kerschl, P.; Handstein, A.; Gutfleisch, O.; Müller, K. The study of magnetocaloric effect in R2Fe17 (R = Y, Pr) alloys. J. Phys. D Appl. Phys. 2004, 37, 2628–2631. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, Y.; Han, J.; Du, H.; Wang, C.; Yang, Y. Magnetocaloric effect in R2Fe17 (R = Sm, Gd, Tb, Dy, Er). J. Magn. Magn. Mater. 2008, 320, 1382–1384. [Google Scholar] [CrossRef]
- Alvarez, P.; Gorria, P.; Sanchez-Llamazares, J.; Perez, M.J.; Franco, V.; Reiffers, M.; Curlik, I.; Gazo, E.; Kovac, J.; Blanco, J.A. Magnetic properties and magneto-caloric effect in pseudo-binary intermetallic (Ce, R)2Fe17 compounds (R = Y, Pr and Dy). Intermetallics 2011, 19, 982–987. [Google Scholar] [CrossRef]
- Bouzidi, W.; Nouri, K.; Bartoli, T.; Sedek, R.; Lassri, H.; Moscovici, J.; Bessais, L. Study of the magnetic and magnetocaloric properties at low-field in Nd2Fe17-xSix intermetallics. J. Magn. Magn. Mater. 2020, 497, 166018. [Google Scholar] [CrossRef]
- Jaballah, H.; Bouzidi, W.; Fersi, R.; Mliki, N.; Bessais, L. Structural, magnetic and magnetocaloric properties of (Pr, Sm)2Fe17 compound at room temperature. J. Phys. Chem. Solids 2022, 161, 110438. [Google Scholar] [CrossRef]
- Horcheni, J.; Nouri, K.; Dhahri, E.; Bessais, L. Crystal structure, critical phenomena and magnetocaloric properties of Ni-substituted ferromagnetic Pr2Fe17 intermetallic compound around room temperature. Solid State Chem. 2023, 326, 124219. [Google Scholar] [CrossRef]
- Xia, Y.; Du, H.; Xu, J.; Zhang, Y.; Wang, C.; Han, J.; Liu, S.; Xu, Q.; Yang, J. The magnetic and magnetocaloric properties of NdFe12-xMox compounds. J. Appl. Phys. 2012, 111, 07A949. [Google Scholar] [CrossRef]
- Bouzidi, W.; Bartoli, T.; Sedek, R.; Bouzidi, A.; Moscovici, J.; Bessais, L. Low-field magnetocaloric effect of NdFe11Ti and SmFe10V2 compounds. J. Mater. Sci. Mater. Electron. 2021, 32, 10579–10586. [Google Scholar] [CrossRef]
- Saidi, M.; Walha, S.; Hlil, E.; Bessais, L.; Jemmali, M. Effect of chromium substitution on structural, magnetic and magnetocaloric properties of GdFe12-xCrx intermetallic compounds, Mössbauer spectrometry and ab initio calculations. J. Solid State Chem. 2021, 297, 122019. [Google Scholar] [CrossRef]
- Gao, P.; Xia, Y.; Gong, J.; Ju, X. Structure and Magnetic Properties of ErFexMn12-x (7.0 ≤ x ≤ 9.0, Δx = 0.2). Nanomaterials 2022, 12, 1586. [Google Scholar] [CrossRef]
- Rietveld, H. A profile refinement method for nuclear and magnetic structures. J. Appl. Crystallogr. 1969, 2, 65–71. [Google Scholar] [CrossRef]
- Rodríguez-Carvajal, J. Recent advances in magnetic structure determination by neutron powder diffraction. Phys. B Condens. Matter. 1993, 192, 55–69. [Google Scholar] [CrossRef]
- Bessais, L.; Djega-Mariadassou, C. Structure and Magnetic Properties of Nanocrystalline Sm(Fe1-xCox)11Ti (x < 2). Phys. Rev. B 2001, 63, 054412. [Google Scholar]
- Piquer, C.; Grandjean, F.; Isnard, O.; Pop, V.; Long, G.J. A magnetic and Mössbauer spectral study of PrFe11Ti and PrFe11TiH. J. Alloys Compd. 2004, 377, 1–7. [Google Scholar] [CrossRef]
- Givord, D.; Laforest, J.; Schweizer, J.; Tasset, F. Temperature dependence of the samarium magnetic form factor in SmCo5. J. Appl. Phys. 1979, 50, 2008–2010. [Google Scholar] [CrossRef]
- Margarian, A.; Dunlop, J.; Day, R.; Kalceff, W. Phase equilibria in the Fe-rich corner of the Nd-Fe-Ti ternary alloy system at 1100 °C. J. Appl. Phys. 1994, 76, 6153–6155. [Google Scholar] [CrossRef]
- Liu, Z.Y.; Jin, Z.P.; Xia, C.S. 873 K isothermal section of phase diagram for Y-Fe-Ti ternary system. Scr. Mater. 1997, 37, 1129–1134. [Google Scholar] [CrossRef]
- Tang, S.; Yang, C.; Wang, B.; Jin, X.; Zhang, S.; Du, Y. Structure and magnetic properties of PrFe11.5-xVxTi0.5 compounds and their nitrides. J. Magn. Magn. Mater. 1998, 189, 341–345. [Google Scholar] [CrossRef]
- Tang, S.; Yin, J.; Jin, Z.; Zhang, J.; Zhang, S.; Du, Y. Structure and magnetic properties of PrFe10VxMo2-x compounds and their nitrides. J. Appl. Phys. 1999, 85, 4687–4689. [Google Scholar] [CrossRef]
- Tereshina, I.; Gaczyński, P.; Rusakov, V.; Drulis, H.; Nikitin, S.; Suski, W.; Tristan, N.; Palewski, T. Magnetic anisotropy and Mössbauer effect studies of PrFe11Ti and PrFe11TiH. J. Phys. Condens. Matter 2001, 13, 8161. [Google Scholar] [CrossRef]
- Kim, H.T.; Kim, Y.B.; Kim, C.S.; Jin, H. Magnetocrystalline anisotropy of (Sm0.5RE0.5)Fe11Ti compounds (RE = Ce, Pr, Nd, Sm, Gd and Tb). J. Magn. Magn. Mater. 1996, 152, 387–390. [Google Scholar] [CrossRef]
- Néel, L. Relation entre la constante d’anisotropie et la loi d’approche à la saturation des ferromagnétiques. J. Phys. Radium 1948, 9, 193–199. [Google Scholar] [CrossRef]
- Denissen, C.; Coehoorn, R.; Buschow, K. 57 Fe Mössbauer study of RFe12-xTx compounds (T= V, Cr, Mo). J. Magn. Magn. Mater. 1990, 87, 51–56. [Google Scholar] [CrossRef]
- Blaha, P.; Schwarz, K.; Sorantin, P.; Trickey, S. Full-potential, linearized augmented plane wave programs for crystalline systems. Comput. Phys. Commun. 1990, 59, 399–415. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef]
- Blaha, P.; Schwarz, K.; Tran, F.; Laskowski, R.; Madsen, G.K.; Marks, L.D. WIEN2k: An APW+ lo program for calculating the properties of solids. J. Chem. Phys. 2020, 152, 074101. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Gunnarsson, A. The Stoner model in the spin-density-functional formalism. Phys. B C 1977, 91, 329–336. [Google Scholar] [CrossRef]
- Trygg, J.; Johansson, B.; Brooks, M.S.S. Ab initio calculation of the magnetism in GdFe12. J. Magn. Magn. Mater. 1992, 104, 1447. [Google Scholar] [CrossRef]
- Liu, X.B.; Altounian, Z.; Ryan, D.H. Magnetocrystalline anisotropy in Gd(Co, Fe) 12B6: A first-principles study. J. Alloys Compd. 2016, 688, 118–122. [Google Scholar] [CrossRef]
- Banerjee, B.K. On a generalised approach to first and second order magnetic transitions. Phys. Lett. 1964, 12, 16–17. [Google Scholar] [CrossRef]
- Zhong, W.; Chen, W.; Ding, W.P.; Zhang, N.; Hu, A.; Du, Y.W.; Yan, Q.J. Structure, composition and magnetocaloric properties in polycrystalline La1-xAxMnO (A = Na, K). J. Eur. Phys. B 1998, 3, 169–174. [Google Scholar] [CrossRef]
- Griffith, L.D.; Mudryk, Y.; Slaughter, J.; Pecharsky, V.K. Material-based figure of merit for caloric materials. J. Appl. Phys. 2018, 123, 034902. [Google Scholar] [CrossRef]
- Jaballah, H.; Charbonnier, V.; Bessais, L.; Mliki, N. Investigation of spin reorientation and magnetocaloric behavior in PrCo5-xCux compounds. Mater. Res. Bull. 2023, 165, 112326. [Google Scholar] [CrossRef]
- Choura-Maatar, S.; Nofal, M.M.; Mnassri, R.; Koubaa, W.C.; Boudjada, N.C.; Cheikhrouhou, A. Enhancement of the magnetic and magnetocaloric properties by Na substitution for Ca of La0.8Ca0.2MnO3 manganite prepared via the Pechini-type sol-gel process. J. Mater. Sci. Mater. Electron. 2020, 31, 1634–1645. [Google Scholar] [CrossRef]
- Sakka, A.; Mnassri, R.; Nofal, M.; Mahjoub, S.; Koubaa, W.C.; Boudjada, N.C.; Oumezzine, M.; Cheikhrouhou, A. Structure, magnetic and field dependence of magnetocaloric properties of Pr0.5RE0.1Sr0.4MnO3 (RE= Eu and Er). J. Magn. Magn. Mater. 2020, 514, 167158. [Google Scholar] [CrossRef]
- Su, L.; Zhang, X.; Dong, Q.; Li, H.T.Y.S.H.; Cheng, Z.H. Evolution of structural, magnetic and magnetocaloric effect in TmFe1-xMnxO3 (x ≤ 0.3). Ceram. Int. 2021, 47, 18286–18294. [Google Scholar] [CrossRef]
- Mazumdar, D.; Das, I. Role of 3d–4f exchange interaction and local anti-site defects in the magnetic and magnetocaloric properties of double perovskite Ho2CoMnO6 compound. J. Appl. Phys. 2021, 129, 063901. [Google Scholar] [CrossRef]
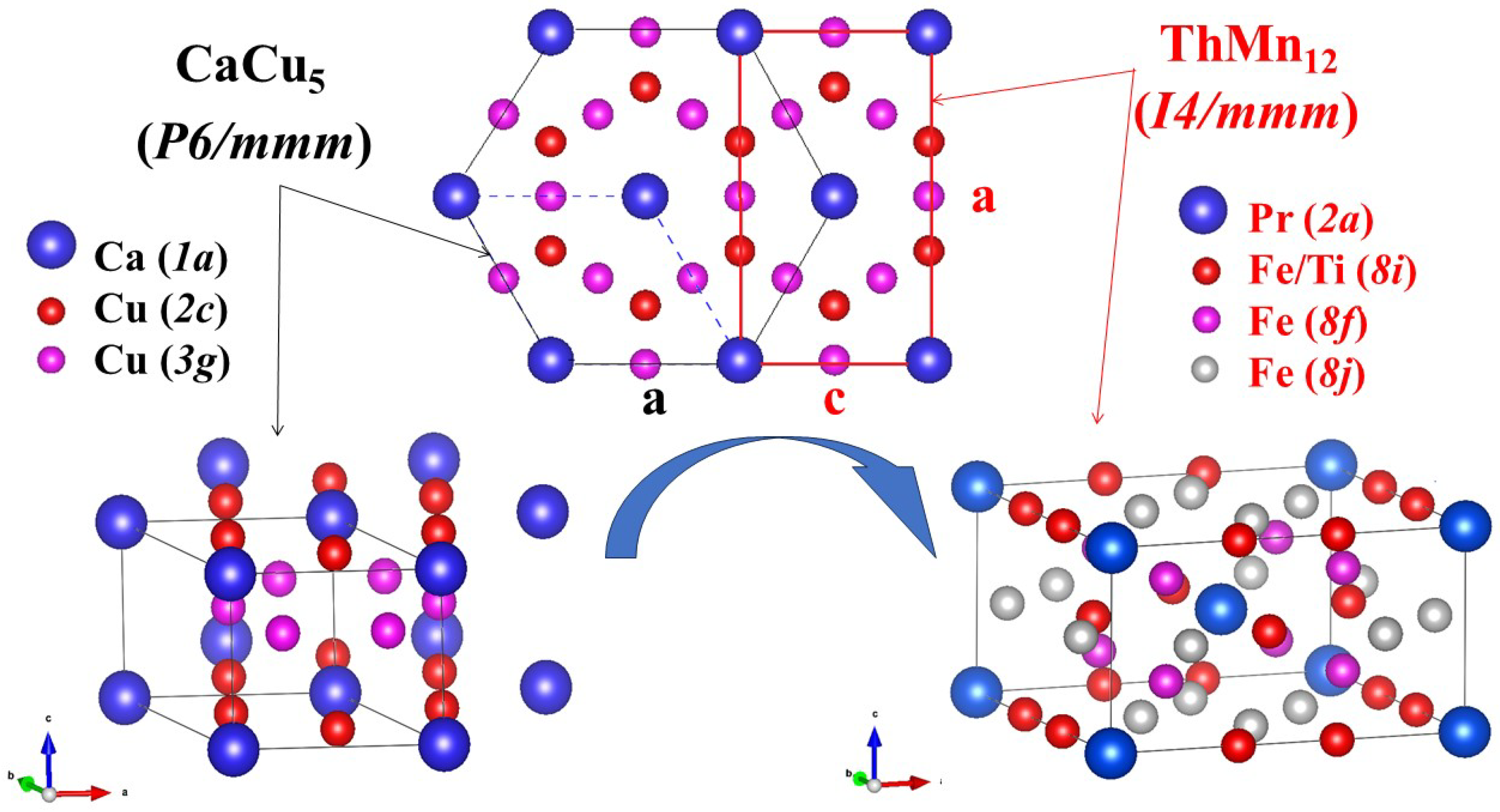

| Sample | PrFeTi | |||
|---|---|---|---|---|
| Space group | ||||
| Cell parameters | (Å) | 8.601(1) | ||
| c (Å) | 4.789(1) | |||
| 0.556 | ||||
| V (Å) | 354.308(1) | |||
| Atom site | x | y | z | Atomic number |
| Pr() | 0 | 0 | 0.344(1) | 2 |
| Fe/Ti() | 0.360(1) | 0 | 0 | 6/2 |
| Fe() | 0.274(1) | 0.5 | 0 | 8 |
| Fe() | 0.25 | 0.25 | 0.25 | 8 |
| Agreement | 6.17 | |||
| factors | 7.5 | |||
| 1.40 |
| Compound | (K) | Ref. |
|---|---|---|
| YFeTi | 525 | [36] |
| PrFeTi | 547 | [30] |
| PrFeTi | 543 | This work |
| NdFeTi | 552 | [24] |
| SmFeTi | 589 | [37] |
| GdFeTi | 604 | [25] |
| (T) | (mm/s) | (mm/s) | WSCV (Å) | ||||
|---|---|---|---|---|---|---|---|
| T(K) | 10 | 300 | 10 | 300 | 10 | 300 | - |
| Fe | 31.2 | 27.1 | 0.08 | −0.08 | 0.13 | 0.09 | 13.1 |
| Fe | 28.7 | 23.8 | 0.01 | −0.10 | 0.11 | 0.09 | 11.6 |
| Fe | 26.3 | 21.8 | −0.01 | −0.12 | 0.06 | 0.04 | 10.6 |
| Pr | - | - | - | - | - | - | 23.3 |
| 28.5 | 24.2 | 0.03 | −0.09 | 0.10 | 0.08 | - | |
| Sample | RCP | TEC | Ref. | ||||
|---|---|---|---|---|---|---|---|
| (T) | (K) | J/(kg·K) | (J/kg) | J(K·kg) | J(K·kg·T) | ||
| PrFeTi | 0.5 | 545 | 1.1 | 23 | 1.1 | 2.2 | This |
| 1 | 1.9 | 48 | 1.9 | 1.9 | work | ||
| 1.5 | 2.5 | 70 | 2.44 | 1.6 | |||
| GdFeAl | 2 | 298 | 0.56 | 25 | - | - | [4] |
| NdFeMo | 5 | 302 | 2.38 | - | - | - | [23] |
| NdFeTi | 1.5 | 552 | 1.5 | - | - | - | [24] |
| SmFeV | 1.5 | 603 | 1.6 | - | - | - | |
| GdFeCr | 1.5 | 580 | 1.82 | 10.5 | - | - | [25] |
| ErFeMn | 1 | 312.5 | 0.7 | - | - | - | [26] |
| 5 | 1.92 | - | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Horcheni, J.; Jaballah, H.; Dhahri, E.; Bessais, L. Exploring Crystal Structure, Hyperfine Parameters, and Magnetocaloric Effect in Iron-Rich Intermetallic Alloy with ThMn12-Type Structure: A Comprehensive Investigation Using Experimental and DFT Calculation. Magnetochemistry 2023, 9, 230. https://doi.org/10.3390/magnetochemistry9110230
Horcheni J, Jaballah H, Dhahri E, Bessais L. Exploring Crystal Structure, Hyperfine Parameters, and Magnetocaloric Effect in Iron-Rich Intermetallic Alloy with ThMn12-Type Structure: A Comprehensive Investigation Using Experimental and DFT Calculation. Magnetochemistry. 2023; 9(11):230. https://doi.org/10.3390/magnetochemistry9110230
Chicago/Turabian StyleHorcheni, Jihed, Hamdi Jaballah, Essebti Dhahri, and Lotfi Bessais. 2023. "Exploring Crystal Structure, Hyperfine Parameters, and Magnetocaloric Effect in Iron-Rich Intermetallic Alloy with ThMn12-Type Structure: A Comprehensive Investigation Using Experimental and DFT Calculation" Magnetochemistry 9, no. 11: 230. https://doi.org/10.3390/magnetochemistry9110230
APA StyleHorcheni, J., Jaballah, H., Dhahri, E., & Bessais, L. (2023). Exploring Crystal Structure, Hyperfine Parameters, and Magnetocaloric Effect in Iron-Rich Intermetallic Alloy with ThMn12-Type Structure: A Comprehensive Investigation Using Experimental and DFT Calculation. Magnetochemistry, 9(11), 230. https://doi.org/10.3390/magnetochemistry9110230







