Abstract
Among the 5d transition metal iridates, Sr2IrO4, which has a layered chalcogenide structure, has received much attention due to its strong spin–orbit coupling (SOC), which produces Mott insulating states and anomalous physical behaviors. In this paper, the microscopic magnetism of Sr2IrO4 is studied with electron spin resonance (ESR) measurements. The Lande factor g of the ferromagnetic resonance signal of Sr2IrO4 shows anomalous behavior compared to typical ferromagnets. It gradually decreases, and the corresponding resonance field Hr increases, with decreasing temperature. The various physical parameters. including the saturated magnetic field Hs derived from M-H, Hr, ΔHpp, the g factor and the intensity I extracted from ESR spectra, are analyzed in detail. Eventually, it is revealed that the anomalous behavior of the g-factor is induced by in-plane Dzyaloshinsky–Moriya interaction (DMI) rather than the SOC effect.
1. Introduction
Spin–orbit coupling (SOC) and the Dzyaloshinsky–Moriya interaction (DMI) have gained significant attention in the field of condensed matter physics due to their roles in creating chiral spin textures and exotic magnetic phases [1,2]. It is well known that SOC plays a critical role in determining a material’s band structure and electronic properties, such as topological insulators, Dirac semimetals, Weyl semimetals with band inversion and novel Mott insulators for 5d transition-metal oxides (TMOs) [3,4]. Orbital characters with different strengths and Bloch states generate different Mott insulating states in 3d, 4d and 5d TMOs. The Dzyaloshinsky–Moriya interaction (DMI) and its accompanied weak ferromagnetism (WFM) are generally believed to be very sensitive to crystal symmetry and antisymmetric spin coupling [5,6,7,8,9,10,11]. The manipulations needed to enhance DMI strength or understand the underlying mechanism has been a hot topic during recent years in the field of spintronics [6]. The study of DMI and external stimuli, such as temperature (T) or magnetic field (H), can produce valuable insights into the fundamental physics underlying peculiar phenomenon in a single-phase compound, such as α-Fe2O3, CuCl2•2H2O, Sr2IrO4, etc. [7,8,9,10,11].
The studies on anomalous transport and its physics in 5d transition-metal oxide (TMO) iridates Srn + 1IrnO3n + 1 (n = 1, 2) have attracted significant attention due to their intriguing insulating nature, possessing a novel Mott ground state with Jeff = 1/2 quantum spin rather than the expected metallic state with S = 1/2 [12,13]. So far, it is known that a strong SOC energy ζSO~0.4 eV is responsible for the peculiar electronic and magnetic properties in Sr2IrO4 [14]. It generates an effective total angular momentum Jeff = 1/2 state with an isotropic mixture of xy, yz and zx orbitals and hybrid up-down spin characters [15,16]. As a result, Jeff = ½ forms a narrow Hubbard band due to reduced hopping factors, such that a small U opens a Mott gap and an unusual Mott insulator is realized [16]. Much work has been performed on understanding the novel electronic structure and unusual transport in Sr2IrO4, such as ARPES, optical conductivity, resonant X-ray scattering (RXS) techniques and first-principles band calculations [12,13,14,15,16,17,18].
However, less work has been focused on studying its large antisymmetric DMI effect on magnetism properties, such as the in-plane WFM arising from the antiphase rotations of the IrO6 octahedra. A zigzag internal magnetic field is generated by the superexchange interaction of the Ir-O-Ir-O-Ir chain [18]. As shown in Figure 1a,b, DMI always causes neighboring magnetic moments to tend to be perpendicular to each other, rather than parallel or antiparallel [19]. Instead of just being parallel or antiparallel to each other, under the competing effects of AFM and FM, the magnetic moments will tend to form an angle that minimizes the energy of the system [20]. By introducing the DMI action constant D (the direction of D in Sr2IrO4 is parallel to the c-axis), the representation of the Hamiltonian quantity is of the form
which allows the two spins S1 and S2 of Ir4+ to be aligned orthogonally, resulting in a lower energy state [21]. Previous studies have shown that the magnitude of the DMI obtained by DFT calculations in Sr2IrO4 is 0.25 meV along the c-axis [21]. The DMI increases with the rotation angle (θOct) of the IrO6 octahedron around the c-axis and reaches a maximum at θOct ≈ 11° (Figure 1c) [18]. Furthermore, it is reported that the appearance of DMI stems from crystal structural distortion and leads to WFM at Tc in Sr2IrO4 [12]. The above results suggest that the large DMI should produce exotic magnetism, rather than SOC, in iridate Sr2IrO4.
HDMI ~ −D12·(S1 × S2),
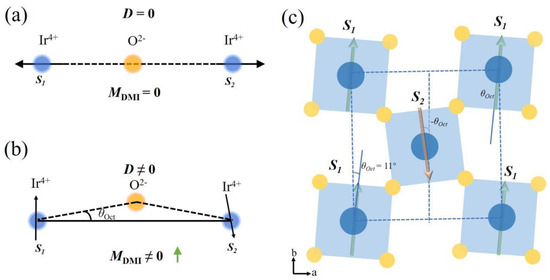
Figure 1.
The schematic illustrations of in-plane spin configurations in Sr2IrO4 without DMI action (a), with DMI action (b) and showing the IrO6 octahedral tilting angle θOct (c), where the green and black arrows represent the spin direction.
To clearly address the DMI’s effect on the magnetic properties of Sr2IrO4, in this article, an ESR technique is used as a measurement probe. ESR is a powerful tool for studying dynamical microscopic magnetism with unpaired electrons, especially in paramagnetic states [22]. Our results show that the g value extracted from ESR spectra is proportional to the DMI. The other derivative magnetic parameters from ESR are also dependent on DMI someway. As a consequence, the DMI of Sr2IrO4 is demonstrated as having a crucial role in the variation of magnetism parameters with T.
2. Experimental
Single crystals of Sr2IrO4 were grown with a flux method by using SrCl2 flux [23]. A mixture of SrCO3 (Innochem (Beijing, China), 99.9%), IrO2 (Western Element (San Jose, CA, USA), 99.99%) and SrCl2 (Aladdin (Hangzhou, China), 99.99%) with a molar ratio of 1.8:1.0:15 was melted at 1300 °C. The melt was slowly cooled down to 900 °C at a rate of 8 °C per hour and then furnace-cooled to room temperature. Plate-like single crystals with typical dimensions of 1 mm × 1 mm × 0.1 mm were found in the solidified melt. The results of X-ray measurement by using a Rigaku-RINT 2400 diffractometer at room temperature were fully consistent with the space group I41/acd previously reported for Sr2IrO4 [12]. The ESR experiments were carried out with a JEOL JES-FA200 ESR spectrometer at X-band frequencies γ ≈ 9.1 GHz in temperatures ranging from 5 to 290 K. Microwave power was set to 1 mW and the magnetic field was parallel to the natural cleavage crystal plane (001). Since the in-plane anisotropy of the Jeff = 1/2 moments is extremely small [12], there is no significant difference in the in-plane magnetism along the a- or b-axis. The in-plane and out-of-plane magnetism were measured by using a commercial superconducting quantum interference device magnetometer (MPMS-XL, Quantum Design, San Diego, CA, USA).
3. Results and Discussions
The compound Sr2IrO4 crystallizes in the layered perovskite structure (space group: I41/acd), consisting of four IrO2 staggered layers (in a unit cell) of corner-sharing IrO6 octahedra with rotational distortion interleaved by Sr-O interlayers [24], as illustrated in Figure 2a. A nonlinear antiferromagnetic spin structure with WFM from a spin canting in-plane ground state has been proposed (Figure 2b). A metamagnetic transition from in-plane interlayer AFM to a WFM is revealed at low temperatures and critical magnetic fields above 2 kOe, as shown in Figure 2c.
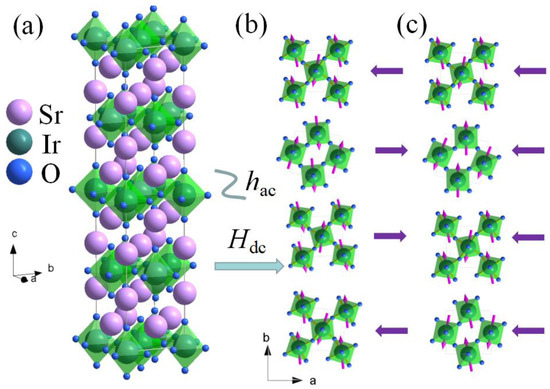
Figure 2.
(a) Crystal structure of Sr2IrO4. IrO6 layers where the Ir atoms (green black) are at the center of corner-sharing oxygen (blue) octahedra are separated by Sr atoms (light purple). (b,c) A metamagnetic transition from AFM to a weak FM above 2 kOe.
Figure 3a presents the temperature (T) dependence of in-plane magnetization (M) at 2–360 K under a magnetic field of 0.1 kOe. The magnetization discrepancy between ZFC and FC curves below Tc suggests the existence of magnetic glassy-like behavior [25]. According to the mean-field model of magnetic glasses, this implies that there exists a competition of magnetic interactions between AFM and FM [26]. The Curie temperature is 226 K, defined by the derivative maximum of |dM/dT|, as shown in Figure 3b. The effective magnetic moment PMeff is around 0.64 μB/f.u., determined by using the Curie–Weiss law with the expression in the temperature regime from 240 to 255 K (Figure 3b), where θ denotes the Weiss constant and C is the Curie constant, which is consistent with the reported effective moment [27,28]. The Curie–Weiss temperature is around 240 K. Instead of a collinear type AFM, this DM type antisymmetric exchange interaction is originated from the rotation of octahedra IrO6 about the c-axis by ~11°, which leads to a transition to a WFM phase at Tc, as previously reported [27]. With decreasing temperature, the value of magnetization is gradually reduced. This implies the DMI (WFM strength) is simultaneously diminished, reflecting the change of structure with decreasing temperature [27]. As T is lowered, the basal bond angle <Ir–O–Ir> increases, the rotation angle (θOct) of IrO6 octahedra around the c axis decreases to ~10.3° at 20 K and the basal bond length dIr−O2 decreases, while the apical bond length dIr−O1 increases [27]. Upon decreasing T to around 100 K, the magnetic-structural coupling occurs as reported by Imtiaz Noor Bhatti [27]. However, there is no trace on this phenomenon in any macromagnetization measurements, such as M-T or M-H, due to the limited detection sensitivity of the magnetic flux method. With the temperature below 11 K, the magnetization rises with lowering T, which might be related to magnetic fluctuation at low temperatures [29].
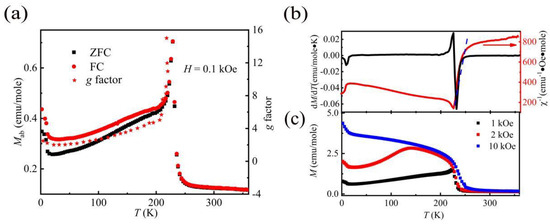
Figure 3.
(a) The temperature dependences of ZFC and FC magnetization at H = 0.1 kOe, and g factor of Sr2IrO4. (b) The temperature dependences of dM/dT and −1. (c) Temperature dependences of ZFC magnetization at H = 1 kOe, 2 kOe and 10 kOe, respectively, where The red arrows represent the red curves corresponding to the right axes.
Figure 3c illustrates the temperature dependence of magnetization, measured in magnetic fields of 1 kOe, 2 kOe and 10 kOe parallel to [010], respectively. It can be seen that the higher H of 2 kOe, corresponding to the critical field-driven in-plane metamagnetic transition, induces a WFM transition and shifts the subsequent AFM transition to a lower temperature of around 150 K. Furthermore, the magnetic field of 10 kOe shifts the Curie temperature to 236 K from 226 K (at H = 0.1 kOe). It realizes the WFM transition and remains in this magnetic state until 2 K. These results indicate that the maximum strength of DMI or WFM is located at Tc.
Figure 4a presents the magnetization curves with in-plane H at temperatures of 2, 10, 50, 100, 150 and 200 K, and out-of-plane H at 2, 10, 50 and 100 K, respectively. An in-plane saturated moment of 0.09 µB/Ir at 2 K is obtained by unit conversion in the WFM state, which is close to the previous report [12]. It is understandable that the in-plane saturated magnetization decreases with temperature due to phonon thermal disturbance [30]. The out-of-plane magnetization is quite negligible and irregular since the c-axis is the hard magnetization direction. However, it is peculiar that the in-plane saturated magnetic field Hs decreases with the increasing temperature, as shown in Figure 4b. This indicates that the DMI strength is enhanced by the temperature increasing, which is consistent with the M-T measurement results (Figure 3a). Furthermore, from Figure 4b, we can see that the change trend of Hs with temperature is similar to the behavior of resonance magnetic field Hr extracted from the ESR measurements, implying there is a close correlation between Hs and Hr. Here, Hr is defined by the magnetic field, corresponding to the center between the lowest and highest values of dP/dH.
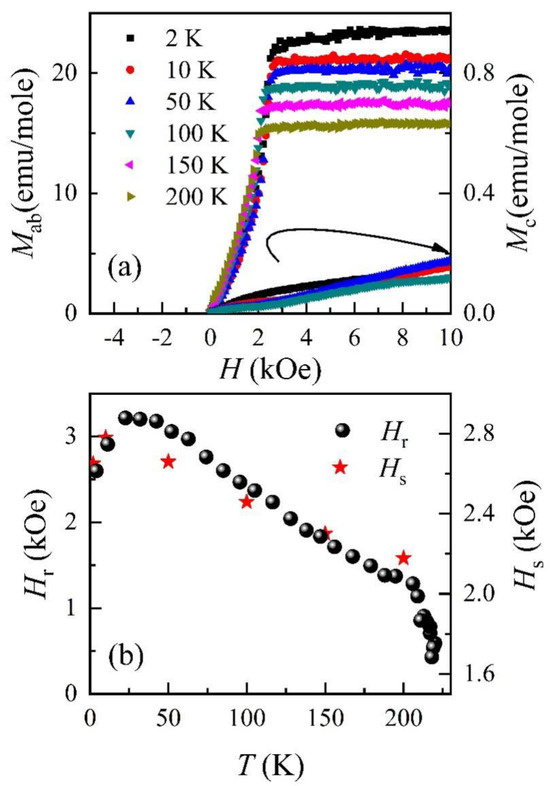
Figure 4.
(a) The magnetic field dependence of in-plane magnetization at 5, 10, 50, 100, 150 and 200 K and out-of-plane magnetization at 5, 10, 50 and 100 K for Sr2IrO4, respectively. (b) The temperature dependences of Hr and Hs.
Figure 5 shows the ESR spectra for Sr2IrO4 in the temperature range from 11 to 230 K with the measurement geometry of the H//ab plane. There is no ESR signal detected for H//c-axis since there is a large magnetic anisotropy mediated by DMI in Sr2IrO4 [13]. Above 230 K (Tc = 226 K), there is no ESR signal observed for the H//ab plane, which should be ascribed to the strong spin–lattice relaxation in the paramagnetic region [12].
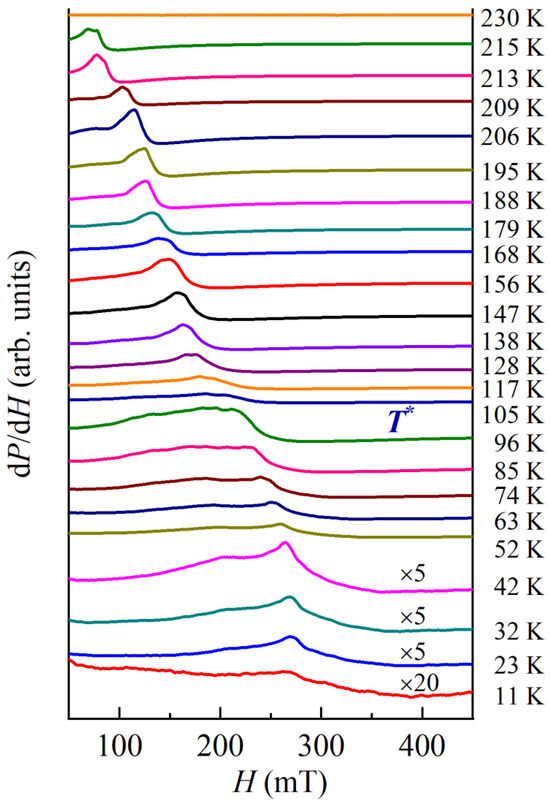
Figure 5.
The differential ESR spectra (dP/dH) at selected temperatures from 11 to 230 K for Sr2IrO4. The amplitude of ESR signals between 11 and 42 K is multiplied for a better view. T* corresponds to the temperature where the DMI is changed drastically due to structural-magnetic coupling.
For all the ESR spectra, the calculated asymmetry ratio A/B of the absorption derivative is less than 2.6. This is indicative of the insulating character of Sr2IrO4 [31,32]. At high temperatures, each spectrum consists of a single line with a Dysonian line shape, indicating the microwave skin depth is smaller than the single crystalline size [31,32], which holds up to the temperature of about T* ≈ 105 K. Below T*, more distortions occur and the resonance line largely broadens, which indicates there emerges more complex magnetic interactions and magnetic inhomogeneity. T* corresponds to the reported temperature where the magneto-structural coupling appears [27].
In Figure 6, the temperature dependences of the intensity I (extracted from double integration of the first derivative ESR spectra dP/dH) and the line width ΔHpp are quantitatively presented. ΔHpp is extracted by the H distance recorded between the highest and lowest peaks of dP/dH. Upon lowering T, the I keeps rising from Tc and then approaches maximum at 95 K just below T*. The peak of I below T* with T should arise from the dramatic change of magneto-structural coupling, evidenced by the crystal lattice parameters around T* [27]. This has never been observed by any macromagnetic measurements such as M-T or M-H since it is a second-order-like structural transition at T*. The c axis of Sr2IrO4 is compressed and the a-axis becomes longer at T*, leading to a reasonable further additional amount of distortion release of octahedra IrO6 with T decreasing, accompanied by the progressively broadened ΔHpp. It is generally believed that the ESR intensity should be proportional to the square of the effective moments of the spins contributing to a given resonance line IESR ~ μ2eff = g2S(S + 1)μB2 [22,33]. Below T*, the monotonous reduction of I is consistent with the M-T behavior since the DMI effect is reduced abruptly, whereas the AFM becomes dominated [27]. Above T*, the change of I is not obvious in the M-T measurements (Figure 3a) due to the spin–lattice relaxation effect. Similar to I behavior, upon decreasing T, the ΔHpp rises, which is characteristic of an insulating nature of Sr2IrO4 except for a symbol contributed from the complicated magnetic interactions. At 95 K just below T*, the appearance of maximum ΔHpp is more solid evidence for the strong coupling between structure and magnetism.
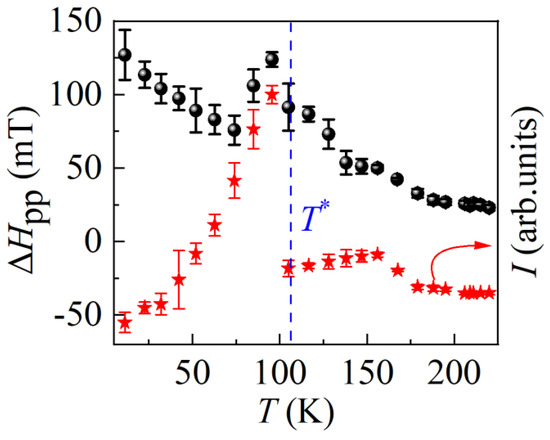
Figure 6.
The temperature dependences of H∆pp and the intensity I with errors of ESR, where the red star represents the intensity and the black ball represents the peak width.
The most striking anomalous feature of Sr2IrO4 is explored via the Hr and g factor. The temperature dependence of the g factor is exhibited in Figure 3a, which is obtained from the main peak of ESR signals calculated by the resonance condition of the first derivative spectra dP/dH in the temperature range of 11–230 K. The g factor shows identical behavior to the temperature dependence of in-plane M, which is a strong hint of the correlation between the g factor and DMI, since M reflects the DMI change with T. The g factor is also a fingerprint of magnetic resonance field Hr. The temperature dependence of Hr is demonstrated in Figure 4b. It can be seen that the trend of Hr vs. T is similar to the Hs behavior. As we know, in a conventional ferromagnet, the magnetic moment should strengthen and the Hs tends to be smaller at lower temperatures. However, in single crystal Sr2IrO4, upon lowering the T, the in-plane magnetic moment decreases when H < 0.2 kOe (Figure 3a) while the Hs becomes larger (Figure 4b). This should be ascribed to the reduction of in-plane DMI with temperature decreasing [6]. Thus, we can conclude that the change of parameters Hr, Hs, M and g factor vs. T are all derived from the DMI ebbing away with T decreasing, rather than SOC interaction. It is well known that the strong SOC results in Jeff = 1/2 as a character of an anomalous Mott insulator in Sr2IrO4. Here, we show another abnormal magnetic property of the g factor and its associated physical parameters driven by DMI, probed by ESR measurements. The results have proved that the ESR technique is very sensitive to structural-magnetic coupling and reliable for detecting the slight modification of WFM by external stimulus such as T, H and even crystalline octahedral distortion.
4. Conclusions
In summary, we have prepared layered single crystals of 5d Sr2IrO4 and studied its anomalous magnetic behavior by M-T, M-H and X-band ESR measurements. It was demonstrated that the crystal structure induces the presence of the DMI action and changes with T, which in turn affects the magnetic behavior of Sr2IrO4. As the temperature decreases, the rotation of IrO6 octahedra distortion decreases, leading to an attenuated DMI among the IrO6 octahedral chains, which eventually results in anomalous magnetic parameters, as probed by ESR measurements. The analysis of the typical magnetic parameters of Hr, Hs, I, g factor and ΔHpp shows that ESR is a powerful tool for characterizing DMI action since it is more sensitive to WFM and even non-perceptual moment change induced by the coupling between structure distortion and magnetism.
Author Contributions
K.W.: writing and testing, L.Y. and Z.L.: data collection, Y.S.: sample preparation, L.H. and F.W.: conceptualization, J.L., B.S. and T.Z.: revising. All authors have read and agreed to the published version of the manuscript.
Funding
Project supported by the National Natural Science Foundation of China (Grant Nos. 12174425, 52171176, 52088101 and U2032220) and International Partnership Program of Chinese Academy of Sciences (113111KYSB20190029).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to the license of contents.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Caretta, L.; Rosenberg, E.; Büttner, F.; Fakhrul, T.; Gargiani, P.; Valvidares, M.; Chen, Z.; Reddy, P.; Muller, D.A.; Ross, C.A.; et al. Interfacial Dzyaloshinskii-Moriya interaction arising from rare-earth orbital magnetism in insulating magnetic oxides. Nat. Commun. 2020, 11, 1090. [Google Scholar] [CrossRef] [PubMed]
- Ishii, K.; Jarrige, I.; Yoshida, M.; Ikeuchi, K.; Mizuki, J.; Ohashi, K.; Takayama, T.; Matsuno, J.; Takagi, H. Momentum-resolved electronic excitations in the Mott insulator Sr2IrO4 studied by resonant inelastic X-ray scattering. Phys. Rev. B 2011, 83, 115121. [Google Scholar] [CrossRef]
- Singh, V.; Pulikkotil, J. Evidence of Slater-type mechanism as origin of insulating state in Sr2IrO4. J. Phys. Condens. Matter 2019, 31, 425501. [Google Scholar] [CrossRef]
- Franke, I.; Baker, P.; Blundell, S.J.; Lancaster, T.; Hayes, W.; Pratt, F.L.; Cao, G. Measurement of the internal magnetic field in the correlated iridates Ca4IrO6, Ca5Ir3O12, Sr3Ir2O7 and Sr2IrO4. Phys. Rev. B 2011, 83, 094416. [Google Scholar] [CrossRef]
- Cetin, M.F.; Lemmens, P.; Gnezdilov, V.; Wulferding, D.; Menzel, D.; Takayama, T.; Ohashi, K.; Takagi, H. Crossover from coherent to incoherent scattering in spin-orbit dominated Sr2IrO4. Phys. Rev. B 2012, 85, 195148. [Google Scholar] [CrossRef]
- Priyamvada, J.; Leonard, F. The microscopic origin of DMI in magnetic bilayers and prediction of giant DMI in new bilayers. NPJ Comput. Mater. 2020, 6, 88. [Google Scholar]
- Jong, W.; Verstelle, J. Antisymmetric exchange interaction and spin-spin relaxation in CuCl2·2H2O. Phys. Lett. A 1972, 40, 403–404. [Google Scholar] [CrossRef]
- Liu, Q.; Kim, T.; Lee, K.; Yang, D.; Kumar, D.; Hu, F.; Yang, H. Dzyaloshinskii-Moriya Torque-Driven Resonance in Antiferromagnetic α-Fe2O3. Adv. Funct. Mater. 2023, 5, 1101–1105. [Google Scholar] [CrossRef]
- Velikov, L.; Rudashevskii, E. Antiferromagnetic resonance in hematite in the weakly ferromagnetic state. Sov. Phys. JETP 1969, 5, 836–839. [Google Scholar]
- Fink, H.; Shaltiel, D. High-Frequency Resonance of a Weak Ferromagnet: MnCO3. Phys. Rev. 1962, 12, 627–631. [Google Scholar] [CrossRef]
- Samuel, J.; Simon, F. Antiferromagnetic Resonance in Systems with Dzyaloshinsky-Moriya Coupling; Orientation Dependence in α-Fe2O3. Phys. Rev. 1964, 7, 136. [Google Scholar]
- Ge, M.; Tan, S.; Huang, Y.; Zhang, L.; Tong, W.; Pi, L.; Zhang, Y. Magnetism of insulator Sr2IrO4 with strong spin–orbit coupling. J. Magn. Magn. Mater. 2013, 345, 13–17. [Google Scholar] [CrossRef]
- Kim, B.J.; Ohsumi, H.; Komesu, T.; Sakai, S.; Morita, T.; Takagi, H.; Arima, T.H. Phase-sensitive observation of a spin-orbital Mott state in Sr2IrO4. Science 2009, 323, 1329–1332. [Google Scholar] [CrossRef]
- Hong, Y.; Jo, Y.; Choi, H.Y.; Lee, N.; Choi, Y.J.; Kang, W. Large magnetic anisotropy in canted antiferromagnetic Sr2IrO4 single crystals. Phys. Rev. B 2016, 93, 094406. [Google Scholar] [CrossRef]
- Cao, G.; Terzic, J.; Zhao, H.D.; Zheng, H.; De Long, L.E.; Riseborough, P.S. Electrical Control of Structural and Physical Properties via Strong Spin-Orbit Interactions in Sr2IrO4. Phys. Rev. Lett. 2018, 120, 017201. [Google Scholar] [CrossRef] [PubMed]
- Kim, B.J.; Jin, H.; Moon, S.J.; Kim, J.Y.; Park, B.G.; Leem, C.S.; Yu, J.; Noh, T.W.; Kim, C.; Oh, S.J.; et al. Novel Jeff = 1/2 Mott state induced by relativistic spin-orbit coupling in Sr2IrO4. Phys. Rev. Lett. 2008, 101, 076402. [Google Scholar]
- Fujiyama, S.; Ohsumi, H.; Komesu, T.; Matsuno, J.; Kim, B.J.; Takata, M.; Arima, T.; Takagi, H. Two-dimensional Heisenberg behavior of Jeff = 1/2 isospins in the paramagnetic state of the spin-orbital Mott insulator Sr2IrO4. Phys. Rev. Lett. 2012, 108, 247212. [Google Scholar] [CrossRef] [PubMed]
- Solovyev, I.V.; Mazurenko, V.V.; Katanin, A.A. Validity and limitations of the superexchange model for the magnetic properties of Sr2IrO4 and Ba2IrO4 mediated by the strong spin-orbit coupling. Phys. Rev. B 2015, 92, 235109. [Google Scholar] [CrossRef]
- Zorko, A.; Nellutla, J.; Brunel, C.; Brunel, L.C.; Bert, F.; Duc, F.; Trombe, J.C.; De Vries, M.A.; Harrison, A.; Mendels, P. Dzyaloshinsky-Moriya anisotropy in the spin-1/2 kagome compound ZnCu3(OH)6Cl2. Phys. Rev. Lett. 2008, 101, 026405. [Google Scholar] [CrossRef] [PubMed]
- Schweflinghaus, B.; Zimmermann, M.; Heide, G.; Bihlmayer, G.; Blügel, S. Role of Dzyaloshinskii-Moriya interaction for magnetism in transition-metal chains at Pt-step edges. Phys. Rev. B 2016, 94, 024403. [Google Scholar] [CrossRef]
- Wei, W.S.; He, Z.D.; Qu, Z.; Du, H.F. Dzyaloshinsky–Moriya interaction (DMI)-induced magnetic skyrmion materials. Rare Met. 2021, 40, 3076–3090. [Google Scholar] [CrossRef]
- Li, L.; Yan, L.Q.; Shi, Y.; Lu, P.; Sun, Y. Evidence and evolution of magnetic polaron in HgCr2Se4 investigated by electron spin resonance. J. Phys. Condens. Matter 2018, 30, 255804. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Yao, L.; Yao, J.; Zhu, W.; Zhang, C. Decreased Energy Gap and Enhanced Conductivity in Zn-Doped Sr2IrO4. J. Supercond. Nov. Magn. 2018, 32, 1583–1587. [Google Scholar] [CrossRef]
- Crawford, M.K.; Subramanian, M.A.; Harlow, R.L.; Fernandez-Baca, J.A.; Wang, Z.R.; Johnston, D.C. Structural and magnetic studies of Sr2IrO4. Phys. Rev. B 1994, 49, 19198–19201. [Google Scholar] [CrossRef] [PubMed]
- Sudipta, M.; Topwal, D. Complex spin glass behavior in Ga2−xFexO3. Appl. Phys. Lett. 2017, 110, 102907. [Google Scholar]
- Kanti, T.; Moessner, R. Dipolar spin glass transition in three dimensions. Phys. Rev. B 2019, 100, 064425. [Google Scholar]
- Bhatti, N.; Rawat, R.; Banerjee, A.; Pramanik, A.K. Temperature evolution of magnetic and transport behavior in 5d Mott insulator Sr2IrO4, significance of magneto-structural coupling. J. Phys. Condens. Matter 2014, 27, 016005. [Google Scholar] [CrossRef] [PubMed]
- Cao, G.; Bolivar, J.; McCall, S.; Crow, J.E.; Guertin, R.P. Weak ferromagnetism, metal-to-nonmetal transition and negative differential resistivity in single-crystal Sr2IrO4. Phys. Rev. B 1998, 57, R11039. [Google Scholar] [CrossRef]
- Wang, C.; Seinige, H.; Cao, G.; Zhou, J.S.; Goodenough, J.B.; Tsoi, M. Temperature dependence of anisotropic magnetoresistance in antiferromagnetic Sr2IrO4. J. Appl. Phys. 2015, 117, 17A310. [Google Scholar] [CrossRef]
- Ge, M.; Zhang, L.; Fan, J.; Zhang, C.; Pi, L.; Tan, S.; Zhang, Y. Critical behavior of the in-plane weak ferromagnet Sr2IrO4. Solid State Commun. 2013, 166, 60–65. [Google Scholar] [CrossRef]
- Feher, G.; Kip, A.F. Electron Spin Resonance Absorption in Metals. Phys. Rev. 1955, 98, 337–348. [Google Scholar] [CrossRef]
- Joh, K.W.; Lee, C.H.; Lee, C.E.; Jeong, Y.H. Origin of electron spin resonance in La0.7Ca0.3MnO3. Phys. Status Solidi (b) 2003, 239, 452–456. [Google Scholar] [CrossRef]
- Wei, N. Electron Spin Resonance Studies of Chalcogenide Manganese Oxides; Institute of Physics, Chinese Academy of Sciences: Beijing, China, 2008; Volume 5, pp. 30–100. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).