Next Article in Journal
Exploring Crystal Structure, Hyperfine Parameters, and Magnetocaloric Effect in Iron-Rich Intermetallic Alloy with ThMn12-Type Structure: A Comprehensive Investigation Using Experimental and DFT Calculation
Previous Article in Journal
Synthesis and Characterization of Hematite, Magnetite and Maghemite Supported on Silica Gel
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Magnetochemistry
Volume 9
Issue 11
10.3390/magnetochemistry9110229
magnetochemistry-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Honey-like Odor Meets Single-Ion Magnet: Synthesis, Crystal Structure, and Magnetism of Cobalt(II) Complex with Aromatic Trans-Cinnamic Acid

by
Petr Halaš
,
Ivan Nemec
and
Radovan Herchel
*
Department of Inorganic Chemistry, Faculty of Science, Palacký University, 17. listopadu 12, CZ-771 46 Olomouc, Czech Republic
*
Author to whom correspondence should be addressed.
Magnetochemistry 2023, 9(11), 229; https://doi.org/10.3390/magnetochemistry9110229
Submission received: 11 October 2023 / Revised: 10 November 2023 / Accepted: 13 November 2023 / Published: 16 November 2023
(This article belongs to the Section Molecular Magnetism)
Browse Figures
Versions Notes

Abstract

:
The hexacoordinate Co(II) complex [Co(neo)2(cin)][BPh4]·½Me2CO (1·½Me2CO) containing trans-cinnamic acid (Hcin) and neocuproine (neo) was prepared. The compound 1·½Me2CO was characterized via single-crystal X-ray analysis, FT-IR spectroscopy, and magnetic measurements. The coordination polyhedron of the complex cation adopts a deformed octahedron shape, and cinnamate exhibits a bidentate mode of coordination, which is unusual for mononuclear Co(II) cinnamate complexes. The analysis of DC magnetic measurements with zero-field splitting (ZFS) spin Hamiltonian revealed large magnetic anisotropy defined by the axial ZFS parameter D = +53.2 cm−1. AC susceptibility measurements revealed the slow relaxation of magnetization under the applied field; thus, 1·½Me2CO behaves as a field-induced single-molecule magnet. The analysis of magnetic properties was also supported by CASSCF/NEVPT2 calculations.

1. Introduction

Single-ion magnets (SIMs), a subgroup of single-molecule magnets (SMMs) where only one metallic center is responsible for the slow relaxation of magnetization, have become increasingly attractive as more and more newly discovered SIMs have exhibited higher relaxation barriers and blocking temperatures, culminating in a series of dysprosocenium complexes [1,2] with the highest blocking temperature yet achieved of TB = 80 K and Ueff = 1541 cm−1 for the [(CpiPr5)Dy(Cp*)][B(C6F5)4] complex (CpiPr5 = penta(isopropyl)cyclopentadienyl, Cp* = pentamethylcyclopentadienyl) [3].
However, as these compounds are usually highly sensitive to air and moisture, more stable alternatives, albeit generally exhibiting lower barriers, are still of much interest, such as the [Dy(bbpen)X] derivatives (bbpen = N,N′-bis(2-hydroxybenzyl)-N,N′-bis(2-pyridylmethyl)ethylenediamine) [4,5] for Ln(III) systems or the (HNEt3)2[Co(bmsab)2] complex (bmsab = N,N′-1,2-phenylenebis(methanesulfonamide)) [6] for 3d metal systems. Out of the 3d metals, Co(II) systems are by far the most promising due to their large spin-orbit coupling and good predisposition for significant magnetic anisotropy; thus, a plethora of cobalt-based SIMs already exist [7,8,9]. Co(II) systems do not exhibit such high barriers but are generally easier to design compared to their Ln(III) counterparts as their coordination sphere is usually limited to 4–6 donor atoms, whereas Ln(III) may contain a much larger number of donor atoms, commonly between 8 and 12. This often leads to the unwanted coordination of either a solvent molecule or a bridging ligand, which might worsen the magnetic properties [10].
The magnetic bistability of SIMs offers a range of applications such as spintronics, quantum computing or high-density data storage [11]. Most often, switching between the spin states is performed with the external magnetic field; however, there has been much interest in the design of systems with alternative ways of effecting the form of switching that may, for example, introduce on/off states of the slow relaxation of magnetization, provide ultrafast changes in magnetization or eliminate the impracticalities associated with external magnetic field switching focused to a scale of single molecules [12,13]. One method of design is based on the introduction of photoswitchable molecules into the metal complex structure, which would induce a change in the magnetic properties [14] upon irradiation, analogously to what has already been observed for ligand-driven light-induced spin change complexes [15,16].
Photoswitchable complexes containing azo (N=N) [17,18] or olefin (C=C) [19,20] moieties have been well known for their cis/trans-photoisomerization property [21] for some time, although not many have been studied for their photomagnetic properties. Their photoisomerization is generally only observed in solution as crystal packing often sterically hinders the switching action in the solid phase; however, some research groups have shown that this can be overcome, for example, by dissolving and setting the sample in a polymer matrix [22] or by utilizing layered polyoxometalate films [23].
The naturally occurring and thermodynamically more stable trans-isomer of cinnamic acid, well known for its honey-like odor, ref. [24], has been historically one of the first widely studied olefin photoisomerisable systems. Dating back to the early 1900s, the first irradiation studies [25,26] showed the possibility of the isolation of the separate geometric isomers, and B. K. Vaidya later reported [27] on a more robust procedure for the isolation of the cis-isomer by simply irradiating a methanolic solution of a trans-cinnamic acid derivative with UV light and subsequently separating the isomers via fractional crystallization or, alternatively, vacuum distillation [28]. A new easier methodology for the preparation of cis-isomers of various cinnamic acid derivatives was introduced by M. L. Salum and co-workers, which involves the irradiation of their ionic liquids in acetonitrile, during which less soluble cis-isomer precipitates out of the solution [29]. Compared to most of its azobenzene counterparts, cis-cinnamic acid shows much better thermal stability and only readily reisomerises to the trans-isomer when heated. Interestingly, only a handful of mononuclear Co(II) complexes containing cinnamic acid as a ligand have been prepared, and in all cases, cinnamic acid coordinates monodentately with the single carboxylate oxygen to the metal center [30,31,32,33].
Based on the aforementioned insights, we decided to utilize trans-cinnamic acid (Hcin) as a co-ligand for the preparation of a new single-ion magnet with a photoswitchable moiety. The cobalt(II) bis(neocuproine) complex seemed to be an excellent initial building block, as a more recent paper by J. Vallejo and co-workers utilized this exact system with the benzoic acid co-ligand to yield a complex exhibiting a slow relaxation of magnetization [34]. Moreover, the neocuproine ligand was beneficial for the preparation of other Co(II) SMMs in the past [35,36,37]. We were successful in the preparation of the title compound [Co(neo)2(cin)][BPh4]·½Me2CO (1·½Me2CO) (Scheme 1), a novel single-ion magnet with a light-switchable moiety, and herein report on its synthesis, crystal structure, and magnetic data measurements.

2. Materials and Methods

2.1. General Considerations and Instrumentation

All chemicals and solvents were purchased from available commercial sources and were used without further purification.
C/H/N elemental analysis was performed on a Thermo Scientific Flash 2000 analyzer. Infrared spectra were obtained on Jasco FT/IR-4700 via the ATR technique. Thermal stability was studied using a Discovery SDT 650 thermal analyzer (TA Instruments) for simultaneous thermogravimetry (TG) and differential scanning calorimetry (DSC) with a 5 °C/min gradient of temperature and a dynamic air atmosphere (50 mL/min).
The shape of the coordination polyhedron was analyzed with Shape 2.1 software [38,39]. The crystal data and computational data were analyzed and visualized with the help of Mercury [40], Diamond [41], and Vesta 3 [42] software.

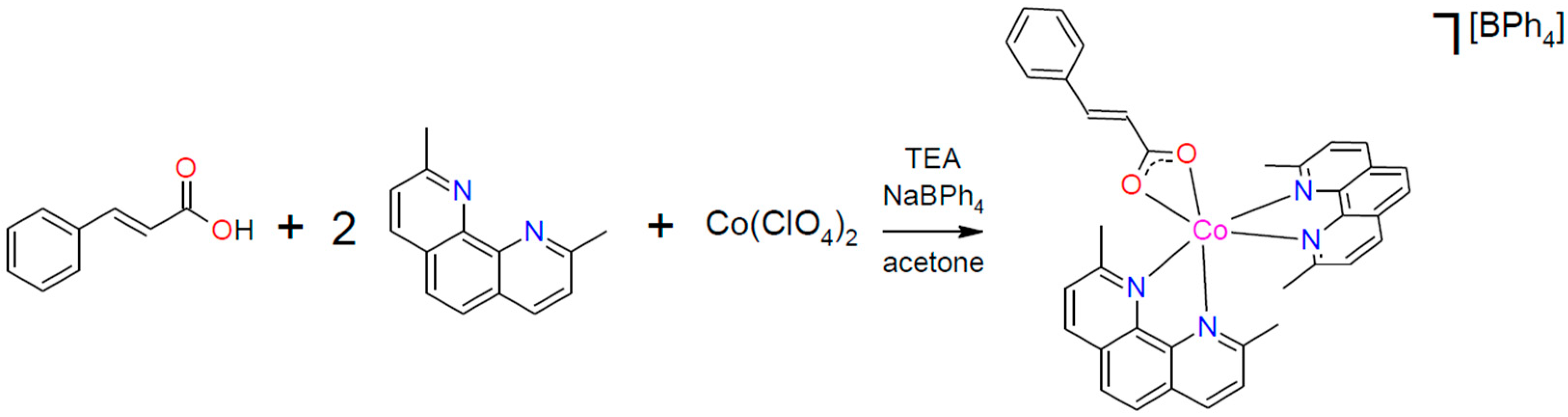
2.2. Synthesis of Compound 1·½Me2CO

To a stirred solution of 45.8 mg (125 µmol) of Co(ClO4)2·6H2O in 5 mL of acetone, 54.3 mg (250 µmol) of neocuproine (neo) hemihydrate was added. Subsequently, 18.5 mg (125 µmol) of trans-cinnamic acid (Hcin) was added, and after its dissolution, 17.3 μL (125 µmol) of triethylamine was added. To this mixture, a filtered solution of 85.5 mg (250 µmol) of sodium tetraphenylborate in 3 mL of acetone was poured in, and the reaction mixture was put into a fridge overnight to yield pink–red crystals of the [Co(neo)2(cin)][BPh4]·½Me2CO product, which were filtered off, washed with acetone and dried in a vacuum desiccator. The yield was 70.2 mg (60%). Large crystals were obtained by letting the reaction mixture stand undisturbed at room temperature for several days. Anal. Calc. values for C62.5H54BCoN4O2.5 are as follows: C, 77.32; H, 5.61; N, 5.77. The findings were as follows: C, 77.20; H, 5.65; N, 5.74. FT-IR (ATR, cm−1): 486 w, 549 w, 591 w, 607 w, 654 w, 683 w, 702 s, 729 m, 742 w, 774 w, 813 w, 851 m, 980 w, 1030 w, 1067 w, 1100 w, 1152 w, 1213 w, 1249 w, 1293 w, 1357 m, 1417 s, 1454 w, 1479 w, 1498 m, 1537 w, 1563 w, 1579 w, 1592 w, 1622 w, 1641 m, 1715 w, and 3055 m.

2.3. X-ray Diffraction Analysis

A suitable single crystal of compound 1 was used for the X-ray diffraction experiment using a Rigaku XtaLAB Synergy-I diffractometer with a microfocused RTG-source PhotonJet-i (Cu) and a HyPix Bantam detector. The structure was solved using the SHELXT [43] program and refined via the full matrix least-squares procedure with Olex2.refine [44] in OLEX2 (version 1.5) [45]. The multi-scan absorption corrections were applied using the program CrysAlisPro 1.171.40.82a [46]. The crystal structure of compound 1 was determined at two different temperatures. Initially, the measurement was conducted at room temperature (1@293K). The quality of structure refinement was sufficient; however, despite observing a small residual density, we were not able to confirm the presence of the co-crystallized acetone molecule. Upon measuring the crystal structure at 100K, we confirmed the presence of half of an acetone molecule per asymmetric unit in the crystal structure of 1@100K. The quality of refinement for 1@100K was significantly better than that of 1@293K; therefore, the structure of 1@100K was used for the discussion of the crystal structure.
The non-routine aspects of refinement were as follows. In each cavity within the crystal structure of the studied compound, there resides one acetone molecule. This molecule exhibits disorder due to a combination of positional and disorder involving a special position. Attempts to model this disorder did not yield a satisfactory model with physically meaningful bond lengths and angles for the acetone molecule. Consequently, solvent density was removed using a solvent masking procedure [47] incorporated in OLEX2. As a result, 66 electrons were found within the 358 Å3 of a void volume per unit cell. This is consistent with the presence of 0.5 acetone per asymmetric unit cell (equivalent to 16 electrons per asymmetric unit, and 64 electrons per unit cell).
X-ray powder diffraction was measured using Rigaku MiniFlex600.

2.4. Magnetic Measurements

Both static and dynamic magnetic field measurements were performed on a Quantum Design MPMS®3 SQUID magnetometer. The temperature-dependent DC magnetic data were acquired at B = 0.2 T, and field-dependent isothermal data were measured in the range B = 0–7 T for T = 2 and 5 K. The magnetic data were corrected for diamagnetic susceptibility and the signal of the eicosane and sample holder. Diamagnetic susceptibility was estimated using Pascal’s constants [48]. The AC susceptibility data were acquired for frequencies 1–1000 Hz for a temperature range up to 6 K, and for a magnetic field of up to 0.5 T.

2.5. Theoretical Calculations

Theoretical calculations were performed with the ORCA 5.0.4 software package [49,50]. First, hydrogen atomic positions were optimized using density functional theory (DFT) on a complex cation fragment extracted from the crystal structure using a BP86 functional [51]. The resolution of identity (RI) approximation [52] with the def2/J auxiliary basis set [53] for Coulomb fitting was employed, and the def2-TZVP basis set for all atoms except for H and C, where less expensive def2-SVP was chosen, was employed [54]. Next, the state-average complete active space self-consistent field (CASSCF) calculations [55] supplemented with N-electron valence second-order perturbation theory (NEVPT2) [56,57] were performed with the active space defined by 7 electrons in 5 d-orbitals, CAS(7e,5o). The same basis sets were used, and additionally, a def2-TZVP/C auxiliary basis set, for correlation fitting [58], and chain-of-sphere approximation (RIJCOSX) [59] were utilized.

3. Results and Discussion

3.1. Synthesis and General Characterization

The synthesis of the title compound was performed in a one-step fashion and did not require an inert atmosphere or anhydrous conditions (Scheme 1). First, the solution of the bis(neocuproine) cobalt(II) precursor complex was prepared by dissolving cobalt perchlorate in acetone, into which two equivalents of neocuproine hemihydrate were added. To this solution, one equivalent of trans-cinnamic acid was added and subsequently neutralized with one equivalent of triethylamine. The perchlorate anion was then replaced with tetraphenylborate by adding a solution of two equivalents of sodium tetraphenylborate in acetone. The bulk crystalline product then crystallized in a fridge overnight. Big monocrystals could be obtained via slow and undisturbed isothermal crystallization at room temperature.
The purity of the bulk sample was confirmed via elemental analysis and X-ray powder diffraction (Figure S1), and was in agreement with the crystal structure determined from a single crystal. As is typical for coordination compounds, the FT-IR spectrum (Figure S2) shows weak and downfield-shifted stretching vibrations of the coordinated cinnamate carboxylate group at 1641 cm−1. Intense C=C/C=N stretching vibrations of the aromatic rings are observed around 1417 cm−1 owing to the high abundance of aromatic rings in the structure. Bending out-of-plane vibrations of C-H groups and aromatic rings can then be observed at 851, 729 and 702 cm−1. C-H stretching vibrations of the methyl groups of neocuproine are present at 3055 cm−1. Additionally, the weak vibration at 1715 cm−1 suggests a presence of acetone in the crystal structure, which is supported by elemental analysis and thermogravimetric measurements (Figure S6), where the gradual loss of acetone can be observed up to 215 °C followed by the decomposition of the complex. Single-crystal X-ray diffraction analysis confirmed that the title compound, compound 1, forms an acetone hemisolvate.
Moreover, the photochemical studies were performed in the solid phase on powdered samples utilizing infrared spectroscopy, as a distinct change in FT-IR spectra is observed for cis- and trans-isomers of cinnamic acid [60]. The individual FT-IR spectra were measured before and after 15 min of simultaneous irradiation with two 6 W UV lamps (254 and 365 nm). Experiments were performed on compound 1·½Me2CO and also dried compound 1 (dried for 30 min at 160 °C). No change in spectra was observed after UV irradiation (Figure S7) for both 1·½Me2CO and 1, and we therefore conclude that no photoisomerization occurs in the aforementioned conditions. It is most likely that the crystal packing blocks the switching action even after the removal of the acetone molecule.

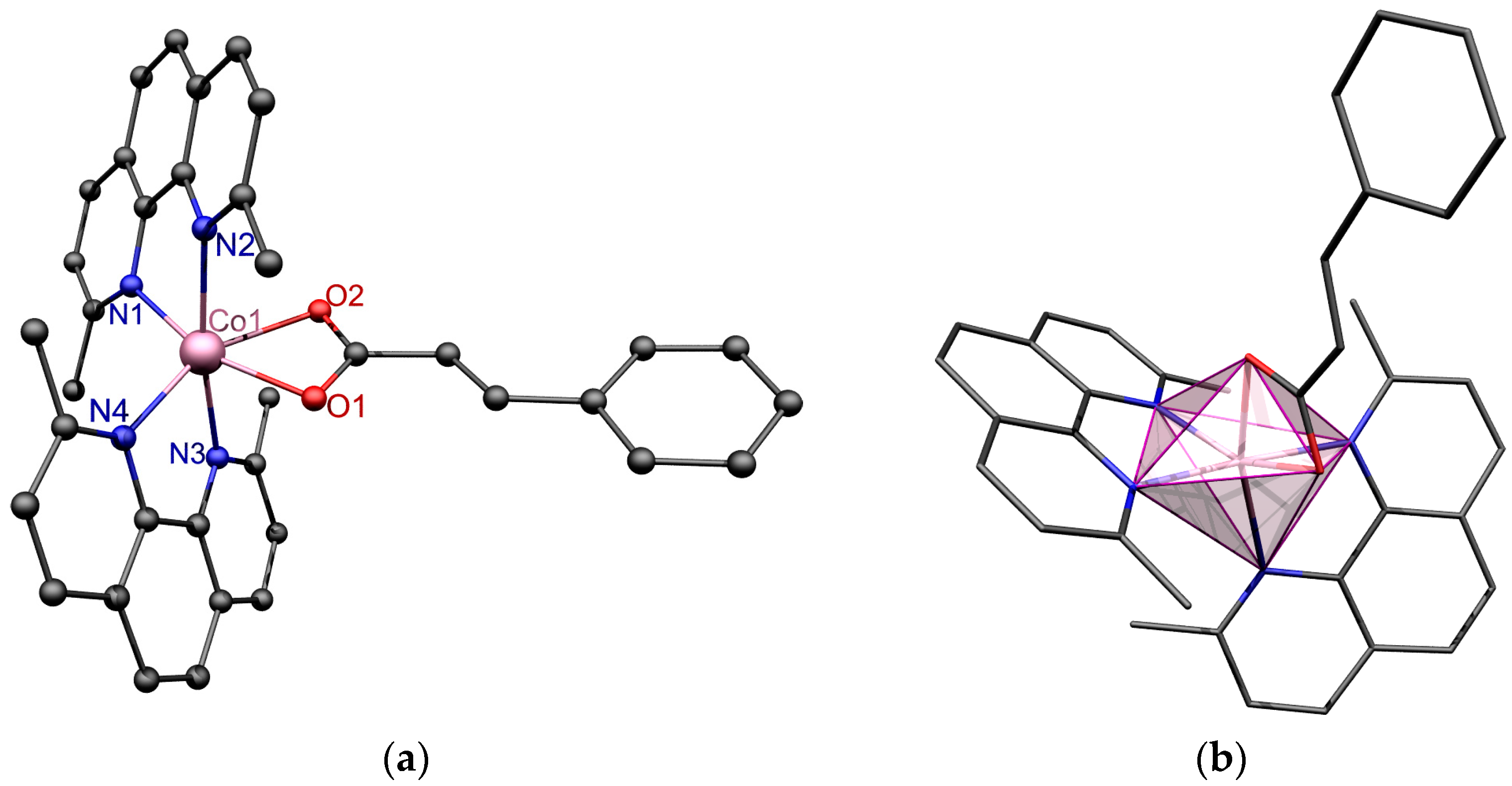
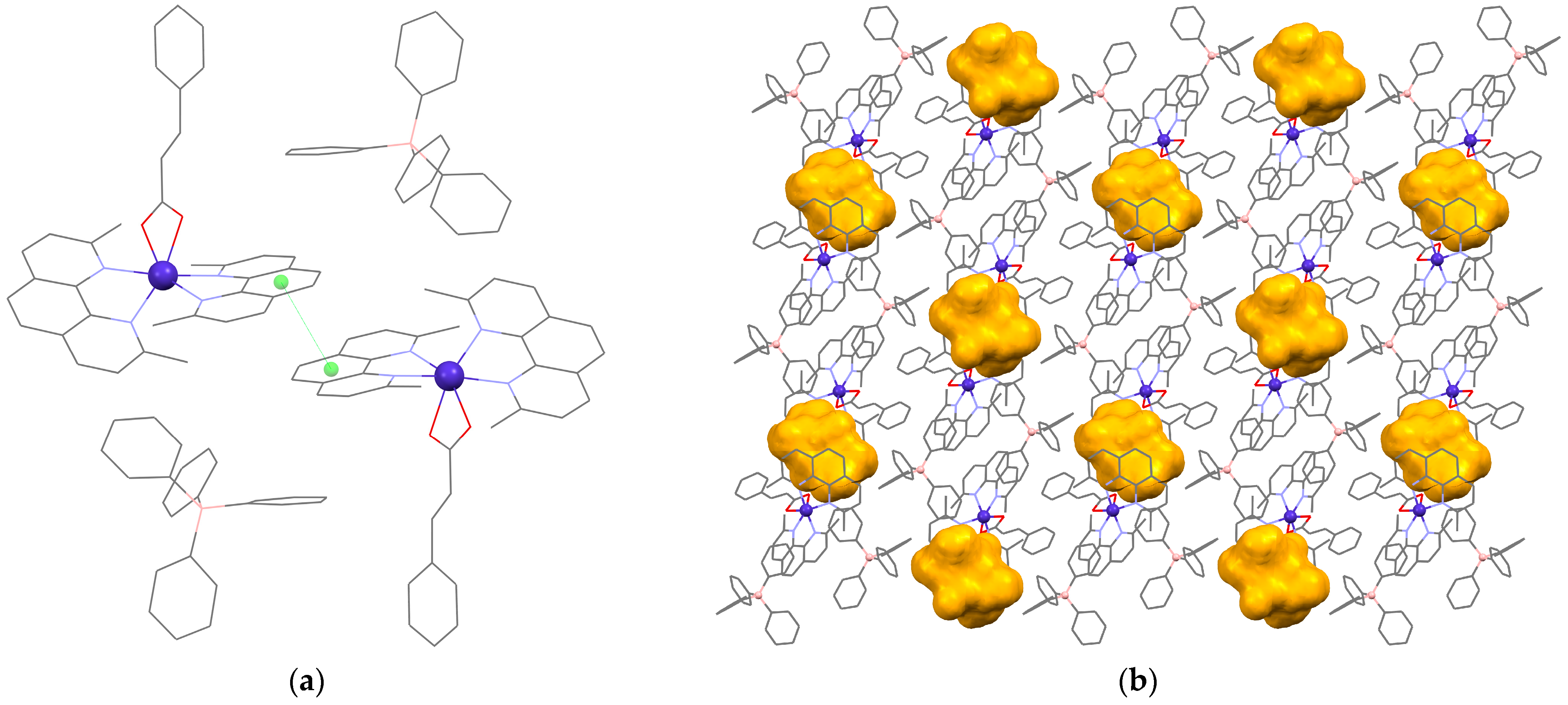
3.2. Description of the Crystal Structure

Prepared single crystals of 1·½Me2CO (Table 1) belong to the monoclinic system with the space group P21/n. The asymmetric unit (Figure 1a) contains a complex cation, [Co(neo)2(cin)]+, and tetraphenylborate anion, [BPh4]−. The cobalt(II) ion is hexacoordinate with the {N4O2} donor set. The geometry of the coordination polyhedron was analyzed with Shape 2.1 software, which determined the shape to be closest to the octahedron (Oh) with a score of 3.150. Inspection of the structure revealed that the deviation from a perfect octahedron is caused mainly by the steric hindrance of the neocuproine methyl groups (Figure 1b). The carboxylate group of the cinnamic acid was coordinated with the metal center with both oxygen atoms almost equidistantly and with bond lengths d(Co1-O1) = 2.134(1) Å and d(Co1-O2) = 2.193(1) Å, and they form an acute angle of ∠(O1-Co1-O2) = 61.12(4)°, which additionally contributes to the deformation of the coordination polyhedron. To our knowledge, this is the first resolved structure of a mononuclear Co(II) complex where the cinnamate ligand is coordinated bidentately to a single cobalt center. Bond lengths and angles of the coordination polyhedron are summarized in Table 2.
Despite the abundant presence of aromatic rings, not many of them form any notable π–π interactions, except for stacking contact between the two neocuproine rings of adjacent complex cations of a unit cell (Figure 2a) with a distance between their centroids of 4.030 Å. The closest distance between the cobalt centers is 10.1549(5) Å, which basically rules out potential magnetic exchange interactions.
The cavity, calculated using a probe radius of 1.2 Å, is situated adjacent to the cinnamate fragment and occupies 6.6% of the unit cell volume (Figure 2b). As previously discussed in Section 3.1, each cavity is occupied by one acetone molecule. The precise modeling of their positions was not carried out due to their involvement in intricate positional disorder (for detailed information, please consult the experimental section).

3.3. Magnetic Properties

3.3.1. Static Magnetic Properties

The temperature- and field-dependent DC magnetic data of 1·½Me2CO are presented in Figure 3. The effective magnetic moment at room temperature was determined to be μeff/μB = 5.12, a value much higher than the calculated spin-only moment of μeff/μB = g S ( S + 1 ) = 3.87 for Co(II) with S = 3/2 and g = 2.0. The gradual decrease in μeff was then observed as the sample was cooled down to 1.8 K with μeff/μB = 3.81. This strongly suggests that complex 1·½Me2CO possesses large magnetic anisotropy due to the zero-field splitting [61]. Isothermal molar magnetization was saturated to the value of Mmol/(NAμB) = 2.35 at 2 K and 7 T, which also reflects large magnetic anisotropy because the expected theoretical value is Mmol/(NAμB) = g∙S = 3 for g = 2.0. Therefore, the simultaneous fit of both temperature- and field-dependent magnetization data was performed using the following spin Hamiltonian (Equation (1)):
H ^ = D S ^ z 2 − S ^ / 3 + E S ^ x 2 − S ^ y 2 + μ B B g S ^
where D and E are axial and rhombic zero-field splitting parameters, respectively, and the last term is the Zeeman term [44]. The analysis was performed for both positive and negative D-parameters; however, only the positive D-parameter was able to reproduce all experimental data properly. The best-fit parameters are D = +53.2 cm−1, gxy = 2.59, gz = 2.0 (fixed) and χTIP = 21.3 × 10−9 m3mol−1 (Figure 3), where χTIP represents temperature-independent paramagnetism [62]. Such a large value of D means that magnetic levels originating from S = 3/2 are separated by Δ = 2D = 106 cm−1. It needs to be mentioned that the fitting procedure was not sensitive to the E parameter.

3.3.2. Dynamic Magnetic Properties

The AC susceptibility measurements were performed to investigate the possibility of the slow relaxation of the magnetization in compound 1·½Me2CO. Therefore, first, AC susceptibility was measured at T = 2 K with a varying static magnetic field as depicted in Figure 4. Evidently, the application of the static magnetic field resulted in an increase in out-of-phase AC susceptibility, and it was possible to analyze experimental data within the range of Bdc = 0.015 to 0.2 T with the one-component Debye model in accordance with Equation (2),
χ 2 π f = χ S + χ T − χ S 1 + i 2 π f τ 1 − α
which led to isothermal (χT) and adiabatic (χS) susceptibilities, relaxation times (τ) and distribution parameters (α)—see Table S1. The low-frequency relaxation channel started to appear above 0.2 T and was not analyzed further.
Next, the field-dependence of τ vs. B was subsequently fitted with Equation (3),
1 τ = b 1 1 + b 2 B 2 + d 1 + e B 2 1 + f B 2 T n
which comprises quantum tunnelling (parameters b1 and b2) and the Raman process (parameters d, e, f and n). As the expected value of n for Kramers ions is nine, it was fixed during fitting [63,64]. The resulting parameters are b1 = 548(67) s−1, b2 = 486(136) T−2, d = 1.60(15) s−1K−9, e = 39(14) T−2, and f = 4.4(4.4) T−2—see Figure 4.
As the field dependence of τ showed a maximum in the range 0.05–0.1 T, the static magnetic field was then fixed to BDC = 0.09 T and the AC susceptibility was measured from 1.8 to 6 K—see Figure 5. Herein, the experimental data were again analyzed with a one-component Debye model (Equation (2)) in the range 1.8–5.0 K, and the resulting parameters are listed in Table S2. The temperature dependence of τ was analyzed with Equation (4),
1 τ = C T n
for the Raman process, which resulted in C = 129(2) s−1K−n and n = 3.16(2)—see Figure 5. The Raman exponent has smaller value than the expected value of 9 for Kramers ions, but when optical and acoustic phonons are considered, values in the range 1–6 are acceptable [33,65,66,67,68].

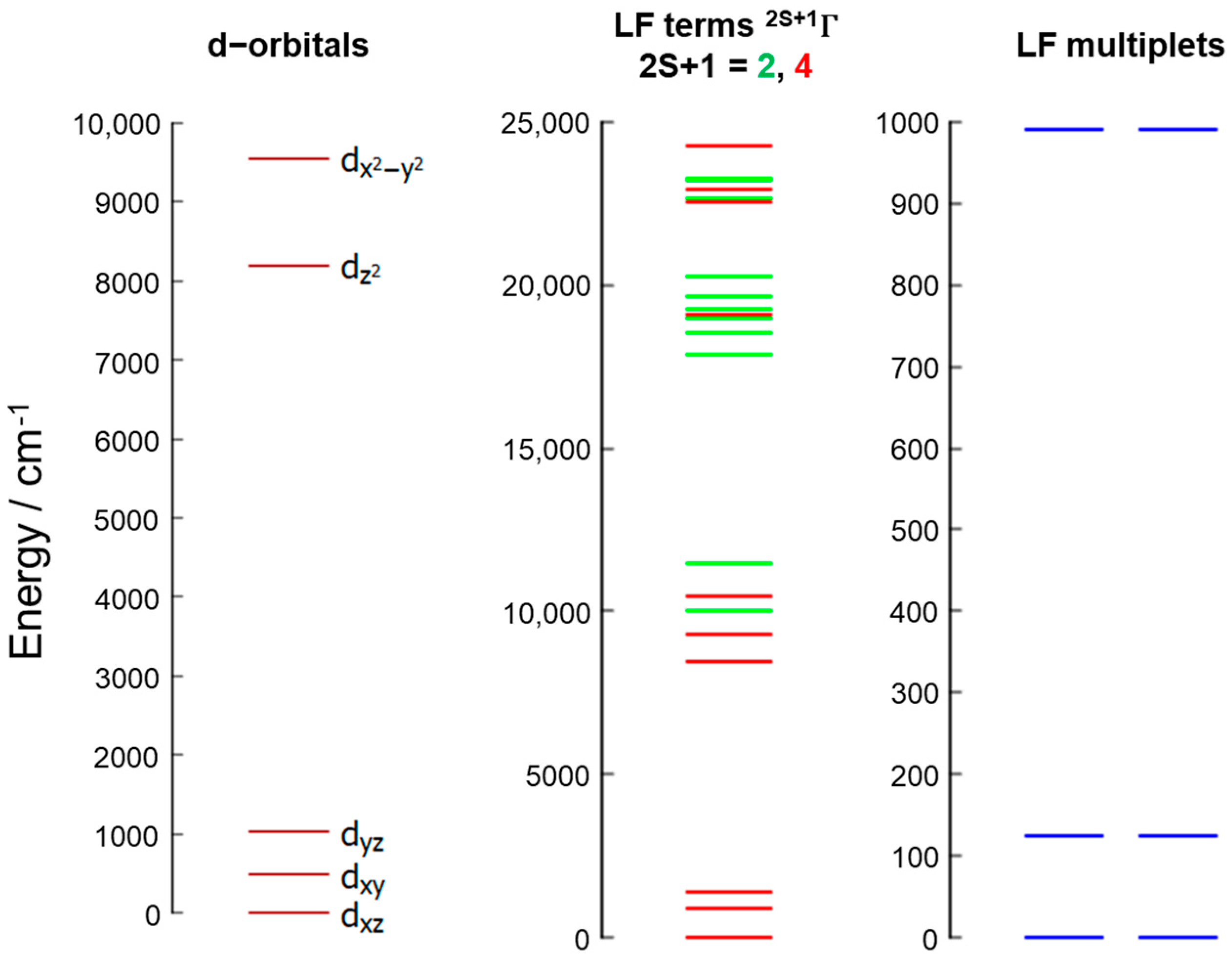
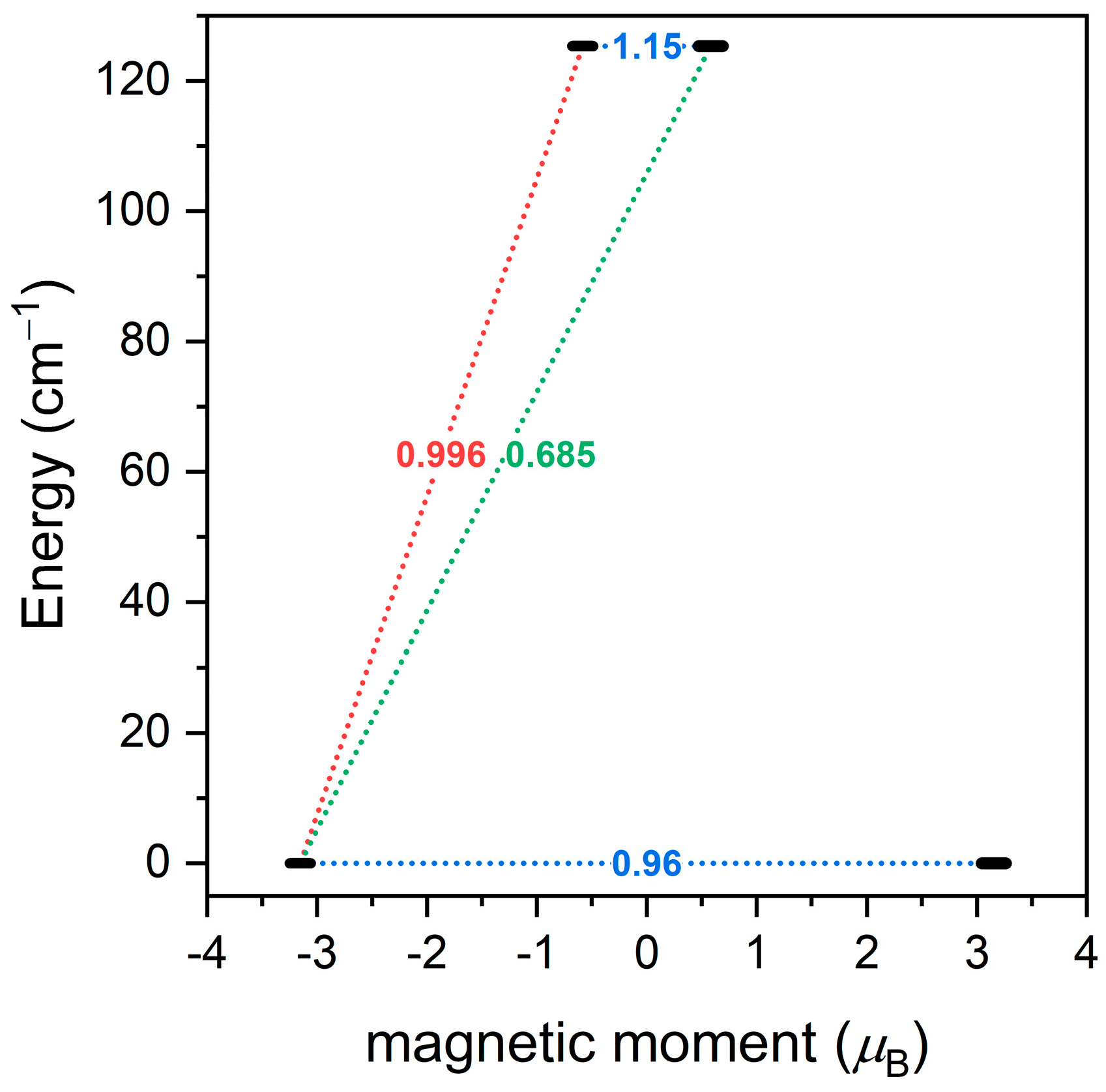
3.4. Theoretical Calculations

With the help of ab initio ligand field theory (AILFT) [69,70], the energies of d-orbitals were calculated and are depicted in Figure 6. The assignment of the corresponding d-orbitals is shown in Figure S3. The splitting of d-orbitals is typical of pseudo-octahedral CoII complexes, in which t2g an eg orbitals within ideal Oh symmetry are split due to the lower symmetry of the real complex under study. Hence, the ground ligand field term, T1g, is also split into three terms within the range 0–1500 cm−1 (Figure 6, middle). Finally, the spin–orbit interactions result in ligand field multiplets, which are shown in Figure 6 (right), where the energy separation of two lowest Kramers doublets is Δ = 125 cm−1, and this value is close to that derived from the fitting of the experimental magnetic data. The further analysis resulted in the zero-field splitting parameters D = 60.7 cm−1, E/D = 0.149, gx = 2.453, gy = 2.666 and gz = 2.004. The actual D-tensor is depicted in Figure S4. As the E/D ratio is non-zero, the resulting magnetic anisotropy can be either of an easy-plane or easy-axis type [71]. Hence, the ground state Kramers doublet was analyzed with the effective spin 1/2, which resulted in g1 = 2.010, g2 = 3.753, g3 = 6.316 and gave = 4.026. Thus, it can be concluded that it holds g1, g2 < gave and gave < g3, which means there is an easy-axis type of the magnetic anisotropy in compound 1 according to CASSCF/NEVPT2 calculations. This is in agreement with the calculated 3D magnetization depicted in Figure S5 (T = 2 K and B = 0.1 T), which shows a shape characteristic of an easy-axis type of anisotropy. Therefore, further analysis was conducted with the SINGLE_ANISO module [72], in order to compute the ab initio magnetization blocking barrier displayed in Figure 7. The corresponding matrix element of the transversal magnetic moment between ground states with opposite magnetization is equal to 0.96; thus, it is larger than 0.1, which suggests a large predisposition for the quantum tunneling of magnetization, which is in line with the experimental AC data.

4. Conclusions

The crystal structure shows an unusual bidentate mode of coordination of cinnamate into a single Co(II) center, contributing to the deformation of the coordination polyhedron. Single-crystal measurement at room temperature most likely led to the formation of voids due to solvent loss.
Dynamic magnetic measurements revealed that the title compound, compound 1·½Me2CO, exhibits a slow relaxation of magnetization in an applied external magnetic field with a predominant Raman process as the relaxation mechanism. Static magnetic measurements, in combination with theoretical calculations, showed that compound 1·½Me2CO possesses large magnetic anisotropy of the axial type due to zero-field splitting with a positive D value of +53.2 cm−1. Despite the evident discrepancy between fitted and calculated rhombicity, the experimental data are in good agreement with CASSCF/NEVPT2 results. It is well known that static magnetic measurements usually cannot determine rhombicity with high precision, and more sensitive methods, such as EPR, would have to be utilized to resolve both E and g-factors more accurately.
To conclude, a Co(II) field-induced single-molecule magnet with a potentially photoisomerizable ligand was prepared and, this opens up an avenue for the further investigation of similar compounds, which would be interesting not only in the field of molecular magnetism, but also in the field of photomagnetism.

Supplementary Materials

The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/magnetochemistry9110229/s1. Figure S1. X-ray powder diffraction of compound 1·½Me2CO measured at room temperature and compared to the simulation calculated from SC-XRD data measured at 293 K. Figure S2. FT-IR spectrum of compound 1·½Me2CO. Figure S3. Assignment of energy levels of d-orbitals of compound 1. Figure S4. D-tensor (NEVPT2) of compound 1. Axes: x—red; y—green; z—blue. Figure S5. Calculated 3D magnetization of compound 1 at T = 2 K and B = 0.1 T. Figure S6. The results of simultaneous TG/DSC thermal analysis of 1·½Me2CO (5 °C/min, 50 mL/min air atmosphere) depicted as TG (in blue) and DSC (green) curves; TG = thermogravimetry, and DSC = differential scanning calorimetry. Figure S7. Top—compound 1·½Me2CO before (blue) and after (red) irradiation. Bottom—compound 1 before (blue) and after (red) irradiation. Table S1. The parameters of the one-component Debye model used to analyze the field-dependent AC susceptibility data of compound 1·½Me2CO; Table S2. The parameters of the one-component Debye model used to analyze the temperature-dependent AC susceptibility data of compound 1·½Me2CO.

Author Contributions

Conceptualization, P.H.; methodology, P.H.; validation, R.H.; formal analysis, P.H., I.N. and R.H.; investigation, P.H. and I.N.; resources, R.H.; data curation, R.H and I.N.; writing—original draft preparation, P.H.; writing—review and editing, R.H. and I.N.; visualization, P.H. and R.H.; supervision, R.H.; project administration, R.H.; funding acquisition, R.H. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Palacký University in Olomouc projects IGA_PrF_2021_009 and IGA_PrF_2022_006.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

All data are contained within the article.

Acknowledgments

The authors would like to thank P. Richterova for the elemental analysis measurement, O. F. Fellner for the X-ray powder diffraction measurement, P. Starha for the TG/DSC measurement and A. Brookfield (The University of Manchester) for the magnetic data measurements.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Goodwin, C.A.; Ortu, F.; Reta, D.; Chilton, N.F.; Mills, D.P. Molecular magnetic hysteresis at 60 kelvin in dysprosocenium. Nature 2017, 548, 439–442. [Google Scholar] [CrossRef] [PubMed]
  2. Guo, F.S.; Day, B.M.; Chen, Y.C.; Tong, M.L.; Mansikkamäki, A.; Layfield, R.A. A dysprosium metallocene single-molecule magnet functioning at the axial limit. Angew. Chem. Int. Ed. 2017, 56, 11445–11449. [Google Scholar] [CrossRef] [PubMed]
  3. Guo, F.S.; Day, B.M.; Chen, Y.C.; Tong, M.L.; Mansikkamäki, A.; Layfield, R.A. Magnetic hysteresis up to 80 kelvin in a dysprosium metallocene single-molecule magnet. Science 2018, 362, 1400–1403. [Google Scholar] [CrossRef] [PubMed]
  4. Liu, J.; Chen, Y.C.; Liu, J.L.; Vieru, V.; Ungur, L.; Jia, J.H.; Chibotaru, L.F.; Lan, Y.; Wernsdorfer, W.; Gao, S.; et al. A stable pentagonal bipyramidal Dy (III) single-ion magnet with a record magnetization reversal barrier over 1000 K. J. Am. Chem. Soc. 2016, 138, 5441–5450. [Google Scholar] [CrossRef]
  5. Santana, F.S.; Perfetti, M.; Briganti, M.; Sacco, F.; Poneti, G.; Ravera, E.; Soares, J.F.; Sessoli, R. A dysprosium single molecule magnet outperforming current pseudocontact shift agents. Chem. Sci. 2022, 13, 5860–5871. [Google Scholar] [CrossRef]
  6. Rechkemmer, Y.; Breitgoff, F.D.; Van Der Meer, M.; Atanasov, M.; Hakl, M.; Orlita, M.; Neugebauer, P.; Neese, F.; Sarkar, B.; Van Slageren, J. A four-coordinate cobalt (II) single-ion magnet with coercivity and a very high energy barrier. Nat. Commun. 2016, 7, 10467. [Google Scholar] [CrossRef]
  7. Herchel, R.; Váhovská, L.; Potočňák, I.; Travnicek, Z. Slow magnetic relaxation in octahedral cobalt (II) field-induced single-ion magnet with positive axial and large rhombic anisotropy. Inorg. Chem. 2014, 53, 5896–5898. [Google Scholar] [CrossRef]
  8. Zadrozny, J.M.; Long, J.R. Slow magnetic relaxation at zero field in the tetrahedral complex [Co(SPh)4]2−. J. Am. Chem. Soc. 2011, 133, 20732–20734. [Google Scholar] [CrossRef]
  9. Jurca, T.; Farghal, A.; Lin, P.H.; Korobkov, I.; Murugesu, M.; Richeson, D.S. Single-molecule magnet behavior with a single metal center enhanced through peripheral ligand modifications. J. Am. Chem. Soc. 2011, 133, 15814–15817. [Google Scholar] [CrossRef]
  10. Ma, X.; Chen, B.; Zhang, Y.Q.; Yang, J.; Shi, Q.; Ma, Y.; Liu, X. Enhancing single-molecule magnet behaviour through decorating terminal ligands in Dy2 compounds. Dalton Trans. 2019, 48, 12622–12631. [Google Scholar] [CrossRef]
  11. Bogani, L.; Wernsdorfer, W. Molecular spintronics using single-molecule magnets. Nat. Mater. 2008, 7, 179–186. [Google Scholar] [CrossRef] [PubMed]
  12. Liedy, F.; Eng, J.; McNab, R.; Inglis, R.; Penfold, T.J.; Brechin, E.K.; Johansson, J.O. Vibrational coherences in manganese single-molecule magnets after ultrafast photoexcitation. Nat. Chem. 2020, 12, 452–458. [Google Scholar] [CrossRef] [PubMed]
  13. Stupakiewicz, A.; Szerenos, K.; Afanasiev, D.; Kirilyuk, A.; Kimel, A.V. Ultrafast nonthermal photo-magnetic recording in a transparent medium. Nature 2017, 542, 71–74. [Google Scholar] [CrossRef] [PubMed]
  14. Rogacz, K.; Brzozowska, M.; Baś, S.; Kurpiewska, K.; Pinkowicz, D. Low-coordinate erbium(III) single-molecule magnets with photochromic behavior. Inorg. Chem. 2022, 61, 16295–16306. [Google Scholar] [CrossRef] [PubMed]
  15. Hasegawa, Y.; Kume, S.; Nishihara, H. Reversible light-induced magnetization change in an azobenzene-attached pyridylbenzimidazole complex of iron(II) at room temperature. Dalton Trans. 2009, 2, 280–284. [Google Scholar] [CrossRef]
  16. Chastanet, G.; Lorenc, M.; Bertoni, R.; Desplanches, C. Light-induced spin crossover—Solution and solid-state processes. Comptes Rendus Chim. 2018, 21, 1075–1094. [Google Scholar] [CrossRef]
  17. Kume, S.; Kurihara, M.; Nishihara, H. Reversible trans–cis photoisomerization of azobenzene-attached bipyridine ligands coordinated to cobalt using a single UV light source and the Co(III)/Co(II) redox change. Chem. Commun. 2001, 17, 1656–1657. [Google Scholar] [CrossRef]
  18. Yutaka, T.; Mori, I.; Kurihara, M.; Tamai, N.; Nishihara, H. Photochemical behavior of azobenzene-conjugated CoII, CoIII, and FeII bis(terpyridine) complexes. Inorg. Chem. 2003, 42, 6306–6313. [Google Scholar] [CrossRef]
  19. Chen, L.; Tan, Y.; Xu, H.; Wang, K.; Chen, Z.H.; Zheng, N.; Li, Y.Q.; Lin, L.R. Enhanced E/Z-photoisomerization and luminescence of stilbene derivative co-coordinated in di-β-diketonate lanthanide complexes. Dalton Trans. 2020, 49, 16745–16761. [Google Scholar] [CrossRef]
  20. Pal, P.; Mukherjee, S.; Maity, D.; Baitalik, S. Synthesis, Structural Characterization, and Luminescence Switching of Diarylethene-Conjugated Ru(II)-Terpyridine Complexes by trans–cis Photoisomerization: Experimental and DFT/TD-DFT Investigation. Inorg. Chem. 2018, 57, 5743–5753. [Google Scholar] [CrossRef]
  21. Guerchais, V.; Le Bozec, H. Metal complexes featuring photochromic ligands. In Molecular Organometallic Materials for Optics. Topics in Organometallic Chemistry; Bozec, H., Guerchais, V., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 28, pp. 171–225. [Google Scholar] [CrossRef]
  22. Lin, L.R.; Wang, X.; Wei, G.N.; Tang, H.H.; Zhang, H.; Ma, L.H. Azobenzene-derived tris-β-diketonate lanthanide complexes: Reversible trans-to-cis photoisomerization in solution and solid state. Dalton Trans. 2016, 45, 14954–14964. [Google Scholar] [CrossRef] [PubMed]
  23. Yamamoto, T.; Umemura, Y.; Einaga, Y. Structure-distortion-induced photomagnetic effect in azobenzene/polyoxometalate Langmuir–Blodgett films. Dalton Trans. 2013, 42, 16014–16020. [Google Scholar] [CrossRef] [PubMed]
  24. Arn, H.; Acree, T.E. Flavornet: A database of aroma compounds based on odor potency in natural products. In Food Flavors: Formation, Analysis and Packaging Influences; Contis, E.T., Ho, C.-T., Mussinan, C.J., Parliment, T.H., Shahidi, F., Spanier, A.M., Eds.; Elsevier: Amsterdam, The Netherlands, 1998; Volume 40, p. 27. ISBN 0167-4501. [Google Scholar]
  25. Stoermer, R. Über die Umlagerung stabiler stereoisomerer äthylenkörper in labile durch ultraviolettes Licht (I). Ber. Dtsch. Chem. Ges. 1909, 42, 4865–4871. [Google Scholar] [CrossRef]
  26. Stoermer, R. Über die Umlagerung der stabilen Stereoisomeren in labile durch ultraviolettes Licht. Ber. Dtsch. Chem. Ges. 1911, 44, 637–668. [Google Scholar] [CrossRef]
  27. Vaidya, B.K. Geometrical inversion in light. Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character 1930, 129, 299–313. [Google Scholar] [CrossRef]
  28. Hocking, M.B. Photochemical and thermal isomerizations of cis-and trans-cinnamic acids, and their photostationary state. Can. J. Chem. 1969, 47, 4567–4576. [Google Scholar] [CrossRef]
  29. Salum, M.L.; Robles, C.J.; Erra-Balsells, R. Photoisomerization of ionic liquid ammonium cinnamates: One-pot synthesis−isolation of Z-cinnamic acids. Org. Lett. 2010, 12, 4808–4811. [Google Scholar] [CrossRef]
  30. Zhu, H.L.; Shao, S.C.; Qiu, X.Y.; Sun, L.; Yang, S.; Ma, J.L. Crystal structure of diaqua-trans-dicinnamato-dihexamethylene-tetraminecobalt(II)dihydrate, Co(C6H12N4)2(C9H7O2)2(H2O)2·2H2O. Z. Krist. New Cryst. Struct. 2003, 218, 545–546. [Google Scholar] [CrossRef]
  31. Sun, H.Y.; Wang, Z.R.; Li, X.; Han, S.; Wang, J.J.; Li, W.F.; Liu, C.L.; Li, C.B. A novel Co(II) based multifunctional metal-organic framework: Synthesis, fluorescence sensing and magnetic analysis. Inorg. Chim. Acta 2019, 486, 750–756. [Google Scholar] [CrossRef]
  32. Fan, X.Y.; Li, K.; Huang, X.; Sun, T.; Yun, R.; Wu, H. Crystal structure of 4-hydroxycinnamato-[tris(1-methylbenzimidazol-2-ylmethyl)amine]cobalt(II) perchlorate–dimethylformamide–ethanol–methanol (1:1:1:1:0.5), Co(C27H27N7)(C9H7O3)](ClO4)·(CH3)2NCHO·C2H5OH·0.5CH3OH. Z. Krist. New Cryst. Struct. 2009, 224, 59–61. [Google Scholar] [CrossRef]
  33. Lehleh, A.; Boutebdja, M.; Beghidja, C.; Beghidja, A. Synthesis, crystal structure and Hirshfeld surface analysis of aqua(3-methoxycinnamato-κO)bis(1,10-phenanthroline-κ2N,N′)cobalt(II) nitrate. Acta Crystallogr. E Crystallogr. Commun. 2022, 78, 1113–1117. [Google Scholar] [CrossRef] [PubMed]
  34. Vallejo, J.; Viciano-Chumillas, M.; Lloret, F.; Julve, M.; Castro, I.; Krzystek, J.; Ozerov, M.; Armentano, D.; De Munno, G.; Cano, J. Coligand effects on the field-induced double slow magnetic relaxation in six-coordinate cobalt (II) single-ion magnets (SIMs) with positive magnetic anisotropy. Inorg. Chem. 2019, 58, 15726–15740. [Google Scholar] [CrossRef] [PubMed]
  35. Nemec, I.; Herchel, R.; Trávníček, Z. Two polymorphic Co(II) field-induced single-ion magnets with enormous angular distortion from the ideal octahedron. Dalton Trans. 2018, 47, 1614–1623. [Google Scholar] [CrossRef]
  36. Smolko, L.; Černák, J.; Kuchár, J.; Rajnák, C.; Titiš, J.; Boča, R. Field-Induced Slow Magnetic Relaxation in Mononuclear Tetracoordinate Cobalt(II) Complexes Containing a Neocuproine Ligand. Eur. J. Inorg. Chem. 2017, 2017, 3080–3086. [Google Scholar] [CrossRef]
  37. Nemec, I.; Fellner, O.F.; Indruchová, B.; Herchel, R. Trigonally Distorted Hexacoordinate Co(II) Single-Ion Magnets. Materials 2022, 15, 1064. [Google Scholar] [CrossRef] [PubMed]
  38. Alvarez, S.; Avnir, D.; Llunell, M.; Pinsky, M. Continuous symmetry maps and shape classification. The case of six-coordinated metal compounds. New J. Chem. 2002, 26, 996–1009. [Google Scholar] [CrossRef]
  39. Alvarez, S. Polyhedra in (inorganic) chemistry. Dalton Trans. 2005, 13, 2209–2233. [Google Scholar] [CrossRef]
  40. Macrae, C.F.; Sovago, I.; Cottrell, S.J.; Galek, P.T.A.; McCabe, P.; Pidcock, E.; Platings, M.; Shields, G.P.; Stevens, J.S.; Towler, M.; et al. Mercury 4.0: From visualization to analysis, design and prediction. J. Appl. Crystallogr. 2020, 53, 226–235. [Google Scholar] [CrossRef]
  41. Diamond 4.6.8-Crystal and Molecular Structure Visualization, Crystal Impact-Dr. H. Putz & Dr. K. Brandenburg GbR, Kreuzherrenstr. 102, 53227 Bonn, Germany. Available online: https://www.crystalimpact.de/diamond (accessed on 2 April 2022).
  42. Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
  43. Sheldrick, G.M. SHELXT–Integrated space-group and crystal-structure determination. Acta Crystallogr. A 2015, 71, 3–8. [Google Scholar] [CrossRef]
  44. Bourhis, L.J.; Dolomanov, O.V.; Gildea, R.J.; Howard, J.A.; Puschmann, H. The anatomy of a comprehensive constrained, restrained refinement program for the modern computing environment–Olex2 dissected. Acta Crystallogr. A 2015, 71, 59–75. [Google Scholar] [CrossRef] [PubMed]
  45. Dolomanov, O.V.; Bourhis, L.J.; Gildea, R.J.; Howard, J.A.; Puschmann, H. OLEX2: A complete structure solution, refinement and analysis program. J. Appl. Crystallogr. 2009, 42, 339–341. [Google Scholar] [CrossRef]
  46. CrysAlisPro, version 1.171.40.82a; Rigaku Oxford Diffraction: Oxford, UK, 2020.
  47. Spek, A.L. PLATON SQUEEZE: A tool for the calculation of the disordered solvent contribution to the calculated structure factors. Acta Cryst. 2015, 71, 9–18. [Google Scholar] [CrossRef]
  48. Boča, R. Theoretical Foundation of Molecular Magnetism; Elsevier: Amsterdam, The Netherlands, 1999. [Google Scholar]
  49. Neese, F.; Wennmohs, F.; Becker, U.; Riplinger, C. The ORCA quantum chemistry program package. J. Chem. Phys. 2020, 152, 224108. [Google Scholar] [CrossRef]
  50. Neese, F. Software update: The ORCA program system—Version 5.0. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2022, 12, e1606. [Google Scholar] [CrossRef]
  51. Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098. [Google Scholar] [CrossRef] [PubMed]
  52. Neese, F. An improvement of the resolution of the identity approximation for the formation of the Coulomb matrix. J. Comput. Chem. 2003, 24, 1740–1747. [Google Scholar] [CrossRef] [PubMed]
  53. Weigend, F. Accurate Coulomb-fitting basis sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057–1065. [Google Scholar] [CrossRef]
  54. Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
  55. Malmqvist, P.Å.; Roos, B.O. The CASSCF state interaction method. Chem. Phys. Lett. 1989, 155, 189–194. [Google Scholar] [CrossRef]
  56. Angeli, C.; Cimiraglia, R.; Evangelisti, S.; Leininger, T.; Malrieu, J.P. Introduction of n-Electron Valence States for Multireference Perturbation Theory. J. Chem. Phys. 2001, 114, 10252–10264. [Google Scholar] [CrossRef]
  57. Angeli, C.; Cimiraglia, R.; Malrieu, J.P. n-Electron Valence State Perturbation Theory: A Fast Implementation of the Strongly Contracted Variant. Chem. Phys. Lett. 2001, 350, 297–305. [Google Scholar] [CrossRef]
  58. Hellweg, A.; Hättig, C.; Höfener, S.; Klopper, W. Optimized accurate auxiliary basis sets for RI-MP2 and RI-CC2 calculations for the atoms Rb to Rn. Theor. Chem. Acc. 2007, 117, 587–597. [Google Scholar] [CrossRef]
  59. Neese, F.; Wennmohs, F.; Hansen, A.; Becker, U. Efficient, approximate and parallel Hartree–Fock and hybrid DFT calculations. A ‘chain-of-spheres’ algorithm for the Hartree–Fock exchange. Chem. Phys. 2009, 356, 98–109. [Google Scholar] [CrossRef]
  60. Hanai, K.; Kuwae, A.; Takai, T.; Senda, H.; Kunimoto, K.-K. A Comparative Vibrational and NMR Study of Cis-Cinnamic Acid Polymorphs and Trans-Cinnamic Acid. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2001, 57, 513–519. [Google Scholar] [CrossRef]
  61. Boča, R. Zero-field splitting in metal complexes. Coord. Chem. Rev. 2004, 248, 757–815. [Google Scholar] [CrossRef]
  62. Kahn, O. Molecular Magnetism; Courier Dover Publications: Mineola, NY, USA, 2021. [Google Scholar]
  63. Shrivastava, K.N. Theory of Spin–Lattice Relaxation. Phys. Status Solidi B 1983, 117, 437–458. [Google Scholar] [CrossRef]
  64. Singh, A.; Shrivastava, K.N. Optical-acoustic two-phonon relaxation in spin systems. Phys. Status Solidi B 1979, 95, 273. [Google Scholar] [CrossRef]
  65. Van Slageren, J.; Vongtragool, S.; Gorshunov, B.; Mukhin, A.A.; Karl, N.; Krzystek, J.; Telser, J.; Müller, A.; Sangregorio, C.; Gatteschi, D.; et al. Frequency domain magnetic resonance spectroscopy of molecular magnetic materials. Phys. Chem. Chem. Phys. 2003, 5, 3837. [Google Scholar] [CrossRef]
  66. Pavlov, A.A.; Aleshin, D.Y.; Savkina, S.A.; Belov, A.S.; Efimov, N.N.; Nehrkorn, J.; Ozerov, M.; Voloshin, Y.Z.; Nelyubina, Y.V.; Novikov, V.V. A Trigonal Prismatic Cobalt(II) Complex as a Single Molecule Magnet with a Reduced Contribution from Quantum Tunneling. ChemPhysChem 2019, 20, 1001. [Google Scholar] [CrossRef]
  67. Misochko, E.Y.; Akimov, A.V.; Korchagin, D.V.; Nehrkorn, J.; Ozerov, M.; Palii, A.V.; Clemente-Juan, J.M.; Aldoshin, S.M. Purely Spectroscopic Determination of the Spin Hamiltonian Parameters in High-Spin Six-Coordinated Cobalt(II) Complexes with Large Zero-Field Splitting. Inorg. Chem. 2019, 58, 16434. [Google Scholar] [CrossRef] [PubMed]
  68. Landart-Gereka, A.; Quesada-Moreno, M.M.; Díaz-Ortega, I.F.; Nojiri, H.; Ozerov, M.; Krzystek, J.; Palacios, M.A.; Colacio, E. Large easy-axis magnetic anisotropy in a series of trigonal prismatic mononuclear cobalt(II) complexes with zero-field hidden single-molecule magnet behaviour: The important role of the distortion of the coordination sphere and intermolecular interactions in the slow relaxation. Inorg. Chem. Front. 2022, 9, 2810. [Google Scholar] [CrossRef]
  69. Atanasov, M.; Ganyushin, D.; Sivalingam, K.; Neese, F. Molecular Electronic Structures of Transition Metal Complexes II; Mingos, D.M.P., Day, P., Dahl, J.P., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 149–220. [Google Scholar]
  70. Singh, S.K.; Eng, J.; Atanasov, M.; Neese, F. Covalency and chemical bonding in transition metal complexes: An ab initio based ligand field perspective. Coord. Chem. Rev. 2017, 344, 2–25. [Google Scholar] [CrossRef]
  71. Nemec, I.; Herchel, R.; Kern, M.; Neugebauer, P.; Van Slageren, J.; Trávníček, Z. Magnetic anisotropy and field-induced slow relaxation of magnetization in tetracoordinate CoII compound [Co(CH3-im)2Cl2]. Materials 2017, 10, 249. [Google Scholar] [CrossRef] [PubMed]
  72. Chibotaru, L.F.; Ungur, L. Ab initio calculation of anisotropic magnetic properties of complexes. I. Unique definition of pseudospin Hamiltonians and their derivation. J. Chem. Phys. 2012, 137, 064112. [Google Scholar] [CrossRef] [PubMed]
Magnetochemistry 09 00229 sch001
Scheme 1. Synthetic procedure for preparation of title compound 1·½Me2CO.
Scheme 1. Synthetic procedure for preparation of title compound 1·½Me2CO.
Magnetochemistry 09 00229 sch001
Magnetochemistry 09 00229 g001
Figure 1. (a) Complex cation of 1 with atom labels of coordination sphere; (b) complex cation with highlighted coordination polyhedron. Hydrogen atoms omitted for clarity.
Figure 1. (a) Complex cation of 1 with atom labels of coordination sphere; (b) complex cation with highlighted coordination polyhedron. Hydrogen atoms omitted for clarity.
Magnetochemistry 09 00229 g001
Magnetochemistry 09 00229 g002
Figure 2. (a) π–π stacking interaction present between the neocuproine rings; centroids represented as green spheres; (b) voids, displayed as yellow surfaces, present in the structure (3 × 3 × 3 packing; view alongside crystallographic b-axis). Hydrogen atoms omitted for clarity.
Figure 2. (a) π–π stacking interaction present between the neocuproine rings; centroids represented as green spheres; (b) voids, displayed as yellow surfaces, present in the structure (3 × 3 × 3 packing; view alongside crystallographic b-axis). Hydrogen atoms omitted for clarity.
Magnetochemistry 09 00229 g002
Magnetochemistry 09 00229 g003
Figure 3. Temperature dependence of the effective magnetic moment, the molar magnetization measured at B = 0.2 T (inset), and the isothermal magnetizations measured at T = 2 and 5 K for 1·½Me2CO. Empty circles—experimental data; full lines—calculated data with parameters in the text.
Figure 3. Temperature dependence of the effective magnetic moment, the molar magnetization measured at B = 0.2 T (inset), and the isothermal magnetizations measured at T = 2 and 5 K for 1·½Me2CO. Empty circles—experimental data; full lines—calculated data with parameters in the text.
Magnetochemistry 09 00229 g003
Magnetochemistry 09 00229 g004
Figure 4. Field-dependent AC susceptibility data for 1·½Me2CO. Top: in-phase χ′ and out-of-phase χ″ molar susceptibilities at T = 2 K (full lines are only guides for the eyes). Middle: frequency dependence of in-phase χ′ and out-of-phase χ″ molar susceptibilities fitted with one-component Debye’s model using Equation (2) (full lines). Bottom: the Argand (Cole–Cole) plot with full lines fitted with Equation (2) and, on the right, the fit of resulting relaxation times, τ, with the combination of quantum tunneling and Raman relaxation processes (red line) using Equation (3).
Figure 4. Field-dependent AC susceptibility data for 1·½Me2CO. Top: in-phase χ′ and out-of-phase χ″ molar susceptibilities at T = 2 K (full lines are only guides for the eyes). Middle: frequency dependence of in-phase χ′ and out-of-phase χ″ molar susceptibilities fitted with one-component Debye’s model using Equation (2) (full lines). Bottom: the Argand (Cole–Cole) plot with full lines fitted with Equation (2) and, on the right, the fit of resulting relaxation times, τ, with the combination of quantum tunneling and Raman relaxation processes (red line) using Equation (3).
Magnetochemistry 09 00229 g004
Magnetochemistry 09 00229 g005
Figure 5. The temperature-dependent AC susceptibility data for 1. Top: in-phase χ’ and out-of-phase χ″ molar susceptibilities at BDC = 0.09 T (full lines are only guides for the eyes). Middle: frequency dependence of in-phase χ’ and out-of-phase χ″ molar susceptibilities fitted with the one-component Debye model using Equation (2) (full lines). Bottom: the Argand (Cole–Cole) plot with full lines fitted with Equation (2) and, on the right, the fit of resulting relaxation times, τ, with the Raman relaxation processes (red line) using Equation (4).
Figure 5. The temperature-dependent AC susceptibility data for 1. Top: in-phase χ’ and out-of-phase χ″ molar susceptibilities at BDC = 0.09 T (full lines are only guides for the eyes). Middle: frequency dependence of in-phase χ’ and out-of-phase χ″ molar susceptibilities fitted with the one-component Debye model using Equation (2) (full lines). Bottom: the Argand (Cole–Cole) plot with full lines fitted with Equation (2) and, on the right, the fit of resulting relaxation times, τ, with the Raman relaxation processes (red line) using Equation (4).
Magnetochemistry 09 00229 g005
Magnetochemistry 09 00229 g006
Figure 6. Energy levels of d-orbitals (left) calculated using ab initio ligand field theory, and ligand field terms (middle) and multiplets (right) calculated using CASSCF/NEVPT2 for compound 1.
Figure 6. Energy levels of d-orbitals (left) calculated using ab initio ligand field theory, and ligand field terms (middle) and multiplets (right) calculated using CASSCF/NEVPT2 for compound 1.
Magnetochemistry 09 00229 g006
Magnetochemistry 09 00229 g007
Figure 7. The results of the SINGLE_ANISO analysis of CASSCF/NEVPT2 calculations for compound 1. The numbers presented in the plots represent the corresponding matrix element of the transversal magnetic moment (for values larger than 0.1, an efficient relaxation mechanism is expected).
Figure 7. The results of the SINGLE_ANISO analysis of CASSCF/NEVPT2 calculations for compound 1. The numbers presented in the plots represent the corresponding matrix element of the transversal magnetic moment (for values larger than 0.1, an efficient relaxation mechanism is expected).
Magnetochemistry 09 00229 g007
Table 1. Crystallographic data and details of the structure refinement of compound 1.
Table 1. Crystallographic data and details of the structure refinement of compound 1.
Compound1@100K1@293K
Empirical formulaC61H51BCoN4O2C61H51BCoN4O2
Formula weight941.79941.79
T/K100.0(1)293(2)
Crystal system, space groupMonoclinic, P21/nMonoclinic, P21/n
Unit cell dimensions
a/Å19.2108(2)19.1252(2)
b/Å11.24860(10)11.49370(10)
c/Å23.3407(2)23.4892(2)
α (°)9090
β (°)94.0510(10)93.9610(10)
γ (°)9090
V/Å35031.20(8)5151.05(8)
Z, Dc/g·cm−34, 1.2434, 1.214
Absorption coefficient (mm−1)3.0422.971
F(000)19721972
Reflections collected/unique (Rint)32,069/9403 (0.0259)9354/7614 (0.0248)
Data/restraints/parameters9403/0/6269354/0/626
Goodness-of-fit on F21.0451.048
Final R indices [I > 2σ(I)]R1 = 0.0359, wR2 = 0.0932R1 = 0.0608, wR2 = 0.1851
R indices (all data)R1 = 0.0401, wR2 = 0.0956R1 = 0.0718, wR2 = 0.1959
CCDC22996892306545
Table 2. Selected interatomic parameters (Å, °) of the coordination polyhedron.
Table 2. Selected interatomic parameters (Å, °) of the coordination polyhedron.
Co1-N12.119(1)
Co1-N22.161(1)
Co1-N32.137(1)
Co1-N42.126(1)
Co1-O12.134(1)
Co1-O22.193(1)
N1-Co1-N278.88(5)
N3-Co1-N479.60(5)
O1-Co1-O261.12(4)
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Halaš, P.; Nemec, I.; Herchel, R. Honey-like Odor Meets Single-Ion Magnet: Synthesis, Crystal Structure, and Magnetism of Cobalt(II) Complex with Aromatic Trans-Cinnamic Acid. Magnetochemistry 2023, 9, 229. https://doi.org/10.3390/magnetochemistry9110229

AMA Style

Halaš P, Nemec I, Herchel R. Honey-like Odor Meets Single-Ion Magnet: Synthesis, Crystal Structure, and Magnetism of Cobalt(II) Complex with Aromatic Trans-Cinnamic Acid. Magnetochemistry. 2023; 9(11):229. https://doi.org/10.3390/magnetochemistry9110229

Chicago/Turabian Style

Halaš, Petr, Ivan Nemec, and Radovan Herchel. 2023. "Honey-like Odor Meets Single-Ion Magnet: Synthesis, Crystal Structure, and Magnetism of Cobalt(II) Complex with Aromatic Trans-Cinnamic Acid" Magnetochemistry 9, no. 11: 229. https://doi.org/10.3390/magnetochemistry9110229

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop