Jahn–Teller Magnets
Abstract
1. Introduction
2. Anti-Jahn–Teller Disproportionation
3. Electron–Hole Dimers
4. Spin Structure of EH Dimers
5. Possible Phase States of JT Magnets with Instability to Charge Transfer
6. Single-Band JT Magnets
6.1. Effective Hamiltonian of a System of Spin–Triplet Composite Bosons: Non-Magnetic Lattice
6.2. , JT Magnets
JT Magnets
6.3. JT Magnets
6.3.1. Isoelectronic Quasi-2D Cuprates and Nickelates
6.3.2. “Silver” JT Magnets
7. Two-Band JT Magnets
7.1. Effective Hamiltonian of a System of Spin–Triplet Composite Bosons: Magnetic Lattice
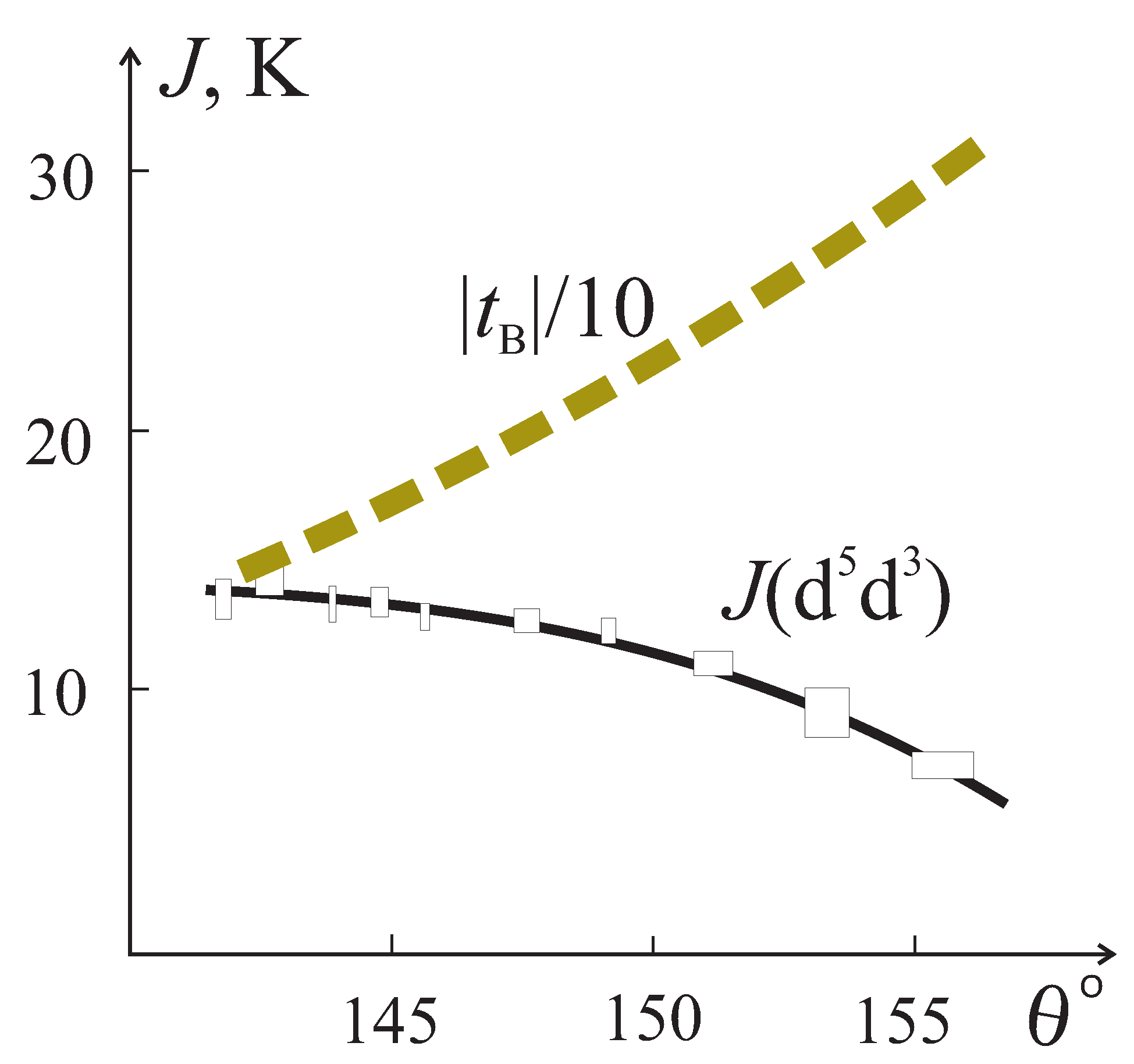
7.2. Chromium Cr Compounds
7.3. Manganites RMnO
7.4. Iron Fe JT Magnets
7.5. JT Ruthenates
7.6. Iron-Based Superconductors
8. Summary
Funding
Acknowledgments
Conflicts of Interest
References
- Bersuker, I. The Jahn-Teller Effect, 1st ed.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2006. [Google Scholar]
- Kugel’, K.I.; Khomskiĭ, D.I. The Jahn-Teller effect and magnetism: Transition metal compounds. Sov. Phys. Uspekhi 1982, 25, 231–256. [Google Scholar] [CrossRef]
- Sugano, S.; Tanabe, Y.; Kamimura, H. Multiplets of Transition-Metal Ions in Crystals; Number v. 33 in Pure and Applied Physics; Academic Press: New York, NY, USA, 1970. [Google Scholar]
- Moskvin, A. Atomy v Krystallah (Atoms in Crystals), 1st ed.; Ural Federal University: Ekaterinburg, Russia, 2018. (In Russian) [Google Scholar]
- Bednorz, J.G.; Müller, K.A. Possible highTc superconductivity in the Ba-La-Cu-O system. Z. Phys. B Condens. Matter 1986, 64, 189–193. [Google Scholar] [CrossRef]
- Ionov, S.P.; Ionova, G.V.; Lubimov, V.S.; Makarov, E.F. Instability of Crystal Lattices with Respect to Electron Density Redistributions. Phys. Status Solidi (B) 1975, 71, 11–57. [Google Scholar] [CrossRef]
- Anderson, P.W. Model for the Electronic Structure of Amorphous Semiconductors. Phys. Rev. Lett. 1975, 34, 953–955. [Google Scholar] [CrossRef]
- Scheurell, S.; Scholz, F.; Olesch, T.; Kemnitz, E. Electrochemical evidence for Cu3+-Cu2+-Cu + transitions in the orthorhombic YBa2Cu3O7−x phase. Supercond. Sci. Technol. 1992, 5, 303–305. [Google Scholar] [CrossRef]
- Larsson, S. Mixed valence model for superconductivity. Braz. J. Phys. 2003, 33, 744–749. [Google Scholar] [CrossRef]
- Wilson, J.A. Again ‘why layered, square-planar, mixed-valent cuprates alone?’—Further pursuit of the ‘chemical’ negative-U Route HTSC Mech. J. Phys. Condens. Matter 2000, 12, R517–R547. [Google Scholar] [CrossRef]
- Hirsch, J.E.; Scalapino, D.J. Double-valence-fluctuating molecules and superconductivity. Phys. Rev. B 1985, 32, 5639–5643. [Google Scholar] [CrossRef]
- Sleight, A.W. Oxide Superconductors: A Chemist’s View. MRS Proc. 1987, 99, 3. [Google Scholar] [CrossRef]
- Kulik, I.O.; Pedan, A.G. Phase transition in a model of superconducting glass. Sov. Phys. JETP 1980, 52, 742–748. [Google Scholar]
- Rice, T.M.; Sneddon, L. Real-Space and -Space Electron Pairing in BaPb1−xBixO3. Phys. Rev. Lett. 1981, 47, 689–692. [Google Scholar] [CrossRef]
- David, W.I.F.; Harrison, W.T.A.; Gunn, J.M.F.; Moze, O.; Soper, A.K.; Day, P.; Jorgensen, J.D.; Hinks, D.G.; Beno, M.A.; Soderholm, L.; et al. Structure and crystal chemistry of the high-Tc superconductor YBa2Cu3O7−x. Nature 1987, 327, 310–312. [Google Scholar] [CrossRef]
- Varma, C.M. Missing valence states, diamagnetic insulators, and superconductors. Phys. Rev. Lett. 1988, 61, 2713–2716. [Google Scholar] [CrossRef] [PubMed]
- Dzyaloshinskii, I.E. Chemical nature of the pairing of holes in high-temperature superconductors. JETP Lett. 1989, 49, 142–144. [Google Scholar]
- Geballe, T.; Moyzhes, B.Y. Qualitative understanding of the highest Tc cuprates. Phys. C Supercond. 2000, 341–348, 1821–1824. [Google Scholar] [CrossRef]
- Mitsen, K.V.; Ivanenko, O.M. Phase diagram of La2–XMxCuO4 Key Underst. Nat. High- Tc Supercond. Phys.-Uspekhi 2004, 47, 493–510. [Google Scholar] [CrossRef]
- Tsendin, K.D.; Popov, B.P.; Denisov, D.V. Explanation of the phase diagram of high-temperature superconductors in terms of the model of negative- U Centres Supercond. Supercond. Sci. Technol. 2006, 19, 313–318. [Google Scholar] [CrossRef]
- Katayama-Yoshida, H.; Kusakabe, K.; Kizaki, H.; Nakanishi, A. General Rule and Materials Design of Negative Effective U System High- Tc Superconductivity. Appl. Phys. Express 2008, 1, 081703. [Google Scholar] [CrossRef]
- Pouchard, M.; Villesuzanne, A. Are Superconductivity Mechanisms a Matter for Chemists? Condens. Matter 2020, 5, 67. [Google Scholar] [CrossRef]
- Mazin, I.I.; Khomskii, D.I.; Lengsdorf, R.; Alonso, J.A.; Marshall, W.G.; Ibberson, R.M.; Podlesnyak, A.; Martínez-Lope, M.J.; Abd-Elmeguid, M.M. Charge Ordering as Alternative to Jahn-Teller Distortion. Phys. Rev. Lett. 2007, 98, 176406. [Google Scholar] [CrossRef]
- Ogg, R.A. Bose-Einstein Condensation of Trapped Electron Pairs. Phase Separation and Superconductivity of Metal-Ammonia Solutions. Phys. Rev. 1946, 69, 243–244. [Google Scholar] [CrossRef]
- Schafroth, M.R. Superconductivity of a Charged Ideal Bose Gas. Phys. Rev. 1955, 100, 463–475. [Google Scholar] [CrossRef]
- Alexandrov, A.S. High-temperature superconductivity: The explanation. Phys. Scr. 2011, 83, 038301. [Google Scholar] [CrossRef]
- Müller, K.A. The Polaronic Basis for High-Temperature Superconductivity. J. Supercond. Nov. Magn. 2017, 30, 3007–3018. [Google Scholar] [CrossRef]
- Pavuna, D.; Dubuis, G.; Bollinger, A.T.; Wu, J.; He, X.; Božović, I. On Local Pairs vs. BCS: Quo Vadis High- Tc Superconductivity. J. Supercond. Nov. Magn. 2017, 30, 731–734. [Google Scholar] [CrossRef]
- Božović, I.; He, X.; Wu, J.; Bollinger, A.T. Dependence of the critical temperature in overdoped copper oxides on superfluid density. Nature 2016, 536, 309–311. [Google Scholar] [CrossRef]
- Pelc, D.; Popčević, P.; Požek, M.; Greven, M.; Barišić, N. Unusual behavior of cuprates explained by heterogeneous charge localization. Sci. Adv. 2019, 5, eaau4538. [Google Scholar] [CrossRef]
- Moskvin, A.S. Perspectives of disproportionation driven superconductivity in strongly correlated 3d compounds. J. Phys. Condens. Matter 2013, 25, 085601. [Google Scholar] [CrossRef]
- Allen, P.B.; Perebeinos, V. Anti-Jahn-Teller polaron in LaMnO3. Phys. Rev. B 1999, 60, 10747–10753. [Google Scholar] [CrossRef]
- Feng, N.; Han, J.; Lin, C.; Ai, Z.; Lan, C.; Bi, K.; Lin, Y.; Xue, K.H.; Xu, B. Anti-Jahn-Teller effect induced ultrafast insulator to metal transition in perovskite BaBiO3. Npj Comput. Mater. 2022, 8, 226. [Google Scholar] [CrossRef]
- Kamimura, H.; Araidai, M.; Ishida, K.; Matsuno, S.; Sakata, H.; Shiraishi, K.; Sugino, O.; Tsai, J.S. First-Principles Calculation of Copper Oxide Superconductors That Supports the Kamimura-Suwa Model. Condens. Matter 2020, 5, 69. [Google Scholar] [CrossRef]
- Moskvin, A.S.; Avvakumov, I.L. Why does the tetrahedrally coordinated Fe drive the superconductivity? In Proceedings of the III International Conference “Fundamental Problems of High-Temperature Superconductivity”, Moscow, Zvenigorod, 13–17 October 2008; p. 215. [Google Scholar]
- Larsson, S. Strong electron correlation and phonon coupling in high Tc superconductors. Phys. C Supercond. 2007, 460–462, 1063–1065. [Google Scholar] [CrossRef]
- Alonso, J.A.; García-Muñoz, J.L.; Fernández-Díaz, M.T.; Aranda, M.A.G.; Martínez-Lope, M.J.; Casais, M.T. Charge Disproportionation in R NiO3 Perovskites: Simultaneous Metal-Insulator and Structural Transition in YNiO3. Phys. Rev. Lett. 1999, 82, 3871–3874. [Google Scholar] [CrossRef]
- Woodward, P.M.; Cox, D.E.; Moshopoulou, E.; Sleight, A.W.; Morimoto, S. Structural studies of charge disproportionation and magnetic order in CaFeO3. Phys. Rev. B 2000, 62, 844–855. [Google Scholar] [CrossRef]
- Uchiyama, H.; Baron, A.Q.R.; Tsutsui, S.; Tanaka, Y.; Hu, W.Z.; Yamamoto, A.; Tajima, S.; Endoh, Y. Softening of Cu-O Bond Stretching Phonons in Tetragonal HgBa2 CuO4 + δ. Phys. Rev. Lett. 2004, 92, 197005. [Google Scholar] [CrossRef] [PubMed]
- Vikhnin, V.S.; Kapphan, S.E. New type charge transfer states in ferroelectric oxides: Actual problems. Radiat. Eff. Defects Solids 2002, 157, 853–856. [Google Scholar] [CrossRef]
- Mazumdar, S. Negative charge-transfer gap and even parity superconductivity in Sr2 RuO4. Phys. Rev. Res. 2020, 2, 023382. [Google Scholar] [CrossRef]
- Green, R.J.; Haverkort, M.W.; Sawatzky, G.A. Bond disproportionation and dynamical charge fluctuations in the perovskite rare-earth nickelates. Phys. Rev. B 2016, 94, 195127. [Google Scholar] [CrossRef]
- Moskvin, A.; Panov, Y. Model of charge triplets for high- Tc cuprates. J. Magn. Magn. Mater. 2022, 550, 169004. [Google Scholar] [CrossRef]
- Moskvin, A.; Panov, Y. Effective-Field Theory for Model High-Tc Cuprates. Condens. Matter 2021, 6, 24. [Google Scholar] [CrossRef]
- Moskvin, A.S. Charge transfer excitons in HTSC cuprates and nickelates. Opt. I Spektrosk. 2023, 131, 491–501. [Google Scholar] [CrossRef]
- Zener, C. Interaction between the d -Shells in the Transition Metals. II. Ferromagnetic Compounds of Manganese with Perovskite Structure. Phys. Rev. 1951, 82, 403–405. [Google Scholar] [CrossRef]
- Merz, M.; Nücker, N.; Schuppler, S.; Arena, D.; Dvorak, J.; Idzerda, Y.U.; Ustinovich, S.N.; Soldatov, A.G.; Shiryaev, S.V.; Barilo, S.N. X-ray absorption of Ba1−XKxBiO3 BaPb1−yBiyO3: Competition Bipolaronic Charg.-Density Wave States. Europhys. Lett. (EPL) 2005, 72, 275–281. [Google Scholar] [CrossRef]
- Chaillout, C.; Santoro, A.; Remeika, J.; Cooper, A.; Espinosa, G.; Marezio, M. Bismuth valence order-disorder study in BaBiO3 by powder neutron diffraction. Solid State Commun. 1988, 65, 1363–1369. [Google Scholar] [CrossRef]
- Rodríguez-Carvajal, J.; Hennion, M.; Moussa, F.; Moudden, A.H.; Pinsard, L.; Revcolevschi, A. Neutron-diffraction study of the Jahn-Teller transition in stoichiometric LaMnO3. Phys. Rev. B 1998, 57, R3189–R3192. [Google Scholar] [CrossRef]
- Huang, Q.; Santoro, A.; Lynn, J.W.; Erwin, R.W.; Borchers, J.A.; Peng, J.L.; Greene, R.L. Structure and magnetic order in undoped lanthanum manganite. Phys. Rev. B 1997, 55, 14987–14999. [Google Scholar] [CrossRef]
- Moskvin, A.S. Disproportionation and electronic phase separation in parent manganite LaMnO3. Phys. Rev. B 2009, 79, 115102. [Google Scholar] [CrossRef]
- Moskvin, A.S.; Ovanesyan, N.S.; Trukhtanov, V.A. Angular dependence of the superexchange interaction Fe3+-O2−-Cr3+. Hyperfine Interact. 1975, 1, 265–281. [Google Scholar] [CrossRef]
- Moskvin, A.S. Dzyaloshinskii Interaction and Exchange-Relativistic Effects in Orthoferrites. J. Exp. Theor. Phys. 2021, 132, 517–547. [Google Scholar] [CrossRef]
- Moskvin, A. Structure–Property Relationships for Weak Ferromagnetic Perovskites. Magnetochemistry 2021, 7, 111. [Google Scholar] [CrossRef]
- Alonso, J.A.; Martínez-Lope, M.J.; Casais, M.T.; Fernández-Díaz, M.T. Evolution of the Jahn-Teller Distortion of MnO6 Octahedra in RMnO3 Perovskites (R = Pr, Nd, Dy, Tb, Ho, Er, Y): A Neutron Diffraction Study. Inorg. Chem. 2000, 39, 917–923. [Google Scholar] [CrossRef]
- Pangburn, E.; Banerjee, A.; Freire, H.; Pépin, C. Incoherent transport in a model for the strange metal phase: Memory-matrix formalism. Phys. Rev. B 2023, 107, 245109. [Google Scholar] [CrossRef]
- Moskvin, A.S.; Panov, Y.D. Nature of the Pseudogap Phase of HTSC Cuprates. Phys. Solid State 2020, 62, 1554–1561. [Google Scholar] [CrossRef]
- Moskvin, A.S.; Panov, Y.D. Phase separation in high-Tc cuprates. J. Phys. Conf. Ser. 2022, 2164, 012014. [Google Scholar] [CrossRef]
- Gong, W.; Greedan, J.; Liu, G.; Bjorgvinsson, M. Crystal structure and magnetic properties of orthorhombic Sr2VO4 with tetrahedral vanadium (IV). J. Solid State Chem. 1991, 95, 213–219. [Google Scholar] [CrossRef]
- Deisenhofer, J.; Schaile, S.; Teyssier, J.; Wang, Z.; Hemmida, M.; Von Nidda, H.A.K.; Eremina, R.M.; Eremin, M.V.; Viennois, R.; Giannini, E.; et al. Electron spin resonance and exchange paths in the orthorhombic dimer system Sr2VO4. Phys. Rev. B 2012, 86, 214417. [Google Scholar] [CrossRef]
- Wang, Z.; Kamenskyi, D.; Cépas, O.; Schmidt, M.; Quintero-Castro, D.L.; Islam, A.T.M.N.; Lake, B.; Aczel, A.A.; Dabkowska, H.A.; Dabkowski, A.B.; et al. High-field electron spin resonance spectroscopy of singlet-triplet transitions in the spin-dimer systems Sr3Cr2O8 and Ba3Cr2O8. Phys. Rev. B 2014, 89, 174406. [Google Scholar] [CrossRef]
- Barone, P.; Yamauchi, K.; Picozzi, S. Jahn-Teller distortions as a novel source of multiferroicity. Phys. Rev. B 2015, 92, 014116. [Google Scholar] [CrossRef]
- Hepting, M. The Rare-Earth Nickelates. In Ordering Phenomena in Rare-Earth Nickelate Heterostructures; Series Title: Springer Theses; Springer International Publishing: Cham, Switzerland, 2017; pp. 13–29. [Google Scholar] [CrossRef]
- Chaloupka, J.; Khaliullin, G. Orbital Order and Possible Superconductivity in LaNiO3/LaMO3 Superlattices. Phys. Rev. Lett. 2008, 100, 016404. [Google Scholar] [CrossRef]
- Gawryluk, D.J.; Klein, Y.M.; Shang, T.; Sheptyakov, D.; Keller, L.; Casati, N.; Lacorre, P.; Fernández-Díaz, M.T.; Rodríguez-Carvajal, J.; Medarde, M. Distortion mode anomalies in bulk PrNiO3: Illustrating the potential of symmetry-adapted distortion mode analysis for the study of phase transitions. Phys. Rev. B 2019, 100, 205137. [Google Scholar] [CrossRef]
- Kumar, D.; Rajeev, K.P.; Alonso, J.A.; Martínez-Lope, M.J. Spin-canted magnetism and decoupling of charge and spin ordering in NdNiO3. Phys. Rev. B 2013, 88, 014410. [Google Scholar] [CrossRef]
- Bousquet, E.; Cano, A. Non-collinear magnetism & multiferroicity: The perovskite case. Phys. Sci. Rev. 2023, 8, 479–508. [Google Scholar] [CrossRef]
- Zhang, J.; Zheng, H.; Ren, Y.; Mitchell, J.F. High-Pressure Floating-Zone Growth of Perovskite Nickelate LaNiO3 Single Crystals. Cryst. Growth Des. 2017, 17, 2730–2735. [Google Scholar] [CrossRef]
- Guo, H.; Li, Z.W.; Zhao, L.; Hu, Z.; Chang, C.F.; Kuo, C.Y.; Schmidt, W.; Piovano, A.; Pi, T.W.; Sobolev, O.; et al. Antiferromagnetic correlations in the metallic strongly correlated transition metal oxide LaNiO3. Nat. Commun. 2018, 9, 43. [Google Scholar] [CrossRef] [PubMed]
- Shamblin, J.; Heres, M.; Zhou, H.; Sangoro, J.; Lang, M.; Neuefeind, J.; Alonso, J.A.; Johnston, S. Experimental evidence for bipolaron condensation as a mechanism for the metal–insulator transition in rare-earth nickelates. Nat. Commun. 2018, 9, 86. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Louca, D.; Yano, S.; Marshall, L.G.; Zhou, J.; Goodenough, J.B. Insulating Pockets in Metallic LaNiO3. Adv. Electron. Mater. 2016, 2, 1500261. [Google Scholar] [CrossRef]
- Wawrzyńska, E.; Coldea, R.; Wheeler, E.M.; Mazin, I.I.; Johannes, M.D.; Sörgel, T.; Jansen, M.; Ibberson, R.M.; Radaelli, P.G. Orbital Degeneracy Removed by Charge Order in Triangular Antiferromagnet AgNiO2. Phys. Rev. Lett. 2007, 99, 157204. [Google Scholar] [CrossRef]
- Chen, H.; Freeman, C.L.; Harding, J.H. Charge disproportionation and Jahn-Teller distortion in LiNiO2 and NaNiO2: A density functional theory study. Phys. Rev. B 2011, 84, 085108. [Google Scholar] [CrossRef]
- Zhang, F.C.; Rice, T.M. Effective Hamiltonian for the superconducting Cu oxides. Phys. Rev. B 1988, 37, 3759–3761. [Google Scholar] [CrossRef]
- Moskvin, A.S. True charge-transfer gap in parent insulating cuprates. Phys. Rev. B 2011, 84, 075116. [Google Scholar] [CrossRef]
- Moskvin, A.S.; Panov, Y.D. Topological Structures in Unconventional Scenario for 2D Cuprates. J. Supercond. Nov. Magn. 2019, 32, 61–84. [Google Scholar] [CrossRef]
- Moskvin, A.S.; Panov, Y.D. Electron–Hole Dimers in the Parent Phase of Quasi–2D Cuprates. Phys. Solid State 2019, 61, 1553–1558. [Google Scholar] [CrossRef]
- Moskvin, A.S. Large Variety of the On-Site Order Parameters and Phase States in Quasi-2D HTSC Cuprates. Phys. Met. Metallogr. 2019, 120, 1252–1259. [Google Scholar] [CrossRef]
- Naito, M.; Krockenberger, Y.; Ikeda, A.; Yamamoto, H. Reassessment of the electronic state, magnetism, and superconductivity in high-Tc cuprates with the Nd2CuO4 structure. Phys. C Supercond. Its Appl. 2016, 523, 28–54. [Google Scholar] [CrossRef]
- Li, D.; Lee, K.; Wang, B.Y.; Osada, M.; Crossley, S.; Lee, H.R.; Cui, Y.; Hikita, Y.; Hwang, H.Y. Superconductivity in an infinite-layer nickelate. Nature 2019, 572, 624–627. [Google Scholar] [CrossRef]
- Panov, Y.D. Critical Temperatures of a Model Cuprate. Phys. Met. Metallogr. 2019, 120, 1276–1281. [Google Scholar] [CrossRef]
- Fischer, P.; Roult, G.; Schwarzenbach, D. Crystal and magnetic structure of silver difluoride-II. Weak 4d-ferromagnetism of AgF2. J. Phys. Chem. Solids 1971, 32, 1641–1647. [Google Scholar] [CrossRef]
- Derzsi, M.; Tokár, K.; Piekarz, P.; Grochala, W. Charge ordering mechanism in silver difluoride. Phys. Rev. B 2022, 105, L081113. [Google Scholar] [CrossRef]
- Bachar, N.; Koteras, K.; Gawraczynski, J.; Trzciński, W.; Paszula, J.; Piombo, R.; Barone, P.; Mazej, Z.; Ghiringhelli, G.; Nag, A.; et al. Charge-Transfer and d d excitations in AgF2. Phys. Rev. Res. 2022, 4, 023108. [Google Scholar] [CrossRef]
- Shen, C.; Žemva, B.; Lucier, G.M.; Graudejus, O.; Allman, J.A.; Bartlett, N. Disproportionation of Ag(II) to Ag(I) and Ag(III) in Fluoride Systems and Syntheses and Structures of (AgF+ )2 AgF4− MF 6− Salts (M = As, Sb, Pt, Au, Ru). Inorg. Chem. 1999, 38, 4570–4577. [Google Scholar] [CrossRef]
- Tokár, K.; Derzsi, M.; Grochala, W. Comparative computational study of antiferromagnetic and mixed-valent diamagnetic phase of AgF2: Crystal, electronic and phonon structure and p-T phase diagram. Comput. Mater. Sci. 2021, 188, 110250. [Google Scholar] [CrossRef]
- Scatturin, V.; Bellon, P.L.; Salkind, A.J. The Structure of Silver Oxide Determined by Means of Neutron Diffraction. J. Electrochem. Soc. 1961, 108, 819. [Google Scholar] [CrossRef]
- Allen, J.P.; Scanlon, D.O.; Watson, G.W. Electronic structures of silver oxides. Phys. Rev. B 2011, 84, 115141. [Google Scholar] [CrossRef]
- Hirschfeld, P.J. Using gap symmetry and structure to reveal the pairing mechanism in Fe-based superconductors. Comptes Rendus Phys. 2016, 17, 197–231. [Google Scholar] [CrossRef]
- Dong, S.; Yu, R.; Yunoki, S.; Liu, J.M.; Dagotto, E. Double-exchange model study of multiferroic RMnO3 perovskites. Eur. Phys. J. B 2009, 71, 339–344. [Google Scholar] [CrossRef][Green Version]
- Stout, J.W.; DeLassus, P.; Graham, C.D.; Rhyne, J.J. CrF2, A Canted Antiferromagnet. AIP Conf. Proc. 1972, 5, 669. [Google Scholar] [CrossRef]
- Jiménez-Mier, J.; Olalde-Velasco, P.; Yang, W.L.; Denlinger, J. X-ray absorption and resonant inelastic x-ray scattering (RIXS) show the presence of Cr+ at the surface and in the bulk of CrF2. In Proceedings of the AIP Conference Proceedings, Ciudad Juárez, Mexico, 4–6 March 2015; p. 020002. [Google Scholar] [CrossRef]
- Raffaelle, R.; Anderson, H.U.; Sparlin, D.M.; Parris, P.E. Transport anomalies in the high-temperature hopping conductivity and thermopower of Sr-doped La(Cr,Mn)O3. Phys. Rev. B 1991, 43, 7991–7999. [Google Scholar] [CrossRef]
- Van Roosmalen, J.; Cordfunke, E. The Defect Chemistry of LaMnO3±δ. J. Solid State Chem. 1994, 110, 109–112. [Google Scholar] [CrossRef]
- Zhou, J.S.; Goodenough, J.B. Paramagnetic phase in single-crystal LaMnO3. Phys. Rev. B 1999, 60, R15002–R15004. [Google Scholar] [CrossRef]
- Ritter, C.; Ibarra, M.R.; De Teresa, J.M.; Algarabel, P.A.; Marquina, C.; Blasco, J.; García, J.; Oseroff, S.; Cheong, S.W. Influence of oxygen content on the structural, magnetotransport, and magnetic properties of LaMnO3+δ. Phys. Rev. B 1997, 56, 8902–8911. [Google Scholar] [CrossRef]
- Kim, Y.J. p-Wave Pairing and Colossal Magnetoresistance in Manganese Oxides. Mod. Phys. Lett. B 1998, 12, 507–518. [Google Scholar] [CrossRef]
- Krivoruchko, V.N. Local spin-triplet superconductivity in half-metallic manganites: A perspective platform for high-temperature topological superconductivity. Low Temp. Phys. 2021, 47, 901–907. [Google Scholar] [CrossRef]
- Markovich, V.; Fita, I.; Wisniewski, A.; Puzniak, R.; Mogilyansky, D.; Titelman, L.; Vradman, L.; Herskowitz, M.; Gorodetsky, G. Metastable diamagnetic response of 20 nm La1−x MnO3 particles. Phys. Rev. B 2008, 77, 014423. [Google Scholar] [CrossRef]
- Kasai, M.; Ohno, T.; Kanke, Y.; Kozono, Y.; Hanazono, M.; Sugita, Y. Current-Voltage Characteristics of YBa2Cu3Oy /La0.7Ca0.3MnOz/YBa2Cu3Oy Trilayered-Type Junctions. Jpn. J. Appl. Phys. 1990, 29, L2219. [Google Scholar] [CrossRef]
- Mitin, A.; Kuz’micheva, G.; Novikova, S. Mixed Oxides of Manganese with Perovskite and Perovskite-related Structures. Russ. J. Inorg. Chem. 1997, 42, 1791. [Google Scholar] [CrossRef]
- Nath, R.; Raychaudhuri, A.K.; Mukovskii, Y.M.; Mondal, P.; Bhattacharya, D.; Mandal, P. Electric field driven destabilization of the insulating state in nominally pure LaMnO3. J. Phys. Condens. Matter 2013, 25, 155605. [Google Scholar] [CrossRef][Green Version]
- Cabassi, R.; Bolzoni, F.; Gilioli, E.; Bissoli, F.; Prodi, A.; Gauzzi, A. Jahn-Teller-induced crossover of the paramagnetic response in the singly valent eg system LaMn7O12. Phys. Rev. B 2010, 81, 214412. [Google Scholar] [CrossRef]
- Schaile, S.; Von Nidda, H.A.K.; Deisenhofer, J.; Loidl, A.; Nakajima, T.; Ueda, Y. Korringa-like relaxation in the high-temperature phase of A -site ordered YBaMn2O6. Phys. Rev. B 2012, 85, 205121. [Google Scholar] [CrossRef]
- Takano, M.; Nakanishi, N.; Takeda, Y.; Naka, S.; Takada, T. Charge disproportionation in CaFeO3 studied with the Mössbauer effect. Mater. Res. Bull. 1977, 12, 923–928. [Google Scholar] [CrossRef]
- Takeda, T.; Kanno, R.; Kawamoto, Y.; Takano, M.; Kawasaki, S.; Kamiyama, T.; Izumi, F. Metal–semiconductor transition, charge disproportionation, and low-temperature structure of Ca1-xSrxFeO3 synthesized under high-oxygen pressure. Solid State Sci. 2000, 2, 673–687. [Google Scholar] [CrossRef]
- Reehuis, M.; Ulrich, C.; Maljuk, A.; Niedermayer, C.; Ouladdiaf, B.; Hoser, A.; Hofmann, T.; Keimer, B. Neutron diffraction study of spin and charge ordering in SrFeO3−δ. Phys. Rev. B 2012, 85, 184109. [Google Scholar] [CrossRef]
- Chakraverty, S.; Matsuda, T.; Ogawa, N.; Wadati, H.; Ikenaga, E.; Kawasaki, M.; Tokura, Y.; Hwang, H.Y. BaFeO3 cubic single crystalline thin film: A ferromagnetic insulator. Appl. Phys. Lett. 2013, 103, 142416. [Google Scholar] [CrossRef]
- Fujioka, J.; Ishiwata, S.; Kaneko, Y.; Taguchi, Y.; Tokura, Y. Variation of charge dynamics upon the helimagnetic and metal–insulator transitions for perovskite AFeO3 (A = Sr and Ca). Phys. Rev. B 2012, 85, 155141. [Google Scholar] [CrossRef]
- Kuzushita, K.; Morimoto, S.; Nasu, S.; Nakamura, S. Charge Disproportionation and Antiferromagnetic Order of Sr3Fe2O7. J. Phys. Soc. Jpn. 2000, 69, 2767–2770. [Google Scholar] [CrossRef]
- Kim, J.H.; Peets, D.C.; Reehuis, M.; Adler, P.; Maljuk, A.; Ritschel, T.; Allison, M.C.; Geck, J.; Mardegan, J.R.L.; Bereciartua Perez, P.J.; et al. Hidden Charge Order in an Iron Oxide Square-Lattice Compound. Phys. Rev. Lett. 2021, 127, 097203. [Google Scholar] [CrossRef]
- Adler, P. Properties of K2NiF4-Type Oxides Sr2FeO4. J. Solid State Chem. 1994, 108, 275–283. [Google Scholar] [CrossRef]
- Adler, P.; Reehuis, M.; Stüßer, N.; Medvedev, S.A.; Nicklas, M.; Peets, D.C.; Bertinshaw, J.; Christensen, C.K.; Etter, M.; Hoser, A.; et al. Spiral magnetism, spin flop, and pressure-induced ferromagnetism in the negative charge-transfer-gap insulator Sr2FeO4. Phys. Rev. B 2022, 105, 054417. [Google Scholar] [CrossRef]
- Itoh, M.; Shikano, M.; Shimura, T. High- and low-spin transition of Ru4+ in the perovskite-related layered system Srn+1RunO3n+1 (N = 1, 2, ∞) Change n. Phys. Rev. B 1995, 51, 16432–16435. [Google Scholar] [CrossRef]
- Grutter, A.J.; Wong, F.J.; Arenholz, E.; Vailionis, A.; Suzuki, Y. Evidence of high-spin Ru and universal magnetic anisotropy in SrRuO3 thin films. Phys. Rev. B 2012, 85, 134429. [Google Scholar] [CrossRef]
- Cao, G.; Song, W.; Sun, Y.; Lin, X. Violation of the Mott–Ioffe–Regel limit: High-temperature resistivity of itinerant magnets Srn+1RunO3n+1 (n = 2,3,∞) and CaRuO3. Solid State Commun. 2004, 131, 331–336. [Google Scholar] [CrossRef]
- Nakatsuji, S.; Maeno, Y. Quasi-Two-Dimensional Mott Transition System Ca2−xSrxRuO4. Phys. Rev. Lett. 2000, 84, 2666–2669. [Google Scholar] [CrossRef] [PubMed]
- Nobukane, H.; Yanagihara, K.; Kunisada, Y.; Ogasawara, Y.; Isono, K.; Nomura, K.; Tanahashi, K.; Nomura, T.; Akiyama, T.; Tanda, S. Co-appearance of superconductivity and ferromagnetism in a Ca2RuO4 nanofilm crystal. Sci. Rep. 2020, 10, 3462. [Google Scholar] [CrossRef] [PubMed]
- Maeno, Y.; Hashimoto, H.; Yoshida, K.; Nishizaki, S.; Fujita, T.; Bednorz, J.G.; Lichtenberg, F. Superconductivity in a layered perovskite without copper. Nature 1994, 372, 532–534. [Google Scholar] [CrossRef]
- Mackenzie, A.P.; Maeno, Y. The superconductivity of Sr2RuO4 and the physics of spin-triplet pairing. Rev. Mod. Phys. 2003, 75, 657–712. [Google Scholar] [CrossRef]
- Mackenzie, A.P.; Scaffidi, T.; Hicks, C.W.; Maeno, Y. Even odder after twenty-three years: The superconducting order parameter puzzle of Sr2RuO4. Npj Quantum Mater. 2017, 2, 40. [Google Scholar] [CrossRef]
- Leggett, A.J.; Liu, Y. Symmetry Properties of Superconducting Order Parameter in Sr2RuO4: A Brief Review. J. Supercond. Nov. Magn. 2021, 34, 1647–1673. [Google Scholar] [CrossRef]
- Ruf, J.P.; Paik, H.; Schreiber, N.J.; Nair, H.P.; Miao, L.; Kawasaki, J.K.; Nelson, J.N.; Faeth, B.D.; Lee, Y.; Goodge, B.H.; et al. Strain-stabilized superconductivity. Nat. Commun. 2021, 12, 59. [Google Scholar] [CrossRef]
- Uchida, M.; Nomoto, T.; Musashi, M.; Arita, R.; Kawasaki, M. Superconductivity in Uniquely Strained RuO2 Films. Phys. Rev. Lett. 2020, 125, 147001. [Google Scholar] [CrossRef]
- Stewart, G.R. Superconductivity in iron compounds. Rev. Mod. Phys. 2011, 83, 1589–1652. [Google Scholar] [CrossRef]
- Chubukov, A.; Hirschfeld, P.J. Iron-based superconductors, seven years later. Phys. Today 2015, 68, 46–52. [Google Scholar] [CrossRef]
- Si, Q.; Yu, R.; Abrahams, E. High-temperature superconductivity in iron pnictides and chalcogenides. Nat. Rev. Mater. 2016, 1, 16017. [Google Scholar] [CrossRef]
- Kreisel, A.; Hirschfeld, P.; Andersen, B. On the Remarkable Superconductivity of FeSe and Its Close Cousins. Symmetry 2020, 12, 1402. [Google Scholar] [CrossRef]
- Carlo, J.P.; Uemura, Y.J.; Goko, T.; MacDougall, G.J.; Rodriguez, J.A.; Yu, W.; Luke, G.M.; Dai, P.; Shannon, N.; Miyasaka, S.; et al. Static Magnetic Order and Superfluid Density of R FeAs (O, F) (R = La, Nd, Ce) and LaFePO Studied by Muon Spin Relaxation: Unusual Similarities with the Behavior of Cuprate Superconductors. Phys. Rev. Lett. 2009, 102, 087001. [Google Scholar] [CrossRef] [PubMed]
- Adamski, A.; Krellner, C.; Abdel-Hafiez, M. Signature of multigap nodeless superconductivity in fluorine-doped NdFeAsO. Phys. Rev. B 2017, 96, 100503. [Google Scholar] [CrossRef]
- Liu, J.; Savici, A.T.; Granroth, G.E.; Habicht, K.; Qiu, Y.; Hu, J.; Mao, Z.Q.; Bao, W. A Triplet Resonance in Superconducting Fe1.03 Se0.4 Te0.6. Chin. Phys. Lett. 2018, 35, 127401. [Google Scholar] [CrossRef]
- Xie, T.; Gong, D.; Ghosh, H.; Ghosh, A.; Soda, M.; Masuda, T.; Itoh, S.; Bourdarot, F.; Regnault, L.P.; Danilkin, S.; et al. Neutron Spin Resonance in the 112-Type Iron-Based Superconductor. Phys. Rev. Lett. 2018, 120, 137001. [Google Scholar] [CrossRef]
- Lee, P.A.; Wen, X.G. Spin-triplet p -wave pairing in a three-orbital model for iron pnictide superconductors. Phys. Rev. B 2008, 78, 144517. [Google Scholar] [CrossRef]
- Baek, S.H.; Grafe, H.J.; Hammerath, F.; Fuchs, M.; Rudisch, C.; Harnagea, L.; Aswartham, S.; Wurmehl, S.; Van Den Brink, J.; Büchner, B. 75As NMR-NQR study in superconducting LiFeAs. Eur. Phys. J. B 2012, 85, 159. [Google Scholar] [CrossRef]
- Hänke, T.; Sykora, S.; Schlegel, R.; Baumann, D.; Harnagea, L.; Wurmehl, S.; Daghofer, M.; Büchner, B.; van den Brink, J.; Hess, C. Probing the Unconventional Superconducting State of LiFeAs by Quasiparticle Interference. Phys. Rev. Lett. 2012, 108, 127001. [Google Scholar] [CrossRef]
- Brydon, P.M.R.; Daghofer, M.; Timm, C.; Van Den Brink, J. Theory of magnetism and triplet superconductivity in LiFeAs. Phys. Rev. B 2011, 83, 060501. [Google Scholar] [CrossRef]
- Brand, J.; Stunault, A.; Wurmehl, S.; Harnagea, L.; Büchner, B.; Meven, M.; Braden, M. Spin susceptibility in superconducting LiFeAs studied by polarized neutron diffraction. Phys. Rev. B 2014, 89, 045141. [Google Scholar] [CrossRef]
- Gifford, J.A.; Chen, B.B.; Zhang, J.; Zhao, G.J.; Kim, D.R.; Li, B.C.; Wu, D.; Chen, T.Y. Determination of spin polarization using an unconventional iron superconductor. AIP Adv. 2016, 6, 115023. [Google Scholar] [CrossRef]
- Hirsch, J.E. Why only hole conductors can be superconductors. In Proceedings of the Oxide-Based Materials and Devices VIII, San Francisco, CA, USA, 29 January–1 February 2017; p. 101051V. [Google Scholar] [CrossRef]
- Hirsch, J.; Marsiglio, F. Understanding electron-doped cuprate superconductors as hole superconductors. Phys. C Supercond. Its Appl. 2019, 564, 29–37. [Google Scholar] [CrossRef]

| JT Configuration JT Ions | Symm. | LS/HS | Local Boson | Lattice | Representative Compounds |
|---|---|---|---|---|---|
| (): Ti, V, Cr | tetra | - | : s = 1 | A S = 0 | -SrVO (Sr,Ba)CrO |
| (): V, Cr, Mn | tetra | LS | : s = 1 | A S = 0 | BaVGeO (?) |
| (): Cr, Mn, Fe | octa | HS | : s = 1 | A S = 3/2 | CrO, CrF SrFeO (Ca,Sr,Ba)FeO (Ca,Sr,Ba)FeO RMnO, LaMnO |
| (): Ru | octa | HS | : s = 1 | A S = 3/2 | (Ca,Sr)RuO (Ca,Sr)RuO, RuO (Ca,Sr)RuO |
| (): Fe, Co | tetra | HS | : s = 1 | A S = 3/2 | FePn, FeCh, NaCoO |
| (): Co, Ni | octa | LS | : s = 1 | A S = 0 | RNiO (Li,Na,Ag)NiO |
| (): Cu, Ni | octa | - | : s = 1 | A S = 0 | CuF, KCuF, KCuF |
| (): Pd, Ag | octa | - | : s = 1 | A S = 0 | AgO (AgAgO) |
| (): Cu, Ni | octa*square | - | : s = 0 | A S = 0 | HTSC cuprates RNiO, CuO |
| (): Pd, Ag | octa*square | - | : s = 0 | A S = 0 | AgF, KAgF CsAgF, LaPdO (?) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moskvin, A. Jahn–Teller Magnets. Magnetochemistry 2023, 9, 224. https://doi.org/10.3390/magnetochemistry9110224
Moskvin A. Jahn–Teller Magnets. Magnetochemistry. 2023; 9(11):224. https://doi.org/10.3390/magnetochemistry9110224
Chicago/Turabian StyleMoskvin, Alexander. 2023. "Jahn–Teller Magnets" Magnetochemistry 9, no. 11: 224. https://doi.org/10.3390/magnetochemistry9110224
APA StyleMoskvin, A. (2023). Jahn–Teller Magnets. Magnetochemistry, 9(11), 224. https://doi.org/10.3390/magnetochemistry9110224







