Abstract
A significant growth of research on digital microfluidics has been achieved over the past several decades, and the field is still attracting increasing attention for fulfilling relevant mechanisms and potential applications. Numerous studies have been devoted to actively manipulating droplets in a variety of fundamental and applicational scenarios. In this work, the deformation of ferromagnetic fluid droplets is studied under an external uniform magnetic field. The droplets are precisely dispersed on the bottom surface of a container assembled with polymer methacrylate (PMMA) plates. Mineral oil is applied instead of air as the surrounding medium for easy stretching and preventing water solvent evaporation in ferrofluid. The design and processing of the container are firstly carried out to observe the shape and characterize the wettability of the droplets in the immiscible mineral oil medium. Furthermore, the droplets’ deformation and the working mechanism are given under the action of the horizontal uniform magnetic field. At different magnetic field intensities, the droplet is stretched in the horizontal direction parallel to the applied field. Due to volume conservation, the dimension in the height reduces correspondingly. With the coupling effect of magnetic force, viscous force and interfacial tension, the contact angle first increases with the magnetic field and then basically remains unchanged upon magnetization saturation. Consistent with the experimental results, the numerical method clearly reveals the field coupling mechanism and the nonlinear deformation of the sessile droplet.
1. Introduction
The shape and wettability manipulation of droplets on a solid surface has become a cutting-edge focus of research in digital microfluidics which is applicable in the printing and coating industry, chemistry, biology, and so on. Up to now, numerous advanced technologies have been developed for the realization of shape and wettability tunability, such as chemical gradient [1], thermal capillary force [2,3], electrostatic force [4,5], optical force [6], magnetic force [7,8,9], etc. There are certain limitations in the adaptability, strength, and breadth of force in terms of the passive method which relies purely on the characteristics of the liquid, solid surface, and surrounding medium. The introduction of active forces mostly requires additional and expensive accessories, which results in the increment of the device cost and a reduction in its reliability. Among them, the magnetic force has attracted increasing attention due to its advantages in remote control without sensitivity to pH and dielectric properties of the liquid medium. To realize magnetization, ferromagnetic fluids are commonly employed as typical media with well-established numerical models to describe the dynamics in terms of channel geometry, magnetic field distribution, and particle concentration [10]. The functional magnetic nanofluid is envisioned for applications in biosensors with magnetic manipulation [11,12]. Moreover, potential aptness in micro-electronic appliances is revealed with a three-dimensional hydrodynamics model established taking into account the nonlinear variation of viscosity with temperature [13]. The magneto microfluidic control mainly focuses on the utilization of magnetic field gradient for magnetic force generation and thus flow manipulation. As a result, the magnitude of the magnetic force is closely related to the shape of the magnet, which puts forward high requirements for fabrication methods. Alternatively, magnetic force can be generated with the contribution of the susceptibility discrepancy between the magnetic and non-magnetic fluid in digital microfluidics. In this case, a uniform magnetic field is adaptable for greatly enhancing the integration of microfluidic devices in the equipment.
There have been numerous reports on the experimental study of active control of ferromagnetic fluid droplets by a magnetic field. The preliminary studies include the shape and instability of droplets under the action of a static magnetic field in terms of the magnetic field strength, temperature, and particle size [14]. A wise selection of different magnetic field configurations can play the required role in the application. Permanent magnets are commonly used to change the wetting characteristics of the droplets, drag the droplets, and realize complex physical or chemical processes such as separation and mixing [7]. In addition, through the design and fabrication of electromagnetic fields, the complex pre-designed movement track can be realized for ferromagnetic fluid droplets in various directions and speeds [15,16]. The superposition of an additional permanent magnetic field in the experimental device facilitates the enhancement of the ferromagnetic fluid droplet magnetization. The deformation and dynamic characteristics of the droplets are verified and analyzed as a function of droplets size, the coil current, and the viscosity of the liquid. The process of splitting, transporting, merging, and mixing of the droplets can be realized on the introduced solid substrate which can be switched between hydrophilic and hydrophobic wetting modes [17]. The speed of the droplets depends significantly on the magnetic field strength. The driving current intensity and frequency are the key parameters of effective mixing [18]. Based on the magnetic approaches, the realization in the detection of DNA control [19] and enzyme-labeled antibodies [20] indicates the potential of its application in biological analysis.
The rotating magnetic field is preferred in certain cases as it can exert both radial and axial forces on the droplets simultaneously. Concerning the frequency and intensity of the magnetic field, an investigation is implemented for the behavior of the droplets [21] and the interaction of magnetic particles [22]. In an experimental study, the movement and resulting merging of the sessile droplets can be realized under a rotational field which can be obtained by rotating a permanent magnet or multiple coils with alternating current applied [23]. The mixing of fluids in the droplet is prompted due to the enhancement of the viscous interaction between the magnetic microspheres and the fluid caused by the circulation flow synchronous with the periodic magnetic field. Both the rotational and translational motion of a magnetic fluid droplet are reported with its shape governed by the magnetic field and the hydrodynamic flows [24].
In this work, the deformation of the ferrofluid sessile droplet is studied under the action of an external horizontal uniform magnetic field. The droplets are placed on a horizontal PMMA plate in a uniform magnetic field generated by a pair of electromagnetic coils. The ferrofluid droplets are placed in the gap between the coils with the generated magnetic field parallel to the bottom of the container. In both experimental and numerical investigations, the ferrofluid droplet is immersed in the surrounding mineral oil for easy stretching and mass conservation. The sessile ferrofluid droplet deforms under the action of the horizontal magnetic field with the intensity shifted by alternating the current value. A comprehensive working mechanism is established through the analysis of the flow field, magnetic distribution, and the involved force.
2. Experimental and Numerical Methods
The experimental setup shown in Figure 1 is mainly composed of a computer, a charge coupled device (CCD) camera, a set of electromagnets, and a container with mineral oil and ferrofluid. To observe the shape and wetting characteristics of ferrofluid droplets, PMMA plates are designed and fabricated by laser cutting for assembling the container in the experimental test. The ferrofluid droplets, with volume set at 1.3 µL, 2.3 µL, 3.4 µL, and 4.8 µL, are placed at the bottom of the container, keeping their remaining surface in contact with the mineral oil introduced to reduce the interfacial tension and prevent the evaporation of the water-based ferrofluid. Water-based ferrofluid (EMG707, Ferrotec, Livermore, CA, USA) is used containing Fe3O4 nanoparticles with a diameter of 10 nm, a volume fraction of 1.8%, and an initial susceptibility of 0.36. The viscosity of ferrofluid is 5 mPa·s at 27 °C. The density of ferrofluid and mineral oil (M5904, Sigma, Alexandria, VA, USA) at 25 °C are 1.1 × 103 kg/m3 and 0.84 × 103 kg/m3, respectively. The ferrofluid droplet is generated by a pipette (Finnpipette, Thermo Scientific, Waltham, MA, USA), which can accurately control the droplet volume within a range of 0.5–10 μL. The magnitude of the magnetic field can be tuned by varying the gap distance and current. In our experiment, the gap is kept at 20.1 mm to ensure the stability, uniformity, and accurate control of the magnetic field. With a fixed gap, the electromagnetic field strength that alters with the current input (0–70 A) is measured by a Gauss meter (Model 410, Lake Shore, Westerville, OH, USA). The calibration of the field is implemented with a comparison with the data given in the manufacturer’s manual sheet. The shape of the droplet is recorded by the CCD camera (Pulnix, progressive scan camera, JAI Inc., Yokohama, Japan) and further analyzed by a customized MATLAB 2019b program.
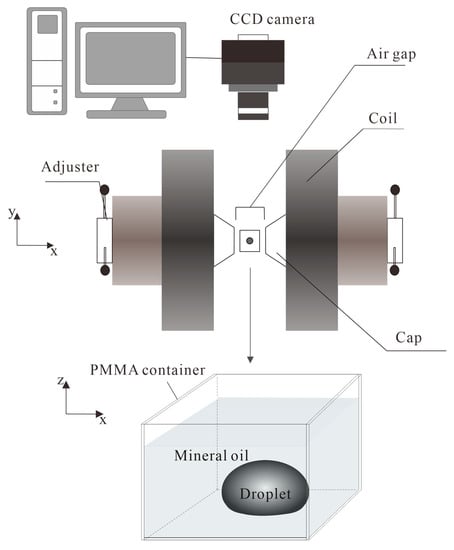
Figure 1.
Experimental setup and imaging system for sessile droplet deformation.
The systematic numerical model is shown in Figure 2a in which the droplet volume is set at 4.8 µL. The size of the container is 6 × 5 × 1.8 mm. Initially, a 1.31844 mm radius hemisphere is placed inside the container to act as a ferrofluid sessile droplet. The physical parameters are the same as the experiment. A uniform magnetic field is generated in X direction with a magnetic potential of 20–3060 A applied on the left wall of the container. The right wall is set with a zero scalar magnetic potential with the others employing the magnetically insulated boundary condition. The initial magnetic field intensity with the corresponding flux density is presented in Figure 2b with various potentials adopted on the boundary. The numerical simulation is implemented with the governing equations solved on a Cartesian staggered grid by the finite element method with the interface tracking between ferrofluid and mineral oil two-phase flow achieved by the level-set method. The calculation is accomplished with the coupling model of the magnetic field, fluid flow, and interface tracking. Subsequently, the initial spherical cap shape of the droplet is deformed and governed by the force balance. Gravitational force is considered in the calculation to have a thorough understanding of the underlying mechanism. The ferrofluid used in the study is assumed as a uniform sample containing 1.8 vol% 10 nm Fe3O4 nanoparticles. The initial shape of the droplet depends on surface tension, viscous force, and gravitational force which is presumed to be constant. The grid-independent study is accomplished by calculation with grids at 288,060 and 550,523. The height and width of the droplets show a relative error of less than 5%. As a result, the following results are provided for the model with grid number 288,060.
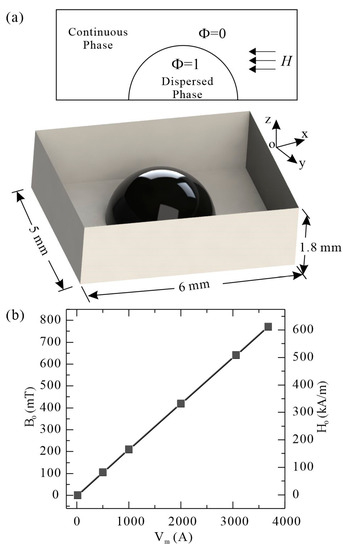
Figure 2.
Computational models and magnetic field parameters: (a) Computational domain and setting; (b) The correspondence between magnetic scale potential and initial magnetic field.
The magnetic field distribution can be solved by Maxwell equations for a non-conducting working fluid,
where H, B, , , and are magnetic field strength, magnetic flux density, magnetic potential, vacuum permeability , and relative permeability. The volumetric force exerted by a magnetic field on an isotropic media with can be expressed as [25,26,27],
where with and stands for the magnetization and susceptibility. The inhomogeneity in both the magnetic field and susceptibility contributes to the magnitude and distribution of the magnetic force density. The permeability of the sample in our study is assumed and defined to vary linearly with the level set function in the computational domain,
where is the level set function. The value of 0 and 1 signifies the relative permeability of vacuum and ferromagnetic fluid, respectively. When lies between 0 and 1, it smooths the distribution of excessive permeability at the interface.
The magnetic force on the droplet purely relies on the magnetic susceptibility, the volume of the droplet and the externally applied magnetic field. By referring to the theoretical work on field-dependent magnetic permeability, the magnetization and susceptibility for ferrofluid are expressed by the Langevin function [28] with magnetic susceptibility shifting with the magnetic field,
where , m, Md, and d are the volume fraction, magnetic moment, saturation magnetization, and diameter of magnetic nanoparticles, k is the Boltzmann constant, and T is the temperature which is taken to have the value of the room temperature. In this work, we customized the magnetization curve of the ferrofluid droplet according to the droplet shape obtained in the experiment with the corresponding -H curve shown in Figure 3. A certain degree of deviation is observed although the magnetization curve fitted by experimental data has the same trend as the regular Langevin equation. It is evident in our study that the magnetization involves the nonlinear region since the maximum field strength reaches 6.15 × 105 A/m at the applied potential of 3680 A. For H less than 6666.7 A/m, the magnetic susceptibility of ferrofluid is around 0.36. The magnetic susceptibility drops sharply when the magnetic field strength exceeds the critical value.
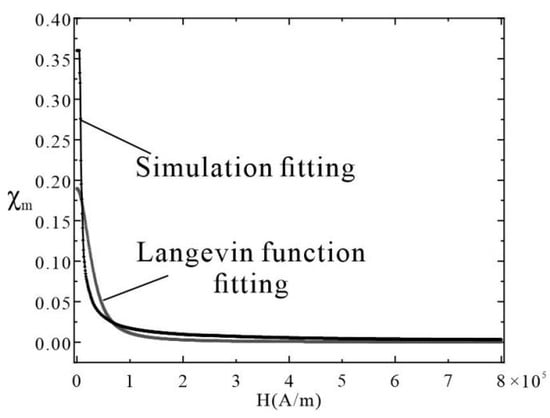
Figure 3.
The magnetization curve -H of the ferrofluid.
The flow field of the incompressible and Newtonian fluid is governed by the following continuity and Navier–Stokes equation,
where u is the velocity of the fluid, is the pressure, is the dynamic viscosity, and is the density of the fluid. The source term is the volumetric force, including the magnetic, gravitational force, and interfacial tension. The discontinuity of physical property parameters is handled by the linear function of the level set equation. The interfacial tension per unit area on the droplet interface can be expressed as [29],
where is the interfacial tension, is the Dirac function, which is only non-zero at the droplet interface, is the interface curvature, and is the unit normal vector of the interface. To characterize the deformation of droplets, the magnetic Bond number is defined as the ratio of the magnetic field force to the interfacial tension at the initial state before stretching,
where is the radius of the droplet. The moving of the contact line is governed by a balance between the interfacial tension and viscous force [30],
where is the normal unit vector of the wall, is the net force along the wetting plane, is the unit vector in the fluid motion direction, is the slip length which defaults to be the grid cell size, and indicates the interface thickness with the default value as half of the grid size which is of the order of the micron in the following calculation. The applied field is also assumed to have a collinear relationship with the liquid magnetization which is independent of temperature.
3. Results Analysis and Discussion
In the experiment, we tested and analyzed the height and base diameter of the droplet at various currents. Different droplet volumes are observed in the experiment, with larger volumes producing greater magnetic field forces, Figure 4. For ferrofluid droplets dispersed on a smooth non-magnetic solid substrate, the liquid partially wet the surface with an ellipsoidal meniscus formed under the effect of gravity and interfacial tension. At the beginning, the numerical calculation is implemented with no magnetic field for the initial value of surface tension by fitting the ferrofluid droplet shape with the experimental image. With a horizontal field applied, the central region of the droplet elongates symmetrically along the field direction due to the magnetic stress which has a maximum at the left and right tip of the droplet. On the boundary, the magnetic field affects the force balance under equilibrium conditions in the form of magnetostrictive pressure, magnetic normal pressure and fluid-magnetic pressure. The increase in current gives rise to the enhancement in magnetic field strength. Consequently, the droplet is stretched horizontally with the height decreasing correspondingly. In the numerical study, the droplet is fixed at 4.8 μL in volume for comparison with the experimental results.
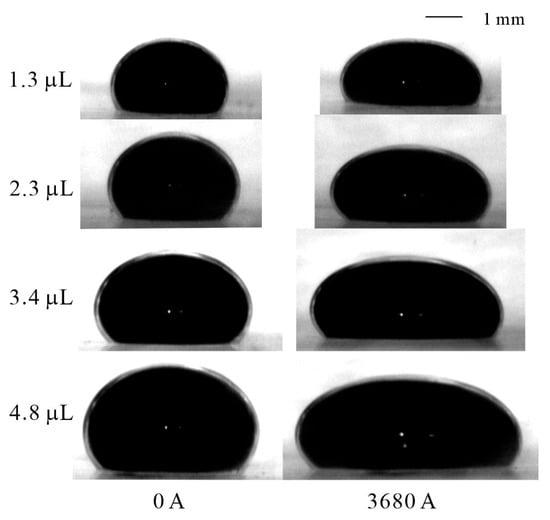
Figure 4.
The experimental results for deformation of droplets at different volumes with and without magnetic field.
The images for the deformed droplet at the volume of 4.8 μL taken at different magnetic potentials are presented in Figure 5a with the red line standing for the interface extracted from the numerical calculation. Both the experimental and numerical results show a stronger deformation at a relatively larger magnetic potential. Upon reaching a critical value of the magnetic potential, the droplet will not continue to the deformation due to the magnetization saturation of the ferrofluid. With the applied magnetic potential at 1000 A, the volume distribution of the droplet at different time steps is shown in Figure 5b. The deformation is almost instant, taking about 40 ms for the initial hemispherical shape to deform to an elliptical shape. In the deformation process, the force balance between the droplet and PMMA surface has a significant effect on the droplet shape, especially in terms of its influence on the contact angle. The enhancement of the magnetic field makes the interface of the sessile drop move farther than the contact line in the horizontal direction, resulting in the increment of the contact angle. It is worth mentioning that the wetting behavior in the experiment will not restore to the original state with the magnetic field turning off due to the surface effect at the contact line, viscous loss, surface dissipation, etc.
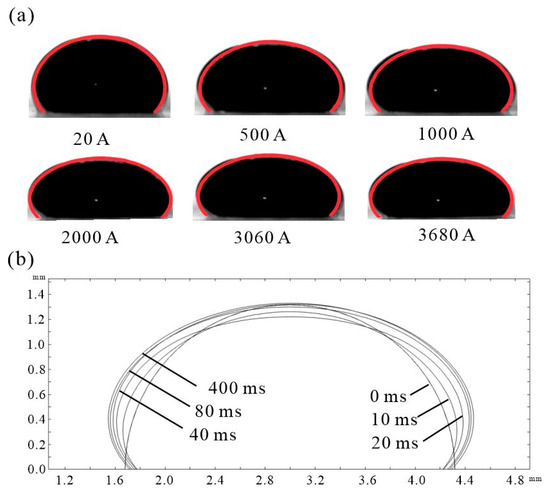
Figure 5.
The volume fraction of the droplet on the XOZ plane: (a) At t = 400 ms and = 20–3680 A, the contour of the droplet is compared with the experiment; (b) At = 1000 A and t = 0–400 ms, the shape of the sessile droplet.
The magnetic field distribution is shown in Figure 6a,b with both the field strength and flux density at a 1000 A magnetic potential. The discrepancy of magnetic susceptibility is defined on the droplet circumferential which is tracked by the level-set method. Moreover, the nonlinear magnetization of ferrofluid is considered as a function of the magnetic flux density. Both the magnetic field gradient and the susceptibility gradient contribute to the magnetic force and act on fluid flow and interface deformation. With the corresponding deformation of the droplet, a further ensuing alteration of the magnetic field distribution results in turn due to the transition of the liquid magnetization varies with the level set function. In addition, the distribution of the magnetic field reflects the effect of the level set function on the smooth assignment of the magnetic permeability. After reaching saturation with the magnetic susceptibility of the ferrofluid varying negligibly with the magnetic field, the balance between magnetic force, surface tension, viscous force, and gravity ensures a stable shape of the droplet. Both the magnetic field strength and flux density follow the negative direction of the X axis. Accordingly, the flow field distribution is shown in Figure 6c. During the stretching process, the flow in the droplet is obviously accelerated with liquid moving to both sides in a regular direction corresponding to the droplet deformation. Upon reaching 400 ms, the magnitude of the velocity decreases to form a stable state. In addition, a higher velocity value appears on both sides of the droplet, resulting in internal circulation.
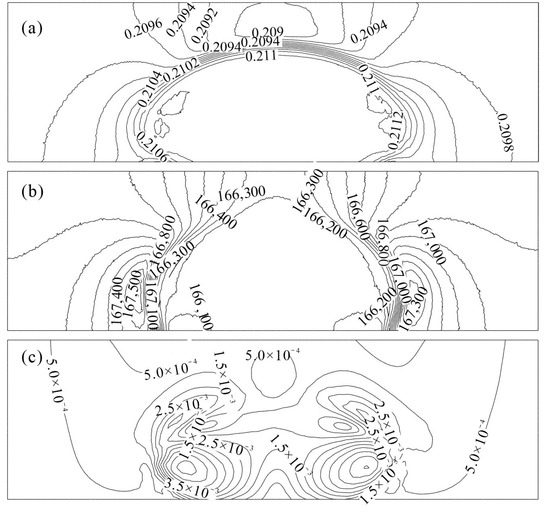
Figure 6.
Distribution on XOZ plane at = 1000 A and t = 400 ms: (a) Magnetic flux density, B (T); (b) Magnetic field strength, H (A/m); (c) Magnitude of velocity.
To further analyze the role in the deformation process of the droplet, the magnitude of the magnetic force and surface tension exerted on the droplet is collected along the horizontal line at the cross-section as shown in Figure 7. Additionally, the volumetric magnetic force is further illustrated separately in terms of the fractions contributed by magnetic field gradients and magnetic susceptibility gradients . In this study, the numerical results show the same magnitude of contribution of the magnetic force component. On both sides of the droplet, the magnetic force points in the direction of elongating the droplet. The component of the magnetic force in the Y and Z directions is negligible compared with that in the X direction. In general, the surface tension is equal at all points on the droplet surface, so that the droplet maintains a state of minimum surface area, forming a spherical shape. As the droplet deforms, an uneven distribution of surface tension emerges on the interface due to the change in curvature. The X-direction component of the interfacial tension, which is larger than that of the magnetic force, points to the interior of the droplet. The higher interfacial tension is mainly concentrated on both sides of the droplet due to the larger curvature that is caused by the deformation of the droplet. A stronger magnetic field would give rise to a severe deformation which enhances the maximum value of interfacial force.
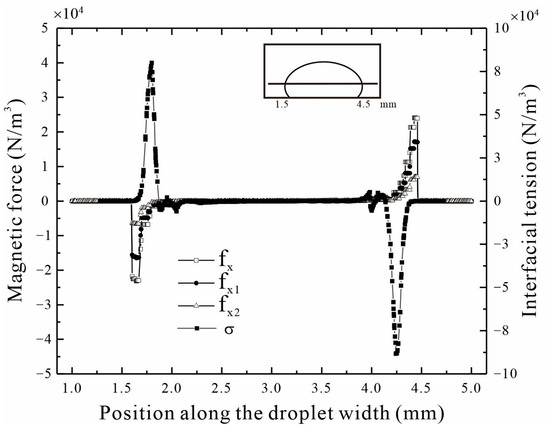
Figure 7.
Distribution of magnetic force in X direction , the magnetic force due to field gradient , the magnetic force due to susceptibility gradient , and interfacial tension in X direction along the droplet width on XOZ plane at =1000 A and t = 400 ms.
To generalize the understanding of the process, the non-dimensional magnetic Bond number is preferred for the characterization of the deformation. Under different magnetic potentials, the magnetic Bond number of the droplets is shown in Figure 8. Before undertaking deformation, the magnetic Bond number is calculated with the data at the initial state by taking the ratio of the maximum value of volumetric magnetic force to the maximum value of the interfacial tension component in X direction. With the increase of the applied magnetic potential, the magnetic Bond number gradually increases and finally tends to be constant. At the initial stage of the deformation, the periphery of the droplet is regular, which results in a relatively small value of the maximum interfacial tension. Hereafter, the droplet deforms rapidly in less than 10 ms with the effect of the wetting and the magnetic force. For the deformed droplet, there would be a sharp decrease in the magnetic Bond number that appears close to the solid wall due to the tremendous increase in the interfacial tension and negligible change in the magnetic force. With the magnetic potential fixed at 1000 A, the droplet no longer deforms significantly after about 0.1 s with a constant magnetic Bond number.
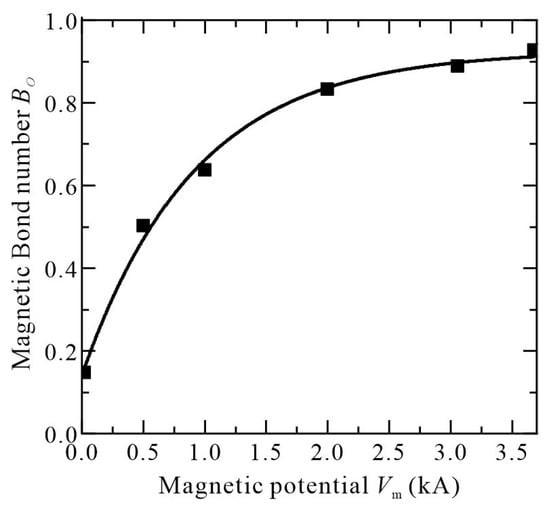
Figure 8.
The magnetic Bond number at various magnetic potentials.
The comparison of the height and width of the droplets under different magnetic Bond numbers is shown in Figure 9a,b. Both the experimental and numerical results are analyzed with typical images for straightforward observation of the droplet shape. With the increase of , the droplets are gradually stretched and finally tend to be stable. The shape and dimension of the sessile droplet are impacted by the generated deformation energy in the process varying with magnetic Bond number due to the shift of the magnitude and distribution of magnetic force inside the droplet. By referring to the definition in Equation (5), the distribution of magnetic force on the droplet is strongly affected by the strength of the magnetic field gradient which is tunable with the magnetic Bond number. Furthermore, the change in orientation of the magnetic moment in the magnetic field results in an alteration in magnetic susceptibility. The shape of the sessile droplet is determined by the combined impact of the above-mentioned factors.
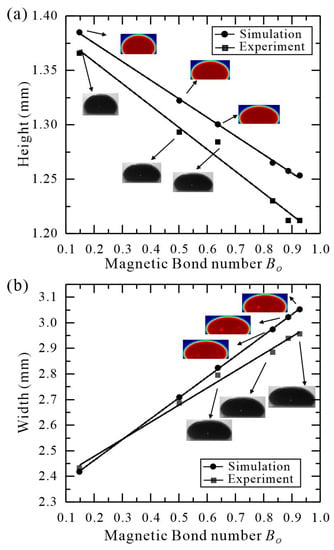
Figure 9.
Comparison of numerical and experimental results at various magnetic Bond numbers: (a) Height; (b) Width.
The significant deformation that occurs at the preliminary stage indicates a vigorous interaction between the magnetic moments which gives rise to a strong internal magnetic force on the sessile ferrofluid droplet. In this study, the maximum magnetic force on the XOZ cut plane varies from 8325.5 to 36,912 N/m3 for potential in the range of 20–3680 A. The magnetization saturation leads to a sharp reduction of the magnetic susceptibility, resulting in a stable magnetic force. The extent of the droplet deformation is almost linearly determined by the magnitude of the magnetic Bond number. The experimental and numerical results agree well with each other, indicating a more comprehensive and systematical study of the partial-wetting sessile ferrofluid droplet deformation in a uniform magnetic field.
4. Conclusions
In this work, the deformation characteristics of ferrofluid in a mineral oil medium are studied in contact with a PMMA plate under the action of the external uniform magnetic field. The effect of the magnetic field on the shape of the droplet is measured by experiments followed by analysis and discussion on the deformation process. For a more comprehensive understanding of the working mechanism, numerical simulation is conducted considering the coupling solution of fluid flow, magnetic field, and interface tracking. The droplet parameter varies with different liquid volumes and magnetic field strength. The increase in liquid volume leads to the increase of magnetic force which affects the equilibrium state on the contact line and thus the motion accordingly. Therefore, the balance established by magnetic force, interfacial tension, and viscous force determines the shape of the sessile droplet including the droplet height, the base diameter, and the contact angle. The results confirm and support the uniform magnetic field to be an effective control method, which has a guiding role in the application of ferrofluid sessile drops in various fields.
Author Contributions
Conceptualization, N.-T.N. and G.-P.Z.; methodology, N.-T.N. and G.-P.Z.; validation, S.-H.W. and S.-Z.Z.; formal analysis, S.-H.W. and L.L.; writing—original draft preparation, S.-H.W.; writing—review and editing, G.-P.Z. and S.-Z.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, 11702134 and the Natural Science Foundation of Jiangsu Province, BK20160797.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
This work was partially supported by the National Natural Science Foundation of China, 11702134 and the Natural Science Foundation of Jiangsu Province, BK20160797.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Aksay, I.A.; Hoge, C.E.; Pask, J.A. Wetting under chemical equilibrium and nonequilibrium conditions. J. Phys. Chem.USA 1974, 78, 1178–1183. [Google Scholar] [CrossRef]
- David, S.; Sefiane, K.; Tadrist, L. Experimental investigation of the effect of thermal properties of the substrate in the wetting and evaporation of sessile drops. Colloids Surf. A 2007, 298, 108–114. [Google Scholar] [CrossRef]
- Nguyen, N.T.; Ting, T.H.; Yap, Y.F.; Wong, T.N.; Chai, J.C.K.; Ong, W.L.; Zhou, J.; Tan, S.H.; Yobas, L. Thermally mediated droplet formation in microchannels. Appl. Phys. Lett. 2007, 91, 084102–084103. [Google Scholar] [CrossRef]
- Hayes, R.A.; Feenstra, B. Video-speed electronic paper based on electrowetting. Nature 2003, 425, 383–385. [Google Scholar] [CrossRef] [PubMed]
- Yi, U.C.; Kim, C.J. Characterization of electrowetting actuation on addressable single-side coplanar electrodes. J. Micromech. Microeng. 2006, 16, 2053. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, G.; Ren, H. Large-Area Optical Switch Using Surface-Expandable Liquid Droplets. J. Disp. Technol. 2017, 12, 1565–1569. [Google Scholar] [CrossRef]
- Nguyen, N.T.; Zhu, G.; Chua, Y.C.; Phan, V.N.; Tan, S.H. Magnetowetting and sliding motion of a sessile ferrofluid droplet in the presence of a permanent magnet. Langmuir 2010, 26, 12553–12559. [Google Scholar] [CrossRef]
- Capobianchi, P.; Lappa, M.; Oliveira, M.S.N. Deformation of a ferrofluid droplet in a simple shear flow under the effect of a constant magnetic field. Comput. Fluids 2018, 173, 313–323. [Google Scholar] [CrossRef]
- Filali, Y.; Er-Riani, M.; El Jarroudi, M. The deformation of a ferrofluid drop under a uniform magnetic field. Int. J. Non-Linear Mech. 2018, 99, 173–181. [Google Scholar] [CrossRef]
- Vafeas, P.; Bakalis, P.; Papadopoulos, P.K. Effect of the magnetic field on the ferrofluid flow in a curved cylindrical annular duct. Phys. Fluids 2019, 31, 117105. [Google Scholar] [CrossRef]
- Volkova, T.I.; Böhm, V.; Naletova, V.A.; Kaufhold, T.; Becker, F.; Zeidis, I.; Zimmermann, K. A ferrofluid based artificial tactile sensor with magnetic field control. J. Magn. Magn. Mater. 2017, 431, 277–280. [Google Scholar] [CrossRef]
- Sharova, O.A.; Merkulov, D.I.; Pelevina, D.A.; Vinogradova, A.S.; Naletova, V.A. Motion of a spherical magnetizable body along a layer of magnetic fluid in a uniform magnetic field. Phys. Fluids 2021, 33, 087107. [Google Scholar] [CrossRef]
- Akbar, N.S.; Al-Zubaidi, A.; Saleem, S.; Alsallami, S.A.M. Variable fluid properties analysis for thermally laminated 3-dimensional magnetohydrodynamic non-Newtonian nanofluid over a stretching sheet. Sci. Rep. 2023, 13, 3231. [Google Scholar] [CrossRef]
- Bacri, J.C.; Salin, D.; Massart, R. Study of the deformation of ferrofluid droplets in a magnetic field. J. Phys. Lett. 1982, 43, 179–184. [Google Scholar] [CrossRef]
- Nguyen, N.T.; Beyzavi, A.; Ng, K.M.; Huang, X. Kinematics and deformation of ferrofluid droplets under magnetic actuation. Microfluid. Nanofluidics 2007, 3, 571–579. [Google Scholar] [CrossRef]
- Nguyen, N.T.; Ng, K.M.; Huang, X. Manipulation of ferrofluid droplets using planar coils. Appl. Phys. Lett. 2006, 89, 648. [Google Scholar] [CrossRef]
- Lehmann, U.; Hadjidj, S.; Parashar, V.K.; Rida, A. Two dimensional magnetic manipulation of microdroplets on a chip. Sens. Actuators B Chem. 2006, 117, 457–463. [Google Scholar] [CrossRef]
- Saroj, S.K.; Asfer, M.; Sunderka, A.; Panigrahi, P.K. Two-fluid mixing inside a sessile micro droplet using magnetic beads actuation. Sens. Actuators A Phys. 2016, 244, 112–120. [Google Scholar] [CrossRef]
- Lehmann, U.; Vandevyver, C.; Parashar, V.K.; Gijs, M.A. Droplet-based DNA purification in a magnetic lab-on-a-chip. Angew. Chem. 2006, 45, 3062–3067. [Google Scholar] [CrossRef]
- Lehmann, U.; De Courten, D.; Vandevyver, C.; Parashar, V.K.; Gijs, M.A.M. On-chip antibody handling and colorimetric detection in a magnetic droplet manipulation system. Microelectron. Eng. 2007, 84, 1669–1672. [Google Scholar] [CrossRef]
- Bacri, J.; Cebers, A.O.; Perzynski, R. Behavior of a magnetic fluid microdrop in a rotating magnetic field. Phys. Rev. Lett. 1994, 72, 2705–2708. [Google Scholar] [CrossRef] [PubMed]
- Cēbers, A.; Javaitis, I. Dynamics of a flexible magnetic chain in a rotating magnetic field. Phys. Rev. E 2004, 69, 021404. [Google Scholar] [CrossRef] [PubMed]
- Shikida, M.; Nagao, N.; Imai, R.; Honda, H.; Okochi, M.; Ito, H.; Sato, K. A palmtop-sized rotary-drive-type biochemical analysis system by magnetic bead handling. J. Micromechanics Microengineering 2008, 18, 35034–35041. [Google Scholar] [CrossRef][Green Version]
- Pelevina, D.A.; Turkov, V.A.; Kalmykov, S.A.; Naletova, V.A. Motions of objects with magnetizable materials along a horizontal plane in a rotating magnetic field. J. Magn. Magn. Mater. 2015, 390, 20–25. [Google Scholar] [CrossRef]
- Shaposhnikov, I.; Shliomis, M. Hydrodynamics of A Magnetizable Medium. 1975. Available online: https://www.researchgate.net/publication/255293888_Hydrodynamics_of_a_magnetizable_medium (accessed on 7 November 2021).
- Rosensweig, R.E. Ferrohydrodynamics; Cambridge University Press: New York, NY, USA, 1985. [Google Scholar]
- Chakrabarty, D.; Dutta, S.; Chakraborty, N.; Ganguly, R. Magnetically actuated transport of ferrofluid droplets over micro-coil array on a digital microfluidic platform. Sens. Actuators B: Chem. 2016, 236, 367–377. [Google Scholar] [CrossRef]
- Stan, C.; Cristescu, C.P.; Balasoiu, M.; Perov, N.; Fetisov, L. Physics. Investigations of a Fe3O4-ferrofluid at different temperatures by means of magnetic measurements. UPB Entific Bull. Ser. A: Appl. Math. 2011, 73, 117–124. [Google Scholar]
- Deshpande, K.B.; Zimmerman, W.B. Simulation of interfacial mass transfer by droplet dynamics using the level set method. Chem. Eng. Sci. 2006, 61, 6486–6498. [Google Scholar] [CrossRef]
- Baldoni, F. A Slip Boundary Condition for the Motion of a Newtonian Droplet on a Solid Surface. Zamm-J. Appl. Math. Mech. 1999, 79, 193–203. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).