Slow Methyl Axes Motions in Perdeuterated Villin Headpiece Subdomain Probed by Cross-Correlated NMR Relaxation Measurements
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample Preparation
2.2. NMR Spectroscopy
3. Results and Discussion
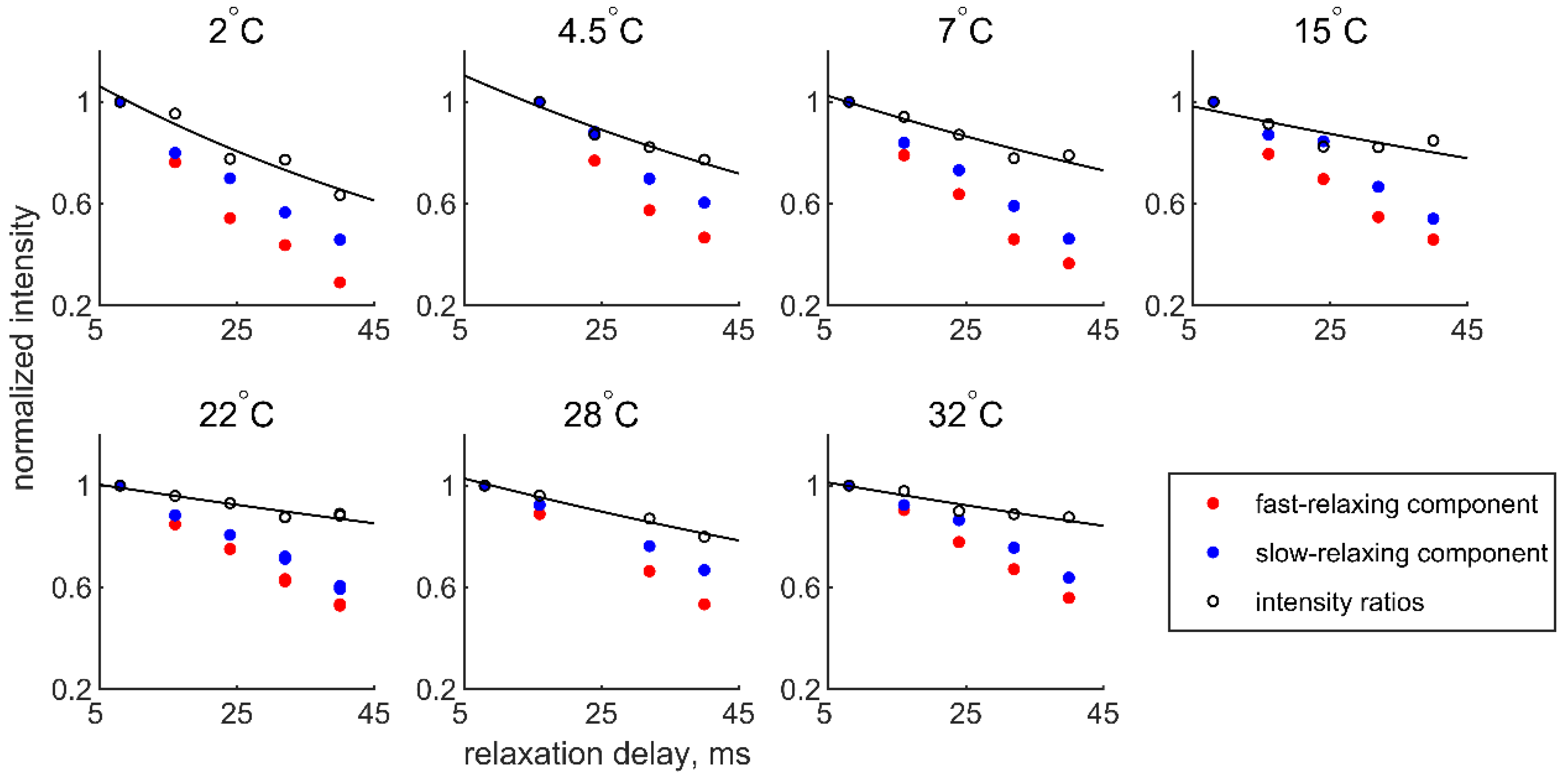
3.1. Summary of the Experimental Approach for Determination of Methyl Order Parameters
3.2. Summary of the Theoretical Expressions
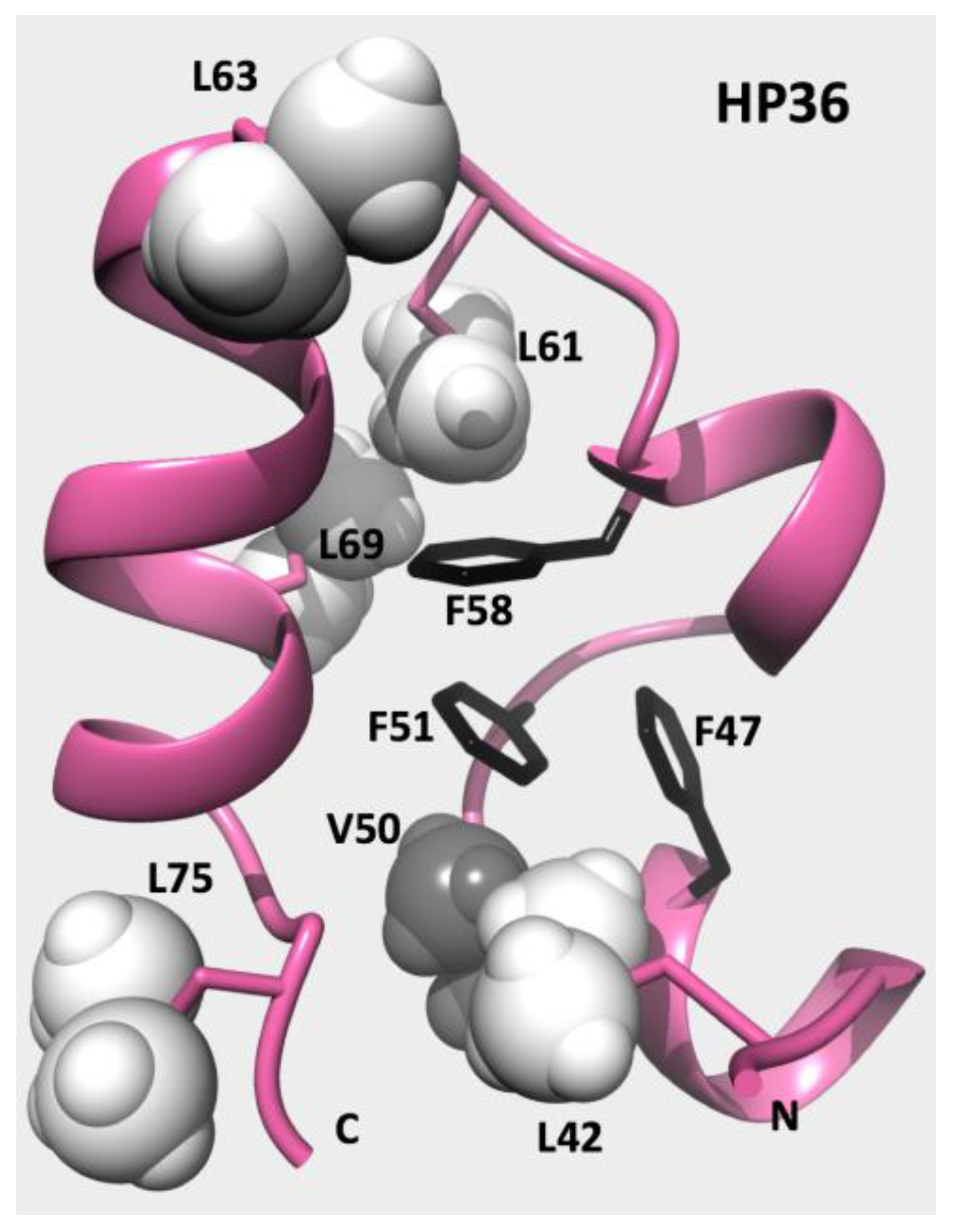
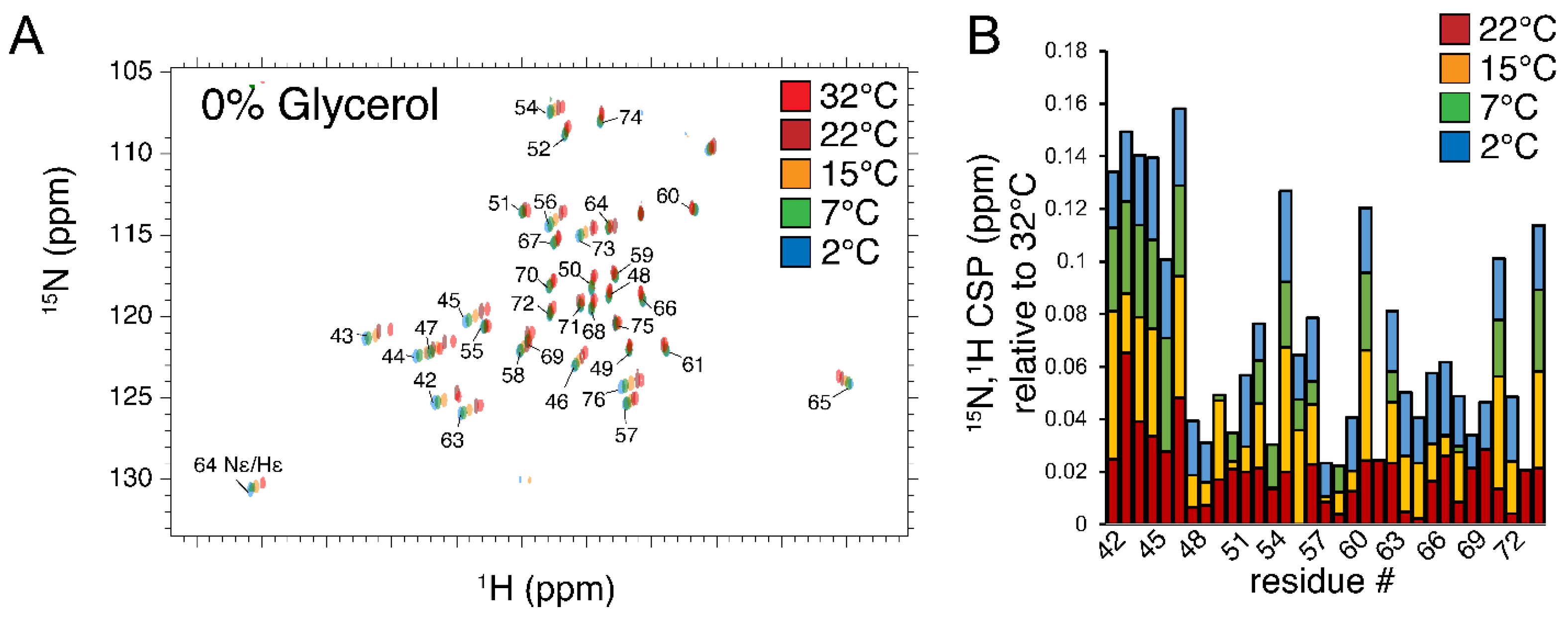
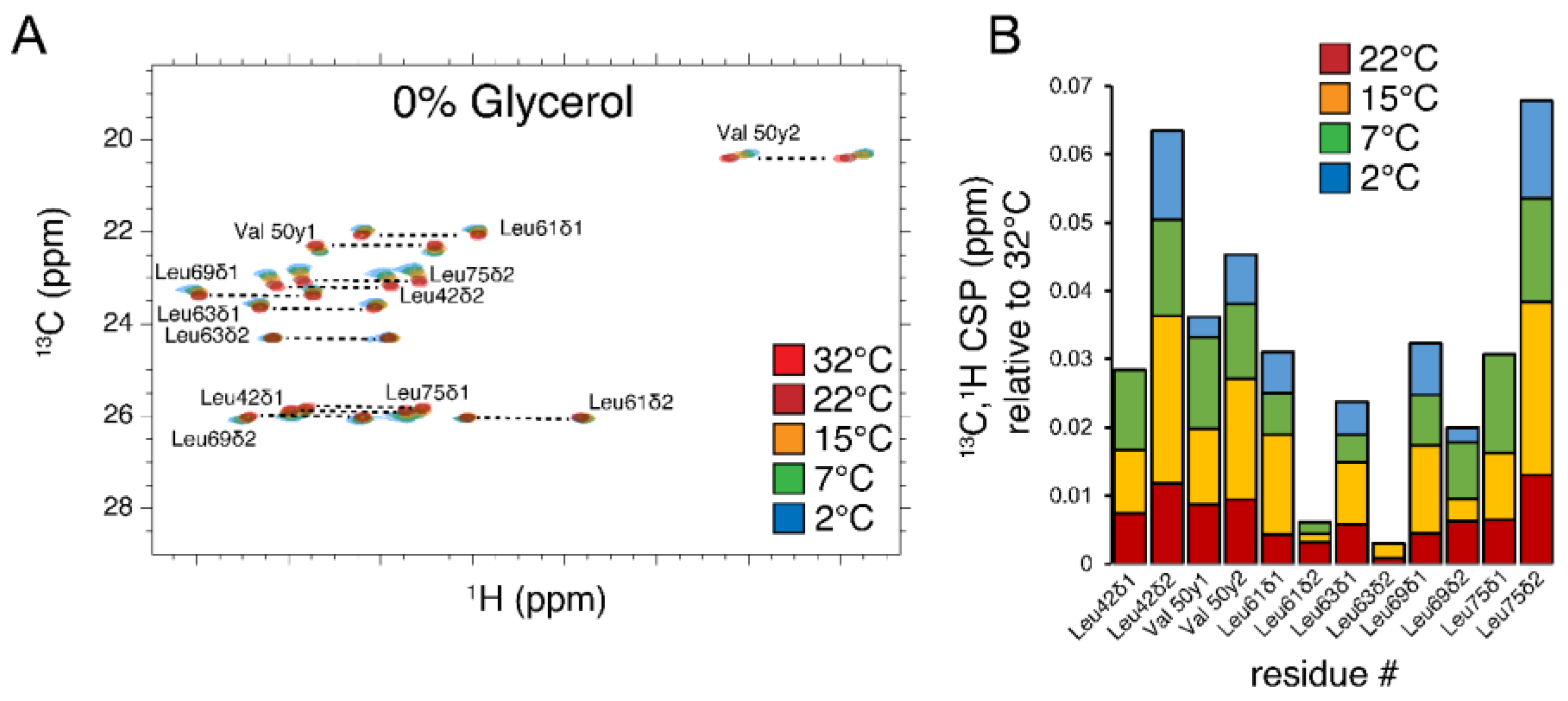
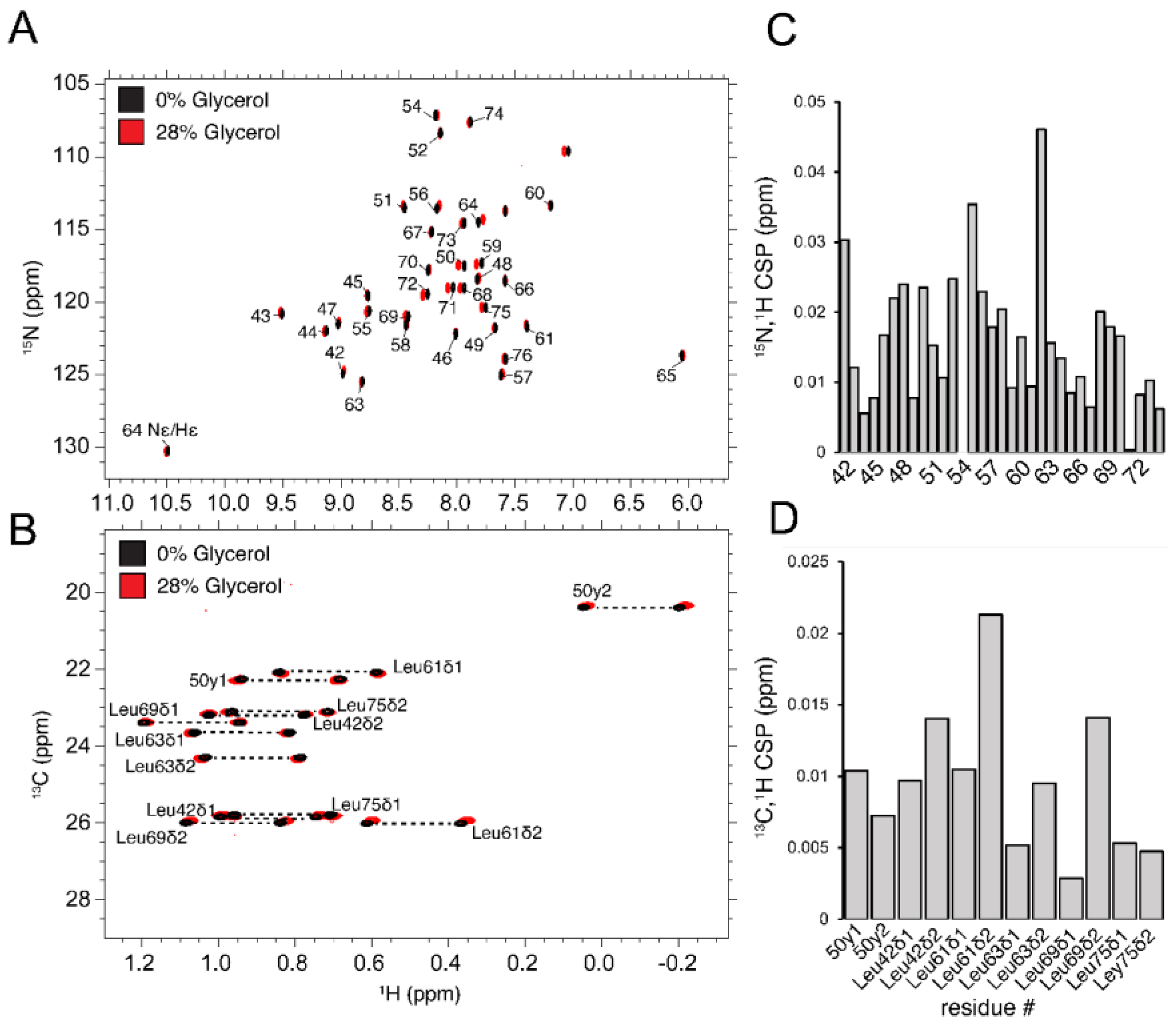
3.3. Summary of Samples, Experimental Conditions, Chemical Shift Perturbation Analysis, and Typical Spectra
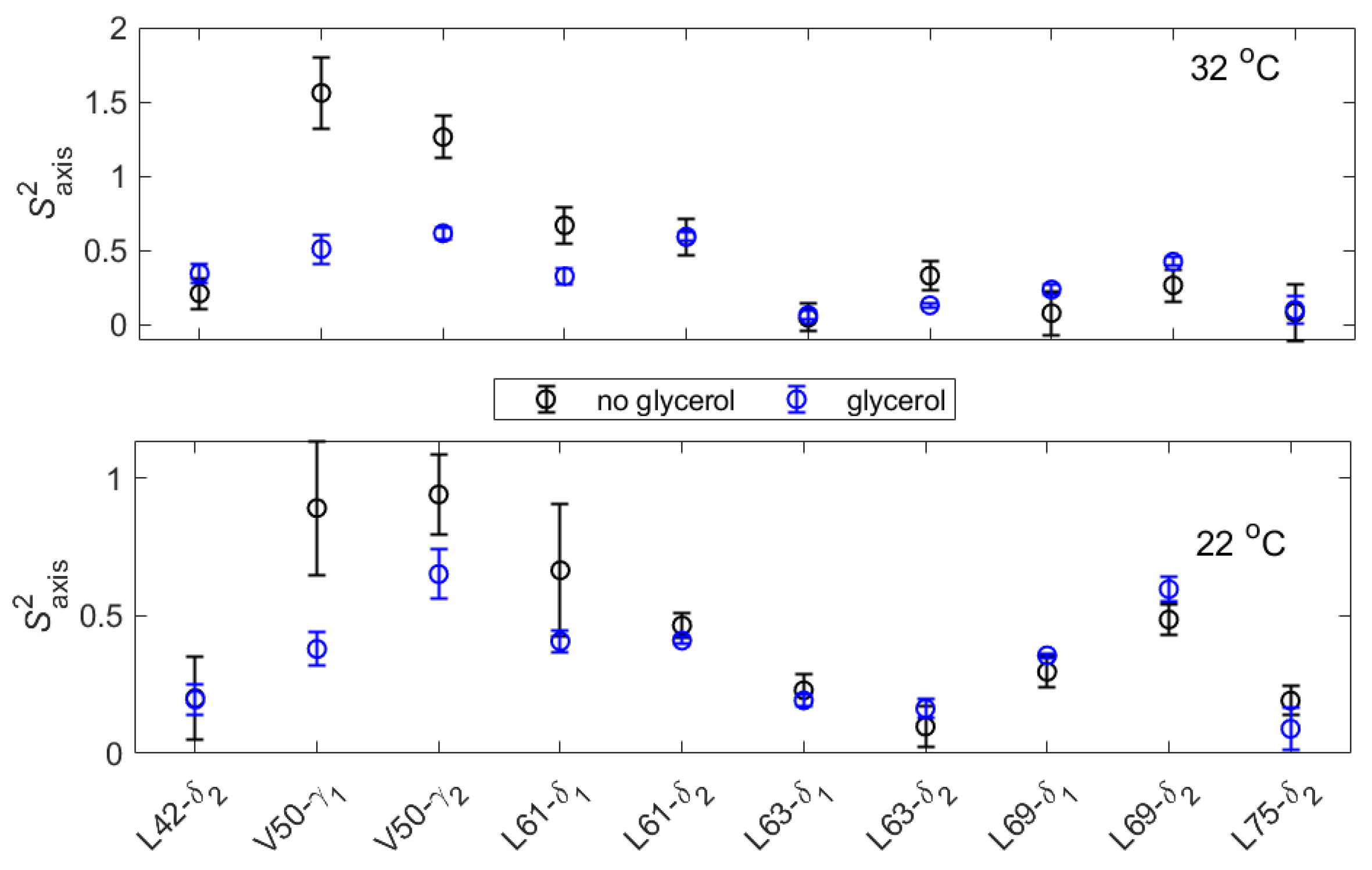
3.4. Overall Tumbling Times and the Effect of Glycerol
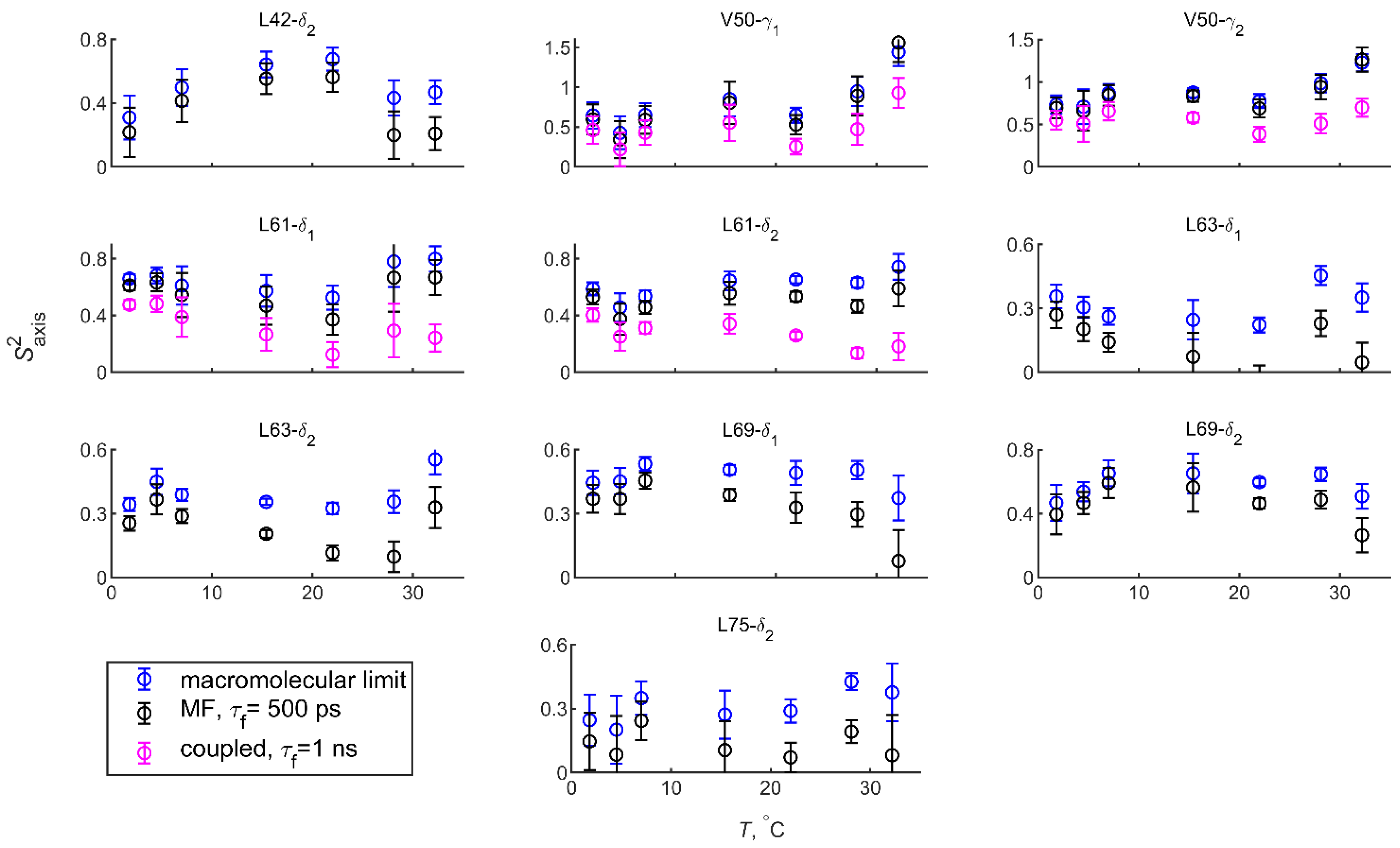
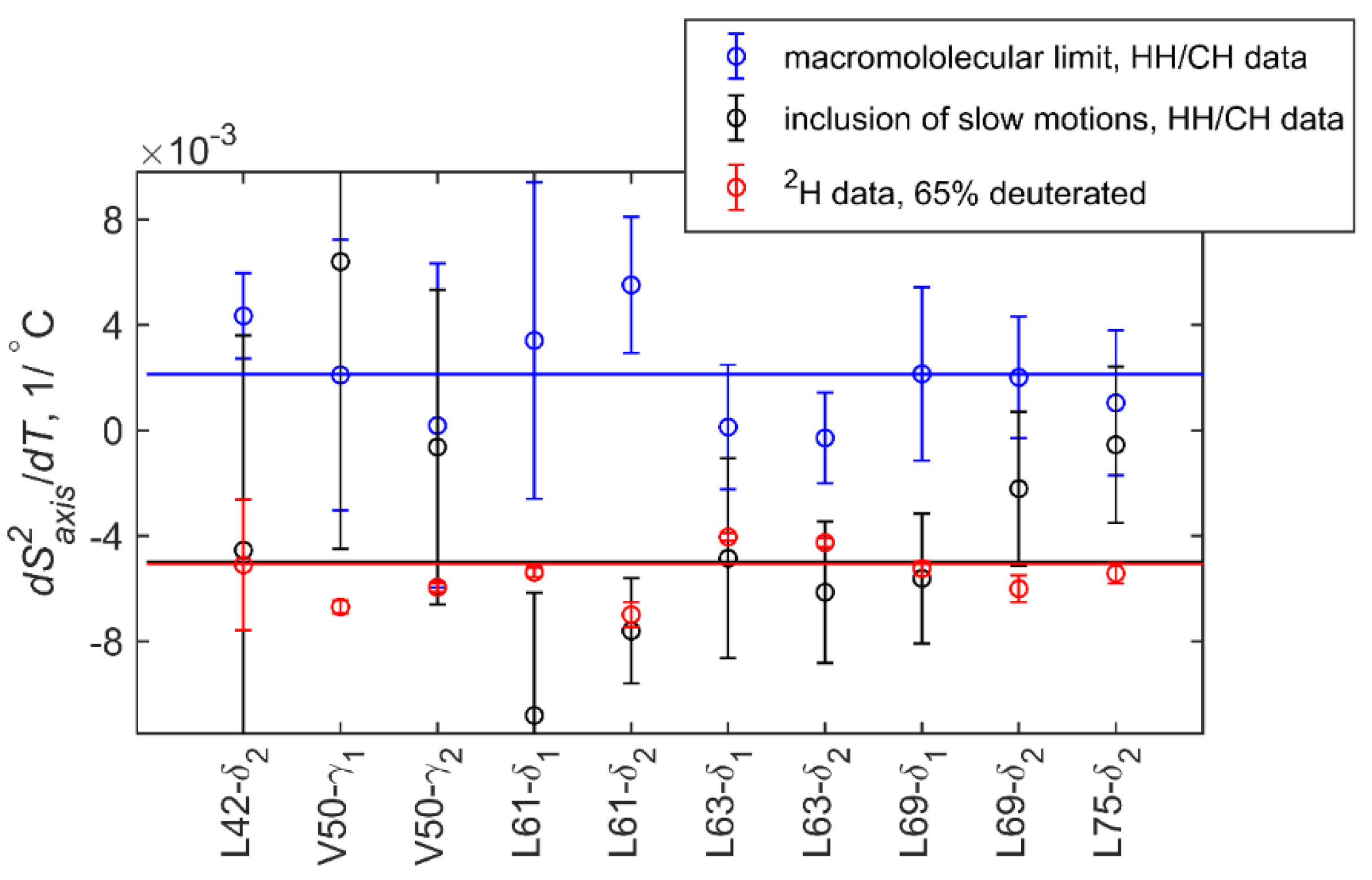
3.5. Methyl Order Parameters and Their Temperature Dependence
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Boswell, Z.K.; Latham, M.P. Methyl-Based NMR Spectroscopy Methods for Uncovering Structural Dynamics in Large Proteins and Protein Complexes. Biochemistry 2019, 58, 144–155. [Google Scholar] [CrossRef]
- Wiesner, S.; Sprangers, R. Methyl groups as NMR probes for biomolecular interactions. Curr. Opin. Struct. Biol. 2015, 35, 60–67. [Google Scholar] [CrossRef] [PubMed]
- Igumenova, T.I.; Frederick, K.K.; Wand, A.J. Characterization of the fast dynamics of protein amino acid side chains using NMR relaxation in solution. Chem. Rev. 2006, 106, 1672–1699. [Google Scholar] [CrossRef]
- Ishima, R.; Petkova, A.P.; Louis, J.M.; Torchia, D.A. Comparison of methyl rotation axis order parameters derived from model-free analyses of (2)H and (13)C longitudinal and transverse relaxation rates measured in the same protein sample. J. Am. Chem. Soc. 2001, 123, 6164–6171. [Google Scholar] [CrossRef]
- Tugarinov, V.; Ceccon, A.; Clore, G.M. Probing Side-Chain Dynamics in Proteins by NMR Relaxation of Isolated (13)C Magnetization Modes in (13)CH(3) Methyl Groups. J. Phys. Chem. B 2021, 125, 3343–3352. [Google Scholar] [CrossRef]
- Millet, O.; Muhandiram, D.R.; Skrynnikov, N.R.; Kay, L.E. Deuterium spin probes of side-chain dynamics in proteins. 1. Measurement of five relaxation rates per deuteron in (13)C-labeled and fractionally (2)H-enriched proteins in solution. J. Am. Chem. Soc. 2002, 124, 6439–6448. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.; Tugarinov, V. Observation and relaxation properties of individual fast-relaxing proton transitions in [(1)(3)CH(3)]-methyl-labeled, deuterated proteins. J. Magn. Reson. 2012, 217, 100–105. [Google Scholar] [CrossRef] [PubMed]
- McKnight, C.J.; Doering, D.S.; Matsudaira, P.T.; Kim, P.S. A thermosTable 35-residue subdomain within villin headpiece. J. Mol. Biol. 1996, 260, 126–134. [Google Scholar] [CrossRef]
- Brewer, S.H.; Vu, D.M.; Tang, Y.F.; Li, Y.; Franzen, S.; Raleigh, D.P.; Dyer, R.B. Effect of modulating unfolded state structure on the folding kinetics of the villin headpiece subdomain. Proc. Natl. Acad. Sci. USA 2005, 102, 16662–16667. [Google Scholar] [CrossRef] [PubMed]
- De Mori, G.M.S.; Colombo, G.; Micheletti, C. Study of the villin headpiece folding dynamics by combining coarse-grained Monte Carlo evolution and all-atom molecular dynamics. Proteins-Struct. Funct. Bioinform. 2005, 58, 459–471. [Google Scholar] [CrossRef]
- Kubelka, J.; Chiu, T.K.; Davies, D.R.; Eaton, W.A.; Hofrichter, J. Sub-microsecond protein folding. J. Mol. Biol. 2006, 359, 546–553. [Google Scholar] [CrossRef] [PubMed]
- Chiu, T.K.; Kubelka, J.; Herbst-Irmer, R.; Eaton, W.A.; Hofrichter, J.; Davies, D.R. High-resolution x-ray crystal structures of the villin headpiece subdomain, an ultrafast folding protein. Proc. Natl. Acad. Sci. USA 2005, 102, 7517–7522. [Google Scholar] [CrossRef]
- Xiao, S.F.; Bi, Y.; Shan, B.; Raleigh, D.P. Analysis of core packing in a cooperatively folded miniature protein: The ultrafast folding Villin Headpiece helical subdomain. Biochemistry 2009, 48, 4607–4616. [Google Scholar] [CrossRef] [PubMed]
- Harpole, K.W.; O’Brien, E.S.; Clark, M.A.; McKnight, C.J.; Vugmeyster, L.; Wand, A.J. The unusual internal motion of the villin headpiece subdomain. Protein Sci. 2016, 25, 423–432. [Google Scholar] [CrossRef]
- Lipari, G.; Szabo, A. Model-Free Approach to the Interpretation of Nuclear Magnetic-Resonance Relaxation in Macromolecules. 1.Theory and Range of Validity. J. Am. Chem. Soc. 1982, 104, 4546–4559. [Google Scholar] [CrossRef]
- Meirovitch, E. The Slowly Relaxing Local Structure Perspective of Protein Dynamics by NMR Relaxation. Isr. J. Chem. 2014, 54, 47–59. [Google Scholar] [CrossRef]
- Tugarinov, V.; Liang, Z.; Shapiro, Y.E.; Freed, J.H.; Meirovitch, E. A structural mode-coupling approach to 15N NMR relaxation in proteins. J. Am. Chem. Soc. 2001, 123, 3055–3063. [Google Scholar] [CrossRef]
- Vugmeyster, L.; Raleigh, D.P.; Palmer, A.G.; Vugmeister, B.E. Beyond the decoupling approximation in the model free approach for the interpretation of NMR relaxation of macromolecules in solution. J. Am. Chem. Soc. 2003, 125, 8400–8404. [Google Scholar] [CrossRef]
- Bi, Y.; Tang, Y.F.; Raleigh, D.P.; Cho, J.H. Efficient high level expression of peptides and proteins as fusion proteins with the N-terminal domain of L9: Application to the villin headpiece helical subdomain. Protein Expr. Purif. 2006, 47, 234–240. [Google Scholar] [CrossRef] [PubMed]
- Nichols, P.J.; Falconer, I.; Griffin, A.; Mant, C.; Hodges, R.; McKnight, C.J.; Vögeli, B.; Vugmeyster, L. Deuteration of nonexchangeable protons on proteins affects their thermal stability, side-chain dynamics, and hydrophobicity. Protein Sci. 2020, 29, 1641–1654. [Google Scholar] [CrossRef]
- Ollerenshaw, J.E.; Tugarinov, V.; Kay, L.E. Methyl TROSY: Explanation and experimental verification. Magn. Reson. Chem. 2003, 41, 843–852. [Google Scholar] [CrossRef]
- Delaglio, F.; Grzesiek, S.; Vuister, G.W.; Zhu, G.; Pfeifer, J.; Bax, A. NMRPipe: A multidimensional spectral processing system based on UNIX pipes. J. Biomol. NMR 1995, 6, 277–293. [Google Scholar] [CrossRef]
- Cavanagh, J.; Fairborther, W.J.; Palmer, A.G.P.; Skelton, N.J.; Rance, M. Protein NMR Spectroscopy. Principles and Practice, 2nd ed.; Elsevier Academic Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Johnson, C.S. Diffusion ordered nuclear magnetic resonance spectroscopy: Principles and applications. Prog. Nucl. Magn. Reson. Spectrosc. 1999, 34, 203–256. [Google Scholar] [CrossRef]
- Wu, D.H.; Chen, A.D.; Johnson, C.S. An Improved Diffusion-Ordered Spectroscopy Experiment Incorporating Bipolar-Gradient Pulses. J. Magn. Reson. Ser. A 1995, 115, 260–264. [Google Scholar] [CrossRef]
- Karlicek, R.F.; Lowe, I.J. A modified pulsed gradient technique for measuring diffusion in the presence of large background gradients. J. Magn. Reson. 1980, 37, 75–91. [Google Scholar] [CrossRef]
- Piotto, M.; Saudek, V.; Sklenár, V. Gradient-tailored excitation for single-quantum NMR spectroscopy of aqueous solutions. J. Biomol. NMR 1992, 2, 661–665. [Google Scholar] [CrossRef]
- Findeisen, M.; Brand, T.; Berger, S. A H-1-NMR thermometer suitable for cryoprobes. Magn. Reson. Chem. 2007, 45, 175–178. [Google Scholar] [CrossRef]
- Tugarinov, V.; Kay, L.E. Relaxation Rates of Degenerate 1H Transitions in Methyl Groups of Proteins as Reporters of Side-Chain Dynamics. J. Am. Chem. Soc. 2006, 128, 7299–7308. [Google Scholar] [CrossRef]
- Kay, L.E.; Torchia, D.A. The effects of dipolar cross correlation on 13C methyl-carbon T1, T2, and NOE measurements in macromolecules. J. Magn. Reson. 1991, 95, 536–547. [Google Scholar] [CrossRef]
- Williamson, M.P. Using chemical shift perturbation to characterise ligand binding. Prog. Nucl. Magn. Reson. Spectrosc. 2013, 73, 1–16. [Google Scholar] [CrossRef]
- Vugmeyster, L.; Trott, O.; McKnight, C.J.; Raleigh, D.P.; Palmer, A.G. Temperature-dependent dynamics of the villin headpiece helical subdomain, an unusually small thermostable protein. J. Mol. Biol. 2002, 320, 841–854. [Google Scholar] [CrossRef]
- Cheng, N.-S. Formula for the Viscosity of a Glycerol−Water Mixture. Ind. Eng. Chem. Res. 2008, 47, 3285–3288. [Google Scholar] [CrossRef]
- Volk, A.; Kähler, C.J. Density model for aqueous glycerol solutions. Exp. Fluids 2018, 59, 75. [Google Scholar] [CrossRef]
- Korchuganov, D.S.; Gagnidze, I.E.; Tkach, E.N.; Schulga, A.A.; Kirpichnikov, M.P.; Arseniev, A.S. Determination of protein rotational correlation time from NMR relaxation data at various solvent viscosities. J. Biomol. NMR 2004, 30, 431–442. [Google Scholar] [CrossRef]
- Vugmeyster, L.; Ostrovsky, D. Temperature dependence of fast carbonyl backbone dynamics in chicken villin headpiece subdomain. J. Biomol. NMR 2011, 50, 119–127. [Google Scholar] [CrossRef]
- Vugmeyster, L.; Griffin, A.; Ostrovsky, D.; Bhattacharya, S.; Nichols, P.J.; McKnight, C.J.; Vögeli, B. Correlated motions of C’–N and Cα–Cβ pairs in protonated and per-deuterated GB3. J. Biomol. NMR 2018, 72, 39–54. [Google Scholar] [CrossRef] [PubMed]
- Reddy Chichili, V.P.; Kumar, V.; Sivaraman, J. Linkers in the structural biology of protein-protein interactions. Protein Sci. A Publ. Protein Soc. 2013, 22, 153–167. [Google Scholar] [CrossRef] [PubMed]
- Walsh, J.D.; Meier, K.; Ishima, R.; Gronenborn, A.M. NMR studies on domain diffusion and alignment in modular GB1 repeats. Biophys. J. 2010, 99, 2636–2646. [Google Scholar] [CrossRef]


| T, °C | 2 | 4.5 | 7 | 15 | 22 | 28 | 32 |
|---|---|---|---|---|---|---|---|
| L42 δ2 | 6.0 ± 2.6 | 8.0 ± 1.9 | 7.6 ± 0.9 | 6.2 ± 0.7 | 3.2 ± 0.8 | 3.1 ± 0.5 | |
| V50 γ1 | 12.5 ± 3.2 | 7.5 ± 3.6 | 10.5 ± 2.4 | 10.1 ± 2.6 | 6.0 ± 0.9 | 7.1 ± 1.4 | 9.4 ± 1.1 |
| V50 γ2 | 14.2 ± 2.1 | 12.5 ± 3.6 | 14.0 ± 1.7 | 10.3 ± 0.6 | 7.1 ± 0.8 | 7.3 ± 0.8 | 8.0 ± 0.7 |
| L61 δ1 | 12.7 ± 0.6 | 12.0 ± 1.0 | 9.8 ± 2.2 | 6.8 ± 1.3 | 4.8 ± 0.8 | 5.8 ± 1.3 | 5.2 ± 0.6 |
| L61 δ2 | 11.3 ± 0.9 | 8.0 ± 1.7 | 8.6 ± 0.6 | 7.6 ± 0.8 | 6.0 ± 0.2 | 4.7 ± 0.3 | 4.9 ± 0.8 |
| L63 δ1 | 6.9 ± 1.1 | 5.4 ± 0.9 | 4.2 ± 0.6 | 2.9 ± 1.1 | 2.0 ± 0.3 | 3.4 ± 0.3 | 2.3 ± 0.4 |
| L63 δ2 | 6.6 ± 0.6 | 7.9 ± 1.1 | 6.3 ± 0.5 | 4.2 ± 0.2 | 3.0 ± 0.3 | 2.6 ± 0.4 | 3.6 ± 0.5 |
| L69 δ1 | 8.6 ± 1.1 | 7.9 ± 1.1 | 8.6 ± 0.5 | 6.0 ± 0.3 | 4.5 ± 0.5 | 3.8 ± 0.3 | 2.4 ± 0.7 |
| L69 δ2 | 9.0 ± 2.1 | 9.4 ± 1.1 | 10.5 ± 1.3 | 7.7 ± 1.5 | 5.5 ± 0.2 | 4.8 ± 0.3 | 3.3 ± 0.5 |
| L75 δ2 | 4.8 ± 2.3 | 3.5 ± 2.8 | 5.6 ± 1.3 | 3.2 ± 1.3 | 2.7 ± 0.5 | 3.2 ± 0.3 | 2.5 ± 0.9 |
| T, °C | 15 | 22 | 32 |
|---|---|---|---|
| L42 δ2 | 5.3 ± 0.8 | 6.3 ± 0.7 | |
| V50 γ1 | 11.0 ± 4.0 | 8.1 ± 0.9 | 8.3 ± 1.2 |
| V50 γ2 | 13.1 ± 1.8 | 12.3 ± 1.4 | 9.5 ± 0.4 |
| L61 δ1 | 11.9 ± 2.6 | 8.5 ± 0.6 | 6.1 ± 0.7 |
| L61 δ2 | 7.7 ± 1.3 | 8.6 ± 0.2 | 9.3 ± 0.4 |
| L63 δ1 | 6.2 ± 0.5 | 5.2 ± 0.3 | 3.0 ± 0.3 |
| L63 δ2 | 6.2 ± 0.6 | 4.8 ± 0.5 | 3.8 ± 0.2 |
| L69 δ1 | 9.5 ± 0.4 | 7.7 ± 0.1 | 5.0 ± 0.4 |
| L69 δ2 | 15.9 ± 2.9 | 11.4 ± 0.7 | 7.2 ± 0.3 |
| L75 δ2 | 3.6 ± 1.1 | 3.4 ± 1.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vugmeyster, L.; Nichols, P.J.; Ostrovsky, D.; McKnight, C.J.; Vögeli, B. Slow Methyl Axes Motions in Perdeuterated Villin Headpiece Subdomain Probed by Cross-Correlated NMR Relaxation Measurements. Magnetochemistry 2023, 9, 33. https://doi.org/10.3390/magnetochemistry9010033
Vugmeyster L, Nichols PJ, Ostrovsky D, McKnight CJ, Vögeli B. Slow Methyl Axes Motions in Perdeuterated Villin Headpiece Subdomain Probed by Cross-Correlated NMR Relaxation Measurements. Magnetochemistry. 2023; 9(1):33. https://doi.org/10.3390/magnetochemistry9010033
Chicago/Turabian StyleVugmeyster, Liliya, Parker J. Nichols, Dmitry Ostrovsky, C. James McKnight, and Beat Vögeli. 2023. "Slow Methyl Axes Motions in Perdeuterated Villin Headpiece Subdomain Probed by Cross-Correlated NMR Relaxation Measurements" Magnetochemistry 9, no. 1: 33. https://doi.org/10.3390/magnetochemistry9010033
APA StyleVugmeyster, L., Nichols, P. J., Ostrovsky, D., McKnight, C. J., & Vögeli, B. (2023). Slow Methyl Axes Motions in Perdeuterated Villin Headpiece Subdomain Probed by Cross-Correlated NMR Relaxation Measurements. Magnetochemistry, 9(1), 33. https://doi.org/10.3390/magnetochemistry9010033






