Next Article in Journal
Magnetic Nanoparticles: An Overview for Biomedical Applications
Previous Article in Journal
Li3V2(PO4)3/Li3PO4 Cathode Materials for Li-Ion Batteries: Synthesis and Characterization
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Magnetochemistry
Volume 8
Issue 9
10.3390/magnetochemistry8090106
magnetochemistry-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Experimental Study of Magnetocaloric Effect in Tetraaquabis(Hydrogen Maleato)Nickel(II), [Ni(C4H3O4)2(H2O)4]—A Potential Realization of a Spin-1 Spatially Anisotropic Square Lattice with Ferromagnetic Interactions

by
Petro Danylchenko
1,
Róbert Tarasenko
1,*,
Erik Čižmár
1,
Vladimír Tkáč
1,
Anna Uhrinová
2,
Alžbeta Orendáčová
1 and
Martin Orendáč
1
1
Institute of Physics, Faculty of Science, Pavol Jozef Šafárik University, Park Angelinum 9, 04154 Košice, Slovakia
2
Department of Chemistry, Biochemistry, and Biophysics, Institute of Pharmaceutical Chemistry, University of Veterinary Medicine and Pharmacy, Komenského 73, 04181 Košice, Slovakia
*
Author to whom correspondence should be addressed.
Magnetochemistry 2022, 8(9), 106; https://doi.org/10.3390/magnetochemistry8090106
Submission received: 21 July 2022 / Revised: 6 September 2022 / Accepted: 14 September 2022 / Published: 16 September 2022
(This article belongs to the Section Magnetic Materials)
Browse Figures
Versions Notes

Abstract

:
An experimental study of the magnetocaloric effect in tetraaquabis(hydrogen maleato)nickel(II), [Ni(C4H3O4)2(H2O)4] powder sample is presented. The magnetocaloric properties of the studied sample were investigated using specific heat and magnetization measurements in magnetic fields up to 9 T in the temperature range from 0.4 to 50 K. A large conventional magnetocaloric effect was found at a temperature of about 3.5 K, where −ΔSM = 8.5 Jkg−1K−1 and 11.2 Jkg−1K−1 for a magnetic field of 5 T and 7 T, respectively. Assuming a substantial role of the crystal field, the temperature dependence of the magnetic specific heat in a zero magnetic field was compared with an S = 1 model with single-ion anisotropy parameters D and E (axial and rhombic). The best agreement was found for the parameters D/kB = −7.82 K and E/kB = −2.15 K. On the other hand, the experimental temperature dependence of −ΔSM shows higher values compared to the theoretical prediction for the mentioned model, indicating the presence of additional factors in the system, such as an exchange interaction between magnetic ions. The first exchange pathway can be realized through maleic rings between the nearest Ni(II) ions. The second exchange pathway can be realized through water molecules approximately along the a crystallographic axis. Broken-symmetry DFT calculations performed using the computational package ORCA provided the values of ferromagnetic exchange interactions, J1/kB = 1.50 K and J2/kB = 1.44 K (using B3LYP functional). The presence of such ferromagnetic correlations in the studied system may explain the enhanced magnetocaloric effect compared with the model of an anisotropic spin-1 paramagnet.

1. Introduction

The magnetocaloric effect (MCE) remains at the center of attention of several scientific communities in recent times [1,2,3,4,5,6,7,8,9,10,11,12]. MCE is based on the heating or cooling of the magnetic refrigerant if a magnetic field is applied. MCE can be used in magnetic cooling at room temperature when it replaces cooling based on adiabatic gas compression and expansion [13,14]. On the other hand, MCE can also be used to achieve low temperatures, which are currently mainly obtained on the basis of the physical properties of the helium-3 isotope. Two parameters are essential for evaluating the magnetocaloric properties of a potential magnetic refrigerant: the magnetic entropy change ΔSM when a magnetic field is applied, and the adiabatic temperature change ΔTad when the magnetic field changes in adiabatic conditions [15,16]. It is important to note that the values of the mentioned parameters should be as large as possible in the given temperature range in which the magnetic refrigerant is used.
Potential magnetic refrigerants currently being studied are based mainly on the physical properties of rare-earth elements [17,18,19,20,21,22,23,24,25,26,27,28]. The enhanced magnetocaloric effect is primarily caused by the large value of the magnetic moment. The main disadvantage of these magnetic refrigerants is their financial and time-consuming difficulty in preparation. For this reason, these materials may not meet one of the essential parameters for choosing a suitable refrigerant [29].
Another possible alternative to rare-earth compounds with enhanced magnetocaloric effect are systems based on Ni(II) ions with spin-1. The main advantages of these systems are their financial availability, the synthesis is not very time-consuming, the number of steps in the synthesis is minimal, and the synthesis does not have many precursors. The magnetocaloric properties of S = 1 Ni(II) systems can be largely modified by the dimensionality of studied systems, the presence of exchange interactions, the type of single-ion anisotropy, and values of corresponding crystal field parameters [3,30,31,32,33]. For example, enhanced MCE, −ΔSM = 10.6 JK−1 kg−1 in a temperature range below 2.3 K, was observed in the tetranuclear nickel complex [Ni4(µ-CO3)2(aetpy)8](ClO4)4 (aetpy = 2-aminoethyl-pyridine) that was identified as a spin-1 Heisenberg diamond cluster with two different coupling constants with J1/kB = −41.4 K and J2/kB = −9.2 K [3]. On the other hand, the analysis of magnetic specific heat and MCE in the Ni(fum)(phen) system (fum = fumarato, phen = 1,10 -phenanthroline) showed that the presence of ferromagnetic interaction forming Ni(II) dimers improves the magnetocaloric properties of the studied system [30].
In this work, we present the experimental study of the magnetocaloric effect in a tetraaquabis(hydrogen maleato)nickel(II), [Ni(C4H3O4)2(H2O)4] (NiHmal) powder sample. The magnetocaloric properties of the studied sample are investigated using specific heat and magnetization measurements in magnetic fields up to 9 T in the temperature range from 0.4 to 50 K. In parallel with the study of magnetocaloric properties, the prediction of the physical model of the studied system is performed using ab initio and broken-symmetry (BS) DFT calculations. Simultaneously, the influence of the spatial realization of the exchange paths on the magnetocaloric properties of NiHmal is discussed.

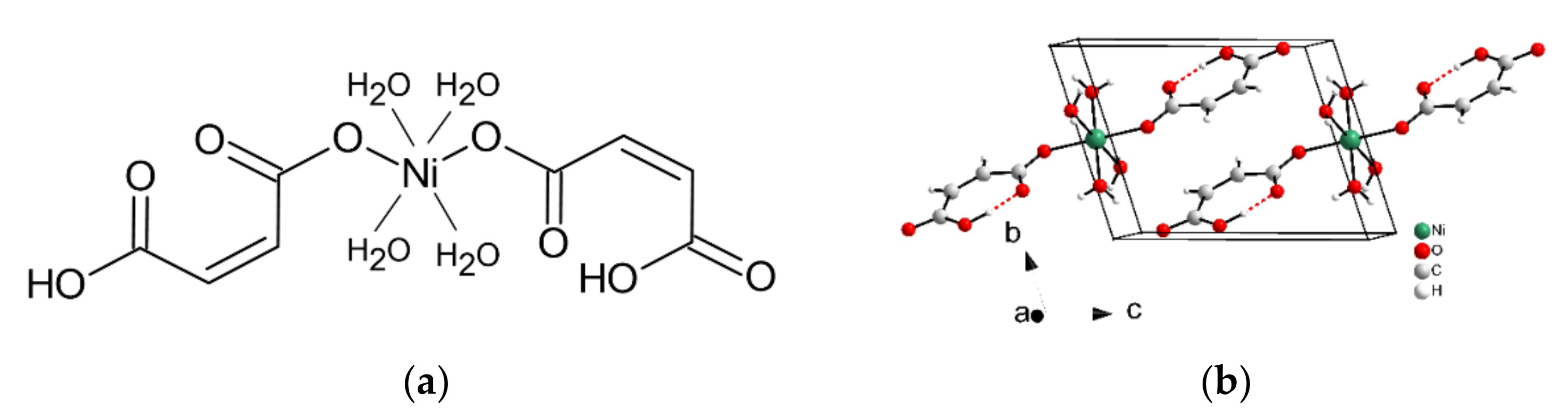
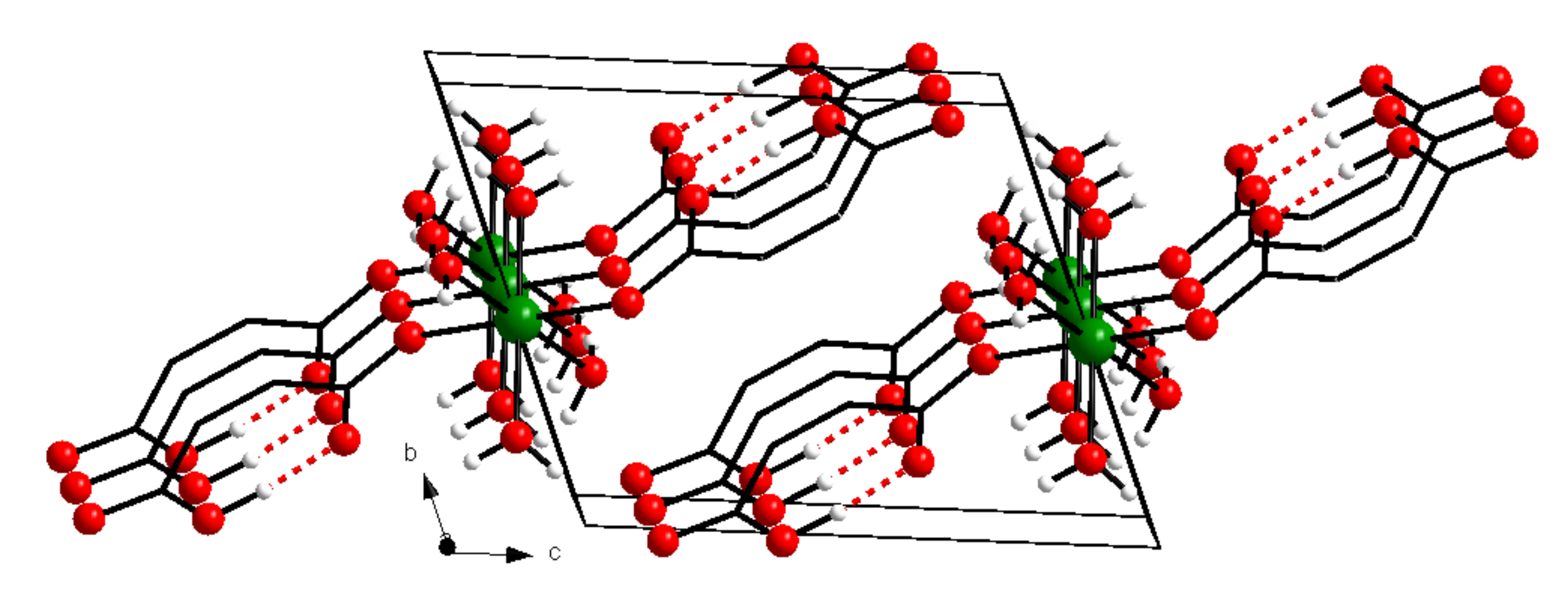
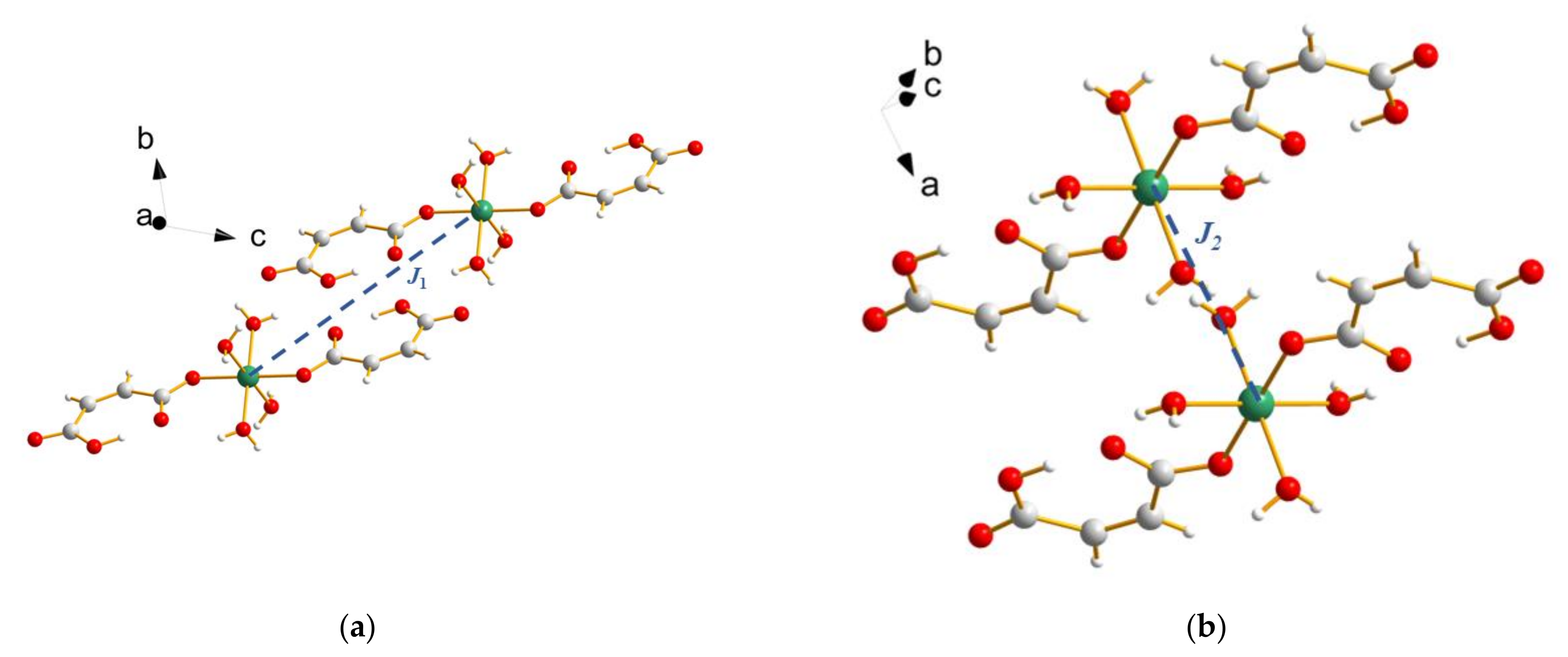
2. Materials and Methods

The synthesis of the studied system was carried out according to the following steps. Nickel sulfate heptahydrate, sodium hydroxide, and maleic acid (99.9%, Sigma-Aldrich—Merck, Darmstadt, Germany) of reagent-grade quality were obtained from commercial sources and were used as received without further purification. All solutions were prepared using deionized water. First, nickel hydroxide was prepared by precipitation of nickel sulfate solution (10 mmol) with sodium hydroxide solution (20 mmol). The resulting precipitate was purified by decantation until a negative test on the sulfate anions and was used for further synthesis without drying. The freshly prepared Ni(OH)2 was dissolved in 10 mL of maleic acid solution (10 mmol) under constant stirring. The obtained solution was filtered off and was placed to open crystallization at room temperature. Within a few days, dark green crystals were formed, isolated by filtration, and freely dried in air (yield: 36%).
The title complex was first prepared by Gupta in 1984 [34], and its molecular structure is shown in Figure 1a. It crystallizes in a triclinic centrosymmetric P-1 space group, and the unit cell of the complex is depicted in Figure 1b. The central Ni(II) atom is coordinated by six oxygen atoms, while four in the equatorial plane originated from molecules of four aqua ligands. There are two hydrogen maleato ligands (Hmal) in the axial position, and they are coordinated through an oxygen atom of a deprotonated carboxyl group. The negative charge -1 of Hmal ligands compensates for the positive charge of the central Ni(II) atom. Axial Ni–O(Hmal) bond distances are 2.078(1) Å, while equatorial Ni–O(aqua) bond distances are 2.025(1) Å and 2.089(1) Å. All O–Ni–O bond angles ranged from 92.45(8)° to 96.73(10)° [35]. The crystal structure is stabilized by strong intramolecular hydrogen bridges involving the non-deprotonated carboxyl groups of Hmal ligands (Figure 2).
The temperature dependence of specific heat of powdered sample pressed in the form of a pellet was obtained using a commercial PPMS system in the temperature range from 0.4 K to 50 K in the magnetic fields up to 9 T. The contribution of the addenda to the specific heat was determined in a separate run. The field dependence of magnetization was collected using a commercial SQUID magnetometer in magnetic fields up to 5 T in the temperature range from 2 K to 20 K. The susceptibility studies were performed in the temperature range from 2 K to 300 K in a magnetic field of 100 mT. Diamagnetic contribution to magnetic susceptibility was subtracted using Pascal constants. The sample pressed in the form of a pellet was fixed in a gelatin capsule using Apiezon N grease. A gelatin capsule with a sample was inserted into a plastic straw and placed using a holder in the device itself.
Ab initio calculations were performed using the ORCA 4.2.1 computational package [36]. The calculations of single-ion anisotropy parameters were based on the state-averaged complete active space self-consistent field (SA-CASSCF) wave functions followed by N-electron valence second-order perturbation theory (NEVPT2) [37,38,39,40,41]. Calculations employed the metal-based d-orbitals as active space CAS (8,5), including the state-averaged approach with all 10 triplet and 15 singlet states equally weighted for Ni(II). The reported ZFS parameters were obtained from the effective Hamiltonian theory [42]. The zeroth-order regular approximation (ZORA) [43,44] was used to account for relativistic effects together with the corresponding segmented all-electron relativistic contracted (SARC) version of the triple-ζ basis set Def2-TZVP(-f) [45,46] for all atoms.
The BS DFT calculation [47] was performed using the B3LYP, BPE0, and TPSSh exchange-correlation functionals [48,49,50]. The exchange coupling was obtained using the Yamaguchi formalism from the single-point approach [51], but the values are later reported using the Hamiltonian in the form H ^ = − J S ^ 1 S ^ 2 .
All calculations utilized the RI approximation and the chain-of-spheres (RIJCOSX) approximation to exact exchange [52] with appropriate decontracted auxiliary basis sets SARC/J and Def2-TZVP/C [53,54]. Increased integration grids (Grid4 for DFT and Grid4X for RIJCOSX) and tight SCF convergence criteria were used.

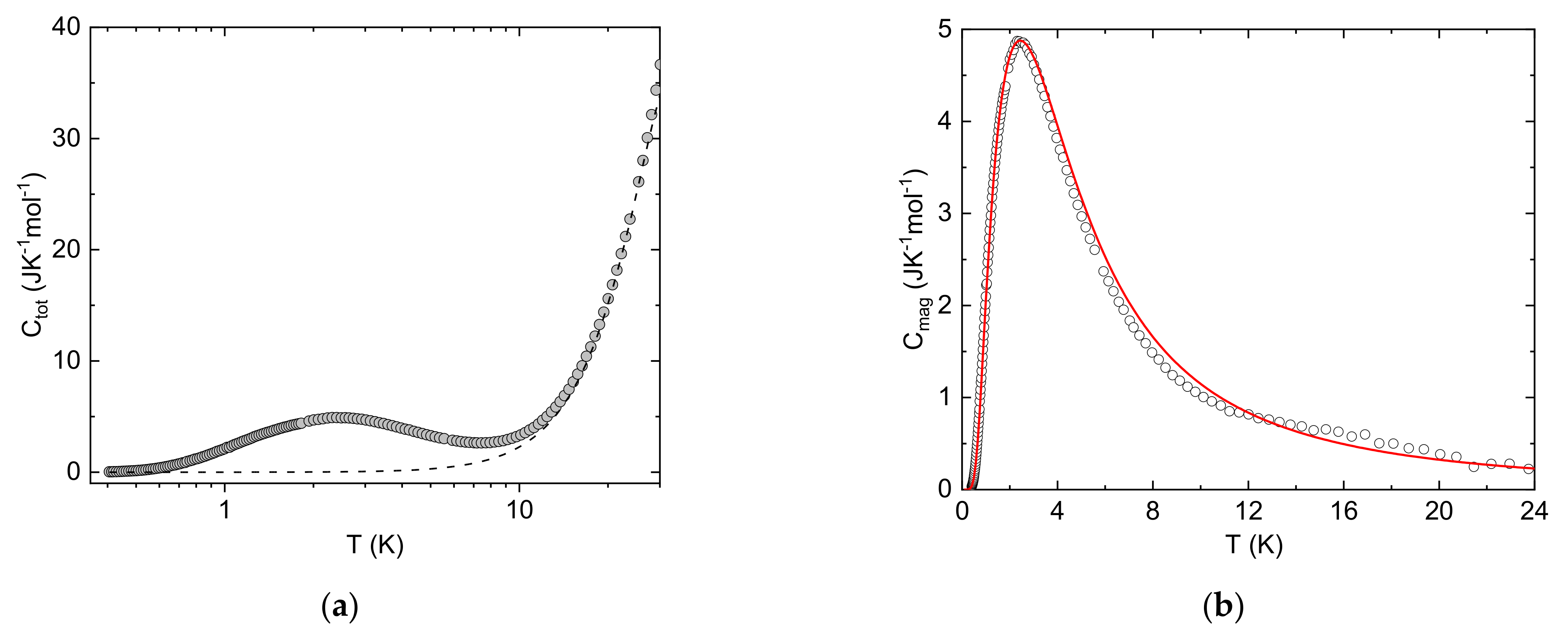
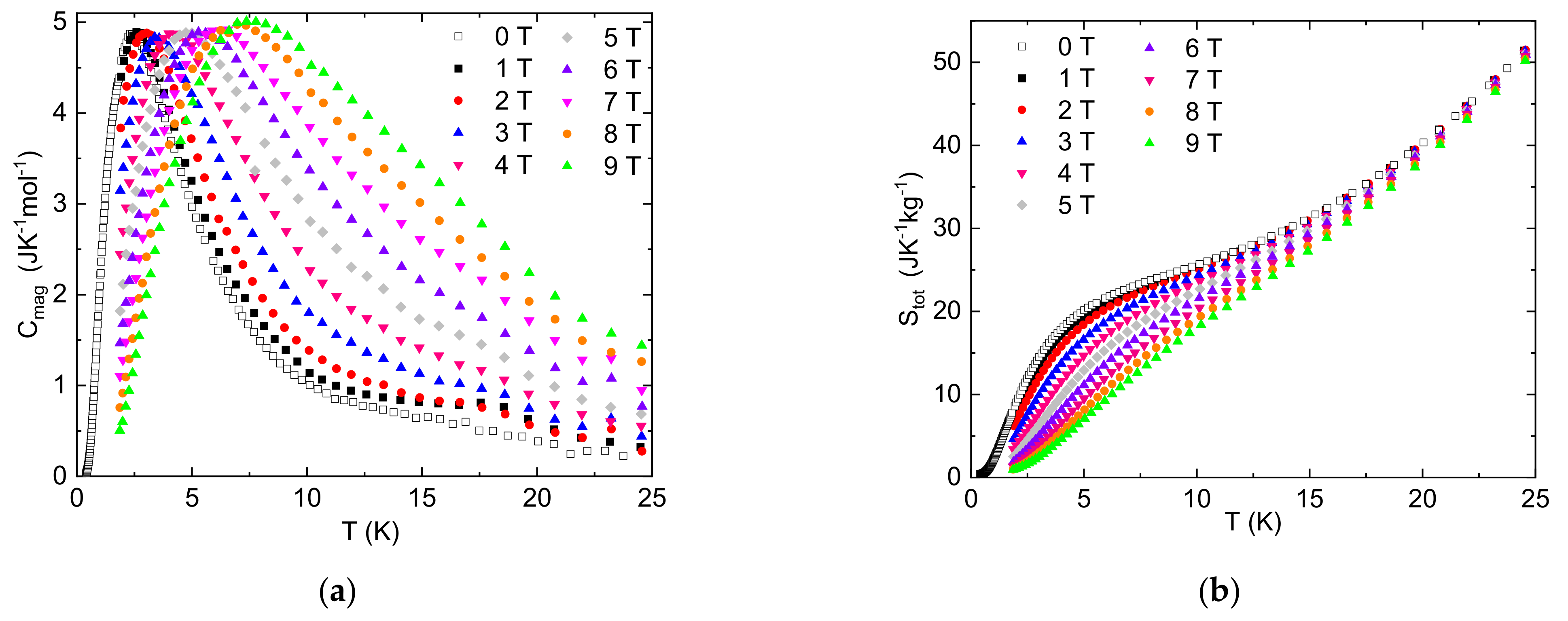
3. Results

The temperature dependence of specific heat of NiHmal in a zero magnetic field is shown in Figure 3a. The round maximum of specific heat in a zero magnetic field can be observed at a temperature of 2.5 K; a monotonous increase was observed at higher temperatures. NiHmal is a magnetic insulator, which means that the total heat capacity is given by the sum of the specific heat of the magnetic and lattice subsystem. In the temperature range from 10.12 K to 26.3 K, the total specific heat can be approximated by the following expression:
C t o t = C m a g + C l a t = a T 2 + b T 3 + c T 5 ,
where a, b, and c are fitting parameters, and the term Cmag ~ T−2 represents the specific heat of the magnetic subsystem. By fitting the experimental data of the specific heat in the temperature range from 10.12 K to 26.3 K, the values of the fitting parameters a = 125.66 JKmol−1, b = 0.00238 JK−4 mol−1, and c = –1.21804 × 10−6 JK−6 mol−1 were obtained.
After subtracting the lattice contribution to the specific heat, the temperature dependence of the magnetic subsystem’s specific heat was obtained, as shown in Figure 3b. In the first approximation based on the crystal structure, only the dominant influence of the crystal field on the magnetic properties of the NiHmal system was assumed, which means the temperature dependence of the specific heat of the magnetic subsystem was compared with the S = 1 model with parameters of uniaxial anisotropy D and rhombic anisotropy E. The best agreement was found for the parameters D/kB = –7.82 K and E/kB = –2.15 K, with g = 2.29. The negative value of the uniaxial anisotropy parameter D points to the easy-axis anisotropy in the studied system, which results from the crystal structure itself based on the deformed octahedron of the Ni(II) ion.
The value of the magnetic entropy below the temperature of 0.4 K for the NiHmal system was estimated from the experimental specific data, similarly for the Ni(fum)(phen) system [30]. First, the magnetic entropy of the experimental data was calculated from the temperature dependence of the specific heat of the magnetic subsystem in the range from 0.4 K to 26 K. The determination of the value of the magnetic entropy in the range from 26 K up to the limit of T → ∞ was realized by standard extrapolation. The sum of these two contributions is equal to 8.88 JK−1 mol−1, representing 97.2% of the total theoretical value of the magnetic entropy for a system with spin-1. Based on this value, it is possible to assume the absence of a phase transition to a magnetically ordered state in a zero magnetic field in the NiHmal system.
The temperature dependence of the specific heat of NiHmal in non-zero magnetic fields up to 9 T is shown in Figure 4a. It can be concluded that with the increase in the magnetic field, the maximum of the specific heat shifts toward higher temperatures. In contrast, the maximum value of the specific heat remains constant up to a magnetic field of 4 T. At higher magnetic fields, an increase in the maximum value of Cmag is also observed.
For further study of the magnetocaloric effect in the NiHmal system, the temperature dependence of the total entropy was calculated from the experimental data of the total heat capacity according to the relation S = ∫ C T T   d T . It should be noted that in the case of obtaining the temperature dependence of the entropy in a zero magnetic field, the obtained dependence was normalized by 0.7 JK−1 kg−1, which means by a part of the entropy below the temperature of 0.4 K. On the other hand, the experimental data values of the total specific heat for all magnetic fields were almost identical at the maximum measured temperature of 50 K. For this reason, it can be concluded that at the mentioned temperature of 50 K, the lattice contribution to the heat capacity largely prevails, and the contributions from the magnetic subsystem are negligible. Based on this knowledge, the calculated temperature dependences of the total entropy in magnetic fields were normalized to have the same value at the highest temperature of 50 K. The temperature dependence of the total entropy Stot is shown in Figure 4b.
Temperature dependence of magnetic susceptibility is presented in Figure 5a. No difference was observed between the data obtained in the field cooling (FC) and zero-field cooling (ZFC) regimes. It could be seen that the susceptibility value increases with decreasing temperature. Such behavior can be explained by the presence of the easy-axis type anisotropy in the studied system. The effective magnetic moment saturates to the value of 3.24 μB, which results in a value of the g factor of ≈ 2.29, typical for Ni(II) ions (Figure 5a, inset).
To evaluate the magnetocaloric properties of the NiHmal system, the field dependences of magnetization were measured in magnetic fields up to 5 T in the temperature range from 2 K to 20 K (Figure 5b). For each temperature, the magnetization increases with increasing magnetic field and decreases with increasing temperature at a constant field. Based on this behavior, predicting a normal magnetocaloric effect in the given system is possible. The Arrott plot for the NiHmal powder sample is shown in Figure 5c. It is evident that the qualitative slope of all curves is similar, and the curves do not show linear behavior for any temperature. Thus, no transition to the magnetically ordered state could be seen from Arrott plots, which is consistent with the results from the specific heat data.
The temperature dependence of the isothermal change of magnetic entropy −ΔSM was calculated from the field dependence of magnetization using the standard Maxwell relation [13]:
Δ S M T , Δ B = ∫ B i B f ∂ M T , B ∂ T d B ,
where ΔB = Bi − Bf, and Bf, and Bi represent the final and initial magnetic fields, respectively. The result of this procedure is shown in Figure 6a. It could be seen that as the magnetic field increases, the maximum value of −ΔSM increases and shifts toward higher temperatures. The data were also compared with −ΔSM obtained from the total entropy data from Figure 4b. It is possible to state a very good agreement between these experimental data, and the small difference between the values obtained from the Maxwell relation and the total entropy can be attributed to the inaccuracies of the specific heat and magnetization measurements. A large conventional magnetocaloric effect was found at a temperature of about 3.5 K, where −ΔSM = 8.5 Jkg−1K−1 and 11.2 Jkg−1K−1 for a magnetic field of 5 T and 7 T, respectively. At the same time, the temperature dependence of −ΔSM was compared with theoretical predictions for S = 1 paramagnet with D/kB = −7.82 K and E/kB = −2.15 K, i.e., with the model that best described the temperature dependence of the specific heat in a zero magnetic field. It is important to note that the theoretical model describes the experimental data relatively well at higher temperatures. Still, significant differences are observed toward lower temperatures, with experimental values larger than the theoretical model. This suggests the presence of other unaccounted factors in the system, such as the exchange interaction between magnetic Ni(II) ions.
The adiabatic temperature change as a function of initial temperature for the NiHmal system, realized under conditions of adiabatic demagnetization to zero magnetic field calculated from the temperature dependence of total entropy, is shown in Figure 6b. The maximum of the -ΔTad value shifts toward higher initial temperatures with an increasing magnetic field value. It could be observed that adiabatic demagnetization from 7 T for initial temperatures of 10 K, 4.2 K, and 2 K yields –ΔTad ≈ 5 K, 2.5 K, and 1.2 K, respectively. The obtained magnetocaloric characteristics of the studied system point to its application potential in the field of magnetocaloric cooling.
As shown above, the simple S = 1 model only considers the parameters of uniaxial anisotropy D and rhombic anisotropy E, which fairly describes the zero-field specific heat of NiHmal and underestimates its isothermal change of magnetic entropy. Therefore, ab initio calculations of the single-ion anisotropy parameters and BS DFT calculation of possible exchange interactions in NiHmal were performed using the structural data obtained in Ref. [35] in ORCA. The single-ion anisotropy parameters of Ni(II) ions in an isolated molecule of NiHmal were predicted using the SA-CASSCF/NEVPT2 method as D/kB = −9.85 K and E/kB = −1.85 K (E/D = 0.188) with diagonal g-tensor components 2.224, 2.240, and 2.279 (an average value of g = 2.247). The inspection of the close contacts between the NiHmal molecules in the unit cell suggests a possibility of two different exchange pathways: π-π bonding between neighboring maleic ligands (J1, Figure 7a) and hydrogen bonds between aqua ligands approximately along the a crystallographic axis (J2, Figure 7b).
For each exchange pathway, a pair of NiHmal molecules were selected. A BS DFT calculation using a single-point approach was performed using the selection of the popular DFT functionals: B3LYP, TPSSh, and PBE0. The results are summarized in Table 1, suggesting a quite strong ferromagnetic (FM) intermolecular exchange interaction in the range between 0.8 K and 1.5 K. The difference between J1 and J2 for each of the selected DFT functional, e.g., J1/kB = 1.50 K and J2/kB = 1.44 K for B3LYP, would suggest the creation of a two-dimensional spatially anisotropic magnetic lattice in NiHmal. Such a relatively strong FM correlation would eventually enhance the isothermal change of magnetic entropy compared to a spin-1 paramagnet with strong single-ion anisotropy [30,32,55].
For example, the analysis of magnetocaloric properties in the Ni(fum)(phen) system showed that this system could be identified as a potential realization of the S = 1 ferromagnetic dimer with D/kB = −11.5 K, E/kB = −3.4 K, and intradimer exchange coupling J/kB = 2.5 K. A large conventional magnetocaloric effect was found at a temperature of about 5.8 K, where −ΔSM = 8.2 Jkg−1K−1 for a magnetic field of 7 T [30]. It should be noted that the molar mass of this system is almost the same as in the NiHmal system. On the other hand, the crystal field parameters for these systems are very close. Nevertheless, the NiHmal system shows better magnetocaloric properties even with smaller values of ferromagnetic interactions, which are, however, realized on a spatially anisotropic square lattice.

4. Conclusions

This work presents an experimental study of the magnetocaloric effect in a tetraaquabis(hydrogen maleato)nickel(II), [Ni(C4H3O4)2(H2O)4] powder sample via magnetization and specific heat measurements in the temperature range from 0.4 K to 50 K in magnetic fields up to 9 T. A large conventional magnetocaloric effect was found at a temperature of about 3.5 K, where −ΔSM = 8.5 Jkg−1K−1 and 11.2 Jkg−1K−1 for a magnetic field of 5 T and 7 T, respectively. The analysis of the magnetocaloric properties of the studied system showed that adiabatic demagnetization from 7 T for initial temperatures of 10 K, 4.2 K, and 2 K leads to the cooling of the sample down to 5 K, 1.7 K, and 0.8 K, respectively. The obtained magnetocaloric characteristics of NiHmal point to its application potential in the field of magnetocaloric cooling. Broken-symmetry DFT calculations performed using the computational package ORCA provided the values of ferromagnetic exchange interactions, J1/kB = 1.50 K and J2/kB = 0.44 K (using B3LYP functional). The presence of such ferromagnetic correlations in the studied system may explain the enhanced magnetocaloric effect compared with the model of an anisotropic spin-1 paramagnet. In the future, a study of the rotational magnetocaloric effect in the NiHmal system on a single crystal will be carried out due to the presence of a large magnetic anisotropy.

Author Contributions

Conceptualization, R.T. and P.D.; investigation, R.T., P.D. and V.T.; software, E.Č.; writing—original draft preparation, R.T.; writing—review and editing, V.T., E.Č., A.U., A.O. and M.O.; visualization, R.T. and P.D.; funding acquisition, M.O. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the Slovak Research and Development Agency Projects numbers APVV-18-0197, APVV-14-0073, and APVV-SK-BY-RD-19-0008 and VEGA Grants No. 1/0426/19, 1/0132/22 of the Scientific Grant Agency of the Ministry of Education, Science, Research and Sport of the Slovak Republic.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

All the data needed to evaluate the conclusions are presented in this paper.

Acknowledgments

Material support from U.S. Steel Košice s.r.o. is greatly appreciated.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Sessoli, R. Chilling with Magnetic Molecules. Angew. Chem.-Int. Ed. 2012, 51, 43–45. [Google Scholar] [CrossRef] [PubMed]
  2. Pęczkowski, P.; Łuszczek, M.; Szostak, E.; Muniraju, N.K.C.; Krztoń-Maziopa, A.; Gondek, Ł. Superconductivity and Appearance of Negative Magnetocaloric Effect in Ba1–XKxBiO3 Perovskites, Doped by Y, La and Pr. Acta Mater. 2022, 222, 117437. [Google Scholar] [CrossRef]
  3. Karl’ová, K.; Strečka, J.; Haniš, J.; Hagiwara, M. Insights into Nature of Magnetization Plateaus of a Nickel Complex [Ni4(μ-CO3)2(Aetpy)8](ClO4)4 from a Spin-1 Heisenberg Diamond Cluster. Magnetochemistry 2020, 6, 59. [Google Scholar] [CrossRef]
  4. Oyarzabal, I.; Echenique-Errandonea, E.; San Sebastián, E.; Rodríguez-Diéguez, A.; Seco, J.M.; Colacio, E. Synthesis, Structural Features and Physical Properties of a Family of Triply Bridged Dinuclear 3d-4f Complexes. Magnetochemistry 2021, 7, 22. [Google Scholar] [CrossRef]
  5. Spichkin, Y.I.; Zvezdin, A.K.; Gubin, S.P.; Mischenko, A.S.; Tishin, A.M. Magnetic Molecular Clusters as Promising Materials for Refrigeration in Low-Temperature Regions. J. Phys. D Appl. Phys. 2001, 34, 1162–1166. [Google Scholar] [CrossRef]
  6. Franco, V.; Blázquez, J.S.; Ipus, J.J.; Law, J.Y.; Moreno-Ramírez, L.M.; Conde, A. Magnetocaloric Effect: From Materials Research to Refrigeration Devices. Prog. Mater. Sci. 2018, 93, 112–232. [Google Scholar] [CrossRef]
  7. Tegus, O.; Brück, E.; Buschow, K.H.J.; De Boer, F.R. Transition-Metal-Based Magnetic Refrigerants for Room-Temperature Applications. Nature 2002, 415, 150–152. [Google Scholar] [CrossRef]
  8. Barclay, J.A.; Steyert, W.A. Materials for Magnetic Refrigeration between 2 K and 20 K. Cryogenics 1982, 22, 73–80. [Google Scholar] [CrossRef]
  9. Czaja, P.; Wróblewski, R.; Grzonka, J.; Przewoźnik, J.; Maziarz, W. Microstructure, Martensitic Transformation, and Inverse Magnetocaloric Effect in Ni48Mn39.5Sn12.5−xAlx Metamagnetic Shape Memory Alloys. Magnetochemistry 2018, 4, 19. [Google Scholar] [CrossRef]
  10. Balli, M.; Mansouri, S.; Jandl, S.; Fournier, P.; Dimitrov, D. Analysis of the Anisotropic Magnetocaloric Effect in RMn2O5 Single Crystals. Magnetochemistry 2017, 3, 36. [Google Scholar] [CrossRef] [Green Version]
  11. Zangana, K. Synthesis, Crystal Structures, and Magnetic Properties of Lanthanide (III) Amino-Phosphonate Complexes. Magnetochemistry 2018, 4, 29. [Google Scholar] [CrossRef]
  12. Castañeda, E.J.G.; Castro, R.E.B.; Briseño, A.C.; Arguijo, B.F.; Castillo, A.A.T.; Rodríguez, A.S.; Galindo, J.T.E.; Sánchez, S.A.P. Effect of Quenching and Normalizing on the Microstructure and Magnetocaloric Effect of a Cu–11Al–9Zn Alloy with 6.5 Wt % Ni–2.5 Wt % Fe. Magnetochemistry 2019, 5, 48. [Google Scholar] [CrossRef]
  13. Gschneidner, A.; Pecharsky, V.K.; Tsokol, A.O. Recent Developments in Magnetocaloric Materials. Rep. Prog. Phys. 2005, 68, 1479–1539. [Google Scholar] [CrossRef]
  14. Guo, D.Q.; Chan, K.C.; Xia, L.; Yu, P. Magneto-Caloric Effect of FexZryB100−x−y Metallic Ribbons for Room Temperature Magnetic Refrigeration. J. Magn. Magn. Mater. 2017, 423, 379–385. [Google Scholar] [CrossRef]
  15. Pecharsky, V.K.; Gschneidner, K.A. Magnetocaloric Effect and Magnetic Refrigeration. J. Magn. Magn. Mater. 1999, 200, 44–56. [Google Scholar] [CrossRef]
  16. Tishin, A.M.; Spichkin, Y.I. The Magnetocaloric Effect and Its Applications; CRC Press: Boca Raton, FL, USA, 2003; p. 475. [Google Scholar]
  17. Wu, Y.D.; Duan, W.W.; Li, Q.Y.; Geng, W.; Zhang, C.; Lv, Q.Q.; He, L.; Chen, J.Q.; Hu, X.Y.; Qin, Y.L.; et al. Giant Conventional and Rotating Magnetocaloric Effects in TbScO3 Single Crystal. J. Alloys Compd. 2022, 894, 162447. [Google Scholar] [CrossRef]
  18. Wu, Y.D.; Qin, Y.L.; Ma, X.H.; Li, R.W.; Wei, Y.Y.; Zi, Z.F. Large Rotating Magnetocaloric Effect at Low Magnetic Fields in the Ising-like Antiferromagnet DyScO3 Single Crystal. J. Alloys Compd. 2019, 777, 673–678. [Google Scholar] [CrossRef]
  19. Ke, Y.J.; Zhang, X.Q.; Ma, Y.; Cheng, Z.H. Anisotropic Magnetic Entropy Change in RFeO3 Single Crystals(R = Tb, Tm, or Y). Sci. Rep. 2016, 6, 19775. [Google Scholar] [CrossRef]
  20. Balli, M.; Jandl, S.; Fournier, P.; Gospodinov, M.M. Anisotropy-Enhanced Giant Reversible Rotating Magnetocaloric Effect in HoMn2O5 Single Crystals. Appl. Phys. Lett. 2014, 104, 232402. [Google Scholar] [CrossRef]
  21. Balli, M.; Jandl, S.; Fournier, P.; Vermette, J.; Dimitrov, D.Z. Unusual Rotating Magnetocaloric Effect in the Hexagonal ErMn O3 Single Crystal. Phys. Rev. B 2018, 98, 184414. [Google Scholar] [CrossRef] [Green Version]
  22. Zhang, X.Q.; Wu, Y.D.; Ma, Y.; Dong, Q.Y.; Ke, Y.J.; Cheng, Z.H. Large Rotating Magnetocaloric Effect in ErAlO3 Single Crystal. AIP Adv. 2017, 7, 056418. [Google Scholar] [CrossRef]
  23. Zhang, H.; Xing, C.; Zhou, H.; Zheng, X.; Miao, X.; He, L.; Chen, J.; Lu, H.; Liu, E.; Han, W.; et al. Giant Anisotropic Magnetocaloric Effect by Coherent Orientation of Crystallographic Texture and Rare-Earth Ion Moments in HoNiSi Ploycrystal. Acta Mater. 2020, 193, 210–220. [Google Scholar] [CrossRef]
  24. Orendáč, M.; Gabáni, S.; Gažo, E.; Pristáš, G.; Shitsevalova, N.; Siemensmeyer, K.; Flachbart, K. Rotating Magnetocaloric Effect and Unusual Magnetic Features in Metallic Strongly Anisotropic Geometrically Frustrated TmB4. Sci. Rep. 2018, 8, 1–10. [Google Scholar] [CrossRef] [PubMed]
  25. Pęczkowski, P.; Zachariasz, P.; Jastrzębski, C.; Piętosa, J.; Drzymała, E.; Gondek, Ł. On the Superconductivity Suppression in Eu1−xPrxBa2Cu3O7−δ. Materials 2021, 14, 3503. [Google Scholar] [CrossRef]
  26. Synoradzki, K.; Nowotny, P.; Skokowski, P.; Toliński, T. Magnetocaloric Effect in Gd5(Si,Ge)4 Based Alloys and Composites. J. Rare Earths 2019, 37, 1218–1223. [Google Scholar] [CrossRef]
  27. Gębara, P. Magnetocaloric Effect of LaFe11.35Co0.6Si1.05 Alloy. Rare Met. 2022, 41, 1563–1569. [Google Scholar] [CrossRef]
  28. Pecharsky, A.O.; Gschneidner, K.A.; Pecharsky, V.K. The Giant Magnetocaloric Effect of Optimally Prepared Gd5Si2Ge2. J. Appl. Phys. 2003, 93, 4722. [Google Scholar] [CrossRef]
  29. Alahmer, A.; Al-Amayreh, M.; Mostafa, A.O.; Al-Dabbas, M.; Rezk, H. Magnetic Refrigeration Design Technologies: State of the Art and General Perspectives. Energies 2021, 14, 4662. [Google Scholar] [CrossRef]
  30. Tarasenko, R.; Danylchenko, P.; Tkáč, V.; Orendáčová, A.; Čižmár, E.; Orendáč, M.; Feher, A. Experimental Study of the Magnetocaloric Effect in [Ni(fum)(phen)]—The Ferromagnetic Dimer with Spin 1. Phys. B Condens. Matter 2020, 576, 411671. [Google Scholar] [CrossRef]
  31. Orendáč, M.; Tarasenko, R.; Tkáč, V.; Orendáčová, A.; Sechovský, V. Specific Heat Study of the Magnetocaloric Effect in the Haldane-Gap S = 1 Spin-Chain Material [Ni(C2H8N2)2NO2](BF4). Phys. Rev. B 2017, 96, 094425. [Google Scholar] [CrossRef]
  32. Ráczová, K.; Cižmár, E.; Feher, A. Magnetocaloric Effect in NiCl2(bipy) at Low Temperatures. Acta Phys. Pol. A 2017, 131, 922–924. [Google Scholar] [CrossRef]
  33. Tarasenko, R.; Orendáčová, A.; Čižmár, E.; Orendáč, M.; Potočňák, I.; Feher, A. Experimental Study of the Magnetocaloric Effect in Ni(en)(H2O)4SO4·2H2O—An S = 1 Molecular Magnet with Easy-Plane Anisotropy. Acta Phys. Pol. A 2017, 131, 904–906. [Google Scholar] [CrossRef]
  34. Gupta, M.P.; Geise, H.J.; Lenstra, A.T.H. IUCr Tetraaquabis(Hydrogen Maleato)Nickel(II), [Ni(C4H3O4)2(H2O)4]. Acta Crystallogr. Sect. C Cryst. Struct. Commun. 1984, 40, 1152–1154. [Google Scholar] [CrossRef]
  35. Sequeira, A.; Rajagopal, H.; Gupta, M.P.; Vanhouteghem, F.; Lenstra, A.T.H.; Geise, H.J. IUCr Tetraaquabis(Hydrogen Maleato)Zinc(II) by Neutron Diffraction and Tetraaquabis(Hydrogen Maleato)Nickel(II) by High-Order X-Ray Diffraction. Acta Crystallogr. Sect. C Cryst. Struct. Commun. 1992, 48, 1192–1197. [Google Scholar] [CrossRef]
  36. Neese, F. Software Update: The ORCA Program System, Version 4.0. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2018, 8, e1327. [Google Scholar] [CrossRef]
  37. Atanasov, M.; Ganyushin, D.; Pantazis, D.A.; Sivalingam, K.; Neese, F. Detailed Ab Initio First-Principles Study of the Magnetic Anisotropy in a Family of Trigonal Pyramidal Iron(II) Pyrrolide Complexes. Inorg. Chem. 2011, 50, 7460–7477. [Google Scholar] [CrossRef] [PubMed]
  38. Angeli, C.; Cimiraglia, R.; Evangelisti, S.; Leininger, T.; Malrieu, J.P. Introduction of N-Electron Valence States for Multireference Perturbation Theory. J. Chem. Phys. 2001, 114, 10252. [Google Scholar] [CrossRef]
  39. Angeli, C.; Cimiraglia, R.; Malrieu, J.P. N-Electron Valence State Perturbation Theory: A Spinless Formulation and an Efficient Implementation of the Strongly Contracted and of the Partially Contracted Variants. J. Chem. Phys. 2002, 117, 9138. [Google Scholar] [CrossRef]
  40. Angeli, C.; Borini, S.; Cestari, M.; Cimiraglia, R. A Quasidegenerate Formulation of the Second Order N-Electron Valence State Perturbation Theory Approach. J. Chem. Phys. 2004, 121, 4043. [Google Scholar] [CrossRef]
  41. Neese, F. Calculation of the Zero-Field Splitting Tensor on the Basis of Hybrid Density Functional and Hartree-Fock Theory. J. Chem. Phys. 2007, 127, 164112. [Google Scholar] [CrossRef]
  42. Maurice, R.; Bastardis, R.; de Graaf, C.; Suaud, N.; Mallah, T.; Guihéry, N. Universal Theoretical Approach to Extract Anisotropic Spin Hamiltonians. J. Chem. Theory Comput. 2009, 5, 2977–2984. [Google Scholar] [CrossRef]
  43. Van Lenthe, E.; Baerends, E.J.; Snijders, J.G. Relativistic Regular Two-component Hamiltonians. J. Chem. Phys. 1998, 99, 4597. [Google Scholar] [CrossRef]
  44. Van Wüllen, C. Molecular Density Functional Calculations in the Regular Relativistic Approximation: Method, Application to Coinage Metal Diatomics, Hydrides, Fluorides and Chlorides, and Comparison with First-Order Relativistic Calculations. J. Chem. Phys. 1998, 109, 392. [Google Scholar] [CrossRef]
  45. Weigend, F.; Ahlrichs, R. Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef] [PubMed]
  46. Pantazis, D.A.; Chen, X.Y.; Landis, C.R.; Neese, F. All-Electron Scalar Relativistic Basis Sets for Third-Row Transition Metal Atoms. J. Chem. Theory Comput. 2008, 4, 908–919. [Google Scholar] [CrossRef] [PubMed]
  47. Nagao, H.; Nishino, M.; Shigeta, Y.; Soda, T.; Kitagawa, Y.; Onishi, T.; Yoshioka, Y.; Yamaguchi, K. Theoretical Studies on Effective Spin Interactions, Spin Alignments and Macroscopic Spin Tunneling in Polynuclear Manganese and Related Complexes and Their Mesoscopic Clusters. Coord. Chem. Rev. 2000, 198, 265–295. [Google Scholar] [CrossRef]
  48. Becke, A.D. Density-functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1998, 98, 5648. [Google Scholar] [CrossRef]
  49. Adamo, C.; Barone, V. Toward Reliable Density Functional Methods without Adjustable Parameters: The PBE0 Model. J. Chem. Phys. 1999, 110, 6158. [Google Scholar] [CrossRef]
  50. Staroverov, V.N.; Scuseria, G.E.; Tao, J.; Perdew, J.P. Comparative Assessment of a New Nonempirical Density Functional: Molecules and Hydrogen-Bonded Complexes. J. Chem. Phys. 2003, 119, 12129. [Google Scholar] [CrossRef]
  51. Yamaguchi, K.; Takahara, Y.; Fueno, T. Ab-Initio Molecular Orbital Studies of Structure and Reactivity of Transition Metal-OXO Compounds. In Applied Quantum Chemistry; Reidel: Dordecht, The Netherlands, 1986; pp. 155–184. [Google Scholar] [CrossRef]
  52. Neese, F.; Wennmohs, F.; Hansen, A.; Becker, U. Efficient, Approximate and Parallel Hartree–Fock and Hybrid DFT Calculations. A ‘Chain-of-Spheres’ Algorithm for the Hartree–Fock Exchange. Chem. Phys. 2009, 356, 98–109. [Google Scholar] [CrossRef]
  53. Weigend, F. Accurate Coulomb-Fitting Basis Sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057–1065. [Google Scholar] [CrossRef] [PubMed]
  54. Hellweg, A.; Hättig, C.; Höfener, S.; Klopper, W. Optimized Accurate Auxiliary Basis Sets for RI-MP2 and RI-CC2 Calculations for the Atoms Rb to Rn. Theor. Chem. Acc. 2007, 117, 587–597. [Google Scholar] [CrossRef]
  55. Liu, J.L.; Chen, Y.C.; Guo, F.S.; Tong, M.L. Recent Advances in the Design of Magnetic Molecules for Use as Cryogenic Magnetic Coolants. Coord. Chem. Rev. 2014, 281, 26–49. [Google Scholar] [CrossRef]
Magnetochemistry 08 00106 g001 550
Figure 1. (a) Molecular structure of NiHmal; (b) Crystal structure of NiHmal. The dashed lines represent hydrogen bonds.
Figure 1. (a) Molecular structure of NiHmal; (b) Crystal structure of NiHmal. The dashed lines represent hydrogen bonds.
Magnetochemistry 08 00106 g001
Magnetochemistry 08 00106 g002 550
Figure 2. Stabilization of the crystal structure by strong intermolecular hydrogen bonds in NiHmal.
Figure 2. Stabilization of the crystal structure by strong intermolecular hydrogen bonds in NiHmal.
Magnetochemistry 08 00106 g002
Magnetochemistry 08 00106 g003 550
Figure 3. (a) Temperature dependence of total specific heat of NiHmal in a zero magnetic field (symbols). The dashed line represents the lattice contribution to the specific heat; (b) Temperature dependence of magnetic specific heat of NiHmal in a zero magnetic field (symbols). The solid line represents the theoretical prediction for S = 1 paramagnet with D/kB = –7.82 K, E/kB = –2.15 K, and g = 2.29.
Figure 3. (a) Temperature dependence of total specific heat of NiHmal in a zero magnetic field (symbols). The dashed line represents the lattice contribution to the specific heat; (b) Temperature dependence of magnetic specific heat of NiHmal in a zero magnetic field (symbols). The solid line represents the theoretical prediction for S = 1 paramagnet with D/kB = –7.82 K, E/kB = –2.15 K, and g = 2.29.
Magnetochemistry 08 00106 g003
Magnetochemistry 08 00106 g004 550
Figure 4. (a) Temperature dependence of the specific heat of the magnetic subsystem of the system NiHmal in different magnetic fields; (b) Temperature dependence of the total entropy of NiHmal in different magnetic fields.
Figure 4. (a) Temperature dependence of the specific heat of the magnetic subsystem of the system NiHmal in different magnetic fields; (b) Temperature dependence of the total entropy of NiHmal in different magnetic fields.
Magnetochemistry 08 00106 g004
Magnetochemistry 08 00106 g005 550
Figure 5. (a) Temperature dependence of the magnetic susceptibility measured in ZFC and FC regimes of NiHmal. Inset: Temperature dependence of the effective magnetic moment of NiHmal; (b) Isothermal magnetization curves of NiHmal powder sample at constant temperatures with temperature steps ΔT = 0.5 K and 1 K in the intervals 2–10 and 11–20 K, respectively; (c) Arrott plot for the NiHmal powder sample.
Figure 5. (a) Temperature dependence of the magnetic susceptibility measured in ZFC and FC regimes of NiHmal. Inset: Temperature dependence of the effective magnetic moment of NiHmal; (b) Isothermal magnetization curves of NiHmal powder sample at constant temperatures with temperature steps ΔT = 0.5 K and 1 K in the intervals 2–10 and 11–20 K, respectively; (c) Arrott plot for the NiHmal powder sample.
Magnetochemistry 08 00106 g005
Magnetochemistry 08 00106 g006 550
Figure 6. (a) Temperature dependence of the isothermal entropy change of NiHmal in different magnetic fields. −ΔSM were obtained from the magnetization curves (symbols); solid lines represent values of −ΔSM calculated from specific heat data. Dashed lines represent values of −ΔSM calculated for S = 1 paramagnet with D/kB = −7.82 K, E/kB = −2.15 K, and g = 2.29; (b) Adiabatic temperature change as a function of initial temperature for the NiHmal system realized under conditions of adiabatic demagnetization to zero magnetic field.
Figure 6. (a) Temperature dependence of the isothermal entropy change of NiHmal in different magnetic fields. −ΔSM were obtained from the magnetization curves (symbols); solid lines represent values of −ΔSM calculated from specific heat data. Dashed lines represent values of −ΔSM calculated for S = 1 paramagnet with D/kB = −7.82 K, E/kB = −2.15 K, and g = 2.29; (b) Adiabatic temperature change as a function of initial temperature for the NiHmal system realized under conditions of adiabatic demagnetization to zero magnetic field.
Magnetochemistry 08 00106 g006
Magnetochemistry 08 00106 g007 550
Figure 7. Schematic representation of the J1 (a) and J2 (b) exchange interactions in the crystal structure of NiHmal.
Figure 7. Schematic representation of the J1 (a) and J2 (b) exchange interactions in the crystal structure of NiHmal.
Magnetochemistry 08 00106 g007
Table
Table 1. Comparison of the exchange coupling in NiHmal obtained from BS DFT calculations for two different exchange paths using selected DFT functionals.
Table 1. Comparison of the exchange coupling in NiHmal obtained from BS DFT calculations for two different exchange paths using selected DFT functionals.
B3LYPTPSShPBE0
J1/kB1.50 K1.18 K0.80 K
J2/kB1.44 K1.04 K0.92 K
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Danylchenko, P.; Tarasenko, R.; Čižmár, E.; Tkáč, V.; Uhrinová, A.; Orendáčová, A.; Orendáč, M. Experimental Study of Magnetocaloric Effect in Tetraaquabis(Hydrogen Maleato)Nickel(II), [Ni(C4H3O4)2(H2O)4]—A Potential Realization of a Spin-1 Spatially Anisotropic Square Lattice with Ferromagnetic Interactions. Magnetochemistry 2022, 8, 106. https://doi.org/10.3390/magnetochemistry8090106

AMA Style

Danylchenko P, Tarasenko R, Čižmár E, Tkáč V, Uhrinová A, Orendáčová A, Orendáč M. Experimental Study of Magnetocaloric Effect in Tetraaquabis(Hydrogen Maleato)Nickel(II), [Ni(C4H3O4)2(H2O)4]—A Potential Realization of a Spin-1 Spatially Anisotropic Square Lattice with Ferromagnetic Interactions. Magnetochemistry. 2022; 8(9):106. https://doi.org/10.3390/magnetochemistry8090106

Chicago/Turabian Style

Danylchenko, Petro, Róbert Tarasenko, Erik Čižmár, Vladimír Tkáč, Anna Uhrinová, Alžbeta Orendáčová, and Martin Orendáč. 2022. "Experimental Study of Magnetocaloric Effect in Tetraaquabis(Hydrogen Maleato)Nickel(II), [Ni(C4H3O4)2(H2O)4]—A Potential Realization of a Spin-1 Spatially Anisotropic Square Lattice with Ferromagnetic Interactions" Magnetochemistry 8, no. 9: 106. https://doi.org/10.3390/magnetochemistry8090106

APA Style

Danylchenko, P., Tarasenko, R., Čižmár, E., Tkáč, V., Uhrinová, A., Orendáčová, A., & Orendáč, M. (2022). Experimental Study of Magnetocaloric Effect in Tetraaquabis(Hydrogen Maleato)Nickel(II), [Ni(C4H3O4)2(H2O)4]—A Potential Realization of a Spin-1 Spatially Anisotropic Square Lattice with Ferromagnetic Interactions. Magnetochemistry, 8(9), 106. https://doi.org/10.3390/magnetochemistry8090106

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop