1. Introduction
Quantum dot cellular automata (QCA) pioneered by Lent et al. [
1,
2,
3] is an emerging technology in nanoelectronics based on the use of the assemblies of quantum dots, which play the role of QCA cells suitable for composing the logic elements in digital integrated circuits. Particularly, the two-electron four-dot square cells can serve as building blocks of wires, fun-outs, majority logical gates and complex circuits [
4,
5,
6,
7,
8,
9,
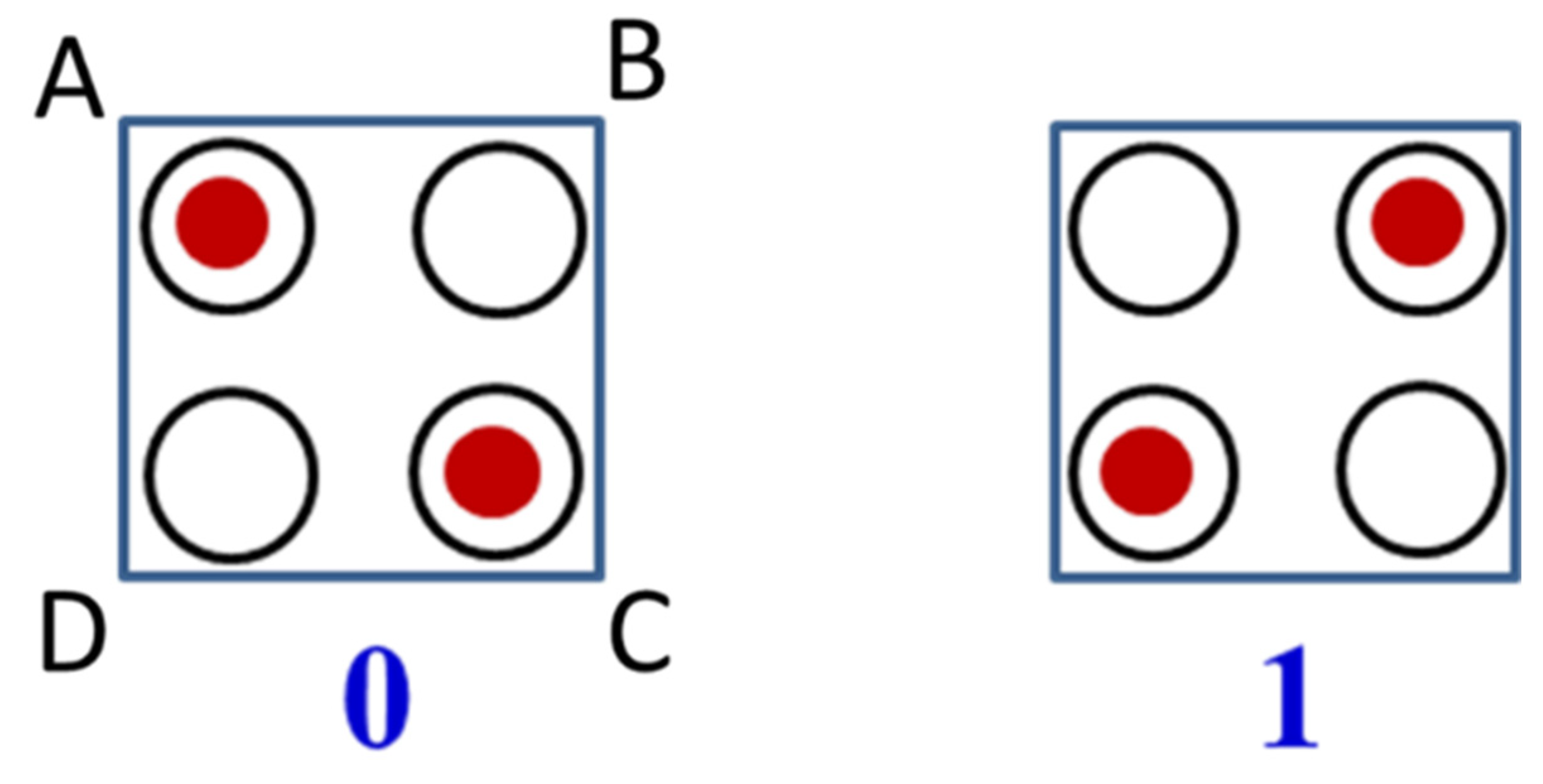
10]. The two antipodal charge configurations of square cell in which the two electrons occupy the diagonals of the molecular square are supported by the interelectronic Coulomb repulsion and can be used to encode binary information (
0 and
1) as shown in
Figure 1. The QCA devices composed of quantum dots have several important potential advantages over standard silicon ones, such as current-free signal propagation and switching, strongly reduced power dissipation in the circuits, and also much smaller size of the logic gates, which allow to achieve much higher density of the devices.
A fundamental idea to scale down the cells by replacing the assemblies of quantum dots with mixed-valence (MV) molecules having similar topology and electronic structure [
4,
11,
12,
13,
14,
15,
16,
17,
18,
19,
20,
21] promises new advantages and allows to employ the controlled chemical design of the molecules with required properties for creating of 2D networks mimicking electronic circuits. Molecular QCA are in the core of interdisciplinary field lying at the borderline of chemistry, physics and molecular electronics. Numerous organic and inorganic MV molecular squares suitable for the design of QCA cells have been obtained, such as, for example, the MV tetramers [(cyclen)
4Ru
II2Ru
III2](pz)
4]
10+ and [Fe
II2Fe
III2(L)
4]
2+ (cyclen = 1,4,7,10-tetraazacyclododecane, pz = pyrazine a nd H
2L = bis[phenyl (2-pyridyl) methanone] thiocarbohydrazone) [
16,
17,
18]. Additionally, the grid-type architectures comprising two-dimensional arrays of molecular cells have been obtained [
21], which has interrelated the synthesis and characterization of the molecular cell prototypes with nanotechnological applications of the controlled 2D monolayers of such cells.
The prerequisite for the efficient quantum-chemical design of molecular cells [
19,
20] is in-depth understanding of the key electronic and vibronic interactions governing the electron delocalization in MV molecules and also a route for possible control of the main functional characteristics of cells. The physical role of different interactions traditionally employed in the models of molecular MV cells is described in detail in [
22,
23,
24] and also reviewed in Refs. [
25,
26] (see also Ref. [
27]). While the inner sphere electron transfer (ET) changes the distribution of the excess charges inside the cell, promoting thus their delocalization, the vibronic coupling with the local “breathing” modes has a competing effect, which consists of self-trapping of the charges. An important role is played by the interelectronic Coulomb repulsion tending to stabilize antipodal (diagonal-type) charge distributions. In conjunction with the vibronic trapping, such effect of the Coulomb repulsion ensures the cell bi-stability required for proper binary information encoding. Finally, the transmission of binary information from cell to cell is carried out through the intercell Coulomb repulsion, which can be modelled by considering the effect of the external electric field produced by the polarized “driver-cell” on the neighboring “working cell”.
In the majority of studies devoted to the theoretical modelling of molecular QCA the intracell interelectronic Coulomb repulsion has been considered as interaction dominating over the ET. Due to that, the antipodal charge configurations prove to be stabilized and hence bistability of the cell is ensured. Approximation of strong Coulomb repulsion has been explicitly invoked in Ref. [
22], allowing thus to essentially simplify the solution of the electronic and vibronic problems. It is worth noting in this context that the concept of charge separation solely due to strong Coulomb repulsion limits the search for systems that could act as molecular cells. To overcome these limitations, we have recently attempted to critically reconsider the parameters regime for achieving functionality with emphasis on the role of the Coulomb repulsion and the vibronic coupling [
28]. It has been demonstrated that bistability and switchability of the square cell can be achieved even in the case of weak or moderate Coulomb interaction provided that the vibronic coupling is strong enough.
Solution of the vibronic problem in [
28] has been performed with the aid of semiclassical adiabatic approximation. Although the latter approximation provides a reliable physical description and an imaginative picture of the main relevant characteristics of a MV molecular cell, the frames of the adiabatic approach are rather limited (see article [
29] devoted to the discussion of this question). The aim of the present study is to demonstrate how by implying the quantum mechanical vibronic theory one can correct the shortcomings of the adiabatic approach as applied to the description of such important features of cell behavior as the degree of non-linearity of the cell-cell response function in the general case when the limit of strong Coulomb repulsion is violated.
2. Cell-Cell Response: Why Do We Need Quantum-Mechanical Approach
The QCA device performs its function through the action of the drive-cell on the working cell [
1,
2,
3,
4]. It is assumed that the first one has a certain polarization, which is transmitted to the adjacent working cell (
Figure 1) via electrostatic field as illustrated in
Figure 2 (upper part). The response of the working cell to the field induced by the polarized driver-cell is described by the so-called cell-cell response function which is defined as dependence of polarization of the working cell
on the polarization
of the driver cell.
The driver-cell is assumed to be polarized in a controllable manner in such a way that the sites disposed in the diagonal AC acquire the electronic densities
ρ while the electronic densities in the sites located on the diagonal BD prove to be equal to 1 −
ρ (the labelling of the sites is that shown in
Figure 1). This means that the driver-cell can be regarded as electric quadrupole with polarization
representing the normalized excess of the electronic density on a certain diagonal of the driver-cell with respect to the density on its another diagonal.
The electrostatic field of polarized driver-cell causes polarization of the neighboring working cell with electronic site densities
ρA,
ρB,
ρC and
ρD, (numeration of the sites is shown in
Figure 1) which are, in general, different. One can define the induced polarization of the working cell as follows:
The efficiency of the effect of the driver-cell on the working cell is characterized by the so-called cell-cell response function
introduced by Lent et al. [
1,
2,
3,
4] and modeled in more recent studies in the framework of different vibronic approaches [
22,
23,
24,
25,
26,
27,
28,
29]. This function characterizes “intercommunication” between the molecular cells. To ensure high performance of QCA-based device the driver-cell should be able to dictate the required charge configuration to the working cell in a strongly non-linear (stepwise) manner. It is also important that as discussed in ref. [
30] the strong non-linearity is able to avoid destructive influence of imperfections in the QCA devices (such as random variation in the cell size, random fields, etc.) on the propagation of the signal.
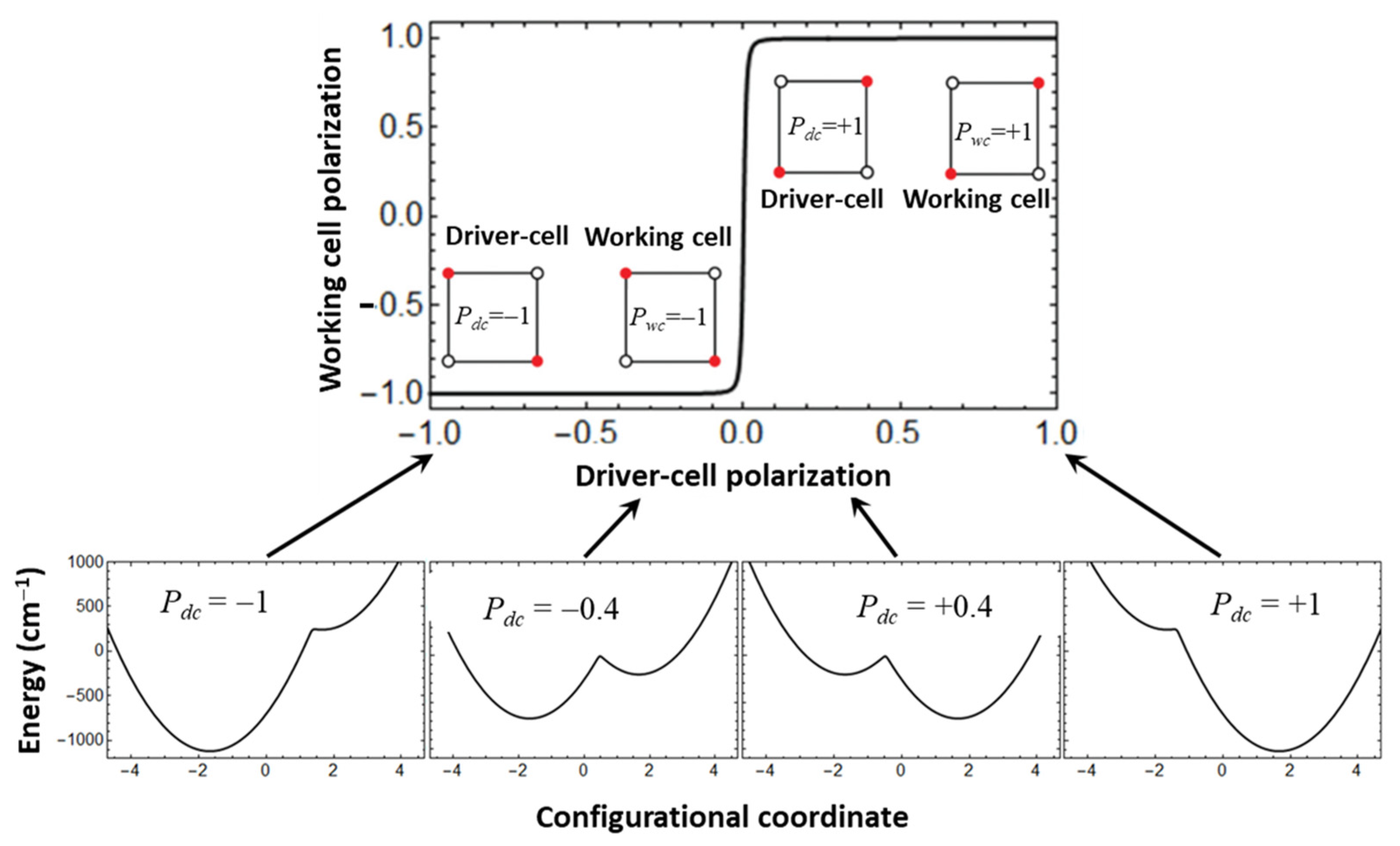
Figure 2 (upper part) illustrates an idealized (but practically unattainable) situation when the cell-cell response function has almost perfect stepwise character, and only the central part of the cell-cell response function being slightly more gradual, with the shape of this central part being determined by the interplay between the ET, vibronic coupling and Coulomb interaction [
29]. As will be discussed below, just the shape of the central non-linear part of cell-cell response function is responsible for switching performance and hence it is of primary importance for the proper action of a QCA-based device. For this reason, the degree of accuracy in the evaluation of cell-cell response in this area is decisive in assessing the applicability of the approach to theoretical modeling.
The two approaches are conventionally used for treating the vibronic problem underlying the localization-delocalization properties of MV clusters, and particularly, the functional properties of MV molecular candidates for the creation of molecular QCA cells with required characteristics [
26]. Application of the first (lower-level) such approach known as semiclassical or adiabatic approximation is illustrated in the lower part of
Figure 2 in which the so-called switching circles (evolution of the lowest adiabatic potential surface of the working cell in course of the change of the driver-cell polarization from −1 to +1) is illustrated for simplest situation of one-dimensional adiabatic potential. At
Pdc ≠ 0 the adiabatic potential is asymmetric due to the action of the quadrupole field of the driver-cell. At the beginning of the switching circle (
Pdc = −1) the working cell is localized in a left deep minimum and its induced polarization acquires the value
Pwc = −1. The left global minimum becomes shallower with decreasing of |
Pdc|, and the second exited (right) minimum appears. The |
Pwc| defined in the global minimum gradually decreases with decreasing |
Pdc| until the latter reaches the narrow critical range of values near
Pdc = 0. In this range, polarization of the working cell abruptly changes from
Pwc = −1 to
Pwc = +1 which is accompanied by interchanging of the global and the excited minima. Finally, at the end of the cycle we arrive at the same energy of the working cell but the cell proves to be localized in the right minimum with polarization
Pwc = +1.
Consideration of the above idealized situation allows to make some preliminary remarks concerning the limits of the applicability of the adiabatic approximation to the description of molecular QCA cells. Indeed, according to the physical sense of the adiabatic approximation its applicability is rather well justified when the system is strongly localized in the deep global minimum as it occurs at Pdc = −1 and Pdc = +1. However, when |Pdc | approaches the critical area (Pdc | ≈ 0) the minima are becoming shallower and the left and the right minima become almost energetically equivalent. As a result, the quantum tunneling effects are expected to play important role in this area.
The above discussion clearly shows that the adiabatic approximation loses its accuracy at weak quadrupole fields, i.e., just in the range of |
Pdc | values playing crucially important roles in switching the cell between
0 and
1 states. Meanwhile, a more exact quantum-mechanical vibronic approach is free from this shortcoming. This is true for the case of strong Coulomb repulsion [
28] for which the quantum-mechanical approach is shown to result in a more smooth
dependence as compared with semiclassical one due to presence of the tunneling processes facilitating reorientation of the cell polarization [
29]. The difference between semiclassical and quantum-mechanical description of cell-cell response is expected to be even more significant for general cases when the intracell Coulomb repulsion is comparable with the ET. Just such a general case will be discussed below.
3. Electronic and Vibronic Interactions in a Two-Electron Mixed-Valence Molecular Square
Let us describe the key ingredients of the model. As a working cell, we consider a square-planar tetramer A-B-C-D (
Figure 1) comprising four diamagnetic centers (spinless cores) and two excess electrons. The latter can occupy either the adjacent cites A-B, B-C, C-D and A-D (sites forming the sides of the square) giving rise to the fourfold degenerate excited Coulomb manifold, or the antipodal sites A-C and B-D located on the diagonals (twofold degenerate ground Coulomb manifold). The Coulomb gap between the ground and the excited Coulomb manifolds will be denoted as
U. The driver-cell can be roughly modelled as electric quadrupole composed of the following four point-charges located at the vertices of the square:
and
(the labels of the redox sites forming the driver-cell are primed to distinguished them from those composing the working cell). This quadrupole admits controllable polarization given by Equation (1) from which it follows that the charges on the driver-cell sites can be thus obtained as follows:
,
. The polarized driver-cell acts on the working cell causing its polarization. To interaction between the two cells is described by the intercell Coulomb energy, which depends both on the polarization of the driver-cell and on the electronic configuration in the working cell. The intercell Coulomb energy will be denoted as
for the configuration in which the charges in the working cell occupy the sites
i and
k. The explicit expressions for all
energies are given in Ref. [
28].
The vibronic coupling is one of the main ingredients determining the properties of the MV systems. The simplest and most convenient way to introduce this interaction is to imply the vibronic Piepho, Krausz and Schatz (PKS) model [
31], which includes only the interaction of the excess electrons with the full-symmetric (“breathing”) modes
,
,
and
located at the redox sites A, B, C, and D, with all these modes being assumed to have the same frequency
ω. The set local modes
can be expressed in terms of symmetry adapted molecular vibrations belonging to the irreducible representations
A1,
E,
B1 of the point group D
4h. The corresponding unitary transformation is the following:
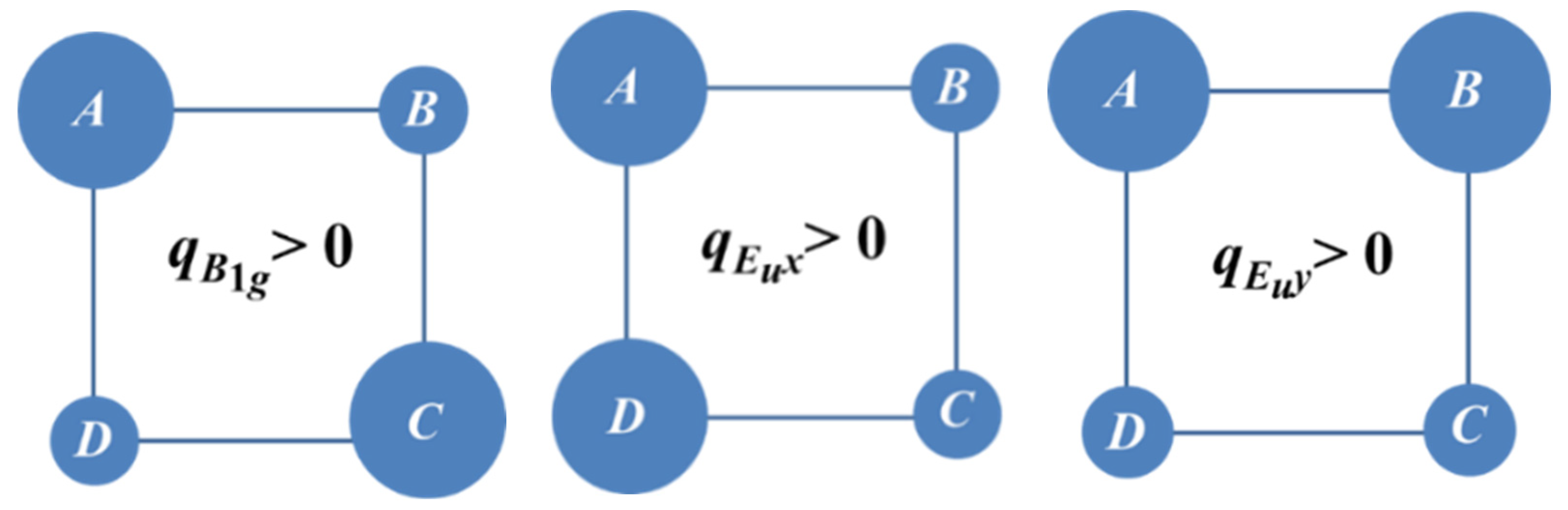
Figure 3 shows the shapes of
Eu and
B1g vibrations illustrating their different physical role. Indeed,
type displacements are interrelated with the ground Coulomb manifold comprising antipodal (diagonal type) charge configurations, while the double degenerate vibration
operates within the excited Coulomb manifold.
The full Hamiltonian of the working cell includes the ET (parameter t) between the neighboring sites of the intracell Coulomb interaction which is the energy gap U between the ground and excited Coulomb manifolds. The Hamiltonian also involves the potential and kinetic energies of the free vibrations and linear vibronic coupling. The ET between the diagonals of the square are assumed to be negligible due to long distance between sites which are not connected through a bridge. The full Hamiltonian also includes the Coulomb field produced by the polarized driver-cell, which is described by the set of intercell Coulomb energies .
The matrix of the full Hamiltonian, which includes all mentioned interactions, is the following:
The matrix in Equation (4) is defined in the electronic basis comprising the states
where
S is the total spin of the electronic pair, which can take on the values
S = 0 and 1. It has been earlier demonstrated (see, for example, ref. [
22]) that the ground state of the cell is has always spin
S = 0 provided that only the electron transfer between the nearest neighboring sites is allowed. For this reason, in the further consideration we will solely focus on the states with
S = 0. The first term in Equation (4) is the Hamiltonian of the free vibrations, where
is the unit
-matrix. Vibronic coupling with
Eu and
B1g - modes is described by the terms
in which
is the vibronic coupling parameter that is the same for all vibrations in the PKS model dealing with equivalent redox sites. The coupling with the full-symmetric mode does not depend on the charge configuration and so it has been eliminated from the matrix in Equation (4) by means of proper redetermination of the reference vibrational configuration.
4. Electronic Densities in a Free Cell: Quantum-Mechanical Results
The subsequent analysis will be based on the quantum-mechanical vibronic approach, which takes into account the kinetic energy of vibrations and for this reason will be referred to as dynamic one. To gain more insight on the vibronic problem let us first consider the pure electronic energy levels. The latter are expressed as follows:
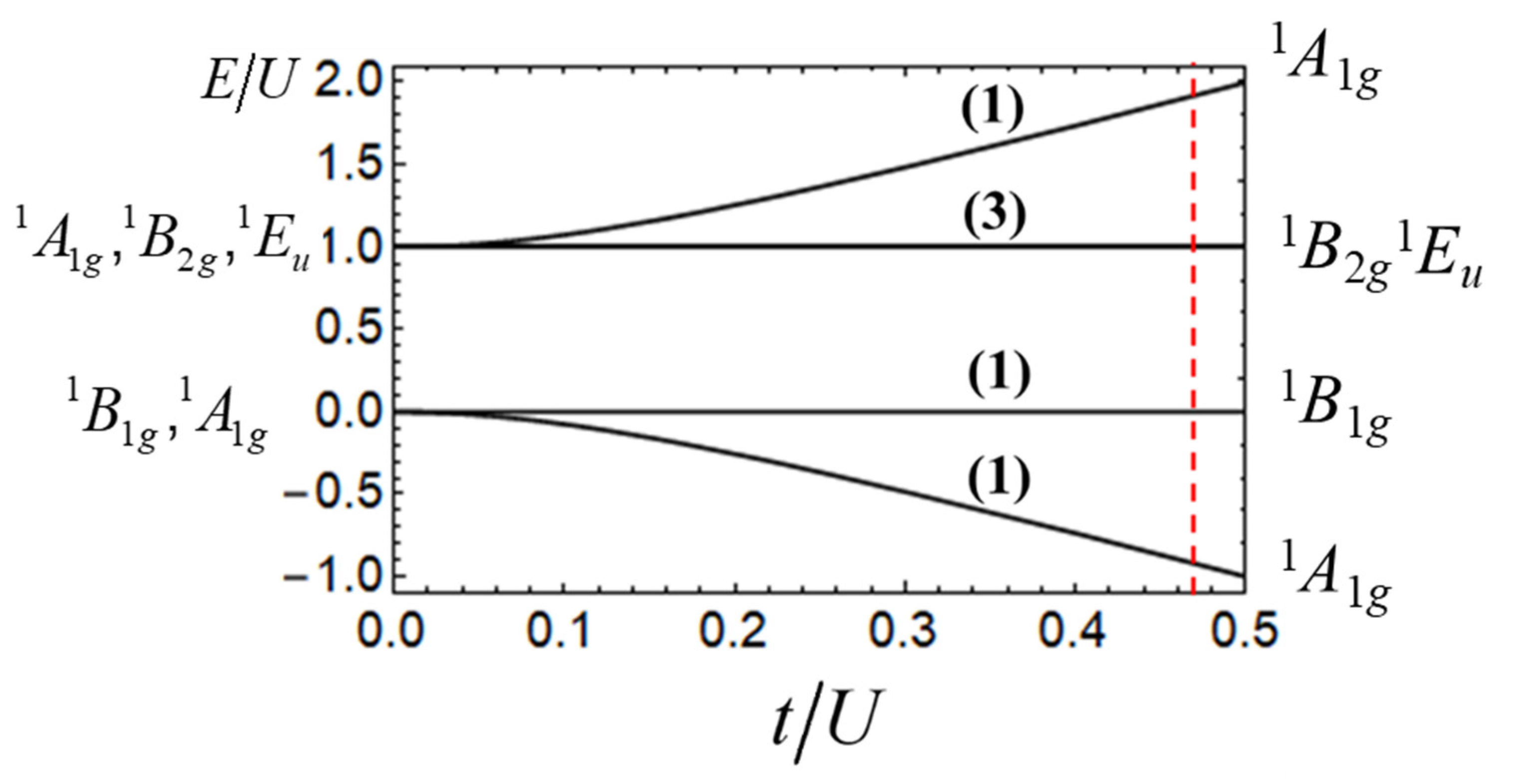
Figure 4 shows the electronic energy pattern presented in the form
E/U vs.
t/U. One can see that at
t = 0 the six levels are grouped into the two sets, (
) and (
), arising from the ground and excited Coulomb manifolds, respectively. Mixing of the states belonging to these two manifolds by the ET processes leads to the splitting of the ground and excited manifolds as shown in
Figure 4. The irreducible representations associated with the levels shows that the inclusion of the vibronic coupling with B1g and Eu vibrations leads to the complicated three-mode vibronic problem combining Jahn-Teller and pseudo-Jahn-Teller problems. This combined vibronic problem can be designated as (
.
Since all PKS vibrations have equal frequencies, we are dealing with the three-dimensional oscillator coupled to six electronic states, and so the total degeneracy of Hilbert space including
N vibrational levels is rather large,
, where
is the number of the vibrational levels involved in the basis set. An efficient symmetry-assisted approach to solve multidimensional dynamic vibronic problems [
32,
33,
34] can be applied to a free cell to essentially reduce the vibronic matrix. Nevertheless, while considering the interacting cells, the symmetry arguments lose their advantages due to lowering the working cell symmetry caused by the electrostatic field of the driver-cell. One can find that for
N = 3 the dimension of vibrational space is
, while for
N = 6 it becomes rather large,
Correspondingly, the dimensions of the full pseudo Jahn-Teller problems (
are
and
= 196,416. Depending on the size of the basis, a certain number of the low lying vibronic levels can be adequately described. The required number of these levels can be estimated as a pseudo Jahn-Teller stabilization energy in
units. Roughly, this can be estimated as
, so that the number of the levels under the potential barrier is
Conventionally, one can estimate that for
N = 6 and
only the ground state can be satisfactorily described, while for
N = 30 the consideration has good accuracy at least for
A more detailed discussion of the multidimensional problem of the vibronic coupling in MV systems is given in Refs. [
32,
33,
34].
Therefore, to solve the dynamic vibronic problem we present the matrix of the full Hamiltonian, Equation (4), in the basis composed of products of the six electronic functions with different localization of the pair and unperturbed vibrational functions representing the wave functions of the three-dimensional harmonic oscillator, where n2, n3 and n4 are the vibrational quantum numbers related to the three active vibrational modes. To obtain a numerical solution of the dynamic problem the infinite matrix has to be truncated. The dimension of the truncated matrix should be large enough to ensure a good convergence that provides a satisfactory accuracy in the evaluation of the low-lying vibronic levels. This dimension depends on the set of parameters involved in the Hamiltonian.
The numerical solution in the truncated basis gives a set of the vibronic energy levels
of the working cell and the corresponding vibronic wave-functions. The latter are obtained as the following superpositions:
where the coefficients
depend on the set of parameters
, and also on the polarization
on the driver-cell. Below we will focus solely on ground vibronic state
, which determine the properties of the cell in the low-temperature limit.
As far as the dynamic vibronic problem is solved, one can evaluate the overall vibronic probabilities of the diagonal-type and side-type two-electron populations in the ground vibronic state
with the aid of the following expressions:
Hereinafter in all sample calculations we use for the intracell distance (side of the molecular square) will have the value To roughly estimate the Coulomb parameters we will use the relative permittivity value that is supposed to mimic the screening effect. With these values, one obtains . We use the fixed values and t = 200 cm−1 for the vibrational PKS quantum and the ET parameter.
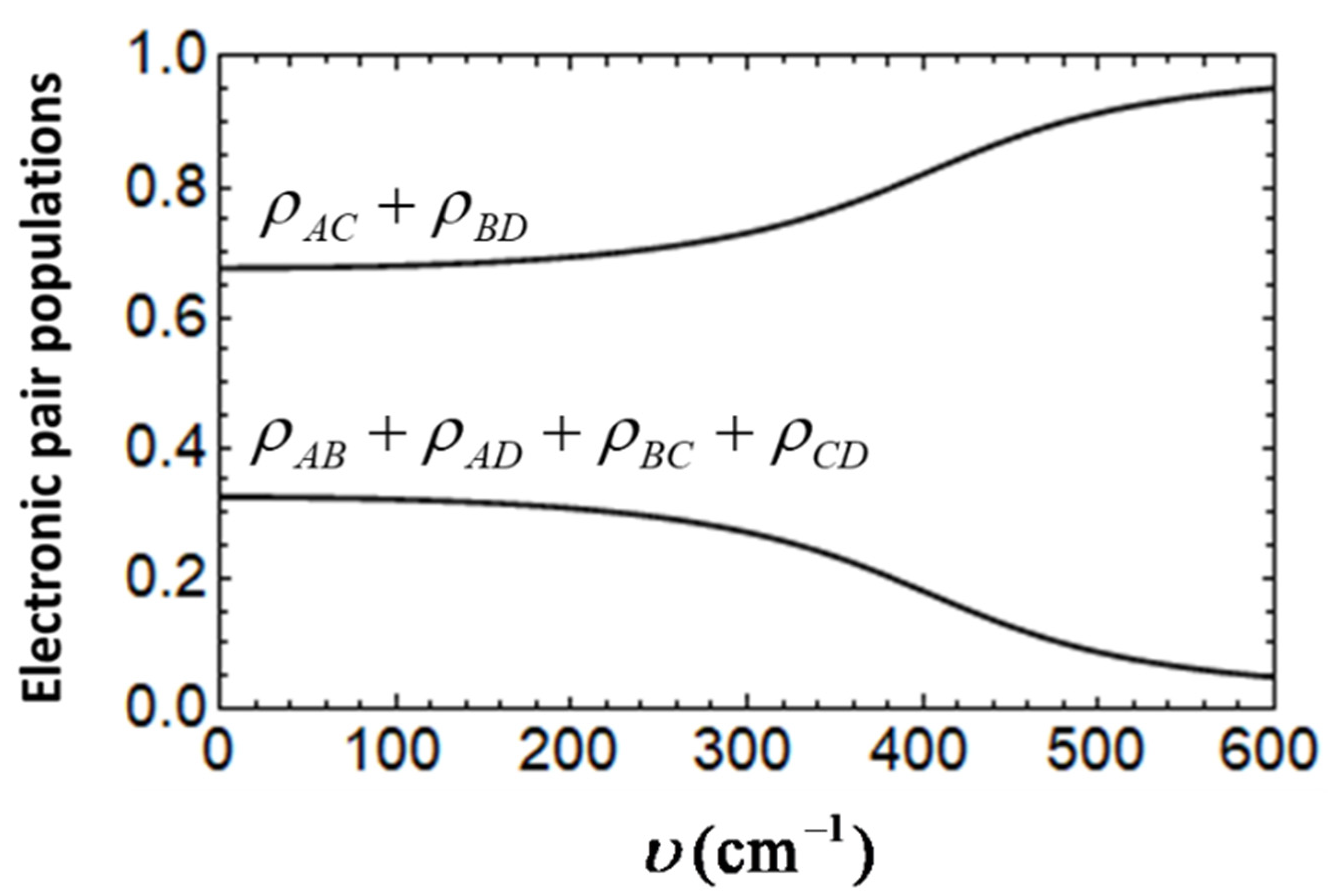
Figure 5 shows the vibronic probabilities for the free cells evaluated as functions of
with the above adopted
and
values. It is seen that at
the overall diagonal-type probability is
while the side-type probability is estimated as
. It is clear that although
around two times exceeds
, the distribution of the electronic density of the two electrons evaluated for the considered set of
t and
U values and
is far from being fully concentrated on the two diagonal positions. This is an indication that we are dealing with the case for which the limit of strong Coulomb repulsion is not achieved.
An increase in
υ leads to the enhancement of the diagonal probability
accompanied by the decrease in
in such a way that at strong vibronic coupling the pair of the excess electrons becomes fully concentrated in the two antipodal positions (
). In general terms, impact of the vibronic coupling is qualitatively the same as that derived within the semiclassical approach [
29]. However, as distinguished from the Born-Oppenheimer states in the adiabatic potential minima representing the broken symmetry states with predominant localization at a certain diagonal, the ground vibronic state obtained by using quantum-mechanical approach corresponds to the unbroken symmetry with equal weights of the resonant states, which are indicative of quantum tunneling. This shows that for a free cell it is reasonable to analyze the overall probabilities
and
rather than the particular probabilities such as
, etc.
It is seen from
Figure 5 that at a weak vibronic coupling (up to
υ ≈ 250 cm
−1)
and
gradually depend on
υ. At this range of the values of
υ the lowest adiabatic potential was shown to possess the only minimum or the two shallow minima separated by a barrier whose top is lower in energy than the energy of the ground vibronic level found from quantum-mechanical treatment. At moderate vibronic coupling, the functions
and
show more rapid changes, which become again more gradual in the limit of strong vibronic coupling when the tunneling is almost fully suppressed. Therefore, the obtained dependences confirm the conclusion derived based on the semiclassical consideration [
28] according to which the strong vibronic coupling is able to effectively restore the dominance of the diagonal-type electronic configurations typical of the strong limit of strong Coulomb repulsion, which is broken down when the inequality
t <<
U fails.
5. Effect of Quantum Tunneling on Cell-Cell Response
Now we apply the quantum-mechanical vibronic approach to the analysis of the response of the working cell to the electrostatic field of the polarized driver-cell. In addition to the set of parameters adopted in
Section 4 we will use the intercell distance
to determine the intercell Coulomb energies
uik.
Figure 6a shows a family of cell-cell response functions calculated with the aid of quantum-mechanical vibronic approach at four different values of
υ. It is seen that for weak vibronic coupling, the cell-cell response is rather weak and almost linear (curves 3 and 4 in
Figure 6a). Increase in the coupling leads to a pronounced non-linearity in the response with the slope of
curve being increased with the increase in
υ (curves 1 and 2 in
Figure 6a). Finally, providing strong vibronic coupling the cell-cell response function shows abrupt stepwise behavior, so that even weak driver-cell polarization causes almost full polarization of the working cell (curve 1 in
Figure 6a).
To facilitate the comparison of quantum-mechanical cell-cell response functions with semiclassical ones calculated with the same values of
υ we have shown a family of the latter functions in
Figure 6b. It is seen that qualitatively the physical role of the vibronic coupling is properly reflected by the adiabatic approximation. It follows from the fact that the slopes of both semiclassical and quantum-mechanical cell-cell response functions increase with the increase in the vibronic coupling. On the other hand, by comparing the two families of curves one can conclude that there are remarkable quantitative differences between the semiclassical and quantum-mechanical functions. Indeed, whereas the semiclassical response exhibits non-linear abrupt at
υ = 300 cm
−1 curve 3 in
Figure 6b), the quantum-mechanical cell-cell response calculated with the same
υ proves to be rather weak and practically linear (curve 3 in
Figure 6a). The difference between semiclassical and quantum-mechanical curves diminishes with the increase in the vibronic coupling, so that at strong coupling (case of
υ = 600 cm
−1) the cell-cell responses evaluated with these two approaches prove to be quite similar in the sense that both curves show abrupt non-linear behavior, with full polarization of the working cell being reached at a weak driver-cell polarization (curves 1 in
Figure 6a,b). Still, even in this case the quantum-mechanically evaluated
-dependences proves to be more gradual as compared with the semiclassical one.
The above noted difference between quantum-mechanical and adiabatic curves can be attributed to the quantum tunneling ignored by the semiclassical approach by its very nature. Indeed, quantum tunneling is a competing factor with respect to the localizing effect of the field of the driver-cell, which tends to stabilize a certain polarization of the working cell. The stronger the vibronic coupling, the smaller the tunneling gap between the ground and the first excited vibronic levels evaluated at
when the lowest levels in the two equivalent potential wells are in resonance. This can be evidenced by comparing the field dependences of the two low-lying vibronic tunnel levels evaluated for
and
(
Figure 7). It is seen that for
the tunneling can be more easily suppressed by the electrostatic field of the driver-cell so that even at very weak polarization of the driver-cell the dependences of the ground and first excited vibronic levels on
are becoming linear. In contrast, at
the tunneling gap is larger and so a higher field is required to ensure linear dependencies of the energies on
. Such difference in tunneling gaps determines the difference in the slopes of the
-dependences and in the saturation
-values as evidenced from comparison of the curves 1 and 2 in
Figure 6a.