Pressure–Temperature Phase Diagram of Multiferroic TbFe2.46Ga0.54(BO3)4
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Symmetry Analysis
3.2. Angular-Dependent Raman Spectra
3.3. Phase Transitions at Atmospheric Pressure
3.4. p–T Phase Diagram
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| FWHM | Full width at half maximum |
| HH | Parallel polarisation of incident and scattered light |
| HV | Cross polarisation of incident and scattered light |
Appendix A. Calculated Intensities of Raman Modes
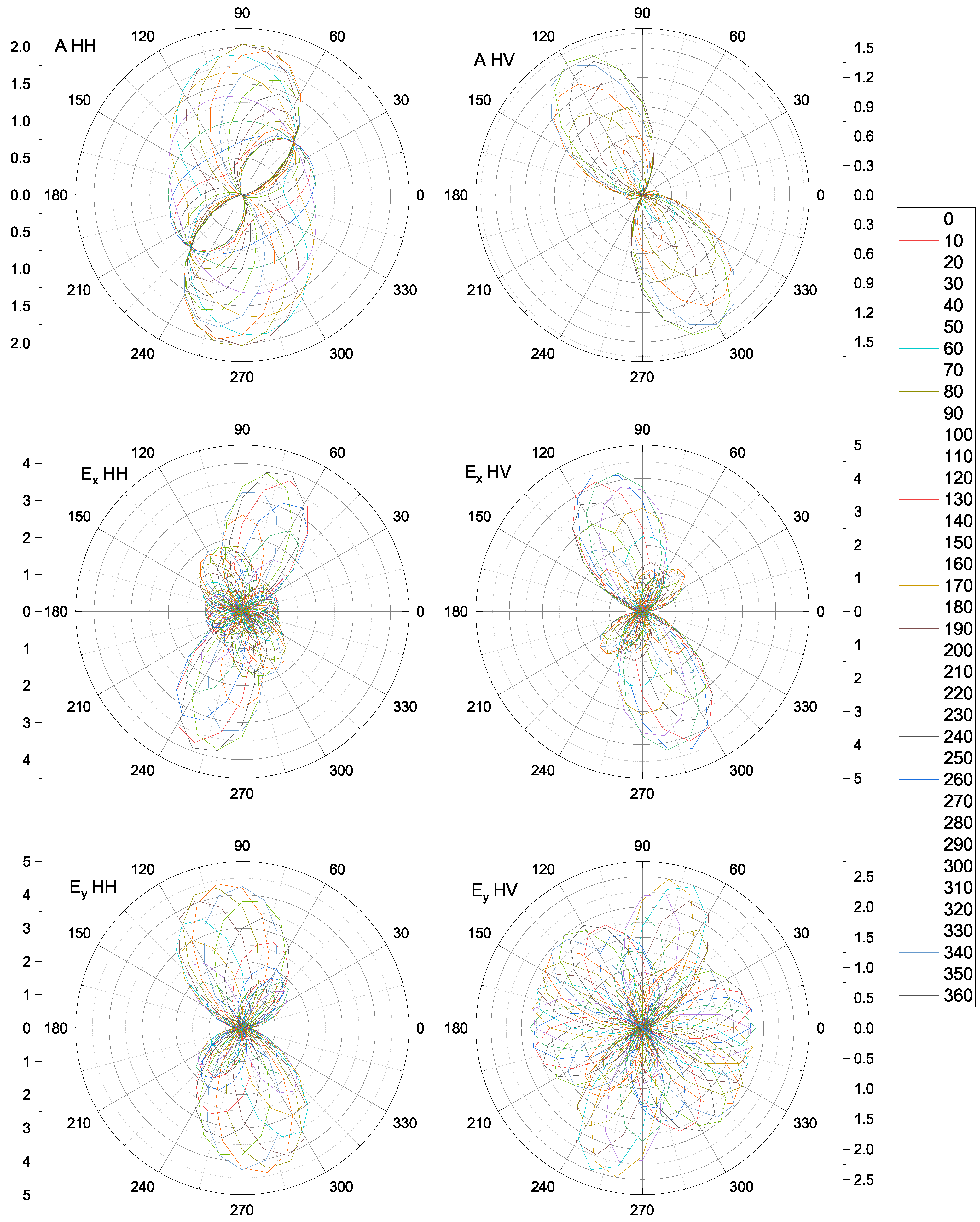
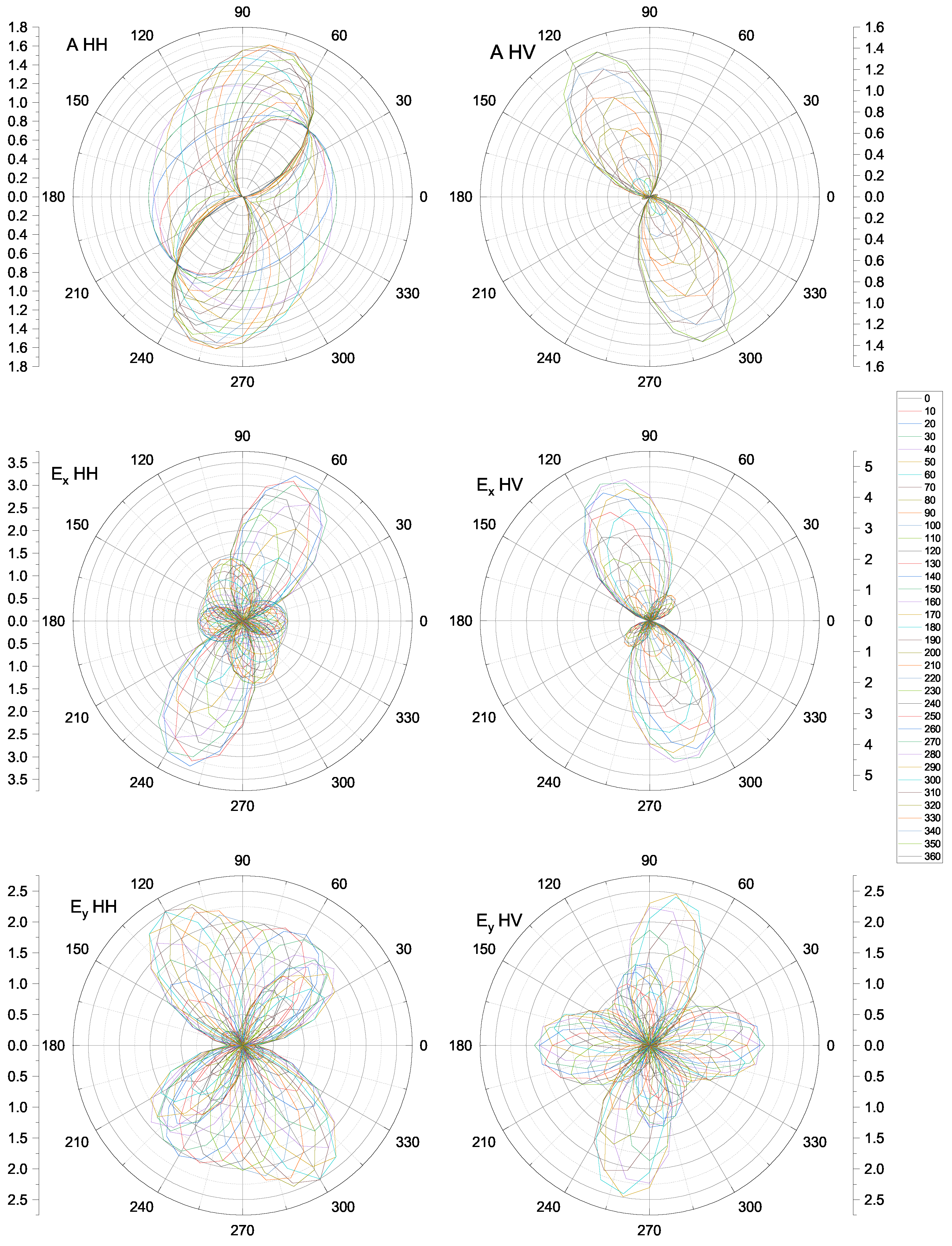
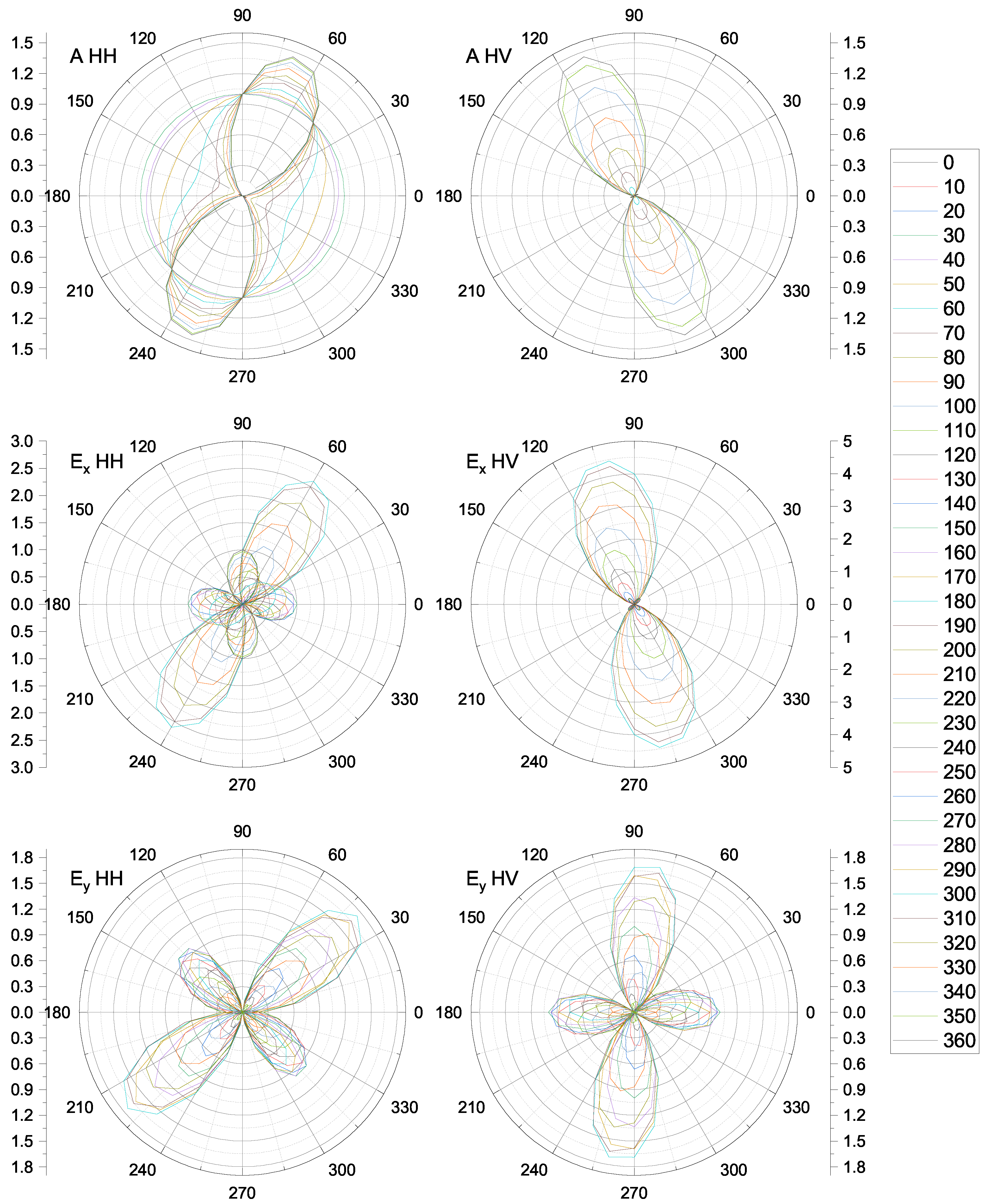

Appendix B. Photos of the TbFe2.46Ga0.54(BO3)4 Crystal in the DAC
References
- Vopson, M.M. Fundamentals of Multiferroic Materials and Their Possible Applications. Crit. Rev. Solid State Mater. Sci. 2015, 40, 223–250. [Google Scholar] [CrossRef]
- Fiebig, M. Revival of the magnetoelectric effect. J. Phys. D Appl. Phys. 2005, 38, R123–R152. [Google Scholar] [CrossRef]
- Eerenstein, W.; Mathur, N.D.; Scott, J.F. Multiferroic and magnetoelectric materials. Nature 2006, 442, 759–765. [Google Scholar] [CrossRef] [PubMed]
- Hinatsu, Y.; Doi, Y.; Ito, K.; Wakeshima, M.; Alemi, A. Magnetic and calorimetric studies on rare-earth iron borates LnFe3(BO3)4 (Ln = Y, La–Nd, Sm–Ho). J. Solid State Chem. 2003, 172, 438–445. [Google Scholar] [CrossRef]
- Krylov, A.S.; Sofronova, S.N.; Gudim, I.A.; Vtyurin, A.N. Magnetoelastic interactions in Raman spectra of Ho1−xNdxFe3(BO3)4 crystals. Solid State Commun. 2013, 174, 26–29. [Google Scholar] [CrossRef]
- Krylov, A.S.; Sofronova, S.N.; Gudim, I.A.; Krylova, S.N.; Kumar, R.; Vtyurin, A.N. Manifestation of magnetoelastic interactions in Raman spectra of HoxNd1−xFe3(BO3)4 crystals. J. Adv. Dielectr. 2018, 8, 1850011. [Google Scholar] [CrossRef]
- Leonyuk, N.I.; Leonyuk, L.I. Growth and characterization of RM3(BO3)4 crystals. Prog. Cryst. Growth. Charact. 1995, 31, 179–278. [Google Scholar] [CrossRef]
- Moshkina, E.; Krylov, A.; Sofronova, S.; Gudim, I.; Temerov, V. Crystal Growth and Raman Spectroscopy Study of Sm1−xLaxFe3(BO3)4 Ferroborates. Cryst. Growth Des. 2016, 16, 6915–6921. [Google Scholar] [CrossRef]
- Moshkina, E.; Krylova, S.; Gudim, I.; Molokeev, M.; Temerov, V.; Pavlovskiy, M.S.; Vtyurin, A.; Krylov, A. Gallium Composition-Dependent Structural Phase Transitions in HoFe3−xGax(BO3)4 Solid Solutions: Crystal Growth, Structure, and Raman Spectroscopy Study. Cryst. Growth Des. 2020, 20, 1058–1069. [Google Scholar] [CrossRef]
- Fausti, D.; Nugroho, A.A.; van Loosdrecht, P.H.; Klimin, S.A.; Popova, M.N.; Bezmaternykh, L.N. Raman scattering from phonons and magnons in RFe3(BO3)4. Phys. Rev. B 2006, 74, 024403. [Google Scholar] [CrossRef]
- Ritter, C.; Balaev, A.; Vorotynov, A.; Petrakovskii, G.; Velikanov, D.; Temerov, V.; Gudim, I. Magnetic structure, magnetic interactions and metamagnetism in terbium iron borate TbFe3(BO3)4: A neutron diffraction and magnetization study. J. Phys. Condens. Matter 2007, 19, 196227. [Google Scholar] [CrossRef]
- Popova, E.A.; Volkov, D.V.; Vasiliev, A.N.; Demidov, A.A.; Kolmakova, N.P.; Gudim, I.A.; Bezmaternykh, L.N.; Tristan, N.; Skourski, Y.; Büchner, B.; et al. Magnetization and specific heat of TbFe3(BO3)4: Experiment and crystal-field calculations. Phys. Rev. B 2007, 75, 224413. [Google Scholar] [CrossRef]
- Pavlovskiy, M.S.; Shaykhutdinov, K.A.; Wu, L.S.; Ehlers, G.; Temerov, V.L.; Gudim, I.A.; Shinkorenko, A.S.; Podlesnyak, A. Observation of soft phonon mode in TbFe3(BO3)4 by inelastic neutron scattering. Phys. Rev. B 2018, 97, 054313. [Google Scholar] [CrossRef]
- Volkov, D.V.; Popova, E.A.; Kolmakov, N.P.; Demidov, A.A.; Tristan, N.; Skourski, Y.; Buechner, B.; Gudim, I.A.; Bezmaternykh, L.N. Magnetic properties of TbFe3(BO3)4). JMMM 2007, 316, e717–e720. [Google Scholar] [CrossRef]
- Stanislavchuk, T.N.; Chukalina, E.P.; Bezmaternykh, L.N. Study of magnetic phase transitions and magnetic structures in a number of rare-earth ferroborates using an erbium spectroscopic probe. J. Opt. Technol. 2007, 74, 139–143. [Google Scholar] [CrossRef]
- Gnatchenko, S.L.; Kachur, I.S.; Piryatinskaya, V.G.; Bedarev, V.A.; Pashchenko, M.I. Spectroscopic and magnetooptical investigations of spin-reorientation phase transition in TbFe3(BO3)4. Low Temp. Phys. 2011, 37, 693–698. [Google Scholar] [CrossRef]
- Szaller, D.; Kocsis, V.; Bordács, S.; Fehér, T.; Rõõm, T.; Nagel, U.; Engelkamp, H.; Ohgushi, K.; Kézsmárki, I. Magnetic resonances of multiferroic TbFe3(BO3)4. Phys. Rev. B 2017, 95, 024427. [Google Scholar] [CrossRef]
- Krylova, S.; Gudim, I.; Aleksandrovsky, A.; Vtyurin, A.; Krylov, A. Electronic band structures of NdFe3(BO3)4 and NdGa3(BO3)4 crystals: Ab initio calculations. Ferroelectrics 2021, 575, 11–17. [Google Scholar] [CrossRef]
- Krylova, S.N.; Aleksandrovsky, A.S.; Roginskii, E.M.; Krylov, A.A.; Gudim, I.A.; Vtyurin, A.N. Optical properties of the HoGa3(BO3)4 crystal: Experiment and ab initio calculation. Ferroelectrics 2020, 559, 135–140. [Google Scholar] [CrossRef]
- Klimin, S.A.; Fausti, D.; Meetsma, A.; Bezmaternykh, L.N.; Van Loosdrecht, P.H.M.; Palstra, T.T.M. Evidence for differentiation in the iron-helicoidal chain in GdFe3(BO3)4. Acta Cryst. B 2005, 61, 481–485. [Google Scholar] [CrossRef]
- Krylov, A.S.; Gudim, I.A.; Krylova, S.N.; Krylov, A.A.; Vtyurin, A.N. Structural phase transition in TbFe2.5Ga0.5(BO3)4 single crystal. Ferroelectrics 2020, 559, 128–134. [Google Scholar] [CrossRef]
- Moshkina, E.; Gudim, I.; Temerov, V.; Krylov, A. Temperature-dependent absorption lines observation in Raman spectra of SmFe3(BO3)4 ferroborate. J. Raman Spectrosc. 2018, 49, 1732–1735. [Google Scholar] [CrossRef]
- Popova, M.N.; Stanislavchuk, T.N.; Malkin, B.Z.; Bezmaternykh, L.N. Phase transitions and crystal-field and exchange interactions in TbFe3(BO3)4 as seen via optical spectroscopy. J. Phys. Condens. Matter 2012, 24, 196002. [Google Scholar] [CrossRef]
- Peschanskii, A.V.; Yeremenko, A.V.; Fomin, V.I.; Bezmaternykh, L.N.; Gudim, I.A. Raman scattering under structural and magnetic phase transitions in terbium ferroborate. Low Temp. Phys. 2014, 40, 171–178. [Google Scholar] [CrossRef]
- Adem, U.; Wang, L.; Fausti, D.; Schottenhamel, W.; van Loosdrecht, P.H.M.; Vasiliev, A.; Bezmaternykh, L.N.; Büchner, B.; Hess, C.; Klingeler, R. Magnetodielectric and magnetoelastic coupling in TbFe3(BO3)4. Phys. Rev. B 2010, 82, 064406. [Google Scholar] [CrossRef]
- Bedarev, V.; Pashchenko, M.; Merenkov, D.; Savina, Y.; Pashchenko, V.; Gnatchenko, S.; Bezmaternykh, L.; Temerov, V. The Faraday effect in TbFe3(BO3)4 and TbAl3(BO3)4 borates. J. Magnet. Magnet. Mater. 2014, 362, 150–153. [Google Scholar] [CrossRef]
- Krylov, A.S.; Gudim, I.A.; Nemtsev, I.; Krylova, S.N.; Shabanov, A.V.; Krylov, A.A. Raman study of HoFe3(BO3)4 at simultaneously high pressure and high temperature: p–T phase diagram. J. Raman Spectrosc. 2017, 48, 1406–1410. [Google Scholar] [CrossRef]
- Krylov, A.; Pavlovskiy, M.; Kitaev, Y.; Gudim, I.; Andryshin, N.; Vtyurin, A.; Jiang, Q.; Krylova, S. Phase transitions and p–T phase diagram of the multiferroic TbFe3(BO3)4 crystal. J. Raman Spectrosc. 2022. [Google Scholar] [CrossRef]
- Datchi, F.; Dewaele, A.; Loubeyre, P.; Letoullec, R.; Godec, Y.L.; Canny, B. Optical pressure sensors for high-pressure–high-temperature studies in a diamond anvil cell. High Press. Res. 2007, 27, 447–463. [Google Scholar] [CrossRef]
- Rashchenko, S.V.; Kurnosov, A.; Dubrovinsky, L.; Litasov, K.D. Revised calibration of the Sm:SrB4O7 pressure sensor using the Sm-doped yttrium-aluminum garnet primary pressure scale. J. Appl. Phys. 2015, 117, 145902. [Google Scholar] [CrossRef]
- Orobengoa, D.; Capillas, C.; Aroyo, M.I.; Perez-Mato, J.M. AMPLIMODES: Symmetry-mode analysis on the Bilbao Crystallographic Server. J. Appl. Crystallogr. 2009, 42, 820–833. [Google Scholar] [CrossRef]
- Perez-Mato, J.M.; Orobengoa, D.; Aroyo, M.I. Mode crystallography of distorted structures. Acta Crystallogr. Sect. A 2010, 66, 558–590. [Google Scholar] [CrossRef]
- Choi, Y.; Kim, K.; Lim, S.Y.; Kim, J.; Park, J.M.; Kim, J.H.; Lee, Z.; Cheong, H. Complete determination of the crystallographic orientation of ReX2 (X = S, Se) by polarized Raman spectroscopy. Nanoscale Horiz. 2020, 5, 308–315. [Google Scholar] [CrossRef]
- Peticolas, W.L.; Nafie, L.; Stein, P.; Fanconi, B. Quantum Theory of the Intensities of Molecular Vibrational Spectra. J. Chem. Phys. 1970, 52, 1576–1584. [Google Scholar] [CrossRef]
- Chang, Y.; He, S.; Sun, M.; Xiao, A.; Zhao, J.; Ma, L.; Qiu, W. Angle-Resolved Intensity of In-Axis/Off-Axis Polarized Micro-Raman Spectroscopy for Monocrystalline Silicon. J. Spectrosc. 2021, 2860007. [Google Scholar] [CrossRef]
- Aroyo, M.I. (Ed.) International Tables for Crystollography. Vol. A. Space Group Symmetry, 6th ed.; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar]
- Litvin, D.B. Magnetic space-group types. Acta Crystallogr. Sect. A 2001, 57, 729–730. [Google Scholar] [CrossRef]
- Wills, A. Magnetic structures and their determination using group theory. J. Phys. IV France 2001, 11, Pr9-133–Pr9-158. [Google Scholar] [CrossRef]
- Litvin, D. Magnetic Group Tables: 1-, 2-, and 3-Dimensional Magnetic Subperiodic Groups and Magnetic Space Groups; International Union of Crystallography: Chester, UK, 2013. [Google Scholar] [CrossRef]
- Cracknell, A.P. Space-Group Selection Rules for Magnetic Crystals. Prog. Theoret. Phys. 1967, 38, 1252–1269. [Google Scholar] [CrossRef][Green Version]
- Shubnikov, A.V.; Belov, N. Colored Symmetry, 6th ed.; Pergamon Press: Oxford, UK, 1964. [Google Scholar]
- Krylov, A.; Vtyurin, A.; Gudim, I.; Nemtsev, I.; Krylova, S. Phase diagram and soft modes behaviour TbFe3−XGaX(BO3)4 solid solutions with huntite structures. Opt. Spectrosc. 2022, 130, 84–91. [Google Scholar]
- Salje, E.K.; Bismayer, U. Hard mode spectroscopy: The concept and applications. Phase Transit. 1997, 63, 1–75. [Google Scholar] [CrossRef]
- Bismayer, U. Hard Mode Spectroscopy of Phase Transitions. Rev. Mineral. Geochem. 2000, 39, 265–283. [Google Scholar] [CrossRef]
- Bismayer, U. Hard mode Raman spectroscopy and its application to ferroelastic and ferroelectric phase transitions. Phase Transit. 1990, 27, 211–267. [Google Scholar] [CrossRef]
- Salje, E.K.H. Hard mode Spectroscopy: Experimental studies of structural phase transitions. Phase Transit. 1992, 37, 83–110. [Google Scholar] [CrossRef]
- Piermarini, G.J.; Block, S.; Barnett, J.D.; Forman, R.A. Calibration of the pressure dependence of the R1 ruby fluorescence line to 195 kbar. J. Appl. Phys. 1975, 46, 2774–2780. [Google Scholar] [CrossRef]
- Ragan, D.D.; Gustavsen, R.; Schiferl, D. Calibration of the ruby R1 and R2 fluorescence shifts as a function of temperature from 0 to 600 K. J. Appl. Phys. 1992, 72, 5539–5544. [Google Scholar] [CrossRef]


| E(x) | E(y) | |||||||
|---|---|---|---|---|---|---|---|---|
| a | 0 | 0 | c | 0 | 0 | 0 | −c | −d |
| 0 | a | 0 | 0 | −c | d | −c | 0 | 0 |
| 0 | 0 | b | 0 | d | 0 | −d | 0 | 0 |
| Raman Shift, cm | HH | HV | Irred. Repres. |
|---|---|---|---|
| 93 | 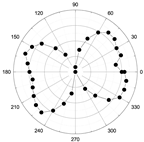 | 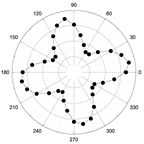 | E |
| 181 | 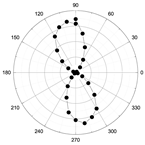 | 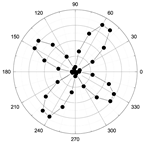 | A |
| 199 |  |  | A |
| 448 | 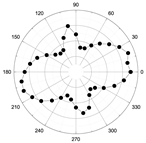 |  | E |
| 482 |  | 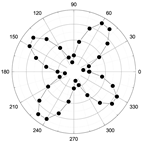 | A |
| 736 | 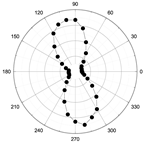 | 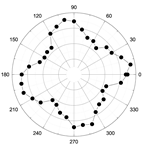 | E |
| 961 | 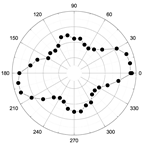 |  | E |
| 991 | 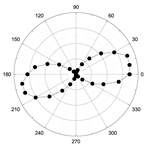 | 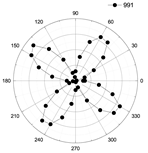 | A |
| 1237 | 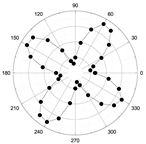 | 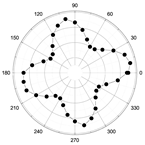 | E |
| 1413 | 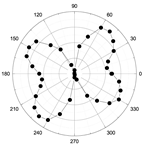 |  | E |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krylov, A.; Krylova, S.; Gudim, I.; Kitaev, Y.; Golovkina, E.; Zhang, H.; Vtyurin, A. Pressure–Temperature Phase Diagram of Multiferroic TbFe2.46Ga0.54(BO3)4. Magnetochemistry 2022, 8, 59. https://doi.org/10.3390/magnetochemistry8060059
Krylov A, Krylova S, Gudim I, Kitaev Y, Golovkina E, Zhang H, Vtyurin A. Pressure–Temperature Phase Diagram of Multiferroic TbFe2.46Ga0.54(BO3)4. Magnetochemistry. 2022; 8(6):59. https://doi.org/10.3390/magnetochemistry8060059
Chicago/Turabian StyleKrylov, Alexander, Svetlana Krylova, Irina Gudim, Yuri Kitaev, Elena Golovkina, Haibo Zhang, and Alexander Vtyurin. 2022. "Pressure–Temperature Phase Diagram of Multiferroic TbFe2.46Ga0.54(BO3)4" Magnetochemistry 8, no. 6: 59. https://doi.org/10.3390/magnetochemistry8060059
APA StyleKrylov, A., Krylova, S., Gudim, I., Kitaev, Y., Golovkina, E., Zhang, H., & Vtyurin, A. (2022). Pressure–Temperature Phase Diagram of Multiferroic TbFe2.46Ga0.54(BO3)4. Magnetochemistry, 8(6), 59. https://doi.org/10.3390/magnetochemistry8060059










