Solid-State Heating Using the Multicaloric Effect in Multiferroics
Abstract
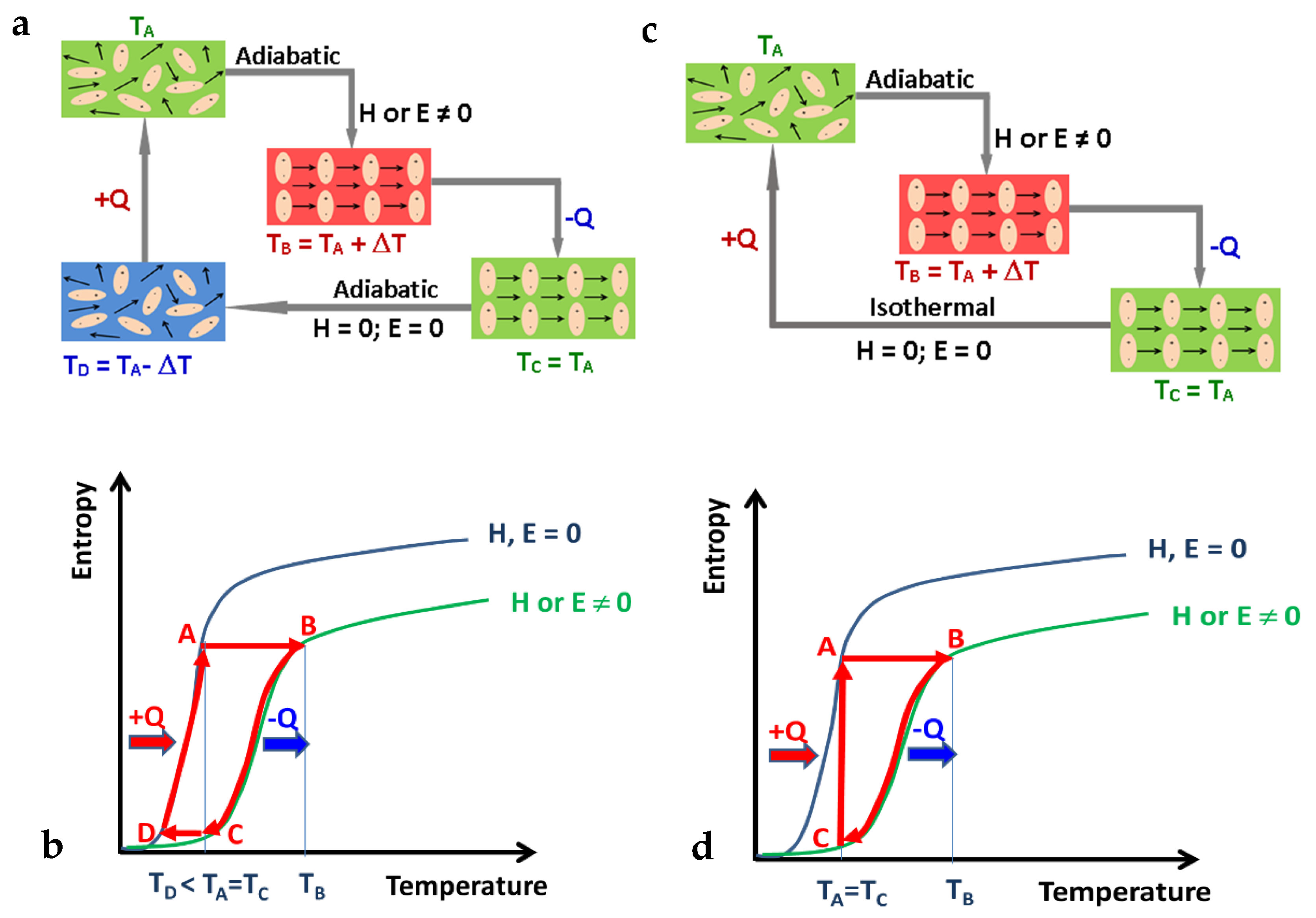
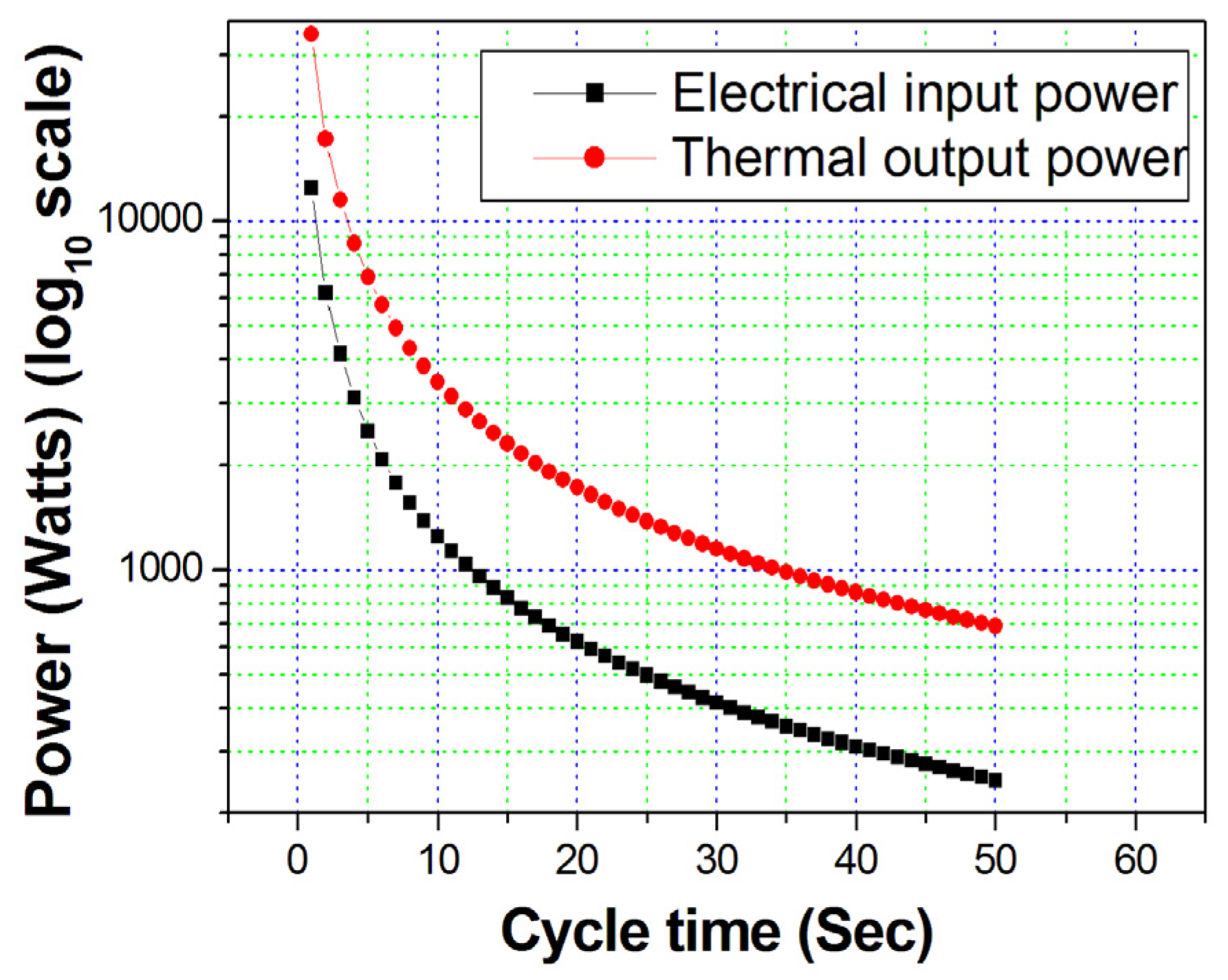
What is the maximum predicted temperature change in the multicaloric effect?
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Mañosa, L.; González-Alonso, D.; Planes, A.; Bonnot, E.; Barrio, M.; Tamarit, J.L.; Aksoy, S.; Acet, M. Giant solid-state baro-caloric effect in the Ni-Mn-In magnetic shape-memory alloy. Nat. Mater. 2010, 9, 478–481. [Google Scholar] [CrossRef]
- Bonnot, E.; Romero, R.; Mañosa, L.; Vives, E.; Planes, A. Elastocaloric Effect Associated with the Martensitic Transition in Shape-Memory Alloys. Phys. Rev. Lett. 2008, 100, 125901. [Google Scholar] [CrossRef]
- Gschneidner, K.A., Jr.; Pecharsky, V.K.; Tsokol, A.O. Recent developments in magnetocaloric materials. Rep. Prog. Phys. 2005, 68, 1479–1539. [Google Scholar] [CrossRef]
- Scott, J. Electrocaloric Materials. Annu. Rev. Mater. Res. 2011, 41, 229–240. [Google Scholar] [CrossRef]
- Castan, T.; Planes, A.; Saxena, A. Thermodynamics of ferrotoroidic materials: Toroidocaloric effect. Phys. Rev. B 2012, 85, 144429. [Google Scholar] [CrossRef]
- Reis, M.S. Oscillating adiabatic temperature change of diamagnetic materials. Solid State Commun. 2012, 152, 921–923. [Google Scholar] [CrossRef]
- Bartlett, J.; Hardy, G.; Hepburn, I.D.; Brockley-Blatt, C.; Coker, P.; Crofts, E.; Winter, B.; Milward, S.; Stafford-Allen, R.; Brownhill, M.; et al. Improved performance of an engineering model cryogen free double adiabatic de-magnetization refrigerator. Cryogenics 2010, 50, 582–590. [Google Scholar] [CrossRef]
- Shakouri, A.; Zhang, Y. On-chip solid-state cooling for integrated circuits using thin-film microrefrigerators. IEEE Trans. Components Packag. Technol. 2005, 28, 65–69. [Google Scholar] [CrossRef]
- Pecharsky, V.K.; Gschneidner, K.A., Jr. Giant magnetocaloric effect in Gd5(Si2Ge2). Phys. Rev. Lett. 1997, 78, 4494–4497. [Google Scholar] [CrossRef]
- Mischenko, A.S.; Zhang, Q.; Scott, J.F.; Whatmore, R.W.; Mathur, N.D. Gian Electrocaloric Effect in Thin-Film PbZr0.95Ti0.05O3. Science 2006, 311, 1270–1271. [Google Scholar] [CrossRef]
- Fiebig, M. Revival of the magnetoelectric effect. J. Phys. D Appl. Phys. 2005, 38, R123–R152. [Google Scholar] [CrossRef]
- Gao, J.; Shen, L.; Wang, Y.; Gray, D.; Li, J.; Viehland, D. Enhanced sensitivity to direct current magnetic field changes in Metglas/Pb(Mg1/3Nb2/3)O3–PbTiO3 laminates. J. Appl. Phys. 2011, 109, 074507. [Google Scholar] [CrossRef]
- Vopsaroiu, M.; Cain, M.; Sreenivasulu, G.; Srinivasan, G.; Balbashov, A. Multiferroic composite for combined detection of static and alternating magnetic fields. Mater. Lett. 2012, 66, 282–284. [Google Scholar] [CrossRef]
- Gajek, M.; Bibes, M.; Fusil, S.; Bouzehouane, K.; Fontcuberta, J.; Barthélémy, A.; Fert, A. Tunnel junctions with multiferroic barriers. Nat. Mater. 2007, 6, 296–302. [Google Scholar] [CrossRef]
- Bibes, M.; Barthélémy, A. Multiferroics: Towards a magnetoelectric memory. Nat. Mater. 2008, 7, 425–426. [Google Scholar] [CrossRef] [PubMed]
- Scott, J.F. Data storage: Multiferroic memories. Nat. Mater. 2007, 6, 256–257. [Google Scholar] [CrossRef] [PubMed]
- Vopsaroiu, M.; Blackburn, J.; Muniz-Piniella, A.; Cain, M.G. Multiferroic magnetic recording read head technology for 1 Tb/in2 and beyond. J. Appl. Phys. 2008, 103, 07F506. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Z.; Deng, C.; Ma, J.; Lin, Y.; Nan, C.W. Demonstration of magnetoelectric read head of multiferroic heterostructures. Appl. Phys. Lett. 2008, 92, 152510. [Google Scholar] [CrossRef]
- Dong, S.; Li, J.F.; Viehland, D. Voltage gain effect in a ring-type magnetoelectric laminate. Appl. Phys. Lett. 2004, 84, 4188. [Google Scholar] [CrossRef]
- Srivastava, V.; Song, Y.; Bhatti, K.; James, R.D. The direct conversion of heat to electricity using multiferroic alloys. Adv. Energy Mater. 2011, 1, 97–104. [Google Scholar] [CrossRef]
- Vopson, M.M. Fundamentals of Multiferroic Materials and Their Possible Applications. Crit. Rev. Solid State Mater. Sci. 2015, 40, 223–250. [Google Scholar] [CrossRef]
- Vopson, M.M. The multicaloric effect in multiferroic materials. Solid State Commun. 2012, 152, 2067–2070. [Google Scholar] [CrossRef]
- Vopson, M.M. Theory of giant-caloric effects in multiferroic materials. J. Phys. D Appl. Phys. 2013, 46, 345304. [Google Scholar] [CrossRef]
- Meng, H.; Li, B.; Ren, W.; Zhang, Z. Coupled caloric effects in multiferroics. Phys. Lett. A 2013, 377, 567–571. [Google Scholar] [CrossRef]
- Alpay, S.P.; Mantese, J.; Trolier-McKinstry, S.; Zhang, Q.; Whatmore, R.W. Next-generation electrocaloric and pyroelectric materials for solid-state electrothermal energy interconversion. Mrs Bull. 2014, 39, 1099–1111. [Google Scholar] [CrossRef]
- Vopson, M.M.; Zhou, D.; Caruntu, G. Multicaloric effect in bi-layer multiferroic composites. Appl. Phys. Lett. 2015, 107, 182905. [Google Scholar] [CrossRef]
- Planes, A.; Castan, T.; Saxena, A. Thermodynamics of multicaloric effects in multiferroics. Philos. Mag. 2014, 94, 1893–1908. [Google Scholar] [CrossRef]
- Liu, Y.; Wei, J.; Janolin, P.E.; Infante, I.C.; Kreisel, J.; Lou, X.; Dkhil, B. Prediction of giant elastocaloric strength and stress-mediated electrocaloric effect in BaTiO3 single crystals. Phys. Rev. B 2014, 90, 104107. [Google Scholar] [CrossRef]
- Patel, S.; Chauhan, A.; Vaish, R. Multiple caloric effects in (Ba0.865Ca0.135Zr0.1089Ti0.8811Fe0.01)O3 ferroelectric ceramic. Appl. Phys. Lett. 2015, 107, 042902. [Google Scholar] [CrossRef]
- Vopson, M.M. The induced magnetic and electric fields’ paradox leading to multicaloric effects in multiferroics. Solid State Commun. 2016, 231, 14–16. [Google Scholar] [CrossRef]
- Zhao, Y.-Q.; Cao, H.-X. Multicaloric effect in multiferroic EuTiO3 thin films. J. Mater. Sci. 2020, 55, 5705–5714. [Google Scholar] [CrossRef]
- Vopson, M.M. Multicaloric effect: An outlook. Phys. B Condens. Matter 2017, 513, 103–105. [Google Scholar] [CrossRef][Green Version]
- Castillo-Villa, P.O.; Soto-Parra, D.E.; Matutes-Aquino, J.A.; Ochoa-Gamboa, R.A.; Planes, A.; Mañosa, L.; González-Alonso, D.; Stipcich, M.; Romero, R.; Ríos-Jara, D.; et al. Caloric effects induced by magnetic and mechanical fields in a Ni 50 Mn 25−x Ga 25 Co x magnetic shape memory alloy. Phys. Rev. B 2011, 83, 174109. [Google Scholar] [CrossRef]
- Castillo-Villa, P.O.; Mañosa, L.; Planes, A.; Soto-Parra, D.E.; Sánchez-Llamazares, J.L.; Flores-Zúñiga, H.; Frontera, C. Elasto-caloric and magnetocaloric effects in Ni-Mn-Sn(Cu) shape-memory alloy. J. Appl. Phys. 2013, 113, 053506. [Google Scholar] [CrossRef]
- Fahler, S.; Roßler, U.K.; Kastner, O.; Eckert, J.; Eggeler, G.; Emmerich, H.; Entel, P.; Muller, S.; Quandt, E.; Albe, K. Caloric Effects in Ferroic Materials: New Concepts for Cooling. Adv. Eng. Mater. 2012, 14, 10–19. [Google Scholar]
- Fodouop, F.K.; Fouokeng, G.C.; Tsokeng, A.T.; Tchoffo, M.; Fai, L.C. Metamagnetoelectric transitions-enhanced multicaloric effect in multiferroics A2Cu2Mo3O12 (A = Rb and Cs) quantum spin chain. Phys. E Low-Dimens. Syst. Nanostruct. 2021, 128, 114616. [Google Scholar] [CrossRef]
- Vopson, M.M.; Fetisov, Y.K.; Caruntu, G.; Srinivasan, G. Measurement Techniques of the Magneto-Electric Coupling in Mul-tiferroics. Materials 2017, 10, 963. [Google Scholar] [CrossRef] [PubMed]
- Neese, B.; Chu, B.; Lu, S.-G.; Wang, Y.; Furman, E.; Zhang, Q.M. Large Electrocaloric Effect in Ferroelectric Polymers Near Room Temperature. Science 2008, 321, 821–823. [Google Scholar] [CrossRef] [PubMed]
- Shen, B.G.; Sun, J.R.; Hu, F.X.; Zhang, H.W.; Cheng, Z.H. Recent Progress in Exploring Magnetocaloric Materials. Adv. Mater. 2009, 21, 4545–4564. [Google Scholar] [CrossRef]
- Nair, B.; Usui, T.; Crossley, S.; Kurdi, S.; Guzmán-Verri, G.G.; Moya, X.; Hirose, S.; Mathur, N.D. Large electrocaloric effects in oxide multi-layer capacitors over a wide temperature range. Nature 2019, 575, 468–472. [Google Scholar] [CrossRef]
- Bartlett, J.; Hardy, G.; Hepburn, I. Performance of a fast response miniature Adiabatic Demagnetisation Refrigerator using a single crystal tungsten magnetoresistive heat switch. Cryogenics 2015, 72, 111–121. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vopson, M.M.; Fetisov, Y.K.; Hepburn, I. Solid-State Heating Using the Multicaloric Effect in Multiferroics. Magnetochemistry 2021, 7, 154. https://doi.org/10.3390/magnetochemistry7120154
Vopson MM, Fetisov YK, Hepburn I. Solid-State Heating Using the Multicaloric Effect in Multiferroics. Magnetochemistry. 2021; 7(12):154. https://doi.org/10.3390/magnetochemistry7120154
Chicago/Turabian StyleVopson, Melvin M., Yuri K. Fetisov, and Ian Hepburn. 2021. "Solid-State Heating Using the Multicaloric Effect in Multiferroics" Magnetochemistry 7, no. 12: 154. https://doi.org/10.3390/magnetochemistry7120154
APA StyleVopson, M. M., Fetisov, Y. K., & Hepburn, I. (2021). Solid-State Heating Using the Multicaloric Effect in Multiferroics. Magnetochemistry, 7(12), 154. https://doi.org/10.3390/magnetochemistry7120154






