The Role of Magnetic Dipole—Dipole Coupling in Quantum Single-Molecule Toroics
Abstract
:1. Introduction
2. Quantum Heisenberg Triangle with Strong On-Site Magnetic Anisotropy
2.1. The Semi-Classical Ising Picture
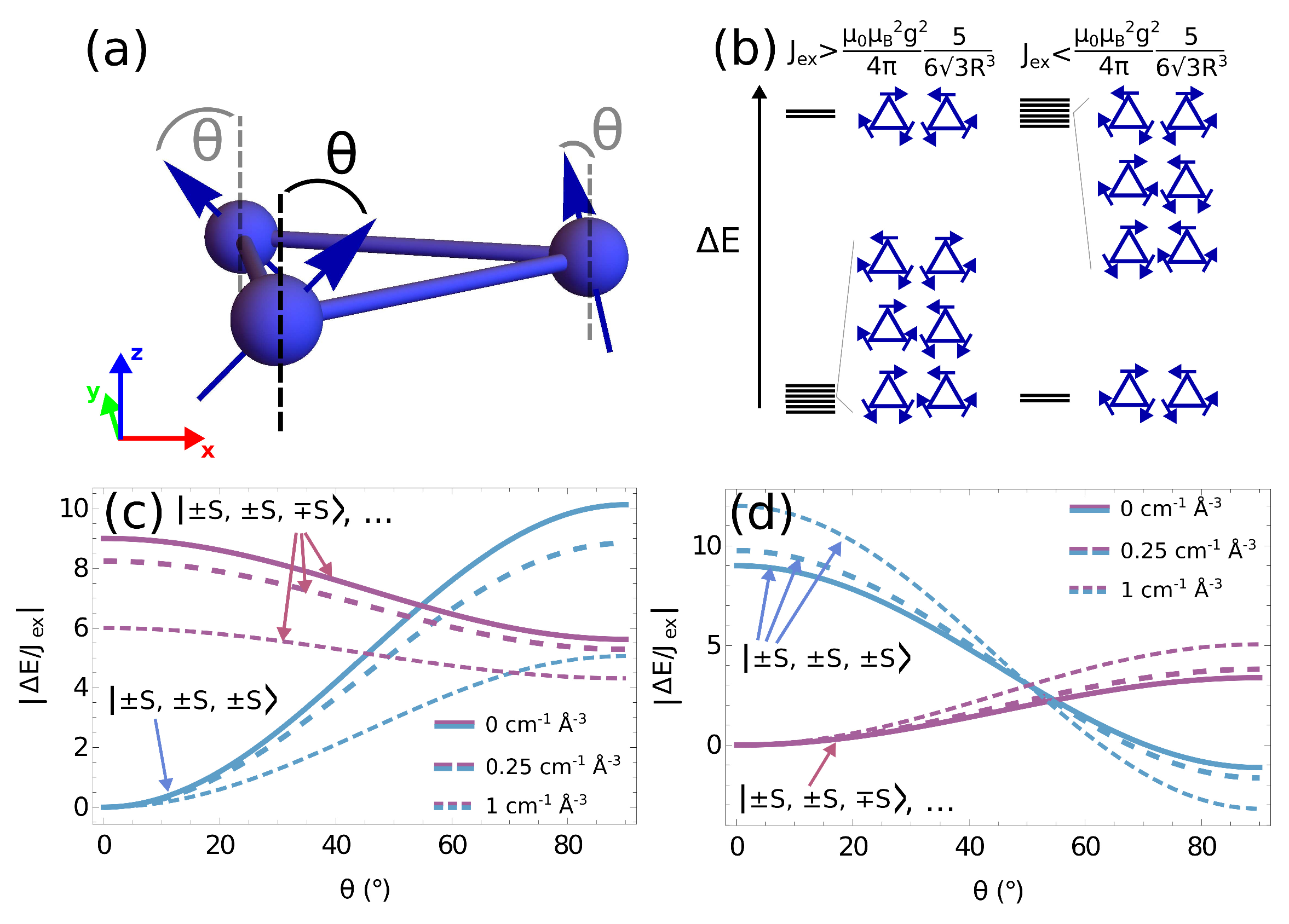
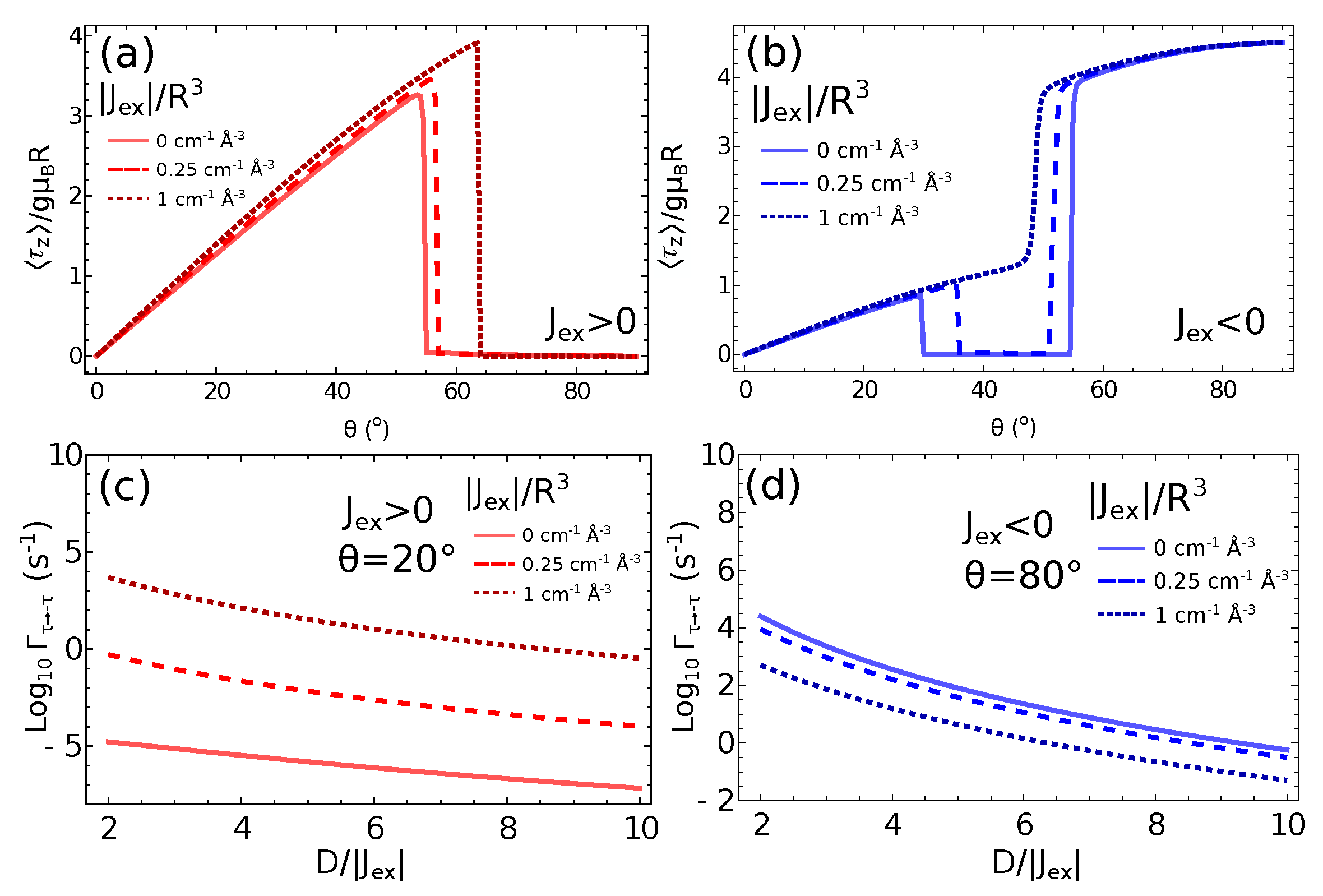
2.2. The Role of Magnetic Dipole–Dipole Coupling in Quantum SMTs
2.3. Tunnelling of the Ground-State Toroidal Moment in a Non-Kramers System
3. Spin Frustration in Molecular Triangles with Vanishing Magnetic Anisotropy
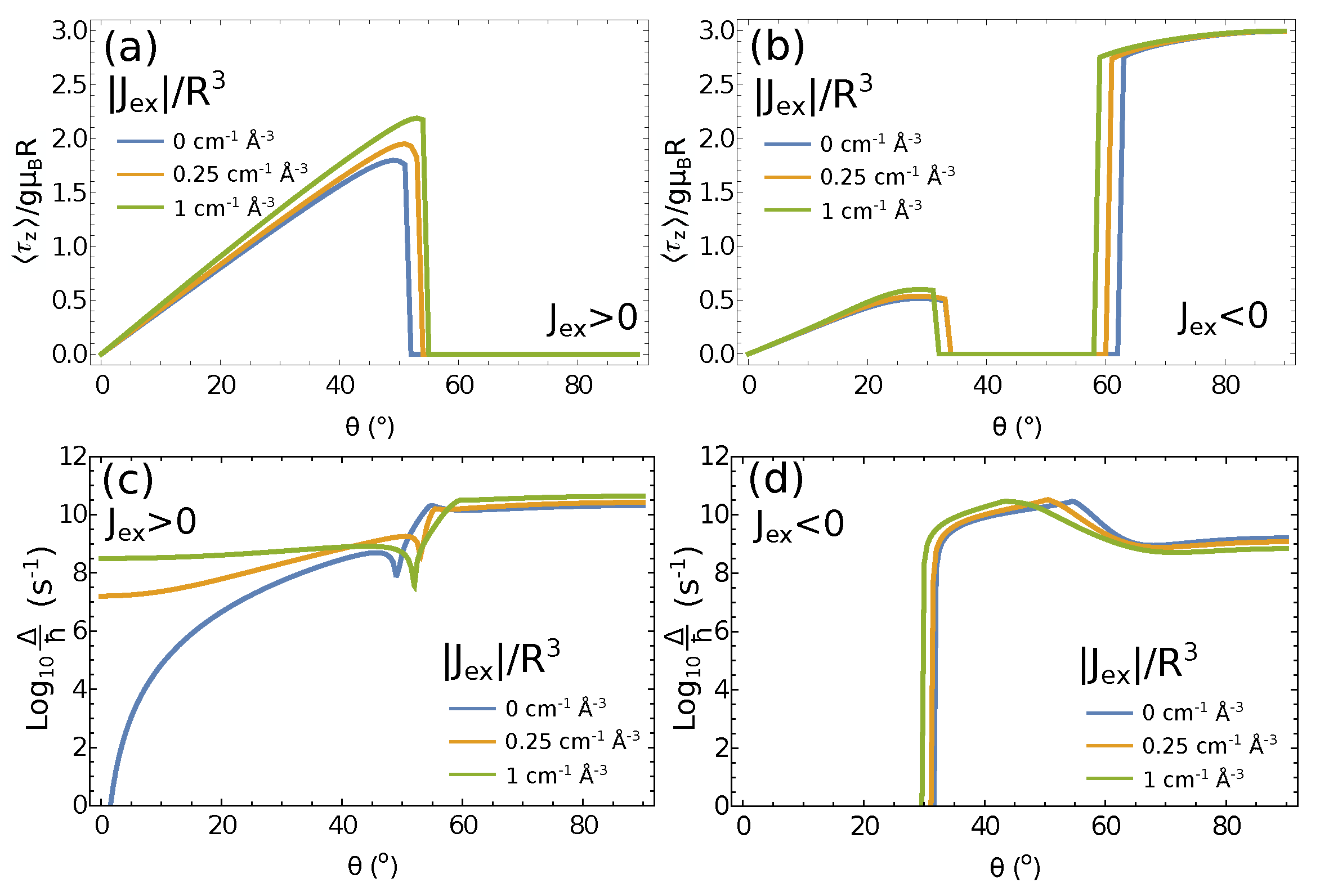
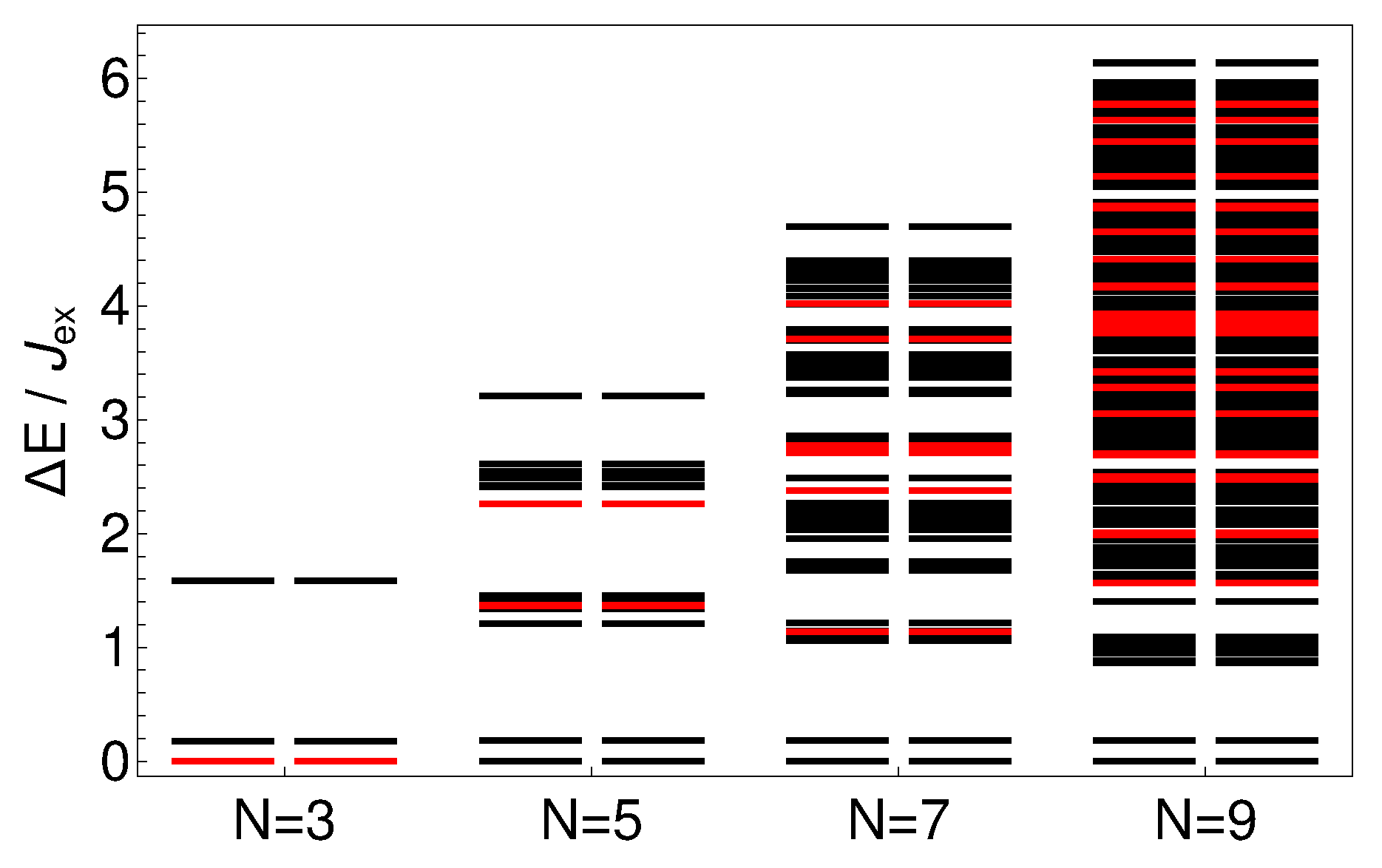
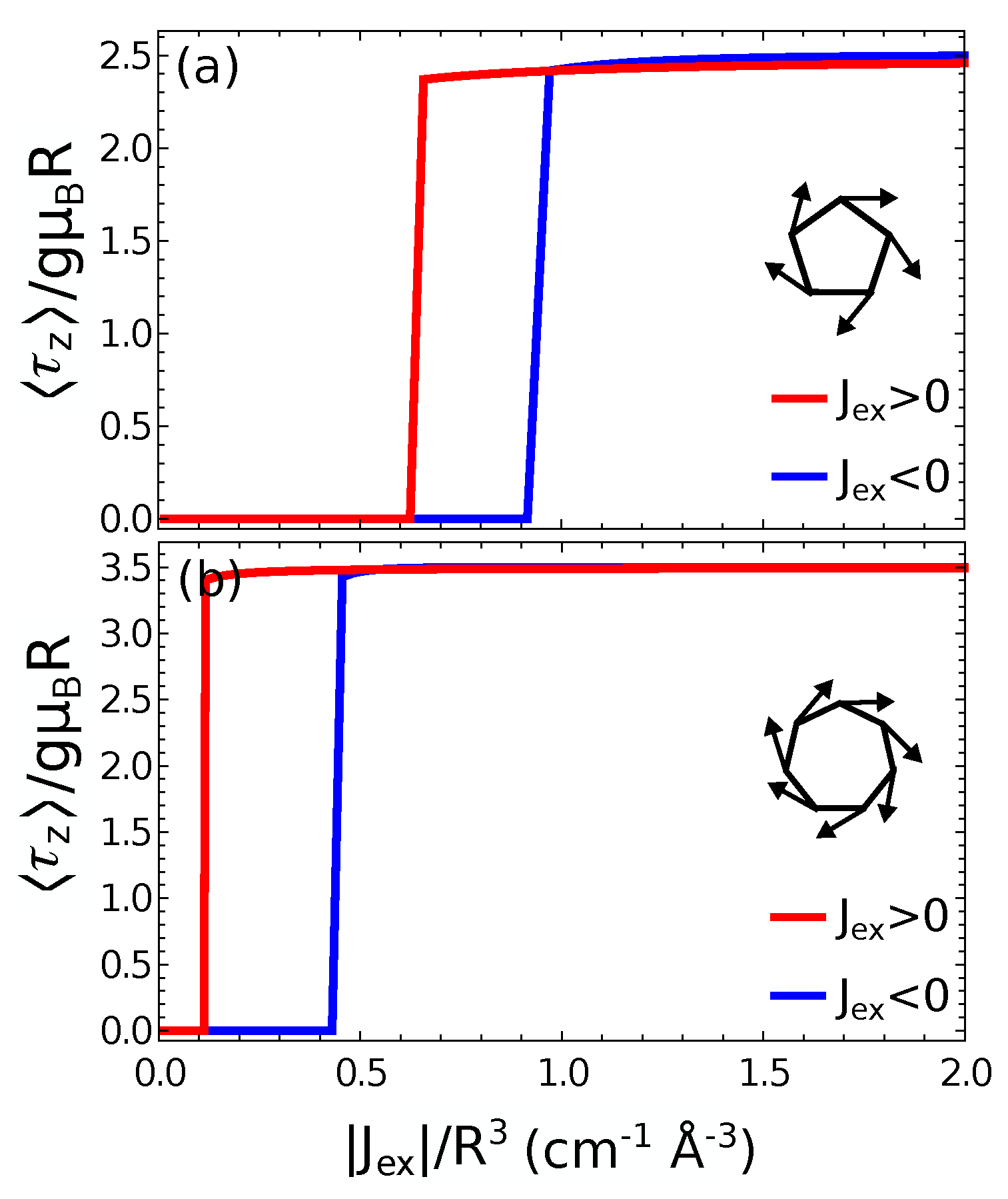
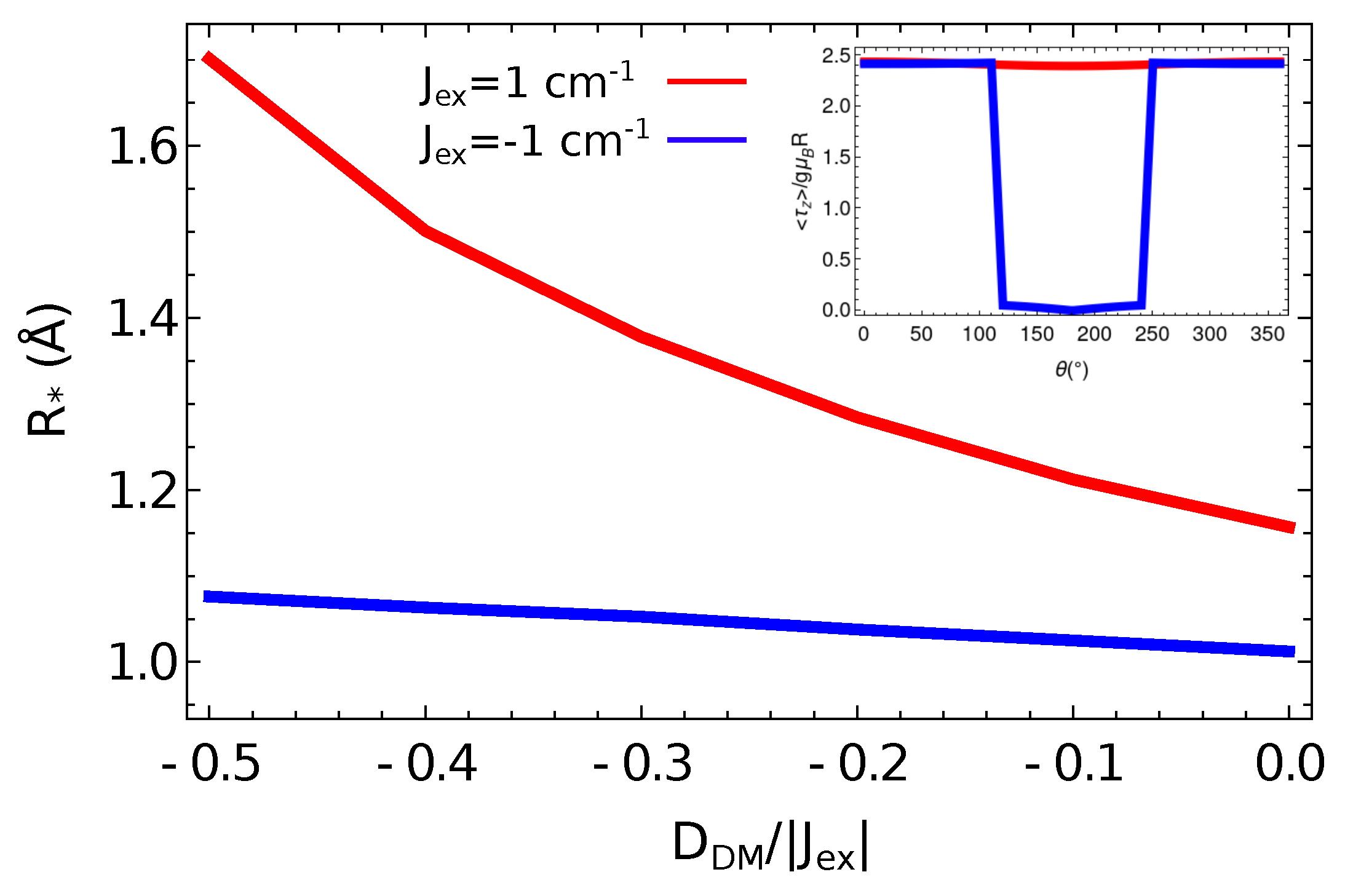
4. Magnetic Dipole–Dipole Interactions in Extended Heisenberg Rings
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SMM | Single-molecule magnet |
| SMT | Single-molecule toroic |
References
- Zel’Dovich, I.B. Electromagnetic interaction with parity violation. Sov. Phys. JETP 1958, 6, 1184–1186. [Google Scholar]
- Wood, C.; Bennett, S.; Cho, D.; Masterson, B.; Roberts, J.; Tanner, C.; Wieman, C.E. Measurement of parity nonconservation and an anapole moment in cesium. Science 1997, 275, 1759–1763. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Marinov, K.; Boardman, A.; Fedotov, V.; Zheludev, N. Toroidal metamaterial. New J. Phys. 2007, 9, 324. [Google Scholar] [CrossRef]
- Wätzel, J.; Berakdar, J. Open-Circuit Ultrafast Generation of Nanoscopic Toroidal Moments: The Swift Phase Generator. Adv. Quantum Technol. 2019, 2, 1970011. [Google Scholar] [CrossRef]
- Ho, C.M.; Scherrer, R.J. Anapole dark matter. Phys. Lett. B 2013, 722, 341–346. [Google Scholar] [CrossRef] [Green Version]
- Lewis, R.R. Anapole moment of a diatomic polar molecule. Phys. Rev. A 1994, 49, 3376. [Google Scholar] [CrossRef] [PubMed]
- Ceulemans, A.; Chibotaru, L.; Fowler, P. Molecular anapole moments. Phys. Rev. Lett. 1998, 80, 1861. [Google Scholar] [CrossRef] [Green Version]
- Pelloni, S.; Faglioni, F.; Soncini, A.; Ligabue, A.; Lazzeretti, P. Magnetic response of dithiin molecules: Is there anti-aromaticity in nature? Chem. Phys. Lett. 2003, 375, 583–590. [Google Scholar] [CrossRef]
- Faglioni, F.; Ligabue, A.; Pelloni, S.; Soncini, A.; Lazzeretti, P. Molecular response to a time-independent non-uniform magnetic-field. Chem. Phys. 2004, 304, 289–299. [Google Scholar] [CrossRef]
- Borschevsky, A.; Iliaš, M.; Dzuba, V.; Flambaum, V.; Schwerdtfeger, P. Relativistic study of nuclear-anapole-moment effects in diatomic molecules. Phys. Rev. A 2013, 88, 022125. [Google Scholar] [CrossRef] [Green Version]
- Pelloni, S.; Faglioni, F.; Zanasi, R.; Lazzeretti, P. Topology of magnetic-field-induced current-density field in diatropic monocyclic molecules. Phys. Rev. A 2006, 74, 012506. [Google Scholar] [CrossRef] [Green Version]
- Carion, R.; Champagne, B.; Monaco, G.; Zanasi, R.; Pelloni, S.; Lazzeretti, P. Ring current model and anisotropic magnetic response of cyclopropane. J. Chem. Theory Comput. 2010, 6, 2002–2018. [Google Scholar] [CrossRef] [PubMed]
- Monaco, G.; Summa, F.F.; Zanasi, R. Program Package for the Calculation of Origin-Independent Electron Current Density and Derived Magnetic Properties in Molecular Systems. J. Chem. Inf. Model. 2020, 61, 270–283. [Google Scholar] [CrossRef] [PubMed]
- Summa, F.F.; Monaco, G.; Lazzeretti, P.; Zanasi, R. Assessment of the performance of DFT functionals in the fulfillment of off-diagonal hypervirial relationships. Phys. Chem. Chem. Phys. 2021, 23, 15268–15274. [Google Scholar] [CrossRef] [PubMed]
- Pelloni, S.; Lazzeretti, P.; Monaco, G.; Zanasi, R. Magnetic-field induced electronic anapoles in small molecules. Rend. Lincei 2011, 22, 105–112. [Google Scholar] [CrossRef]
- Summa, F.F.; Monaco, G.; Zanasi, R.; Lazzeretti, P. Dynamic Toroidisability as Ubiquitous Property of Atoms and Molecules in Optical Electric Fields. J. Chem. Phys. 2022, 156, 054106. [Google Scholar] [CrossRef]
- Dubovik, V.; Tugushev, V. Toroid moments in electrodynamics and solid-state physics. Phys. Rep. 1990, 187, 145–202. [Google Scholar] [CrossRef]
- Spaldin, N.A.; Fiebig, M.; Mostovoy, M. The toroidal moment in condensed-matter physics and its relation to the magnetoelectric effect. J. Phys. Condens. Matter 2008, 20, 434203. [Google Scholar] [CrossRef] [Green Version]
- Soncini, A.; Chibotaru, L.F. Toroidal magnetic states in molecular wheels: Interplay between isotropic exchange interactions and local magnetic anisotropy. Phys. Rev. B 2008, 77, 220406. [Google Scholar] [CrossRef] [Green Version]
- Tang, J.; Hewitt, I.; Madhu, N.; Chastanet, G.; Wernsdorfer, W.; Anson, C.E.; Benelli, C.; Sessoli, R.; Powell, A.K. Dysprosium triangles showing single-molecule magnet behavior of thermally excited spin states. Angew. Chem. 2006, 118, 1761–1765. [Google Scholar] [CrossRef]
- Chibotaru, L.F.; Ungur, L.; Soncini, A. The origin of nonmagnetic Kramers doublets in the ground state of dysprosium triangles: Evidence for a toroidal magnetic moment. Angew. Chem. 2008, 120, 4194–4197. [Google Scholar] [CrossRef]
- Wang, Y.X.; Shi, W.; Li, H.; Song, Y.; Fang, L.; Lan, Y.; Powell, A.K.; Wernsdorfer, W.; Ungur, L.; Chibotaru, L.F.; et al. A single-molecule magnet assembly exhibiting a dielectric transition at 470 K. Chem. Sci. 2012, 3, 3366–3370. [Google Scholar] [CrossRef]
- Xue, S.; Chen, X.H.; Zhao, L.; Guo, Y.N.; Tang, J. Two bulky-decorated triangular dysprosium aggregates conserving vortex-spin structure. Inorg. Chem. 2012, 51, 13264–13270. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Z.H.; Ma, X.F.; Wang, H.L.; Zou, H.H.; Mo, K.Q.; Zhang, Y.Q.; Yang, Q.Z.; Li, B.; Liang, F.P. A triangular Dy 3 single-molecule toroic with high inversion energy barrier: Magnetic properties and multiple-step assembly mechanism. Inorg. Chem. Front. 2018, 5, 3155–3162. [Google Scholar] [CrossRef]
- Langley, S.K.; Vignesh, K.R.; Gupta, T.; Gartshore, C.J.; Rajaraman, G.; Forsyth, C.M.; Murray, K.S. New examples of triangular terbium (III) and holmium (III) and hexagonal dysprosium (III) single molecule toroics. Dalton Trans. 2019, 48, 15657–15667. [Google Scholar] [CrossRef]
- Das, C.; Vaidya, S.; Gupta, T.; Frost, J.M.; Righi, M.; Brechin, E.K.; Affronte, M.; Rajaraman, G.; Shanmugam, M. Single-molecule magnetism, enhanced magnetocaloric effect, and toroidal magnetic moments in a family of Ln4 squares. Chemistry 2015, 21, 15639–15650. [Google Scholar] [CrossRef] [Green Version]
- Gusev, A.; Herchel, R.; Nemec, I.; Shul’gin, V.; Eremenko, I.L.; Lyssenko, K.; Linert, W.; Travnicek, Z. Tetranuclear lanthanide complexes containing a hydrazone-type ligand. Dysprosium [2 × 2] gridlike single-molecule magnet and toroic. Inorg. Chem. 2016, 55, 12470–12476. [Google Scholar] [CrossRef]
- Fernandez Garcia, G.; Guettas, D.; Montigaud, V.; Larini, P.; Sessoli, R.; Totti, F.; Cador, O.; Pilet, G.; Le Guennic, B. A Dy4 Cubane: A New Member in the Single-Molecule Toroics Family. Angew. Chem. 2018, 130, 17335–17339. [Google Scholar] [CrossRef]
- Ungur, L.; Langley, S.K.; Hooper, T.N.; Moubaraki, B.; Brechin, E.K.; Murray, K.S.; Chibotaru, L.F. Net toroidal magnetic moment in the ground state of a {Dy6}-triethanolamine ring. J. Am. Chem. Soc. 2012, 134, 18554–18557. [Google Scholar] [CrossRef] [Green Version]
- Holmberg, R.J.; Kuo, C.J.; Gabidullin, B.; Wang, C.W.; Clérac, R.; Murugesu, M.; Lin, P.H. A propeller-shaped μ 4-carbonate hexanuclear dysprosium complex with a high energetic barrier to magnetisation relaxation. Dalton Trans. 2016, 45, 16769–16773. [Google Scholar] [CrossRef]
- Lu, J.; Montigaud, V.; Cador, O.; Wu, J.; Zhao, L.; Li, X.L.; Guo, M.; Le Guennic, B.; Tang, J. Lanthanide (III) hexanuclear circular helicates: Slow magnetic relaxation, toroidal arrangement of magnetic moments, and magnetocaloric effects. Inorg. Chem. 2019, 58, 11903–11911. [Google Scholar] [CrossRef] [PubMed]
- Novitchi, G.; Pilet, G.; Ungur, L.; Moshchalkov, V.V.; Wernsdorfer, W.; Chibotaru, L.F.; Luneau, D.; Powell, A.K. Heterometallic Cu II/Dy III 1D chiral polymers: Chirogenesis and exchange coupling of toroidal moments in trinuclear Dy 3 single molecule magnets. Chem. Sci. 2012, 3, 1169–1176. [Google Scholar] [CrossRef] [Green Version]
- Vignesh, K.R.; Soncini, A.; Langley, S.K.; Wernsdorfer, W.; Murray, K.S.; Rajaraman, G. Ferrotoroidic ground state in a heterometallic {Cr III Dy III 6} complex displaying slow magnetic relaxation. Nat. Commun. 2017, 8, 1023. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vignesh, K.R.; Langley, S.K.; Swain, A.; Moubaraki, B.; Damjanović, M.; Wernsdorfer, W.; Rajaraman, G.; Murray, K.S. Slow Magnetic Relaxation and Single-Molecule Toroidal Behaviour in a Family of Heptanuclear {CrIIILnIII6}(Ln= Tb, Ho, Er) Complexes. Angew. Chem. 2018, 130, 787–792. [Google Scholar] [CrossRef]
- Ashtree, J.M.; Borilović, I.; Vignesh, K.R.; Swain, A.; Hamilton, S.H.; Whyatt, Y.L.; Benjamin, S.L.; Phonsri, W.; Forsyth, C.M.; Wernsdorfer, W.; et al. Tuning the Ferrotoroidic Coupling and Magnetic Hysteresis in Double-Triangle Complexes {Dy3MIIIDy3} via the MIII-linker. Eur. J. Inorg. Chem. 2021, 2021, 435–444. [Google Scholar] [CrossRef]
- Lin, S.Y.; Wernsdorfer, W.; Ungur, L.; Powell, A.K.; Guo, Y.N.; Tang, J.; Zhao, L.; Chibotaru, L.F.; Zhang, H.J. Coupling Dy3 triangles to maximize the toroidal moment. Angew. Chem. Int. Ed. 2012, 51, 12767–12771. [Google Scholar] [CrossRef]
- Li, X.L.; Wu, J.; Tang, J.; Le Guennic, B.; Shi, W.; Cheng, P. A planar triangular Dy 3+ Dy 3 single-molecule magnet with a toroidal magnetic moment. Chem. Commun. 2016, 52, 9570–9573. [Google Scholar] [CrossRef]
- Lin, S.Y.; Wu, J.; Xu, Z. The effect of additional methyl on the magnetic relaxation and toroidal moment of Dy 6 complex. RSC Adv. 2017, 7, 47520–47526. [Google Scholar] [CrossRef] [Green Version]
- Nielsen, M.A.; Chuang, I. Quantum computation and quantum information. In Mathematical Structures in Computer Science; United States of America by Cambridge University Press: New York, NY, USA, 2002; Volume 17, p. 1115. [Google Scholar]
- Crabtree, J.M.; Soncini, A. Toroidal quantum states in molecular spin-frustrated triangular nanomagnets with weak spin–orbit coupling: Applications to molecular spintronics. Phys. Rev. B 2018, 98, 094417. [Google Scholar] [CrossRef]
- Rao, S.; Ashtree, J.; Soncini, A. Toroidal moment in a family of spin-frustrated heterometallic triangular nanomagnets without spin–orbit coupling: Applications in a molecular spintronics device. Phys. B Condens. Matter 2020, 592, 412237. [Google Scholar] [CrossRef]
- Trif, M.; Troiani, F.; Stepanenko, D.; Loss, D. Spin-electric coupling in molecular magnets. Phys. Rev. Lett. 2008, 101, 217201. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Trif, M.; Troiani, F.; Stepanenko, D.; Loss, D. Spin electric effects in molecular antiferromagnets. Phys. Rev. B 2010, 82, 045429. [Google Scholar] [CrossRef] [Green Version]
- Plokhov, D.; Zvezdin, A.; Popov, A. Macroscopic quantum dynamics of toroidal moment in Ising-type rare-earth clusters. Phys. Rev. B 2011, 83, 184415. [Google Scholar] [CrossRef] [Green Version]
- Pavlyukh, Y. Toroidal spin states in molecular magnets. Phys. Rev. B 2020, 101, 144408. [Google Scholar] [CrossRef]
- Liu, J.; Mrozek, J.; Myers, W.K.; Timco, G.A.; Winpenny, R.E.; Kintzel, B.; Plass, W.; Ardavan, A. Electric field control of spins in molecular magnets. Phys. Rev. Lett. 2019, 122, 037202. [Google Scholar] [CrossRef] [Green Version]
- Rao, S.V. Development and Application of Theoretical Models for Molecular Magnetism. Ph.D. Thesis, University of Melbourne, Melbourne, VIC, Australia, 2019. [Google Scholar]
- Abragam, A.; Bleaney, B. Electron Paramagnetic Resonance of Transition Ions; OUP Oxford: Oxford, UK, 2012. [Google Scholar]
- Noodleman, L. Valence bond description of antiferromagnetic coupling in transition metal dimers. J. Chem. Phys. 1981, 74, 5737–5743. [Google Scholar] [CrossRef]
- Bellini, V.; Olivieri, A.; Manghi, F. Density-functional study of the Cr 8 antiferromagnetic ring. Phys. Rev. B 2006, 73, 184431. [Google Scholar] [CrossRef]
- Vélez, E.; Alberola, A.; Polo, V. A density functional theory study of the magnetic exchange coupling in dinuclear manganese (II) inverse crown structures. J. Phys. Chem. A 2009, 113, 14008–14013. [Google Scholar] [CrossRef]
- Craig, D.P.; Thirunamachandran, T. Molecular Quantum Electrodynamics: An Introduction to Radiation-Molecule Interactions; Courier Corporation: Chelmsford, MA, USA, 1998. [Google Scholar]
- Luzon, J.; Bernot, K.; Hewitt, I.J.; Anson, C.E.; Powell, A.K.; Sessoli, R. Spin chirality in a molecular dysprosium triangle: The archetype of the noncollinear Ising model. Phys. Rev. Lett. 2008, 100, 247205. [Google Scholar] [CrossRef]
- Rousset, E.; Piccardo, M.; Boulon, M.E.; Gable, R.W.; Soncini, A.; Sorace, L.; Boskovic, C. Slow magnetic relaxation in lanthanoid crown ether complexes: Interplay of Raman and anomalous phonon bottleneck processes. Chem. Eur. J. 2018, 24, 14768–14785. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Islam, M.F.; Nossa, J.F.; Canali, C.M.; Pederson, M. First-principles study of spin-electric coupling in a {Cu_ {3}} single molecular magnet. Phys. Rev. B 2010, 82, 155446. [Google Scholar] [CrossRef]
- Ferrer, S.; Lloret, F.; Pardo, E.; Clemente-Juan, J.M.; Liu-Gonzalez, M.; Garcia-Granda, S. Antisymmetric exchange in triangular tricopper (II) complexes: Correlation among structural, magnetic, and electron paramagnetic resonance parameters. Inorg. Chem. 2012, 51, 985–1001. [Google Scholar] [CrossRef] [PubMed]
- Baniodeh, A.; Magnani, N.; Lan, Y.; Buth, G.; Anson, C.E.; Richter, J.; Affronte, M.; Schnack, J.; Powell, A.K. High spin cycles: Topping the spin record for a single molecule verging on quantum criticality. NPJ Quantum Mater. 2018, 3, 10. [Google Scholar] [CrossRef] [Green Version]
- Fu, Z.; Qin, L.; Sun, K.; Hao, L.; Zheng, Y.Z.; Lohstroh, W.; Günther, G.; Russina, M.; Liu, Y.; Xiao, Y.; et al. Low-temperature spin dynamics of ferromagnetic molecular ring {Cr8Y8}. NPJ Quantum Mater. 2020, 5, 32. [Google Scholar] [CrossRef]
- Choi, K.Y.; Matsuda, Y.H.; Nojiri, H.; Kortz, U.; Hussain, F.; Stowe, A.C.; Ramsey, C.; Dalal, N.S. Observation of a Half Step Magnetization in the {Cu3}-Type Triangular Spin Ring. Phys. Rev. Lett. 2006, 96, 107202. [Google Scholar] [CrossRef] [Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hymas, K.; Soncini, A. The Role of Magnetic Dipole—Dipole Coupling in Quantum Single-Molecule Toroics. Magnetochemistry 2022, 8, 58. https://doi.org/10.3390/magnetochemistry8050058
Hymas K, Soncini A. The Role of Magnetic Dipole—Dipole Coupling in Quantum Single-Molecule Toroics. Magnetochemistry. 2022; 8(5):58. https://doi.org/10.3390/magnetochemistry8050058
Chicago/Turabian StyleHymas, Kieran, and Alessandro Soncini. 2022. "The Role of Magnetic Dipole—Dipole Coupling in Quantum Single-Molecule Toroics" Magnetochemistry 8, no. 5: 58. https://doi.org/10.3390/magnetochemistry8050058
APA StyleHymas, K., & Soncini, A. (2022). The Role of Magnetic Dipole—Dipole Coupling in Quantum Single-Molecule Toroics. Magnetochemistry, 8(5), 58. https://doi.org/10.3390/magnetochemistry8050058





