Oxygen Deficiency and Migration-Mediated Electric Polarization in Magnetic Fe,Co-Substituted SrTiO3−δ
Abstract
1. Introduction
2. DFT Modeling
3. Results
3.1. Representative Configurations
3.2. Electric Polarization and O Migration
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| STFC | SrTiFeCoO |
| STF | SrTiFeO |
| STC | SrTiCoO |
| STO | SrTiO |
| TM | Transition Metal |
| FE | Ferroelectric |
| FM | Ferromagnetic |
| AFM | Antiferromagnetic |
| DFT | Density Functional Theory |
| PAW | Projector-augmented-wave |
| GGA | Generalized Gradient Approximation |
| GGA+U | Generalized Gradient Approximation with Hubbard-like correction |
| PBE | Perdew-Burke-Ernzerhof |
| HSE | Heyd–Scuseria–Ernzerhof |
| NEB | Nudged Elastic Band |
Appendix A. Configurations of Oxygen Vacancies for
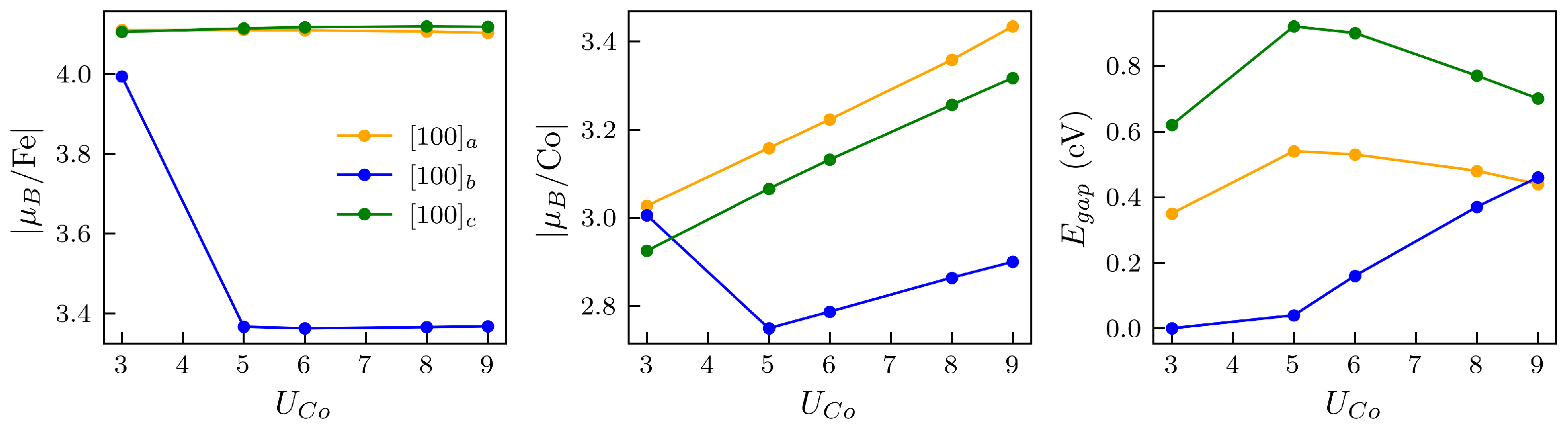
Appendix B. GGA+U: Selection of Hubbard +U Parameters
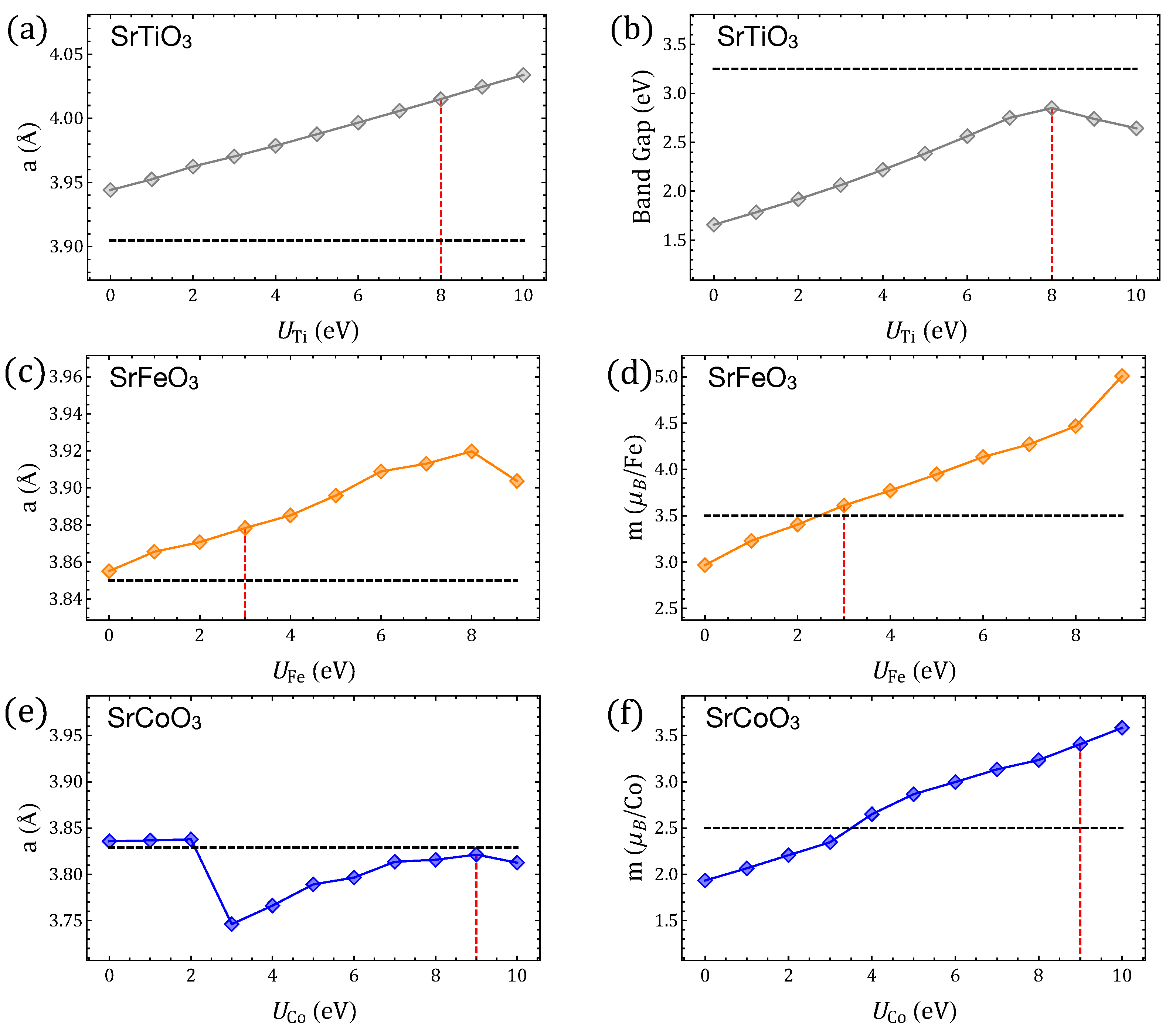
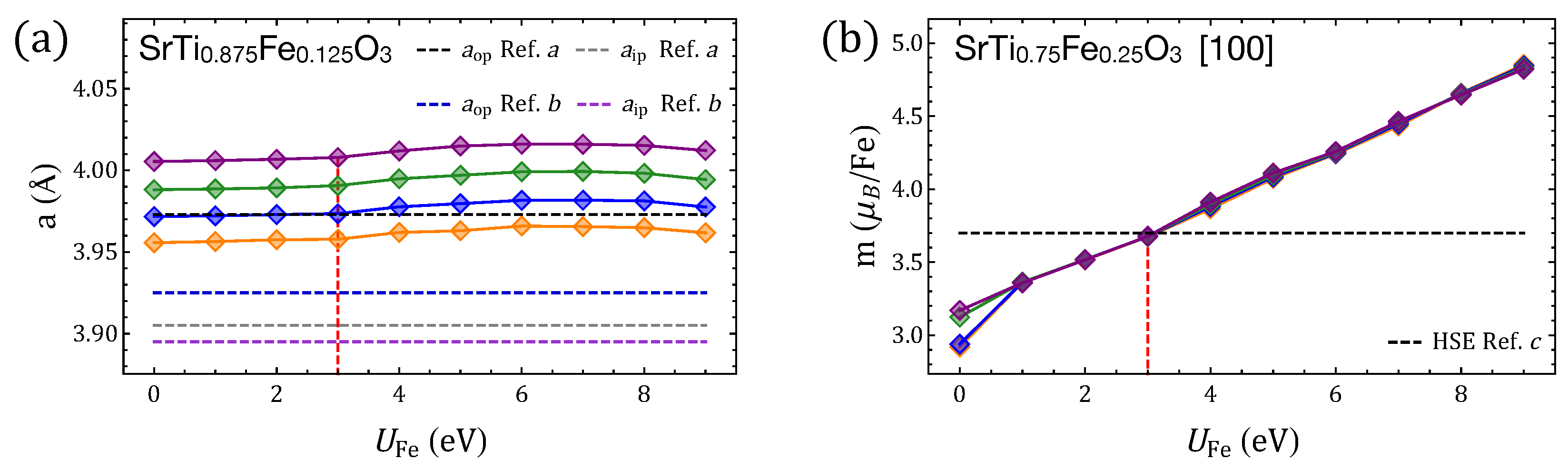
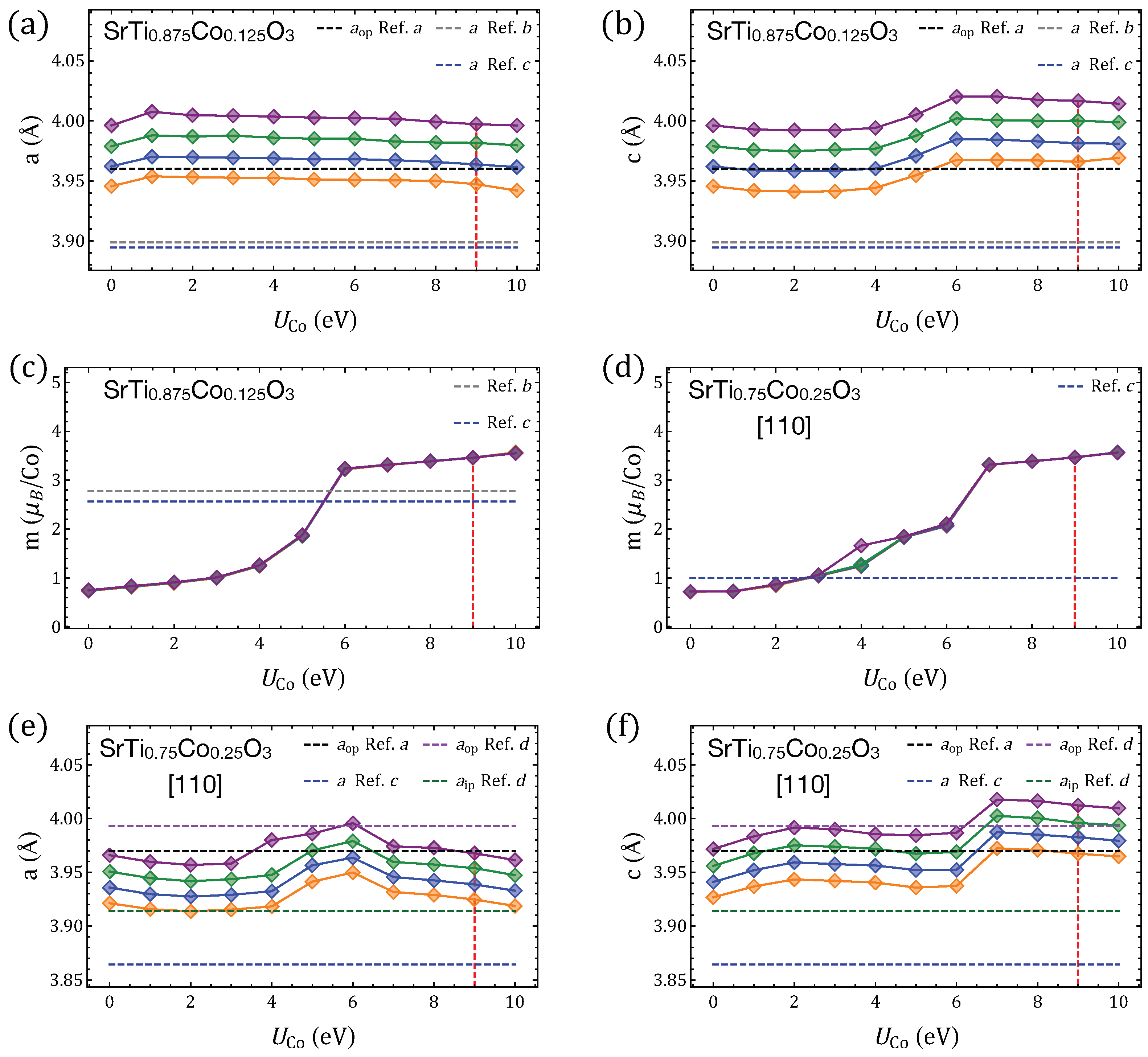
Appendix C. Oxygen-Vacancy Migration
Appendix C.1. Migration Path between δ01 Vacancies in Figure 2: [100]a and [100]c
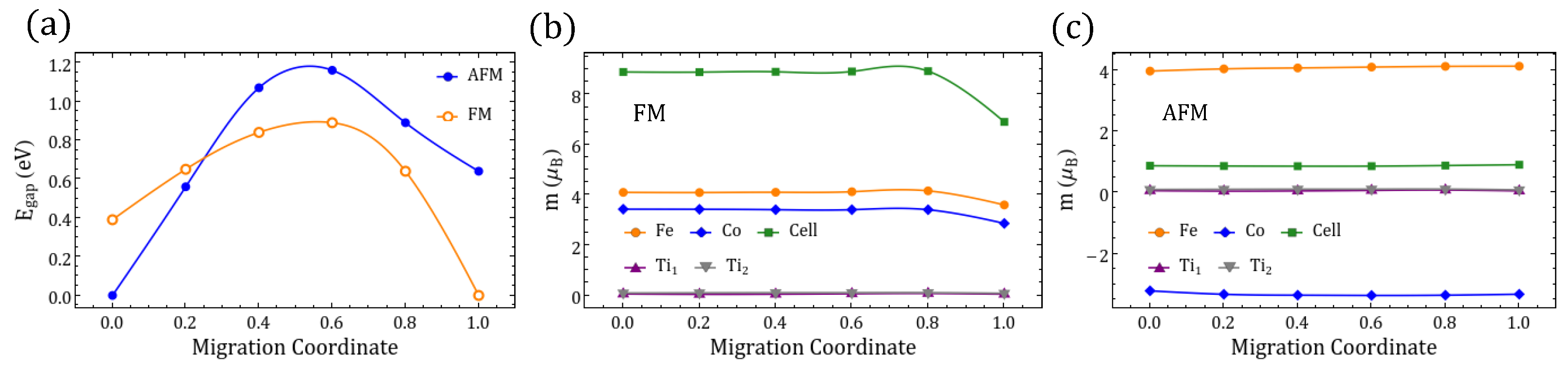
Appendix C.2. Migration Path between δ02 Vacancies in Figure 2: and
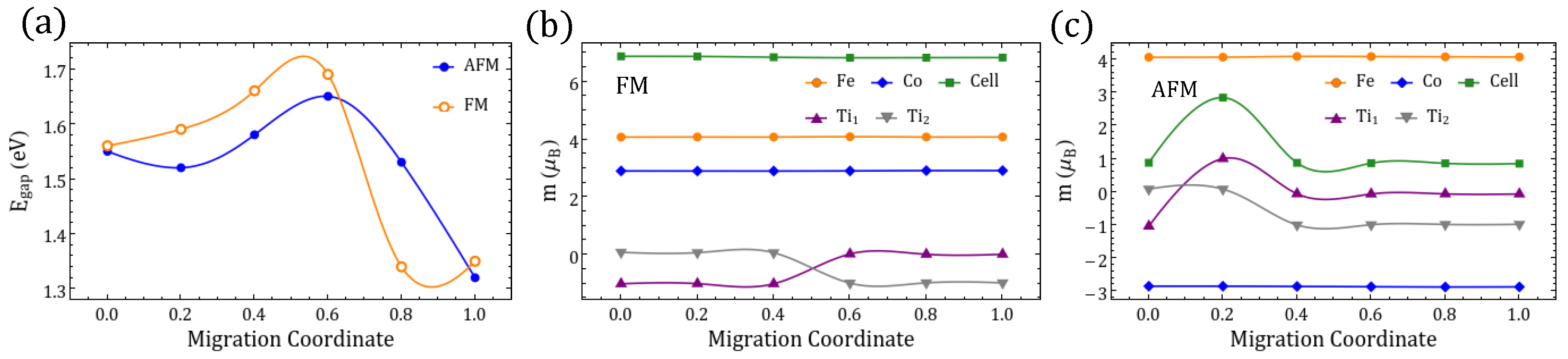
Appendix C.3. Other Migration Paths for δ01
Appendix C.3.1. Migration Connecting Symmetry-Equivalent Vacancies: The Case of [100]c

Appendix C.3.2. Migration Connecting Nonequivalent Vacancies: The Case of [100]a and [100]b
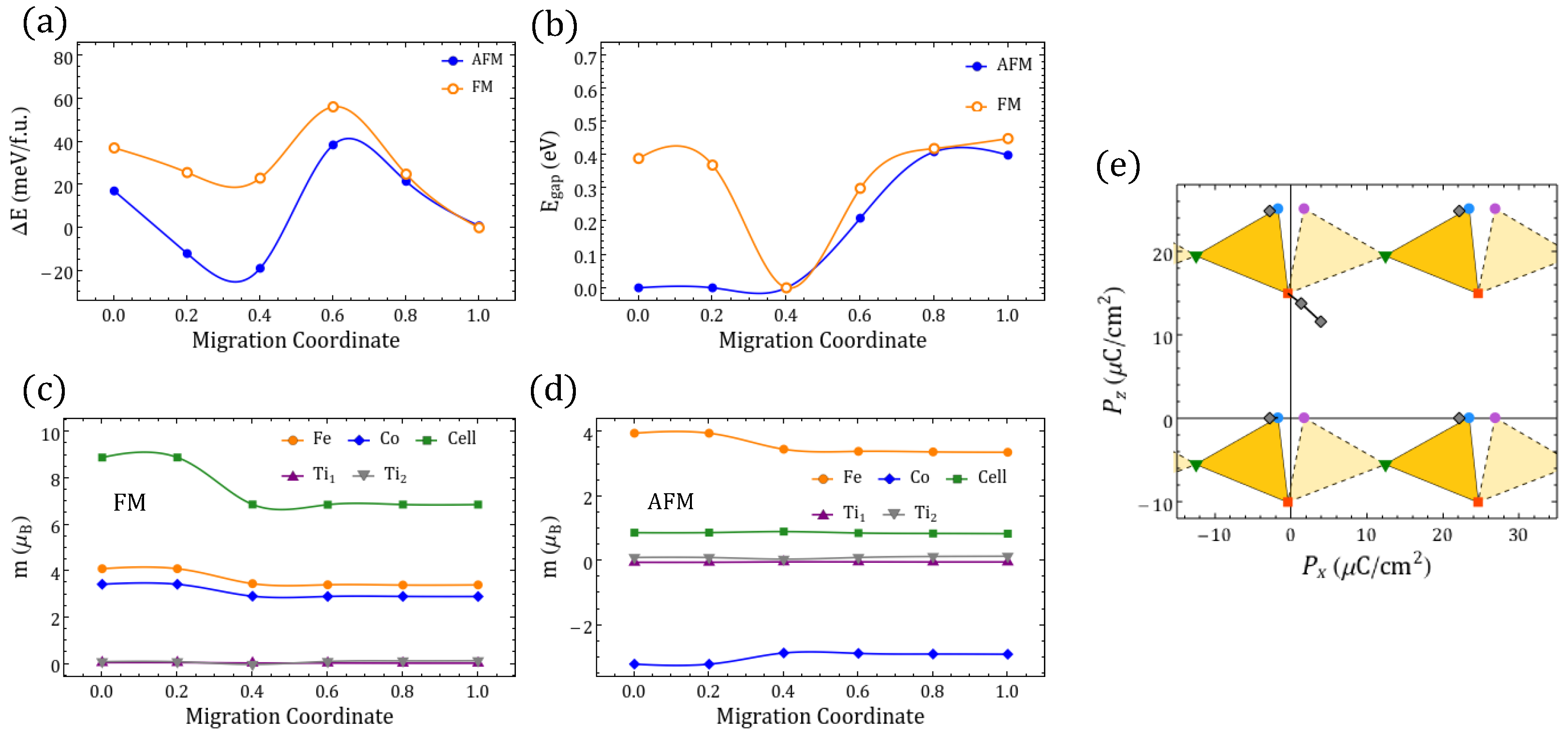
Appendix C.4. Other Migration Paths for δ02
Appendix C.4.1. Migration Path between δ02 Vacancies: and
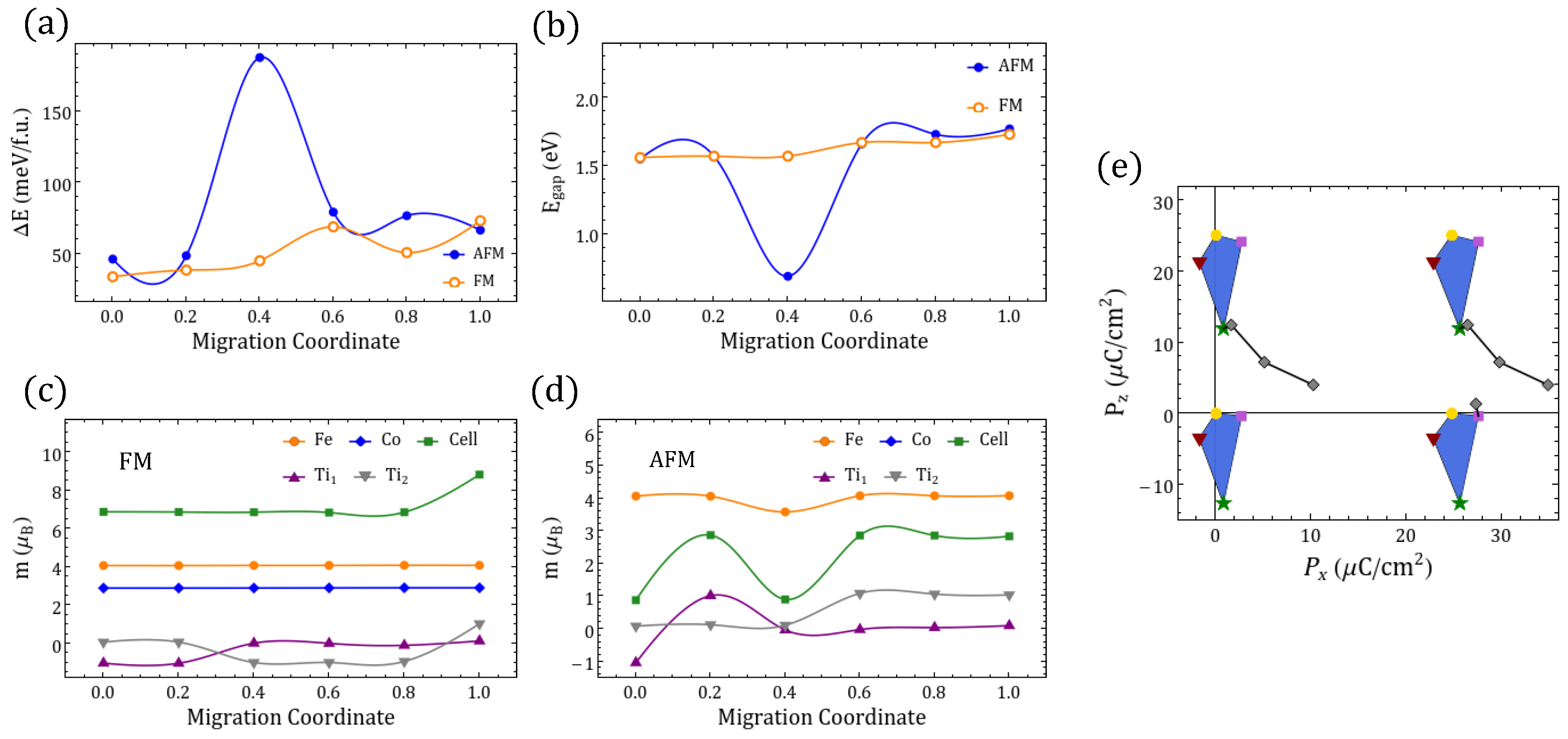
Appendix C.4.2. Migration Path between δ02 Vacancies: and

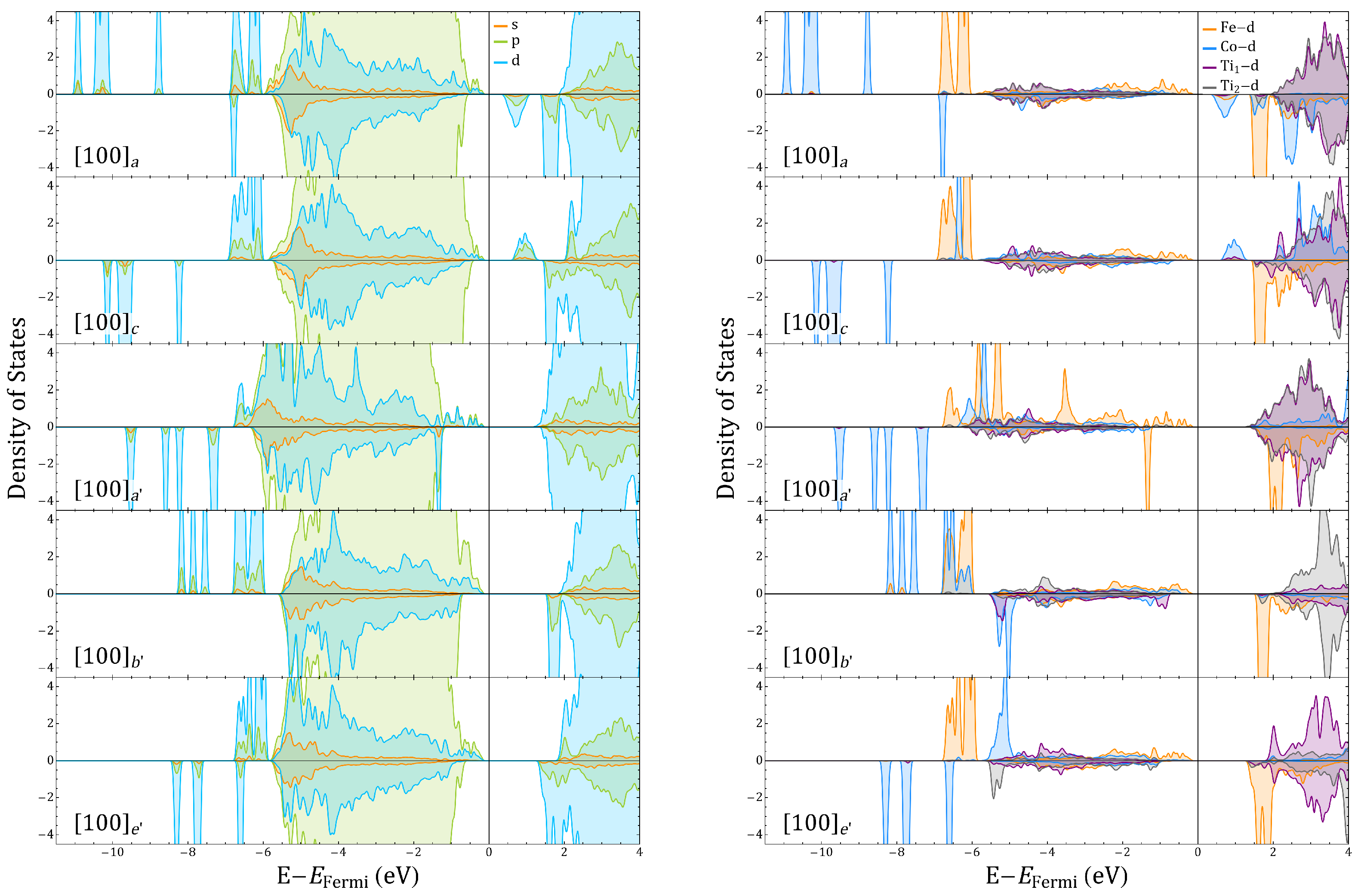
Appendix D. Projected Density of States
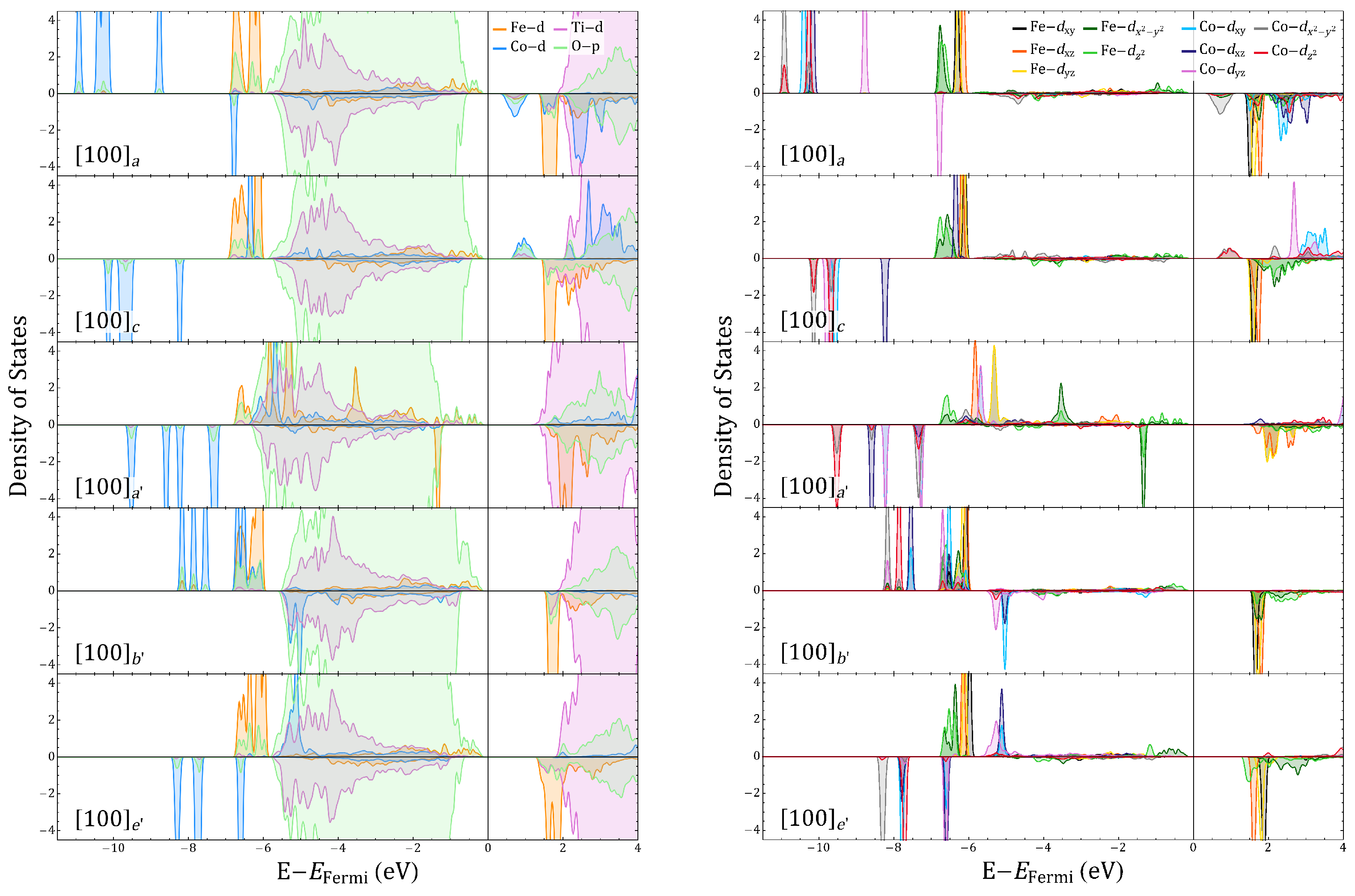
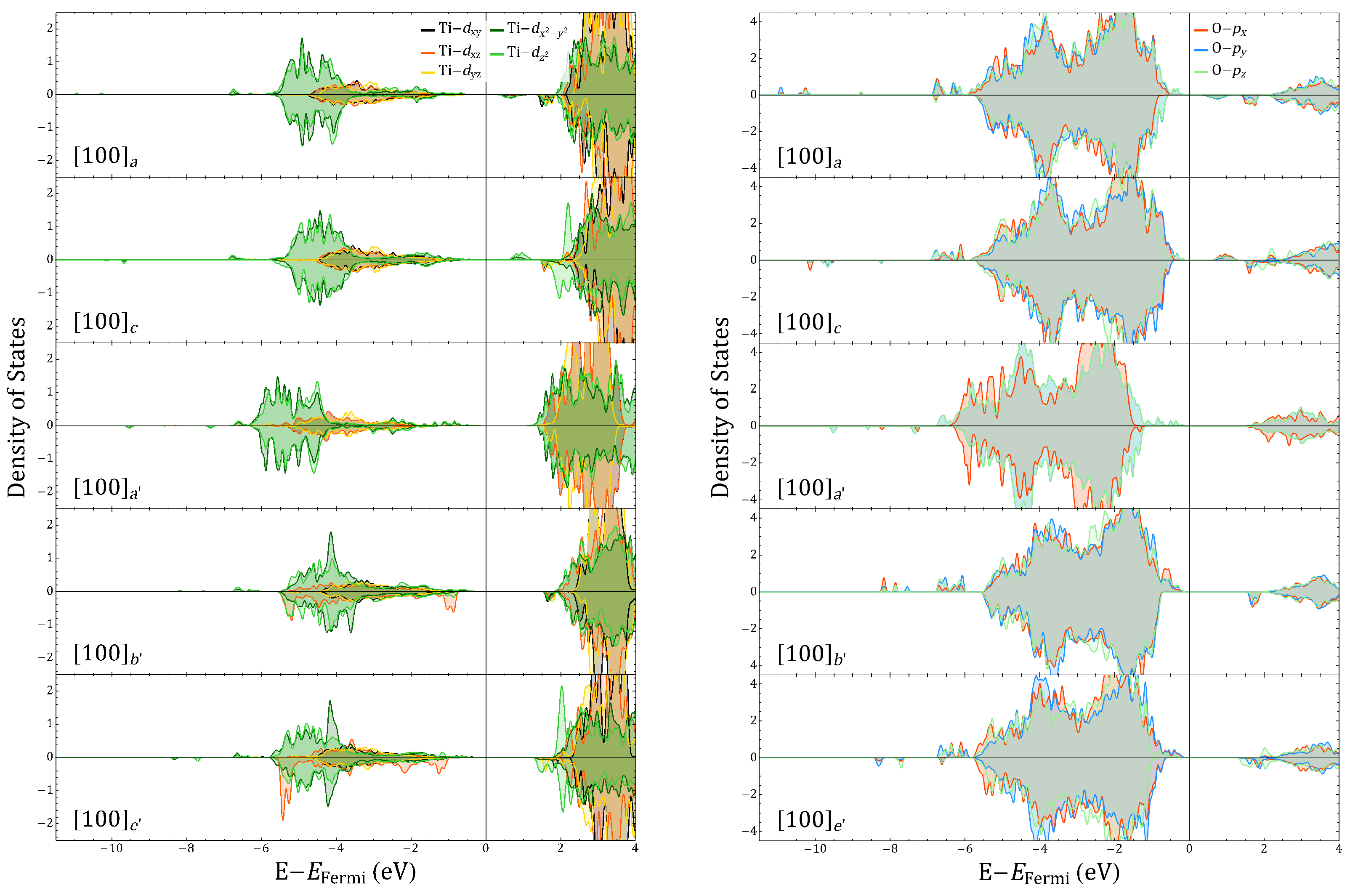
Appendix E. Robustness against Different Functionals
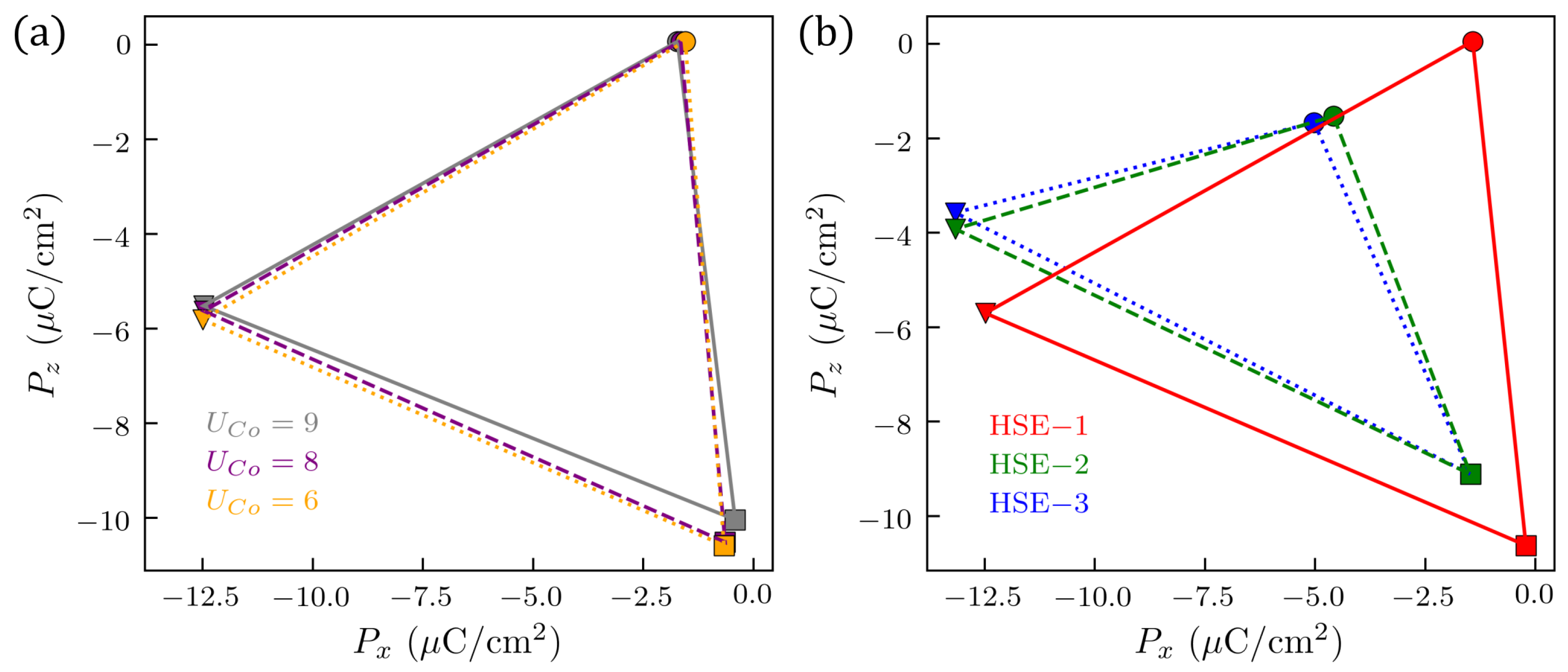
References
- Spaldin, N.A.; Ramesh, R. Advances in magnetoelectric multiferroics. Nat. Mater. 2019, 18, 203. [Google Scholar] [CrossRef] [PubMed]
- Fiebig, M.; Lottermoser, T.; Meier, D.; Trassin, M. The evolution of multiferroics. Nat. Rev. Mater. 2016, 1, 16046. [Google Scholar] [CrossRef]
- Marthinsen, A.; Faber, C.; Aschauer, U.; Spaldin, N.A.; Selbach, S.M. Coupling and competition between ferroelectricity, magnetism, strain, and oxygen vacancies in AMnO3 perovskites. MRS Commun. 2016, 6, 182. [Google Scholar] [CrossRef]
- Goto, T.; Kim, D.H.; Sun, X.; Onbasli, M.C.; Florez, J.M.; Ong, S.P.; Vargas, P.; Ackland, K.; Stamenov, P.; Aimon, N.M.; et al. Magnetism and Faraday Rotation in Oxygen-Deficient Polycrystalline and Single-Crystal Iron-Substituted Strontium Titanate. Phys. Rev. Appl. 2017, 7, 024006. [Google Scholar] [CrossRef]
- Florez, J.M.; Ong, S.P.; Onbasli, M.C.; Dionne, G.F.; Vargas, P.; Ceder, G.; Ross, C.A. First-principles insights on the magnetism of cubic SrTi1−xCoxO3−δ. Appl. Phys. Lett. 2012, 100, 252904. [Google Scholar] [CrossRef]
- Tang, A.S.; Onbasli, M.C.; Sun, X.; Ross, C.A. Thickness-Dependent Double-Epitaxial Growth in Strained SrTi0.7Co0.3O3−δ Films. ACS Appl. Mater. Interfaces 2018, 10, 7469. [Google Scholar] [CrossRef]
- Pai, Y.; Tylan-Tyler, A.; Irvin, P.; Levy, J. Physics of SrTiO3-based heterostructures and nanostructures: A review. Rep. Prog. Phys. 2018, 81, 036503. [Google Scholar] [CrossRef]
- Aschauer, U.; Spaldin, N.A. Competition and cooperation between antiferrodistortive and ferroelectric instabilities in the model perovskite SrTiO3. J. Phys. Condens. Matter 2014, 26, 122203. [Google Scholar] [CrossRef]
- Shin, D.; Latini, S.; Schäfer, C.; Sato, S.A.; Giovannini, U.D.; Hübener, H.; Rubio, A. Quantum Paraelectric Phase of SrTiO3 from First Principles. Phys. Rev. B 2021, 104, L060103. [Google Scholar] [CrossRef]
- Latini, S.; Shin, D.; Sato, S.A.; Schäfer, C.; Giovannini, U.D.; Hübener, H.; Rubio, A. The Ferroelectric Photo Ground State of SrTiO3: Cavity Materials Engineering. Proc. Natl. Acad. Sci. USA 2021, 118, e2105618118. [Google Scholar] [CrossRef]
- Xu, T.; Shimada, T.; Mori, M.; Fujimoto, G.; Wang, J.; Kitamura, T. Defect Engineering for Nontrivial Multiferroic Orders in SrTiO3. Phys. Rev. Mater. 2020, 4, 124405. [Google Scholar] [CrossRef]
- Hemberger, J.; Lunkenheimer, P.; Viana, R.; Böhmer, R.; Loidl, A. Electric-field-dependent dielectric constant and nonlinear susceptibility in SrTiO3. Phys. Rev. B 1995, 52, 13159. [Google Scholar] [CrossRef] [PubMed]
- Haeni, J.H.; Irvin, P.; Chang, W.; Uecker, R.; Reiche, P.; Li, Y.L.; Choudhury, S.; Tian, W.; Hawley, M.E.; Craigo, B.; et al. Room-temperature ferroelectricity in strained SrTiO3. Nature 2004, 430, 758. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.S.; Kim, D.J.; Kim, T.H.; Noh, T.W.; Choi, J.S.; Park, B.H.; Yoon, J.-G. Observation of room-temperature ferroelectricity in tetragonal strontium titanate thin films on SrTiO3 (001) substrates. Appl. Phys. Lett. 2007, 91, 042908. [Google Scholar] [CrossRef]
- Jang, H.W.; Kumar, A.; Denev, S.; Biegalski, M.D.; Maksymovych, P.; Bark, C.W.; Nelson, C.T.; Folkman, C.M.; Baek, S.H.; Balke, N.; et al. Ferroelectricity in Strain-Free SrTiO3 Thin Films. Phys. Rev. Lett. 2010, 104, 197601. [Google Scholar] [CrossRef]
- Choi, M.; Oba, F.; Tanaka, I. Role of Ti Antisitelike Defects in SrTiO3. Phys. Rev. Lett. 2009, 103, 185502. [Google Scholar] [CrossRef]
- Kim, Y.S.; Kim, J.; Moon, S.J.; Choi, W.S.; Chang, Y.J.; Yoon, J.-G.; Yu, J.; Chung, J.-S.; Noh, T.W. Localized electronic states induced by defects and possible origin of ferroelectricity in strontium titanate thin films. Appl. Phys. Lett. 2009, 94, 202906. [Google Scholar] [CrossRef]
- Klyukin, K.; Alexandrov, V. Effect of intrinsic point defects on ferroelectric polarization behavior of SrTiO3. Phys. Rev. B 2017, 95, 035301. [Google Scholar] [CrossRef]
- Yang, F.; Zhang, Q.; Yang, Z.; Gu, J.; Liang, Y.; Li, W.; Wang, W.; Jin, K.; Gu, L.; Guo, J. Room-temperature ferroelectricity of SrTiO3 films modulated by cation concentration. Appl. Phys. Lett. 2015, 107, 082904. [Google Scholar] [CrossRef]
- Sokolovic, I.; Schmid, M.; Diebold, U.; Setvin, M. Incipient ferroelectricity: A route towards bulk-terminated. Phys. Rev. Mater. 2019, 3, 034407. [Google Scholar] [CrossRef]
- Hallsteinsen, I.; Nord, M.; Bolstad, T.; Vullum, P.-E.; Boschker, J.E.; Longo, P.; Takahashi, R.; Holmestad, R.; Lippmaa, M.; Tybell, T. Effect of Polar (111)-Oriented SrTiO3 on Initial Perovskite Growth. Cryst. Growth Des. 2016, 16, 2357. [Google Scholar] [CrossRef]
- Xu, T.; Shimada, T.; Araki, Y.; Wang, J.; Kitamura, T. Multiferroic Domain Walls in Ferroelectric PbTiO3 with Oxygen Deficiency. Nano Lett. 2015, 16, 454–458. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.; Park, K.; Lee, H.J.; Song, M.S.; Lee, K.C.; Namkung, J.; Lee, J.H.; Park, J.; Chae, S.C. Enhanced ferroelectric switching speed of Si-doped HfO2 thin film tailored by oxygen deficiency. Sci. Rep. 2021, 11, 6290. [Google Scholar] [CrossRef] [PubMed]
- Cheng, S.; Li, M.; Deng, S.; Bao, S.; Tang, P.; Duan, W.; Ma, J.; Nan, C.; Zhu, J. Manipulation of Magnetic Properties by Oxygen Vacancies in Multiferroic YMnO3. Adv. Funct. Mater. 2016, 26, 3589–3598. [Google Scholar] [CrossRef]
- Agrawal, P.; Guo, J.; Yu, P.; Hebert, C.; Passerone, D.; Erni, R.; Rossell, M.D. Strain-driven oxygen deficiency in multiferroic SrMnO3 thin films. Phys. Rev. B 2016, 94, 104101. [Google Scholar] [CrossRef]
- Glinchuk, M.D.; Eliseev, E.A.; Li, G.; Zeng, J.; Kalinin, S.V.; Morozovska, A.N. Ferroelectricity induced by oxygen vacancies in relaxors with perovskite structure. Phys. Rev. B 2018, 98, 094102. [Google Scholar] [CrossRef]
- Abd El-Naser, A.; Abdel-Khalek, E.K.; Nabhan, E.; Rayan, D.A.; Gaafar, M.S.; Abd El-Aal, N.S. Study the influence of oxygen-deficient (δ = 0.135) in SrFeO3−δ nanoparticles perovskite on structural, electrical and magnetic properties. Philos. Mag. 2020, 101, 710–728. [Google Scholar] [CrossRef]
- Wang, Y.-G.; Tang, X.-G.; Liu, Q.-X.; Jiang, Y.-P.; Jiang, L.-L. Room Temperature Tunable Multiferroic Properties in Sol-Gel-Derived Nanocrystalline Sr(Ti1−xFex)O3−δ Thin Films. Nanomaterials 2017, 7, 264. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Z.; Hu, Q.; Zhang, C.; Wang, D.; Li, L. Room temperature multiferroic properties of Fe-doped nonstoichiometric SrTiO3 ceramics at both A and B sites. Solid State Commun. 2019, 289, 22. [Google Scholar] [CrossRef]
- Florez, J.M.; Onbasli, M.C.; Kim, D.H.; Ong, S.P.; Ceder, G.; Vargas, P.; Ross, C.A. Abstract: M32.00014, APS March Meeting 2015. 2015, Volume 60. Number 1. Available online: http://meetings.aps.org/link/BAPS.2015.MAR.M32.14 (accessed on 31 December 2021).
- Mitra, C.; Lin, C.; Posadas, A.B.; Demkov, A.A. Role of Oxygen Vacancies in Room-Temperature Ferromagnetism in Cobalt-Substituted SrTiO3. Phys. Rev. B 2014, 90, 125130. [Google Scholar] [CrossRef]
- Posadas, A.B.; Mitra, C.; Lin, C.; Dhamdhere, A.; Smith, D.J.; Tsoi, M.; Demkov, A.A. Oxygen Vacancy-Mediated Room-Temperature Ferromagnetism in Insulating Cobalt-Substituted SrTiO3 Epitaxially Integrated with Silicon. Phys. Rev. B 2013, 87, 144422. [Google Scholar] [CrossRef]
- Sluchinskaya, I.A.; Lebedev, A.I. Cobalt in Strontium Titanate as a New Off-Center Magnetic Impurity. Phys. Solid State 2019, 61, 390. [Google Scholar] [CrossRef]
- Opazo, M.A.; Ong, S.P.; Vargas, P.; Ross, C.A.; Florez, J.M. Oxygen-vacancy tuning of magnetism in SrTi0.75Fe0.125Co0.125O3−δ perovskite. Phys. Rev. Mater. 2019, 3, 014404. [Google Scholar] [CrossRef]
- Liu, Y.; Baumann, S.; Schulze-Küppers, F.; Mueller, D.N.; Guillon, O. Co and Fe co-doping influence on functional properties of SrTiO3 for use as oxygen transport membranes. J. Eur. Ceram. Soc. 2018, 38, 5058. [Google Scholar] [CrossRef]
- Phoon, B.L.; Lai, C.W.; Juan, J.C.; Show, P.L.; Chen, W.H. A review of synthesis and morphology of SrTiO3 for energy and other applications. Int. J. Energy Res. 2019, 43, 5151. [Google Scholar] [CrossRef]
- Mroziński, A.; Molin, S.; Karczewski, J.; Miruszewski, T.; Jasiński, P. Electrochemical properties of porous Sr0.86Ti0.65Fe0.35O3 oxygen electrodes in solid oxide cells: Impedance study of symmetrical electrodes. Int. J. Hydrogen Energy 2019, 44, 1827. [Google Scholar] [CrossRef]
- Kim, D.H.; Aimon, N.M.; Bi, L.; Florez, J.M.; Dionne, G.F.; Ross, C.A. Magnetostriction in epitaxial SrTi1-xFexO3-delta perovskite films with x = 0.13 and 0.35. J. Phys. Condens. Matter 2013, 25, 026002. [Google Scholar] [CrossRef]
- Ning, S.; Zhang, Q.; Occhialini, C.; Comin, R.; Zhong, X.; Ross, C.A. Voltage Control of Magnetism above Room Temperature in Epitaxial SrCo1−xFexO3−δ. ACS Nano 2020, 14, 8949. [Google Scholar] [CrossRef]
- Inkinen, S.; Yao, L.; van Dijken, S. Reversible Thermal Strain Control of Oxygen Vacancy Ordering in an Epitaxial La0.5Sr0.5CoO3−δ Film. Phys. Rev. Mater. 2020, 4, 046002. [Google Scholar] [CrossRef]
- Assat, G.; Tarascon, J.-M. Fundamental understanding and practical challenges of anionic redox activity in Li-ion batteries. Nat. Energy 2018, 3, 373. [Google Scholar] [CrossRef]
- Myeong, S.; Cho, W.; Jin, W.; Hwang, J.; Yoon, M.; Yoo, Y.; Nam, G.; Jang, H.; Han, J.-G.; Choi, N.-S.; et al. Understanding voltage decay in lithium-excess layered cathode materials through oxygen-centred structural arrangement. Nat. Commun. 2018, 9, 3285. [Google Scholar] [CrossRef] [PubMed]
- Rawat, K.; Fong, D.D.; Aidhy, D.S. Breaking Atomic-Level Ordering via Biaxial Strain in Functional Oxides: A DFT Study. J. Appl. Phys. 2021, 129, 095301. [Google Scholar] [CrossRef]
- Iijima, S.; Yang, W.; Matsumura, S.; Ohnishi, I. Atomic Resolution Imaging of Cation Ordering in Niobium–Tungsten Complex Oxides. Commun Mater 2021, 2, 1. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Jonsson, H.; Mills, G.; Jacobsen, K.W. Nudged elastic band method for finding minimum energy paths of transitions. In Classical and Quantum Dynamics in Condensed Phase Simulations; Berne, B.J., Ciccotti, G., Coker, D.F., Eds.; World Scientific: Singapore, 1998. [Google Scholar]
- Rohrbach, A.; Hafner, J.; Kresse, G. Electronic correlation effects in transition-metal sulfides. J. Phys. Condens. Matter 2003, 15, 979. [Google Scholar] [CrossRef]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118, 8207. [Google Scholar] [CrossRef]
- Resta, R. Macroscopic polarization in crystalline dielectrics: The geometric phase approach. Rev. Mod. Phys. 1994, 66, 899. [Google Scholar] [CrossRef]
- Zhou, W.X.; Ariando, A. Review on Ferroelectric/Polar Metals. Jpn. J. Appl. Phys. 2020, 59, SI0802. [Google Scholar] [CrossRef]
- Hadjimichael, M.; Li, Y.; Zatterin, E.; Chahine, G.A.; Conroy, M.; Moore, K.; Connell, E.N.O.; Ondrejkovic, P.; Marton, P.; Hlinka, J.; et al. Metal–Ferroelectric Supercrystals with Periodically Curved Metallic Layers. Nat. Mater. 2021, 20, 4. [Google Scholar] [CrossRef] [PubMed]
- Momma, K.; Izumi, F. VESTA 3 for Three-Dimensional Visualization of Crystal, Volumetric and Morphology Data. J. Appl. Cryst. 2011, 44, 1272. [Google Scholar] [CrossRef]
- Palmer, D.C. CrystalMaker; CrystalMaker Software Ltd.: Oxfordshire, UK, 2014; Available online: www.crystalmaker.com (accessed on 31 December 2021).
- Ong, S.P.; Richards, W.D.; Jain, A.; Hautier, G.; Kocher, M.; Cholia, S.; Gunter, D.; Chevrier, V.L.; Persson, K.A.; Ceder, G. Python Materials Genomics (pymatgen): A robust, open-source python library for materials analysis. Comput. Mater. Sci. 2013, 68, 314. [Google Scholar] [CrossRef]
- Makov, G.; Payne, M.C. Periodic boundary conditions in ab initio calculations. Phys. Rev. B 1995, 51, 4014. [Google Scholar] [CrossRef] [PubMed]
- Emery, A.A.; Wolverton, C. High-Throughput DFT Calculations of Formation Energy, Stability and Oxygen Vacancy Formation Energy of ABO3 Perovskites. Sci. Data 2017, 4, 1. [Google Scholar] [CrossRef] [PubMed]
- Tahini, H.A.; Tan, X.; Schwingenschlögl, U.; Smith, S.C. Formation and Migration of Oxygen Vacancies in SrCoO3 and Their Effect on Oxygen Evolution Reactions. ACS Catal. 2016, 6, 5565. [Google Scholar] [CrossRef]
- Wang, L.; Maxisch, T.; Ceder, G. Oxidation energies of transition metal oxides within the GGA+U framework. Phys. Rev. B 2006, 73, 195107. [Google Scholar] [CrossRef]
- Lee, Y.-L.; Kleis, J.; Rossmeisl, J.; Morgan, D. Ab initio energetics of LaBO3 (001) (B = Mn, Fe, Co, and Ni) for solid oxide fuel cell cathodes. Phys. Rev. B 2009, 80, 224101. [Google Scholar] [CrossRef]
- Hombo, J.; Matsumoto, Y.; Kawano, T. Electrical conductivities of SrFeO3−δ and BaFeO3−δ perovskites. J. Solid State Chem. 1990, 84, 138. [Google Scholar] [CrossRef]
- Jahn, H.A.; Teller, E. Stability of Polyatomic Molecules in Degenerate Electronic States-I—Orbital Degeneracy, Proceedings of the Royal Society of London. Ser.-Math. Phys. Sci. 1937, 161, 220. [Google Scholar]
- Tkacz-Śmiech, K.; Koleżyński, A.; Ptak, W.S. Chemical Bond in Ferroelectric Perovskites. Ferroelectrics 2000, 237, 57. [Google Scholar] [CrossRef]
- Xu, S.; Jacobs, R.; Morgan, D. Factors Controlling Oxygen Interstitial Diffusion in the Ruddlesden-Popper Oxide La2−xSrxNiO4+δ. Chem. Mater. 2018, 30, 7166. [Google Scholar] [CrossRef]
- Resta, R.; Vanderbilt, D. Theory of Polarization: A Modern Approach. Top. Appl. Phys. 2007, 105, 31–61. [Google Scholar]
- Vanderbilt, D. Berry Phases in Electronic Structure Theory: Electric Polarization, Orbital Magnetization and Topological Insulators; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Jadaun, P.; Xiao, D.; Niu, Q.; Banerjee, S.K. Topological classification of crystalline insulators with space group symmetry. Phys. Rev. B 2013, 88, 085110. [Google Scholar] [CrossRef]
- Raeliarijaona, A.; Fu, H. Persistence of strong and switchable ferroelectricity despite vacancies. Sci. Rep. 2017, 7, 41301. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.H.; Liu, X.Q.; Chen, X.M. Review of experimental progress of hybrid improper ferroelectricity in layered perovskite oxides. J. Phys. D Appl. Phys. 2022, 55, 113001. [Google Scholar] [CrossRef]
- Reyes-Lillo, S.E.; Rabe, K.M.; Neaton, J.B. Ferroelectricity in [111]-oriented epitaxially strained SrTiO3 from first principles. Phys. Rev. Mater. 2019, 3, 030601. [Google Scholar] [CrossRef]
- Ritzmann, A.M.; noz-García, A.B.M.; Pavone, M.; Keith, J.A.; Carter, E.A. Ab Initio DFT+U Analysis of Oxygen Vacancy Formation and Migration in La1−xSrxFeO3−δ (x = 0, 0.25, 0.50). Chem. Mater. 2013, 25, 3011. [Google Scholar] [CrossRef]
- Tahini, H.A.; Tan, X.; Lou, S.N.; Scott, J.; Amal, R.; Ng, Y.H.; Smith, S.C. Mobile Polaronic States in α-MoO3: An ab Initio Investigation of the Role of Oxygen Vacancies and Alkali Ions. ACS Appl. Mater. Interfaces 2016, 8, 10911. [Google Scholar] [CrossRef]
- He, X.; Mo, Y. Accelerated materials design of Na0.5Bi0.5TiO3 oxygen ionic conductors based on first principles calculations. Phys. Chem. Chem. Phys. 2015, 17, 18035. [Google Scholar] [CrossRef]
- Chroneos, A.; Vovk, R.V.; Goulatis, I.L.; Goulatis, L.I. Oxygen transport in perovskite and related oxides: A brief review. J. Alloys Compd. 2010, 494, 190. [Google Scholar] [CrossRef]
- Souza, R.A.D. Oxygen Diffusion in SrTiO3 and Related Perovskite Oxides. Adv. Funct. Mater. 2015, 25, 6326. [Google Scholar] [CrossRef]
- Mayeshiba, T.T.; Morgan, D.D. Factors controlling oxygen migration barriers in perovskites. Solid State Ion. 2016, 296, 71. [Google Scholar] [CrossRef]
- Vives, S.; Meunier, C. Defect cluster arrangements and oxygen vacancy migration in Gd doped ceria for different interatomic potentials. Solid State Ion. 2015, 283, 137. [Google Scholar] [CrossRef]
- Souza, R.A.D.; Ramadan, A.; Hörner, S. Modifying the barriers for oxygen-vacancy migration in fluorite-structured CeO2 electrolytes through strain: A computer simulation study. Energy Environ. Sci. 2012, 5, 5445. [Google Scholar] [CrossRef]
- Kong, F.; Liang, C.; Wang, L.; Zheng, Y.; Perananthan, S.; Longo, R.C.; Ferraris, J.P.; Kim, M.; Cho, K. Kinetic Stability of Bulk LiNiO2 and Surface Degradation by Oxygen Evolution in LiNiO2-Based Cathode Materials. Adv. Energy Mater. 2019, 9, 1802586. [Google Scholar] [CrossRef]
- Goikoetxea, J.; Friedrich, C.; Bihlmayer, G.; Blügel, S.; Arnau, A.; Blanco-Rey, M. Multiplet effects in the electronic correlation of one-dimensional magnetic transition metal oxides on metals. Phys. Rev. B 2022, 106, 035130. [Google Scholar] [CrossRef]
- Allen, J.P.; Watson, G.W. Occupation matrix control of d- and f-electron localisations using DFT + U. Phys. Chem. Chem. Phys. 2014, 16, 21016. [Google Scholar] [CrossRef]
- Lü, W.; Li, C.; Zheng, L.; Xiao, J.; Lin, W.; Li, Q.; Wang, X.R.; Huang, Z.; Zeng, S.; Han, K.; et al. Multi-Nonvolatile State Resistive Switching Arising from Ferroelectricity and Oxygen Vacancy Migration. Adv. Mater. 2017, 29, 1606165. [Google Scholar] [CrossRef]
- Liao, Z.; Gao, P.; Bai, X.; Chen, D.; Zhang, J. Evidence for electric-field-driven migration and diffusion of oxygen vacancies in Pr0.7Ca0.3MnO3. J. Appl. Phys. 2012, 111, 114506. [Google Scholar] [CrossRef]
- Hanzig, J.; Mehner, E.; Jachalke, S.; Hanzig, F.; Zschornak, M.; Richter, C.; Leisegang, T.; Stöcker, H.; Meyer, D.C. Dielectric to pyroelectric phase transition induced by defect migration. New J. Phys. 2015, 17, 023036. [Google Scholar] [CrossRef]
- Leighton, C. Electrolyte-based ionic control of functional oxides. Nat. Mater. 2019, 18, 13. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Ahn, E.; Seo, Y.-S.; Kim, Y.; Jeon, T.-Y.; Cho, J.; Lee, I.; Jeen, H. Redox-Driven Nanoscale Topotactic Transformations in Epitaxial SrFe0.8Co0.2O3−x under Atmospheric Pressure. Phys. Rev. Appl. 2018, 10, 054035. [Google Scholar] [CrossRef]
- Ishiwata, S.; Tokunaga, M.; Kaneko, Y.; Okuyama, D.; Tokunaga, Y.; Wakimoto, S.; Kakurai, K.; Arima, T.; Taguchi, Y.; Tokura, Y. Versatile helimagnetic phases under magnetic fields in cubic perovskite SrFeO3. Phys. Rev. B 2011, 84, 5. [Google Scholar] [CrossRef]
- Kinoshita, M.; Sakai, H.; Hayashi, N.; Tokura, Y.; Takano, M.; Ishiwata, S. Contrasting Magnetic Behaviors in Rhodium- and Ruthenium-Doped Cubic Perovskite SrFeO3: Nearly Ferromagnetic Metal versus Spin-Glass Insulator. Angew. Chem. Int. Ed. 2016, 55, 49. [Google Scholar] [CrossRef] [PubMed]
- Long, Y.; Kaneko, Y.; Ishiwata, S.; Taguchi, Y.; Tokura, Y. Synthesis of cubic SrCoO3 single crystal and its anisotropic magnetic and transport properties. J. Phys. Condens. Matter 2011, 23, 24. [Google Scholar] [CrossRef]
- Kim, D.H.; Bi, L.; Jiang, P.; Dionne, G.F.; Ross, C.A. Magnetoelastic effects in SrTi1−xMxO3 (M = Fe, Co, or Cr) epitaxial thin films. Phys. Rev. B 2011, 84, 014416. [Google Scholar] [CrossRef]
- Bi, L.; Kim, H.-S.; Dionne, G.; Gerald, F.; Ross, C.A. Structure, magnetic properties and magnetoelastic anisotropy in epitaxial Sr(Ti1−xCox)O3 films. New J. Phys. 2010, 12, 4. [Google Scholar] [CrossRef]
- Pascanut, C.; Dragoe, N.; Berthet, P. Magnetic and transport properties of cobalt-doped perovskites SrTi1−xCoxO3 (x ≤ 0.5). J. Magn. Magn. Mater. 2006, 305, 1. [Google Scholar] [CrossRef]
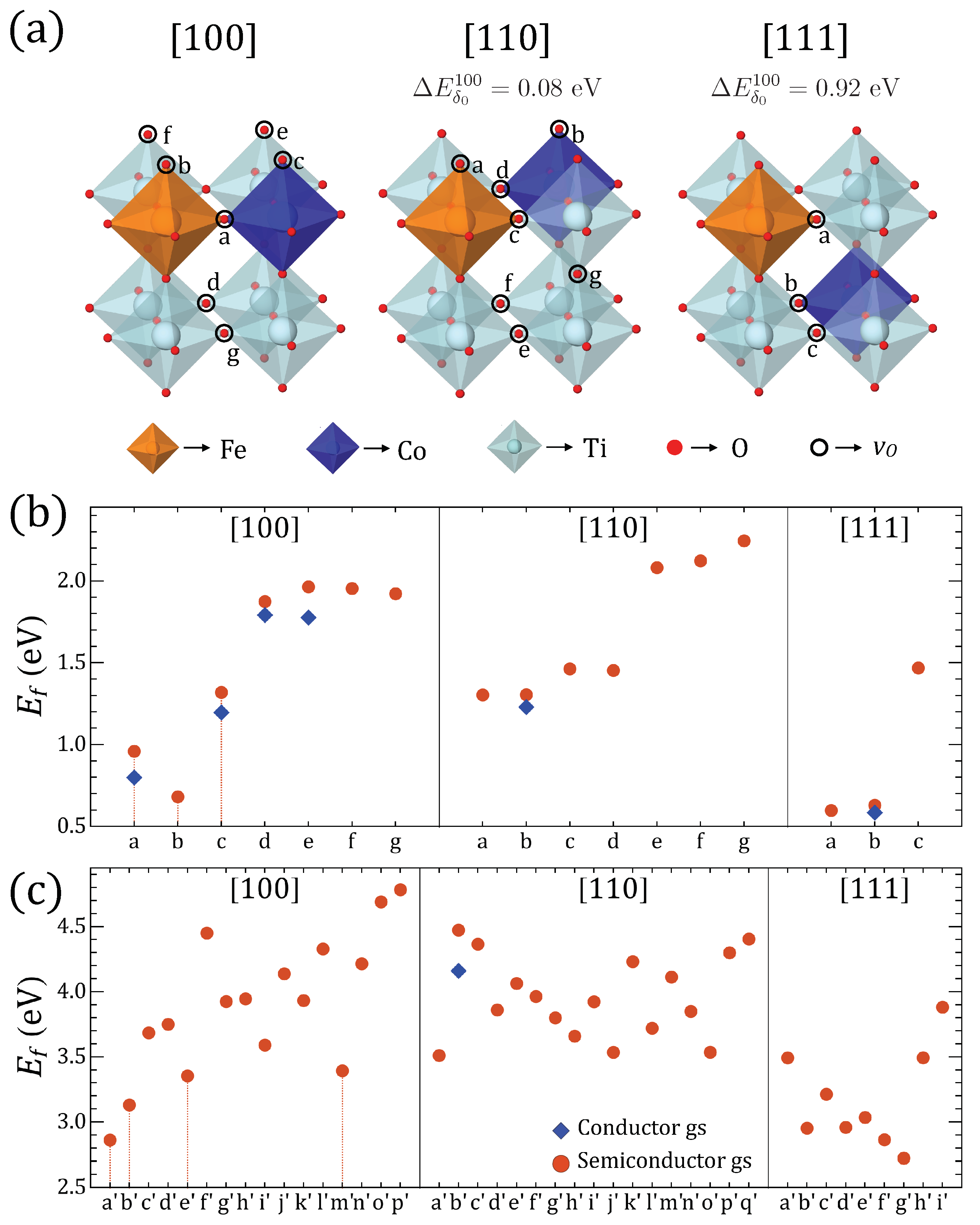
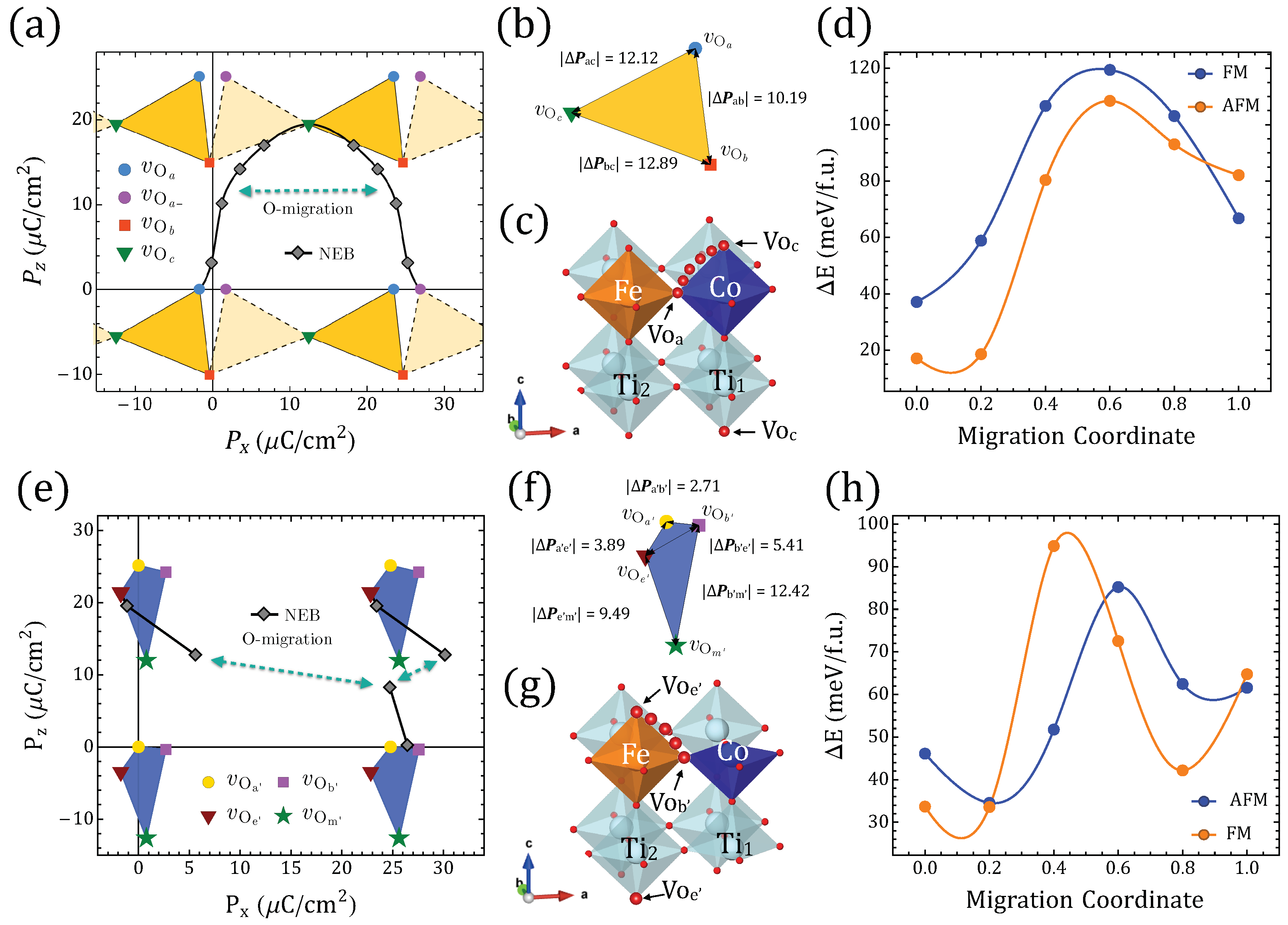
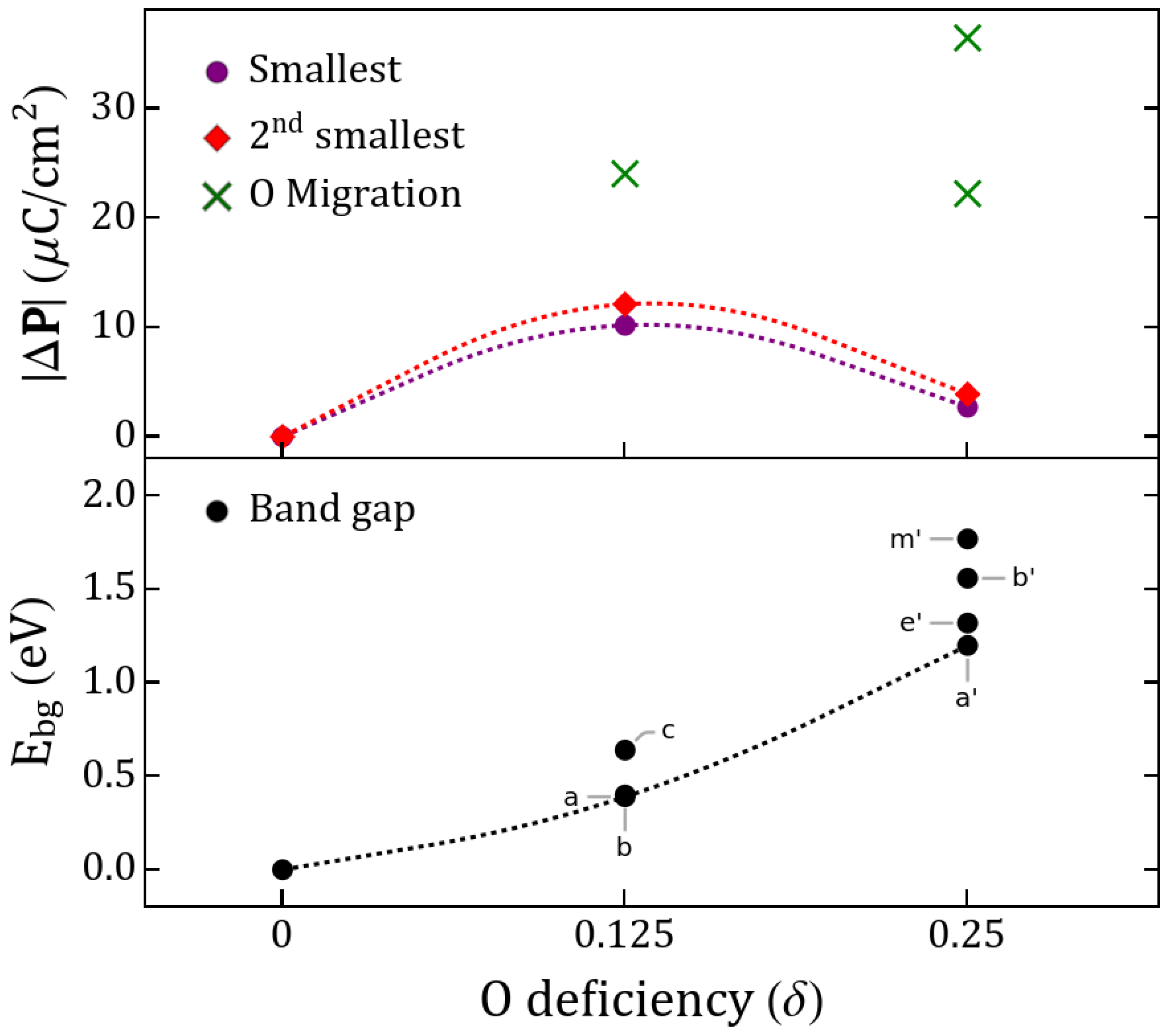
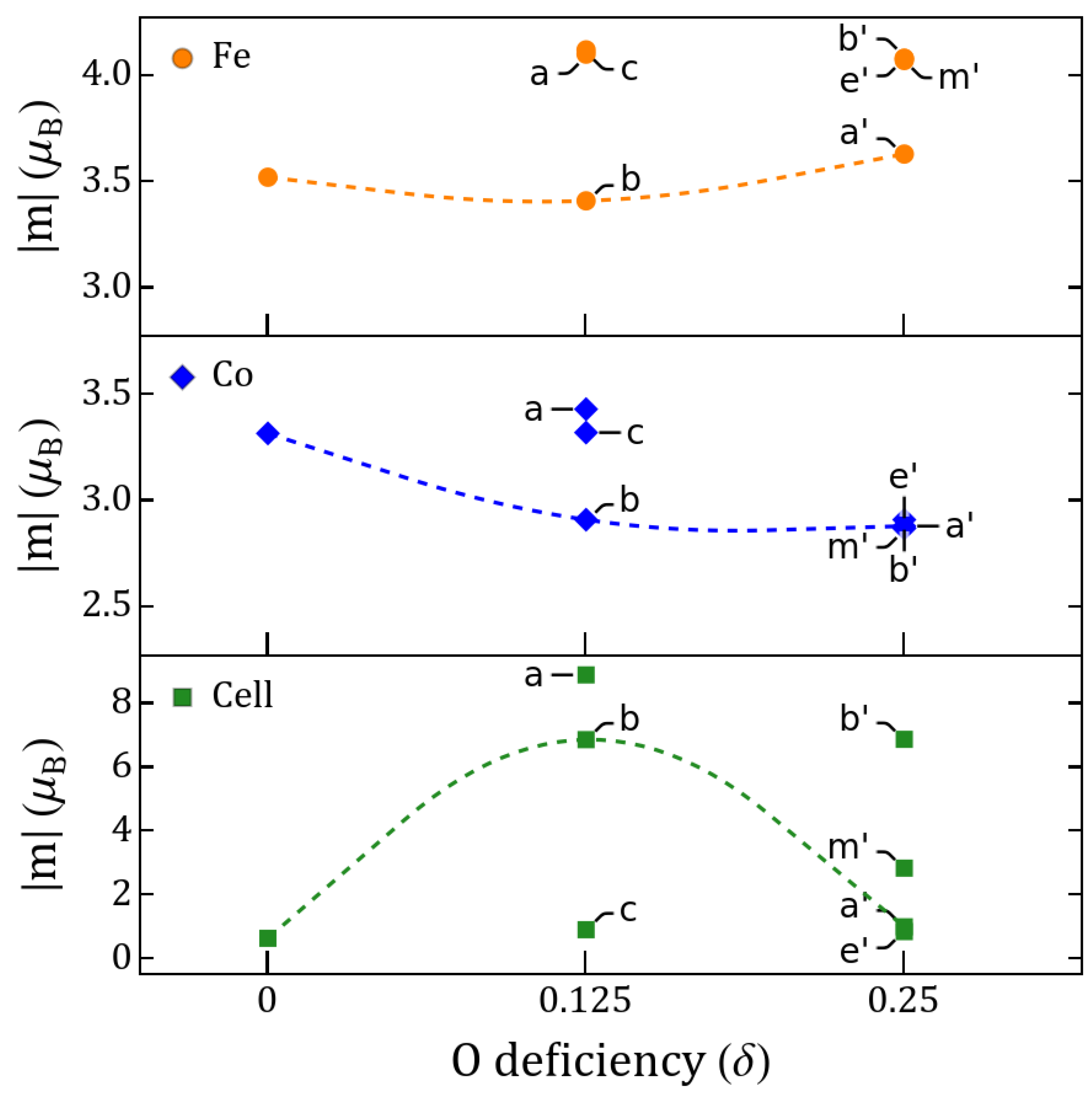

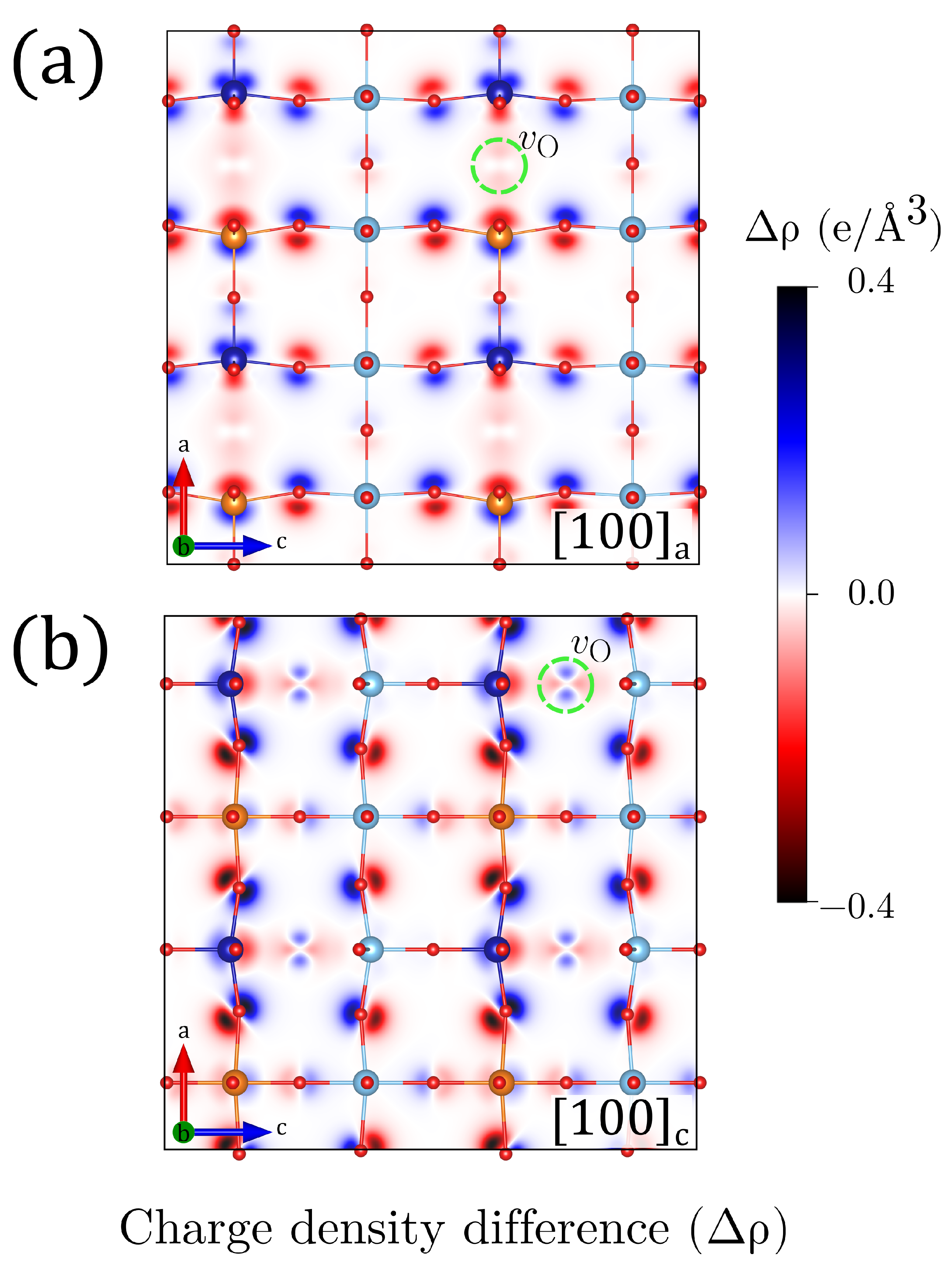
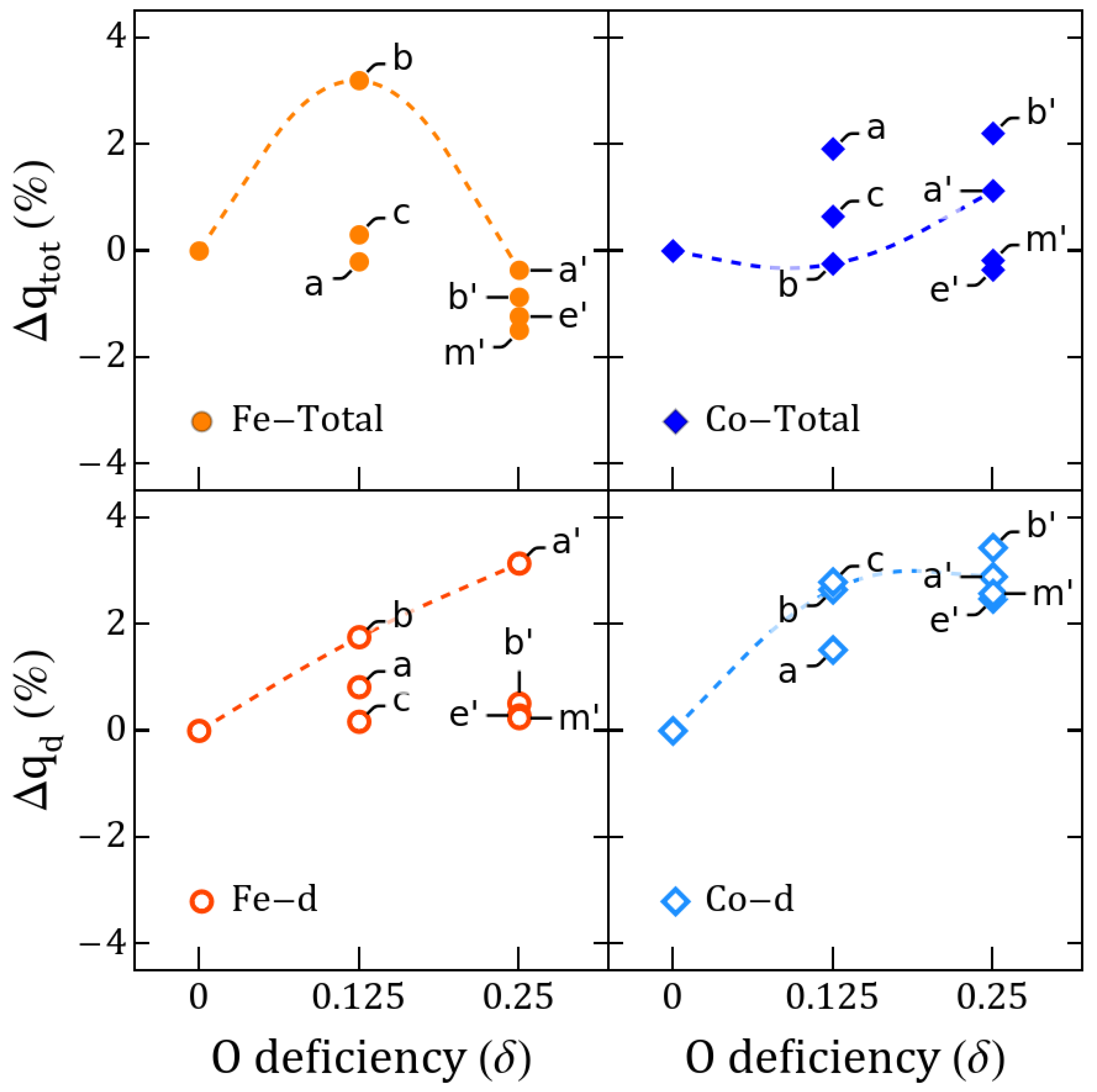
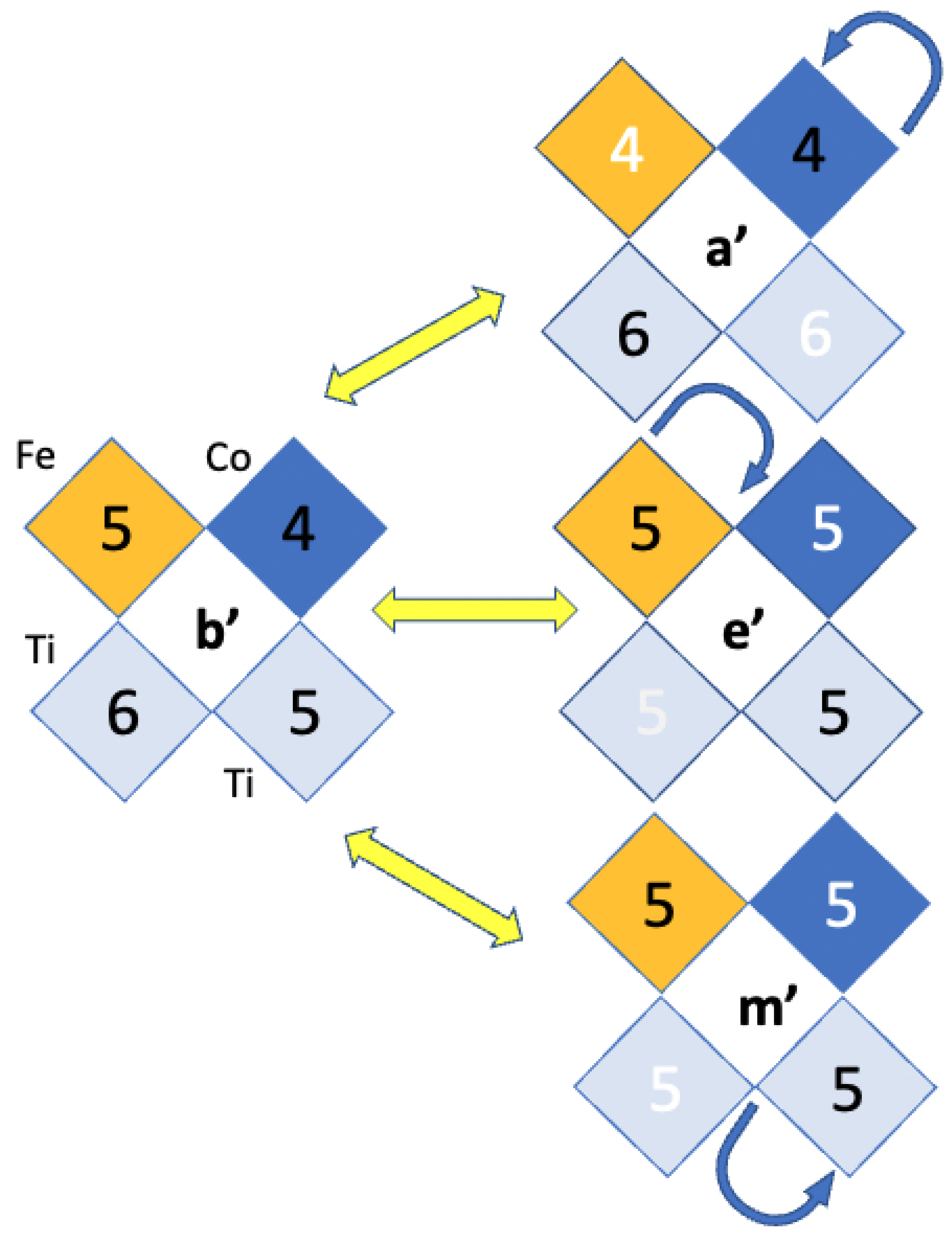
| Vacancy | a (Å) | b (Å) | c (Å) | Volume (Å3) | Order | (meV/f.u.) | (eV) | Space Group | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 8.01113 | 8.00104 | 8.00101 | 512.843 | 3.96 | 3.21 | 0.87 | AFM | 17.1 | 0.0 | P4mm | |
| 8.03717 | 7.9533 | 8.01124 | 512.094 | 4.10 | 3.43 | 8.90 | FM | 37.1 | 0.39 | Pmm2 | |
| 8.03101 | 7.97895 | 8.03229 | 514.696 | 3.37 | 2.90 | 0.84 | AFM | 0.8 | 0.40 | P1 | |
| 8.03693 | 7.97111 | 8.03031 | 514.442 | 3.41 | 2.91 | 6.87 | FM | 0. | 0.45 | P1 | |
| 8.00861 | 7.99924 | 8.03576 | 514.793 | 3.60 | 2.87 | 6.91 | FM | 66.8 | 0.0 | Pm | |
| 7.9939 | 8.01455 | 8.02041 | 513.847 | 4.12 | 3.32 | 0.91 | AFM | 82.1 | 0.64 | Pmm2 | |
| 7.93281 | 8.0405 | 8.04098 | 512.883 | 3.63 | 2.88 | 1.00 | AFM | 0. | 1.20 | P4/mmm | |
| 7.92617 | 8.04598 | 8.04597 | 513.122 | 3.64 | 2.87 | 7.02 | FM | 20.2 | 1.14 | P4/mmm | |
| 8.08034 | 8.07529 | 7.97517 | 520.313 | 4.08 | 2.91 | 6.88 | FM | 33.7 | 1.56 | P1 | |
| 8.10709 | 8.03554 | 8.00719 | 521.573 | 4.07 | 2.85 | 0.88 | AFM | 46.1 | 1.55 | Pm | |
| 7.96727 | 8.09836 | 8.04881 | 519.323 | 4.07 | 2.87 | 0.85 | AFM | 61.6 | 1.32 | Pm | |
| 7.96523 | 8.10383 | 8.04897 | 519.551 | 4.09 | 2.92 | 6.84 | FM | 64.8 | 1.35 | P1 | |
| 8.03584 | 8.10503 | 7.9565 | 518.213 | 4.08 | 2.87 | 2.84 | AFM | 66.5 | 1.77 | Pmm2 | |
| 8.04113 | 8.10629 | 7.95194 | 518.337 | 4.09 | 2.92 | 8.83 | FM | 73.1 | 1.73 | Pmm2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cortés Estay, E.A.; Ong, S.P.; Ross, C.A.; Florez, J.M. Oxygen Deficiency and Migration-Mediated Electric Polarization in Magnetic Fe,Co-Substituted SrTiO3−δ. Magnetochemistry 2022, 8, 144. https://doi.org/10.3390/magnetochemistry8110144
Cortés Estay EA, Ong SP, Ross CA, Florez JM. Oxygen Deficiency and Migration-Mediated Electric Polarization in Magnetic Fe,Co-Substituted SrTiO3−δ. Magnetochemistry. 2022; 8(11):144. https://doi.org/10.3390/magnetochemistry8110144
Chicago/Turabian StyleCortés Estay, Emilio A., Shyue P. Ong, Caroline A. Ross, and Juan M. Florez. 2022. "Oxygen Deficiency and Migration-Mediated Electric Polarization in Magnetic Fe,Co-Substituted SrTiO3−δ" Magnetochemistry 8, no. 11: 144. https://doi.org/10.3390/magnetochemistry8110144
APA StyleCortés Estay, E. A., Ong, S. P., Ross, C. A., & Florez, J. M. (2022). Oxygen Deficiency and Migration-Mediated Electric Polarization in Magnetic Fe,Co-Substituted SrTiO3−δ. Magnetochemistry, 8(11), 144. https://doi.org/10.3390/magnetochemistry8110144








