On the Distribution of Magnetic Moments in a System of Magnetic Nanoparticles
Abstract
1. Introduction
2. Fittings to the Magnetization Curves
2.1. Samples
2.2. Models
2.3. Fittings
3. Approximation to the Actual Magnetic Moment Distribution of an Ideal Sample
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Formula for the Magnetization
References
- Pankhurst, Q.A.; Connolly, J.; Jones, S.K.; Dobson, J. Applications of magnetic nanoparticles in biomedicine. J. Phys. D Appl. Phys. 2003, 36, R167–R181. [Google Scholar] [CrossRef]
- Nguyen, M.D.; Tran, H.V.; Xu, S.; Lee, T.R. Fe3O4 Nanoparticles: Structures, Synthesis, Magnetic Properties, Surface Functionalization, and Emerging Applications. Appl. Sci. 2021, 11, 1301. [Google Scholar] [CrossRef] [PubMed]
- Liberti, P.A.; Rao, C.G.; Terstappen, L.W.M.M. Optimization of ferrofluids and protocols for the enrichment of breast tumor cells in blood. J. Magn. Magn. Mater. 2001, 225, 301–307. [Google Scholar] [CrossRef]
- Kim, D.K.; Mikhaylova, M.; Wang, F.H.; Kehr, J.; Bjelke, B.; Zhang, Y.; Tsakalakos, T.; Muhammed, M. Starch-Coated Superparamagnetic Nanoparticles as MR Contrast Agents. Chem. Mater. 2003, 15, 4343–4351. [Google Scholar] [CrossRef]
- Navarathne, D.; Ner, Y.; Jain, M.; Grote, J.G.; Sotzing, G.A. Fabrication of DNA-magnetite hybrid nanofibers for water detoxification. Mater. Lett. 2011, 65, 219–221. [Google Scholar] [CrossRef]
- Dadfar, S.M.; Roemhild, K.; Drude, N.I.; von Stillfried, S.; Knüchel, R.; Kiessling, F.; Lammers, T. Iron oxide nanoparticles: Diagnostic, therapeutic and theranostic applications. Adv. Drug Deliv. Rev. 2019, 138, 302–325. [Google Scholar] [CrossRef]
- Farinha, P.; Coelho, J.M.P.; Reis, C.P.; Gaspar, M.M. A Comprehensive Updated Review on Magnetic Nanoparticles in Diagnostics. Nanomaterials 2021, 11, 3432. [Google Scholar] [CrossRef]
- Fernández-Barahona, I.; Muñoz-Hernando, M.; Ruiz-Cabello, J.; Herranz, F.; Pellico, J. Iron Oxide Nanoparticles: An Alternative for Positive Contrast in Magnetic Resonance Imaging. Inorganics 2020, 8, 28. [Google Scholar] [CrossRef]
- Roger, J.; Pons, J.N.; Massart, R.; Halbreich, A.; Bacri, J.C. Some biomedical applications of ferrofluids. Eur. Phys. J. Appl. Phys. 1999, 5, 321–325. [Google Scholar] [CrossRef]
- Palzer, J.; Eckstein, L.; Slabu, I.; Reisen, O.; Neumann, U.P.; Roeth, A.A. Iron Oxide Nanoparticle-Based Hyperthermia as a Treatment Option in Various Gastrointestinal Malignancies. Nanomaterials 2021, 11, 3013. [Google Scholar] [CrossRef] [PubMed]
- Asmatulu, R.; Zalich, M.A.; Claus, R.O.; Riffle, J.S. Synthesis, characterization and targeting of biodegradable magnetic nanocomposite particles by external magnetic fields. J. Magn. Magn. Mater. 2005, 292, 108–119. [Google Scholar] [CrossRef]
- Turrina, C.; Berensmeier, S.; Schwaminger, S.P. Bare Iron Oxide Nanoparticles as Drug Delivery Carrier for the Short Cationic Peptide Lasioglossin. Pharmaceuticals 2021, 14, 405. [Google Scholar] [CrossRef] [PubMed]
- Stanicki, D.; Vangijzegem, T.; Ternad, I.; Laurent, S. An update on the applications and characteristics of magnetic iron oxide nanoparticles for drug delivery. Expert Opin. Drug Deliv. 2022, 19, 321–335. [Google Scholar] [CrossRef] [PubMed]
- Gupta, R.B.; Kompella, U.B. (Eds.) Nanoparticle Technology for Drug Delivery; CRC Press: Philadelphia, PA, USA, 2006. [Google Scholar]
- Bean, C.P.; Livingston, J.D. Superparamagnetism. J. Appl. Phys. 1959, 30, 120–129. [Google Scholar] [CrossRef]
- Kaiser, R.; Miskolczy, G. Magnetic Properties of Stable Dispersions of Subdomain Magnetite Particles. J. Appl. Phys. 1970, 41, 1064–1072. [Google Scholar] [CrossRef]
- O’grady, K.; Bradbury, A. Particle size analysis in ferrofluids. J. Magn. Magn. Mater. 1983, 39, 90407–90416. [Google Scholar] [CrossRef]
- Bacri, J.C.; Perzynski, R.; Salin, D.; Cabuil, V.; Massart, R. Magnetic colloidal properties of ionic ferrofluids. J. Magn. Magn. Mater. 1986, 62, 90731–90737. [Google Scholar] [CrossRef]
- Xu-Fei, W.; Li-Qun, S. Polydispersity effects on the magnetization of diluted ferrofluids: A lognormal analysis. Chin. Phys. B 2010, 19, 107502. [Google Scholar] [CrossRef]
- Herdan, G. Small Particles Statistics; Butterworths Scientic Publications Ltd.: London, UK, 1960. [Google Scholar]
- Reimers, G.W.; Khalafalla, S.E. Preparing Magnetic Fluids by a Peptizing Method; US Department of the Interior: Washington, DC, USA, 1972. [Google Scholar]
- Hadjipanayis, G.C.; Siegel, R.R.W. NATO Advanced Study Institute on Nanophase Materials: Synthesis-Properties—Applications; Springer: Dordrecht, The Netherlands, 1993. [Google Scholar]
- Sjøgren, C.E.; Briley-Sæbø, K.; Hanson, M.; Johansson, C. Magnetic characterization of iron oxides for magnetic resonance imaging. Magn. Reson. Med. 1994, 31, 268–272. [Google Scholar] [CrossRef]
- Li, S.; Irvin, G.C.; Simmons, B.; Rachakonda, S.; Ramannair, P.; Banerjee, S.; John, V.T.; Mcpherson, G.L.; Zhou, W.; Bose, A. Structured materials syntheses in a self-assembled surfactant mesophase. Colloids Surf. A Physicochem. Eng. Asp. 2000, 174, 275–281. [Google Scholar] [CrossRef]
- Santra, S.; Tapec, R.; Theodoropoulou, N.; Dobson, J.; Hebard, A.; Tan, W. Synthesis and Characterization of Silica-Coated Iron Oxide Nanoparticles in Microemulsion: The Effect of Nonionic Surfactants. Langmuir 2001, 17, 2900–2906. [Google Scholar] [CrossRef]
- Tillotson, T.M.; Gash, A.E.; Simpson, R.L.; Hrubesh, L.W.; Satcher, J.H., Jr.; Poco, J.F. Nanostructured energetic materials using sol-gel methodologies. J. Non Cryst. Solids 2001, 285, 338–345. [Google Scholar] [CrossRef]
- Deng, Y.; Wang, L.; Yang, W.; Fu, S.; Elaïssari, A. Preparation of magnetic polymeric particles via inverse microemulsion polymerization process. J. Magn. Magn. Mater. 2003, 257, 987–990. [Google Scholar] [CrossRef]
- Gupta, A.K.; Curtis, A.S.G. Lactoferrin and ceruloplasmin derivatized superparamagnetic iron oxide nanoparticles for targeting cell surface receptors. Biomaterials 2004, 25, 3029–3040. [Google Scholar] [CrossRef]
- Popplewell, J.; Sakhnini, L. The dependence of the physical and magnetic properties of magnetic fluids on particle size. J. Magn. Magn. Mater. 1995, 149, 72–78. [Google Scholar] [CrossRef]
- Woodward, R.C.; Heeris, J.S.; Pierre, T.G.; Saunders, M.; Gilbert, E.P.; Rutnakornpituk, M.; Zhang, Q.; Riffle, J.S. A comparison of methods for the measurement of the particle-size distribution of magnetic nanoparticles. Int. Union Crystallogr. 2007, 40, 495–500. [Google Scholar] [CrossRef]
- Chen, D.X.; Sanchez, A.; Taboada, E.; Roig, A.; Sun, N.; Gu, H.C. Size determination of superparamagnetic nanoparticles from magnetization curve. J. Appl. Phys. 2009, 105, 83924. [Google Scholar] [CrossRef]
- Cótica, L.F.; Santos, I.A.; Girotto, E.M.; Ferri, E.V.; Coelho, A.A. Surface spin disorder effects in magnetite and poly(thiophene)-coated magnetite nanoparticles. J. Appl. Phys. 2010, 108, 64325. [Google Scholar] [CrossRef]
- Yoon, S.H. Determination of the Size Distribution of Magnetite Nanoparticles from Magnetic Measurements. J. Magn. 2011, 16, 368–373. [Google Scholar] [CrossRef][Green Version]
- Bacri, J.C.; Perzynski, R.; Salin, D. Magnetic and thermal behaviour of γ-Fe2O3 fine grains. J. Magn. Magn. Mater. 1988, 71, 90002–90011. [Google Scholar] [CrossRef]
- Jarjayes, O.; Fries, P.H.; Bidan, G. Magnetic properties of fine maghemite particles in an electroconducting polymer matrix. J. Magn. Magn. Mater. 1994, 137, 205–218. [Google Scholar] [CrossRef]
- Vaishnava, P.P.; Senaratne, U.; Buc, E.C.; Naik, R.; Naik, V.M.; Tsoi, G.M.; Wenger, L.E. Magnetic properties of Fe2O3 nanoparticles incorporated in a polystyrene resin matrix. Phys. Rev. B 2007, 76, 024413. [Google Scholar] [CrossRef]
- Chantrell, R.W.; Popplewell, J.; Charles, S.W. The coercivity of a system of single domain particles with randomly oriented easy axes and a distribution of particle size. J. Magn. Magn. Mater. 1980, 15, 1123–1124. [Google Scholar] [CrossRef]
- Kommareddi, N.S.; Tata, M.; John, V.T.; McPherson, G.L.; Herman, M.F.; Lee, Y.S.; O’Connor, C.J.; Akkara, J.A.; Kaplan, D.L. Synthesis of superparamagnetic Polymer–Ferrite composites using surfactant microstructures. Chem. Mater. A 1996, 8, 801–809. [Google Scholar] [CrossRef]
- Caruntu, D.; Caruntu, G.; Connor, C.J. Magnetic properties of variable-sized Fe3O4 nanoparticles synthesized from non-aqueous homogeneous solutions of polyols. J. Phys. D Appl. Phys. 2007, 40, 5801–5809. [Google Scholar] [CrossRef]
- Simeonidis, K.; Mourdikoudis, S.; Tsiaoussis, I.; Angelakeris, M.; Dendrinou-Samara, C.; Kalogirou, O. Structural and magnetic features of heterogeneously nucleated Fe-oxide nanoparticles. J. Magn. Magn. Mater. 2008, 320, 1631–1638. [Google Scholar] [CrossRef]
- Sasayama, T.; Yoshida, T.; Saari, M.M.; Enpuku, K. Comparison of volume distribution of magnetic nanoparticles obtained from M-H curve with a mixture of log-normal distributions. J. Appl. Phys. 2015, 117, 17D155. [Google Scholar] [CrossRef]
- Van Rijssel, J.; Kuipers, B.W.M.; Erné, B.H. Bimodal distribution of the magnetic dipole moment in nanoparticles with a monomodal distribution of the physical size. J. Magn. Magn. Mater. 2015, 380, 325–329. [Google Scholar] [CrossRef]
- Bender, P.; Balceris, C.; Ludwig, F.; Posth, O.; Bogart, L.K.; Szczerba, W.; Castro, A.; Nilsson, L.; Costo, R.; Gavilán, H.; et al. Distribution functions of magnetic nanoparticles determined by a numerical inversion method. New J. Phys. 2017, 19, 073012. [Google Scholar] [CrossRef]
- Berkov, D.V.; Görnert, P.; Buske, N.; Gansau, C.; Mueller, J.; Giersig, M.; Neumann, W.; Su, D. New method for the determination of the particle magnetic moment distribution in a ferrofluid. J. Phys. D Appl. Phys. 2000, 33, 331–337. [Google Scholar] [CrossRef]
- Cótica, L.F.; Freitas, V.F.; Dias, G.S.; Santos, I.A.; Vendrame, S.C.; Khalil, N.M.; Mainardes, R.M.; Staruch, M.; Jain, M. Simple and facile approach to synthesize magnetite nanoparticles and assessment of their effects on blood cells. J. Magn. Magn. Mater. 2012, 324, 559–563. [Google Scholar] [CrossRef]
- Kilcoyne, S.H.; Cywinski, R. Ferritin: A model superparamagnet. J. Magn. Magn. Mater. 1995, 140, 626–627. [Google Scholar] [CrossRef]
- Makhlouf, S.A.; Parker, F.T.; Berkowitz, A.E. Magnetic hysteresis anomalies in ferritin. Phys. Rev. B 1997, 55, 14717. [Google Scholar] [CrossRef]
- Seehra, M.S.; Babu, V.S.; Manivannan, A.; Lynn, J.W. Neutron scattering and magnetic studies of ferrihydrite nanoparticles. Phys. Rev. B 2000, 61, 3513–3518. [Google Scholar] [CrossRef]
- Seehra, M.S.; Punnoose, A. Deviations from the Curie-law variation of magnetic susceptibility in antiferromagnetic nanoparticles. Phys. Rev. B 2001, 64, 132410. [Google Scholar] [CrossRef]
- Punnoose, A.; Phanthavady, T.; Seehra, M.S.; Shah, N.; Huffman, G.P. Magnetic properties of ferrihydrite nanoparticles doped with Ni, Mo, and Ir. Phys. Rev. B 2004, 69, 054425. [Google Scholar] [CrossRef]
- Millan, A.; Urtizberea, A.; Silva, N.J.O.; Palacio, F.; Amaral, V.S.; Snoeck, E.; Serin, V. Surface effects in maghemite nanoparticles. J. Magn. Magn. Mater. 2007, 312, 5–9. [Google Scholar] [CrossRef]
- Silva, N.J.O.; Amaral, V.S.; Carlos, L.D. Relevance of magnetic moment distribution and scaling law methods to study the magnetic behavior of antiferromagnetic nanoparticles: Application to ferritin. Phys. Rev. B 2005, 71, 184408. [Google Scholar] [CrossRef]
- Tiwari, S.D.; Rajeev, K.P. Effect of distributed particle magnetic moments on the magnetization of NiO nanoparticles. Solid State Commun. 2012, 152, 1080–1083. [Google Scholar] [CrossRef]
- Rani, C.; Tiwari, S.D. Estimation of particle magnetic moment distribution for antiferromagnetic ferrihydrite nanoparticles. J. Magn. Magn. Mater. 2015, 385, 272–276. [Google Scholar] [CrossRef]
- Li, C.Y.; Karna, S.K.; Wang, C.W.; Li, W.H. Spin Polarization and Quantum Spins in Au Nanoparticles. Int. J. Mol. Sci. 2013, 14, 17618–17642. [Google Scholar] [CrossRef] [PubMed]
- Hou, Y.; Kondoh, H.; Ohta, T.; Gao, S. Size-controlled synthesis of nickel nanoparticles. Appl. Surf. Sci. 2005, 241, 218–222. [Google Scholar] [CrossRef]
- Quesenberry, C.P.; Kent, J. Selecting Among Probability Distributions Used in Reliability. Technometrics 1982, 24, 59–65. [Google Scholar] [CrossRef]
- Silva, E.L.; Lisboa, P. Analysis of the characteristic features of the density functions for gamma, Weibull and log-normal distributions through RBF network pruning with QLP. In Proceedings of the 6th Conference on 6th WSEAS International Conference On Artificial Intelligence, Dallas, TX, USA, 22–24 March 2007; Volume 6, pp. 223–228. [Google Scholar]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Gilles, C.; Bonville, P.; Rakoto, H.; Broto, J.; Wong, K.; Mann, S. Magnetic hysteresis and superantiferromagnetism in ferritin nanoparticles. J. Magn. Magn. Mater. 2002, 241, 430–440. [Google Scholar] [CrossRef]
- Feller, W. An Introduction to Probability Theory and Its Applications, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 1971; Volume 2. [Google Scholar]
- Penrose, R. A generalized inverse for matrices. Math. Proc. Camb. Philos. Soc. 1955, 51, 406–413. [Google Scholar] [CrossRef]
- Penrose, R. On best approximate solutions of linear matrix equations. Math. Proc. Camb. Philos. Soc. 1956, 52, 17–19. [Google Scholar] [CrossRef]
- Rehberg, I.; Richter, R.; Hartung, S.; Lucht, N.; Hankiewicz, B.; Friedrich, T. Measuring magnetic moments of polydisperse ferrofluids utilizing the inverse Langevin function. Phys. Rev. B 2019, 100, 134425. [Google Scholar] [CrossRef]
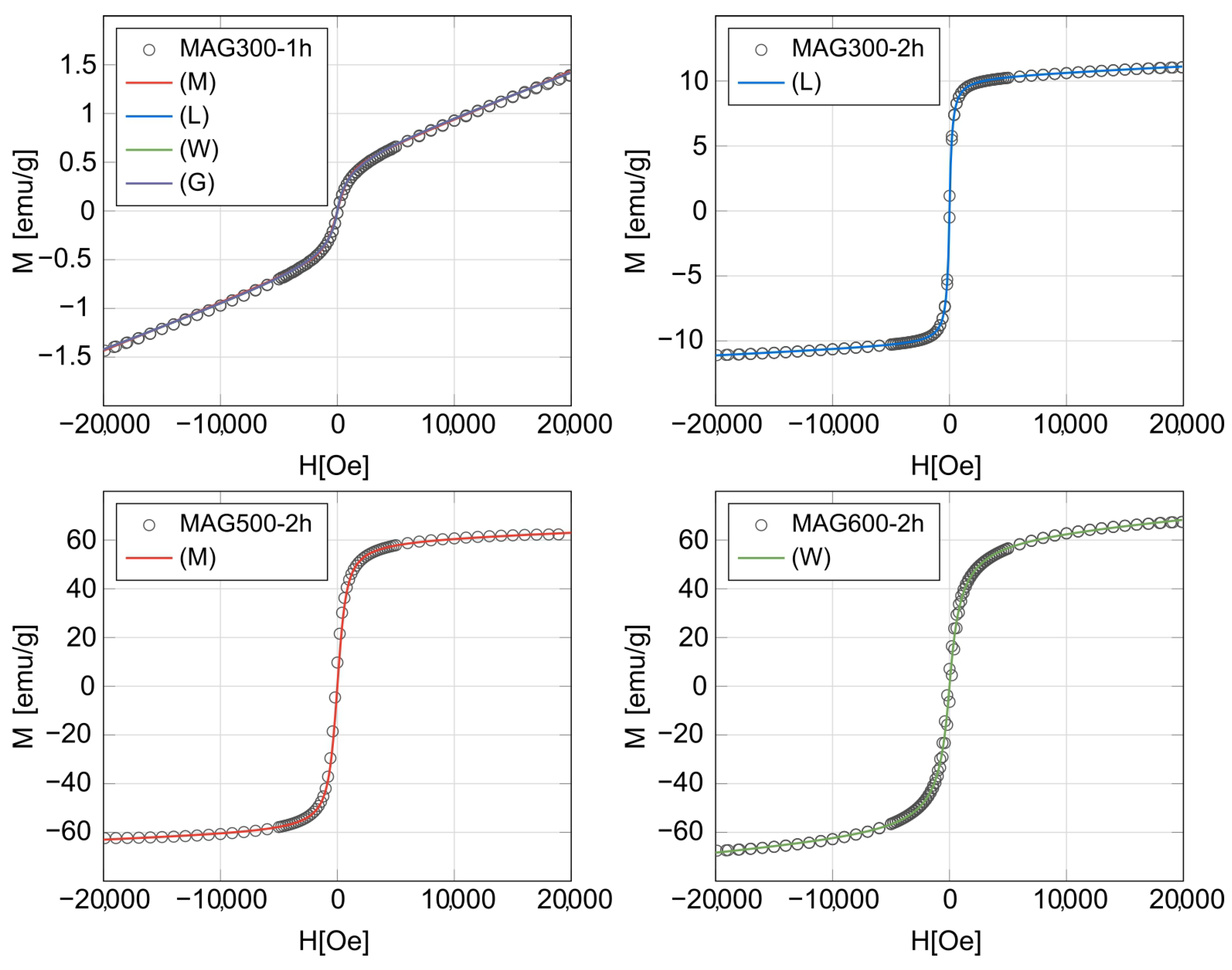

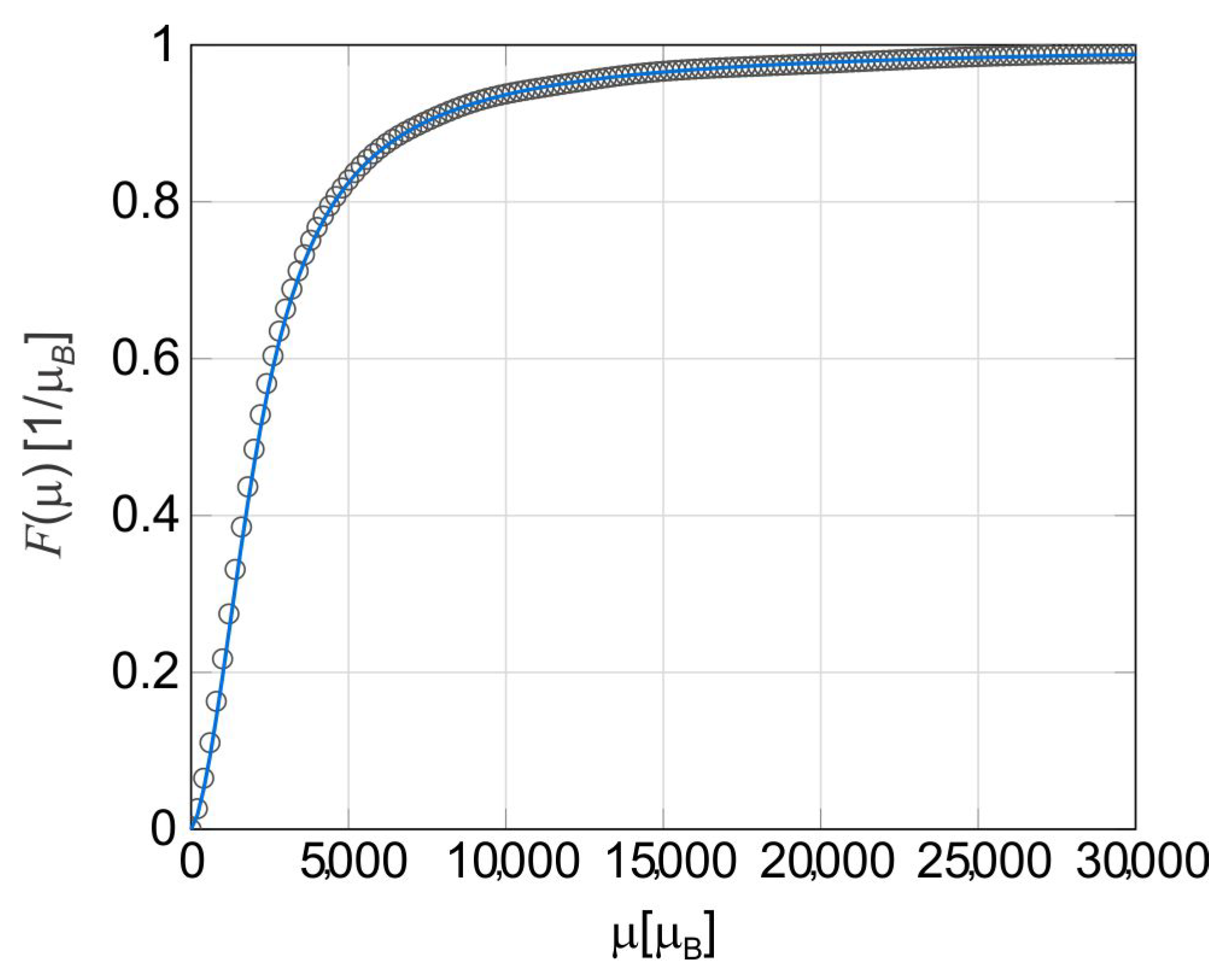
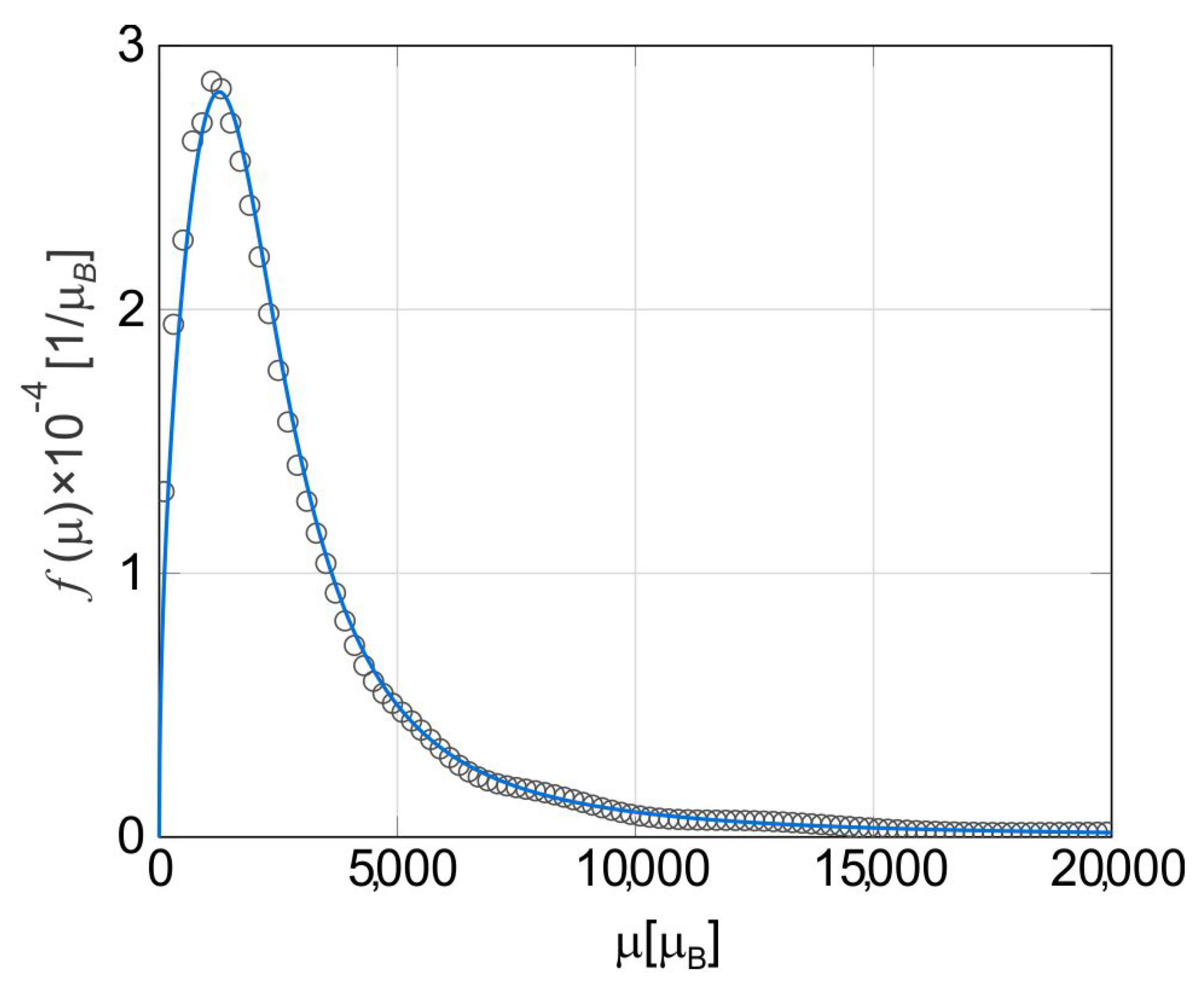
| Model | M (emu/g) | AIC | ||||||
|---|---|---|---|---|---|---|---|---|
| Mag300-1h | ||||||||
| (M) | 4.9 | 0.47 | 11,042.3 | 0.999133 | −750.955 | |||
| (L) | 4.5 | 0.54 | 3133.78 | 1.03 | 1.09 | 5327.46 | 0.999261 | −774.827 |
| (G) | 4.5 | 0.24 | 12,531.1 | 0.02 | 24.0 | 106.96 | 0.999264 | −775.482 |
| (W) | 4.5 | 0.56 | 1912.33 | 0.57 | 1.96 | 3062.9 | 0.999264 | −775.337 |
| Mag300-2h | ||||||||
| (M) | 5.0 | 10.2 | 42,216.1 | 0.999860 | −222.430 | |||
| (L) | 4.3 | 10.3 | 28,108.2 | 0.69 | 3.12 | 35,634.2 | 0.999898 | −271.347 |
| (G) | 4.2 | 10.3 | 17,798.2 | 1.95 | 3.20 | 34,762.0 | 0.999896 | −269.014 |
| (W) | 4.2 | 10.3 | 37,355.8 | 1.40 | 3.28 | 34,033.7 | 0.999896 | −268.319 |
| Mag500-2h | ||||||||
| (M) | 16.7 | 60.5 | 14,924.9 | 0.998594 | 348.987 | |||
| (L) | 15.7 | 60.7 | 14,376.2 | 0.19 | 44.7 | 14,640.8 | 0.998595 | 350.913 |
| (G) | 15.6 | 60.7 | 580.66 | 25.2 | 44.8 | 14,614.0 | 0.998595 | 350.908 |
| (W) | 15.2 | 60.8 | 15,757.3 | 5.16 | 45.2 | 14,494.8 | 0.998596 | 350.880 |
| Mag600-2h | ||||||||
| (M) | 63.2 | 57.7 | 10,937.0 | 0.999038 | 628.309 | |||
| (L) | 45.1 | 61.1 | 6405.28 | 0.68 | 81.6 | 8071.44 | 0.999162 | 608.134 |
| (G) | 39.1 | 62.6 | 5723.98 | 1.14 | 103 | 6545.34 | 0.999176 | 605.332 |
| (W) | 40.1 | 62.3 | 6898.42 | 1.10 | 101 | 6657.45 | 0.999177 | 605.160 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodríguez, M.J.J.; Vieira, D.S.; Nery, R.C.; Dias, G.S.; Santos, I.A.d.; Mendes, R.d.S.; Cotica, L.F. On the Distribution of Magnetic Moments in a System of Magnetic Nanoparticles. Magnetochemistry 2022, 8, 129. https://doi.org/10.3390/magnetochemistry8100129
Rodríguez MJJ, Vieira DS, Nery RC, Dias GS, Santos IAd, Mendes RdS, Cotica LF. On the Distribution of Magnetic Moments in a System of Magnetic Nanoparticles. Magnetochemistry. 2022; 8(10):129. https://doi.org/10.3390/magnetochemistry8100129
Chicago/Turabian StyleRodríguez, Max Javier Jáuregui, Denner Serafim Vieira, Renato Cardoso Nery, Gustavo Sanguino Dias, Ivair Aparecido dos Santos, Renio dos Santos Mendes, and Luiz Fernando Cotica. 2022. "On the Distribution of Magnetic Moments in a System of Magnetic Nanoparticles" Magnetochemistry 8, no. 10: 129. https://doi.org/10.3390/magnetochemistry8100129
APA StyleRodríguez, M. J. J., Vieira, D. S., Nery, R. C., Dias, G. S., Santos, I. A. d., Mendes, R. d. S., & Cotica, L. F. (2022). On the Distribution of Magnetic Moments in a System of Magnetic Nanoparticles. Magnetochemistry, 8(10), 129. https://doi.org/10.3390/magnetochemistry8100129








