Electronic Structure of Tyrosyl D Radical of Photosystem II, as Revealed by 2D-Hyperfine Sublevel Correlation Spectroscopy
Abstract
1. Introduction
2. Materials and Methods
2.1. Preparation of Spinach PSII Membranes
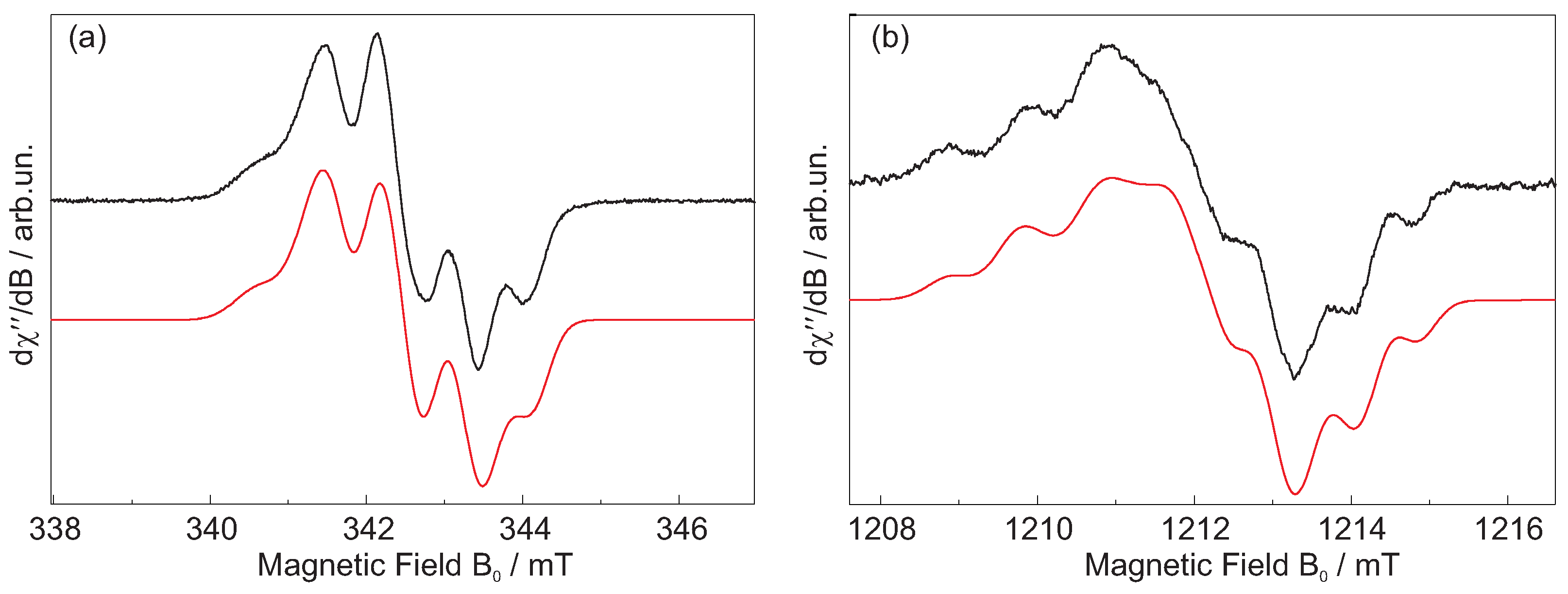
2.2. EPR Spectroscopy
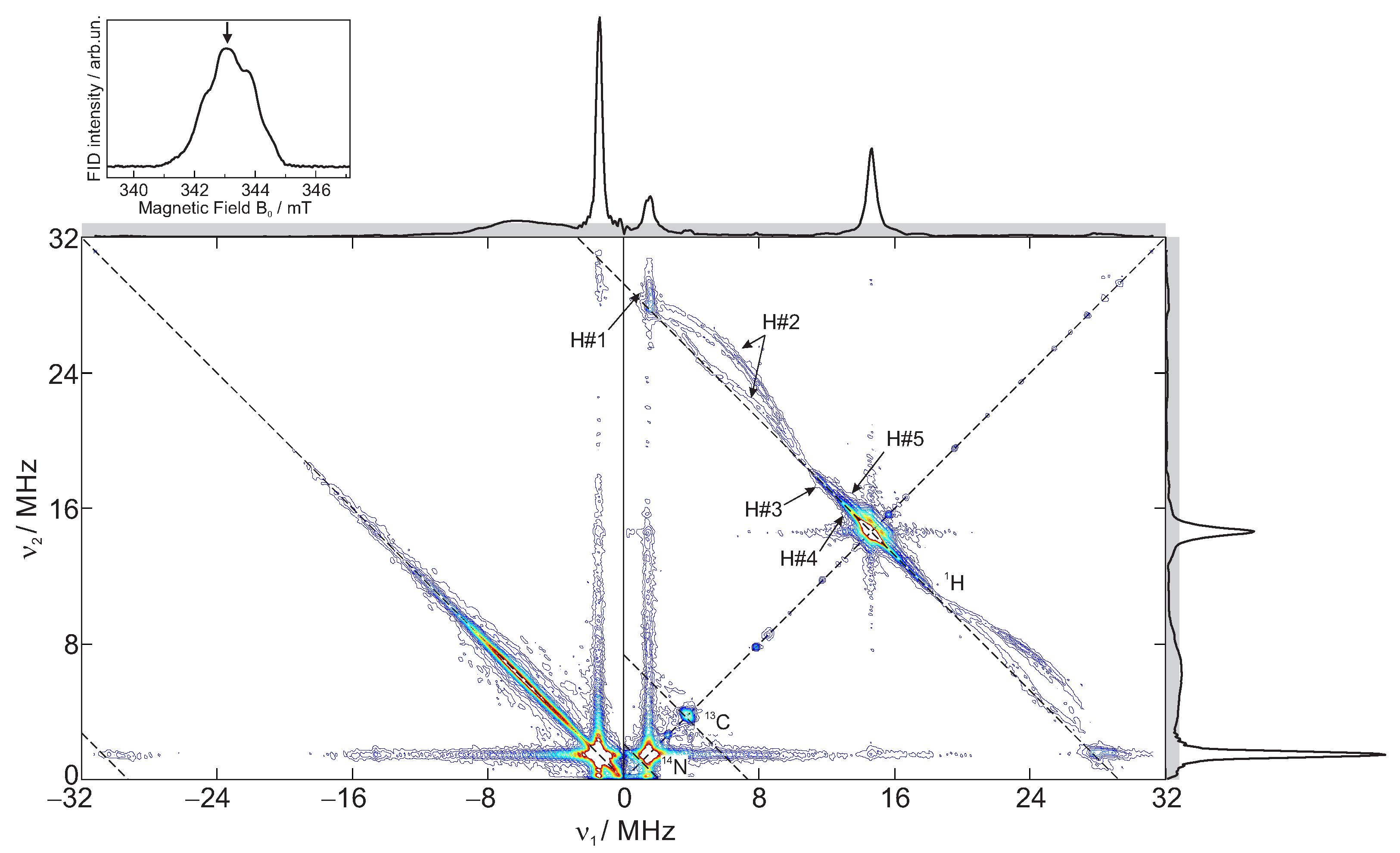
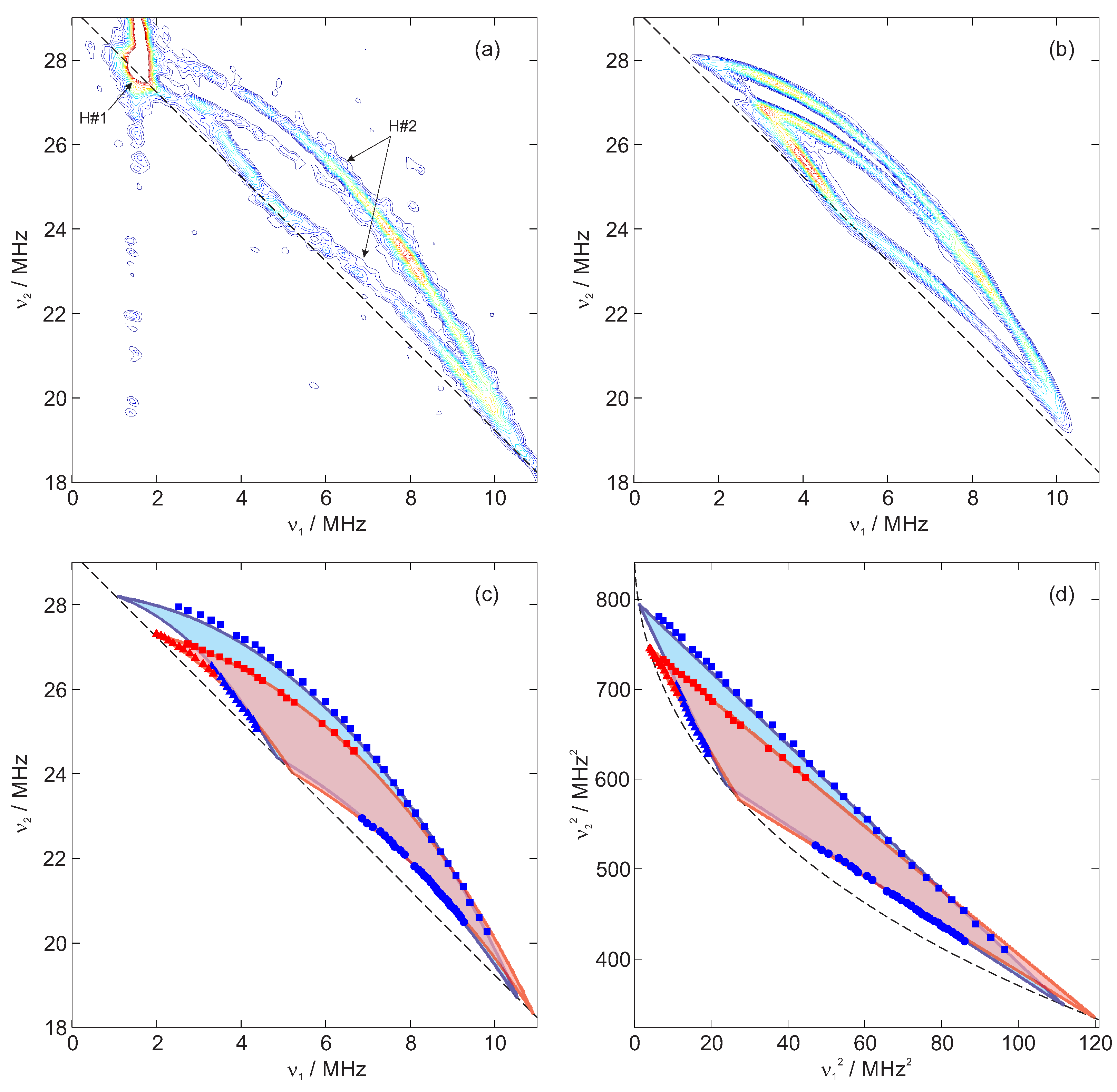
2.3. Analysis of HYSCORE Spectra
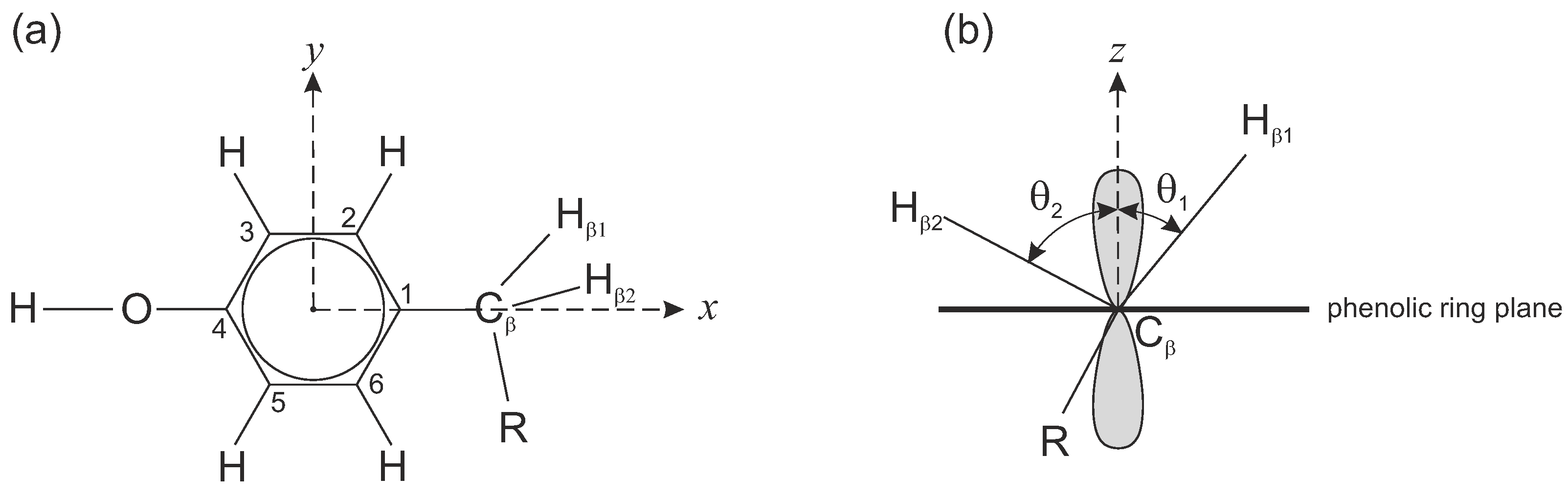
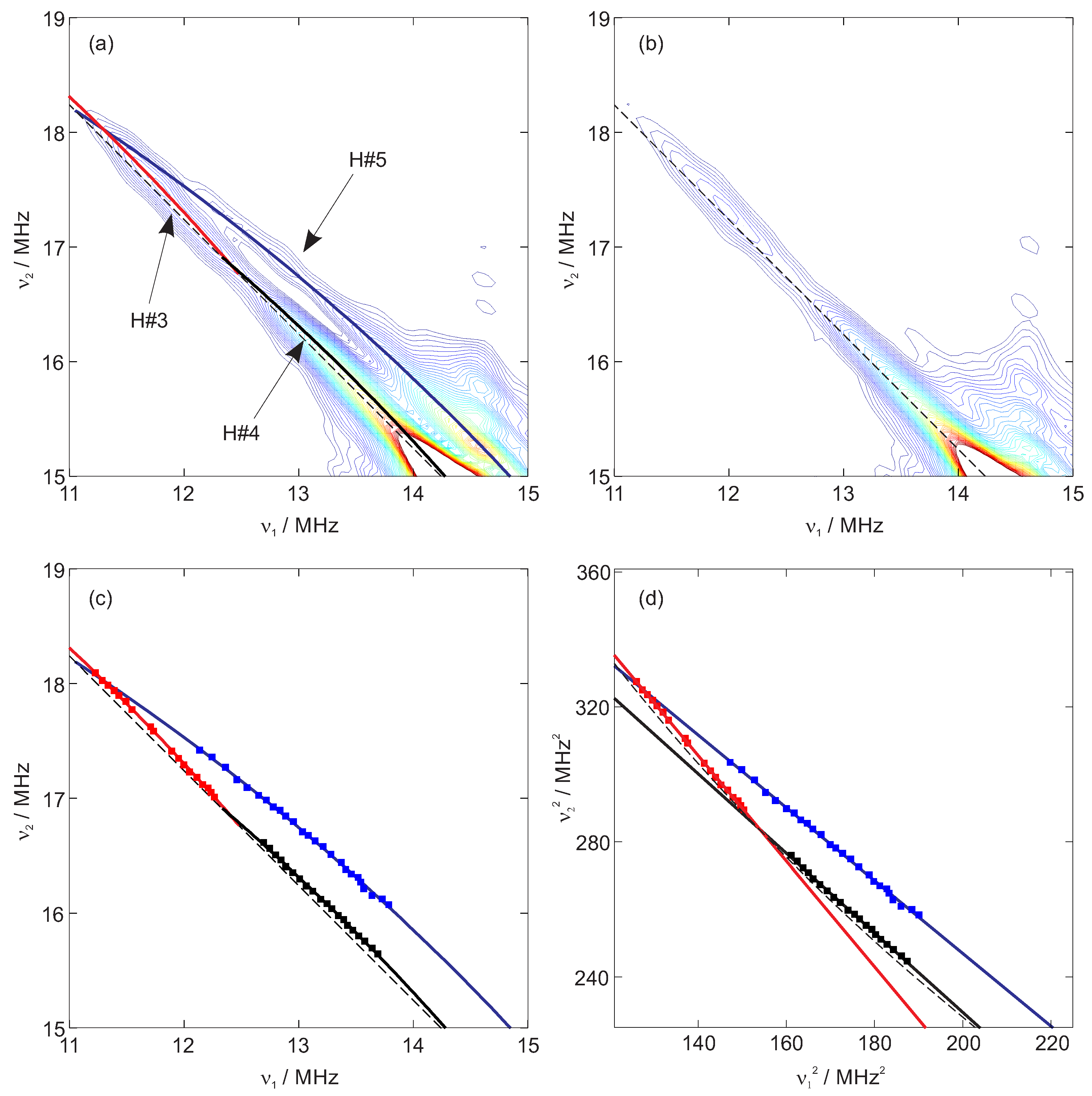
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cox, N.; Pantazis, D.A.; Lubitz, W. Current Understanding of the Mechanism of Water Oxidation in Photosystem II and Its Relation to XFEL Data. Annu. Rev. Biochem. 2020, 89, 795–820. [Google Scholar] [CrossRef] [PubMed]
- Umena, Y.; Kawakami, K.; Shen, J.; Kamiya, N. Crystal structure of oxygen-evolving photosystem II at a resolution of 1.9Å. Nature 2011, 473, 55–60. [Google Scholar] [CrossRef]
- Suga, M.; Akita, F.; Hirata, K.; Ueno, G.; Murakami, H.; Nakajima, Y.; Shimizu, T.; Yamashita, K.; Yamamoto, M.; Ago, H.; et al. Native structure of photosystem II at 1.95 angstrom resolution viewed by femtosecond X-ray pulses. Nature 2015, 517, 99–103. [Google Scholar] [CrossRef]
- Kok, B.; Forbush, B.; McGloin, M. Cooperation of Charges in Photosynthetic O2 Evolution–I. A Linear Four Step Mechanism. Photochem. Photobiol. 1970, 11, 457–475. [Google Scholar] [CrossRef]
- Diner, B.; Britt, R. The redox-active tyrosine Yz and YD. In Photosystem II: The Light-Driven Water: Plastoquinone Oxidoreductase; Wydrzynski, T., Satoh, K., Eds.; Springer: Dordrecht, The Netherlands, 2005; pp. 207–233. [Google Scholar]
- Styring, S.; Sjöholm, J.; Mamedov, F. Two tyrosines that changed the world: Interfacing the oxidizing power of photochemistry to water splitting in photosystem II. Biochim. Biophys. Acta Bioenerg. 2012, 1817, 76–87. [Google Scholar] [CrossRef] [PubMed]
- Koulougliotis, D.; Tang, X.; Diner, B.; Brudvig, G. Spectroscopic Evidence for the Symmetric Location of Tyrosines D and Z in Photosystem II. Biochemistry 1995, 34, 2850–2856. [Google Scholar] [CrossRef] [PubMed]
- Faller, P.; Debus, R.J.; Brettel, K.; Sugiura, M.; Rutherford, A.W.; Boussac, A. Rapid formation of the stable tyrosyl radical in photosystem II. Proc. Natl. Acad. Sci. USA 2001, 98, 14368–14373. [Google Scholar] [CrossRef] [PubMed]
- Nakamura, S.; Noguchi, T. Infrared Detection of a Proton Released from Tyrosine YD to the Bulk upon Its Photo-oxidation in Photosystem II. Biochemistry 2015, 54, 5045–5053. [Google Scholar] [CrossRef]
- Saito, K.; Shen, J.R.; Ishida, T.; Ishikita, H. Short Hydrogen Bond between Redox-Active Tyrosine YZ and D1-His190 in the Photosystem II Crystal Structure. Biochemistry 2011, 50, 9836–9844. [Google Scholar] [CrossRef] [PubMed]
- Sirohiwal, A.; Neese, F.; Pantazis, D.A. Microsolvation of the Redox-Active Tyrosine-D in Photosystem II: Correlation of Energetics with EPR Spectroscopy and Oxidation-Induced Proton Transfer. J. Am. Chem. Soc. 2019, 141, 3217–3231. [Google Scholar] [CrossRef]
- Renger, G.; Renger, T. Photosystem II: The machinery of photosynthetic water splitting. Photosynth. Res. 2008, 98, 53–80. [Google Scholar] [CrossRef] [PubMed]
- Rappaport, F.; Blanchard-Desce, M.; Lavergne, J. Kinetics of electron transfer and electrochromic change during the redox transitions of the photosynthetic oxygen-evolving complex. Biochim. Biophys. Acta Bioenerg. 1994, 1184, 178–192. [Google Scholar] [CrossRef]
- Haumann, M.; Liebisch, P.; Müller, C.; Barra, M.; Grabolle, M.; Dau, H. Photosynthetic O2 Formation Tracked by Time-Resolved X-ray Experiments. Science 2005, 310, 1019–1021. [Google Scholar] [CrossRef] [PubMed]
- Klauss, A.; Haumann, M.; Dau, H. Seven Steps of Alternating Electron and Proton Transfer in Photosystem II Water Oxidation Traced by Time-Resolved Photothermal Beam Deflection at Improved Sensitivity. J. Phys. Chem. B 2015, 119, 2677–2689. [Google Scholar] [CrossRef]
- Styring, S.; Rutherford, A.W. In the oxygen-evolving complex of photosystem II the S0 state is oxidized to the S1 state by D+ (signal IIslow). Biochemistry 1987, 26, 2401–2405. [Google Scholar] [CrossRef]
- Vass, I.; Styring, S. pH-Dependent charge equilibria between tyrosine-D and the S states in photosystem II. Estimation of relative midpoint redox potentials. Biochemistry 1991, 30, 830–839. [Google Scholar] [CrossRef]
- Buser, C.A.; Thompson, L.K.; Diner, B.A.; Brudvig, G.W. Electron-transfer reactions in manganese-depleted photosystem II. Biochemistry 1990, 29, 8977–8985. [Google Scholar] [CrossRef]
- Debus, R.J.; Barry, B.A.; Babcock, G.T.; McIntosh, L. Site-directed mutagenesis identifies a tyrosine radical involved in the photosynthetic oxygen-evolving system. Proc. Natl. Acad. Sci. USA 1988, 85, 427–430. [Google Scholar] [CrossRef] [PubMed]
- Vermaas, W.F.; Renger, G.; Dohnt, G. The reduction of the oxygen-evolving system in chloroplasts by thylakoid components. Biochim. Biophys. Acta Bioenerg. 1984, 764, 194–202. [Google Scholar] [CrossRef]
- Messinger, J.; Renger, G. Generation, oxidation by the oxidized form of the tyrosine of polypeptide D2, and possible electronic configuration of the redox states S0, S-1, and S-2 of the water oxidase in isolated spinach thylakoids. Biochemistry 1993, 32, 9379–9386. [Google Scholar] [CrossRef] [PubMed]
- Ananyev, G.M.; Sakiyan, I.; Diner, B.A.; Dismukes, G.C. A Functional Role for Tyrosine-D in Assembly of the Inorganic Core of the Water Oxidase Complex of Photosystem II and the Kinetics of Water Oxidation. Biochemistry 2002, 41, 974–980. [Google Scholar] [CrossRef]
- Boerner, R.; Bixby, K.; Nguyen, A.; Noren, G.; Debus, R.; Barry, B. Removal of stable tyrosine radical D+ affects the structure or redox properties of tyrosine Z in manganese-depleted photosystem II particles from Synechocystis 6803. J. Biol. Chem. 1993, 268, 1817–1823. [Google Scholar] [CrossRef]
- Havelius, K.G.V.; Styring, S. pH Dependent Competition between YZ and YD in Photosystem II Probed by Illumination at 5 K. Biochemistry 2007, 46, 7865–7874. [Google Scholar] [CrossRef] [PubMed]
- Deak, Z.; Vass, I.; Strying, S. Redox interaction of Tyrosine-D with the S-states of the water-oxidizing complex in intact and chloride-depleted Photosystem II. Biochim. Biophys. Acta Bioenerg. 1994, 1185, 65–74. [Google Scholar] [CrossRef]
- Feyziyev, Y.; Rotterdam, B.J.; Bernát, G.; Styring, S. Electron transfer from cytochrome b559 and tyrosineD to the S2 and S3 states of the water oxidizing complex in photosystem II. Chem. Phys. 2003, 294, 415–431. [Google Scholar] [CrossRef]
- Mamedov, F.; Smith, P.J.; Styring, S.; Pace, R.J. Relaxation behaviour of the tyrosine YD radical in photosystem II: Evidence for strong dipolar interaction with paramagnetic centers in the S1 and S2 states. Phys. Chem. Chem. Phys. 2004, 6, 4890–4896. [Google Scholar] [CrossRef]
- Rutherford, A.; Boussac, A.; Faller, P. The stable tyrosyl radical in Photosystem II: Why D? Biochim. Biophys. Acta Bioenerg. 2004, 1655, 222–230. [Google Scholar] [CrossRef]
- Saito, K.; Ishida, T.; Sugiura, M.; Kawakami, K.; Umena, Y.; Kamiya, N.; Shen, J.R.; Ishikita, H. Distribution of the Cationic State over the Chlorophyll Pair of the Photosystem II Reaction Center. J. Am. Chem. Soc. 2011, 133, 14379–14388. [Google Scholar] [CrossRef]
- Diner, B.A.; Bautista, J.A.; Nixon, P.J.; Berthomieu, C.; Hienerwadel, R.; Britt, R.D.; Vermaas, W.F.J.; Chisholm, D.A. Coordination of proton and electron transfer from the redox-active tyrosine, YZ, of Photosystem II and examination of the electrostatic influence of oxidized tyrosine, YD˙(H+). Phys. Chem. Chem. Phys. 2004, 6, 4844–4850. [Google Scholar] [CrossRef]
- Jeans, C.; Schilstra, M.J.; Ray, N.; Husain, S.; Minagawa, J.; Nugent, J.H.A.; Klug, D.R. Replacement of Tyrosine D with Phenylalanine Affects the Normal Proton Transfer Pathways for the Reduction of P680+ in Oxygen-Evolving Photosystem II Particles from Chlamydomonas. Biochemistry 2002, 41, 15754–15761. [Google Scholar] [CrossRef] [PubMed]
- Magnuson, A.; Rova, M.; Mamedov, F.; Fredriksson, P.O.; Styring, S. The role of cytochrome b559 and tyrosineD in protection against photoinhibition during in vivo photoactivation of Photosystem II. Biochim. Biophys. Acta Bioenerg. 1999, 1411, 180–191. [Google Scholar] [CrossRef]
- Deligiannakis, Y.; Ivancich, A.; Rutherord, A. 2D-Hyperfine sublevel correlation spectroscopy of tyrosyl radicals. Spectrochim. Acta Part A 2002, 58, 1191–1200. [Google Scholar] [CrossRef]
- Mino, H.; Astashkin, A.V.; Kawamori, A. An EPR and pulsed ENDOR study of the structure of tyrosine Z• in Tris-treated photosystem II. Spectrochim. Acta Part A 1997, 53, 1465–1483. [Google Scholar] [CrossRef]
- Teutloff, C.; Pudollek, S.; Keßen, S.; Broser, M.; Zouni, A.; Bittl, R. Electronic structure of the tyrosine D radical and the water-splitting complex from pulsed ENDOR spectroscopy on photosystem II single crystals. Phys. Chem. Chem. Phys. 2009, 11, 6715–6726. [Google Scholar] [CrossRef] [PubMed]
- Mark, B.; Coates, C.S.; Sugimura, S.; Baldansuren, A.; Ku, J.; Debus, R.J.; Lakshmi, K. Determining the Electronic Structure of Paramagnetic Intermediates in membrane proteins: A high-resolution 2D 1H hyperfine sublevel correlation study of the redox-active tyrosines of photosystem II. Biochim. Biophys. Acta Biomembr. 2020, 1862, 183422. [Google Scholar] [CrossRef] [PubMed]
- Warncke, K.; McCracken, J.; Babcock, G.T. Structure of the YD Tyrosine Radical in Photosystem II as Revealed by 2H Electron Spin Echo Envelope Modulation (ESEEM) Spectroscopic Analysis of Hydrogen Hyperfine Interactions. J. Am. Chem. Soc. 1994, 116, 7332–7340. [Google Scholar] [CrossRef]
- Chatterjee, R.; Coates, C.S.; Milikisiyants, S.; Lee, C.I.; Wagner, A.; Poluektov, O.G.; Lakshmi, K.V. High-Frequency Electron Nuclear Double-Resonance Spectroscopy Studies of the Mechanism of Proton-Coupled Electron Transfer at the Tyrosine-D Residue of Photosystem II. Biochemistry 2013, 52, 4781–4790. [Google Scholar] [CrossRef]
- Sjöholm, J.; Mamedov, F.; Styring, S. Spectroscopic Evidence for a Redox-Controlled Proton Gate at Tyrosine D in Photosystem II. Biochemistry 2014, 53, 5721–5723. [Google Scholar] [CrossRef]
- Hasler, L.; Ghanotakis, D.; Fedtke, B.; Spyridaki, A.; Miller, M.; Müller, S.A.; Engel, A.; Tsiotis, G. Structural Analysis of Photosystem II: Comparative Study of Cyanobacterial and Higher Plant Photosystem II Complexes. J. Struct. Biol. 1997, 119, 273–283. [Google Scholar] [CrossRef] [PubMed]
- McDermott, A.E.; Yachandra, V.K.; Guiles, R.D.; Cole, J.L.; Dexheimer, S.L.; Britt, R.D.; Sauer, K.; Klein, M.P. Characterization of the manganese oxygen-evolving complex and the iron-quinone acceptor complex in photosystem II from a thermophilic cyanobacterium by electron paramagnetic resonance and x-ray absorption spectroscopy. Biochemistry 1988, 27, 4021–4031. [Google Scholar] [CrossRef]
- Yachandra, V.K.; Sauer, K.; Klein, M.P. Manganese Cluster in Photosynthesis: Where Plants Oxidize Water to Dioxygen. Chem. Rev. 1996, 96, 2927–2950. [Google Scholar] [CrossRef]
- Boussac, A.; Kuhl, H.; Un, S.; Rögner, M.; Rutherford, A.W. Effect of Near-Infrared Light on the S2-State of the Manganese Complex of Photosystem II from Synechococcus elongatus. Biochemistry 1998, 37, 8995–9000. [Google Scholar] [CrossRef]
- Zahariou, G.; Ioannidis, N.; Sanakis, Y.; Pantazis, D.A. Arrested Substrate Binding Resolves Catalytic Intermediates in Higher-Plant Water Oxidation. Angew. Chem. Int. Ed. 2021, 60, 3156–3162. [Google Scholar] [CrossRef] [PubMed]
- Berthold, D.A.; Babcock, G.T.; Yocum, C.F. A highly resolved, oxygen-evolving photosystem II preparation from spinach thylakoid membranes: EPR and electron-transport properties. FEBS Lett. 1981, 134, 231–234. [Google Scholar] [CrossRef]
- Ford, R.; Evans, M. Isolation of a photosystem 2 preparation from higher plants with highly enriched oxygen evolution activity. FEBS Lett. 1983, 160, 159–164. [Google Scholar] [CrossRef]
- Stoll, S.; Schweiger, A. EasySpin, a comprehensive software package for spectral simulation and analysis in EPR. J. Magn. Reson. 2006, 178, 42–55. [Google Scholar] [CrossRef] [PubMed]
- Dikanov, S.A.; Tyryshkin, A.M.; Bowman, M.K. Intensity of Cross-Peaks in Hyscore Spectra of S = 1/2, I = 1/2 Spin Systems. J. Magn. Reson. 2000, 144, 228–242. [Google Scholar] [CrossRef]
- Dikanov, S.; Bowman, M. Cross-Peak Lineshape of Two-Dimensional ESEEM Spectra in Disordered S = 1/2, I = 1/2 Spin Systems. J. Magn. Reson. Ser. A 1995, 116, 125–128. [Google Scholar] [CrossRef]
- Schweiger, A.; Jeschke, G. Principles of Pulse Electron Paramagnetic Resonance; Oxford University Press: New York, NY, USA, 2001. [Google Scholar]
- Stoll, S.; Calle, C.; Mitrikas, G.; Schweiger, A. Peak suppression in ESEEM spectra of multinuclear spin systems. J. Magn. Reson. 2005, 177, 93–101. [Google Scholar] [CrossRef] [PubMed]
- O’ Malley, P.J.; MacFarlane, A.J.; Rigby, S.E.; Nugent, J.H. The geometry and spin density distribution of the tyrosyl radical: A molecular orbital study. Biochim. Biophys. Acta Bioenerg. 1995, 1232, 175–179. [Google Scholar] [CrossRef][Green Version]
- McConnell, H.M.; Chesnut, D.B. Negative Spin Densities in Aromatic Radicals. J. Chem. Phys. 1957, 27, 984–985. [Google Scholar] [CrossRef]
- McConnell, H.M. Spin Density Matrices for Paramagnetic Molecules. J. Chem. Phys. 1958, 28, 1188–1192. [Google Scholar] [CrossRef]
- Heller, C.; McConnell, H.M. Radiation Damage in Organic Crystals. II. Electron Spin Resonance of (CO2H)CH2CH(CO2H) in β-Succinic Acid. J. Chem. Phys. 1960, 32, 1535–1539. [Google Scholar] [CrossRef]
- Fessenden, R.W.; Schuler, R.H. Electron Spin Resonance Studies of Transient Alkyl Radicals. J. Chem. Phys. 1963, 39, 2147–2195. [Google Scholar] [CrossRef]
- Nakazawa, S.; Ishii, A.; Minagawa, J.; Ono, T. Application of 2D-HYSCORE spectroscopy to tyrosine radicals YD and YZ in photosystem II for evaluation of spin density distributions. Chem. Phys. Lett. 2005, 405, 318–322. [Google Scholar] [CrossRef]
- Force, D.A.; Randall, D.W.; Britt, R.D.; Tang, X.S.; Diner, B.A. 2H ESE-ENDOR study of hydrogen bonding to the tyrosine radicals YD.bul. and YZ.bul. of photosystem II. J. Am. Chem. Soc. 1995, 117, 12643–12644. [Google Scholar] [CrossRef]
- Keßen, S.; Teutloff, C.; Kern, J.; Zouni, A.; Bittl, R. High-Field 2H-Mims-ENDOR Spectroscopy on PSII Single Crystals: Hydrogen Bonding of YD. ChemPhysChem 2010, 11, 1275–1282. [Google Scholar] [CrossRef]
- Gilchrist, M.L.; Ball, J.A.; Randall, D.W.; Britt, R.D. Proximity of the manganese cluster of photosystem II to the redox-active tyrosine YZ. Proc. Natl. Acad. Sci. USA 1995, 92, 9545–9549. [Google Scholar] [CrossRef]
- Farrar, C.T.; Gerfen, G.J.; Griffin, R.G.; Force, D.A.; Britt, R.D. Electronic Structure of the YD Tyrosyl Radical in Photosystem II: A High-Frequency Electron Paramagnetic Resonance Spectroscopic and Density Functional Theoretical Study. J. Phys. Chem. B 1997, 101, 6634–6641. [Google Scholar] [CrossRef]
- Hofbauer, W.; Zouni, A.; Bittl, R.; Kern, J.; Orth, P.; Lendzian, F.; Fromme, P.; Witt, H.T.; Lubitz, W. Photosystem II single crystals studied by EPR spectroscopy at 94 GHz: The tyrosine radical Y. Proc. Natl. Acad. Sci. USA 2001, 98, 6623–6628. [Google Scholar] [CrossRef]
- Fotinou, C.; Kokkinidis, M.; Fritzsch, G.; Haase, W.; Michel, H.; Ghanotakis, D.F. Characterization of a Photosystem II core and its three-dimensional crystals. Photosynth. Res. 1993, 37, 41–48. [Google Scholar] [CrossRef] [PubMed]
| Hyperfine Coupling Constants in MHz | ||||||||
|---|---|---|---|---|---|---|---|---|
| Peak No. | a | T | Assignment | |||||
| H#1 | 32.0 | 25.9 | 25.9 | 27.9 | 2.0 | 0.38 | ||
| H#2 | −27.5 | −8.1 | −19.9 | −18.5 | 5.2 | 3.8 | 0.27 | 3 |
| H#2 | −25.5 | −8.0 | −19.1 | −17.5 | 4.8 | 3.1 | 0.25 | 5 |
| H#3 | 8.6 | 4.3 | 4.3 | 5.7 | 1.4 | −0.08 | 2, 6, | |
| H#4 | 4.6 | 0.2 | 0.2 | 1.7 | 1.5 | protein | ||
| H#5 | 7.2 | −4.8 | −4.8 | −0.8 | 4.0 | H-bond | ||
| 3,5 Proton | 2,6 Proton | Proton | Proton | Comment | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 10 | 15 | 26 | 3.5 | 3.5 | 8.8 | 26.6 | 26.6 | 31.7 | 3.5 | 3.5 | 8.8 | spinach Mn-depleted, pH = 6.5 [33] |
| −24.4 | −8.4 | −21.9 | 4.7 | 7.4 | 4.7 | 30.6 | 24.3 | 24.3 | 7.4 | 4.7 | 4.7 | C. reinhardtii, Mn-depleted, pH = 6.5 [57] |
| 8 | 19.8 | 27.4 | 25.9 | Synechocystis, Mn-depleted, pH = 8.7 [36] | ||||||||
| 7.6 | 18.8 | 25.5 | ||||||||||
| −27.5 | −8.1 | −19.9 | 8.6 | 4.3 | 4.3 | 32.0 | 25.9 | 25.9 | 8.6 | 4.3 | 4.3 | spinach, S, pH = 6.5 [this study] |
| −25.5 | −8.0 | −19.1 | ||||||||||
| −25.7 | −7.6 | −19.0 | 4.7 | 7.4 | 1.5 | 32.2 | 26.8 | 26.0 | 9.3 | 3.4 | 4.0 | T. elongatus, S [35] |
| −27.3 | −8.4 | −20.2 | 4.5 | 7.1 | 1.4 | |||||||
| −29.07 | −7.85 | −22.46 | 5.02 | 9.29 | 3.02 | 32.88 | 27.79 | 27.34 | 8.27 | 3.32 | 2.89 | 3ox model computational [11] |
| −26.44 | −6.83 | −20.58 | 4.83 | 9.11 | 2.95 | |||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chrysina, M.; Zahariou, G.; Ioannidis, N.; Sanakis, Y.; Mitrikas, G. Electronic Structure of Tyrosyl D Radical of Photosystem II, as Revealed by 2D-Hyperfine Sublevel Correlation Spectroscopy. Magnetochemistry 2021, 7, 131. https://doi.org/10.3390/magnetochemistry7090131
Chrysina M, Zahariou G, Ioannidis N, Sanakis Y, Mitrikas G. Electronic Structure of Tyrosyl D Radical of Photosystem II, as Revealed by 2D-Hyperfine Sublevel Correlation Spectroscopy. Magnetochemistry. 2021; 7(9):131. https://doi.org/10.3390/magnetochemistry7090131
Chicago/Turabian StyleChrysina, Maria, Georgia Zahariou, Nikolaos Ioannidis, Yiannis Sanakis, and George Mitrikas. 2021. "Electronic Structure of Tyrosyl D Radical of Photosystem II, as Revealed by 2D-Hyperfine Sublevel Correlation Spectroscopy" Magnetochemistry 7, no. 9: 131. https://doi.org/10.3390/magnetochemistry7090131
APA StyleChrysina, M., Zahariou, G., Ioannidis, N., Sanakis, Y., & Mitrikas, G. (2021). Electronic Structure of Tyrosyl D Radical of Photosystem II, as Revealed by 2D-Hyperfine Sublevel Correlation Spectroscopy. Magnetochemistry, 7(9), 131. https://doi.org/10.3390/magnetochemistry7090131






