The Internal Field in a Ferromagnetic Crystal with Chiral Molecular Packing of Achiral Organic Radicals

Abstract

The achiral organic radical dinitrophenyl nitronyl nitroxide crystallizes in two enantiomorphs, both being chiral tetragonal space groups that are mirror images of each other. Muon-spin rotation experiments have been performed to study the magnetic properties of these crystals and demonstrate that long-range magnetic order is established below a temperature of 1.10(1) K. Two oscillatory components are detected in the muon data, which show two different temperature dependences.

1. Introduction

The impetus to synthesize purely organic ferromagnets [1,2] arises from the aim to achieve a goal that was once thought to be impossible: that of realising ferromagnetism in materials containing atoms that only have s and p electrons. Heisenberg’s celebrated theory of ferromagnetism [3], which was formulated back in the 1920s and that first introduced the concept of the exchange interaction, provided a rationalisation for the apparent mandatory requirement for atoms containing d and f electrons. Purely organic materials can contain unpaired spins, and organic radical molecules are relatively common, however few are stable enough to be assembled into crystalline structures. Moreover, even when that is possible, it is another matter to attempt to ferromagnetically align these spins. Ferromagnets are, in fact, rather rare, even among the elements (and, of course, the elemental ferromagnets that do exist are only in the d- or f-blocks).

Organic ferromagnetism was first achieved using a nitronyl nitroxide organic radical [4]. The unpaired electron density in nitronyl nitroxides is predominantly distributed over the two NO moieties with only some smaller spin density being distributed over the rest of the molecule. The central carbon atom of the ONCNO moiety is a node of the singly-occupied molecular orbital. Nitronyl nitroxides are chemically stable, but the vast majority of them do not show a long range ferromagnetic order. Therefore, the discovery of long-range ferromagnetism in the $\beta$ phase of para-nitrophenyl nitronyl nitroxide (C${}_{13}$H${}_{16}$N${}_3$O${}_4$, abbreviated to p-NPNN), was a major milestone, even though the transition temperature proved to be a disappointingly low 0.65 K [4]. A $\lambda$-type peak in the heat capacity at the critical temperature and a divergence in the ac susceptibility [4,5,6] indicated the transition to ferromagnetic order. $\mu$SR experiments on p-NPNN show the development of coherent spin precession oscillations below $T_{\mathrm{C}}$ [7,8]. A number of other nitronyl nitroxide systems were studied while using this technique [9,10,11,12,13], but the transition temperatures are all below 1 K.

Chirality [14] has recently been used in designing new chiral catalysts [15], developing organic spin filters [16], and investigating spin-dependent tunnelling through chiral molecules [17,18,19]. It has an important role in photochemistry that may have been important in the origin of life [20]. Therefore, the phenomenon of structural or magnetic chirality is an attractive feature to engineer in nitronyl nitroxide magnets, however preparing a chiral molecular crystal from achiral radicals in a controlled manner is a formidable task. It was first achieved ten years ago through the preparation of a crystal containing nitronyl nitroxide radicals, in which there is a chiral packing of the molecular units [21]. The compound is 3,5-dinitrophenyl nitronyl nitroxide (DNPNN), a molecule that is itself achiral (see the molecular structure depicted in Figure 1a) and optically inactive when dissolved in a solvent, but that is found to crystallize in two enantiomorphs, one of which is a chiral tettragonal space group of P4${}_3$ (see Figure 1b). This has a left-handed, counterclockwise stacking of radical molecules along the fourfold screw axes. The other enantiomorph has the P4${}_1$ space group and is its mirror image. The magnetic susceptibility fits to a one-dimensional Heisenberg ferromagnetic model with intrachain $2J/k_{\mathrm{B}}=12$ K (and weak interchain $2z{J}^{\prime }/k_{\mathrm{B}}\approx 1$ K). On the basis of magnetic susceptibility and heat capacity measurements [21], the system is believed to undergo a ferromagnetic phase transition at $T_{\mathrm{C}}=1.1$ K, and the entropy that is found by heat capacity is equal to $Rln2$, as expected for a system of $S=\frac{1}{2}$ spins. The magnetic behaviour of the left-handed form and right-handed form are identical, but it is possible to prepare crystals of one type or the other [21]. In this paper, we report the results of a muon-spin rotation ($\mu$SR) study of this compound that shed further light on the magnetic properties of this material.

2. $\mathit{\mu }$SR Experiment

The technique of muon-spin rotation [22,23,24,25] is very effective in establishing three-dimensional ordering in low-dimensional magnets [26,27]. This is because, below the critical temperature, a spontaneous precession of the muon spin-polarization in zero-applied field can be observed (see e.g., Refs. [28,29,30,31] for examples in organic and molecular magnets), with its frequency being proportional to the order parameter. Of course, ordering can be detected using thermodynamic measurements, but these are often dominated by the effect of intrachain interactions in low-dimensional magnets. For example, three-dimensional ordering in a very anisotropic spin chain is only associated with a tiny fraction of the total entropy. As the sample is cooled, very long correlated segments begin to develop on the individual chains well in advance of the appearance of long range order [32]). Therefore, $\mu$SR experiments provide a clear and unambiguous signal of long range order. Furthermore, the magnetic susceptibility measurements can be dominated by magnetic impurities and, so, it is desirable to have a test of intrinsic magnetic order. $\mu$SR provides this, as it is a volume probe; muons stop throughout the bulk of a sample and, therefore, can provide volume fraction information. Moreover, muons do not require hydrogen-containing samples to be deuterated, which makes $\mu$SR a more convenient technique for studying nitronyl nitroxide magnets in comparision to neutron scattering.

The MuSR spectrometer at the ISIS Pulsed Neutron and Muon Facility based at the Rutherford Appleton Laboratory was used to perform the $\mu$SR experiments. This spectrometer is equipped with a dilution refrigerator. In the experiment, spin-polarized positive muons (${\mu }^{+}$, momentum 28 MeV/c) were implanted into an array of small crystals of DNPNN that we prepared according to the method described in [21]. Our sample contained a mixture of crystals with different handedness, however one would not expect a $\mu$SR experiment to be able to distinguish between the samples that are mirror images of each other. The muons stop quickly (in <10${}^{-9}$ s), without a significant loss of spin-polarization. The observed quantity is the time evolution of the average muon spin polarization $P_z\left(t\right)$, which can be inferred [22,23,24,25] via the asymmetry in the angular distribution of emitted decay positrons, being parameterized by an asymmetry function $A\left(t\right)$ that is proportional to $P_z\left(t\right)$. Figure 2 shows two representative spectra for our sample of DNPNN. In the higher temperature data, a relaxing signal is observed, which is consistent with spin fluctuations, but not magnetic order. However, below $T_{\mathrm{C}}$, an oscillatory signal develops that contains two distinct frequency components (that are apparent from the beating pattern observed in the 0.65 K data in Figure 2). This identifies the presence of bulk long range magnetic order in the sample.

The $\mu$SR data are well described by the fitting function

$$A\left(t\right)=\left[\sum _{i=1}^2{A}_i{e}^{-{\mathsf{\Lambda }}_{i}t}cos\left(2\pi {\nu }_{i}t\right)\right]+A_3{e}^{-{\sigma }^2{t}^2}+A_{\mathrm{bg}},$$

(1)

where ${\mathsf{\Lambda }}_i$ is a relaxation rate and ${\nu }_i$ is a muon precession frequency (that is equal to ${\gamma }_{\mu }{B}_i/2\pi$, with $B_i$ being the magnetic field at the ith muon site, and ${\gamma }_{\mu }=2\pi \times 135.5$ MHz T${}^{-1}$ being the muon gyromagnetic ratio), and $A_{\mathrm{bg}}$ as the background contribution from those muons that stop outside the sample. The ratio of $A_1$ to $A_2$ was fixed across the temperature range (with $A_2/A_1\approx 3$) although there is some temperature dependence in the total oscillatory amplitude $A_1+A_2$ in our fits. In addition to the two oscillatory components, there is also a small Gaussian contribution (amplitude $A_3$ and relaxation rate $\sigma$) of unknown origin, although such components are commonly found in organic and molecular magnets [26]. These fits allow the extraction of the precession frequencies as a function of temperature, and these are plotted in Figure 3a. Their magnitudes, both reaching $\approx 1$ MHz as $T\to 0$, are typical for precession signals that are measured in nitronyl nitroxide magnets [8,9,10,11,12,13], which result from a relatively dilute array of spin-$\frac{1}{2}$ moments, one per radical molecule. Both of the precession frequencies follow a typical temperature dependence for a magnetic order parameter and that can be fitted using the phenomenological function $\nu \left(T\right)=\nu \left(0\right){(1-{(T/T_{\mathrm{C}})}^{\alpha })}^{\beta }$ (the best fit parameters given in

Table 1. Parameters for fitting the temperature dependence of the precession frequencies to $\nu \left(T\right)=\nu \left(0\right){(1-{(T/T_{\mathrm{C}})}^{\alpha })}^{\beta }$.

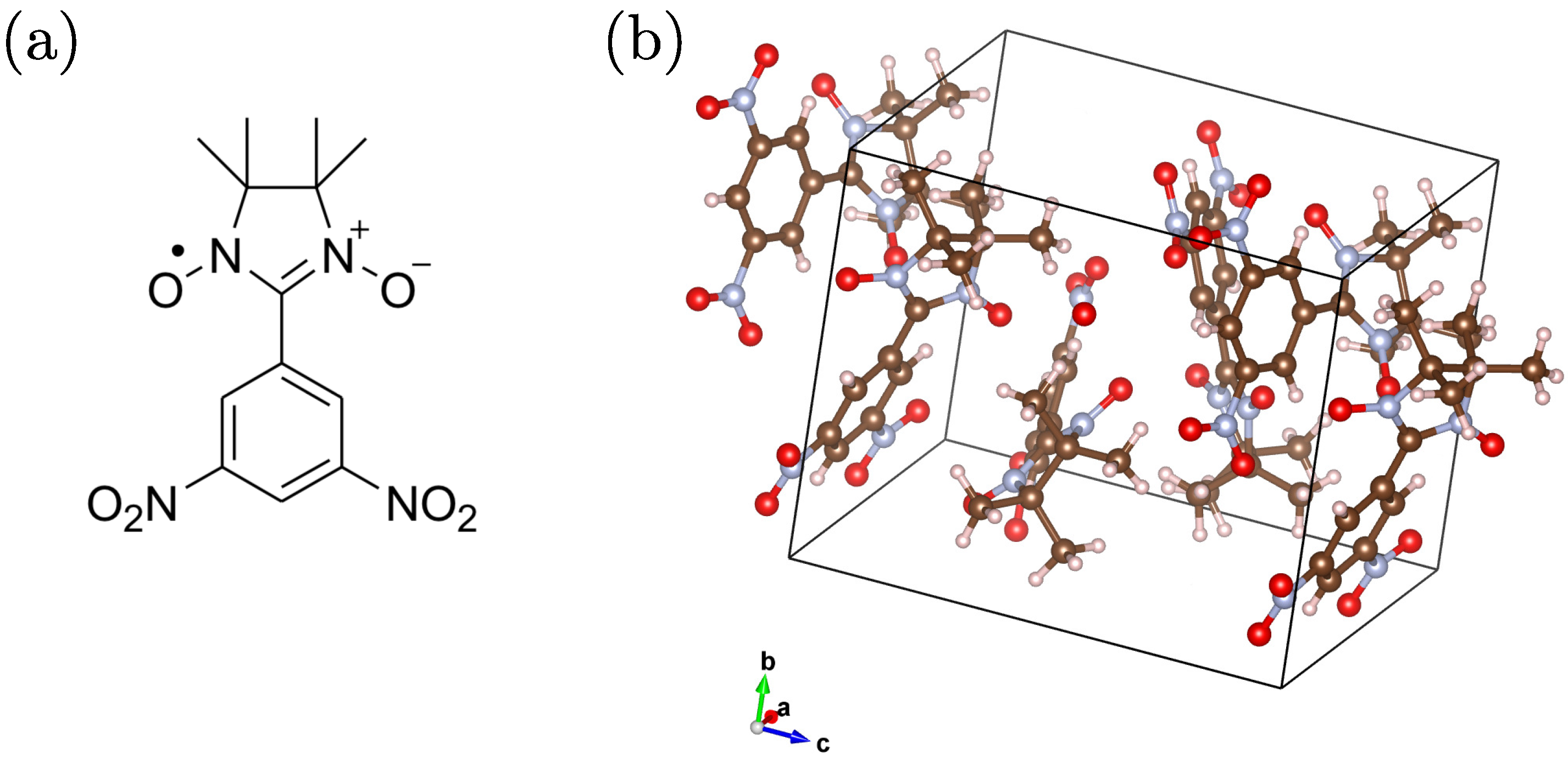
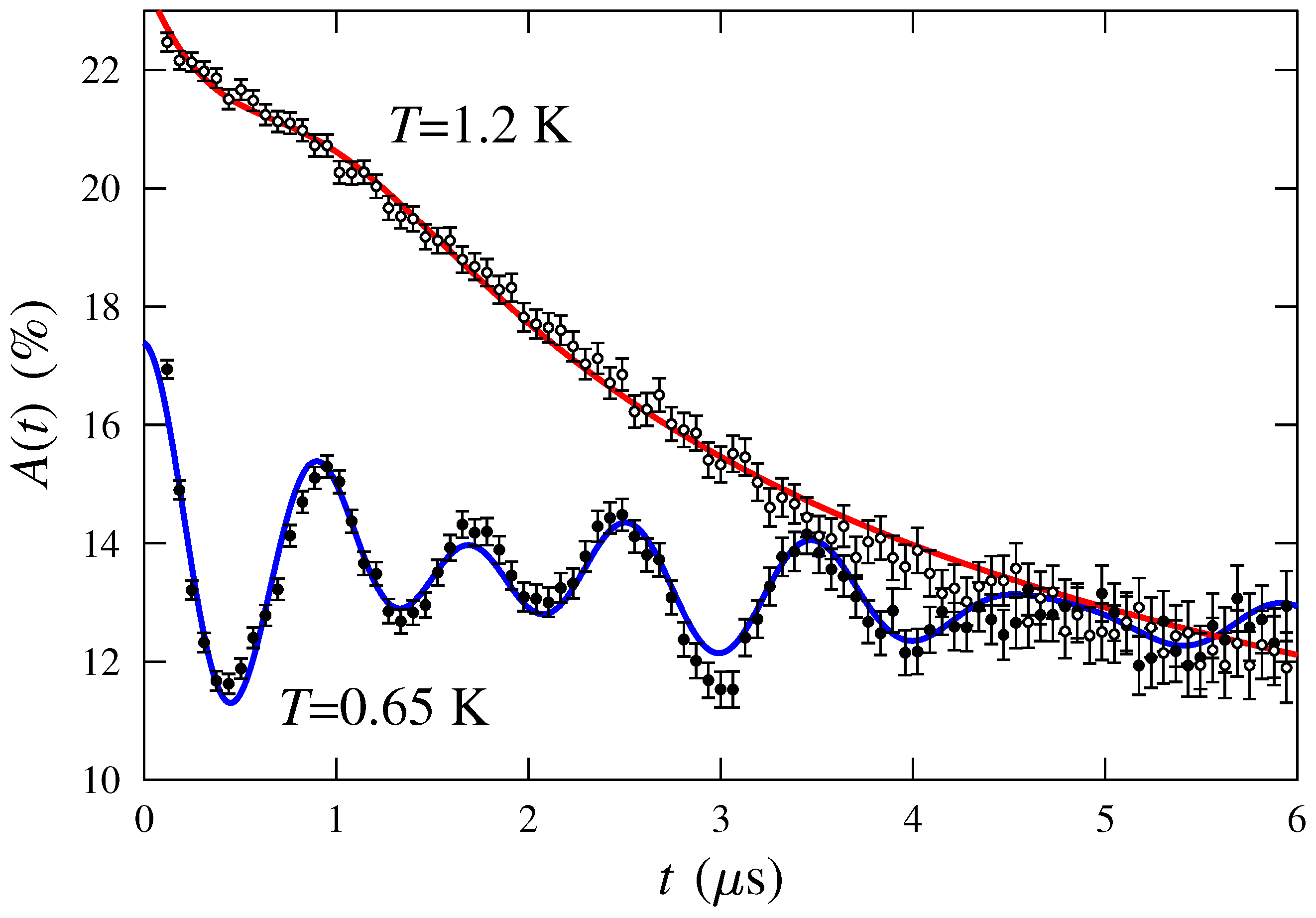
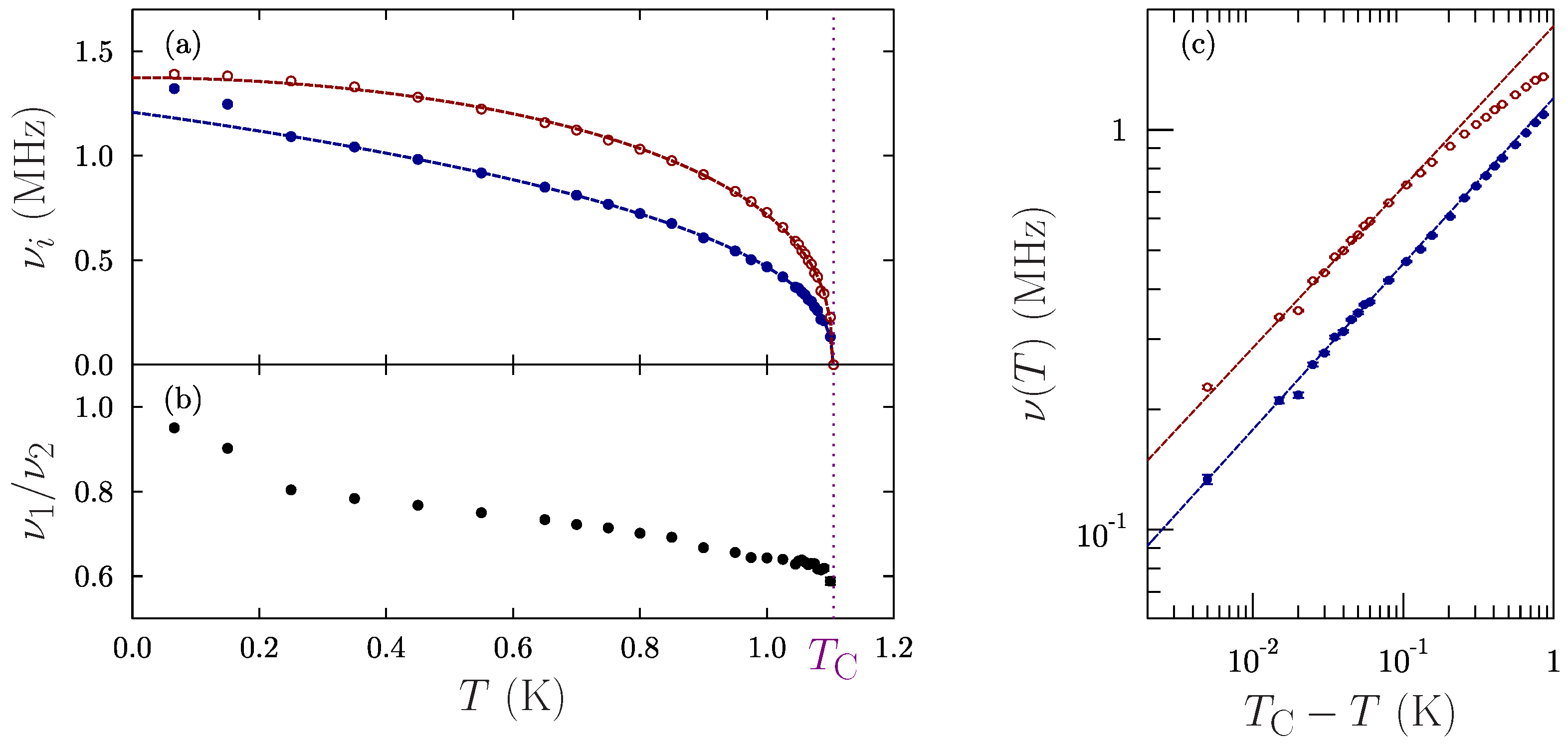
Parameter	Frequency 1	Frequency 2
$T_{\mathrm{C}}$ (K)	1.105(1)	1.104(1)
$\nu \left(0\right)$ (MHz)	1.21(2)	1.37(2)
$\alpha$	1.03(6)	1.96(14)
$\beta$	0.41(1)	0.37(1)

) and they provide a well constrained estimate of the critical temperature as $T_{\mathrm{C}}=1.105\left(1\right)$ K, which is consistent with the earlier measurements using magnetic susceptibility and heat capacity [21]. The value of $\alpha$, which is averaged over the two frequencies, is ≈1.5, as expected for magnons in a three-dimensional ferromagnet, so one can speculate that there are some structure factors that affect the sensitivity of two different sites to an additional antiferromagnetic component. Although the statistical error on our determination of $T_{\mathrm{C}}$ is 1 mK, the possible thermal offsets and calibration errors could lead to an uncertainty, which is an order of magnitude greater, and so our final determination of $T_{\mathrm{C}}$ from these measurements is 1.10(1) K.

Figure 3a also reveals a surprising feature, namely that the two precession frequencies do not follow exactly the same temperature dependence. Although they both collapse to zero at $T_{\mathrm{C}}$, they approach the same limit as $T\to 0$, but become increasingly different as $T\to T_{\mathrm{C}}$. This can be very clearly seen by plotting the ratio of the two frequencies as a function of temperature, as shown in Figure 3b. It is common in $\mu$SR data to find more than one frequency in the ordered state, but the individual frequencies usually follow the same temperature dependence, since they all are expected to be proportional to the order parameter, and so should only differ by a temperature-independent scaling factor. We return to this point in the following section.

Close to the transition, the two frequencies are expected to follow a scaling law $\nu \left(T\right)\propto M\left(T\right)\propto {(T_{\mathrm{C}}-T)}^{\beta }$, where $M\left(T\right)$ is the magnetization (or staggered magnetization for an antiferromagnet) and $\beta$ is a critical exponent. The value of $\beta$ can be crudely extracted using the phenomenological function that is discussed above, but a better estimate is obtained by focussing on the data measured close to the transition using the scaling plot that is shown in Figure 3c. This shows that scaling behaviour is followed well in the region $T_{\mathrm{C}}-T\ll 1$ and it yields $\beta =0.40\left(2\right)$ for the higher frequency and $\beta =0.41\left(2\right)$ for the lower frequency; hence, the two values are consistent with one another within error (and slightly larger than 0.37, the value obtained for frequency 2 by the less reliable phenomenological fit listed in Table 1). This is close to the value that is expected for the three-dimensional Heisenberg model ($\beta =0.369$ [33]). It is also much larger than the value that is found for a chiral antiferromagnetic layered molecular magnet [34]. We note that our measured value is even closer to the theoretical value for the O(4) model ($\beta =0.39$ [35]), although the link with such a model is not clear.

We carried out density functional theory (DFT) calculations to understand the nature of the muon stopping sites [36]. The calculations were carried out using the MuFinder software [37] and the plane-wave-based code Castep [38] while using the local density approximation. Muons, which were modelled by an ultrasoft hydrogen pseudopotential, were initialised in range of low-symmetry positions and the structure was allowed to relax (keeping the unit cell fixed) until the change in energy per ion was less than $2\times {10}^{-5}$ eV. We used a cutoff energy of 545 eV and a $1\times 1\times 1$ Monkhorst-Pack grid for k-point sampling. The calculations were made on both the unit cell and a supercell in order to check for any self-interaction effects between the muons.

The lowest-energy diamagnetic muon sites are found around 1 Å from those oxygen atoms that are bonded to the five-membered ring in the DNPNN molecule. Sites that are close to the nitrogen atoms on these rings are also stabilised, but they are found around 0.55 eV higher in energy. In addition, sites close to the aromatic ring are also stable, although these are found around 0.45 eV high in energy than the oxygen sites. The calculations were repeated with muonium implanted instead of the bare muon and leading to a very similar range of sites with slightly different energies. The oxygen site is still found to be the lowest-energy configuration.

3. Discussion

The demonstration of long range order below 1.10(1) K in DNPNN is the main result of this study. This value can be compared with other quasi-one-dimensional organic ferromagnets (all of which are driven into long-range three-dimensional order due to the weak interchain interactions), and some selected values are included in

Table 2. Magnetic properties of selected one-dimensional ferromagnets. p-NPNN=para-nitrophenyl nitronyl nitroxide, Me=CH${}_3$, DMSO = C${}_2$H${}_6$SO, p-CDTV = 3-(4-chlorophenyl)-1,5-dimethyl-6-thioxoverdazyl, TMSO = C${}_4$H${}_8$SO and CHAC = C${}_6$H${}_{11}$NH${}_3$CuCl${}_3$, p-CDpOV = 3-(4-chlorophenyl)-1,5-diphenyl-6-oxoverdazyl, TMCuC = tetramethylammonium copper trichloride, CHAB = C${}_6$H${}_{11}$NH${}_3$CuBr${}_3$, 2-BiMNN = 2-benzimidazolyl nitronyl nitroxide, F4BiMNN = 2-(4,5,6,7-tetrafluorobenzimidazol-2-yl)-nitronyl nitroxide (F4BImNN).

Compound	Reference	$\mathit{J}/{\mathit{k}}_{\mathit{B}}$ (K)	${\mathit{T}}_{\mathit{c}}$ (K)	${\mathit{k}}_{\mathit{B}}{\mathit{T}}_{\mathit{c}}/\mathit{J}$
$\gamma$-NPNN	[6]	2.15	0.65	0.30
Me${}_3$NHCuCl${}_3·$2H${}_2$O	[39]	0.85	0.165	0.19
CuCl${}_2$(DMSO)	[40,41]	45	4.8	0.11
p-CDTV	[42]	6.0	0.67	0.11
CuCl${}_2$(TMSO)	[40,41]	39	3	0.08
CHAC	[43,44]	45–53	2.18	0.04–0.05
p-CDpOV	[45]	5.5	0.21	0.038
TMCuC	[41,46,47]	30, 45	1.24	0.03–0.04
CHAB	[48]	55	1.50	0.027
2-BImNN	[49]	22	1.0	0.045
F4BImNN	[50]	22	0.72	0.033
DNPNN	[21], this work	5.6	1.015	0.18

. These show that DNPNN can be considered a to be fairly good approximation to a one-dimensional ferromagnet due to its relatively low value of $k_{\mathrm{B}}{T}_{\mathrm{C}}/J$ (the quoted value of J is obtained from heat capacity measurements [21]), but, when compared to other examples, the interchain interactions are still significant.

The different temperature dependence of the two precession frequencies is an intriguing feature of the data. This is in stark contrast to many $\mu$SR studies of ordered magnets, where multiple precession frequencies can be observed but all follow the same temperature dependence, albeit with a different scaling factor. A good example of this is found in [FeCp${}_2^{*}$][MnCr(ox)${}_3$], which consists of layers of bimetallic oxalate that are separated by paramagnetic decamethylferrocenium and which that ferromagnetically below 5.17(3) K [51,52]. In this compound, $\mu$SR data show three distinct precession signals, presumably originating from three different muon sites in this rather complex structure, but, apart from different scaling factors, they all follow the same temperature dependence [53]. This scaling arises because the observed precession frequency is given by ${\gamma }_{\mu }{B}_{\mathrm{dip}}\left({\mathit{r}}_{\mu }\right)/\left(2\pi \right)$, where ${\gamma }_{\mu }$ is the muon gyromagnetic ratio and the dipolar field at the muon site is given by $B_{\mathrm{dip}}^{\alpha }\left({\mathit{r}}_{\mu }\right)={\sum }_i{D}_i^{\alpha \beta }\left({\mathit{r}}_{\mu }\right)m_i^{\beta }$, a sum over the magnetic ions in the crystal (see e.g., [25]); the magnetic moment of the ith ion is ${\mathit{m}}_i$ and $D_i^{\alpha \beta }\left({\mathit{r}}_{\mu }\right)$ is the dipolar tensor that is given by

$$D_i^{\alpha \beta }\left({\mathit{r}}_{\mu }\right)=\frac{{\mu }_0}{4\pi R_i^3}\left(\frac{3R_i^{\alpha }{R}_i^{\beta }}{R_i^2}-{\delta }^{\alpha \beta }\right),$$

(2)

where ${\mathit{R}}_i\equiv (R_i^x,R_i^y,R_i^z)={\mathit{r}}_{\mu }-{\mathit{r}}_i$ and ${\mathit{r}}_i$ is the position of the ith ion. Thus, if the magnetic moments in the sample at temperature T take the value ${\mathit{m}}_i\left(T\right)={\mathit{m}}_i\left(0\right)f\left(T\right)$, where $f\left(T\right)$ is the temperature dependence of the order parameter, the precession frequency that is corresponding to the jth muon site ${\mathit{r}}_{\mu ,j}$ will take the value

$${\nu }_j\left(T\right)={\nu }_j\left(0\right)f\left(T\right),$$

(3)

the value of ${\nu }_j\left(0\right)$ being a function of ${\mathit{r}}_{\mu ,j}$, but $f\left(T\right)$ being independent of j. Therefore, the only way in which one can explain two precession frequencies following different temperature dependences is if the magnetic structure (i.e. the arrangement of magnetic moments) is itself temperature dependent.

The magnetic moment in nitronyl nitroxide magnets results from the spin density delocalized over the O–N–C–N–O moiety [54,55]. The calculations of the dipolar field $B_{\mathrm{dip}}^{\alpha }\left({\mathit{r}}_{\mu }\right)={\sum }_i{D}_i^{\alpha \beta }\left({\mathit{r}}_{\mu }\right)m_i^{\beta }$ for the three candidate muon sites were performed, while assuming ferromagnetic order along the c-direction and with a 1${\mu }_{\mathrm{B}}$ moment being delocalized over the O–N–C–N–O moiety (with equal spin density on the nitrogen and oxygen atoms, and weak negative spin density on the central carbon, as found in p-NPNN [54]). These calculations resulted in fields that were an order of magnitude higher than we observe, due to the fact that there is a very large coupling between the muon and molecule closest to it. If instead, as found in p-NPNN [8], the muon brings an electron that forms a singlet state with the molecule to which it is closest, then the magnetic moment on that molecule will be switched off. Repeating the calculation while assuming this local molecular singlet state gives values that are closer to the experimental values, although still too large. Including the contribution from the Lorentz field ($B_{\mathrm{L}}={\mu }_{0}M/3$) and demagnetizing field ($B_{\mathrm{demag}}=-NM$, where N is the demagnetizing factor, probably somewhere between ≈1/2 and 1), gives a precession frequency $\approx 4.6$–$4.8$ MHz for the lowest-energy state close to the oxygen, ≈3–4 MHz for the site close to the nitrogen atom, and ≈1.5–3 MHz for the site that is close to the aromatic ring (the uncertainty in these values reflecting the uncertainty in N, which is less important for the oxygen site for which the local field is dominated by a component of the dipolar field perpendicular to the magnetization and, hence, to the demagnetizing field $B_{\mathrm{demag}}$). These frequencies are of the right order of magnitude, but they are all still too large, perhaps reflecting a magnetic state that is more complex than simple ferromagnetic order.

It is believed that the dominant exchange interaction in DNPNN is between the spin density on this O–N–C–N–O moiety on one molecule and the ortho-carbon atom of the phenyl group in the adjacent, $\pi /2$-rotated molecule [21]. This gives rise to one-dimensional spin chains along the helical molecular packing. In order to produce three-dimensional long range order, it is the role of the weak coupling between the chains that produces correlations whose length becomes infinite at $T_{\mathrm{C}}$. It is possible that these weaker interactions, which, as noted earlier, are still significant in size, might be competing to produce the three-dimensional ordered state in zero-field, thereby resulting in a helical component to the ordered state, albeit with a strong ferromagnetic component. If these weaker interactions were temperature dependent, then the balance of competition could shift, resulting in changes to the pitch of the helix and, therefore, altering the field measured at the two different muon sites. Anisotropic (Dzyaloshinskii–Moriya) exchange could be another possible source of this effect, which can favour spin canting (and, hence, a ferromagnetic component) in an otherwise antiferromagnetic system. However, in a material that is composed of only carbon, hydrogen, oxygen, and nitrogen atoms, one would not normally expect anisotropic exchange (which is mainly due to the spin-orbit interaction) to be particularly strong. It is also possible that the chiral packing of the molecular units in crystals of DNPNN may result in noncollinear order. We speculate that it is the finely balanced competition between these different interchain interactions that results in a strong temperature sensitivity of the detailed magnetic structure, which results in the differing temperature dependences being measured at the two distinct muon sites.

4. Conclusions

The $\mu$SR results that are presented in this paper confirm the magnetic transition previously observed [21] in DNPNN, a nitronyl nitroxide magnet with a chiral crystal structure, to be a bulk effect, a transition to three-dimensional order below 1.10 K. Our results reveal a two-component precession signal that develops below $T_{\mathrm{C}}$, and only spin relaxation is observed above the transition. The temperature dependence of the precession frequencies is unusual and the two frequencies follow markedly different temperature dependences. Although many nitronyl nitroxide magnets have been studied since the discovery of ferromagnetism in p-NPNN [4], these results highlight the special nature of DNPNN that appears to be a particularly interesting example of this family and deserving of further study.