Estimation of the Electricity Storage Volume Density of Compact SMESs of a New Concept Based on Si Microfabrication Technologies
Abstract
1. Introduction
1.1. Background and Motivation of the Research
1.2. A Novel Approach to Increase the w and Mass Producibility of SMES
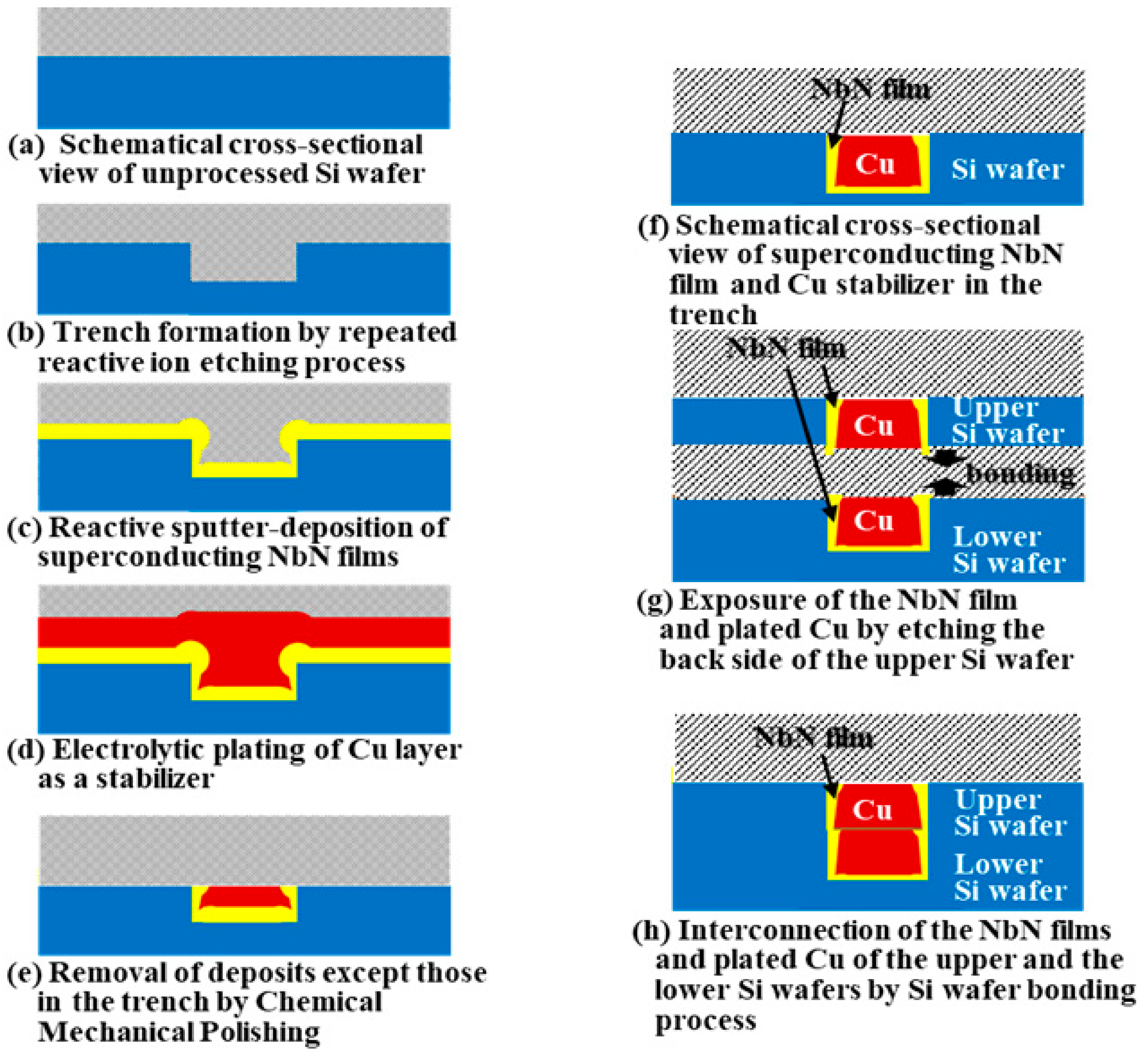
1.3. Experimental Proof of Concept Using Superconducting NbN Thin Films
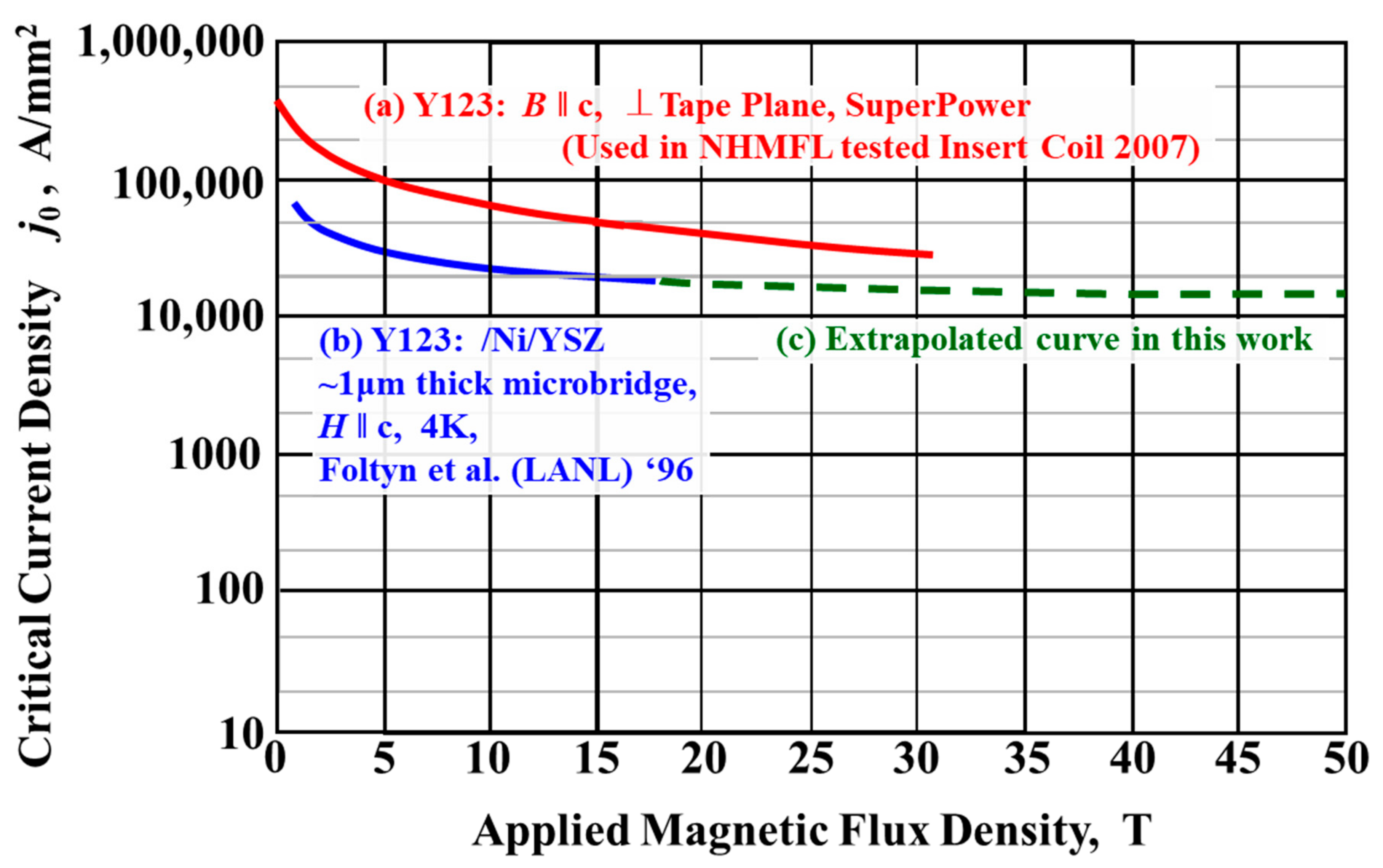
1.4. Replacement of NbN by YBa2Cu3O7-δ to Increase Electricity Storage Volume Density
1.5. Aim of This Work
2. Method of Estimation
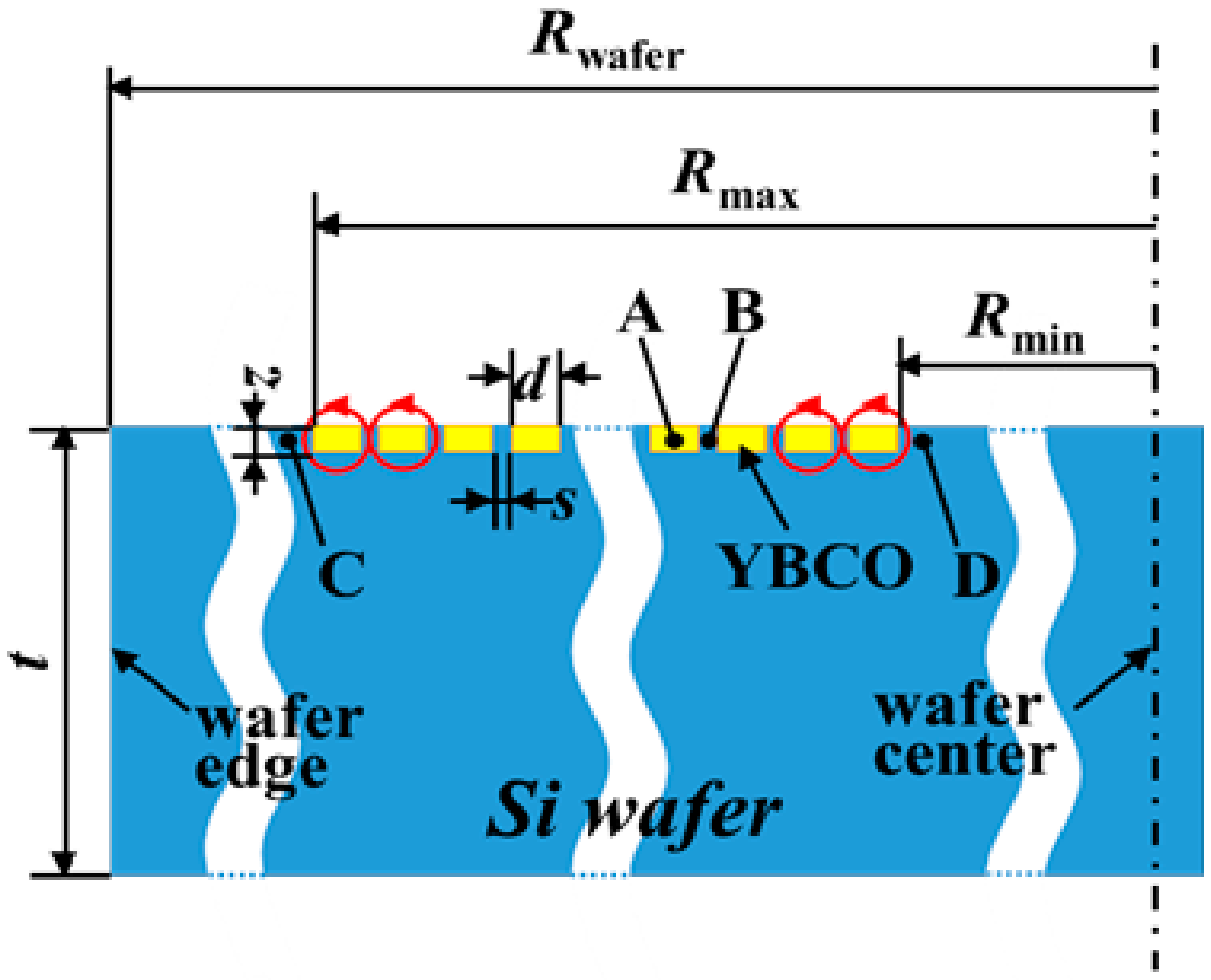
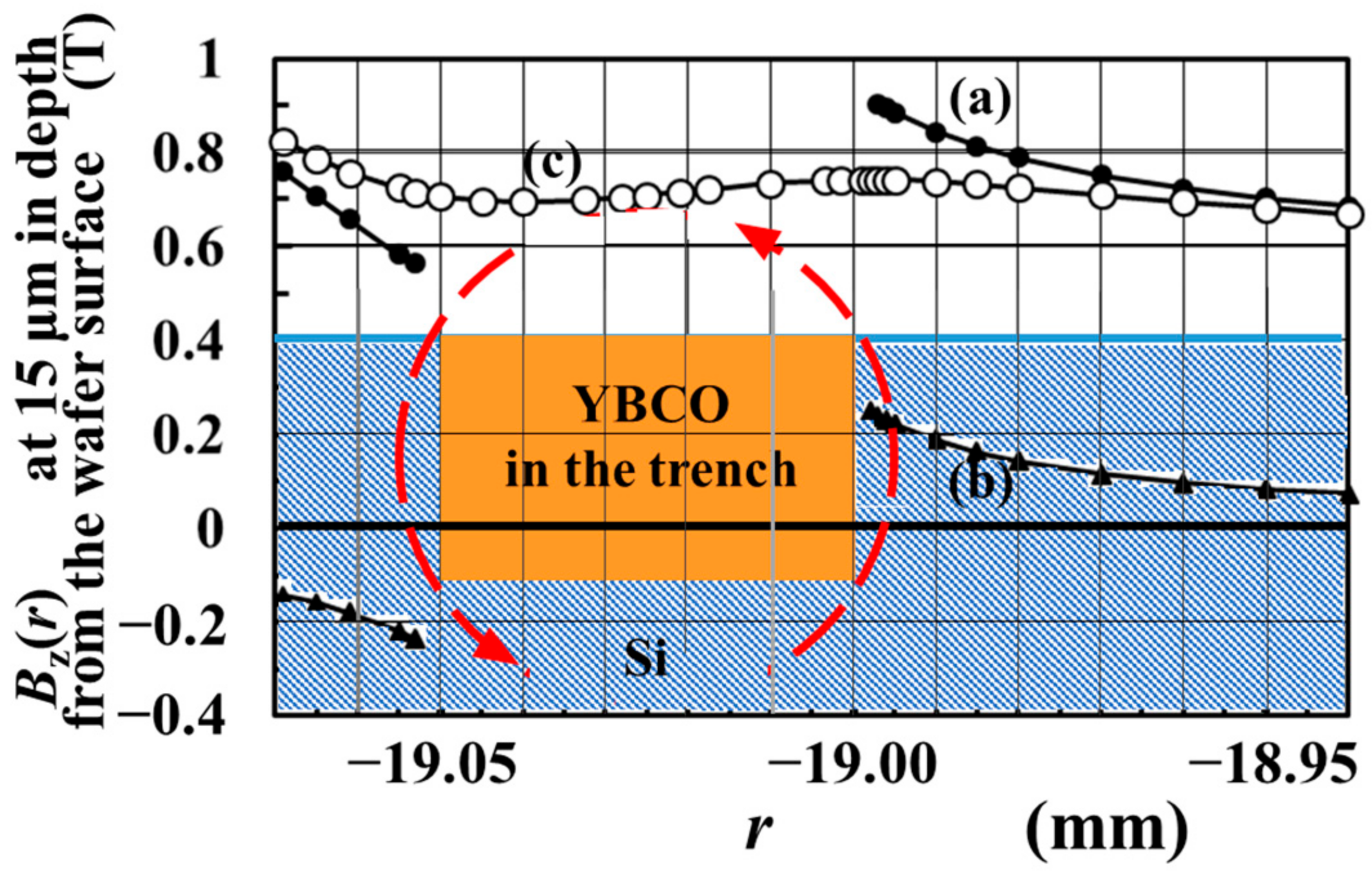
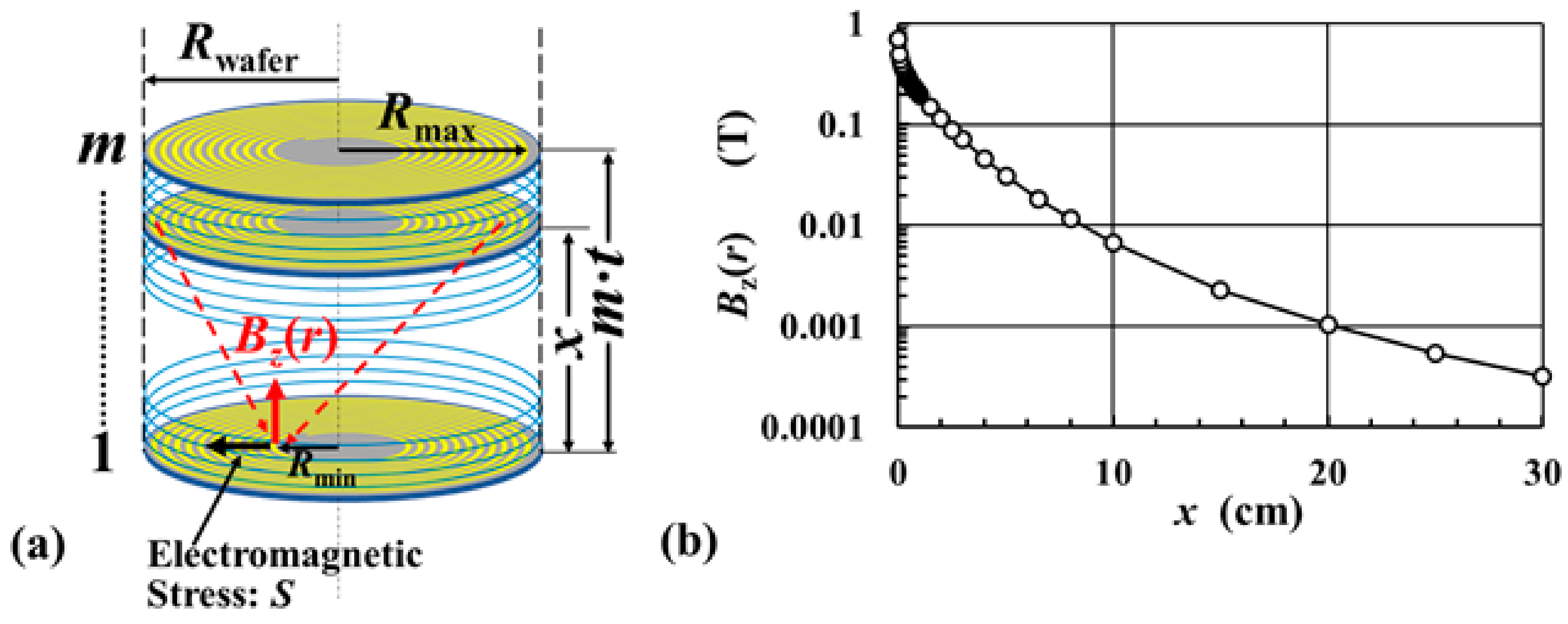
2.1. Calculation of Magnetic Flux Density in a Wafer Coil
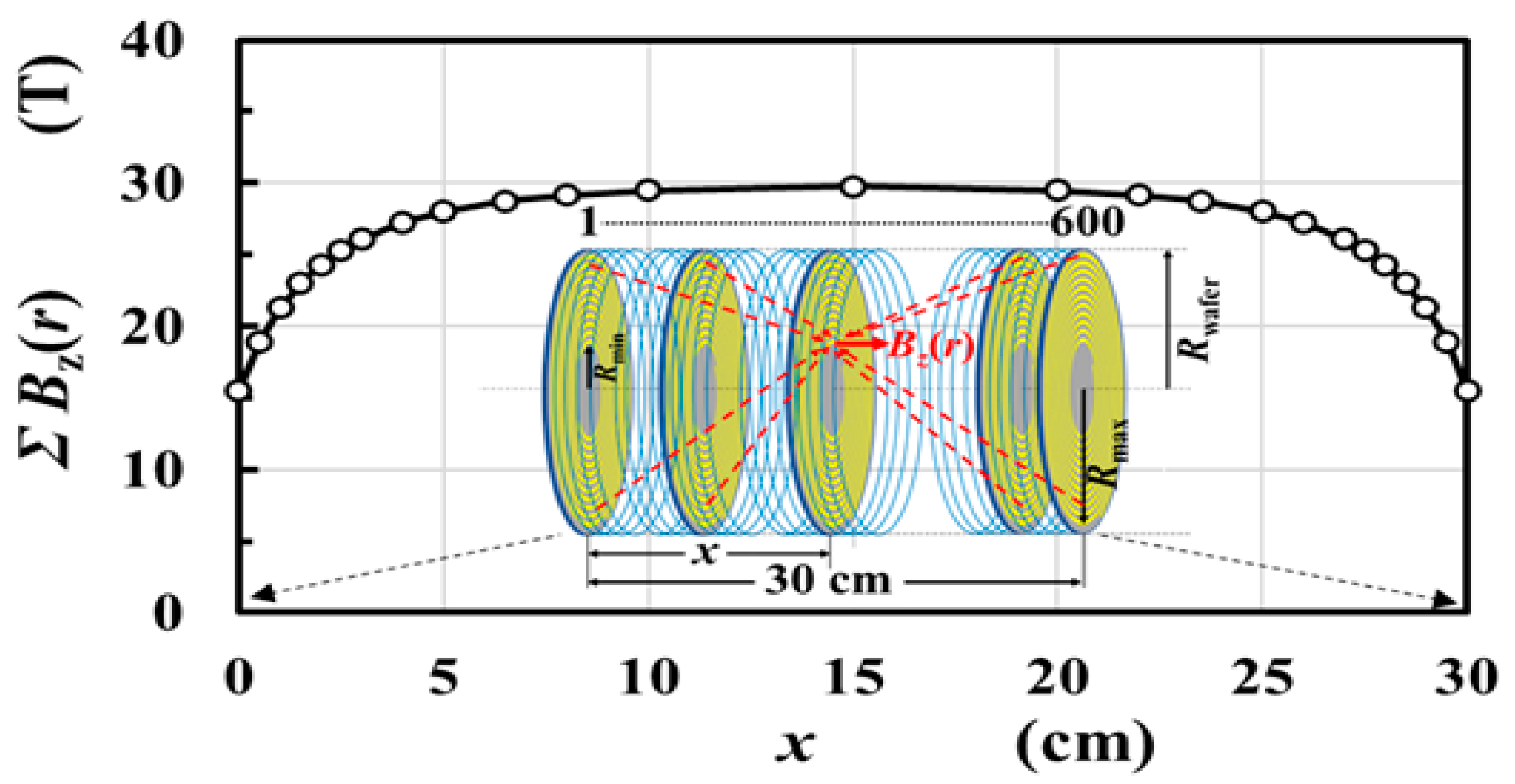
2.2. Calculation of Magnetic Flux Density in a Stack of Wafer Coils
2.3. Calculation of Inductance of the Wafer Coil Stack
2.4. Calculation of Electricity Storage Volume Density of the Wafer Coil Stack
2.5. Electromagnetic Hoop Stress
2.6. Consideration of Magnertic Flux Density Dependent jc in the Calculation
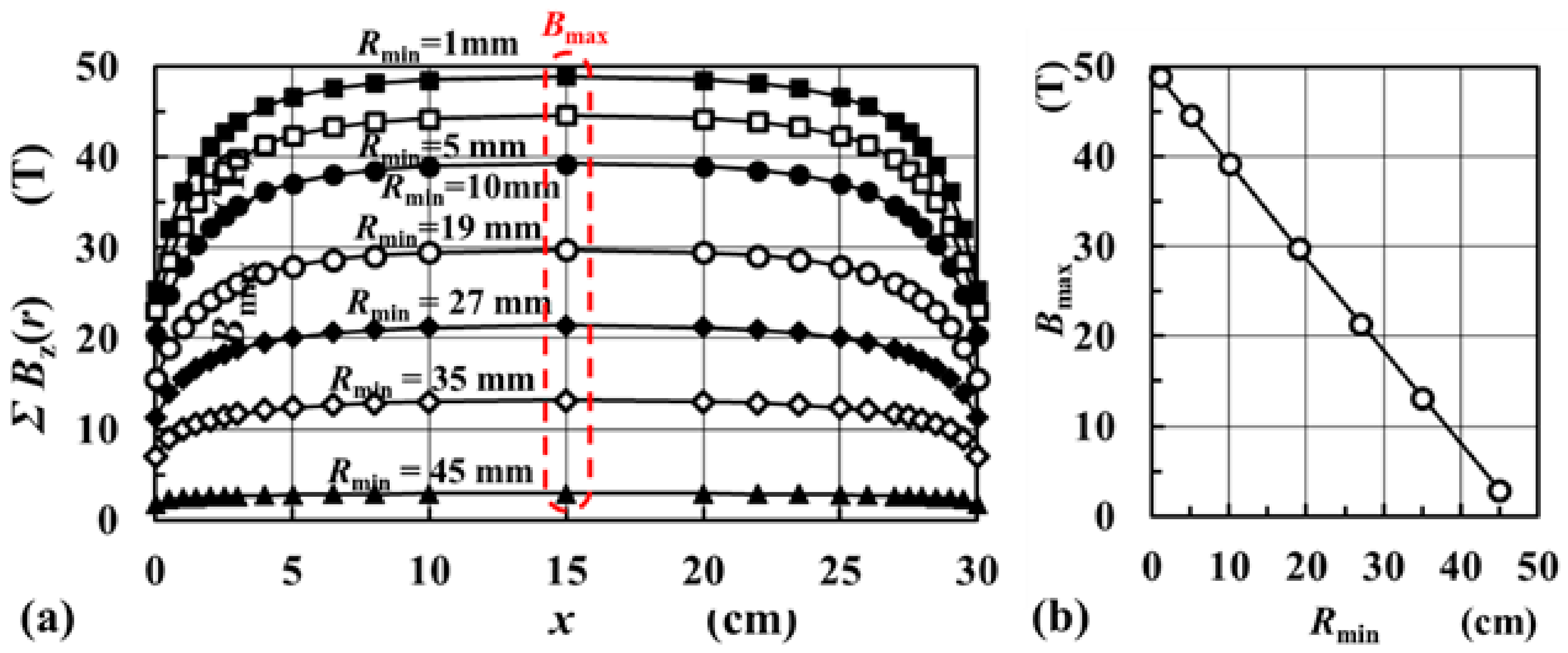
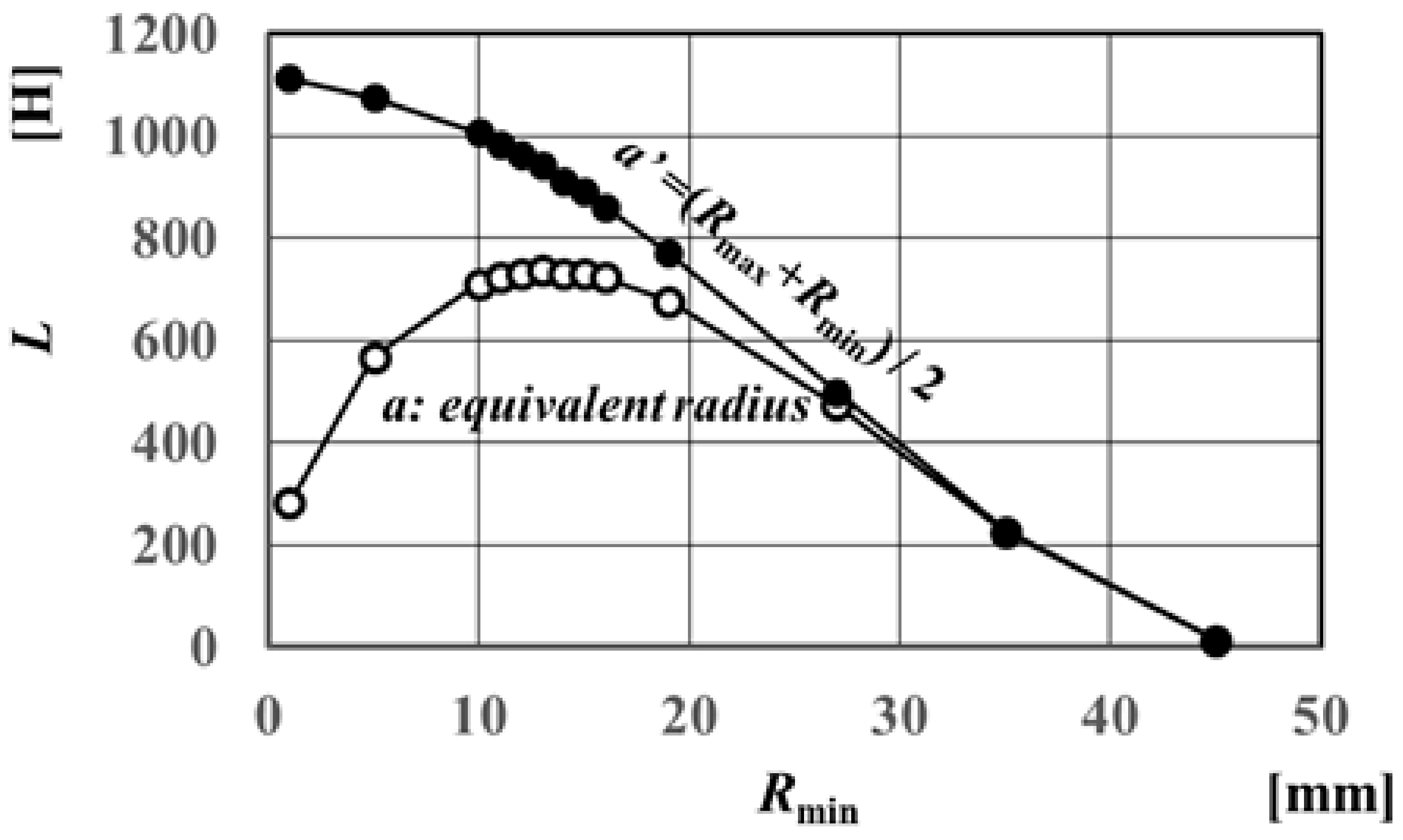
2.7. Effects of the Wafer Coil Design and the Hight of the Wafer Coil Stack on the Electricity Storage Volume Density
2.8. Comparison of the Effects of the Wafer Coil Design and the Height of the Wafer Coil Stack under Two Different Magnetic Flux Density-Dependent jc
3. Results
4. Discussion
4.1. Possibility of SMES to Rank with or Surpass Capacitors in Electricity Storage Volume Density
4.2. Improvement for Lower Cost and Compatibility for Mass Production
4.3. Applications of the Compact SMES Which Ranks with or Surpass the Commercially Available Capacitors
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Panasonic Electric Double Layer Capacitor (Gold Capacitor) Radial Lead Type Series: HL. Available online: https://industrial.panasonic.com/cdbs/www-data/pdf/RDH0000/ABC0000C106.pdf (accessed on 13 February 2021).
- Nippon Chemi-Con Electric Double Layer Capacitor Dlcaptm DXE Series. Available online: https://www.chemi-con.co.jp/catalog/pdf/dl-je/dl-sepa-je/dl-dxe-je-2020.pdf (accessed on 13 February 2021).
- Electric Double Layer Capacitors “EVerCAPⓇ” JJD Screw Terminal Type, High Energy Density Type. Available online: https://www.nichicon.co.jp/english/products/evercap/index.html (accessed on 13 February 2021).
- VISHAY 196 HVC ENYCAPTM Hybrid Energy Storage Capacitors. Available online: https://www.vishay.com/docs/28409/196hvc.pdf (accessed on 13 February 2021).
- Venkataratum, K.; Rao, V.V.; Rao, K.N.V.S.; Kumar, A.A. Optimurn Design of Superconducting Magnet Coil for a Micro SMES Unit. IEEE Trans. Appl. Supercond. 1999, 9, 350–353. [Google Scholar] [CrossRef]
- Shikimachi, K.; Hirano, N.; Nagaya, S.; Kawashima, H.; Higashikawa, K.; Nakamura, T. System Coordination of 2 GJ Class YBCO SMES for Power System Control. IEEE Trans. Appl. Supercond. 2009, 19, 2012–2018. [Google Scholar] [CrossRef]
- Katagiri, T.; Nakabayashi, H.; Nijo, Y.; Tamada, T.; Noda, T.; Hirano, N.; Nagaya, T.; Nagaya, S. Field Test Result of 10MVA/20MJ SMES for Load Fluctuation Compensation. IEEE Trans. Appl. Supercond. 2009, 19, 1993–1998. [Google Scholar] [CrossRef]
- Zimmermann, A.W.; Sharkh, S.M. Design of a 1 MJ/100 kW high temperature superconducting magnet for energy storage. Energy Rep. 2020, 6, 180–188. [Google Scholar] [CrossRef]
- Kumar, A.; Jeyan, J.V.M.L.; Agarwal, A. Electromagnetic Analysis on 2.5 MJ High Temperature Superconducting Magnetic Energy Storage (SMES) Coil to be used in Uninterruptible Power Applications. Mater. Today Proc. 2020, 21, 1755–1762. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Song, N.H.; Gao, Z.Y.; Zhang, F.Y.; Jing, L.W.; Guo, W.Y.; Teng, Y.P.; Zhang, R.L.; Xin, Z.Z.; Zhang, D.; et al. Manufacture and Tests of a Bi2223/YBCO Coil for a 1-MJ/0.5MVA Fault Current Limitter-Magnetic Energy Storage System. J. Supercond. Novel Mag. 2019, 32, 521–528. [Google Scholar] [CrossRef]
- Chen, Z.; Geng, G.; Fang, J. Influence of AC Loss on Stress and Strain of Superconducting Coils. J. Supercond. Novel Magn. 2019, 32, 549–555. [Google Scholar] [CrossRef]
- Vyas, G.; Dondapai, R.S. Investigation on the structural behavior of superconducting magnetic energy storage (SMES) devices. J. Energy Storage 2020, 28, 101212. [Google Scholar] [CrossRef]
- Kumar, A.; Muruga Lal Jeyan, J.V.; Agarwal, A. Numerical analysis on 10MJ solenoidal high temperature superconducting magnetic energy storage system to evaluate magnetic flux and Lorentz force distribution. Phys. C Amst. Neth. 2019, 558, 17–24. [Google Scholar] [CrossRef]
- Watanabe, T.; Nagaya, S.; Hirano, N.; Awaji, S.; Oguro, H.; Ishiyama, A.; Hojo, M.; Nishikawa, M. Progress of “Yoroi-Coil Structure” in Mechanical Strength with High Current Density. IEEE Trans. Appl. Supercond. 2017, 27, 4602305. [Google Scholar] [CrossRef]
- Nishijima, G.; Oguro, H.; Awaji, S.; Watanabe, K.; Shikimachi, K.; Hirano, N.; Nagaya, S. Transport Characteristics of CVD-YBCO Coated Conductor under Hoop Stress. IEEE Trans. Appl. Supercond. 2008, 18, 1131–1134. [Google Scholar] [CrossRef]
- Morandi, A.; Trevisani, L.; Negrini, F.; Ribani, P.L.; Fabbri, M. Feasibility of Superconducting Magnetic Energy Storage on Board of Ground Vehicles with Present State-of-the-Art Superconductors. IEEE Trans. Appl. Supercond. 2012, 22, 5700106. [Google Scholar] [CrossRef]
- Ko, C.-T.; Chen, K.-N. Wafer-level bonding/stacking technology for 3D integration. Microelectron. Reliab. 2010, 50, 481–488. [Google Scholar] [CrossRef]
- Sumitomo Heavy Industries, Ltd. Cryocoolers. Available online: https://www.shi.co.jp/english/products/precision/cold/index.html (accessed on 13 February 2021).
- Sugimoto, N.; Motohiro, T. Anisotropic I-V characteristics of spontaneously emerged periodic stripes of superconducting NbN thin films on Si trench sidewall by RF magnetron sputtering. Vacuum 2012, 93, 13–21. [Google Scholar] [CrossRef]
- Sugimoto, N.; Iguchi, N.; Kusano, Y.; Fukano, T.; Hioki, T.; Ichiki, A.; Bessho, T.; Motohiro, T. Compact SMES with a superconducting film in a spiral groove on a Si wafer formed by MEMS technology with possible high-energy storage volume density comparable to rechargeable batteries. Supercond. Sci. Technol. 2017, 30, 015014. [Google Scholar] [CrossRef]
- Sasaki, M.; Hsu, C.-W.; Suzuki, Y.; Hioki, T.; Noh, J.-H.; Takai, O.; Watanabe, H.; Doy, H.; Motohiro, T. Fabrication of 3-stepped spiral trench with smooth sidewall at nano-level to deposit superconducting material for energy storage. Int. J. Nanotechnol. 2018, 15, 858–872. [Google Scholar] [CrossRef]
- Wang, M.; Li, J.; Ngo, K.; Xie, H. Silicon molding techniques for integrated power MEMS inductors, Sens. Actuators A 2011, 166, 157–163. [Google Scholar] [CrossRef]
- Suzuki, Y.; Iguchi, N.; Adachi, K.; Hioki, T.; Ichiki, A.; Hsu, C.-W.; Kumagai, S.; Sasaki, M.; Motohiro, T. Stress control of reactively sputtered thick NbN film on Si wafer changing the location of the substrate Si wafer against the Nb target on a magnetron cathode. IOP Conf. Series J. Phys. Conf. Series 2017, 871, 012071. [Google Scholar] [CrossRef]
- Suzuki, Y.; Iguchi, N.; Adachi, K.; Ichiki, A.; Hioki, T.; Hsu, C.-W.; Sato, R.; Kumagai, S.; Sasaki, M.; Noh, J.-H.; et al. Complete fabrication of a traversable 3 μm thick NbN film superconducting coil with Cu plated layer of 42 m in length in a spiral three-storied trench engraved in a Si wafer of 76.2 mm in diameter formed by MEMS technology for a compact SMES with high energy storage volume density. IOP Conf. Ser. J. Phys. Conf. Ser. 2017, 897, 012019. [Google Scholar] [CrossRef]
- Manabe, T.; Kondo, W.; Mizuta, S.; Kumagai, T. Cristallization of YBa2Cu3O7-y films on SrTiO3(100) by postannealing of precursors prepared by dipping-pyrolysis process. J. Mater. Res. 1994, 9, 858–865. [Google Scholar] [CrossRef]
- Motoki, T.; Ikeda, S.; Honda, G.; Nagaishi, T.; Nakamura, S.; Shimoyama, J. Dramatic effects of chlorine addition on expanding synthesis conditions for fluorine-free metal–organic decomposition YBa2Cu3Oy films. Appl. Phys. Express 2017, 10, 023102. [Google Scholar] [CrossRef]
- Ichiki, Y.; Adachi, K.; Suzuki, Y.; Kawahara, M.; Ichiki, A.; Hioki, T.; Hsu, C.-W.; Kumagai, S.; Sasaki, M.; Noh, J.-H.; et al. Replacement of NbN by YBa2Cu3O7-δ in superconducting thin film coil in a spiral trench on a Si-wafer for compact SMESs. IOP Conf. Ser. J. Phys. Conf. Ser. 2018, 1054, 012065. [Google Scholar] [CrossRef]
- National High Magnetic Field Laboratory. Data of YBCO Tape, Magnetic Field Perpendicular to the Tape-Plane. REBCO: SP26 Tape, 50 μm Substrate, 7.5% Zr. Measured at National High Magnetic Field Laboratory (NHMFL) by V. Braccini, J. Jaroszynski and A. Xu. 2007. Available online: https://nationalmaglab.org/magnet-development/applied-superconductivity-center/ (accessed on 13 February 2021).
- Braccini, V.; Xu, A.; Jaroszynski, J.; Xin, Y.; Larbalestier, D.C.; Chen, Y.; Carota, G.; Dackow, J.; Kesgin, I.; Yao, Y.; et al. Properties of recent IBAD-MOCVD coated conductors relevant to their high field, low temperature magnet use. Supercond. Sci. Technol. 2010, 24, 035001. [Google Scholar] [CrossRef]
- Slideum Directory Jc vs. B—Florida State University. Data of YBCO: /Ni/YSZ ~1 μm Thick Microbridge, Magnetic Field in Parallel with c-Axis of the YBCO Thin Film, 4 K, Foltyn et al. (LANL) ‘96. Available online: https://slideum.com/doc/1756013/jc-vs-b---florida-state-university (accessed on 13 February 2021).
- Sekitani, T.; Miura, N.; Ikeda, S.; Matsuda, Y.H.; Shiobara, Y. Upper critical field for optimally-doped YBa2Cu3O7-δ. Phys. B Amst. Neth. 2004, 346/347, 319–324. [Google Scholar] [CrossRef]
- Ichiki, Y.; Ichiki, A.; Hioki, T.; Sasaki, M.; Noh, J.-H.; Takai, O.; Honma, H.; Motohiro, T. Estimation of electricity storage capacity of compact SMESs composed of stack of Si-wafers loaded with superconducting thin film coils in spiral trenches formed by MEMS process. IOP Conf. Ser. J. Phys. Conf. Ser. 2019, 1293, 012058. [Google Scholar] [CrossRef]
- Motohiro, T.; Sasaki, M.; Noh, J.-H.; Takai, O.; Honma, H. Estimation of Electricity Storage Density of Compact SMESs Composed of Si-wafer Stacks Loaded with Superconducting Thin Film Coils in Spiral Trenches under the Constraints of the Critical Magnetic Flux Density, J. Phys. Conf. Ser. 2020, 1590, 012045. [Google Scholar] [CrossRef]
- Rombolà, G.; Ballarini, V.; Chiodoni, A.; Gozzelino, L.; Mezzetti, E.; Menetti, B.; Pirri, C.F.; Tresso, E.R.F. Sputtering deposition of buffer layers for Si/YBCO integrated microelectronics. Int. J. Mod. Phys. B 2005, 19, 4605–4617. [Google Scholar] [CrossRef]
- Botta, D.; Camerlingo, C.; Chiodoni, A.; Fabbri, F.; Gerbaldo, R.; Chigo, G.; Gozzelino, L.; Laviano, F.; Minetti, B.; Pirri, C.F.; et al. Intrinsic pinning and current percolation signatures in E-J characteristics of Si/YSZ/CeO2/YBCO layouts. Eur. Phys. J. B 2005, 48, 359–365. [Google Scholar] [CrossRef]
- Shimadzu Europa GmbH. Press Information 2018, New Nexgen GC CAGC-100, A-ENG-18008. 10 April 2018. Available online: https://www.shimadzu.eu/new-nexgen-gc-cagc-100 (accessed on 13 February 2021).
- Nishino, M.; Takemori, Y.; Matsuoka, S.; Kanai, M.; Nishimoto, T.; Ueda, M.; Komori, K. Development of μGC (Micro Gas Chromatography) with High Performance Micromachined Chip Column. IEEJ Trans. Electr.Electron. Eng. 2009, 4, 358–364. [Google Scholar] [CrossRef]
- Sekiya, N.; Monjunaga, Y. A novel REBCO wire structure that improves coil quality factor in MHz range and its effect on wireless power transfer system. IEEE Trans. Appl. Supercond. 2017, 27, 6602005. [Google Scholar] [CrossRef]
- Nomura, S.; Tsutsui, H.; Shimada, R. Feasibility Study on Large Scale SMES for Daily Load Leveling Using Force-Balanced Helical Coils. IEEE Trans. Appl. Supercond. 2013, 23, 5700904. [Google Scholar] [CrossRef]
- Penthia, T.; Panda, A.K.; Patnaik, N.; Mohanty, P.R. Performance of SMES system with non-linear dynamic control approach for pulsed load compensation. IET Gener. Transm. Distrib. 2020, 14, 1872–1881. [Google Scholar] [CrossRef]
- NTT R&D Forum 2020 Connect E03_j. Available online: https://www.rd.ntt/_assets/pdf/forum/2020/E03_j.pdf (accessed on 13 February 2021).




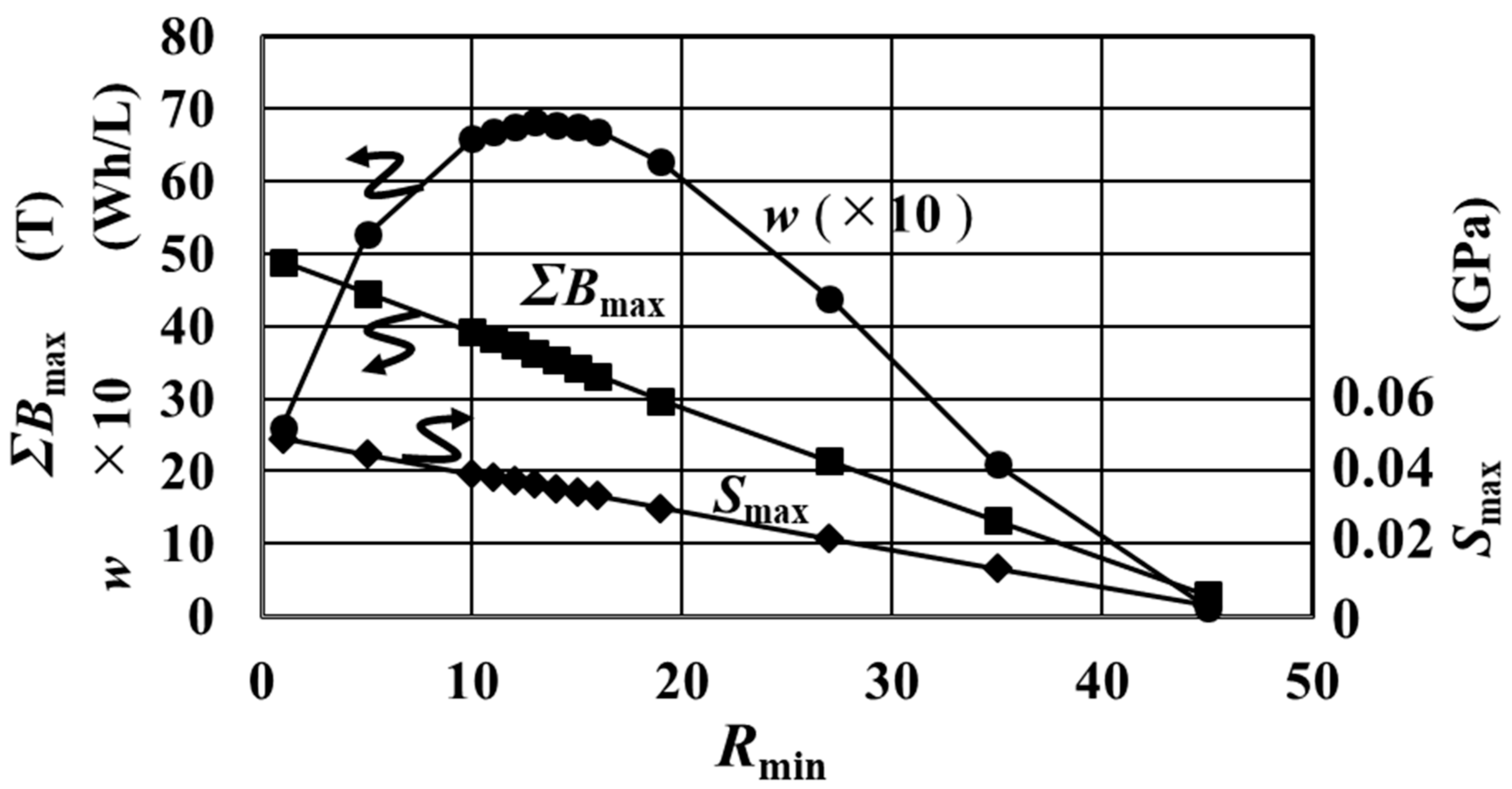
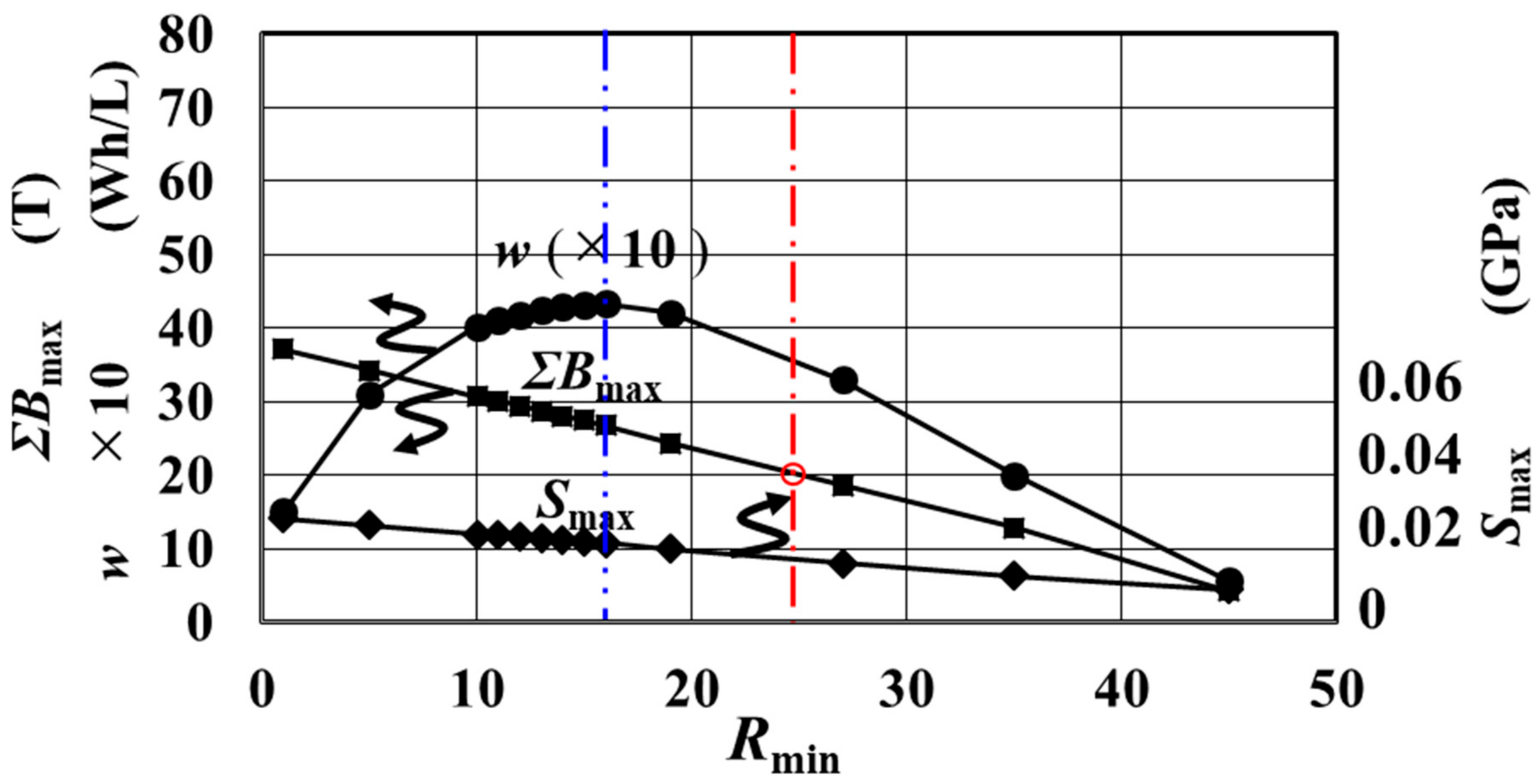

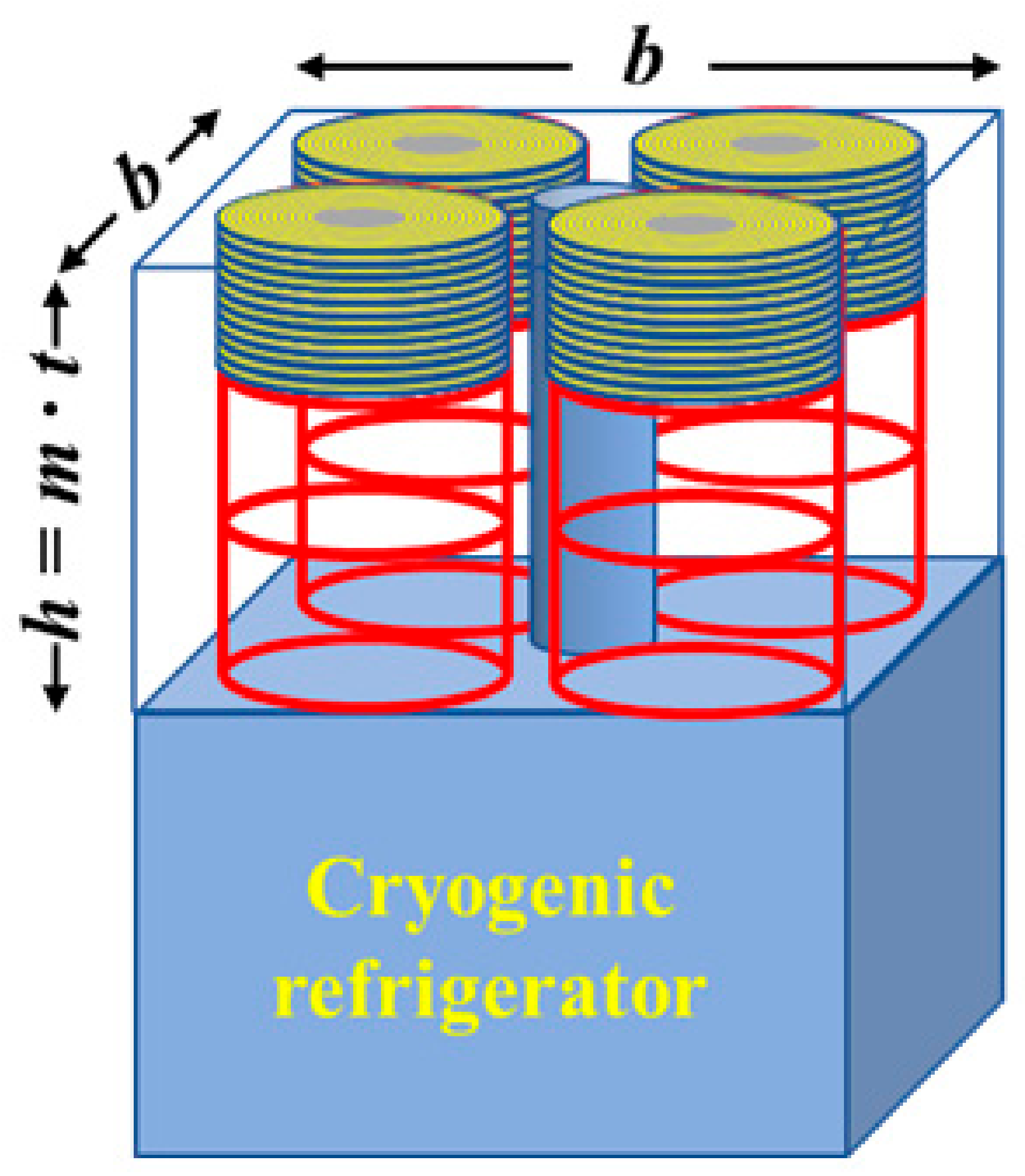
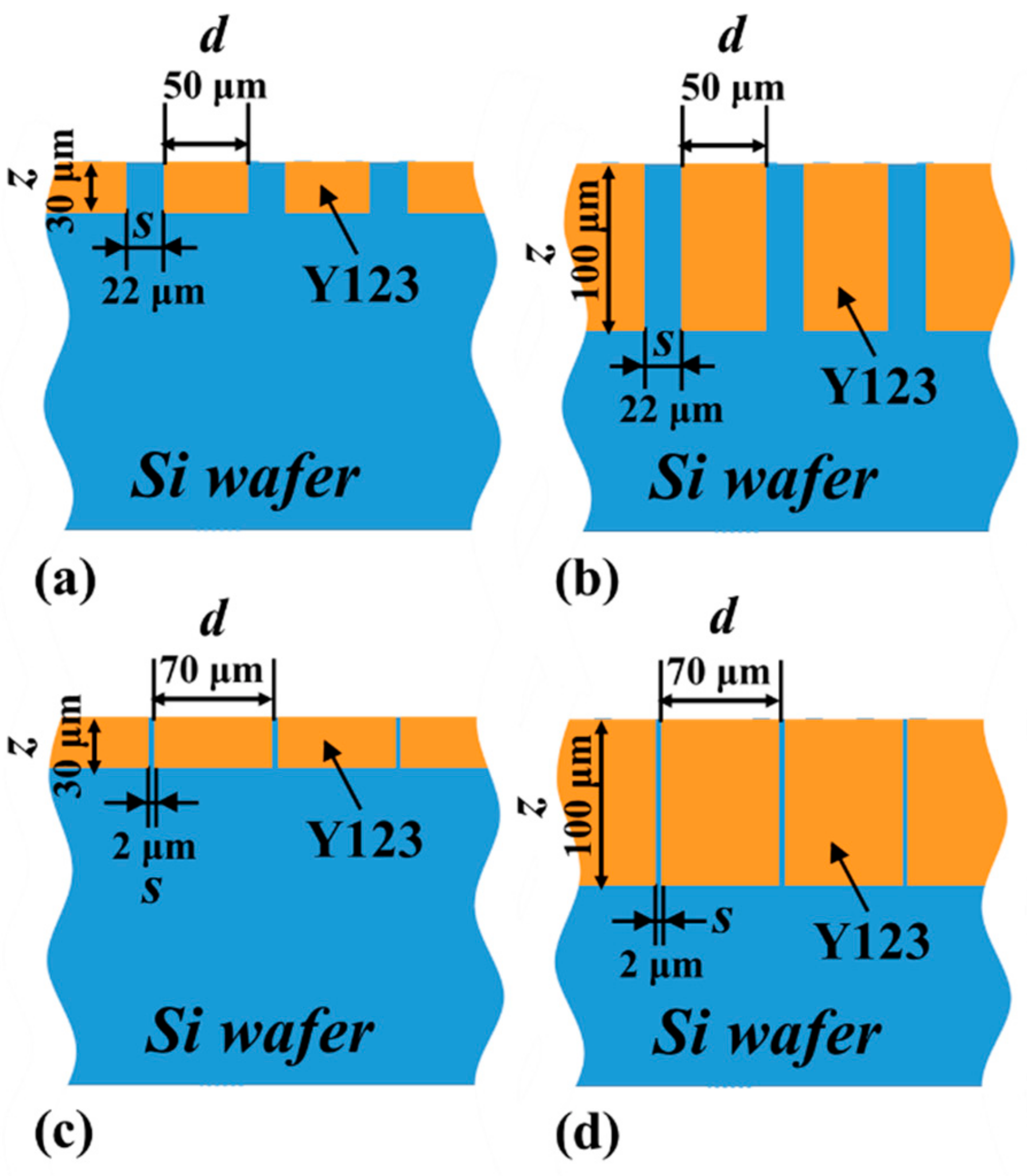
| Fig. | jc-B Curve | d (μm) | s (μm) | z (μm) | m | w@20T (Wh/L) | Rmin (mm) | Smax (GPa) | Bmax (T) | wpeak (Wh/L) | Rmin (mm) | Smax (GPa) | ∑Bmax (T) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Figure S1a | (b), (c) in Figure 4 Equation (11) | 50 | 22 | 30 | 600 | 3.6 | 24.7 | 0.017 | 20 | 4.3 | 15.3 | 0.021 | 26.7 |
| Figure S1b | 100 | 5 | 40.6 | 0.020 | 36.5 | 13.7 | 0.057 | 81.4 | |||||
| Figure S2a | 30 | 200 | 3.5 | 21.5 | 0.017 | 3.9 | 14.8 | 0.020 | 24.0 | ||||
| Figure S2b | 100 | 5.8 | 40.0 | 0.017 | 33.8 | 13.5 | 0.052 | 74.2 | |||||
| Figure S3a | 70 | 2 | 30 | 600 | 4.3 | 31.4 | 0.024 | 7.6 | 15.0 | 0.038 | 36.0 | ||
| Figure S3b | 100 | 6.8 | 43.5 | 0.020 | 69.4 | 13.7 | 0.105 | 110 | |||||
| Figure S4a | 30 | 200 | 4.5 | 29.3 | 0.024 | 6.9 | 14.6 | 0.035 | 32.0 | ||||
| Figure S4b | 100 | 6 | 42.5 | 0.020 | 60.0 | 13.9 | 0.094 | 99.0 | |||||
| Figure S5a | (a) in Figure 4 Equation (12) | 50 | 22 | 30 | 600 | 5.1 | 36.9 | 0.038 | 20 | 9.8 | 19.0 | 0.047 | 37.0 |
| Figure S5b | 100 | 6.1 | 44.5 | 0.038 | 48.2 | 17.5 | 0.070 | 86.1 | |||||
| Figure S6a | 30 | 200 | 5.6 | 34.9 | 0.038 | 9.3 | 19.4 | 0.045 | 33.8 | ||||
| Figure S6b | 100 | 6.7 | 43.7 | 0.038 | 44.9 | 17.4 | 0.066 | 77.8 | |||||
| Figure S7a | 70 | 2 | 30 | 600 | 5.1 | 40.3 | 0.052 | 14.9 | 18.8 | 0.072 | 42.6 | ||
| Figure S7b | 100 | 5.6 | 45.8 | 0.052 | 80.0 | 17.5 | 0.114 | 110 | |||||
| Figure S8a | 30 | 200 | 5.1 | 39.8 | 0.052 | 14.1 | 19.1 | 0.068 | 41.6 | ||||
| Figure S8b | 100 | 6.4 | 45.4 | 0.053 | 73.6 | 16.6 | 0.011 | 102 |
| Fig. | jc-B Curve | d (μm) | s (μm) | z (μm) | m | w@20T (Wh/L) | w@30T (Wh/L) | w@40T (Wh/L) | w@50T (Wh/L) | w@60T (Wh/L) | w@70T (Wh/L) | w@80T (Wh/L) | w@90T (Wh/L) | w@100T (Wh/L) | wpeak@∑Bmax (Wh/L) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Figure S1a | (b,c)in Figure 4 Equation (11) | 50 | 22 | 30 | 600 | 3.6 | 4.3@26.7T | ||||||||
| Figure S1b | 100 | 5 | 11.3 | 18.4 | 25 | 30 | 34.8 | 36.5@81.4T | |||||||
| Figure S2a | 30 | 200 | 3.5 | 3.9@24T | |||||||||||
| Figure S2b | 100 | 5.75 | 12 | 18.5 | 25 | 33.8@74.2T | |||||||||
| Figure S3a | 70 | 2 | 30 | 600 | 4.3 | 6.9 | 7.6@36T | ||||||||
| Figure S3b | 100 | 6.8 | 8.6 | 19.8 | 27.8 | 39 | 47.8 | 55.6 | 62.5 | 67.4 | 69.4@110T | ||||
| Figure S4a | 30 | 200 | 4.5 | 6.9@32T | |||||||||||
| Figure S4b | 100 | 6 | 13.4 | 20 | 29.5 | 37.4 | 47.6 | 53.8 | 60.0@99T | ||||||
| Figure S5a | (a) in Figure 4 Equation (12) | 50 | 22 | 30 | 600 | 5.1 | 9.8@37T | ||||||||
| Figure S5b | 100 | 6.1 | 14 | 20 | 30.2 | 39.6 | 43 | 48.2@86.1T | |||||||
| Figure S6a | 30 | 200 | 5.6 | 9.3@33.8T | |||||||||||
| Figure S6b | 100 | 6.7 | 14.4 | 22.2 | 30.6 | 38.6 | 42.9 | 44.9@77.8T | |||||||
| Figure S7a | 70 | 2 | 30 | 600 | 5.1 | 9.8 | 14 | 14.9@42.6T | |||||||
| Figure S7b | 100 | 5.6 | 10 | 22.3 | 31 | 43.6 | 52.7 | 62.6 | 69.5 | 80.0@110T | |||||
| Figure S8a | 30 | 200 | 5.1 | 10.8 | 14.1@41.6T | ||||||||||
| Figure S8b | 100 | 6.4 | 14.2 | 23.4 | 33.4 | 44.2 | 54.2 | 62.6 | 70.2 | 73.6@102T |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Motohiro, T.; Sasaki, M.; Noh, J.-h.; Takai, O. Estimation of the Electricity Storage Volume Density of Compact SMESs of a New Concept Based on Si Microfabrication Technologies. Magnetochemistry 2021, 7, 44. https://doi.org/10.3390/magnetochemistry7030044
Motohiro T, Sasaki M, Noh J-h, Takai O. Estimation of the Electricity Storage Volume Density of Compact SMESs of a New Concept Based on Si Microfabrication Technologies. Magnetochemistry. 2021; 7(3):44. https://doi.org/10.3390/magnetochemistry7030044
Chicago/Turabian StyleMotohiro, Tomoyoshi, Minoru Sasaki, Joo-hyong Noh, and Osamu Takai. 2021. "Estimation of the Electricity Storage Volume Density of Compact SMESs of a New Concept Based on Si Microfabrication Technologies" Magnetochemistry 7, no. 3: 44. https://doi.org/10.3390/magnetochemistry7030044
APA StyleMotohiro, T., Sasaki, M., Noh, J.-h., & Takai, O. (2021). Estimation of the Electricity Storage Volume Density of Compact SMESs of a New Concept Based on Si Microfabrication Technologies. Magnetochemistry, 7(3), 44. https://doi.org/10.3390/magnetochemistry7030044






