Magnetic Normal Mode Calculations in Big Systems: A Highly Scalable Dynamical Matrix Approach Applied to a Fibonacci-Distorted Artificial Spin Ice
Abstract
1. Introduction
2. Theoretical Approach
3. Application to a Fibonacci Lattice
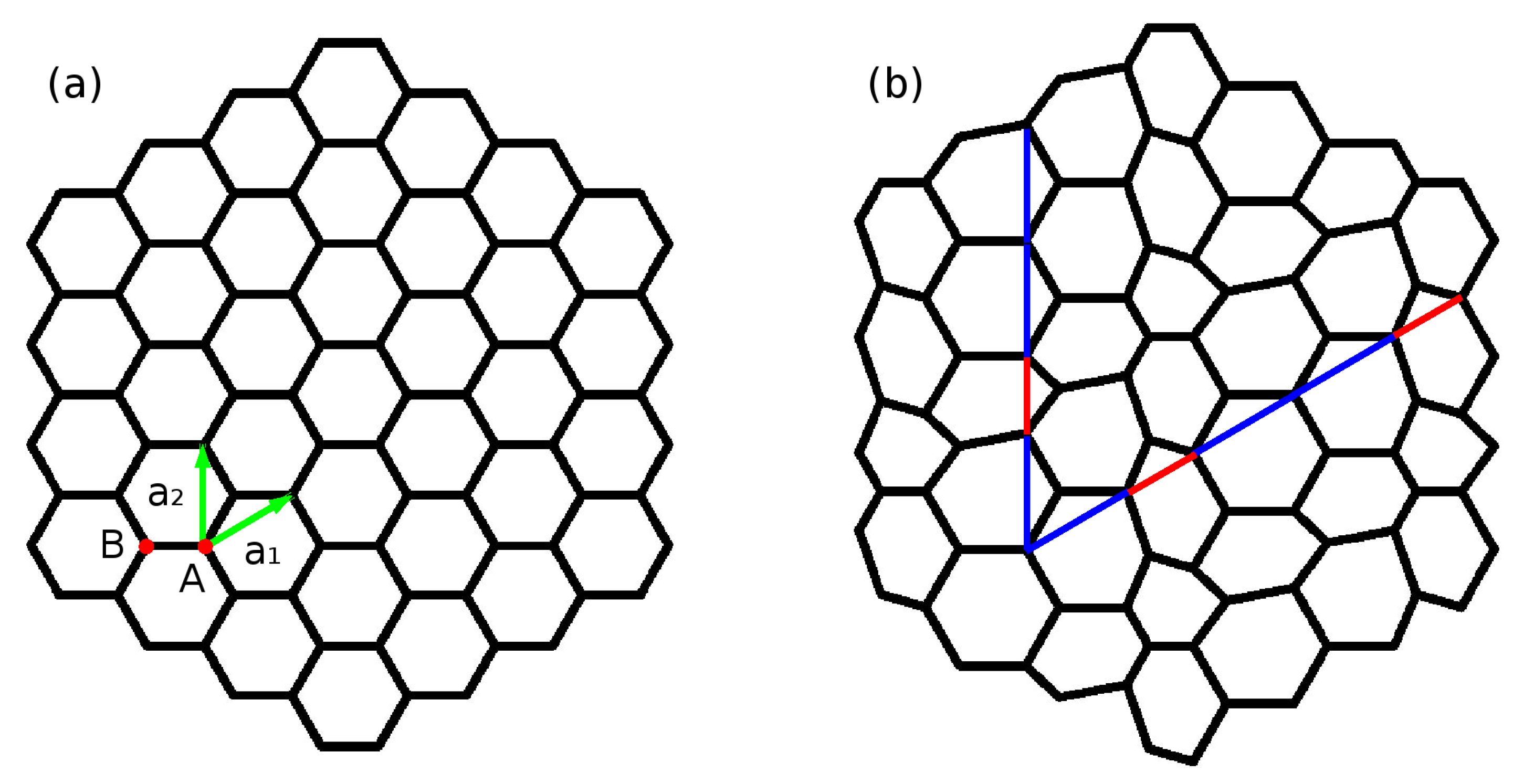
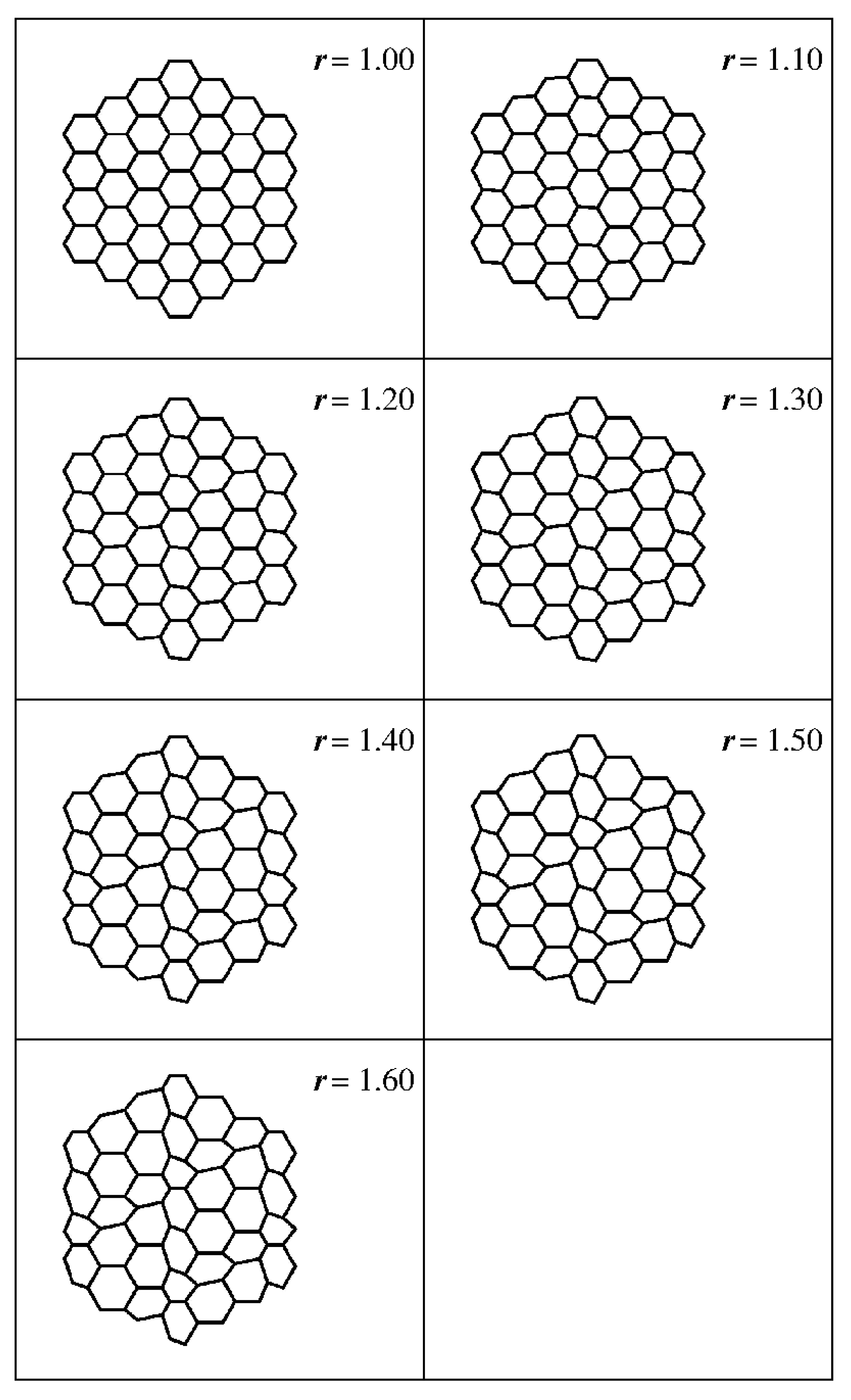
3.1. System Structure
3.2. Calculation Methods
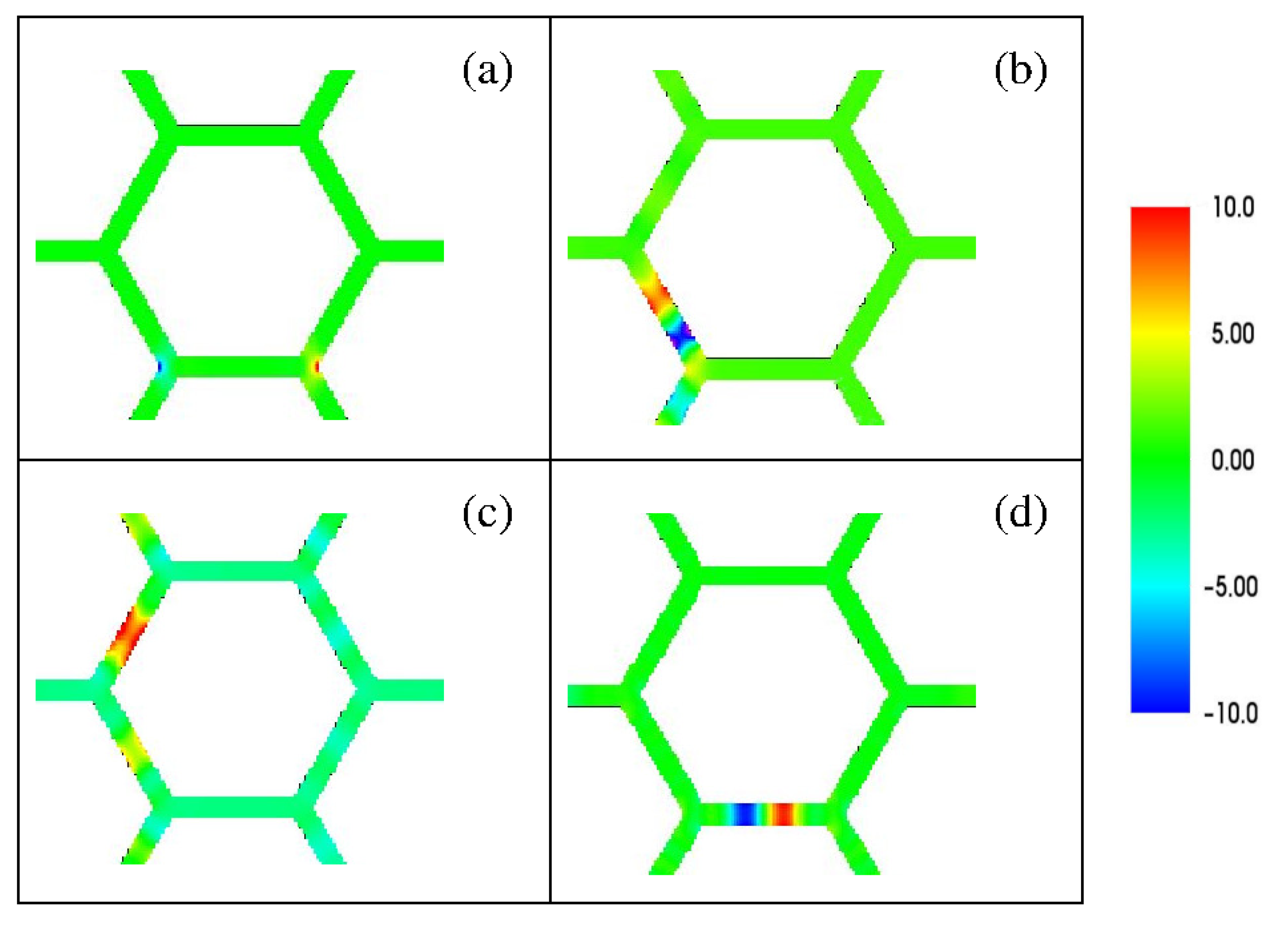
3.3. Unperturbed System: Mode Profiles
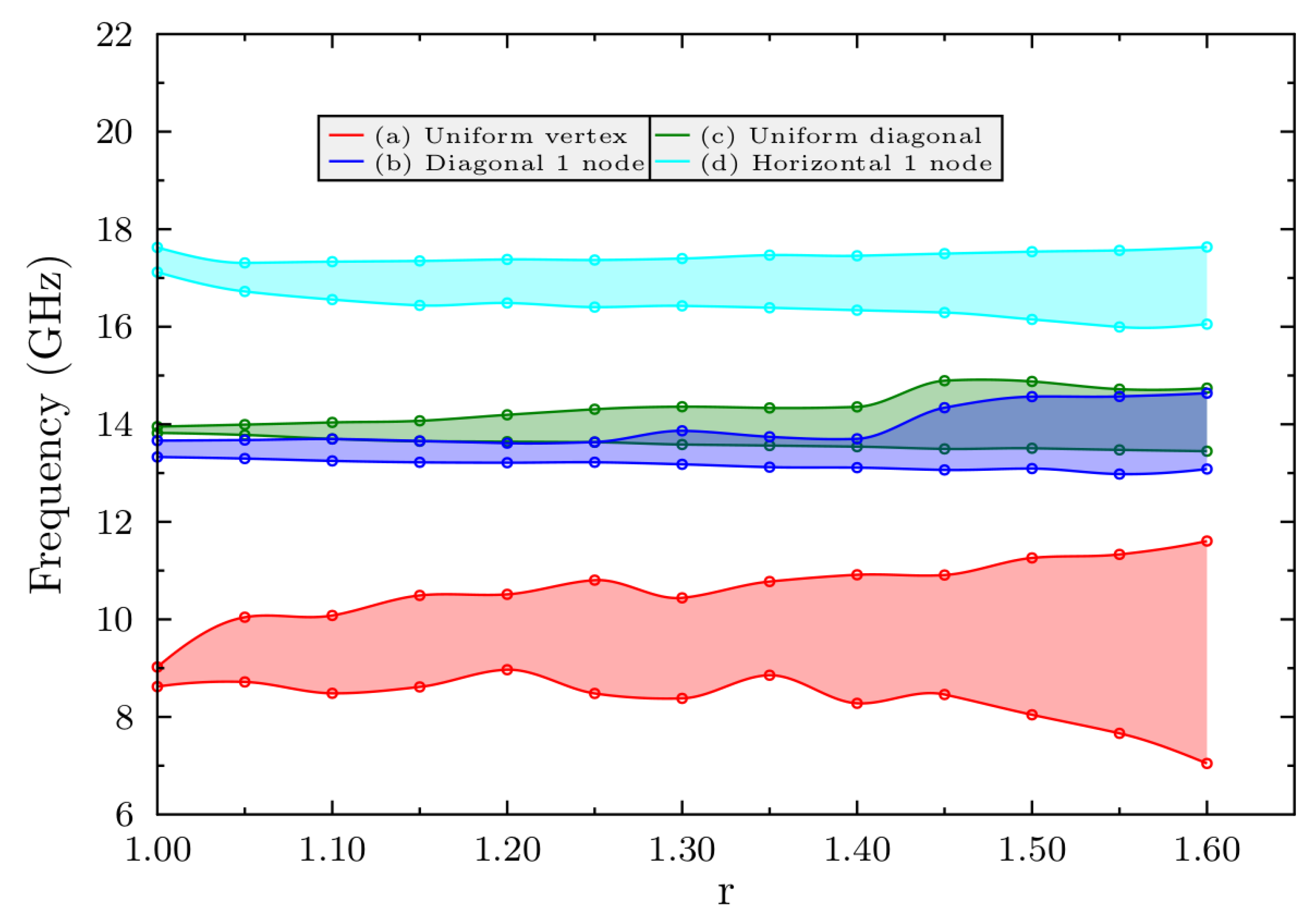
3.4. Perturbed System: Mode Frequency Dispersion and Bands
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Reformulated Dynamical Matrix Formalism
References
- Krawczyk, M.; Grundler, D. Review and prospects of magnonic crystals and devices with reprogrammable band structure. J. Phys. Condens. Matter 2014, 26, 123202. [Google Scholar] [CrossRef]
- Wang, R.F.; Nisoli, C.; Freitas, R.S.; Li, J.; McConville, W.; Cooley, B.J.; Lund, M.S.; Samarth, N.; Leighton, C.; Crespi, V.H.; et al. Artificial ‘spin ice’ in a geometrically frustrated lattice of nanoscale ferromagnetic islands. Nat. Lett. 2006, 439, 303. [Google Scholar] [CrossRef]
- Dion, T.; Arroo, D.M.; Yamanoi, K.; Kimura, T.; Gartside, J.C.; Cohen, L.F.; Kurebayashi, H.; Branford, W.R. Tunable magnetization dynamics in artificial spin ice via shape anisotropy modification. Phys. Rev. B 2019, 100, 054433. [Google Scholar] [CrossRef]
- Di, K.; Zhang, V.L.; Kuok, M.H.; Lim, H.S.; Ng, S.C.; Narayanapillai, K.; Yang, H. Band structure of magnonic crystals with defects: Brillouin spectroscopy and micromagnetic simulations. Phys. Rev. B 2014, 90, 060405(R). [Google Scholar] [CrossRef]
- Manzin, A.; Barrera, G.; Celegato, F.; Coïsson, M.; Tiberto, P. Influence of lattice defects on the ferromagnetic resonance behaviour of 2D magnonic crystals. Sci. Rep. 2016, 6, 22004. [Google Scholar] [CrossRef] [PubMed]
- Drisko, J.; Marsh, T.; Cumings, J. Topological frustration of artificial spin ice. Nat. Commun. 2017, 8, 14009. [Google Scholar] [CrossRef]
- Montoncello, F.; Giovannini, L.; Farmer, B.; De Long, L.E. Dynamic origin of segment magnetization reversal in thin-film Penrose tilings. J. Magn. Magn. Mater. 2017, 423, 158–163. [Google Scholar] [CrossRef]
- Farmer, B.; Bhat, V.S.; Sklenar, J.; Teipel, E.; Ketterson, J.W.J.B.; Hastings, J.T.; De Long, L.E. Magnetic response of aperiodic wire networks based on Fibonacci distortions of square antidot lattices. J. Appl. Phys. 2015, 117, 17B714. [Google Scholar] [CrossRef]
- Bhat, V.S.; Sklenar, J.; Farmer, B.; Woods, J.; Hastings, J.T.; Lee, S.J.; Ketterson, J.B.; De Long, L.E. Controlled Magnetic Reversal in Permalloy Films Patterned into Artificial Quasicrystals. Phys. Rev. Lett. 2013, 111, 077201. [Google Scholar] [CrossRef]
- Brown, W.F.J. Interscience tracts on Physics and Astronomy. In 18. Micromagnetics; Marshack, R.E., Ed.; John Wiley & Sons: New York, NY, USA, 1963; Volume 18, pp. 1–143. [Google Scholar]
- Fangohr, H.; Fischbacher, T.; Franchin, M.; Bordignon, G.; Generowicz, J.; Knittel, A.; Walter, M.; Albert, M. NMAG User Manual Documentation Release 0.2.1. 2012. Available online: http://nmag.soton.ac.uk/nmag/current/manual/singlehtml/manual.html (accessed on 5 March 2021).
- Donahue, M.J.; Porter, D.G. OOMMF User’s Guide, Version 1.0, Interagency Report NISTIR 6376; National Institute of Standards and Technology: Gaithersburg, MD, USA, 1999.
- De Wiele, B.V.; Montoncello, F. A continuous excitation approach to determine time-dependent dispersion diagrams in 2D magnonic crystals. J. Phys. D Appl. Phys. 2014, 47, 315002. [Google Scholar] [CrossRef]
- Xiong, L.L.; Adeyeye, A.O. Dynamic behavior of Ni80Fe20 nanowires with controlled periodic width modulation. Appl. Phys. Lett. 2016, 108, 262401. [Google Scholar] [CrossRef]
- Liu, C.; Chen, J.; Liu, T.; Heimbach, F.; Yu, H.; Xiao, Y.; Hu, J.; Liu, M.; Chang, H.; Stueckler, T.; et al. Long-distance propagation of short-wavelength spin waves. Nat. Commun. 2018, 9, 738. [Google Scholar] [CrossRef]
- Labbé, S.; Bertin, P.Y. Microwave polarizability of ferrite particles with non-uniform magnetization. J. Magn. Magn. Mater. 1999, 206, 93. [Google Scholar] [CrossRef]
- Grimsditch, M.; Giovannini, L.; Montoncello, F.; Nizzoli, F.; Leaf, G.K.; Kaper, H.G. Magnetic normal modes in ferromagnetic nanoparticles: A dynamical matrix approach. Phys. Rev. B 2004, 70, 054409. [Google Scholar] [CrossRef]
- Rivkin, K.; Ketterson, J.B. Micromagnetic simulations of absoption spectra. J. Magn. Magn. Mater. 2006, 306, 204. [Google Scholar] [CrossRef][Green Version]
- Fiedler, G.; Fidler, J.; Lee, J.; Schrefl, T.; Stamps, R.; Braun, H.B.; Suess, D. Direct calculation of the attempt frequency of magnetic structures using the finite element method. J. Appl. Phys. 2010, 111. [Google Scholar] [CrossRef]
- Buijnsters, F.J.; Fasolino, A.; Katsnelson, M.I. Zero modes in magnetic systems: General theory and an efficient computational scheme. Phys. Rev. B 2014, 89, 174433. [Google Scholar] [CrossRef]
- Montoncello, F.; Giovannini, L.; Nizzoli, F.; Zivieri, R.; Consolo, G.; Gubbiotti, G. Spin-wave activation by spin-polarized current pulse in magnetic nanopillars. J. Magn. Magn. Mater. 2010, 322, 2330. [Google Scholar] [CrossRef]
- Dmytriiev, O.; Dvornik, M.; Mikhaylovskiy, R.V.; Franchin, M.; Fangohr, H.; Giovannini, L.; Montoncello, F.; Berkov, D.V.; Semenova, E.K.; Gorn, N.L.; et al. Dynamic magnetic response of infinite arrays of ferromagnetic particles. Phys. Rev. B 2012, 86, 104405. [Google Scholar] [CrossRef]
- Montoncello, F.; Giovannini, L. Bandwidth broadening and asymmetric softening of collective spin waves in magnonic crystals. Appl. Phys. Lett. 2014, 104, 242407. [Google Scholar] [CrossRef]
- Rivkin, K.; Saslow, W.; Chandrasehkhar, V.; De Long, L.E.; Ketterson, J.B. Dynamic magnetic response of infinite arrays of ferromagnetic particles. Phys. Rev. B 2007, 75, 174408. [Google Scholar] [CrossRef]
- Bhat, V.; Woods, J.; De Long, L.E.; Hastings, J.T.; Metlushko, V.V.; Rivkin, K.; Heinonen, O.; Sklenar, J.; Ketterson, J.B. Broad-band FMR study of ferromagnetic thin films patterned with antidot lattices. Physica C 2012, 479, 83. [Google Scholar] [CrossRef]
- Greenberg, N.; Kunza, A. Disordered kagomé spin ice. AIP Adv. 2018, 8, 055711. [Google Scholar] [CrossRef]
- Ding, J.; Kostylev, M.; Adeyeye, A.O. Magnonic Crystal as a Medium with Tunable Disorder on a Periodical Lattice. Phys. Rev. Lett. 2011, 107, 047205. [Google Scholar] [CrossRef]
- Kruglyak, V.V.; Sokolovskii, M.L.; Tkachenko, V.S.; Kuchko, A.N. Spin-wave spectrum of a magnonic crystal with an isolated defect. J. Appl. Phys. 2006, 99, 08C906. [Google Scholar] [CrossRef]
- Frotanpour, A.; Woods, J.; Farmer, B.; Kaphle, A.P.; De Long, L.E.; Giovannini, L.; Montoncello, F. Magnetization dynamics of a Fibonacci-distorted kagome artificial spin ice. Phys. Rev. B 2020, 102, 224435. [Google Scholar] [CrossRef]
- Smith, J.O. Mathematics of the Discrete Fourier Transform (DFT). W3K Publishing. 2007. Available online: http://www.w3k.org/books/ (accessed on 5 March 2021).
- Stewart, G.W. A Krylov–Schur Algorithm for Large Eigenproblems. SIAM J. Matrix Anal. Appl. 2002, 23, 601–614. [Google Scholar] [CrossRef]
- Hernandez, V.; Roman, J.E.; Tomas, A. Evaluation of Several Variants of Explicitly Restarted Lanczos Eigensolvers and Their Parallel Implementations. In Proceedings of the High Performance Computing for Computational Science—VECPAR 2006: 7th International Conference, Rio de Janeiro, Brazil, 10–13 June 2006; Daydé, M., Palma, J.M.L.M., Coutinho, Á.L.G.A., Pacitti, E., Lopes, J.C., Eds.; Revised Selected and Invited Papers. Springer: Berlin/Heidelberg, Germany, 2007; pp. 403–416. [Google Scholar] [CrossRef]
- Morgan, R.B.; Zeng, M. A harmonic restarted Arnoldi algorithm for calculating eigenvalues and determining multiplicity. Linear Algebra Appl. 2006, 415, 96. [Google Scholar] [CrossRef]
- Morgan, R.B.; Scott, D.S. Generalizations of Davidson’s Method for Computing Eigenvalues of Sparse Symmetric Matrices. SIAM J. Sci. Stat. Comput. 1986, 7, 817–825. [Google Scholar] [CrossRef]
- Levine, D.; Steinhardt, P.J. Quasicrystals: A New Class of Ordered Structures. Phys. Rev. Lett. 1984, 53, 2477–2480. [Google Scholar] [CrossRef]
- Levine, D.; Steinhardt, P.J. Quasicrystals. I. Definition and structure. Phys. Rev. B 1986, 34, 596–616. [Google Scholar] [CrossRef] [PubMed]
- Tzounas, G.; Dassios, I.; Liu, M.; Milano, F. Comparison of Numerical Methods and Open-Source Libraries for Eigenvalue Analysis of Large-Scale Power Systems. Appl. Sci. 2020, 10, 7592. [Google Scholar] [CrossRef]
- Bhat, V.S.; Heimbach, F.; Stasinopoulos, I.; Grundler, D. Magnetization dynamics of topological defects and the spin solid in a kagome artificial spin ice. Phys. Rev. B 2016, 93, 140401. [Google Scholar] [CrossRef]
- Montoncello, F.; Giovannini, L. Vortex mode dynamics and bandwidth tunability in a two-dimensional array of interacting magnetic disks. Appl. Phys. Lett. 2012, 100, 182406. [Google Scholar] [CrossRef]
- Gubbiotti, G.; Carlotti, G.; Okuno, T.; Grimsditch, M.; Giovannini, L.; Montoncello, F.; Nizzoli, F. Spin dynamics in thin nanometric elliptical Permalloy dots: A Brillouin light scattering investigation as a function of dot eccentricity. Phys. Rev. B 2005, 72, 184419. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giovannini, L.; Farmer, B.W.; Woods, J.S.; Frotanpour, A.; De Long, L.E.; Montoncello, F. Magnetic Normal Mode Calculations in Big Systems: A Highly Scalable Dynamical Matrix Approach Applied to a Fibonacci-Distorted Artificial Spin Ice. Magnetochemistry 2021, 7, 34. https://doi.org/10.3390/magnetochemistry7030034
Giovannini L, Farmer BW, Woods JS, Frotanpour A, De Long LE, Montoncello F. Magnetic Normal Mode Calculations in Big Systems: A Highly Scalable Dynamical Matrix Approach Applied to a Fibonacci-Distorted Artificial Spin Ice. Magnetochemistry. 2021; 7(3):34. https://doi.org/10.3390/magnetochemistry7030034
Chicago/Turabian StyleGiovannini, Loris, Barry W. Farmer, Justin S. Woods, Ali Frotanpour, Lance E. De Long, and Federico Montoncello. 2021. "Magnetic Normal Mode Calculations in Big Systems: A Highly Scalable Dynamical Matrix Approach Applied to a Fibonacci-Distorted Artificial Spin Ice" Magnetochemistry 7, no. 3: 34. https://doi.org/10.3390/magnetochemistry7030034
APA StyleGiovannini, L., Farmer, B. W., Woods, J. S., Frotanpour, A., De Long, L. E., & Montoncello, F. (2021). Magnetic Normal Mode Calculations in Big Systems: A Highly Scalable Dynamical Matrix Approach Applied to a Fibonacci-Distorted Artificial Spin Ice. Magnetochemistry, 7(3), 34. https://doi.org/10.3390/magnetochemistry7030034







