Chassis Influence on the Exposure Assessment of a Compact EV during WPT Recharging Operations
Abstract
1. Introduction
2. Materials and Methods
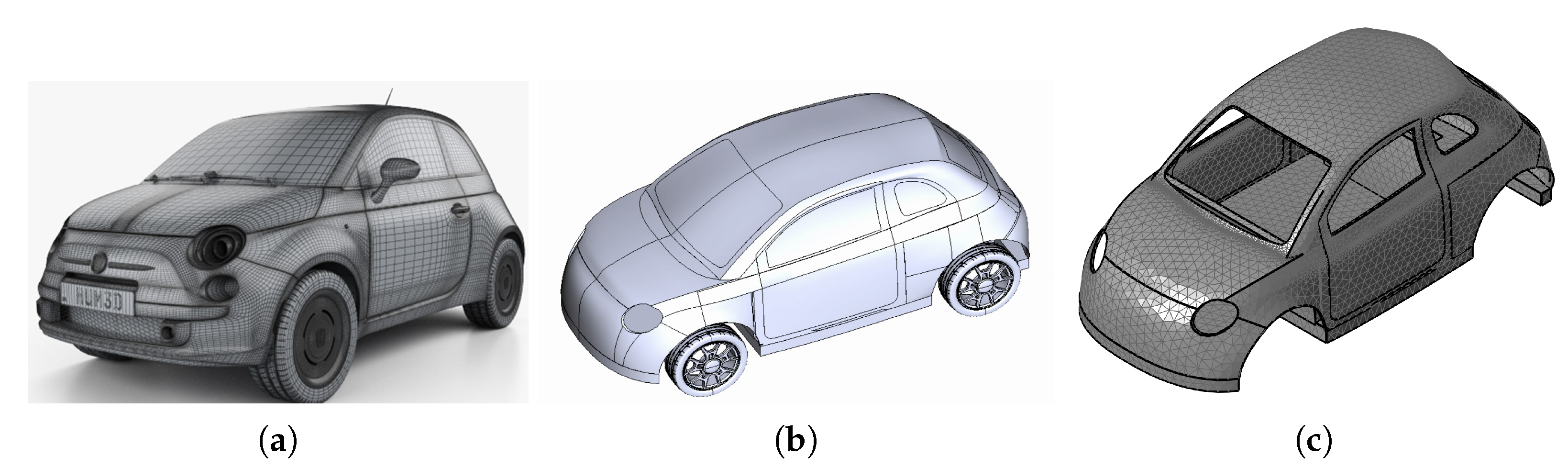
2.1. Car Modeling
2.2. WPT System Configuration
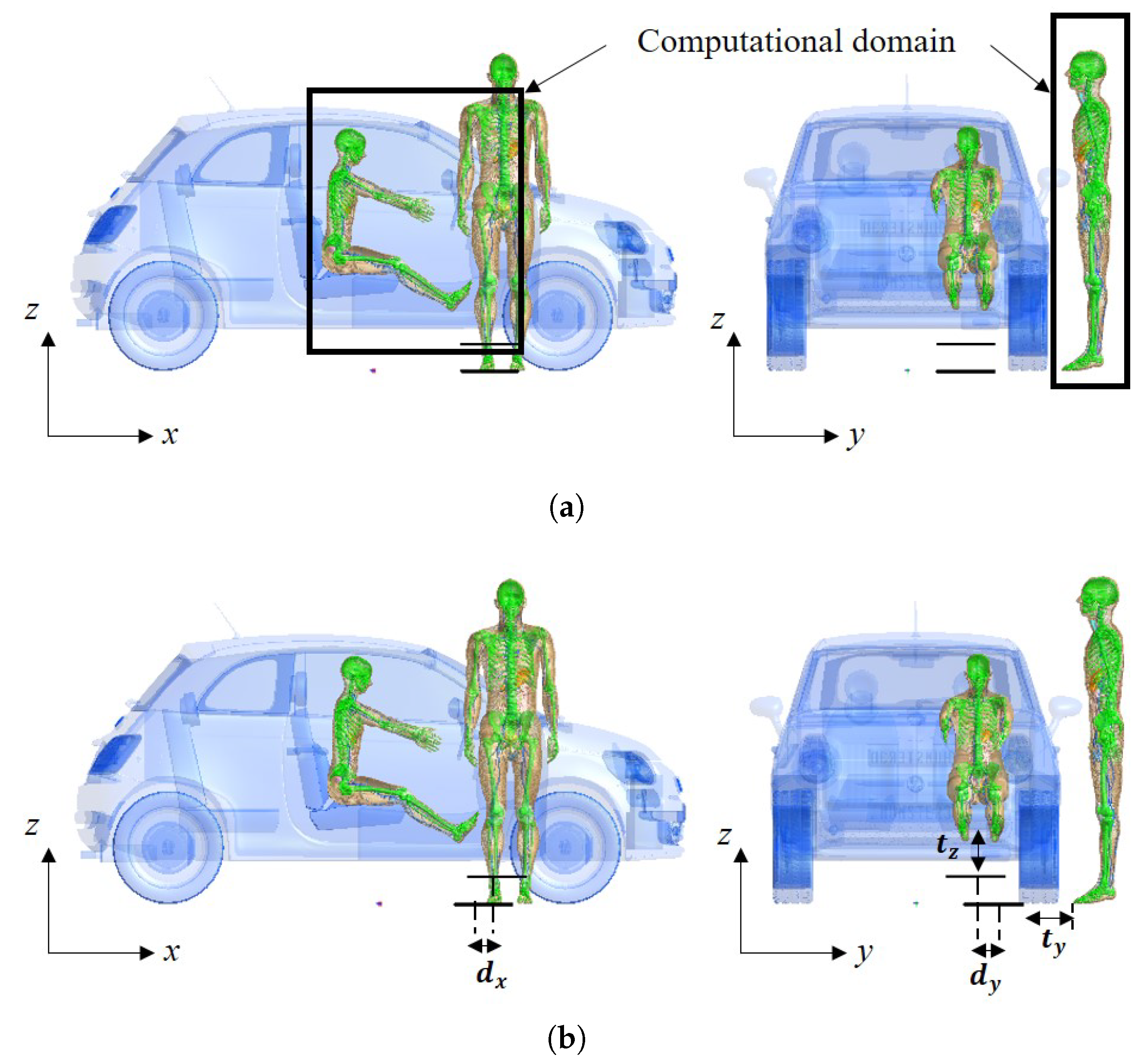
2.3. Exposure Scenarios for Numerical Dosimetry
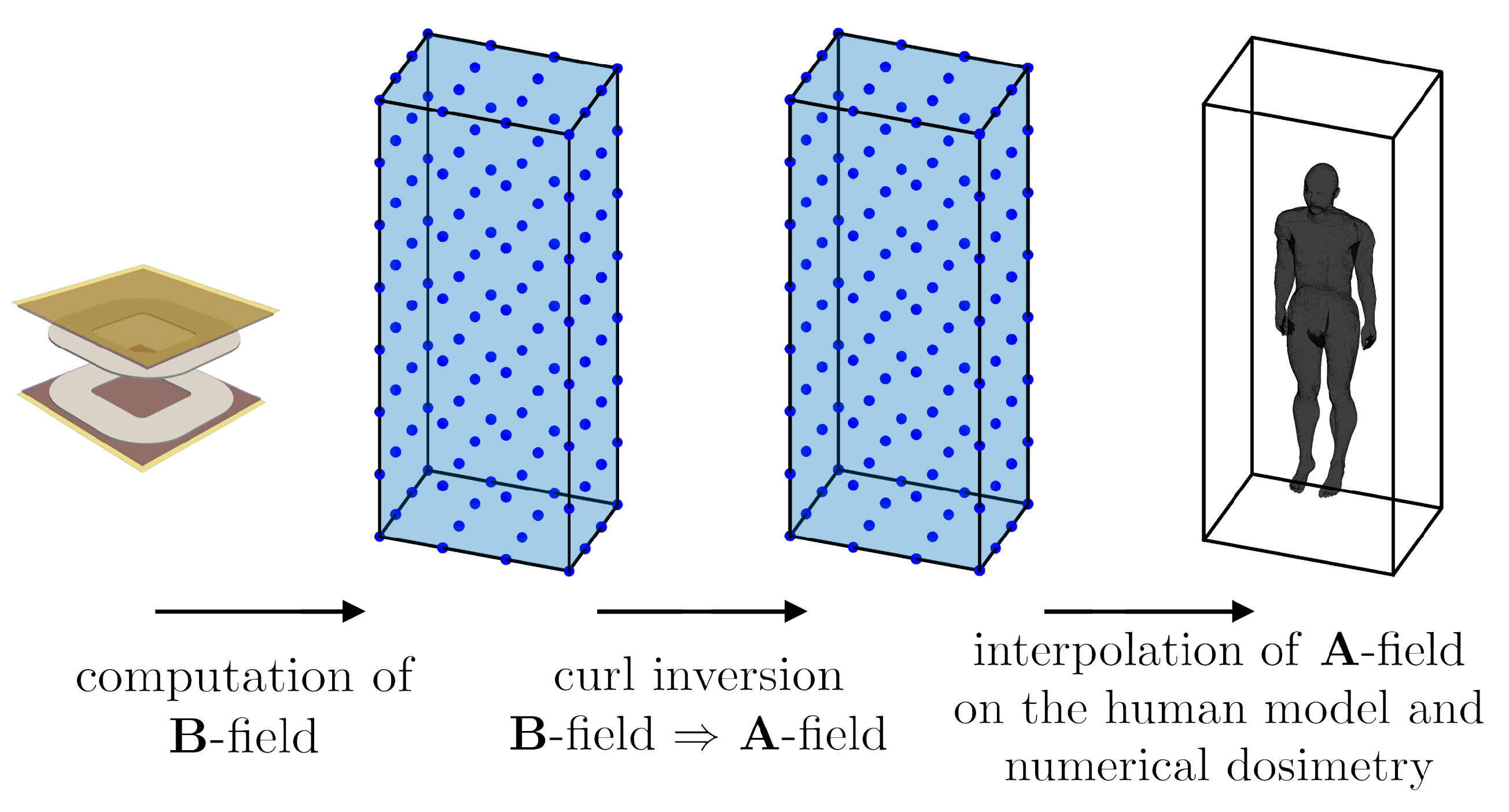
2.4. Magnetic Field Evaluation
2.5. LF Dosimetry
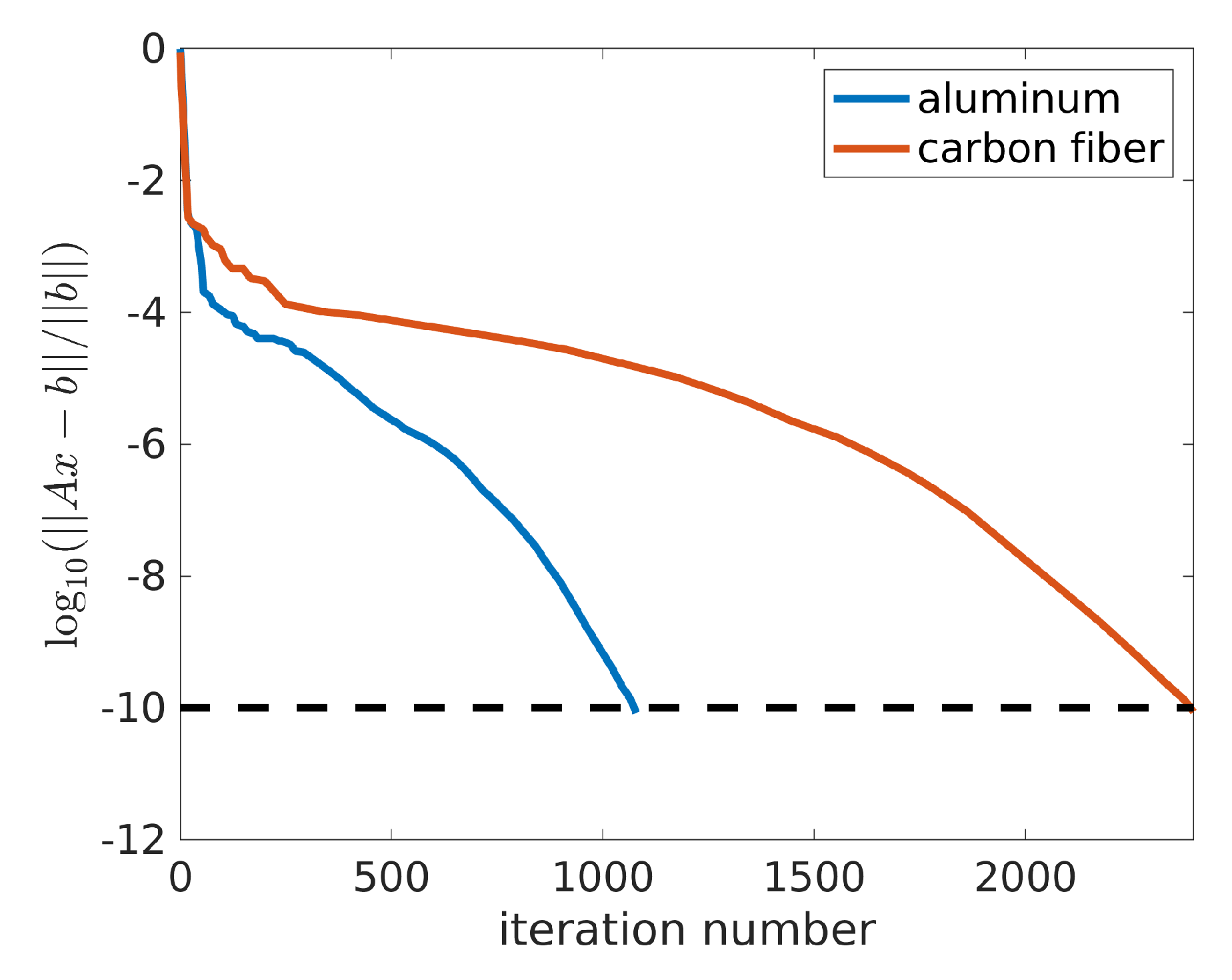
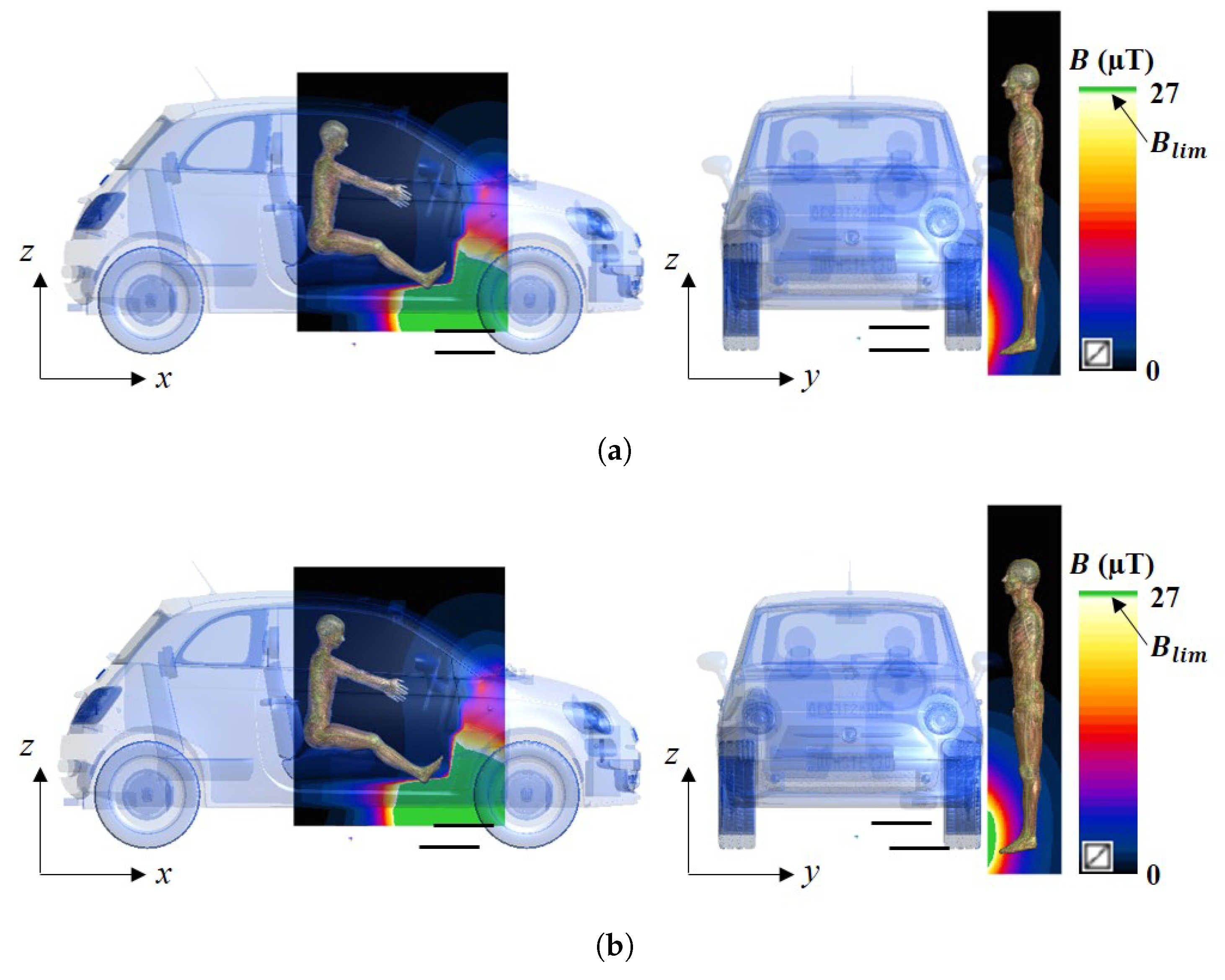
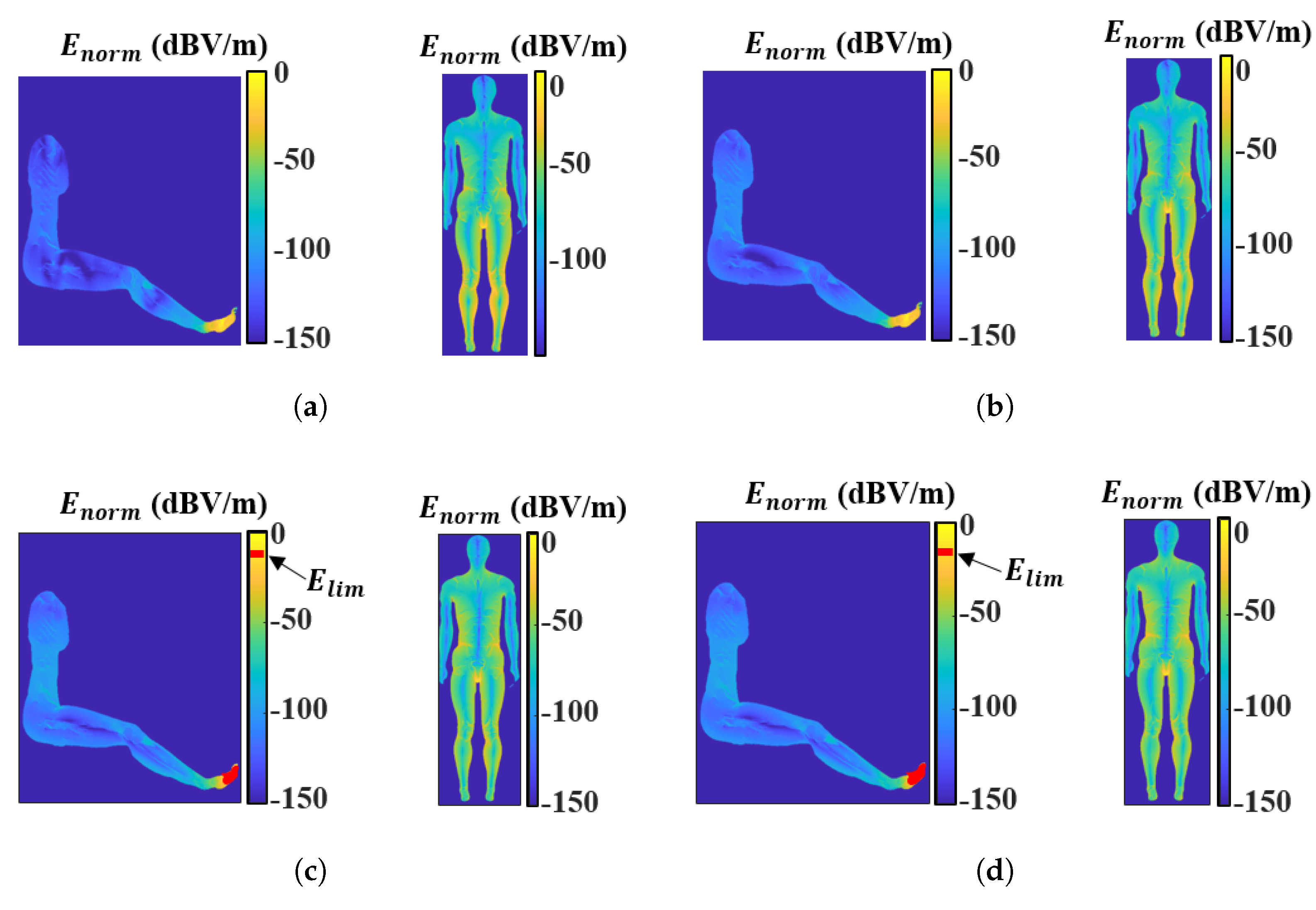
3. Numerical Dosimetry Results
3.1. RL Numerical Dosimetry
3.2. BR Numerical Dosimetry
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- International Energy Agency (IEA). Global Energy and CO2 Status Report; IEA: Paris, France, 2018.
- International Energy Agency (IEA). Global EV Outlook; IEA: Paris, France, 2019.
- Machura, P.; De Santis, V.; Li, Q. Driving range of Electric Vehicles charged by Wireless Power Transfer. IEEE Trans. Veh. Technol. 2020, 69, 5968–5982. [Google Scholar] [CrossRef]
- Romo, J.; Cañibano, E.; Merino, J.C. Lightweighting and passive safety for urban electric vehicle. In Proceedings of the 2017 Electric Vehicles International Conference (EV), Bucharest, Romania, 5–6 October 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Shimamoto, T.; Laakso, I.; Hirata, A. In-situ electric field in human body model in different postures for wireless power transfer system in an electrical vehicle. Phys. Med. Biol. 2015, 60, 163–173. [Google Scholar] [CrossRef]
- Cirimele, V.; Freschi, F.; Giaccone, L.; Pichon, L.; Repetto, M. Human exposure assessment in Dynamic Inductive Power Transfer for automotive applications. IEEE Trans. Magn. 2017, 53, 1–4. [Google Scholar] [CrossRef]
- De Santis, V.; Campi, T.; Cruciani, S.; Laakso, I.; Feliziani, M. Assessment of the induced electric fields in a Carbon-Fiber Electrical Vehicle equipped with a Wireless Power Transfer system. Energies 2018, 11, 684. [Google Scholar] [CrossRef]
- Arduino, A.; Bottauscio, O.; Chiampi, M.; Giaccone, L.; Liorni, I.; Kuster, N.; Zilberti, L.; Zucca, M. Accuracy assessment of numerical dosimetry for the evaluation of human exposure to Electric Vehicle inductive charging systems. IEEE Trans. Electromag. Compat. 2020, 62, 1939–1950. [Google Scholar] [CrossRef]
- Dawson, T.; Stuchly, M. Analytic validation of a three-dimensional scalar-potential finite-difference code for low-frequency magnetic induction. Appl. Comput. Electrom. 1996, 11, 72–81. [Google Scholar]
- Zang, M.; Cimala, C.; Clemens, M.; Dutiné, J.; Timm, T.; Schmuelling, B. A Co-Simulation Scalar-Potential Finite Difference Method for the Numerical Analysis of Human Exposure to Magneto-Quasi-Static Fields. IEEE Trans. Magn. 2017, 53, 1–4. [Google Scholar] [CrossRef]
- Freschi, F.; Giaccone, L.; Repetto, M. Algebraic formulation of nonlinear surface impedance boundary condition coupled with BEM for unstructured meshes. Eng. Anal. Bound. Elem. 2018, 88, 104–114. [Google Scholar] [CrossRef]
- Laakso, I.; De Santis, V.; Cruciani, S.; Campi, T.; Feliziani, M. Modelling of induced electric fields based on incompletely known magnetic fields. Phys. Med. Biol. 2017, 62, 6567. [Google Scholar] [CrossRef]
- Freschi, F.; Giaccone, L.; Cirimele, V.; Canova, A. Numerical assessment of low-frequency dosimetry from sampled magnetic fields. Phys. Med. Biol. 2018, 63, 015029. [Google Scholar] [CrossRef]
- Conchin Gubernati, A.; Freschi, F.; Giaccone, L.; Campi, T.; De Santis, V.; Laakso, I. Comparison of numerical techniques for the evaluation of human exposure from measurement data. IEEE Trans. Magn. 2019, 55, 1–4. [Google Scholar] [CrossRef]
- Campi, T.; Cruciani, S.; De Santis, V.; Maradei, F.; Feliziani, M. Magnetic field behavior in a carbon-fiber electrical vehicle charged by a wireless power transfer system. In Proceedings of the 2017 International Symposium on Electromagnetic Compatibility-EMC EUROPE, Angers, France, 4–7 September 2017; pp. 1–6. [Google Scholar] [CrossRef]
- IEC 61980-1. Electric Vehicle Wireless Power Transfer (WPT) Systems-Part 1: General Requirements; IEC: Geneva, Switzerland, 2015. [Google Scholar]
- International SAE J2954-Wireless Power Transfer for Light-Duty Plug-In/Electric Vehicles and Alignment Methodology; SAE: Warrendale, PA, USA, 2019.
- Hasgall, P.A.; Di Gennaro, F.; Baumgartner, C.; Neufeld, E.; Lloyd, B.; Gosselin, M.; Payne, D.; Klingenböck, A.; Kuster, N. IT’IS Database for Thermal and Electromagnetic Parameters of Biological Tissues. 2018. Available online: www.itis.swiss/database (accessed on 12 December 2020).
- De Santis, V.; Chen, X.L.; Laakso, I.; Hirata, A. An equivalent skin conductivity model for low-frequency magnetic field dosimetry. Biomed. Phys. Eng. Express 2015, 1, 1–10. [Google Scholar] [CrossRef]
- De Santis, V.; Chen, X.L.; Cruciani, S.; Campi, T.; Feliziani, M. A novel homogenization procedure to model the skin layers in LF numerical dosimetry. Phys. Med. Biol. 2016, 61, 4402–4411. [Google Scholar] [CrossRef]
- Tonti, E. A direct discrete formulation of field laws: The cell method. Comput. Model. Eng. Sci. 2001, 2, 237–258. [Google Scholar] [CrossRef]
- Hirata, A.; Ito, F.; Laakso, I. Confirmation of quasi-static approximation in SAR evaluation for a wireless power transfer system. Phys. Med. Biol. 2013, 58, N241–N249. [Google Scholar] [CrossRef]
- Kim, M.; Yun, I. An efficient implementation of the generalized minimum residual algorithm with a new preconditioner for the boundary element method. Eng. Anal. Bound. Elem. 2011, 35, 1214–1224. [Google Scholar] [CrossRef]
- Mandel, J. On block diagonal and Schur complement preconditioning. Numer. Math. 1990, 58, 79–93. [Google Scholar] [CrossRef]
- ICNIRP. Guidelines for Limiting Exposure to Time-Varying Electric and Magnetic Fields (1 Hz–100 kHz). Health Phys. 2010, 99, 818–836. [Google Scholar] [CrossRef]
- Kos, B.; Valič, B.; Miklavčič, D.; Kotnik, T.; Gajšek, P. Pre- and post-natal exposure of children to EMF generated by domestic induction cookers. Phys. Med. Biol. 2011, 56, 6149–6160. [Google Scholar] [CrossRef]
- Laakso, I.; Hirata, A. Reducing the staircasing error in computational dosimetry of low-frequency electromagnetic fields. Phys. Med. Biol. 2012, 57, 25–34. [Google Scholar] [CrossRef] [PubMed]
- De Santis, V.; Chen, X.L. On the issues related to compliance assessment of ICNIRP 2010 basic restrictions. J. Rad. Prot. 2014, 34, N31. [Google Scholar] [CrossRef] [PubMed]
- Diao, Y.; Gomez-Tames, J.; Rashed, E.A.; Kavet, R.; Hirata, A. Spatial averaging schemes of in situ electric field for low-frequency magnetic field Eexposures. IEEE Access 2019, 7, 184320–184331. [Google Scholar] [CrossRef]
- Giaccone, L. Compliance of non-sinusoidal or pulsed magnetic fields generated by industrial sources with reference to human exposure guidelines. In Proceedings of the 2020 International Symposium on Electromagnetic Compatibility-EMC EUROPE, Rome, Italy, 23–25 September 2020; pp. 1–6. [Google Scholar] [CrossRef]


| Exposure | Chassis | Overexposure | |||
|---|---|---|---|---|---|
| Scenario | Material | (V/m) | (V/m) | (V/m) | (dB) |
| Ella–Aligned | aluminum | 8.26 | 1.84 | 0.71 | −18.48 |
| Ella–Misaligned | 7.69 | 1.36 | 0.57 | −19.22 | |
| Duke–Aligned | 0.27 | 0.11 | 0.07 | −44.11 | |
| Duke–Misaligned | 0.53 | 0.25 | 0.12 | −39.56 | |
| Ella–Aligned | carbon fiber | 19.21 | 5.86 | 1.71 | −16.48 |
| Ella–Misaligned | 24.00 | 6.94 | 1.76 | −16.23 | |
| Duke–Aligned | 0.76 | 0.36 | 0.14 | −38.11 | |
| Duke–Misaligned | 0.90 | 0.44 | 0.17 | −36.45 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Santis, V.; Giaccone, L.; Freschi, F. Chassis Influence on the Exposure Assessment of a Compact EV during WPT Recharging Operations. Magnetochemistry 2021, 7, 25. https://doi.org/10.3390/magnetochemistry7020025
De Santis V, Giaccone L, Freschi F. Chassis Influence on the Exposure Assessment of a Compact EV during WPT Recharging Operations. Magnetochemistry. 2021; 7(2):25. https://doi.org/10.3390/magnetochemistry7020025
Chicago/Turabian StyleDe Santis, Valerio, Luca Giaccone, and Fabio Freschi. 2021. "Chassis Influence on the Exposure Assessment of a Compact EV during WPT Recharging Operations" Magnetochemistry 7, no. 2: 25. https://doi.org/10.3390/magnetochemistry7020025
APA StyleDe Santis, V., Giaccone, L., & Freschi, F. (2021). Chassis Influence on the Exposure Assessment of a Compact EV during WPT Recharging Operations. Magnetochemistry, 7(2), 25. https://doi.org/10.3390/magnetochemistry7020025








