Geometrically Constrained Skyrmions
Abstract
1. Introduction
2. Results
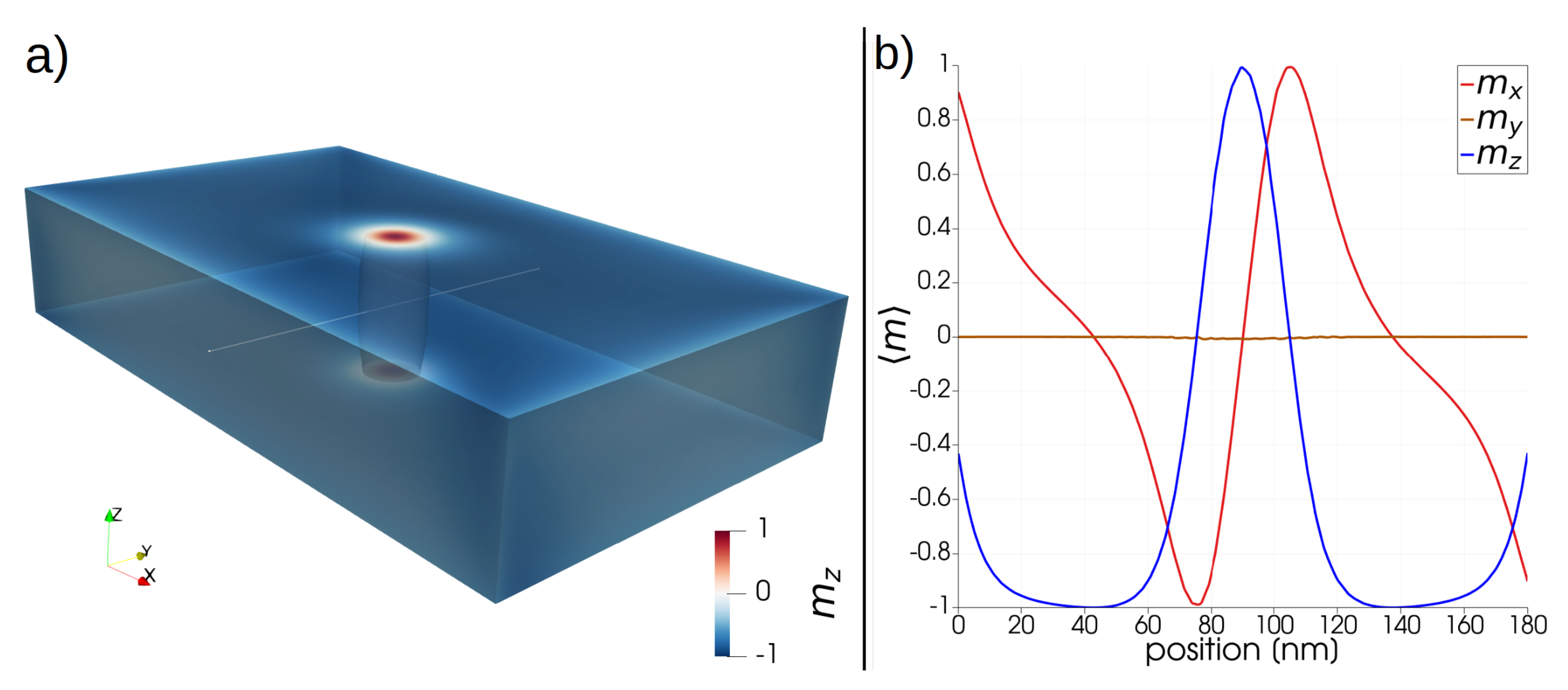
2.1. Chiral Magnetization States in a Helimagnetic Rectangular Platelet
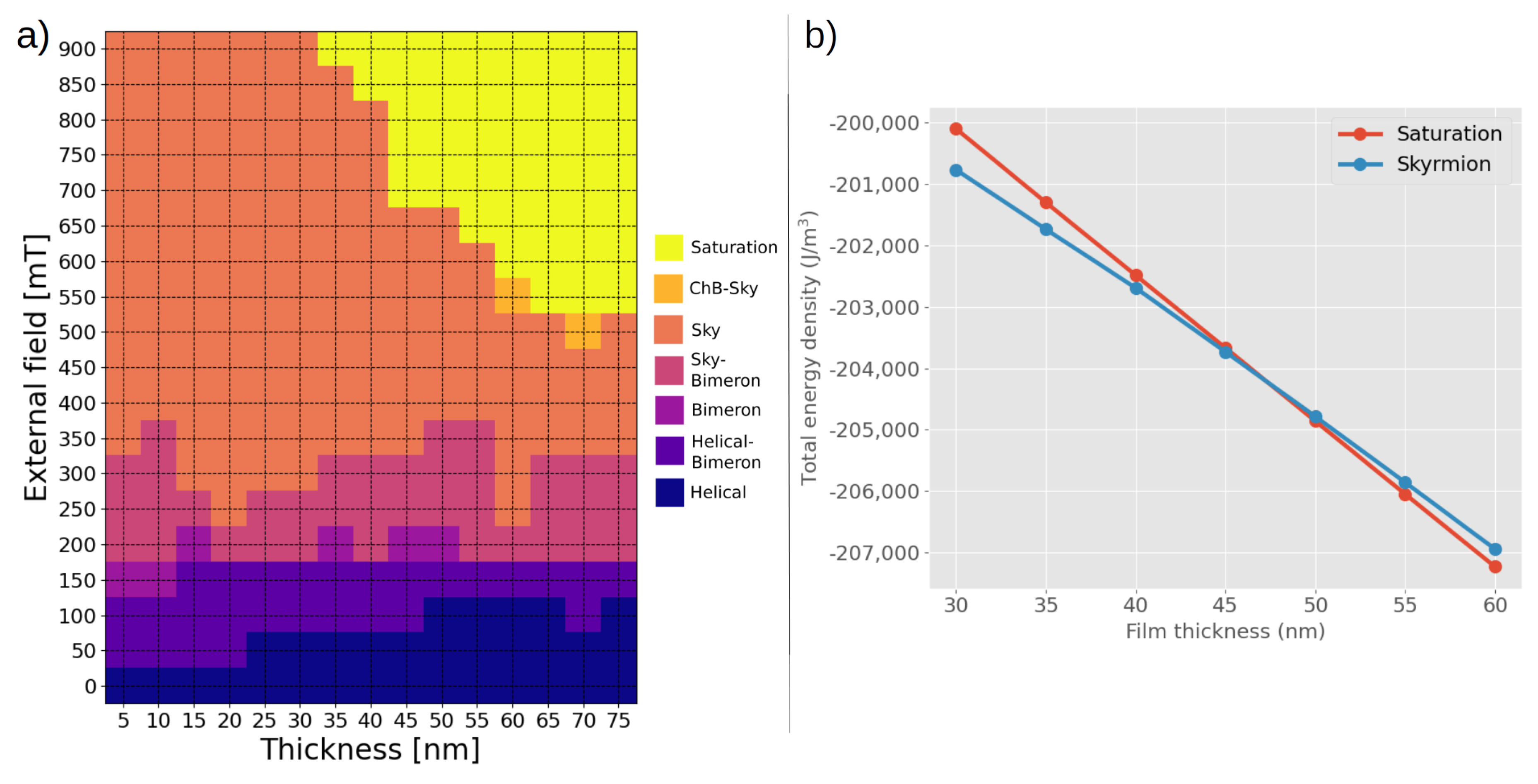
2.2. Phase Diagram of the Magnetization States
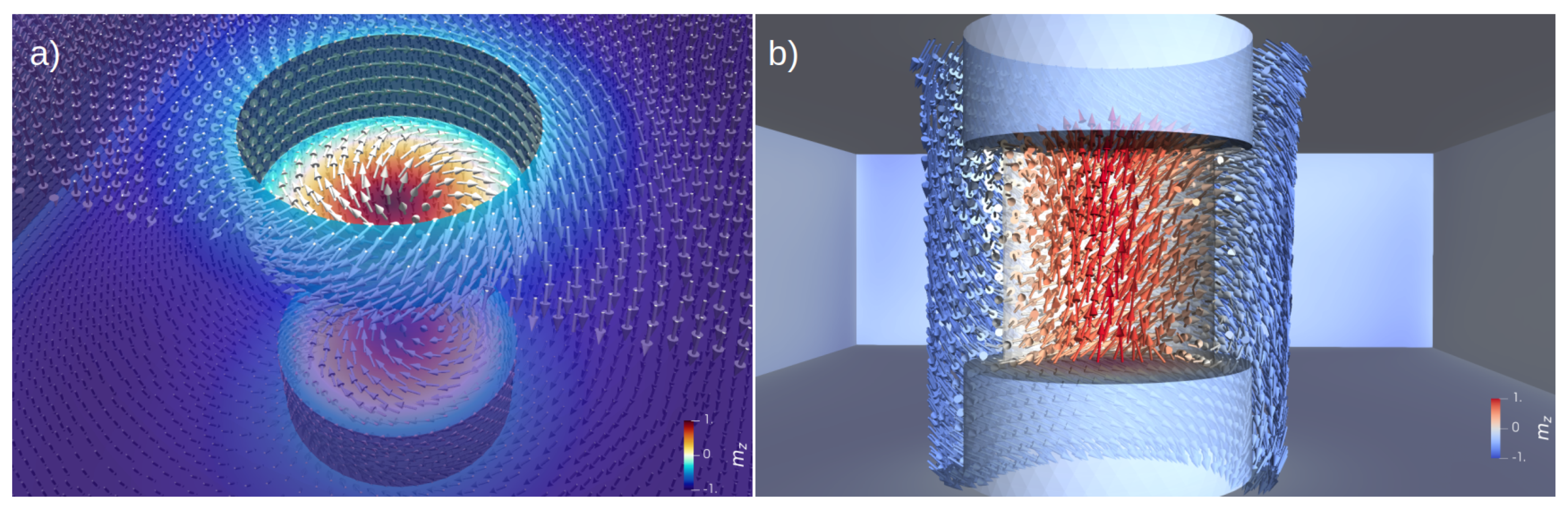
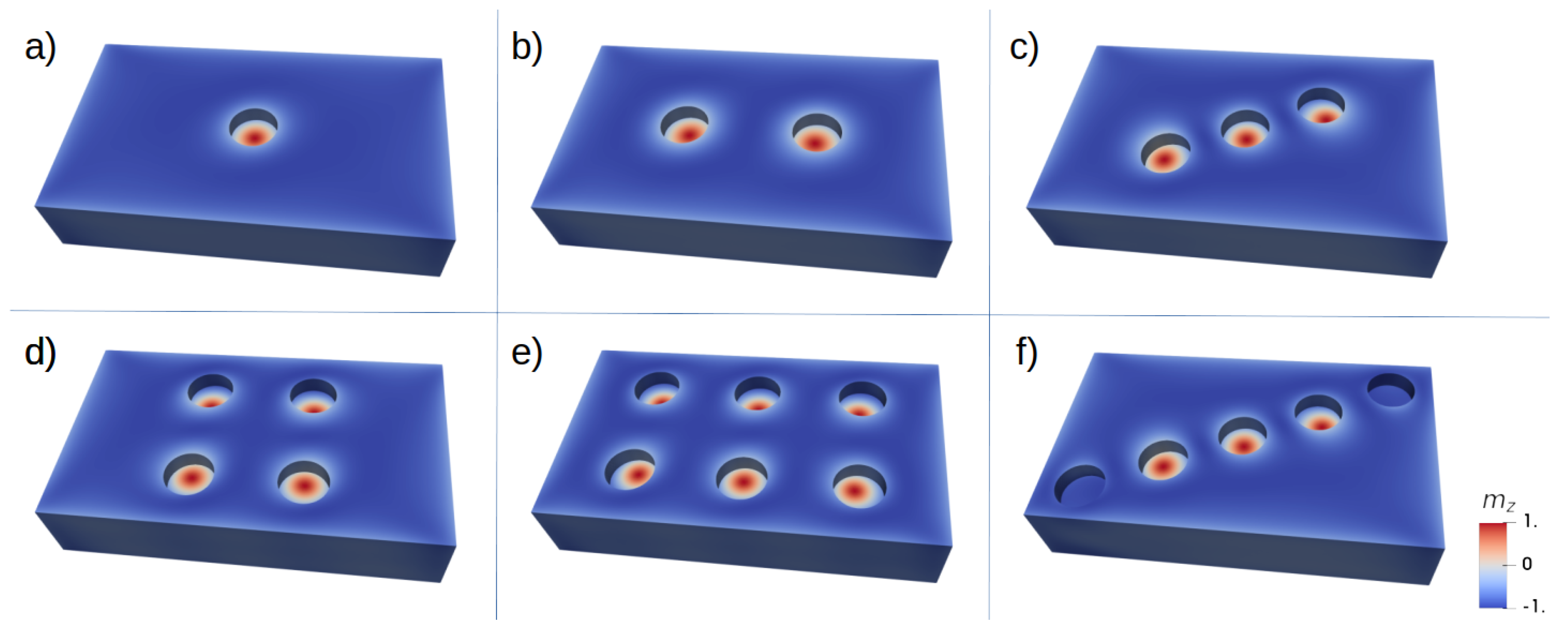
2.3. Geometrically Constrained Skyrmions
3. Discussion
4. Materials and Methods
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DMI | Dzyaloshinksii-Moryia interaction |
| LLG | Landau-Lifshitz-Gilbert equation |
| FEM | Finite Element Method |
| BEM | Boundary Element Method |
| GPU | Graphical Processing Unit |
| 3D | three-dimensional |
| ChB | chiral bobber |
Appendix A. Energy Minimization
References
- Finocchio, G.; Büttner, F.; Tomasello, R.; Carpentieri, M.; Kläui, M. Magnetic skyrmions: From fundamental to applications. J. Phys. D Appl. Phys. 2016, 49, 423001. [Google Scholar] [CrossRef]
- Everschor-Sitte, K.; Masell, J.; Reeve, R.M.; Kläui, M. Perspective: Magnetic skyrmions—Overview of recent progress in an active research field. J. Appl. Phys. 2018, 124, 240901. [Google Scholar] [CrossRef]
- Back, C.; Cros, V.; Ebert, H.; Everschor-Sitte, K.; Fert, A.; Garst, M.; Ma, T.; Mankovsky, S.; Monchesky, T.L.; Mostovoy, M.; et al. The 2020 skyrmionics roadmap. J. Phys. D Appl. Phys. 2020, 53, 363001. [Google Scholar] [CrossRef]
- Muhlbauer, S.; Binz, B.; Jonietz, F.; Pfleiderer, C.; Rosch, A.; Neubauer, A.; Georgii, R.; Boni, P. Skyrmion Lattice in a Chiral Magnet. Science 2009, 323, 915–919. [Google Scholar] [CrossRef]
- Yu, X.; Onose, Y.; Kanazawa, N.; Park, J.; Han, J.; Matsui, Y.; Nagaosa, N.; Tokura, Y. Real-space observation of a two-dimensional skyrmion crystal. Nature 2010, 465, 901–904. [Google Scholar] [CrossRef] [PubMed]
- Oike, H.; Kikkawa, A.; Kanazawa, N.; Taguchi, Y.; Kawasaki, M.; Tokura, Y.; Kagawa, F. Interplay between topological and thermodynamic stability in a metastable magnetic skyrmion lattice. Nat. Phys. 2016, 12, 62–66. [Google Scholar] [CrossRef]
- Iwasaki, J.; Mochizuki, M.; Nagaosa, N. Universal current-velocity relation of skyrmion motion in chiral magnets. Nat. Commun. 2013, 4, 1463. [Google Scholar] [CrossRef]
- Iwasaki, J.; Mochizuki, M.; Nagaosa, N. Current-induced skyrmion dynamics in constricted geometries. Nat. Nanotechnol. 2013, 8, 742–747. [Google Scholar] [CrossRef]
- Xuan, S.; Liu, Y. Nonuniform gyrotropic oscillation of skyrmion in a nanodisk. AIP Adv. 2018, 8, 045312. [Google Scholar] [CrossRef]
- Yu, X.Z.; Kanazawa, N.; Onose, Y.; Kimoto, K.; Zhang, W.Z.; Ishiwata, S.; Matsui, Y.; Tokura, Y. Near room-temperature formation of a skyrmion crystal in thin-films of the helimagnet FeGe. Nat. Mater. 2011, 10, 106–109. [Google Scholar] [CrossRef]
- Boulle, O.; Vogel, J.; Yang, H.; Pizzini, S.; de Souza Chaves, D.; Locatelli, A.; Menteş, T.O.; Sala, A.; Buda-Prejbeanu, L.D.; Klein, O.; et al. Room-temperature chiral magnetic skyrmions in ultrathin magnetic nanostructures. Nat. Nanotechnol. 2016, 11, 449. [Google Scholar] [CrossRef] [PubMed]
- Heinze, S.; Von Bergmann, K.; Menzel, M.; Brede, J.; Kubetzka, A.; Wiesendanger, R.; Bihlmayer, G.; Blügel, S. Spontaneous atomic-scale magnetic skyrmion lattice in two dimensions. Nat. Phys. 2011, 7, 713–718. [Google Scholar] [CrossRef]
- Yu, X.; Kanazawa, N.; Zhang, W.; Nagai, T.; Hara, T.; Kimoto, K.; Matsui, Y.; Onose, Y.; Tokura, Y. Skyrmion flow near room temperature in an ultralow current density. Nat. Commun. 2012, 3, 988. [Google Scholar] [CrossRef] [PubMed]
- Fert, A.; Cros, V.; Sampaio, J. Skyrmions on the track. Nat. Nanotechnol. 2013, 8, 152–156. [Google Scholar] [CrossRef]
- Seki, S.; Yu, X.; Ishiwata, S.; Tokura, Y. Observation of skyrmions in a multiferroic material. Science 2012, 336, 198–201. [Google Scholar] [CrossRef]
- Rybakov, F.N.; Borisov, A.B.; Bogdanov, A.N. Three-dimensional skyrmion states in thin films of cubic helimagnets. Phys. Rev. B 2013, 87, 094424. [Google Scholar] [CrossRef]
- Rybakov, F.N.; Borisov, A.B.; Blügel, S.; Kiselev, N.S. New spiral state and skyrmion lattice in 3D model of chiral magnets. New J. Phys. 2016, 18, 045002. [Google Scholar] [CrossRef]
- Beg, M.; Carey, R.; Wang, W.; Cortés-Ortuño, D.; Vousden, M.; Bisotti, M.A.; Albert, M.; Chernyshenko, D.; Hovorka, O.; Stamps, R.L.; et al. Ground state search, hysteretic behaviour, and reversal mechanism of skyrmionic textures in confined helimagnetic nanostructures. Sci. Rep. 2015, 5, 17137. [Google Scholar] [CrossRef]
- Ma, F.; Zhou, Y.; Braun, H.B.; Lew, W.S. Skyrmion-Based Dynamic Magnonic Crystal. Nano Lett. 2015, 15, 4029–4036. [Google Scholar] [CrossRef]
- Parkin, S.S.P.; Hayashi, M.; Thomas, L. Magnetic Domain-Wall Racetrack Memory. Science 2008, 320, 190–194. [Google Scholar] [CrossRef] [PubMed]
- Bedau, D.; Kläui, M.; Rüdiger, U.; Vaz, C.A.F.; Bland, J.A.C.; Faini, G.; Vila, L.; Wernsdorfer, W. Angular dependence of the depinning field for head-to-head domain walls at constrictions. J. Appl. Phys. 2007, 101, 09F509. [Google Scholar] [CrossRef]
- Bogart, L.K.; Eastwood, D.S.; Atkinson, D. The effect of geometrical confinement and chirality on domain wall pinning behavior in planar nanowires. J. Appl. Phys. 2008, 104, 033904. [Google Scholar] [CrossRef]
- Garcia-Sanchez, F.; Kákay, A.; Hertel, R.; Asselin, P. Depinning of Transverse Domain Walls from Notches in Magnetostatically Coupled Nanostrips. Appl. Phys. Express 2011, 4, 033001. [Google Scholar] [CrossRef]
- Suess, D.; Vogler, C.; Bruckner, F.; Heistracher, P.; Slanovc, F.; Abert, C. Spin Torque Efficiency and Analytic Error Rate Estimates of Skyrmion Racetrack Memory. Sci. Rep. 2019, 9, 4827. [Google Scholar] [CrossRef]
- Liu, Y.H.; Li, Y.Q. A mechanism to pin skyrmions in chiral magnets. J. Phys. Condens. Matter 2013, 25, 076005. [Google Scholar] [CrossRef]
- Hanneken, C.; Kubetzka, A.; Bergmann, K.V.; Wiesendanger, R. Pinning and movement of individual nanoscale magnetic skyrmions via defects. New J. Phys. 2016, 18, 055009. [Google Scholar] [CrossRef]
- Müller, J.; Rosch, A. Capturing of a magnetic skyrmion with a hole. Phys. Rev. B 2015, 91, 054410. [Google Scholar] [CrossRef]
- Karube, K.; White, J.S.; Reynolds, N.; Gavilano, J.L.; Oike, H.; Kikkawa, A.; Kagawa, F.; Tokunaga, Y.; Rønnow, H.M.; Tokura, Y.; et al. Robust metastable skyrmions and their triangular–square lattice structural transition in a high-temperature chiral magnet. Nat. Mater. 2016, 15, 1237–1242. [Google Scholar] [CrossRef] [PubMed]
- Mandru, A.O.; Yıldırım, O.; Tomasello, R.; Heistracher, P.; Penedo, M.; Giordano, A.; Suess, D.; Finocchio, G.; Hug, H.J. Coexistence of distinct skyrmion phases observed in hybrid ferromagnetic/ferrimagnetic multilayers. Nat. Commun. 2020, 11, 6365. [Google Scholar] [CrossRef] [PubMed]
- Rybakov, F.N.; Borisov, A.B.; Blügel, S.; Kiselev, N.S. New Type of Stable Particlelike States in Chiral Magnets. Phys. Rev. Lett. 2015, 115, 117201. [Google Scholar] [CrossRef] [PubMed]
- Zheng, F.; Rybakov, F.N.; Borisov, A.B.; Song, D.; Wang, S.; Li, Z.A.; Du, H.; Kiselev, N.S.; Caron, J.; Kovács, A.; et al. Experimental observation of chiral magnetic bobbers in B20-type FeGe. Nat. Nanotechnol. 2018, 13, 451–455. [Google Scholar] [CrossRef] [PubMed]
- Ross, C. Patterned Magnetic Recording Media. Annu. Rev. Mater. Res. 2001, 31, 203–235. [Google Scholar] [CrossRef]
- Hayashi, M.; Thomas, L.; Rettner, C.; Moriya, R.; Jiang, X.; Parkin, S.S.P. Dependence of Current and Field Driven Depinning of Domain Walls on Their Structure and Chirality in Permalloy Nanowires. Phys. Rev. Lett. 2006, 97, 207205. [Google Scholar] [CrossRef]
- Wilson, M.N.; Butenko, A.B.; Bogdanov, A.N.; Monchesky, T.L. Chiral skyrmions in cubic helimagnet films: The role of uniaxial anisotropy. Phys. Rev. B 2014, 89, 094411. [Google Scholar] [CrossRef]
- Brearton, R.; van der Laan, G.; Hesjedal, T. Magnetic skyrmion interactions in the micromagnetic framework. Phys. Rev. B 2020, 101, 134422. [Google Scholar] [CrossRef]
- Lin, S.Z.; Reichhardt, C.; Batista, C.D.; Saxena, A. Particle model for skyrmions in metallic chiral magnets: Dynamics, pinning, and creep. Phys. Rev. B 2013, 87, 214419. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, G.P.; Fangohr, H.; Liu, J.P.; Xia, W.X.; Xia, J.; Morvan, F.J. Skyrmion-skyrmion and skyrmion-edge repulsions in skyrmion-based racetrack memory. Sci. Rep. 2015, 5, 7643. [Google Scholar] [CrossRef] [PubMed]
- Sampaio, J.; Cros, V.; Rohart, S.; Thiaville, A.; Fert, A. Nucleation, stability and current-induced motion of isolated magnetic skyrmions in nanostructures. Nat. Nanotechnol. 2013, 8, 839. [Google Scholar] [CrossRef]
- Duine, R. Skyrmions singled out. Nat. Nanotechnol. 2013, 8, 800–802. [Google Scholar] [CrossRef]
- Bruno, P. Geometrically Constrained Magnetic Wall. Phys. Rev. Lett. 1999, 83, 2425–2428. [Google Scholar] [CrossRef]
- Garst, M.; Waizner, J.; Grundler, D. Collective spin excitations of helices and magnetic skyrmions: Review and perspectives of magnonics in non-centrosymmetric magnets. J. Phys. D Appl. Phys. 2017, 50, 293002. [Google Scholar] [CrossRef]
- Cortés-Ortuño, D.I.; Beg, M.; Nehruji, V.; Breth, L.; Pepper, R.; Kluyver, T.; Downing, G.; Hesjedal, T.; Hatton, P.; Lancaster, T.; et al. Proposal for a micromagnetic standard problem for materials with Dzyaloshinskii-Moriya interaction. New J. Phys. 2018. [Google Scholar] [CrossRef]
- Lebech, B.; Bernhard, J.; Freltoft, T. Magnetic structures of cubic FeGe studied by small-angle neutron scattering. J. Phys. Condens. Matter 1989, 1, 6105–6122. [Google Scholar] [CrossRef]
- Zhao, X.; Jin, C.; Wang, C.; Du, H.; Zang, J.; Tian, M.; Che, R.; Zhang, Y. Direct imaging of magnetic field-driven transitions of skyrmion cluster states in FeGe nanodisks. Proc. Natl. Acad. Sci. USA 2016, 113, 4918–4923. [Google Scholar] [CrossRef]
- Fredkin, D.; Koehler, T. Hybrid method for computing demagnetizing fields. IEEE Trans. Magn. 1990, 26, 415–417. [Google Scholar] [CrossRef]
- Koehler, T.; Fredkin, D. Finite element methods for micromagnetics. IEEE Trans. Magn. 1992, 28, 1239–1244. [Google Scholar] [CrossRef]
- Hertel, R.; Christophersen, S.; Börm, S. Large-scale magnetostatic field calculation in finite element micromagnetics with H2-matrices. J. Magn. Magn. Mater. 2019, 477, 118–123. [Google Scholar] [CrossRef]
- Gilbert, T.L. A phenomenological theory of damping in ferromagnetic materials. IEEE Trans. Magn. 2004, 40, 3443–3449. [Google Scholar] [CrossRef]
- Riegel, J.; Mayer, W.; van Havre, Y. FreeCAD (0.18). Available online: https://www.freecadweb.org/ (accessed on 12 December 2020).
- Schöberl, J. NETGEN An advancing front 2D/3D-mesh generator based on abstract rules. Comput. Vis. Sci. 1997, 1, 41–52. [Google Scholar] [CrossRef]
- Ayachit, U. The ParaView Guide: A Parallel Visualization Application; Kitware: Clifton Park, NY, USA, 2015. [Google Scholar]
- Ahnert, K.; Mulansky, M. Odeint—Solving Ordinary Differential Equations in C++. AIP Conf. Proc. 2011, 1389, 1586–1589. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pathak, S.A.; Hertel, R. Geometrically Constrained Skyrmions. Magnetochemistry 2021, 7, 26. https://doi.org/10.3390/magnetochemistry7020026
Pathak SA, Hertel R. Geometrically Constrained Skyrmions. Magnetochemistry. 2021; 7(2):26. https://doi.org/10.3390/magnetochemistry7020026
Chicago/Turabian StylePathak, Swapneel Amit, and Riccardo Hertel. 2021. "Geometrically Constrained Skyrmions" Magnetochemistry 7, no. 2: 26. https://doi.org/10.3390/magnetochemistry7020026
APA StylePathak, S. A., & Hertel, R. (2021). Geometrically Constrained Skyrmions. Magnetochemistry, 7(2), 26. https://doi.org/10.3390/magnetochemistry7020026






