1. Introduction
Flow past a stretching plate has been a topic of the research for around half a century [
1]. One of the aspects of this flow is its effect on the heat and mass transfer [
2]. The forced convective heat transfer on a stretching sheet with injection, suction, and blowing with variable temperature are studied by Grubka and Bobba [
3]. They showed the thermodynamic aspects of the problem is affected significantly by the flow characteristics. The application of this problem is in the industry of the wire drawing [
4] manufacturing of hot rolling glass fiber [
5], drawing plastic sheet [
6], cooling and drying of papers [
7], melting of polymers [
8], etc. The temperature field in a flow over a stretching plate with a uniform heat flux [
6] and with variable heat flux [
8] including the distribution of heat transfer reveals the effect of flux distribution on the thermal balance in the volume. Hooshmand et al. solved the flow past a stretching plate and the solution obtained reveals that for constant surface temperature the skin friction coefficient increases with the Reynolds number [
9]. The research also contains the effect of thermal radiation on a stretching plate [
9,
10]. Flow and heat transfer of a fluid through a porous medium over a stretching surface with internal heat generation/absorption and suction/blowing is studied by Cortell [
11].
Transient flow is solved analytically for the case of unsteady boundary-layer flows caused by an impulsively stretching plate [
12]. There is a great difference between the solution of Liao [
12] and the simple model in boundary-layer flow derived by Mehmood [
13]. Hydro-magnetic effects adjacent [
14] to a stretching vertical sheet and inside the boundary-layer flow [
15] was studied by researchers. Furthermore, the geometry is varied from plate [
1,
9,
12] to cylinder [
15,
16,
17,
18]. The effect of magnetohydrodynamics (MHD) on the flow and heat transfer due to a stretching cylinder was studied by Ishak et al. [
19]. Existence of a solution and prior bounds for steady stagnation flow toward a stretching cylinder by Mastroberardino and Paullet [
20] and Aligned and non-aligned radial stagnation flow on a stretching cylinder by Weidman and Ali [
21] showed that the concentration of the flow can increase the heat transfer locally.
Stretching of the cylinder can cause slip effects [
22] and vacillation [
23]. Those effects can be controlled by hydro-magnetic effects [
24]. The MHD control is used in various applications such as two-phase flow-induced vibrations in the vertical heated upward flow [
25,
26,
27], hemodynamic [
28,
29,
30], and polymer applications [
31,
32,
33]. The problem is solved in Cartesian [
34,
35,
36,
37,
38,
39,
40,
41] and cylindrical coordinates [
42,
43]. In the International Plastics Handbook [
44] and Mechanical and Thermophysical Properties of Polymer Liquid Crystals [
45] thermal and physical properties of polymers are given and used for the current study. The Rosseland approximation [
46].
Previous work on MHD flow [
47] with radiation heat transfer [
10,
48,
49,
50] with models [
51,
52] and methods [
53,
54], in various media [
55,
56,
57,
58,
59,
60,
61,
62,
63,
64,
65,
66,
67,
68,
69,
70,
71,
72,
73].
The media can be categorized as porous [
55], convective [
56], microchannel [
57], square cavity [
58], gravity flows [
59], gravity currents [
60], suspensions [
61], shear-thinning [
62], porous gravity currents [
63], power-law gravity currents [
64], vertically graded porous media [
65], confining boundaries [
66], gravity porous media [
67], propagative [
68,
69,
70], pressure-dependent [
71], rheological [
72], and varying cross-sections and inclinations [
73]. The literature is very broad but few papers consider all the effects in one study. The importance of this work is in considering all those parameters in one problem.
Hayat et al. solved the Jeffrey fluid problem with Cattaneo–Christov heat flux (a combination of transient thermal and velocity), double stratification, and chemical reaction effects [
74]. Modified Fourier’s law (parabolic heat conduction) showed decreases in temperature at higher thermal relaxation. MHD effects on homogeneous (first-order kinetics
) and heterogeneous (cubic autocatalytic kinetics
) reactions have been studied by Khan et al. [
75]. They showed that homogeneous reactions are governed by first-order kinetics, but the effect of MHD on boundary chemical flux was not considered. MHD effects on mixed convective flow caused by a rotating disk were studied by Hayat et al. [
76] without the chemical reaction. The impacts of Joule heating, Brownian model, Buongiorno model, and non-linear thermal radiation on Walter-B fluid is addressed in [
77]. Khan et al. [
77] ignored the effect of a self-sustained chemical reaction and the reaction caused by Brownian diffusion and thermophoresis diffusion effects. Rashid [
78] studied the flow of magnetite Fe
O
nano liquid over a stretching sheet. Heat source/sink, non-linear radiation, velocity, and thermal slip aspects were considered by them, but chemical reactions are ignored.
Considering all the above, the goal of the present article was to investigate the MHD effects in a steady-state fully developed non-Newtonian incompressible flow over an axisymmetric stretching sheet and the Rosseland approximation model in the chemical reactive environment where the Brownian and thermophoresis effects affect the transport of diluted species. Furthermore, the chemical reaction will affect the thermal balance of the system with released heat and with heating at a specific rate. In the next section, the complex nature of the governing equations describing the flows of the system are presented. Similarity transformation is used to reduce the governing equations of the problem into a system of non-linear ordinary differential equations. The resulting system of coupled equations are solved and discussed in the last section. A parameter study on chemical reactions including thermal radiation parameter, Brinkman number, Prandtl number, Hartmann number, power-law index, heat source coefficient, Brownian parameter, thermophoresis parameter, and chemical reaction parameter is performed. Numerical values are expressed in terms of graphs to investigate the influence of various flow, controlling parameters such as radiation parameter, Prandtl number, magnetic parameter, chemical parameter, and power-law parameter. The conclusions are presented in the conclusion section.
2. Governing Equations
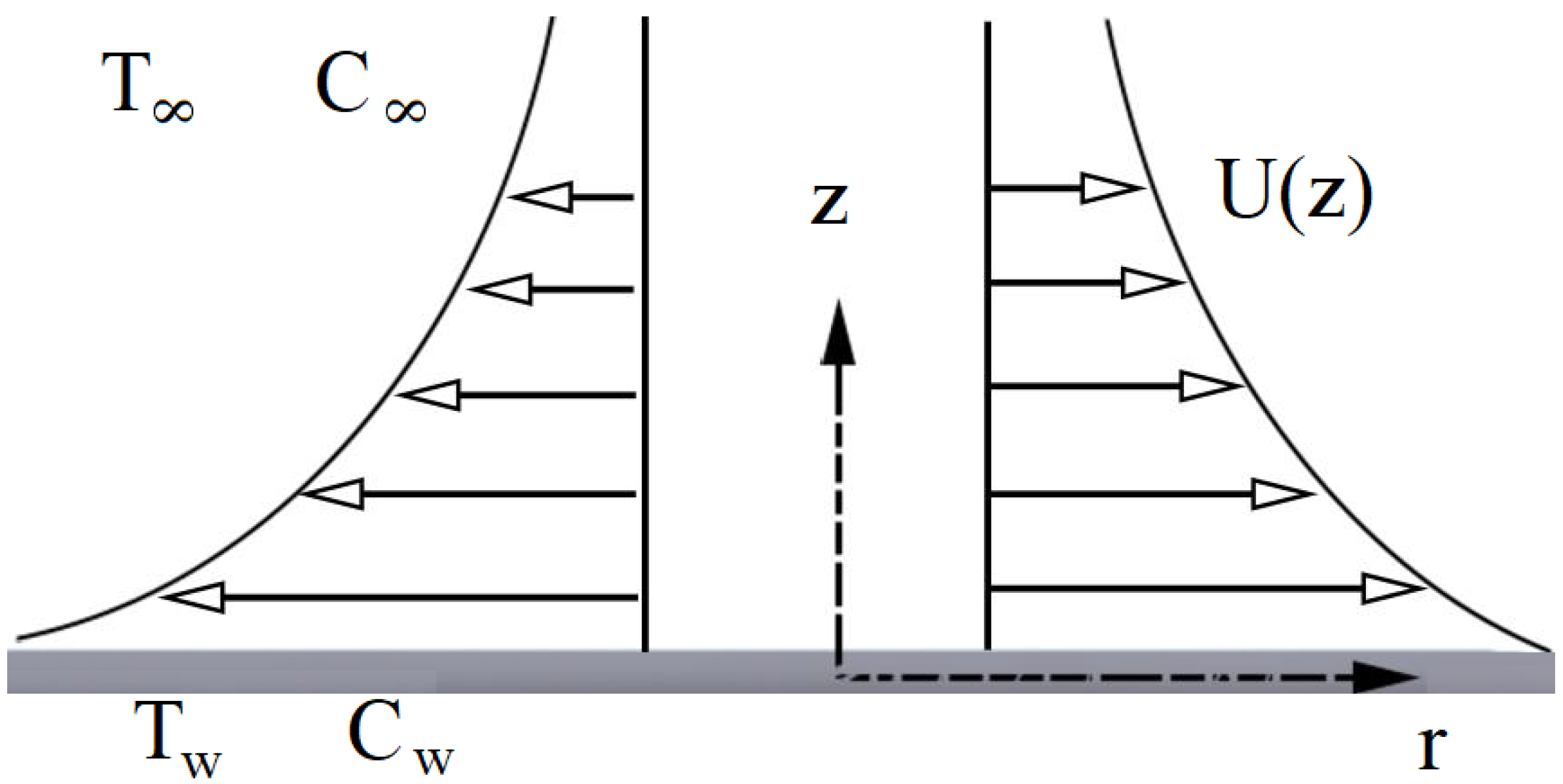
To study the MHD effects on chemical reaction near an infinitely radially stretching sheet, an axisymmetric two-dimensional sketch as shown in
Figure 1 is well considered. The fluid is considered to be an incompressible liquid. To understand the effect of melting, non-Newtonian models are considered. As exemplified, the fluid in contact with the surface of the non-permeable stretching sheet will travel along with the sheet without any slippage.
In cylindrical coordinates the continuity is:
and the momentum equation is:
where power-law indexes for common materials are presented in
Table 1.
The energy equation for thermal balance is:
where
qr is modeled by Rosseland approximation:
For the optically thick medium with the optical thickness (
×
r) greater than 3 and the boundary layer [
38] and using a linear approximation for temperature (
) the energy balance is:
The governing boundary-layer equations for mass transfer is
boundary conditions are:
where shrink rates for common plastics are presented in
Table 2.
The governing equations can be reduced to ordinary differential equations, using the similarity transformation. The equivalent stream formulations (
) of momentum and energy equations by the dimensionless temperature definition (
) are:
where
Furthermore, the mass transfer equation by considering the dimensionless concentration definition (
) is:
The
r component of velocity is assumed to have the following profile:
where
is
and stream function is
the resulted axial velocity component is:
the magnetic field distribution is:
the heat source coefficient is:
Since the non-dimensional momentum and energy equations are:
with boundary conditions of:
The velocity, temperature, and concentration profiles are obtained by solving Equations (24)–(26) with boundary conditions (27)–(33) by assigning numerical values to the parameter encounter in the problem. Dimensionless parameters are as follow:
The Schmidt number (Sc) is a dimensionless number defined as the ratio of momentum diffusivity (kinematic viscosity) and mass diffusivity:
Lewis number is a dimensionless number which is the ratio of thermal diffusivity to mass diffusivity,
, (or) Schmidt number to Prandtl number
Brownian motion parameter is
thermophoresis parameter is
chemical reaction parameter is
3. Results and Discussion
The non-linear ordinary differential Equations (24)–(26) with boundary conditions (27)–(33) have been solved by implementing the Runge–Kutta–Fehlberg fourth–fifth-order method with shooting technique. The work presents a study on the physical aspects of MHD on the chemical reactions on non-Newtonian fluid flow over stretching surface which has a significant role in food processing, polymer manufacturing, chemical engineering industries, and metallurgy. The mathematical modeling of the physical problem, which is coupled heat and mass transfer problem, include the non-linear set of partial differential equations. The coupled non-linear equations are solved for different values of parameters. To validate the compatibility of the computed solution,
Table 3 is developed to compare the present work with past works, with which this comparison shows excellent agreement. The schematic details of the compared model are the same as the current problem, which is shown in
Figure 1.
A set of non-linear ordinary differential equations are of third order in
f, second order in
and
, and are first reduced into a system of simultaneous ordinary equations. The system of ODE is in the form of
where
and the function g is
Using trial and error or some scientific approach, one attempts to get as close to the boundary value as possible. The most essential step of this method is to choose the appropriate finite value for far-field boundary conditions. Here, infinity condition is taken at a large but finite value of
, where no considerable variations in velocity, temperature and so on occur. We run our bulk computations with the value at
= 5, which is sufficient to achieve far-field boundary conditions asymptotically for all values of the parameters considered.
Figure 1 shows the schematic of the flow model where the
z-axis represents the horizontal direction and the
r-axis is normal to it. It is assumed that the sheet has an infinite radius and the surface is exposed to stretching by specific velocity. Before discussing the results, first the results of the current problem are compared with earlier research.
Table 3 presents a comparison of the
f between the present results and those obtained previously [
51] for the special case of,
Ha = 0,
n = 0, and non-linear stretching (
m = −1/3). That shows the results could be interpreted in perspective of previous studies and the working hypotheses. They are the same in geometry. Since the most important parameter is compared, and they are found to be in excellent agreement. Furthermore, the value of the local Nusselt number is compared for the case of
and
, which shows that the current method underestimates that value, but they are generally in good agreement. Numerical values are expressed in terms of graphs to investigate the influence of the Hartmann number as well as the chemical reaction parameter, Brownian motion, and thermo-phoresis parameter. General results of solved parameters are plotted in
Figure 2,
Figure 3 and
Figure 4.
Figure 2,
Figure 3 and
Figure 4 demonstrate that with an increase in curvature of the cylinder we would have an increase in velocity, temperature, and concentration profiles, respectively. As shown in
Figure 2 the
function decrease as the distance from the wall increases. The Figure is a plot of results obtained for
. Radial velocity distributions show that the inside the boundary layer the velocity decrease gradually as a result of non-linear viscosity of the fluid. This is because an increase in Hartmann number will increase the intensity of body force, which acts as a blowing boundary condition at the stretching surface and hence tends to thicken the boundary layer.
Figure 3 reveals the concentration distribution versus the non-dimensional distance. The Figure is a plot of results obtained for
. It is observed that for increasing values of distance, the dimensionless concentration decreases, and the velocity boundary-layer thickness increases and decreases the temperature distribution. It is realized that an increase in the value of chemical reaction parameter decreases the concentration of species in the boundary layer, whereas the velocity and temperature of the fluid are not significant with an increase in chemical reaction parameter.
Figure 4 exposes the temperature distribution versus the non-dimensional distance. The Figure is a plot of results obtained for
. It is observed that for increasing values of distance, the dimensionless temperature decreases, and the velocity boundary-layer thickness increases and decreases the temperature distribution.
The findings and their implications are summarized in
Table 4, where all the important results, by different parameter, are presented.
Table 4 explains the effect of radiation parameter, Prandtl number, Brinkmann number, non-Newtonian power index, Hartmann number, and volumetric heat generation on boundary later thickness and Nusselt number. Future research directions may also be done by considering Brownian motion effects and Soret effects. Boundary-layer characteristics in
Table 4 are symbolized by parameter
. It is observed that for increasing values of Hartman number, the velocity and the boundary-layer thickness increase and decrease the temperature distribution. It could be understood by the curvature of the velocity and temperature profile. Specific results of the magnetic parameter on the chemical reaction at the boundary are plotted in
Figure 5,
Figure 6 and
Figure 7. As shown in
Figure 5, the
function at the stretched wall decrease as the Hartmann increase. The Figure is a plot of results obtained for
. Concentration distributions plotted in
Figure 3 shows that inside the boundary layer the concentration decreases while the magnetic force makes the figure curvier and causes lower gradients in the stretched surface. This is because an increase in Hartmann number will increase the intensity of body force, which acts as a negative pressure gradient force near the stretching surface and hence tends to thicken the boundary layer. Furthermore, an increase of thermophoresis parameter in the medium decreases the boundary flux of concentration.
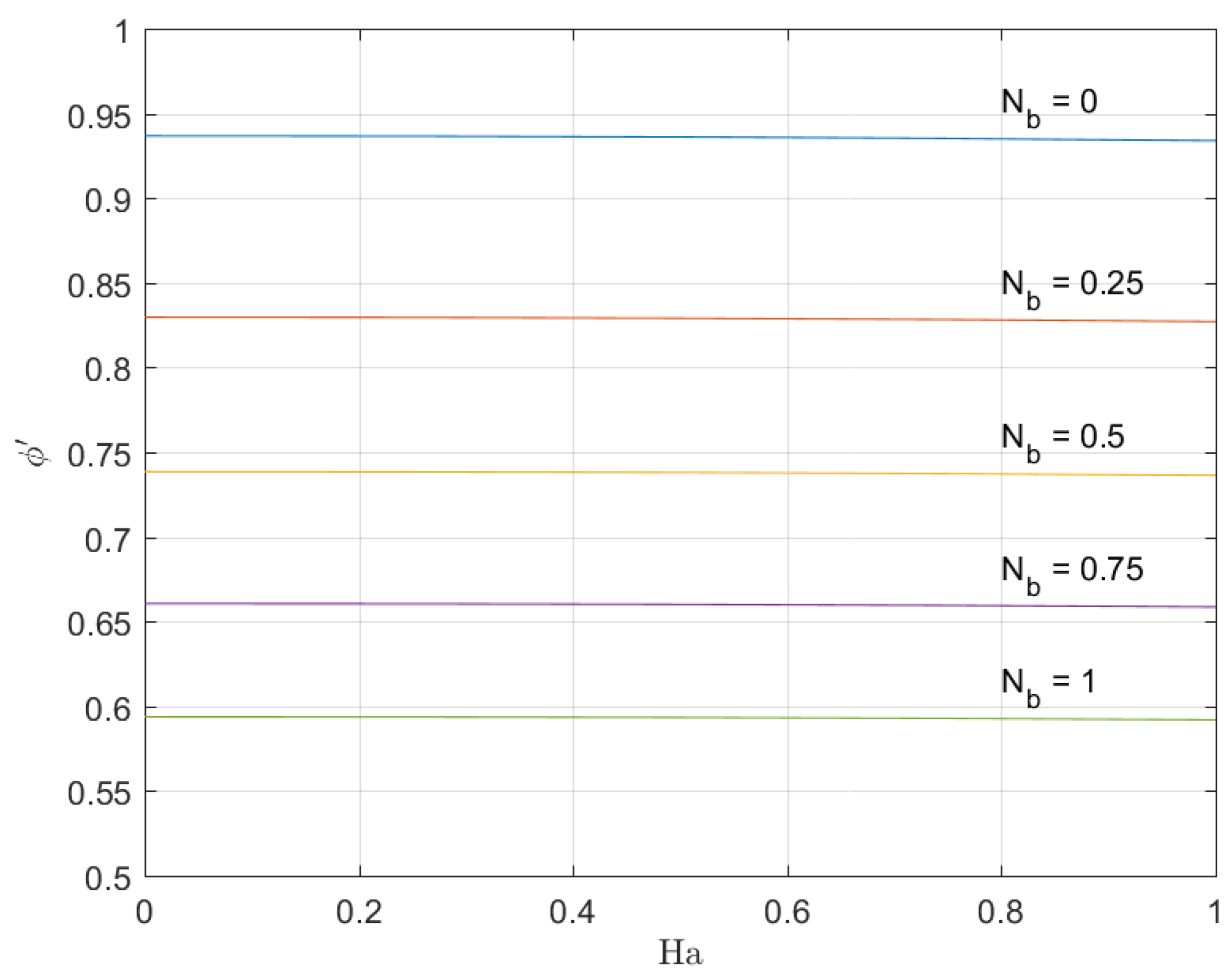
Figure 6 reveals the concentration gradients at the moving wall versus the non-dimensional magnetic parameter for various Brownian parameters. The Figure is a plot of results obtained for
. It is observed that for increasing values of Hartmann number, the dimensionless concentration flux decreases, and the concentration boundary-layer thickness increases and decreases the concentration flux distribution near the wall. Furthermore, the increase of Brownian parameter in the medium decreases the boundary flux of concentration.
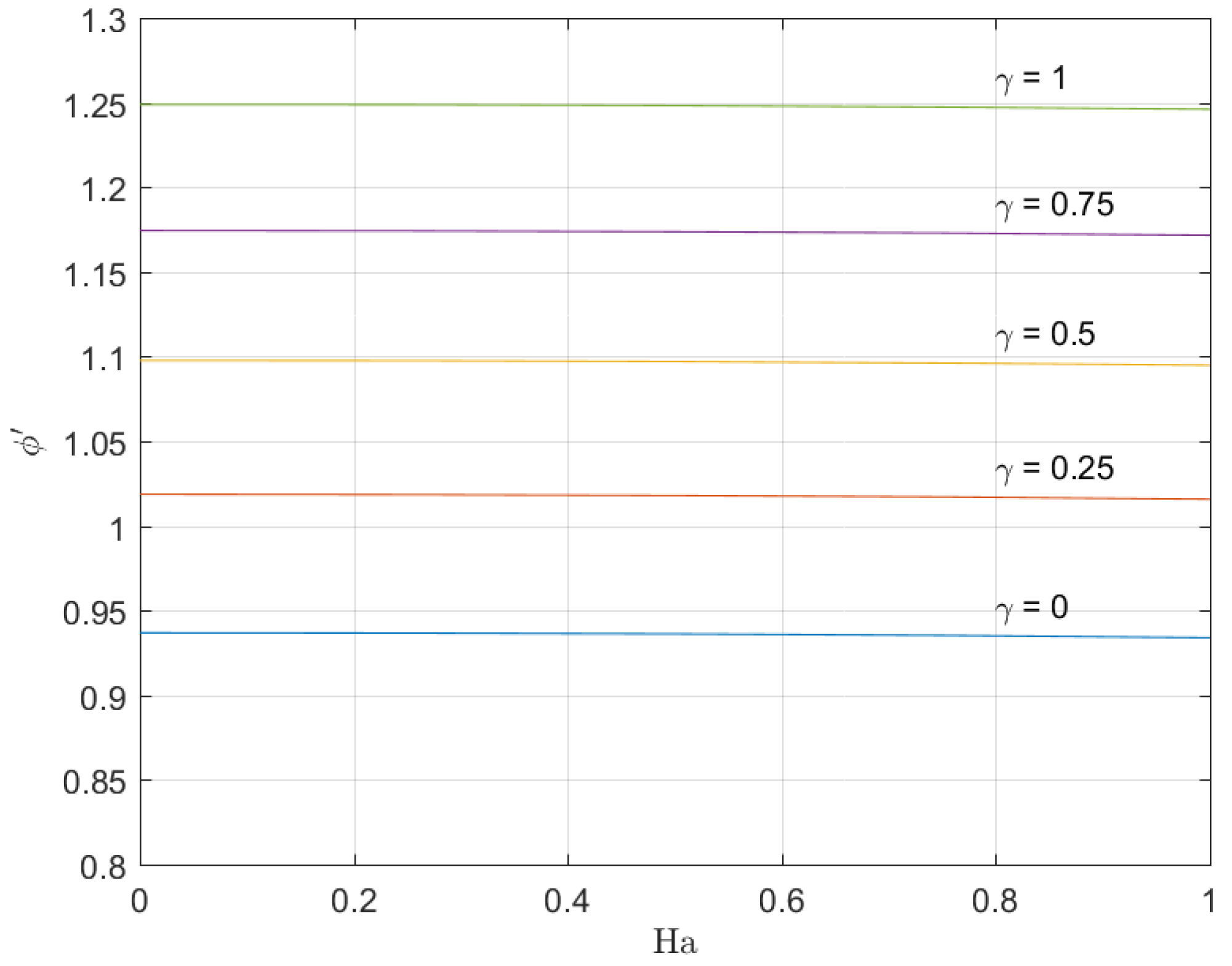
Figure 7 exposes the temperature distribution versus the non-dimensional distance. The Figure is a plot of results obtained for
. It is observed that for increasing values of Hartmann number, the dimensionless concentration gradients decrease and the concentration boundary-layer thickness increase and decrease the concentration flux distribution near the wall. Furthermore, the increase in chemical reaction parameter in the medium increase the boundary flux of concentration. The findings and their implications are summarized in
Table 5 where all the important results, by different parameter, are presented.
As the MHD affected the chemical reaction indirectly, its effect should be considered by the coupling with other parameters. Because the goal of the present article is to investigate the MHD effects in a steady-state fully developed incompressible flow over an axisymmetric stretching sheet, in
Figure 5,
Figure 6 and
Figure 7, the rate of the chemical reaction is released which is almost independent of MHD effect. The plots are given versus the MHD parameter instead of diffusion and reaction parameters to show the dominance of the chemical parameter over the MHD parameter. If just the MHD parameter changes over a broader range, the results here show the effect to be more visible, while in
Figure 5,
Figure 6 and
Figure 7 the importance is discussed for the base levels coming from chemical parameters.