Next Article in Journal
Optical-Based (Bio) Sensing Systems Using Magnetic Nanoparticles
Next Article in Special Issue
Spontaneous Magnetization and Optical Activity in the Chiral Series {(L-proline)nV[Cr(CN)6]x} (0 < n < 3)
Previous Article in Journal
Magnetic Field Effects on Chemical Reaction of Power-Law Fluid over an Axisymmetric Stretched Sheet
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Magnetochemistry
Volume 5
Issue 4
10.3390/magnetochemistry5040058
magnetochemistry-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

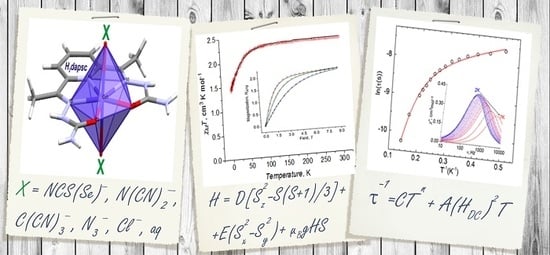
A Series of Field-Induced Single-Ion Magnets Based on the Seven-Coordinate Co(II) Complexes with the Pentadentate (N3O2) H2dapsc Ligand

by
Vyacheslav A. Kopotkov
1,*,
Denis V. Korchagin
1,*,
Valentina D. Sasnovskaya
1,
Ildar F. Gilmutdinov
2 and
Eduard B. Yagubskii
1,*
1
Institute of Problems of Chemical Physics, Russian Academy of Sciences, Semenov’s av., 1, Chernogolovka 142432, Russia
2
Institute of Physics, Kazan Federal University, 16a Kremlyovskaya st., Kazan 420008, Russia
*
Authors to whom correspondence should be addressed.
Magnetochemistry 2019, 5(4), 58; https://doi.org/10.3390/magnetochemistry5040058
Submission received: 18 September 2019 / Revised: 7 October 2019 / Accepted: 15 October 2019 / Published: 18 October 2019
(This article belongs to the Special Issue Feature Papers in Magnetochemistry)
Browse Figures
Review Reports Versions Notes

Abstract

:
A series of five new mononuclear pentagonal bipyramidal Co(II) complexes with the equatorial 2,6-diacetylpyridine bis(semicarbazone) ligand (H2dapsc) and various axial pseudohalide ligands (SCN, SeCN, N(CN)2, C(CN)3, and N3) was prepared and structurally characterizated: [Co(H2dapsc)(SCN)2]∙0.5C2H5OH (1), [Co(H2dapsc)(SeCN)2]∙0.5C2H5OH (2), [Co(H2dapsc)(N(CN)2)2]∙2H2O (3), [Co(H2dapsc)(C(CN)3)(H2O)](NO3)∙1.16H2O (4), and {[Co(H2dapsc)(H2O)(N3)][Co(H2dapsc)(N3)2]}N3∙4H2O (5). The combined analyses of the experimental DC and AC magnetic data of the complexes (1–5) and two other earlier described those of this family [Co(H2dapsc)(H2O)2)](NO3)2∙2H2O (6) and [Co(H2dapsc)(Cl)(H2O)]Cl∙2H2O (7), their theoretical description and the ab initio CASSCF/NEVPT2 calculations reveal large easy-plane magnetic anisotropies for all complexes (D = + 35 − 40 cm−1). All complexes under consideration demonstrate slow magnetic relaxation with dominant Raman and direct spin–phonon processes at static magnetic field and so they belong to the class of field-induced single-ion magnets (SIMs).

Graphical Abstract

1. Introduction

Large uniaxial magnetic anisotropy has a crucial role in the enhancement of the blocking temperature of magnetization reversal in single molecular magnets (SMMs) [1,2,3,4]. One of the approaches to increase magnetic anisotropy is to use special ligands with a less-common coordination since the anisotropy depends on the coordination number of the metal centers [5,6]. The magnetic anisotropy can be improved by a rational ligand design [7,8,9,10,11,12,13,14,15]. The “ligand approach” has already led to a variety of mononuclear 3d metal ion—based SMMs (so-called single-ion magnets (SIMs)) with improved characteristics [6]. Among them, the two-coordinate complex of Fe(I) exhibited an effective spin-reversal barrier of Ueff = 226 cm−1 [7] and recently reported that the linear two-coordinated Co(II) imido complex has the energy barrier of 413 cm–1 [13], the largest yet observed for a 3d-based SMM. However, low coordinate complexes are not very stable which restricts their possible utility in different applications. At the same time, the experimental and theoretical studies of stable seven-coordinated metal centers with pentagonal bipyramidal geometry showed that such centers are highly promising as anisotropic spin carriers [16,17,18,19,20,21,22,23,24,25]. In this context, 3d-metallocomplexes with the pentadentate Schiff-base H2dapsc ligand (H2dapsc = 2,6-diacetylpyridine bis(semicarbazone), Figure 1) and its analogues are of considerable interest. These complexes reveal the rare occurrence of pentagonal bipyramidal stereochemistry about a central metal ion, which results from pentacoordination of the nearly planar H2dapsc (N3O2), and two labile apical ligands (H2O and/or Cl, NO3, and others) perpendicular to the equatorial pentagon plane [26,27,28,29,30]. Although the complexes of H2dapsc and its analogues have long been known, the study of their magnetic properties [17,19,20,21,31,32,33,34] and their use as building blocks for the preparation of magnetic polynuclear assemblies [21,35,36,37,38] are started only in last time. It has been shown that some of these Ni(II), Fe(II), and Co(II) mononuclear complexes with the H2dapbh, H2dapsc, and H4daps ligands (Figure 1) demonstrate slow magnetic relaxation. In contrast to the Ni(II) and Fe(II) complexes which reveal strong uniaxial magnetic anisotropy (D < 0) [20,21,31,35] characteristic of SIMs, the known Co(II) complexes with H2dapbh and H2daps ligands revealed a large easy-plane magnetic anisotropy (D > 0) [17,19,20,32,33,34]. Although D-parameter has a positive value which in accordance with the theory should not allow the SIM behavior, these Co(II) complexes show slow relaxation of magnetization in the presence of static magnetic field (so-called field-induced SIMs). Ruis, Luis, and co-workers gave the explanation of the presence of the field-induced slow magnetic relaxation for Kramer ions, such as Co(II), with prevailing easy-plane magnetic anisotropy [39]. The origin of this large non-uniaxial anisotropy is due to the mixing of the ground electronic state with the excited electronic states because of spin-orbit coupling.
In this paper, we present the synthesis and crystal structures of the five new seven-coordination Co(II) complexes with H2dapsc equatorial and different pseudohalide axial (SCN−, SeCN−, [N(CN)2]−, [C(CN)3]−, N3−) ligands: [Co(H2dapsc)(SCN)2]∙0.5C2H5OH (1), [Co(H2dapsc)(SeCN)2]∙0.5C2H5OH (2), [Co(H2dapsc)(N(CN)2)2]∙2H2O (3), [Co(H2dapsc)(C(CN)3)(H2O)](NO3)∙1.16H2O (4), and {[Co(H2dapsc)(H2O)(N3)][Co(H2dapsc)(N3)2]}N3···4H2O (5). Molecular and crystal structures of these complexes were investigated by single crystal X-ray diffraction method. The DC and AC magnetic properties of these complexes and two other described those of this family [Co(H2dapsc)(H2O)2)](NO3)2∙2H2O [28] (6) and [Co(H2dapsc)(Cl)(H2O)]Cl∙2H2O [29] (7) were studied. The detailed theoretical analysis of magnetic properties was provided. The effect of modification of axial ligands on magnetic anisotropy was traced.

2. Results and Discussion

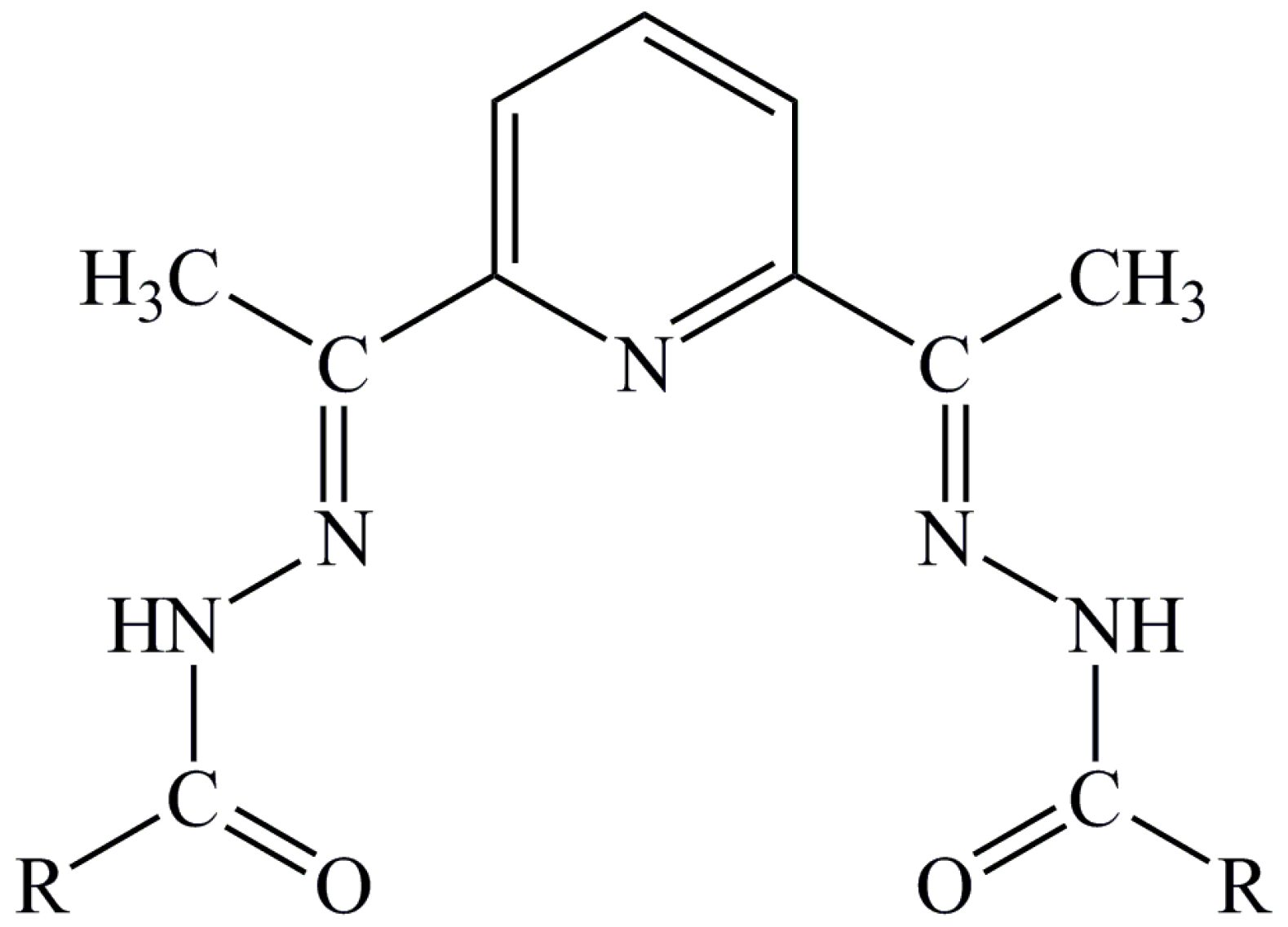
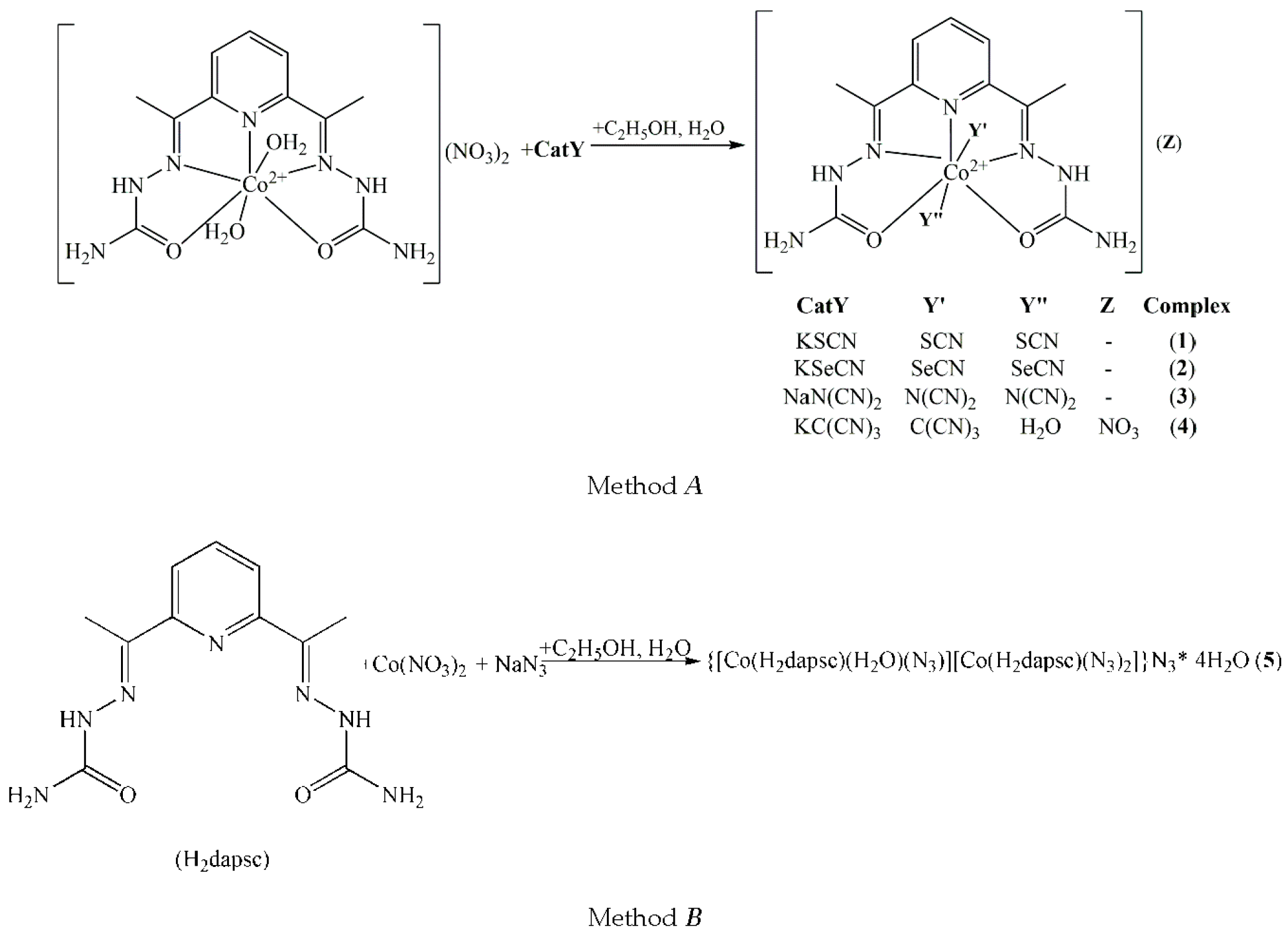
2.1. Synthesis and Characterization

The Co(II) complexes with H2dapsc ligand and pseudohalide anions were synthesized using the following two approaches: (A) the substitution of the terminal ligands (H2O) in the starting Co2+ complex with H2dapsc ligand [Co(H2dapsc)(H2O)2](NO3)2 [28,29] for pseudohalide anions; and (B) the reaction between Co2+ nitrate, H2dapsc ligand, and a precursor of the pseudohalide anions, Scheme 1.
The IR spectra of the obtained complexes are quite similar. The presence of the H2dapsc ligand was confirmed by the following characteristic vibrations: ν(N–H) and ν(C=N) vibrations of the amino and imino groups were located in the 3150–3350 cm−1 and 1650–1700 cm−1 region, respectively. Bands for ν(C≡N) and ν(–N=N+=N−) stretching vibrations of the pseudohalide anions in 1–5 were observed in the 2050–2200 cm−1 region.

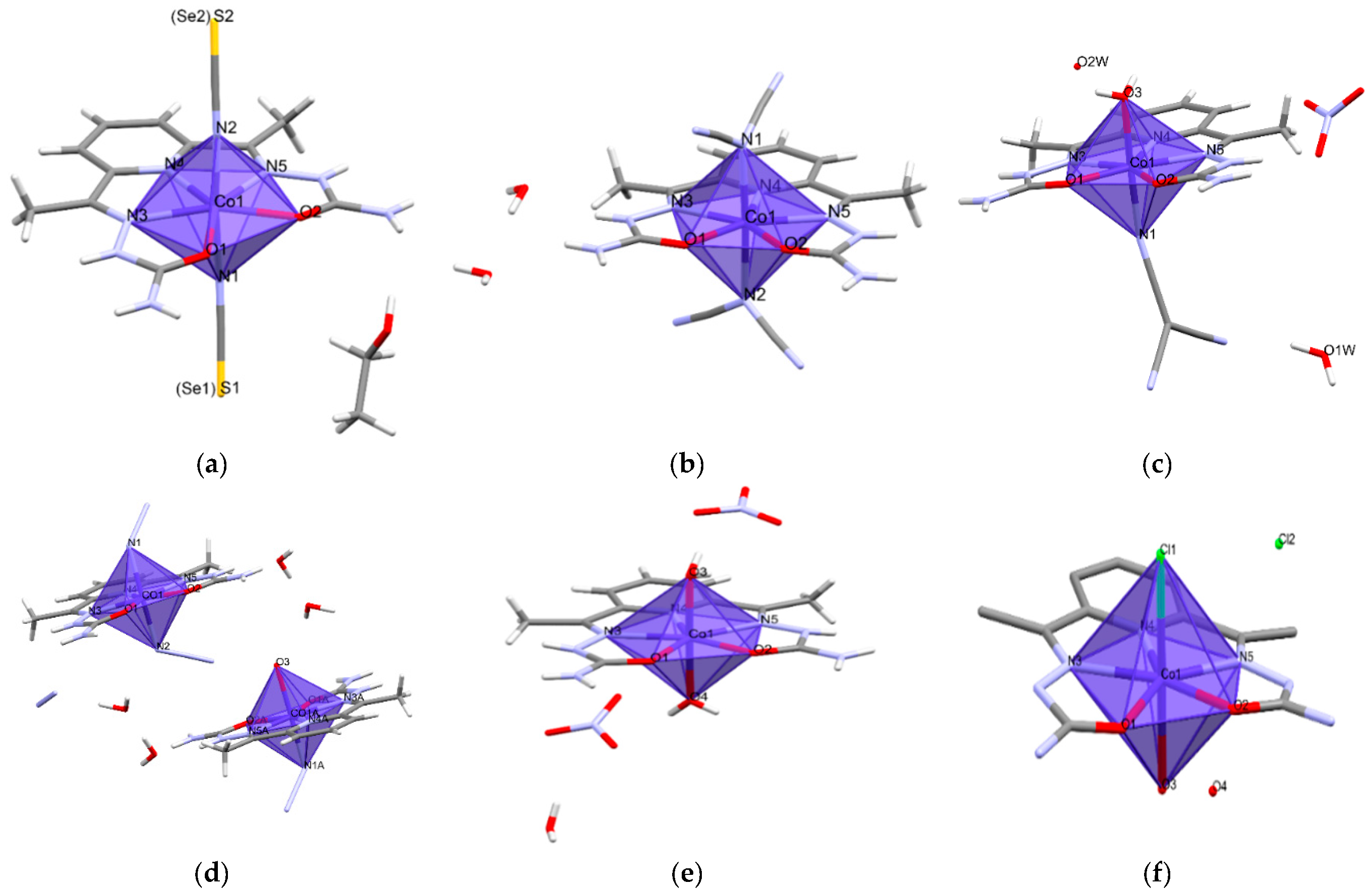
2.2. Description of the Structure

Compounds 1 and 2 are isostructural. They crystallize in the monoclinic space group P21/c with a half solvate EtOH molecule per one molecule of complex (Figure 2a). Solvate EtOH molecule occupies special positions (center of symmetry) with 1/2 occupancies. Compound 3 crystallizes in the triclinic space group P-1 with a two solvate water molecules per one molecule of complex (Figure 2b). In contradistinction to neutral 1–3 complexes, 4 is cationic. It crystallizes in the monoclinic space group P21/c with a one nitrate-anion and two solvate water molecules, one of them (O2w) has site occupation factor ~0.16 (Figure 2c). Complex 4 contains apical ligands of different nature: Tricyanomethanide-anion ([C(CN)3]− = tcm) and H2O, whereas in the complexes 1–3 the apical ligands are the same SCN–, SeCN–, [N(CN)2]−, respectively.
It is surprising that crystals of 5 contain two complexes in the same lattice linked by hydrogen bonds (see below): Neutral [Co(H2dapsc)(N3)2] and cationic [Co(H2dapsc)(N3)(H2O)]+, Figure 2d. Compound 5 crystallizes in the monoclinic space group C2/c with a two solvate water molecules per one molecule of complexes (Figure 2d). Isolated azide anion in special position plays the role of counterion. The structure of both complexes is very close so that we could solve and refine the crystal structure with one molecule of the complex in asymmetric unit (in order to minimize number of parameters).
Crystal structures 6 and 7 have been previously studied (Figure 2e,f) and described [28,29].
In all complexes the central Co(II) ion has a pentagonal bipyramidal coordination environment formed by five equatorial N3O2 (N3, N4, N5, O1, and O2) atoms from the H2dapsc ligand and two axial N(O) atoms (N1, N2(O3)) from the axial NCS– NCSe–, N(CN)2–, tcm, N3–, or H2O ligands. In previously studied compounds 6 [28] and 7 [29] axial ligands are two water molecules and water molecule and chloride-anion, respectively. In compound 3, the relatively rare monodentate coordination of the N(CN)2− ligand is realized. Usually (>75% of cases), dicyanamide anion acts as a polydentate bridging ligand [40]. Interestingly, the monodentate type of coordination is more characteristic of the tcm anion than on the dicyanamide anion. The number of examples of mono- and polydentate coordination of tcm ligands in Cambridge Structural Database [40] are almost the same. The axial bond angle N(1)-Co(1)-N(2) for 1 (or 2) and 3 are ~174 and ~177°, respectively. In complexes 4 and 5 it has been found the smallest and the largest axial bond angles N(1)-Co(1)-O(3) 171.21(9) and 178.51(9), respectively. The axial Co-N(O) bond lengths in the complexes 1, 2, and 4 are slightly shorter than the equatorial Co-N(O) bond distances while in 3 Co-Nax bonds are similar to Co-(N)Oeq (Table S2). At the same time, the Co-Oeq bond lengths in 3 are slightly shorter than in other complexes. In complexes 1 and 2 the equatorial N-Co-O(N) bond angles are in the more large range 69.8–77.8° than in 3 (70.2–75.6°), that together with approximately equal bond lengths in the coordination polyhedron CoN5O2 of 3 indicates to a more distorted pentagonal bipyramidal geometry of Co(II) complexes 1 and 2. Indeed, the SHAPE software [41,42] gave the deviation parameters of 0.058 for 3 and 0.312 (0.314) for 1 (2), Table S1, which in the case of 1 (2) is larger from zero of the ideal D5h symmetry that confirms more distorted coordination polyhedra of 1 and 2 complexes. The equatorial N-Co-O(N) bond angles in 3 (70.2–75.6°) and 4 (70.1–76.2°) are similar but the strong distortion of axial bond angle N(1)-Co(1)-O(3) and the difference of axial and equatorial bond lengths (see Table S2) in 4 leads to the relatively large deviation parameter 0.294 as in the case of complexes 1 and 2. In spite of similarity azide and isothiocyanate anions, Co(II) coordination environment in 5 is closer to 3 than 1 or 2 (see Table S2). Also the SHAPE program (Table S1) gave the deviation parameters of 0.105 and 0.072 for neutral [Co(H2dapsc)(N3)2] and cationic [Co(H2dapsc)(N3)(H2O)]+ in 5 that shows less distorted coordination polyhedra of these complexes than in the cases of 1 and 2.
Figure S1a,b shows the fragments of crystal structures of 1 and 2. Crystal structures are stabilized by the number of intermolecular hydrogen bonds (H-bonds) between complexes itself, and between complexes and solvate EtOH molecules (Table S3). The Co(II) ions in crystal packing are not well isolated with the closest intermolecular Co···Co separations being 6.96 (1) and 7.01Å (2). In case of 3, the closest intermolecular Co···Co separations are somewhat larger (7.48Å), apparently due to the larger size of the apical ligands or the presence of a larger number of solvate water molecules in the crystal structure.
The presence of not only solvate water molecules but also isolated counterions (NO3– and N3–) in the crystal structures of 4 and 5 gave the largest from shortest intermolecular Co···Co separations (7.66 and 7.73 Å, respectively) among all structures under consideration. Crystal structures of 3−5 is also stabilized by the large number of H-bonds with the amino and imino groups of H2dapsc ligands, solvate water molecules, and NO3− anions (Figures S1c,d and S2, Table S3). It should be noted that the strong distorted axial bond angle N(1)-Co(1)-O(3) in 4 complex can be the result of stacking interactions of tcm ligands of adjacent molecules (Figure S3) and/or H-bonds involving a water ligand.
As it has been already noted in the works [28,29], the crystal structures of 6 and 7 are stabilized by an extensive network of hydrogen bonds involving the complex cations, the nitrate or chloride anions, and the solvent water molecules (Figure S1e,f). In crystal packings of 6 and 7 Co(II) ions are not well isolated with the closest intermolecular Co···Co separations being 6.65 and 6.75 Å, respectively, these values are the two smallest values from all compound under consideration.

2.3. Magnetic Properties

2.3.1. Static Magnetic Measurements

The temperature dependencies of magnetic susceptibility for complexes 1–7 were performed in the temperature range of 2.0–300 K under a 5000 Oe DC field. The shapes of the χMT versus T curves of all complexes are similar. At room temperature, χMT products are in the range of 2.36–2.61 cm3∙K∙mol (Figure 3). These values are higher than the spin only value for Co(II) with S = 3/2 (1.875 cm3 K mol−1) due to an orbital contribution to the magnetic moment. Upon cooling, χMT remains almost constant in the temperature range from 300 to 60 K after which point it starts to decrease for all the compounds and reaches the values of ≈1.4–1.6 cm3∙K∙mol−1 at 2 K (Figure 3). The room-temperature χMT value 5.14 cm3∙K∙mol−1 for 5 is in good agreement with the paramagnetic response of the two magnetically non-interacting Co(II) ions with S = 3/2 (Figure 3e). The decrease of the χMT at low temperatures is due to the intrinsic magnetic anisotropy of the Co(II) centers [43]. Field dependences of magnetization for all complexes at 2 K (insets on Figure 3) saturate at values of around 2.15–2.28 NAμB that is significantly lower than the value of 3NAμB, corresponding to the pure spin S = 3/2 ground state with g = 2. This fact indicates the presence of considerable magnetic anisotropy in the complexes.
To describe the DC magnetic properties, we use the following zero-field splitting (ZFS) spin Hamiltonian:
H ^ = D [ S ^ Z 2 − 1 3 S ( S + 1 ) ] + E ( S ^ X 2 − S ^ Y 2 ) + μ B ( B X g X S ^ X + B Y g Y S ^ Y + B Z g Z S ^ Z )
here S = 3/2 is the spin of the high-spin Co(II) ion, D and E are axial and rhombic ZFS parameters, and gα (α = X, Y, Z) are the principle values of the g-tensor. The set of the best-fit parameters for the observed temperature dependences of χMT (Figure 3) and field dependences of magnetization at different temperatures (Figure 3) is presented in the Table 1. These parameters agree well with the calculated by SA-CASSCF/NEVPT2 methods set of parameters (Table 1). The complexes exhibit positive axial magnetic anisotropy (D) with non-zero rhombicity parameter (Table 1). The sign and the magnitudes of D for 1–7 are in the range of previously reported those for the seven-coordinate pentagonal bipyramidal Co(II) complexes [24,25,33,34].

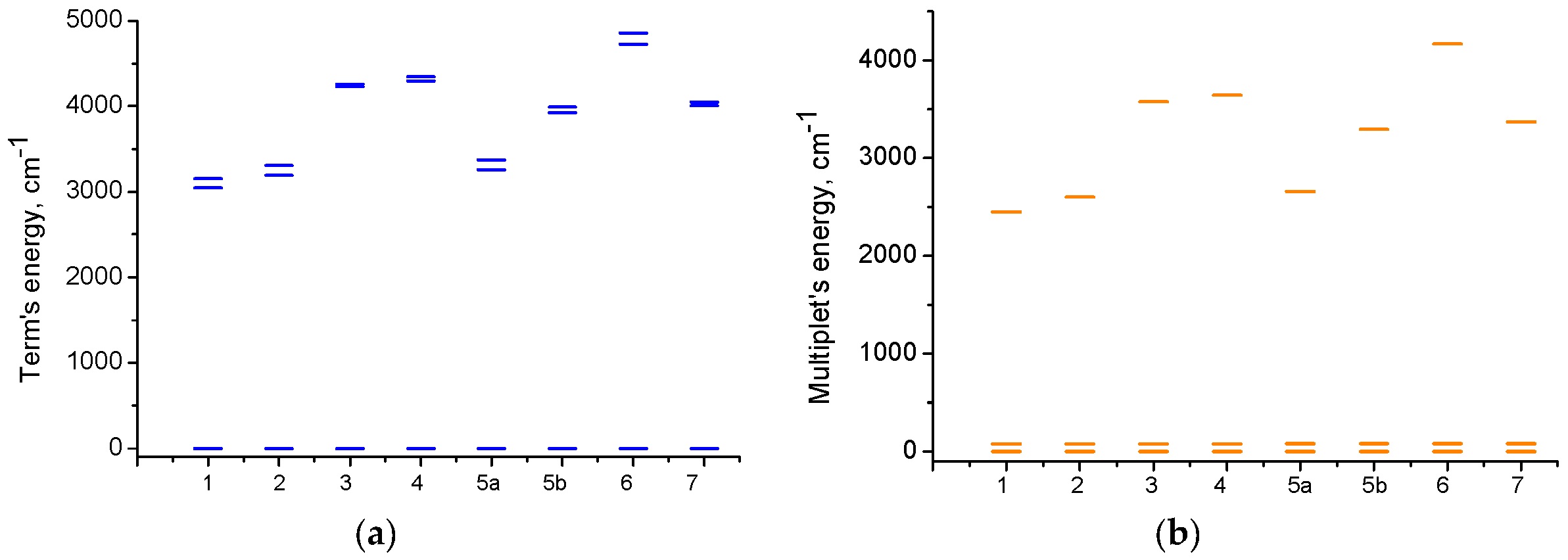
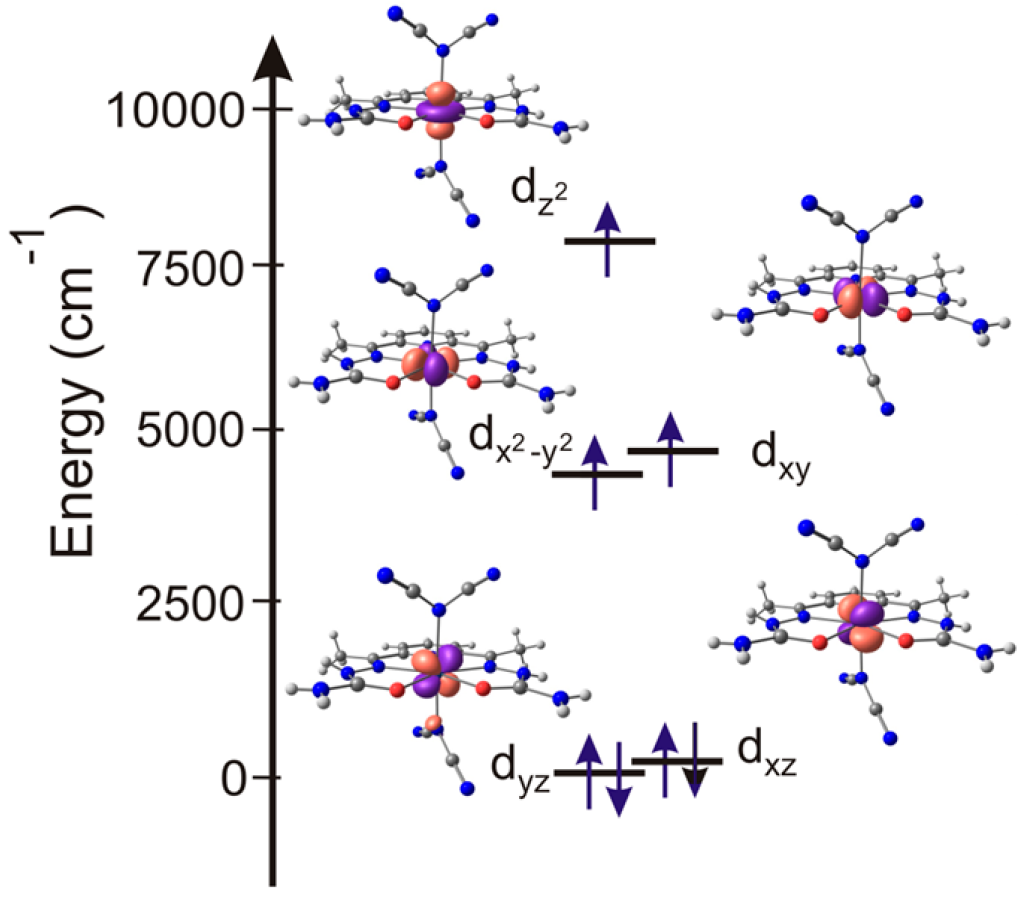
2.3.2. Quantum Chemical Calculations

The first excited quartet term lies above 3047 cm−1 is well separated from the excited ones for all complexes (Figure 4a). This is also reflected in the ligand field multiplets (Kramers doublets) calculated with the spin–orbit coupling, where in all cases, two lowest Kramers doublets can be described with the ZFS formalism using S = 3/2, because the third doublet is also well separated from the ground state by an energy gap more than 2450 cm−1 (Figure 4b).
The values of the ZFS parameters D and E/D as well as the g values calculated by introducing the spin-orbit coupling (SOC) operators, extracted with the aid of the effective Hamiltonian approach, are listed in Table 1, orientation of the corresponding magnetic axes are given in Figure 5.
The results of the calculations are in good agreement in both magnitude and sign with the experimental data for all complexes. The analysis of the g-tensor components shows the closeness of gx and gy values that confirms the correctness of the choice of gx= gy in analysis of magnetic data. The rhombicity parameter E/D = |Dx-Dy|/2 is small enough this fact correlates with the proximity of the gx and gy values.
Splitting of the d-orbitals (Figure 5) has been calculated and analyzed within the ab initio ligand field theory (AILFT). Two doubly occupied low-lying states (dyz and dxz) are close in energy and are well separated from single occupied one-electron states (see Table 2). The analysis of individual excited states contributions to the total D value (Table 3) shows, that the main contribution with positive sign goes from the third and fourth quartet excited states, also major contribution from doublet state goes from various excited doublet states (these three or four states give about 100% of the calculated total D value). It should be noted that 1 and 2 complexes are different from other by the nature of SOC contributions of doublet excited states (Table 3).

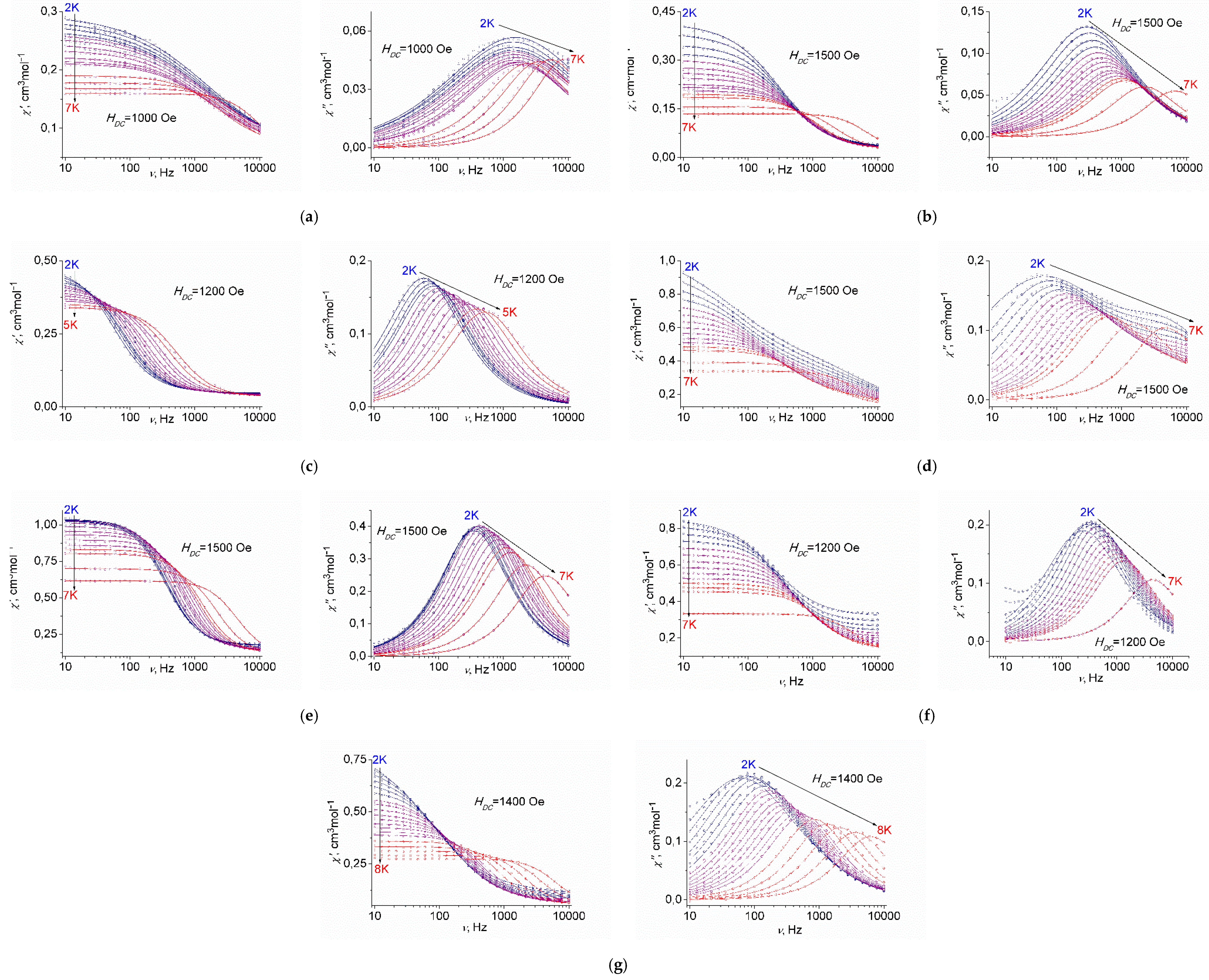
2.3.3. AC Susceptibility Data

To probe the possible SIM properties of compounds 1–7 alternating current susceptibilities as a function of frequency were measured at different temperatures for each compound in zero and non-zero DC field. In the absence of DC field, no obvious frequency dependence in the in-phase (χ′) and out-of–phase (χ″) can be observed for all compounds. The DC field-dependencies of AC susceptibility were recorded under fields of 0–3000 Oe at 2.0 K and two frequencies (100 Hz, 1000 Hz) in search of an optimal field for the suppression of quantum tunneling of magnetization (QTM), Figure S4. When applying a DC field of 1000–2000 Oe, a maximum of χ″ was observed for all complexes, Figure S4. To probe the relaxation behavior of complexes 1–7, the frequency dependence of AC susceptibility was studied in the presence of the optimal static DC field for each complex at different temperatures (Figure 6). Both the χ′ and χ″ susceptibilities show frequency-dependent signals indicating slow relaxation of magnetization. These results clearly indicate that the mononuclear complexes 1–7 are field-induced SIMs. The χ″ peaks for different frequencies appear one after another and the frequency dependence data show the clear and steady shift of the peaks towards higher frequencies with increasing temperature that is characteristic of SMMs. In contrast to complexes 1–3 and 5–7, in which one set of maxima is observed on the frequency dependencies of χ″ (Figure 6), in the complex 4 at T < 5 K, there is a second high frequency set of maxima (Figure 6), which indicates the existence of the two-step relaxation processes in 4 [44,45]. Only the main low frequency peaks in 4 will be discussed here. More detailed information on the effects of the applied DC field on the slow magnetic relaxation processes and the reasons for observing two or even three relaxation processes in Co(II) complexes can be obtained from the works of Boča and co-workers [46,47,48,49]. The obtained data for the AC susceptibility were fitted in cc-fit program [50] by using the one- and two-component generalized Debye model for the complexes 1–3, 5–7 and 4, respectively [45,51], which gave the values and distribution of the relaxation time (τ and α; Tables S4–S10). The α values are in the range 0.02−0.34 for all complexes suggesting the narrow distribution of relaxation time. The best representation of the obtained parameters is Cole-Cole plots (Figure S5). The simulations using these parameter sets are in a good agreement with the experimental data. For all complexes, the relaxation times (τ) were plotted versus T−1, giving Arrhenius–like curves (Figure S5), which were successfully fitted in whole temperature range with following equation:
τ − 1 = C T n + A ( H D C ) 2 T
where the first and second terms describe Raman and direct spin–phonon processes, respectively. The direct one-phonon process is dominating at low temperatures, while the contribution of the two-phonon Raman process becomes important with increasing temperature. The best-fit parameters for 1–7 are summarized in Table 4. The Orbach process was not included in the relaxation time τ approximation for these complexes because there is no any real energy barrier between spin states in the Co(II) complexes with D > 0 [39,52,53]. As regards the process of fast temperature independent relaxation via QTM, this process is partially or completely suppressed in the presence of a small external DC field [54].

3. Materials and Methods

General remarks: The ligand H2dapsc and complexes [Co(H2dapsc)(H2O)2](NO3)2∙2H2O (6), [Co(H2dapsc)(H2O)(Cl)]Cl 2H2O (7) were prepared by a methods described in references [27,28,29]. All other chemicals were used as supplied from Aldrich.

3.1. Synthesis

[Co(H2dapsc)(SCN)2]∙0.5C2H5OH (1). Method A. The complex [Co(H2dapsc)(H2O)2](NO3)∙2H2O [28] (0.146 g, 0.5 mmol) was dissolved in ethanol (15 mL). The solution was heated to 50 °C and stirred for 10–15 min, and then KSCN (97 mg, 1 mmol) in methanol (5 mL) was added. The resulting clear solution was filtered and cooled. The solution was slowly evaporated at 20 °C for one to three days. The precipitated red brown crystals were filtered off, washed with a small amount of water, and dried in vacuo. For 1 yield: 40%. Anal. calc. for CoC15H21N9O3S2 (498.46): C, 36.11; H, 4.21; N, 25.29%. Found: C, 35.81; H, 4.63; N, 25.03%. IR data (cm−1): ν(N–H) = 3176, 3334; ν(C≡N) = 2075; ν (C=N) = 1652.
Complexes [Co(H2dapsc)(SeCN)2]∙0.5C2H5OH (2), [Co(H2dapsc)(N(CN)2)2]∙2H2O (3) and [Co(H2dapsc)(C(CN)3)(H2O)](NO3)∙2H2O (4) were obtained similarly to complex (1) using KSeCN, NaN(CN)2, and KC(CN)3 instead of KSCN (Scheme 1). For 2 yield: 36%. Anal. calc. for CoC15H21N9O3Se2 (592.25): C, 30.42; H, 3.57; N, 21.29%. Found: C, 30.73; H, 3.49; N, 21.78%. Characteristic IR data (cm−1): ν(N–H) = 3167, 3328; ν(C≡N) = 2087; ν(C=N) = 1661. For 3 yield: 73%. Anal. calc. for CoC15H19N13O4 (504.34): C, 35.72; H, 3.80; N, 36.10%. Found: C, 35.93; H, 3.99; N, 35.87%. Characteristic IR data (cm−1): ν(N–H) = 3182, 3311; ν(C≡N) = 2160; ν(C=N) = 1668. For 4 yield: 66%. Anal. calc. for CoC15H19N11O7.16 (526.92): C, 34.16; H, 3.61; N, 29.23%. Found: C, 34.63; H, 3.45; N, 29.81%. Characteristic IR data (cm−1): ν(N–H) = 3176, 3305; ν(C≡N) = 2185; ν(C=N) = 1663.
{[Co(H2dapsc)(H2O)(N3)][Co(H2dapsc)(N3)2]N3}∙4H2O (5). Method B. The ligand dapsc (2,6-diacetylpyridinebis(semicarazone)) (148 mg, 0.5 mmol) was suspended in ethanol-water mixture (4:1, 20 mL) at 55°C. Then a solutions of cobalt(II) nitrate hexahydrate (146 mg, 0.5 mmol) in 4 mL water and NaN3 (65 mg, 1 mmol) in the same amount of water were added to the ligand suspension. The resulting clear solution was filtered and cooled. The solution was slowly evaporated at 20°C for one to three days. The precipitated red brown crystals were filtered off, washed with a small amount of water, and dried in vacuo. For 5 yield: 53%. Anal. calc. for Co2C22H40N26O9 (930.60): C, 28.39; H, 4.33; N, 39.13%. Found: C, 28.53; H, 4.68; N, 38.41%. Characteristic IR data (cm−1): ν(N–H) = 3174, 3305; ν(–N=N+=N−) = 2017, 2046; ν (C=N) = 1662.

3.2. X-ray Crystal Structure

X-ray data for a single crystals of 1–5 were collected on a CCD diffractometer Agilent XCalibur with EOS detector (Agilent Technologies UK Ltd., Yarnton, Oxfordshire, UK) using graphite-monochromated MoKα radiation (λ= 0.71073 Å) and treated by CrysAlisPro software for cell refinement, data collection, and data reduction with empirical absorption correction (Scale3AbsPack) of the experimental intensities [55]. The structure was solved by direct methods and refined against all F2 data (SHELXTL) [56]. All non-hydrogen atoms were refined with anisotropic thermal parameters, positions of hydrogen atoms were obtained from difference Fourier syntheses and refined with riding model constraints. The X-ray crystal structures data have been deposited with the Cambridge Crystallographic Data Center, with reference codes CCDC 1952369- 1952373. Selected crystallographic parameters and the data collection and refinement statistics are given in Table S11.

3.3. Physical Measurements

The C, H, and N elemental analyses were carried out with a vario MICRO cube analyzing device. IR spectra were recorded on a Vertex 70 V instrument in the range from 600 to 4000 cm–1 using polycrystalline samples. Absorption bands in the IR spectra were assigned on the basis of literature data. Static magnetic properties measurements (DC magnetization) were performed using vibrating sample magnetometer (VSM) installed to physical properties measurements system (PPMS-9, Quantum Design). Dynamic magnetic properties measurements (AC magnetization) were performed using AC Measurement System (ACMS) installed to the PPMS-9 set-up.
The sample in polycrystalline (powder) form was loaded into a gelatin capsule and glued to the standard sample holder. In order to get magnetic properties of the metal center diamagnetic contribution of sample holder and the ligand was subtracted. For this purpose, the sample holder with the capsule were measured independently. The diamagnetic contribution from ligand was calculated using Pascal’s constants.

3.4. Computational Calculations

Quantum chemical calculations of the ZFS (D-tensor) and g-tensor parameters for all complexes were performed with post-Hartree-Fock multireference wavefunction (WF) approach based on the state averaged complete active space self-consistent field calculations (SA-CASSCF) [57,58,59] complemented by the N-electron valence second-order perturbation theory (NEVPT2) [60,61,62,63]. In the state-averaged approach, all multiplets for a given electron configuration were equally weighted. Scalar relativistic effects were taken into account by a standard second-order Douglas-Kroll-Hess (DKH) procedure [64]. For calculations a segmented all-electron relativistically contracted version [65] of Ahlrichs polarized triple-ζ basis set def2-TZVP [66,67,68] was used for all atoms. Dominant spin–orbit coupling contributions from excited states were calculated through quasi-degenerate perturbation theory (QDPT) [69], in which an approximation to the Breit–Pauli form of the spin–orbit coupling operator (SOMF approximation) [70] and the effective Hamiltonian theory [71] were utilized. The CASSCF active space was constructed from five MOs with predominant contribution of 3d-AOs and seven electrons, corresponding to Co(II) ion—CAS (7.5). All possible multiplet states arising from the d7 configuration were included into WF expansion – 10 quartet (S = 3/2) and 40 doublet (S = 1/2) states. The ab initio ligand field theory [72,73] analysis was done for CAS (7.5) calculations. Atomic coordinates have been taken from the single crystal X-ray diffraction data. In selected inconsistent structures, positions of hydrogen atoms were optimized employing density functional theory with BP86 functional and Ahlrichs polarized basis set def2-TZVP. Molecular frame of axes has been chosen in such a way that Z axis goes along Co ion and donor atoms of axial ligands, X axis lies in the plane of the H2dapsc ligand, while Y axis is orthogonal to it. All calculations were done by the ORCA program (ver. 4.0.1.2) [74,75].

4. Conclusions

The five new Co(II) heptacoordinate complexes with the equatorial 2,6-diacetylpyridine bis(semicarbazone) ligand (H2dapsc) and various axial pseudohalide ligands were synthesized. The complexes reveal distorted pentagonal bipyramidal geometry which results from pentacoordination of the nearly planar H2dapsc (N3O2), and two the same or different apical ligands (SCN−, SeCN−, [N(CN)2]−, [C(CN)3]−, N3−, and H2O) perpendicular to the equatorial pentagon plane. In the case the N3− apical ligand, the crystals of 5 contain two different complexes in the same lattice linked by hydrogen bonds: Neutral [Co(H2dapsc)(N3)2] and cationic [Co(H2dapsc)(N3)(H2O)]+. The theoretical analysis of DC susceptibility exhibited the positive magnetic anisotropy (D) for all complexes with non-zero rhombicity parameter. The calculated values of magnetic anisotropy are in good agreement with the experimental values of D (Table 1), which for all complexes under consideration are close to 35−40 cm−1, indicating a weak effect of the nature of axial ligands on the magnitude of magnetic anisotropy parameter for the seven-coordinate mononuclear Co(II) complexes with easy-plane magnetic anisotropy. It is well established that the large positive D parameter in pentagonal bipyramidal Co(II) complexes is a result of the spin–orbit mixing of the ground quartet state with excited states, two being quartets and the others are doublets, Table 3 [20,33,34]. An analysis of the literature data on the influence of the coordination environment on the ZFS parameter in the Co(II) seven-coordinated complexes shows that the D value increases in the case of weaker axially coordinated σ-ligands and a more symmetric equatorial ligand [20,33,34]. To increase the positive D value, the energy difference between the ground and quartet excited states should be reduced, which will lead to an increase of the interaction between them. The introduction of weak σ-donors into the apical positions of the complexes will reduce the energy difference between these orbitals and thereby enhance the coupling and increase the positive D value. Table S12 presents the D parameters of the synthesized 1–7 complexes compared to the D parameters of previously reported mononuclear pentagonal-bipyramidal Co(II) complexes with the 2,6-diacethylpyridine-based opened acyclic ligands. The Co(II) complexes with the equatorial H4daps ligand (13–15, Table S12) clearly demonstrate the effect of the nature of axial ligands on the D value [34]. Among them, complex 13 has the highest positive D value among the seven-coordination cobalt systems and contains two weak σ-donor ligands (MeOH) in the axial positions. Full or partial replacement of these donors by stronger σ-ligands (NCS−) leads to a decrease of D value. Along with spin-orbit coupling of the ground state with an excited quartet states, mixing with doublet states also has a significant effect on the parameter of easy-plane magnetic anisotropy in the pentagonal bipyramidal Co(II) complexes (Table 3). Note in this connection that in the complex 13, the equatorial coordination environment is more symmetrical compared to the complexes 14, 15, since unlike the latters, complex 13 contains an equatorial ligand in a dianionic conjugated form (H2daps), which increases the positive contribution to D parameter [34]. As for the complexes 1–7 (Table S12) synthesized by us, the high positive D value for complex 6 compared to complexes 3, 4, and 7 is the result of the presence of weak donor ligands (H2O) in the axial positions of 6. The experimental D values for isostructural complexes 1 and 2 with axial ligands NCS− and NCSe− are somewhat different (Table S12), while the theoretical D values for these complexes are almost identical (38.02 and 37.73 cm−1, respectively, Table 1) and actually coincide with the D value for complex 15 with a neutral equatorial ligand H4daps and two axial ligands NCS−(Table S12). Relatively high D value for the azide complex 5 (Table S12), which has an unusual structure containing two different complexes (neutral and cationic) in the same crystal lattice, possibly related to a more symmetric coordination environment in the azide complexes compared to complexes 1 and 2. Coordination polyhedra in 5 are less distorted than in latters.
The complexes 1–7 demonstrate the slow magnetic relaxation in weak DC field, i.e., are field-induced SIMs. For all complexes, the relaxation is well described in the whole temperature range by combination of Raman and direct spin–phonon processes (Table 4).

Supplementary Materials

The following are available online at https://www.mdpi.com/2312-7481/5/4/58/s1, Table S1. Shape analysis for the metal centers of complexes 1–7; Table S2. Selected bond lengths (Å) and angles (°) in coordination polyhedra of 1–7; Figure S1. Fragments of crystal structures of 1 (a), 2 (b), 3 (c), 4 (d), 6 (e) and 7 (f); Table S3. Geometric parameters of H-bonds in crystal structures 1–5; Figure S2. Fragments of 5 crystal structure: ac projection (a) and ab projection (b); Figure S3. Stacking interactions of tcm ligands of adjacent molecules in the crystal structure of 4; Figure S4 The DC field-dependencies of AC susceptibility (χ″) at 2.0 K and two frequencies (100 Hz, 1000 Hz) for 1 and 5; Figure S5 Argand (Cole−Cole) plots from 2.0 to 7 K and Arrhenius plots of relaxation times as ln(τ) versus 1/T under DC fields for 1 (a), 2(b), 3 (c), 4 (d), 5 (e), 6 (f) and 7 (g); Tables S4–S10. Best fit parameters of the generalized Debye model for the Cole-Cole plot of complexes 1–7 under DC fields; Table S11. Crystal data and structure refinement for 1–5; Table S12. Magnetic anisotropy parameters (D parameters) for seven-coordinated Co(II) complexes with the 2,6-diacethylpyridine-based opened acyclic ligands (Figure 1, main text).

Author Contributions

V.A.K. and V.D.S. synthesized the complexes and prepared the crystals; D.V.K. solved crystal structures, performed quantum chemical calculations, analyzed DC and AC magnetic data and wrote the paper together with E.B.Y. and V.A.K.; I.F.G. performed measurements on SQUID magnetometer; E.B.Y. supervised overall work and organized the project.

Funding

This work was supported by the Program No. P13 of Presidium of the Russian Academy of Sciences, project No. 0089-2018-1245. The work was done on the topic of the State task (No. 0089-2019-0011) with using of the Analytical Center for Collective Use tool base of the IPCP RAS. D.V.K. acknowledges the Ministry of Science and Higher Education of the Russian Federation (Agreement no. 14.W03.31.0001). The magnetic measurements were carried out at the Federal Center of Shared Facilities of Kazan federal university. The work of I.F.G. was funded by a subsidy allocated to Kazan Federal University for state assignments in the sphere of scientific activities (project No. 3.8138.2017/8.9).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Milios, C.; Winpenny, R. Cluster-Based Single-Molecule Magnet. In Molecular Nanomagnets and Related Phenomena, 1st ed.; Gao, S., Ed.; Springer: Berlin/Heidelberg, Germany, 2015; Volume 164, pp. 1–109. [Google Scholar]
  2. Neese, F.; Pantazis, D. What is not required to make a single molecule magnet. Faraday Discuss. 2011, 148, 229–238. [Google Scholar] [CrossRef] [PubMed]
  3. Waldmann, O. A Criterion for the Anisotropy Barrier in Single-Molecule Magnets. Inorg. Chem. 2007, 46, 10035–10037. [Google Scholar] [CrossRef] [PubMed]
  4. Aldoshin, S.M.; Korchagin, D.V.; Palii, A.V.; Tsukerblat, B.S. Some new trends in the design of single molecule magnets. Pure Appl. Chem. 2017, 89, 1119–1144. [Google Scholar] [CrossRef]
  5. Bar, A.K.; Pichon, C.; Sutter, J.P. Magnetic anisotropy in two- to eight-coordinated transition-metal complexes: Recent developments in molecular magnetism. Coord. Chem. Rev. 2016, 308, 346–380. [Google Scholar] [CrossRef]
  6. Craig, G.; Murrie, M. 3d single-ion magnets. Chem. Soc. Rev. 2015, 44, 2135–2147. [Google Scholar] [CrossRef] [Green Version]
  7. Zadrozny, J.M.; Xiao, D.J.; Atanasov, M.; Long, G.J.; Grandjean, F.; Neese, F.; Long, J.R. Magnetic blocking in a linear iron (I) complex. Nat. Chem. 2013, 5, 577–581. [Google Scholar] [CrossRef]
  8. Gómes-Coca, S.; Cremades, E.; Aliaga-Alcalde, N.; Ruiz, E. Mononuclear Single-Molecule Magnets: Tailoring the Magnetic Anisotropy of First-Row Transition-Metal Complexes. J. Amer. Chem. Soc. 2013, 135, 7010–7018. [Google Scholar] [CrossRef]
  9. Poulten, R.C.; Page, M.J.; Algarra, A.G.; Le Roy, J.J.; Lopez, I.; Carter, E.; Llobet, A.; Macgregor, S.A.; Mahon, M.F.; Murphy, D.M.; et al. Synthesis, Electronic Structure, and Magnetism of [Ni(6-Mes)2]+: A Two-Coordinate Nickel(I) Complex Stabilized by Bulky N-Heterocyclic Carbenes. J. Am. Chem. Soc. 2013, 135, 13640–13643. [Google Scholar] [CrossRef]
  10. Ruamps, R.; Maurice, R.; Batchelor, L.; Boggio-Pasqua, M.; Guillot, R.; Barra, A.; Liu, J.; Bendeif, E.; Pillet, S.; Hill, S.; et al. Giant Ising-Type Magnetic Anisotropy in Trigonal Bipyramidal Ni(II) Complexes: Experiment and Theory. J. Amer. Chem. Soc. 2013, 135, 3017–3026. [Google Scholar] [CrossRef]
  11. Saber, M.R.; Dunbar, K.R. Ligands effects on the magnetic anisotropy of tetrahedral cobalt complexes. Chem. Commun. 2014, 50, 12266–12269. [Google Scholar] [CrossRef]
  12. Zhang, Y.-Z.; Gómez-Coca, S.; Brown, A.J.; Saber, M.R.; Zhang, X.; Dunbar, K.R. Trigonal antiprismatic Co(II) single molecule magnets with large uniaxial anisotropies: importance of Raman and tunneling mechanisms. Chem. Sci. 2016, 7, 6519–6527. [Google Scholar] [CrossRef] [PubMed]
  13. Yao, X.-N.; Du, J.-Z.; Zhang, Y.-Q.; Leng, X.-B.; Yang, M.-W.; Jiang, S.-D.; Wang, Z.-X.; Ouyang, Z.-W.; Deng, L.; Wang, B.-W.; et al. Two-Coordinate Co(II) Imido Complexes as Outstanding Single-Molecule Magnets. J. Am. Chem. Soc. 2017, 139, 373–380. [Google Scholar] [CrossRef] [PubMed]
  14. Palii, A.V.; Korchagin, D.V.; Yureva, E.A.; Akimov, A.V.; Misochko, E.Y.; Shilov, G.V.; Talantsev, A.D.; Morgunov, R.B.; Aldoshin, S.M.; Tsukerblat, B.S. Single-Ion Magnet Et4N[CoII(hfac)3] with Nonuniaxial Anisotropy: Synthesis, Experimental Characterization, and Theoretical Modeling. Inorg. Chem. 2016, 55, 9696–9706. [Google Scholar] [CrossRef] [PubMed]
  15. Tupolova, Y.P.; Shcherbakov, I.N.; Popov, L.D.; Lebedev, V.E.; Tkachev, V.V.; Zakharov, K.V.; Vasiliev, A.N.; Korchagin, D.V.; Palii, A.V.; Aldoshin, S.M. Field-induced single-ion magnet behavior of a hexacoordinated Co(II) complex with easy-axis-type magnetic anisotropy. Dalton Trans. 2019, 48, 6960–6970. [Google Scholar] [CrossRef] [PubMed]
  16. Platas-Iglesias, C.; Vaiana, L.; Esteban-Gómez, D.; Avecilla, F.; Real, J.; de Blas, A.; Rodríguez-Blas, T. Electronic Structure Study of Seven-Coordinate First-Row Transition Metal Complexes Derived from 1,10-Diaza-15-crown-5: A Successful Marriage of Theory with Experiment. Inorg. Chem. 2005, 44, 9704–9713. [Google Scholar] [CrossRef]
  17. Batchelor, L.; Sangalli, M.; Guillot, R.; Guihéry, N.; Maurice, R.; Tuna, F.; Mallah, T. Pentanuclear Cyanide-Bridged Complexes Based on Highly Anisotropic CoII Seven-Coordinate Building Blocks: Synthesis, Structure, and Magnetic Behavior. Inorg. Chem. 2011, 50, 12045–12052. [Google Scholar] [CrossRef]
  18. Venkatakrishnan, T.; Sahoo, S.; Bréfuel, N.; Duhayon, C.; Paulsen, C.; Barra, A.; Ramasesha, S.; Sutter, J. Enhanced Ion Anisotropy by Nonconventional Coordination Geometry: Single-Chain Magnet Behavior for a [{FeIIL}2{NbIV(CN)8}] Helical Chain Compound Designed with Heptacoordinate Fe(II). J. Am. Chem. Soc. 2010, 132, 6047–6056. [Google Scholar] [CrossRef]
  19. Huang, X.; Zhou, C.; Shao, D.; Wang, X. Field-Induced Slow Magnet Relaxation in Cobalt(II) Compounds with Pentagonal Bipyramid Geometry. Inorg. Chem. 2014, 53, 12671–12673. [Google Scholar] [CrossRef]
  20. Ruamps, R.; Batchelor, L.; Maurice, R.; Gogoi, N.; Jiménez-Lozano, P.; Guihéry, N.; de Graaf, C.; Barra, A.; Sutter, J.; Mallah, T. Origin of the Magnetic Anisotropy in Heptacoordinate NiII and CoII Complexes. Chem. Eur. J. 2013, 19, 950–956. [Google Scholar] [CrossRef]
  21. Gogoi, N.; Thlijeni, M.; Duhayon, C.; Sutter, J. Heptacoordinated Nickel(II) as an Ising-Type Anisotropic Building Unit: Illustration with a Pentanuclear [(NiL)3{W(CN)8}2] Complex. Inorg. Chem. 2013, 52, 2283–2285. [Google Scholar] [CrossRef]
  22. Regueiro-Figueroa, M.; Lima, L.; Blanco, V.; Esteban-Gomez, D.; de Blas, A.; Rodriguez-Blas, T.; Delgado, R.; Platas-Iglesias, C. Reasons behind the relative abundances of heptacoordinate complexes along the late first-row transition metal series. Inorg. Chem. 2014, 53, 12859–12869. [Google Scholar] [CrossRef]
  23. Gavey, E.L.; Pilkington, M. Coordination complexes of 15-membered pentadentate aza, oxoaza and thiaaza Schiff base macrocycles “Old Complexes Offer New Attractions”. Coord. Chem. Rev. 2015, 296, 125–152. [Google Scholar] [CrossRef]
  24. Shao, D.; Zhang, S.; Zhang, Y.; Wang, X. Probing the Effect of Axial Ligands on Easy-Plany Anisotropy of Pentagonal-Bipyramidal Cobalt(II) Single-Ion Magnets. Inorg. Chem. 2016, 55, 10859–10869. [Google Scholar] [CrossRef]
  25. Drahoš, B.; Herchel, R.; Trávníček, Z. Impact of Halogenido Coligands on Magnetic Anisotropy in Seven-Coordinate Co(II) Complexes. Inorg. Chem. 2017, 56, 5076–5088. [Google Scholar] [CrossRef]
  26. Giordano, T.J.; Palenik, G.J.; Palenic, R.C.; Sullivan, D.A. Pentagonal-Bipyramidal Complexes. Synthesis and Characterization of Aqua(nitrato)[2,6-diacetylpyridinebis-(benzonic acid hydrazone)]cobalt(II) Nitrate and Diaqua[2,6-diacetylpyridinebis(benzonic acid hydrazone)]nickel(II) Nitrate Dihydrate. Inorg. Chem. 1979, 18, 2445–2450. [Google Scholar] [CrossRef]
  27. Ivanovic-Burmazovic, I.; Andjelkovic, K. Transition metal complexes with bis(hydrazone) ligands of 2,6-diacetylpyridine hepta-coordination of 3d metals. In Book Advances Inorganic Chemistry, 1st ed.; van Eldik, R., Ed.; Elsevier: Amsterdam, The Netherlands, 2004; Volume 55, pp. 315–360. [Google Scholar]
  28. Carcelli, M.; Ianelli, S.; Pelagatti, P.; Pelizzi, G. Structural characterization of a new ligand mode of 2,6-diacetylpyridine bis(semicarbazone), H2daps. Inorg. Chim. Acta 1999, 292, 121–126. [Google Scholar] [CrossRef]
  29. Palenik, G.J.; Wester, D.W. Pentagonal-bipyramidal complexes. Crystal and molecular structures of chloroaqua(2,6-diacetylpyridine bis(semicarbazone))manganese(II), -iron(II), -cobalt(II), and -zinc(II) chloride dihydrates. Inorg. Chem. 1978, 17, 864–870. [Google Scholar] [CrossRef]
  30. Palenik, G.J.; Wester, D.W.; Rychlewska, U.; Palenik, R.C. Pentagonal-bipyramidal complexes. Synthesis and crystal structures of diaqua[2,6-diacetylpyridine bis(semicarbazone)]chromium(III) hydroxide dinitrate hydrate and dichloro[2,6-diacetylpyridine bis(semicarbazone)]iron(III) chloride dihydrate. Inorg. Chem. 1976, 15, 1814–1819. [Google Scholar] [CrossRef]
  31. Bar, A.; Pichon, C.; Gogoi, N.; Duhayon, C.; Ramasesha, S.; Sutter, J. Single-ion magnet behaviour of heptacoordinated Fe(II) complexes: on the importance of supramolecular organization. Chem. Commun. 2015, 51, 3616–3619. [Google Scholar] [CrossRef]
  32. Habib, F.; Korobkov, I.; Murugesu, M. Exposing the intermolecular nature of the second relaxation pathway in a mononuclear cobalt(II) single-molecule magnet with positive anisotropy. Dalton Trans. 2015, 44, 6368–6373. [Google Scholar] [CrossRef] [PubMed]
  33. Dey, M.; Dutta, S.; Sarma, B.; Deka, R.C.; Gogoi, N. Modulation of the coordination environment: a convenient approach to tailor magnetic anisotropy in seven coordinate Co(II) complexes. Chem. Commun. 2016, 52, 753–756. [Google Scholar] [CrossRef] [PubMed]
  34. Mondal, A.K.; Mondal, A.; Dey, B.; Konar, S. Influence of the Coordination Environment on Easy-Plane Magnetic Anisotropy of Pentogonal Bipyramidal Cobalt(II) Complexes. Inorg. Chem. 2018, 57, 9999–10008. [Google Scholar] [CrossRef] [PubMed]
  35. Bar, A.; Gogoi, N.; Pichon, C.; Goli, V.; Thlijeni, M.; Duhayon, C.; Suaud, N.; Guihery, N.; Barra, A.; Ramasesha, S.; et al. Pentagonal Bipyramid FeII Complexes: Robust Ising-Spin Units towards Heteropolynuclear Nanomagnets. Chem. Eur. J. 2017, 23, 4380–4396. [Google Scholar] [CrossRef] [PubMed]
  36. Kopotkov, V.A.; Sasnovskaya, V.D.; Korchagin, D.V.; Morgunov, R.B.; Aldoshin, S.M.; Simonov, S.V.; Zorina, L.V.; Schaniel, D.; Woike, T.; Yagubskii, E.B. The first photochromic bimetallic assemblies based on Mn(III) and Mn(II) Schiff-base (salpn, dapsc) complexes and pentacyanonitrosylferrate(II). CrystEngComm. 2015, 17, 3866–3876. [Google Scholar] [CrossRef]
  37. Sasnovskaya, V.D.; Kopotkov, V.A.; Talantsev, A.D.; Morgunov, R.B.; Yagubskii, E.B.; Simonov, S.V.; Zorina, L.V.; Mironov, V.S. Synthesis, Structure, and Magnetic Properties of 1D {[MnIII(CN)6][MnII(dapsc)]}n Coordination Polymers: Origin of Unconventional Single-Chain Magnet Behavior. Inorg. Chem. 2017, 56, 8926–8943. [Google Scholar] [CrossRef]
  38. Pichon, C.; Suaud, N.; Duhayon, C.; Guihéry, N.; Sutter, J. Cyano-Bridged Fe(II)−Cr(III) Single-Chain Magnet Based on Pentagonal Bipyramid Units: On the Added Value of Aligned Axial Anisotropy. J. Amer. Chem. Soc. 2018, 140, 7698–7704. [Google Scholar] [CrossRef]
  39. Gomez-Coca, S.; Urtizberea, A.; Cremades, E.; Alonso, P.; Camon, A.; Ruiz, E.; Luis, F. Origin of slow magnetic relaxation in Kramers ions with non-uniaxial anisotropy. Nat. Commun. 2014, 5, 1–8. [Google Scholar] [CrossRef]
  40. Groom, C.R.; Bruno, I.J.; Lightfoot, M.P.; Ward, S.C. The Cambridge Structural Database. Acta Cryst. 2016, B72, 171–179. [Google Scholar] [CrossRef]
  41. Casanova, D.; Alemany, P.; Bofill, J.; Alvarez, S. Shape and symmetry of heptacoordinate transition-metal complexes: structural trends. Chem. Eur. J. 2003, 9, 1281–1295. [Google Scholar] [CrossRef]
  42. Alvarez, S.; Alemany, P.; Casanova, D.; Cirera, J.; Llunell, M.; Avnir, D. Shape maps and polyhedral interconversion paths in transition metal chemistry. Coord. Chem. Rev. 2005, 249, 1693–1708. [Google Scholar] [CrossRef]
  43. Mabbs, F.; Machin, D. Magnetism and Transition Metal Complexes, 2nd ed.; Dover Publications Inc.: New York, NY, USA, 2008; pp. 1–206. [Google Scholar]
  44. Guo, Y.; Xu, G.; Gamez, P.; Zhao, L.; Lin, S.; Deng, R.; Tang, J.; Zhang, H.J. Two-step relaxation in a linear tetranuclear dysprosium(III) aggregate showing single-molecule magnet behavior. J. Am. Chem. Soc. 2010, 132, 8538–8539. [Google Scholar] [CrossRef] [PubMed]
  45. Guo, Y.; Xu, G.F.; Guo, Y.; Tang, J. Relaxation dynamics of dysprosium(III) single molecule magnets. Dalton Trans. 2011, 40, 9953–9963. [Google Scholar] [CrossRef] [PubMed]
  46. Varga, F.; Rajnák, C.; Titiš, J.; Moncoľ, J.; Boča, R. Slow magnetic relaxation in a Co(II) octahedral-tetrahedral system formed of a [CoL3]2+ core with L = bis(diphenylphosphanoxido) methane and tetrahedral [CoBr4]2− counter anions. Dalton Trans. 2017, 46, 4148–4151. [Google Scholar] [CrossRef]
  47. Rajnák, C.; Titiš, J.; Moncoľ, J.; Renz, F.; Boča, R. Field-Supported Slow Magnetic Relaxation in Hexacoordinate CoII Complexes with Easy Plane Anisotropy. Eur. J. Inorg. Chem. 2017, 2017, 1520–1525. [Google Scholar] [CrossRef]
  48. Titiš, J.; Rajnák, C.; Valigura, D.; Boča, R. Breaking the Magic Border of One Second for Slow Magnetic Relaxation of Cobalt-Based Single Ion Magnets. Inorg. Chem. 2018, 57, 14314–14321. [Google Scholar]
  49. Mandal, S.; Mondal, S.; Rajnák, C.; Titiš, J.; Boča, R.; Mohanta, S. Syntheses, crystal structures and magnetic properties of two mixed-valence Co(III)Co(II) compounds derived from Schiff base ligands: field-supported single-ion-magnet behavior with easy-plane anisotropy. Dalton Trans. 2017, 46, 13135–13144. [Google Scholar] [CrossRef] [PubMed]
  50. Chilton, N.F. CC-fit, The University of Manchester, UK. 2014. Available online: http://www.nfchilton.com/cc-fit.html.
  51. Cole, K.S.; Cole, R.H. Dispersion and Absorption in Dielectrics, I. Alternating Current Characteristics. J. Chem. Phys. 1941, 9, 341–351. [Google Scholar] [CrossRef]
  52. Ishikawa, R.; Horii, Y.; Nakanishi, R.; Ueno, S.; Breedlove, B.; Yamashita, M.; Kawata, S. Field-Induced Single-Ion Magnetism Based on Spin-Phonon Relaxation in a Distorted Octahedral High-Spin Cobalt(II) Complex. Eur. J. Inorg. Chem. 2016, 2016, 3233–3239. [Google Scholar] [CrossRef]
  53. Korchagin, D.V.; Palii, A.A.V.; Yureva, E.A.; Akimov, A.V.; Misochko, E.Y.; Shilov, G.V.; Talantsev, A.D.; Morgunov, R.B.; Shakin, A.A.; Aldoshin, S.M.; et al. Evidence of field induced slow magnetic relaxation in: cis-[Co(hfac)2(H2O)2] exhibiting tri-axial anisotropy with a negative axial component. Dalton Trans. 2017, 46, 7540–7548. [Google Scholar] [CrossRef]
  54. Gatteschi, D.; Sessoli, R. Quantum tunneling of magnetization and related phenomena in molecular materials. Angew. Chem. Int. Ed. 2003, 42, 268–297. [Google Scholar] [CrossRef]
  55. Agilent. CrysAlis PRO Version 171.35.19; Agilent Technologies UK Ltd.: Yarnton, Oxfordshire, UK, 2011. [Google Scholar]
  56. Sheldrick, G.M. SHELXTL v. 6.14, Structure Determination Software Suite; Bruker AXS: Madison, WI, USA, 2000. [Google Scholar]
  57. Roos, B.O.; Taylor, P.R.; Siegbahn, P.E. A complete active space SCF method (CASSCF) using a density matrix formulated super-CI approach. Chem. Phys. 1980, 48, 157–173. [Google Scholar] [CrossRef]
  58. Per, S.; Heiberg, A.; Roos, B.; Levy, B. A Comparison of the Super-CI and the Newton-Raphson Scheme in the Complete Active Space SCF Method. Phys. Scr. 1980, 21, 323–327. [Google Scholar]
  59. Siegbahn, P.; Almlöf, J.; Heiberg, A.; Roos, B. The complete active space SCF (CASSCF) method in a Newton–Raphson formulation with application to the HNO molecule. J. Chem. Phys. 1981, 74, 2384–2396. [Google Scholar] [CrossRef]
  60. Angeli, C.; Cimiraglia, R.; Evangelisti, S.; Leininger, T.; Malrieu, J. Introduction of n-electron valence states for multireference perturbation theory. J. Chem. Phys. 2001, 114, 10252–10264. [Google Scholar] [CrossRef]
  61. Angeli, C.; Cimiraglia, R.; Malrieu, J. N-electron valence state perturbation theory: a fast implementation of the strongly contracted variant. Chem. Phys. Lett. 2001, 350, 297–305. [Google Scholar] [CrossRef]
  62. Angeli, C.; Cimiraglia, R. Multireference perturbation configuration interaction V. Third-order energy contributions in the Møller–Plesset and Epstein–Nesbet partitions. Theor. Chem. Acc. 2002, 107, 313–317. [Google Scholar] [CrossRef]
  63. Angeli, C.; Cimiraglia, R.; Malrieu, J. n-electron valence state perturbation theory: A spinless formulation and an efficient implementation of the strongly contracted and of the partially contracted variants. J. Chem. Phys. 2002, 17, 9138–9153. [Google Scholar] [CrossRef]
  64. Hess, B.A. Relativistic electronic-structure calculations employing a two-component no-pair formalism with external-field projection operators. Phys. Rev. A 1986, 33, 3742–3748. [Google Scholar] [CrossRef] [Green Version]
  65. Pantazis, D.A.; Chen, X.-Y.; Landis, C.R.; Neese, F. All-Electron Scalar Relativistic Basis Sets for Third-Row Transition Metal Atoms. J. Chem. Theory Comput. 2008, 4, 908–919. [Google Scholar] [CrossRef]
  66. Schafer, A.; Huber, C.; Ahlrichs, R. Fully optimized contracted Gaussian basis sets of triple zeta valence quality for atoms Li to Kr. J. Chem. Phys. 1994, 100, 5829–5835. [Google Scholar] [CrossRef]
  67. Schafer, A.; Horn, H.; Ahlrichs, R. Fully optimized contracted Gaussian basis sets for atoms Li to Kr. J. Chem. Phys. 1992, 97, 2571–2577. [Google Scholar] [CrossRef]
  68. Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef] [PubMed]
  69. Ganyushin, D.; Neese, F. First-principles calculations of zero-field splitting parameters. J. Chem. Phys. 2006, 125, 024103-11. [Google Scholar] [CrossRef] [PubMed]
  70. Neese, F. Efficient and accurate approximations to the molecular spin-orbit coupling operator and their use in molecular g-tensor calculations. J. Chem. Phys. 2005, 122, 034107-13. [Google Scholar] [CrossRef] [PubMed]
  71. Maurice, R.; Bastardis, R.; Graaf, C.; Suaud, N.; Mallah, T.; Guihéry, N. Universal Theoretical Approach to Extract Anisotropic Spin Hamiltonians. J. Chem. Theory Comput. 2009, 5, 2977–2984. [Google Scholar] [CrossRef]
  72. Atanasov, M.; Ganyushin, D.; Sivalingam, K.; Neese, F. A Modern First-Principles View on Ligand Field Theory Through the Eyes of Correlated Multireference Wavefunctionsin. In Molecular Electronic Structures of Transition Metal Complexes II, 1st ed.; Mingos, D., Day, P., Dahl, J., Eds.; Springer-Verlag: Berlin/Heidelberg, Germany, 2012; Volume 143, pp. 149–220. [Google Scholar]
  73. Singh, S.; Eng, J.; Atanasov, M.; Neese, F. Covalency and chemical bonding in transition metal complexes: An ab initio based ligand field perspective. Coord. Chem. Rev. 2017, 344, 2–25. [Google Scholar] [CrossRef]
  74. Neese, F. The ORCA program system. Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
  75. Neese, F. Software update: the ORCA program system, version 4.0. Comput. Mol. Sci. 2018, 8, e1327-6. [Google Scholar] [CrossRef]
Magnetochemistry 05 00058 g001 550
Figure 1. Molecular structure of the pentadentate ligand H2dapsc (R = NH2) and some its analogues: H2dapbh (R = C6H5), H2biph (R = C6H4-C6H5), and H4daps (R = 2-OHC6H4).
Figure 1. Molecular structure of the pentadentate ligand H2dapsc (R = NH2) and some its analogues: H2dapbh (R = C6H5), H2biph (R = C6H4-C6H5), and H4daps (R = 2-OHC6H4).
Magnetochemistry 05 00058 g001
Magnetochemistry 05 00058 sch001 550
Scheme 1. Synthesis of complexes 1–5. Methods A and B are described in the text.
Scheme 1. Synthesis of complexes 1–5. Methods A and B are described in the text.
Magnetochemistry 05 00058 sch001
Magnetochemistry 05 00058 g002 550
Figure 2. The molecular structures of 1 (2) (a), 3 (b), 4 (c), 5 (d), 6 (e), and 7 (f). Disordering of solvate molecules is omitted for clarity (see text).
Figure 2. The molecular structures of 1 (2) (a), 3 (b), 4 (c), 5 (d), 6 (e), and 7 (f). Disordering of solvate molecules is omitted for clarity (see text).
Magnetochemistry 05 00058 g002
Magnetochemistry 05 00058 g003 550
Figure 3. Temperature dependence of χMT obtained at 0.5 T for 1 (a), 2(b), 3 (c), 4 (d), 5 (e), 6 (f), and 7 (g). The insets: Magnetization versus magnetic field measured at T= 2, 3, and 5 K for these complexes. The empty circles represent the experimental data and black solid lines represent the fitted using Equation (1) with the parameters listed in Table 1.
Figure 3. Temperature dependence of χMT obtained at 0.5 T for 1 (a), 2(b), 3 (c), 4 (d), 5 (e), 6 (f), and 7 (g). The insets: Magnetization versus magnetic field measured at T= 2, 3, and 5 K for these complexes. The empty circles represent the experimental data and black solid lines represent the fitted using Equation (1) with the parameters listed in Table 1.
Magnetochemistry 05 00058 g003
Magnetochemistry 05 00058 g004 550
Figure 4. The lowest energy levels from SA-CASSCF(7,5)/NEVPT2 calculations for 1–7 (the ground and excited quartet states (a) and the lowest ligand field multiplets/Kramers doublets result from the spin–orbit coupling (b).
Figure 4. The lowest energy levels from SA-CASSCF(7,5)/NEVPT2 calculations for 1–7 (the ground and excited quartet states (a) and the lowest ligand field multiplets/Kramers doublets result from the spin–orbit coupling (b).
Magnetochemistry 05 00058 g004
Magnetochemistry 05 00058 g005 550
Figure 5. d-AO diagram according to ab initio ligand field theory (AILFT) analysis for 3.
Figure 5. d-AO diagram according to ab initio ligand field theory (AILFT) analysis for 3.
Magnetochemistry 05 00058 g005
Magnetochemistry 05 00058 g006 550
Figure 6. Frequency-dependence of in-phase (χ’) and out-of-phase (χ″) AC susceptibility in the temperature range of 2–8 K for 1 (a), 2(b), 3 (c), 4 (d), 5 (e), 6 (f), and 7 (g) under a DC fields.
Figure 6. Frequency-dependence of in-phase (χ’) and out-of-phase (χ″) AC susceptibility in the temperature range of 2–8 K for 1 (a), 2(b), 3 (c), 4 (d), 5 (e), 6 (f), and 7 (g) under a DC fields.
Magnetochemistry 05 00058 g006
Table
Table 1. The CASSCF/NEVPT2 quantum chemical calculated and fitted magnetic parameters for 1–7.
Table 1. The CASSCF/NEVPT2 quantum chemical calculated and fitted magnetic parameters for 1–7.
12345a5b67
ZFS and g values based on CASSCF/NEVPT2 calculations with CAS(7,5)
D (cm−1)38.0237.7337.5137.4939.9339.5838.9938.94
E/D0.02270.02130.00650.00930.01620.01430.01430.0133
gx2.34422.33662.32202.32062.35902.34902.32842.3511
gy2.36412.35542.32692.32862.37362.36172.35592.3625
gz2.00492.00231.99361.99431.99711.99491.99252.0009
giso2.23772.23142.21482.21452.24322.23522.22562.2382
Analysis of the experimental magnetic data
D (cm−1)35.638.2035.333.6040.438.0235.61
E/D0.170.000.1010.149−0.0180.16
gx,y/gz2.29/2.142.36/1.902.28/2.132.26/2.002.48/2.002.28/2.162.45/2.11
giso2.242.262.232.182.332.242.34
χTIP−1.0 × 10−41.0 × 10−45.0 × 10−4−5.0 × 10−4−
Table
Table 2. Relative energies (cm−1) of ligand field one-electron states (in the basis of d-AOs) from AILFT analysis (SA-CASSCF(7,5)/NEVPT2).
Table 2. Relative energies (cm−1) of ligand field one-electron states (in the basis of d-AOs) from AILFT analysis (SA-CASSCF(7,5)/NEVPT2).
d-AO12345a5b67
dyz0.00.00.00.00.00.00.00.0
dxz253.2274.5119.3326.3513.4254.8330.2339.0
dx2-y22888.03026.54437.74652.23779.54244.35142.24371.6
dxy3499.53688.24741.34770.74019.64445.75241.44531.5
dz28044.88141.77885.87817.57742.27005.56019.46732.7
Table
Table 3. Main contributions of the excited states to total D values (cm−1).
Table 3. Main contributions of the excited states to total D values (cm−1).
Excited StateContributions to Total D, cm−1
No.Mult12345a5b67
3417.2616.7915.0315.6517.4517.0917.0316.62
4415.2714.7915.1414.9016.2616.3014.2015.74
52--13.2813.5111.6513.1513.6312.82
62-4.56-
72 −1.55−1.51−1.33−1.61−1.58−1.53
826.484.71−1.59−1.55−1.59−1.57−1.51−1.63
Table
Table 4. Parameters for the magnetic relaxation of complexes 1–7 obtained by fit of the experimental relaxation times to Equation 2.
Table 4. Parameters for the magnetic relaxation of complexes 1–7 obtained by fit of the experimental relaxation times to Equation 2.
1234567
n9 (Fixed*)7.4(3)7.3(2)5.6(3)5.8(4)4.2(2)9 (Fixed*)
A, Oe−2s−1K−11.03(2) × 10−34.10(9) × 10−41.29(2) × 10−47.7(6) × 10−52.9(1) × 10−42.9(1) × 10−41.11(3) × 10−4
C, s−1K−n1.06(6) × 10−30.02(1)0.017(6)0.4(2)0.26(6)0.26(6)2.43(5) × 10−4
* Fixed n = 9, since during approximation the parameter n exceeded this value, which is characteristic for the Raman process (~CT9).

Share and Cite

MDPI and ACS Style

Kopotkov, V.A.; Korchagin, D.V.; Sasnovskaya, V.D.; Gilmutdinov, I.F.; Yagubskii, E.B. A Series of Field-Induced Single-Ion Magnets Based on the Seven-Coordinate Co(II) Complexes with the Pentadentate (N3O2) H2dapsc Ligand. Magnetochemistry 2019, 5, 58. https://doi.org/10.3390/magnetochemistry5040058

AMA Style

Kopotkov VA, Korchagin DV, Sasnovskaya VD, Gilmutdinov IF, Yagubskii EB. A Series of Field-Induced Single-Ion Magnets Based on the Seven-Coordinate Co(II) Complexes with the Pentadentate (N3O2) H2dapsc Ligand. Magnetochemistry. 2019; 5(4):58. https://doi.org/10.3390/magnetochemistry5040058

Chicago/Turabian Style

Kopotkov, Vyacheslav A., Denis V. Korchagin, Valentina D. Sasnovskaya, Ildar F. Gilmutdinov, and Eduard B. Yagubskii. 2019. "A Series of Field-Induced Single-Ion Magnets Based on the Seven-Coordinate Co(II) Complexes with the Pentadentate (N3O2) H2dapsc Ligand" Magnetochemistry 5, no. 4: 58. https://doi.org/10.3390/magnetochemistry5040058

APA Style

Kopotkov, V. A., Korchagin, D. V., Sasnovskaya, V. D., Gilmutdinov, I. F., & Yagubskii, E. B. (2019). A Series of Field-Induced Single-Ion Magnets Based on the Seven-Coordinate Co(II) Complexes with the Pentadentate (N3O2) H2dapsc Ligand. Magnetochemistry, 5(4), 58. https://doi.org/10.3390/magnetochemistry5040058

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop