Evidence of Photo-Thermal Effects on the First-Order Thermo-Induced Spin Transition of [{Fe(NCSe)(py)2}2(m-bpypz)] Spin-Crossover Material
Abstract
1. Introduction
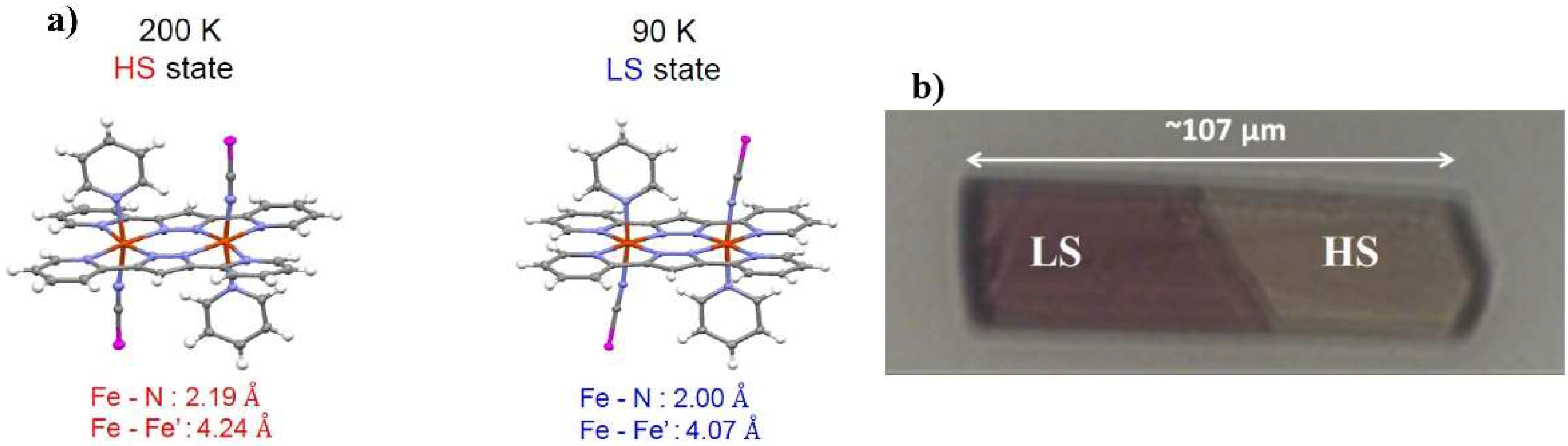
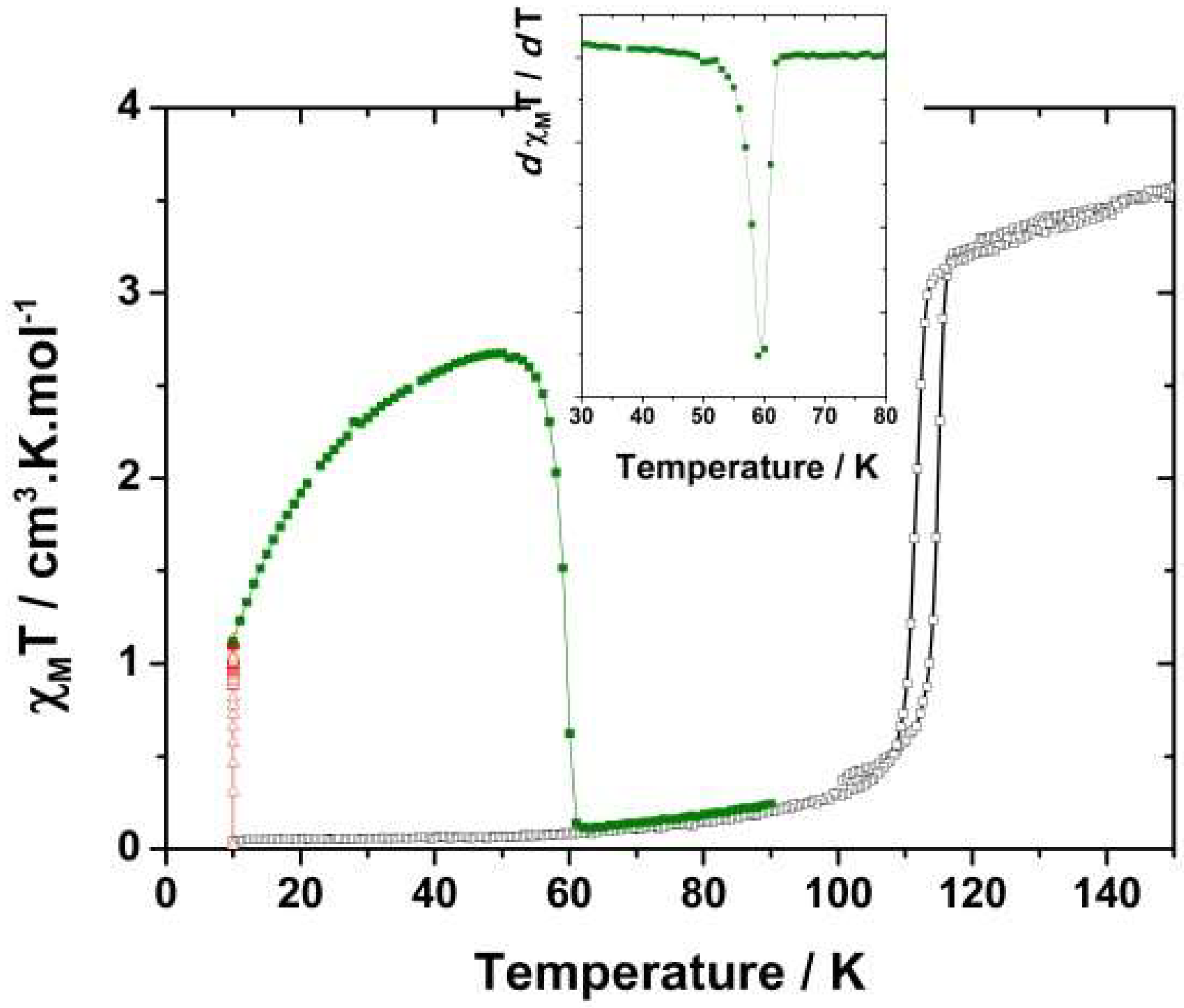
2. Experiments and Results
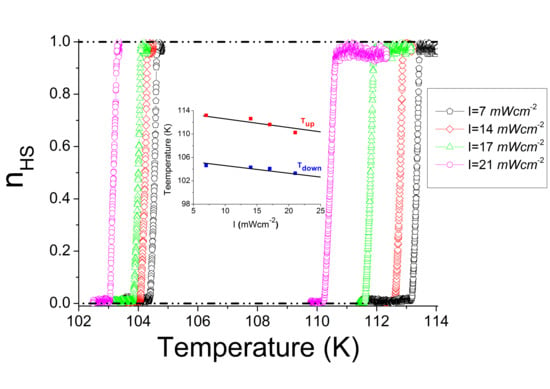
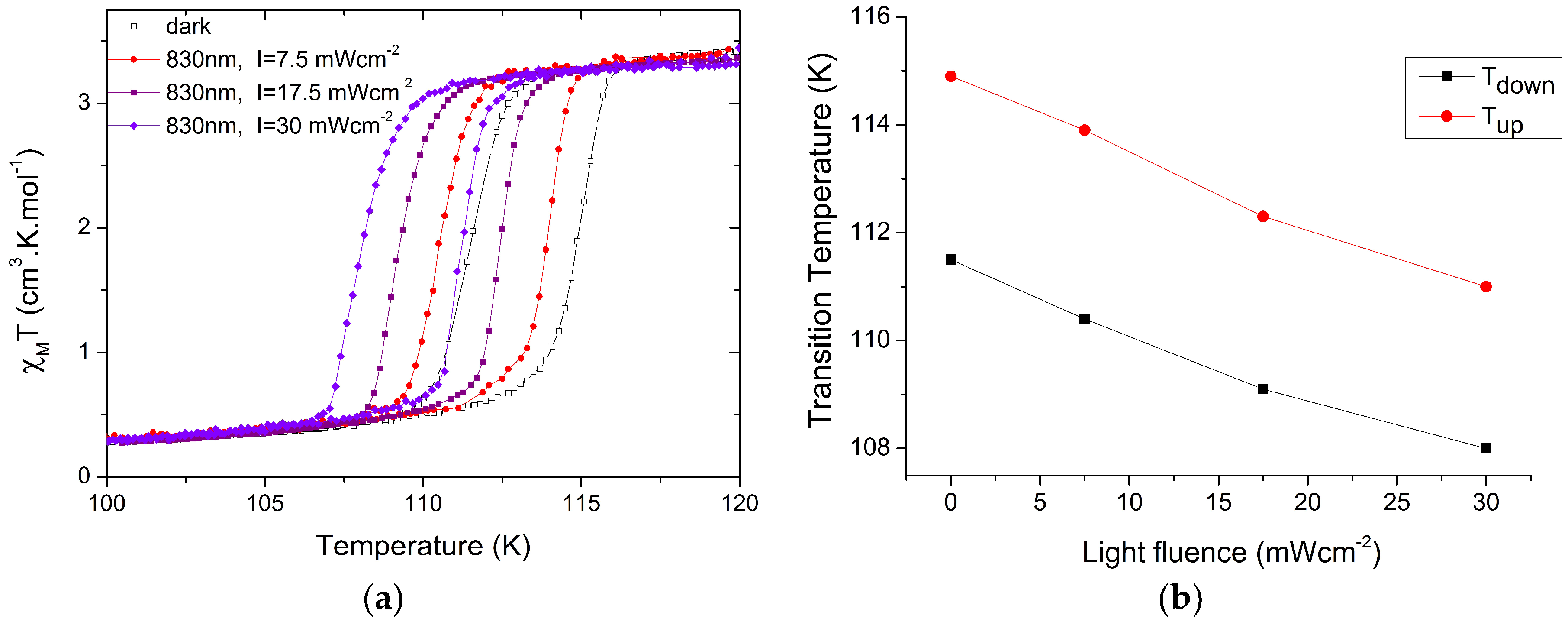
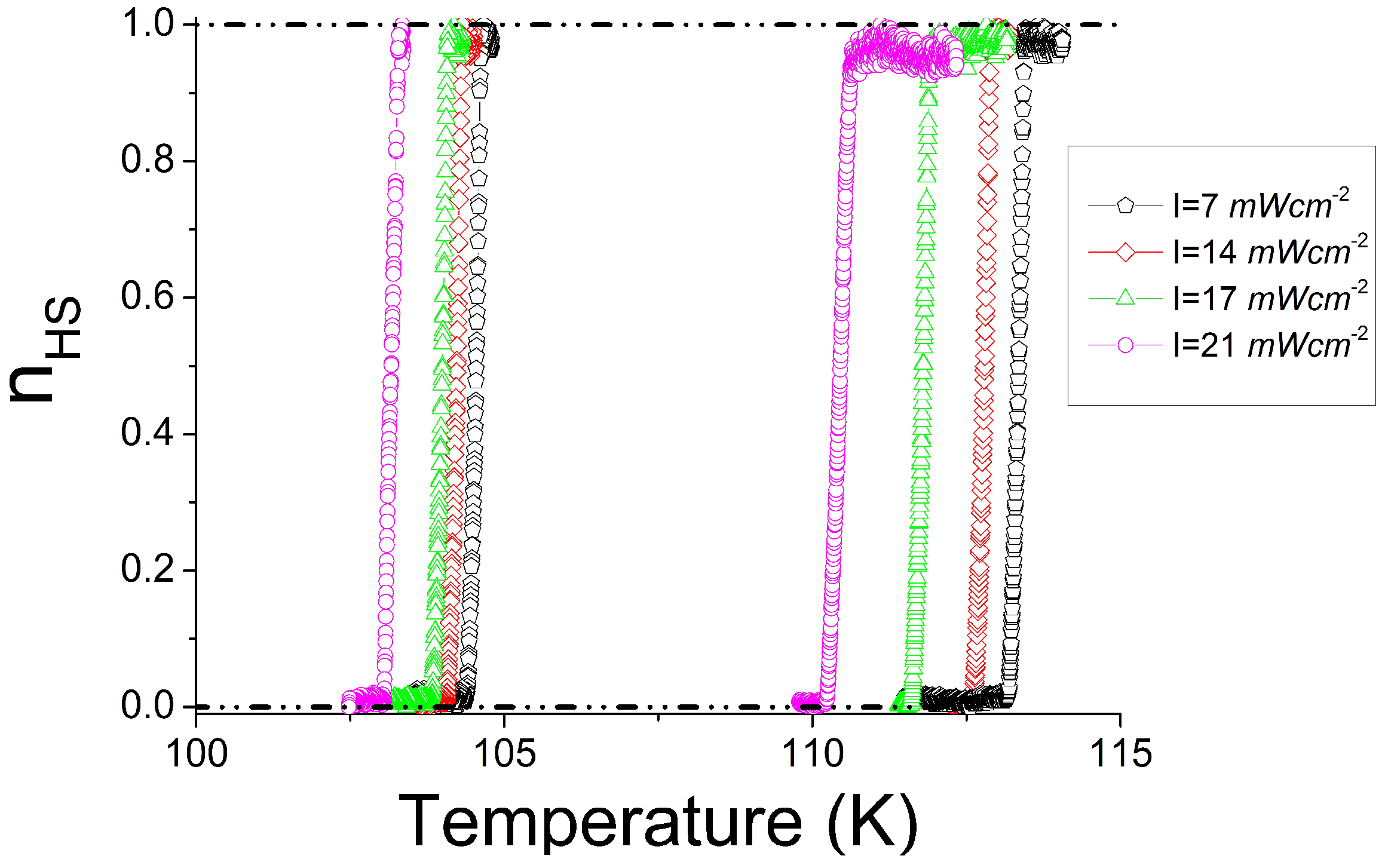
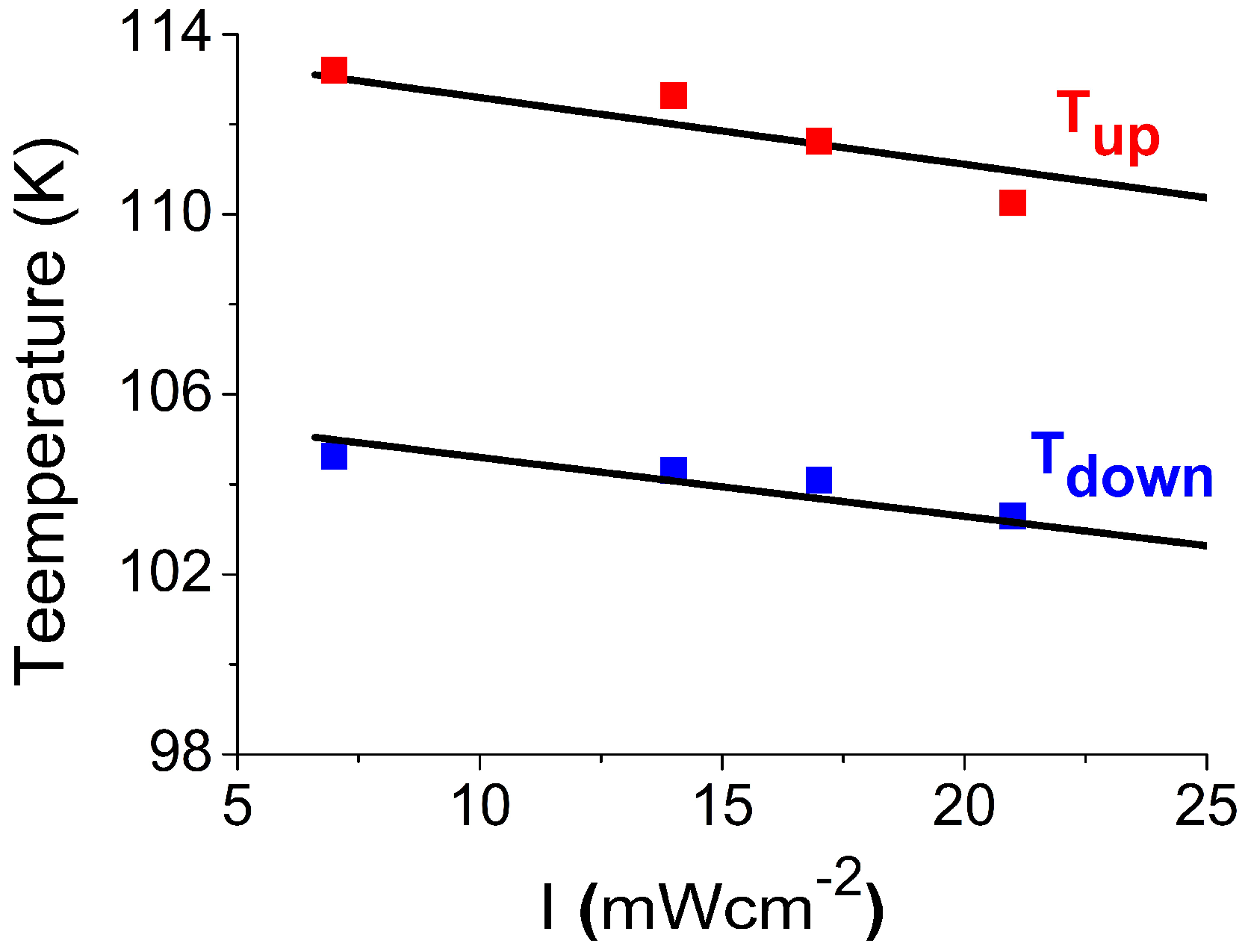
2.1. Photo-Magnetic Studies under Various Shining Intensities
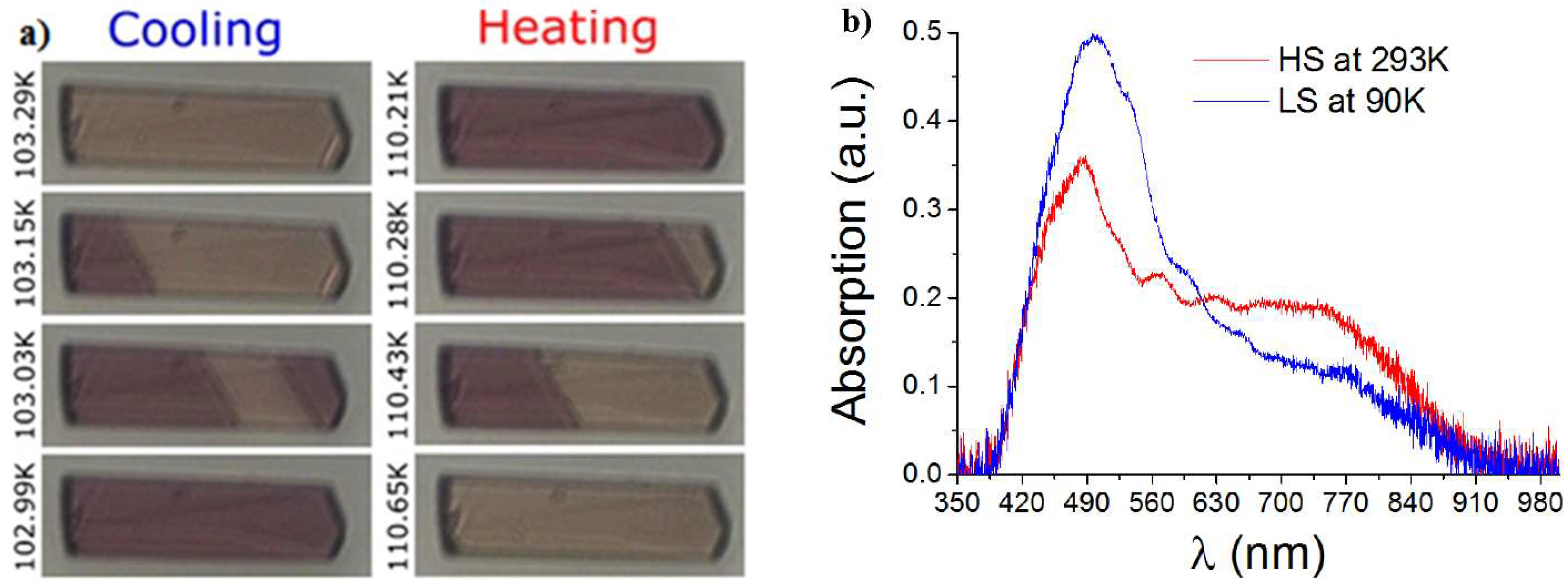
2.2. Optical Microscopy Thermal Hysteresis and Photo-Heating Effects
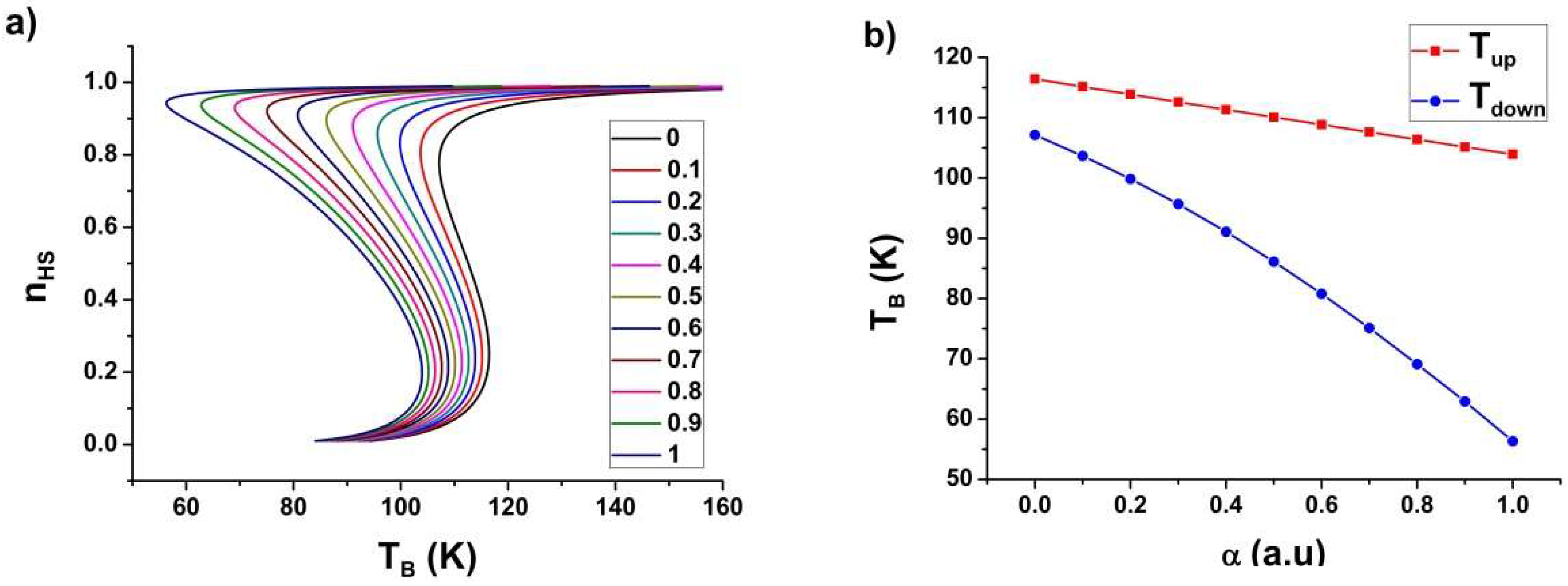
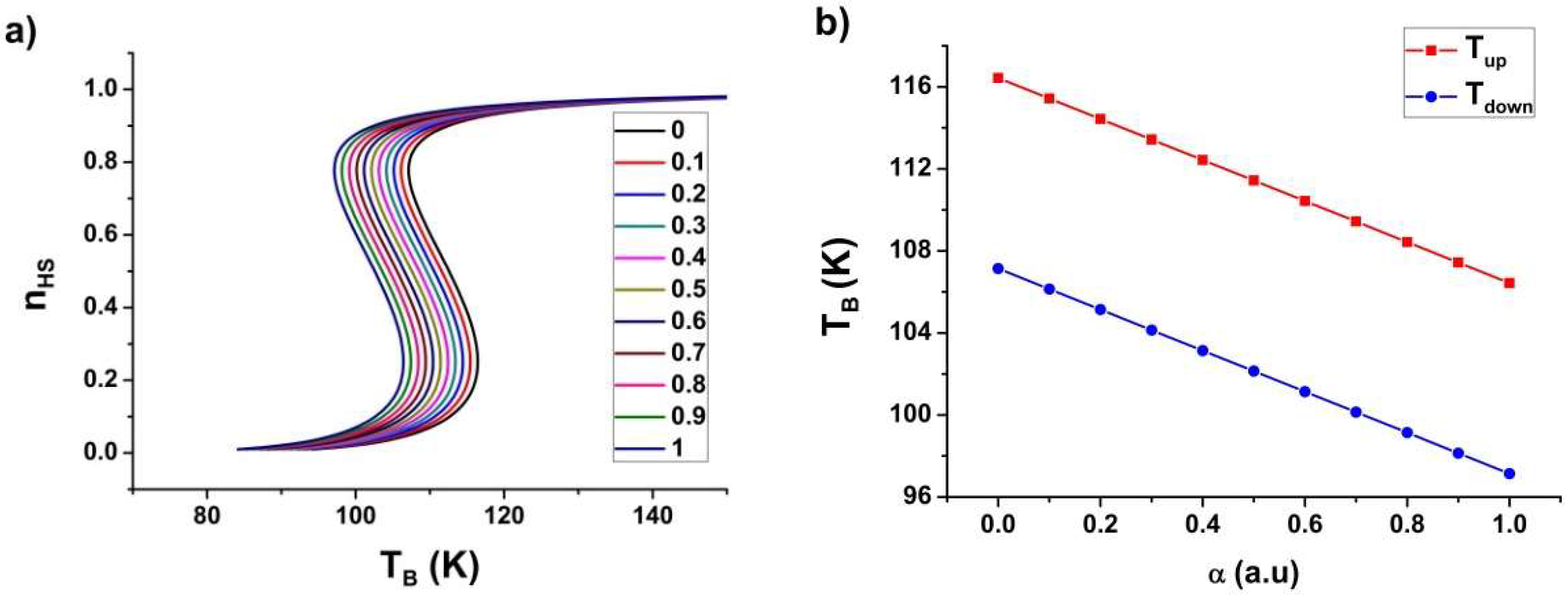
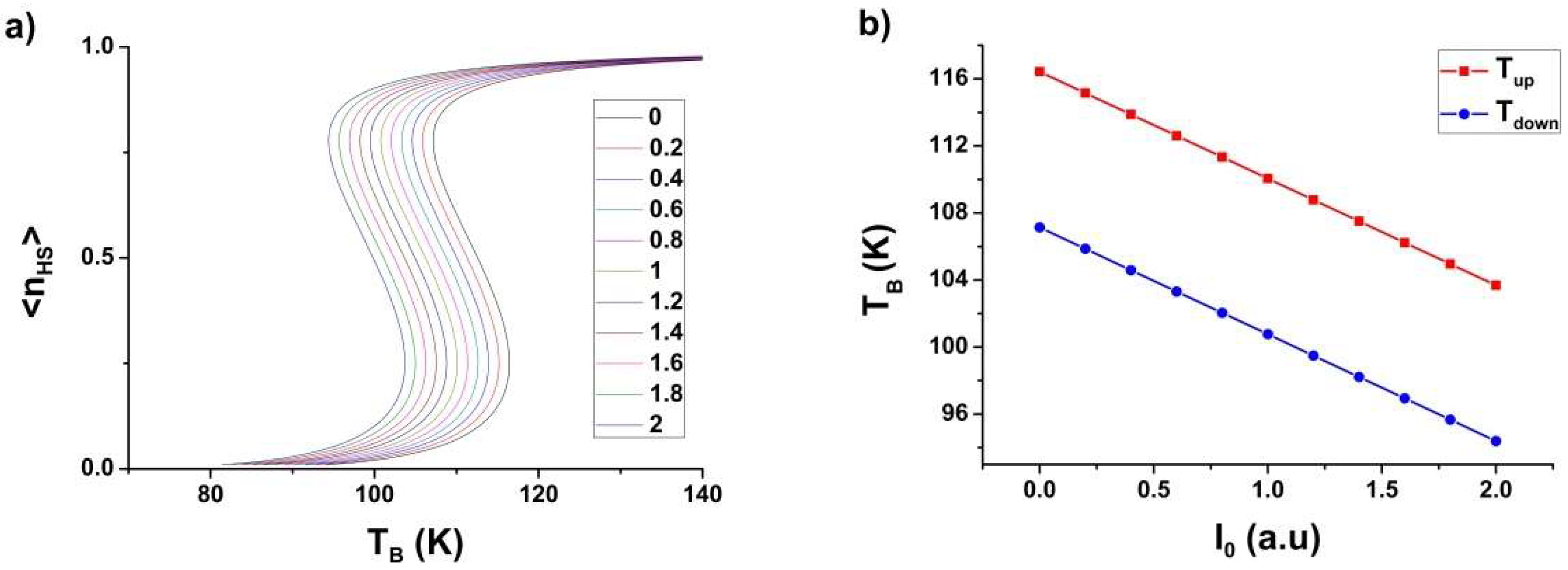
3. Theory of the Photo-Heating Effects
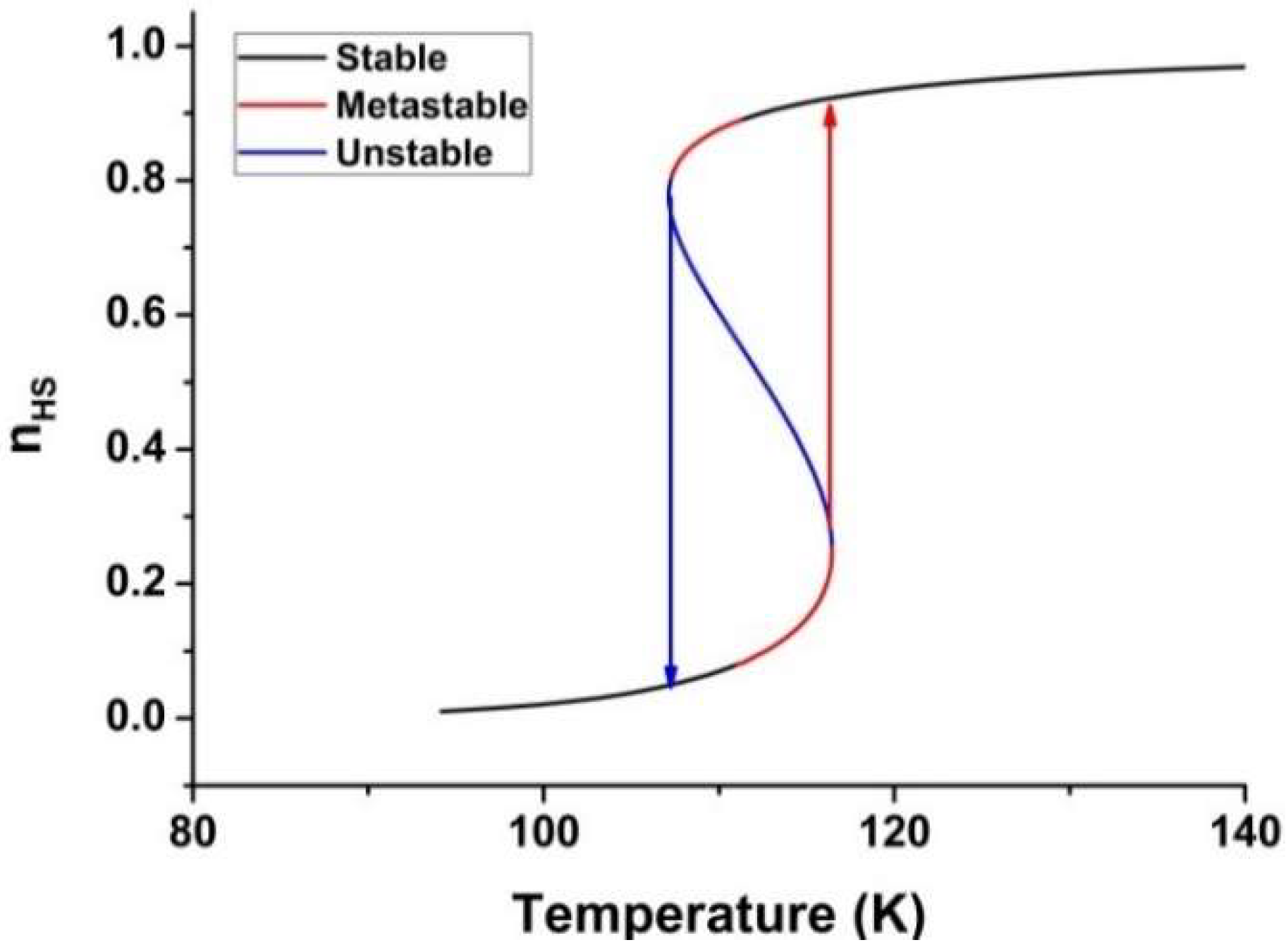
3.1. The Thermally-Induced Spin Transition
3.2. Light-Induced Photo-Heating Effect
3.3. Effect of Light Absorption
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| SCO | Spin Crossover |
| HS | High-Spin |
| LS | Low-Spin |
| LIESST | Light-Induced Excited Spin-State Trapping |
| LITH | Light-Induced Thermal Hysteresis |
| OM | Optical Microscopy |
References
- Gütlich, P.; Hauser, A. Thermal and light-induced spin crossover in iron(II) complexes. Coord. Chem. Rev. 1990, 97, 1–22. [Google Scholar] [CrossRef]
- Sorai, M.; Seki, S. Magnetic Heat Capacity Due to Cooperative Low-Spin 1A 1 ⇌ High-Spin 5T2 Transition in Fe(phen)2(NCS)2 Crystal. J. Phys. Soc. Japan 1972, 33, 575. [Google Scholar] [CrossRef]
- Halcrow, M.A. Spin-Crossover Materials: Properties and Applications; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2013. [Google Scholar]
- Quintero, C.M.; Felix, G.; Suleimanov, I.; Sanchez Costa, J.; Molnar, G.; Salmon, L.; Nicolazzi, W.; Bousseksou, A. Hybrid spin-crossover nanostructures. Beilstein J. Nanotechnol. 2014, 5, 2230–2239. [Google Scholar] [CrossRef]
- Peng, H.; Tricard, S.; Felix, G.; Molnar, G.; Nicolazzi, W.; Salmon, L.; Bousseksou, A. Re-Appearance of Cooperativity in Ultra-Small Spin-Crossover [Fe(pz){Ni(CN)}] Nanoparticles. Angew. Chem. Int. Ed. Engl. 2014. [Google Scholar] [CrossRef]
- Jureschi, C.M.; Linares, J.; Rotaru, A.; Ritti, M.H.; Parlier, M.; Dîrtu, M.M.; Wolff, M.; Garcia, Y. Pressure sensor via optical detection based on a 1D spin transition coordination polymer. Sensors 2015, 15, 2388–2398. [Google Scholar] [CrossRef]
- Boukheddaden, K.; Ritti, M.H.; Bouchez, G.; Sy, M.; Dîrtu, M.M.; Parlier, M.; Linares, J.; Garcia, Y. Quantitative Contact Pressure Sensor Based on Spin Crossover Mechanism for Civil Security Applications. J. Phys. Chem. C 2018, 122, 7597–7604. [Google Scholar] [CrossRef]
- Decurtins, S.; Gütlich, P.; Hasselbach, K.M.; Hauser, A.; Spiering, H. Light-induced excited-spin-state trapping in iron(II) spin-crossover systems. Optical spectroscopic and magnetic susceptibility study. Inorgan. Chem. 1985, 24, 2174–2178. [Google Scholar] [CrossRef]
- Hauser, A. Reversibility of light-induced excited spin state trapping in the Fe(ptz)6(BF4)2, and the Zn1−xFex(ptz)6(BF4)2 spin-crossover systems. Chem. Phys. Lett. 1986, 124, 543–548. [Google Scholar] [CrossRef]
- Hauser, A.; Adler, J.; Gütlich, P. Light-induced excited spin state trapping (LIESST) in [Fe(2-mephen)3]2+ embedded in polymer matrices. Chem. Phys. Lett. 1988, 152, 468–472. [Google Scholar] [CrossRef]
- Desaix, A.; Roubeau, O.; Jeftic, J.; Haasnoot, J.G.; Boukheddaden, K.; Codjovi, E.; Linarès, J.; Noguès, M.; Varret, F. Light-induced bistability in spin transition solids leading to thermal and optical hysteresis. Eur. Phys. J. B 1998, 6, 183–193. [Google Scholar] [CrossRef]
- Gütlich, P.; Garcia, Y.; Goodwin, H.A. Spin crossover phenomena in Fe(ii) complexes. Chem. Soc. Rev. 2000, 29, 419–427. [Google Scholar] [CrossRef]
- Varret, F.; Boukheddaden, K.; Codjovi, E.; Enachescu, C.; Linarès, J. On the Competition Between Relaxation and Photoexcitations in Spin Crossover Solids under Continuous Irradiation. In Spin Crossover in Transition Metal Compounds II; Springer: Berlin/Heidelberg, Germany, 2004; Volume 234, pp. 199–229. [Google Scholar]
- Hauser, A. Light-Induced Spin Crossover and the High-Spin→Low-Spin Relaxation. In Spin Crossover in Transition Metal Compounds; Chem, T.C., Ed.; Springer: New York, NY, USA, 2004; Volume 234, pp. 155–198. [Google Scholar]
- Varret, F.; Boukheddaden, K.; Codjovi, E.; Maurin, I.; Tokoro, H.; Ohkoshi, S.; Hashimoto, K. Light-induced thermal hysteresis and intensity thresholds in molecular switcheable solids, by mean-field macroscopic master equation approach: Discussion of the experimental data obtained for Co–Fe Prussian Blue Analogues. Polyhedron 2005, 24, 2857–2863. [Google Scholar] [CrossRef]
- Boukheddaden, K.; Sy, M. Direct Optical Microscopy Observation of Photo-Induced Effects and Thermal Relaxation in a Spin Crossover Single Crystal. Curr. Inorg. Chem. 2016, 6, 40–48. [Google Scholar] [CrossRef]
- Bousseksou, A.; Negre, N.; Goiran, M.; Salmon, L.; Tuchagues, J.P.; Boillot, M.L.; Boukheddaden, K.; Varret, F. Dynamic triggering of a spin-transition by a pulsed magnetic field. Eur. Phys. J. B 2000, 13, 451–456. [Google Scholar]
- Ould Moussa, N.; Ostrovskii, D.; Garcia, V.M.; Molnár, G.; Tanaka, K.; Gaspar, A.B.; Real, J.A.; Bousseksou, A. Bidirectional photo-switching of the spin state of iron(II) ions in a triazol based spin crossover complex within the thermal hysteresis loop. Chem. Phys. Lett. 2009, 477, 156–159. [Google Scholar] [CrossRef]
- Mahfoud, T.; Molnar, G.; Bonhommeau, S.; Cobo, S.; Salmon, L.; Demont, P.; Tokoro, H.; Ohkoshi, S.; Boukheddaden, K.; Bousseksou, A. Electric-field-induced charge-transfer phase transition: A promising approach toward electrically switchable devices. J. Am. Chem. Soc. 2009, 131, 15049–15054. [Google Scholar] [CrossRef]
- Rotaru, A.; Dugay, J.; Tan, R.P.; Guralskiy, I.A.; Salmon, L.; Demont, P.; Carrey, J.; Molnar, G.; Respaud, M.; Bousseksou, A. Nano-electromanipulation of spin crossover nanorods: Towards switchable nanoelectronic devices. Adv. Mater. 2013, 25, 1745–1749. [Google Scholar] [CrossRef]
- Prins, F.; Monrabal-Capilla, M.; Osorio, E.A.; Coronado, E.; van der Zant, H.S. Room-temperature electrical addressing of a bistable spin-crossover molecular system. Adv. Mater. 2011, 23, 1545–1549. [Google Scholar] [CrossRef]
- Cavallini, M. Status and perspectives in thin films and patterning of spin crossover compounds. Phys. Chem. Chem. Phys. 2012, 14, 11867–11876. [Google Scholar] [CrossRef] [PubMed]
- Shepherd, H.J.; Molnár, G.; Nicolazzi, W.; Salmon, L.; Bousseksou, A. Spin Crossover at the Nanometre Scale. Eur. J. Inorg. Chem. 2013, 2013, 653–661. [Google Scholar] [CrossRef]
- Cavallini, M.; Bergenti, I.; Milita, S.; Kengne, J.C.; Gentili, D.; Ruani, G.; Salitros, I.; Meded, V.; Ruben, M. Thin deposits and patterning of room-temperature-switchable one-dimensional spin-crossover compounds. Langmuir 2011, 27, 4076–4081. [Google Scholar] [CrossRef]
- Naik, A.D.; Stappers, L.; Snauwaert, J.; Fransaer, J.; Garcia, Y. A biomembrane stencil for crystal growth and soft lithography of a thermochromic molecular sensor. Small 2010, 6, 2842–2846. [Google Scholar] [CrossRef] [PubMed]
- Basak, S.; Hui, P.; Chandrasekar, R. Flexible and Optically Transparent Polymer Embedded Nano/Micro Scale Spin Crossover Fe(II) Complex Patterns/Arrays. Chem. Mater. 2013, 25, 3408–3413. [Google Scholar] [CrossRef]
- Gütlich, P.G. Spin Crossover in Transition Metal Compounds I–III, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Linares, J.; Codjovi, E.; Garcia, Y. Pressure and Temperature Spin Crossover Sensors with Optical Detection. Sensors 2012, 12, 4479–4492. [Google Scholar] [CrossRef] [PubMed]
- Bousseksou, A.; Molnar, G.; Salmon, L.; Nicolazzi, W. Molecular spin crossover phenomenon: Recent achievements and prospects. Chem. Soc. Rev. 2011, 40, 3313–3335. [Google Scholar] [CrossRef]
- Gütlich, P.; Gaspar, A.B.; Garcia, Y. Spin state switching in iron coordination compounds. Beilstein J. Organ. Chem. 2013, 9, 342–391. [Google Scholar] [CrossRef] [PubMed]
- Cavallini, M.; Melucci, M. Organic Materials for Time–Temperature Integrator Devices. ACS Appl. Mater. Interfaces 2015, 7, 16897–16906. [Google Scholar] [CrossRef] [PubMed]
- Gentili, D.; Demitri, N.; Schäfer, B.; Liscio, F.; Bergenti, I.; Ruani, G.; Ruben, M.; Cavallini, M. Multi-modal sensing in spin crossover compounds. J. Mater. Chem. C 2015, 3, 7836–7844. [Google Scholar] [CrossRef]
- Naik, A.D.; Robeyns, K.; Meunier, C.F.; Léonard, A.F.; Rotaru, A.; Tinant, B.; Filinchuk, Y.; Su, B.L.; Garcia, Y. Selective and Reusable Iron(II)-Based Molecular Sensor for the Vapor-Phase Detection of Alcohols. Inorg. Chem. 2014, 53, 1263–1265. [Google Scholar] [CrossRef]
- Shepherd, H.J.; Gural’skiy, I.A.; Quintero, C.M.; Tricard, S.; Salmon, L.; Molnar, G.; Bousseksou, A. Molecular actuators driven by cooperative spin-state switching. Nat. Commun. 2013, 4, 2607. [Google Scholar] [CrossRef]
- Sy, M.; Garrot, D.; Slimani, A.; Paez-Espejo, M.; Varret, F.; Boukheddaden, K. Reversible Control by Light of the High-Spin Low-Spin Elastic Interface inside the Bistable Region of a Robust Spin-Transition Single Crystal. Angew. Chem. Int. Ed. 2016, 55, 1755–1759. [Google Scholar] [CrossRef] [PubMed]
- Paez-Espejo, M.; Sy, M.; Boukheddaden, K. Unprecedented Bistability in Spin-Crossover Solids Based on the Retroaction of the High Spin Low-Spin Interface with the Crystal Bending. J. Am. Chem. Soc. 2018, 140, 11954–11964. [Google Scholar] [CrossRef] [PubMed]
- Pronschinske, A.; Bruce, R.C.; Lewis, G.; Chen, Y.; Calzolari, A.; Buongiorno-nardelli, M.; Shultz, D.A.; You, W.; Dougherty, D.B. Iron(ii) spin crossover films on Au(111): Scanning probe microscopy and photoelectron spectroscopy. Chem. Commun. 2013, 49, 10446–10452. [Google Scholar] [CrossRef]
- Bi, H.; Yin, K.; Xie, X.; Zhou, Y.; Wan, S.; Banhart, F.; Sun, L. Microscopic bimetallic actuator based on a bilayer of graphene and graphene oxide. Nanoscale 2013, 5, 9123–9128. [Google Scholar] [CrossRef]
- Bartual-Murgui, C.; Salmon, L.; Akou, A.; Thibault, C.; Molnar, G.; Mahfoud, T.; Sekkat, Z.; Real, J.A.; Bousseksou, A. High quality nano-patterned thin films of the coordination compound {Fe(pyrazine)[Pt(CN)4]} deposited layer-by-layer. New J. Chem. 2011, 35, 2089–2094. [Google Scholar] [CrossRef]
- Cobo, S.; Molnar, G.; Carcenac, F.; Szilagyi, P.A.; Salmon, L.; Vieu, C.; Bousseksou, A. Thin films of Prussian blue: Sequential assembly, patterning and electron transport properties at the nanometric scale. J. Nanosci. Nanotechnol. 2010, 10, 5042–5050. [Google Scholar] [CrossRef]
- Volatron, F.; Catala, L.; Rivière, E.; Gloter, A.; Stéphan, O.; Mallah, T. Spin-crossover coordination nanoparticles. Inorg. Chem. 2008, 47, 6584–6586. [Google Scholar] [CrossRef] [PubMed]
- Moulet, L.; Daro, N.; Etrillard, C.; Létard, J.-F.; Grosjean, A.; Guionneau, P. Rational Control of Spin-Crossover Particle Sizes: From Nano- to Micro-Rods of [Fe(Htrz)2(trz)](BF4). Magnetochemistry 2016, 2, 10. [Google Scholar] [CrossRef]
- Salmon, L.; Catala, L. Spin-crossover nanoparticles and nanocomposite materials. C. R. Chim. 2018, 21, 1230–1269. [Google Scholar] [CrossRef]
- Pillet, S.; Hubsch, J.; Lecomte, C. Single crystal diffraction analysis of the thermal spin conversion in [Fe(btr)2(NCS)2](H2O): Evidence for spin-like domain formation. Eur. Phys. J. B 2004, 38, 541–552. [Google Scholar] [CrossRef]
- Legrand, V.; Pillet, S.; Carbonera, C.; Souhassou, M.; Letard, J.F.; Guionneau, P.; Lecomte, C. Optical, Magnetic and Structural Properties of the Spin-Crossover Complex [Fe(btr)2(NCS)2]·H2O in the Light-Induced and Thermally Quenched Metastable States. Eur. J. Inorg. Chem. 2007, 2007, 5693–5706. [Google Scholar] [CrossRef]
- Slimani, A.; Varret, F.; Boukheddaden, K.; Chong, C.; Mishra, H.; Haasnoot, J.; Pillet, S. Visualization and quantitative analysis of spatiotemporal behavior in a first-order thermal spin transition: A stress-driven multiscale process. Phys. Rev. B 2011, 84, 094442. [Google Scholar] [CrossRef]
- Chong, C.; Slimani, A.; Varret, F.; Boukheddaden, K.; Collet, E.; Ameline, J.C.; Bronisz, R.; Hauser, A. The kinetics features of a thermal spin transition characterized by optical microscopy on the example of [Fe(bbtr)3](ClO4)2 single crystals: Size effect and mechanical instability. Chem. Phys. Lett. 2011, 504, 29–33. [Google Scholar] [CrossRef]
- Slimani, A.; Varret, F.; Boukheddaden, K.; Garrot, D.; Oubouchou, H.; Kaizaki, S. Velocity of the high-spin low-spin interface inside the thermal hysteresis loop of a spin-crossover crystal, via photothermal control of the interface motion. Phys. Rev. Lett. 2013, 110, 087208–087213. [Google Scholar] [CrossRef] [PubMed]
- Sy, M.; Varret, F.; Boukheddaden, K.; Bouchez, G.; Marrot, J.; Kawata, S.; Kaizaki, S. Structure-driven orientation of the high-spin-low-spin interface in a spin-crossover single crystal. Angew. Chem. Int. Ed. 2014, 53, 7539–7542. [Google Scholar] [CrossRef] [PubMed]
- Fourati, H.; Milin, E.; Slimani, A.; Chastanet, G.; Abid, Y.; Triki, S.; Boukheddaden, K. Interplay between a crystal’s shape and spatiotemporal dynamics in a spin transition material. Phys. Chem. Chem. Phys. 2018, 20, 10142–10154. [Google Scholar] [CrossRef] [PubMed]
- Varret, F.; Slimani, A.; Boukheddaden, K.; Chong, C.; Mishra, H.; Collet, E.; Haasnoot, J.; Pillet, S. The propagation of the thermal spin transition of [Fe(btr)2(NCS)2][middle dot]H2O single crystals, observed by optical microscopy. New J. Chem. 2011, 35, 2333–2340. [Google Scholar] [CrossRef]
- Fourati, H.; Bouchez, G.; Paez-Espejo, M.; Triki, S.; Boukheddaden, K. Spatio-temporal Investigations of the Incomplete Spin Transition in a Single Crystal of [Fe(2-pytrz)2{Pt(CN)4}]·3H2O: Experiment and Theory. Crystals 2019, 9, 46. [Google Scholar] [CrossRef]
- Sy, M.; Traiche, R.; Fourati, H.; Singh, Y.; Varret, F.; Boukheddaden, K. Spatiotemporal Investigations on Light-Driven High-Spin–Low-Spin Interface Dynamics in the Thermal Hysteresis Region of a Spin-Crossover Single Crystal. J. Phys. Chem. C 2018, 122, 20952–20962. [Google Scholar] [CrossRef]
- Renz, F.; Spiering, H.; Goodwin, H.A.; Gütlich, P. Light-perturbed hysteresis in an iron(II) spin-crossover compound observed by the Mössbauer effect. Hyperfine Interact. 2000, 126, 155–158. [Google Scholar] [CrossRef]
- Gütlich, P.; Hauser, A.; Spiering, H. Thermal and Optical Switching of Iron(II) Complexes. Angewandte Chem. Int. 1994, 33, 2024–2054. [Google Scholar] [CrossRef]
- Letard, J.F.; Guionneau, P.; Rabardel, L.; Howard, J.A.; Goeta, A.E.; Chasseau, D.; Kahn, O. Structural, Magnetic, and Photomagnetic Studies of a Mononuclear Iron(II) Derivative Exhibiting an Exceptionally Abrupt Spin Transition. Light-Induced Thermal Hysteresis Phenomenon. Inorg. Chem. 1998, 37, 4432–4441. [Google Scholar] [CrossRef]
- Bertoni, R.; Cammarata, M.; Lorenc, M.; Matar, S.F.; Létard, J.-F.; Lemke, H.T.; Collet, E. Ultrafast Light-Induced Spin-State Trapping Photophysics Investigated in Fe(phen)2(NCS)2 Spin-Crossover Crystal. Acc. Chem. Res. 2015, 48, 774–781. [Google Scholar] [CrossRef] [PubMed]
- Cannizzo, A.; Milne, C.J.; Consani, C.; Gawelda, W.; Bressler, C.; van Mourik, F.; Chergui, M. Light-induced spin crossover in Fe(II)-based complexes: The full photocycle unraveled by ultrafast optical and X-ray spectroscopies. Coord. Chem. Rev. 2010, 254, 2677–2686. [Google Scholar] [CrossRef]
- Cook, T.; McDougall, I.; Proctor, W.; Winson, P.H. Cryogenics at Oxford Instruments. Cryogenics 1981, 21, 259–266. [Google Scholar] [CrossRef]
- Chong, C.; Mishra, H.; Boukheddaden, K.; Denise, S.; Bouchez, G.; Collet, E.; Ameline, J.-C.; Naik, A.D.; Garcia, Y.; Varret, F. Electronic and Structural Aspects of Spin Transitions Observed by Optical Microscopy. The Case of [Fe(ptz)6](BF4)2. J. Phys. Chem. B 2010, 114, 1975–1984. [Google Scholar] [CrossRef]
- Nakano, K.; Suemura, N.; Kawata, S.; Fuyuhiro, A.; Yagi, T.; Nasu, S.; Morimoto, S.; Kaizaki, S. Magnetic behavior and Mossbauer spectra of spin-crossover pyrazolate bridged dinuclear diiron(II) complexes: X-ray structures of high-spin and low-spin [(Fe(NCBH3)(py))2(mu-bpypz)2]. Dalton Trans. 2004, 982–988. [Google Scholar] [CrossRef] [PubMed]
- Létard, J.F.; Real, J.A.; Moliner, N.; Gaspar, A.B.; Capes, L.; Cador, O.; Kahn, O.J. Am. Light Induced Excited Pair Spin State in an Iron(II) Binuclear Spin-Crossover Compound. Am. Chem. Soc. 1999, 121, 10630–10631. [Google Scholar] [CrossRef]
- Letard, J.F.; Carbonera, C.; Real, J.A.; Kawata, S.; Kaizaki, S. Photomagnetism of a series of dinuclear Iron(II) complexes. Chemistry 2009, 15, 4146–4155. [Google Scholar] [CrossRef]
- Chastanet, G.; Carbonera, C.; Mingotaud, C.; Létard, J.F.J. Atypical photomagnetic properties in a series of binuclear iron(II) spin crossover complexes. J. Mater. Chem. 2004, 14, 3516–3523. [Google Scholar] [CrossRef]
- Chastanet, G.; Desplanches, C.; Baldé, C.; Rosa, P.; Marchivie, M.; Guionneau, P. A critical review of the T(LIESST) temperature in spin crossover materials—What it is and what it is not. Chem. Squared Chem. 2018, 2, 2. [Google Scholar] [CrossRef]
- Boukheddaden, K.; Nishino, M.; Miyashita, S. Molecular dynamics and transfer integral investigations of an elastic anharmonic model for phonon-induced spin crossover. Phys. Rev. Lett. 2008, 100, 177206–177209. [Google Scholar] [CrossRef] [PubMed]
- Boukheddaden, K.; Miyashita, S.; Nishino, M. Elastic interaction among transition metals in one-dimensional spin-crossover solids. Phys. Rev. B 2007, 75, 094112–094122. [Google Scholar] [CrossRef]
- Konishi, Y.; Tokoro, H.; Nishino, M.; Miyashita, S. Monte Carlo simulation of pressure-induced phase transitions in spin-crossover materials. Phys. Rev. Lett. 2008, 100, 067206–067209. [Google Scholar] [CrossRef] [PubMed]
- Nishino, M.; Enachescu, C.; Miyashita, S.; Rikvold, P.A.; Boukheddaden, K.; Varret, F. Macroscopic nucleation phenomena in continuum media with long-range interactions. Sci. Rep. 2011, 1, 162. [Google Scholar] [CrossRef] [PubMed]
- Enachescu, C.; Nishino, M.; Miyashita, S.; Stoleriu, L.; Stancu, A. Monte Carlo Metropolis study of cluster evolution in spin-crossover solids within the framework of a mechanoelastic model. Phys. Rev. B 2012, 86, 054114–054120. [Google Scholar] [CrossRef]
- Slimani, A.; Boukheddaden, K.; Varret, F.; Nishino, M.; Miyashita, S. Properties of the low-spin high-spin interface during the relaxation of spin-crossover materials, investigated through an electro-elastic model. J. Chem. Phys. 2013, 139, 194706–194713. [Google Scholar] [CrossRef]
- Slimani, A.; Boukheddaden, K.; Varret, F.; Oubouchou, H.; Nishino, M.; Miyashita, S. Microscopic Spin-Distortion Model for Switchable Molecular Solids: Spatiotemporal Study of the Deformation Field and Local Stress at the Thermal Spin Transition. Phys. Rev. B Condens. Matter Mater. Phys. 2013, 87, 014111. [Google Scholar] [CrossRef]
- Spiering, H.; Boukheddaden, K.; Linares, J.; Varret, F. Total Free Energy of a Spin-Crossover Molecular System. Phys. Rev. B Condens. Matter Mater. Phys. 2004, 70, 184106. [Google Scholar] [CrossRef]
- Boukheddaden, K. Monte Carlo investigations on surface elastic energy of spin-crossover solids: Direct access to image pressure and the Eshelby constant. Phys. Rev. B 2013, 88, 134105. [Google Scholar] [CrossRef]
- Traiche, R.; Sy, M.; Oubouchou, H.; Bouchez, G.; Varret, F.; Boukheddaden, K. Spatiotemporal Observation and Modeling of Remarkable Temperature Scan Rate Effects on the Thermal Hysteresis in a Spin-Crossover Single Crystal. J. Phys. Chem. C 2017, 121, 11700–11708. [Google Scholar] [CrossRef]
- Gandolfi, C.; Morgan, G.G.; Albrecht, M. A magnetic iron(iii) switch with controlled and adjustable thermal response for solution processing. Dalton Trans. 2012, 41, 3726–3730. [Google Scholar] [CrossRef]
- Brooker, S. Spin crossover with thermal hysteresis: Practicalities and lessons learnt. Chem. Soc. Rev. 2015, 44, 2880–2892. [Google Scholar] [CrossRef] [PubMed]
- Létard, J.-F.; Chastanet, G.; Nguyen, O.; Marcén, S.; Marchivie, M.; Guionneau, P.; Chasseau, D.; Gütlich, P. Spin Crossover Properties of the [Fe(PM-BiA)2(NCS)2] Complex—Phases I and II. Monatsh. Chem. Chem. Mon. 2003, 134, 165–182. [Google Scholar] [CrossRef]
- Ichiyanagi, K.; Hebert, J.; Toupet, L.; Cailleau, H.; Guionneau, P.; Létard, J.F.; Collet, E. Nature and mechanism of the photoinduced spin transition in [Fe(PM−BiA)2(NCS)2]. Phys. Rev. B 2006, 73. [Google Scholar] [CrossRef]
- Boukheddaden, K.; Paez-Espejo, M.; Varret, F.; Sy, M. Autocatalytic spin-crossover transition: Nonlinear dynamics induced by a photothermal instability. Phys. Rev. B 2014, 89, 224303–224311. [Google Scholar] [CrossRef]
- Fouche, O.; Degert, J.; Jonusauskas, G.; Daro, N.; Letard, J.F.; Freysz, E. Mechanism for optical switching of the spin crossover [Fe(NH2-trz)3](Br)2·3H2O compound at room temperature. Phys. Chem. Chem. Phys. 2010, 12, 3044–3052. [Google Scholar] [CrossRef] [PubMed]
- Boukheddaden, K.; Shteto, I.; Hôo, B.; Varret, F. Dynamical model for spin-crossover solids. I. Relaxation effects in the mean-field approach. Phys. Rev. B 2000, 62, 14796–14805. [Google Scholar] [CrossRef]
- Paez-Espejo, M.; Sy, M.; Varret, F.; Boukheddaden, K. Quantitative macroscopic treatment of the spatiotemporal properties of spin crossover solids based on a reaction diffusion equation. Phys. Rev. B 2014, 89, 024306–024313. [Google Scholar] [CrossRef]
- Bousseksou, A.; Nasser, J.; Linares, J.; Boukheddaden, K.; Varret, F. Ising-like model for the two-step spin-crossover. J. Phys. I Fr. 1992, 2, 1381–1403. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boukheddaden, K.; Fourati, H.; Singh, Y.; Chastanet, G. Evidence of Photo-Thermal Effects on the First-Order Thermo-Induced Spin Transition of [{Fe(NCSe)(py)2}2(m-bpypz)] Spin-Crossover Material. Magnetochemistry 2019, 5, 21. https://doi.org/10.3390/magnetochemistry5020021
Boukheddaden K, Fourati H, Singh Y, Chastanet G. Evidence of Photo-Thermal Effects on the First-Order Thermo-Induced Spin Transition of [{Fe(NCSe)(py)2}2(m-bpypz)] Spin-Crossover Material. Magnetochemistry. 2019; 5(2):21. https://doi.org/10.3390/magnetochemistry5020021
Chicago/Turabian StyleBoukheddaden, Kamel, Houcem Fourati, Yogendra Singh, and Guillaume Chastanet. 2019. "Evidence of Photo-Thermal Effects on the First-Order Thermo-Induced Spin Transition of [{Fe(NCSe)(py)2}2(m-bpypz)] Spin-Crossover Material" Magnetochemistry 5, no. 2: 21. https://doi.org/10.3390/magnetochemistry5020021
APA StyleBoukheddaden, K., Fourati, H., Singh, Y., & Chastanet, G. (2019). Evidence of Photo-Thermal Effects on the First-Order Thermo-Induced Spin Transition of [{Fe(NCSe)(py)2}2(m-bpypz)] Spin-Crossover Material. Magnetochemistry, 5(2), 21. https://doi.org/10.3390/magnetochemistry5020021