Figure 1.
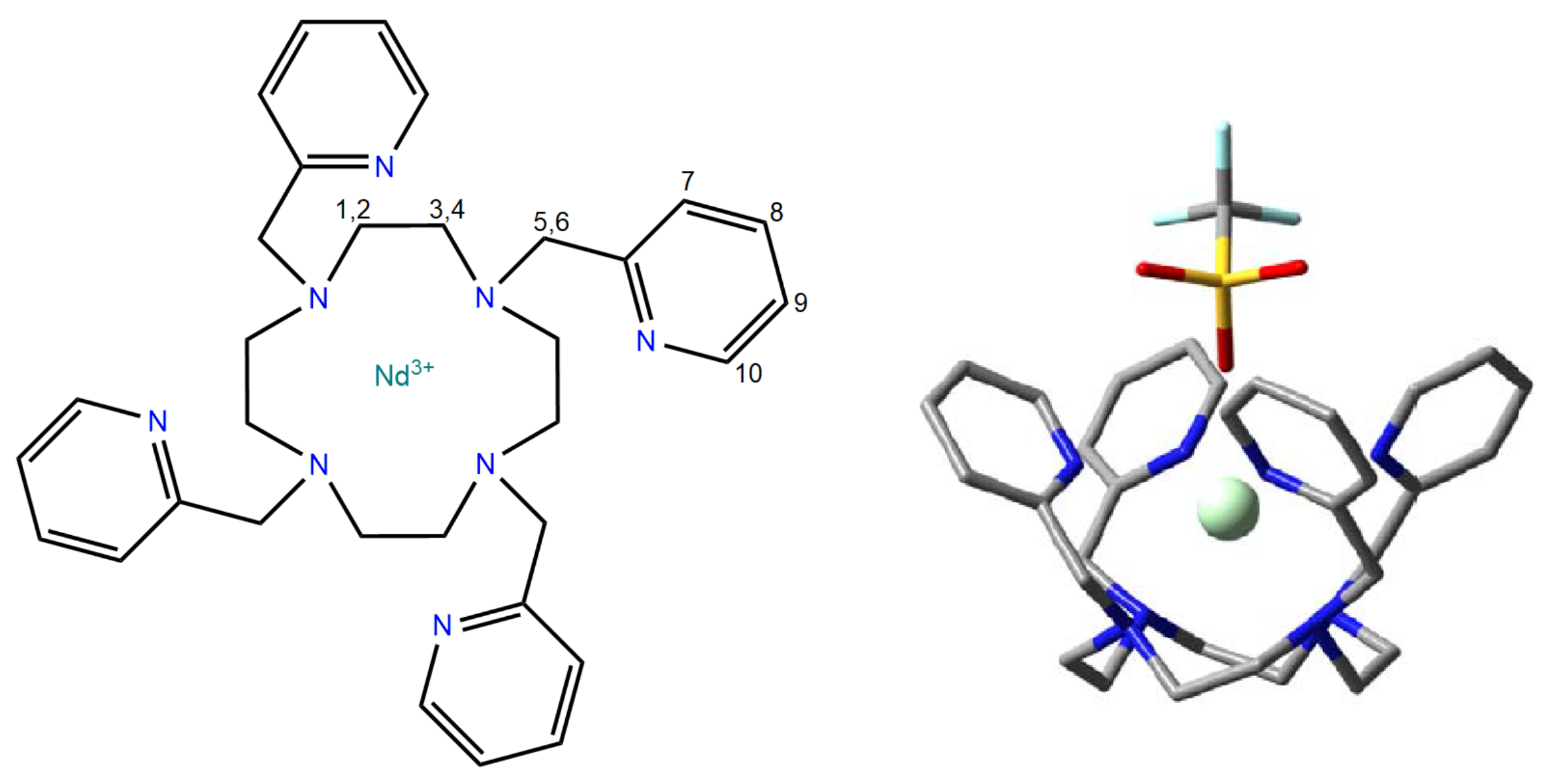
Structure of the cyclen complex [ NdL ]. Labels refer to the 10 chemically distinct H atoms, with 1,3,5 representing equatorial CH protons and 2,4,6 representing axial protons. Colours indicate atom type (grey C, blue N, red O, yellow S, light blue F).
Figure 1.
Structure of the cyclen complex [ NdL ]. Labels refer to the 10 chemically distinct H atoms, with 1,3,5 representing equatorial CH protons and 2,4,6 representing axial protons. Colours indicate atom type (grey C, blue N, red O, yellow S, light blue F).
Figure 2.
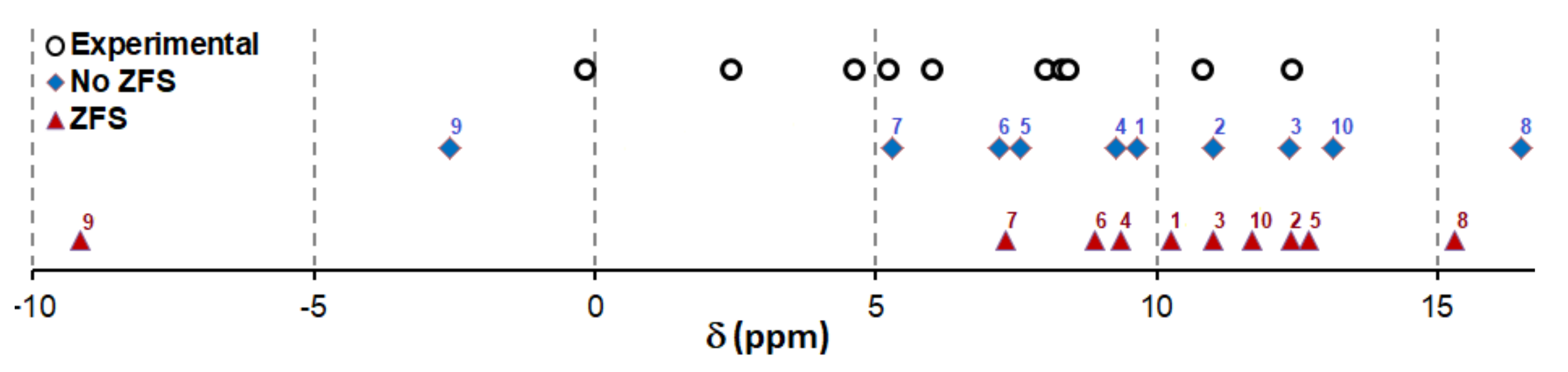
Experimental and computed pNMR spectra for [ NdL
]
with and without ZFS at 298.15K. For numbering of protons see
Figure 1.
Figure 2.
Experimental and computed pNMR spectra for [ NdL
]
with and without ZFS at 298.15K. For numbering of protons see
Figure 1.
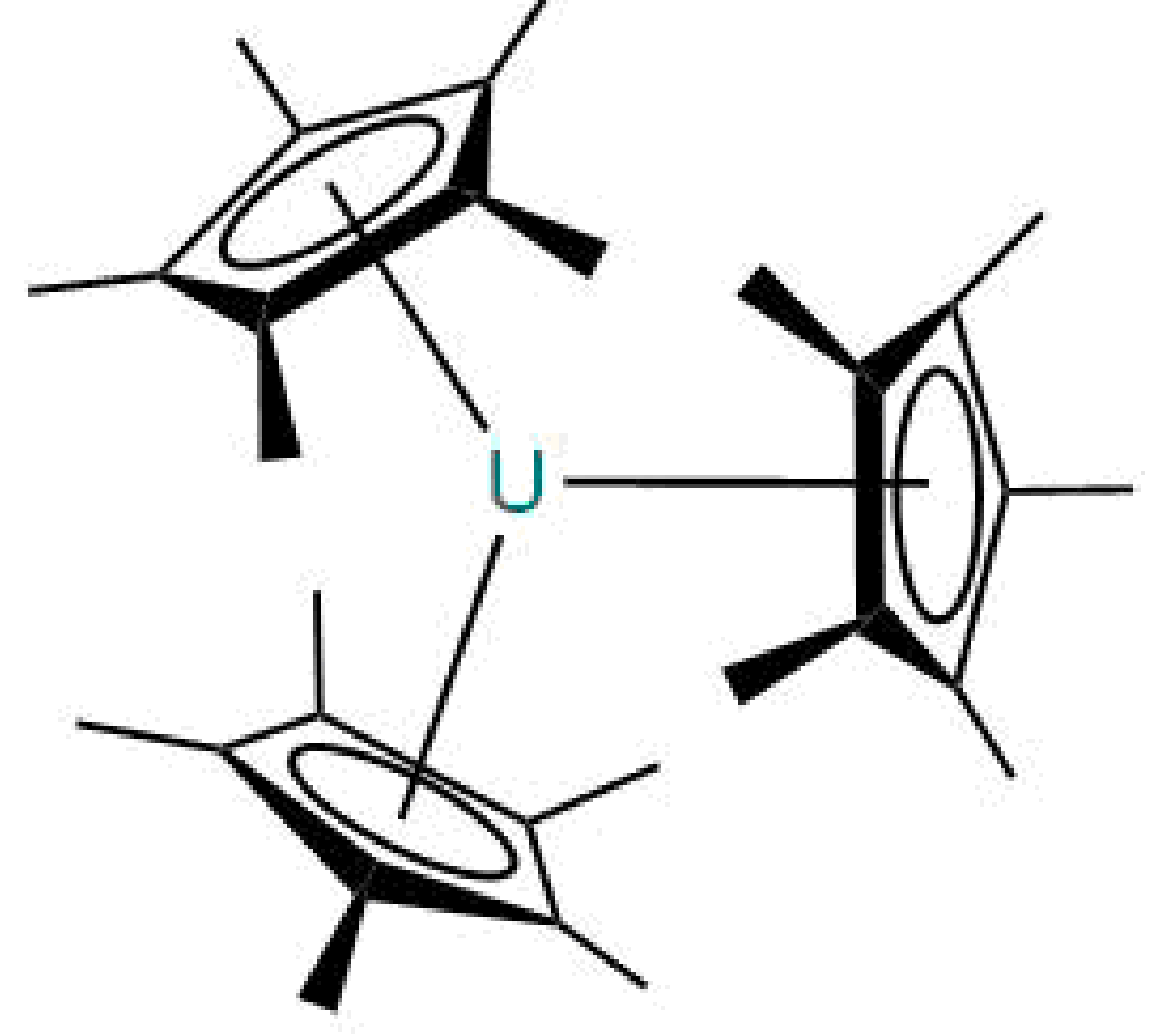
Figure 3.
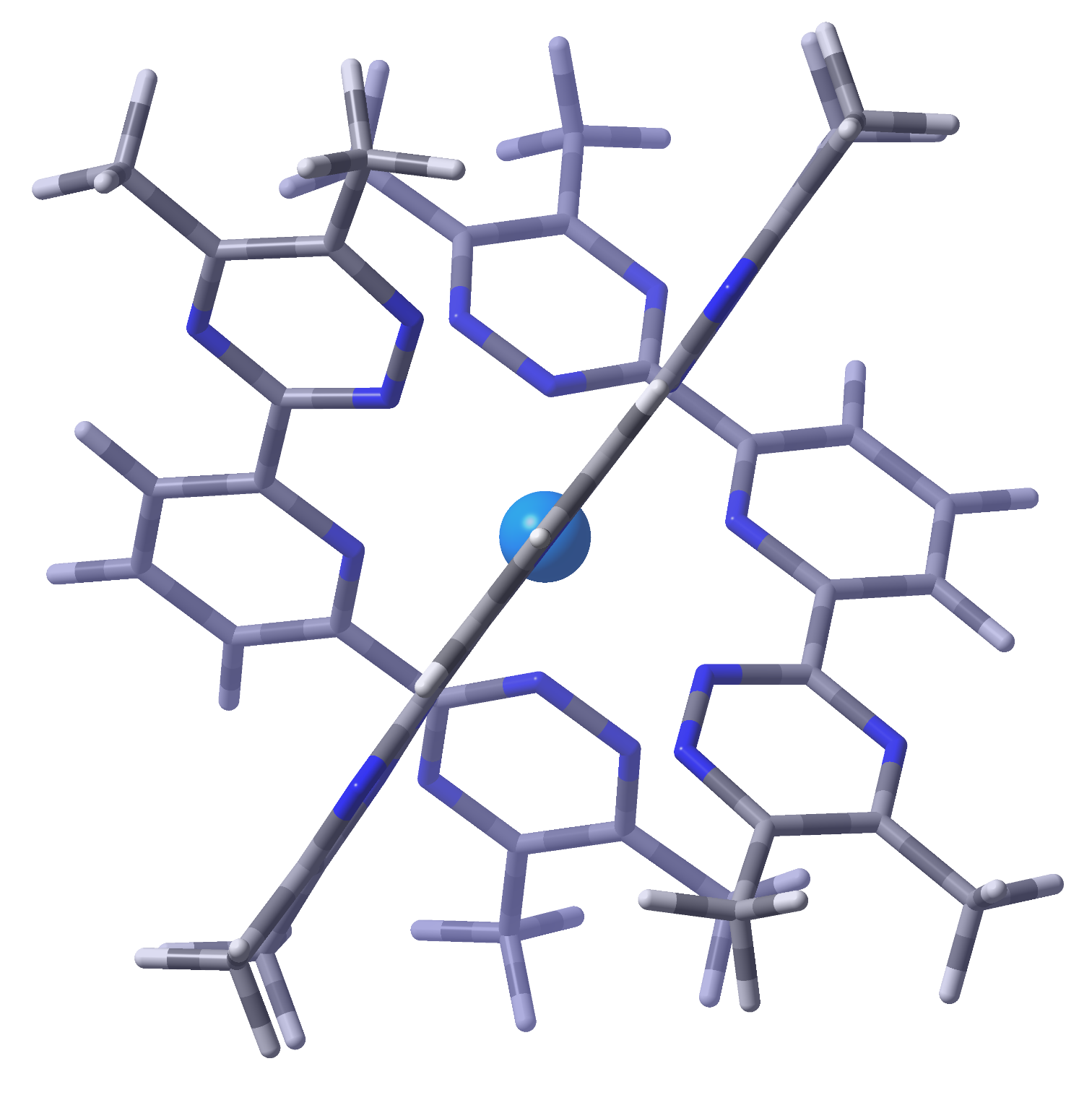
(a) The MeBTP ligand, labels identify the four types of chemically equivalent H, (b) The full structure of Tris(2,6-bis(5,6-dialkyl-1,2,4-triazin-3-yl)pyridine) uranium(III).
Figure 3.
(a) The MeBTP ligand, labels identify the four types of chemically equivalent H, (b) The full structure of Tris(2,6-bis(5,6-dialkyl-1,2,4-triazin-3-yl)pyridine) uranium(III).
Figure 4.
Stereochemistry of U(MeBTP), showing the three planar ligands, staggered with approximate 3-fold rotational symmetry.
Figure 4.
Stereochemistry of U(MeBTP), showing the three planar ligands, staggered with approximate 3-fold rotational symmetry.
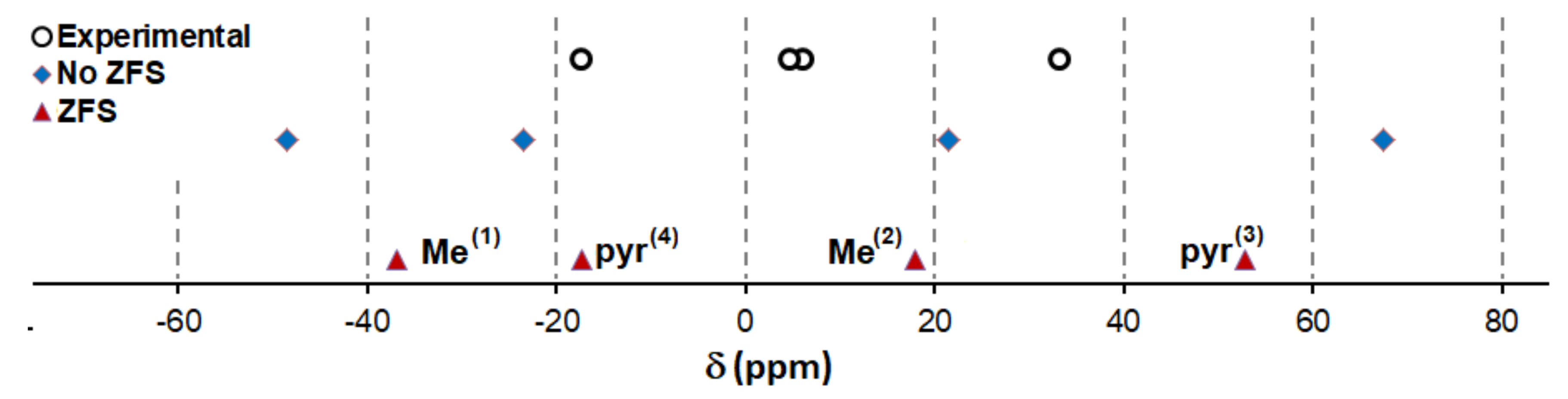
Figure 5.
Experimental and predicted pNMR shifts of U(MeBTP)
with and without ZFS at 303K. For numbering of protons see
Figure 3. The order is consistent in all cases.
Figure 5.
Experimental and predicted pNMR shifts of U(MeBTP)
with and without ZFS at 303K. For numbering of protons see
Figure 3. The order is consistent in all cases.
Figure 6.
The structure and stereochemistry of U(CMe).
Figure 6.
The structure and stereochemistry of U(CMe).
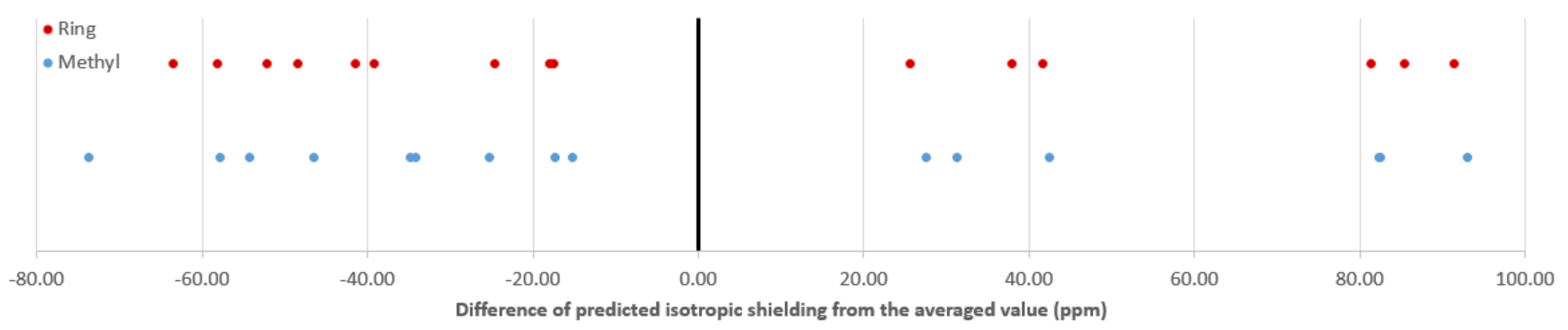
Figure 7.
Difference of the predicted isotropic shielding of individual C nuclei from the averaged value at 298 K.
Figure 7.
Difference of the predicted isotropic shielding of individual C nuclei from the averaged value at 298 K.
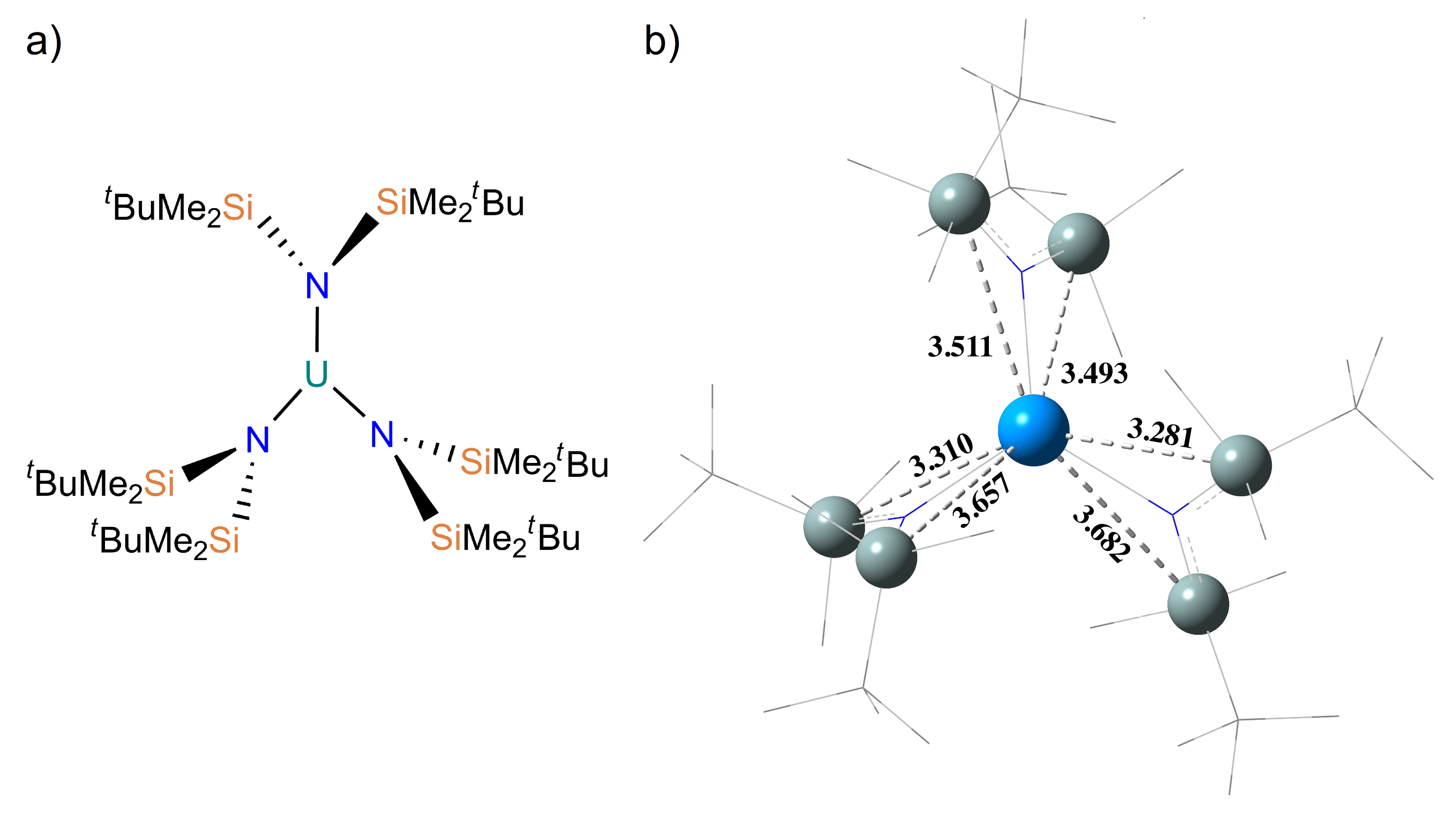
Figure 8.
(a) Chemical structure of U(N(SiMeBu)), (b) Stereochemistry of U(N(SiMeBu)) with uranium and silicon nuclei shown as spheres and the remaining non-hydrogen nuclei in wireframe. Stated distances are in Angstroms.
Figure 8.
(a) Chemical structure of U(N(SiMeBu)), (b) Stereochemistry of U(N(SiMeBu)) with uranium and silicon nuclei shown as spheres and the remaining non-hydrogen nuclei in wireframe. Stated distances are in Angstroms.
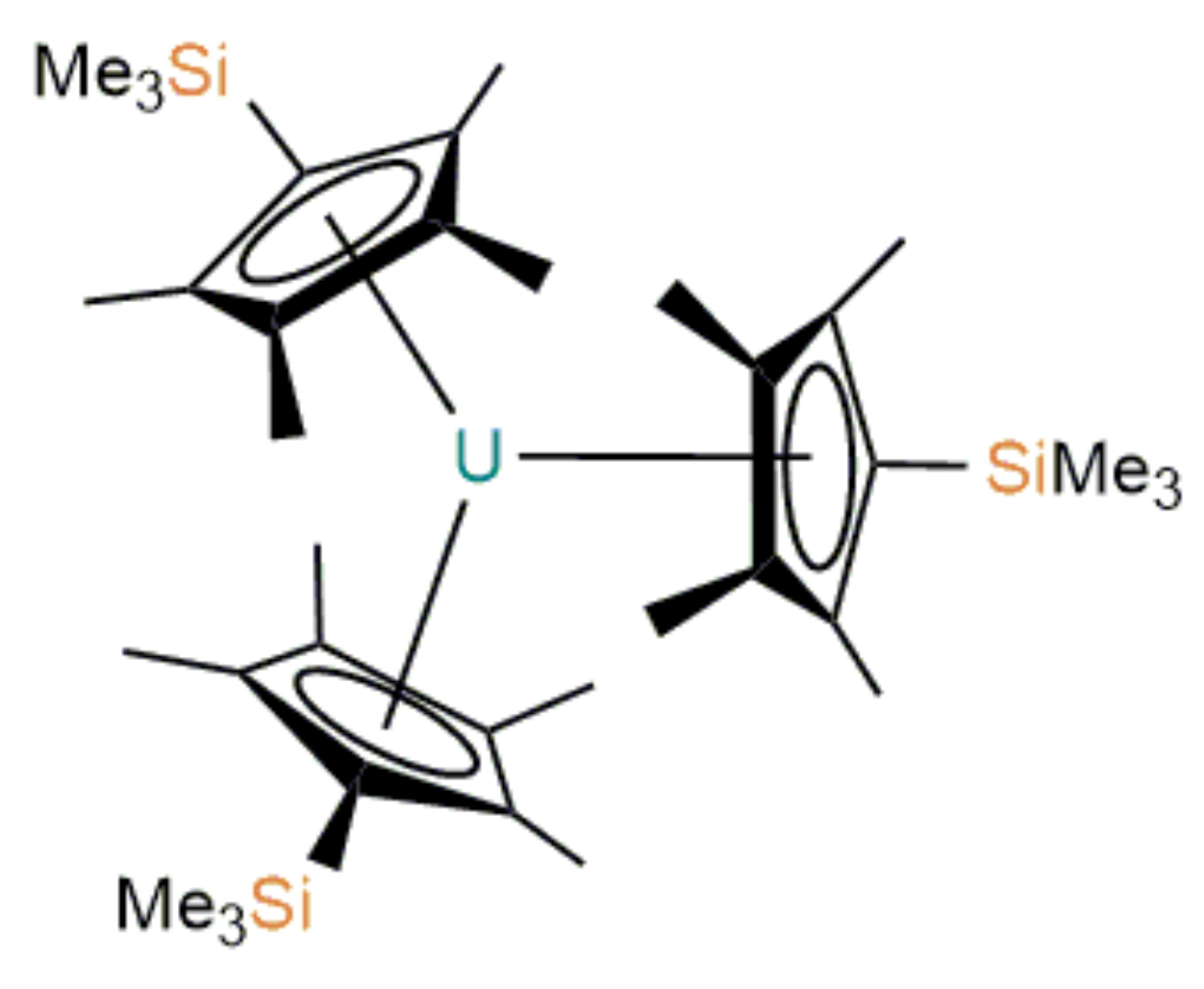
Figure 9.
Tris(trimethylsilylcyclopentadienyl)uranium(lll), U(CMeSiMe).
Figure 9.
Tris(trimethylsilylcyclopentadienyl)uranium(lll), U(CMeSiMe).
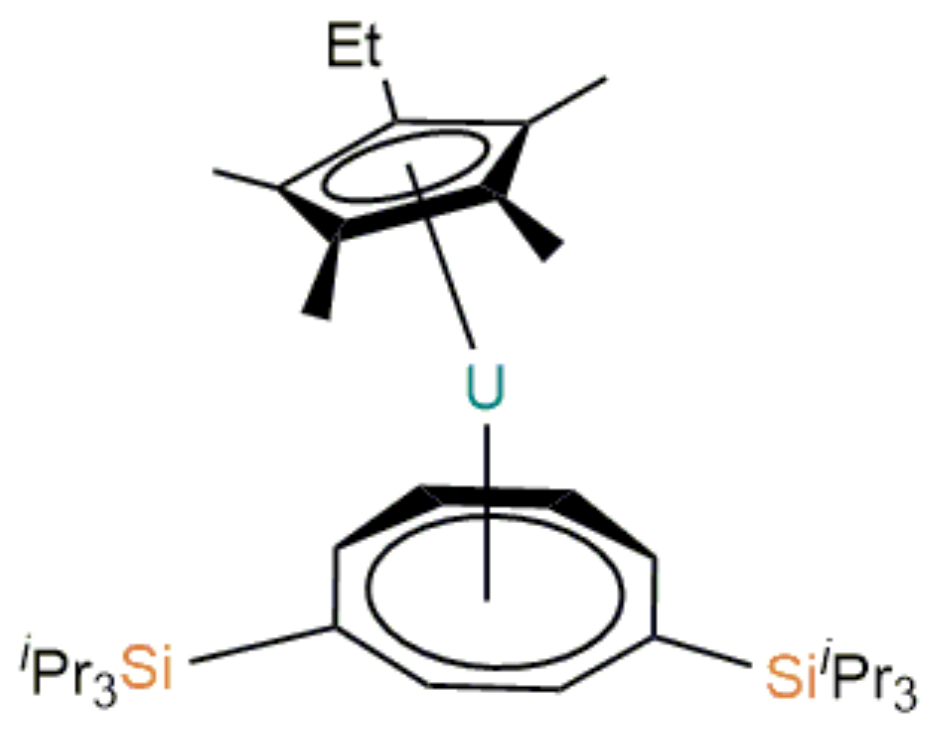
Figure 10.
U(-CMeEt)(-(1,4-CH(SiPr)).
Figure 10.
U(-CMeEt)(-(1,4-CH(SiPr)).
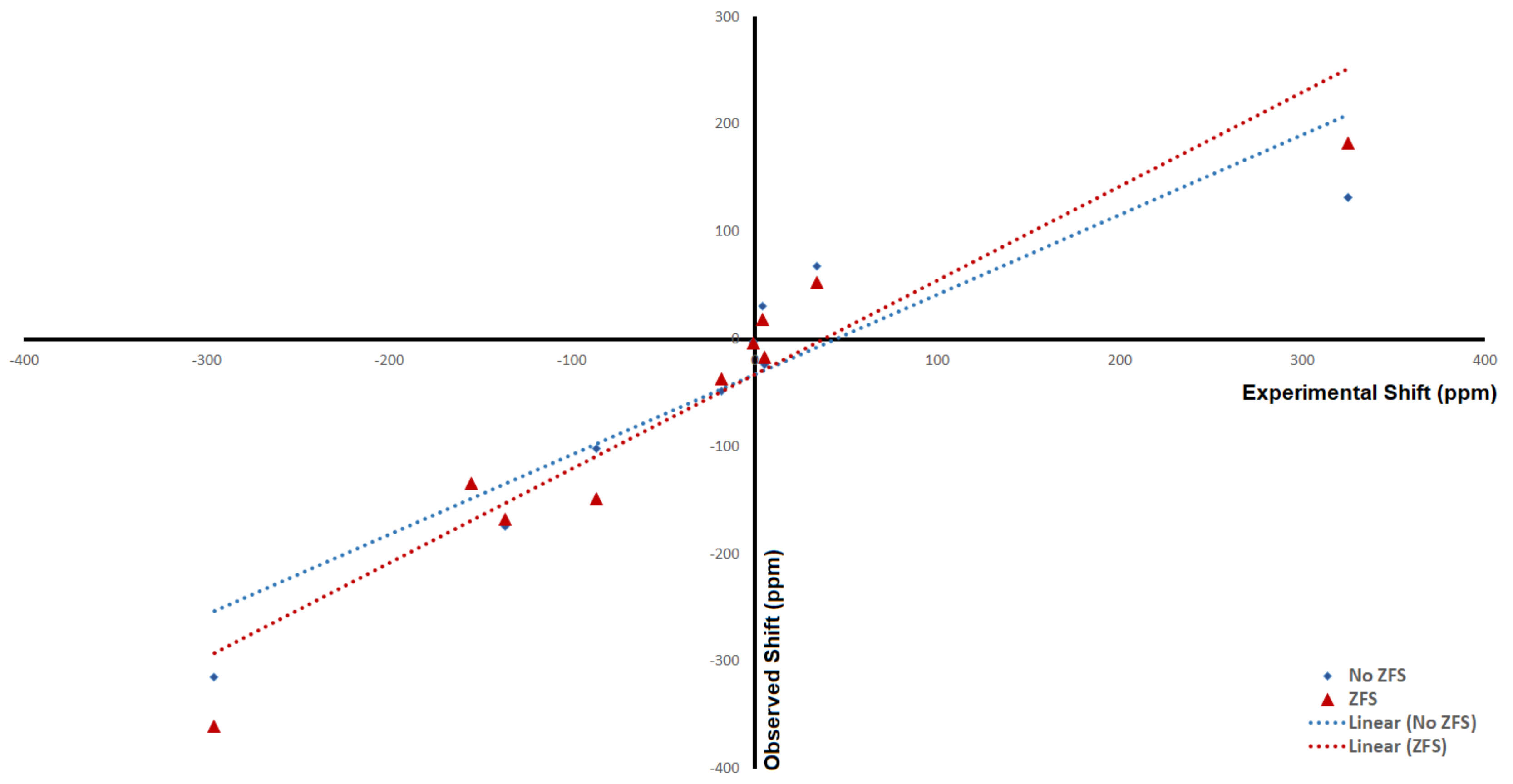
Figure 11.
Calculated results against experimental results.
Figure 11.
Calculated results against experimental results.
Table 1.
Decomposition of the components of the Zeeman and hyperfine coupling matrices by isotropic and anisotropic components, indicates a identity matrix.
Table 1.
Decomposition of the components of the Zeeman and hyperfine coupling matrices by isotropic and anisotropic components, indicates a identity matrix.
| Matrix | | O(1) Component | O() Components | O() Components |
|---|
| | | , | |
| | | , | , , |
Table 2.
Classification of components of the matrix.
Table 2.
Classification of components of the matrix.
| Hyperfine | Zeeman | Order in | Decomposition |
|---|
| Method 1 | Method 2 |
|---|
| Isotropic | | Free electron | | 2nd | Contact | Contact |
| Scalar | | Iso. g-shift | | 4th | Contact | Contact |
| Relativistic | | Aniso. g-shift | | 4th | Contact | Pseudocontact |
| Isotropic | | Free electron | | 4th | Contact | Contact |
| SO Correction | | Iso. g-shift | | 6th | Contact | - |
| | | Aniso. g-shift | | 6th | Contact | - |
| Anisotropic | | Free electron | | 2nd | Pseudocontact | Pseudocontact |
| Scalar | | Iso. g-shift | | 4th | Pseudocontact | Pseudocontact |
| Relativistic | | Aniso. g-shift | | 4th | Pseudocontact | Pseudocontact |
| Symmetric | | Free electron | | 4th | Pseudocontact | Pseudocontact |
| Anisotropic | | Iso. g-shift | | 6th | Pseudocontact | - |
| SO Correction | | Aniso. g-shift | | 6th | Pseudocontact | - |
| Asymmetric | | Free electron | | 4th | Pseudocontact | Pseudocontact |
| Anisotropic | | Iso. g-shift | | 6th | Pseudocontact | - |
| SO Correction | | Aniso. g-shift | | 6th | Pseudocontact | - |
Table 3.
One of the Kramers pair wave functions of U(MeBTP), spin-orbit corrected, SA-CASSCF(3,7) wave function, with 14 quartet and 25 doublet states. The second state can be inferred, via Kramers degeneracy, exchanging the weights of each state with that of the corresponding state. States with weight less than 0.01 are omitted.
Table 3.
One of the Kramers pair wave functions of U(MeBTP), spin-orbit corrected, SA-CASSCF(3,7) wave function, with 14 quartet and 25 doublet states. The second state can be inferred, via Kramers degeneracy, exchanging the weights of each state with that of the corresponding state. States with weight less than 0.01 are omitted.
| Quartet | Doublet |
|---|
| | | | | |
| Weight | Root | Weight | Root | Weight | Root | Weight | Root | Weight | Root | Weight | Root |
| 0.076 | 1 | 0.068 | 2 | 0.021 | 1 | 0.048 | 1 | 0.012 | 5 | 0.011 | 3 |
| 0.048 | 2 | 0.020 | 3 | 0.024 | 2 | 0.089 | 3 | 0.017 | 7 | 0.019 | 6 |
| 0.064 | 3 | 0.042 | 4 | 0.019 | 3 | 0.021 | 4 | 0.030 | 10 | 0.012 | 9 |
| 0.018 | 5 | 0.014 | 9 | 0.051 | 5 | | | | | 0.017 | 10 |
| 0.017 | 6 | 0.012 | 12 | 0.011 | 11 | | | | | | |
Table 4.
Relative energies (cm) for the 10 lowest spin-orbit states of the six compounds studied here, showing the increased gap between first and second excited pairs compared to that of the first pair and the ground state pair.
Table 4.
Relative energies (cm) for the 10 lowest spin-orbit states of the six compounds studied here, showing the increased gap between first and second excited pairs compared to that of the first pair and the ground state pair.
| States | [ NdL ] | U(MeBTP) | U(CMe) | U(N(SiMeBu)) | U(CMeSiMe) | U(-CMeEt)
* (-(1,4-CH(SiPr)) |
|---|
| 1–2 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3–4 | 41 | 44 | 580 | 190 | 61 | 374 |
| 5–6 | 139 | 260 | 1365 | 432 | 144 | 841 |
| 7–8 | 218 | 387 | 2495 | 1101 | 1034 | 1190 |
| 9–10 | 265 | 464 | 2552 | 1269 | 1183 | 1255 |
Table 5.
Calculated
H pNMR shifts of [ NdL
]
organised in increasing
. For numbering of protons see
Figure 1. The reference chemical shift is
ppm (TMS) and the temperature is 298.15K.
Table 5.
Calculated
H pNMR shifts of [ NdL
]
organised in increasing
. For numbering of protons see
Figure 1. The reference chemical shift is
ppm (TMS) and the temperature is 298.15K.
| Component | | | H | H | H | H | H |
|---|
| | Order | | No ZFS | ZFS | No ZFS | ZFS | No ZFS | ZFS | No ZFS | ZFS | No ZFS | ZFS |
| | 2 | | −0.07 | −0.07 | 0.44 | 0.44 | 3.63 | 3.62 | 2.51 | 2.51 | 1.04 | 1.04 |
| | | 4 | | 0.12 | 0.12 | −0.70 | −0.70 | −5.77 | −5.76 | −3.99 | −3.99 | −1.66 | −1.66 |
| | | 4 | | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | −0.01 | 0.00 | -0.01 | 0.00 | 0.00 |
| | 2 | | 0.00 | −10.86 | 0.00 | 3.33 | 0.00 | 2.78 | 0.00 | 0.10 | 0.00 | 0.97 |
| | | 4 | | 0.00 | 17.27 | 0.00 | −5.30 | 0.00 | −4.42 | 0.00 | −0.17 | 0.00 | −1.54 |
| | | 4 | | 6.41 | 6.60 | −1.95 | −2.01 | −1.68 | -1.72 | 0.01 | 0.00 | −0.56 | −0.57 |
| Orbital Contribution | | | 27.59 | 28.40 | 28.11 | 23.66 | 23.00 |
| Contact | Method 1 | | | 0.04 | 0.04 | −0.26 | −0.26 | −2.14 | −2.15 | −1.48 | −1.49 | −0.62 | −0.61 |
| | Method 2 | | | 0.04 | 0.04 | −0.26 | −0.26 | −2.14 | −2.15 | −1.48 | −1.48 | −0.62 | −0.61 |
| Pseudocontact | Method 1 | | | 6.41 | 13.01 | −1.95 | −3.98 | −1.68 | −3.37 | 0.01 | −0.07 | −0.56 | −1.14 |
| | Method 2 | | | 6.41 | 13.00 | −1.95 | −3.98 | −1.68 | −3.37 | 0.01 | −0.08 | −0.56 | −1.14 |
| Total isotropic shielding | | 34.05 | 40.64 | 26.18 | 24.16 | 24.29 | 22.59 | 22.19 | 22.12 | 21.82 | 21.24 |
| Delta | | −2.46 | −9.06 | 5.40 | 7.42 | 7.29 | 8.99 | 9.39 | 9.46 | 9.76 | 10.35 |
| Component | | | H | H | H | H | H |
| | Order | | No ZFS | ZFS | No ZFS | ZFS | No ZFS | ZFS | No ZFS | ZFS | No ZFS | ZFS |
| | 2 | | 9.86 | 9.84 | 20.51 | 20.49 | 3.28 | 3.28 | −2.90 | −2.89 | 25.96 | 25.93 |
| | | 4 | | −15.67 | −15.65 | −32.62 | −32.58 | −5.22 | −5.21 | 4.61 | 4.60 | −41.29 | −41.24 |
| | | 4 | | 0.00 | −0.02 | 0.00 | −0.05 | 0.00 | −0.01 | 0.00 | 0.01 | 0.00 | −0.06 |
| | 2 | | 0.00 | −2.27 | 0.00 | −2.41 | 0.00 | 2.26 | 0.00 | 8.47 | 0.00 | −2.02 |
| | | 4 | | 0 0.00 | 3.61 | 0.00 | 3.83 | 0.00 | −3.60 | 0.00 | −13.47 | 0.00 | 3.22 |
| | | 4 | | 1.81 | 1.83 | 1.42 | 1.46 | −1.36 | −1.39 | −5.16 | −5.30 | 1.20 | 1.24 |
| Orbital Contribution | | | 23.14 | 29.04 | 23.77 | 27.35 | 29.11 |
| Contact | Method 1 | | | −5.81 | −5.83 | −12.11 | −12.14 | −1.94 | −1.94 | 1.71 | 1.72 | −15.33 | −15.38 |
| | Method 2 | | | −5.81 | −5.81 | −12.11 | −12.09 | −1.94 | −1.93 | 1.71 | 1.71 | −15.33 | −15.31 |
| Pseudocontact | Method 1 | | | 1.81 | 3.17 | 1.42 | 2.88 | −1.36 | −2.74 | −5.16 | −10.30 | 1.20 | 2.41 |
| | Method 2 | | | 1.81 | 3.15 | 1.42 | 2.83 | −1.36 | −2.74 | −5.16 | −10.29 | 1.20 | 2.38 |
| Total isotropic shielding | | 19.13 | 20.48 | 18.35 | 19.78 | 20.48 | 19.10 | 23.90 | 18.77 | 14.98 | 16.18 |
| Delta | | 12.45 | 11.10 | 13.23 | 11.80 | 11.10 | 12.48 | 7.68 | 12.81 | 16.60 | 15.41 |
Table 6.
Calculated
H pNMR shifts for the methyl H atoms of U(MeBTP)
in ppm at 303K). For numbering of protons see
Figure 3. The final, ZFS corrected, computational values are highlighted.
Table 6.
Calculated
H pNMR shifts for the methyl H atoms of U(MeBTP)
in ppm at 303K). For numbering of protons see
Figure 3. The final, ZFS corrected, computational values are highlighted.
| Component | | | | Methyl H | | Methyl H |
|---|
| | Order | | No ZFS | ZFS | | No ZFS | ZFS |
| | 2 | | −113.43 | −69.47 | | 28.79 | 17.63 |
| | | 4 | | 166.55 | 102.00 | | −42.28 | −25.89 |
| | | 4 | | −0.00 | 8.85 | | 0.00 | −2.25 |
| | 2 | | 0.00 | 2.26 | | 0.00 | 6.82 |
| | | 4 | | 0.00 | −3.32 | | −0.00 | −10.01 |
| | | 4 | | −2.12 | −0.85 | | −6.27 | −2.54 |
| Ave. Calc. U-H distance, Angstrom | 7.16 | | 6.15 |
| Orbital Contribution | 28.96 | | 29.88 |
| Reference shift | 31.58 | | 31.58 |
| Contact | Method 1 | 53.12 | 41.38 | | −13.48 | −10.51 |
| | | Method 2 | 53.12 | 32.53 | | -13.48 | -8.26 |
| Pseudocontact | Method 1 | −2.12 | −1.91 | | −6.27 | −5.73 |
| | | Method 2 | −2.12 | 6.94 | | −6.27 | −7.98 |
| Total isotropic shielding | 79.96 | 68.43 | | 10.13 | 13.65 |
| Delta | | | −48.38 | −36.85 | | 30.46 | 17.93 |
| Experimental shift [4] | −18.04 | | 4.59 |
Table 7.
Calculated
H pNMR shifts for the ring H atoms of U(MeBTP)
in ppm at 303K. For numbering see
Figure 5. The final, ZFS corrected, computational values are highlighted.
Table 7.
Calculated
H pNMR shifts for the ring H atoms of U(MeBTP)
in ppm at 303K. For numbering see
Figure 5. The final, ZFS corrected, computational values are highlighted.
| Component | | | | Ortho-Pyridine H | | Para-Pyridine H |
|---|
| | Order | | No ZFS | ZFS | | No ZFS | ZFS |
| | 2 | | −49.74 | −30.46 | | 155.85 | 95.45 |
| | | 4 | | 73.03 | 44.72 | | −228.84 | −140.15 |
| | | 4 | | −0.00 | 3.88 | | 0.00 | −12.16 |
| | 2 | | 0.00 | −10.72 | | 0.00 | −15.21 |
| | | 4 | | 0.00 | 15.73 | | 0.00 | 22.34 |
| | | 4 | | 10.01 | 4.03 | | 14.48 | 5.83 |
| Calculated U–H distance, Angstrom | 5.52 | | 6.38 |
| Orbital Contribution | 21.75 | | 22.56 |
| Reference shift | 31.58 | | 31.58 |
| Contact | Method 1 | 23.29 | 18.14 | | −72.99 | −56.86 |
| | | Method 2 | 23.29 | 14.26 | | −72.99 | −44.70 |
| Pseudocontact | Method 1 | 10.01 | 9.04 | | 14.48 | 12.96 |
| | | Method 2 | 10.01 | 12.92 | | 14.48 | 0.80 |
| Total isotropic shielding | 55.05 | 48.94 | | −35.95 | −21.35 |
| Delta | | | −23.47 | −17.36 | | 67.53 | 52.92 |
| Experimental shift [4] | 5.64 | | 33.95 |
Table 8.
Calculated H pNMR shifts for U(CMe) in ppm at 298K. The final, ZFS corrected, computational values are highlighted.
Table 8.
Calculated H pNMR shifts for U(CMe) in ppm at 298K. The final, ZFS corrected, computational values are highlighted.
| A | g | Order | | No ZFS | ZFS |
|---|
| | 2 | | −6.02 | −5.13 |
| | | 4 | | 7.83 | 6.68 |
| | | 4 | | −0.00 | 1.12 |
| | 2 | | −0.00 | −2.36 |
| | | 4 | | 0.00 | 3.07 |
| | | 4 | | 2.83 | 1.61 |
| Orbital Contribution | 29.95 |
| Contact | Method 1 | 1.82 | 2.67 |
| | | Method 2 | 1.82 | 1.55 |
| Pseudocontact | Method 1 | 2.83 | 2.32 |
| | | Method 2 | 2.83 | 3.44 |
| Total isotropic shielding | 34.60 | 34.94 |
| Reference shift, 31.58 ppm (TMS) |
| Delta | | | −3.02 | −3.36 |
| Experimental shift [77] | −0.90 |
Table 9.
Calculated C pNMR shifts for U(CMe) in ppm with no spin-orbit corrections to the hyperfine term at 298 K). The final, ZFS corrected, computational values are highlighted.
Table 9.
Calculated C pNMR shifts for U(CMe) in ppm with no spin-orbit corrections to the hyperfine term at 298 K). The final, ZFS corrected, computational values are highlighted.
| Component | | | Cyclopentadienyl | | Methyl |
|---|
| | Order | | No ZFS | ZFS | | No ZFS | ZFS |
| | 2 | | 256.34 | 218.66 | | −343.69 | −293.18 |
| | | 4 | | −333.83 | −284.76 | | 447.59 | 381.80 |
| | | 4 | | −0.00 | −47.79 | | 0.00 | 64.07 |
| | 2 | | −0.01 | −64.23 | | −0.01 | −11.63 |
| | | 4 | | 0.01 | 83.65 | | 0.01 | 15.14 |
| | | 4 | | 77.50 | 43.90 | | 13.76 | 7.88 |
| Orbital Contribution | 57.01 | | 173.62 |
| Reference shift | 189.03 | | 189.03 |
| Contact | Method 1 | −77.49 | −113.89 | | 103.89 | 152.69 |
| | | Method 2 | −77.49 | −66.10 | | 103.89 | 88.62 |
| Pseudocontact | Method 1 | 77.51 | 63.31 | | 13.76 | 11.39 |
| | | Method 2 | 77.51 | 15.53 | | 13.76 | 75.46 |
| Total isotropic shielding | 57.02 | 6.44 | | 291.27 | 337.70 |
| Delta | | | 132.00 | 182.59 | | -102.25 | −148.68 |
| Experimental shift [77] | 324.80 | | −86.70 |
Table 10.
Calculated C pNMR shifts for U(CMe) in ppm with spin-orbit corrections to the hyperfine term at 298 K). The final, ZFS corrected, computational values are highlighted.
Table 10.
Calculated C pNMR shifts for U(CMe) in ppm with spin-orbit corrections to the hyperfine term at 298 K). The final, ZFS corrected, computational values are highlighted.
| Component | | | Cyclopentadienyl | | Methyl |
|---|
| | Order | | No ZFS | ZFS | | No ZFS | ZFS |
| Isotropic Hyperfine Contribution | |
| | 2 | | 256.34 | 218.66 | | −343.69 | −293.18 |
| | | 4 | | −333.83 | −284.76 | | 447.59 | 381.80 |
| | | 4 | | −0.00 | −47.79 | | 0.00 | 64.07 |
| | 4 | | 74.44 | 63.50 | | −5.38 | −4.59 |
| | | 6 | | −96.94 | −82.69 | | 7.00 | 5.97 |
| | | 6 | | −0.00 | −13.88 | | 0.00 | 1.00 |
| Anisotropic Hyperfine Contribution | |
| | 2 | | −0.01 | −64.23 | | −0.01 | −11.63 |
| | | 4 | | 0.01 | 83.65 | | 0.01 | 15.14 |
| | | 4 | | 77.50 | 43.90 | | 13.76 | 7.88 |
| | 4 | | 0.00 | 127.76 | | 0.00 | 10.78 |
| | | 6 | | −0.00 | −166.38 | | −0.00 | −14.04 |
| | | 6 | | −152.63 | −86.94 | | −12.76 | −7.31 |
| | 4 | | −0.00 | 0.00 | | −0.00 | −0.00 |
| | | 6 | | −0.00 | −0.00 | | −0.00 | 0.00 |
| | | 6 | | −0.00 | −0.01 | | 0.00 | 0.00 |
| Orbital Contribution | 57.01 | | 173.62 |
| Reference shift | 189.03 | | 189.03 |
| Method 1 | | |
| Contact | —no SOC | | −77.49 | −113.89 | | 103.89 | 152.69 |
| | | —with SOC | | −99.99 | −146.96 | | 105.52 | 155.08 |
| Pseudocontact | —no SOC | | 77.51 | 63.31 | | 13.76 | 11.39 |
| | | —with SOC | | −75.13 | −62.25 | | 1.00 | 0.82 |
| Isotropic shielding | —no SOC | | 57.02 | 6.44 | | 291.27 | 337.70 |
| | —with SOC | | −118.11 | −133.18 | | 280.14 | 329.52 |
| Delta | —no SOC | | 132.00 | 182.59 | | −102.25 | −148.68 |
| | | —with SOC | | 307.14 | 341.23 | | −91.11 | −140.50 |
| | Order | | No ZFS | ZFS | | No ZFS | ZFS |
| Method 2 | | | | |
| Contact | —no SOC | | −77.49 | −66.10 | | 103.89 | 88.62 |
| | | —with SOC | | −3.05 | −2.61 | | 137.46 | 84.04 |
| Pseudocontact | —no SOC | | 77.51 | 15.53 | | 13.76 | 75.46 |
| | | —with SOC | | 77.51 | 143.29 | | 13.76 | 86.24 |
| Isotropic shielding | —no SOC | | 57.02 | 6.44 | | 291.27 | 337.70 |
| | | —with SOC | | 131.47 | 197.69 | | 324.84 | 343.9 |
| Delta | —no SOC | | 132.00 | 182.59 | | −102.25 | −148.68 |
| | | —with SOC | | 57.57 | −8.66 | | −135.81 | −154.87 |
| Experimental shift [77] | 324.80 | | −86.70 |
Table 11.
Calculated Si pNMR shifts of U(N(SiMeBu)) in ppm at 298 K. The final, ZFS corrected, computational values are highlighted.
Table 11.
Calculated Si pNMR shifts of U(N(SiMeBu)) in ppm at 298 K. The final, ZFS corrected, computational values are highlighted.
| A | g | Order | | No ZFS | ZFS |
|---|
| | 2 | | −624.79 | −608.68 |
| | | 4 | | 889.64 | 866.71 |
| | | 4 | | −0.00 | 48.19 |
| | 2 | | −0.00 | −6.14 |
| | | 4 | | −0.00 | 8.74 |
| | | 4 | | 37.26 | 39.49 |
| Contact | Method 1 | 264.85 | 306.22 |
| | | Method 2 | 264.85 | 258.03 |
| Pseudocontact | Method 1 | 37.26 | 42.09 |
| | | Method 2 | 37.26 | 90.28 |
| Orbital Contribution | 344.04 |
| Reference shift | 331.60 |
| Total isotropic shielding | 646.15 | 692.34 |
| Delta | | | −314.54 | |
| Experimental shift [2] | −296.00 |
Table 12.
Calculated Si pNMR shifts of U(CMeSiMe) in ppm at K. The final, ZFS corrected, computational values are highlighted.
Table 12.
Calculated Si pNMR shifts of U(CMeSiMe) in ppm at K. The final, ZFS corrected, computational values are highlighted.
| A | g | Order | | No ZFS | ZFS |
|---|
| | 2 | | −389.29 | −376.21 |
| | | 4 | | 532.93 | 515.02 |
| | | 4 | | 0.00 | 4.55 |
| | 2 | | 0.00 | 0.99 |
| | | 4 | | 0.00 | −1.36 |
| | | 4 | | −19.09 | −20.19 |
| Ave. Calc. U–H distance, Angstrom | 4.16 |
| Contact | Method 1 | 143.64 | 143.36 |
| | | Method 2 | 143.64 | 138.81 |
| Pseudocontact | Method 1 | −19.09 | −20.56 |
| | | Method 2 | −19.09 | −16.01 |
| Orbital Contribution | 358.12 |
| Reference shift | 346.58 |
| Total isotropic shielding | 482.66 | 480.93 |
| Delta | | | −136.08 | |
| Experimental shift [79,80] | −155.00 |
Table 13.
Calculated Si pNMR shifts of U(CMeEt)(1,4-CH(SiPr) in ppm at K. The final, ZFS corrected, computational values are highlighted.
Table 13.
Calculated Si pNMR shifts of U(CMeEt)(1,4-CH(SiPr) in ppm at K. The final, ZFS corrected, computational values are highlighted.
| A | g | Order | | No ZFS | ZFS |
|---|
| | 2 | | −324.51 | −298.57 |
| | | 4 | | 512.84 | 471.85 |
| | | 4 | | 0.00 | 30.66 |
| | 2 | | 0.00 | −6.60 |
| | | 4 | | −0.00 | 10.43 |
| | | 4 | | 5.66 | 6.25 |
| Contact | Method 1 | 188.33 | 203.95 |
| | | Method 2 | 188.33 | 173.28 |
| Pseudocontact | Method 1 | 5.66 | 10.08 |
| | | Method 2 | 5.66 | 40.74 |
| Orbital Contribution | 326.64 |
| Reference shift | 346.34 |
| Total isotropic shielding | 520.64 | 540.66 |
| Delta | | | −174.29 | |
| Experimental shift [1] | −136.70 |