DFT Protocol for EPR Prediction of Paramagnetic Cu(II) Complexes and Application to Protein Binding Sites
Abstract
:1. Introduction
2. Results and Discussion
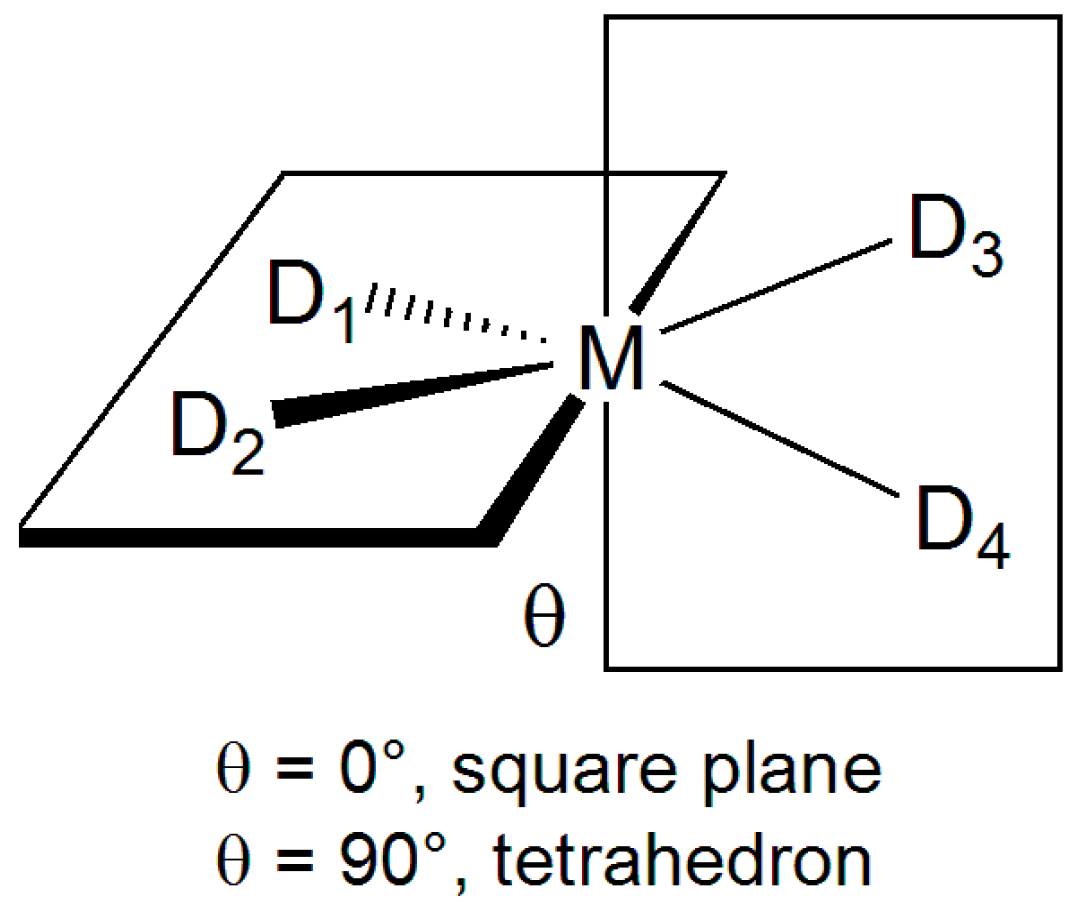
2.1. Geometry Optimization
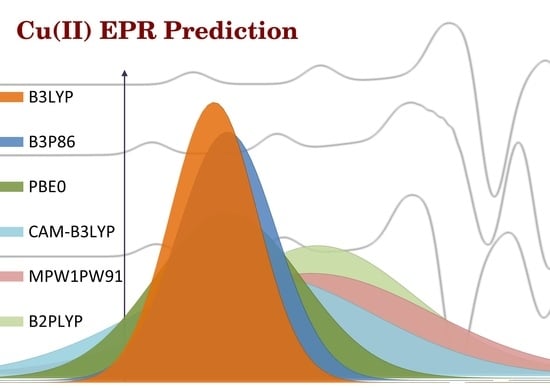
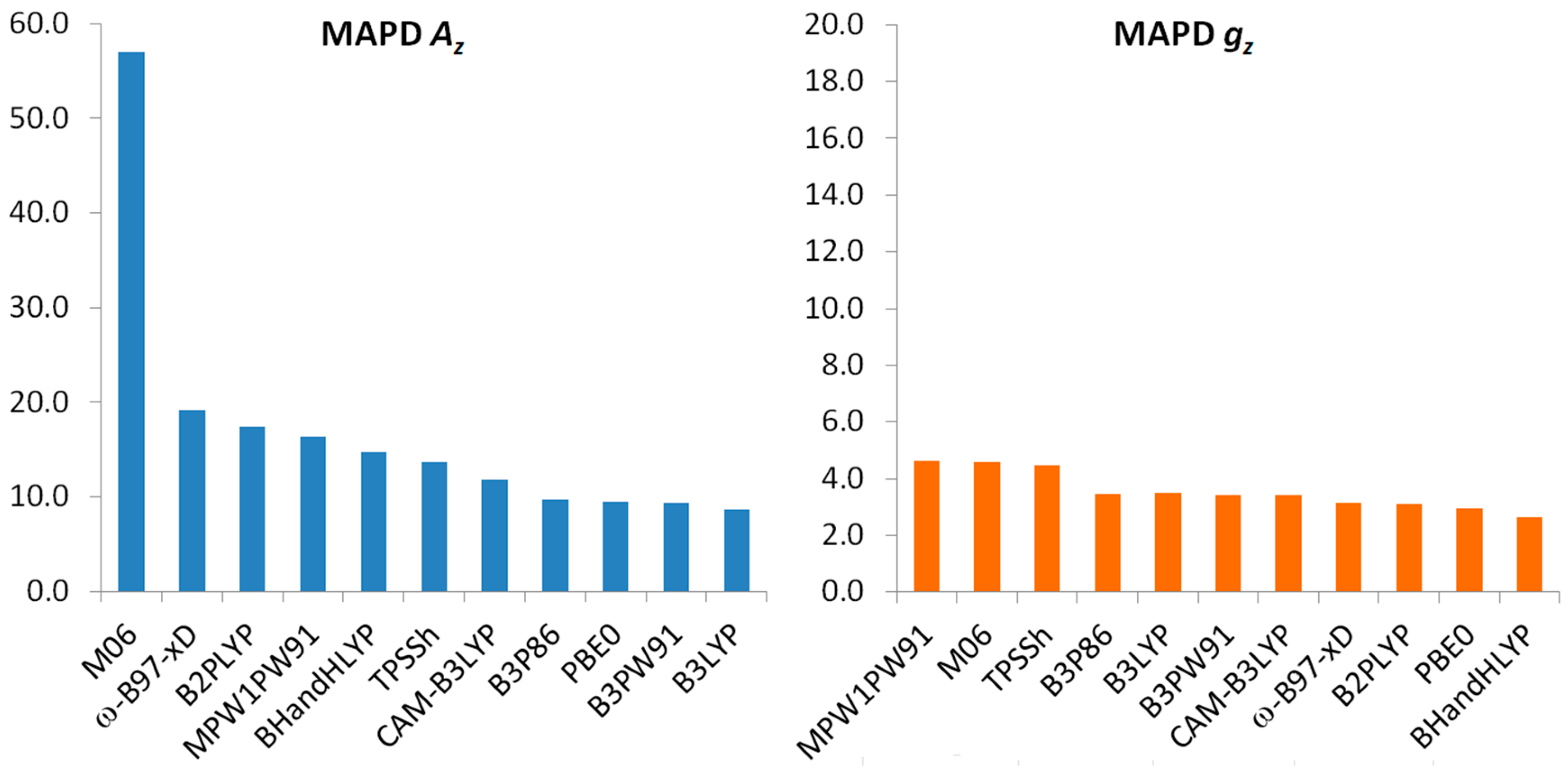
2.2. Prediction Accuracy of the Methods
2.3. Prediction of Az
2.4. Prediction of gz
2.5. Effect of the Geometry Optimization on the Prediction of Az
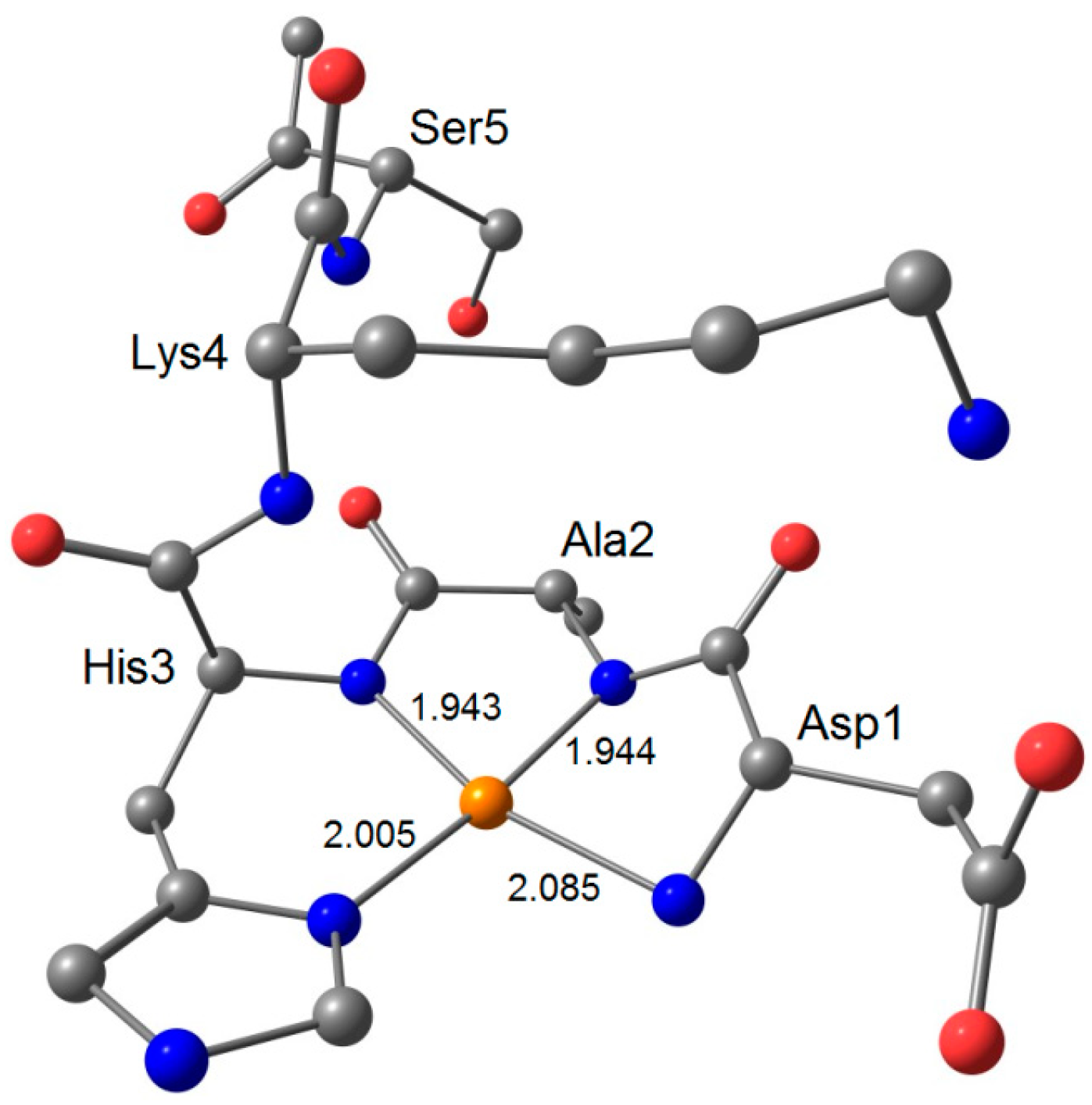
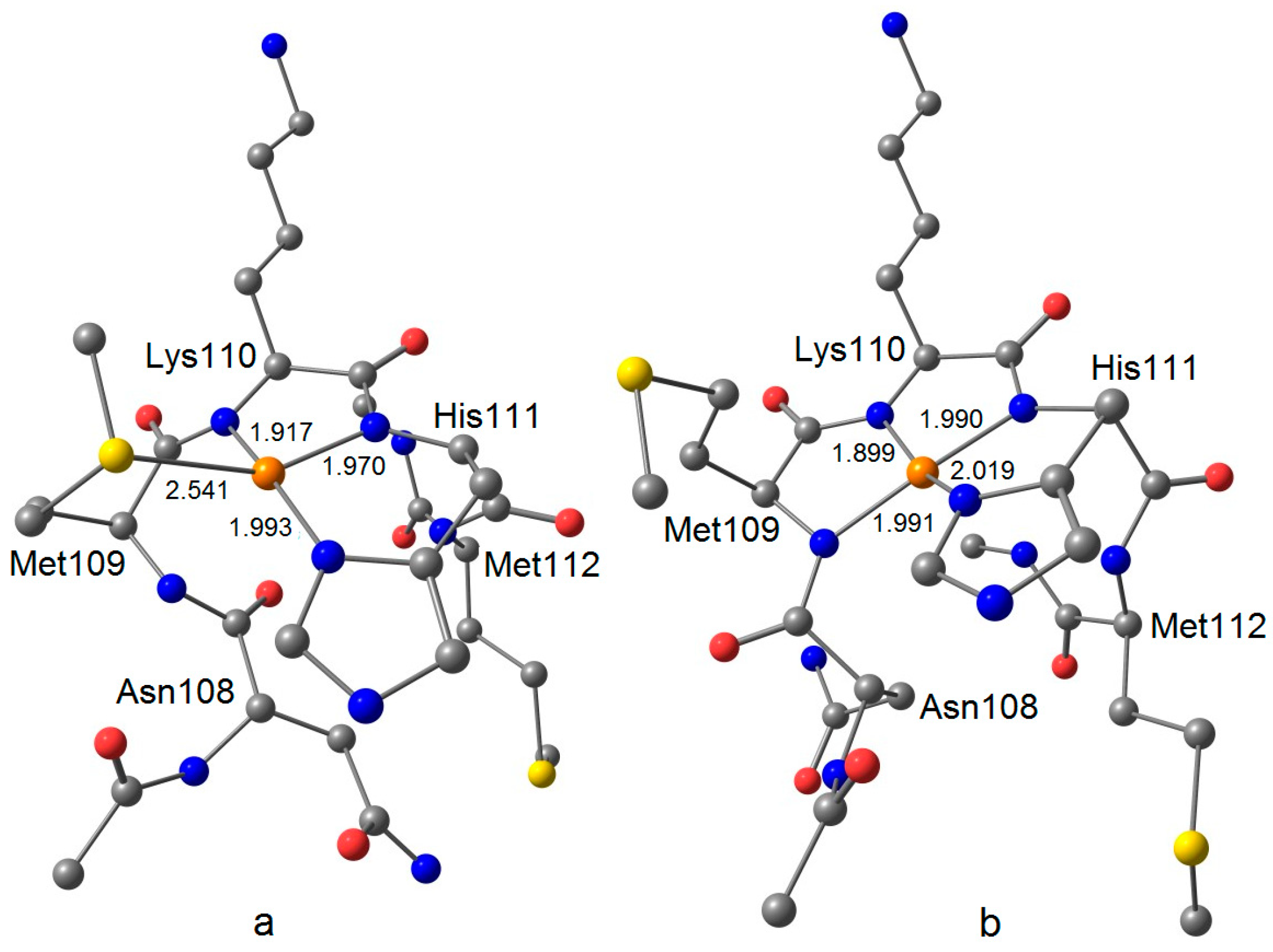
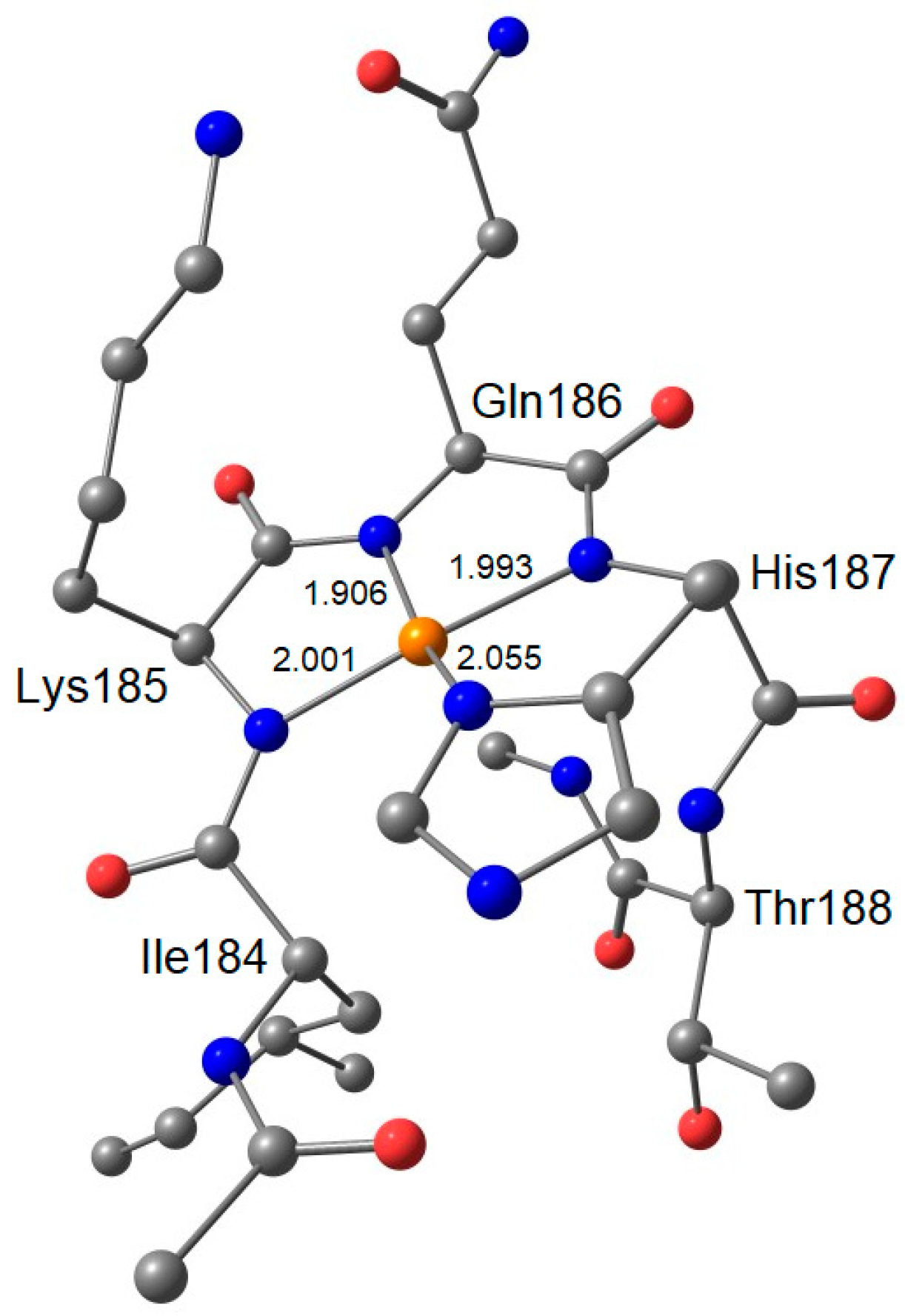
2.6. Application to the Interaction of Cu(II) with Human Serum Albumin and Prion Protein
3. Materials and Methods
3.1. Computational Details
3.2. Theory Background
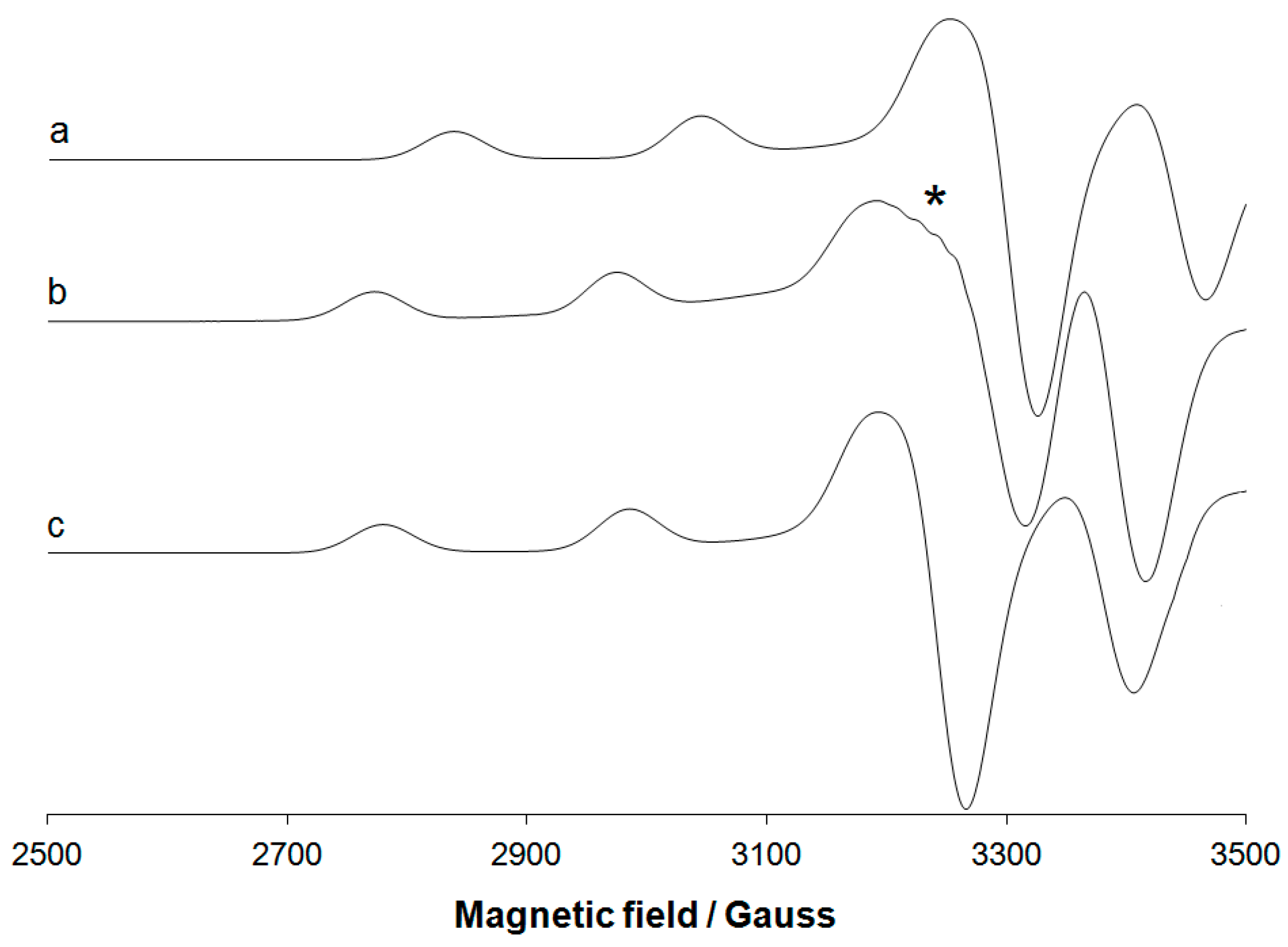
3.3. Experimental EPR Spectra
3.4. Chemicals
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References and Note
- Boal, A.K.; Rosenzweig, A.C. Structural Biology of Copper Trafficking. Chem. Rev. 2009, 109, 4760–4779. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Festa, R.A.; Thiele, D.J. Copper: An essential metal in biology. Curr. Biol. 2011, 21, R877–R883. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Blackburn, N.J.; Yan, N.; Lutsenko, S. Copper in Eukaryotes. In Binding, Transport and Storage of Metal Ions in Biological Cells; Maret, W., Wedd, A., Eds.; The Royal Society of Chemistry: Cambridge, UK, 2014; pp. 524–555. [Google Scholar]
- Rehder, D. Bioinorganic Chemistry; Oxford University Press: Oxford, UK, 2014. [Google Scholar]
- Allen, S.E.; Walvoord, R.R.; Padilla-Salinas, R.; Kozlowski, M.C. Aerobic Copper-Catalyzed Organic Reactions. Chem. Rev. 2013, 113, 6234–6458. [Google Scholar] [CrossRef] [Green Version]
- Munnik, P.; de Jongh, P.E.; de Jong, K.P. Recent Developments in the Synthesis of Supported Catalysts. Chem. Rev. 2015, 115, 6687–6718. [Google Scholar] [CrossRef]
- Joost, M. Synthesis and Original Reactivity of Copper and Gold Complexes; Springer International Publishing: Basel, Switzerland, 2015. [Google Scholar]
- Tisato, F.; Marzano, C.; Porchia, M.; Pellei, M.; Santini, C. Copper in diseases and treatments, and copper-based anticancer strategies. Med. Res. Rev. 2010, 30, 708–749. [Google Scholar] [CrossRef] [PubMed]
- Santini, C.; Pellei, M.; Gandin, V.; Porchia, M.; Tisato, F.; Marzano, C. Advances in Copper Complexes as Anticancer Agents. Chem. Rev. 2014, 114, 815–862. [Google Scholar] [CrossRef]
- Tabti, R.; Tounsi, N.; Gaiddon, C.; Bentouhami, E.; Désaubry, L. Progress in Copper Complexes as Anticancer Agents. Med. Chem. 2017, 7, 875–879. [Google Scholar] [CrossRef]
- Lee, J.D. Concise Inorganic Chemistry; Chapman & Hall: London, UK, 1996. [Google Scholar]
- Cotton, F.A.; Wilkinson, G.; Murillo, C.A.; Bochmann, M. Advanced Inorganic Chemistry, 6th ed.; Wiley-Interscience: New York, NY, USA, 1999. [Google Scholar]
- Gaăzo, J.; Bersuker, I.B.; Garaj, J.; Kabešová, M.; Kohout, J.; Langfelderová, H.; Melník, M.; Serator, M.; Valach, F. Plasticity of the coordination sphere of copper(II) complexes, its manifestation and causes. Coord. Chem. Rev. 1976, 19, 253–297. [Google Scholar] [CrossRef]
- Hathaway, B.J. A New Look at the Stereochemistry and Electronic Properties of Complexes of the Copper(II) Ion; Struct. Bonding (Berlin); Springer: Berlin, Germany, 1984; pp. 55–118. [Google Scholar]
- Hathaway, B.J.; Billing, D.E. The electronic properties and stereochemistry of mono-nuclear complexes of the copper(II) ion. Coord. Chem. Rev. 1970, 5, 143–207. [Google Scholar] [CrossRef]
- Roessler, M.M.; Salvadori, E. Principles and applications of EPR spectroscopy in the chemical sciences. Chem. Soc. Rev. 2018, 47, 2534–2553. [Google Scholar] [CrossRef]
- Peisach, J.; Blumberg, W.E. Structural Implications derived from the Analysis of Electron Paramagnetic Resonance Spectra of Natural and Artificial Copper Proteins. Arch. Biochem. Biophys. 1974, 165, 691–708. [Google Scholar] [CrossRef]
- Chasteen, D.N. Vanadyl(IV) EPR Spin Probe. Inorganic and Biochemical Aspects. In Biological Magnetic Resonance; Berliner, L.J., Reuben, J., Eds.; Plenum Press: New York, NY, USA, 1981; Volum 3, pp. 53–119. [Google Scholar]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Neese, F. A critical evaluation of DFT, including time-dependent DFT, applied to bioinorganic chemistry. JBIC J. Biol. Inorg. Chem. 2006, 11, 702–711. [Google Scholar] [CrossRef] [PubMed]
- Neese, F. Prediction of molecular properties and molecular spectroscopy with density functional theory: From fundamental theory to exchange-coupling. Coord. Chem. Rev. 2009, 253, 526–563. [Google Scholar] [CrossRef]
- Cohen, A.J.; Mori-Sánchez, P.; Yang, W. Challenges for Density Functional Theory. Chem. Rev. 2012, 112, 289–320. [Google Scholar] [CrossRef] [PubMed]
- Tsipis, A.C. DFT flavor of coordination chemistry. Coord. Chem. Rev. 2014, 272, 1–29. [Google Scholar] [CrossRef]
- van Mourik, T.; Bühl, M.; Gaigeot, M.-P. Density functional theory across chemistry, physics and biology. Philos. Trans. R. Soc. A 2014, 372, 20120488. [Google Scholar] [CrossRef]
- Kirste, B. Applications of Density Functional Theory to Theoretical Organic Chemistry. Chem. Sci. J. 2016, 7, 127. [Google Scholar] [CrossRef]
- Mardirossian, N.; Head-Gordon, M. Thirty years of density functional theory in computational chemistry: An overview and extensive assessment of 200 density functionals. Mol. Phys. 2017, 115, 2315–2372. [Google Scholar] [CrossRef]
- Cossi, M.; Barone, V.; Cammi, R.; Tomasi, J. Ab initio study of solvated molecules: A new implementation of the polarizable continuum model. Chem. Phys. Lett. 1996, 255, 327–335. [Google Scholar] [CrossRef]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef]
- Sciortino, G.; Lihi, N.; Czine, T.; Maréchal, J.-D.; Lledós, A.; Garribba, E. Accurate prediction of vertical electronic transitions of Ni(II) coordination compounds via time dependent density functional theory. Int. J. Quantum Chem. 2018, e25655. [Google Scholar] [CrossRef]
- Bagno, A.; Rastrelli, F.; Saielli, G. Toward the Complete Prediction of the 1H and 13C NMR Spectra of Complex Organic Molecules by DFT Methods: Application to Natural Substances. Chem.-Eur. J. 2006, 12, 5514–5525. [Google Scholar] [CrossRef]
- Toukach, F.V.; Ananikov, V.P. Recent advances in computational predictions of NMR parameters for the structure elucidation of carbohydrates: Methods and limitations. Chem. Soc. Rev. 2013, 42, 8376–8415. [Google Scholar] [CrossRef]
- Willoughby, P.H.; Jansma, M.J.; Hoye, T.R. A guide to small-molecule structure assignment through computation of (1H and 13C) NMR chemical shifts. Nat. Protoc. 2014, 9, 643–660. [Google Scholar] [CrossRef]
- Saladino, A.C.; Larsen, S.C. Density Functional Theory Calculations of the Electron Paramagnetic Resonance Parameters for VO2+ Complexes. J. Phys. Chem. A 2003, 107, 1872–1878. [Google Scholar] [CrossRef]
- Neese, F. Metal and ligand hyperfine couplings in transition metal complexes: The effect of spin-orbit coupling as studied by coupled perturbed Kohn-Sham theory. J. Chem. Phys. 2003, 118, 3939–3948. [Google Scholar] [CrossRef]
- Munzarová, M.L. DFT Calculations of EPR Hyperfine Coupling Tensors. In Calculation of NMR and EPR Parameters; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2004; pp. 461–482. [Google Scholar]
- Micera, G.; Garribba, E. Is the Spin-Orbit Coupling Important in the Prediction of the 51V Hyperfine Coupling Constants of VIVO2+ Species? ORCA Versus Gaussian Performance and Biological Applications. J. Comput. Chem. 2011, 32, 2822–2835. [Google Scholar] [CrossRef]
- Sanna, D.; Sciortino, G.; Ugone, V.; Micera, G.; Garribba, E. Nonoxido VIV Complexes: Prediction of the EPR Spectrum and Electronic Structure of Simple Coordination Compounds and Amavadin. Inorg. Chem. 2016, 55, 7373–7387. [Google Scholar] [CrossRef]
- Pietrzyk, P.; Podolska, K.; Sojka, Z. Molecular interpretation of EPR parameters—Computational spectroscopy approaches. In Electron Paramagnetic Resonance; Gilbert, B.C., Murphy, D.M., Chechik, V., Eds.; The Royal Society of Chemistry: Cambridge, UK, 2013; Volume 23, pp. 264–311. [Google Scholar]
- Conradie, M.M.; Conradie, J.; Ghosh, A. Capturing the spin state diversity of iron(III)-aryl porphyrins: OLYP is better than TPSSh. J. Inorg. Biochem. 2011, 105, 84–91. [Google Scholar] [CrossRef]
- Fritscher, J.; Hrobárik, P.; Kaupp, M. Computational Studies of Electron Paramagnetic Resonance Parameters for Paramagnetic Molybdenum Complexes. 1. Method Validation on Small and Medium-Sized Systems. J. Phys. Chem. B 2007, 111, 4616–4629. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical hybrid density functional with perturbative second-order correlation. J. Chem. Phys. 2006, 124, 034108. [Google Scholar] [CrossRef]
- Munzarová, M.L.; Kubáček, P.; Kaupp, M. Mechanisms of EPR Hyperfine Coupling in Transition Metal Complexes. J. Am. Chem. Soc. 2000, 122, 11900–11913. [Google Scholar] [CrossRef]
- Gorelsky, S.; Micera, G.; Garribba, E. Equilibrium Between the Octahedral and Square Pyramidal Form and the Influence of an Axial Ligand on the Molecular Properties of VIVO Complexes: A Spectroscopic and DFT Study. Chem.-Eur. J. 2010, 16, 8167–8180. [Google Scholar] [CrossRef]
- Remenyi, C.; Reviakine, R.; Arbuznikov, A.V.; Vaara, J.; Kaupp, M. Spin-orbit effects on hyperfine coupling tensors in transition metal complexes using hybrid density functionals and accurate spin-orbit operators. J. Phys. Chem. A 2004, 108, 5026–5033. [Google Scholar] [CrossRef]
- Stein, M.; van Lenthe, E.; Baerends, E.J.; Lubitz, W. g- and A-tensor calculations in the zero-order approximation for relativistic effects of Ni complexes Ni(mnt)2− and Ni(CO)3H as model complexes for the active center of [NiFe]-hydrogenase. J. Phys. Chem. A 2001, 105, 416–425. [Google Scholar] [CrossRef]
- van Lenthe, E.; van der Avoird, A.; Wormer, P.E.S. Density functional calculations of molecular hyperfine interactions in the zero order regular approximation for relativistic effects. J. Chem. Phys. 1998, 108, 4783–4796. [Google Scholar] [CrossRef]
- Belanzoni, P.; van Lenthe, E.; Baerends, E.J. An evaluation of the density functional approach in the zero order regular approximation for relativistic effects: Magnetic interactions in small metal compounds. J. Chem. Phys. 2001, 114, 4421–4433. [Google Scholar] [CrossRef] [Green Version]
- Ames, W.M.; Larsen, S.C. Density Functional Theory Investigation of EPR Parameters for Tetragonal Cu(II) Model Complexes with Oxygen Ligands. J. Phys. Chem. A 2009, 113, 4305–4312. [Google Scholar] [CrossRef]
- Ames, W.M.; Larsen, S.C. DFT calculations of the EPR parameters for Cu(II) DETA imidazole complexes. Phys. Chem. Chem. Phys. 2009, 11, 8266–8274. [Google Scholar] [CrossRef]
- Ames, W.M.; Larsen, S.C. DFT Calculations of EPR Parameters for Copper(II)-Exchanged Zeolites Using Cluster Models. J. Phys. Chem. A 2010, 114, 589–594. [Google Scholar] [CrossRef]
- Nomenclature and Symbolism for Amino Acids and Peptides. Eur. J. Biochem. 1984, 138, 9–37. [CrossRef] [Green Version]
- Bühl, M.; Kabrede, H. Geometries of Transition-Metal Complexes from Density-Functional Theory. J. Chem. Theory Comput. 2006, 2, 1282–1290. [Google Scholar] [CrossRef]
- Bühl, M.; Reimann, C.; Pantazis, D.A.; Bredow, T.; Neese, F. Geometries of Third-Row Transition-Metal Complexes from Density-Functional Theory. J. Chem. Theory Comput. 2008, 4, 1449–1459. [Google Scholar] [CrossRef] [Green Version]
- Tyagi, S.; Hathaway, B.J. Crystal structure and electronic properties of bis(2,2′-bipyridyl)-thiocyanatocopper(II) tetrafluoroborate. J. Chem. Soc. Dalton Trans. 1981, 2029–2033. [Google Scholar] [CrossRef]
- Glass, R.S.; Steffen, L.K.; Swanson, D.D.; Wilson, G.S.; de Gelder, R.; de Graaff, R.A.G.; Reedijk, J. Bis(trithiacyclononane)metal(II) compounds and Jahn-Teller distortions from octahedral geometry, electrochemistry, spectroscopy, and crystal structures of the copper bis(tetrafluoroborate) bis(acetonitrile) complex at 177 K and the cadmium bis(tetrafluoroborate) and copper bis(tetrafluoroborate) bis(nitromethane) complexes at 300 K. Inorg. Chim. Acta 1993, 207, 241–252. [Google Scholar] [CrossRef]
- Comba, P.; Hambley, T.W.; Lawrance, G.A.; Martin, L.L.; Renold, P.; Várnagy, K. Template syntheses of chiral tetradentate ligands derived from l-amino acids. Structural and spectroscopic characterization of the free ligands and of their copper(II) complexes. J. Chem. Soc. Dalton Trans. 1991, 277–283. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Perdew, J.P. Density-functional approximation for the correlation energy of the inhomogeneous electron gas. Phys. Rev. B 1986, 33, 8822–8824. [Google Scholar] [CrossRef]
- Perdew, J.P. Erratum: Density-functional approximation for the correlation energy of the inhomogeneous electron gas. Phys. Rev. B 1986, 34, 7406. [Google Scholar] [CrossRef]
- Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244–13249. [Google Scholar] [CrossRef]
- Yanai, T.; Tew, D.P.; Handy, N.C. A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef] [Green Version]
- Chai, J.-D.; Head-Gordon, M. Systematic optimization of long-range corrected hybrid density functionals. J. Chem. Phys. 2008, 128, 084106. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Exchange functionals with improved long-range behavior and adiabatic connection methods without adjustable parameters: The mPW and mPW1PW models. J. Chem. Phys. 1998, 108, 664–675. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Erratum: Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1997, 78, 1396. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, revision D.01; Gaussian, Inc.: Wallingford, CT, USA, 2010. [Google Scholar]
- Tao, J.; Perdew, J.P.; Staroverov, V.N.; Scuseria, G.E. Climbing the Density Functional Ladder: Nonempirical Meta–Generalized Gradient Approximation Designed for Molecules and Solids. Phys. Rev. Lett. 2003, 91, 146401. [Google Scholar] [CrossRef]
- Staroverov, V.N.; Scuseria, G.E.; Tao, J.; Perdew, J.P. Comparative assessment of a new nonempirical density functional: Molecules and hydrogen-bonded complexes. J. Chem. Phys. 2003, 119, 12129–12137. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. A new local density functional for main-group thermochemistry, transition metal bonding, thermochemical kinetics, and noncovalent interactions. J. Chem. Phys. 2006, 125, 194101. [Google Scholar] [CrossRef] [Green Version]
- Grimme, S.; Mück-Lichtenfeld, C.; Würthwein, E.-U.; Ehlers, A.W.; Goumans, T.P.M.; Lammertsma, K. Consistent Theoretical Description of 1,3-Dipolar Cycloaddition Reactions. J. Phys. Chem. A 2006, 110, 2583–2586. [Google Scholar] [CrossRef]
- Schwabe, T.; Grimme, S. Double-hybrid density functionals with long-range dispersion corrections: Higher accuracy and extended applicability. Phys. Chem. Chem. Phys. 2007, 9, 3397–3406. [Google Scholar] [CrossRef]
- Schwabe, T.; Grimme, S. Theoretical Thermodynamics for Large Molecules: Walking the Thin Line between Accuracy and Computational Cost. Acc. Chem. Res. 2008, 41, 569–579. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. Density Functionals with Broad Applicability in Chemistry. Acc. Chem. Res. 2008, 41, 157–167. [Google Scholar] [CrossRef] [Green Version]
- Medvedev, M.G.; Bushmarinov, I.S.; Sun, J.; Perdew, J.P.; Lyssenko, K.A. Density functional theory is straying from the path toward the exact functional. Science 2017, 355, 49–52. [Google Scholar] [CrossRef]
- Kallay, C.; David, A.; Timari, S.; Nagy, E.M.; Sanna, D.; Garribba, E.; Micera, G.; De Bona, P.; Pappalardo, G.; Rizzarelli, E.; et al. Copper(II) complexes of rat amylin fragments. Dalton Trans. 2011, 40, 9711–9721. [Google Scholar] [CrossRef]
- It must be highlighted that the aquaion [Cu(H2O)6]2+, due to their highly conformational and coordination variability, was excluded from this analysis.
- Madhu, V.; Das, S.K. Near-IR absorption due to supramolecular electronic interaction in an extended 3D hydrogen-bonding network material: synthesis, crystal structure and properties of [4,4′-H2bpy][Cu(mnt)2]. Polyhedron 2004, 23, 1235–1242. [Google Scholar] [CrossRef]
- Fabiano, E.; Constantin, L.A.; Cortona, P.; Della Sala, F. Global Hybrids from the Semiclassical Atom Theory Satisfying the Local Density Linear Response. J. Chem. Theory Comput. 2015, 11, 122–131. [Google Scholar] [CrossRef]
- Harris, W.R. Equilibrium model for speciation of aluminum in serum. Clin. Chem. 1992, 38, 1809–1818. [Google Scholar]
- Harford, C.; Sarkar, B. Amino Terminal Cu(II)- and Ni(II)-Binding (ATCUN) Motif of Proteins and Peptides: Metal Binding, DNA Cleavage, and Other Properties. Acc. Chem. Res. 1997, 30, 123–130. [Google Scholar] [CrossRef]
- Giroux, E.L.; Durieux, M.; Schechter, P.J. A study of zinc distribution in human serum. Bioinorg. Chem. 1976, 5, 211–218. [Google Scholar] [CrossRef]
- Foote, J.W.; Delves, H.T. Distribution of zinc amongst human serum globulins determined by gel filtration-affinity chromatography and atomic-absorption spectrophotometry. Analyst 1984, 109, 709–711. [Google Scholar] [CrossRef] [PubMed]
- Bal, W.; Sokołowska, M.; Kurowska, E.; Faller, P. Binding of transition metal ions to albumin: Sites, affinities and rates. Biochim. Biophys. Acta, Gen. Subj. 2013, 1830, 5444–5455. [Google Scholar] [CrossRef] [PubMed]
- Bal, W.; Christodoulou, J.; Sadler, P.J.; Tucker, A. Multi-metal binding site of serum albumin. J. Inorg. Biochem. 1998, 70, 33–39. [Google Scholar] [CrossRef]
- Stewart, A.J.; Blindauer, C.A.; Berezenko, S.; Sleep, D.; Sadler, P.J. Interdomain zinc site on human albumin. Proc. Natl. Acad. Sci. USA 2003, 100, 3701–3706. [Google Scholar] [CrossRef] [PubMed]
- Di Natale, G.; Grasso, G.; Impellizzeri, G.; La Mendola, D.; Micera, G.; Mihala, N.; Nagy, Z.; Õsz, K.; Pappalardo, G.; Rigó, V.; et al. Copper(II) Interaction with Unstructured Prion Domain Outside the Octarepeat Region: Speciation, Stability, and Binding Details of Copper(II) Complexes with PrP106−126 Peptides. Inorg. Chem. 2005, 44, 7214–7225. [Google Scholar] [CrossRef] [PubMed]
- Brown, D.R.; Guantieri, V.; Grasso, G.; Impellizzeri, G.; Pappalardo, G.; Rizzarelli, E. Copper(II) complexes of peptide fragments of the prion protein. Conformation changes induced by copper(II) and the binding motif in C-terminal protein region. J. Inorg. Biochem. 2004, 98, 133–143. [Google Scholar] [CrossRef]
- WinEPR SimFonia, version 1.25; Chong, D.P. (Ed.) Bruker Analytische Messtechnik GmbH: Karlshrue, Germany, 1996. [Google Scholar]
- Prusiner, S. Molecular biology of prion diseases. Science 1991, 252, 1515–1522. [Google Scholar] [CrossRef]
- Prusiner, S.B. Biology and Genetics of Prions Causing Neurodegeneration. Annu. Rev. Genet. 2013, 47, 601–623. [Google Scholar] [CrossRef] [Green Version]
- Saá, P.; Harris, D.A.; Cervenakova, L. Mechanisms of prion-induced neurodegeneration. Expert Rev. Mol. Med. 2016, 18, e5. [Google Scholar] [CrossRef] [PubMed]
- Brown, D.R.; Qin, K.; Herms, J.W.; Madlung, A.; Manson, J.; Strome, R.; Fraser, P.E.; Kruck, T.; von Bohlen, A.; Schulz-Schaeffer, W.; et al. The cellular prion protein binds copper in vivo. Nature 1997, 390, 684–687. [Google Scholar] [CrossRef] [PubMed]
- Millhauser, G.L. Copper and the Prion Protein: Methods, Structures, Function, and Disease. Annu. Rev. Phys. Chem. 2007, 58, 299–320. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Walter, E.D.; Chattopadhyay, M.; Millhauser, G.L. The Affinity of Copper Binding to the Prion Protein Octarepeat Domain: Evidence for Negative Cooperativity. Biochemistry 2006, 45, 13083–13092. [Google Scholar] [CrossRef] [PubMed]
- Stevens, D.J.; Walter, E.D.; Rodríguez, A.; Draper, D.; Davies, P.; Brown, D.R.; Millhauser, G.L. Early Onset Prion Disease from Octarepeat Expansion Correlates with Copper Binding Properties. PLoS Pathog. 2009, 5, e1000390. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jones, C.E.; Abdelraheim, S.R.; Brown, D.R.; Viles, J.H. Preferential Cu2+ Coordination by His96 and His111 Induces β-Sheet Formation in the Unstructured Amyloidogenic Region of the Prion Protein. J. Biol. Chem. 2004, 279, 32018–32027. [Google Scholar] [CrossRef]
- Eric, D.W.; Daniel, J.S.; Ann, R.S.; Micah, P.V.; Andrew Dei, R.; Glenn, L.M. Copper Binding Extrinsic to the Octarepeat Region in the Prion Protein. Curr. Protein Pept. Sci. 2009, 10, 529–535. [Google Scholar] [CrossRef]
- Jobling, M.F.; Stewart, L.R.; White, A.R.; McLean, C.; Friedhuber, A.; Maher, F.; Beyreuther, K.; Masters, C.L.; Barrow, C.J.; Collins, S.J.; et al. The Hydrophobic Core Sequence Modulates the Neurotoxic and Secondary Structure Properties of the Prion Peptide 106-126. J. Neurochem. 1999, 73, 1557–1565. [Google Scholar] [CrossRef]
- Giachin, G.; Mai, P.T.; Tran, T.H.; Salzano, G.; Benetti, F.; Migliorati, V.; Arcovito, A.; Longa, S.D.; Mancini, G.; D’Angelo, P.; et al. The non-octarepeat copper binding site of the prion protein is a key regulator of prion conversion. Sci. Rep. 2015, 5, 15253. [Google Scholar] [CrossRef] [Green Version]
- Grasso, D.; Grasso, G.; Guantieri, V.; Impellizzeri, G.; La Rosa, C.; Milardi, D.; Micera, G.; Õsz, K.; Pappalardo, G.; Rizzarelli, E.; et al. Environmental Effects on a Prion′s Helix II Domain: Copper(II) and Membrane Interactions with PrP180–193 and Its Analogues. Chem.-Eur. J. 2006, 12, 537–547. [Google Scholar] [CrossRef]
- Bruschi, M.; De Gioia, L.; Mitrić, R.; Bonačić-Koutecký, V.; Fantucci, P. A DFT study of EPR parameters in Cu(II) complexes of the octarepeat region of the prion protein. Phys. Chem. Chem. Phys. 2008, 10, 4573–4583. [Google Scholar] [CrossRef] [PubMed]
- Ames, W.M.; Larsen, S.C. Insight into the copper coordination environment in the prion protein through density functional theory calculations of EPR parameters. JBIC J. Biol. Inorg. Chem. 2009, 14, 547–557. [Google Scholar] [CrossRef] [PubMed]
- Davies, P.; McHugh, P.C.; Hammond, V.J.; Marken, F.; Brown, D.R. Contribution of Individual Histidines to Prion Protein Copper Binding. Biochemistry 2011, 50, 10781–10791. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez-Guerra Pedregal, J.; Gómez-Orellana, P.; Maréchal, J.-D. ESIgen: Electronic Supporting Information Generator for Computational Chemistry Publications. J. Chem. Inf. Model. 2018, 58, 561–564. [Google Scholar] [CrossRef] [PubMed]
- Neese, F. The ORCA program system. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Neese, F. ORCA—An Ab Initio, DFT and Semiempirical Program Package, Version 4.0; Max-Planck-Institute for Chemical Energy Conversion: Mülheim, Germany, 2017. [Google Scholar]
- Pisano, L.; Varnagy, K.; Timari, S.; Hegetschweiler, K.; Micera, G.; Garribba, E. VIVO Versus VIV Complex Formation by Tridentate (O, Narom, O) Ligands: Prediction of Geometry, EPR 51V Hyperfine Coupling Constants, and UV-Vis Spectra. Inorg. Chem. 2013, 52, 5260–5272. [Google Scholar] [CrossRef]
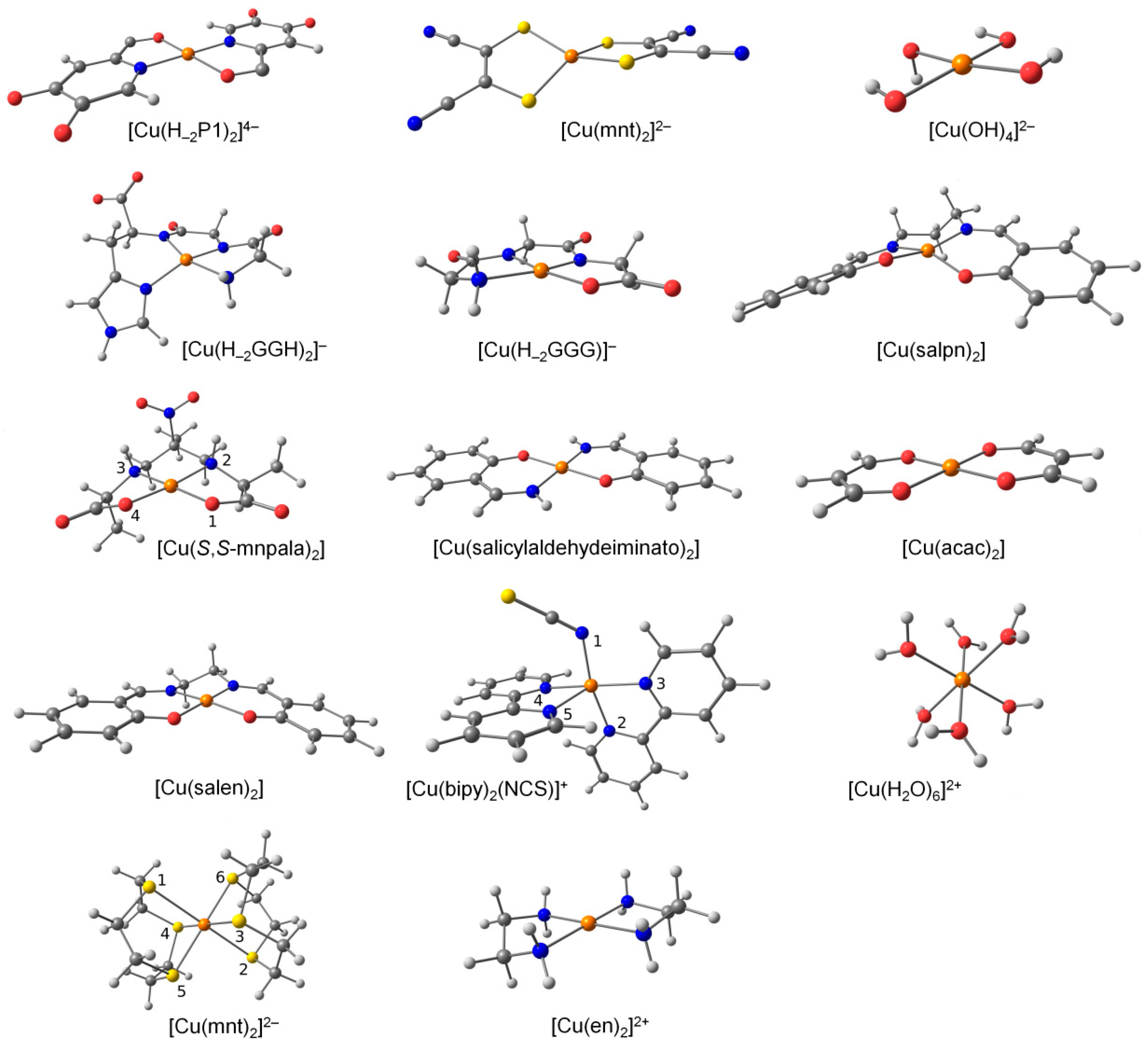
| Parameter 2 | [Cu(bipy)2(NCS)]+ 3 | [Cu(ttcn)]2+ 4 | [Cu(S,S-mnpala)] 5 | |||
|---|---|---|---|---|---|---|
| Exptl. | Calcd. | Exptl. | Calcd. | Exptl. | Calcd. | |
| Cu−D(1) | 1.996 | 1.962 | 2.504 | 2.697 | 1.911 | 1.908 |
| Cu−D(2) | 2.070 | 2.070 | 2.504 | 2.697 | 1.980 | 2.064 |
| Cu−D(3) | 1.994 | 2.044 | 2.342 | 2.417 | 1.986 | 2.058 |
| Cu−D(4) | 1.979 | 2.060 | 2.342 | 2.417 | 1.920 | 1.921 |
| Cu−D(5) | 2.119 | 2.252 | 2.487 | 2.429 | – | – |
| Cu−D(6) | – | – | 2.487 | 2.429 | – | – |
| D(1)−Cu−D(4) | 92.4 | 90.1 | 91.7 | 93.2 | 92.2 | 97.5 |
| D(1)−Cu−D(3) | 92.8 | 92.9 | 88.3 | 86.8 | 174.6 | 177.8 |
| D(2)−Cu−D(3) | 80.1 | 79.0 | 91.7 | 93.2 | 98.2 | 96.1 |
| D(3)−Cu−D(4) | 174.7 | 170.5 | 180.0 | 180.0 | 85.3 | 82.8 |
| D(3)−Cu−D(5) | 98.4 | 111.9 | 92.0 | 91.3 | – | – |
| D(2)−Cu−D(5) | 104.5 | 97.3 | 87.0 | 86.1 | – | – |
| Functional | MAPD Az | SD Az | MPD Az |
|---|---|---|---|
| M06 | 57.0 | 40.3 | 9.0 |
| ω-B97-xD | 19.1 | −9.9 | −0.5 |
| MPW1PW91 | 17.1 | 11.7 | −17.1 |
| B2PLYP | 17.4 | 9.4 | 1.9 |
| BHandHLYP | 14.8 | 9.8 | 6.9 |
| TPSSh | 13.7 | 12.6 | 4.2 |
| CAM-B3LYP | 11.8 | 11.5 | −28.4 |
| PBE0 | 9.5 | 7.1 | −5.0 |
| B3P86 | 9.7 | 4.7 | 9.6 |
| B3PW91 | 9.4 | 4.5 | 5.7 |
| B3LYP | 8.6 | 4.2 | −17.1 |
| Functional | MAPD gz | SD gz | MPD gz |
|---|---|---|---|
| M06 | 4.6 | 6.9 | 1.4 |
| MPW1PW91 | 4.6 | 2.1 | −4.5 |
| TPSSh | 4.5 | 1.9 | −2.7 |
| CAM-B3LYP | 3.4 | 2.5 | 3.9 |
| B3P86 | 3.5 | 1.1 | −2.2 |
| B3LYP | 3.5 | 1.1 | −18.2 |
| B3PW91 | 3.4 | 1.1 | −2.1 |
| ω-B97-xD | 3.1 | 2.5 | −2.9 |
| B2PLYP | 3.1 | 3.5 | −2.9 |
| BHandHLYP | 2.7 | 3.5 | 1.0 |
| PBE0 | 2.9 | 1.1 | −4.3 |
| Protein | gx | gy | gz | Ax1 | Ay1 | Az1 |
|---|---|---|---|---|---|---|
| HSA 2 | 2.045 | 2.045 | 2.173 | 22.0 | 22.0 | 206.6 |
| AspAlaHisLysSer–NHCH3 3 | 2.041 | 2.042 | 2.135 | 16.1 | 20.9 | 204.4 |
| PrP(106–126) [Cu(H–1L)]+ 4 | 5 | 5 | 2.220 | 5 | 5 | 174 |
| Ac–AsnMetLysHisMet–NHCH3 3 | 2.037 | 2.061 | 2.155 | 0.8 | 30.3 | 158.9 |
| PrP (106–126) [Cu(H–2L)] 6 | 5 | 5 | 2.198 | 5 | 5 | 198 |
| Ac–AsnMetLysHisMet–NHCH3 3 | 2.044 | 2.045 | 2.143 | 9.9 | 12.5 | 194.2 |
| PrP (180–193) [Cu(H–2L)] 7 | 5 | 5 | 2.185 | 5 | 5 | 196 |
| Ac–IleLysGlnHisThr–NHCH3 3 | 2.045 | 2.047 | 2.148 | 9.8 | 11.7 | 191.5 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sciortino, G.; Lubinu, G.; Maréchal, J.-D.; Garribba, E. DFT Protocol for EPR Prediction of Paramagnetic Cu(II) Complexes and Application to Protein Binding Sites. Magnetochemistry 2018, 4, 55. https://doi.org/10.3390/magnetochemistry4040055
Sciortino G, Lubinu G, Maréchal J-D, Garribba E. DFT Protocol for EPR Prediction of Paramagnetic Cu(II) Complexes and Application to Protein Binding Sites. Magnetochemistry. 2018; 4(4):55. https://doi.org/10.3390/magnetochemistry4040055
Chicago/Turabian StyleSciortino, Giuseppe, Giuseppe Lubinu, Jean-Didier Maréchal, and Eugenio Garribba. 2018. "DFT Protocol for EPR Prediction of Paramagnetic Cu(II) Complexes and Application to Protein Binding Sites" Magnetochemistry 4, no. 4: 55. https://doi.org/10.3390/magnetochemistry4040055
APA StyleSciortino, G., Lubinu, G., Maréchal, J.-D., & Garribba, E. (2018). DFT Protocol for EPR Prediction of Paramagnetic Cu(II) Complexes and Application to Protein Binding Sites. Magnetochemistry, 4(4), 55. https://doi.org/10.3390/magnetochemistry4040055