Next Article in Journal
DFT Protocol for EPR Prediction of Paramagnetic Cu(II) Complexes and Application to Protein Binding Sites
Next Article in Special Issue
Microstructure and Magnetic Properties of Grain Refined Pr2Co14B Melt-Spun Ribbons
Previous Article in Journal
Synthesis, Structure and Magnetic Study of a Di-Iron Complex Containing N-N Bridges
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Magnetochemistry
Volume 4
Issue 4
10.3390/magnetochemistry4040054
magnetochemistry-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Structural, Magnetic, and Mössbauer Studies of Transition Metal-Doped Gd2Fe16Ga0.5TM0.5 Intermetallic Compounds (TM = Cr, Mn, Co, Ni, Cu, and Zn)

by
J. N. Dahal
1,2,*,
K. S. Syed Ali
3,
S. R. Mishra
2 and
J. Alam
2
1
Department of Physics and Astronomy, Georgia Southern University, Savannah, GA 31419, USA
2
Department of Physics and Materials Science, The University of Memphis, Memphis, TN 38152, USA
3
Department of Science, Harmony Science Academy, 12005 Forestgate Dr., Dallas, TX 75243, USA
*
Author to whom correspondence should be addressed.
Magnetochemistry 2018, 4(4), 54; https://doi.org/10.3390/magnetochemistry4040054
Submission received: 9 September 2018 / Revised: 9 November 2018 / Accepted: 19 November 2018 / Published: 27 November 2018
(This article belongs to the Special Issue Permanent Magnets)
Browse Figures
Versions Notes

Abstract

:
The effect of transition metal substitution for Fe and the structural and magnetic properties of Gd2Fe16Ga0.5TM0.5 (TM = Cr, Mn, Co, Ni, Cu, and Zn) compounds were investigated in this study. Rietveld analysis of X-ray data indicates that all the samples crystallize in the hexagonal Th2Ni17 structure. The lattice parameters a, c, and the unit cell volume show TM ionic radii dependence. Both Ga and TM atoms show preferred site occupancy for 12j and 12k sites. The saturation magnetization at room temperature was observed for Co, Ni, and Cu of 69, 73, and 77 emu/g, respectively, while a minimum value was observed for Zn (62 emu/g) doping in Gd2Fe16Ga0.5TM0.5. The highest Curie temperature of 590 K was observed for Cu doping which is 15 and 5% higher than Gd2Fe17 and Gd2Fe16Ga compounds, respectively. The hyperfine parameters viz. hyperfine field and isomer shift show systematic dependence on the TM atomic number. The observed magnetic and Curie temperature behavior in Gd2Fe16Ga0.5TM0.5 is explained on the basis of Fe(3d)-TM(3d) hybridization. The superior Curie temperature and magnetization value of Co-, Ni-, and Cu-doped Gd2Fe16Ga0.5TM0.5 compounds as compared to pure Gd2Fe17 or Gd2Fe16Ga makes Gd2Fe16Ga0.5TM0.5 a potential candidate for high-temperature industrial magnet applications.

1. Introduction

The rare-earth intermetallic compounds R2Fe17 have energy product (BH)max and Hc to be about 26 MGOe and 15 kOe, respectively [1]. Beside these properties, they exhibit low Curie temperature (Tc). For example, 473 K for Gd2Fe17 and 300 K for Dy2Fe17 along with low magnetic anisotropies [2]. Various strategies have been employed addressing issues related to improving magnetic anisotropy, magnetization, and Curie temperature of R2Fe17 compounds. Metalloids such as C, N, and H atoms are added to improve the magnetic anisotropy and Curie temperature [3,4,5,6]. However, high-temperature processing of these interstitially modified compounds is difficult. Subsequently, the addition of non-magnetic atoms such as Al, Ga, and Si for iron in the R2Fe17−xMx compound was investigated and showed Curie temperature enhancement at high non-magnetic atom content. Among Al, Si, and Ga, Ga substituted compounds show high Tc, e.g., for Sm2Fe16Ga, Tc was ~485 K [7]; for Dy2Fe16Ga, Tc was ~462 K [8]. However, this improvement in Tc is overshadowed by a concomitant deterioration in saturation magnetization as iron atoms are being replaced by non-magnetic atoms.
The Curie temperatures Tc in the R2Fe17 compounds is explained on the basis of exchange interaction strength between Fe–Fe pairs [9]. This is based on the assumption that the exchange interactions favor ferromagnetic (r > rc) or antiferromagnetic (r < rc) properties, where rc ~2.5 Å. Hence, Tc is assumed dependent on the competition between ferromagnetic and antiferromagnetic exchange interactions between neighboring pairs of Fe–Fe ions located at various crystallographic positions. This means that Tc enhancement can be achieved via lattice unit cell expansion, except in Si-substituted RE2Fe17−xSix, favoring ferromagnetic exchange interaction between Fe–Fe pairs. Usually, such lattice expansion is possible either via substituting for Fe ions by ions with the larger ionic radii [10,11] or via insertion of interstitial atoms in the unit cell [12,13]. It was observed that there are two ingredients influencing TC value: local magnetic moment values and exchange interaction values [14].
Among R2Fe17 intermetallic, Gd2Fe17 is of special interest, as it has the highest Curie temperature, TC. Among the doped R2Fe17−xMx (M = Al, Si, Ga), Ga-doped compounds display higher Tc [15]. In this regard, the present work investigates the effect of doping transition metal (TM) atoms in Ga-doped Gd2Fe16Ga0.5TM0.5 compounds and compares the results with Gd2Fe17. It is expected that the doping of TM atoms with ionic radii greater than Fe will bring unit cell volume expansion and hence improve Fe–Fe exchange interaction enough to couple Fe–Fe moments ferromagnetically, thus improving the Curie temperature of the compound. Furthermore, there also lies the possibility of improving magnetic moment of Fe via Fe–TM 3d band hybridization, which can either bring band narrowing or increase exchange splitting by moving the 3d↑ states below the Fermi level or allow charge transfer out of the 3d band, provided that the spin-down density of states exceed the spin-up density [16].
This study discusses the change in the structural and magnetic properties in R2Fe17 compounds when Fe is substituted in R2Fe16Ga0.5TM0.5 compounds with transition metal TM = Cr, Mn, Co, Ni, Cu, and Zn. The main aim of the study is to bring structural and band-related changes to R2Fe17 compounds so as to improve Tc without affecting the saturation magnetization.

2. Experimental Section

The raw materials of Gd, Fe, Ga, and TM (TM = Cr, Mn, Co, Ni, Cu, and Zn) with 99.9% purity were purchased from Sigma Aldrich, USA. The parent alloys Gd2Fe16Ga0.5TM0.5 were prepared by arc melting the stoichiometric amount of the aforementioned elements under a high purity argon atmosphere. The ingots were melted several times to ensure the high degree of homogeneity.
X-ray diffraction (XRD) experiment was carried out with Cu Kα (λ ~1.5406 Å) radiation using a Bruker (D8 Advance) diffractometer. The powder X-ray data sets were collected in the 2θ range from 20 to 75° with a step size of 0.042° and a collection time of 2 s/step. The XRD analysis was performed by the well-known structural refinement Rietveld method [17] using the JANA2006 [18] software package to fit the experimental and calculated diffraction patterns. The initial crystal structure parameters were used as given by Liao et al. [19]. In the hexagonal setting, Gd was fixed at the 2b and 2d site (0, 0, 0.25) and (0.333, 0.667, 0.75), Fe is fixed at 4f, 6g, 12j, and 12k (0.333, 0.667, 0.105), (0.5, 0, 0), (0.333, 0.969, 0.25), and (0.167, 0.333, 0.985). The profile was constructed using a pseudo-Voigt function. Profile asymmetry was introduced by employing the multi-term Simpson rule integration devised by Howard [20]. A surface roughness correction was also applied using the Pitschke, Hermann, and Matter [21] model. In this technique, structural parameters, lattice parameters, peak shift, background profile shape, and preferred orientation parameters were used to minimize the difference between a calculated profile and the observed data.
Magnetic properties of the powder sample were investigated at room temperature (RT) using a vibrating sample magnetometer (VSM) in the maximum field of 1.2 T. To minimize the effect of the demagnetizing field, the samples were compacted at 3000 psi, cut into rectangular parallelepiped with the length-to-width ratio greater than 3, and embedded in epoxy. A modified thermogravimetric analyzer (DuPont 910) equipped with a permanent magnet was used to determine the Curie temperature of composite samples. In this procedure, magnetic material is placed inside an empty, tared, TGA pan located near a strong magnet. The material is then heated. At the Curie temperature, Tc, the magnetic properties disappear (i.e., the material goes from ferromagnetic to paramagnetic), and the reduced attraction for the magnet results in a sharp apparent weight loss or gain (depending on the TGA design).
The Mössbauer spectra of the samples were obtained at RT using a 25 mCi 57Co source in a Rh foil mounted on a constant acceleration drive system (SEE Co., Minneapolis, MN, USA) in transmission geometry. The velocity scale of the Mössbauer spectrometer was calibrated by measuring the hyperfine field of α-Fe foil, at room temperature. The Mössbauer spectra were analyzed using WMoss software from SEE Co. They were fitted using a standard nonlinear least squares minimization routine with sub-spectra intensities constrained to match crystallographic probabilities.

3. Results and Discussion

The raw powder profile for Gd2Fe16Ga0.5TM0.5 systems is presented in Figure 1a. The inset in Figure 1a, the enlarged 2θ view between 41.5 and 43.3°, shows that there is a shift in 2θ towards the lower angle, which indicates the expansion of the unit cell with the substitution of increasing atomic number of TM in the compound. This observation is in accordance with the increasing size of the substitution atom whose metallic radii increases from TM = Cr to Zn (Table 1). The refined Rietveld profiles are presented in Figure 1b for Gd2Fe16Ga0.5TM0.5 systems. In Table 1, the Robs values are calculated from the observed and calculated structure factors. Since it is a mixed system, the Robs possibly adds errors (less than 5%) in the structure factor. These small errors reflect on the low angle, and the intensity counts range is between 25 and 100, which is minimal. This error may be because of multiple factors such as background errors, the preferred orientation, multiplicity factors, and instrumental errors. Moreover, these errors are minimal when compared to the high angle reflection 2θ range of 35–45°. The refined structural parameters viz. lattice parameters a, c, the c/a ratio, the unit cell volume, and the reliability indices are given in Table 1. From the Rietveld analysis, the refined profile indicates that Gd2Fe16Ga0.5TM0.5 compounds crystallize in the hexagonal Th2Ni17 structure with the P63/mmc symmetry group. Figure 2 show the lattice parameters as a function of the TM atomic number in Gd2Fe16Ga0.5TM0.5. It can be observed in Figure 2 that the variation in lattice parameter, a, is more pronounced than that in c in the doped compounds. This is also evident from the variation in the c/a ratio (Table 1), which indicates the anisotropic expansion of unit cell volume with TM atom doping. The doping of Cr up to Co brings lattice contraction while Ni, Cu, and Zn brings about lattice expansion. The observed trend in lattice parameter closely follows TM metallic radii (Figure 2).
The atomic site occupancy for Gd, Fe, Ga, and TM atoms derived from Rietveld refinement are listed in Table 2. The site notations are given for rhombohedral structure with corresponding hexagonal notation viz. 6c(4f), 9d(6g), 18f(12j), and 18h(12k). The crystallographic site preference exhibited by TM in Gd2Fe16Ga0.5TM0.5 is listed in Table 2. It is evident from Table 2 that Ga prefers 12j and 12k sites, and TM avoids 4f sites and prefers to remain closer to Ga at 12j and 12k sites. The TM atoms display occupancy preference with the order 12j~12k > 6g > 4f. Thus, the 6c(4f) dumbbell site is the least affected site by the TM substitution. Results of site occupancy are in close conformity with the previous Neutron diffraction [22,23] and 57Fe Mössbauer studies [24,25,26] on R2Fe17−xGax where Ga atoms preferentially occupy mainly the 18h(12k) site in the Th2Zn17 structure for x < 4. The number of Fe and R nearest neighbors (NNs) for Fe atoms at various crystallographic sites in R2Fe17 compounds is as follows; at the Fe 6c site (dumbbell site), there are 13 Fe NNs and 1 R NNs; at the Fe 9d site, there are 10 Fe NNs and 2 R NNs; at Fe 18f, there are 10 Fe NNs and 2 R NNs; at the Fe 18h site there are 9 Fe NNs and 3 R NNs. In addition, the Wigner–Seitz cell volume follows 6c(4f) > 18h(12k) > 18f(12j) > 9d(6g). This shows that Ga and TM atoms for 12j and 12k sites suggest that the Ga affinity for R atoms surpasses the Wigner–Seitz site volume [15].
The Fe–Fe site-to-site bond distances are listed in Table 3 and are plotted in Figure 3. It can be observed in Table 3 that the 4f-4f bond distances are smallest (~2.40 Å), and 12k-12k (2.46 Å) and 12j-12j (2.57 Å) distances are greatest of all. Other bond distances such as 6g-12j, 6g-12k, and 12k-12k have values close to 2.45 Å and do not show much variation with TM doping. It is to be noted that because of the aforementioned variation in bond distances, it is highly unlikely that these bond-length changes will have a drastic effect on the Curie temperature of the compounds. In fact, a slight reduction in bond distances is observed up to Cu substitution, which ideally should lead to an increase in antiferromagnetic exchange coupling between Fe–Fe moments and hence Curie temperature reduction. The observed changes in bond distances are in line with the metallic radii of the TM atoms (Figure 2).
RT magnetization vs. field plot for Gd2Fe16Ga0.5TM0.5 is shown in Figure 4. The RT magnetic parameters derived from the hysteresis curves are plotted in Figure 5 and are listed in Table 4. The “law of approach” to saturation magnetization was used to determine the saturation magnetization, Ms. The law of approach describes the relationship between magnetization M on the applied magnetic field for H greater than coercive field Hc. The magnetization near Ms can be written as [27], M = M s ( 1 − a H − b H 2 ) + κ H , where M is the magnetization, H is the applied magnetic field, and MS is the saturation magnetization attained at a high field. The term κH represents the field-induced increase in the spontaneous magnetization of the domains. This term is very small at a temperature well below the Curie temperature and could be neglected. The term “a” is generally interpreted as due to microstress and ignored in the high field region, and “b” as due to crystal anisotropy. Where magneto-crystalline is a dominant term, a plot of M vs. 1/H2 in the high field region gives a straight line, the intercept of which (with the M-axis) gives the Ms and the slope of which gives the magneto-crystalline anisotropy constant. Interesting variation in Ms is noticed with the TM atom doping. The Ms was observed to decrease first with Cr and Mn doping and then increase with TM atomic number up to Cu, and it decreased for Zn and Ga doping. The highest Ms ~77 emu/g was observed with Cu doping in Gd2Fe16Ga0.5TM0.5, while a low Ms was observed upon Cr (60 emu/g), Mn (57 emu/g), and Zn (59 emu/g) doping. As compared to Gd2Fe17 (67 emu/g), Gd2Fe16Ga0.5Cu0.5 (77 emu/g) showed an increase of 15% in the Ms value. The observed variation in Ms can be attributed to the Fe(3d)-TM(3d) hybridization effect of orbitals. The extent of Fe(3d)-3d hybridization raises or lowers the bandwidth, which eventually changes the magnetic moment of Fe atoms [28,29]. The electronic configuration of TM atoms is Cr ([Ar]4s13d5), Mn [Ar]4s23d5, Fe [Ar]4s23d6, Co [Ar]4s23d7, Ni [Ar]4s23d8, Cu [Ar]4s13d10, Zn [Ar]4s23d10, and Ga [Ar] 4s2 4p13d10). In the case of early transition metals, 3d states are positioned at higher energies than those of Fe. Due to exchange splitting, 3d↓ spin-down states moved up in energy and were therefore close to the 3d states of early transition metals. Thus, the hybridization of 3d states of early transition metals is stronger with 3d↓ spin-down states than with 3d↑ spin-up states of Fe. As a result, the fraction of spin down 3d↓ states of early transition metals found in the energy region of Fe–3d is increased. Since the Fermi level is situated in this region, anti-ferromagnetic coupling follows. For the late transition metals, the situation is reversed, and ferromagnetic coupling follows [30,31,32]. Given this explanation, Cr- and Mn-doped Gd2Fe16Ga0.5TM0.5 show lower magnetization while Co-, Ni-, and Cu-doped samples show increasingly higher magnetization. A rather rapid decrease in Ms has been reported in Er2Fe17−xMnx with increasing Mn content and has been attributed to the antiferromagnetic coupling between Fe and Mn [33]. The lower magnetization values of Zn and Ga results from the magnetic dilution effect upon replacing magnetic Fe with non-magnetic Zn and Ga atoms.
The measured Curie temperature, Tc, of Gd2Fe16Ga0.5TM0.5 compounds is plotted in Figure 5 as a function of TM atomic number. It is evident from Figure 5 that the TM doping affects the Tc of Gd2Fe16Ga0.5TM0.5 compounds. The Curie temperature reaches a maximum value of 587 K for Co doping followed by a reduction in Tc with increasing TM atomic number. A 15% increase in Tc was observed upon Co doping in Gd2Fe16Ga0.5TM0.5 as compared to that of Gd2Fe17 (513 K) and a 4% increase as compared to Gd2Fe16Ga (559K). In the Fe-rich R2Fe17 intermetallic, the Tc is mainly determined by the strength and number of Fe–Fe exchange interactions. The strength of Fe–Fe exchange interaction is strongly dependent on the interatomic Fe–Fe distances described [9,34,35,36]. Accordingly, the exchange interactions between iron atoms situated at distances smaller (greater) than 2.45−2.50 Å are negative (positive). In the R2Fe17 majority of Fe–Fe, distances favor a negative interaction [37]. The negative exchange interaction can be reduced either by volume expansion or by reducing the number of Fe–Fe pairs with negative exchange interactions. The low TC observed in parent Gd2Fe17 compound is believed to be due to the short Fe–Fe interatomic distances found at the 4f(6c) sites in the hexagonal (rhombohedral) structure, which couple antiferromagnetically since their separation is ~2.4 Å (Figure 3), which is less than 2.45 Å needed for ferromagnetic ordering [38]. It is to be noted that the increase in Tc has been reported earlier with higher Al, Ga, and Si content (at x > 2) in R2Fe17−xMx (M = Al, Ga, and Si) [15] but with a concomitant reduction in Ms due to large Fe replacement with non-magnetic atoms. A Tc value of 581 K has been reported earlier in the YGdFe16CoGa [39] compound, but a reported Tc ~586 K of Gd2Fe16Ga0.5Co0.5 exceeds that of the former compounds. Thus, the observed increase in Tc in TM-doped Gd2Fe16Ga0.5TM0.5 compounds is highest with a minimum replacement of Fe atoms.
The Friedel model [40] can also be used to explain the observed variation in Tc. According to this model, the strength of interaction between two magnetic moments would be strong and ferromagnetic, if λ/d > 1, where distance “d” between these magnetic atoms is smaller than the distance “λ” covered by the main peak of the Friedel oscillations. In compounds containing 3d transition metals, it has been established that the magnetic coupling is governed mainly by the NN interactions and is proportional to the lattice parameters. Furthermore, λ is found to be inversely proportional to the Fermi wave vector, kf. For the 3d band in the R2Fe17 compounds, kf is large. Substitution of TM decreases the holes in the 3d-band and hence decreases kf. The substitution of Ga leads to lattice expansion and hence increases “d”, which will have an effect of reducing the λ/d ratio. Since the substitution of Co, Ni, and Cu brings in lattice volume reduction as compared to R2Fe16Ga; there is hence an increase in the λ/d > 1 and Tc [39,40]. The reported theoretical studies attribute changes in the Curie temperature in substituted R2Fe17−xTx (T = Al, Si, Ga, and Ti) intermetallic to be electronic in origin other than due to the simple volume expansion effect and hence bond distances [41,42,43]. The effect of the substitution is to fill out the Fe–3d spin-up sub-bands, which alter the magnetic moment of the compound and hence the strength of exchange interaction [41,44]. In fact, theoretical calculations performed using the LSDA+U method showed enhancement between Fe–Fe atoms in the presence of Ga in Gd2Fe17−xGax compounds, which in turn was shown to enhance Tc for low Ga (x < 3) content [45]. Thus, the higher Tc values of Gd2Fe16Ga0.5TM0.5 as compared to that of pure Gd2Fe17 could be attributed to this effect as well. In comparison to various doped intermetallic such as Gd2Fe16Ga (~410 K) [46], Gd2Fe16Ga0.5Ti0.5 (556 K) [47], Dy2Fe16Ga (~462 K) [8], Ce2Fe16Ga (~320 K) [48], Sm2Fe16Ga (~505 K) [49], or Sm2Fe16.2Ti0.8 (~435 K) [50], the reported compound Gd2Fe16Ga0.5TM0.5 with Co, Ni, and Cu substitution certainly exhibits higher Tc and Ms, thus ensuring their potential use as high-temperature permanent magnet applications.
The room temperature (RT) Mössbauer spectra for Gd2Fe16Ga0.5TM0.5 are shown in Figure 6. The intermetallic R2Fe17 with a Th2Ni17 structure have the easy direction of magnetization and hyperfine field lying in the basal plane along the a or b axes of the unit cell [51,52]. This easy basal plane direction of magnetization complicates the Mössbauer spectral analysis of R2Fe17 compounds because it involves four crystallographically inequivalent iron sites. The reason for the inequivalent iron site is the vector character of the hyperfine field and tensor character of the electric field gradient [53]. Thus, this inequivalency demands further magnetic splitting of g, j, and k iron sites. Mössbauer studies of Gd2Fe16Ga0.5TM0.5 have been conducted accordingly, either with 8 or 10 magnetic sextets, with an absence or presence of impurity phase, respectively [48,54,55,56]. The Mössbauer spectral analysis was carried out with magnetic sextets assigned to the 4f, 6g, 12j, and 12k sites in Gd2Fe17. The 6g, 12j, and 12k sites were further split into 2, 3, and 2 corresponding to the site occupancies of Fe atoms in the crystal structure of R2Fe17 with the planar anisotropy. The intensities of the six absorption lines of each sextet were assumed to follow the 3:2:1 intensity ratio expected for randomly oriented powder samples in zero magnetic fields and a single common line-width was assumed for all eight sextets. The isomer shifts (IS, δ) for the magnetically inequivalent sites were constrained to be the same, whereas the hyperfine field (HF, Bhf) was expected to vary at pairs of magnetically inequivalent sites due to variations in the dipolar and orbital contributions to the magnetic hyperfine fields [57]. The 57Fe Mössbauer spectra show hyperfine split sextets in Gd2Fe16Ga0.5TM0.5, revealing that the samples are magnetically ordered, and all of them have different sub-spectra with different magnetic hyperfine fields.
The hyperfine parameters derived from the fitting are listed in Table 5, and weighted average (Wt.Avg.) hyperfine field (HF) and isomer shifts (IS, δ) are plotted in Figure 7. There exists a direct correlation between hyperfine field values of a site to its near neighbor (NN) iron sites. In case of Th2Ni17 structure, 12k site has 9 NN Fe sites (1(4f), 2(6g), 4(12j), 2(12k)), 12j has 10 NN Fe sites (2 (4f), 2(6g), 2(12j), 4(12k)), 6g has 10 NN Fe sites (2(4f), 0(6g), 4(12j), 4(12k)), and 4f site has 11 NN Fe sites (1(4f), 3(6g), 6(12j), 3(12k)). Following the NN distribution, the observed HF values are in 4f(6c) > 12j(18f) > 6g(9d) > 12k(18h) sequence, which is similar to the sequence observed in other R2Fe17 compounds [58,59]. It is obvious that 4f (6c) site has the maximum hyperfine field, since it has the maximum number of Fe nearest neighbors, whereas, the 18h (12k) site has the minimum number of Fe neighbors and consequently has the least HF value. Although 6g(9d) and 12j(18f) sites have the same number of Fe neighbors, the former has comparatively smaller Fe-Fe distances, and hence a larger hyperfine field, Table 3 and Table 5. The Cu and Mn-doped Gd2Fe16Ga0.5TM0.5 display a low Wt. Avg. HF values as compared to other TM doped Gd2Fe16Ga0.5TM0.5 compounds. The Wt. Avg. HF value reaches the maximum for Gd2Fe17 and Gd2Fe16Ga0.5Co0.5, to a value ~252 kOe followed with a gradual decline in its value, reaching a value of 246 kOe for Gd2Fe16Ga1. This decrease in HF value results from the decreased magnetic exchange interactions resulting from Fe replacement with non-magnetic Cu, Zn, and Ga atoms. Furthermore, under the first approximation, the hyperfine field is assumed proportional to the magnetic moment. We obtained the Fe moment using the hyperfine coupling constant of 150 kOe/μB, which has been reported for Y–Fe systems [60,61]. The average value of Fe magnetic moment for Gd2Fe16Ga0.5TM0.5 is plotted in Figure 5. In general, Fe magnetic moment holds up to the value of 1.68 μB only for Fe, Co, and Ni substitution in Gd2Fe16Ga0.5TM0.5.
The isomer shift values were assigned in relation to the Wigner–Seitz cell volume, i.e., the greater the Wigner–Seitz cell volume, the greater the isomer shift (Table 5) [62]. Therefore, as V(4f) > V(12j)~V(12k) > V(6g), their corresponding IS is as follows: δ4f > δ12j~δ12k > δ6g. The room temperature values of Wt.Avg. IS for Gd2Fe16Ga0.5TM0.5 are negative, and the magnitudes of IS increase with an increasing TM atomic number in Gd2Fe16Ga0.5TM0.5. The IS is proportional to the total s-electron charge density at the iron nucleus, which is the sum of the spin-up and spin-down s-electron density and lattice site volume; an increasing s-electron density at the iron nucleus is indicated by a decreasing isomer shift. The observed behavior of the IS value could be attributed to the competition between lattice site volume and the complex nature of hybridization in Fe–Ga–TM [63,64], which all affect the s-electron charge density at the iron nucleus. A volume contraction is observed until TM = Ni, followed by unit cell expansion until TM = Zn doping in Gd2Fe16Ga0.5TM0.5. However, the Wt.Avg. IS value becomes less negative with TM = Co and onward. Thus, this behavior of IS indicates electronic effects at play in dictating IS behavior of the Gd2Fe16Ga0.5TM0.5 compound. The increased IS value with Co, Ni, Cu, Zn, and Ga in Gd2Fe16Ga0.5TM0.5 could be associated with the increased number of the 3d electrons, which increases the shielding of the s-electrons from the nucleus. In earlier TM atoms viz. Cr and Mn, the 3d band is broader and heavily hybridized with the conduction band [40]. These make electrons freer and thus have a greater presence at the Fe nucleus, which makes IS more negative. The increased screening of s-electrons via 3d electrons beyond TM = Fe doping in Gd2Fe16Ga0.5TM0.5 could be the reason for enhanced IS.

4. Conclusions

The effect of double substitution of Ga and TM in Gd2Fe16Ga0.5TM0.5 on structural and magnetic properties was compared with Gd2Fe17 compounds. These compounds were found to crystallize in a hexagonal Th2Ni17 structure. Lattice parameters and unit cell volume of TM-doped Gd2Fe16Ga0.5TM0.5 compounds showed dependence on the atomic radii of the TM dopant. The variance of the c/a ratio with the substation in these compounds showed anisotropic unit cell volume expansion. The Rietveld analysis showed the preferred occupancy of TM for 12k and Ga for 12k and 12j sites. Overall, no direct correlation was observed between the trend in Curie temperature and bond distances. The observed Tc reached a maximum value of 587 K for cobalt substitution, which is 15% higher than the Tc value of Gd2Fe17. Furthermore, 15% and 14% enhancement in Ms was observed for Cu-substituted Gd2Fe16Ga0.5TM0.5 compound as compared to Dy2Fe17 and Dy2Fe16Ga1 compounds, respectively. Furthermore, unlike other doped compounds of intermetallic RE2Fe17−xMx (M = Al, Si, Ga), where improvements in Tc is compromised with the reduction in Ms, in the present studied compound Gd2Fe16Ga0.5TM0.5, even small TM doping (TM = Co, Ni, and Cu) brought about a simultaneous enhancement in Ms and Tc. The combined magnetic and Mössbauer study points to the fact that the observed improvement in Tc and Ms could be attributed to electronic effects resulting from Fe–3d hybridization with a substituted TM atom electronic shell. A concomitant improvement in Ms and Tc is desirable for the magnetic industry. The study elucidates that the judicious selection of dopants and its content can improve the Ms and Tc of the R2Fe17 intermetallic compounds.

Author Contributions

Data Curation, Methodology and writing original draft preparation, J.N.D.; Revising/Editing the original draft, S.R.M.; Rietveld analysis, K.S.S.A.; Revising the paper, J.A.

Funding

This research was funded by NSF-CMMI (Grant #: 1029780) and NSF-TN-SCORE (Grant #: EPS-10004083).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. National Imports LLC. Permanent Magnet Selection and Design Handbook; Magcraft, Advance Magnetic Materials: Vienna, VA, USA, 2007. [Google Scholar]
  2. Strnat, K.J. Chapter 2—Rare earth-cobalt permanent magnets. Handb. Ferromagn. Mater. 1988, 4, 131–209. [Google Scholar]
  3. Coey, J.M.D.; Sun, H. Improved magnetic properties by treatment of iron-based rare earth intermetallic compounds in ammonia. J. Magn. Magn. Mater. 1990, 87, L251. [Google Scholar] [CrossRef]
  4. Coey, J.M.D.; Sun, H.; Otani, Y.; Hurley, D.P.F. Gas-phase carbonation of R2Fe17; R = Y, Sm. J. Magn. Magn. Mater. 1991, 98, 76–78. [Google Scholar] [CrossRef]
  5. Zhong, X.P.; Radwanski, R.J.; de Boer, F.R.; Jacobs, T.H.; Buschow, K.H.J. Magnetic and crystallographic characteristics of rare-earth ternary carbides derived from R2Fe17 compounds. J. Magn. Magn. Mater. 1990, 86, 333–340. [Google Scholar] [CrossRef]
  6. Buschow, K.H.J.; Coehoorn, R.; de Mooij, D.B.; de Waard, K.; Jacobs, T.H. Structure and magnetic properties of R2Fe17Nx compounds. J. Magn. Magn. Mater. 1990, 92, L35. [Google Scholar] [CrossRef]
  7. Xu, R.; Zhen, L.; Yang, D.; Wu, J.; Wang, X.; Wang, Q.; Chen, C.; Dai, L. Effect of Ga on the structural stablity of Sm2(FeGa)17 compounds. Mater. Lett. 2002, 57, 146. [Google Scholar] [CrossRef]
  8. Shen, B.G.; Cheng, Z.H.; Gong, H.Y.; Liang, B.; Yan, Q.W.; Zhan, W.S. Magnetic anisotropy of Dy2Fe17−xGax compounds. Solid State Commun. 1995, 95, 813–816. [Google Scholar] [CrossRef]
  9. Givord, D.; Lemaire, R. Magnetic transition and anomalous thermal expansion in R2Fe17 compounds. IEEE Trans. Magn. 1974, 10, 109–113. [Google Scholar] [CrossRef]
  10. Jacobs, T.H.; Buschow, K.H.J.; Zhou, G.F.; Li, X.; de Boer, F.R. Magnetic interactions in R2Fe17−xAlx compounds (R = Ho, Y). J. Magn. Magn. Mater. 1992, 116, 220–230. [Google Scholar] [CrossRef]
  11. Shen, B.G.; Wang, F.W.; Kong, L.S.; Cao, L. Magnetic anisotropy of Sm2Fe17−xGax compounds with 0 ⩽x ⩽6. J. Phys. Condens. Matter 1993, 5, L685. [Google Scholar] [CrossRef]
  12. Sun, H.; Coey, J.M.D.; Otani, Y.; Hurley, D.P.F. Magnetic properties of a new series of rare-earth iron nitrides: R2Fe17Ny(y approximately 2.6). J. Phys. Condens. Matter 1990, 2, 6465. [Google Scholar] [CrossRef]
  13. De Mooij, D.B.; Buschow, K.H.J. Formation and magnetic properties of the compounds R2Fe14C. J. Less-Common Met. 1988, 142, 349–357. [Google Scholar] [CrossRef]
  14. Lukoyanov, A.V.; Kokorina, E.E.; Medvedev, M.V.; Nekrasov, I.A. Ab initio exchange interactions and magnetic properties of Gd2Fe17 iron sublattice: Rhombohedral vs. hexagonal phases. Phys. Rev. B 2009, 80, 104409. [Google Scholar] [CrossRef]
  15. Rao, K.V.S.R.; Ehrenberg, H.; Markandeyulu, G.; Varadaraju, U.V.; Venkatesan, M.; Suresh, K.G.; Murthy, V.S.; Schmidt, P.C.; Fuess, H. On the Structural and Magnetic Properties of R2Fe17–x(A,T)x (R =Rare Earth; A Al, Si, Ga; T= Transition Metal)Compounds. Phys. Status Solid (a) 2002, 189, 373–388. [Google Scholar] [CrossRef]
  16. Coey, J.M.D. New permanent magnets; manganese compounds. J. Phys. Condens. Matter 2014, 26, 064211. [Google Scholar] [CrossRef] [PubMed]
  17. Rietveld, H.M. A profile refinement method for nuclear and magnetic structures. J. Appl. Cryst. 1969, 2, 65–71. [Google Scholar] [CrossRef] [Green Version]
  18. Petříček, V.; Dušek, M.; Palatinus, L. Crystallographic Computing System JANA2006: General features. Z. Kristallogr. 2014, 229, 345. [Google Scholar] [CrossRef]
  19. Liao, L.X.; Altounican, Z.; Ryan, D.H. Cobalt site preferences in iron rare-earth-based compounds. Phy. Rev. B 1993, 47, 11230–11241. [Google Scholar] [CrossRef] [Green Version]
  20. Howard, C.J. The approximation of asymmetric neutron powder diffraction peaks by sums of Gaussians. J. Appl. Crystallogr. 1982, 15, 615–620. [Google Scholar] [CrossRef]
  21. Pitschke, W.; Hermann, H.; Mattern, N. The influence of surface roughness on diffracted X-ray intensities in Bragg–Brentano geometry and its effect on the structure determination by means of Rietveld analysis. Powder Diffr. 1993, 8, 74–83. [Google Scholar] [CrossRef]
  22. Yang, Q.W.; Yan, Q.W.; Zhang, P.L.; Shen, B.G.; Lang, F.W.; Kong, L.S.; Gou, C.; Chen, D.F.; Cheng, Y.F. A neutron powder diffraction study of the structure of Ho2Fe17−xGaxC2 (x = 4.0 and 5.5). J. Phys. Condens. Mater. 1994, 6, 3567–3572. [Google Scholar]
  23. Hu, Z.; Yelon, W.B.; Mishra, S.; Long, G.J.; Pringle, O.A.; Middleton, D.P.; Buschow, K.H.J.; Grandjean, F. A magnetic, neutron diffraction, and Mössbauer spectral study of Nd2Fe15Ga2 and the Tb2Fe17−xGax solid solutions. J. Appl. Phys. 1994, 76, 443. [Google Scholar] [CrossRef]
  24. Morariu, M.; Rogalski, M.S. 57Fe Mössbauer study of Y2Fe16M compounds and their nitrides with M = Ga, V. Phys. Status Solidi A 1994, 141, 223–230. [Google Scholar] [CrossRef]
  25. Cadogan, J.M.; Li, H.S.; Margarian, A.; Dunlop, J.B. On the ternary intermetallic phases formed by YFe12−xGax (1⩽x⩽ 2). Mater. Lett. 1993, 18, 39–43. [Google Scholar] [CrossRef]
  26. Li, H.-S.; Suharyana; Cadogan, J.M.; Ju, B.-P.; Shen, B.-G.; Wang, F.-W.; Zhan, W.-S. A Mossbauer study of Sm2Fe14Ga3Cx (x=0–2.5). IEEE Trans. Mag. 1995, 31, 3716–3718. [Google Scholar]
  27. Chikazumi, S.; Graham, C.D. Physics of Ferromagnetism, 2nd ed.; Oxford University Press: New York, NY, USA, 2009; Volume 94. [Google Scholar]
  28. Huang, M.Z.; Ching, W.Y. Effects of Al substitution in Nd2Fe17 studied by first principles calculations. J. Appl. Phys. 1994, 76, 7046. [Google Scholar] [CrossRef]
  29. Huang, M.Z.; Ching, W.Y. First principles calculation of the electronic and magnetic properties of Nd2Fe17−xMx (M = Si, Ga) solid solutions. J. Appl. Phys. 1996, 79, 5545. [Google Scholar] [CrossRef]
  30. Akai, M.; Akai, H.; Kanamori, J. Electronic Structure of Impurities in Ferromagnetic Iron. II. 3d and 4d Impurities. J. Phys. Soc. Jpn. 1985, 54, 4257–4264. [Google Scholar] [CrossRef]
  31. Drittler, B.; Stefanou, N.; Blugel, S.; Zeller, R.; Dederichs, P.H. Electronic structure and magnetic properties of dilute Fe alloys with transition-metal impurities. Phys. Rev. B 1989, 40, 8203. [Google Scholar] [CrossRef]
  32. Mirbt, S.; Eriksson, O.; Johansson, B.; Skriver, H.L. Magnetic coupling in 3d transition-metal monolayers and bilayers on bcc (100) iron. Phys. Rev. B 1995, 52, 15070. [Google Scholar] [CrossRef]
  33. Wang, J.L.; Ibarra, M.R.; Marquina, C.; García-Landa, B.; Li, W.X.; Tang, N.; Wang, W.Q.; Yang, F.M.; Wu, G.H. Effect of Mn substitution on the volume and magnetic properties of Er2Fe17. J. Appl. Phys. 2002, 92, 1453. [Google Scholar] [CrossRef]
  34. Neél, L. Propriétés magnétiques de l’état métallique et énergie d’interaction entre atomes magnétiques. Ann. Phys. 1936, 5, 232–279. [Google Scholar] [CrossRef]
  35. Li, Z.W.; Morrish, A.H. Negative exchange interactions and Curie temperatures for Sm2Fe17 and Sm2Fe17Ny. Phys. Rev. B 1997, 55, 3670. [Google Scholar] [CrossRef]
  36. Dahal, J.N.; Wang, L.; Mishra, S.R.; Nguyen, V.V.; Liu, J.P. Synthesis and magnetic properties of SrFe12−x−yAlxCoyO19 nanocomposites prepared via autocombustion technique. J. Alloy. Comp. 2014, 595, 213–220. [Google Scholar] [CrossRef]
  37. Shen, B.G.; Cheng, Z.H.; Liang, B.; Guo, H.Q.; Zhang, J.X.; Gong, H.Y.; Wang, F.W.; Yan, Q.W.; Zhan, W.S. Structure and magnetocrystalline anisotropy of R2Fe17−xGax compounds with higher Ga concentration. Appl. Phys. Lett. 1995, 67, 1621. [Google Scholar] [CrossRef]
  38. Valeanu, M.; Plugaru, N.; Burzo, E. Effect of nitrogenation on the magnetic properties of Y2Fe17−xMx compounds, with M = Al, Ga or Si. Solid State Commun. 1994, 89, 519–522. [Google Scholar] [CrossRef]
  39. Srilatha, R.; Markandeyulu, G.; Murty, V. Effect of Co on the Magnetic Properties of YGdFe17−xCoxGa. IEEE Trans. Magn. 2006, 42, 917. [Google Scholar] [CrossRef]
  40. Friedel, J.; Leman, G.; Olszewski, S. On the Nature of the Magnetic Couplings in Transitional Metals. J. Appl. Phys. Suppl. 1961, 32, 325S. [Google Scholar] [CrossRef]
  41. Sabirianov, R.F.; Jaswal, S.S. Electronic structure and magnetism in Sm2Fe17−xAx (A = Al, Ga, Si). J. Appl. Phys. 1996, 79, 5942. [Google Scholar] [CrossRef]
  42. Li, H.-S.; Coey, J.M.D. Handbook of Magnetic Materials; Buschow, K.H.J., Ed.; Elsevier: Amsterdam, The Netherlands, 1991; Volume 6, Chapter I; p. 1. [Google Scholar]
  43. Ching, W.Y.; Huang, M.Z. Band Theoretical Investigation of Curie Temperatures of Modified R2Fe17-Based Intermetallic Compounds. J. Appl. Phys. 1996, 79, 4602. [Google Scholar] [CrossRef]
  44. Hu, B.-P.; Li, H.-S.; Shen, B.-G.; Wang, F.-W.; Cadogan, J.M.; Zhan, W.-S. A 57Fe Mossbauer study of Gd2Fe17−xGaxC2 (x = 0–6). J. Appl. Phys. 1996, 79, 5713. [Google Scholar] [CrossRef]
  45. Kokorina, E.E.; Medvedev, M.V.; Nekrasov, I.A. Ab Initio Exchange Interactions and Magnetic Properties of Intermetallic Compound Gd2Fe17−xGax. Solid State Phenom. 2010, 168–169, 196–199. [Google Scholar] [CrossRef]
  46. Cheng, Z.H.; Shen, B.G.; Liang, B.; Zhang, J.X.; Wang, F.W.; Zhang, S.Y.; Zhao, J.G.; Zhan, W.S. Ga-concentration dependence of magnetocrystalline anisotropy in Gd2Fe17−xGax Compounds. J. Appl. Phys. 1995, 78, 1385. [Google Scholar] [CrossRef]
  47. Pokharel, G.; Ali, K.S.S.; Mishra, S.R. Structural, magnetic and Mossbauer studies of Ti doped Gd2Fe17−xTix and Gd2Fe16Ga1−xTix (0 ≤ x ≤1). J. Magn. Magn. Mater. 2015, 382, 31–42. [Google Scholar] [CrossRef]
  48. Long, G.J.; Mishra, S.R.; Pringle, O.A.; Hu, Z.; Yelon, W.B.; Grandjean, F.; Middleton, D.P.; Buschow, K.H.J. A magnetic, neutron diffraction, and Mossbauer spectral study of the Ce2Fe17-xGax solid solutions. J. Magn. Magn. Mater. 1997, 176, 217–232. [Google Scholar] [CrossRef]
  49. Maruyama, F. Exchange interactions in R2Fe17−xGax (R =Y, Sm, Gd, Tb, Ho and Tm) compounds. J. Solid State Chem. 2005, 178, 3020–3026. [Google Scholar] [CrossRef]
  50. Paoluzi, A.; Pareti, L. Magnetocrystalline anisotropy of Fe and Sm sublattices in Sm2Fe17: Effects of Ti substitution for Fe. J. Mang. Magn. Mater. 1998, 189, 89–95. [Google Scholar] [CrossRef]
  51. Liao, L. Cobalt Site in Iron Rare-Earth Based Compounds. Ph.D. Thesis, McGill University, Montréal, QC, Canada, 1992. [Google Scholar]
  52. Gubbens, P.C.M.; Buschow, K.H.J. Magnetic phase transition in Tm2Fe17. J. Appl. Phys. 1973, 44, 3739. [Google Scholar] [CrossRef]
  53. Isnard, O.; Hautot, D.; Long, G.J.; Grandjean, F. A structural, magnetic, and Mössbauer spectral study of Dy2Fe17 and its hydrides. J. Appl. Phys. 2000, 88, 2750. [Google Scholar] [CrossRef]
  54. Buschow, K.H.J.; Wieringen, J.S.V. Crystal structure and magnetic properties of cerium-iron compounds. Phys. Status Solidi 1970, 42, 231–239. [Google Scholar] [CrossRef]
  55. Levinson, L.M.; Rosenberg, E.; Shaulov, A.; Strnat, K. Mössbauer Study of Some 2–17 Lanthanide-Iron Compounds. J. Appl. Phys. 1970, 41, 910. [Google Scholar] [CrossRef]
  56. Alp, E.E.; Umarji, A.M.; Malik, S.K.; Shenoy, G.K.; Huang, M.Q.; Boltich, E.B.; Wallace, W.E. 57Fe Mössbauer studies on Si-substituted Er2Fe17. J. Magn. Magn. Mater. 1987, 68, 305–308. [Google Scholar] [CrossRef]
  57. Wang, J.L.; Campbell, S.J.; Tegus, O.; Marquina, C.; Ibarra, M.R. Magnetovolume effect and magnetic properties of Dy2Fe17−xMnx. Phys. Rev. B 2007, 75, 174423. [Google Scholar] [CrossRef]
  58. Grandjean, F.; Isnard, O.; Long, G.J. Magnetic and Mossbauer spectral evidence for the suppression of the magnetic spin reorientation in Tm2Fe17 by deuterium. Phys. Rev. B 2002, 65, 064429. [Google Scholar] [CrossRef]
  59. Long, G.J.; Isnard, O.; Grandjean, F. A Mossbauer spectral study of the magnetic properties of Ho2Fe17 and Ho2Fe17D3.8. J. Appl. Phys. 2002, 91, 1423. [Google Scholar] [CrossRef]
  60. Gubbens, P.C.M.; van Apeldoorn, J.H.F.; van der Kraan, A.M.; Buschow, K.H.J. Mossbauer effect investigation of Y-Fe compounds. J. Phys. F Met. Phys. 1974, 4, 921. [Google Scholar] [CrossRef]
  61. Dubiel, S.M. Relationship between the magnetic hyperfine field and the magnetic moment. J. Alloy. Comp. 2009, 488, 18–22. [Google Scholar] [CrossRef] [Green Version]
  62. Long, G.J.; Pringle, O.A.; Grandjean, F.; Buschow, K.H.J. A Mössbauer effect study of the microscopic magnetic properties of Nd2Fe17 and Nd2Fe17N2.6. J. Appl. Phys. 1992, 72, 4845. [Google Scholar] [CrossRef]
  63. Halasa, N.A.; de Pasquali, G.; Drickamer, H.G. High-pressure studies on ferrites. Phys. Rev. B 1974, 10, 154. [Google Scholar] [CrossRef]
  64. Drickamer, H.G.; Frank, C.W. Electronic Transitions and the High-Pressure Chemistry and Physics of Solids; Chapman and Hall: London, UK, 1973. [Google Scholar]
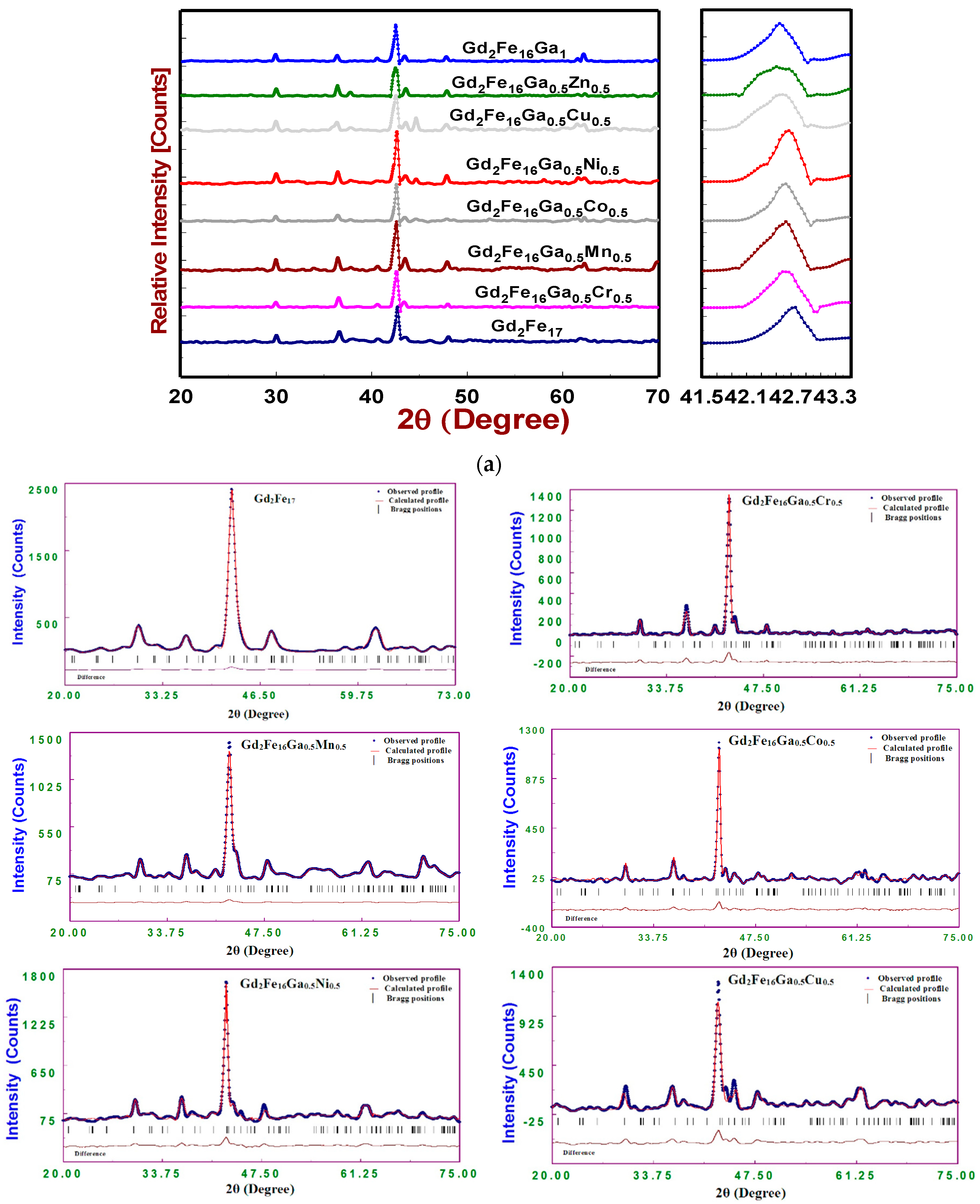
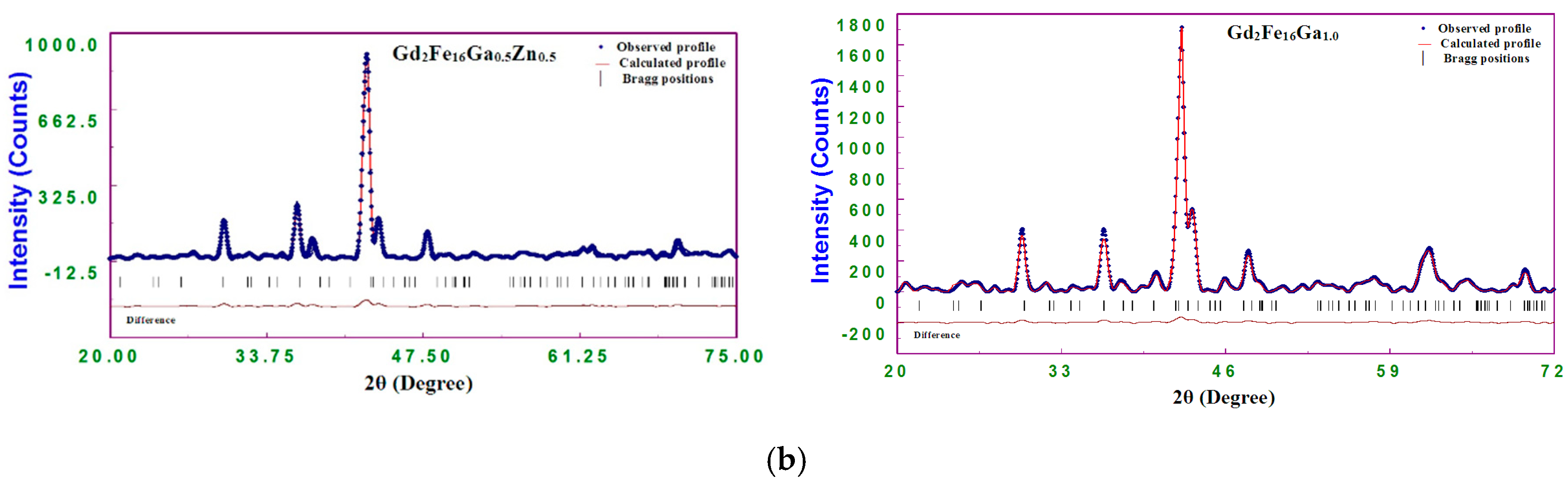
Magnetochemistry 04 00054 g001a 550Magnetochemistry 04 00054 g001b 550
Figure 1. (a) XRD powder profile for Gd2Fe17 and Gd2Fe16Ga0.5TM0.5 (TM = Cr, Mn, Co, Ni, Cu, Zn, and Ga). (b) Rietveld refined XRD data of Gd2Fe17 and Gd2Fe16Ga0.5TM0.5 (TM = Cr, Mn, Co, Ni, Cu, Zn, and Ga).
Figure 1. (a) XRD powder profile for Gd2Fe17 and Gd2Fe16Ga0.5TM0.5 (TM = Cr, Mn, Co, Ni, Cu, Zn, and Ga). (b) Rietveld refined XRD data of Gd2Fe17 and Gd2Fe16Ga0.5TM0.5 (TM = Cr, Mn, Co, Ni, Cu, Zn, and Ga).
Magnetochemistry 04 00054 g001aMagnetochemistry 04 00054 g001b
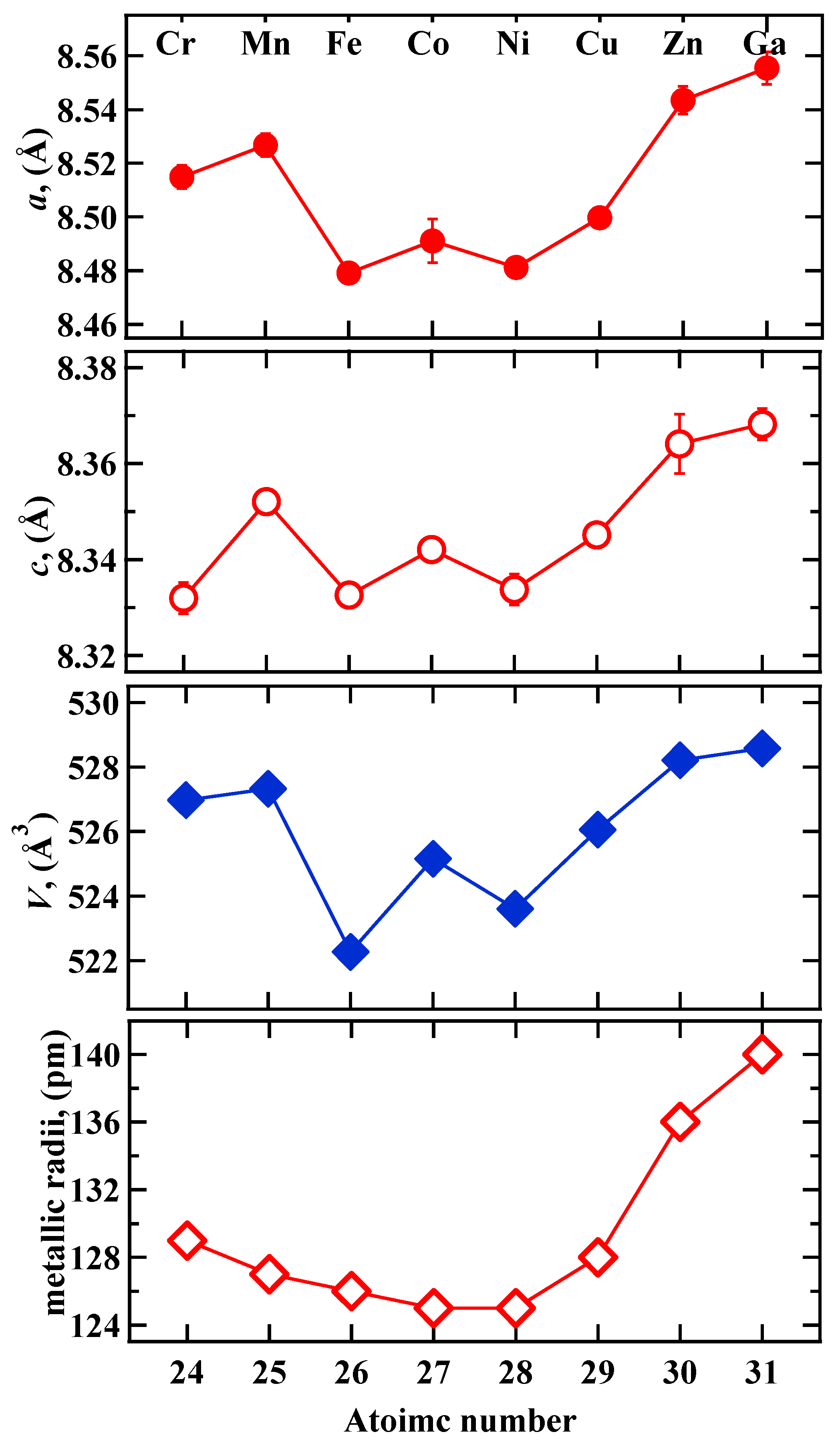
Magnetochemistry 04 00054 g002 550
Figure 2. Lattice parameters obtained via Rietveld refinement, and metallic radii of Gd2Fe16Ga0.5TM0.5 as a function of TM atomic number.
Figure 2. Lattice parameters obtained via Rietveld refinement, and metallic radii of Gd2Fe16Ga0.5TM0.5 as a function of TM atomic number.
Magnetochemistry 04 00054 g002
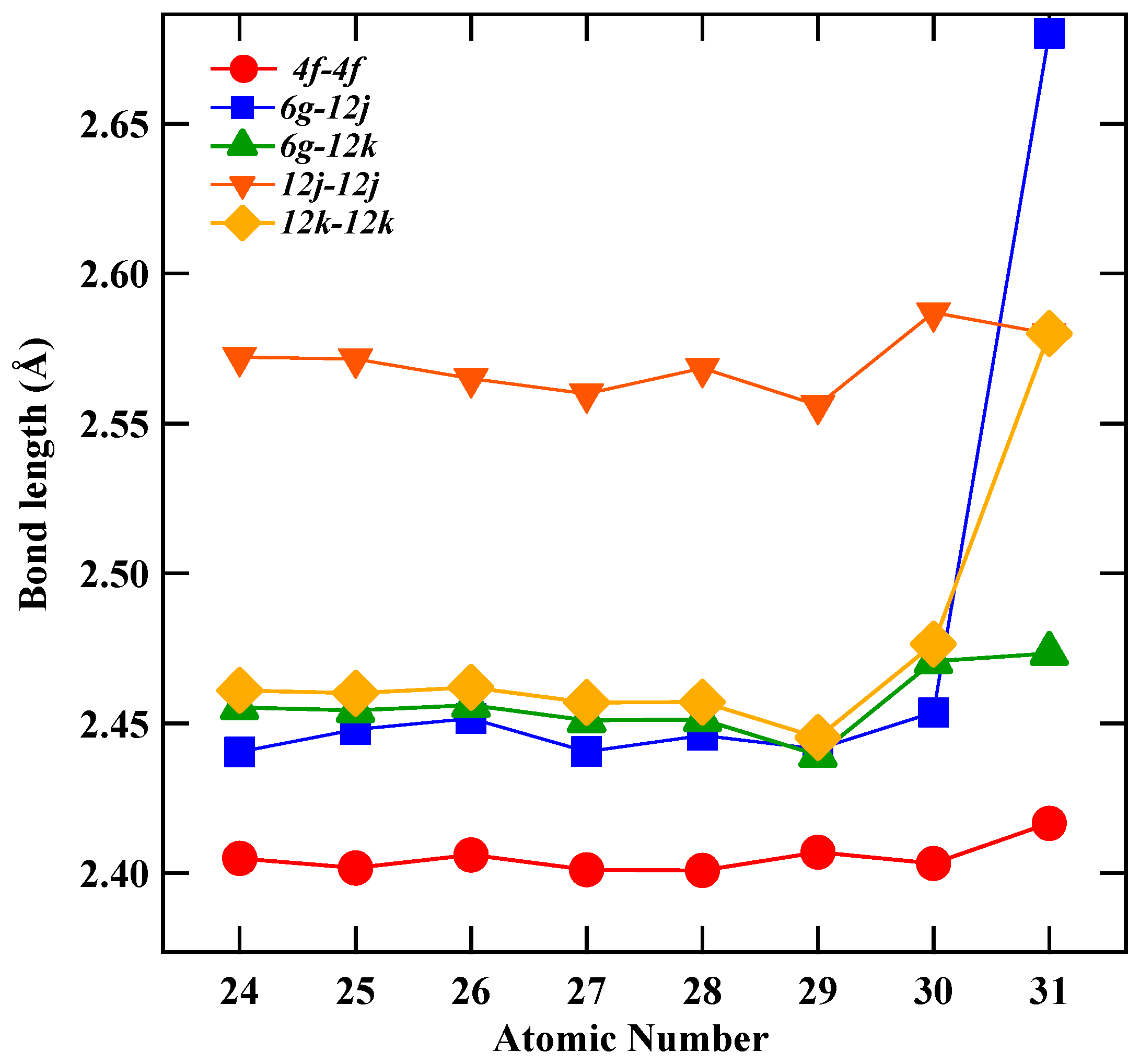
Magnetochemistry 04 00054 g003 550
Figure 3. Atomic site–site bond lengths as a function of TM atomic number in Gd2Fe16Ga0.5TM0.5 (TM = Cr, Mn, Co, Ni, Cu, Zn, and Ga) derived from Rietveld refinement.
Figure 3. Atomic site–site bond lengths as a function of TM atomic number in Gd2Fe16Ga0.5TM0.5 (TM = Cr, Mn, Co, Ni, Cu, Zn, and Ga) derived from Rietveld refinement.
Magnetochemistry 04 00054 g003
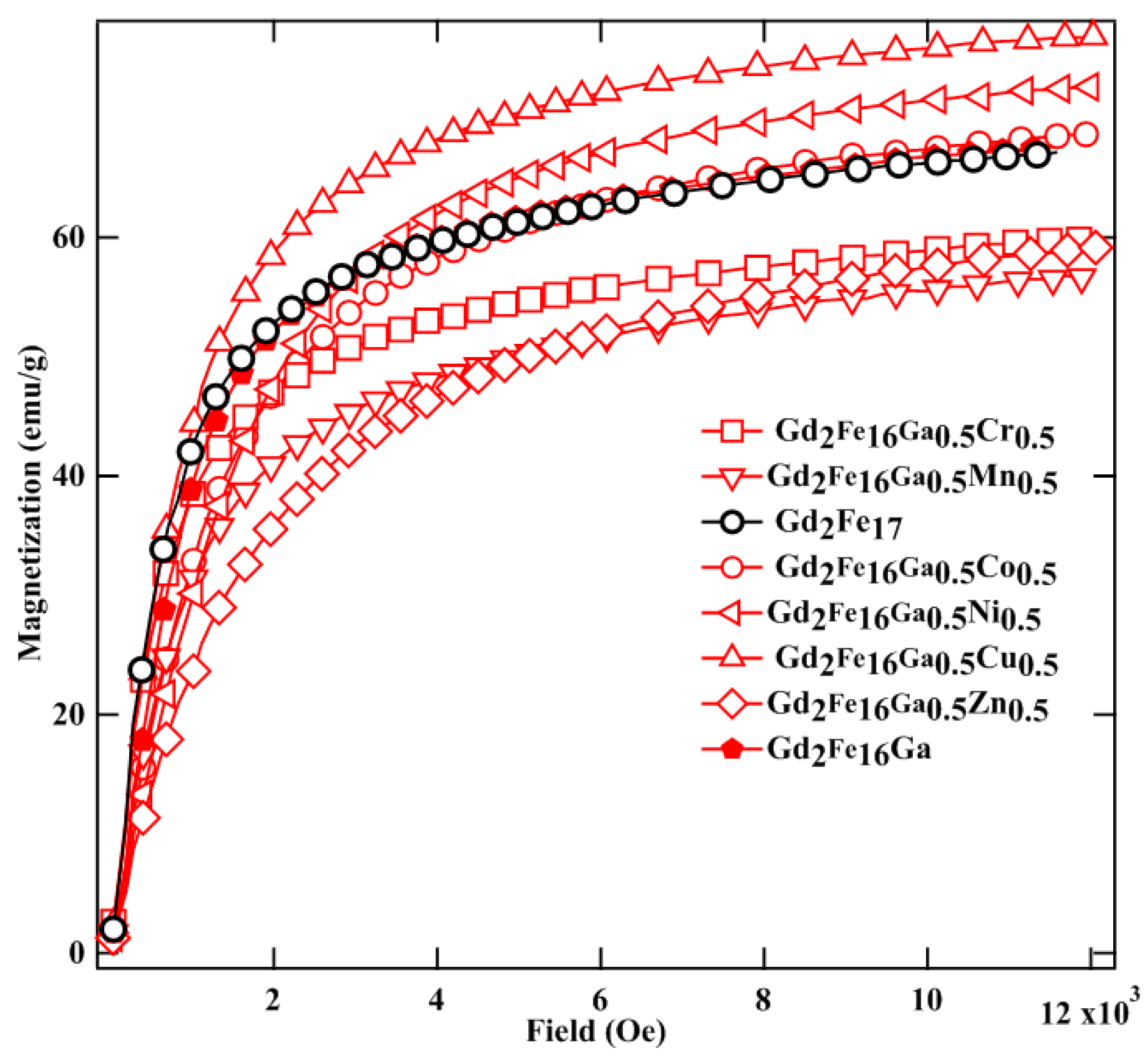
Magnetochemistry 04 00054 g004 550
Figure 4. Room temperature M vs. H plot of Gd2Fe17 and Gd2Fe16Ga0.5TM0.5 (TM = Cr, Mn, Co, Ni, Cu, Zn, and Ga).
Figure 4. Room temperature M vs. H plot of Gd2Fe17 and Gd2Fe16Ga0.5TM0.5 (TM = Cr, Mn, Co, Ni, Cu, Zn, and Ga).
Magnetochemistry 04 00054 g004
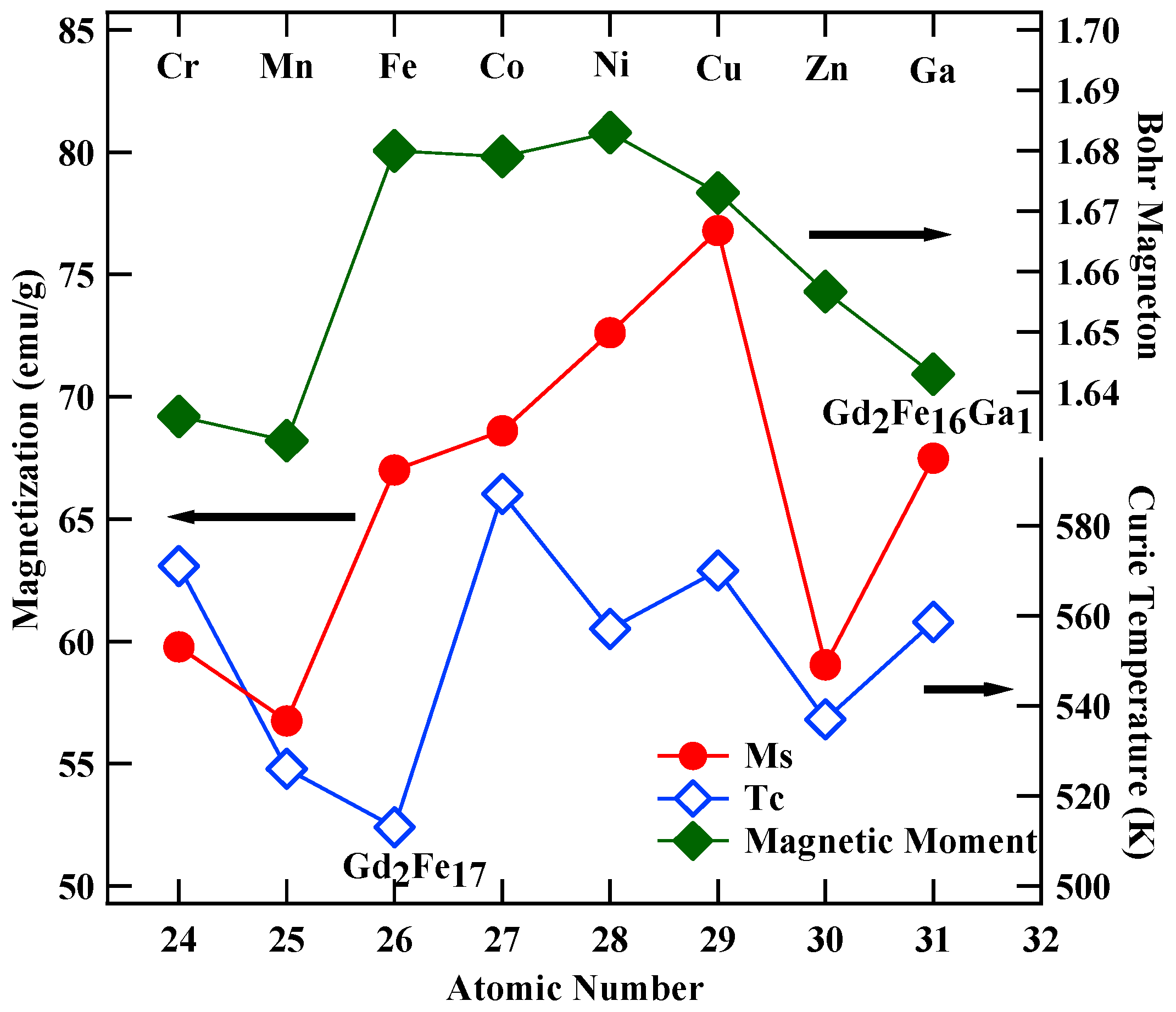
Magnetochemistry 04 00054 g005 550
Figure 5. Saturation magnetization, Ms, Curie temperature, Tc, and Bohr magneton number as a function of TM atomic number in Gd2Fe17 and Gd2Fe16Ga0.5TM0.5 (TM = Cr, Mn, Co, Ni, Cu, Zn, and Ga).
Figure 5. Saturation magnetization, Ms, Curie temperature, Tc, and Bohr magneton number as a function of TM atomic number in Gd2Fe17 and Gd2Fe16Ga0.5TM0.5 (TM = Cr, Mn, Co, Ni, Cu, Zn, and Ga).
Magnetochemistry 04 00054 g005
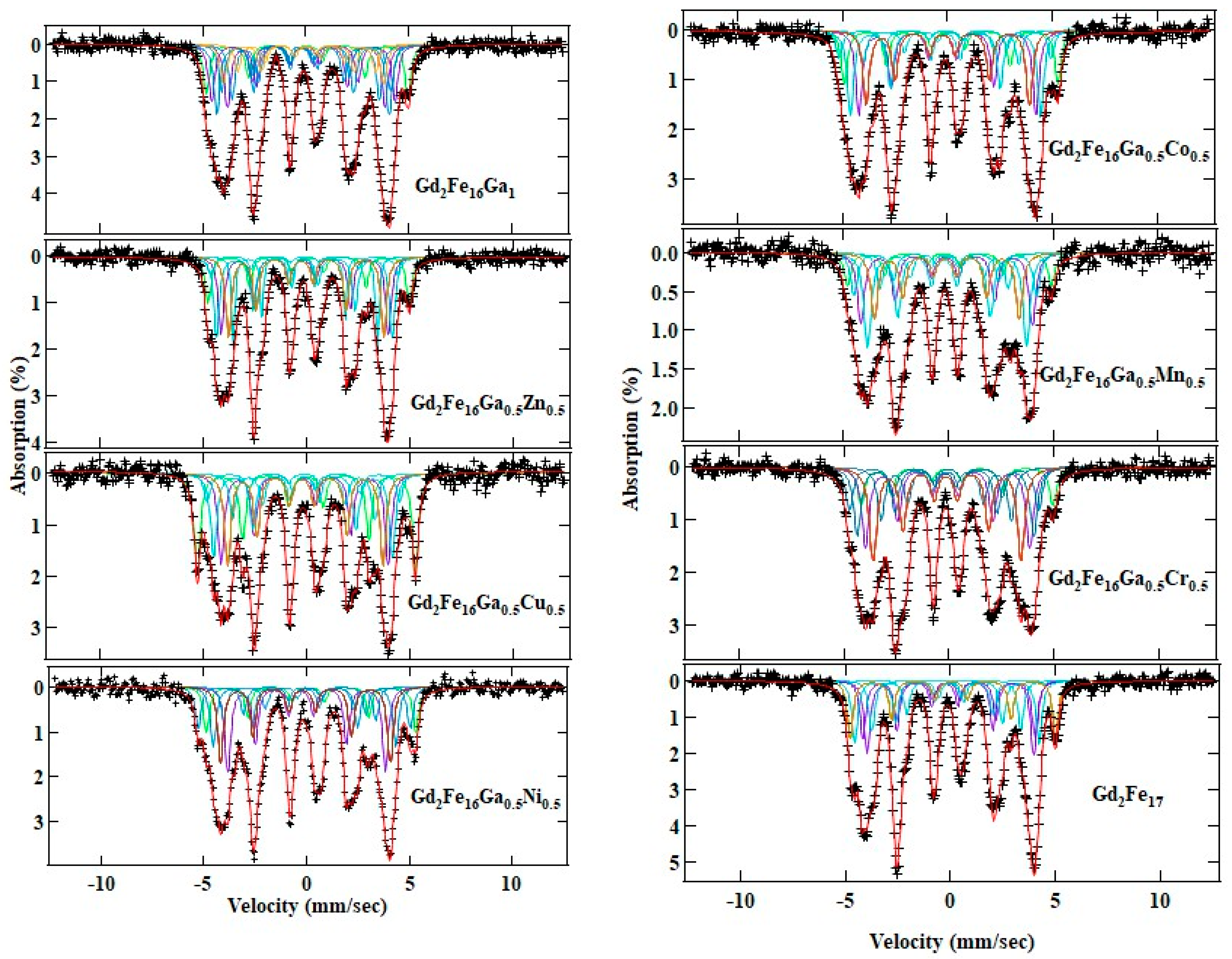
Magnetochemistry 04 00054 g006 550
Figure 6. Fitted RT Mössbauer spectra of Gd2Fe17 and Gd2Fe16Ga0.5TM0.5 (TM = Cr, Mn, Co, Ni, Cu, Zn, and Ga).
Figure 6. Fitted RT Mössbauer spectra of Gd2Fe17 and Gd2Fe16Ga0.5TM0.5 (TM = Cr, Mn, Co, Ni, Cu, Zn, and Ga).
Magnetochemistry 04 00054 g006
Magnetochemistry 04 00054 g007 550
Figure 7. Weighted average hyperfine parameters, hyperfine field, and isomer shift, as a function of TM atomic number for Gd2Fe17 and Gd2Fe16Ga0.5TM0.5 (TM = Cr, Mn, Co, Ni, Cu, Zn, and Ga).
Figure 7. Weighted average hyperfine parameters, hyperfine field, and isomer shift, as a function of TM atomic number for Gd2Fe17 and Gd2Fe16Ga0.5TM0.5 (TM = Cr, Mn, Co, Ni, Cu, Zn, and Ga).
Magnetochemistry 04 00054 g007
Table
Table 1. Structural parameters derived from Rietveld refinement of powder XRD data of Gd2Fe17 and Gd2Fe16Ga0.5TM0.5 (TM = Cr, Mn, Co, Ni, Cu, Zn, and Ga).
Table 1. Structural parameters derived from Rietveld refinement of powder XRD data of Gd2Fe17 and Gd2Fe16Ga0.5TM0.5 (TM = Cr, Mn, Co, Ni, Cu, Zn, and Ga).
ParameterCrMnGd2Fe17
Fe		CoNi Cu ZnGd2Fe16Ga
Ga
Metallic radii (pm)127126129125125128136140
a (Å)8.5149(43)8.5267(42)8.4791(21)8.4911(81)8.4812(24)8.4997(32)8.5435(52)8.5555(61)
c (Å)8.3320(32)8.3521(22)8.3326(6)8.3421(8)8.3338(32)8.3451(16)8.3641(62)8.3682(33)
c/a0.97850.97950.98270.98240.98260.98180.97900.9781
Cell Volume (Å3)526.97527.32522.2634525.15523.60526.06528.21528.5749
Robs (%)5.674.442.484.533.213.992.316.43
wRobs (%)4.325.213.555.314.214.873.657.12
Rp (%)6.227.879.128.117.327.225.3210.55
wRp (%)7.878.8610.549.328.3210.117.7812.54
Table
Table 2. Atomic site occupancy derived from Rietveld refinement for Gd2Fe17 and Gd2Fe16Ga0.5TM0.5 (TM = Cr, Mn, Co, Ni, Cu, Zn, and Ga).
Table 2. Atomic site occupancy derived from Rietveld refinement for Gd2Fe17 and Gd2Fe16Ga0.5TM0.5 (TM = Cr, Mn, Co, Ni, Cu, Zn, and Ga).
TMGd1(2b)Gd2(2d)Fe(4f)Fe(6g)Fe(12j)Fe(12k)Ga(4f)Ga(6g)Ga(12j)Ga(12k)TM(4f)TM(6g)TM(12j)TM(12k)
Cr0.08610.08090.15810.23600.45800.49560.00470.00680.01480.01120.00720.00320.01590.0181
Mn0.08290.08460.15100.23270.43790.50170.00420.00610.01280.01080.00820.00410.01660.0188
Fe0.08540.08150.17060.25800.49730.5293
Co0.08350.08270.15090.24100.45890.48910.00570.01180.01120.01150.00470.00930.01440.0157
Ni0.08610.08090.15180.25270.43230.48240.00810.01170.00620.01710.00690.01030.01470.0162
Cu0.08390.08210.15030.24350.45210.48030.00520.01210.01180.01090.00510.00830.01510.0169
Zn0.08160.08390.15110.23210.43100.49560.00450.00580.01240.01020.00750.00420.01790.0129
Ga0.08120.08360.14550.23140.42850.48630.00940.019380.03090.0341
Table
Table 3. Interatomic Fe–Fe distances (in Å) for Gd2Fe17 and Gd2Fe16yGa0.5TM0.5 (TM = Cr, Mn, Co, Ni, Cu, Zn, and Ga) obtained from Rietveld refinement.
Table 3. Interatomic Fe–Fe distances (in Å) for Gd2Fe17 and Gd2Fe16yGa0.5TM0.5 (TM = Cr, Mn, Co, Ni, Cu, Zn, and Ga) obtained from Rietveld refinement.
Fe–Fe SitesCrMnFeCoNiCuZnGa
4f-4f2.4050(4)2.4018(13)2.4061(3)2.4012(5)2.4010(11)2.4070(3)2.4032(2)2.4166(21)
6g-12j2.4405(9)2.4479(9)2.4516(2)2.4406(16)2.4460(3)2.4414(7)2.4536(3)2.6801(3)
6g-12k2.4552(13)2.4543(5)2.4560(2)2.4510(7)2.4513(3)2.4394(11)2.4707(2)2.4734(3)
12j-12j2.5721(3)2.5715(2)2.5650(1)2.5600(7)2.5684(2)2.5561(2)2.587(21)2.5800(3)
12k-2k2.4610(13)2.4600(13)2.4620(4)2.4570(2)2.4571(11)2.4453(11)2.4764(11)2.5800(12)
Table
Table 4. Room temperature saturation magnetization, Ms, and Curie temperature, Tc, of Gd2Fe17 and Gd2Fe16Ga0.5TM0.5 (TM = Cr, Mn, Co, Ni, Cu, Zn, and Ga).
Table 4. Room temperature saturation magnetization, Ms, and Curie temperature, Tc, of Gd2Fe17 and Gd2Fe16Ga0.5TM0.5 (TM = Cr, Mn, Co, Ni, Cu, Zn, and Ga).
Gd2Fe16Ga0.5TM0.5Ms (emu/g)Tc (K)
Cr59.78571
Mn56.75526
Gd2Fe1767.00513
Co68.61587
Ni72.61557
Cu76.79570
Zn59.04537
Gd2Fe16Ga167.49559
Table
Table 5. RT Mössbauer hyperfine parameters for Gd2Fe17 and Gd2Fe16Ga0.5TM0.5 (TM = Cr, Mn, Co, Ni, Cu, Zn, and Ga).
Table 5. RT Mössbauer hyperfine parameters for Gd2Fe17 and Gd2Fe16Ga0.5TM0.5 (TM = Cr, Mn, Co, Ni, Cu, Zn, and Ga).
TM 4f6g16g212j112j212j312k112k2DoubletWt.Avg.
CrB (kOe)303231.6244.1212.5271.2278.5198255.3 245.424
IS (mm/s)0.102−0.121−0.121−0.1−0.1−0.10.0110.011 −0.0576
QS (mm/s)0.3510.1160.1620.073−0.157−0.0090.35−0.0446
Area (%)10.015.217.812.54.318.59.911.7
MnB (kOe)302.3230254.3210.1265.2275.1202255.6 244.882
IS (mm/s)0.078−0.117−0.117−0.124−0.124−0.1240.0390.039 −0.0608
QS (mm/s)0.280.0930.093−0.1570.149−0.0790.434−0.17
Area (%)8.216.317.68.723.110.610.76.2
(Gd2Fe17)B (kOe)304246.2254.6220.5272.3286.3205.6260.2 252.1
IS (mm/s)0.07−0.13−0.13−0.115−0.115−0.1150.0350.035 −0.0603
QS (mm/s)0.0670.2960.21−0.0190.009−0.1160.358−0.487
Area (%)13.815.519.86.113.611.96.1611.7
CoB (kOe)315.2242.7262.9215.6271.3283203.2264.6 251.932
IS (mm/s)0.11−0.119−0.119−0.098−0.098−0.0980.0560.056 −0.0417
QS (mm/s)0.1390.2720.238−0.3990.015−0.0390.263−0.245
Area (%)11.51618.17.118.45.910.110.8
NiB (kOe)310.1239.1257.4220.6276.7285.2201.9263.344.4252.524
IS (mm/s)0.113−0.129−0.129−0.09−0.09−0.090.0440.0440.5−0.0432
QS (mm/s)0.2650.4580.055−0.0360.042−0.0790.1380.151−0.5
Area (%)11.03.59.38.018.68.314.316.68.4
CuB (kOe)312.2234.5252.1214.8269.2290.3200.2268.045.9251.032
IS (mm/s)0.113−0.137−0.137−0.128−0.128−0.1280.0620.0620.387−0.0567
QS (mm/s)0.0210.1720.102−0.005−0.083−0.103−0.358−0.17−0.39
Area (%)22.020.820.410.318.76.51.92.62.8
ZnB (kOe)303.4234.5252.3217.1265.0280.7211.3256.4 248.689
IS (mm/s)0.088−0.141−0.141−0.101−0.101−0.1010.0620.062 −0.0459
QS (mm/s)0.0410.2520.1250.098−0.0001−0.0330.178−0.145
Area (%)11.319.418.813.219.54.33.49.1
GaB (kOe)304.8235.6238.3222.8255.1283.8208.2252.9 246.529
IS (mm/s)0.059−0.109−0.109−0.113−0.113−0.1130.050.05 −0.0518
QS (mm/s)0.025−0.0860.2110.2160.275−0.0230.093−0.147
Area (%)12.314.015.313.511.717.36.89.9

Share and Cite

MDPI and ACS Style

Dahal, J.N.; Ali, K.S.S.; Mishra, S.R.; Alam, J. Structural, Magnetic, and Mössbauer Studies of Transition Metal-Doped Gd2Fe16Ga0.5TM0.5 Intermetallic Compounds (TM = Cr, Mn, Co, Ni, Cu, and Zn). Magnetochemistry 2018, 4, 54. https://doi.org/10.3390/magnetochemistry4040054

AMA Style

Dahal JN, Ali KSS, Mishra SR, Alam J. Structural, Magnetic, and Mössbauer Studies of Transition Metal-Doped Gd2Fe16Ga0.5TM0.5 Intermetallic Compounds (TM = Cr, Mn, Co, Ni, Cu, and Zn). Magnetochemistry. 2018; 4(4):54. https://doi.org/10.3390/magnetochemistry4040054

Chicago/Turabian Style

Dahal, J. N., K. S. Syed Ali, S. R. Mishra, and J. Alam. 2018. "Structural, Magnetic, and Mössbauer Studies of Transition Metal-Doped Gd2Fe16Ga0.5TM0.5 Intermetallic Compounds (TM = Cr, Mn, Co, Ni, Cu, and Zn)" Magnetochemistry 4, no. 4: 54. https://doi.org/10.3390/magnetochemistry4040054

APA Style

Dahal, J. N., Ali, K. S. S., Mishra, S. R., & Alam, J. (2018). Structural, Magnetic, and Mössbauer Studies of Transition Metal-Doped Gd2Fe16Ga0.5TM0.5 Intermetallic Compounds (TM = Cr, Mn, Co, Ni, Cu, and Zn). Magnetochemistry, 4(4), 54. https://doi.org/10.3390/magnetochemistry4040054

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop