A Co(II)-Hydrazone Schiff Base Single Ion Magnet Exhibiting Field Induced Slow Relaxation Dynamics †
Abstract
:1. Introduction
2. Results and Discussion
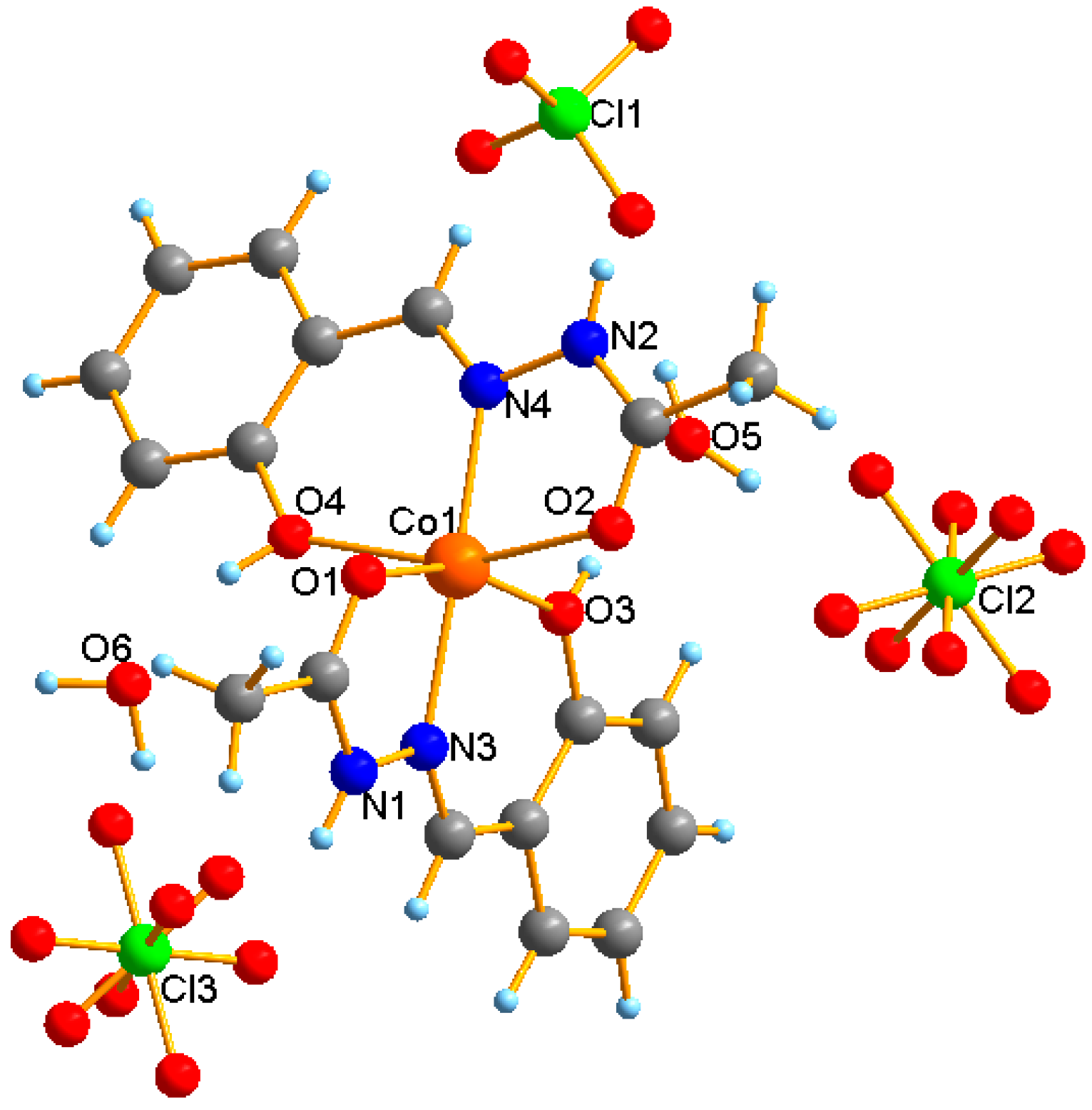
2.1. X-ray Crystal Structure of [Co(HL)2](ClO4)2·2H2O (1)
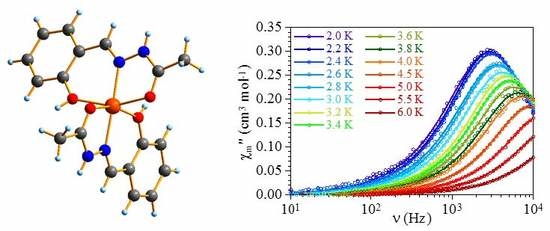
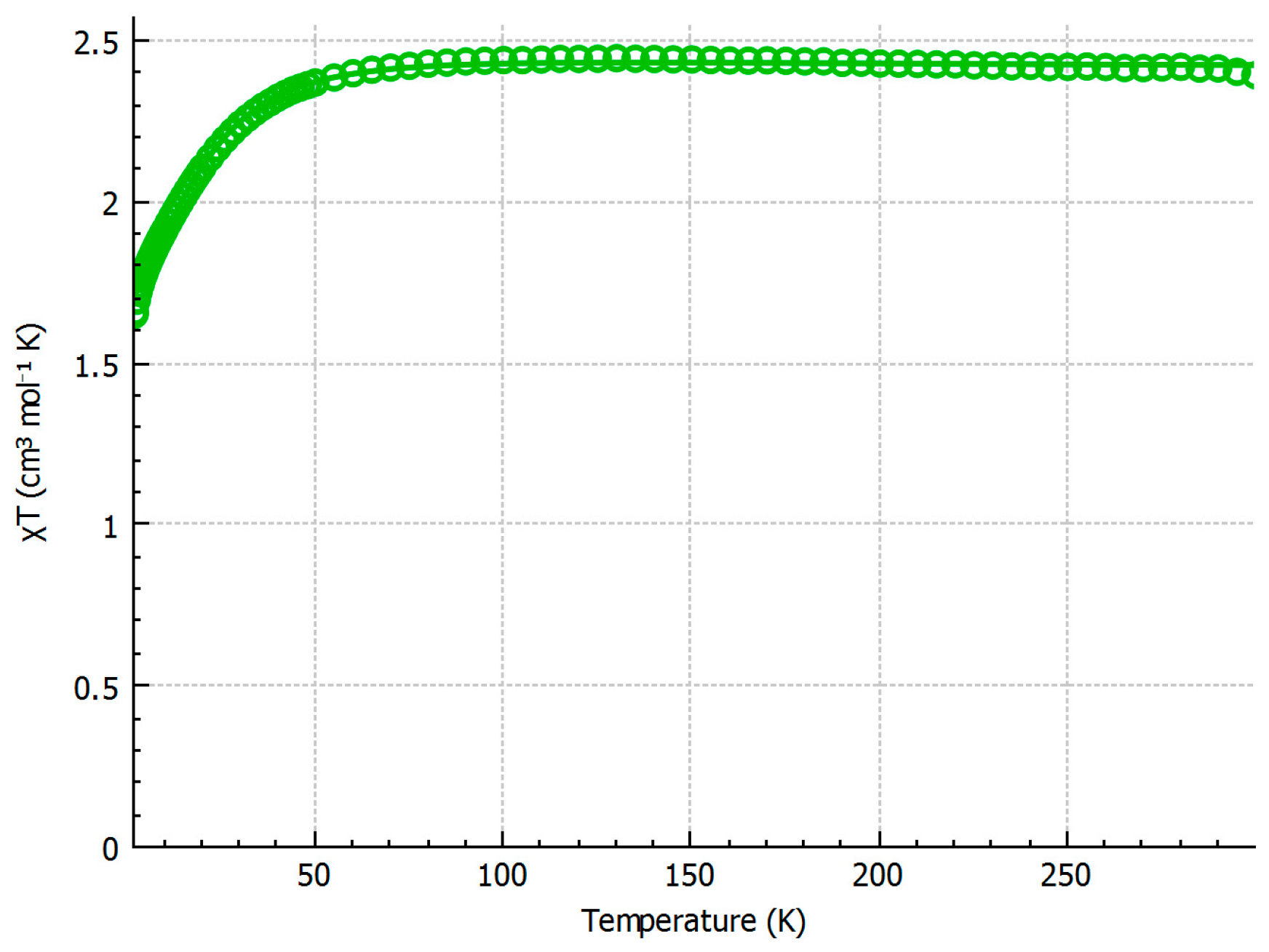
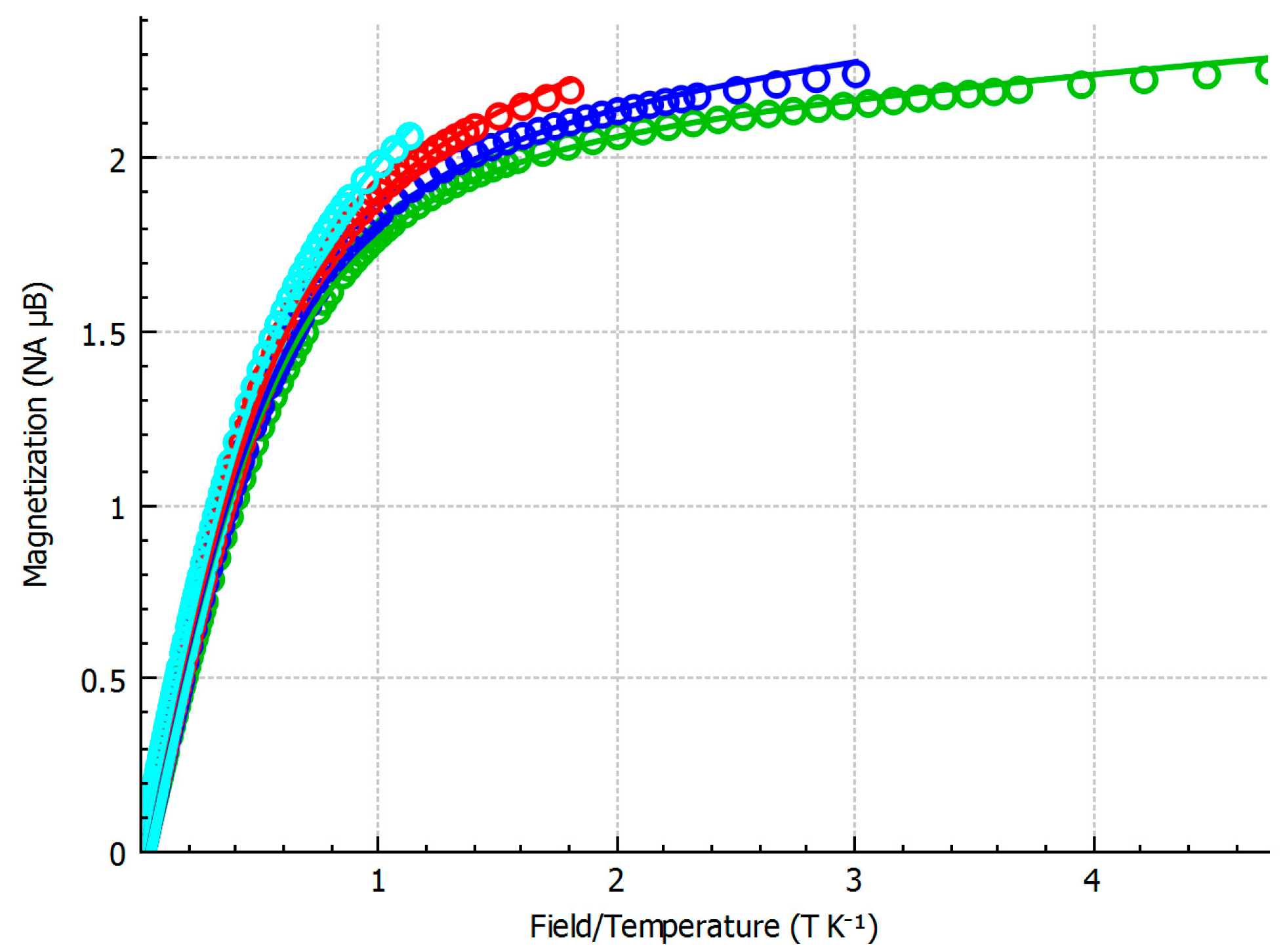
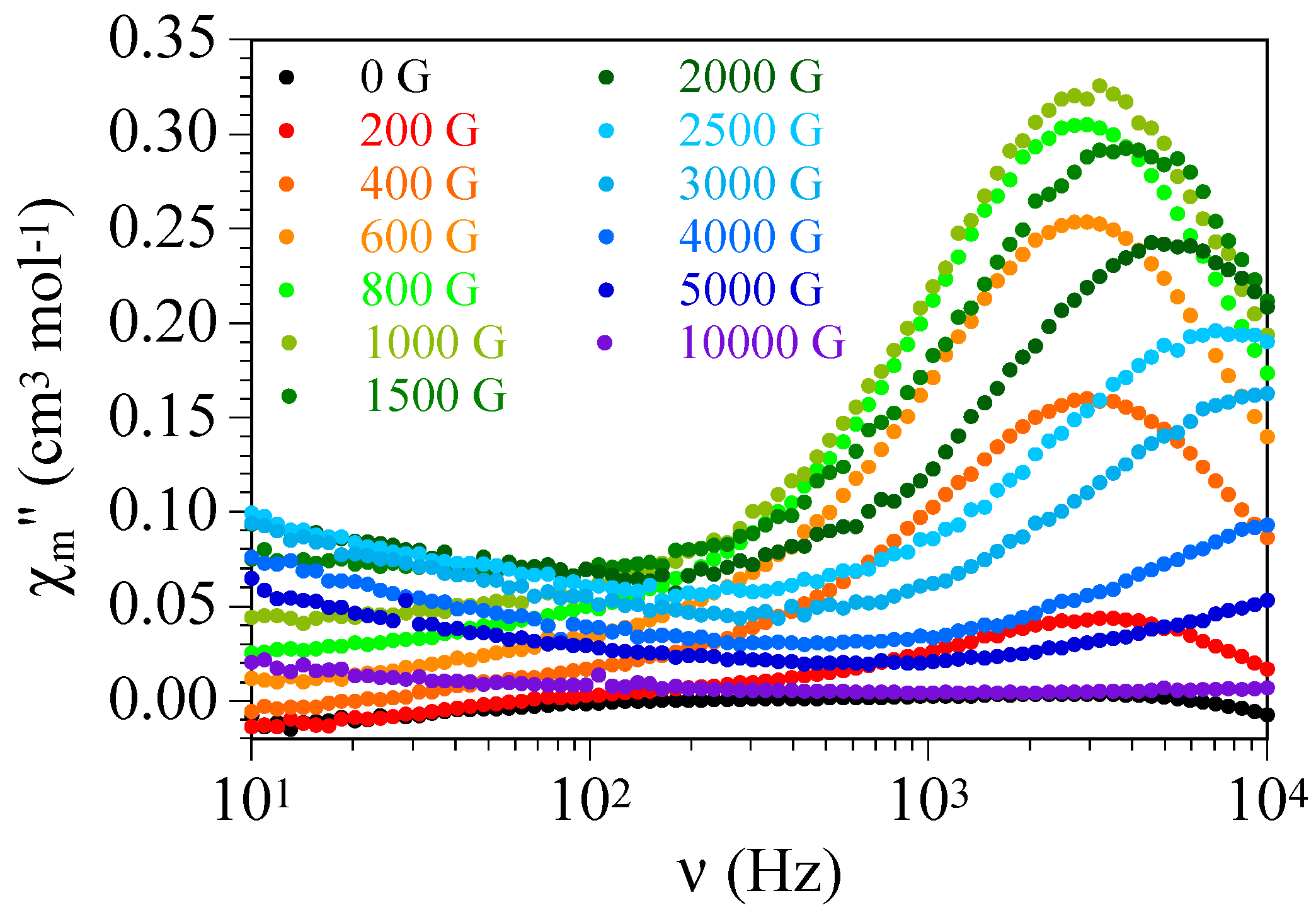
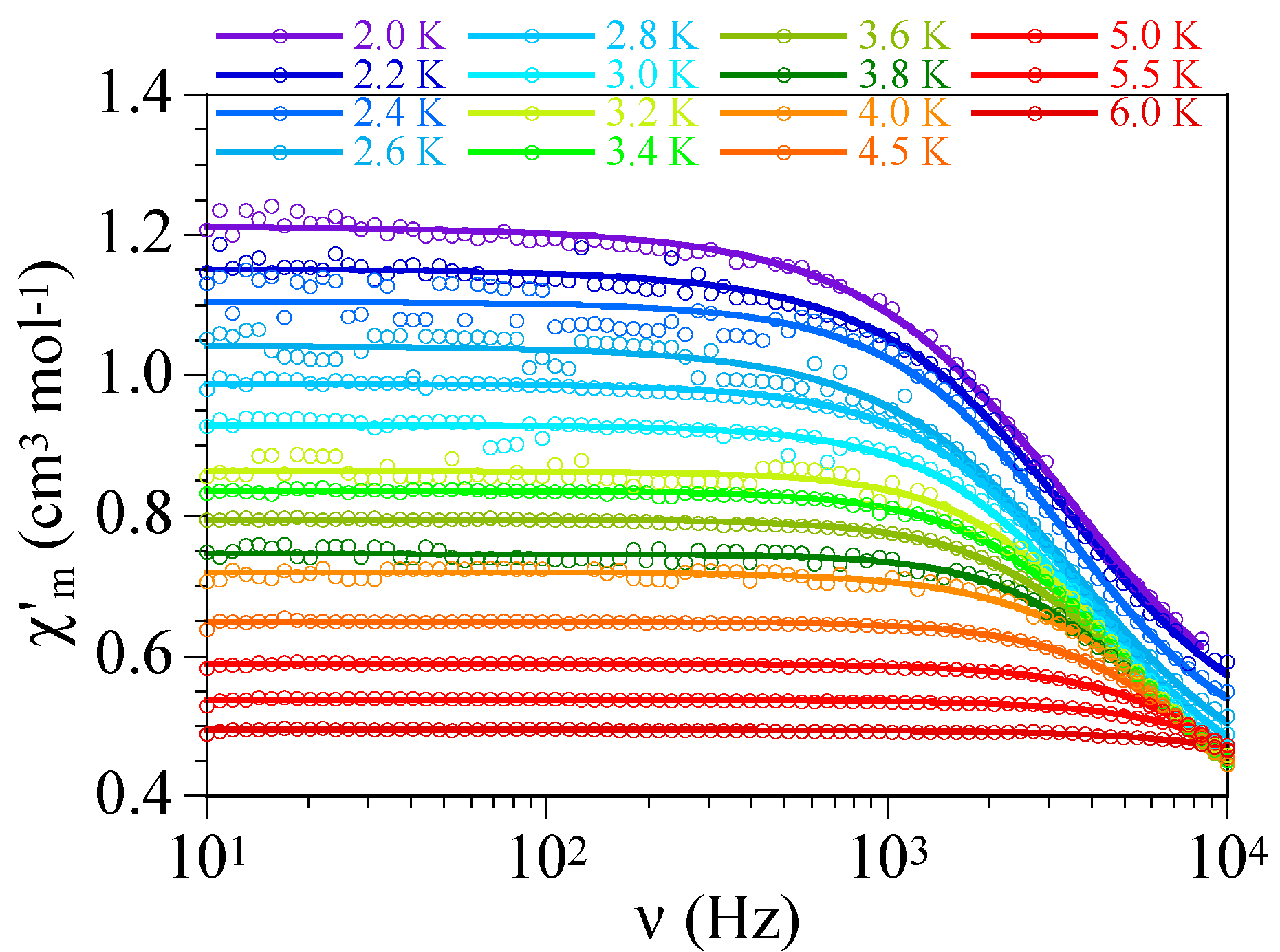
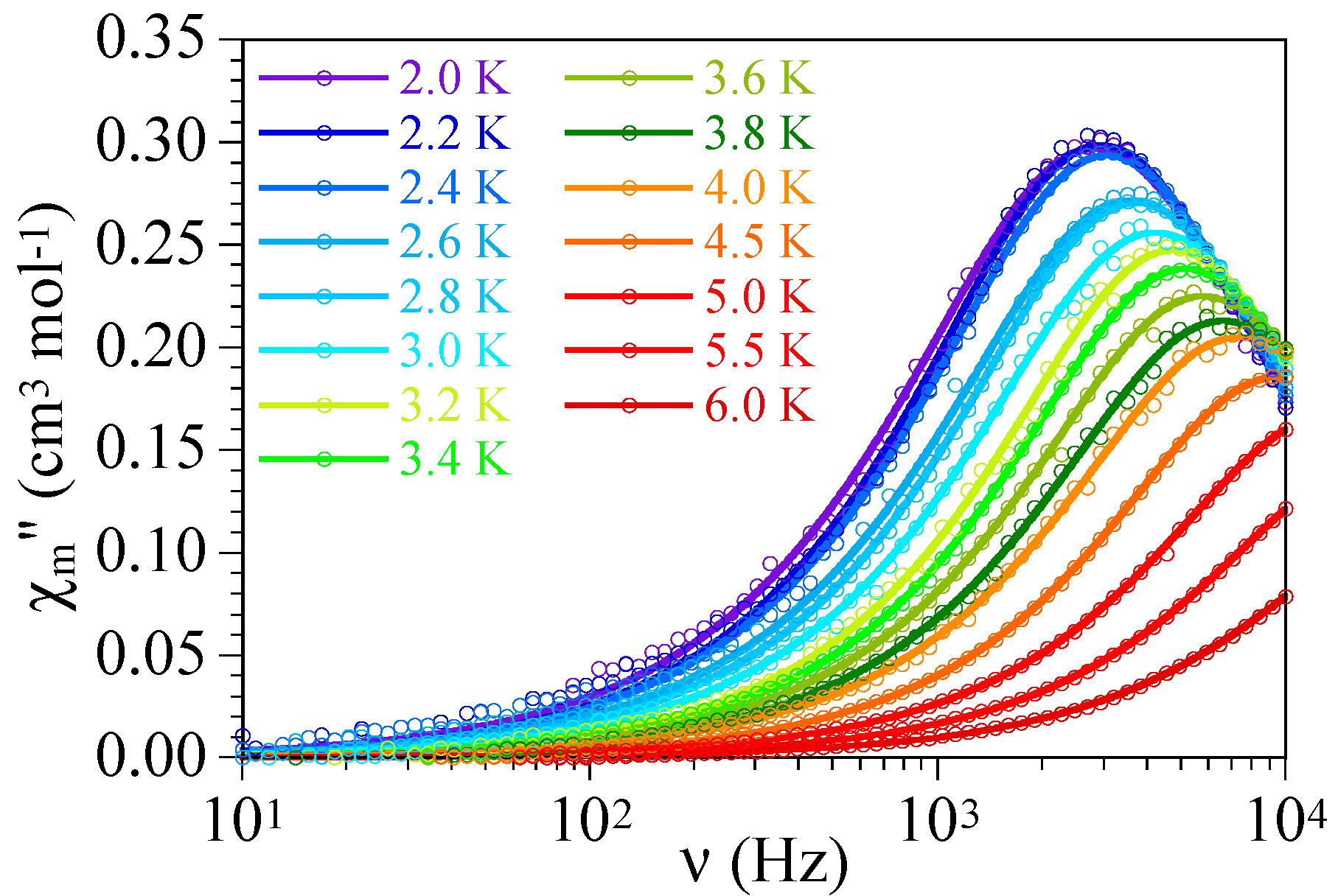
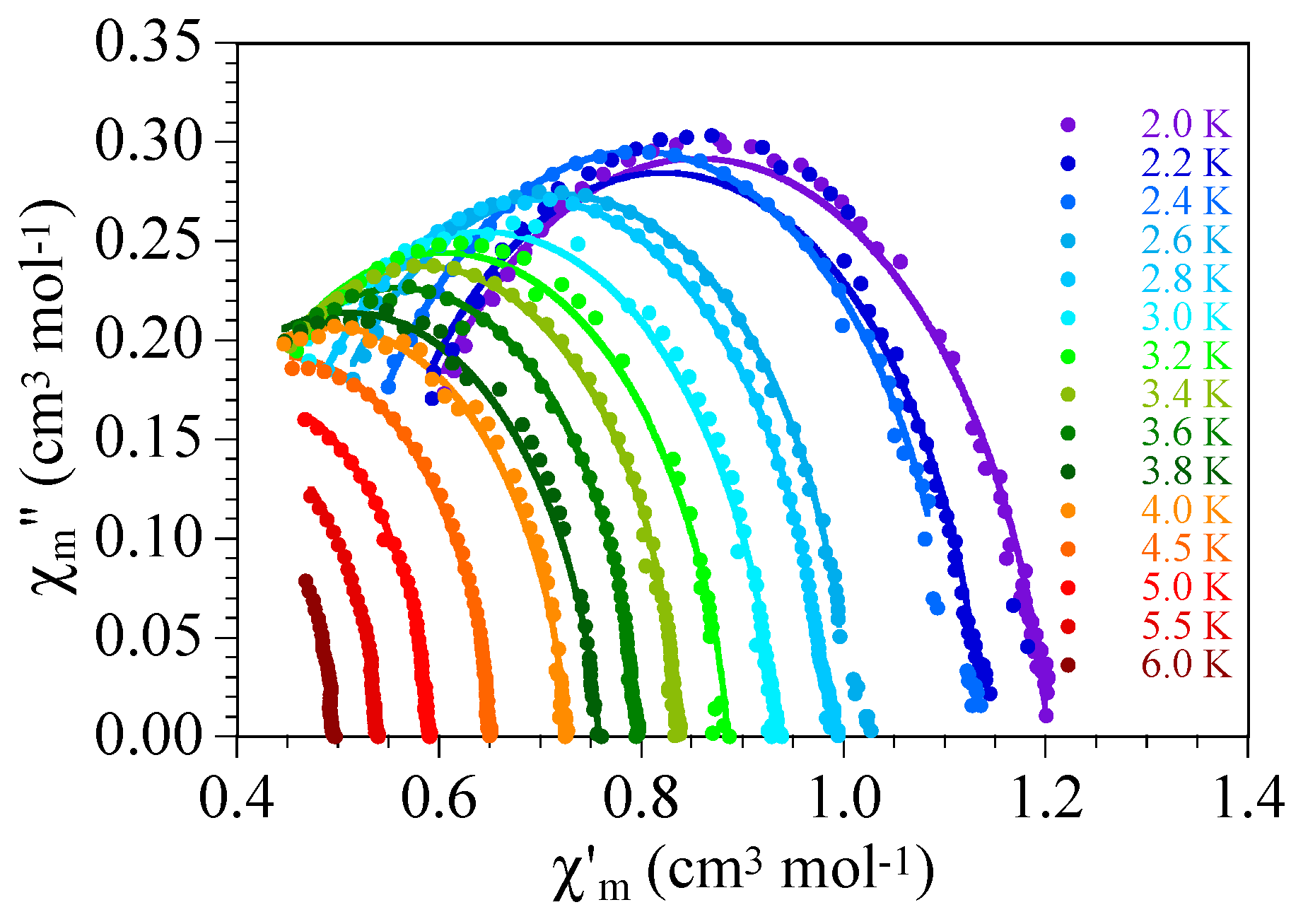
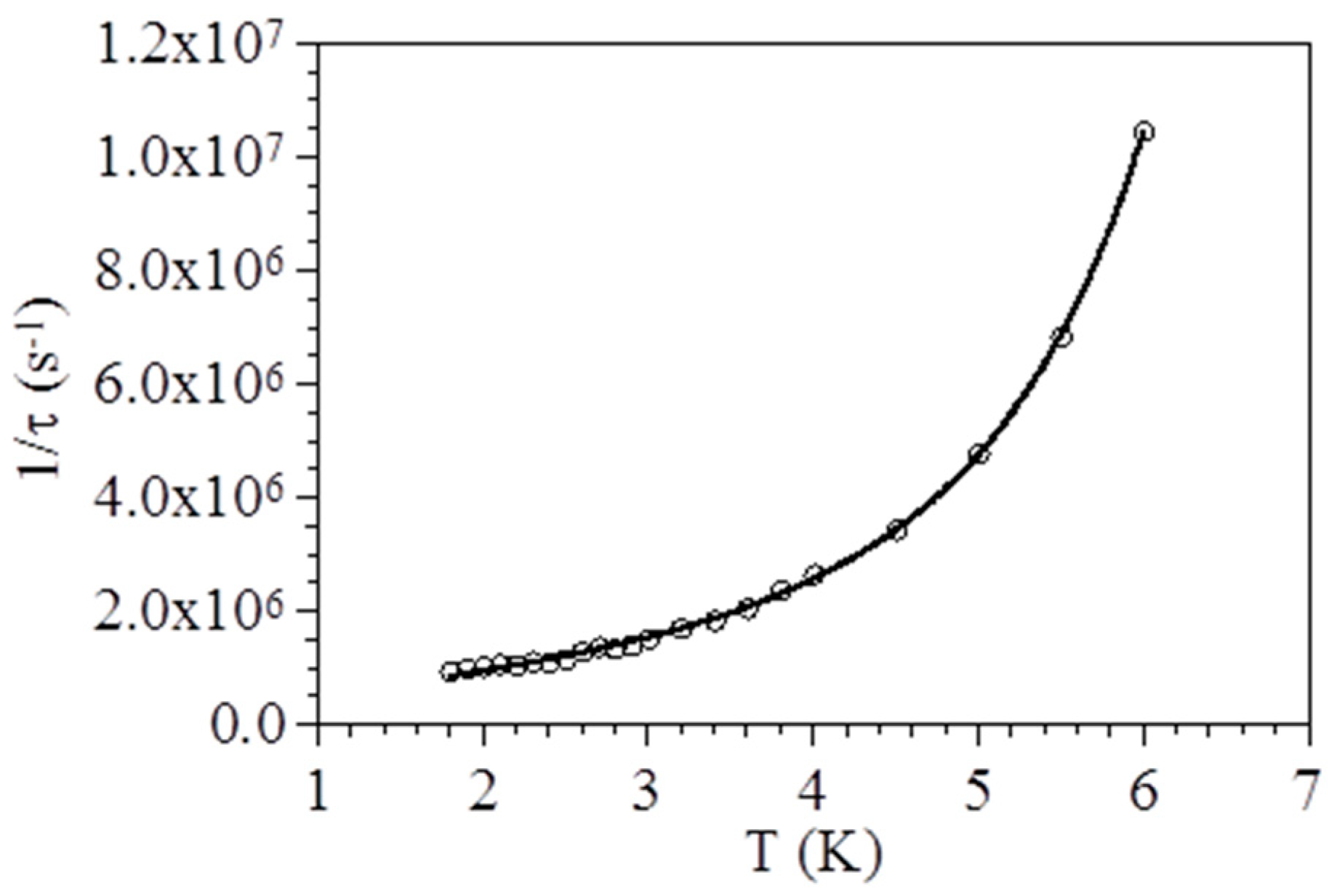
2.2. Magnetic Studies
3. Materials and Methods
3.1. Syntheses
3.1.1. Synthesis of the Hydrazone Ligand [HL]
3.1.2. Synthesis of [Co(HL)2](ClO4)2·2H2O (1)
3.2. Physical Measurements
3.3. X-ray Crystallography
4. Conclusions
Funding
Author Contributions
Acknowledgments
Conflicts of Interest
Notes
References
- Vincent, R.; Klyatskaya, S.; Ruben, M.; Wernsdorfer, W.; Balestro, F. Electronic read-out of a single nuclear spin using a molecular spin transistor. Nature 2012, 488, 357–360. [Google Scholar] [CrossRef] [PubMed]
- Aromí, G.; Aguilà, D.; Gamez, P.; Luis, F.; Roubeau, O. Design of magnetic coordination complexes for quantum computing. Chem. Soc. Rev. 2012, 41, 537–546. [Google Scholar] [CrossRef] [Green Version]
- Timco, G.A.; Faust, T.B.; Tuna, F.; Winpenny, R.E.P. Linking heterometallic rings for quantum information processing and amusement. Chem. Soc. Rev. 2011, 40, 3067–3075. [Google Scholar] [CrossRef] [PubMed]
- Ishikawa, N.; Sugita, M.; Ishikawa, T.; Koshihara, S.Y.; Kaizu, Y. Lanthanide Double-Decker Complexes Functioning as Magnets at the Single-Molecular Level. J. Am. Chem. Soc. 2003, 125, 8694–8695. [Google Scholar] [CrossRef] [PubMed]
- Ishikawa, N.; Sugita, M.; Ishikawa, T.; Koshihara, S.; Kaizu, Y. Mononuclear Lanthanide Complexes with a Long Magnetization Relaxation Time at High Temperatures: A New Category of Magnets at the Single-Molecular Level. J. Phys. Chem. B 2004, 108, 11265–11271. [Google Scholar] [CrossRef]
- AlDamen, M.A.; Clemente-Juan, J.M.; Coronado, E.; Marti-Gastaldo, C.; Gaita-Arino, A. Mononuclear lanthanide single-molecule magnets based on polyoxometalates. J. Am. Chem. Soc. 2008, 130, 8874–8875. [Google Scholar] [CrossRef] [PubMed]
- AlDamen, M.A.; Cardona-Serra, S.; Clemente-Juan, J.M.; Coronado, E.; Alejandro, G.-A.; Carlos, M.-G.; Fernando, L.; Oscar, M. Mononuclear Lanthanide Single Molecule Magnets Based on the Polyoxometalates [Ln(W5O18)2]9− and [Ln(β2-SiW11O39)2]13−(LnIII = Tb, Dy, Ho, Er, Tm, and Yb). Inorg. Chem. 2009, 48, 3467–3479. [Google Scholar] [CrossRef]
- Baldoví, J.J.; Cardona-Serra, S.; Clemente-Juan, J.M.; Coronado, E.; Gaita-Arin, A.; Palii, A. Rational Design of Single-Ion Magnets and Spin Qubits Based on Mononuclear Lanthanoid Complexes. Inorg. Chem. 2012, 51, 12565–12574. [Google Scholar] [CrossRef]
- Rinehart, J.D.; Long, J.R. Slow magnetic relaxation in a trigonal prismatic uranium(III) complex. J. Am. Chem. Soc. 2009, 131, 12558–12559. [Google Scholar] [CrossRef]
- Rinehart, J.D.; Meihaus, K.R.; Long, J.R. Observation of a Secondary Slow Relaxation Process for the Field-Induced Single-Molecule Magnet U(H2BPz2)3. J. Am. Chem. Soc. 2010, 132, 7572–7573. [Google Scholar] [CrossRef]
- Magnani, N.; Apostolidis, C.; Morgenstern, A.; Colineau, E.; Griveau, J.C.; Bolvin, H.; Walter, O.; Caciuffo, R. Magnetic memory effect in a transuranic mononuclear complex. Angew. Chem. Int. Ed. 2011, 50, 1696–1698. [Google Scholar] [CrossRef] [PubMed]
- Antunes, M.A.; Pereira, L.C.J.; Santos, I.C.; Mazzanti, M.; Marçalo, J.; Almeida, M. [U(TpMe2)2(bipy)]+: A Cationic Uranium(III) Complex with Single-Molecule-Magnet Behavior. Inorg. Chem. 2011, 50, 9915–9917. [Google Scholar] [CrossRef] [PubMed]
- Goodwin, C.A.P.; Ortu, F.; Reta, D.; Chilton, N.F.; Mills, D.P. Molecular magnetic hysteresis at 60 kelvin in dysprosocenium. Nature 2017, 548, 439–442. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guo, F.-S.; Day, B.M.; Chen, Y.-C.; Tong, M.-L.; Mansikkamäki, A.; Layfield, R.A. A Dysprosium Metallocene Single-Molecule Magnet Functioning at the Axial Limit. Angew. Chem. Int. Ed. 2017, 56, 11445–11449. [Google Scholar] [CrossRef] [PubMed]
- Guo, F.-S.; Day, B.M.; Chen, Y.-C.; Tong, M.-L.; Mansikkamäki, A.; Layfield, R.A. Magnetic hysteresis up to 80 kelvin in a dysprosium metallocene single-molecule magnet. Science 2018. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Coca, S.; Cremades, E.; Aliaga-Alcalde, N.; Ruiz, E. Mononuclear Single-Molecule Magnets: Tailoring the Magnetic Anisotropy of First-Row Transition-Metal Complexes. J. Am. Chem. Soc. 2013, 135, 7010–7018. [Google Scholar] [CrossRef] [PubMed]
- Freedman, D.E.; Harman, W.H.; Harris, T.D.; Long, G.J.; Chang, C.J.; Long, J.R. Slow Magnetic Relaxation in a High-Spin Iron(II) Complex. J. Am. Chem. Soc. 2010, 132, 1224–1225. [Google Scholar] [CrossRef]
- Harman, W.H.; Harris, T.D.; Freedman, D.E.; Fong, H.; Chang, A.; Rinehart, J.D.; Ozarowski, A.; Sougrati, M.T.; Grandjean, F.; Long, G.J.; et al. Slow magnetic relaxation in a family of trigonal pyramidal iron(II) pyrrolide complexes. J. Am. Chem. Soc. 2010, 132, 18115–18126. [Google Scholar] [CrossRef]
- Rechkemmer, Y.; Breitgoff, F.D.; van der Meer, M.; Atanasov, M.; Hakl, M.; Orlita, M.; Neugebauer, P.; Neese, F.; Sarkar, B.; van Slageren, J. A four-coordinate cobalt(II) single-ion magnet with coercivity and a very high energy barrier. Nat. Commun. 2016, 7, 10467. [Google Scholar] [CrossRef] [Green Version]
- Ruamps, R.; Batchelor, L.J.; Guillot, R.; Zakhia, G.; Barra, A.-L.; Wernsdorfer, W.; Guihéry, N.; Mallah, T. Ising-type magnetic anisotropy and single molecule magnet behaviour in mononuclear trigonal bipyramidal Co(II) complexes. Chem. Sci. 2014, 5, 3418–3424. [Google Scholar] [CrossRef]
- Poulten, R.C.; Page, M.J.; Algarra, A.G.; Le Roy, J.J.; López, I.; Carter, E.; Llobet, A.; Macgregor, S.A.; Mahon, M.F.; Murphy, D.M.; et al. Synthesis, Electronic Structure, and Magnetism of [Ni(6-Mes)2]+: A Two-Coordinate Nickel(I) Complex Stabilized by Bulky NHeterocyclic Carbenes. J. Am. Chem. Soc. 2013, 135, 13640–13643. [Google Scholar] [CrossRef] [PubMed]
- Jurca, T.; Farghal, A.; Lin, P.-H.; Korobkov, I.; Murugesu, M.; Richeson, D.S.J. Single-Molecule Magnet Behavior with a Single Metal Center Enhanced through Peripheral Ligand Modifications. Am. Chem. Soc. 2011, 133, 15814–15817. [Google Scholar] [CrossRef] [PubMed]
- Zadrozny, J.M.; Long, J.R. Slow Magnetic Relaxation at Zero Field in the Tetrahedral Complex [Co(SPh)4]2–. J. Am. Chem. Soc. 2011, 133, 20732–20734. [Google Scholar] [CrossRef] [PubMed]
- Saber, M.R.; Dunbar, K.R. Ligands effects on the magnetic anisotropy of tetrahedral cobalt complexes. Chem. Commun. 2014, 50, 12266–12269. [Google Scholar] [CrossRef] [PubMed]
- Smolko, L.; Černak, J.; Dušek, M.; Miklovič, J.; Titiš, J.; Boča, R. Three tetracoordinate Co(II) complexes [Co(biq)X2] (X = Cl, Br, I) with easy-plane magnetic anisotropy as field-induced single-molecule magnets. Dalton Trans. 2015, 44, 17565–17571. [Google Scholar] [CrossRef]
- Vaidya, S.; Upadhyay, A.; Singh, S.K.; Gupta, T.; Tewary, S.; Langley, S.K.; Walsh, J.P.S.; Murray, K.S.; Rajaraman, G.; Shanmugam, M. A synthetic strategy for switching the single ion anisotropy in tetrahedral Co(II) complexes. Chem. Commun. 2015, 51, 3739–3742. [Google Scholar] [CrossRef]
- Vaidya, S.; Singh, S.K.; Shukla, P.; Ansari, K.; Rajaraman, G.; Shanmugam, M. Role of Halide Ions on the Nature of Magnetic Anisotropy in Tetrahedral Co(II) Complexes. Chem. A Eur. J. 2017, 23, 9546–9559. [Google Scholar] [CrossRef]
- Zadrozny, J.M.; Telser, J.; Long, J.R. Slow magnetic relaxation in the tetrahedral cobalt(II) complexes [Co(EPh)4]2 (E = O, S, Se). Polyhedron 2013, 64, 209–217. [Google Scholar] [CrossRef]
- Vallejo, J.; Castro, I.; Ruiz-Garcia, R.; Cano, J.; Julve, M.; Lloret, F.; De Munno, G.; Wernsdorfer, W.; Pardo, E. Field-Induced Slow Magnetic Relaxation in a Six-Coordinate Mononuclear Cobalt(II) Complex with a Positive Anisotropy. J. Am. Chem. Soc. 2012, 134, 15704–15707. [Google Scholar] [CrossRef]
- Colacio, E.; Ruiz, J.; Ruiz, E.; Cremades, E.; Krzystek, J.; Carretta, S.; Cano, J.; Guidi, T.; Wernsdorfer, W.; Brechin, E.K. Slow magnetic relaxation in a Co(II)-Y(III) single-ion magnet with positive axial zero-field splitting. Angew. Chem. Int. Ed. 2013, 52, 9130–9134. [Google Scholar] [CrossRef]
- Herchel, R.; Vahovska, L.; Potočňak, I.; Travniček, Z. Slow Magnetic Relaxation in Octahedral Cobalt(II) Field-Induced Single-Ion Magnet with Positive Axial and Large Rhombic Anisotropy. Inorg. Chem. 2014, 53, 5896–5898. [Google Scholar] [CrossRef] [PubMed]
- Diaz-Torres, R.; Menelaou, M.; Roubeau, O.; Sorrenti, A.; Brandariz-de-Pedro, G.; Sanudo, E.C.; Teat, S.J.; Fraxedas, J.; Ruiz, E.; Aliaga-Alcalde, N. Multiscale study of mononuclear CoII SMMs based on curcuminoid ligands. Chem. Sci. 2016, 7, 2793–2803. [Google Scholar] [CrossRef] [PubMed]
- Palii, A.V.; Korchagin, D.V.; Yureva, E.A.; Akimov, A.V.; Misochko, E.Y.; Shilov, G.V.; Talantsev, A.D.; Morgunov, R.B.; Aldoshin, S.M.; Tsukerblat, B.S. Single-Ion Magnet Et4N[CoII(hfac)3] with Nonuniaxial Anisotropy: Synthesis, Experimental Characterization, and Theoretical Modeling. Inorg. Chem. 2016, 55, 9696–9706. [Google Scholar] [CrossRef] [PubMed]
- Valigura, D.; Rajnak, C.; Moncol, J.; Titiš, J.; Boča, R. A mononuclear Co(II) complex formed from pyridinedimethanol with manifold slow relaxation channels. Dalton Trans. 2017, 46, 10950–10956. [Google Scholar] [CrossRef]
- Varga, F.; Rajnak, C.; Titis, J.; Moncol, J.; Boca, R. Slow magnetic relaxation in a Co(II) octahedraltetrahedral system formed of a [CoL3]2+ core with L = bis(diphenylphosphanoxido) methane and tetrahedral [CoBr4]2− counter anions. Dalton Trans. 2017, 46, 4148–4151. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Coca, S.; Urtizberea, A.; Cremades, E.; Alonso, P.J.; Camon, A.; Ruiz, E.; Luis, F. Origin of slow magnetic relaxation in Kramers ions with non-uniaxial anisotropy. Nat. Commun. 2014, 5, 4300. [Google Scholar] [CrossRef] [Green Version]
- Sertphon, D.; Murray, K.S.; Phonsri, W.; Jover, J.; Ruiz, E.; Telfer, S.G.; Alkaş, A.; Harding, P.; Harding, D.J. Slow Relaxation of Magnetization in a Bis-mer-Tridentate Octahedral Co(II) Complex. Dalton Trans. 2018, 47, 859–867. [Google Scholar] [CrossRef]
- Zhu, Y.-Y.; Cui, C.; Zhang, Y.-Q.; Jia, J.-H.; Guo, X.; Gao, C.; Qian, K.; Jiang, S.-D.; Wang, B.-W.; Wang, Z.-M.; et al. Zero-field slow magnetic relaxation from single Co(II) ion: A transition metal single-molecule magnet with high anisotropy barrier. Chem. Sci. 2013, 4, 1802–1806. [Google Scholar] [CrossRef]
- Peng, Y.; Mereacre, V.; Anson, C.E.; Zhang, Y.; Bodenstein, T.; Fink, K.; Powell, A.K. Field-Induced Co(II) Single-Ion Magnets with mer-Directing Ligands but Ambiguous Coordination Geometry. Inorg. Chem. 2017, 56, 6056–6066. [Google Scholar] [CrossRef]
- Mabbs, F.E.; Machin, D.J. Magnetism and Transition Metal Complexes; Dover Publications: New York, NY, USA, 2008. [Google Scholar]
- Chilton, N.F.; Anderson, R.P.; Turner, L.D.; Soncini, A.; Murray, K.S. PHI: Apowerful new program for the analysis of anisotropic monomeric and exchange-coupled polynuclear d- and f block complexes. J. Comput. Chem. 2013, 34, 1164–1175. [Google Scholar] [CrossRef]
- Aubin, S.M.J.; Sun, Z.; Pardi, L.; Krzystek, J.; Folting, K.; Brunel, L.; Rheingold, A.L.; Christou, G.; Hendrickson, D.N. Reduced Anionic Mn12 Molecules with Half-Integer Ground States as Single-Molecule Magnets. Inorg. Chem. 1999, 38, 5329. [Google Scholar] [CrossRef]
- Hagiwara, M.; Nagata, K. Magnetic behaviors of complex nature found in an oxide glass system containing deposited magnetite clusters at the superparamagnetic state. J. Magn. Magn. Mater. 1998, 177–181, 91–92. [Google Scholar] [CrossRef]
- Chandrasekhar, V.; Dey, A.; Mota, A.J.; Colacio, E. Slow Magnetic Relaxation in Co(III)–Co(II) Mixed-Valence Dinuclear Complexes with a CoIIO5X (X = Cl, Br, NO3) Distorted-Octahedral Coordination Sphere. Inorg. Chem. 2013, 52, 4554–4561. [Google Scholar] [CrossRef] [PubMed]
- Sheldrick, G.M. A short history of SHELX. Acta Crystallogr. A 2008, 64, 112–122. [Google Scholar] [CrossRef] [PubMed]
- Altomare, A.; Burla, M.C.; Camalli, M.; Cascarano, G.L.; Giacovazzo, C.; Guagliardi, A.; Moliterni, A.G.G.; Polidori, G.; Spagna, R.J. SIR97: A new tool for crystal structure determination and refinement. Appl. Cryst. 1999, 32, 115–119. [Google Scholar] [CrossRef]
- Betteridge, P.W.; Carruthers, J.R.; Cooper, R.I.; Prout, K.; Watkin, D.J. CRYSTALS version 12: software for guided crystal structure analysis. J. Appl. Cryst. 2003, 36, 1487. [Google Scholar] [CrossRef]
- Meulenaer, J.D.; Tompa, H. The absorption correction in crystal structure analysis. Acta Crystallogr. 1965, 19, 1014–1018. [Google Scholar] [CrossRef]
| Atoms | Distance (Å) | Atoms | Angle (°) | Atoms | Angle (°) |
|---|---|---|---|---|---|
| Co1-O1 | 2.0804(2) | O4-Co1-O2 | 158.26(7) | O1-Co1-N4 | 106.53(7) |
| Co1-O2 | 2.0911(2) | O4-Co1-O1 | 87.18(7) | O3-Co1-N4 | 91.30(7) |
| Co1-O3 | 2.0803(2) | O2-Co1-O1 | 87.33(7) | O4-Co1-N3 | 91.94(7) |
| Co1-O4 | 2.0929(2) | O4-Co1-O3 | 100.71(7) | O2-Co1-N3 | 107.42(7) |
| Co1-N3 | 2.0713(2) | O2-Co1-O3 | 91.03(7) | O1-Co1-N3 | 77.90(7) |
| Co1-O22 | 2.0750(2) | O1-Co1-O3 | 161.26(7) | O3-Co1-N3 | 84.82(7) |
| O4-Co1-N4 | 83.82(7) | N4-Co1-N3 | 173.64(7) | ||
| O2-Co1-N4 | 77.63(7) |
| D-H···A | d(D-H) Å | d(H···A) Å | d(D···A) Å | <(DHA) ° |
|---|---|---|---|---|
| N2-H21···O7 | 0.85 | 2.05 | 2.891(4) | 173 |
| N1-H11···O11 | 0.84 | 2.12 | 2.929(4) | 161 |
| N1-H11···O14 | 0.84 | 2.09 | 2.894(4) | 159 |
| O3-H31···O5 | 0.82 | 1.84 | 2.564(4) | 146 |
| O4-H41···O6 | 0.82 | 1.75 | 2.541(4) | 163 |
| O5-H52···O8 | 0.83 | 2.07 | 2.872(4) | 165 |
| O5-H51···O11 | 0.82 | 2.33 | 3.093(4) | 155 |
| O5-H51···O12 | 0.82 | 1.98 | 2.588(4) | 130 |
| O5-H51···O13 | 0.82 | 2.45 | 3.245(4) | 163 |
| O5-H51···O14 | 0.82 | 2.56 | 3.224(4) | 138 |
| O6-H1···O8 | 0.90 | 1.98 | 2.886(4) | 180 |
| O6-H2···O15 | 0.90 | 2.56 | 3.138(4) | 122 |
| O6-H2···O16 | 0.90 | 1.76 | 2.660(4) | 180 |
| O6-H2···O17 | 0.90 | 2.48 | 3.248(4) | 143 |
| T (K) | α | χs (cm3 mol−1) | χT (cm3 mol−1) | |
|---|---|---|---|---|
| 2.0 | 0.0999 | 0.658 | 1.344 | 9.63 × 10−7 |
| 2.1 | 0.0881 | 0.663 | 1.337 | 9.40 × 10−7 |
| 2.2 | 0.0532 | 0.676 | 1.324 | 9.42 × 10−7 |
| 2.3 | 0.0458 | 0.683 | 1.317 | 9.04 × 10−7 |
| 2.4 | 0.0542 | 0.680 | 1.320 | 9.06 × 10−7 |
| 2.5 | 0.0590 | 0.685 | 1.315 | 8.64 × 10−7 |
| 2.6 | 0.0594 | 0.701 | 1.299 | 7.71 × 10−7 |
| 2.7 | 0.0612 | 0.708 | 1.292 | 7.26 × 10−7 |
| 2.8 | 0.0434 | 0.710 | 1.290 | 7.47 × 10−7 |
| 2.9 | 0.0370 | 0.718 | 1.282 | 7.09 × 10−7 |
| 3.0 | 0.0502 | 0.723 | 1.277 | 6.60 × 10−7 |
| 3.2 | 0.0280 | 0.742 | 1.258 | 5.87 × 10−7 |
| 3.4 | 0.0214 | 0.754 | 1.247 | 5.42 × 10−7 |
| 3.6 | 0.0213 | 0.766 | 1.234 | 4.86 × 10−7 |
| 3.8 | 0.0377 | 0.774 | 1.226 | 4.20 × 10−7 |
| 4.0 | 0.0326 | 0.784 | 1.216 | 3.76 × 10−7 |
| 4.5 | 0.0121 | 0.811 | 1.189 | 2.91 × 10−7 |
| 5.0 | 0.0158 | 0.830 | 1.170 | 2.09 × 10−7 |
| 5.5 | 0.0209 | 0.850 | 1.150 | 1.46 × 10−7 |
| 6.0 | 0.0361 | 0.872 | 1.129 | 9.57 × 10−8 |
| 1 | |
|---|---|
| Formula | C12H16Cl2CoN4O13 |
| Mol. Wt. (g mol−1) | 650.24 |
| T (K) | 120 |
| λ Å | 0.71073 |
| Crystal system | Triclinic |
| Space gr. | P-1 |
| a (Å) | 10.1953(13) |
| b (Å) | 10.5394(14) |
| c (Å) | 13.6540(18) |
| α (°) | 78.889(6) |
| β (°) | 69.501(6) |
| γ (°) | 69.266(6) |
| V Å3 | 1281.3(3) |
| Z | 2 |
| D g.cm−3 | 1.685 |
| µ mm−1 | 0.956 |
| F (000) | 666 |
| Crystal size mm3 | 0.08 × 0.10 × 0.17 |
| θ range ° | 2 to 28 |
| Reflections collected | 47,212 |
| Ind. reflections | 6201 |
| R(int) | 0.037 |
| Reflections used | 4781 |
| Parameters refined | 391 |
| S | 1.07 |
| Final R indices [I > 3σ(I)] | R = 0.0451 wR = 0.0524 |
| Δρmax and Δρmin e·Å−3 | 0.7 and −1.14 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sadhukhan, D.; Ghosh, P.; Gómez-García, C.J.; Rouzieres, M. A Co(II)-Hydrazone Schiff Base Single Ion Magnet Exhibiting Field Induced Slow Relaxation Dynamics. Magnetochemistry 2018, 4, 56. https://doi.org/10.3390/magnetochemistry4040056
Sadhukhan D, Ghosh P, Gómez-García CJ, Rouzieres M. A Co(II)-Hydrazone Schiff Base Single Ion Magnet Exhibiting Field Induced Slow Relaxation Dynamics. Magnetochemistry. 2018; 4(4):56. https://doi.org/10.3390/magnetochemistry4040056
Chicago/Turabian StyleSadhukhan, Dipali, Prithwi Ghosh, Carlos J. Gómez-García, and Mathieu Rouzieres. 2018. "A Co(II)-Hydrazone Schiff Base Single Ion Magnet Exhibiting Field Induced Slow Relaxation Dynamics" Magnetochemistry 4, no. 4: 56. https://doi.org/10.3390/magnetochemistry4040056
APA StyleSadhukhan, D., Ghosh, P., Gómez-García, C. J., & Rouzieres, M. (2018). A Co(II)-Hydrazone Schiff Base Single Ion Magnet Exhibiting Field Induced Slow Relaxation Dynamics. Magnetochemistry, 4(4), 56. https://doi.org/10.3390/magnetochemistry4040056