Abstract
The complex [Dy(L)(tta)3] with L the chiral 3-(2-pyridyl)-4-aza[6]-helicene ligand (tta− = 2-thenoyltrifluoroaacetonate) has been synthesized in its racemic form and structurally and magnetically characterized. [Dy(L)(tta)3] behaves as a single molecule magnet in its crystalline phase with the opening of a hysteresis loop at 0.50 K. These magnetic properties were interpreted with ab initio calculations.
1. Introduction
The design of single molecule magnet (SMM), with the aim of enhancing its peculiar magnetic properties, has been a prolific field in the scientific community for decades [1,2,3]. Indeed, SMMs can pave the way towards a new generation of materials as, for example, molecular qubits for quantum computing [4], memory storage devices [5] or spin valves [6]. In this framework, lanthanide ions are commonly exploited in the effort of reaching slower relaxation rates for the reversal of the magnetization. Indeed, lanthanides are well classified by looking at their electron density distribution, ranging from oblate (planar) to prolate (axial) distribution [7]. This is mainly due to their strong spin-orbit coupling, which leads to ground states with large angular momentum J and strong magnetic anisotropy. The crystal field, induced by the donor atoms of the ligands, acts only as a perturbation on the electron density distribution, leading to a fine-tuning of the electronic properties and so of the molecular magnetism. As a consequence, the careful choice of the lanthanide ion and of the ligands (and the induced symmetry) can be used to engineer novel SMMs. However, a complete elucidation of these magneto-structural correlations for these complexes is still missing, even if progresses have been done recently [8,9,10,11].
For all the applications mentioned above, it is crucial to study the correlation between the SMM behavior and other physical properties such as luminescence or redox activity [12]. The versatility of ligand chemistry can be exploited in this sense and may offer the possibility to have in a single compound, for instance, a magnetic emitting nanodevice [13,14,15]. Indeed, lanthanides have been intensively studied for their peculiar luminescence that covers a broad range of frequencies (from visible to near IR) with sharp line shape emission bands and long lifetime of the excited states [16,17,18,19,20,21,22]. However, they show very low absorption coefficients, since the f–f transitions are indeed prohibited (Laporte rule) [23]. This results in ineffective direct excitation processes, especially in dilute solution. To tackle this problem, indirect sensitization, using for example MLCT (Metal-Ligand Charge Transfer) transitions, has been developed by means of ligands functionalization with organic chromophores acting as antennae [24]. In the case where the antenna is chiral, the solid-state properties might change between the enantiopure and the racemic crystals. Besides, the magnetic properties of these atoms can be used to modify the light absorption in chiral compounds, an effect known as magneto-chiral dichroism [25,26].
A first example of the coupling between a DyIII-based SMM and a chiral antenna has been reported recently with the complex [Dy(L)(hfac)3] with L = 3-(2-pyridyl)-4-aza[6]-helicene and hfac = 1,1,1,5,5,5-hexafluoroacetylacetone [27]. The DyIII ion, with its 6H15/2 ground state, easily leads to Ising type of magnetic anisotropy in coordination spheres like N2O6 and this is achieved with the common bidentate 2,2′-bipyridine (bpy) ligand and three hfac− ligands [13,28,29,30]. On the other hand, a 2,2′-bipyridine (bpy) ligand has been functionalized with a [6]-helicene to enhance the luminescence. Indeed, the latter presents a π-conjugated backbone of aromatic rings, configurationally stable for n ≥ 5, and its peculiar topology results in intense emission [31,32]. Moreover, [n]-helicene ligands are helically-shaped, so they possess a chirality despite the absence of enantiocenter. Due to these intrinsic properties, this family of ligands is widely employed for various applications, ranging from organic molecular electronics [33], probes for detection of chirality and sensing devices [34] to molecular junction [35].
In the case of the [Dy(L)(hfac)3] SMM [27], the chirality of the ligand results in two possible crystal structures (racemic and enantiopure) with similar molecular arrangement but different packings. Interestingly, racemic and enantiopure crystals show notable different magnetic behavior, with the opening of a magnetic hysteresis only in the case of the enantiopure. Moreover, the calculated different nature (antiferromagnetic and ferromagnetic) of the dipolar couplings between first-neighbors allows explaining the magnetic measurements (e.g., temperature dependence of χMT).
With the aim to enhance the magnetic properties in this series of compounds, we present herein a novel derivative in which the hfac− ligands have been replaced by tta− (2-thenoyltrifluoroaacetonate) ligands. Indeed, it is well known that the swapping of these two ligands in such specific N2O6 environment enhances the magnetic properties [36,37,38], even if in other coordination environments the opposite effect has been recently observed [39]. Therefore, we report the synthesis, the single crystal X-ray structural analysis and the magnetic characterization along with extensive ab initio calculations of the novel compound [Dy(L)(tta)3] (1).
2. Results and Discussion
2.1. Structure
Complex 1 was obtained by the coordination reaction of the chiral 3-(2-pyridyl)-4-aza[6]-helicene [39,40] ligand (L) and tris(2-thenoyltrifluoroaacetonate)bis(aqueous)DyIII in CH2Cl2 (Scheme 1).
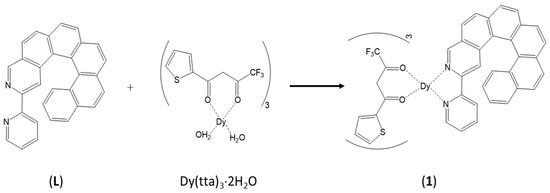
Scheme 1.
Synthetic route to obtain complex 1.
1 crystallizes in the triclinic centrosymmetric space group P-1 (Figure 1 and Figure S1, Table S1). The DyIII ion is surrounded by two nitrogen atoms and six oxygen atoms coming from the three 2-thenoyltrifluoroacetonate (tta−) anions and the L ligand. The N2O6 coordination polyhedron can be described as a distorted square antiprism environment (D4d symmetry on the basis of SHAPE analysis, Table S2) [41]. Thus, the replacement of the 1,1,1,5,5,5-hexafluoroacetylacetonate anions with tta− ones confers an higher symmetry for the coordination environment [27]. As already noted, such observation was already done for another complex stemming from this group and a significant positive impact on the magnetic properties was observed [37,38].
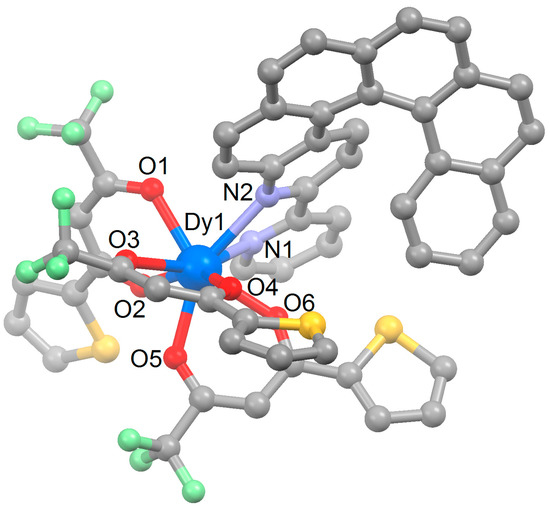
Figure 1.
Molecular structure of 1. Hydrogen atoms and molecules of crystallization are omitted for clarity. Selected bond lengths: Dy1–N1, 2.560(3) Å; Dy1–N2, 2.549(3) Å; Dy1–O1, 2.341(3) Å; Dy1–O2, 2.296(3) Å; Dy1–O3, 2.359(3) Å; Dy1–O4, 2.356(3) Å; Dy1–O5, 2.322(3) Å; Dy1–O6, 2.341(3) Å.
Starting from the racemic mixture of L, both enantiomers are present in the cell (P-1 space group symmetry). The crystal packing reveals that heterochiral dimers are formed with the presence of π–π interactions between the 2,2′-bipyridyl moieties (Figure 2) while an organic network runs along the a-axis thank to π–π interactions between the helicenic parts. The Dy–Dy shortest intermolecular distance was measured equal to 8.935 Å which is similar to the distance measured in the complex involving the Dy(hfac)3 metallo-precursor.

Figure 2.
Crystal packing of 1 along the a-axis. “Spacefill” and “ball and sticks” representations are used for L ligands and organometallic moieties, respectively.
2.2. Magnetic Properties
2.2.1. Static Magnetic Measurements
The temperature dependence of χMT for the sample 1 is represented in Figure 3. The room temperature value is 13.96 cm3·K·mol−1 in good agreement with the expected value of 14.17 cm3·K·mol−1 for an isolated DyIII ion [42]. Upon cooling, χMT decreases monotonically down to 11.20 cm3·K·mol−1 due to the thermal depopulation of the MJ states. Below 5 K, the more rapid decrease could be attributed to the presence of weak dipolar antiferromagnetic interactions as determined by quantum calculations on the analogue complex involving hfac− ancillary ligands [27]. The field dependence of the magnetization measured at 2.0 K reaches the value of 5.12 Nβ under a magnetic field of 50 kOe, in agreement with the expected value (5 Nβ) for an Ising ground state (Inset of Figure 3).

Figure 3.
Temperature dependence of χMT for 1 (black circles). The inset shows the field variations of the magnetization at 2 K. Full red lines correspond to the simulated curves from ab initio calculations.
2.2.2. Dynamic Magnetic Measurements
The out-of-phase component of the ac susceptibility (χM′′) of 1 was measured using immobilized crunched single crystals. It shows frequency dependence in zero external dc field with clear maxima on the χM′′ vs. ν curves (ν the frequency of the ac oscillating field) up to 13 K (Figure 4a). The frequency dependence of the ac susceptibility can be analyzed in the framework of the extended Debye model (Figures S2 and S3) [43,44]. The temperature dependence of the relaxation time at zero field is extracted between 2.0 and 14.0 K (Table S3). Formally, four different relaxation mechanisms coexist: Direct, Raman, Orbach and QTM [2]. The former disappears in the absence of external field while the second and the third are field-independent. The latest is the only temperature independent mechanism. Fitting of the zero-field data with only Raman and QTM is not satisfactory while Raman + Orbach + QTM leads to unrealistic results owing to over-parameterization. The only realistic picture is given by the Orbach + QTM combination. The relaxation time follows the Arrhenius law τ = τ0 exp(Δ/kT) only above 12 K with τ0 = 2.6(2) × 10−6 s and Δ = 38.7(2) cm−1 (Figure 4d, open squares) with dominant QTM mechanism (τQTM = 7.0(3) × 10−4 s) at low temperature.

Figure 4.
(a) Frequency dependence of χM′′ between 2 and 14 K; (b) scan field of the frequency dependence of χM′′ at 2 K; (c) frequency dependence of χM′′ between 2 and 14 K under an applied magnetic field of 1000 Oe; and (d) temperature variation of the relaxation time measured in zero field (open squares) and in an external field of 1000 Oe (full squares) with the best fitted curve (red lines) in the temperature range of 2–14 K.
In order to reduce the QTM operating in this system, the optimal magnetic field of 1000 Oe was determined by a scan field (Figure 4b). The application of this moderate external dc field induces a slowing down of the magnetic relaxation with a shift of the maxima of the χM′′ vs. ν curve at lower frequencies (Figure 4c). It must be mentioned that at moderate fields at least two relaxation processes coexist which merge into one at higher fields than 800 Oe (Figure 4b). Any attempts to fit the thermal behavior of the relaxation time with a combination of the previously mentioned mechanisms fail with a reasonable set of data. The thermal dependence of the relaxation time of the magnetization (Figures S4 and S5 and Table S4) can be fitted considering a combination of two thermally dependent regimes between 3.0 and 14.0 K (Orbach processes) (τ0 = 2.0(7) × 10−7 s and Δ0 = 68.1(3) cm−1, τ1 = 4.9(6) × 10−4 s and Δ1 = 16.0(5) cm−1). Relaxation times on the order of few seconds is slow enough to observe the opening of the hysteresis loop at 0.50 K (Figure 5) which remains opened at higher temperatures (Figure S6). One must mention that the hysteresis loop of the racemic form of [Dy(L)(hfac)3] [27] was closed at the same temperature.

Figure 5.
Magnetic hysteresis loop of 1 measured at 0.5 K at a sweep rate of 16 Oe·s−1.
2.2.3. Ab Initio Calculations
Various theoretical models, with various pros and cons, are available to predict the magnetic properties of lanthanides, ranging from complete active space ab initio methods (e.g., CASSCF or CASPT2) to semi-empirical methods (e.g., radial effective charge model, REC) [45]. To study the electronic structure of the present compound, we choose SA-CASSCF/RASSI-SO calculations as a good compromise between accuracy with respect to the experimental evidence and “first principle” theoretical model.
Calculations were performed for 1 to understand the observed magnetic properties comparing with the ab initio calculated electronic structure (see computational details). The calculated χMT vs. T and M vs. H (Figure 3) curves fairly well reproduce the experimental curves, even if the agreement for the χMT vs. T data is still semi-quantitative. Calculations confirm the axial character of the magnetic anisotropy tensor of the ground Kramers doublet with large gz values of 19.55 and almost negligible gx and gy values. The gz value for DyIII is close to the expected gz = 20 for a pure MJ = |±15/2> ground state. This is confirmed by the calculated composition of MJ = 0.94 |±15/2> + 0.06 |±11/2> for the ground doublet state of 1 (see Table S5 for the wavefunction composition). The calculated ground-state easy axis (Figure 6) for the DyIII ion is oriented perpendicular to the plane formed by the 2,2′-bipyridine moieties as expected for an oblate ion with this coordination sphere [31,36].

Figure 6.
Representation of complex 1 with the theoretical orientation of the easy magnetic axis of the DyIII center.
Even if the uniaxiality of the anisotropy is not strictly associated to slow relaxation of the magnetization [46], in most of the cases reported in the literature for DyIII this assumption is valid. Indeed, in this case, the magnetic relaxation pathways can also be easily interpreted on the basis of magnetic transition moments (Figure 7) calculated with the SINGLE_ANISO program [47,48]. It has to be pointed out that in the latter not all the contributions are included. Indeed, the coupling of spin-phonon degrees of freedom in the SMM relaxation is not taken into account in the ab initio model whereas it has been recently evidenced of general importance [49,50]. However, these discrepancies are common in literature [3,51,52] and the magnetic transition moments calculated in this work still leads to a fairly good qualitative picture. Indeed, no direct transition between the two MJ states of the ground doublet or Orbach processes from the ground state are expected whereas relaxation mechanisms involving states from the third MJ state are highly probable. A non-negligible Orbach process has been also found between the second and third MJ states. The calculations indicate a difference between the calculated energy barrier (Δ = 82 cm−1) and the experimental barrier (Δ = 39–68 cm−1). However, the discrepancy between these values can be, reasonably, ascribed in the spin-phonon contributions mentioned above.

Figure 7.
Computed magnetization blocking barrier in complex 1 for the DyIII ion. Numbers provided on each arrow are the mean absolute values for the corresponding matrix elements of the magnetic transition dipole moment.
3. Materials and Methods
3.1. Synthesis. General Procedures and Materials
The precursor Dy(tta)3·2H2O [53] (tta− = 2-thenoyltrifluoroacetonate anion) and the ligand 3-(2-pyridyl)-4-aza[6]-helicene [40,54] L were synthesized following previously reported methods. All other reagents were commercially available and used without further purification.
3.2. Synthesis of Complex [Dy(tta)3(L)]·CH2Cl2·C7H8 (1)
Dy(tta)3·2H2O (17.2 mg, 0.02 mmol) were dissolved in 5 mL of CH2Cl2 and then added to a solution of 5 mL of CH2Cl2 containing 8.3 mg of L (0.02 mmol). After 20 min of stirring, 30 mL of toluene were layered at 4 °C in the dark. Slow diffusion following by slow evaporation lead to yellow single crystals which are suitable for X-ray studies. Yield: 15.2 mg (54% based on Dy). Anal. Calcd (%) for C62H40Cl2DyF9N2O6S3: C 52.78, H 2.84, N 1.99; found: C 52.72, H 2.81 N, 2.09. I.R. 3426 (m), 2923 (w), 1604 (s), 1588 (m), 1566 (m), 1493 (m), 1468 (m), 1429 (m), 1256 (s), 117 (m), 1091 (w), 1046 (w), 991 (w), 963 (w), 848 (w), 815 (w), 797 (s), 773 (m), 755 (m), 654 (m), 542 (m), 503 (m) cm−1.
3.3. Crystallography
Single crystal of [Dy(tta)3(L)]·CH2Cl2·C7H8 (1) was mounted on a APEXII Bruker-AXS diffractometer for data collection (MoKα radiation source, λ = 0.71073 Å). The structure was solved by direct methods using the SIR-97 program and refined with a full matrix least-squares method on F2 using the SHELXL-97 program [55,56]. Crystallographic data are summarized in Table S1. Complete crystal structure results as a CIF file including bond lengths, angles, and atomic coordinates are deposited as Supporting Information. CCDC number is 1510324 for compound 1.
3.4. Physical Measurements
The elementary analyses of the compound were performed at the Centre Régional de Mesures Physiques de l’Ouest, Rennes, France. The dc magnetic susceptibility measurements were performed on solid polycrystalline sample with a Quantum Design MPMS-XL SQUID magnetometer between 2 and 300 K in an applied magnetic field of 0.02 T for temperatures in the range 2–20 K, 0.2 T between 20 and 80 K and 1 T for temperatures between 80 and 300 K. These measurements were all corrected for the diamagnetic contribution as calculated with Pascal’s constants. The ultra-low temperature measurements (below 1.8 K) were performed with the help of a 3He insert.
3.5. Computational Details
Wavefunction-based calculations were carried out on molecular structures of 1 by using the SA-CASSCF/RASSI-SO approach, as implemented in the MOLCAS quantum chemistry package (versions 8.0) [57]. In this approach, the relativistic effects are treated in two steps on the basis of the Douglas–Kroll Hamiltonian. First, the scalar terms were included in the basis-set generation and were used to determine the spin-free wavefunctions and energies in the complete active space self-consistent field (CASSCF) method [58]. Next, spin-orbit coupling was added within the restricted-active-space-state-interaction (RASSI-SO) method, which uses the spin-free wavefunctions as basis states [59,60]. The resulting wavefunctions and energies are used to compute the magnetic properties and g-tensors of the lowest states from the energy spectrum by using the pseudo-spin S = 1/2 formalism in the SINGLE-ANISO routine [47,48]. Cholesky decomposition of the bielectronic integrals was employed to save disk space and speed-up the calculations [61]. For 1 the active space of the self consistent-field (CASSCF) method consisted of the nine 4f electrons of the DyIII ion spanning the seven 4f orbitals, i.e., CAS(9,7)SCF. State-averaged CASSCF calculations were performed for all of the sextets (21 roots), all of the quadruplets (224 roots), and 300 out of the 490 doublets (due to hardware limitations) of the DyIII ion. Twenty-one sextets, 128 quadruplets, and 107 doublets were mixed through spin–orbit coupling in RASSI-SO. All atoms were described by ANO-RCC basis sets [62,63,64]. The following contractions were used: [8s7p4d3f2g1h] for Dy, [4s3p2d1f] for the O and N atoms, [3s2p1d] for the C and F atoms, [4s3p1d] for the S atoms and [2s1p] for the H atoms. The atomic positions were extracted from the X-ray crystal structures. Only the position of the H and F atoms were optimized on the YIII parent complexes with the Gaussian 09 (revision D.01) package [65] employing the PBE0 hybrid functional [66,67]. The “Stuttgart/Dresden” basis sets [68] and effective core potentials were used to describe the yttrium atom, whereas all other atoms were described with the SVP basis sets [69].
4. Conclusions
In the course of intermixing chirality offered by the nature of the ligands and SMM properties, we extend herein the family of [6]-helicene-based lanthanide SMM [27]. We report the synthesis of the complex [Dy(L)(tta)3] with L the chiral 3-(2-pyridyl)-4-aza[6]-helicene ligand (tta− = 2-thenoyltrifluoroaacetonate). Its racemic form was structurally and magnetically characterized. [Dy(L)(tta)3] behaves as a single molecule magnet in its crystalline phase. As expected, the substitution of hfac− ligands by tta− moieties enhances the magnetic behavior with the opening of an hysteresis loop at 0.50 K that was only observed for the enantiopure forms in the case of [Dy(L)(hfac)3] [27]. The electronic structure of the complex has been elucidated by mean of SA-CASSCF/RASSI-SO calculations, highlighting the nature of the ground state and contributing in the interpretation of experimental evidences. A qualitative picture of the magnetization blocking barrier is also reported. In the near future, we will pursue our investigation of chiral lanthanide-based SMMs that may offer new perspectives in both the domains of molecular magnetism and chirality with the potential access of properties such as circularly polarized luminescence (CPL) activity that remains anecdotic for lanthanide compounds to date.
Supplementary Materials
The following are available online at www.mdpi.com/2312-7481/3/1/2/s1, Figure S1: ORTEP view of 1. Thermal ellipsoids are drawn at 30% probability. Hydrogen atoms and solvent molecules of crystallization are omitted for clarity., Figure S2: Frequency dependence of the ac susceptibility components χM′ and χM′′ at 10 K and in zero external dc field for compound 1 with the best fitted curve with extended Debye model, Figure S3: Frequency dependence of the ac susceptibility components χM′ and χM′′ at 10 K and in 1000 Oe external dc field for compound 1 with the best fitted curve with extended Debye model; Figure S4: Cole–Cole plots using the ac data performed under zero magnetic field. The black lines correspond to the fit with a generalized Debye model; Figure S5: Cole–Cole plots using the ac data performed under 1000 Oe magnetic field. The black lines correspond to the fit with a generalized Debye model; Figure S6: Magnetic hysteresis loop of 1 measured at 0.5, 1.0 and 1.5 K; Table S1: X-ray crystallographic data of 1; Table S2: SHAPE analysis for 1; Table S3: Best fitted parameters (χT, χS, τ and α) with the extended Debye model 1 at zero field in the temperature range 2.0–15 K; Table S4: Best fitted parameters (χT, χS, τ and α) with the extended Debye model 1 at 1 kOe in the temperature range 1.8–5 K; Table S5: Computed energies, g-tensor and wavefunction composition of the ground state doublet in the effective spin ½ model for 1.
Acknowledgments
This work was supported by Région Bretagne, Rennes Métropole, CNRS, Université de Rennes 1. G.F.G gratefully acknowledges the European Commission through the ERC-AdG 267746 MolNanoMas (project N. 267746) and the ANR (ANR-13-BS07-0022-01) for financial support. J.C. with N.S. and J.-K.O.-Y., respectively, thank the ANR (ANR-10-BLAN-724-1-NCPCHEM) and the Chinese Scholarship Council for financial support. B.L.G. and G.F.G. thank the French GENCI/IDRIS-CINES center for high-performance computing resources.
Author Contributions
J.-K.O.-Y., and N.S. performed the organic syntheses; F.P. performed the coordination chemistry, crystallizations, the single crystal X-ray diffraction experiments and structure refinements; O.C. performed the magnetic measurements; J.F.G. analyzed the magnetic measurements; G.F.-G., F.T., and B.L.G. performed the ab initio calculations; J.C., and L.O. discussed the results and commented on the manuscript; and F.P., O.C., and B.L.G. conceived and designed the experiments and contributed equally to the writing of the article.
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| SMM | Single Molecule Magnet |
| TTF | TetraThiaFulvalene |
| CH2Cl2 | Dichloromethane |
| hfac | 1,1,1,5,5,5-hexafluoroacetylacetonate |
| tta | 2-thenoyltrifluoroacetonate |
| PCM | Polarizable Continuum Model |
| CASSCF | Complete Active Space Self-Consistent Field |
| RASSI-SO | Restricted Active Space State Interaction—Spin-Orbit |
References
- Sessoli, R.; Powell, A.K. Strategies towards single molecule magnets based on lanthanide ions. Coord. Chem. Rev. 2009, 253, 2328–2341. [Google Scholar] [CrossRef]
- Liddle, S.T.; van Slageren, J. Improving f-element single molecule magnets. Chem. Soc. Rev. 2015, 44, 6655–6669. [Google Scholar] [CrossRef] [PubMed]
- Pedersen, K.S.; Dreiser, J.; Weihe, H.; Sibille, R.; Johannesen, H.V.; Sorensen, M.A.; Nielsen, B.E.; Sigrist, M.; Mutka, H.; Rols, S.; et al. Design of Single-Molecule Magnets: Insufficiency of the Anisotropy Barrier as the Sole Criterion. Inorg. Chem. 2015, 54, 7600–7606. [Google Scholar] [CrossRef] [PubMed]
- Pedersen, K.S.; Ariciu, A.; McAdams, S.; Weihe, H.; Bendix, J.; Tuna, F.; Piligkos, S. Toward Molecular 4f Single-Ion Magnet Qubits. J. Am. Chem. Soc. 2016, 138, 5801–5804. [Google Scholar] [CrossRef] [PubMed]
- Mannini, M.; Pineider, F.; Sainctavit, P.; Danieli, C.; Otero, E.; Sciancalepore, C.; Talarico, A.M.; Arrio, M.-A.; Cornia, A.; Gatteschi, D. Magnetic memory of a single-molecule quantum magnet wired to a gold surface. Nat. Mater. 2009, 8, 194–197. [Google Scholar] [CrossRef] [PubMed]
- Rocha, A.R.; García-Suaŕez, V.M.; Bailey, S.W.; Lambert, C.J.; Ferrer, J.; Sanvito, S. Towards Molecular Spintronics. Nat. Mater. 2005, 4, 335–339. [Google Scholar] [CrossRef] [PubMed]
- Rinehart, J.D.; Long, J.R. Exploiting single-ion anisotropy in the design of f-element single-molecule magnets. Chem. Sci. 2011, 2, 2078–2085. [Google Scholar] [CrossRef]
- Lucaccini, E.; Briganti, M.; Perfetti, M.; Vendier, L.; Costes, J.-P.; Totti, F.; Sessoli, R.; Sorace, L. Relaxation Dynamics and Magnetic Anisotropy in a Low-Symmetry DyIII Complex. Chem. Eur. J. 2016, 22, 5552–5562. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Zhang, L.; Tang, J. Lanthanide single molecule magnets: Progress and perspective. Dalton. Trans. 2015, 44, 3923–3929. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Jung, J.; Zhang, L.; Tang, J.; Le Guennic, B. Elucidating the Magnetic Anisotropy and Relaxation Dynamics of Low-Coordinate Lanthanide Compounds. Inorg. Chem. 2016, 55, 1905–1911. [Google Scholar] [CrossRef] [PubMed]
- Cucinotta, G.; Perfetti, M.; Luzon, J.; Etienne, M.; Car, P.E.; Caneschi, A.; Calvez, G.; Bernot, K.; Sessoli, R. Magnetic Anisotropy in a Dysprosium/DOTA Single-Molecule Magnet: Beyond Simple Magneto-Structural Correlations. Angew. Chem. Int. Ed. 2012, 51, 1606–1610. [Google Scholar] [CrossRef] [PubMed]
- Pointillart, F.; Le Guennic, B.; Cador, O.; Maury, O.; Ouahab, L. Lanthanide and Ion and Tetrathiafulvalene-Based Ligand as a “Magic” Couple toward Luminescence, Single Molecule Magnets, and Magnetostructural Correlations. Acc. Chem. Res. 2015, 48, 2834–2842. [Google Scholar] [CrossRef] [PubMed]
- Pointillart, F.; Jung, J.; Berraud-Pache, R.; Le Guennic, B.; Dorcet, V.; Golhen, S.; Cador, O.; Maury, O.; Guyot, Y.; Decurtins, S.; et al. Luminescence and Single-Molecule Magnet Behavior in Lanthanide Complexes Involving a Tetrathiafulvalene-Fused Dipyridophenazine Ligand. Inorg. Chem. 2015, 54, 5384–5397. [Google Scholar] [CrossRef] [PubMed]
- Long, J.; Vallat, R.; Ferreira, R.A.S.; Carlos, L.D.; Almeida Paz, F.A.; Guari, Y.; Larionova, J. A bifunctional luminescent single-ion magnet: Towards correction between luminescence studies and magnetic slow relaxation processes. Chem. Commun. 2012, 48, 9974–9976. [Google Scholar] [CrossRef] [PubMed]
- Pointillart, F.; Le Guennic, B.; Golhen, S.; Cador, O.; Maury, O.; Ouahab, L. A redox active luminescent ytterbium single-molecule magnet. Chem. Commun. 2013, 49, 615–617. [Google Scholar] [CrossRef] [PubMed]
- Sabbatini, N.; Guardigli, M.; Manet, I. Handbook of the Physics and Chemistry of Rare Earths; Elsevier: Amsterdam, The Netherlands, 1996; Volume 23, p. 69. [Google Scholar]
- Comby, S.; Bünzli, J.-C.G. Handbook on the Physics and Chemistry of Rare Earths; Elsevier: Amsterdam, The Netherlands, 2007; Volume 37, Chapter 235. [Google Scholar]
- Parker, D. Luminescent Lanthanide Sensors for pH, pO2 and Selected Anions. Coord. Chem. Rev. 2000, 205, 109–130. [Google Scholar] [CrossRef]
- Parker, D. Excitement in f block: Structure, dynamics and function of nine-coordinate chiral lanthanide complexes in aqueous media. Chem. Soc. Rev. 2004, 33, 156–165. [Google Scholar] [CrossRef] [PubMed]
- Bünzli, J.-C.G.; Piguet, C. Taking advantage of luminescent lanthanide ions. Chem. Soc. Rev. 2005, 34, 1048–1077. [Google Scholar] [CrossRef] [PubMed]
- Eliseeva, S.V.; Bünzli, J.-C.G. Lanthanide luminescence for functional materials and bio-sciences. Chem. Soc. Rev. 2010, 39, 189–227. [Google Scholar] [CrossRef] [PubMed]
- D’Aléo, A.; Pointillart, F.; Ouahab, L.; Andraud, C.; Maury, O. Charge transfer excited states sensitization of lanthanide emitting from the visible to the near-infra-red. Coord. Chem. Rev. 2012, 256, 1604–1620. [Google Scholar] [CrossRef]
- VanVleck, J.H. The Puzzle of rare-earth Spectra in Solids. J. Phys. Chem. 1937, 41, 67–80. [Google Scholar] [CrossRef]
- Wang, X.; Chang, H.; Xie, J.; Zhao, B.; Liu, B.; Xu, S.; Pei, W.; Ren, N.; Huang, L.; Huang, W. Recent developments in Lanthanide-based luminescent probes. Coord. Chem. Rev. 2014, 273–274, 201–212. [Google Scholar] [CrossRef]
- Train, C.; Ghoerghe, R.; Krstic, V.; Chamoreau, L.; Ovanesyan, N.S.; Rikken, G.L.J.A.; Gruselle, M.; Verdaguer, M. Strong magneto-chiral dichroism in enantiopure chiral ferromagnets. Nat. Mater. 2008, 7, 729–734. [Google Scholar] [CrossRef] [PubMed]
- Sessoli, R.; Boulon, M.-E.; Caneschi, A.; Mannini, M.; Poggini, L.; Wilhelm, F.; Rogalev, A. Strong magneto-chiral dichroism in a paramagnetic molecular helix observed by hard X-rays. Nat. Phys. 2014, 11, 69–74. [Google Scholar] [CrossRef] [PubMed]
- Ou-Yang, J.-K.; Saleh, N.; Fernandez Garcia, G.; Norel, L.; Pointillart, F.; Guizouarn, T.; Cador, O.; Totti, F.; Ouahab, L.; Crassous, J.; et al. Improved Slow Magnetic Relaxation in Optically Pure Helicene-Based DyIII Single Molecule Magnet. Chem. Commun. 2016, 52, 14474–14477. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Li, X.L.; Wang, T.W.; Song, Y.; You, X.Z. Slow Relaxation Processes and Single-Ion Magnetic Behaviors in Dysprosium-Containing Complexes. Inorg. Chem. 2010, 49, 969–976. [Google Scholar] [CrossRef] [PubMed]
- Li, D.-P.; Wang, T.-W.; Li, C.-H.; Liu, D.-S.; Li, Y.-Z.; You, X.-Z. Single-ion magnets based on mononuclear lanthanide complexes with chiral Schiff base ligands [Ln(FTA)3L] (Ln = Sm, Eu, Gd, Tb and Dy). Chem. Commun. 2010, 46, 2929–2931. [Google Scholar] [CrossRef] [PubMed]
- Norel, L.; Bernot, K.; Feng, M.; Roisnel, T.; Caneschi, A.; Sessoli, R.; Rigaut, S. A carbon-rich ruthenium decorated dysprosium single molecule magnet. Chem. Commun. 2012, 48, 3948–3950. [Google Scholar] [CrossRef] [PubMed]
- Bosson, J.; Gouin, J.; Lacour, J. Cationic triangulenes and helicenes: Synthesis, chemical stability, optical properties and extended applications of these unusual dyes. Chem. Soc. Rev. 2014, 43, 2824–2840. [Google Scholar] [CrossRef] [PubMed]
- Saleh, N.; Shen, C.; Crassous, J. Helicene-based transition metal complexes: Synthesis, properties and applications. Chem. Sci. 2014, 5, 3680–3694. [Google Scholar] [CrossRef]
- Storch, J.; Zadny, J.; Strasak, T.; Kubala, M.; Syroka, J.; Dusek, M.; Cirkva, V.; Matejka, P.; Krbal, M.; Vacek, J. Synthesis and Characterization of a Helicene-Based Imidazolium Salt and its Application in Organic Molecular Electronics. Chem. Eur. J. 2014, 21, 2343–2347. [Google Scholar] [CrossRef] [PubMed]
- Mendola, D.; Saleh, N.; Hellou, N.; Vanthuyne, N.; Roussel, C.; Toupet, L.; Castiglione, F.; Melone, F.; Caronna, T.; Fontana, F.; et al. Synthesis and Structural Properties of Aza[n]helicene Platinum Complex: Control of Cis and Trans Stereochemistry. Inorg. Chem. 2016, 55, 2009–2017. [Google Scholar] [CrossRef] [PubMed]
- Vacek, J.; Vacek Chocholousova, J.; Stara, I.G.; Stary, I.; Dubi, Y. Mechanical tuning of conductance and thermopower in helicene molecular junctions. Nanoscale 2015, 7, 8793–8802. [Google Scholar] [CrossRef] [PubMed]
- Jung, J.; da Cunha, T.T.; Le Guennic, B.; Pointillart, F.; Pereira, C.L.M.; Luzon, J.; Golhen, S.; Cador, O.; Maury, O.; Ouahab, L. Magnetic Studies of Redox-Active Tetrathiafulvalene-Based Complexes: Dysprosium vs. Ytterbium Ananlogues. Eur. J. Inorg. Chem. 2014, 2014, 3888–3894. [Google Scholar] [CrossRef]
- Cosquer, G.; Pointillart, F.; Golhen, S.; Cador, O.; Ouahab, L. Slow Magnetic Relaxation in Condensed versus Dispersed Dysprosium(III) Mononuclear Complexes. Chem. Eur. J. 2013, 19, 7895–7905. [Google Scholar] [CrossRef] [PubMed]
- Da Cunha, T.T.; Jung, J.; Boulon, M.-E.; Campo, G.; Pointillart, F.; Pereira, C.L.M.; Le Guennic, B.; Cador, O.; Bernot, K.; Pineider, F.; et al. Magnetic Poles Determinations and Robustness of Memory Effect upon Solubilization in a DyIII-Based Single Ion Magnet. J. Am. Chem. Soc. 2013, 135, 16332–16335. [Google Scholar] [CrossRef] [PubMed]
- Jiménez, J.R.; Díaz-Ortega, I.F.; Ruiz, E.; Aravena, D.; Pope, S.J.A.; Colacio, E.; Herrera, J.M. Lanthanide tetrazolate complexes combining Single-Molecule Magnet and luminescence properties: The effect of the replacement of tetrazolate N3 by β-diketonate ligands on the anisotropy energy barrier. Chem. Eur. J. 2016, 22, 14548–14559. [Google Scholar] [CrossRef] [PubMed]
- Saleh, N.; Moore, B., II; Srebro, M.; Vanthuyne, N.; Toupet, L.; Williams, J.A.G.; Roussel, C.; Deol, K.K.; Muller, G.; Autschbach, J.; et al. Acid/Base-Triggered Switching of Circularly Polarized Luminescence and Electronic Circular Dichroism in Organic and Organometallic Helicenes. Chem. Eur. J. 2015, 21, 1673–1681. [Google Scholar] [CrossRef] [PubMed]
- Llunell, M.; Casanova, D.; Cirera, J.; Bofill, J.M.; Alemany, P.; Alvarez, S.S. SHAPE, version 2.1; University of Barcelona: Barcelona, Spain, 2013.
- Kahn, O. Molecular Magnetism; VCH: Weinhem, Germany, 1993. [Google Scholar]
- Dekker, C.; Arts, A.F.M.; Wijn, H.W.; van Duyneveldt, A.J.; Mydosh, J.A. Activated dynamics in a two-dimensional Ising spin glass: Rb2Cu1−xCoxF4. Phys. Rev. B 1989, 40, 11243–11251. [Google Scholar] [CrossRef]
- Cole, K.S.; Cole, R.H. Dipersion and Absorption in Dielectrics I. Alternating Current Charcateristics. J. Chem. Phys. 1941, 9, 341–351. [Google Scholar] [CrossRef]
- Baldovi, J.J.; Duan, Y.; Morales, R.; Gaita-Ariño, A.; Ruiz, E.; Coronado, E. Rational design of lanthanoid Single-Ion Magnets: Predictive power of the theoretical models. Chem. Eur. J. 2016, 22, 13532–13539. [Google Scholar] [CrossRef] [PubMed]
- Lucaccini, E.; Sorace, L.; Perfetti, M.; Costes, J.-P.; Sessoli, R. Beyond the anisotropy barrier: Slow relaxation of the magnetization in both easy-axis and easy-plane Ln(trensal) complexes. Chem. Commun. 2014, 50, 1648–1651. [Google Scholar] [CrossRef] [PubMed]
- Chibotaru, L.F.; Ungur, L. Ab initio calculation of anisotropic magnetic properties of complexes. I. Unique definition of pseudospin Hamiltonians and their derivation. J. Chem. Phys. 2012, 137, 064112–064122. [Google Scholar] [CrossRef] [PubMed]
- Chibotaru, L.F.; Ungur, L.; Soncini, A. The Origin of Nonmagnetic Kramers Doublets in the Ground State of Dysprosium Triangles: Evidence for a Toroidal Magnetic Moment. Angew. Chem. Int. Ed. 2008, 47, 4126–4129. [Google Scholar] [CrossRef] [PubMed]
- Lunghi, A.; Totti, F. The role of Anisotropic Exchange in Single Molecule Magnets: A CASSCF/NEVPT2 Study of the Fe4 SMM Building Block [Fe2(OCH3)2(dbm)4] Dimer. Inorganics 2016, 4, 28–38. [Google Scholar] [CrossRef]
- Tesi, L.; Lunghi, A.; Atzori, M.; Lucaccini, E.; Sorace, L.; Totti, F.; Sessoli, R. Giant spin-phonon bottleneck effects in evaporable vanadyl-based molecules with long spin coherence. Dalton Trans. 2016, 45, 16635–16643. [Google Scholar] [CrossRef] [PubMed]
- Zadrozny, J.M.; Long, J.R. Slow Magnetic Relaxation at Zero Field in the tetrahedral Complex [Co(SPh)4]2−. J. Am. Chem. Soc. 2011, 133, 20732–20734. [Google Scholar] [CrossRef] [PubMed]
- Freedman, D.E.; Harman, W.H.; Harris, T.D.; Long, G.H.; Chang, C.J.; Long, J.R. Slow Magnetic Relaxation in a High-Spin Iron(II) Complex. J. Am. Chem. Soc. 2010, 132, 1224–1225. [Google Scholar] [CrossRef] [PubMed]
- Vooshin, A.I.; Shavaleev, N.M.; Kazakov, V.P. Chemiluminescence of praseodymium (III), neodymium (III) and ytterbium (III) β-diketonates in solution excited from 1,2-dioxetane decomposition and singlet-singlet energy transfer from ketone to rare-earth β-diketonates. J. Lumin. 2000, 91, 49–58. [Google Scholar] [CrossRef]
- Saleh, N.; Srebro, M.; Reynaldo, T.; Vanthuyne, N.; Toupet, L.; Chang, V.Y.; Muller, G.; Williams, J.A.G.; Roussel, C.; Autschbach, J.; et al. Enantio-Enriched CPL-active helicene-bipyridine-rhenium complexes. Chem. Commun. 2015, 51, 3754–3757. [Google Scholar] [CrossRef] [PubMed]
- Sheldrick, G.M. SHELX97—Programs for Crystal Structure Analysis (Release 97-2); Institüt für Anorganische Chemie der Universität: Göttingen, Germany, 1998. [Google Scholar]
- Altomare, A.; Burla, M.C.; Camalli, M.; Cascarano, G.L.; Giacovazzo, C.; Guagliardi, A.; Moliterni, A.G.G.; Polidori, G.; Spagna, R. SIR97: A new tool for crystal structure determination and refinement. J. Appl. Cryst. 1999, 32, 115–119. [Google Scholar] [CrossRef]
- Aquilante, F.; de Vico, L.; Ferré, N.; Ghigo, G.; Malmqvist, P.A.; Neogrady, P.; Bondo Pedersen, T.; Pitonak, M.; Reiher, M.; Roos, B.O.; et al. MOLCAS 7: The Next Generation. J. Comput. Chem. 2010, 31, 224–247. [Google Scholar] [CrossRef] [PubMed]
- Roos, B.O.; Taylor, P.R.; Siegbahn, P.E.M. A complete active space SCF method (CASSCF) using a density matrix formulated super-CI approach. Chem. Phys. 1980, 48, 157–288. [Google Scholar] [CrossRef]
- Malmqvist, P.A.; Roos, B.O.; Schimmelpfennig, B. The restricted active space (RAS) state interaction approach with spin-orbit coupling. Chem. Phys. Lett. 2002, 357, 230–240. [Google Scholar] [CrossRef]
- Malmqvist, P.A.; Roos, B.O. The CASSCF state interaction method. Chem. Phys. Lett. 1989, 155, 189–194. [Google Scholar] [CrossRef]
- Aquilante, F.; Malmqvist, P.-A.; Pedersen, T.-B.; Ghosh, A.; Roos, B.O. Decomposition-Based Multiconfiguration Second-Order Perturbation Theory (CD-CASPT2): Application to the Spin-State Energetics of CoIII(diiminato)(NPh). J. Chem. Theory Comput. 2008, 4, 694–702. [Google Scholar] [CrossRef] [PubMed]
- Roos, B.O.; Lindh, R.; Malmqvist, P.-A.; Veryazov, V.; Widmark, P.-O. Main Group Atoms and Dimers Studied with a New Relativistic ANO Basis Set. J. Phys. Chem. A 2004, 108, 2851–2858. [Google Scholar] [CrossRef]
- Roos, B.O.; Lindh, R.; Malmqvist, P.-A.; Veryazov, V.; Widmark, P.-O. New Relativistic ANO Basis Sets for Transition Metal Atoms. J. Phys. Chem. A 2005, 109, 6576–6586. [Google Scholar] [CrossRef] [PubMed]
- Roos, B.O.; Lindh, R.; Malmqvist, P.-A.; Veryazov, V.; Widmark, P.-O.; Borin, A.-C. New relavistic Atomic Natural Orbital Basis Sets for lanthanide Atoms with Applications to the Ce Diatom and LuF3. J. Phys. Chem. A 2008, 112, 11431–11435. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision A.02; Gaussian Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Dolg, M.; Stoll, H.; Preuss, H. A combination of quasirelativistic pseudopotential and ligand field calculations for lanthanoid compounds. Theor. Chim. Acta 1993, 85, 441–450. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef] [PubMed]
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).