Next Article in Journal
Magneto-Luminescence Correlation in the Textbook Dysprosium(III) Nitrate Single-Ion Magnet
Next Article in Special Issue
Recent Advances in Organic Radicals and Their Magnetism
Previous Article in Journal
Strain Engineering of the CeNi5 System
Previous Article in Special Issue
Magnetic Behavior of Carboxylate and β-Diketonate Lanthanide Complexes Containing Stable Organometallic Moieties in the Core-Forming Ligand
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Magnetochemistry
Volume 2
Issue 4
10.3390/magnetochemistry2040040
magnetochemistry-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

The Rise of Single-Ion Magnets as Spin Qubits

by
You-Song Ding
,
Yi-Fei Deng
and
Yan-Zhen Zheng
*
Frontier Institute of Science and Technology (FIST), State Key Laboratory of Mechanical Behavior of Materials and MOE Key Laboratory for Nonequilibrium Synthesis and Modulation of Condensed Matter, Xi’an Jiaotong University, Xi’an 710054, China
*
Author to whom correspondence should be addressed.
Magnetochemistry 2016, 2(4), 40; https://doi.org/10.3390/magnetochemistry2040040
Submission received: 31 August 2016 / Revised: 8 October 2016 / Accepted: 25 October 2016 / Published: 16 November 2016
(This article belongs to the Special Issue Molecules in Quantum Information)
Browse Figures
Versions Notes

Abstract

:
Recent studies revealed that magnetic molecules with single spin centers showed exciting phenomena related to quantum information processing, such as long quantum coherence times and Rabi oscillations. In this review, we go over these phenomena according to the essential metal ions, from which we can see the development of single-ion magnets as spin qubits is booming, especially quantum coherence times have been significantly enhanced from nanoseconds to hundreds of microseconds in a short period. Hence, the correlations between the molecular structures and quantum coherence are becoming clearer. In this regard, some chemical approaches to designing better spin qubits have been discussed.

1. Introduction

Single-ion magnets (SIMs) are a kind of molecular magnets that contain only one spin center surrounded by organic ligands [1,2,3,4,5], and show potential applications for high-density information storage, molecular spintronic devices and quantum information processing (QIP) units [6,7,8,9]. In this review, we will focus on the topic of SIMs for QIP applications.
For classical computation, the data are encoded in binary digits (bits), each of which is a well-defined state (0 or 1). In contrast, qubits take the advantage of superposition of quantum microstates. The basic set for qubits is |ψ> = α|0> + β|1>. Hence, a qubit can be either |1> or |0>, or any arbitrary superposition of these two states [10,11,12]. The key point for being a good qubit is to have long transverse relaxation time T2. Moreover, the spin-lattice relaxation time T1, which describes transitions from, say, |1> to |0>, is also very important because to observe the Rabi oscillations both T1 and T2 must be long enough. Because the period of coherent Rabi oscillations 1/ΩR, induced by an external stimulus (usually microwaves) between different qubit states, is actually used to evaluate the quality of a quantum system, the coherence time divided by half of the Rabi period, which is defined as QM = 2ΩRT2 (QM is the qubit figure of merit) and represented by the number of coherent single-qubit operations, is useful to evaluate the performance of spin qubit. Only when the QM is large enough, can the material then be used for QIP [13]. Other than the long coherence times, the possibility of building quantum logical gates is also very important [14].
Up to date, suitable physical carriers for qubits are found in ion traps [15,16], photons [17], nuclear spins [18], superconducting circuits [19,20], spin-based systems [21], atomic impurities in solids [22,23] and coordination molecules [12,24,25,26,27]. Among those candidates, the coordination molecules are extremely exciting due to the ready chemical design and detailed magneto-structural correlations. Specifically, the primary factors influencing the quantum decoherence such as the magnitude of spins, spin-orbit coupling effects and nuclear spin bath, and other peripheral factors such as the donor atoms of the coordinating ligands and solvent molecules can be systematically clarified, which can in turn guide the design of better molecular qubits [28,29,30,31,32,33,34]. Previously, such examples were only demonstrated by molecules with multi-metal centers [12,34]. More recently, new systems based on single-ion magnetic molecules were identified with even better performance owing to the well isolated environment. More excitingly, quantum logic gates such as the Controlled-NOT (CNOT) gate based on multiqubit can be readily achieved by chemical linkage of molecules [35,36,37,38] and quantum state can be read out by a single nuclear spin in TbPc2 [39,40]. Here below, we discussed these exciting topics according to the comprising metal centers, highlighting their advantages for QIP applications.

2. Single-Ion Magnetic Molecules with Transition Metal Centers

As the valence electrons for 3d transition metals locate in outer d orbits, the ligands coordinating to the transition metals have great impact on the electronic structure of the central cations, which then significantly influence the property of quantum coherence. The story starts from the simplest spin-1/2 systems such as V(IV) and Cu(II) ions with only two-level states, spin-up and spin-down.

2.1. V(IV) Based Spin Qubits

Pioneering work searching for potential spin qubits started from the V(IV) ion with small spin-1/2 state and large nuclear spin I = 7/2 (see Table 1). The first example is the complex (Bu4N)2[V(C8S8)3] 1 [41], in which the V(IV) ion is coordinated to six S ions, providing a nuclear spin free peripheral environment (Figure 1a). The hyperfine coupling of the electron spin and nuclear spin produces multiple states detected by electron paramagnetic resonance (EPR) spectrum (Figure 1b). Eight separate transitions were found to be potentially available for quantum information processing. The coherence time T2 is 1.2 μs at 80 K (performed on a 1 mM solution of 1 in butyronitrile). Rabi oscillations are observed by transient nutation experiments (Figure 1d), and the Rabi frequencies yielded from the nutation data at 3486 Oe at corresponding microwave power (B1) attenuations, namely are 28.1 MHz, 17.6 MHz, and 10.2 MHz for 3 dB, 7 dB, and 11 dB.
Subsequently, a series of V(IV) complexes (Ph4P)2[V(C8S8)3] 2, (Ph4P)2[V(β-C3S5)3] 3, (Ph4P)2[V(α-C3S5)3] 4, and (Ph4P)2[V(C3S4O)3] 5, based on carbonsulfides (Figure 2a–d), were prepared to test the electronic donating ability on the quantum coherence times [42]. The similar S6 coordination environment is maintained. Interestingly, the longest T2 was found for 2 of 4 μs at 80 K, indicating the weaker donating ability is better since the donating ability sequence is C8S82− < β-C3S52− < α-C3S52− < C3S4O2−. In addition, the solvent effect on quantum coherence was investigated. Several solvents including some deuterated ones such as PrCN, PrCN/DMF, DMF/Tol, d7-DMF/d8-Tol and CS2 were chosen and found they have little effect on T1. In contrast, T2 is significantly affected, e.g., T2 for complex 2 in CS2 is 1.18 μs (120 K), which is about 10 times longer than that in PrCN (0.108 μs, 120 K). Moreover, T2 is temperature-dependent. At 10 K T2 of 2 in CS2 solution is enhanced to 675(7) μs, even longer than some prominent solid-state qubits [43,44]. Remarkably, Rabi oscillations were observed for all four complexes (Figure 2e), and QM for 2 was found to be 36,000, which is very high among molecule-based spin qubits. Hence, this series of V(IV) complexes indicates the spin qubits are significantly affected by nuclear spin bath.
The second class of mononuclear V(IV) based spin qubits contains the VO2+ unit with distinct short V=O double bond (about 1.6 Å), which is much shorter than other coordination bonds bound to the central V(IV) ions in a typical square pyramidal geometry. Such strong bond is believed to be responsible for a special d-orbital splitting which leaves the dxy orbital being in the lowest place in energy levels and well separated from the other orbitals. This is evident in the complex VO(dpm)2 6 (dpm− = dipivaloylmethanate) (Figure 3a) [45] whose V=O bond length is 1.59 Å, while other V–O single bonds averages at 1.96 Å. AC magnetic susceptibility study gives out-of-phase signals up to 80 K for frequencies lower than 10 kHz, which is the highest one among all reported molecular magnets. The relaxation time T1 at 80 K reached 13.42 μs (Figure 3d). By pulsed EPR spectroscopy, the coherence time was detected. When complex 6 was dissolved in CH2Cl2-toluene (1 mM), T2 reaches 2.1 μs at 80 K, and with 1:10 dispersion of diamagnetic TiO(dpm)2, this T2 can be further preserved up to 220 K. T1 was also determined by pulsed EPR spectroscopy, which gave the consistent results for AC magnetic susceptibility study, conforming that the two techniques are actually probing the same process. Complexes VO(acac)2 7 and VO(dbm)2 8) (acac− = acetylacetonate, and dbm− = dibenzoylmethanate) (Figure 3b,c) share a similar coordination environment to 6 [46]. The V=O bond distances are 1.585 Å and 1.578 Å for 7 and 8, respectively. Both of 7 and 8 show out-of-phase AC signals under a static magnetic field of 0.2 T up to 40 K, which is associated with a giant spin-phonon bottleneck effect. Moreover, a pronounced crystal size dependence of the relaxation time was observed in complexes 6–8.
Another mononuclear V(IV) based spin qubit with short V=O bond (1.58 Å) is the complex VOPc 9 (Pc = Phthalocyanine) (Figure 4a) [31,48]. Together with its d1 electron configuration, this molecule makes a perfect two level system for spin qubit. Moreover, the out-of-phase signals of AC magnetic susceptibility for the frequency of 10 kHz can be observed up to 40 K under an applied static magnetic field of 0.2 T. An extraordinarily long T1 (2.4 s at 7 K) was obtained by Q-band EPR measurements in 0.5 mM D2SO4-solution, and T2 is 20 μs at 20 K under the same condition [31]. When VOPc is mixed with the isostructural diamagnetic host TiOPc in molar ratio of 1:1000, quantum coherence could be detected up to room temperature. T1 of 1.1 μs at 300 K was obtained by inversion recovery experiments and by echo decay experiments, echo decay traces (Figure 4b) were detected up to room temperature with T2 of 0.83 μs. Hence, for the first time, Rabi oscillation at room temperatures was detected in a solid state molecular system (Figure 4c). Besides, the quantum states of this electron spins based system can be efficiently initialized with high thermal stability, representing a promising qubit.
More recently, a new mononuclear V(IV) complex (Ph4P)2[VO(α-C3S5)2] 10 was reported, which enhances the quantum coherence by strong V=O double bond [47]. As shown in Figure 5a, the structure of 10 is similar to 4 except for the apical O atom. For comparison, the dynamic magnetism of both complexes was studied. Under a static magnetic field of 0.2 T, complex 4 displays slow magnetic relaxations below 10 K; while for complex 10, the temperature is raised up to 40 K. Their quantum coherences were detected by continuous-wave and pulsed EPR measurements on diluted samples. For 4, it was dispersed by [(Ph)4P]2[Ti(α-C3S5)3] in a molar ratio of 1:19, which gives T1 of 0.71 μs and T2 of 0.19 μs at 150 K (Figure 5c). Complex 10 was mixed with [(Ph)4P]2[MoO(α-C3S5)2] in a molar ratio of 1:19 for pulsed EPR measurements. At room temperature (293 K), both T1 and T2 of 10 remain high, namely 3.37 μs and 1.04 μs (Figure 5b). Rabi oscillations are also clearly observed at 293 K for diluted 10 and at 60 K for diluted 4, indicating the enhancement of O substitution.

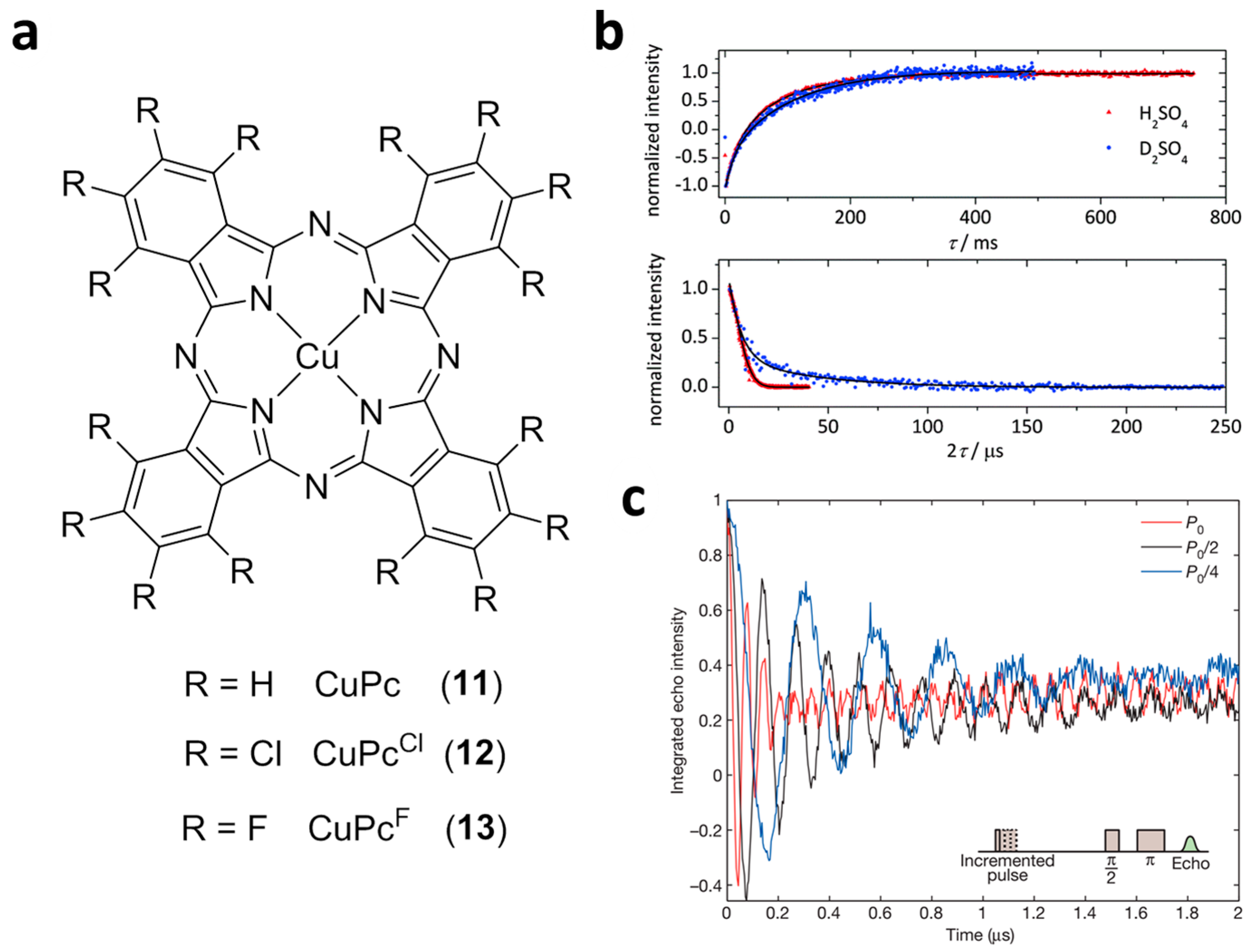
2.2. Cu(II) Based Single-Ion Spin Qubits

Except for V(IV), Cu(II) is another ion with spin-1/2 state. Several examples of mononuclear Cu(II) complexes have been reported as potential single-ion spin qubits (Table 2). The first one is CuPc 11 (Figure 6a) [31,49]. By organic-molecular-beam deposition, complex 11 and free phthalocyanine are able to assemble a monoatomic layer onto the layer of perylene-3,4,9,20-tetracarboxylic dianhydride. With the Hahn echo sequence, T2 for 11 was determined to be 1 μs at 80 K. Moreover, Rabi oscillations of a 0.1% CuPc:H2Pc were clearly observed at 5 K (Figure 6c) [49]. The impact of solvent deuteration on electron spin relaxation has been investigated by dissolving 11 in H2SO4 and D2SO4 [31]. For D2SO4, T2 is about 41 μs at 7 K, which is five times longer than those in H2SO4 (Figure 6b). The ligand effect on the quantum coherence times was also investigated using complexes CuPcCl 12 and CuPcF 13. All the three complexes share a similar T2 value of 40 μs at 7 K, indicating the ligand field effect is little in this series [31].
(PPh4)2[Cu(mnt)2] 14 (mnt2− = maleonitriledithiolate or 1,2-dicyanoethylene-1,2-dithiolate) is another high-performance single-ion spin qubit that displays long quantum coherence times at room temperature [50]. The Cu(II) ion in 14 is coordinated to four S ions in a square planner geometry (Figure 7a). The H atoms in this complex can be fully replaced by deuterium and its Ni analogy is diamagnetic, allowing a magnetic dilution study. At 294 K, electron spin echo-detected EPR measurements of the highly diluted sample (0.0001% of 14 in (PPh4)2[Ni(mnt)2]) gave T1 of 0.48 μs and T2 of 0.6 μs (Figure 7b). Towards lower temperatures with 0.01% deuterated 14 in deuterated (PPh4)2[Ni(mnt)2], T2 is prolonged to 68 μs at 7 K. Moreover, Rabi-like oscillations of the echo intensities were clearly observed by nutation measurements of the same sample at 15 K with a merit QM ≈ 3400.

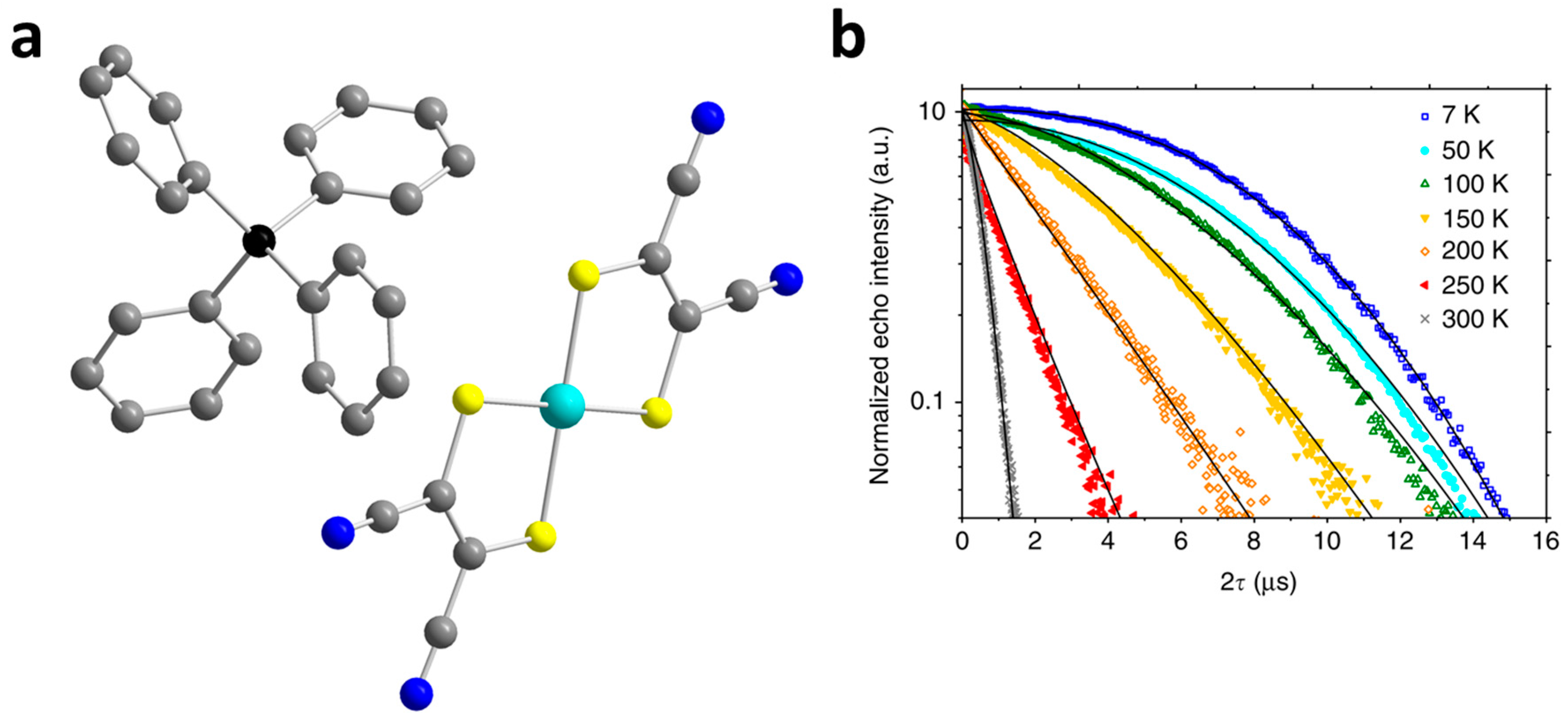
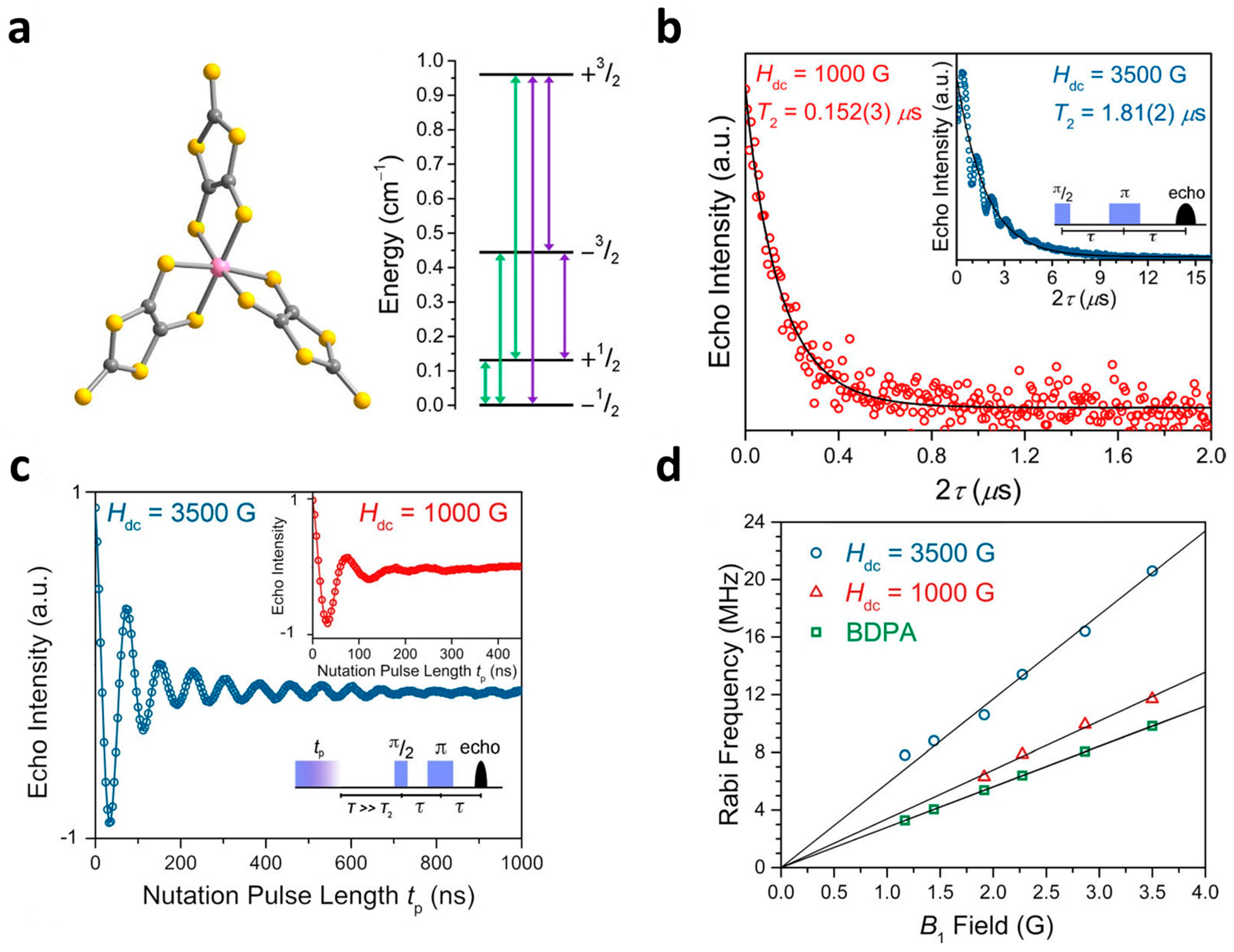
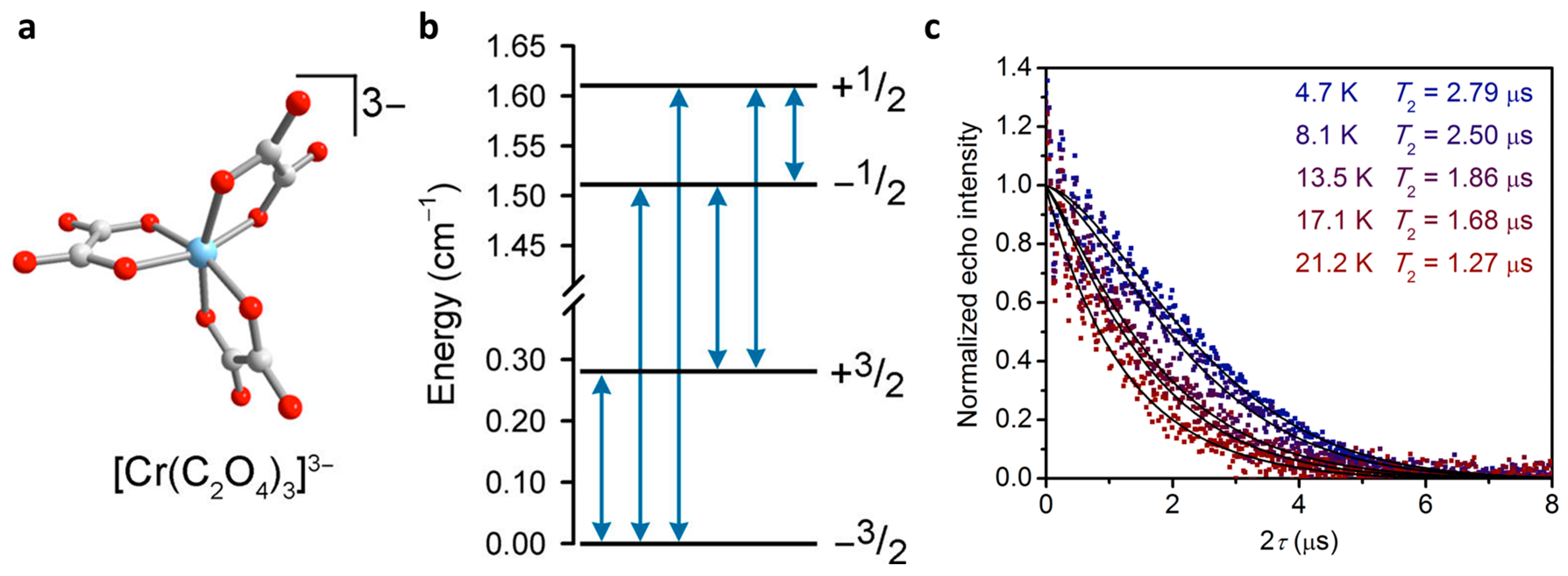
2.3. Other Transition Metals

Only two Cr(III) (spin-3/2) based single-spin qubits have been reported so far (Table 3). The first one is (Ph4P)3[Cr(C3S5)3] 15, in which the Cr(III) ion is coordinated to six S atoms with a first-circle nuclear spin free coordination environment (Figure 8a) [51]. By magnetometer and continuous-wave EPR spectroscopy, D = +0.326(8) cm−1 and E = −0.107(5) cm−1 were determined, which gave a rhombicity |E/D| of 0.31. The high rhombicity would afford highly mixed MS levels at low magnetic fields, producing significant intensity of forbidden EPR transitions with multiple MS pairs for quantum studies. Pulsed X-band EPR spectroscopy measurement was carried out on deuterated 15 in (d20-Ph4P)3[Ga(C3S5)3] (1%) (Figure 8b). T1 sharply drops from 29(3) ms at 5 K to 875(5) μs at 30 K, while T2 drops from 1.81(3) μs to 0.82(2) μs upon the same temperature change. Moreover, Rabi oscillations were clearly observed at 5 K with linear ΩR against B1, indicating the provenance of the nutations (Figure 8c,d).
The other Cr(III) based single-ion spin qubit is K3[Cr(C2O4)3] 16 (Figure 9a) [33]. The |D| value of 16 is about 0.7 cm−1 and the E value is about 0.06 cm−1 [52]. The inherent scalability and tunability engendered by zero-field splitting are illustrated in Figure 9b. The transitions between the multiple MS pairs can be used as qubits, which is in accordance with the study of complex 15 [51]. T2 for 16 is about 1.27 μs at 22 K, obtained by two-pulse Hahn echo sequence on 1 mM solutions of 16 in 1:1 (v/v) H2O/glycerol (Figure 9c) [33].
A series of analogous complexes K3[Fe(C2O4)3] 17, (Ph4P)3[Fe(CN)6] 18, K3[Ru(C2O4)3] 19, (Ph4P)3[Ru(CN)6] 20, (Ph4P)3[Os(CN)6] 21 and 16 were used to study the influence of spin-spin and spin-orbit couplings on quantum coherence [33]. Complexes 19, 16 and 17 possess spin states of s = 1/2, 3/2, and 5/2 with the same coordination environment, which gives an opportunity to understand the impact of spin magnitude on quantum coherence (Figure 10a). At low temperature, T2 value for 19 is the longest one (3.44 μs at 5 K and 2.01 μs at 14 K), followed by 16 (2.79 μs at 5 K and 1.86 μs at 14 K) and then 17 (1.83 μs at 5 K and 0.81 μs at 14 K). This result indicates a larger spin increases the intermolecular dipolar interaction and hence enhances the decoherence rate [53,54,55]. However, at a higher temperature (22 K), T2 for 16 becomes the longest, reaching 1.27 μs, which may also indicate spin magnitude can be varied without significantly compromising T2 in certain conditions as long as it is appropriate for signal detection. As the spin states for complexes 18, 20, 21 are all 1/2, and the free ion SOC effects on T2 can be compared. T2 for those three complexes are in the order Fe(III) < Ru(III) < Os(III), which is coincident with the increase of SOC constants, namely 464 cm−1, 880 cm−1, and 3100 cm−1 for 18, 20 and 21 (Figure 10a and Table 3) [56,57,58]. Rabi oscillations and pulse sequence for a solution of 19 at 5 K, Hdc = 2812 G, and relative B1 of 2.0 was observed (Figure 10b). Note that 21 is the only Os complex regarded as potential qubit.
Another Fe(III) based single-ion spin qubit is the complex (Ph4P)3[Fe(C5O5)3] 22 (Figure 11a) [59,60]. Variable-frequency CW EPR measurements at low temperatures (5 K) and high frequencies (208 GHz) on this trigonally distorted six-coordinate iron(III) complexes with O6 coordination environments reveal a sharp resonance near g = 2.00 and negative D value of −0.30 cm−1. To evaluate the spin qubit viability of 22, its diamagnetic analogy (Ph4P)3[Ga(C5O5)3] was used for preparations of diluted samples, (Ph4P)3[Fe0.002Ga0.998(C5O5)3] 22a and the deuterated (Ph4P-d20)3[Fe0.002Ga0.998(C5O5)3] 22b for pulsed EPR studies. At 5 K, T1 are 11.3 μs and 8.0 μs for 22a and 22b, respectively. These values drop dramatically as increasing temperatures, which eventually went down to 1.18 μs and 0.82(1) μs, respectively, at 15 K. T2 values for 22a and 22b at 5 K are 0.74 μs and 1.60 μs, respectively, highlighting the enhancement of T2 with deuteration. Similar to T1, T2 also decay rapidly upon warming, ultimately down to 0.34 μs for 22a at 15 K. Moreover, clear Rabi oscillations were observed for both 22a and 22b at 10 K (Figure 11c,d) with liner dependence of ΩR against B1, proving the qubit characteristic [59]. By multi-frequency pulsed EPR spectroscopic measurements, a high to low degree of MS mixing in the high-spin qubit was discovered in 22, which highlights the possibility of long T1 and T2 parameters in high-spin species through control of MS level mixing [60].
As far as we know, few mononuclear Mn and Co complexes were reported as potential spin qubits. The only investigation of these two ions was found in complexes MnPc (23) and CoPc (24), which were used to reveal the influences of central ion on quantum coherence behavior of complexes 9, 11–13 [31]. Pulsed Q-band EPR spectroscopy was measured on 0.5 mM D2SO4 solution of complexes 9, 11, 23 and 24 because they have the same ligand Pc. T1 for those complexes were found to be in the order of 23 (0.69 ms) < 24 (11.1 ms) < 11 (103 ms) < 9 (2.4 s) at 7 K, which is in accord with the conclusion that smaller SOC effects generate longer spin-lattice relaxation times [33,61]. The T2 values at 7 K are 22 μs, 41 μs, 14 μs and 9.44 μs for 9, 11, 23 and 24, respectively.

3. Single-Ion Magnetic Molecules with Single 4f Spins

Lanthanide-based SIMs have been intensively investigated for more than 10 years and have achieved significant progress in information storage and spintronic aspects, such as, (i) high magnetic hysteresis temperature (30 K) [62]; (ii) high magnetic anisotropic energy barrier (1000 K) [63]; and (iii) surface deposition of molecular magnets without changing the original magnetism [64,65,66,67]. In contrast, the attempts of using lanthanide-based SIMs as spin qubits have just begun [8,9,68,69]. Examples we will discuss include some lanthanide polyoxometalates [70,71,72,73], the famous TbPc2 [39,40,74,75] and one Yb complex [76], see also Table 4.

3.1. Single-Lanthanide Polyoxometalates as Spin Qubits

Though the magnetism of free Gd(III) ion is very isotropic, Gd(III) complexes with special coordination environments can behave as single-molecule magnets at very low temperatures [70,77]. The tungsten-based polyoxometalates are such ligand beds for Gd(III) ions. Compounds [Gd(P5W30O110)]12− (25) and [Gd(W5O18P)2]9− (GdW10) (Figure 12) show slow magnetic relaxation behaviors below 300 mK. The relaxation times for GdW10 follow the activated behavior with an energy barrier of 2.2 K. However, for 25, relaxation times depend weakly on temperature and show a strong deviation from the expected thermally activated behavior. Qualitative fitting of their EPR data proves that the magnetic anisotropy is raised by mixing ground and excited states, resulting in easy-axial magnetic anisotropy for GdW10 and an easy-plane magnetic anisotropy for 25. This difference further influences their application as spin qubits. Pulsed X-band EPR experiments give coherence figure of merit QM > 50 for 25 with observation of Rabi oscillations at 5 K, proving the possibility of spin qubits [71].
Another single-lanthanide polyoxometalate for spin qubit is the complex [Ho(W5O18P)2]9− (26) [72,73], an analogy of GdW10 with a different lanthanide center. The Ho(III) ion is encapsulated between two W5O18 POM units that provide a square-antiprismatic coordination geometry with D4d symmetry (Figure 13a). By high-frequency and X-band EPR measurements, the hyperfine-split mJ = ±4 ground states can be observed (Figure 13b). The tunneling gap is about 9 GHz, which make 26 suitable for spin qubits [72]. The dilution study of 26 was carried out on Na9[HoxY(1–x)(W5O18)2]·nH2O, where x ranges from 0.001 to 0.25 [73]. For x = 0.001, a long T2 of 8.4 μs was detected together with T1 of 20 μs at 5 K (Figure 13c). Interestingly, T2 remains at higher concentrations for a long period (about 8.0 μs for x = 0.01 and 0.7 μs for x = 0.1) at 5 K. The main contribution to those narrow resonances is found to be a Gaussian distribution in the B 4 4 parameter. Thus, by exploiting optimal operating points or atomic clock transitions between hyperfine states, quantum coherence times could be significantly protected regardless of spin concentrations [73].

3.2. Tb(III) Based Nuclear-Spin Qubits

TbPc2 27, one of the high-performance SIMs, has also been identified as one promising qubit for several reasons [39,40,74,75]. (I) The synthesis of this complex is facile and controllable with various functional groups [78]; (II) The magnetic properties are robust, which can be retained after sublimation at 820 K on a copper surface [64]; (III) The two Pc ligands have a conjugated p system, which can easily conduct electrons; while the valence state for Tb(III) is very stable, so that the current flow does not damage the complex [39]; (IV) The flat Pc ligands help graft the complexes on various surfaces, including gold, carbon nanotube, graphite, etc. With all these characteristics, it is possible to make 27 a spintronic devices (Figure 14a). Magnetic studies of 27 reveal a strong uniaxial magnetic anisotropy with ground J = 6 state separated from the excited states by an energy gap of more than 400 cm−1 [1,79]. With the nuclear spin I = 3/2, strong hyperfine coupling between the ground state and the nuclear spin makes the ground states split into four sub-states (Figure 14b), which can be functionalized as quantum microstates. The coherence time T2 for 27 is about 64.0 μs with isotope-dependent relaxation times, while T1 is more than 10 s. Moreover, Rabi oscillations are observed (Figure 14c,d) [40].

3.3. Yb(III) Based Spin Qubits

For Yb(III) ions, the ground state is a Kramers doublet with J = 7/2, which can be approximated as an effective spin-1/2 system at low temperatures [76]. Its isotopes include I = 1/2 (171Yb), I = 5/2 (173Yb) and 0 for the others. To detect the quantum coherence of Yb(trensal) 28 (H3trensal = 2,2′,2″-tris(salicylideneimino)triethylamine), sample of 7% 28 in diamagnetic Lu(trensal) was prepared for EPR measurements (Figure 15a) [76]. Fitting the echo-detected field-swept (EDFS) X-band pulsed EPR spectrum gave both spin-lattice relaxation times T1 and quantum coherence times T2 (Figure 15c). The T1 values are in accord with ac susceptibility studies on bulk 28, which exhibits strong temperature dependence behavior and can be described by a power law [80]. On the contrary, T2 is weakly temperature dependent and reaches 0.5 μs at 3 K. Clear oscillatory behavior was observed at 5 K (Figure 15d). The peak widths show little difference for all isotopes, but for the damping, the oscillations at “I = 0 lines” are much stronger than other isotopes. Besides, more than 70 Rabi oscillations can be observed extending to 4 μs. Together with the coherence figure of merit QM of about 40, complex 28 is an excellent candidate for QIP.

3.4. Lanthanide-Doped Spin Qubits

By doping lanthanide ions into some inorganic crystals, many solid-state qubits were found, despite that it is hard to control the environment of lanthanide ions [13,81,82,83,84,85,86]. Typical examples include doping Er(III) ions into CaWO4, which gives Er(III):CaWO4 with T2 of 50 μs at 2.5 K and QM of 1400 [13] and Pr(III):Y2SiO5 with long phase memory time of 82 ms [82]. Other lanthanide elements using a similar doping method include Nd(III) [84] and Eu(III) [86].

4. Conclusions and Perspectives

From the above analyses, we can see the practice of SIMs for spin qubits is still in its infancy, especially for lanthanide based SIMs, yet many exciting results have been achieved in the field. These include: (i) long quantum coherence times (e.g., complex 2 exhibits T2 = 657 μs at 7 K; complex 10 exhibits T2 = 1 μs for at room-temperature; while T1 reaches 10 s for TbPc2 at low temperatures); (ii) Rabi oscillations are well observed in many well isolated molecules; (iii) electrically read-out of a single nuclear spin using a molecular spintronic device was achieved; (iv) chemical linkage for CNOT gate operations was demonstrated. Last but not least, the decoherence-structural correlation of SIMs is becoming clearer, which is extremely encouraging for chemists who are working on this field because this knowledge may help to design better spin qubits. The key points can be summarized as follows. Firstly, the quantum states must exist, which may arise from hyperfine coupling of the electron spin and nuclear spin or the spin orbital coupling with a proper energy gap (reasonably between 2 and 20 GHz). Secondly, the ligands, especially the atoms directly coordinated to the metal center, would significantly influence the electronic structure of the center ions. Nuclear spin free atoms are often favorable in this area, such as C and S. Besides, if there is an H atom in the ligands, deuteration often helps to protect the quantum coherence. Finally, the concentration, which is often adjusted by solvents or diamagnetic analogy, is also crucial. Nuclear spin free solvents (e.g., CS2) can effectively enhance the coherence time. Since all these factors are chemically controllable, it is very encouraging for chemists to design high performance single spin qubits based on the toolbox of synthetic chemistry. Only if the quantum coherence time is long enough at room temperature can the realization of QIP for daily usage be expected.

Acknowledgments

This work was supported by “973 project” (2012CB619402), NSFC (21473129, 21503155, IRT13034 and 21620102002), “National Young 1000-Plan” program, Fundamental Research Funds for Central Universities and Wuhan National High Magnetic Field Center (2015KF06).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Ishikawa, N.; Sugita, M.; Ishikawa, T.; Koshihara, S.Y.; Kaizu, Y. Lanthanide double-decker complexes functioning as magnets at the single-molecular level. J. Am. Chem. Soc. 2003, 125, 8694–8695. [Google Scholar] [CrossRef] [PubMed]
  2. Rinehart, J.D.; Long, J.R. Exploiting single-ion anisotropy in the design of f-element single-molecule magnets. Chem. Sci. 2011, 2, 2078–2085. [Google Scholar] [CrossRef]
  3. Woodruff, D.N.; Winpenny, R.E.P.; Layfield, R.A. Lanthanide Single-Molecule Magnets. Chem. Rev. 2013, 113, 5110–5148. [Google Scholar] [CrossRef] [PubMed]
  4. Feltham, H.L.C.; Brooker, S. Review of purely 4f and mixed-metal nd-4f single-molecule magnets containing only one lanthanide ion. Coord. Chem. Rev. 2014, 276, 1–33. [Google Scholar] [CrossRef]
  5. Craig, G.A.; Murrie, M. 3d single-ion magnets. Chem. Soc. Rev. 2015, 44, 2135–2147. [Google Scholar] [CrossRef] [PubMed]
  6. Gatteschi, D.; Sessoli, R.; Villain, J. Molecular Nanomagnets; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
  7. Benelli, C.; Gatteschi, D. Introduction to Molecular Magnetism: From Transition Metals to Lanthanides; Wiley-VCH Verlag GmbH & Co.: Weinheim, Germany, 2015. [Google Scholar]
  8. Gao, S. Molecular Nanomagnets and Related Phenomena; Springer: New York, NY, USA, 2015; Volume 164. [Google Scholar]
  9. Layfield, R.A.; Murugesu, M. Lanthanides and Actinides in Molecular Magnetism; Wiley-VCH: Weinheim, Germany, 2015. [Google Scholar]
  10. Bennett, C.H.; DiVincenzo, D.P. Quantum information and computation. Nature 2000, 404, 247–255. [Google Scholar] [CrossRef] [PubMed]
  11. Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
  12. Aromi, G.; Aguila, D.; Gamez, P.; Luis, F.; Roubeau, O. Design of magnetic coordination complexes for quantum computing. Chem. Soc. Rev. 2012, 41, 537–546. [Google Scholar] [CrossRef] [PubMed]
  13. Bertaina, S.; Gambarelli, S.; Tkachuk, A.; Kurkin, I.N.; Malkin, B.; Stepanov, A.; Barbara, B. Rare-earth solid-state qubits. Nat. Nanotechnol. 2007, 2, 39–42. [Google Scholar] [CrossRef] [PubMed]
  14. Ladd, T.D.; Jelezko, F.; Laflamme, R.; Nakamura, Y.; Monroe, C.; O Brien, J.L. Quantum computers. Nature 2010, 464, 45–53. [Google Scholar] [CrossRef] [PubMed]
  15. Cirac, J.I.; Zoller, P. Quantum computations with cold trapped ions. Phys. Rev. Lett. 1995, 74, 4091–4094. [Google Scholar] [CrossRef] [PubMed]
  16. Monroe, C.; Kim, J. Scaling the ion trap quantum processor. Science 2013, 339, 1164–1169. [Google Scholar] [CrossRef] [PubMed]
  17. Knill, E.; Laflamme, R.; Milburn, G.J. A scheme for efficient quantum computation with linear optics. Nature 2001, 409, 46–52. [Google Scholar] [CrossRef] [PubMed]
  18. Gershenfeld, N.A.; Chuang, I.L. Bulk spin-resonance quantum computation. Science 1997, 275, 350–356. [Google Scholar] [CrossRef] [PubMed]
  19. Clarke, J.; Wilhelm, F.K. Superconducting quantum bits. Nature 2008, 453, 1031–1042. [Google Scholar] [CrossRef] [PubMed]
  20. Devoret, M.H.; Schoelkopf, R.J. Superconducting circuits for quantum information: An outlook. Science 2013, 339, 1169–1174. [Google Scholar] [CrossRef] [PubMed]
  21. Loss, D.; DiVincenzo, D.P. Quantum computation with quantum dots. Phys. Rev. A 1998, 57, 120. [Google Scholar] [CrossRef]
  22. Awschalom, D.D.; Bassett, L.C.; Dzurak, A.S.; Hu, E.L.; Petta, J.R. Quantum spintronics: Engineering and manipulating atom-like spins in semiconductors. Science 2013, 339, 1174–1179. [Google Scholar] [CrossRef] [PubMed]
  23. Hanson, R.; Awschalom, D.D. Coherent manipulation of single spins in semiconductors. Nature 2008, 453, 1043–1049. [Google Scholar] [CrossRef] [PubMed]
  24. Sato, K.; Nakazawa, S.; Rahimi, R.; Ise, T.; Nishida, S.; Yoshino, T.; Mori, N.; Toyota, K.; Shiomi, D.; Yakiyama, Y.; et al. Molecular electron-spin quantum computers and quantum information processing: Pulse-based electron magnetic resonance spin technology applied to matter spin-qubits. J. Mater. Chem. 2009, 19, 3739–3754. [Google Scholar] [CrossRef]
  25. Luis, F.; Repollés, A.; Martínez-Pérez, M.J.; Aguilà, D.; Roubeau, O.; Zueco, D.; Alonso, P.J.; Evangelisti, M.; Camón, A.; Sesé, J. Molecular prototypes for spin-based CNOT and SWAP quantum gates. Phys. Rev. Lett. 2011, 107, 117203. [Google Scholar] [CrossRef] [PubMed]
  26. Lehmann, J.; Gaita-Ari Nmacr, A.; Coronado, E.; Loss, D. Spin qubits with electrically gated polyoxometalate molecules. Nat. Nanotechnol. 2007, 2, 312–317. [Google Scholar] [CrossRef] [PubMed]
  27. Leuenberger, M.N.; Loss, D. Quantum computing in molecular magnets. Nature 2001, 410, 789–793. [Google Scholar] [CrossRef] [PubMed]
  28. Ardavan, A.; Rival, O.; Morton, J.J.; Blundell, S.J.; Tyryshkin, A.M.; Timco, G.A.; Winpenny, R.E. Will spin-relaxation times in molecular magnets permit quantum information processing? Phys. Rev. Lett. 2007, 98, 057201. [Google Scholar] [CrossRef] [PubMed]
  29. Wedge, C.J.; Timco, G.A.; Spielberg, E.T.; George, R.E.; Tuna, F.; Rigby, S.; McInnes, E.; Winpenny, R.; Blundell, S.J.; Ardavan, A. Chemical engineering of molecular qubits. Phys. Rev. Lett. 2012, 108, 107204. [Google Scholar] [CrossRef] [PubMed]
  30. Kaminski, D.; Webber, A.L.; Wedge, C.J.; Liu, J.; Timco, G.A.; Vitorica-Yrezabal, I.J.; McInnes, E.J.; Winpenny, R.E.; Ardavan, A. Quantum spin coherence in halogen-modified Cr7Ni molecular nanomagnets. Phys. Rev. B 2014, 90, 184419. [Google Scholar] [CrossRef]
  31. Bader, K.; Winkler, M.; van Slageren, J. Tuning of molecular qubits: Very long coherence and spin-lattice relaxation times. Chem. Commun. 2016, 52, 3623–3626. [Google Scholar] [CrossRef] [PubMed]
  32. Fielding, A.J.; Fox, S.; Millhauser, G.L.; Chattopadhyay, M.; Kroneck, P.M.; Fritz, G.; Eaton, G.R.; Eaton, S.S. Electron spin relaxation of copper (II) complexes in glassy solution between 10 and 120 K. J. Magn. Reson. 2006, 179, 92–104. [Google Scholar] [CrossRef] [PubMed]
  33. Graham, M.J.; Zadrozny, J.M.; Shiddiq, M.; Anderson, J.S.; Fataftah, M.S.; Hill, S.; Freedman, D.E. Influence of Electronic Spin and Spin–Orbit Coupling on Decoherence in Mononuclear Transition Metal Complexes. J. Am. Chem. Soc. 2014, 136, 7623–7626. [Google Scholar] [CrossRef] [PubMed]
  34. Repollés Rabinad, A.M. Quantum Computing with Molecular Magnets; Prensas de la Universidad de Zaragoza: Zaragoza, Spain, 2016; Volume 131. [Google Scholar]
  35. Timco, G.A.; Carretta, S.; Troiani, F.; Tuna, F.; Pritchard, R.J.; Muryn, C.A.; McInnes, E.J.; Ghirri, A.; Candini, A.; Santini, P. Engineering the coupling between molecular spin qubits by coordination chemistry. Nat. Nanotechnol. 2009, 4, 173–178. [Google Scholar] [CrossRef] [PubMed]
  36. Lan, Y.; Klyatskaya, S.; Ruben, M.; Fuhr, O.; Wernsdorfer, W.; Candini, A.; Corradini, V.; Rizzini, A.L.; Del Pennino, U.; Troiani, F. Magnetic interplay between two different lanthanides in a tris-phthalocyaninato complex: A viable synthetic route and detailed investigation in the bulk and on the surface. J. Mater. Chem. C 2015, 3, 9794–9801. [Google Scholar] [CrossRef] [Green Version]
  37. Aguilà, D.; Barrios, L.A.; Velasco, V.; Roubeau, O.; Repollés, A.; Alonso, P.J.; Sesé, J.; Teat, S.J.; Luis, F.; Aromí, G. Heterodimetallic [LnLn′] lanthanide complexes: Toward a chemical design of two-qubit molecular spin quantum gates. J. Am. Chem. Soc. 2014, 136, 14215–14222. [Google Scholar] [CrossRef] [PubMed]
  38. Ferrando-Soria, J.; Pineda, E.M.; Chiesa, A.; Fernandez, A.; Magee, S.A.; Carretta, S.; Santini, P.; Vitorica-Yrezabal, I.J.; Tuna, F.; Timco, G.A. A modular design of molecular qubits to implement universal quantum gates. Nat. Commun. 2016, 7, 11377. [Google Scholar] [CrossRef] [PubMed]
  39. Vincent, R.; Klyatskaya, S.; Ruben, M.; Wernsdorfer, W.; Balestro, F. Electronic read-out of a single nuclear spin using a molecular spin transistor. Nature 2012, 488, 357–360. [Google Scholar] [CrossRef] [PubMed]
  40. Thiele, S.; Balestro, F.; Ballou, R.; Klyatskaya, S.; Ruben, M.; Wernsdorfer, W. Electrically driven nuclear spin resonance in single-molecule magnets. Science 2014, 344, 1135–1138. [Google Scholar] [CrossRef] [PubMed]
  41. Zadrozny, J.M.; Niklas, J.; Poluektov, O.G.; Freedman, D.E. Multiple Quantum Coherences from Hyperfine Transitions in a Vanadium(IV) Complex. J. Am. Chem. Soc. 2014, 136, 15841–15844. [Google Scholar] [CrossRef] [PubMed]
  42. Zadrozny, J.M.; Niklas, J.; Poluektov, O.G.; Freedman, D.E. Millisecond Coherence Time in a Tunable Molecular Electronic Spin Qubit. ACS Cent. Sci. 2015, 1, 488–492. [Google Scholar] [CrossRef] [PubMed]
  43. Stanwix, P.L.; Pham, L.M.; Maze, J.R.; Le Sage, D.; Yeung, T.K.; Cappellaro, P.; Hemmer, P.R.; Yacoby, A.; Lukin, M.D.; Walsworth, R.L. Coherence of nitrogen-vacancy electronic spin ensembles in diamond. Phys. Rev. B 2010, 82, 201201. [Google Scholar] [CrossRef]
  44. Koehl, W.F.; Buckley, B.B.; Heremans, F.J.; Calusine, G.; Awschalom, D.D. Room temperature coherent control of defect spin qubits in silicon carbide. Nature 2011, 479, 84–87. [Google Scholar] [CrossRef] [PubMed]
  45. Tesi, L.; Lucaccini, E.; Cimatti, I.; Perfetti, M.; Mannini, M.; Atzori, M.; Morra, E.; Chiesa, M.; Caneschi, A.; Sorace, L. Quantum coherence in a processable vanadyl complex: New tools for the search of molecular spin qubits. Chem. Sci. 2016, 7, 2074–2083. [Google Scholar] [CrossRef]
  46. Tesi, L.; Lunghi, A.; Atzori, M.; Lucaccini, E.; Sorace, L.; Totti, F.; Sessoli, R. Giant spin-phonon bottleneck effects in evaporable vanadyl-based molecules with long spin coherence. Dalton. Trans. 2016, 45, 16635–16643. [Google Scholar] [CrossRef] [PubMed]
  47. Atzori, M.; Morra, E.; Tesi, L.; Albino, A.; Chiesa, M.; Sorace, L.; Sessoli, R. Quantum Coherence Times Enhancement in Vanadium (IV)-based Potential Molecular Qubits: The Key Role of the Vanadyl Moiety. J. Am. Chem. Soc. 2016, 138, 11234–11244. [Google Scholar] [CrossRef] [PubMed]
  48. Atzori, M.; Tesi, L.; Morra, E.; Chiesa, M.; Sorace, L.; Sessoli, R. Room-Temperature Quantum Coherence and Rabi Oscillations in Vanadyl Phthalocyanine: Toward Multifunctional Molecular Spin Qubits. J. Am. Chem. Soc. 2016, 138, 2154–2157. [Google Scholar] [CrossRef] [PubMed]
  49. Warner, M.; Din, S.; Tupitsyn, I.S.; Morley, G.W.; Stoneham, A.M.; Gardener, J.A.; Wu, Z.; Fisher, A.J.; Heutz, S.; Kay, C.W. Potential for spin-based information processing in a thin-film molecular semiconductor. Nature 2013, 503, 504–508. [Google Scholar] [CrossRef] [PubMed]
  50. Bader, K.; Dengler, D.; Lenz, S.; Endeward, B.; Jiang, S.; Neugebauer, P.; van Slageren, J. Room temperature quantum coherence in a potential molecular qubit. Nat. Commun. 2014, 5, 6304. [Google Scholar] [CrossRef] [PubMed]
  51. Fataftah, M.S.; Zadrozny, J.M.; Coste, S.C.; Graham, M.J.; Rogers, D.M.; Freedman, D.E. Employing Forbidden Transitions as Qubits in a Nuclear Spin-Free Chromium Complex. J. Am. Chem. Soc. 2016, 138, 1344–1348. [Google Scholar] [CrossRef] [PubMed]
  52. Mor, H.H.; Weihe, H.; Bendix, J. Fitting of EPR spectra: The importance of a flexible bandwidth. J. Magn. Reson. 2010, 207, 283–286. [Google Scholar]
  53. Stamp, P.C.; Gaita-Arino, A. Spin-based quantum computers made by chemistry: Hows and whys. J. Mater. Chem. 2009, 19, 1718–1730. [Google Scholar] [CrossRef]
  54. Morello, A.; Stamp, P.; Tupitsyn, I.S. Pairwise decoherence in coupled spin qubit networks. Phys. Rev. Lett. 2006, 97, 207206. [Google Scholar] [CrossRef] [PubMed]
  55. Bertaina, S.; Gambarelli, S.; Mitra, T.; Tsukerblat, B.; Müller, A.; Barbara, B. Quantum oscillations in a molecular magnet. Nature 2008, 453, 203–206. [Google Scholar] [CrossRef] [PubMed]
  56. Bendix, J.; Brorson, M.; Schaffer, C.E. Accurate empirical spin-orbit coupling parameters. zeta. nd for gaseous ndq transition metal ions. The parametrical multiplet term model. Inorg. Chem. 1993, 32, 2838–2849. [Google Scholar] [CrossRef]
  57. Bendix, J.; Steenberg, P.; Søtofte, I. Isolation and molecular structure of hexacyanoruthenate (III). Inorg. Chem. 2003, 42, 4510–4512. [Google Scholar] [CrossRef] [PubMed]
  58. Albores, P.; Slep, L.D.; Baraldo, L.M.; Baggio, R.; Garland, M.T.; Rentschler, E. Crystal structure and electronic and magnetic properties of hexacyanoosmate (III). Inorg. Chem. 2006, 45, 2361–2363. [Google Scholar] [CrossRef] [PubMed]
  59. Zadrozny, J.M.; Freedman, D.E. Qubit Control Limited by Spin–Lattice Relaxation in a Nuclear Spin-Free Iron (III) Complex. Inorg. Chem. 2015, 54, 12027–12031. [Google Scholar] [CrossRef] [PubMed]
  60. Zadrozny, J.M.; Graham, M.J.; Krzyaniak, M.D.; Wasielewski, M.R.; Freedman, D.E. Unexpected suppression of spin-lattice relaxation via high magnetic field in a high-spin iron (III) complex. Chem. Commun. 2016, 52, 10175–10178. [Google Scholar] [CrossRef] [PubMed]
  61. Du, J.; Eaton, G.R.; Eaton, S.S. Electron spin relaxation in vanadyl, copper (II), and silver (II) porphyrins in glassy solvents and doped solids. J. Magn. Reson. Ser. A 1996, 119, 240–246. [Google Scholar] [CrossRef]
  62. Gupta, S.K.; Rajeshkumar, T.; Rajaraman, G.; Murugavel, R. An air-stable Dy (iii) single-ion magnet with high anisotropy barrier and blocking temperature. Chem. Sci. 2016, 7, 5181–5191. [Google Scholar] [CrossRef]
  63. Liu, J.; Chen, Y.; Jia, J.; Liu, J.; Vieru, V.; Ungur, L.; Chibotaru, L.F.; Lan, Y.; Wernsdorfer, W.; Gao, S. A Stable Pentagonal-Bipyramidal Dy (III) Single-Ion Magnet with a Record Magnetization Reversal Barrier over 1000 K. J. Am. Chem. Soc. 2016, 138, 5441–5450. [Google Scholar] [CrossRef] [PubMed]
  64. Stepanow, S.; Honolka, J.; Gambardella, P.; Vitali, L.; Abdurakhmanova, N.; Tseng, T.; Rauschenbach, S.; Tait, S.L.; Sessi, V.; Klyatskaya, S. Spin and orbital magnetic moment anisotropies of monodispersed bis (phthalocyaninato) terbium on a copper surface. J. Am. Chem. Soc. 2010, 132, 11900–11901. [Google Scholar] [CrossRef] [PubMed]
  65. Margheriti, L.; Chiappe, D.; Mannini, M.; Car, P.E.; Sainctavit, P.; Arrio, M.A.; de Mongeot, F.B.; Cezar, J.C.; Piras, F.M.; Magnani, A. X-Ray Detected Magnetic Hysteresis of Thermally Evaporated Terbium Double-Decker Oriented Films. Adv. Mater. 2010, 22, 5488–5493. [Google Scholar] [CrossRef] [PubMed]
  66. Gonidec, M.; Biagi, R.; Corradini, V.; Moro, F.; De Renzi, V.; Del Pennino, U.; Summa, D.; Muccioli, L.; Zannoni, C.; Amabilino, D.B. Surface supramolecular organization of a terbium (III) double-decker complex on graphite and its single molecule magnet behavior. J. Am. Chem. Soc. 2011, 133, 6603–6612. [Google Scholar] [CrossRef] [PubMed]
  67. Mannini, M.; Bertani, F.; Tudisco, C.; Malavolti, L.; Poggini, L.; Misztal, K.; Menozzi, D.; Motta, A.; Otero, E.; Ohresser, P. Magnetic behaviour of TbPc2 single-molecule magnets chemically grafted on silicon surface. Nat. Commun. 2014, 5, 5582. [Google Scholar] [CrossRef] [PubMed]
  68. Gaita-Ariño, A.; Prima-Garcia, H.; Cardona-Serra, S.; Escalera-Moreno, L.; Rosaleny, L.E.; Baldovi, J.J. Coherence and organisation in lanthanoid complexes: From single ion magnets to spin qubits. Inorg. Chem. Front. 2016, 3, 568–577. [Google Scholar] [CrossRef]
  69. Clemente-Juan, J.M.; Coronado, E.; Gaita-Ariño, A. Magnetic polyoxometalates: From molecular magnetism to molecular spintronics and quantum computing. Chem. Soc. Rev. 2012, 41, 7464–7478. [Google Scholar] [CrossRef] [PubMed]
  70. Martínez-Pérez, M.J.; Cardona-Serra, S.; Schlegel, C.; Moro, F.; Alonso, P.J.; Prima-García, H.; Clemente-Juan, J.M.; Evangelisti, M.; Gaita-Ariño, A.; Sesé, J. Gd-based single-ion magnets with tunable magnetic anisotropy: Molecular design of spin qubits. Phys. Rev. Lett. 2012, 108, 247213. [Google Scholar] [CrossRef] [PubMed]
  71. Baldovi, J.J.; Cardona-Serra, S.; Clemente-Juan, J.M.; Coronado, E.; Gaita-Ariño, A.; Prima-Garcia, H. Coherent manipulation of spin qubits based on polyoxometalates: The case of the single ion magnet [GdW30P5O110]14−. Chem. Commun. 2013, 49, 8922–8924. [Google Scholar] [CrossRef] [PubMed]
  72. Ghosh, S.; Datta, S.; Friend, L.; Cardona-Serra, S.; Gaita-Ariño, A.; Coronado, E.; Hill, S. Multi-frequency EPR studies of a mononuclear holmium single-molecule magnet based on the polyoxometalate [HoIII(W5O18)2]9−. Dalton. Trans. 2012, 41, 13697–13704. [Google Scholar] [CrossRef] [PubMed]
  73. Shiddiq, M.; Komijani, D.; Duan, Y.; Gaita-Ariño, A.; Coronado, E.; Hill, S. Enhancing coherence in molecular spin qubits via atomic clock transitions. Nature 2016, 531, 348–351. [Google Scholar] [CrossRef] [PubMed]
  74. Urdampilleta, M.; Klayatskaya, S.; Ruben, M.; Wernsdorfer, W. Magnetic Interaction between a Radical Spin and a Single-Molecule Magnet in a Molecular Spin-Valve. ACS Nano 2015, 9, 4458–4464. [Google Scholar] [CrossRef] [PubMed]
  75. Urdampilleta, M.; Klyatskaya, S.; Cleuziou, J.; Ruben, M.; Wernsdorfer, W. Supramolecular spin valves. Nat. Mater. 2011, 10, 502–506. [Google Scholar] [CrossRef] [PubMed]
  76. Pedersen, K.S.; Ariciu, A.; McAdams, S.; Weihe, H.; Bendix, J.; Tuna, F.; Piligkos, S. Toward Molecular 4f Single-Ion Magnet Qubits. J. Am. Chem. Soc. 2016, 138, 5801–5804. [Google Scholar] [CrossRef] [PubMed]
  77. Holmberg, R.J.; Ungur, L.; Korobkov, I.; Chibotaru, L.F.; Murugesu, M. Observation of unusual slow-relaxation of the magnetisation in a Gd-EDTA chelate. Dalton. Trans. 2015, 44, 20321–20325. [Google Scholar] [CrossRef] [PubMed]
  78. Ganivet, C.R.; Ballesteros, B.; de la Torre, G.; Clemente Juan, J.M.; Coronado, E.; Torres, T. Influence of Peripheral Substitution on the Magnetic Behavior of Single-Ion Magnets Based on Homo-and Heteroleptic TbIII Bis (phthalocyaninate). Chem. Eur. J. 2013, 19, 1457–1465. [Google Scholar] [CrossRef] [PubMed]
  79. Ishikawa, N.; Sugita, M.; Wernsdorfer, W. Quantum Tunneling of Magnetization in Lanthanide Single-Molecule Magnets: Bis (phthalocyaninato) terbium and Bis (phthalocyaninato) dysprosium Anions. Angew. Chem. Int. Ed. 2005, 44, 2931–2935. [Google Scholar] [CrossRef] [PubMed]
  80. Pedersen, K.S.; Dreiser, J.; Weihe, H.; Sibille, R.; Johannesen, H.V.; Sørensen, M.A.; Nielsen, B.E.; Sigrist, M.; Mutka, H.; Rols, S. Design of single-molecule magnets: Insufficiency of the anisotropy barrier as the sole criterion. Inorg. Chem. 2015, 54, 7600–7606. [Google Scholar] [CrossRef] [PubMed]
  81. Bertaina, S.; Shim, J.H.; Gambarelli, S.; Malkin, B.Z.; Barbara, B. Spin-orbit qubits of rare-earth-metal ions in axially symmetric crystal fields. Phys. Rev. Lett. 2009, 103. [Google Scholar] [CrossRef] [PubMed]
  82. Fraval, E.; Sellars, M.J.; Longdell, J.J. Method of Extending Hyperfine Coherence Times in Pr3+: Y2SiO5. Phys. Rev. Lett. 2004, 92, 77601. [Google Scholar] [CrossRef] [PubMed]
  83. Ohlsson, N.; Mohan, R.K.; Kröll, S. Quantum computer hardware based on rare-earth-ion-doped inorganic crystals. Opt. Commun. 2002, 201, 71–77. [Google Scholar] [CrossRef]
  84. Longdell, J.J.; Sellars, M.J. Experimental demonstration of quantum-state tomography and qubit-qubit interactions for rare-earth-metal-ion-based solid-state qubits. Phys. Rev. A 2004, 69, 032307. [Google Scholar] [CrossRef]
  85. Rippe, L.; Nilsson, M.; Kröll, S.; Klieber, R.; Suter, D. Experimental demonstration of efficient and selective population transfer and qubit distillation in a rare-earth-metal-ion-doped crystal. Phys. Rev. A 2005, 71, 062328. [Google Scholar] [CrossRef]
  86. Fraval, E.; Sellars, M.J.; Longdell, J.J. Dynamic decoherence control of a solid-state nuclear-quadrupole qubit. Phys. Rev. Lett. 2005, 95, 030506. [Google Scholar] [CrossRef] [PubMed]
Magnetochemistry 02 00040 g001 550
Figure 1. (a) Molecular structure of [V(C8S8)3]2− in 1 (Green, V; yellow, S; gray, C) and energies of spin states with increasing applied dc field for 1 oriented; (b) Echo-detected, field-swept, X-band spectrum of a 1 mM solution of 1 in butyronitrile at 20 K (blue line); (c) Integrated echo intensity as a function of delay time (τ) for 1 under an applied dc field of 3486 Oe at 80 K with graphical depiction of Hahn-echo pulse sequence. Inset: Temperature dependence of T2 for 1; (d) Rabi oscillations collected on a 1 mM solution of 1 at 20 K, Hdc = 3486 Oe, and 11 dB attenuation of B1 (adapted with permission from [41]).
Figure 1. (a) Molecular structure of [V(C8S8)3]2− in 1 (Green, V; yellow, S; gray, C) and energies of spin states with increasing applied dc field for 1 oriented; (b) Echo-detected, field-swept, X-band spectrum of a 1 mM solution of 1 in butyronitrile at 20 K (blue line); (c) Integrated echo intensity as a function of delay time (τ) for 1 under an applied dc field of 3486 Oe at 80 K with graphical depiction of Hahn-echo pulse sequence. Inset: Temperature dependence of T2 for 1; (d) Rabi oscillations collected on a 1 mM solution of 1 at 20 K, Hdc = 3486 Oe, and 11 dB attenuation of B1 (adapted with permission from [41]).
Magnetochemistry 02 00040 g001
Magnetochemistry 02 00040 g002 550
Figure 2. Molecular structures of 2–5 (a–d) (Green, V; yellow, S; gray, C; red, O; Ph4P groups are omitted for clarity); (e) Rabi oscillations for 2−5 that verify quantum control in each member of the series. Data were recorded in 1:1 DMF/Tol at 20 K, and 14 dB attenuation of B1. The spin-flip operation time of 52 ns is highlighted (adapted with permission from [42]).
Figure 2. Molecular structures of 2–5 (a–d) (Green, V; yellow, S; gray, C; red, O; Ph4P groups are omitted for clarity); (e) Rabi oscillations for 2−5 that verify quantum control in each member of the series. Data were recorded in 1:1 DMF/Tol at 20 K, and 14 dB attenuation of B1. The spin-flip operation time of 52 ns is highlighted (adapted with permission from [42]).
Magnetochemistry 02 00040 g002
Magnetochemistry 02 00040 g003 550
Figure 3. (a–c) Molecular structures of 6−8 (Green, V; gray, C; red, O; hydrogen atoms are omitted for clarity); (d) Frequency dependence of the imaginary component of the AC susceptibility of bulk 6 in Bdc = 0.2 T multiplied by temperature to be readable in the whole 2–80 K temperature range; (e) Pulsed EPR Hahn echo decay traces for a frozen 1 mM CH2Cl2-toluene solution of 6 at indicated temperatures recorded at 343 mT. In the Inset the employed pulse sequence; (f) Rabi oscillations for a frozen 1 mM CH2Cl2-toluene solution of 6 recorded at 4.3 K at 10 dB microwave attenuation (adapted with permission from [45]).
Figure 3. (a–c) Molecular structures of 6−8 (Green, V; gray, C; red, O; hydrogen atoms are omitted for clarity); (d) Frequency dependence of the imaginary component of the AC susceptibility of bulk 6 in Bdc = 0.2 T multiplied by temperature to be readable in the whole 2–80 K temperature range; (e) Pulsed EPR Hahn echo decay traces for a frozen 1 mM CH2Cl2-toluene solution of 6 at indicated temperatures recorded at 343 mT. In the Inset the employed pulse sequence; (f) Rabi oscillations for a frozen 1 mM CH2Cl2-toluene solution of 6 recorded at 4.3 K at 10 dB microwave attenuation (adapted with permission from [45]).
Magnetochemistry 02 00040 g003
Magnetochemistry 02 00040 g004 550
Figure 4. (a) Molecular structures of 9 (Green, V; gray, C; red, O; blue, N; hydrogen atoms are omitted for clarity); (b) Echo decay traces for 9 at indicated temperatures performed at 345 mT. Solid lines are the best fits; (c) Rabi oscillations recorded for 9 at 300 K for different microwave attenuations performed at 345 mT (adapted with permission from [48]).
Figure 4. (a) Molecular structures of 9 (Green, V; gray, C; red, O; blue, N; hydrogen atoms are omitted for clarity); (b) Echo decay traces for 9 at indicated temperatures performed at 345 mT. Solid lines are the best fits; (c) Rabi oscillations recorded for 9 at 300 K for different microwave attenuations performed at 345 mT (adapted with permission from [48]).
Magnetochemistry 02 00040 g004
Magnetochemistry 02 00040 g005 550
Figure 5. (a) Molecular structure of 10 (Green, V; yellow, S; gray, C; Ph4P groups are omitted for clarity); (b) Echo decay traces for diluted 10 at indicated temperatures performed at X-band; (c) Echo decay traces for diluted 4 at indicated temperatures performed at X-band. Solid lines are the best fits (adapted with permission from [47]).
Figure 5. (a) Molecular structure of 10 (Green, V; yellow, S; gray, C; Ph4P groups are omitted for clarity); (b) Echo decay traces for diluted 10 at indicated temperatures performed at X-band; (c) Echo decay traces for diluted 4 at indicated temperatures performed at X-band. Solid lines are the best fits (adapted with permission from [47]).
Magnetochemistry 02 00040 g005
Magnetochemistry 02 00040 g006 550
Figure 6. (a) Structures of complexes 11–13; (b) Inversion recovery experiment (up) and Hahn echo experiment (down) for relaxation data of 11 in H2SO4 (red triangles) and D2SO4 (blue circles) at Q-band and 7 K (adapted with permission from [31]); (c) Rabi oscillations of a 0.1% CuPc:H2Pc film recorded at 5 K and 330.5 mT for different microwave powers (adapted with permission from [49]).
Figure 6. (a) Structures of complexes 11–13; (b) Inversion recovery experiment (up) and Hahn echo experiment (down) for relaxation data of 11 in H2SO4 (red triangles) and D2SO4 (blue circles) at Q-band and 7 K (adapted with permission from [31]); (c) Rabi oscillations of a 0.1% CuPc:H2Pc film recorded at 5 K and 330.5 mT for different microwave powers (adapted with permission from [49]).
Magnetochemistry 02 00040 g006
Magnetochemistry 02 00040 g007 550
Figure 7. (a) Molecular structure of 14 (Aqua, Cu; yellow, S; blue, N; black, P; gray, C; hydrogen atoms are omitted for clarity); (b) Temperature-dependent Hahn echo decay curves for 14Cu0.001%. Solid lines are the best fits (adapted with permission from [50]).
Figure 7. (a) Molecular structure of 14 (Aqua, Cu; yellow, S; blue, N; black, P; gray, C; hydrogen atoms are omitted for clarity); (b) Temperature-dependent Hahn echo decay curves for 14Cu0.001%. Solid lines are the best fits (adapted with permission from [50]).
Magnetochemistry 02 00040 g007
Magnetochemistry 02 00040 g008 550
Figure 8. (a) Molecular structure of [Cr(C3S5)3]3− in 15 (Pink, Cr; yellow, S; gray, C, Ph4P groups are omitted for clarity) and calculated splitting of the MS energy levels with Hdc = 2000 G aligned along the z-axis of the molecule (arrows illustrate the allowed (green) and forbidden (purple) transitions within the s = 3/2 manifold); (b) Hahn-echo decay curves for 1% of deuterated 15 in (d20-Ph4P)3[Ga(C3S5)3] at 5 K. Lines are best fits; (c) Rabi oscillations at Hdc = 3500 and 1000 G and Rabi frequency dependence on B1; (d) Rabi frequency plotted as a function of increasing B1 for 1% of deuterated 15 in (d20-Ph4P)3[Ga(C3S5)3] and BDPA (1,3-bisdiphenylene-2-phenylallyl radical) at 5 K (adapted with permission from [51]).
Figure 8. (a) Molecular structure of [Cr(C3S5)3]3− in 15 (Pink, Cr; yellow, S; gray, C, Ph4P groups are omitted for clarity) and calculated splitting of the MS energy levels with Hdc = 2000 G aligned along the z-axis of the molecule (arrows illustrate the allowed (green) and forbidden (purple) transitions within the s = 3/2 manifold); (b) Hahn-echo decay curves for 1% of deuterated 15 in (d20-Ph4P)3[Ga(C3S5)3] at 5 K. Lines are best fits; (c) Rabi oscillations at Hdc = 3500 and 1000 G and Rabi frequency dependence on B1; (d) Rabi frequency plotted as a function of increasing B1 for 1% of deuterated 15 in (d20-Ph4P)3[Ga(C3S5)3] and BDPA (1,3-bisdiphenylene-2-phenylallyl radical) at 5 K (adapted with permission from [51]).
Magnetochemistry 02 00040 g008
Magnetochemistry 02 00040 g009 550
Figure 9. (a) Molecular structure of [Cr(C2O4)3]3− in 16 (Light blue, Cr; red, O; gray, C; cations are omitted for clarity); (b) Calculated splitting of the MS energy levels with Hdc = 1000 G aligned along the z-axis of the molecule. Blue arrows indicate the six potential qubits; (c) T2 decay curves for 16 at indicated temperatures. Lines are best fits (adapted with permission from [33]).
Figure 9. (a) Molecular structure of [Cr(C2O4)3]3− in 16 (Light blue, Cr; red, O; gray, C; cations are omitted for clarity); (b) Calculated splitting of the MS energy levels with Hdc = 1000 G aligned along the z-axis of the molecule. Blue arrows indicate the six potential qubits; (c) T2 decay curves for 16 at indicated temperatures. Lines are best fits (adapted with permission from [33]).
Magnetochemistry 02 00040 g009
Magnetochemistry 02 00040 g010 550
Figure 10. (a) Depictions of the molecular structures of 16, 17 and 19 (left) and 18, 20 and 21 (right) (cations are omitted for clarity); (b) Rabi oscillations and pulse sequence for a solution of 19 at 5 K (adapted with permission from [33]).
Figure 10. (a) Depictions of the molecular structures of 16, 17 and 19 (left) and 18, 20 and 21 (right) (cations are omitted for clarity); (b) Rabi oscillations and pulse sequence for a solution of 19 at 5 K (adapted with permission from [33]).
Magnetochemistry 02 00040 g010
Magnetochemistry 02 00040 g011 550
Figure 11. (a) Molecular structure of [Fe(C5O5)3]3− in 22 (Brown, Fe; red, O; gray, C; the Ph4P groups are omitted for clarity); (b) Magnetic field dependence of the MS levels of the s = 5/2 state in 22 for a magnetic field aligned perpendicular to the molecular z-axis (adapted with permission from [60]); (c) Rabi oscillations at Hdc = 1608 G with indicated B1 for 22a at 10 K(adapted with permission from [59]; (d) Rabi oscillations at Hdc = 1608 G with indicated B1 for 22b at 10 K (adapted with permission from [60].
Figure 11. (a) Molecular structure of [Fe(C5O5)3]3− in 22 (Brown, Fe; red, O; gray, C; the Ph4P groups are omitted for clarity); (b) Magnetic field dependence of the MS levels of the s = 5/2 state in 22 for a magnetic field aligned perpendicular to the molecular z-axis (adapted with permission from [60]); (c) Rabi oscillations at Hdc = 1608 G with indicated B1 for 22a at 10 K(adapted with permission from [59]; (d) Rabi oscillations at Hdc = 1608 G with indicated B1 for 22b at 10 K (adapted with permission from [60].
Magnetochemistry 02 00040 g011
Magnetochemistry 02 00040 g012 550
Figure 12. (a) Molecular structures of GdW10 and 25; energy levels of GdW10 and 25 for Hdc = 10 mT; (b) Ac magnetic susceptibility measured at indicated temperatures and the relaxation times for GdW10 and 25 (adapted with permission from [70]); (c) Rabi oscillations for 25 at indicated microwave (adapted with permission from [71].
Figure 12. (a) Molecular structures of GdW10 and 25; energy levels of GdW10 and 25 for Hdc = 10 mT; (b) Ac magnetic susceptibility measured at indicated temperatures and the relaxation times for GdW10 and 25 (adapted with permission from [70]); (c) Rabi oscillations for 25 at indicated microwave (adapted with permission from [71].
Magnetochemistry 02 00040 g012
Magnetochemistry 02 00040 g013 550
Figure 13. (a) Polyhedral representation, molecular structures and separate view along the axial z-direction of 26 (adapted with permission from [72]); (b) Zeeman diagrams corresponding to the hyperfine-split mJ = ±4 ground states (adapted with permission from [72]); (c) Field-swept T2 recorded at 5.0 K at indicated frequencies and fields for Na9[HoxY(1–x)(W5O18)2]·nH2O (x = 0.001) (adapted with permission from [73]).
Figure 13. (a) Polyhedral representation, molecular structures and separate view along the axial z-direction of 26 (adapted with permission from [72]); (b) Zeeman diagrams corresponding to the hyperfine-split mJ = ±4 ground states (adapted with permission from [72]); (c) Field-swept T2 recorded at 5.0 K at indicated frequencies and fields for Na9[HoxY(1–x)(W5O18)2]·nH2O (x = 0.001) (adapted with permission from [73]).
Magnetochemistry 02 00040 g013
Magnetochemistry 02 00040 g014 550
Figure 14. (a) Artist’s view of a nuclear spin qubit transistor based on a single 27 molecule. The four anisotropic nuclear spin states of the Tb3+ (colored circles) can be manipulated by an electric field pulse (adapted with permission from [40]); (b) The two ground states are each split into four different sub-states owing to the hyperfine coupling with the nuclear spin (I = 3/2). Colored lines denote the Iz components: purple, −3/2; blue, −1/2; green, 1/2; and red, 3/2. Two processes are responsible for the magnetization reversal (adapted with permission from [39]); (c) Ramsey interference fringes obtained by repeating time-dependent external magnetic field and pulse sequence for 100 times at 40 mK (adapted with permission from [40]); (d) Rabi oscillations obtained by repeating the above sequence in (c) for 100 times at 40 mK (adapted with permission from [40]).
Figure 14. (a) Artist’s view of a nuclear spin qubit transistor based on a single 27 molecule. The four anisotropic nuclear spin states of the Tb3+ (colored circles) can be manipulated by an electric field pulse (adapted with permission from [40]); (b) The two ground states are each split into four different sub-states owing to the hyperfine coupling with the nuclear spin (I = 3/2). Colored lines denote the Iz components: purple, −3/2; blue, −1/2; green, 1/2; and red, 3/2. Two processes are responsible for the magnetization reversal (adapted with permission from [39]); (c) Ramsey interference fringes obtained by repeating time-dependent external magnetic field and pulse sequence for 100 times at 40 mK (adapted with permission from [40]); (d) Rabi oscillations obtained by repeating the above sequence in (c) for 100 times at 40 mK (adapted with permission from [40]).
Magnetochemistry 02 00040 g014
Magnetochemistry 02 00040 g015 550
Figure 15. (a) Molecular structure of Yb(trensal) in 28 (Pink, Yb; red, O; blue, N; gray, C, hydrogen atoms are omitted for clarity); (b) Zeeman diagram of the I = 5/2 isotope; (c) Temperature dependence of T1 and T2 determined by pulsed EPR for 7% 28 in Lu(trensal); (d) Echo intensity, proportional to the expectation value ⟨Sz⟩, as a function of the length of the nutation pulse (tp) at selected field positions at T = 5 K (microwave attenuation = 3 dB) and its corresponding Fourier transforms (adapted with permission from [76]).
Figure 15. (a) Molecular structure of Yb(trensal) in 28 (Pink, Yb; red, O; blue, N; gray, C, hydrogen atoms are omitted for clarity); (b) Zeeman diagram of the I = 5/2 isotope; (c) Temperature dependence of T1 and T2 determined by pulsed EPR for 7% 28 in Lu(trensal); (d) Echo intensity, proportional to the expectation value ⟨Sz⟩, as a function of the length of the nutation pulse (tp) at selected field positions at T = 5 K (microwave attenuation = 3 dB) and its corresponding Fourier transforms (adapted with permission from [76]).
Magnetochemistry 02 00040 g015
Table
Table 1. V(IV) based single-ion spin qubits.
Table 1. V(IV) based single-ion spin qubits.
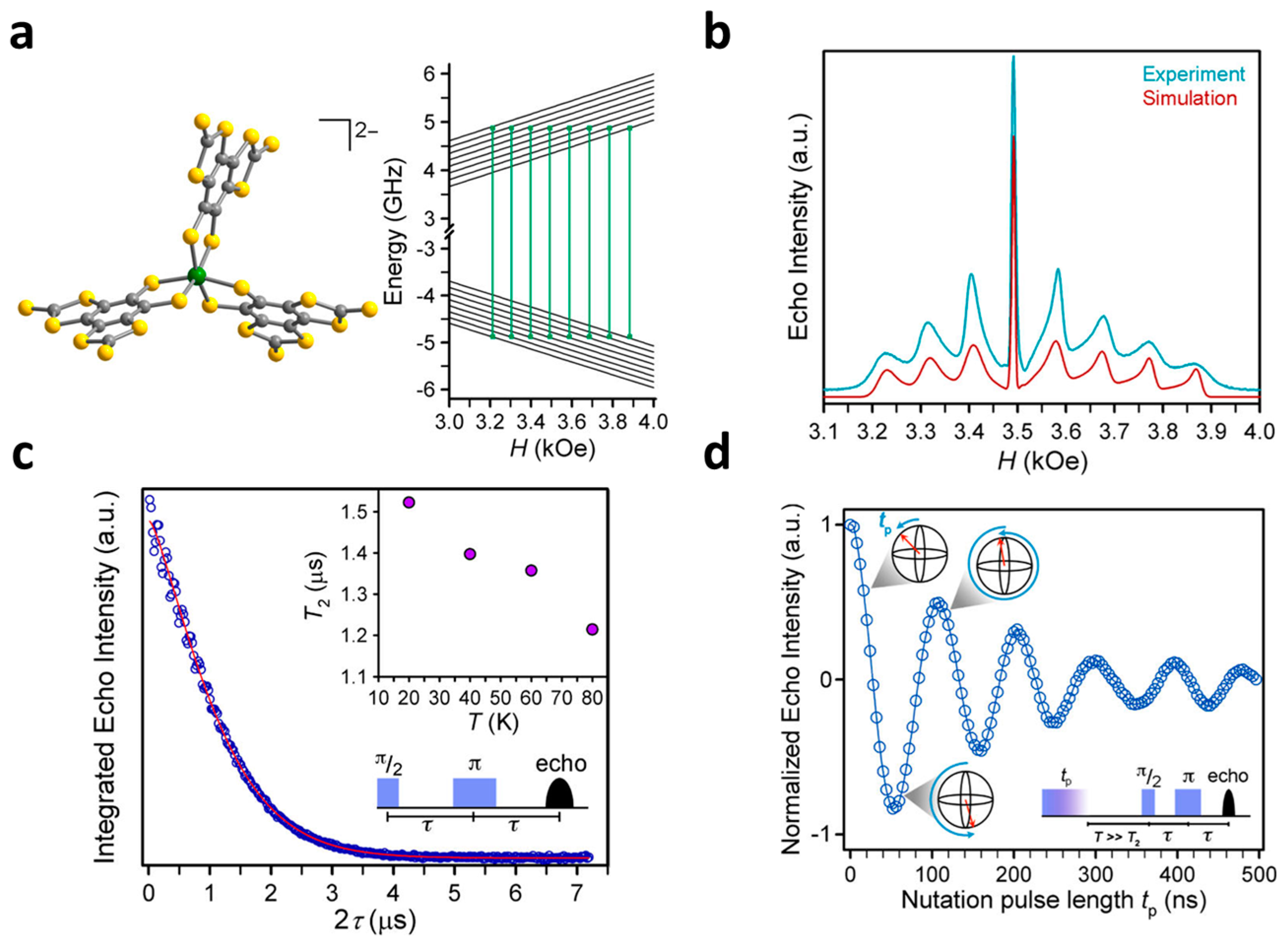
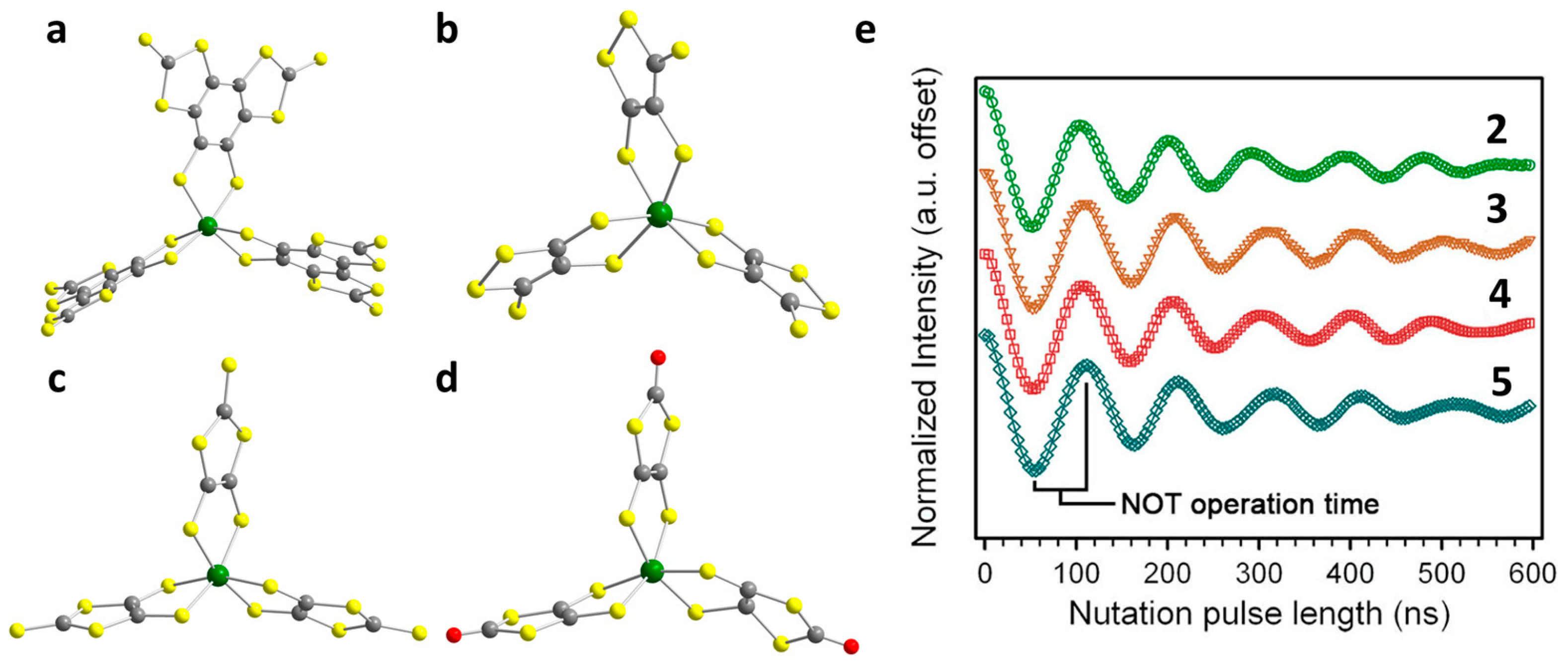
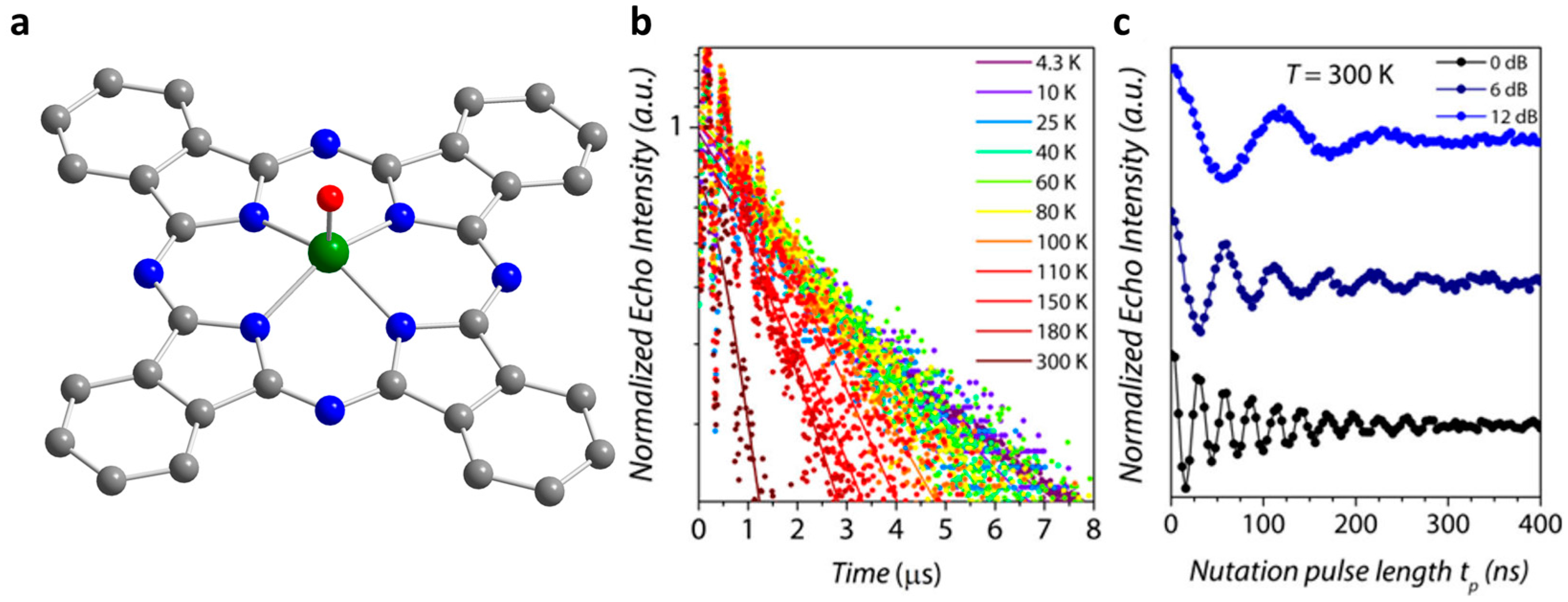
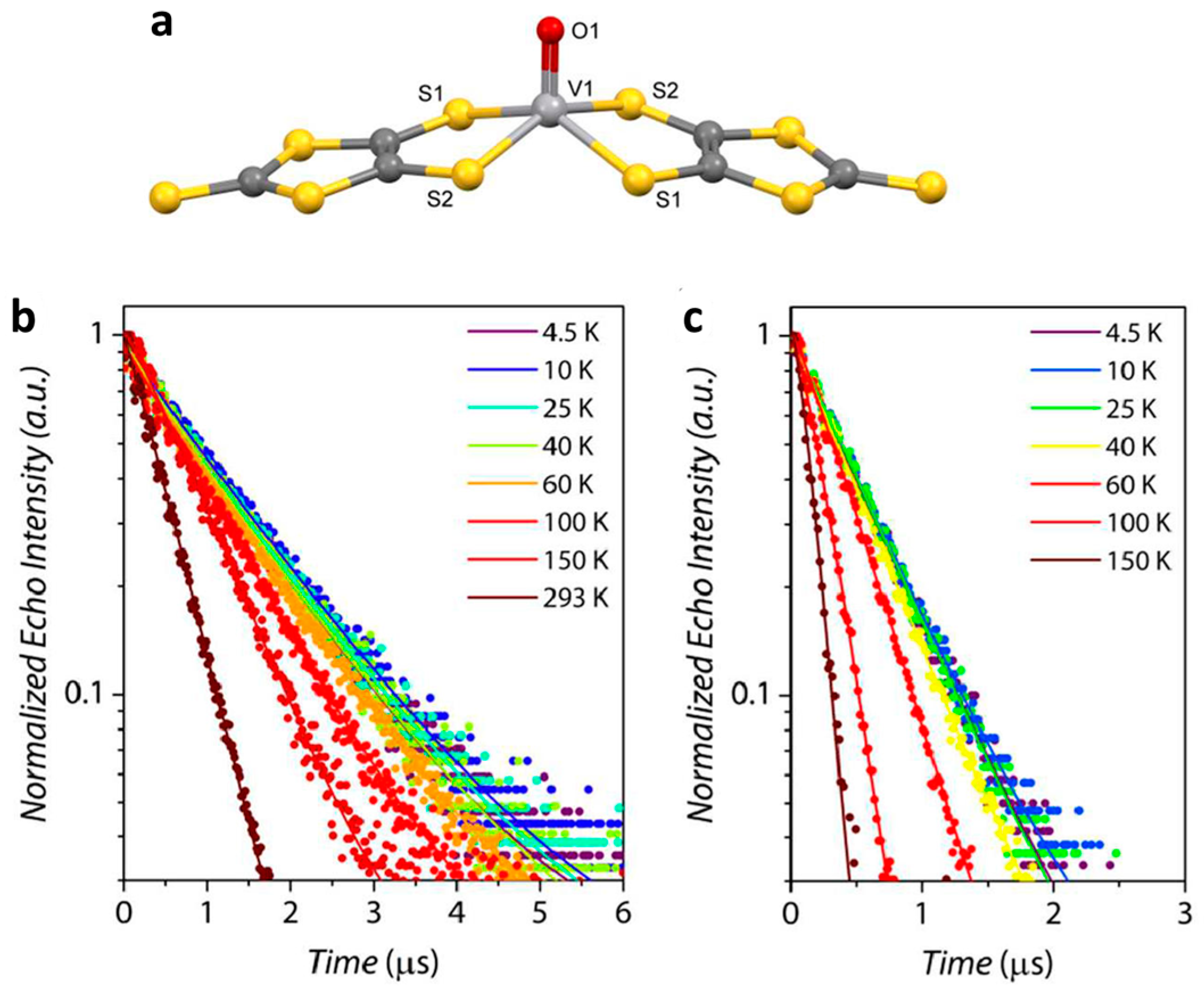
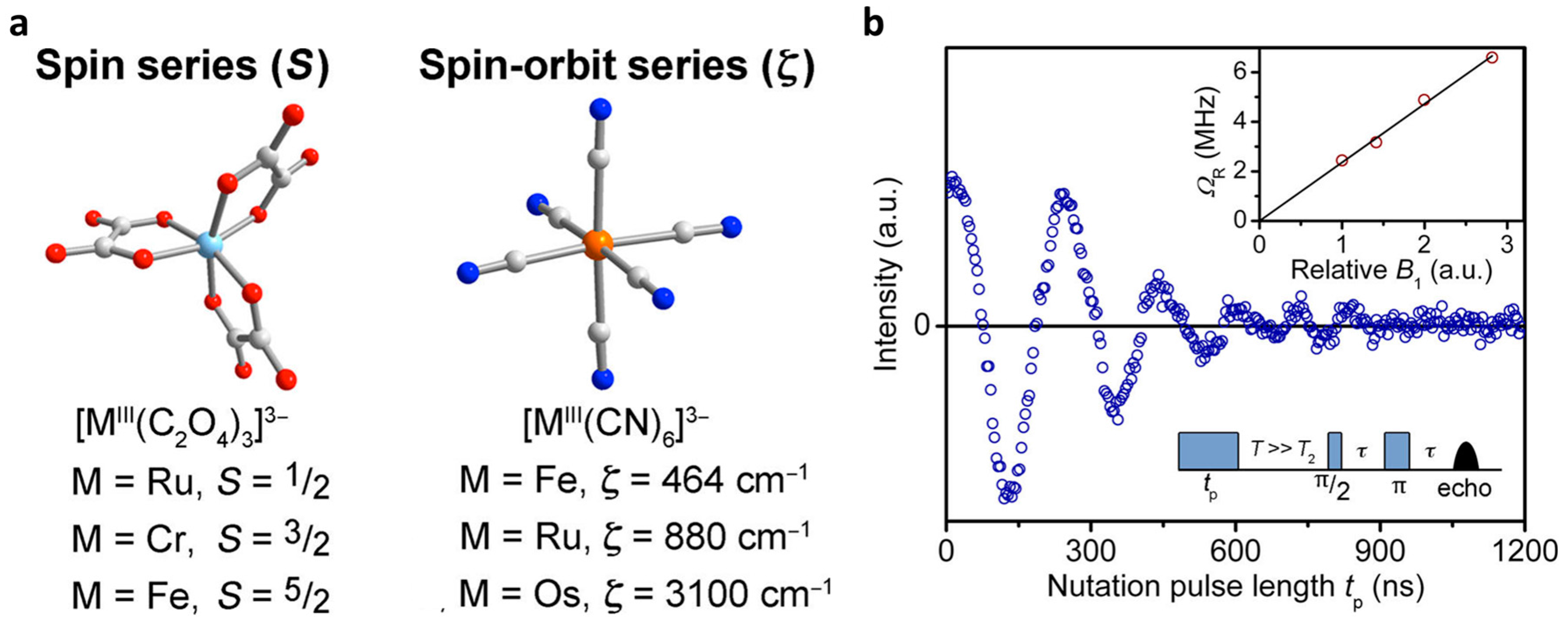
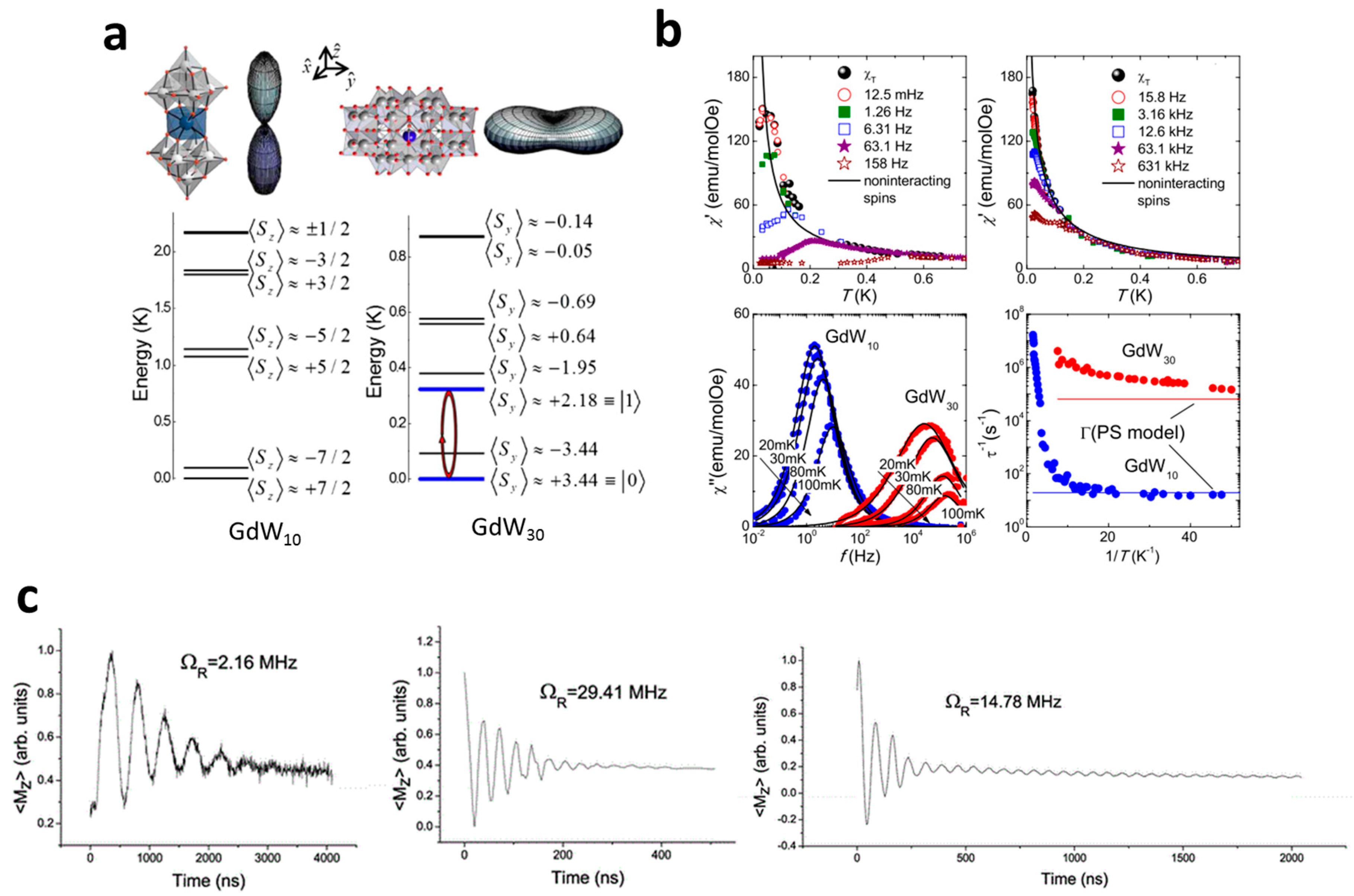
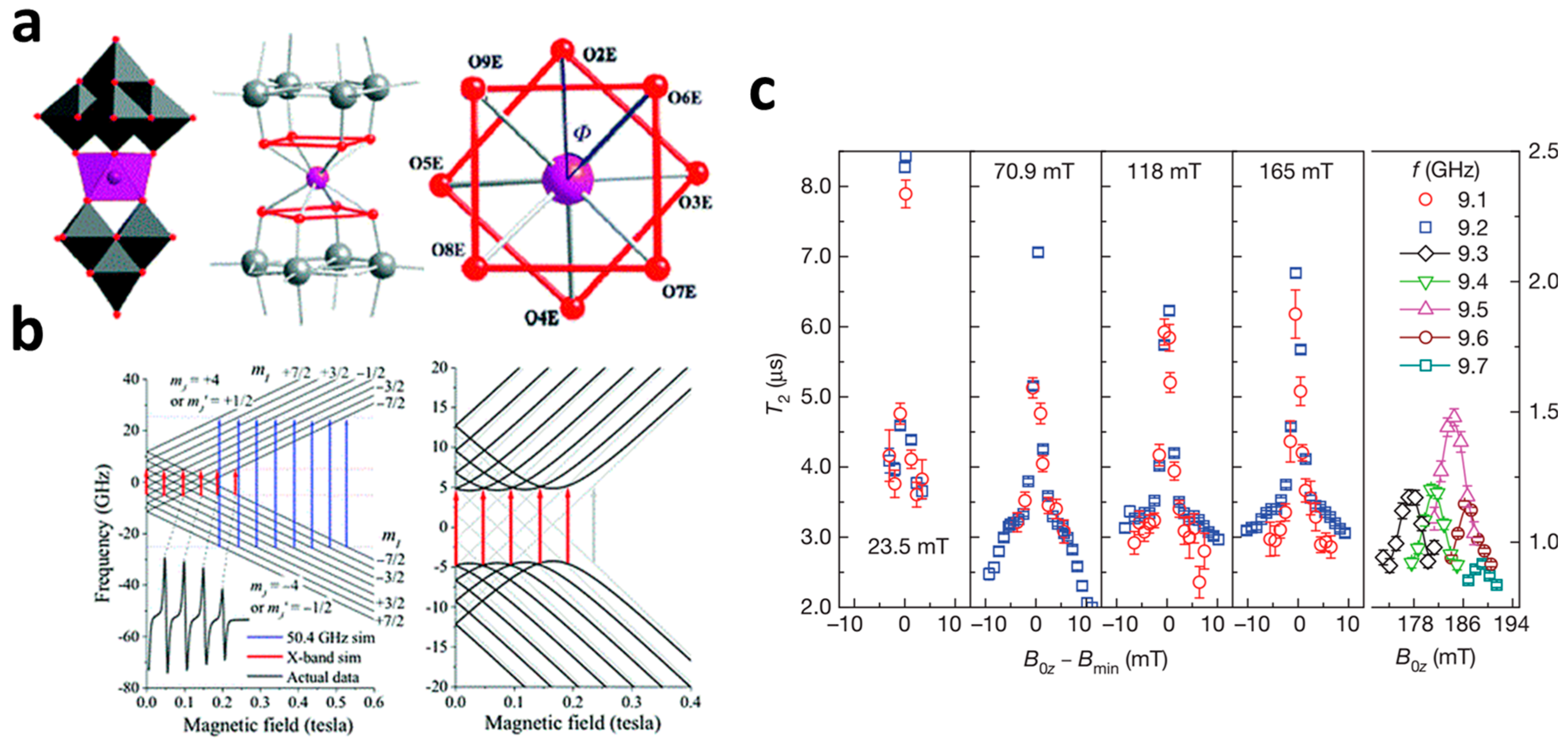
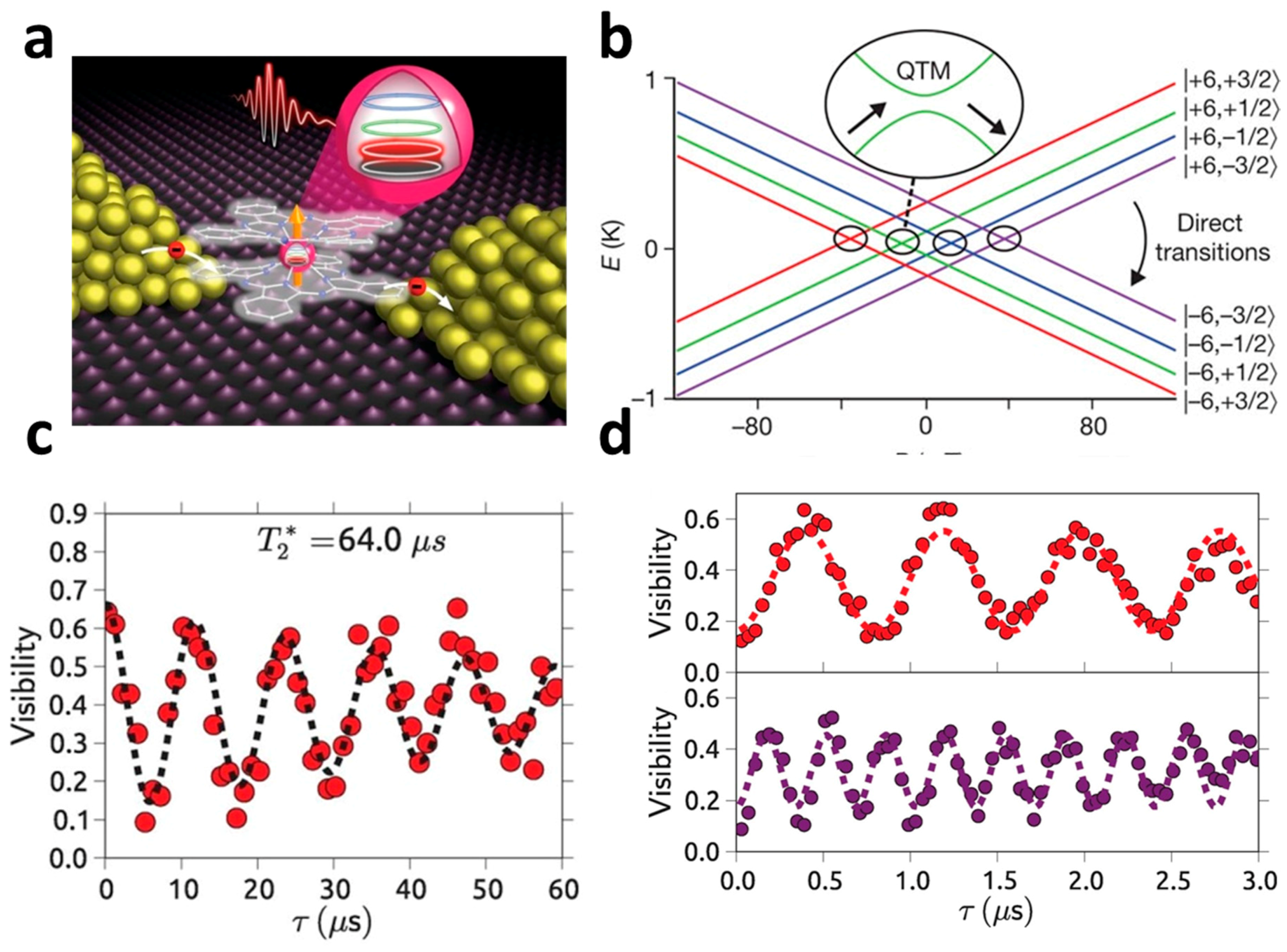
ComplexT1/μsT2/μs aT2/μs bTR/K cRef.
(Bu4N)2[V(C8S8)3] (1)-1.2 (80 K)1.52 (20 K)20[41]
(Ph4P)2[V(C8S8)3] (2)4.90 (120 K)1.18 (120 K)675(7) (10 K)20[42]
(Ph4P)2[V(β-C3S5)3] (3)2.24 (120 K)0.86 (120 K)6.13 (10 K)20[42]
(Ph4P)2[V(α-C3S5)3] (4)0.71 (150 K)0.19 (150 K)6.01 (10 K)60[42,47]
(Ph4P)2[V(C3S4O)3] (5)3.16 (120 K)0.96 (120 K)2.79 (10 K)20[42]
VO(dpm)2 (6)6 (110 K)0.1 (220 K)2.5 (10 K)4.3[45]
VO(acac)2 (7)≈102 (40 K)---[46]
VO(dbm)2 (8)≈102 (40 K)---[46]
VOPc (9)2.4 × 106 (7 K)22 (10 K)--[31]
VOPc (9)1.1 (300 K)0.83 (300 K)-300[48]
[(Ph)4P]2[VO(α-C3S5)2] (10)3.37 (293 K)1.04 (293 K)-293[47]
a Reported T2 values at the highest temperatures; b Best T2 values; c Reported temperatures for Rabi oscillations.
Table
Table 2. Cu(II) based single-ion spin qubits.
Table 2. Cu(II) based single-ion spin qubits.
ComplexT1/μsT2/μs aT2/μs bTR/K cRef.
CuPc (11)105 (7 K)1.0 (80 K)41 (7 K)5[31,49]
CuPcCl (12)105 (7 K)40 (7 K)--[31]
CuPcF (13)6 × 104 (7 K)40 (7 K)--[31]
(PPh4)2[Cu(mnt)2] (14)0.48 (294 K)0.6 (294 K)68 (7 K)15[50]
a Reported T2 values at the highest temperatures; b Best T2 values; c Reported temperatures for Rabi oscillations.
Table
Table 3. Other transition metals based single-ion spin qubits.
Table 3. Other transition metals based single-ion spin qubits.
ComplexT1/μsT2/μs aT2/μs bTR/K cRef.
(Ph4P)3[Cr(C3S5)3] (15)875 (30 K)0.82 (30 K)1.81 (5 K)5 K[51]
K3[Cr(C2O4)3] (16)-1.27 (22 K)2.79 (5 K)-[33]
K3[Fe(C2O4)3] (17)-0.45 (22 K)1.83 (5 K)-[33]
(Ph4P)3[Fe(CN)6] (18)-0.60 (22 K)2.38 (5 K)-[33]
K3[Ru(C2O4)3] (19)-0.41 (22 K)3.44 (5 K)5[33]
(Ph4P)3[Ru(CN)6] (20)-1.29 (22 K)2.55 (5 K)-[33]
(Ph4P)3[Os(CN)6] (21)-1.04 (22 K)4.12 (5 K)-[33]
(Ph4P)3[Fe(C5O5)3] (22)1.18 (15K)0.498 (40 K)1.63 (5 K)10[59]
MnPc (23)690 (7 K)14 (7 K)--[31]
CoPc (24)1.11 × 104 (7 K)9.44 (7 K)--[31]
a Reported T2 values at the highest temperatures; b Best T2 values; c Reported temperatures for Rabi oscillations.
Table
Table 4. 4f based single-ion spin qubits.
Table 4. 4f based single-ion spin qubits.
ComplexT1/μsT2/μs aT2/μs bTR/K cRef
[Gd(P5W30O110)] K14nH2O (25)1.6 (6 K)0.41 (6 K)-5[70,71]
[Ho(W5O18P)2]9− (26)20 (5 K)-8.4 (5 K)-[73]
TbPc2 (27)--64 (40 mK)0.04[40]
Yb(trensal)3 (28)0.2 (20 K)0.17 (15 K)0.53 (2.7 K)5[76]
a Reported T2 values at the highest temperatures; b Best T2 values; c Reported temperatures for Rabi oscillations.

Share and Cite

MDPI and ACS Style

Ding, Y.-S.; Deng, Y.-F.; Zheng, Y.-Z. The Rise of Single-Ion Magnets as Spin Qubits. Magnetochemistry 2016, 2, 40. https://doi.org/10.3390/magnetochemistry2040040

AMA Style

Ding Y-S, Deng Y-F, Zheng Y-Z. The Rise of Single-Ion Magnets as Spin Qubits. Magnetochemistry. 2016; 2(4):40. https://doi.org/10.3390/magnetochemistry2040040

Chicago/Turabian Style

Ding, You-Song, Yi-Fei Deng, and Yan-Zhen Zheng. 2016. "The Rise of Single-Ion Magnets as Spin Qubits" Magnetochemistry 2, no. 4: 40. https://doi.org/10.3390/magnetochemistry2040040

APA Style

Ding, Y. -S., Deng, Y. -F., & Zheng, Y. -Z. (2016). The Rise of Single-Ion Magnets as Spin Qubits. Magnetochemistry, 2(4), 40. https://doi.org/10.3390/magnetochemistry2040040

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop