Abstract
Information concerning the structures of compounds of rare earth elements with carboxylic acids and a β-diketone containing stable organometallic moieties that we obtained previously is presented. Additional results for 15 complexes with the [Gd2O2] core allowed confirming and improving the correlation between JGd–Gd′ and the Gd…Gd distance for complexes of this type that we found earlier. For the first time, dc and ac magnetic measurements were carried out for the formerly-described complex [Dy2(O2CCym)4(NO3)2(DMSO)4] (2), Cym = (η5-C5H4)Mn(CO)3), and two new binuclear complexes, namely [Dy2(O2CFc)4(NO3)2(DMSO)4] (3), and [Dy2(O2CFc)6(DMSO)2(H2O)2] (4), Fc = (η5-C5H4)Fe(η5-C5H5)). For binuclear [Dy2(O2CCym)6(DMSO)4] (1), as well as for a 1D-polymer [Dy(O2CCym)(acac)2(H2O)]n (6), ac magnetic measurements were carried out more precisely. The characteristics of a single-molecule magnet and of a single-chain magnet were determined for Complexes 2 and 6, respectively.
1. Introduction
Single-molecule magnets (SMM) are molecule-scale objects that demonstrate properties characteristic of bulk magnetic materials. In compounds of this kind, the classical phenomenon of residual magnetization retention is based on magnetic anisotropy on molecular and atomic levels. The majority of currently-known SMMs are the coordination compounds whose molecules contain a few metal ions with rather a large number of unpaired electrons and can retain residual magnetization for some time at very low temperatures. Compounds of this kind may be regarded as elements of high-density magnetic memory, i.e., promising components for data storage. A powerful impetus to the developments in this field was given by studies of the magnetic properties of the {Mn12} cluster [1,2]. Currently, close attention of researchers is given to coordination compounds of lanthanides in the context of molecular magnetism.
The interest in coordination compounds of rare earth elements (REE) is currently rather high [3,4], primarily due to their unique magnetic properties [5,6,7,8,9]. Among them, considerable attention is paid to β-diketonate and carboxylate derivatives. The latter class of compounds is characterized by a wide structural variety that is mainly reached due to the ability of carboxylic groups to show various structural functions. It is also attained by incorporation of additional ligands [10]. The most popular approach to the design of lanthanide-containing SMM involves the use of ligand field symmetry to increase the anisotropy of isolated Ln3+ ions [11]. At the same time, beside the specifics of the local symmetry of Dy3+, a considerable role may belong to the ligand nature (electrostatic aspect) [12]. Therefore, the suggestion of new core-forming ligands for directed design of SMM is of undoubted interest.
An interesting, but insufficiently studied group among carboxylate and β-diketonate lanthanide derivatives comprises complexes in which the core-forming (carboxylate/β-diketone) ligand contains stable organometallic moieties, viz. derivatives of ferrocene (bis(η5-cyclopentadienyl)iron, (η5-C5H5)2Fe), and cymantrene (η5-cyclopentadienyltricarbonylmanganese, (η5-C5H5)Mn(CO)3), the derivatives of cymantrene- and ferrocene-carboxylic acids in particular (Scheme 1).
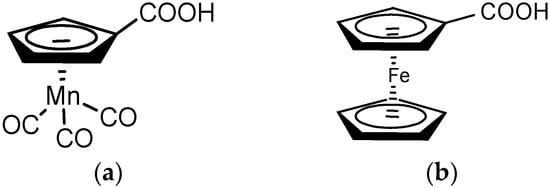
Scheme 1.
(a) cymantrenecarboxylic acid (CymCO2H); (b) ferrocenecarboxylic acid (FcCO2H).
These ligands are bulky; they also have a highly polarizable π-system. Therefore, both steric and electronic effects may play a significant role in metal carboxylates/β-diketonates. Such compounds also represent the original type of heterometallic complexes, since they are potentially able to combine specific properties of the metal ion and of the organometallic fragment. For example, in the aspect of magnetic properties, the reversible conversion of the ferrocenyl group to paramagnetic ferrocenium in the solid state of ferrocenecarboxylates is of interest [13,14].
This paper provides a review of our previous (2011–2016) and new synthetic and structural results of studies on the magnetic behavior of cymantrene- and ferrocene-carboxylates of dysprosium.
2. Results and Discussion
First of all, no information about cymantrenecarboxylates of rare earth metals and their magnetic properties was available before our first publication [15]. To date, we have obtained cymantrenecarboxylates with various structures, both binuclear [15,16,17,18] and polymeric complexes [19,20,21].
The first complexes of this type that we obtained included two similar series of heteroleptic cymantrenecarboxylates of light lanthanides, [Ln2(μ-O,η2-O2CCym)2(μ2-O,O′-O2CCym)2(η2-O2CCym)2L4] nL, containing molecules of volatile tetrahydrofuran (Ln = Nd, n = 0; Ln = Gd, Eu, n = 1; L = THF) [15] or pyridine (Ln = Pr, Sm, Eu, Gd, n = 2, L = Py) [16] as neutral ligands. The obtained complexes had a binuclear structure typical of lanthanide carboxylates (Figure 1).
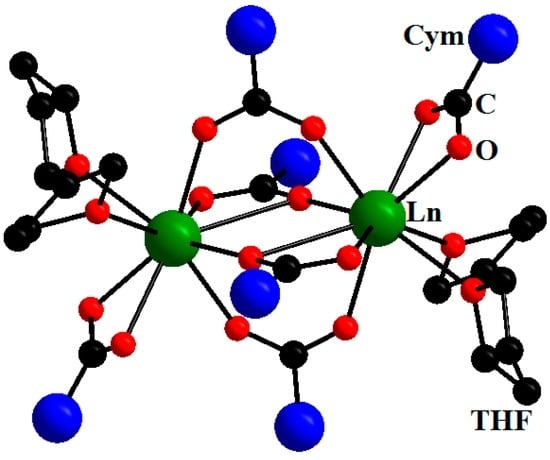
Figure 1.
Molecular structure of [Ln2(μ-O,η2-O2CCym)2(μ2-O,O′-O2CCym)2(η2-O2CCym)2(THF)4]. Reproduced from the work [15] with the change in appearance.
Furthermore, a series of binuclear complexes that contained relatively low volatile DMSO as the neutral ligand was obtained, namely [Ln2(μ-O,η2-O2CCym)2(μ2-O,O′-O2CCym)2(η2-O2CCym)2(DMSO)4]; Ln = Ce, Nd, Eu, Gd [17]; Ln = Tb, Dy [18].
The first representatives of lanthanide cymantrenecarboxylates with the ratio Ln:Mn = 1:2 were binuclear compounds [Ln2(μ2-O2CCym)2(μO,η2-O2CCym)2(η2-NO3)2(η2-DME)2] (Ln = Pr, Eu, Gd, Tb, Dy, Ho, Er; DME (1,2-dimethoxyethane)) [19] and [Ln2(μ2-O,O′-O2CCym)4(η2-NO3)2(DMSO)4] (Ln = Tb, Dy) [18]. The [Ln2(O2CCym)4(NO3)2(DME)2] complexes are built similarly to binuclear complexes with THF, pyridine and DMSO, except that the role of chelating anions is played by nitrate ions, whereas chelate molecules of DME are the neutral ligands. Yet another type of compound with the Ln:Mn ratio of 1:2 is the mixed acetate-cymantrenecarboxylate complexes [20]. In the case of heavier lanthanides (Ho, Er, Tm), binuclear complexes [Ln2(μ2-O2CCym)2-(η2-O2CCym)2-(η2-OAc)2(H2O)4]∙5H2O were obtained (Figure 2), while 1D polymers [Ln(O2CCym)2-(OAc)(A)x]n∙mSolv (x = 1, 2; A = MeOH, H2O; Solv = i-PrOH, THF, H2O) were obtained in the cases of Ln = Nd, Gd, Dy (Figure 3) [20].
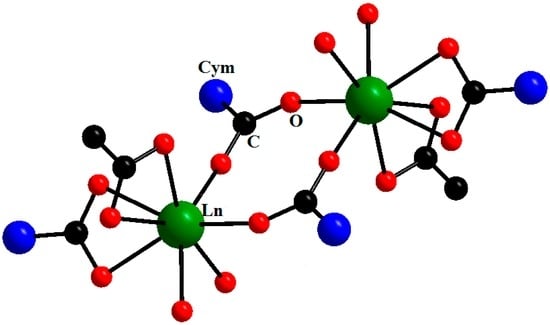
Figure 2.
Molecular structure of [Ln2(μ2-O2CCym)4(OAc)2(H2O)4]∙5H2O (Ln = Ho, Er, Tm). Reproduced from the work [20] with the change in appearance.
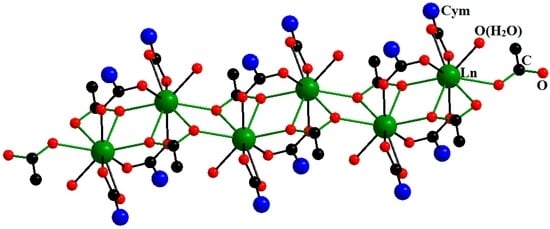
Figure 3.
Molecular structure of [Ln(O2CCym)2(OAc)(A)x]n∙mSolv (Ln = Nd, Gd, Dy; x = 1, 2; A = MeOH, H2O; Solv = i-PrOH, THF, H2O). Reproduced from the work [20] with the change in appearance.
All of the polymers include a common ladder structure {Ln(OAc)}n formed by tetradentate acetate ligands and Ln3+ ions. Cymantrenecarboxylate anions form the periphery of the polymer chain, where they play the role of monodentate, chelate or bridging ligands. The diversity of coordinating functions of the cymantrenecarboxylate residues determines the variety of the polymer structures.
The 1D-polymeric complexes [Ln(η2-O2CCym)2(μ2-O2CCym)4Ln(ROH)4]n·mSolv (Ln = Nd, Gd, Dy, Ho, Er; R = H, Me; Cym = (η5-C5H4)Mn(CO)3; Solv (solvent molecule)) that we obtained appeared to be rather interesting. The polymeric chains of these compounds contain two types of alternating coordination centers, namely, Ln3+ ions that coordinate the water/methanol molecules and the oxygen atoms of bridging carboxylate anions and Ln3+ ions that coordinate the oxygen atoms of bridging and chelate carboxylate anions; in both cases, the coordination number (CN) of Ln equals eight (Figure 4) [21].
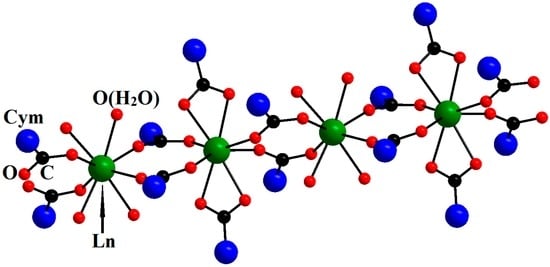
Figure 4.
Molecular structure of [Ln(η2-O2CCym)2(μ-O2CCym)4Ln(H2O)4]n. Reproduced from the work [21] with the change in appearance.
To synthesize cymantrenecarboxylates with the ratio Ln:Mn = 1:1, we suggested an original technique with the use of hydrated lanthanide acetylacetonates as the starting reagents [22]. 1D-polymeric complexes [Ln(O2CCym)(acac)2(H2O)]n (Ln = Eu, Gd, Tb, Dy, Ho, Er) were obtained. The structure of the complexes is formed of [Ln(acac)2(H2O)] moieties, in which the lanthanide ion is chelated by two acac ligands, while the bridging cymantrenecarboxylate anions bind the adjacent [Ln(acac)2(H2O)] moieties into an infinite chain. The coordination number of Ln3+ is seven, which is a comparatively small value for lanthanide complexes (Figure 5).
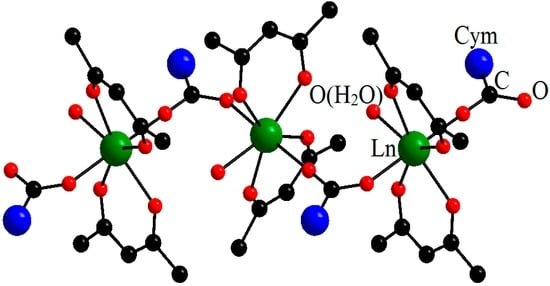
Figure 5.
Molecular structure of [Ln(O2CCym)(acac)2(H2O)]n (Ln = Eu–Er). Reproduced from the work [22] with the change in appearance.
Moreover, new REE ferrocenecarboxylates [Ln2(μ-O,η2-OOCFc)2(μ2-O,O′-OOCFc)2(η2-NO3)2(DMSO)4] (Ln = Gd, Tb, Y) and [Gd2(μ-O,η2-OOCFc)2(η2-OOCFc)4(DMSO)2(H2O)2]·2DMSO·2CH2Cl2 were obtained and characterized [23]. Two new compounds were obtained in this study: [Dy2(O2CFc)4(NO3)2(DMSO)4] (3), which is isostructural with [Ln2(O2CFc)4(NO3)2(DMSO)4] (Ln = Gd, Tb, Y) [23], and [Dy2(O2CFc)6(DMSO)2(H2O)2]∙2DMSO∙3MePh (4).
A number of hitherto unknown ferrocenoylacetonate complexes of rare earth elements, [Ln(fca)3(bpy)]∙MeC6H5 (Ln = Pr, Eu, Gd, Tb, Dy, Ho (fca = Fc(CO)CH(CO)Me; bpy = 2,2′-bipyridyl)) (Figure 6) [24] and [Ln(fca)2(NO3)(bpy)]∙nMeC6H5 (Ln = Sm, Eu, Dy, Er, Yb), were synthesized and characterized by X-ray single crystal analysis [25].
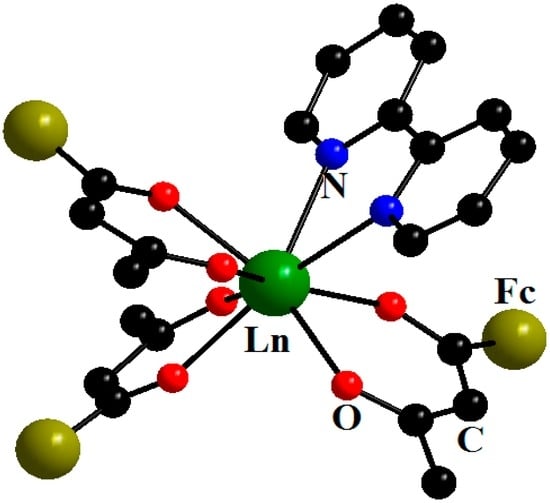
Figure 6.
Molecular structure of [Ln(fca)3(bpy)] (Ln = Pr, Eu, Gd, Tb, Dy, Ho); here and below, the ferrocene moieties are simplified for clarity. Reproduced from the work [24] with the change in appearance.
Thus, we proposed methods for the synthesis of new compounds, determined their molecular and crystal structures, studied their thermal behavior, as well as luminescent properties for Eu derivatives [15,16,17,18,19,20,21,22,23,24,25], but a detailed study of the magnetic behavior of some of the complexes was not carried out.
The diamagnetism of cymantrene and ferrocene moieties distinguishes lanthanide cymantrene- and ferrocene-carboxylates from all of the other Fe-Ln and Mn-Ln heterometallic compounds since their magnetism is caused only by the contribution of Ln3+ ions. The dc magnetic susceptibility for most of the complexes was studied in the temperature range of 2–300 K in an applied magnetic field of 5000 Oe. It was shown that their magnetic behavior was determined by the lanthanide ions, and the χT (300 K) values for all of the compounds agreed satisfactorily with the theoretical values [26].
Among compounds of light lanthanides (Ce-Gd), complexes of Gd3+ are of particular interest due to the electronic structure of this ion: it has the maximum possible number of unpaired electrons (S = 7/2) among 4f-elements. Moreover, it is an isotropic ion with zero contribution from spin-orbital coupling, which considerably facilitates the mathematical description of magnetism for Gd3+ complexes. The experimental χmT(T) dependences for binuclear and polynuclear Gd3+ complexes with the [Gd2O2] core are usually interpreted using equations derived from the Heisenberg–Dirac–Van Vleck Hamiltonian H = −JSGdSGd′ (J: exchange coupling constant) with isotropic spin and the quantum number SGd = SGd′ = 7/2 [27,28].
For binuclear Gd3+ complexes both ferromagnetic and antiferromagnetic interactions with small absolute values J have been observed (below 0.2 cm−1). The ferromagnetic nature of the Gd…Gd interaction was supported by magnetization measurements in the 0–5 T range at 2 K [29]. Relative expanded uncertainties Ur(J) are not presented in the literature (see the references in the work [30] and in Table 1). The fitting procedure leads to Jex, g and (R = Σ[(χm)obs − (χm)calc]2/Σ[(χm)obs]2), which allows one to evaluate Ur(J). Ur(J) must be not less than 10% (±0.01).

Table 1.
The Gd…Gd′ distances and the exchange coupling parameter JGd-Gd′ for [Gd2O2] complexes.
The problem of establishing the magnetostructural correlation for gadolinium complexes with the [Gd2O2] core has been considered earlier [31,32,33]. The experimental data that we obtained for [Gd2(O2CCym)6(THF)4]·THF [15] and [Gd2(O2CCym)6(py)4]·2py [16] and the available sufficiently abundant data for 34 gadolinium complexes with the [Gd2O2] motive allowed us to suggest a correlation between the JGd-Gd′ value and the Gd…Gd distance in the complexes [30]. The determined empirical dependence was satisfactorily approximated by a fourth degree polynomial with R2 = 0.854 [30]. It was found that the antiferromagnetic interaction between the Gd3+ ions weakens with an increase in the distance; at DGd…Gd′ above ~4.10 Å, it changes to ferromagnetic coupling that passes through a maximum (at DGd…Gd′ ≈ 4.25 Å) and approaches zero at DGd…Gd′ > 4.50 Å (Figure 7). The authors [34] also note that within the framework of the [Gd2O2] core, exchange coupling is ferromagnetic when the Gd…Gd distance is larger than ~4.0–4.1 Å, while the exchange coupling is antiferromagnetic when this parameter is smaller.
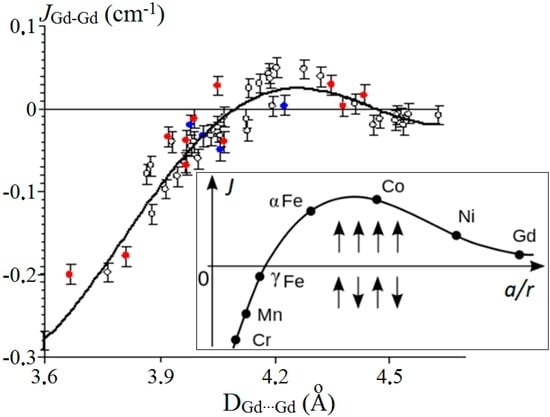
Figure 7.
Approximation of the dependence of JGd-Gd′ vs. Gd…Gd′ distance for 49 [Gd2O2] complexes (o, values used for building of the plot in the work [30]; , values reported in the work [30], but not used for building of the correlation; , newly-added data (Table 1)). The relative expanded uncertainties are shown. Insert: Bethe–Slater curve [35].
The validity of this correlation was confirmed by the data for four [Gd2O2] complexes synthesized by us (marked with asterisks in Table 1 and by blue points in Figure 7) [30]. The plot of the dependence is similar to the Bethe–Slater curve (Figure 7, insert) which represents the magnitude of direct exchange as a function of a/r ratio, where a is the distance between two nearby atoms, and r is the radius of the unfilled electron shell [35].
In the work [30], the results of the studies carried out before the year 2013 were summarized. However, presently, this problem is still under research [34]. Therefore, we decided to supplement the information provided in our earlier work [30] with both our and literature data, which is presented in this paper (Table 1 and red points in Figure 7).
Taking into account additional findings, together with the previously used data, allowed enhancing the reliability of the correlation (R2 = 0.875). As can be seen from Figure 7, these data also confirm the validity of the correlation that we found.
It should be noted that small negative J values are observed in the area of long Gd…Gd distances (Figure 7). This may be due to the influence of factors other than Gd…Gd distance, which we have neglected. However, the relative expanded uncertainty suggests that small positive J values are also possible in this region. The J values corresponding to the longest Gd…Gd distances are very close to zero, as expected.
Furthermore, the following dysprosium compounds were studied: [Dy2(O2CCym)6(DMSO)4] (1), [Dy2(O2CCym)4(NO3)2(DMSO)4] (2), [Dy2(O2CFc)4(NO3)2(DMSO)4] (3), [Dy2(O2CFc)6(DMSO)2(H2O)2]·2DMSO·3MePh (4), [Dy(η2-O2CCym)2(μ-O2CCym)4Dy(H2O)4]n (5), [Dy(O2CCym)(acac)2(H2O)]n (6) and [Dy(fca)3(bpy)]∙MeC6H5 (7).
Binuclear cymantrenecarboxylates 1 were 2 were prepared and structurally characterized earlier [18]; dysprosium ferrocenecarboxylates 3 and 4 are newly obtained.
The cymantrenecarboxylate anion is the core-forming ligand in Compounds 1 and 2, whereas the ferrocenecarboxylate anion plays this role in Structures 3 and 4. Structures 1, 2, 3 and 4 are formed by centrosymmetric dimers (Figure 8).
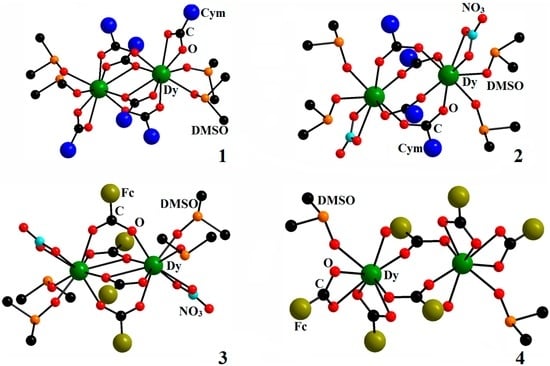
Figure 8.
Molecular structures of Compounds 1 [18] (reproduced with the change in appearance), 2 [18] (reproduced with the change in appearance), 3 and 4.
The coordination number of Dy atoms in Structure 1 is nine. The coordination polyhedron is best described as a three-cap trigonal prism. The structure of the dimer of Compound 2 is similar to the structure of Compound 1 with the replacement of chelate ligands, i.e., the {η2-O2CCym} ligand, for {η2-NO3}. Furthermore, on transition from Compounds 1 to 2, the chelate-bridging {μ-O,η2-O2CCym} cymantrenecarboxylate ligands turn in such a way that they become purely bridging {μ2-O,O′-O2CCym} ligands, which results in a decrease in the CN from nine (1) down to eight (2) and a considerable increase in the Dy…Dy′ distance from 4.0513(6)–4.1775(4) Å, respectively. In Structure 3, two Dy atoms are bound by two bridging and two chelate-bridging O2CFc ligands, similarly to Structure 1. Coordination of Dy is also complemented by a NO3− chelate ion and two oxygen atoms of DMSO molecules (CN = 9); the Dy…Dy′ distance is 4.042 Å. In Structure 4, two Dy atoms are bound by two O2CFc bridging ligands; coordination of Dy is complemented by two O2CFc chelate ligands and two oxygen atoms from molecules of DMSO and water (CN = 8); the Dy…Dy’ distance is 4.376 Å.
DC magnetic measurements were carried out for Complexes 2, 3 and 4 for the first time. The χmT values of complexes at 300 K (Table 2) correspond to two magnetically-isolated free Dy3+ ions (6H15/2, S = 5/2, L = 5, g = 4/3).

Table 2.
Magnetic characteristics of Complexes 1–4.
As the temperature decreases to 100 K, the χmT values of dysprosium complexes weakly depend on temperature, but on further temperature lowering, the absolute values decrease considerably. The minimum values are attained at 2 K (Figure S1, Table 2). This behavior is caused by the splitting of mJ levels in the zero field due to the ligand field effect, by the Zeeman effect under the external field and/or by weak antiferromagnetic coupling between the lanthanide ions.
To explore the presence of the slow relaxation of magnetization in the case of Dy complexes, dynamic measurements of ac magnetic susceptibility as a function of temperature at variable frequencies were performed for polycrystalline powder samples of some complexes in the temperature range of 2–12 K. Such measurements for Complexes 2–4 were also carried out for the first time.
For binuclear complex [Dy2(O2CCym)6(DMSO)4] (1), we have measured the ac magnetic susceptibility in the dc field with the intensities H = 0 and 5 kOe only for three frequencies earlier [18]. In the zero external field, the temperature dependences of the imaginary component contain the frequency-dependent signal and a noticeable increase in χ″, but no distinctly detected maximum was observed. As the field intensity increases to H = 5 kOe, the maximum in the χ″ (T) dependences is observed in the range 4.5–5 K at all frequencies (only three frequencies (100 Hz, 1 kHz and 10 kHz)) at which the measurements were carried out [18].
In this work, Complex 1 was studied in the temperature range of 2–5 K in zero, 1000 and 2000 Oe external fields for a wide range of frequencies (10–10,000 Hz). A frequency-dependent signal χ″ is observed in this temperature range, but the position of the maximum in the χ″(ν) plot does not change with the temperature variation (Figure S2), which may be due to the quantum tunneling effect. On application of the magnetic field with up to an H = 2000 Oe strength, the maximum in the χ″ (T) plot is observed at all of the measurement temperatures, but no shift of the maximum is observed (Figure S3). This behavior of the χ″(ν) plot indicates that slow magnetic relaxation is present, but the effect of quantum tunneling decreases insignificantly upon the application of an external magnetic field.
Furthermore, we carried out studies for binuclear complex [Dy2(O2CCym)4(NO3)2(DMSO)4] (2). For Complex 2, non-zero χ″ values are observed even in the zero field (Figure 9).
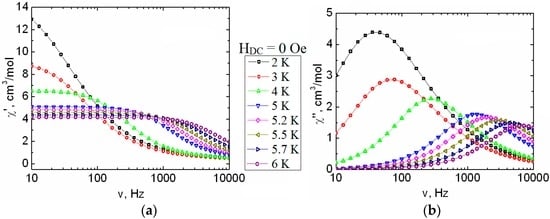
Figure 9.
Frequency dependence of the in-phase (χ′, a) and out-of-phase (χ″, b) parts of ac susceptibility, between 2 and 6 K, for 2 in the zero dc field. Solid lines are visual guides.
The τ vs. T−1 plot for Complex 2 is presented in Figure S4 and Figure 10 (empty squares). Fitting the τ(T−1) plot to the Arrhenius equation in the temperature range of 2–6 K allowed us to determine the potential barrier of magnetization reversal, ΔE/kB = 53 K, and the pre-exponential factor, τ0 = 3.2·10−9 s.
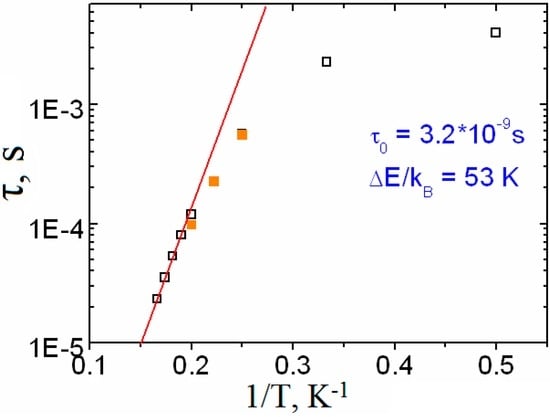
Figure 10.
τ vs. T−1 plot for [Dy2(O2CCym)4(NO3)2(DMSO)4] (2) in a zero (□) and 1000 Oe () dc field. The solid red line is the best fit to the Arrhenius law (τ0 = 3.2 × 10−9 s, ΔE/kB = 53 K) (this study).
The magnetization dynamics of 2 was also studied under an applied dc magnetic field in order to minimize the probability of quantum tunneling (Figure S5). It was found that the external magnetic field did not affect considerably the relaxation processes in Complex 2 (Figure 10).
No non-zero out-of-phase component of ac magnetic susceptibility χ″ was found for Complex 3 at temperatures above 2 K in the frequency range of 10–10,000 Hz, both in the zero magnetic field and under an external magnetic field of 5000 Oe (Figures S6–S8).
In the case of the new complex [Dy2(O2CFc)6(DMSO)2(H2O)2] (4), a frequency-dependent signal χ″ is almost not observed in the zero external field at 2 K. On increasing the dc field strength to H = 2500 Oe, a χ″(ν) growth is observed at all magnetic field strengths applied for the measurements, but no maximum was found on the χ″(ν) plots (Figure S9).
The study of binuclear Complexes 1–4 that we performed has shown that Complex 2 has the best SMM characteristics, whereas no SMM properties were found in Complex 3. Interestingly, the lowering of the coordination number in the corresponding pairs 1 and 2, and 3 and 4 takes place. The results obtained agree with the concept that changes in local molecular symmetry and even insignificant distortion of coordination geometry [41], as well as possible dipole coupling of Dy(III) ions [42] have a considerable effect on SMM characteristics. The enhancement of SMM properties with the lowering of the coordination number observed in our case is in agreement with the recent theoretical study [43].
Studies of polymeric complex [Dy(η2-O2CCym)2(μ-O2CCym)4Dy(H2O)4]n (5) (whose molecular structure is shown in Figure 4) were performed previously [21]. Maxima were observed in the zero field on the frequency dependences of out-of-phase component χ″ at low temperatures (2–3 K), which confirms the presence of slow relaxation of the magnetization (Figure S10). Analysis of the isotherms of frequency dependences gave the relaxation time. Figure S11 shows the dependence of relaxation time on inverse temperature in the temperature range of 2.0–3.5 K. Using the Arrhenius law τ = τ0∙exp(ΔE/kBT), the pre-exponential factor (τ0 = 4.3 × 10−6 s) and the relaxation energy barrier (ΔE/kB = 4.1 K) were determined. The shape of ln(τ) vs. (1/T) and χ″(χ′) plots (Figure S12) allow us to believe that relaxation is thermally activated and that a purely quantum mode takes place below the temperature studied (T < 2 K). A unit of the polymeric chain [Dy(η2-O2CCym)2(μ-O2CCym)4Dy(H2O)4]n (5) contains two Dy atoms, one of which coordinates four O atoms of {μ-O2CCym) ligands and four O atoms of H2O molecules (Figure 4). The second Dy atom coordinates four O atoms of {μ-O2Ccym} and four O atoms of {η2-O2CCym} ligands. The coordination number of Dy atoms is eight; the {Dy(μ-O2CCym)4(H2O)4} polyhedron is a two-cap trigonal prism. The {Dy(η2-O2CCym)2(μ-O2CCym)4} polyhedron is strongly distorted and is most similar to a trigonal dodecahedron with the central segments of the trapezohedra occupied by η2-O2C moieties. It has been shown [44] that the existence of magnetic centers with differing anisotropy can give rise to two different mechanisms of magnetic relaxation that correspond to two different positions of dysprosium atoms. Though Structure 5 contains two crystallographically different Dy centers, studies have shown that only one mechanism of thermally-activated magnetic relaxation is present.
The structure of a polymeric complex [Dy(O2CCym)(acac)2(H2O)]n (6) is formed by polymeric chains (Figure 5); the coordination number of Dy is seven; the polyhedron is a pentagonal bipyramid. Previously, incomplete study of this complex was carried out [21]. The temperature dependences of the out-of-phase alternating-current (ac) magnetic susceptibility in the zero external magnetic field were obtained. However, no application of an external magnetic field was made. In this study, the dynamics of the magnetization was probed by ac susceptibility measurements for Complex 6. At 2 K, an ac relaxation mode for 6 appears around 2000 Oe. From the complete study of the ac susceptibility as a function of temperature and frequency at 2000 Oe (Figure 11), the characteristic relaxation time of the magnetization was estimated between 2 and 10 K (Figure S15). As shown by the non-thermally-activated dependence of the relaxation time in this temperature range, quantum tunneling of the magnetization is obviously dominating the relaxation process in 6 even under the applied dc field. Nevertheless, an attempt to extrapolate the Arrhenius behavior above 10 K leads to a rough estimation of the SMM energy gap of about 42 K, with a pre-exponential factor of 4.3 × 10−7 s. The value of τ0, which is at least four orders of magnitude larger than expected for typical vibrations of the network, further confirms that the estimation value of ΔE/kB should be considered as a lower limit of the actual energy barrier for the thermally-activated relaxation process in 6.
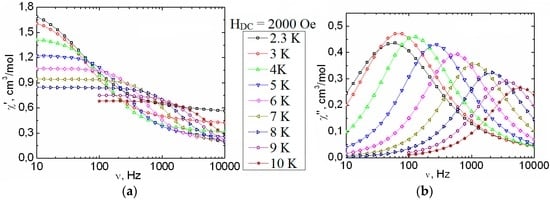
Figure 11.
Frequency dependence of the in-phase (χ′, a) and out-of-phase (χ″, b) parts of ac susceptibility, between 2 and 10 K, for 6 in a 2000 Oe dc field. Solid lines are visual guides.
To give a fuller picture, we also present our data [24] for ferrocenoylacetonate [Dy(fca)3(bpy)]∙MeC6H5 (7). The structure of 7 contains the [Dy(fca)3(bpy)] complex (Figure 6) and solvate molecules of MeC6H5. Bpy…bpy stacking interactions bind complexes into centrosymmetric dimers. The solvate molecule of MeC6H5 that is arranged in rather a spacious cavity is not involved in stacking interactions. Detailed studies of dc and ac magnetic susceptibility were carried out. SMM properties were detected at temperatures up to 32 K. Most likely, owing to the electron-donating effect of ferrocenyl moieties [45,46], the complex has an extremely high magnetization reversal barrier, Δeff/kB = 241 K, which is a record value for lanthanide β-diketonates. This result illustrates the importance of the effect of the crystal field on the SMM properties of dysprosium complexes.
3. Experimental Section
3.1. Materials and Methods
The following commercial reagents and solvents were used for the syntheses: hydrated dysprosium salts Dy(NO3)3 5H2O, DyCl3.6H2O and acetylacetonate Dy(acac)3·3H2O, from Alfa Aesar (Heysham, Lancashire, UK), cymantrene from Aldrich (St. Louls, MO, USA), acetylferrocene (Alfa Aesar, 97%) and solvents (MeOH, DMSO, C6H5Me, CHCl3, C2H5OH) from Alfa Aesar. Cymantrenecarboxylic acid was synthesized according to a known procedure by the reaction of cymantrenyllithium obtained from n-butyllithium and cymantrene in THF at −45 °C, with solid CO2 [47]. Before use in the synthesis, cymantrenecarboxylic acid was sublimed in vacuo to remove traces of Mn2+. Methanol was dehydrated before use by distillation over magnesium; toluene was successively distilled over P2O5 and sodium; DMSO was purified by freezing.
Magnetic susceptibility measurements were performed with the use of a Quantum Design magnetometer/susceptometer PPMS-9 (Quantum Design, San Diego, CA, USA). This instrument works between 1.8 and 350 K for dc applied fields ranging from −9 to 9 T. For ac susceptibility measurements, an oscillating ac field of 1 or 5 Oe with a frequency between 10 and 10,000 Hz was employed. Measurements were performed on polycrystalline samples sealed in polyethylene bags and covered with mineral oil in order to prevent field-induced torqueing of the crystals. The magnetic data were corrected for the sample holder, mineral oil and diamagnetic contribution.
X-ray powder diffraction analysis was carried out on a Bruker D8 ADVANCE X-ray diffractometer (CuKα, Ni-filter, LYNXEYE detector, reflection geometry) (Bruker, Karslruhe, Germany).
Experimental data from single crystals were obtained on a Bruker SMART APEX2 diffractometer [48] (Table S1). Absorption for 3 and 4 was taken into account by a semiempirical method based on equivalents using SADABS software [49]. For Compound 3, the model of the isostructural Tb complex was used [23]. The positions of hydrogen atoms were calculated from geometrical considerations and refined using the “riding” model. The structure of 4 was determined using a combination of the direct method and Fourier syntheses. The structures of 3 and 4 were refined by the full-matrix anisotropic-isotropic least squares method. All of the calculations were carried out using SHELXS-2014 and SHELXL-2014 software [50]. CCDC 1493047 and 1493048 contain the supplementary crystallographic data for Compounds 3 and 4. These data can be obtained free of charge via http://www.ccdc.cam.ac.uk/conts/retrieving.html or from the Cambridge Crystallographic Data Centre, 12 Union Road, Cambridge CB2 1EZ, U.K.; fax: (+44) 1223-336-033; or e-mail: deposit@ccdc.cam.ac.uk.
3.2. Synthesis of Complexes 1–4
Dysprosium complexes [Dy2(O2CCym)6(DMSO)4] (1), [Dy2(O2CCym)4(NO3)2(DMSO)4] (2) and [Dy(O2CCym)(acac)2(H2O)]n (5) were synthesized using the procedures that we developed previously [18,22]. The complex [Dy2(O2CFc)4(NO3)2(DMSO)4] (3) was prepared according to the procedure used for the synthesis of its Gd and Tb isostructural analogs [23]. The complex [Dy2(O2CFc)6(DMSO)2(H2O)2]∙2DMSO∙3MePh (4) was obtained according to the procedure reported previously for the complex [Gd2(O2CFc)6(DMSO)2(H2O)2]·2DMSO·2CH2Cl2 [23], except that boiling toluene (25 mL) was used for the extraction of the substance, and the resulting solution was kept at 4 °C for two days.
4. Conclusions
In summary, we have obtained new findings on the magnetism of the lanthanide complexes with stable organometallic ligands. The analysis of complementary data on exchange coupling in binuclear complexes of gadolinium with two bridging oxygen atoms has shown the validity of the correlation between JGd-Gd′ and the Gd…Gd distance that we suggested earlier.
Dynamic ac magnetic susceptibility measurements have shown that the presence of more than one dysprosium atom in a molecule adversely affects the molecular magnet properties, since, as a rule, SMM properties in polynuclear SMM are demonstrated by each lanthanide atom rather than by the exchange coupled systems as in complexes of d-elements. A considerable drawback of polynuclear lanthanide complexes lies in the existence of dipole-dipole coupling that accelerates relaxation processes and in their tendency to quantum tunneling, which noticeably decreases the real relaxation times. Furthermore, SMM characteristics are considerably affected by changes in local molecular symmetry and even insignificant distortion of coordination geometry. It has been shown also that the increase of the coordination number weakens the SMM properties of similar Dy complexes.
Supplementary Materials
The following are available online at www.mdpi.com/2312-7481/2/4/38/s1. Table S1: Crystal data and structure refinement for 3, 4, Figure S1: Plots of χT vs. temperature for 1–4 (, 1 [18]; ▲, 2; , 3; , 4). The measurements were carried out in an external magnetic field H = 5000 Oe, Figure S2: Frequency dependences of the in-phase (χ′, a) and out-of-phase (χ″, b) parts of the ac susceptibility, between 2 and 6 K, for [Dy2(O2CCym)6(DMSO)4] (1) in the zero dc field (this study). Solid lines are visual guides, Figure S3: Frequency dependences of the in-phase (χ′, a) and out-of-phase (χ″, b) parts of the ac susceptibility, at 2 K, for [Dy2(O2CCym)6(DMSO)4] (1) in the zero, 1000 and 2000 Oe dc field (this study). Solid lines are visual guides, Figure S4: τ vs. T−1 plot for [Dy2(O2CCym)4(NO3)2(DMSO)4] (2) in the zero magnetic field. The solid red line is the best fit to the Arrhenius law (τ0 = 3.2·10−9 s, ΔE/kB = 53 K) (this study), Figure S5: Frequency dependences of the in-phase (χ′, a) and out-of-phase (χ″, b) parts of the ac susceptibility, between 4 and 5 K, for [Dy2(O2CCym)4(NO3)2(DMSO)4] (2) in a 1000 Oe dc field (this study). Solid lines are visual guides, Figure S6: Frequency dependences of the in-phase (χ′, a) and out-of-phase (χ″, b) parts of the ac susceptibility, between 2 and 4 K, for [Dy2(O2CFc)4(NO3)2(DMSO)4] (3) in the zero dc field (this study). Solid lines are visual guides, Figure S7: Frequency dependences of the in-phase (χ′, a) and out-of-phase (χ″, b) parts of the ac susceptibility, between 2 and 24 K, for [Dy2(O2CFc)4(NO3)2(DMSO)4] (3) in a 5000 Oe dc field (this study). Solid lines are visual guides, Figure S8: Frequency dependences of the in-phase (χ′, a) and out-of-phase (χ″, b) parts of the ac susceptibility, at 2 K, for [Dy2(O2CFc)4(NO3)2(DMSO)4] (3) in the zero, 500, 1000 and 1500 Oe dc field (this study). Solid lines are visual guides, Figure S9: Frequency dependences of the in-phase (χ′, a) and out-of-phase (χ″, b) parts of the ac susceptibility, at 2 K, for [Dy2(O2CFc)6(DMSO)2(H2O)2] (4) in the zero, 1000, 1500, 2000 and 2500 Oe dc-field (this study). Solid lines are visual guides, Figure S10: Frequency dependences of the in-phase (a) and out-of-phase (b) parts of the ac susceptibility of [Dy(η2-O2CCym)2(μ-O2CCym)4Dy(H2O)4]n (5) (Hdc = 0 Oe) [21], Figure S11: Plot of ln(τ) vs. 1/T [Dy(η2-O2CCym)2(μ-O2CCym)4Dy(H2O)4]n (5) obtained from the frequency dependences of χ″ in the zero magnetic field [21], Figure S12: Cole-Cole dependence for [Dy2(O2CCym)6(H2O)4]n (5) (HDC = 0 Oe), Figure S13: Frequency dependences of the in-phase (a) and out-of-phase (b) parts of the ac susceptibility of [Dy(CymCO2)(acac)2(H2O)]n (6) (Hdc = 0 Oe) (this study), Figure S14: Frequency dependences of out-of-phase (χ″) parts of the ac susceptibility at 2.3 K, for [Dy(CymCO2)(acac)2(H2O)]n (6) in the zero, 1000 and 2000 Oe dc field (this study). Solid lines are visual guides, Figure S15: τ vs. T−1 plot for [Dy(CymCO2)(acac)2(H2O)]n (6) in a 2000 Oe dc field. The solid red line is the best fit to the Arrhenius law (this study).
Acknowledgments
This study was financially supported by the Russian Science Foundation (Grant 14-13-00938).
Author Contributions
P.S.K. and A.V.G. synthesized the complexes. N.N.E. and P.S.K. performed the experiments. A.B.I performed the structural experiments. Z.V.D. conceived of and designed the experiments. Z.V.D., P.S.K. and N.N.E. wrote the paper. V.M.N. supervised and managed the project.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Caneschi, A.; Gatteschi, R.; Sessoli, R.; Barra, A.L.; Brunel, L.C.; Guillot, M. Alternating current susceptibility, high field magnetization, and millimeter band EPR evidence for a ground S = 10 state in [Mn12O12(CH3COO)16(H2O)4]∙2CH3COOH∙4H2O. J. Am. Chem. Soc. 1991, 113, 5873–5874. [Google Scholar] [CrossRef]
- Sessoli, R.; Gatteschi, D.; Caneschi, A.; Novak, M.A. Magnetic bistability in a metal-ion cluster. Nature 1993, 365, 141–142. [Google Scholar] [CrossRef]
- Sessoli, R.; Powell, A.K. Strategies towards single molecule magnets based on lanthanide ions. Coord. Chem. Rev. 2009, 253, 2328–2341. [Google Scholar] [CrossRef]
- Bünzli, J.-C.G. Lanthanide coordination chemistry: From old concepts to coordination polymers. J. Coord. Chem. 2014, 67, 3706–3733. [Google Scholar] [CrossRef]
- Castro, G.; Regueiro-Figueroa, M.; Esteban-Gomez, D.; Perez-Lourido, P.; Platas-Iglesias, C.; Valencia, L. Magnetic anisotropies in rhombic lanthanide(III) complexes do not conform to bleaney’s theory. Inorg. Chem. 2016, 55, 3490–3497. [Google Scholar] [CrossRef] [PubMed]
- Gregson, M.; Chilton, N.F.; Ariciu, A.-M.; Tuna, F.; Crowe, I.F.; Lewis, W.; Blake, A.J.; Collison, D.; McInnes, E.J.L.; Winpenny, R.E.P.; et al. A Monometallic Lanthanide Bis(methanediide) Single molecule magnet with a large energy barrier and complex spin relaxation behaviour. Chem. Sci. 2016, 7, 155–165. [Google Scholar] [CrossRef]
- Pointillart, F.; Guizouarn, T.; Lefeuvre, S.; Golhen, S.; Cador, O.; Ouahab, L. Rational design of a lanthanide-based complex featuring Different single-molecule magnets. Chem. Eur. J. 2015, 21, 16929–16934. [Google Scholar] [CrossRef] [PubMed]
- Anastasiadis, N.C.; Kalofolias, D.A.; Philippidis, A.; Tzani, S.; Raptopoulou, C.P.; Psycharis, V.; Milios, C.J.; Escuer, A.; Perlepes, S.P. A family of dinuclear lanthanide(III) complexes from the use of a tridentate Schiff base: Structural and physical studies, and the case of a DyIII2 emissive single-molecule magnet. Dalton Trans. 2015, 44, 10200–10209. [Google Scholar] [CrossRef] [PubMed]
- Yatoo, M.A.; Cosquer, G.; Morimoto, M.; Irie, M.; Breedlove, B.K.; Yamashita, M. 1D chains of lanthanoid ions and a dithienylethene ligand showing slow relaxation of the magnetization. Magnetochemistry 2016, 2, 21–28. [Google Scholar] [CrossRef]
- Huang, C. Rare Earth Coordination Chemistry: Fundamentals and Applications; John Wiley & Sons: Singapore, 2010. [Google Scholar]
- Woodruff, D.N.; Winpenny, R.E.P.; Layfield, R.A. Lanthanide Single-Molecule Magnets. Chem. Rev. 2013, 113, 5110–5148. [Google Scholar] [CrossRef] [PubMed]
- Chilton, N.F.; Langley, S.K.; Moubaraki, B.; Soncini, A.; Batten, S.R.; Murray, K.S. Single molecule magnetism in a family of mononuclear β-diketonate lanthanide(III) complexes: Rationalization of magnetic anisotropy in complexes of low symmetry. Chem. Sci. 2013, 4, 1719–1730. [Google Scholar] [CrossRef]
- Mereacre, V.; Schlageter, M.; Powell, A.K. A temperature induced ferrocene-ferrocenium interconversion in a ferrocene functionalized μ3-O chromium carboxylate. J. Magn. Magn. Mater. 2015, 381, 478–480. [Google Scholar] [CrossRef]
- Mereacre, V.; Schlageter, M.; Eichhöfer, A.; Bauer, T.; Wolny, J.A.; Schünemann, V.; Powell, A.K. Unusual metal-ligand charge transfer in ferrocene functionalized μ3-O iron carboxylates observed with Mössbauer spectroscopy. J. Magn. Magn. Mater. 2016, 407, 87–91. [Google Scholar] [CrossRef]
- Koroteev, P.S.; Kiskin, M.A.; Dobrokhotova, Z.V.; Bogomyakov, A.M.; Efimov, N.N.; Novotortsev, V.M. Synthesis, structure, solid-state thermal decomposition and magnetic properties of binuclear Nd, Gd and Eu cymantrenecarboxylates. Polyhedron 2011, 30, 2523–2529. [Google Scholar] [CrossRef]
- Koroteev, P.S.; Dobrokhotova, Z.V.; Kiskin, M.A.; Lermontov, A.S.; Efimov, N.N.; Bogomyakov, A.S.; Tyurin, A.V.; Bykov, M.A.; Demina, L.I.; Velikodny, Y.A.; et al. Synthesis, structure, thermal behavior, thermodynamic, magnetic and luminescent properties of Pr, Sm, Eu, and Gd cymantrenecarboxylates. Polyhedron 2012, 43, 36–46. [Google Scholar] [CrossRef]
- Koroteev, P.S.; Dobrokhotova, Z.V.; Ilyukhin, A.B.; Motornova, M.S.; Novotortsev, V.M. Synthesis, structure, solid-state thermolysis, and catalytic properties of binuclear Ce, Nd, Eu, and Gd cymantrenecarboxylate complexes with DMSO. Russ. Chem. Bull. 2012, 61, 1069–1078. [Google Scholar] [CrossRef]
- Koroteev, P.S.; Efimov, N.N.; Dobrokhotova, Z.V.; Ilyukhin, A.B.; Gavrikov, A.V.; Novotortsev, V.M. Binuclear and polynuclear cymantrenecarboxylate complexes of heavy lanthanides. Russ. J. Coord. Chem. 2015, 41, 149–161. [Google Scholar] [CrossRef]
- Koroteev, P.S.; Dobrokhotova, Z.V.; Ilyukhin, A.B.; Efimov, N.N.; Kirdyankin, D.I.; Tyurin, A.V.; Velikodny, A.Y.; Kovba, M.L.; Novotortsev, V.M. Lanthanide cymantrenecarboxylate complexes with an Ln:Mn ratio of 1:2 as precursors for LnMn2O5 phases. Synthesis, structure, physicochemical properties, and thermal decomposition. Polyhedron 2013, 65, 110–121. [Google Scholar] [CrossRef]
- Koroteev, P.S.; Dobrokhotova, Z.V.; Ilyukhin, A.B.; Efimov, N.N.; Kirdyankin, D.I.; Tyurin, A.V.; Gavrikov, A.V.; Novotortsev, V.M. Polymeric lanthanide acetates with peripheral cymantrenecarboxylate groups—Synthesis, magnetism and thermolysis. Polyhedron 2015, 85, 941–952. [Google Scholar] [CrossRef]
- Koroteev, P.S.; Dobrokhotova, Z.V.; Ilyukhin, A.B.; Efimov, N.N.; Gavrikov, A.V.; Novotortsev, V.M. Polymer lanthanide cymantrenecarboxylates. Russ. J. Coord. Chem. 2015, 41, 805–816. [Google Scholar] [CrossRef]
- Gavrikov, A.V.; Koroteev, P.S.; Dobrokhotova, Z.V.; Ilyukhin, A.B.; Efimov, N.N.; Kirdyankin, D.I.; Bykov, M.A.; Ryumin, M.A.; Novotortsev, V.M. Novel heterometallic polymeric lanthanide acetylacetonates with bridging cymantrenecarboxylate groups—Synthesis, magnetism and thermolysis. Polyhedron 2015, 102, 48–59. [Google Scholar] [CrossRef]
- Koroteev, P.S.; Dobrokhotova, Z.V.; Efimov, N.N.; Ilyukhin, A.B.; Novotortsev, V.M. New binuclear ferrocenecarboxylates of rare-earth metals as precursors for ferrites: Syntheses, structures, and solid-phase thermolysis. Russ. J. Coord. Chem. 2014, 40, 495–504. [Google Scholar] [CrossRef]
- Koroteev, P.S.; Dobrokhotova, Z.V.; Ilyukhin, A.B.; Efimov, N.N.; Rouzieres, M.; Kiskin, M.; Clerac, R.; Novotortsev, V.M. Synthesis, structure, and physical properties of new rare earth ferrocenoylacetonates. Dalton Trans. 2016, 45, 6405–6417. [Google Scholar] [CrossRef] [PubMed]
- Koroteev, P.S.; Dobrokhotova, Z.V.; Ilyukhin, A.B.; Efimov, N.N.; Novotortsev, V.M. Synthesis, structure, and magnetic properties of lanthanide ferrocenoylacetonates with nitrate and 2,2′-bipyridine ligands. J. Coord. Chem. 2016, 69, 2723–2735. [Google Scholar] [CrossRef]
- Benelli, C.; Gatteschi, D. Magnetism of lanthanides in molecular materials with transition-metal ions and organic radicals. Chem. Rev. 2002, 102, 2369–2387. [Google Scholar] [CrossRef] [PubMed]
- Kahn, O. Molecular Magnetism; Wiley-Blackwell: New York, NY, USA, 1993; p. 380. [Google Scholar]
- Panagiotopoulos, A.; Zafiropoulos, T.F.; Perlepes, S.P.; Bakalbassis, E.; Masson-Ramade, I.; Kahn, O.; Terzis, A.; Raptopoulou, C.P. Molecular structure and magnetic mroperties of acetato-bridged lanthanide(III) dimers. Inorg. Chem. 1995, 34, 4918–4920. [Google Scholar] [CrossRef]
- Costes, J.P.; Clemente-Juan, J.M.; Dahan, F.; Nicodeme, F.; Verelst, M. Unprecedented Ferromagnetic Interaction in Homobinuclear Erbium and Gadolinium Complexes: Structural and Magnetic Studies. Angew. Chem. Int. Ed. 2002, 41, 323–325. [Google Scholar] [CrossRef]
- Koroteev, P.S.; Efimov, N.N.; Dobrokhotova, Z.V.; Fomina, I.G.; Ilyukhin, A.B.; Eremenko, I.L.; Novotortsev, V.M. Magnetostructural correlation for the Gd complexes with bridging oxygen. Russ. Chem. Bull. Int. Ed. 2013, 62, 1768–1771. [Google Scholar] [CrossRef]
- John, D.; Urland, W. Crystal Structure and Magnetic Behaviour of the New Gadolinium Carboxylates Gd2(ClF2CCOO)6(hypy)2, Gd2(F3CCOO)6(hypy)2, Gd2(F2HCCOO)6(hypy)2 and Gd2(Cl2HCCOO)6(H2O)2(hypy)2. Eur. J. Inorg. Chem. 2006, 3503–3509. [Google Scholar] [CrossRef]
- Roy, L.E.; Hughbanks, T. Magnetic Coupling in Dinuclear Gd Complexes. J. Am. Chem. Soc. 2006, 128, 568–575. [Google Scholar] [CrossRef] [PubMed]
- Cañadillas-Delgado, L.; Fabelo, O.; Cano, J.; Pasán, J.; Delgado, F.S.; Lloret, F.; Julve, M.; Ruiz, C. Dinuclear and two- and three-dimensional gadolinium(III) complexes with mono- and dicarboxylate ligands: Synthesis, structure and magnetic properties. CrystEngComm 2009, 11, 2131–2142. [Google Scholar] [CrossRef]
- Ito, M.; Hamada, D.; Ono, H.; Matsumoto, N.; Sunatsuki, Y.; Re, N. Binuclear tetra-acetate bridged Gd(III) complex [Gd2(μ2-O2CMe)4(H2L)2](ClO4)2·2H2O·2MeOH (H2L = bis(5-methylimidazol-4-yl-methyliden eamino propyl)methylamine): Synthesis, structure, and magnetic properties. Inorg. Chim. Acta 2016, 443, 274–278. [Google Scholar] [CrossRef]
- Tumanski, S. Handbook of Magnetic Measurements; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2011; p. 62. [Google Scholar]
- Bag, P.; Rastogi, C.K.; Biswas, S.; Sivakumar, S.; Mereacre, V.; Chandrasekhar, V. Homodinuclear lanthanide {Ln2} (Ln = Gd, Tb, Dy, Eu) complexes prepared from an o-vanillin based ligand: Luminescence and single-molecule magnetism behavior. Dalton Trans. 2015, 44, 4328–4340. [Google Scholar] [CrossRef] [PubMed]
- Long, J.; Habib, F.; Lin, P.; Korobkov, I.; Enright, G.; Ungur, L.; Wernsdorfer, W.; Chibotaru, L.F.; Murugesu, M. Single-molecule magnet behavior for an antiferromagnetically superexchange-coupled dinuclear dysprosium(III) complex. J. Am. Chem. Soc. 2011, 133, 5319–5328. [Google Scholar] [CrossRef] [PubMed]
- Sakamoto, S.; Fujinami, T.; Nishi, K.; Matsumoto, N.; Mochida, N.; Ishida, T.; Sunatsuki, Y.; Re, N. Carbonato-Bridged NiII2LnIII2 (LnIII = GdIII, TbIII, DyIII) Complexes Generated by Atmospheric CO2 Fixation and Their Single-Molecule-Magnet Behavior: [(μ4-CO3)2{NiII(3-MeOsaltn)(MeOH or H2O)LnIII(NO3)}2]·solvent [3-MeOsaltn = N,N′-Bis(3-methoxy-2-oxybenzylidene)-1,3-propanediaminato]. Inorg. Chem. 2013, 52, 7218–7229. [Google Scholar] [PubMed]
- Ehama, K.; Ohmichi, Y.; Sakamoto, S.; Fujinami, T.; Matsumoto, N.; Mochida, N.; Ishida, T.; Sunatsuki, Y.; Tsuchimoto, M.; Re, N. Synthesis, Structure, Luminescent, and Magnetic Properties of Carbonato-Bridged ZnII2LnIII2 Complexes [(μ4-CO3)2{ZnIILnLnIII(NO3)}2] (LnIII = GdIII, TbIII, DyIII; L1 = N,N′-Bis(3-methoxy-2-oxybenzylidene)-1,3-propanediaminato, L2 = N,N′-Bis(3-ethoxy-2-oxybenzylidene)-1,3-propanediaminato). Inorg. Chem. 2013, 52, 12828–12841. [Google Scholar] [PubMed]
- Koroteev, P.S.; Ilyukhin, A.B.; Efimov, N.N.; Minin, V.V.; Tyurin, A.V.; Dobrokhotova, Z.V.; Novotortsev, V.M. Charge transfer adducts of binuclear rare earth 3,5-dinitrobenzoates with N,N-dimethylaniline and toluene. Polyhedron 2015, 89, 238–249. [Google Scholar] [CrossRef]
- Katoh, K.; Horii, Y.; Yasuda, N.; Wernsdorfer, W.; Toriumi, K.; Breedlove, B.K.; Yamashita, M. Multiple-decker phthalocyaninato dinuclear lanthanoid(III) single-molecule magnets with dual-magnetic relaxation processes. Dalton Trans. 2012, 41, 13582–13600. [Google Scholar] [CrossRef] [PubMed]
- Katoh, K.; Asano, R.; Miura, A.; Horii, Y.; Morita, T.; Breedlove, B.K.; Yamashita, M. Effect of f–f interactions on quantum tunnelling of the magnetization: Mono- and dinuclear Dy(III) phthalocyaninato triple-decker single-molecule magnets with the same octacoordination environment. Dalton Trans. 2014, 43, 7716–7725. [Google Scholar] [CrossRef] [PubMed]
- Ungur, L.; Chibotaru, L.F. Strategies toward High-Temperature Lanthanide-Based Single-Molecule Magnets. Inorg. Chem. 2016. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Xu, G.; Gamez, P.; Zhao, L.; Lin, S.; Deng, R.; Tang, J.; Zhang, H. Two-step relaxation in a linear tetranuclear dysprosium(III) aggregate showing single-molecule magnet behavior. J. Am. Chem. Soc. 2010, 132, 8538–8539. [Google Scholar] [CrossRef] [PubMed]
- McKinney, J.D.; Anderson, P.A.; Hamor, T.A.; Jones, C.J.; Paxton, K.; Porch, A. The synthesis, solid state conductivity and X-ray crystal structure of [Fe{η5-C5H5)(E-η5-C5H4–CH=CH-9-C16H9)][1,4-{(CN)2C=}2C6H4]. J. Organomet. Chem. 1998, 558, 147–153. [Google Scholar] [CrossRef]
- Perevalova, É.G.; Grandberg, K.I.; Zharikova, N.A.; Gubin, S.P.; Nesmeyanov, A.N. Electronic influence of ferrocenyl as a substituent. Russ. Chem. Bull. 1966, 15, 796–802. [Google Scholar] [CrossRef]
- Nesmeyanov, A.N.; Anisimov, K.N.; Kolobova, N.E.; Makarov, Y.V. Metalation of cyclopentadienyltricarbonylmanganese. Russ. Chem. Bull. 1968, 17, 672. [Google Scholar] [CrossRef]
- Bruker. APEX2 and SAINT; Bruker AXS Inc.: Madison, WI, USA, 2007. [Google Scholar]
- Sheldrick, G.M. SADABS; University of Göttingen: Göttingen, Germany, 1997. [Google Scholar]
- Sheldrick, G. Crystal structure refinement with SHELXL. Acta Crystallogr. Sect. C 2015, 71, 3–8. [Google Scholar] [CrossRef] [PubMed]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).