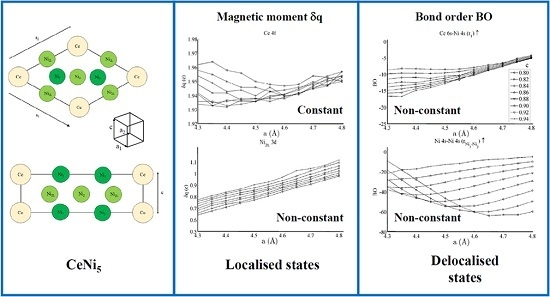
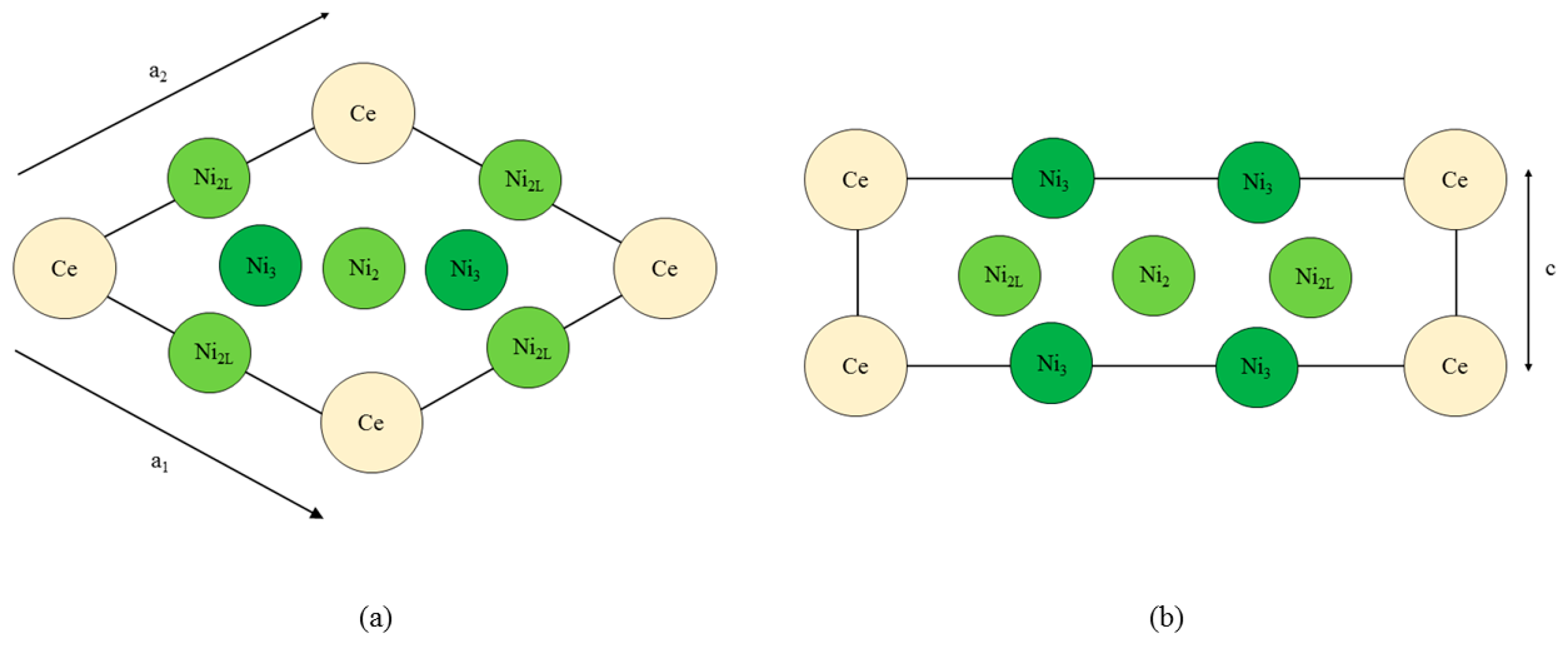
Strain Engineering of the CeNi5 System
Abstract
:1. Introduction
2. Theory
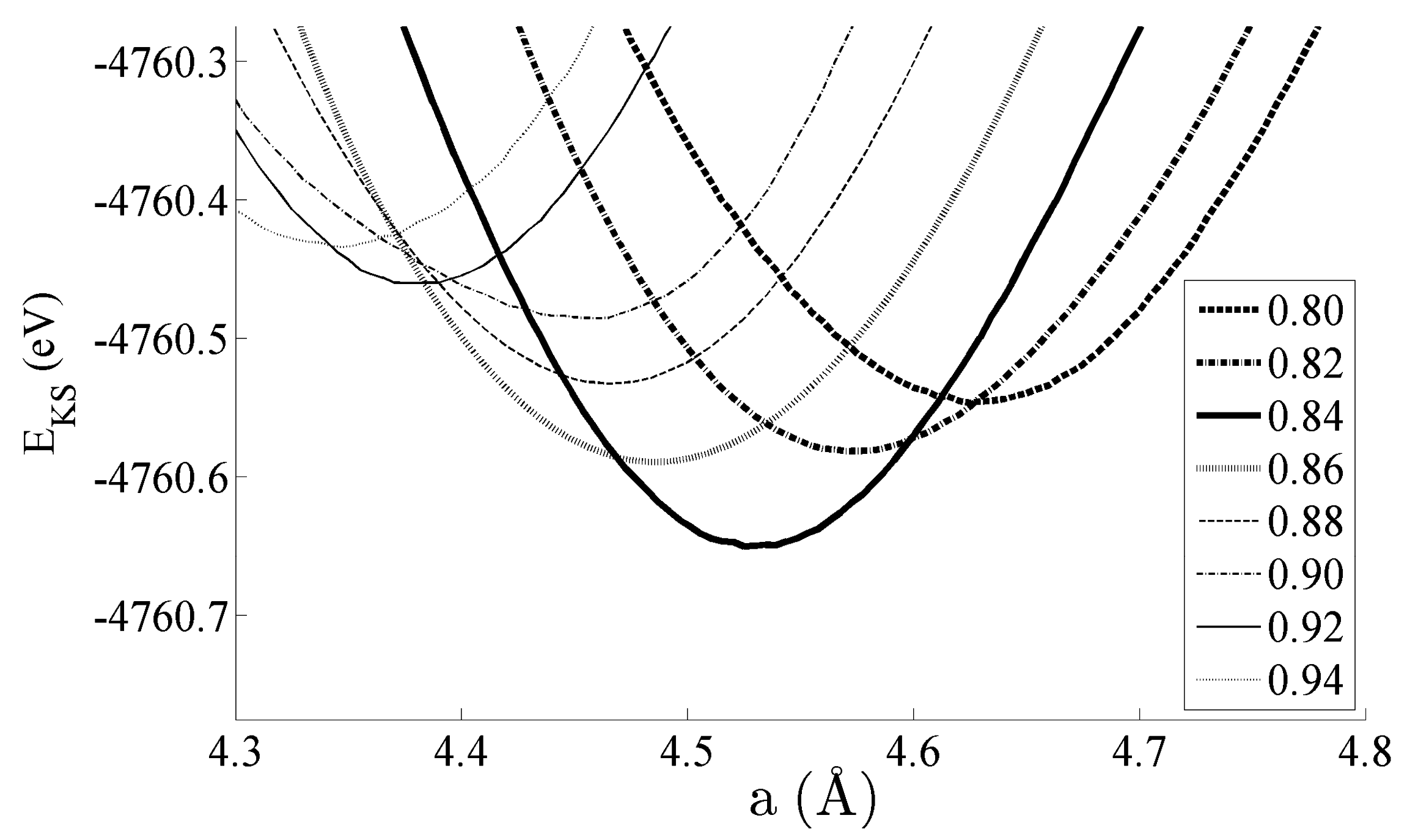
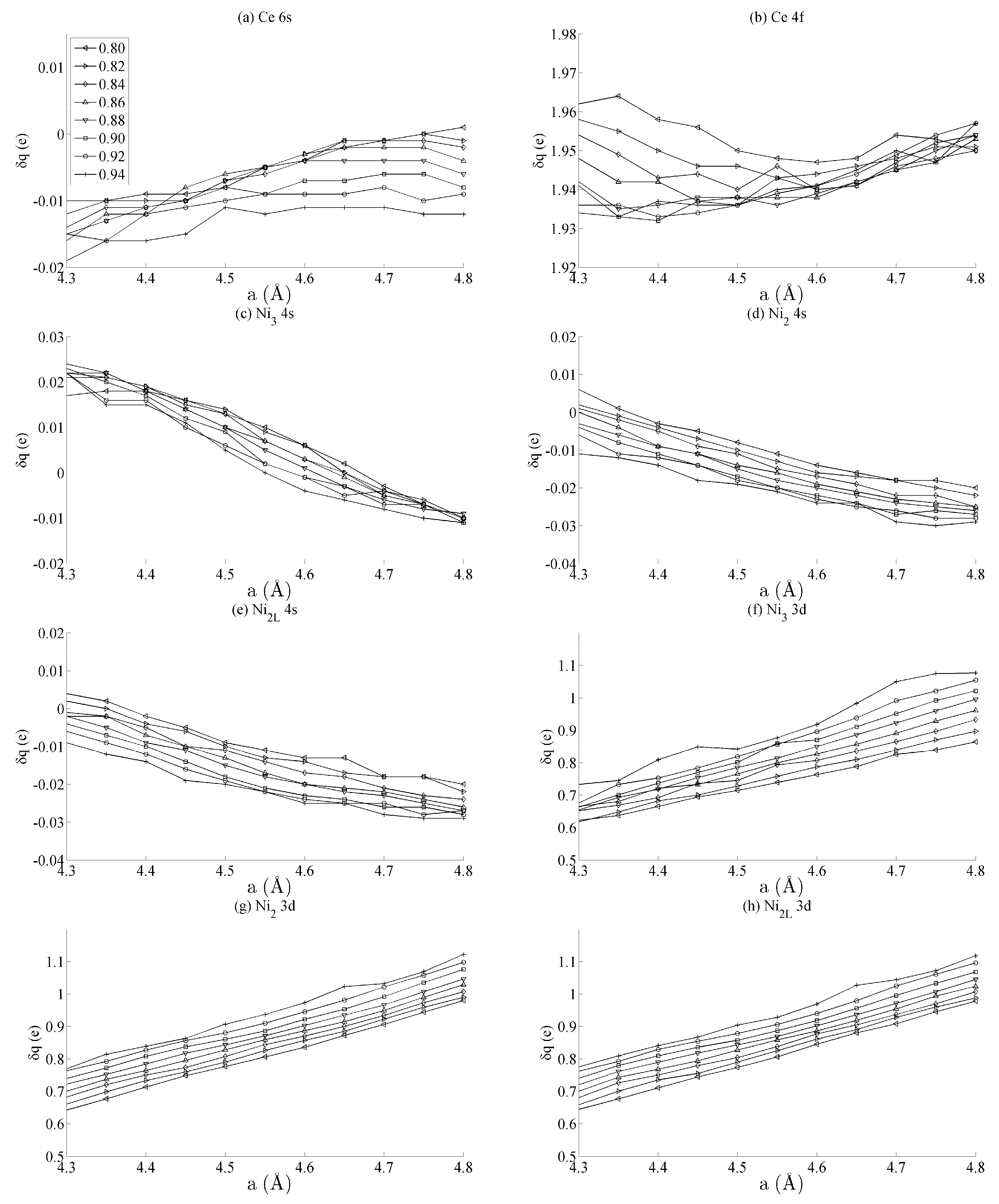
3. Results and Discussion
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Dantzer, P. Properties of intermetallic compounds suitable for hydrogen storage applications. Mater. Sci. Eng. A 2002, 329–331, 313–320. [Google Scholar] [CrossRef]
- Wang, J.; Jorda, J.L.; Pisch, A.; Flükiger, R. Experimental study of the CeNi5-CeCu5 system. Intermetallics 2006, 14, 695–701. [Google Scholar] [CrossRef]
- Nordstrom, L.; Brooks, M.S.S.; Johansson, B. Theoretical study of the enhanced paramagnetism in CeNix (x = 1, 2, and 5). Phys. Rev. B 1992, 46, 3458–3464. [Google Scholar] [CrossRef]
- Gignoux, D.; Givord, F.; Lemaire, R.; Tasset, F. Thermal dependence of the susceptibility densities in CeNi5. J. Phys. Colloq. 1982, 43, 257–261. [Google Scholar] [CrossRef]
- Grechnev, G.E.; Logosha, A.V.; Panfilov, A.S.; Kuchin, A.G.; Vasijev, A.N. Effect of pressure on the magnetic properties of YNi5, LaNi5, and CeNi5. Low Temp. Phys. 2011, 37, 138–143. [Google Scholar] [CrossRef]
- Knyazev, Y.V.; Kuz’min, Y.I.; Kuchin, A.G. Optical properties of CeNi5 and CeNi4M (M = Al, Cu) compounds. J. Alloys Compd. 2011, 509, 557–559. [Google Scholar] [CrossRef]
- Coldea, M.; Andreica, D.; Bitu, M.; Crisan, V. Spin fluctuations in YNi5 and CeNi5. J. Magn. Magn. Mater. 1996, 157–158, 627–628. [Google Scholar] [CrossRef]
- Reiffers, M.; Della Mea, M.; Bauer, E.; Pristáš, G. Pressure and field effects on spin fluctuations in CeNi5. J. Magn. Magn. Mater. 2004, 272–276, 605–607. [Google Scholar] [CrossRef]
- Moriya, T.; Takahashi, Y. Spin fluctuations in itinerant electron magnetism. J. Phys. Colloq. 1978, 39, 1466–1471. [Google Scholar] [CrossRef]
- Sun, Y.; Thompson, S.E.; Nishida, T. Physics of strain effects in semiconductors and metal-oxide-semiconductor field-effect transistors. J. Appl. Phys. 2007, 101, 104503. [Google Scholar] [CrossRef]
- Fischetti, M.V.; Laux, S.E. Band structure, deformation potentials, and carrier mobility in strained Si, Ge and SiGe alloys. J. Appl. Phys. 1996, 80, 2234–2252. [Google Scholar] [CrossRef]
- Fu, D.Y.; Zhang, R.; Wang, B.G.; Liu, B.; Xie, Z.L.; Xiu, X.Q.; Lu, H.; Zheng, Y.D.; Edwards, G. Biaxial and uniaxial strain effects on the ultraviolet emission efficiencies of AlxGa1−xN films with different Al concentrations. J. Appl. Phys. 2010, 108, 103107. [Google Scholar] [CrossRef]
- Steel, F.M.; Tuttle, B.R.; Shen, X.; Pantelides, S.T. Effects of strain on the electrical properties of silicon carbide. J. Appl. Phys. 2013, 114, 013702. [Google Scholar] [CrossRef]
- Shuttleworth, I.G. Controlled FCC/on-top binding of H/Pt(111) using surface stress. Appl. Surf. Sci. 2016, 378, 286–292. [Google Scholar] [CrossRef]
- Stamenkovic, V.R.; Fowler, B.; Mun, B.S.; Wang, G.; Ross, P.N.; Lucas, C.A.; Marković, N.M. Improved Oxygen Reduction Activity on Pt3Ni(111) via Increased Surface Site Availability. Science 2007, 315, 493–497. [Google Scholar] [CrossRef] [PubMed]
- Soler, J.M.; Artacho, E.; Gale, J.D.; García, A.; Junquera, J.; Ordejón, P.; Sánchez-Portal, D. The SIESTA method for ab initio order-N materials simulation. J. Phys. Condens. Matter 2002, 14, 2745–2779. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef] [PubMed]
- Junquera, J.; Paz, Ó.; Sánchez-Portal, D.; Artacho, E. Numerical atomic orbitals for linear-scaling calculations. Phys. Rev. B 2001, 64, 235111. [Google Scholar] [CrossRef]
- Troullier, N.; Martins, J.L. Efficient pseudopotentials for plane-wave calculations. Phys. Rev. B. 1991, 4, 1993–2006. [Google Scholar] [CrossRef]
- Troullier, N.; Martins, J.L. Efficient pseudopotentials for plane-wave calculations. II. Operators for fast iterative diagonalization. Phys. Rev. B. 1991, 43, 8861–8869. [Google Scholar] [CrossRef]
- Kleinman, L.; Bylander, D.M. Efficacious form for model pseudopotentials. Phys. Rev. Lett. 1982, 48, 1425–1428. [Google Scholar] [CrossRef]
- Moreno, J.; Soler, J.M. Optimal meshes for integrals in real- and reciprocal-space unit cells. Phys. Rev. B. 1992, 45, 13891–13898. [Google Scholar] [CrossRef]
- Petukhov, A.G.; Mazin, I.I.; Chioncel, L.; Lichtenstein, A.I. Correlated metals and the LDA + U method. Phys. Rev. B 2003, 67, 1531061–1531064. [Google Scholar] [CrossRef]
- Shuttleworth, I.G. The magnetic properties of Ce/Pd surface alloys investigated using DFT. Chem. Phys. Lett. 2014, 605–606, 5–9. [Google Scholar] [CrossRef]
- Hirshfeld, F.L. Bonded-atom fragments for describing molecular charge densities. Theor. Chim. Acta 1977, 44, 129–138. [Google Scholar] [CrossRef]
- Guerra, C.F.; Handgraaf, J.-W.; Baerends, E.J.; Bickelhaupt, F.M. Voronoi deformation density (VDD) charges: Assessment of the Mulliken, Bader, Hirshfeld, Weinhold, and VDD methods for charge analysis. J. Comput. Chem. 2004, 25, 189–210. [Google Scholar] [CrossRef] [PubMed]
- Bickelhaupt, F.M.; Van Eikema Hommes, N.J.R.; Guerra, C.F.; Baerends, E.J. The carbon-lithium electron pair bond in (CH3Li)n (n = 1, 2, 4). Organometallics 1996, 15, 2923–2931. [Google Scholar] [CrossRef]
- Dronskowski, R.; Blöchl, P.E. Crystal Orbital Hamilton Populations (COHP). Energy-Resolved Visualization of Chemical Bonding in Solids based on Density-Functional Calculations. J. Phys. Chem. 1993, 97, 8617–8624. [Google Scholar] [CrossRef]
- Shuttleworth, I.G. Comparative investigation of the c(2 × 2)-Si/Cu(011) and (√3 × √3)R30°-Cu2Si/Cu(111) surface alloys using DFT. Appl. Surf. Sci. 2012, 258, 3475–3484. [Google Scholar] [CrossRef]
- Butler, B.; Givord, D.; Givord, F.; Palmer, S.B. The elastic constants of CeNi5. J. Phys. C Solid State Phys. 1980, 13, L743–L746. [Google Scholar] [CrossRef]
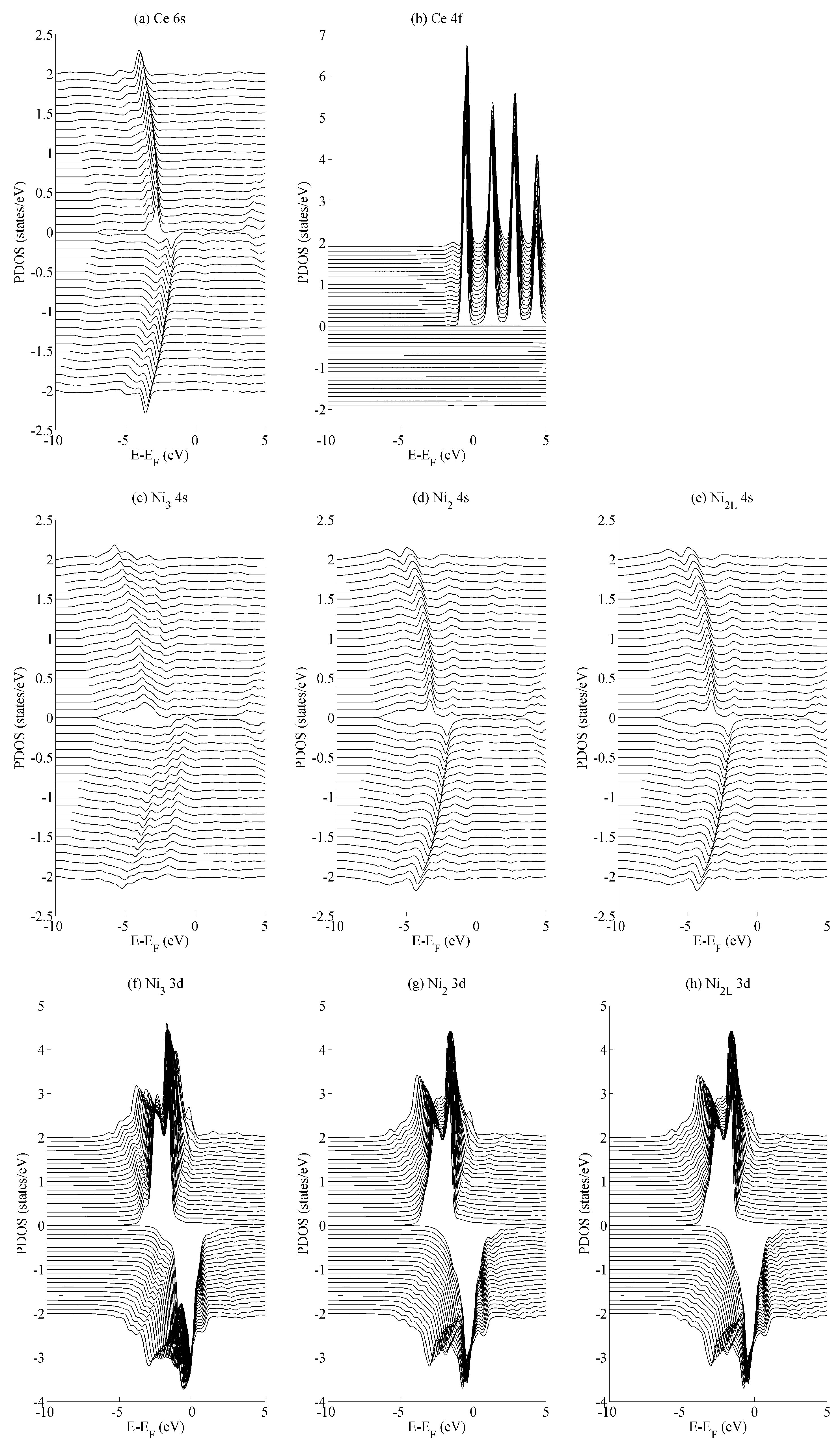
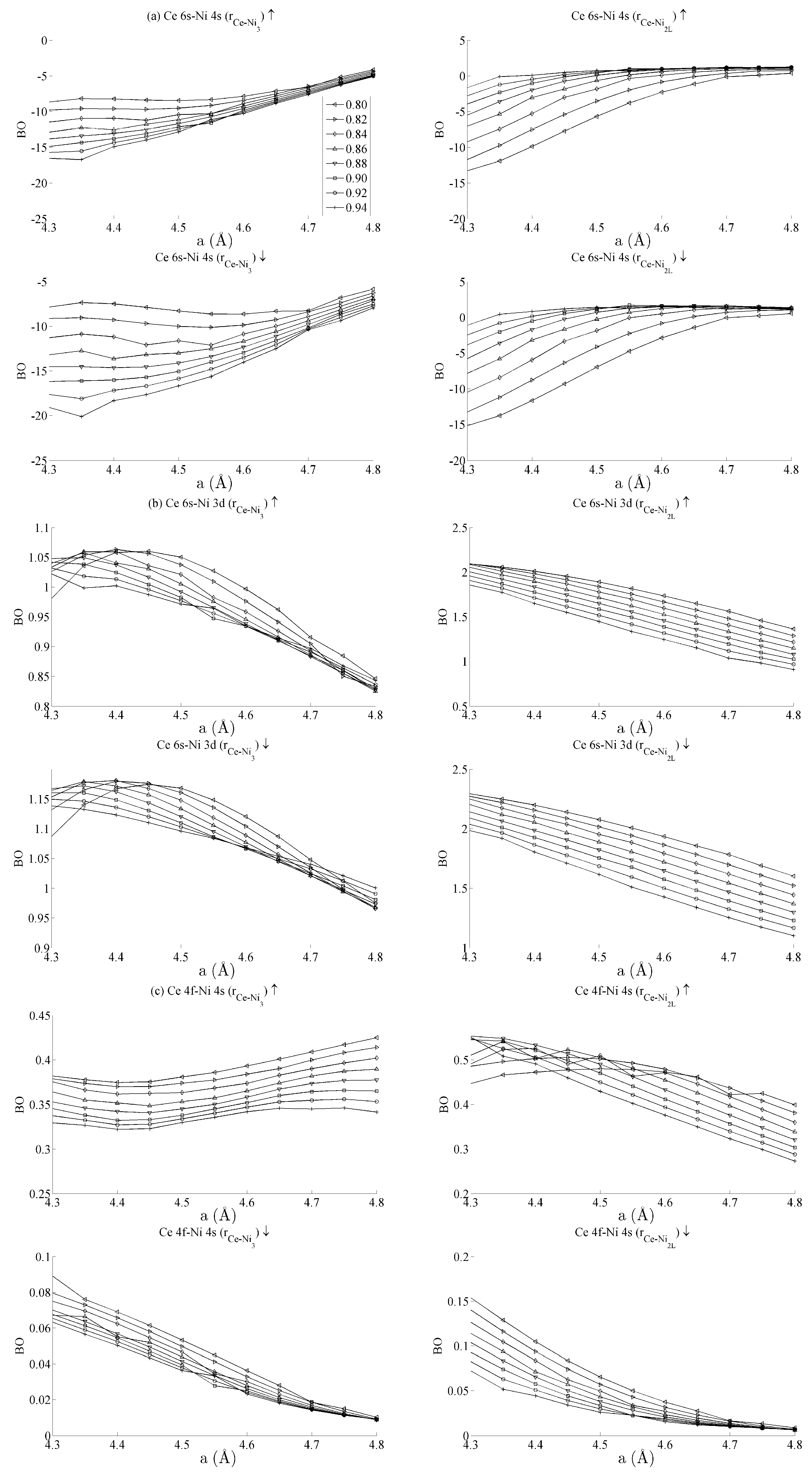
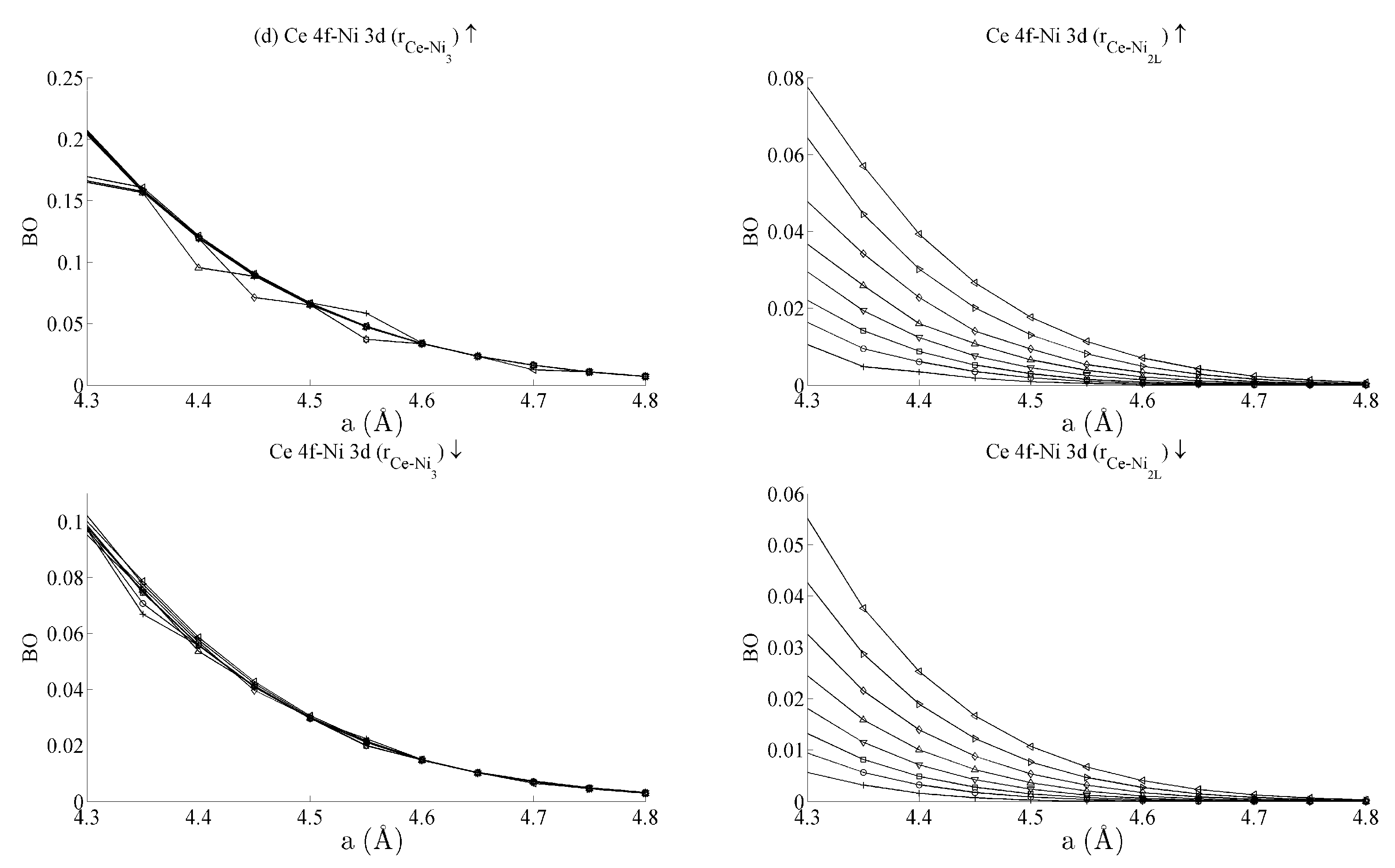

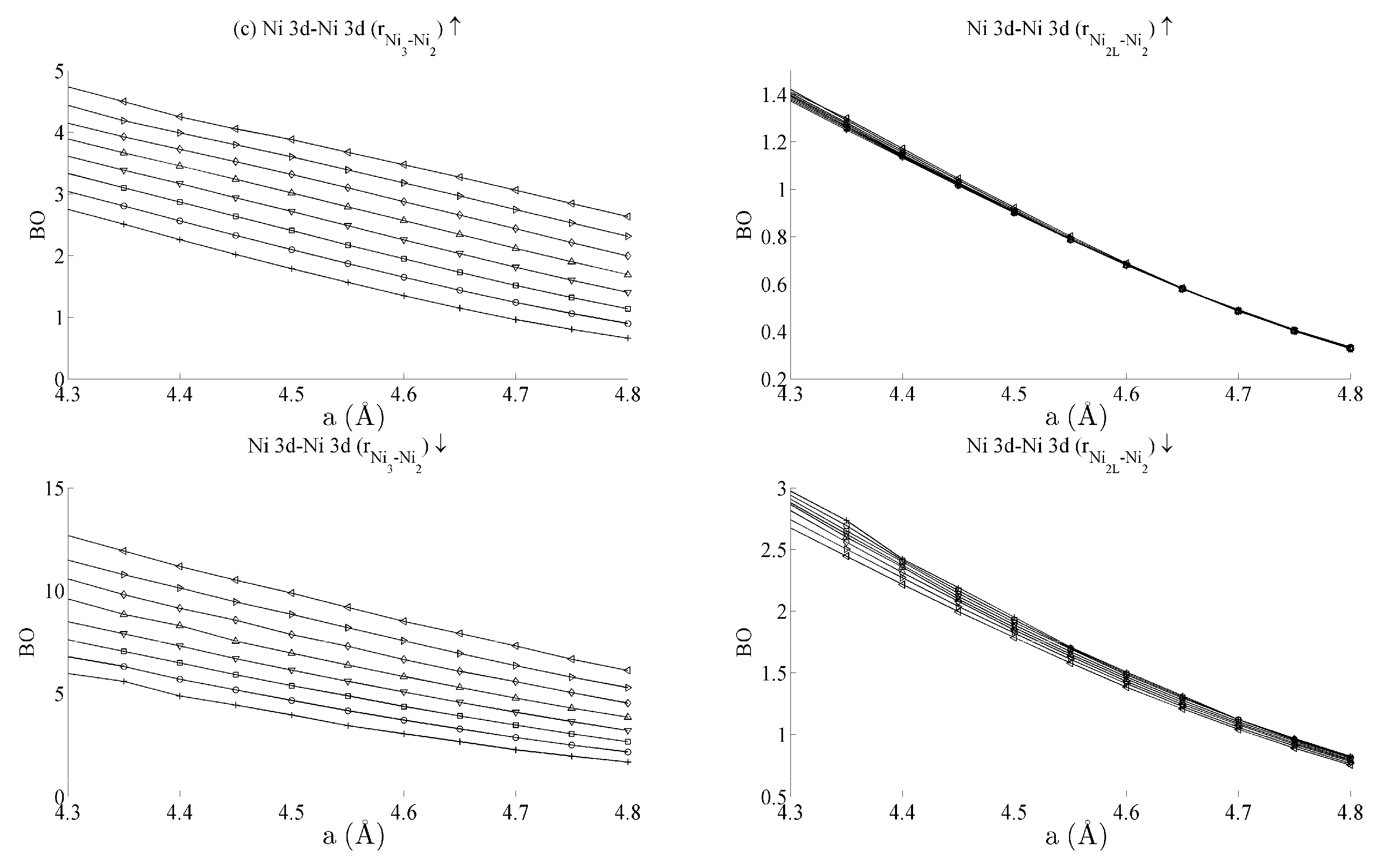
| Interaction | r | Spin | ||
|---|---|---|---|---|
| Ce 6s–Ni 4s | Ce–Ni3 | ↑ | −12.5 | 5 |
| Ce–Ni2L | ↑ | −5.0 | 6 | |
| Ce–Ni3 | ↓ | −12.4 | 5 | |
| Ce–Ni2L | ↓ | −5.0 | 6 | |
| Ce 6s–Ni 3d | Ce–Ni3 | ↑ | 0.9 | 0.1 |
| Ce–Ni2L | ↑ | 1.5 | 0.5 | |
| Ce–Ni3 | ↓ | 1.05 | 0.1 | |
| Ce–Ni2L | ↓ | 1.75 | 0.75 | |
| Ce 4f–Ni 4s | Ce–Ni3 | ↑ | 0.35 | 0.05 |
| Ce–Ni2L | ↑ | 0.40 | 0.15 | |
| Ce–Ni3 | ↓ | 0.04 | 0.04 | |
| Ce–Ni2L | ↓ | 0.075 | 0.075 | |
| Ce 4f–Ni 3d | Ce–Ni3 | ↑ | 0.1 | 0.1 |
| Ce–Ni2L | ↑ | 0.05 | 0.03 | |
| Ce–Ni3 | ↓ | 0.05 | 0.05 | |
| Ce–Ni2L | ↓ | 0.03 | 0.03 |
| Interaction | r | Spin | ||
|---|---|---|---|---|
| Ni 4s–Ni 4s | Ni3–Ni2 | ↑ | −40 | 20 |
| Ni2L–Ni2 | ↑ | −15 | 15 | |
| Ni3–Ni2 | ↓ | −40 | 40 | |
| Ni2L–Ni2 | ↓ | −20 | 20 | |
| Ni 4s–Ni 3d | Ni3–Ni2 | ↑ | 9 | 3 |
| Ni2L–Ni2 | ↑ | 3.25 | 0.5 | |
| Ni3–Ni2 | ↓ | 10 | 2 | |
| Ni2L–Ni2 | ↓ | 4 | 0.6 | |
| Ni 3d–Ni 3d | Ni3–Ni2 | ↑ | 3 | 2 |
| Ni2L–Ni2 | ↑ | 0.75 | 0.65 | |
| Ni3–Ni2 | ↓ | 7.5 | 5 | |
| Ni2L–Ni2 | ↓ | 1.75 | 1.25 |
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shuttleworth, I. Strain Engineering of the CeNi5 System. Magnetochemistry 2016, 2, 39. https://doi.org/10.3390/magnetochemistry2040039
Shuttleworth I. Strain Engineering of the CeNi5 System. Magnetochemistry. 2016; 2(4):39. https://doi.org/10.3390/magnetochemistry2040039
Chicago/Turabian StyleShuttleworth, Ian. 2016. "Strain Engineering of the CeNi5 System" Magnetochemistry 2, no. 4: 39. https://doi.org/10.3390/magnetochemistry2040039
APA StyleShuttleworth, I. (2016). Strain Engineering of the CeNi5 System. Magnetochemistry, 2(4), 39. https://doi.org/10.3390/magnetochemistry2040039