Supramolecular Complexes for Quantum Simulation

Abstract

Simulating the evolution of quantum systems on a classical computer is a yellow very challenging task, which could be easily tackled by digital quantum simulators. These are intrinsically quantum devices whose parameters can be controlled in order to mimic the evolution of a broad class of target Hamiltonians. We describe here a quantum simulator implemented on a linear register of molecular Cr₇Ni qubits, linked through Co²⁺ ions which act as switches of the qubit–qubit interaction. This allows us to implement one- and two-qubit gates on the chain with high-fidelity, by means of uniform magnetic pulses. We demonstrate the effectiveness of the scheme by numerical experiments in which we combine several of these elementary gates to implement the simulation of the transverse field Ising model on a set of three qubits. The very good agreement with the expected evolution suggests that the proposed architecture can be scaled to several qubits.

1. Introduction

Simulating the evolution of a large quantum mechanical system on a classical computer is highly inefficient, due to the exponential growth of the Hilbert space with the system size. As a consequence, many important problems in physics and chemistry cannot be tackled. However, this difficulty can be overcome if we “let the computer itself be built of quantum mechanical elements which obey quantum mechanical laws”, as envisioned more than thirty years ago by R. Feynman [1].

In recent years, different schemes have been proposed to realize quantum simulators of many relevant models in condensed matter physics, quantum field theories, and quantum chemistry [2]. Quantum simulators can be classified in two categories. In analog simulators, a certain quantum system directly emulates another one; whereas in digital simulators, the state of the target system is encoded in qubits and the time evolution of its wavefunction can be discretized into a sequence of logical gates. While analog architectures are restricted to specific target problems, digital ones can be programmed to simulate broad classes of Hamiltonian. They are, indeed, small quantum computers. However, while several thousands or even millions of qubits are needed for the non-trivial implementation of quantum algorithms such as Shor’s code for factoring large numbers in primes or Grover’s search code [3]—thus requiring an amazing degree of control on the hardware—only a few dozens of qubits would outperform a classical computer in simulating quantum systems. Hence, the physical implementation of a digital quantum simulator is much less demanding than a useful quantum computer and seems within reach of present technology.

In this perspective, molecular nanomagnets (MNMs) [4] represent attractive candidate qubits [5,6,7,8,9,10,11] thanks to their wide tunability both at the intermolecular and at the intramolecular level, and to the possibility of providing a detailed microscopic description in terms of a quantum spin Hamiltonian. Among the most widely investigated systems for quantum information processing are Cr₇Ni antiferromagnetic (AF) rings. These are characterized by a $S=1/2$ ground state, and coherence times above 10 $\mathsf{\mu }$s have been demonstrated on properly engineered variants [12]. Rabi oscillations within the computational doublet (corresponding to single-qubit gates) have already been performed on ensembles of MNMs [13,14,15], as well as two-qubit operations in dimers of permanently coupled molecular qubits [16,17]. However, an important and much more challenging step towards the realization of a digital quantum simulator is the physical implementation of two-qubit entangling gates on a scalable architecture. Indeed, this implies the ability to turn the interaction between pairs of qubits on and off at will.

To this aim, we have recently introduced a scalable quantum computation scheme which allows one to control the qubits on a linear register by using uniform magnetic pulses as the only manipulation tool [18,19,20]. It is based on two classes of magnetic units that play two distinct roles: effective $S=1/2$ spins are used to encode the qubits, whereas interposed molecular complexes (or ions) are used as switches of the effective qubit–qubit interaction. The scheme relies on a weak qubit–switch exchange interaction. In this limit, an external magnetic field keeps the switch frozen in its ground state, thus leaving the qubits decoupled. Hence, single qubit gates can be implemented by magnetic pulses resonant with the qubit gap. Conversely, conditional gates between neighboring pairs of qubits are performed by temporarily bringing the switch to an excited state by a microwave pulse of suitable phase and duration. This excitation corresponds to turning on the qubit–qubit interaction.

Here we show that the implementation of such a scheme is particularly efficient on an $\mathcal{ABAB}$ chain of molecular qubits, and we discuss the scalability of the proposed architecture. We employ an extended version of the supra-molecular assembly introduced in [20], in which Cr₇Ni rings are employed to encode the qubits, whereas Co ions act as switches of the qubit–qubit interaction. The perpendicular arrangement of the Cr₇Ni qubits makes the $\mathcal{A}$ and $\mathcal{B}$ transitions spectroscopically distinguishable, thanks to the anisotropy of the $\underline{g}$ tensors of the rings. We demonstrate the scalability of our scheme and its robustness with respect to gating errors by numerically simulating the transverse-field Ising model on a chain of three qubits, which requires the concatenation of many elementary gates. The article is organized as follows: we first review the basic concepts of a digital quantum simulator (Section 2.1); then we introduce the scalable supra-molecular setup (Section 3.1) for its realization. In Section 3.2, we describe the scheme to implement quantum gates with uniform pulses; in the second part of the paper (Section 3.3), we show the performance of our architecture on registers consisting of two or three qubits, we provide numerical experiments to demonstrate how the proposed simulator would work, we discuss the scalability of the architecture (Section 4), and we draw some conclusions based on the current work (Section 5).

2. Methods

2.1. Digital Quantum Simulation

We provide here a quick overview on the operating principles of a digital quantum simulator. To this end, we exploit the mathematical formalization introduced by Lloyd [21], who translated Feynman’s intuition into quantum information perspectives. Most Hamiltonians of physical interest can be written as the sum of L local terms, $\widehat{\mathcal{H}}={\sum }_k^L{\widehat{\mathcal{H}}}_k$. Hence, the system dynamics can be approximated by a sequence of local unitary operators according to the first-order Trotter–Suzuki formula ($\hslash =1$):

$$\widehat{U}\left(t\right)=e^{-i\widehat{\mathcal{H}}t}={(e^{-i{\widehat{\mathcal{H}}}_1\mathsf{\tau }}\cdots e^{-i{\widehat{\mathcal{H}}}_L\mathsf{\tau }})}^N+O\left({\mathsf{\tau }}^2\right),$$

(1)

where $\mathsf{\tau }=t/N$ and the total digital error of this approximation can be made as small as desired by choosing a sufficiently large N [21]. Commuting terms in the Hamiltonian do not require any Trotter decomposition. As we will show below, higher order decompositions [22] can be used to reduce N, while keeping the same digital error. The Trotter–Suzuki formula reduces the simulation to the sequential implementation of local unitary operators, each one corresponding to a small time interval $t/N$. This can be obtained by a proper sequence of single- and two-qubit gates, which thus constitute the basic building blocks of any quantum simulation algorithm. The problem then reduces to finding a suitable mapping between the physical hardware (consisting of many qubits, described by means of Pauli matrices) and the target Hamiltonian.

The mapping of $s=1/2$ models onto an array of qubits is straightforward. Let us consider here two kinds of significant local terms in the target Hamiltonian, namely one- (${\widehat{\mathcal{H}}}_{\mathsf{\alpha }}^{\left(1\right)}$) and two-body (${\widehat{\mathcal{H}}}_{\mathsf{\alpha }\mathsf{\beta }}^{\left(2\right)}$) terms, with $\mathsf{\alpha },\mathsf{\beta }=x,y,z$. The unitary time evolution corresponding to one-body terms ${\widehat{\mathcal{H}}}_{\mathsf{\alpha }}^{\left(1\right)}=b{\widehat{s}}_{\mathsf{\alpha }}$ is directly implemented by single-qubit rotations ${\widehat{R}}_{\mathsf{\alpha }}\left(b\mathsf{\tau }\right)\equiv e^{-ib\mathsf{\tau }{\widehat{s}}_{\mathsf{\alpha }}}$. Conversely, two-body terms describe a generic spin–spin interaction of the form ${\widehat{\mathcal{H}}}_{\mathsf{\alpha }\mathsf{\beta }}^{\left(2\right)}=\mathsf{\lambda }{\widehat{s}}_{1\mathsf{\alpha }}{\widehat{s}}_{2\mathsf{\beta }}$, for any choice of $\mathsf{\alpha },\mathsf{\beta }=x,y,z$. The evolution operator $e^{-i{\widehat{\mathcal{H}}}_{\mathsf{\alpha }\mathsf{\beta }}^{\left(2\right)}\mathsf{\tau }}$ can be decomposed as [18]:

$$e^{-i\mathsf{\lambda }{\widehat{s}}_{1\mathsf{\alpha }}{\widehat{s}}_{2\mathsf{\beta }}\mathsf{\tau }}=[{\widehat{u}}_{1\mathsf{\alpha }}\otimes {\widehat{u}}_{2\mathsf{\beta }}]e^{-i\widehat{\Lambda }\mathsf{\tau }}{[{\widehat{u}}_{1\mathsf{\alpha }}\otimes {\widehat{u}}_{2\mathsf{\beta }}]}^{†},$$

(2)

with $\widehat{\Lambda }=\mathsf{\lambda }{\widehat{s}}_{1z}{\widehat{s}}_{2z}$, ${\widehat{u}}_x={\widehat{R}}_y(\mathsf{\pi }/2)$, ${\widehat{u}}_y={\widehat{R}}_x(3\mathsf{\pi }/2)$, ${\widehat{u}}_z=\widehat{I}$. The Ising evolution operator $e^{-i\mathsf{\lambda }{\widehat{s}}_{1z}{\widehat{s}}_{2z}\mathsf{\tau }}$ can be easily obtained by combining the two-qubit controlled-phase (C$\mathsf{\phi }$) gate with single qubit rotations.

Even if in the present work we focus our attention on the simulation of spin-1/2 Hamiltonians, it is worth mentioning that many other Hamiltonians can be mapped onto the state of a qubits register by properly re-writing them in terms of Pauli operators. For instance, the simulation of Hamiltonians involving $S>1/2$ spins can be performed by encoding the state of each spin-S onto that of $2S$ qubits [18]. Furthermore, fermionic operators can be expressed in terms of Pauli matrices by exploiting the Jordan–Wigner transformation, thus allowing the simulation of models of great interest in condensed matter physics or quantum chemistry [23].

3. Results

3.1. Scalable Supra-Molecular Setup

In this section, we describe the supra-molecular setup proposed as a quantum simulator, inspired by the platform of [18]. The elementary unit of the scalable array consists of an $\mathcal{AB}$ pair of qubits linked by an interposed switch, in which $\mathcal{A}$ and $\mathcal{B}$ transitions are spectroscopically distinguishable. As a physical implementation of this architecture, we consider a couple of perpendicularly arranged Cr₇Ni rings, connected through a Co²⁺ complex, as reported in [20]. This two-qubit unit can be extended to form the $\mathcal{ABAB}$ one-dimensional register schematically shown in Figure 1. We exploit the anisotropy of the $\underline{g}$ tensors of the orthogonally arranged Cr₇Ni rings to selectively address $\mathcal{A}$ or $\mathcal{B}$ transitions. As explained below, in order to get a conditional excitation of odd (even) pairs of qubits, we also require to spectroscopically distinguish the transitions associated with odd (even) switches (see below), labeled S₁ and S₂ in Figure 1. In the present setup, S₁ and S₂ can be obtained by rotating the same Co²⁺ ion, thanks to the large anisotropy of its $\underline{g}$ tensor (see

Table 1. Parameters of the spin Hamiltonian (3). Only diagonal components have been assumed for both $\underline{g}$ and $\underline{J}$ tensors. Exchange couplings are in $\mathsf{\mu }$eV.

	${\underline{\mathit{g}}}_{\mathit{A}}$	${\underline{\mathit{g}}}_{\mathit{B}}$	${\underline{\mathit{g}}}_{\mathit{S}1}$	${\underline{\mathit{g}}}_{\mathit{S}2}$	$\underline{\mathit{J}}$	${\underline{\mathit{J}}}^{\prime }$
x	1.78	1.74	1.78	1.78	12	6
y	1.78	1.78	4.25	6.50	−28	−14
z	1.74	1.78	6.50	4.25	−14	−28

).

The spin Hamiltonian describing the hardware is given by:

$$\begin{array}{ccc}\hfill \widehat{H}& =& \sum _k{\mathsf{\mu }}_B\left({\widehat{\mathbf{S}}}_{2k-1}·{\underline{g}}_{\mathcal{A}}+{\widehat{\mathbf{S}}}_{2k}·{\underline{g}}_{\mathcal{B}}+{\widehat{\mathbf{s}}}_{2k-1}·{\underline{g}}_{S1}+{\widehat{\mathbf{s}}}_{2k}·{\underline{g}}_{S2}\right)·\mathbf{B}\hfill \\ & +& \sum _k[{\widehat{\mathbf{s}}}_{2k-1}·(\underline{J}·{\widehat{\mathbf{S}}}_{2k-1}+{\underline{J}}^{\prime }·{\widehat{\mathbf{S}}}_{2k})+{\widehat{\mathbf{s}}}_{2k}·(\underline{J}·{\widehat{\mathbf{S}}}_{2k+1}+{\underline{J}}^{\prime }·{\widehat{\mathbf{S}}}_{2k})],\hfill \end{array}$$

(3)

where capital ($\mathbf{S}$) and lowercase ($\mathbf{s}$) letters are used to indicate the effective spin 1/2 operators of the logical Cr₇Ni qubits and of the Co²⁺ switches, respectively. $\mathcal{A}$ qubits and S₁ switches are labeled by odd indices, while $\mathcal{B}$ qubits and S₂ switches by even indices. The spectroscopic tensors ${\underline{g}}_{\mathcal{A}}$, ${\underline{g}}_{\mathcal{B}}$ (${\underline{g}}_{S1}$, ${\underline{g}}_{S2}$) describe the interaction of the qubits (switches) with an external magnetic field B, and ${\mathsf{\mu }}_B$ is the Bohr magneton. Finally, $\underline{J}$ and ${\underline{J}}^{\prime }$ are exchange tensors describing the interaction of the switches with $\mathcal{A}$ and $\mathcal{B}$ qubits, respectively. The parameters employed in the simulations are listed in Table 1.

${\underline{g}}_{\mathcal{A}}$, ${\underline{g}}_{\mathcal{B}}$, and ${\underline{g}}_{S1}$ were determined by X-, K-, Q-, and W-band electron paramagnetic resonance (EPR) performed on the elementary Cr₇Ni–Co–Cr₇Ni unit [20], while $\underline{J}$ and ${\underline{J}}^{\prime }$ were reduced by a factor of three with respect to the experimental values of [20], in order to improve the scalability of the setup (see discussion below). A similar reduction could be achieved chemically by adding an extra phenyl group between the ring and the central node.

3.2. Quantum Gates with Uniform Magnetic Pulses

We describe here a scheme for performing one- and two-qubit gates (which constitute the essential building blocks of digital quantum simulation algorithms) on a scalable platform, based on the ideas of [19,20]. As discussed below, this scheme can be exploited for proof-of-principle experiments of quantum simulation on short chains of molecular qubits. The qubit–qubit coupling is switched by a single (Co²⁺) ion, interposed between the Cr₇Ni qubits, as in the newly synthesized family of complexes Cr₇Ni–Co–Cr₇Ni. A necessary condition for the scheme to work is that as long as the switch is in the ground state, the effective qubit–qubit interaction (resulting from virtual excitations of the switch) is small enough that the associated unwanted evolution is very slow on the timescale of the quantum gates. On one hand, this condition is fulfilled if the difference between the excitation energies of the qubits and of the switch is much larger than the qubit–switch coupling. On the other hand, to enable conditional dynamics, this coupling must be large enough to make the excitation energy of the switch sufficiently dependent on the state of the qubits. This requires a suitable chemical engineering of the qubit–switch bond. In the present implementation, the feasibility of the scheme relies on a weak Co-ring coupling, if compared to the difference between the Co and ring Zeeman interaction with an applied field.

We first focus on the two-qubit elementary unit, and let z be the direction of the external field. Since $\mathsf{\Delta }g{\mathsf{\mu }}_{B}B\gg J,J^{\prime }$, in a field of a few Teslas, the eigenstates of the Hamiltonian are factorized and we can define the computational basis within the low-energy subspace corresponding to the Co frozen into its ground state $M_{Co}=-1/2$. Here $\mathsf{\Delta }g=g_{zS1\left(S2\right)}-g_{zA\left(B\right)}$, and we associate the logical $|0\rangle$ and $|1\rangle$ to the $|M=-1/2\rangle$ and $|M=1/2\rangle$ state of each ring. It is therefore possible to implement single-qubit rotations by EPR pulses resonant with the $|M=-1/2\rangle \to |M=1/2\rangle$ Cr₇Ni gaps. Notice that the $\mathcal{A}$ and $\mathcal{B}$ transitions are made significantly inequivalent by the anisotropy of the Cr₇Ni $\underline{g}$ tensor ($g_{z\mathcal{A}}=1.74\ne g_{z\mathcal{B}}=1.78$, see Table 1), combined with the asymmetric coupling to the switch ($J_z=-14\mathsf{\mu }eV\ne J_z^{\prime }=-28\mathsf{\mu }eV$). Indeed, the z component of the exchange interaction yields a renormalization of the magnetic field felt by the qubits: $B\to B-\frac{J_z}{2g_{z\mathcal{A}}{\mathsf{\mu }}_B}$ for qubit $\mathcal{A}$ and $B\to B-\frac{J_z^{\prime }}{2g_{z\mathcal{B}}{\mathsf{\mu }}_B}$ for qubit $\mathcal{B}$. This leads to an energy difference $\left(g_{z\mathcal{B}}-g_{z\mathcal{A}}\right){\mathsf{\mu }}_{B}B-\frac{J_z^{\prime }-J_z}{2}$ between the $|00\rangle \to |01\rangle$ and $|00\rangle \to |10\rangle$ transitions and allows us to independently rotate $\mathcal{A}$ and $\mathcal{B}$ qubits.

Conversely, the entangling two-qubit gate controlled-$\mathsf{\phi }$ (C$\mathsf{\phi }$) is obtained by exciting and de-exciting the $|11\rangle$ component of the two-qubit wavefunction to a state outside the computational basis, corresponding to a rotation of the central Co²⁺ ion state. This allows us to implement a conditional (two-qubit) dynamics because the energy cost of this rotation depends on the states of the two molecular qubits by an amount of the order of J. Hence, C$\mathsf{\phi }$ can be implemented by a pulse resonant with the $|11\rangle \equiv |1/2,1/2\rangle \otimes |M_{Co}=-1/2\rangle \to |1/2,1/2\rangle \otimes |M_{Co}=1/2\rangle$ gap, followed by a repetition of the same pulse that brings the state back to $|11\rangle$ with an additional phase $\mathsf{\phi }$. The other two-qubit states are left unaffected by the pulse sequence, as required by the controlled-phase gate [3]. The value of $\mathsf{\phi }$ is controlled by the phase difference between the first and the second pulse.

Below we extend this scheme for quantum computation to a chain of three qubits, schematically shown in the inset of Figure 2. Qubits Q₁ and Q₃ belong to the $\mathcal{A}$ sublattice, while Q₂ to the $\mathcal{B}$ sublattice. In Figure 2, we also report the energy level diagram as a function of the applied magnetic field (along the z-axis). The computational three-qubit basis is defined in the low-energy subspace where both switches S₁ and S₂ are frozen into their $M=-1/2$ ground state, corresponding to the red lines in Figure 2. Quantum gates are implemented in a static field $B=4$ T, by means of gaussian EPR pulses. Single-qubit rotations of $\mathcal{A}$ and $\mathcal{B}$ qubits are obtained by pulses resonant with the gaps indicated by blue arrows. In this three-qubit setup, the rotation of Q₁ and Q₃ qubits ($\mathcal{A}$ sublattice) occurs in two steps via the intermediate excitation of the degenerate $|0q_{2}1\rangle$ and $|1q_{2}0\rangle$ states. Conversely, C${\mathsf{\phi }}_{12}$ (C${\mathsf{\phi }}_{23}$) gates on the 12 (23) pair of qubits are implemented by a conditional excitation of the $|1_1{1}_2{q}_3\rangle$ ($|q_1{1}_2{1}_3\rangle$) component of the wave-function (red arrows in Figure 2) to the excited states (green lines), corresponding to the flip of the switch S₁ (S₂). Notice that if the pulse is applied along the y direction, the implementation of this gate is fast, owing to the large value of $g_{S1\left(S2\right)}$. Moreover, the exchange interaction in Equation (3) is sufficiently large to allow us to employ large oscillating fields (50 G), since the desired transition is spectroscopically well resolved from all the others. Consequently, the C$\mathsf{\phi }$ gate can be performed in only about 12 ns.

3.3. Numerical Experiments

In order to quantify the performance of the elementary gates, we compute the fidelity $\mathcal{F}\equiv \left|\langle {\mathsf{\psi }}_I|\mathsf{\psi }\rangle \right|$, which is a well-known figure of merit of the proximity of two quantum states [3]. Here $|{\mathsf{\psi }}_I\rangle$ is the final state that would result from an ideal implementation of the gates, while $|\mathsf{\psi }\rangle$ is the actual final state, obtained by numerically simulating the evolution of the wave-function, subject to the static Hamiltonian 3 and to the sequence of pulses required to implement such gates. The fidelities calculated for two and three qubit setups in the implementation of single-qubit rotations, C$\mathsf{\phi }$ gates, as well as in the simulation of spin Hamiltonian terms ${\widehat{\mathcal{H}}}_{\mathsf{\alpha }\mathsf{\beta }}^{\left(2\right)}$ are reported in

Table 2. Fidelity ($\mathcal{F}$) of single- [${\widehat{R}}_x\left(\mathsf{\varphi }\right)$] and two-qubit gates (controlled-$\mathsf{\phi }$), and to simulate the elementary terms of a generic two-body spin Hamiltonian (for $\mathsf{\lambda }\mathsf{\tau }=\mathsf{\pi }/2$). Single-qubit rotations correspond to simulating single-spin terms of the spin Hamiltonian (with $\mathsf{\varphi }=b\mathsf{\tau }$). The fidelity has been computed on a random initial state. The second and third lines of the Table compare the calculations performed on $n=2$ and $n=3$ qubits. The fidelities obtained in the rotations on the two $\mathcal{A}$ and $\mathcal{B}$ sublattices have been averaged to get ${\widehat{R}}_x(\mathsf{\pi }/2)$. The same has been done for the two-body terms on qubit-pairs 12 and 23.

$\mathcal{F}$	${\widehat{\mathit{R}}}_{\mathit{x}}(\mathsf{\pi }/2)$	${\widehat{\mathit{U}}}_{\mathit{C}\mathsf{\phi }=\mathsf{\pi }/3}$	${\widehat{\mathcal{H}}}_{\mathit{z}\mathit{z}}^{\left(2\right)}$	${\widehat{\mathcal{H}}}_{\mathit{z}\mathit{x}}^{\left(2\right)}$	${\widehat{\mathcal{H}}}_{\mathit{x}\mathit{x}}^{\left(2\right)}$
$n=2$	99.997%	99.988%	99.984%	99.984%	99.971%
$n=3$	99.990%	99.982%	99.980%	99.972%	99.870%

. In order to simplify the simulation of the term $\mathsf{\lambda }{\widehat{s}}_{1z}{\widehat{s}}_{2z}$—which yields a phase-difference between parallel and anti-parallel spin components—we simultaneously apply two pulses for a conditional excitation/de-excitation of both $|00\rangle$ and $|11\rangle$ components of the two-qubit wave-function to a state in which the Co spin is reversed. This directly adds the desired phase to $|00\rangle$ and $|11\rangle$, without requiring additional single-qubit phase-gates.

It is worth noting that the reported fidelities are very high. The small errors are predominantly caused by imperfect operation of the switches. Indeed, the permanent Co-rings couplings ($\underline{J}$ and ${\underline{J}}^{\prime }$) lead to a small residual qubit–qubit interaction, even when the switch is in the off-state. The analytic form of this residual coupling can be deduced at second-order perturbation theory level. Indeed, since $\mathsf{\Delta }g{\mathsf{\mu }}_{B}B\gg J,J^{\prime }$, the exchange terms in (3) act as a small perturbation with respect to the energy cost of flipping a pair of neighboring spins. This allows us to eliminate the switch degrees of freedom in the subspace in which $M_{Co}=-1/2$, and to obtain a residual qubit–qubit interaction expressed by:

$${\widehat{H}}_{res}={\mathsf{\Gamma }}_{xx}{\widehat{S}}_{1x}{\widehat{S}}_{2x}+{\mathsf{\Gamma }}_{yy}{\widehat{S}}_{1y}{\widehat{S}}_{2y}+{\mathsf{\lambda }}_1{\widehat{S}}_{1z}+{\mathsf{\lambda }}_2{\widehat{S}}_{2z}+C,$$

(4)

with

$$\begin{array}{ccc}\hfill {\mathsf{\Gamma }}_{xx}& =& -\frac{g_{z\mathcal{A}}{J}_y{J}_x^{\prime }\left(g_{zS}^2-g_{z\mathcal{B}}^2\right)+J_x\left[J_x^{\prime }{g}_{zS}\left(2g_{zS}^2-g_{z\mathcal{B}}^2-g_{z\mathcal{A}}^2\right)+J_y{g}_{z\mathcal{B}}\left(g_{zS}^2-g_{z\mathcal{A}}^2\right)\right]}{4{\mathsf{\mu }}_{B}B\left(g_{zS}^2-g_{z\mathcal{A}}^2\right)\left(g_{zS}^2-g_{z\mathcal{B}}^2\right)}\hfill \\ \hfill {\mathsf{\Gamma }}_{yy}& =& -\frac{g_{z\mathcal{B}}{J}_y{J}_x^{\prime }\left(g_{zS}^2-g_{z\mathcal{A}}^2\right)+J_y^{\prime }\left[J_y{g}_{zS}\left(2g_{zS}^2-g_{z\mathcal{B}}^2-g_{z\mathcal{A}}^2\right)+J_x{g}_{z\mathcal{A}}\left(g_{zS}^2-g_{z\mathcal{B}}^2\right)\right]}{4{\mathsf{\mu }}_{B}B\left(g_{zS}^2-g_{z\mathcal{A}}^2\right)\left(g_{zS}^2-g_{z\mathcal{B}}^2\right)}\hfill \\ \hfill {\mathsf{\lambda }}_1& =& -\frac{J_z}{2}-\frac{2g_{zS}{J}_x{J}_y+g_{z\mathcal{A}}\left(J_x^2+J_y^2\right)}{8{\mathsf{\mu }}_{B}B\left(g_{zS}^2-g_{z\mathcal{A}}^2\right)}\hfill \\ \hfill {\mathsf{\lambda }}_2& =& -\frac{J_z^{\prime }}{2}-\frac{2g_{zS}{J}_x^{\prime }{J}_y^{\prime }+g_{z\mathcal{B}}\left(J_x^{\prime 2}+J_y^{\prime 2}\right)}{8{\mathsf{\mu }}_{B}B\left(g_{zS}^2-g_{z\mathcal{B}}^2\right)}.\hfill \end{array}$$

Here, in the limit of small qubit–switch exchange interaction, the leading term is given by a first order correction to the magnetic field felt by the qubits, induced by $J_z$ and $J_z^{\prime }$. Two-qubit XX and YY interactions emerge as a second-order effect, which induce an unwanted two-qubit evolution—even when the switch is turned off—by mixing states $|01\rangle$ and $|10\rangle$ of the computational basis. To obtain high-fidelity single qubit gates, these interactions should be small, so that the associated dynamics occurs on a time-scale much longer than the gating time (∼10–20 ns). For the here-reported parameters, we have estimated that the time required to reduce the fidelity in an idle evolution of a couple of qubits to 0.9 is of the order of several $\mathsf{\mu }$s. The effect increases by increasing the number n of qubits, but remains negligible for $n=3$. Remarkably, this timescale is much longer than $1/\mathsf{\Gamma }$, since the combination of the perpendicular arrangement of the rings and of the highly anisotropic behavior of Co²⁺ leads to a significant splitting of the $|01\rangle$ and $|10\rangle$ states, thus effectively suppressing the residual inter-qubit interaction. Hence, the fidelities of the elementary gates for $n=2$ and $n=3$ are very similar and practically unaffected by the unwanted evolution.

Even if the demonstration of the elementary single- and two-qubit gates is in principle sufficient to ensure the implementation of quantum simulation algorithms, the actual feasibility of such simulations needs to be quantitatively assessed by testing whether the complex sequences of gates needed are robust with respect to errors. To demonstrate the effectiveness of the proposed scheme, we have performed numerical experiments in which many gates have been concatenated to implement quantum simulation algorithms on a chain of three qubits. As a paradigmatic example, we report the digital quantum simulation of the transverse field Ising model, described by the target Hamiltonian:

$${\widehat{\mathcal{H}}}_{TIM}=\mathsf{\lambda }\left({\widehat{s}}_{1z}{\widehat{s}}_{2z}+{\widehat{s}}_{2z}{\widehat{s}}_{3z}\right)+b\left({\widehat{s}}_{1x}+{\widehat{s}}_{2x}+{\widehat{s}}_{3x}\right).$$

(5)

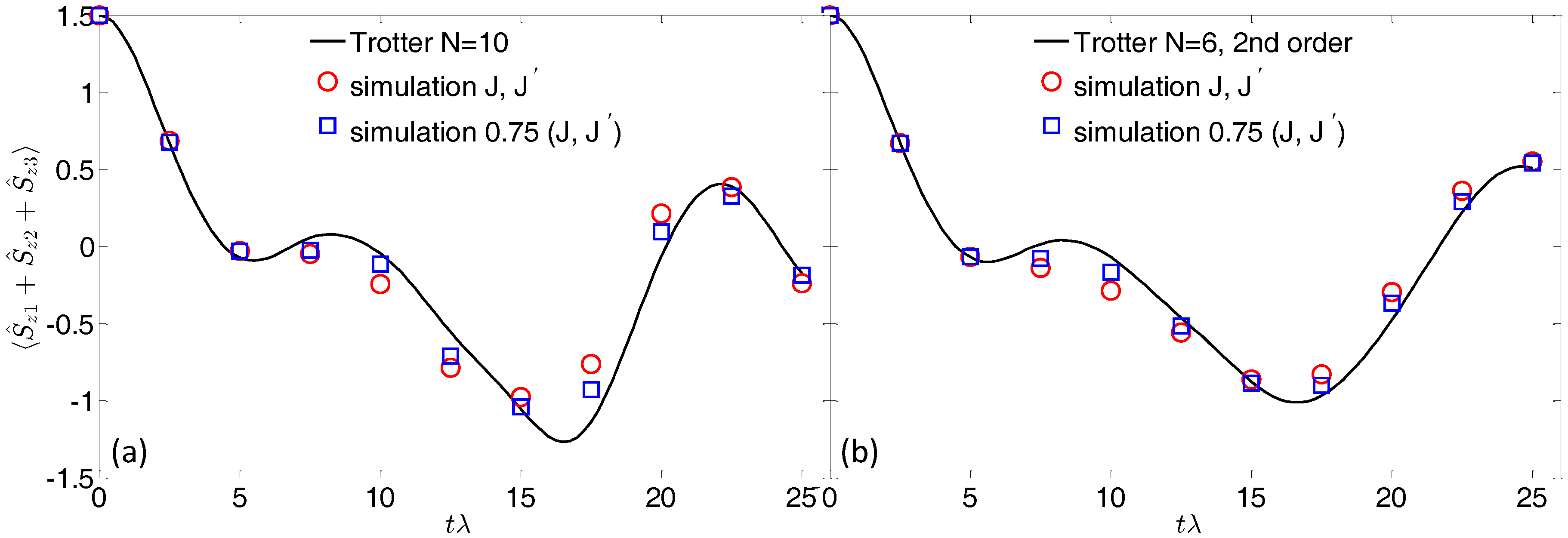
If we exploit the first order expansion 1, simulating the evolution induced by ${\widehat{\mathcal{H}}}_{TIM}$ requires the implementation of three single-qubit rotations and four conditional gates per Trotter step. Figure 3a shows the time evolution of the final magnetization of the three qubits, calculated by using $N=10$ Trotter steps. This is the typical quantity that can be extracted in a pulse-EPR experiment on a bulk crystal of molecular nanomagnets (see, e.g., [24]). The polarization detectors either measure the entire polarization pattern or selectively record the on-resonance polarization, thus targeting the transitions of each qubit. In the former case, the qubits polarization can be obtained by subtracting the contribution of the Co switches (which are practically frozen into the $M_{Co}=-1/2$ ground state) from the entire polarization.

By analyzing Figure 3, we note that the agreement with the expected evolution (continuous line) is generally good. However, since we are now considering the sequential application of many gates (the total simulation time is about 300 ns), the effect of the residual qubit–qubit interaction is much more pronounced than in the case of a single gate. On the one hand, this is a direct consequence of increasing the computational time; on the other hand, errors accumulated in the implementation of each gate can combine non-linearly, leading (for significantly large errors) to unreliable results.

We can point out different ways to reduce the detrimental effect of the residual coupling. As noted above, with a static field of 4 T, the oscillation induced by ${\widehat{H}}_{eff}$ occurs on a timescale of several $\mathsf{\mu }$s, which is much longer than the time required for the whole simulation. Hence, simulated (blue) points reported in Figure 3a are in good agreement with the exact evolution (continuous line). The analytic expression (4) can be exploited to further improve the simulation. Indeed, we note that ${\mathsf{\Gamma }}_{xx}$ and ${\mathsf{\Gamma }}_{yy}$ can be controlled by the strength of the applied field or by the size of the Co-ring exchange. Hence, increasing the magnetic field or reducing J (red points in Figure 3) leads to a better agreement between the exact and simulated time evolution.

Alternatively, a strategy to reduce the total number of gates (hence the error associated with the unwanted evolution) is to exploit a second order Trotter–Suzuki expansion [22]. For instance, we can decompose the target Hamiltonian into four terms: ${\widehat{\mathcal{H}}}_{TIM}={\widehat{\mathcal{H}}}_1+{\widehat{\mathcal{H}}}_2+{\widehat{\mathcal{H}}}_3+{\widehat{\mathcal{H}}}_4$, with ${\widehat{\mathcal{H}}}_1=b{\widehat{s}}_{2x}$, ${\widehat{\mathcal{H}}}_2=b({\widehat{s}}_{1x}+{\widehat{s}}_{3x})$, ${\widehat{\mathcal{H}}}_3=\mathsf{\lambda }{\widehat{s}}_{1z}{\widehat{s}}_{2z}$, ${\widehat{\mathcal{H}}}_4=\mathsf{\lambda }{\widehat{s}}_{2z}{\widehat{s}}_{3z}$. Then, we approximate the unitary evolution associated to ${\widehat{\mathcal{H}}}_{TIM}$ by:

$$\widehat{U}\left(\mathsf{\tau }\right)=e^{-i({\widehat{\mathcal{H}}}_1+{\widehat{\mathcal{H}}}_2+{\widehat{\mathcal{H}}}_3+{\widehat{\mathcal{H}}}_4)\mathsf{\tau }}=e^{-i{\widehat{\mathcal{H}}}_1\frac{\mathsf{\tau }}{2}}{e}^{-i{\widehat{\mathcal{H}}}_3\frac{\mathsf{\tau }}{2}}{e}^{-i{\widehat{\mathcal{H}}}_2\mathsf{\tau }}{e}^{-i{\widehat{\mathcal{H}}}_4\mathsf{\tau }}{e}^{-i{\widehat{\mathcal{H}}}_3\frac{\mathsf{\tau }}{2}}{e}^{-i{\widehat{\mathcal{H}}}_1\frac{\mathsf{\tau }}{2}}+O\left({\mathsf{\tau }}^3\right).$$

(6)

This is a second order expansion of the exponential, meaning that the associated error is $O\left({\mathsf{\tau }}^3\right)$, with $\mathsf{\tau }=t/N$. Consequently, Equation (6) gives a better approximation of the exact evolution for short t, while expansion 1 is preferable for long times. By exploiting Equation (6), the total number of gates per step is increased (four rotations and six conditional gates), but we can reduce the number of Trotter steps to $N=6$, while keeping (for small $\mathsf{\tau }$) a digital error similar to that obtained with $N=10$ steps in the first order decomposition. This reduces the total number of gates required for the simulation and leads to a better agreement between the expected and simulated evolution, reported in panel (b) of Figure 3.

4. Discussion

The proposed schemes for quantum information processing can be extended to finite chains of Cr₇Ni rings connected through interposed divalent ions. Similar one-dimensional chains have already been made, involving single Cr₇Ni units and rotaxanes [25]. The key step consists of including two functional groups per Cr₇Ni ring and per switch. The inclusion of two different functionalities is challenging but entirely feasible, as suggested in [20].

Given the ability to overcome these issues experimentally, it is crucial to gain a deeper insight into the theoretical scalability of the proposed schemes. Indeed, the extension of the two-qubit setup to a multi-qubit register raises some fundamental issues concerning the propagation of errors. In the proposed implementation, we can identify two main sources of error: decoherence, and the already mentioned imperfect operation of the switch. First, we notice that spin relaxation is substantially negligible in these systems [26]. Hence, the harmful effect of decoherence is mainly associated with the pure dephasing of the qubits and of the switch. The corresponding errors increase with the overall computational time. We stress that the proposed platform allows us to simultaneously manipulate non-overlapping parts of the register, thus drastically reducing the computation time and decoherence-induced errors with respect to a serial implementation. This limits the class of target Hamiltonians which can be simulated, but greatly increases the performance of the setup, by reducing the computational time. Suppose, for instance, that we need to induce a two-qubit evolution on each pair of neighboring qubits (as in the simulation of many translationally invariant Hamiltonians). This can be performed first by simultaneously turning on the interaction between all the $n/2$ “even" bonds, and then simultaneously on the remaining $n/2$ “odd” bonds. As stated above, excitations of the “even” switches can be made spectroscopically distinguishable from the excitation of the “odd” switches by proper chemical engineering.

We now examine the scaling of the errors with the number of qubits in the register. Both the effect of decoherence and of the residual inter-qubit interaction are enhanced by increasing the number of qubits, since they influence idle and manipulated qubits on an equal footing. It can be shown [27] that the total decoherence error ($\mathsf{\epsilon }=1-{\mathcal{F}}^2$) on a set of non-interacting qubits scales as $\mathsf{\epsilon }\propto n\frac{t}{T_2}$ (per Trotter step). It is worth noting that, in a parallel implementation, t is limited by the value it assumes for a chain of three qubits, whereas in a serial scheme, it increases linearly with n. By proper chemical engineering of the qubits, $T_2$ as large as ∼15 $\mathsf{\mu }$s can be obtained, thus enabling the implementation of many quantum gates before degradation occurs [12].

We now analyze the effect of an imperfect operation of the switch on scalability. As a consequence of the always-on residual interaction, an unwanted evolution of the qubits is induced, even in the idle configuration. The effect of this imperfect decoupling between the qubits increases with n, thus limiting the maximum number of qubits which can be independently rotated. As noted above, the gap between $|01\rangle$ and $|10\rangle$ states leads to a non-linear scaling of the unwanted evolution time with $1/\mathsf{\Gamma }$. For instance, by halving the Co-ring exchange interaction, we gain an order of magnitude in the timescale of the unwanted interaction. Hence, the $\mathcal{AB}$ structure of the one-dimensional register is a key-resource for the scalability of the present setup. Other possible strategies to reduce the effect of the unwanted qubit–qubit residual coupling involve the use of $S>1/2$ switches with a sizeable zero-field splitting, which increases the gap between computational and auxiliary states, as reported in [19]. A further possibility to improve the performance of the switch would be to employ dimers or triangular spin units with a singlet ground state [18].

5. Conclusions

We have described a scheme for quantum information processing and digital quantum simulation on permanently-coupled molecular qubits. The proposed platform consists of a linear chain of Cr₇Ni rings, linked through Co²⁺ ions to form an $\mathcal{ABAB}$ register. By using uniform magnetic pulses as the only manipulation tool, many interesting model Hamiltonians can be simulated. To demonstrate the experimental feasibility of the scheme and the performance of the setup, we have performed extensive numerical experiments on subsets of two- and three-qubits by using state-of-the-art parameters. Finally, we have discussed the scalability of the proposed architecture.