Enhanced Magnetocaloric Effect and Single-Molecule Magnet Behavior in a Series of Sulfur-Containing Ligand-Based Ln9 Clusters (Ln = Gd, Tb, and Dy)
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials and Characterization
2.2. Syntheses of Complexes 1–3
2.3. Single-Crystal Structure Determination
3. Results and Discussion
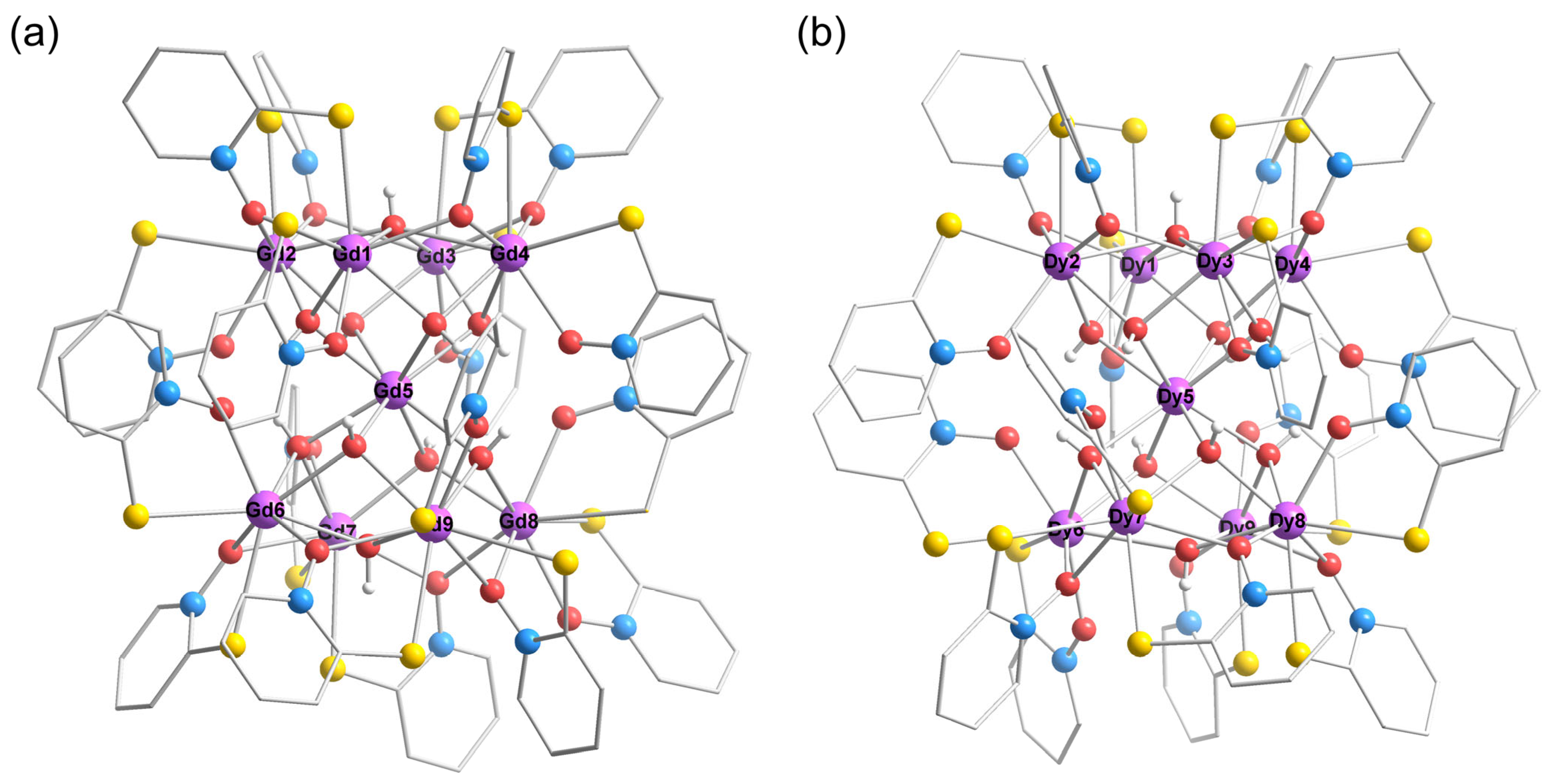
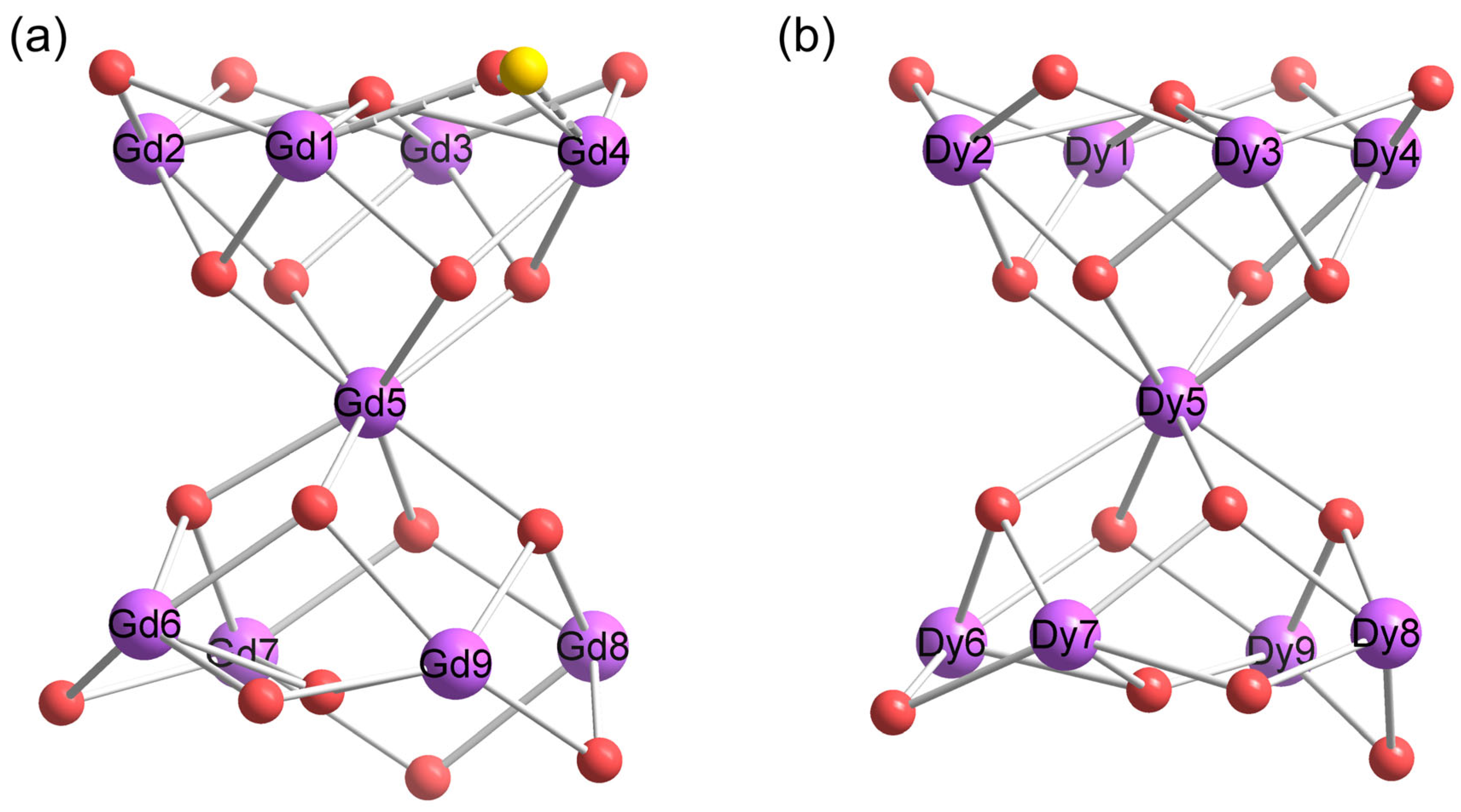
3.1. Crystal Structure
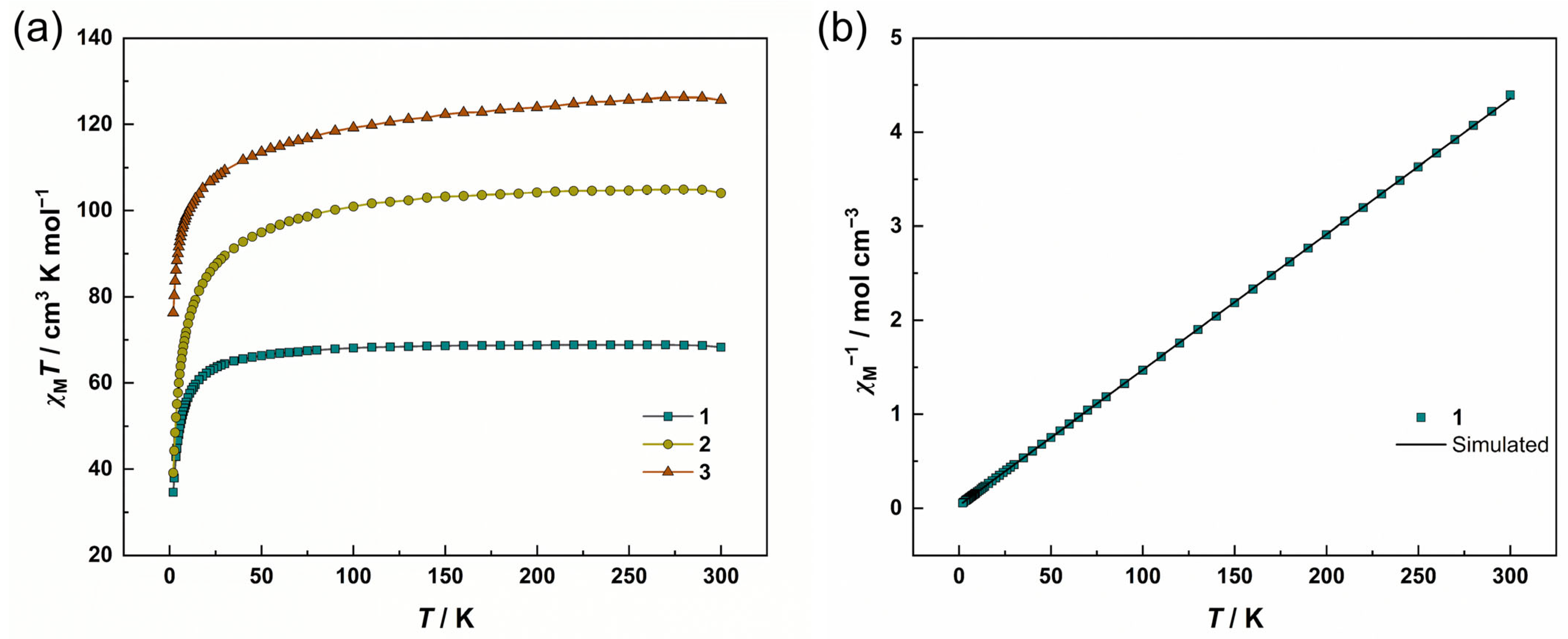
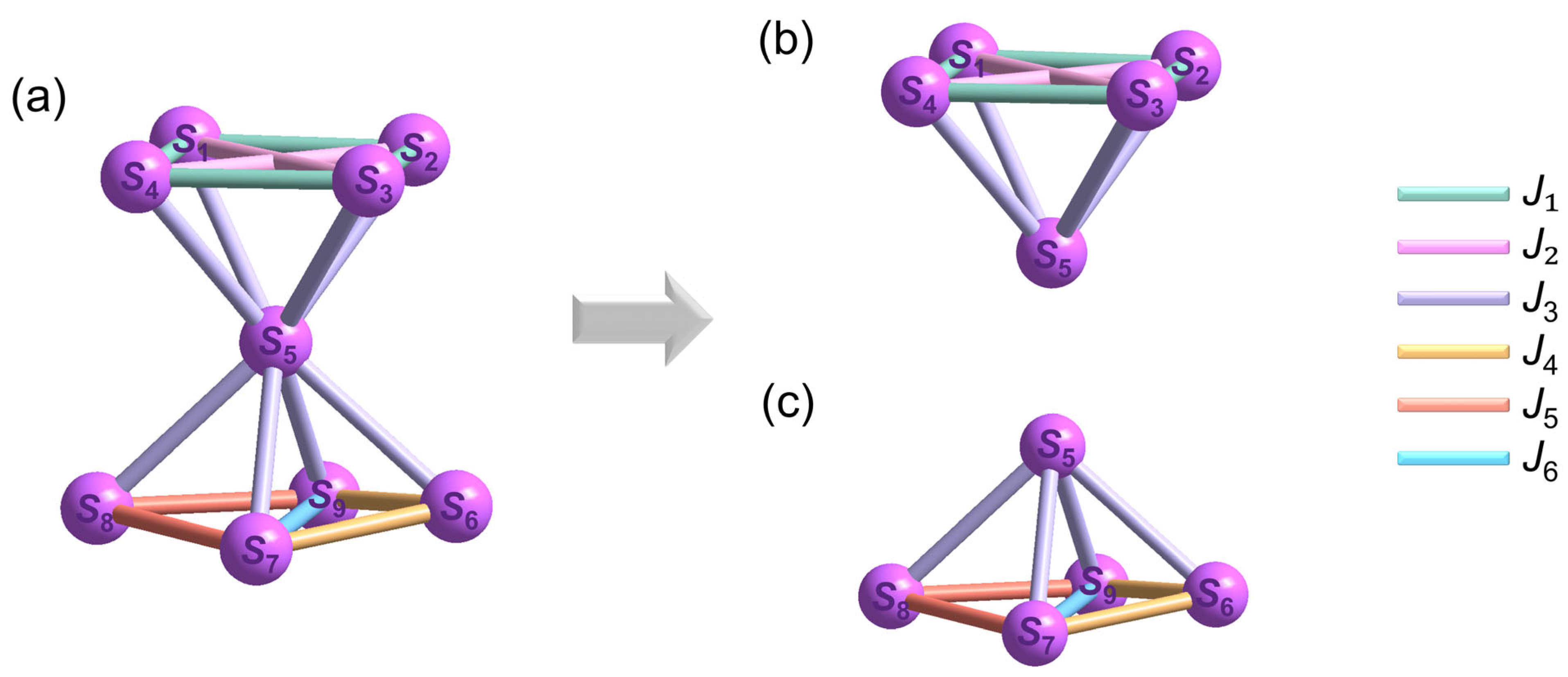
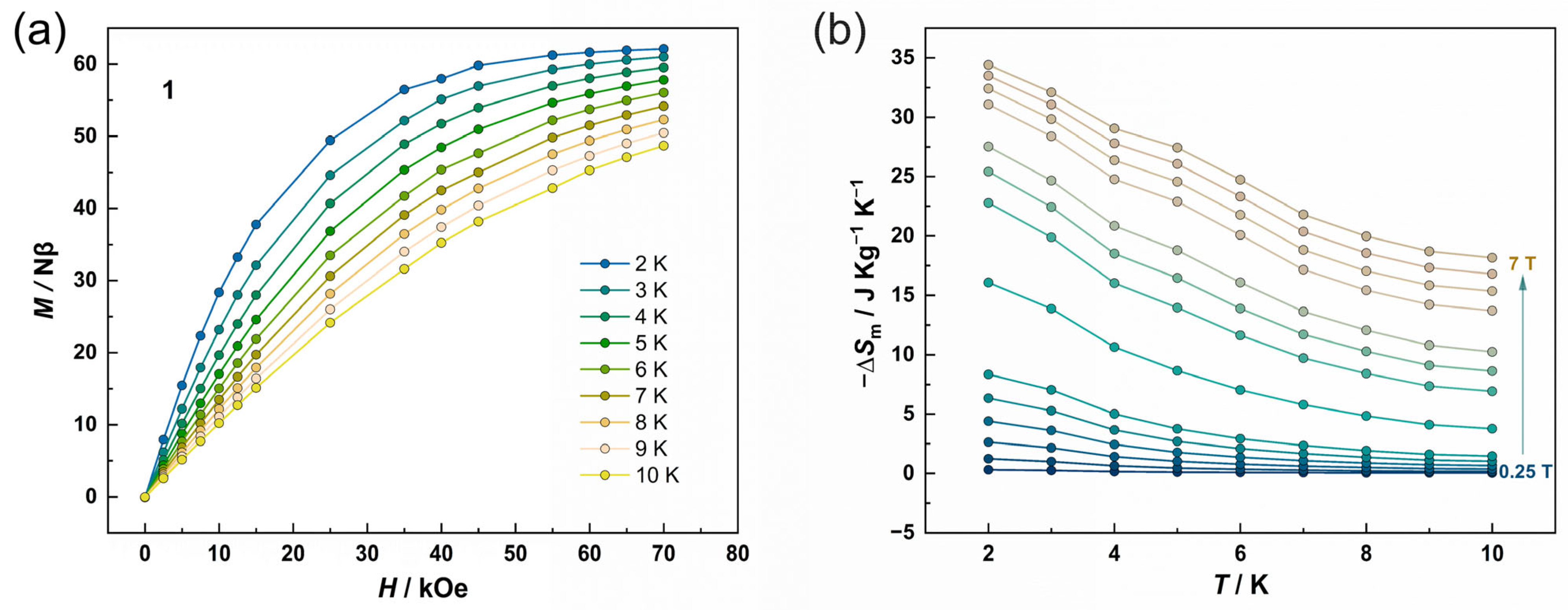
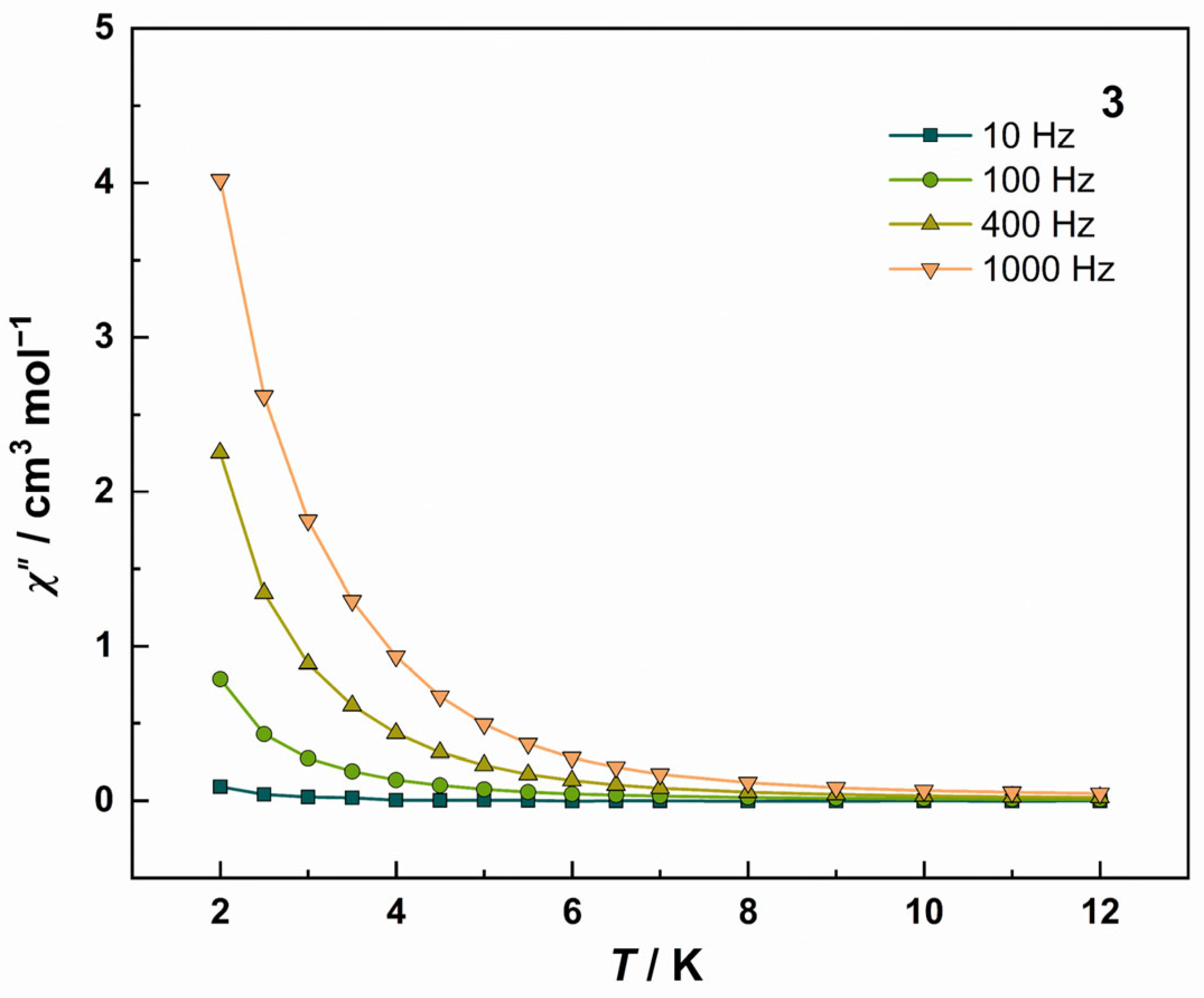
3.2. Magnetic Properties
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lucia, U.; Grisolia, G. Magnetocaloric refrigeration in the context of sustainability: A review of thermodynamic bases, the state of the art, and future prospects. Energies 2024, 17, 3585. [Google Scholar] [CrossRef]
- Zhao, S.; Wang, P.; Chen, W.; Wang, L.; Wang, Q.C.; Chen, W.Q. Supply and demand conflicts of critical heavy rare earth element: Lessons from gadolinium. Resour. Conserv. Recycl. 2023, 199, 1–9. [Google Scholar] [CrossRef]
- Nehan, P.Z.Z.; Vitayaya, O.; Munazat, D.R.; Manawan, M.T.E.; Darminto, D.; Kurniawan, B. The magnetocaloric effect properties for potential applications of magnetic refrigerator technology: A review. Phys. Chem. Chem. Phys. 2024, 26, 14476–14504. [Google Scholar] [CrossRef]
- Zheng, Y.-Z.; Zhou, G.-J.; Zheng, Z.; Winpenny, R.E.P. Molecule-based magnetic coolers. Chem. Soc. Rev. 2014, 43, 1462–1475. [Google Scholar] [CrossRef] [PubMed]
- Pecharsky, V.K.; Gschneidner, K.A. Magnetocaloric effect and magnetic refrigeration. J. Magn. Magn. Mater. 1999, 200, 44–56. [Google Scholar] [CrossRef]
- De Haas, W.J. Extremely low temperatures. Nature 1933, 132, 372–373. [Google Scholar] [CrossRef]
- Phan, M.H.; Yu, S.C. Review of the magnetocaloric effect in manganite materials. J. Magn. Magn. Mater. 2007, 308, 325–340. [Google Scholar] [CrossRef]
- Hu, J.J.; Peng, Y.; Liu, S.J.; Wen, H.R. Recent advances in lanthanide coordination polymers and clusters with magnetocaloric effect or single-molecule magnet behavior. Dalton Trans. 2021, 50, 15473–15487. [Google Scholar] [CrossRef]
- Konieczny, P.; Sas, W.; Czernia, D.; Pacanowska, A.; Fitta, M. Magnetic cooling: A molecular perspective. Dalton Trans. 2022, 51, 12762–12780. [Google Scholar] [CrossRef] [PubMed]
- Zhong, X.; Hu, J.-J.; Yao, S.-L.; Zhang, R.-J.; Wang, J.-J.; Cai, D.-G.; Luo, T.-K.; Peng, Y.; Liu, S.-J.; Wen, H.-R. Gd(III)-based inorganic polymers, metal-organic frameworks and coordination polymers for magnetic refrigeration. CrystEngComm 2022, 24, 2370–2382. [Google Scholar] [CrossRef]
- Fan, C.H.; Bai, K.P.; Luo, Q.C.; Han, T.; Huang, C.; Zheng, Y.Z.; Chen, W.P. A new family of SO42−-templated 3d-4f high-nuclearity clusters: Syntheses, structures, and magnetic properties. Chin. J. Chem. 2024, 42, 2438–2444. [Google Scholar] [CrossRef]
- Liu, S.J.; Han, S.D.; Zhao, J.P.; Xu, J.L.; Bu, X.H. In-situ synthesis of molecular magnetorefrigerant materials. Coord. Chem. Rev. 2019, 394, 39–52. [Google Scholar] [CrossRef]
- Liu, J.L.; Chen, Y.C.; Tong, M.L. Molecular design for cryogenic magnetic coolants. Chem. Rec. 2016, 16, 825–834. [Google Scholar] [CrossRef]
- Han, S.D.; Miao, X.H.; Liu, S.J.; Bu, X.H. Magnetocaloric effect and slow magnetic relaxation in two dense (3,12)-connected lanthanide complexes. Inorg. Chem. Front. 2014, 1, 549–552. [Google Scholar] [CrossRef]
- Zheng, X.Y.; Jiang, Y.H.; Zhuang, G.L.; Liu, D.P.; Liao, H.G.; Kong, X.J.; Long, L.S.; Zheng, L.S. A gigantic molecular wheel of {Gd140}: A new member of the molecular wheel family. J. Am. Chem. Soc. 2017, 139, 18178–18181. [Google Scholar] [CrossRef]
- Luo, X.M.; Hu, Z.B.; Lin, Q.F.; Cheng, W.W.; Cao, J.P.; Cui, C.H.; Mei, H.; Song, Y.; Xu, Y. Exploring the performance improvement of magnetocaloric effect based Gd-exclusive cluster Gd60. J. Am. Chem. Soc. 2018, 140, 11219–11222. [Google Scholar] [CrossRef] [PubMed]
- Zhitomirsky, M.E. Enhanced magnetocaloric effect in frustrated magnets. Phys. Rev. B 2003, 67, 1–7. [Google Scholar] [CrossRef]
- Chang, L.X.; Xiong, G.; Wang, L.; Cheng, P.; Zhao, B. A 24-Gd nanocapsule with a large magnetocaloric effect. Chem. Commun. 2013, 49, 1055–1057. [Google Scholar] [CrossRef]
- Ho, T.L. Hard soft acids bases (HSAB) principle and organic-chemistry. Chem. Rev. 1975, 75, 1–20. [Google Scholar] [CrossRef]
- Zheng, X.Y.; Kong, X.J.; Zheng, Z.P.; Long, L.S.; Zheng, L.S. High-nuclearity lanthanide-containing clusters as potential molecular magnetic coolers. Acc. Chem. Res. 2018, 51, 517–525. [Google Scholar] [CrossRef]
- Zheng, X.Y.; Xie, J.; Kong, X.J.; Long, L.S.; Zheng, L.S. Recent advances in the assembly of high-nuclearity lanthanide clusters. Coord. Chem. Rev. 2019, 378, 222–236. [Google Scholar] [CrossRef]
- Iki, N.; Tanaka, T.; Hiro-oka, S.; Shinoda, K. Self-assembly of a trilanthanide(III) core sandwiched between two thiacalix[4] arene ligands. Eur. J. Inorg. Chem. 2016, 2016, 5020–5027. [Google Scholar] [CrossRef]
- Tian, H.W.; Hong, J.Q.; Wang, K.; del Rosal, I.; Maron, L.; Zhou, X.G.; Zhang, L.X. Unprecedented reaction mode of phosphorus in phosphinidene rare-earth complexes: A joint experimental-theoretical study. J. Am. Chem. Soc. 2018, 140, 102–105. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.P.; Wang, D.; Zhou, Z.H.; Zhao, G.Y.; Li, Q.; Bi, Y.F.; Zheng, Z.P. Thiacalix[4]arene-sandwiched sandglass-like Ln9 Clusters (Ln = Tb and Eu): Insights into the selective luminescence quenching properties by p-nitrobenzene derivatives. Inorg. Chem. 2022, 61, 20814–20823. [Google Scholar] [CrossRef] [PubMed]
- Ying, J.; Gao, N.; Mou, H.C.; Tian, A.X. Rare earth mono-substituted Keggin dimmers: Structures, electrochemical, supercapacitor and magnetic properties. J. Solid State Chem. 2022, 314, 1–11. [Google Scholar] [CrossRef]
- Ohama, K.; Komiya, M.; Yamatoya, T.; Sawamura, R.; Karashimada, R.; Gao, S.; Ozawa, Y.; Osada, K.; Aoki, I.; Nagasaki, T.; et al. Albumin nanoparticle electrostatically loaded with highly anionic Gd-thiacalixarene complex for MRI-guided neutron capture therapy. Colloids Surf., A 2024, 699, 1–13. [Google Scholar] [CrossRef]
- Marin, R.; Gálico, D.A.; Gayfullina, R.; Moilanen, J.O.; Carlos, L.D.; Jaque, D.; Murugesu, M. A zero-field single-molecule magnet with luminescence thermometry capabilities containing soft donors. J. Mater. Chem. C 2022, 10, 13946–13953. [Google Scholar] [CrossRef]
- Chen, S.M.; Xiong, J.; Zhang, Y.Q.; Yuan, Q.; Wang, B.W.; Gao, S. A soft phosphorus atom to "harden" an erbium(III) single-ion magnet. Chem. Sci. 2018, 9, 7540–7545. [Google Scholar] [CrossRef]
- Liu, S.S.; Lang, K.; Zhang, Y.Q.; Yang, Q.; Wang, B.W.; Gao, S. A distinct magnetic anisotropy enhancement in mononuclear dysprosium-sulfur complexes by controlling the Dy-ligand bond length. Dalton Trans. 2016, 45, 8149–8153. [Google Scholar] [CrossRef]
- Canaj, A.B.; Dey, S.; Céspedes, O.; Wilson, C.; Rajaraman, G.; Murrie, M. There is nothing wrong with being soft: Using sulfur ligands to increase axiality in a Dy(III) single-ion magnet. Chem. Commun. 2020, 56, 1533–1536. [Google Scholar] [CrossRef] [PubMed]
- Tziotzi, T.G.; Gracia, D.; Dalgarno, S.J.; Schnack, J.; Evangelisti, M.; Brechin, E.K.; Milios, C.J. A {Gd12Na6} molecular quadruple-wheel with a record magnetocaloric effect at low magnetic fields and temperatures. J. Am. Chem. Soc. 2023, 145, 7743–7747. [Google Scholar] [CrossRef]
- Braun, J.; Seufert, D.; Anson, C.E.; Tang, J.K.; Powell, A.K. An effectively uncoupled Gd8 cluster formed through fixation of atmospheric CO2 showing excellent magnetocaloric properties. Int. J. Mol. Sci 2024, 25, 264. [Google Scholar] [CrossRef]
- Wang, Y.F.; Wang, Y.X.; Yang, Q.Q.; Yin, B. Auxiliary rather than dominant. the role of direct Dy-S coordination in single-molecule magnet unveiled via ab initio study. J. Phys. Chem. A 2024, 128, 5285–5297. [Google Scholar] [CrossRef]
- Kumari, N.; Jassal, M.; Agrawal, A.K. Effect of metal ion on UV protective and antimicrobial properties of in-situ synthesized pyrithione complexes on cellulosic textiles. Mater. Today Commun. 2023, 34, 1–13. [Google Scholar] [CrossRef]
- Han, T.; Wang, X.Q.; Guo, T.; Cao, H.S.; Chen, W.P.; He, L. Modulation of the magnetic dynamics in two air-stable sulfur-ligated dysprosium complexes via polymerization. Dalton Trans. 2023, 52, 7551–7557. [Google Scholar] [CrossRef]
- Yuan, F.; Li, T.; Zhang, M.; Qian, H. Synthesis and crystal structure of tri(pyrithione) cerium complex and its catalytic property for oxidation of benzoin to benzil. Synth. React. Inorg. Met.-Org. Nano-Met. Chem. 2013, 43, 1510–1513. [Google Scholar] [CrossRef]
- Niu, D.Z.; Mu, L.L.; Lu, Z.S.; Song, B.L.; Sun, B.W. Synthesis and crystal structure of Pr3(DMSO)2 (Hmpo=2-mercaptopyridine N-oxide). J. Chem. Crystallogr. 2004, 34, 195–198. [Google Scholar] [CrossRef]
- Xiong, R.G.; Zuo, J.L.; You, X.Z.; Huang, X.Y. Synthesis and X-ray structure of the first lanthanide 2-mercaptopyridine N-oxide complex, tris-(1-hydroxy-2(1H)-pyridinethionato-O,S) bis sulfinylbis(methane) samarium(III). Polyhedron 1996, 15, 3321–3324. [Google Scholar] [CrossRef]
- Hu, Y.H.; Weng, L.H.; Huang, L.G.; Chen, X.T.; Wu, D.X.; Kang, B.S. Structure of tris(2-mercaptopyridine 1-oxido)cobalt(III) acetonitrile solvate. Acta Crystallogr. Sect. C Cryst. Struct. Commun. 1991, 47, 2655–2656. [Google Scholar] [CrossRef]
- West, D.X.; Frank, C.A. 2 series of rare-earth complexes of the 2-thiopyridine N-oxide anion. J. Inorg. Nucl. Chem. 1979, 41, 49–53. [Google Scholar] [CrossRef]
- Wang, T.; Wang, H.; Sun, W. Sandglass-like Ln9 nanoclusters with magnetocaloric effect and lanthanide-centered luminescence. Cryst. Growth Des. 2024, 24, 8076–8084. [Google Scholar] [CrossRef]
- Pandey, P.; Chauhan, D.; Walawalkar, M.G.; Gupta, S.K.; Meyer, F.; Rajaraman, G.; Murugavel, R. Hourglass-shaped homo- and heteronuclear nonanuclear lanthanide clusters: Structures, magnetism, photoluminescence, and theoretical analysis. Inorg. Chem. 2024, 63, 11963–11976. [Google Scholar] [CrossRef]
- Hu, P.; Li, S.H.; Cao, L.H.; Liu, A.G.; Zhuang, G.L.; Ji, L.D.; Li, B. Construction of a high nuclear gadolinium cluster with enhanced magnetocaloric effect through structural transition. Acs Omega 2022, 7, 38782–38788. [Google Scholar] [CrossRef]
- Casanova, D.; Cirera, J.; Llunell, M.; Alemany, P.; Avnir, D.; Alvarez, S. Minimal distortion pathways in polyhedral rearrangements. J. Am. Chem. Soc. 2004, 126, 1755–1763. [Google Scholar] [CrossRef]
- Panguluri, S.P.K.; Jourdain, E.; Chakraborty, P.; Klyatskaya, S.; Kappes, M.M.; Nonat, A.M.; Charbonnière, L.J.; Ruben, M. Yb-to-Eu cooperative sensitization upconversion in a multifunctional molecular nonanuclear lanthanide cluster in solution. J. Am. Chem. Soc. 2024, 146, 13083–13092. [Google Scholar] [CrossRef] [PubMed]
- Knighton, R.C.; Soro, L.K.; Lecointre, A.; Pilet, G.; Fateeva, A.; Pontille, L.; Francés-Soriano, L.; Hildebrandt, N.; Charbonnière, L.J. Upconversion in molecular hetero-nonanuclear lanthanide complexes in solution. Chem. Commun. 2021, 57, 53–56. [Google Scholar] [CrossRef] [PubMed]
- Hu, P.; Cao, L.H.; Liu, A.G.; Zhang, Y.Q.; Zhang, T.L.; Li, B. Modulating the relaxation dynamics via structural transition from a dinuclear dysprosium cluster to a nonanuclear cluster. Dalton Trans. 2021, 50, 12814–12820. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Qin, Y.R.; Ge, Y.; Cui, Y.F.; Zhang, X.M.; Li, Y.H.; Yao, J.L. Rationally assembled nonanuclear lanthanide clusters: Dy9 displays slow relaxation of magnetization and Tb9 serves as luminescent sensor for Fe3+, CrO42− and Cr2O72−. New J. Chem. 2019, 43, 19344–19354. [Google Scholar] [CrossRef]
- Griffiths, K.; Kühne, I.A.; Tizzard, G.J.; Coles, S.J.; Kostakis, G.E.; Powell, A.K. Twists to the spin structure of the Ln9-diabolo motif exemplified in two {Zn2Ln2}Ln9{Zn2} coordination clusters. Inorg. Chem. 2019, 58, 2483–2490. [Google Scholar] [CrossRef]
- Wang, H.S.; Long, Q.Q.; Yin, C.L.; Xu, Z.W.; Pan, Z.Q. Syntheses, crystal structures and magnetic properties of sandglass Dy9III and irregular tetrahedron Dy4III complexes. Polyhedron 2018, 141, 69–76. [Google Scholar] [CrossRef]
- Chen, H.F.; Yang, X.P.; Jiang, D.M.; Shi, D.L.; Zhang, L.J. Construction of NIR luminescent polynuclear lanthanide-based nanoclusters with sensing properties towards metal ions. Dalton Trans. 2018, 47, 13880–13886. [Google Scholar] [CrossRef]
- Zheng, X.Y.; Peng, J.B.; Livera, M.; Luo, Y.; Wang, Y.Y.; Kong, X.J.; Long, L.S.; Zheng, Z.P.; Zheng, L.S. Selective formation of chromogen I from N-acetyl-D-glucosamine upon lanthanide coordination. Inorg. Chem. 2017, 56, 110–113. [Google Scholar] [CrossRef]
- Mylonas-Margaritis, I.; Kitos, A.A.; Panteli, C.C.; Skordi, K.; Tasiopoulos, A.J.; Bekiari, V.; Escuer, A.; Perlepes, S.P. 2-hydroxybenzophenone-controlled self-assembly of enneanuclear lanthanide(III) hydroxo coordination clusters with an “hourglass”-like topology. Inorg. Chem. Commun. 2017, 83, 118–122. [Google Scholar] [CrossRef]
- Omagari, S.; Nakanishi, T.; Kitagawa, Y.; Seki, T.; Fushimi, K.; Ito, H.; Meijerink, A.; Hasegawa, Y. Critical role of energy transfer between terbium ions for suppression of back energy transfer in nonanuclear terbium clusters. Sci. Rep. 2016, 6, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Greisch, J.F.; Chmela, J.; Harding, M.E.; Klopper, W.; Kappes, M.M.; Schooss, D. Gas-phase photoluminescence characterization of stoichiometrically pure nonanuclear lanthanoid hydroxo complexes comprising europium or gadolinium. Inorg. Chem. 2016, 55, 3316–3323. [Google Scholar] [CrossRef] [PubMed]
- Zou, H.H.; Sheng, L.B.; Chen, Z.L.; Liang, F.P. Lanthanide nonanuclear clusters with sandglass-like topology and the SMM behavior of dysprosium analogue. Polyhedron 2015, 88, 110–115. [Google Scholar] [CrossRef]
- Omagari, S.; Nakanishi, T.; Seki, T.; Kitagawa, Y.; Takahata, Y.; Fushimi, K.; Ito, H.; Hasegawa, Y. Effective photosensitized energy transfer of nonanuclear terbium clusters using methyl salicylate derivatives. J. Phys. Chem. A 2015, 119, 1943–1947. [Google Scholar] [CrossRef]
- Nakanishi, T.; Suzuki, Y.; Doi, Y.; Seki, T.; Koizumi, H.; Fushimi, K.; Fujita, K.; Hinatsu, Y.; Ito, H.; Tanaka, K.; et al. Enhancement of optical faraday effect of nonanuclear Tb(III) complexes. Inorg. Chem. 2014, 53, 7635–7641. [Google Scholar] [CrossRef]
- Greisch, J.F.; Harding, M.E.; Schäfer, B.; Ruben, M.; Klopper, W.; Kappes, M.M.; Schooss, D. Characterization of nonanuclear europium and gadolinium complexes by gas-phase luminescence spectroscopy. J. Phys. Chem. Lett. 2014, 5, 1727–1731. [Google Scholar] [CrossRef]
- Zhang, B.; Xiao, T.; Liu, C.M.; Li, Q.; Zhu, Y.Y.; Tang, M.S.; Du, C.X.; Song, M.P. Systematic study of the luminescent europium-based nonanuclear clusters with modified 2-hydroxybenzophenone ligands. Inorg. Chem. 2013, 52, 13332–13340. [Google Scholar] [CrossRef]
- Singh-Wilmot, M.A.; Sinclair, R.A.; Andrews, M.; Rowland, C.; Cahill, C.L.; Murugesu, M. Nonanuclear lanthanide(III) nanoclusters: Structure, luminescence and magnetic properties. Polyhedron 2013, 53, 187–192. [Google Scholar] [CrossRef]
- Xu, X.B.; Zhao, L.; Xu, G.F.; Guo, Y.N.; Tang, J.K.; Liu, Z.L. A diabolo-shaped Dy9 cluster: Synthesis, crystal structure and magnetic properties. Dalton Trans. 2011, 40, 6440–6444. [Google Scholar] [CrossRef]
- Alexandropoulos, D.I.; Mukherjee, S.; Papatriantafyllopoulou, C.; Raptopoulou, C.P.; Psycharis, V.; Bekiari, V.; Christou, G.; Stamatatos, T.C. A new family of nonanuclear lanthanide clusters displaying magnetic and optical properties. Inorg. Chem. 2011, 50, 11276–11278. [Google Scholar] [CrossRef] [PubMed]
- Baril-Robert, F.; Petit, S.; Pilet, G.; Chastanet, G.; Reber, C.; Luneau, D. Site-selective lanthanide doping in a nonanuclear yttrium(III) cluster revealed by crystal structures and luminescence spectra. Inorg. Chem. 2010, 49, 10970–10976. [Google Scholar] [CrossRef]
- Petit, S.; Baril-Robert, F.; Pilet, G.; Reber, C.; Luneau, D. Luminescence spectroscopy of europium(III) and terbium(III) penta-, octa- and nonanuclear clusters with β-diketonate ligands. Dalton Trans. 2009, 6809–6815. [Google Scholar] [CrossRef] [PubMed]
- Volpe, M.; Bombieri, G.; Clemente, D.A.; Foresti, E.; Grillone, M.D. Synthesis and physico-chemical characterization of a new series of hydroxide ion acetylacetonate lanthanide(III)-ditungsten decacarbonyl hydride complexes. J. Alloys Compd. 2004, 374, 382–386. [Google Scholar] [CrossRef]
- Addamo, M.; Bombieri, G.; Foresti, E.; Grillone, M.D.; Volpe, M. Assembling process of charged nonanuclear cationic lanthanide(III) clusters assisted by dichromium decacarbonyl hydride. Inorg. Chem. 2004, 43, 1603–1605. [Google Scholar] [CrossRef]
- Xu, G.; Wang, Z.M.; He, Z.; Lu, Z.; Liao, C.S.; Yan, C.H. Synthesis and structural characterization of nonanuclear lanthanide complexes. Inorg. Chem. 2002, 41, 6802–6807. [Google Scholar] [CrossRef]
- Hubert-Pfalzgraf, L.G.; Miele-Pajot, N.; Papiernik, R.; Vaissermann, J. A novel example of self-assembly in lanthanide chemistry: Synthesis and molecular structure of Na(EtOH)6Y9(μ4-O)2(μ3-OH)8{μ-η2-MeC(O)CHC(O)OEt}8{η2-MeC(O)CHC(O)OEt}8. J. Chem. Soc. Dalton Trans. 1999, 4127–4130. [Google Scholar] [CrossRef]
- Chilton, N.F.; Anderson, R.P.; Turner, L.D.; Soncini, A.; Murray, K.S. PHI: A powerful new program for the analysis of anisotropic monomeric and exchange-coupled polynuclear d- and f-block complexes. J. Comput. Chem. 2013, 34, 1164–1175. [Google Scholar] [CrossRef]
- Singh, M.K.; Rajeshkumar, T.; Kumar, R.; Singh, S.K.; Rajaraman, G. Role of (1,3) {Cu-Cu} interaction on the magneto-caloric effect of trinuclear {CuII-GdIII-CuII} complexes: Combined DFT and experimental studies. Inorg. Chem. 2018, 57, 1846–1858. [Google Scholar] [CrossRef] [PubMed]
- Rajeshkumar, T.; Singh, S.K.; Rajaraman, G. A computational perspective on magnetic coupling, magneto-structural correlations and magneto-caloric effect of a ferromagnetically coupled {GdIII-GdIII} pair. Polyhedron 2013, 52, 1299–1305. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Geng, Y.-W.; Guo, T.; Wang, X.-Q.; Han, T. Enhanced Magnetocaloric Effect and Single-Molecule Magnet Behavior in a Series of Sulfur-Containing Ligand-Based Ln9 Clusters (Ln = Gd, Tb, and Dy). Magnetochemistry 2025, 11, 70. https://doi.org/10.3390/magnetochemistry11090070
Geng Y-W, Guo T, Wang X-Q, Han T. Enhanced Magnetocaloric Effect and Single-Molecule Magnet Behavior in a Series of Sulfur-Containing Ligand-Based Ln9 Clusters (Ln = Gd, Tb, and Dy). Magnetochemistry. 2025; 11(9):70. https://doi.org/10.3390/magnetochemistry11090070
Chicago/Turabian StyleGeng, Ya-Wei, Tong Guo, Xiao-Qin Wang, and Tian Han. 2025. "Enhanced Magnetocaloric Effect and Single-Molecule Magnet Behavior in a Series of Sulfur-Containing Ligand-Based Ln9 Clusters (Ln = Gd, Tb, and Dy)" Magnetochemistry 11, no. 9: 70. https://doi.org/10.3390/magnetochemistry11090070
APA StyleGeng, Y.-W., Guo, T., Wang, X.-Q., & Han, T. (2025). Enhanced Magnetocaloric Effect and Single-Molecule Magnet Behavior in a Series of Sulfur-Containing Ligand-Based Ln9 Clusters (Ln = Gd, Tb, and Dy). Magnetochemistry, 11(9), 70. https://doi.org/10.3390/magnetochemistry11090070




