Abstract
The article is devoted to the theoretical development of the mechanisms of molecular refrigeration, the area combining molecular magnetism and material science with promise for low-temperature physics and quantum computing, where conventional principles of refrigeration become inefficient. Given this general trend, we propose the concept of the magnetothermal effect in magnetically anisotropic complexes of 3d metal ions, caused by fast magnetic field quenching. Within this concept, the most topical case of an axially magnetically anisotropic system isolated from the environment by adiabatic envelope is analyzed. We evaluate the temperature change as a function of the initial temperature and magnetic field and also its dependence on the sign and the magnitude of the axial zero-field splitting parameter and the Debye temperature. Correlations are revealed between the sign of the magnetic anisotropy (dictated by the sign of the axial zero field splitting parameter) and the sign of the thermal effect (heating versus cooling) caused by field quenching. The temperature change is shown to be negative (cooling) in the case of complexes exhibiting easy-axis-type magnetic anisotropy, while for the case of easy-plane-type anisotropy, it proves to be positive (heating). The thermal effects are shown to have an efficient control by varying the initially applied field. These findings allow us to propose complexes exhibiting easy-axis-type magnetic anisotropy as candidates for achieving a low-temperature refrigeration effect caused by fast field quenching and also to employ the established magnetothermal correlations to the analysis of magnetic anisotropy.
1. Introduction
The magnetocaloric effect (MCE) represents the basis for attractive refrigeration technologies for commercial and cryogenic applications [1,2,3,4] and also for better understanding of the magneto-physical properties of magnetic materials. Most studies in this area are devoted to the creation of efficient refrigerants operating at nearly room temperature; however, refrigerants functioning at low and ultra-low temperatures [1,3,4] are an important as well as cost-effective alternative to dilution refrigerants using a mixture of 3He and 4He isotopes. Recently, the problem of finding low-temperature coolants has become increasingly important in connection with the development of quantum computers requiring cryogenic conditions for operating. While magnetically ordered crystals are promising as coolants operating at room temperatures, molecular nanomagnets can act as coolants, demonstrating MCE at low temperatures [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23]. To date, extensive research devoted to MCE has been carried out. Polynuclear high-spin clusters of 3d metals [11,12,13,14,15,16,17,18,19], lanthanide-based clusters [20,21], and mixed 3d-4f structures of various topology have been shown to be promising as magnetic coolants [22,23]. Some dimeric and monomeric 4f-based compounds exhibit significant MCE [24,25,26,27]. The mononuclear 3d metals-based systems with spin S = 5/2 [28], S = 3/2 [29], and S = 1 [30,31], which possess little anisotropy, have been shown to exhibit relatively high MCE. Important advances in the field of MCE have been achieved by using crystalline systems. Very recently, the low-temperature magnetocaloric responses in solid-state magnets have been extensively studied with the aim to develop high-performing MC materials for magnetic refrigeration and in-depth understanding of their magneto physical characteristics [32,33,34]. Thus, in ref. [32], a remarkable low-temperature magnetocaloric response in GdNaGeO4 oxide was discovered, and this system was found to be an excellent candidate for application in low-temperature magnetic refrigeration. The influence of substitutions (Fe, Mn, Cu, and Al) on the magnetic properties and magnetocaloric effect of the GdCo2 compounds was revealed in ref. [33]. Finally, the new material Gd11O10(SiO4)(PO4)3 for cryogenic magnetic refrigeration application was synthesized, and its structure, magnetic properties, and cryogenic magnetocaloric performances were studied in detail [34].
Noting the achievements reached in the field of solid-state magnetic resonance, it is also necessary to mention the undoubted advantages of nanomagnets, which include the possibility of the chemical control of their structure and properties (especially magnetic anisotropy [5,6,7]) to achieve maximum effect. Although high anisotropy is generally considered undesirable, highly anisotropic compounds are ideal candidates for observing the so-called rotational MCE [8,9], where the field can be effectively modulated by rotating the sample. This method not only allows the use of highly anisotropic clusters but also enables rapid switching of the field when needed [10].
Recently, we analyzed the magnetothermal processes expected in mononuclear magnetically anisotropic paramagnetic complexes of 3d ions [35], which are induced, as in the conventional MCE, by changing the magnetic field. However, unlike traditional approaches in the MCE area, we focused on the case when the field is switched off “suddenly”, which leads to a violation of the thermodynamic equilibrium between different parts of the system. A similar approach has been reported in refs. [36,37] dealing with the modeling of non-equilibrium magnetothermal processes in Heisenberg-type and Ising-type dimers. The classical definition of MCE assumes that quasi-equilibrium reversible processes generated by the relatively slow change of the magnetic field do not involve the spin–lattice relaxation. Although, according to the adopted terminology, the magnetothermal effect considered in [35,36,37] cannot be referred to as MCE, these two kinds of effects are somewhat close in nature. The approach developed in refs. [35,36,37] assumes the experimental conditions of the efficient heat exchange between the magnetic molecule and its surroundings so that the system maintains the same temperature at the end of the relaxation process as that which existed before the field switching off. The quantitative measure of such process is the heat release, which is the thermal energy passing as heat from the spin subsystem composed of anisotropic mononuclear 3d metal complexes to the phonon bath and further on to the surrounding area or from the surrounding area to the phonon bath and then to the spin subsystem depending on the sign of the thermal effect.
An even more interesting experimental situation may occur when the sample is isolated from its surrounding with an adiabatic envelope. Under this condition, sudden magnetic field switching off is expected to lead to increasing or decreasing temperature depending on the sign of the thermal effect. To evaluate the temperature change, the theoretical approach developed in [35,36,37] should be essentially modified. A new approach and its application to the analysis of the thermal effects are discussed in this article.
2. Theoretical Approach
We consider a mononuclear 3d metal complex with spin S = 1 (e.g., high-spin Ni(II) complex) exhibiting axial magnetic anisotropy. Magnetic anisotropy in magnetic materials and metal clusters has long been studied in connection with the EPR, and this fundamental property of magnetic materials has become even more relevant in the development of field of single molecular magnets (for a detailed overview, see ref. [38]).
Such a complex is described by the following spin-Hamiltonian:
The first term in Equation (1) is the axial zero-field splitting (ZFS) operator, where D is the axial ZFS parameter (for a detailed overview, see ref. [38]), is the spin-projection operator, and Z is the anisotropy axis. The second term represents the Zeeman interaction, where is the external magnetic field, which is applied along the Z axis; is the axial g-tensor component; is the Bohr magneton. Depending on the sign of the parameter D, the system can exhibit either easy-axis-type magnetic anisotropy (D < 0) or easy-plane-type anisotropy (D > 0).
Although we consider only a fairly simple S = 1 system to illustrate the background of the proposed concept, the main results seem to extend to complexes possessing arbitrary spin values. In fact, the basic Hamiltonian describing anisotropy, Equation (1), is applicable to any spin value, while the remaining evaluations for the high spin values remain the same, but of course, the expressions become more complex. In particular, the expressions for the energy levels, Equation (2), yield simple generalization. At the same time, for , the spin-Hamiltonian involves high-order terms (), but the corresponding contributions are usually small and should be taken into account when the experimental data (for instance, EPR) clearly indicate their presence.
The eigenvalues of the Hamiltonian, Equation (1), are the following:
Figure 1 shows the field dependences of the eigenvalues, Equation (2), evaluated for two signs of D. It is seen that at D < 0 (Figure 1a), the zero-field ground state of the system is the doublet , while the excited state is the singlet . In the field directed along the anisotropy axis, the ground doublet is split in such a way that the Zeeman sublevel with proves to be the ground state. This is a case of an easy-axis-type magnetic anisotropy. At D > 0, the —state is the ground one at zero field (Figure 1b). This state is non-magnetic, so we deal with the easy-plane-type anisotropy. In this case, at non-zero field, the ground state depends on the ratio between the Zeeman energy and the ZFS parameter D. In the case of a weak field, i.e., , the ground state possesses , while for a strong field, i.e., , the Zeeman sublevel with becomes the ground state. Below, we show that this difference in the energy spectra related to the cases of D < 0 and D > 0 determines the difference in the thermal effect (cooling versus heating) caused by fast magnetic field switching off. It is also demonstrated that the difference between the weak and the strong field cases in systems with D > 0 proves to be important, although the thermal effect does not depend on the field.
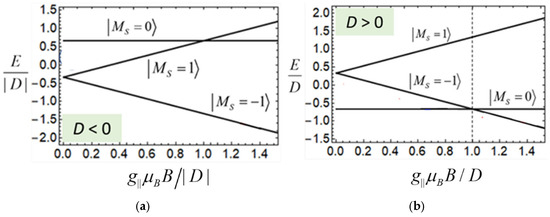
Figure 1.
Field dependencies of the energies of the mononuclear complex, with S = 1 exhibiting axial magnetic anisotropy with D < 0 (a) and D > 0 (b). Magnetic field is directed along the anisotropy axis. The Zeeman levels are characterized by the magnetic quantum number MS.
It is convenient to set the zero-field level as a reference energy so that the eigenvalues of the Hamiltonian, Equation (1), acquire the following form:
Let us assume that at the beginning of the process, the system is exposed to the magnetic field B directed along the anisotropy axis Z, and it is in a thermodynamic equilibrium state characterized by temperature T. Taking into account Equation (3), one obtains the following expressions for the Boltzmann populations of the spin states:
where kB is the Boltzmann constant, and the denominator in these expressions represents a partition function. At fast field switching off, the energy exchange between the spin subsystem and the thermal bath does not have time to occur, so the same populations also remain immediately after field switching off. However, these populations reach non-equilibrium because the energy pattern is changed when the field is switched off. It is also notable that the temperature of the phonon subsystem does not change in the course of the switching off event and remains equal to the temperature T, which characterizes the initial (before the field switching off) equilibrium state.
In course of the subsequent relaxation process, the system comes to the new equilibrium state characterized by the final temperature Tfin. Immediately after the field is switched off, the internal energy of the spin subsystem is given by the sum of the zero-field spin-state energies weighted by their populations defined in Equation (4):
where is the Avogadro constant, and the symbol init is used to specify the internal energy of the spin subsystem at the beginning of the relaxation process. With the adopted choice of the reference energy, i.e., one obtains
In the subsequent relaxation process, the heat exchange occurs between the spin subsystem and the phonon bath, in course of which the final (fin) equilibrium state is established. This final state is characterized by the following Boltzmann populations of the zero-field states:
This allows us to write down the following expression for the final internal energy of the spin subsystem:
The thermal balance in the entire system, including spin subsystem and phonon bath, is maintained provided that
where is the heat capacity of the phonon subsystem, which comes from the acoustic phonons. It is assumed that the temperature is low enough that the optical phonon branches are not excited. In this particular but important case, the phonon heat capacity can be described by the Debye law:
where is the Debye temperature. The number of oscillating units in Equation (10) is assumed to be the same as the number of spins in Equation (5), which seems to be a good approximation as applied to the long-wave acoustic phonons participating in phonon heat capacity, when each spin complex can be imagined to be oscillating as a whole. Then, one obtains
Substitution of Equations (6), (8) and (11) into Equation (9) results in the following final equation for :
By solving this equation, we find as a function of the initial temperature T and also the temperature change as a function of T.
The approach described so far can be reformulated in terms of the so-called “spin temperature”. The latter can be used to describe a nonequilibrium state in certain systems, particularly those with strong spin–lattice interactions. While equilibrium states are characterized by a uniform temperature throughout the volume, nonequilibrium states can exhibit spatially varying temperatures or a temperature different from the temperature of a system in equilibrium with its environment.
Within this approach, it is assumed that the nonequilibrium state of the spin subsystem, formed immediately after the field is switched off, can be treated as a quasi-equilibrium state, with the term “equilibrium” referring exclusively to the spin subsystem and not to the entire system. This state is characterized by a spin temperature that differs from the temperature of the phonon subsystem (the latter remains unaffected by the rapid field switching off and retains its initial temperature T). The initial internal energy of the spin subsystem is then expressed through the spin temperature as follows:
By equating Equations (6) and (13), one obtains the following expression for the spin temperature:
Now, the thermal balance condition can be written as follows:
where the value is the heat capacity of the spin subsystem. We thus obtain
By substituting Equations (16) and (11) into Equation (15), one arrives at the following final equation:
It should be emphasized that Equation (17) is equivalent to Equation (12) provided that is defined by Equation (14).
3. Results and Discussion
Figure 2 and Figure 3 show the series of the dependencies of the temperature change of the system induced by fast magnetic field switching off on the initial temperature T. The results are shown for various negative (Figure 2) and positive (Figure 3) values of D and various values of θD and B, provided that the system is isolated from the environment by an adiabatic shell. In all calculations, it is assumed that , which is in the typical range for Ni(II) complexes.
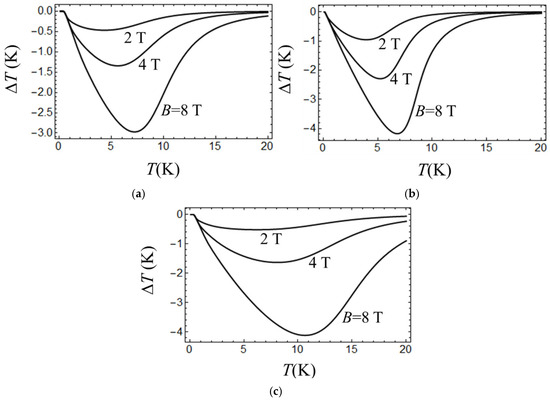
Figure 2.
Temperature change evaluated as function of the initial temperature T at D = −5 cm−1, θD = 100 K (a); D = −2 cm−1, θD = 100 K; (b) and D = −5 cm−1, θD = 200 K (c) and different values of the initial magnetic field shown in the plots.
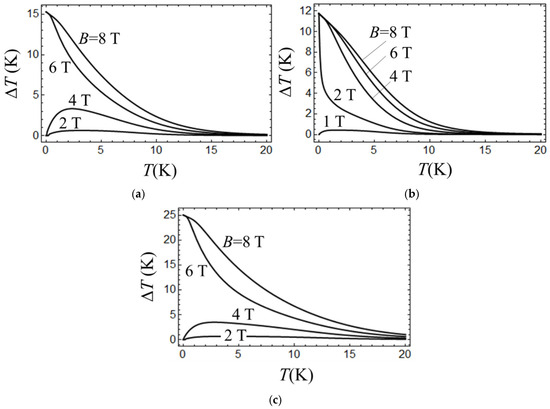
Figure 3.
The value evaluated as function of T at D = 5 cm−1, θD = 100 K (a); D = 2 cm−1, θD = 100 K; (b) and D = 5 cm−1, θD = 200 K (c) at different values of the magnetic field shown in the plots.
It follows from Figure 2 that at D < 0, the temperature change is negative (the temperature is decreased) at finite values of T, which means that sudden magnetic field switching off leads to the magnetic cooling in system with easy-axis-type magnetic anisotropy. This magnetic cooling disappears in the limits of low and high temperatures and reaches maximum at a finite temperature corresponding to the minimum in vs. T curve. By comparing curves in Figure 2a,b, one can see that decrease in the temperature is higher for larger ratio B/D, and its maximum is shifted towards higher T with the increase in this ratio (compare the curves in Figure 2a,b). It is also seen that the cooling effect is stronger for systems with higher θD (compare Figure 2a,c).
To better understand this behavior, let us focus on Figure 4, in which the temperature dependencies of the nonequilibrium populations of the energy levels (established immediately after the magnetic field is turned off) are compared with the corresponding equilibrium populations. Figure 4a shows these populations evaluated in the case of D < 0. The nonequilibrium populations of the ground and excited levels in this case are expressed as follows:
where and are the nonequilibrium populations of the states defined by Equation (4). Similarly, the equilibrium populations of the levels are the following:
where the equilibrium states populations are given by
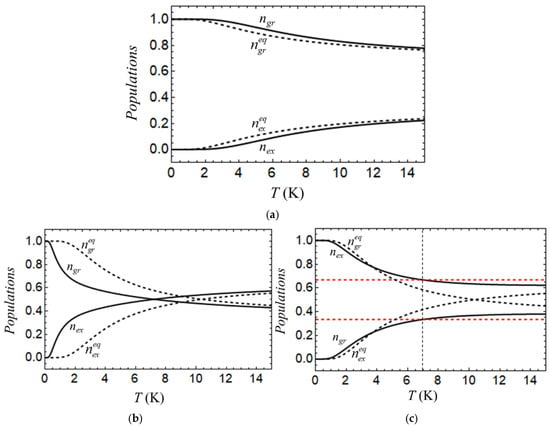
Figure 4.
Temperature dependencies of nonequilibrium populations ngr and nex of the ground and excited levels (solid black lines) arising upon fast magnetic field switching off: D = −5 cm−1, B = 4 T (a); D = 5 cm−1, B = 4 T (b); and D = 5 cm−1, B = 8 T (c). Temperature dependencies of equilibrium populations and of the ground and excited levels (dashed black lines) evaluated with the same D values at B = 0. At D < 0 (case (a)), the level with MS = ±1 is ground, and that with MS = 0 is excited, while at D > 0 (cases (b) and (c)), the ground and excited levels are those with MS = 0 and MS = ±1, respectively. Red dashed lines in case (c) show the equilibrium populations in the high-temperature limit.
It follows from Figure 4a that in the case of D < 0, the excited level with MS = 0 proves to be underpopulated, while the ground level with MS = ±1 is overpopulated, which means that in the course of subsequent spin–lattice relaxation, the heat is absorbed from the phonon subsystem, initially having the temperature T, to the spin system. As a result, the final temperature Tfin established in the system upon relaxation proves to be lower than T, as shown in Figure 2. It is also seen from Figure 4a that the difference between the equilibrium and nonequilibrium populations is vanishing in the low- and the high-temperature limits and passes through the maximum at some finite temperature. Comparing Figure 4a with Figure 2, one can see that just the maximal difference between the populations gives the greatest decrease in temperature.
In contrast, in the case of positive D values, is always positive at finite temperatures; i.e., sudden field switching off causes heating of the system (Figure 3), with the heating effect being stronger for larger B/D and/or higher θD. As distinguished from the case of D < 0, for D > 0, the shape of the curve proves to be dependent on whether < 1 (weak field) or > 1 (strong field). It is seen from the plots in Figure 3 that at weak field, is vanishing in the low-temperature limit, while at the finite temperatures, it increases with the increase in T, passes through the maximum, and finally decreases with further increase in T. On the other hand, at strong field, the low-temperature limit of tends to the nonzero value. In the latter case, the low-temperature limit of Tfin is shown to satisfy the following equation:
where . The increase in T in the case of strong field leads to a monotonic decrease in , as follows from the high-field plots in Figure 3 (see, e.g., the curves with B = 8 T and 6 T in Figure 3a).
The described features of the thermal process in the case of D > 0 can be understood by examining Figure 4b,c, which compare the equilibrium and nonequilibrium populations evaluated for this case. When D is positive, the equilibrium and nonequilibrium populations of the ground and excited levels are defined by Equations (22) and (23), respectively:
The nonequilibrium and equilibrium populations of the states, presented in the right parts of Equations (22) and (23), are given by Equations (4) and (20), respectively.
In the case of a weak field (Figure 4b), one obtains and , which means that fast magnetic field switching off creates a nonequilibrium state with an overpopulated excited level (MS = ±1 level, Figure 1b), while the ground level with MS = 0 is underpopulated. As a result, the heat is transferred from the spin subsystem to the phonon bath in course of the relaxation process, which leads to an increase in the temperature of the system relative to the initial temperature T. The difference in the equilibrium and nonequilibrium populations disappears in the low- and the high-temperature limits (Figure 4b), and hence, heating in these limits disappears as well.
The conditions and are also fulfilled for a strong magnetic field (Figure 4c), which is indicative of the heating process in this case. However, as distinguished from the above-considered cases in which the difference between the equilibrium and nonequilibrium populations of each level disappears in the low-temperature limit, now, this difference is maximal at T = 0 K, and it monotonically decreases with the increase in T. This explains the monotonic decrease in in the case of D > 0 and strong magnetic field, as described above (see, e.g., the curves with B = 8 T and 6 T in Figure 3a). Another notable feature of this case is the occurrence of inverted populations at low temperatures. In the high-temperature limit, the equilibrium population reaches its maximum value of 2/3 for the excited doublet (MS = ±1) and minimum value of 1/3 for the non-degenerate ground state (MS = 0). Population inversion occurs when the excited doublet level population exceeds 2/3 and falls for the singlet ground level below 1/3. For D = 5 cm−1 and B = 8 T (Figure 4c), these conditions are satisfied provided that T < 7 K.
Since the spin subsystem is effectively hotter in the nonequilibrium state with inverted population than in any state without it, the system exhibits greater heating when inversion occurs (compare the curves at high fields, where inversion takes place, with those at low fields in Figure 3).
The described features of the thermal processes can be also understood on the basis of the spin-temperature formalism introduced at the end of Section 2. Figure 5 shows the spin temperature Tspin evaluated as function of T for the cases of negative (Figure 5a) and positive (Figure 5b,c) D and different values of the magnetic field. It is seen that at D < 0, the spin temperature is lower than T (Figure 5a), which is the consequence of underpopulation of the excited level (Figure 4a). As a result, the heat is transferred from the phonons that initially have the temperature T to the spin subsystem whose spin temperature is lower than T, and hence, the final temperature Tfin established in course of the relaxation process proves to be lower than the initial temperature T. This is in accord with the negative sign of ΔT (see Figure 2). The difference T–Tspin is the increasing function of B (Figure 5a), which explains that cooling is more efficient for a higher magnetic field (compare, e.g., the curves in Figure 2a found for different B-values).
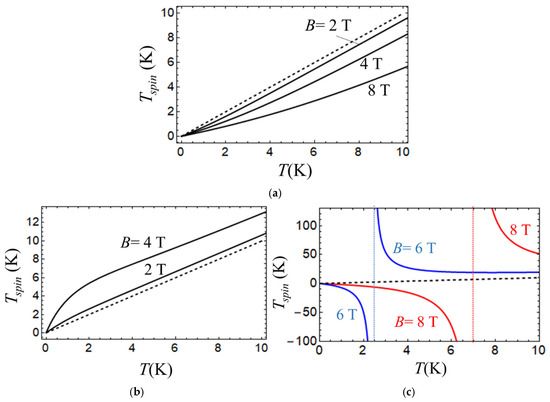
Figure 5.
Spin temperature evaluated as function of T at D = −5 cm−1 (a) and D = 5 cm−1 (b), (c) at different values of the magnetic field shown in the plots. To compare Tspin with T, the latter is also shown in the plots by dashed lines.
In contrast, at a positive D and weak field, the spin temperature is higher than T (Figure 5b) due to overpopulation of the excited level (see Figure 4b), so the heat is transferred from the spin subsystem to the phonons. As a result, the final temperature of the entire system is higher than the initial temperature T; that is, the system heats up. Figure 5b shows that the difference between Tspin and T increases with the increase in B, giving rise to stronger heating for a stronger initially applied field (see the plots in Figure 3, which are related to the weak field case). Finally, for D > 0 and a strong magnetic field, there are two ranges of T exhibiting different signs of Tspin (Figure 5c). Below some critical temperature Tc, the spin temperature becomes negative (Figure 5c), indicating population inversion at low T. For T > Tc, the spin temperature is positive and exceeds the lattice temperature, Tspin > T, as in the weak field case shown in Figure 5b.
The critical temperature Tc at which the spin temperature changes the sign is the temperature at which and . It follows from Figure 5c that Tc increases with the increase in the field. As indicated above, in the case of equilibrium distribution, such populations occur in the high-temperature limit. Then, the inverted populations (at and , Figure 4c) occurring at T < Tc correspond to the negative spin temperature. When T approaches Tc from the left, Tspin → −∞, while if T approaches Tc from the right, Tspin → +∞. Since the negative absolute temperatures are actually “higher” than all positive temperatures, including “infinite temperature”, in the case of Tspin < 0, the heat is also transferred from the spin subsystem to the phonons, giving rise to heating of the system ( > 0) in agreement with those plots in Figure 3, which are related to the strong field case.
4. Concluding Remarks
We studied the magnetothermal processes that are expected under fast (sudden) magnetic field switching off in 3d metal spin complexes exhibiting axial magnetic anisotropy. We focused on the relatively simple case of a complex with S = 1, at which the ZFS is operative. This work considers a magnetothermal process in an adiabatically confined system, where fast magnetic field switching off leads to a temperature change in the system. The approach developed here has allowed us to evaluate the temperature change ΔT as function of the initial temperature and magnetic field and also the dependence of ΔT upon the sign and the magnitude of the axial ZFS parameter and the Debye temperature.
The main result is the established correlation between the sign of the magnetic anisotropy parameter D and the sign of the thermal effect caused by the field quenching. It was demonstrated that ΔT is negative at D < 0 (cooling), while for D > 0, it is positive (heating). The revealed condition for cooling can be useful in the design of molecular-based refrigeration systems. It was also shown that cooling and heating can be effectively controlled by a varying magnetic field. Finally, it was demonstrated that the established magnetothermal correlations necessitate interpretation based on the analysis of nonequilibrium and equilibrium populations and also the application of spin-temperature formalism.
Author Contributions
Conceptualization, A.P. and B.T.; methodology, A.P., V.B. and B.T.; software, A.P. and V.B.; writing—original draft preparation, A.P., V.B. and B.T.; writing—review and editing, A.P. and B.T.; funding acquisition, A.P. and V.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Russian Science Foundation (Project No. 25-13-00010), Ministry of Science and Higher Education of the RF (No. 124013100858-3).
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding authors.
Acknowledgments
A.P. and V.B. acknowledge financial support from the Russian Science Foundation (Project No. 25-13-00010). The data previously obtained under financial support of the Ministry of Science and Higher Education of the RF and published in ref. [24] were used in the discussions (A.P. and V.B., state assignment No. 124013100858-3).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, Y.; Pan, H.; Liu, S. Research Progress of High Efficiency Magnetic Refrigeration Technology and Magnetic Materials. J. Supercond. Nov. Magn. 2025, 38, 86. [Google Scholar] [CrossRef]
- Paramanik, T.; Das, I. Near room temperature giant magnetocaloric effect and giant negative magnetoresistance in Co, Ga substituted Ni–Mn–In Heusler alloy. J. Alloys Compd. 2016, 654, 399–403. [Google Scholar] [CrossRef]
- Pełka, R.; Konieczny, P.; Zieliński, P.M.; Wasiutyński, T.; Miyazaki, Y.; Inaba, A.; Sieklucka, B. Magnetocaloric effect in {[Fe(pyrazole)4]2[Nb(CN)8]·4H2O} n molecular magnet. J. Magn. Magn. Mat. 2014, 354, 359–362. [Google Scholar] [CrossRef]
- Cao, H. Refrigeration below 1 kelvin. J. Low Temp. Phys. 2021, 204, 175–205. [Google Scholar] [CrossRef]
- Raza, A.; Perfetti, M. Electronic structure and magnetic anisotropy design of functional metal complexes. Coord. Chem. Rev. 2023, 490, 215213. [Google Scholar] [CrossRef]
- Konieczny, P.; Sas, W.; Czernia, D.; Pacanowska, A.; Fitta, M.; Pełka, R. Magnetic cooling: A molecular perspective. Dalton Trans. 2022, 51, 12762–12780. [Google Scholar] [CrossRef] [PubMed]
- Evangelisti, M.; Roubeau, O.; Palacios, E.; Camón, A.; Hooper, T.N.; Brechin, E.K.; Alonso, J.J. Cryogenic Magnetocaloric Effect in a Ferromagnetic Molecular Dimer. Angew. Chem. Int. Ed. 2011, 50, 6606–6609. [Google Scholar] [CrossRef] [PubMed]
- Konieczny, P.; Pełka, R.; Czernia, D.; Podgajny, D. Rotating Magnetocaloric Effect in an Anisotropic Two-Dimensional CuII [WV(CN)8]3– Molecular Magnet with Topological Phase Transition: Experiment and Theory. Inorg. Chem. 2017, 56, 11971–11980. [Google Scholar] [CrossRef] [PubMed]
- Konieczny, P.; Czernia, D.; Kajiwara, T. Rotating magnetocaloric effect in highly anisotropic TbIII and DyIII single molecular magnets. Sci. Rep. 2022, 12, 16601. [Google Scholar] [CrossRef]
- Beckmann, C.; Ehrens, J.; Schnack, J. Rotational magnetocaloric effect of anisotropic giant-spin molecular magnets. J. Magn. Magn. Mater. 2019, 482, 113–119. [Google Scholar] [CrossRef]
- Garlatti, E.; Carretta, S.; Schnack, J.; Amoretti, G.; Santini, P. Theoretical design of molecular magnets for magnetic refrigeration. Appl. Phys. Lett. 2013, 103, 202410. [Google Scholar] [CrossRef]
- Evangelisti, M.; Candini, A.; Ghirri, A.; Affronte, M. Spin-enhanced magnetocaloric effect in molecular nanomagnets. Appl. Phys. Lett. 2005, 87, 072504. [Google Scholar] [CrossRef]
- Evangelisti, M.; Candini, A.; Affronte, M.; Pasca, E.; de Jongh, L.J.; Scott, R.T.W.; Brechin, E.K. Magnetocaloric effect in spin-degenerated molecular nanomagnets. Phys. Rev. B 2009, 79, 104414. [Google Scholar] [CrossRef]
- Manoli, M.; Johnstone, R.D.L.; Parsons, S.; Murrie, M.; Affronte, M.; Evangelisti, M.; Brechin, E.K. A Ferromagnetic Mixed-Valent Mn Supertetrahedron: Towards Low-Temperature Magnetic Refrigeration with Molecular Clusters. Angew. Chem. Int. Ed. 2007, 46, 4456–4460. [Google Scholar] [CrossRef] [PubMed]
- Manoli, M.; Collins, A.; Parsons, S.; Candini, A.; Evangelisti, M.; Brechin, E.K. Mixed-valent Mn supertetrahedra and planar discs as enhanced magnetic coolers. J. Am. Chem. Soc. 2008, 130, 11129–11139. [Google Scholar] [CrossRef] [PubMed]
- Agapaki, E.; Charkiolakis, E.K.; Nichol, G.S.; Gracia, D.; Evangelisti, M.; Brechin, E.K. Magnetocaloric effect in a high-spin ferromagnetic molecular cluster. Front. Chem. 2024, 12, 1494609. [Google Scholar] [CrossRef]
- Affronte, M.; Ghirri, A.; Carretta, S.; Amoretti, G.; Piligkos, S.; Timco, G.A.; Winpenny, R.E.P. Engineering molecular rings for magnetocaloric effect. Appl. Phys. Lett. 2004, 84, 3468–3470. [Google Scholar] [CrossRef]
- Spichkin, Y.I.; Zvezdin, A.K.; Gubin, S.P.; Mischenko, A.S.; Tishin, A.M. Magnetic molecular clusters as promising materials for refrigeration in low-temperature regions. J. Phys. D Appl. Phys. 2001, 34, 1162–1166. [Google Scholar] [CrossRef]
- Evangelisti, M.; Luis, F.; de Jongh, L.J.; Affronte, M. Magnetothermal properties of molecule-based materials. J. Mater. Chem. 2006, 16, 2534–2549. [Google Scholar] [CrossRef]
- Zheng, X.Y.; Kong, X.J.; Zheng, Z.; Long, L.S.; Zheng, L.S. High-nuclearity lanthanide-containing clusters as potential molecular magnetic coolers. Acc. Chem. Res 2018, 51, 517–525. [Google Scholar] [CrossRef]
- Fang, M.; Dang, Y.; Ma, M.; Shao, Y.; Luan, Y.; Tang, Z.; Ma, Y.; Shi, B. Two tetranuclear lanthanide complexes respectively featuring magnetocaloric effect and slow magnetization relaxation. J. Mol. Struct. 2025, 1334, 141750. [Google Scholar] [CrossRef]
- Zheng, Y.-Z.; Evangelisti, M.; Winpenny, R.E.P. Co–Gd phosphonate complexes as magnetic refrigerants. Chem. Sci. 2011, 2, 99–102. [Google Scholar] [CrossRef]
- Zheng, Y.-Z.; Evangelisti, M.; Winpenny, R.E.P. Large Magnetocaloric Effect in a Wells–Dawson Type {Ni6Gd6P6}Cage. Angew. Chem. Int. Ed. 2011, 50, 3692–3695. [Google Scholar] [CrossRef]
- Chen, W.; Wang, J.; Yang, F.; Zhang, Y.; Li, L. Structural and magnetic properties of RE2O2SO4 (RE = Gd, Tb, Dy and Ho) oxides featuring large direct and inverse magnetocaloric effect. Ceram. Int. 2024, 50, 35706–35713. [Google Scholar] [CrossRef]
- Wu, B.; Zhang, Y.; Guo, D.; Wang, J.; Ren, Z. Structure, magnetic properties and cryogenic magneto-caloric effect (MCE) in RE2FeAlO6 (RE = Gd, Dy, Ho) oxides. Ceram. Int. 2021, 47, 6290–6297. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, B.; Li, S.; Zhu, J.; Wu, B.; Wang, J.; Ren, Z. Cryogenic magnetic properties and magnetocaloric effects (MCE) in B-site disordered RE2CuMnO6 (RE = Gd, Dy, Ho and Er) double perovskites (DP) compounds. Ceram. Int. 2021, 47, 18205–18212. [Google Scholar] [CrossRef]
- Das, M.; Roy, S.; Mandal, P. Giant reversible magnetocaloric effect in a multiferroic GdFeO3 single crystal. Phys. Rev. B 2017, 96, 174405. [Google Scholar] [CrossRef]
- Chen, Y.C.; Guo, F.S.; Liu, J.L.; Leng, J.D.; Vrábel, P.; Orendáč, M.; Tong, M.L. Switching of the magnetocaloric effect of MnII glycolate by water molecules. Chem. Eur. J. 2014, 20, 3029–3035. [Google Scholar] [CrossRef]
- Wang, S.; Wang, Y.; He, J.; Wang, D.; Bu, K.; Zhang, X.; Huang, F. Syntheses, crystal structures and magnetic properties of two new chromium chalcogenides Cr(en)3SbSe4 and Cr(en)2AsSe3. J. Alloys Compd. 2018, 768, 970–977. [Google Scholar] [CrossRef]
- Tarasenko, R.; Danylchenko, P.; Tkáč, V.; Orendáčová, A.; Čižmár, E.; Orendáč, M.; Feher, A. Experimental study of the magnetocaloric effect in [Ni(fum)(phen)]–The ferromagnetic dimer with spin 1. Phys. B Condens. Matter 2020, 576, 411671. [Google Scholar] [CrossRef]
- Danylchenko, P.; Tarasenko, R.; Čižmár, E.; Tkáč, V.; Uhrinová, A.; Orendáčová, A.; Orendáč, M. Experimental study of magnetocaloric effect in tetraaquabis (hydrogen maleato) nickel (II), [Ni(C4H3O4)2(H2O)4]—A potential realization of a spin-1 spatially anisotropic square lattice with ferromagnetic interactions. Magnetochemistry 2022, 8, 106. [Google Scholar] [CrossRef]
- Zhang, Y.; Na, Y.; Xie, Y.; Zhao, X. Unveiling the structural and magnetic properties of RENaGeO4 (RE = Gd, Dy, and Ho) oxides and remarkable low-temperature magnetocaloric responses in GdNaGeO4 oxide. J. Mater. Chem. A 2025, 13, 19923–19932. [Google Scholar] [CrossRef]
- Souca, G.; Dudric, R.; Küpper, K.; Tiusan, C.; Tetean, R. Band Structure Calculations, Magnetic Properties and Magneto-caloric Effect of GdCo1.8M0.2 Compounds with M = Fe, Mn, Cu, AI. Magnetochemistry 2024, 10, 53–73. [Google Scholar] [CrossRef]
- Chen, W.; Lin, J.; Wang, X.; Li, L. Structural, magnetic, and cryogenic magnetocaloric properties of Gd11O10(SiO4)(PO4)3 phosphosilicate. J. Magn. Magn. Mater. 2025, 626, 173107–173113. [Google Scholar] [CrossRef]
- Palii, A.; Tsukerblat, B. Thermal processes in anisotropic metal complexes induced by non-adiabatic switching of magnetic field. Dalton Trans. 2024, 53, 9161–9270. [Google Scholar] [CrossRef]
- Palii, A.; Belonovich, V.; Aldoshin, S.; Tsukerblat, B. Modelling thermal effects in Heisenberg dimers initiated by fast magnetic field switching off. J. Chem. Phys. 2025, 163, 024130. [Google Scholar] [CrossRef]
- Palii, A.; Belonovich, V.; Aldoshin, S.; Tsukerblat, B. Non-equilibrium magnetothermal effects in Ising dimers: Relevance to the problem of low-temperature magnetic refrigeration. Phys. Chem. Chem. Phys. 2025, 27, 16607–16619. [Google Scholar] [CrossRef]
- Boča, R. Zero-field splitting in metal complexes. Coord. Chem. Rev. 2004, 248, 757–815. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).