Abstract
Two iron(III) spin crossover complexes [Fe(5Cl-L)(NCS)] (1) and [Fe(5Cl-L)(NCSe)] (2) were synthesized with the pentadentate Schiff base ligand 5Cl-L and thiocyanato and selenocyanato as coligands. 5Cl-L, as an asymmetric {N3O2} donor Schiff base, was synthesized by a condensation reaction of 5-chlorosalicyladehyde using the asymmetric N-(2-aminoethyl)-1,3-propanediamine. The complexes exhibited a spin crossover at 280 (1) and 293 K (2), respectively, and were subjected to electron spin resonance (ESR) and Mössbauer spectroscopy at 77, 295 and 325 K. Ab initio CASSCF calculations followed by the NEVPT2 method were applied for predicting the g-tensor components as well as Mössbauer parameters.
1. Introduction
Since the first coordination compounds introduced by Cambi et al. showed the phenomenon of spin crossover in the early 1930s, there have been major developments in the field of these compounds that have also led to promising applications [1,2]. Numerous theoretical considerations of the effect and the associated mechanism have also been reported, especially for thermally induced spin transitions. These include a multitude of thermodynamic aspects and models [3]. In addition to thermally induced spin transitions, many other possible stimuli have been explored, i.e., light irradiation, which gave insights into the widely analyzed LIESST effect [4]. Besides physical stimuli, chemical stimuli like volatile organic compounds have also been reported, which were implemented into polymer matrices [5,6].
Mononuclear iron(III) complexes with a pentadentate N3O2-donor ligand L have been widely studied and these systems with an asymmetric ligand often show a spin transition/crossover (ST/SCO) [7,8,9,10,11,12,13,14,15]. The ligand field strength ΔLFS influences the enthalpy of the spin transition, ΔH ~ ΔLFS, and consequently the critical temperature T1/2 = ΔH/ΔS [16,17]. The ligand field strength can be tuned by a monodentate pseudohalido coligand positioned at the sixth coordination site [14,18,19,20,21,22,23].
Two iron(III) mononuclear complexes [Fe(5Cl-L)(NCS)] (1) and [Fe(5Cl-L)(NCSe)] (2) (5Cl-L is a pentadentate ligand resulting from the Schiff condensation of 5-chlorosalicylaldehyde with asymmetric N-(2-aminoethyl)-1,3-propanediamine) were identified as spin crossover systems (Figure 1) [23]. The spin transition is rather gradual with the onset around 150 K and completion near room temperature, where T1/2 = 280 K (1) and 293 K (2), respectively. The solid-state cooperativity is rather small in this class of complexes [16,17,23].
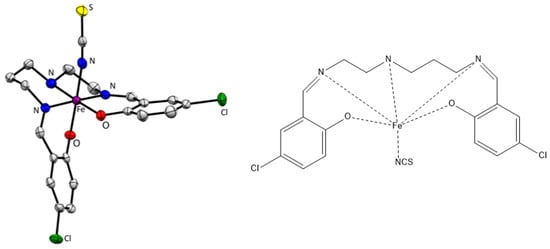
Figure 1.
Molecular structure of 1 at 100 K; thermal ellipsoids were drawn at a 50% probability level (ORTEP) [23].
An analogous system [Fe(3,5Cl-L)(NCSe)] with a bisubstituted ligand 3,5Cl-L shows a thermally induced spin crossover with a broad hysteresis width of 24 K between 123 K (warming) and 99 K (cooling). Other complexes of the [Fe(3,5X-L)(Y)] type with X = Cl or Br and Y = Cl−, N3−, NCS−, and NCSe− are in the high-spin state over the whole temperature interval [24].
In this study, we report the Mössbauer and electron spin resonance (ESR) data for 1 and 2. The molecular parameters extracted from the experimental data are compared with the ab initio calculations at the CASSCF + NEVPT2 and DFT level, respectively.
2. Results
2.1. Mössbauer Results
57Fe Mössbauer measurements were carried out for 1 and 2 at 77 K, 295 K and 325 K with the sample perpendicular to the γ-radiation source (Figure 2). The isomer shifts and quadrupole splitting for 1 and 2 at 295 K and 325 K show typical values for iron(III) in the high-spin state [25]. Additionally, these values for the Fe(III)-HS state are in good agreement with values from the literature for similar pentadentate Schiff base-based SCO complexes [26]. For 1 at 325 K, the asymmetric Lorentz fit resulted in an isomer shift δ = 0.287 mm·s−1 and a quadrupole splitting ∆EQ = 0.640 mm·s−1 (Table 1). In comparison to the values at 295 K, the isomer shift (δ = 0.285 mm·s−1) nearly stays the same while the quadrupole splitting (∆EQ = 0.870 mm·s−1) decreases. This indicates a higher symmetry of the ligand field caused by a stronger vibration of the ligand around the central ion, which is induced by the heating process. The ratio asymmetry of the full widths at half maximum (FWHM) and peak areas are due to increasing relaxation rates near the spin crossover point. As the temperature decreases to 77 K, the asymmetry disappears, which leads to the conclusion that the texture effect is temperature dependent on the condition that the crystal structure remains the same [27]. In addition, the spin–lattice relaxation rate decreases with lower temperature, as can be seen in the FWHM ratio (w/w’ = 1.029) [28]. The Lorentz fit exhibits an isomer shift (δ = 0.221 mm·s−1) and quadrupole splitting (∆EQ = 2.739 mm·s−1), which is characteristic for iron(III) in the LS state [25]. The relatively high quadrupole splitting can be explained by the asymmetric structural contribution of the pseudo-octahedral coordination, which can be observed following inspection of the ESR-g-components.
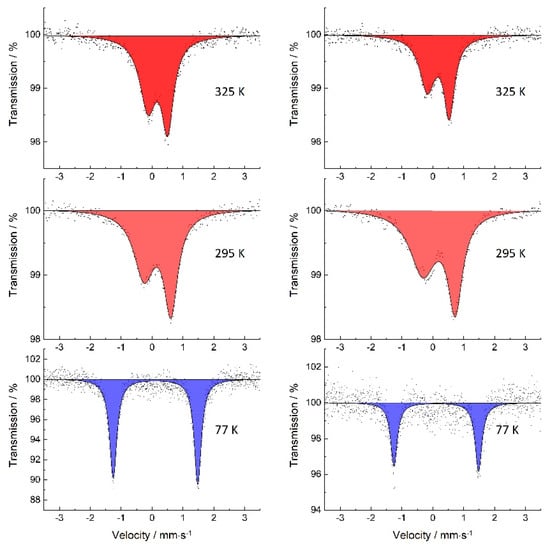
Figure 2.
57Fe Mössbauer spectra of 1 (left) and 2 (right) at 325 K (top) and at 298 K (middle) both in the HS state (S = 5/2) and at 77 K (bottom) in the LS state (S = 1/2).

Table 1.
Parameters of the Mössbauer spectra for 1 and 2.
Complex 2 shows a similar behavior. The values for isomer shift and quadrupole splitting Fe(III) in the HS state can also be assigned to this compound. This is shown by a comparison with existing literature [26]. In addition, the increasing quadrupole splitting from ∆EQ = 0.712 mm·s−1 at 325 K to ∆EQ = 1.3739 mm·s−1 at 295 K shows a stronger tendency compared to 1. For 1 and 2, the asymmetry of the peak areas A and A’ in the 77 K spectrum can be most likely assigned to texture effects arising from preferred crystal fracturing during the sample preparation [29].
2.2. Electron Spin Resonance Results
The ESR measurements were performed at 77 K and 295 K. The spectra of both samples show a low-spin state of iron(III) at 77 K (Figure 3). The components g1, g2 and g3 of the g-tensor (77 K) have only small differences (Table 2).
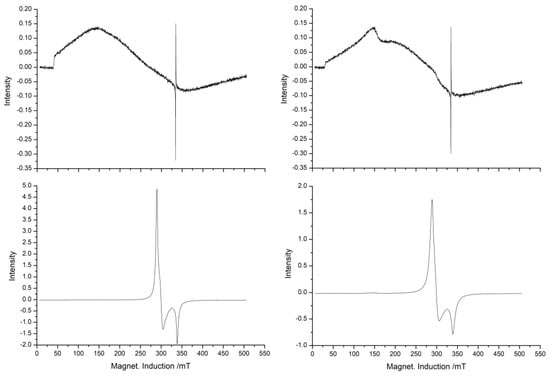
Figure 3.
ESR spectra of 1 (left) and 2 (right) at 295 K (top) and 77 K (bottom).

Table 2.
ESR parameters of sample 1 and 2.
At 295 K, compound 1 shows a rather broad absorption (ΔB ≈ 250 mT), which is dominated by strongly interacting high-spin states of the iron(III) ions. In addition, 2 demonstrates small absorption at g′ = 4.3, which is possibly caused by iron(III) ions in rhombical distorted polyhedrons.
The values of the FWHM at 298 K are 257 mT (1) and 252 mT (2) and 40.3 mT (1) and 46.0 mT (2) at 77 K. Using a Cu(II) reference sample, the spin densities were determined quantitatively for 1 with ~3.2 × 1021 spins/g and for 2 with ~1.8 × 1021 spins/g. Both spin density values are estimations due to the line broadness and the signal backgrounds. Differences in the spectra could be seen in the second derivative of the spectra taken at 77 K. Here, the signals of 1 are much broader than for 2, although the averages for 1 and 2 are nearly the same. The reasons for this may be statistical distributions of the g-components, or different equilibrium parts of the high-spin–low-spin equilibrium. In principle, these facts can also be observed in the results of the Mössbauer measurements. At 77 K, the values of δ and ΔEQ are the same for both samples. The absolute values of δ at 77 K can be seen in correspondence to the strong g-anisotropy (g1 – g3 = 0.317).
The ESR spectra taken at 295 K show differences in the shape, which are also in correspondence to the related Mössbauer spectra. During the transfer from 77 K to 295 K, the ΔEQ values became smaller (may be due to thermal fluctuations), but the δ values became larger. Moreover, the semi quantitative evaluation of the ESR-signals highlights the relationship of the spin numbers of [Fe(5Cl-L)(NCS)]:[Fe(5Cl-L)(NCSe)] = 1.81:1. This is in correspondence to the magnetic data [23].
2.3. Ab Initio Calculations
Low-temperature structures were used for the calculation, for which a low-spin state was proved on the basis of experimental data. The SA-CASSCF/NEVPT2 (ORCA 4.2.1) correctly predict the low-spin ground state for these complexes, whereas the first excited sextet state lies only ~800 cm−1 above it (Table 3). This proves the association of the spin crossover. The calculated values of the g-factor components reflect the presence of strong g-anisotropy, despite the slight inconsistency with experimental g-values. The DFT values of isomer shift and quadrupole splitting are, on the other hand, in good agreement with the experiment, which corresponds to the low-spin state of complexes 1 and 2 at ~100 K.

Table 3.
Calculated energies and key parameters for studied complexes.
3. Materials and Methods
3.1. Experimental Section
All reagents and solvents were purchased from Sigma Aldrich, St. Louis, MO, USA and used without further purification. Dark reddish-brown crystals of the complexes 1 and 2 were obtained by following the synthesis path described elsewhere [23].
[Fe(5Cl–L)(Cl)]: Calculated: C, 47.19%; H, 3.96%; N, 8.69%; C/N, 5.43. Found: C, 46.0%; H, 4.36%; N, 9.07%; C/N, 5.07; IR (ATR): v(N–H) = 3268 cm−1, v(C–H) = 2902 cm−1, v(C=N) = 1616 cm−1.
[Fe(5Cl–L)(NCS)] (1): Calculated: C, 47.4%; H, 3.78%; N, 11.1%; S, 6.33%; C/N, 4.29. Found: C, 46.2%; H, 3.72%; N, 11.0%; S, 6.50%; C/N, 4.20; IR (ATR): v(N–H) = 3248 cm−1, v(C–H) = 2927 cm−1, v(NCS) = 2101, 2061 cm−1, v(C=N) = 1610 cm−1.
[Fe(5Cl–L)(NCSe)] (2): Calculated: C, 43.4%; H, 3.46%; N, 10.1%; C/N, 4.29. Found: C, 41.5%; H, 3.39%; N, 9.64%; C/N, 4.30; IR (ATR): v(N–H) = 3233 cm−1, v(C–H) = 2927 cm−1, v(NCSe) = 2101, 2071 cm−1, v(C=N) = 1610 cm−1.
3.2. Mössbauer Measurements
The Mössbauer measurements were performed using a standard transmission spectrometer (Wissenschaftliche Elektronik GmbH, Ortenberg, Germany) at 77 K and a Miniaturized Mössbauer Spectrometer MIMOS II with the sample perpendicular with respect to the 57Co/Rh source at 295 K and 325 K in transmission mode. All isomer shifts were given relative to α-Fe at room temperature. The measurement time was less than 48 h. The data were plotted using OriginPro 8.5.1 and fitted with Recoil 1.05. The samples 1 and 2 were put into a spherical sample holder and the cap was subsequently rotated to align the crystals in the x-y-plane.
3.3. Electron Spin Resonance Measurements
The ESR measurements were conducted at 77 K and 295 K using an X-band spectrometer (ERS 300, ZWG/Magnettech, Berlin, Germany).
3.4. Ab Initio Calculations
All quantum-chemical calculations were performed with the ORCA 4.2.1 computational package using the X-ray structures of the studied complexes [30]. The relativistic effects were included in the calculations with zero-order regular approximation (ZORA) together with the scalar relativistic contracted version of the def2-TZVPP basis set for Fe atoms, def2-TZVP basis set for S, Se, N, O, Cl atoms and def2-SV(P) basis set for C, H atoms. Ab initio calculations were based on state average complete active space self-consistent field (SA-CASSCF) wave functions complemented by N-electron valence second-order perturbation theory (NEVPT2) [31,32,33,34,35]. The active space of the CASSCF calculations comprised of five electrons in five metal-based d-orbitals. The state averaged approach was used, in which all 10 triplet and 15 singlet states were equally weighted. For calculations, the RI approximation was used with appropriate decontracted auxiliary basis set and the chain-of-spheres (RIJCOSX) approximation for exact exchange. Increased integration grids (Grid4 and GridX5) and tight SCF convergence criteria were used. Energies of multiplets (Kramers doublets) were calculated through quasi-degenerate perturbation theory in which an approximation for the Breit–Pauli form of the spin–orbit coupling operator (SOMF) was utilized [36,37]. The g-factor components were calculated using the effective Hamiltonian theory.
In addition, the density functional theory (DFT) method has been used for calculation of the ESR and Mössbauer parameters. The ESR g-tensor was calculated through solution of the coupled-perturbed SCF equations using the hybrid PBE0 exchange–correlation functional in combination with the spin–orbit mean field representation of the spin–orbit coupling operator [38,39]. For the calculation of the Mössbauer parameters, the hybrid TPSSh functional was used along with CP(PPP) basis set for Fe atoms [40]. The isomer shifts δ were estimated using the formula δ = α(ρ0 − C) + β, where ρ0 is the electron density at the nucleus. The constants α, β and C are calibration parameters for a given DFT method [36,37,41].
4. Conclusions
We investigated two iron(III) spin transition complexes with an asymmetric N3O2 donor Schiff base ligand by Mössbauer and ESR spectroscopy. Mössbauer spectra were measured at a perpendicular angle at 77 K, 295 K and 325 K. The results of these measurements suggest that the texture effect can mostly be eliminated at low temperatures due to the reduced anisotropic mean-square vibrational amplitudes [28]. The spin–lattice relaxations can be observed by determination of the FWHM ratio. The remaining asymmetries could be assigned to the Goldanskii–Karyagin effect, but this is very unlikely given the studied complexes [29,42,43,44,45]. It should be noted that this effect is rare and has not yet been observed for the class of compounds described in this paper. Final clarification would only be possible by Mössbauer measurements below 77 K, but these could not be carried out in the context of this study [46]. Furthermore, by increasing the temperature up to 325 K, the FHWM and quadrupole splitting decrease due to the relaxation effects and the higher symmetry of the ligand field caused by a stronger vibration of the ligand around the central ion [47,48].
The ESR measurements, performed at 77 K and 295 K, are in good agreement with the Mössbauer results and the magnetic measurements [23]. In addition, the ESR line widths of the two compounds show that the spin–lattice relaxation of the electronic spins will be much faster at the approximation of room temperature. Therefore, the thermal fluctuations will be enlarged. This will result in an averaging out of the small spin couplings and modulation of the ESR fine structure in the HS-iron(III) spectra. This causes the broad ESR lines observed at room temperature [49,50].
Ab initio calculations support the existence of the low-spin state of 1 and 2 at 100 K and 120 K proved by SA-CASSCF/NEVPT2 calculations and DFT values of isomer shift and quadrupole splitting. The calculated g-values show a strong anisotropy, which was also observed in the ESR measurements, and are in correspondence with the isomer shifts at 77 K. The calculated Mössbauer parameters are in good agreement with the performed measurements.
The measured and calculated values shown provide further insight into the presented type of coordination compound. They can be used for future comparisons of similar complexes. This applies in particular to the Mössbauer values. Further investigations must be carried out in the future with nuclear forward scattering (NFS), nuclear inelastic scattering (NIS) or extended X-ray absorption fine structure (EXAFS) spectroscopy [51].
Author Contributions
Conceptualization, C.K. and M.S.K.; Investigation, J.T.; Supervision, F.R.; Writing—original draft, S.K. and R.L.; Writing—review and editing, M.M., B.E., R.S. and R.B. All authors have read and agreed to the published version of the manuscript.
Funding
Slovak grant agencies and the DAAD (D/SK) project are acknowledged for the financial support.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable
Data Availability Statement
Data are available from the corresponding author by requirement.
Acknowledgments
The Laboratory of Nano and Quantum Engineering (LNQE) of Leibniz University Hannover is acknowledged for their material support. Special thanks must be given to V. Ksenofontov and S. Shylin from the Johannes Gutenberg-University Mainz for their support with Mössbauer spectroscopy. The authors would like to dedicate this paper to Reinhard Stößer, who passed away during the writing of this manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Cambi, L.; Szegö, L. Berichte der deutschen chemischen Gesellschaft (A and B Series). Eur. J. Inorg. Chem. 1931, 64, 2591. [Google Scholar]
- Li, G.; Stefanczyk, O.; Kumar, K.; Guérin, L.; Okuzono, K.; Tran, K.; Kilic, M.S.; Nakabayashi, K.; Imoto, K.; Namai, A.; et al. Near-Infrared Light-Induced Spin-State Switching Based on Fe (II)–Hg (II) Spin-Crossover Network. Angew. Chem. Int. Ed. 2025, 64, e202423095. [Google Scholar] [CrossRef] [PubMed]
- Nicolazzi, W.; Bousseksou, A. Thermodynamical aspects of the spin crossover phenomenon. Comptes Rendus Chim. 2018, 21, 1060–1074. [Google Scholar] [CrossRef]
- Létard, J.F.; Capes, L.; Chastanet, G.; Moliner, N.; Létard, S.; Real, J.A.; Kahn, O. Critical temperature of the LIESST effect in iron (II) spin crossover compounds. Chem. Phys. Lett. 1999, 313, 115–120. [Google Scholar] [CrossRef]
- Sun, L.; Rotaru, A.; Robeyns, K.; Garcia, Y. A colorimetric sensor for the highly selective, ultra-sensitive, and rapid detection of volatile organic compounds and hazardous gases. Ind. Eng. Chem. Res. 2021, 60, 8788–8798. [Google Scholar] [CrossRef]
- Tran, K.; Sander, P.; Kilic, M.S.; Brehme, J.; Sindelar, R.; Renz, F. Facile Approach for the Fabrication of Vapor Sensitive Spin Transition Composite Nanofibers. Eur. J. Inorg. Chem. 2024, 27, e202400363. [Google Scholar] [CrossRef]
- Goodwin, H.A. Spin transitions in six-coordinate iron (II) complexes. Coord. Chem. Rev. 1976, 18, 293. [Google Scholar] [CrossRef]
- Gütlich, P. Spin crossover in iron (II)-complexes. Met. Complexes 1981, 44, 83–195. [Google Scholar]
- König, E. Nature and dynamics of the spin-state interconversion in metal complexes. Nature and dynamics of the spin-state interconversion in metal complexes. Complex Chem. 1991, 76, 51–152. [Google Scholar]
- Gütlich, P.; Hauser, A.; Spiering, H. Thermisch und optisch schaltbare Eisen (II)-Komplexe. Angew. Chem. 1994, 106, 2109–2141. [Google Scholar] [CrossRef]
- Gütlich, P.; Garcia, Y.; Goodwin, H.A. Spin crossover phenomena in Fe (II) complexes. Chem. Soc. Rev. 2000, 29, 419–427. [Google Scholar] [CrossRef]
- Gütlich, P.; Garcia, Y.; van Koningsbruggen, P.J.; Renz, F. Introduction to Physical Techniques in Molecular Magnetism, Part 1—Structural and Magnetic Methods; Palacio, F., Schweizer, J., Ressouche, E., Eds.; University Press: Zaragoza, Spain, 2000. [Google Scholar]
- Hauser, A.; Jeftic, J.; Romstedt, H.; Hinek, R.; Spering, H. Cooperative phenomena and light-induced bistability in iron(II) spin-crossover compounds. Coord. Chem. Rev. 1999, 190–192, 471–491. [Google Scholar] [CrossRef]
- Gütlich, P.; Goodwin, H.A. Spin Crossover in Transition Metal Compounds I, II, III, in Topics in Current Chemistry; Springer: Berlin, Germany, 2004; pp. 233–235. [Google Scholar]
- Gütlich, P.; van Koningsbruggen, P.J.; Renz, F. Recent advances of spin crossover research. Struct. Bond. 2004, 107, 27–75. [Google Scholar]
- Augustín, P.; Boča, R. Magnetostructural relationships for Fe (III) spin crossover complexes. Nova Biotechnol. Chim. 2015, 14, 96–103. [Google Scholar] [CrossRef]
- Boča, R. Thermodynamics and cooperativeness of the spin crossover. Nova Biotechnol. Chim. 2020, 19, 138–153. [Google Scholar] [CrossRef]
- Nemec, I.; Herchel, R.; Boča, R.; Trávníček, Z.; Svoboda, I.; Fuess, H.; Linert, W. Tuning of spin crossover behaviour in iron (III) complexes involving pentadentate Schiff bases and pseudohalides. Dalton Trans. 2011, 40, 10090–10099. [Google Scholar] [CrossRef]
- Boča, R.; Fukuda, Y.; Gembický, M.; Herchel, R.; Jaroščiak, R.; Linert, W.; Renz, F.; Yuzurihara, J. Spin crossover in mononuclear and binuclear iron (III) complexes with pentadentate Schiff-base ligands. Chem. Phys. Lett. 2000, 325, 411–419. [Google Scholar] [CrossRef]
- Boča, R.; Nemec, I.; Šalitroš, I.; Pavlik, J.; Herchel, R.; Renz, F. Interplay between spin crossover and exchange interaction in iron (III) complexes. Pure Appl. Chem. 2009, 81, 1357–1383. [Google Scholar] [CrossRef]
- Šalitroš, I.; Boča, R.; Dlháň, Ľ.; Gembický, M.; Kožíšek, J.; Linares, J.; Moncoľ, J.; Nemec, I.; Perašínová, L.; Renz, F.; et al. Unconventional spin crossover in dinuclear and trinuclear iron (III) complexes with cyanide and metallacyanido bridges. Eur. J. Inorg. Chem. 2009, 2009, 3141–3154. [Google Scholar] [CrossRef]
- Renz, F.; Kerep, P.; Hill, D.; Klein, M. Complexes based on ethylene- and propylene-bridged-pentadentate-Fe (III)-units allow interplay between magnetic centers and multistability investigated by Mössbauer spectroscopy. Hyperfine Interact. 2006, 168, 981–987. [Google Scholar] [CrossRef]
- Krüger, C.; Augustín, P.; Nemec, I.; Trávniček, Z.; Oshio, H.; Boča, R.; Renz, F. Spin crossover in iron (III) complexes with pentadentate schiff base ligands and pseudohalido coligands. Eur. J. Inorg. Chem. 2013, 2013, 902–915. [Google Scholar] [CrossRef]
- Rajnák, C.; Mičová, R.; Moncoľ, J.; Dlháň, Ľ.; Krüger, C.; Renz, F.; Boča, R. Spin-crossover in an iron (III) complex showing a broad thermal hysteresis. Dalton Trans. 2021, 50, 472–475. [Google Scholar] [CrossRef] [PubMed]
- Hayami, S.; Gu, Z.; Yoshiki, H.; Fujishima, A.; Sato, O. Iron (III) spin-crossover compounds with a wide apparent thermal hysteresis around room temperature. J. Am. Chem. Soc. 2001, 123, 11644–11650. [Google Scholar] [CrossRef] [PubMed]
- Preiss, A.; Heyer, L.; Klimke, S.; Klingelhöfer, G.; Renz, F. Mössbauer investigation of Schiff base iron (III) coordination compounds. Hyperfine Interact. 2017, 238, 74. [Google Scholar] [CrossRef]
- Nihei, M.; Shiga, T.; Maeda, Y.; Oshio, H. Spin crossover iron (III) complexes. Coord. Chem. Rev. 2007, 251, 2606–2621. [Google Scholar] [CrossRef]
- Grunert, M.; Reiman, S.; Spiering, H.; Kitchen, J.A.; Brooker, S.; Gütlich, P. Mixed Spin-State [HS-LS] Pairs in a Dinuclear Spin-Transition Complex: Confirmation by Variable-Temperature 57Fe Mössbauer Spectroscopy. Angew. Chem. 2008, 120, 3039–3041. [Google Scholar] [CrossRef]
- Grandjean, F.; Long, G.J. Best Practices and Protocols in Mössbauer Spectroscopy. Chem. Mater. 2021, 33, 3878–3904. [Google Scholar] [CrossRef]
- Neese, F. The ORCA program system. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Neese, F. ORCA—An Ab Initio, Density Functional and Semi-Empirical Program Package, Version 4.2.1; Max-Planck-Institut für Kohlenforschung: Mülheim, Germany, 2024. [Google Scholar]
- Atanasov, M.; Ganyushin, D.; Pantazis, D.A.; Sivalingam, K.; Neese, F. Detailed ab initio first-principles study of the magnetic anisotropy in a family of trigonal pyramidal iron (II) pyrrolide complexes. Inorg. Chem. 2011, 50, 7460. [Google Scholar] [CrossRef]
- Angeli, C.; Borini, S.; Cestari, M.; Cimiraglia, R. A quasidegenerate formulation of the second order n-electron valence state perturbation theory approach. J. Chem. Phys. 2004, 121, 4043. [Google Scholar] [CrossRef]
- Angeli, C.; Cimiraglia, R.; Evangelisti, S.; Leininger, T.; Malrieu, J. –P. Introduction of n-electron valence states for multireference perturbation theory. J. Chem. Phys. 2001, 114, 10252. [Google Scholar] [CrossRef]
- Angeli, C.; Cimiraglia, R.; Malrieu, J. –P. n-electron valence state perturbation theory: A spinless formulation and an efficient implementation of the strongly contracted and of the partially contracted variants. J. Chem. Phys. 2002, 117, 9138. [Google Scholar] [CrossRef]
- Ganyushin, D.; Neese, F. First principles calculations of zero-field splitting parameters. J. Chem. Phys. 2006, 125, 24103. [Google Scholar] [CrossRef] [PubMed]
- Neese, F.J. Calculation of the zero-field splitting tensor on the basis of hybrid density functional and Hartree-Fock theory. Chem. Phys. 2007, 127, 164112. [Google Scholar]
- Neese, F. Efficient and accurate approximations to the molecular spin-orbit coupling operator and their use in molecular g-tensor calculations. J. Chem. Phys. 2005, 122, 34107. [Google Scholar] [CrossRef]
- Neese, F. Prediction of electron paramagnetic resonance g values using coupled perturbed Hartree-Fock and Kohn-Sham theory. J. Chem. Phys. 2001, 115, 11080. [Google Scholar] [CrossRef]
- Sinnecker, S.; Slep, L.; Bill, E.; Neese, F. Performance of Nonrelativistic and Quasi-Relativistic Hybrid DFT for the Prediction of Electric and Magnetic Hyperfine Parameters in 57Fe Mössbauer Spectra. Inorg. Chem. 2005, 44, 2245–2254. [Google Scholar] [CrossRef]
- Römelt, M.; Ye, S.; Neese, F. Calibration of modern density functional theory methods for the prediction of 57Fe Mössbauer isomer shifts: Meta-GGA and double-hybrid functionals. Inorg. Chem. 2009, 48, 784–785. [Google Scholar] [CrossRef]
- Ericsson, T.; Wäppling, R. Texture Effects in 3/2-1/2 Mössbauer Spectra. J. Phys. Colloq. 1976, 37, C6–C719. [Google Scholar] [CrossRef]
- Goldanskii, V.I.; Gorodinskii, G.M.; Karyagin, S.V.; Korytko, L.A.; Krizhanskii, L.M.; Makarov, E.F.; Suzdalev, I.P. VV Khrapov English transl. Proc. Acad. Sci. USSR Phys. Chem. Dect. 1963, 147, 766. [Google Scholar]
- Karyagin, S.V. The possible reason for the asymmetry of doublet components of Mössbauers absorption spectrum in certain powdery tin compounds. Proc. Acad. Sci. USSR Phys. Chem. Sect. 1964, 148, 110. [Google Scholar]
- Gütlich, P.; Bill, E.; Trautwein, A.X. Mössbauer Spectroscopy and Transition Metal Chemistry; Springer: Berlin, Germany, 2011; pp. 210–220. [Google Scholar]
- Vieira, B.J.; Coutinho, J.T.; Santos, I.C.; Pereira, L.C.; Waerenborgh, J.C.; da Gama, V. [Fe(nsal2trien)]SCN, a new two-step iron (III) spin crossover compound, with symmetry breaking spin-state transition and an intermediate ordered state. Inorg. Chem. 2013, 52, 3845–3850. [Google Scholar] [CrossRef]
- von Rhein, N.; Krewald, V. The temperature dependence of Mössbauer quadrupole splitting values: A quantum chemical analysis. Chem. Commun. 2025, 61, 2512–2515. [Google Scholar] [CrossRef] [PubMed]
- Koczorowski, T.; Szczolko, W.; Bakun, P.; Wicher, B.; Sobotta, L.; Gdaniec, M.; Teubert, A.; Mielcarek, J.; Tykarska, E.; Korecki, J.; et al. The valence and spin state tuning of iron (II/III) porphyrazines with bulky pyrrolyl periphery in solution and solid state. Molecules 2022, 27, 7820. [Google Scholar] [CrossRef]
- Halcrow, M.A. Spin-Crossover Materials, Properties and Applications; John Wiley and Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Wickman, H.H.; Klein, M.P.; Shirley, D.A. Paramagnetic Hyperfine Structure and Relaxation Effects in Mössbauer Spectra: Fe57 in Ferrichrome A. Phys. Rev. 1966, 152, 345. [Google Scholar] [CrossRef]
- Paulsen, H.; Grünsteudel, H.; Meyer-Klaucke, W.; Gerdan, M.; Grünsteudel, H.F.; Chumakov, A.I.; Rüffer, R.; Winkler, H.; Toftlund, H.; Trautwein, A.X. The spin-crossover complex [Fe(tpa)(NCS)2] Investigated by synchrotron-radiation based spectroscopies. Eur. Phys. J. B-Condens. Matter Complex Syst. 2001, 23, 463–472. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).