Abstract
We have investigated for the first time the temperature, size, and ion-doping concentration dependence of the magnetic properties, band-gap energy, and specific heat of CuFeO2 in both bulk materials and nanoparticles using a microscopic model (the s-d model) and Green’s function theory. Variations in the ionic radii of the dopant elements compared to those of the host ions introduce strain effects, which alter the exchange-interaction constants. Consequently, the influence of ion doping on the various properties of CuFeO2 nanoparticles has been elucidated at a microscopic level. The magnetization exhibits an increase when CuFeO2 is doped with Mn at the Fe site or Li and Ca at the Cu site, whereas doping with Sc or Mg at the Fe site leads to a decrease in magnetization. Regarding the band-gap energy, it increases upon doping with Mg and Sc at the Fe site, while doping with Mn at the Fe site or with Li and Ca at the Cu site results in a decrease. The temperature dependence of the specific heat reveals two distinct peaks, corresponding to the two magnetic phase-transition temperatures. The theoretical results show good qualitative agreement with experimental data, confirming the validity of the proposed model.
1. Introduction
Delafossite structures are of particular interest due to their unique superlattice structure, which is generally represented by the formula ABO2 (where A = Li, Na; B = Cr, Mn, Fe, Co, Ni). CuFeO2 (CFO) is one such delafossite-structured material. It is known as a prototypical type-II multiferroic, where the electric polarization is induced by specific spin patterns. Its linear magnetoelectric mechanism is distinct from those involving cycloidal magnetism [1,2]. CFO exhibits multiferroic behavior, meaning that the polarization can be induced either by applying a magnetic field or through doping at the Fe site with various ions, including Al [3,4,5], Ga [6], Rh [7], Ni [8], Mn, Co [9,10,11], Mg [12], Eu [13] ions, Y [14], or Li doping at the Cu site [15].
The substitution of cations A and B enables the development of novel properties with significant implications for both fundamental studies and technological applications. Magnetoelectric ordering, for example, positions these materials as promising candidates for information storage, processing, and transmission [16,17], while magnetoelastic coupling offers potential for advanced force-sensor technologies [18]. Additionally, the coexistence of electrical and elastic orders facilitates the design of ferroelectric materials for piezoelectric and optical devices [19]. A key challenge remains the creation of multifunctional devices capable of integrating several functionalities simultaneously. Moreover, CFO, as a p-type semiconductor, demonstrates considerable promise for applications in lithium-ion battery anodes [20], solar photocathodes [21,22,23], solar energy conversion [24], supercapacitors [25], and water-splitting catalysts [26].
Magnetic susceptibility and neutron diffraction studies indicate that CFO undergoes two distinct phase transitions as the temperature decreases. The first Neel temperature occurs at approximately 16 K, marking a transition from a paramagnetic state to a collinear-incommensurate antiferromagnetic structure. The second Neel temperature is observed near 11 K, where the magnetic structure shifts to a collinear-commensurate antiferromagnetic state [27,28]. Notably, the phase transition at 11 K corresponds to the magnetic transition to the ground state of the collinear four-sublattice (4SL) phase, also known as the phase [29]. The results of Ye et al. [29] suggest that the pronounced magnetoelastic coupling in CFO is closely linked to its multiferroic behavior. It arises from the strong spontaneous spin–lattice coupling inherent to the geometrically frustrated triangular lattice antiferromagnetic structure of CFO.
In addition, defects play an important role in regulating the magnetic properties of CFO. Zhu et al. [5] reported that a previously overlooked biquadratic interaction is essential to reproduce the ground state and excited states of CFO. In Co ion-doped CFO, the strain between distorted and undistorted FeO6 and CoO6 octahedra leads to distinct effects on the spin reorientation transition and spontaneous electric polarization [9]. The substitution of Mn3+ at the Fe site in CFO appears to influence magnetic and electric polarization behavior, possibly linked to the partial alleviation of spin frustration [10]. Increasing Cr ion doping in CFO nanoparticles has been observed to elevate both magnetization and transition temperatures [30]. Magnetic measurements by Ye et al. [31] on Mn-doped CFO ceramics indicated that low-doped CFO (x = 0.00–0.03) exhibited purely antiferromagnetic behavior, while higher doping levels (x = 0.05–0.10) resulted in the coexistence of ferromagnetism and antiferromagnetism. For x = 0.10, the sample displays the highest magnetization. Additionally, Peng et al. [32,33] reported that rare-earth-ion substitution at the Fe site reduces the magnetic transition temperatures and . This may be attributed to magnetic dilution effects and variations in exchange-interaction strength. The magnetic properties of Eu-doped bulk CFO were investigated through positron annihilation by Dai et al. [13].
The band-gap energy is essential for investigating the electrical properties of materials, including both pure and ion-doped CFO. However, there are still inconsistencies in the literature regarding its optical characteristics and reported band-gap values. For pure CFO, the band-gap energy has been documented in the range of 1.2 to 1.63 eV [34,35,36,37]. In contrast, CFO nanostructures, such as powders, thin films, and nanoplates, typically exhibit higher band-gap values [38,39,40,41,42]. These discrepancies in band-gap measurements can largely be attributed to differences in synthesis techniques, such as pulsed laser deposition, solid-state reaction processes, or the sol–gel method.
Doping with various ions, such as Al, Mg, Ni, Sc, Zr, Sn, Li, and Ca, significantly influences the band-gap energy of CFO, as reported experimentally by several authors [5,13,27,34,42,43,44,45]. An increase in is observed in CFO doped with Mg, Sc, and Zr at the Fe site [32,34], whereas a decrease occurs in CFO doped with Ni, Sn, and Ga at the Fe site [27,44,45], as well as in CFO doped with Li or Ca at the Cu site [15,42]. Let us emphasize that till now, the doping effects on the band-gap energy in CFO are not investigated theoretically.
There is a limited number of theoretical studies investigating the magnetic properties of CFO. Maouhoubi et al. [28] employed the Density Functional Theory (DFT) to examine the temperature dependence of magnetization, magnetic susceptibility, and specific heat in CFO. Their goal was to study the phase transitions and to determine the Neel temperatures and . Zhu et al. [5] introduced a magnetic cluster expansion method that considers all symmetry-allowed interactions in Al-doped CFO. Additionally, Petrenko et al. [46] demonstrated that a Heisenberg model with weak anisotropy provides a significantly better description of CFO’s magnetic data than the widely accepted two-dimensional Ising model. Experimental and theoretical DFT studies are combined by Santiago et al. [47] to study the electronic and magnetic properties of CuMnO2 nanoparticles.
It should be emphasized that the majority of theoretical studies are conducted using Density Functional Theory (DFT). In contrast, in this work, we employ a microscopic model combined with Green’s function theory. DFT is an exceptionally powerful method for investigating many-body problems; however, it is primarily limited to ground-state properties at zero temperature. Our approach, by comparison, allows for the investigation of the entire temperature range, providing a finite-temperature analysis that encompasses the full excitation spectrum. Specifically, it enables the exploration of the complete phase diagram, determined by the various excitation energies present in the system. A limitation of our method is that collective properties are incorporated from the outset: the fundamental degrees of freedom are not individual electrons, but rather effective spins associated with underlying quasi-particles. While DFT allows, at least in principle, for the calculation of all system parameters from first principles, our method requires the adoption of additional models to determine these quantities. Nevertheless, we believe that both DFT and the Green’s function approach are appropriate and, to some extent, complementary methods for the description of many-body systems.
In our previous papers [48,49], we investigated the ferroelectric and phonon properties of multiferroic CFO. The aim of this work is to study the doping effects on the magnetic properties and band gap of CFO in both bulk materials and nanoparticles, using for the first time a microscopic model and Green’s function theory. Notably, the optical properties of doped CFO have not been considered theoretically so far. We explain the doping effects on microscopic level and tried to clarify the existing discrepancies in the reported magnetic and band-gap results in doped CFO. In addition, we obtain some results that we hope will be confirmed experimentally in the near future.
2. The Model
The compound CFO is associated with the Rm space group, characterized by alternating layers of non-magnetic Cu+-O2−-Cu+ and magnetic Fe3+ ions along the c-axis. Within this structure, the Fe3+ ions form a planar triangular arrangement, giving rise to antiferromagnetic interactions. CFO also has semiconducting properties in addition to magnetic, which can be described by the s-d model:
is the Heisenberg Hamiltonian:
In this system, and its z component represent the spin operators for the localized spins at site i. The parameter denotes the nearest-neighbor exchange interaction, including both intra-plane () and inter-plane () interactions. The next-nearest-neighbor interactions within each hexagonal plane are neglected. The term corresponds to the exchange interaction in the doped states, while x represents the ion-doping concentration. The parameter denotes the easy-axis single-site anisotropy, which is considerably smaller than . An external magnetic field is represented by h. The Fe3+ ions with S = 5/2 spin are responsible for the magnetic properties.
is the Hamiltonian of the conduction electrons in the Wannier representation:
where represents the probability amplitude for a conduction electron to hop between sites, commonly referred to as the hopping integral. The operators and denote the Fermi annihilation and creation operators for an electron at site i, respectively.
The Hamiltonian describes, within the single-band approximation, the exchange interaction between conduction electrons and magnetic ions:
The interaction I between the spin operator and the conduction electron one is short range. Consequently, this Hamiltonian effectively accounts for the interaction of the electron only with the atom at which it is located. The can be represented in terms of the Fermi creation and annihilation operators as follows: , .
The magnetization is observed from
Here, S denotes the spin quantum number, . represents the spin excitations obtained from the spin Green’s function , calculated using the method of Tserkovnikov [50].
We calculated the band gap using the equation:
where and correspond to the energy at the top of the valence band and the energy at the bottom of the conduction band, respectively. The electronic energies are determined by the following expression:
They are determined by the poles of the electronic Green’s function , where is the band energy, = ±1, and M is the magnetization.
3. Numerical Results and Discussion
We performed the numerical calculations based on the JAVA software platform and using a self-consistent iterative procedure. The starting parameters for the iterative process are the model parameters defined below at T = 0 K. The numerical calculations use the following model values: = −0.456 meV, = −0.132 meV, D = 0.068 meV [29], S = 5/2, and I = 0.2 eV.
3.1. Temperature and Size Dependence of the Magnetization in CFO
Initially, we examine the temperature dependence of the magnetization M in bulk CFO under an external magnetic field of h = 40 kOe. The results are shown in Figure 1. As the temperature increases, M rises, reaches a maximum at = 16 K, and then decreases sharply. It is important to note that at = 11 K, the curve changes its slope and becomes steeper above . This behavior indicates that the decrease in magnetization below is closely linked to the dominant antiferromagnetic ordering. A similar behaviour has been observed by Zhang et al. [27].
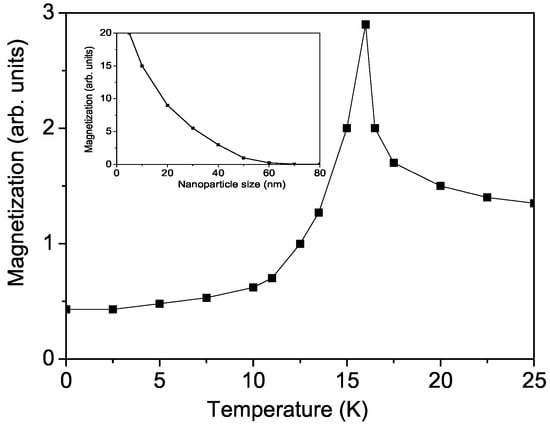
Figure 1.
The temperature dependence of the magnetization M in CFO for h = 40 kOe applied in plane. Inset: the size dependence of the magnetization M in CFO, h = 0.
It is important to note that while the bulk CFO compound is antiferromagnetic, CFO nanoparticles (NPs) exhibit weak ferromagnetism. This behavior arises due to surface and size effects, including uncompensated surface spins, the number of neighboring spins, and changes in symmetry [48]. The NP is defined by fixing the origin at an arbitrary spin at the center of the particle. The remaining spins are arranged within the particle on shells (cuboctahedra surrounded by triangular and square walls). The shells are labeled with n = 0, 1, …, and N, where n = 0 represents the central spin, and n = N corresponds to the surface shell of the system. The distance between the shells is 1.16 nm [35]. Due to defects, uncompensated spins, and surface disorder, the exchange-interaction constant at the surface, denoted as , differs from that in the bulk, J. This difference can result in being either smaller or larger than J. This effect is demonstrated for CFO NPs in the inset of Figure 1, where . The magnetization M increases as the NP size d decreases. However, experimental data for are currently unavailable.
3.2. Doping Dependence of the Magnetization in CFO NPs
Magnetization can also be modified by substituting various ions at the Fe or Cu sites. The incorporation of doping ions in place of Fe or Cu results in changes to the microstructure of CFO, leading to lattice distortion. The magnetic properties of CFO are primarily attributed to the 5d orbitals of Fe, particularly the Fe-Fe interactions. Consequently, replacing Fe sites to introduce new magnetic interactions has been widely employed to study CFO magnetism. In this work, we will explore the effect of different doping ions, such as Mn4+ or Mg2+, on the magnetic properties of CFO NPs. The ionic radius of the host Fe3+ ion is 0.69 Å, while the ionic radius of the substituted Mn4+ ion is smaller, 0.67 Å. This substitution induces compressive strain, leading to a decrease in the lattice parameters. In our model, this means that the exchange-interaction constant in the doped state, denoted as , which is inversely proportional to the lattice parameters, is greater than that in the undoped state J, i.e., . Moreover, the difference in valencies between the donor ion and the substituted ion disrupts the charge neutrality of the low-dimensional system. To maintain the balance between positive and negative charges, oxygen anion vacancies appear. This leads to a reduction in the unit cell volume, i.e., a decrease in the distance between the spins and an increase in the exchange-interaction constant between them. Oxygen anion vacancies also lead to the formation of charge transfer reactions, in which interactions arise between Fe ions with different valencies, i.e., Fe2+-Fe4+. Thus, the compressive strain and Fe2+-Fe4+ interactions lead to an increase in the spontaneous magnetization M, resulting in the emergence of a weak ferromagnetism. The corresponding result is shown in Figure 2, curve 1, for x = 0–0.05. It is assumed that in this doping interval, no clusters or secondary phases of the doping ions are formed, as shown in [29,32,51]. It is important to note that at low doping concentrations, primarily antiferromagnetic behavior is observed, while in the higher-doped NPs, a coexistence of antiferromagnetism and ferromagnetism is seen. In this way, we have explained the relationship between the magnetic properties of CFO and the microstructure at a microscopic level. Our findings regarding the doping dependence of the spontaneous magnetization are consistent with the experimental data of Ye et al. [29].
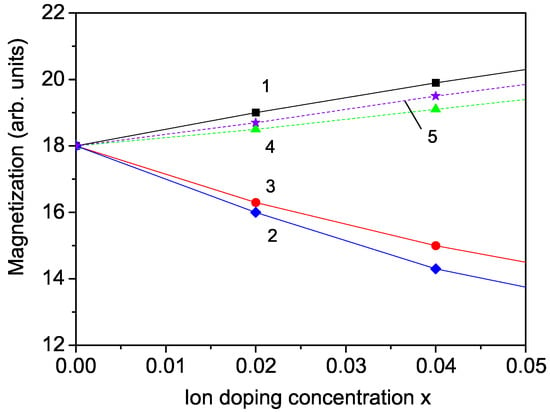
Figure 2.
Doping concentration dependence of the magnetization M in a CFO NP with d = 20 nm for (1) Mn, (2) Sc, (3) Mg ions at the Fe site, (4) Li, and (5) Ca ions at the Cu site.
Next, we consider the substitution of the Fe3+ ion with Sc3+, whose ionic radius r = 0.885 Å is larger compared to that of the Fe ion. This leads to lattice-structure distortion. A tensile strain appears, the lattice parameters increase, and we have in our model the following relation of the exchange-interaction constants of the doped and undoped NP: . Therefore, we determine that the magnetization M decreases increasing the dopant concentration x. The result is demonstrated in Figure 2, curve 2. Moreover, the two magnetic phase-transition temperatures and decrease (not shown here), which coincides with the experimental data of Peng et al. [32].
Let us emphasize that by doping with Y3+ ions at the Fe3+ ions we observe a tensile strain, because the ionic radius of the Y ion (1.04 Å) is larger than that of the Fe ion (0.69 Å), i.e., the magnetization M has to be reduced. However, due to the larger magnetic moment of the doped Y3+ ion compared to that of the Fe3+ ion, the magnetization M increases, as also observed experimentally by Huang et al. [14] in Y-doped CFO ceramics.
The opposite result compared to that by Mn ion doping is obtained by substituting the Fe3+ with Mg2+ ions. The ionic radius of the doping Mg ion is 0.86 Å, i.e., larger than that of the host Fe ion. This leads to a tensile strain, to an increase in the lattice parameters, and to the following relation of the exchange-interaction constants: . So, from Equation (5), we observe a decrease in the magnetization M with increasing Mg dopant. The result is shown in Figure 2, curve 3, and coincides with the reported experimental data of Bera et al. [12] in CFO thin films and Chang et al. [34] in bulk CFO.
Now, we will consider the substitution effects of ion doping in CFO NPs at the Cu+ sites, for example with Li+. The ionic radii of the both ions are 0.91 Å and 0.90 Å, respectively, i.e., there appears a small compressive strain. The exchange-interaction constants at the doped states are larger than those in the undoped ones: . This leads to a small increase in the magnetization M (see Figure 2, curve 4). A similar behavior is also reported by Dai et al. [15] in bulk CFO. We obtain a similar result for Ca-doped CFO at the Cu site; see Figure 2, curve 5. It is important to note that the stability of the antiferromagnetic phase at low temperatures is affected by Li doping, as both antiferromagnetic and ferromagnetic phases coexist, and Li doping enhances the ferromagnetic interactions.
Therefore, the magnetic transition of the sample is influenced by a range of factors, including lattice distortions, changes in ion valence states, variations in microscopic defect types, and alterations in magnetic interactions.
3.3. Size and Temperature Dependence of the Band Gap Energy in CFO
Delafossite CFO is a p-type oxide semiconductor with a band gap of approximately 1.5 eV [36], which has garnered significant interest for applications in solar energy harvesting and oxide electronics. The band gap of CFO is primarily attributed to the charge-transfer transition between the O-2p and Fe-3d states. Initially, we investigate the temperature dependence of the band gap for bulk CFO. The result is shown in Figure 3. The band gap decreases with increasing temperature, consistent with the experimental data of Chen et al. [35]. It is important to note that the temperature dependence of the band gap is governed by the temperature dependence of the magnetization (see Equation (7)). Therefore, from a theoretical perspective, a reduction in is expected as the temperature increases.
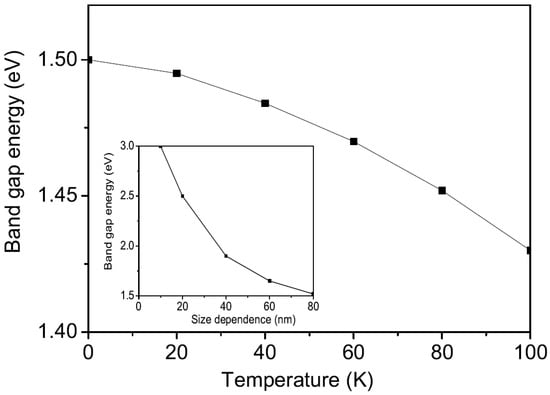
Figure 3.
The temperature dependence of the band-gap energy in CFO. Inset: the size dependence of the band-gap energy in CFO.
Using Equation (7), we have calculated the size dependence of the band-gap energy for CFO NPs with the relation and found that it increases as the NP size d decreases, as shown in the inset of Figure 3. This behavior is in agreement with the results of Moharam et al. [38]. In NPs, the band gap is larger because the number of overlapping orbitals is reduced compared to the bulk material. Higher band-gap values in various CFO nanostructures, such as thin films and nanoplates, have also been reported in [39,40,41,42]. It is worth emphasizing that nano-sized CFO can be utilized in optoelectronic devices, such as photoelectrochemical cells and/or photovoltaic cells.
3.4. Ion-Doping Dependence of the Band-Gap Energy in CFO NPs
The band gap plays a critical role in determining the optoelectronic properties of materials, making its tunability essential. The ability to modulate the band gap over a wide energy range has positioned perovskites as promising candidates for applications such as photovoltaics, lasers, light-emitting devices, photodetectors, and high-energy particle detection. Notably, semiconductor materials with narrower band gaps are key to enhancing the absorption of the visible solar spectrum.
At first, we will consider the effects of Mn and Mg ion doping at the Fe site in CFO NPs. As discussed already in Section 3.2, a compressive strain appears in the first case, whereas a tensile strain appears in the second one. This is due to the different ionic radii of the dopants and the host ion—Fe—which causes changes in the exchange-interaction constants at the doped states compared to the undoped ones J. They are dependant on the distance between the spins, i.e., on the lattice parameters being inversely proportional. The results are shown in Figure 4, curves 1 and 3. Through the Mn doping of CFO, the band-gap energy decreases, whereas with Mg doping, it increases. The Mg doping at the Fe sites results in increase the p-type carrier concentration and an electron deficiency, thereby increasing the optical band gap . Moreover, the conductivity is enhanced as the number of electron holes in CFO. Bera et al. [12], Chang et al. [34], and Elkhouni et al. [51] have also observed an increase in the band-gap energy in Mg-doped CFO thin films and bulk CFO, respectively, at the Fe site.
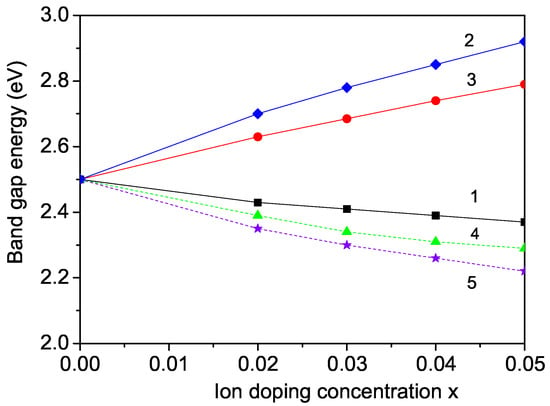
Figure 4.
Doping concentration dependence of the band-gap energy in a CFO NP with d = 20 nm for (1) Mn, (2) Sc, and (3) Mg ions at the Fe site, (4) Li, and (5) Ca ions at the Cu site.
For the effect of Mn ion doping on the band-gap energy of CFO, there are no experimental data. However, our result of the doping dependence of the magnetization for Mn-doped CFO (see Section 3.2) is in accordance with the experimental data of Ye et al. [29]. Therefore, we assume that the doping dependence of the band-gap energy is also correct.
In Figure 4, curve 2 demonstrates the Sc-doping dependence of the band-gap energy in Sc-doped CFO NP. It can be seen that increases with increasing x in agreement with the experimental data of Peng et al. [32].
We also calculated the dependence of the band-gap energy on the doping concentration for Li and Ca-doped CFO NP at the Cu site. The results are shown in Figure 4, curves 4 and 5, respectively. It can be seen that by Li and Ca substitution at the Cu site, decreases with increasing x. Unfortunately, there are no experimental data for in Li-doped CFO. However the increase in by Li substitution at the Cu site observed in Section 3.2, which is also reported by Dai et al. [15] in bulk CFO, gives us hope that our result is correct. We can conclude that in order to enhance the photoconductivity and incident photon-to-current efficiency of CFO, we have to increase the carrier concentrations of Ca2+ ions by doping, thus enhancing the photocatalytic efficiency of CFO. It must be mentioned, that Xiong et al. [42] reported that the optical band gap in CFO nanoplates decreased with increasing the Ca dopant, which is in agreement with our result. Chang et al. [34] affirmed that the doping of CFO with Ca enhances the photocatalytic efficiency of CFO, which also confirms our result.
It must be mentioned that Ca2+ ions (r = 1 Å) can also be substituted at the Fe3+ site, causing a tensile strain. Moreover, the spin value of Ca is zero, S = 0. Therefore, the magnetization M will decrease with an increase in the doping Ca concentration x, which coincides with the result of Elkhouni et al. [51] in (Cu,Mg)-doped CFO nanoplates. This would lead to an increase in the band-gap energy (not shown here), opposite to the substitution at the Cu site. Unfortunately, there are no such experimental data for .
Let us note that more experimental and theoretical works are needed to clarify the influence of various doping ions on the optical properties of CFO—bulk materials and nanostructures.
3.5. Temperature Dependence of the Specific Heat in CFO
To validate our model, we have calculated the temperature dependence of the specific heat for bulk CFO using the equation , where H represents the full Hamiltonian. Longitudinal and transverse correlation functions are involved, which are computed using the spectral theorem from the corresponding Green’s functions. The result for is shown in Figure 5, curve 1. Two peaks are observed at the two phase-transition temperatures in CFO: = 11 K and at = 16 K. A similar behavior has been reported by Maouhoubi et al. [28], providing evidence that our model is valid. It must be emphasized that CFO exhibits successive magnetic transitions as the temperature decreases: first from a paramagnetic state to a partially disordered phase at (approximately 16 K), and subsequently to an antiferromagnetic phase at (around 11 K) (refer to the Introduction). The transitions at and are reflected in the magnetic susceptibility curve by a peak at and a pronounced drop at [27].
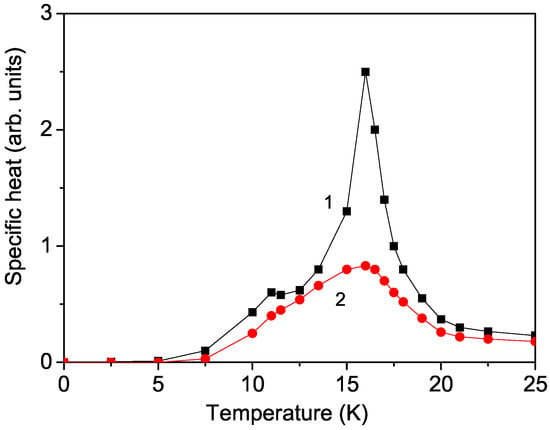
Figure 5.
Temperature dependence of the specific heat in CFO for different magnetic fields h: (1) 0, (2) 60 kOe applied in the plane.
When a strong external magnetic field h is applied, the specific heat decreases, and the peaks become smaller (see Figure 5, curve 2). The reduction in the peaks at and in the specific heat may be attributed to the suppression of spin fluctuations due to the increasing magnetic field. Unfortunately, this magnetic field dependence of has not been reported till now.
4. Conclusions
Using a microscopic model and Green’s function theory, the temperature, size, and doping concentration dependencies of various properties, such as magnetization, band-gap energy, and specific heat in CFO NPs are investigated. We have provided a microscopic explanation for the effects of ion doping on these properties. The exchange-interaction constants, which are inversely proportional to the lattice parameters, can be modified by ion doping. This is due to the differing radii of the doping ions compared to the host ions and the strains that arise. The magnetization M increases with doping by Mn at the Fe site and by Li or Ca at the Cu site, while it decreases in Sc and Mg-doped CFO. The band-gap energy increases in Mg and Sc-doped CFO at the Fe site, whereas it decreases by Mn doping at the Fe site or Li and Ca doping at the Cu site. Thus, incorporating Mn, Li, or Ca can enhance the photocatalytic efficiency of CFO by narrowing the band gap. The link between microstructure and magnetic properties indicates that structural distortions, vacancy defects, and spin modulation disruptions are critical factors affecting the magnetic behavior of CFO. These results highlight CFO’s potential as a multifunctional material, serving both as a transparent conducting oxide and a magnetic material. However, further experimental and theoretical studies are necessary to fully understand the impact of various dopants on the properties of bulk and nanostructured CFO.
The temperature dependence of the specific heat shows two peaks at the magnetic phase-transition temperatures, which decrease when an external magnetic field is applied.
The theoretical results are in good qualitative agreement with the experimental data. In addition, we have obtained results that we hope will be confirmed experimentally in the near future.
Author Contributions
Conceptualization, J.M.W.; Methodology, A.T.A.; Software, I.N.A.; Formal analysis, A.T.A.; Investigation, A.T.A., I.N.A. and J.M.W.; Writing—original draft, J.M.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Derived data supporting the findings of this study are available from the corresponding author upon reasonable request.
Acknowledgments
One of the authors, A.T.A., acknowledges financial support by the Bulgarian National Fund Scientific Studies (contract KP-06-N88/6).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Kimura, T.; Goto, T.; Shintani, H.; Ishizaka, K.; Arima, T.; Tokura, Y. Magnetic control of ferroelectric polarization. Nature 2003, 426, 55. [Google Scholar] [CrossRef]
- Choi, Y.J.; Yi, H.T.; Lee, S.; Huang, Q.; Kiryukhin, W.; Cheong, S.-W. Ferroelectricity in an Ising chain magnet. Phys. Rev. Lett. 2008, 100, 047601. [Google Scholar] [CrossRef]
- Seki, S.; Yamasaki, Y.; Shiomi, Y.; Iguchi, S.; Onose, Y.; Tokura, Y. Impurity-doping-induced ferroelectricity in the frustrated antiferromagnet CuFeO2. Phys. Rev. B 2007, 75, 100403(R). [Google Scholar] [CrossRef]
- Mitsuda, S.; Matsumoto, T.; Wada, T.; Kurihara, K.; Urata, Y.; Yoshizawa, H.; Mekata, M. Magnetic ordering of CuFe1−xAlxO2. Physica B 1995, 213, 194. [Google Scholar] [CrossRef]
- Zhu, W.; Wang, P.; Zhu, H.; Li, X.; Zhao, J.; Xu, C.; Xiang, K. Mechanism of Type-II Multiferroicity in Pure and Al-Doped CuFeO2. Phys. Rev. Lett. 2025, 134, 066801. [Google Scholar] [CrossRef] [PubMed]
- Haraldsen, J.T.; Fishman, R.S. Effect of interlayer interactions and lattice distortions on the magnetic ground state and spin dynamics of a geometrically frustrated triangular-lattice antiferromagnet. Phys. Rev. B 2010, 82, 144441. [Google Scholar] [CrossRef]
- Kundys, B.; Maignan, A.; Pelloquin, D.; Simon, C. Magnetoelectric interactions in polycrystalline multiferroic antiferromagnets CuFe1−xRhxO2 (x = 0.00 and x = 0.05). Solid State Sci. 2009, 11, 1035–1039. [Google Scholar] [CrossRef]
- Kongkaew, T.; Sinsarp, A.; Osotchan, T.; Limphirat, W.; Subannajui, K. Magnetic properties and chemical state of nickel doped Cu FeO2 delafossite oxide powders prepared by sol-gel method. Mater. Today Proc. 2018, 5, 10932. [Google Scholar] [CrossRef]
- Xiao, G.; Xia, Z.; Wei, M.; Huang, S.; Shi, L.; Zhang, X.; Wu, H.; Yang, F.; Song, Y.; Ouyang, Z. Modulation of Jahn-Teller effect on magnetization and spontaneous electric polarization of CuFeO2. J. Magn. Magn. Mater. 2018, 449, 214. [Google Scholar] [CrossRef]
- Xiao, G.; Xia, Z.C.; Xiaoxing, Z.; Song, Y.; Huang, S.; Yang, F.; Jiang, D.; Deng, H.; Ouyang, Z.; Shi, L. Impact of Mn3+ substitution on magnetization and electric polarization behavior in geometry frustrated CuFe1−xMnxO2. J. Mater. Sci. Mater. Electr. 2019, 30, 9531. [Google Scholar] [CrossRef]
- Hayashi, K.; Fukatsu, R.; Nozaki, T.; Miyazaki, Y.; Kajitani, T. Structural, magnetic, and ferroelectric properties of CuFe1−xMnxO2. Phys. Rev. B 2013, 87, 064418. [Google Scholar] [CrossRef]
- Bera, A.; Deb, K.; Bera, T.; Sinthika, S.; Thapa, R.; Saha, B. Effect of Mg substitution in delafossite structured CuFeO2 thin film deposited on FTO coated glass substrate and its diode characteristics. Thin Solid Films 2017, 642, 316. [Google Scholar] [CrossRef]
- Dai, H.; Xie, X.; Chen, Z.; Ye, F.; Li, T.; Yang, Y. Microstructure evolution and magnetic properties of Eu doped CuFeO2 multiferroic ceramics studied by positron annihilation. Ceram. Intern. 2018, 44, 13894. [Google Scholar] [CrossRef]
- Huang, B.; Wu, L.; Ren, H.; Zhang, Q.; Lin, H.; Xu, S.; Xiong, D.; Deng, W. Effect of Y3+ doping of rare earth element on microstructure and antiferromagnetism of CuFeO2 ceramics. J. Ceram. Intern. 2024, 6, 9372. [Google Scholar] [CrossRef]
- Dai, H.; Ye, F.; Li, T.; Chen, Z.; Cao, X.; Wang, B. Impact of Li doping on the microstructure, defects, and physical properties of CuFeO2 multiferroic ceramics. Ceram. Intern. 2019, 45, 24570. [Google Scholar] [CrossRef]
- Ahmed, S.; Atif, M.; Rehman, A.U.; Bashir, S.; Iqbal, N.; Khalid, W.; Ali, Z.; Nadeem, M. Enhancement in the magnetoelectric and energy storage properties of core-shell-like CoFe2O4-BaTiO3 multiferroic nanocomposite. J. Alloys Compd. 2021, 883, 160875. [Google Scholar] [CrossRef]
- Rovillain, P.; de Sousa, R.; Gallais, Y.; Sacuto, A.; Measson, M.A.; Colson, D.; Forget, A.; Bibes, M.; Barthelemy, A.; Cazayous, M. Electric-field control of spin waves at room temperature in multiferroic BiFeO3. Nat. Mater. 2010, 9, 975. [Google Scholar] [CrossRef]
- Bieńkowski, A.; Szewczyk, R. The possibility of utilizing the high permeability magnetic materials in construction of magnetoelastic stress and force sensors. Sens. Actuators A 2004, 113, 270. [Google Scholar] [CrossRef]
- Alikin, D.; Turygin, A.; Ushakov, A.; Kosobokov, M.; Alikin, Y.; Hu, Q.; Liu, X.; Xu, Z.; Wei, X.; Shur, V. Competition between ferroelectric and ferroelastic domain wall dynamics during local switching in rhombohedral PMN-PT single crystals. Nanomater 2022, 12, 3912. [Google Scholar] [CrossRef]
- Kim, J.-H.; Kim, J.Y.; Choi, Y.H.; Youn, D.H. Facile CuFeO2 microcrystal synthesis for lithium ion battery anodes via microwave heating. J. Mater. Sci. Mater. Electron. 2020, 31, 9408. [Google Scholar] [CrossRef]
- Idrissi, M.E.; Mei, B.; Abd-Lefdil, M.; Atourki, L. Making Solar Hydrogen: A Review of the Challenges and Strategies of Synthesizing CuFeO2 Photocathodes for Photoelectrochemical Water Splitting. Molecules 2025, 30, 1152. [Google Scholar] [CrossRef]
- Wei, J.; Guo, C.; Hou, D.; Jia, D.; Xue, H.; Tian, J.; Jiang, T. High Density Facet Junctions in Nano-Stepped CuFeO2 Enable Efficient Charge Separation for Selective Photocatalytic CO2 Reduction to CH4. Inorg. Chem. Front, 2025; in press. [Google Scholar] [CrossRef]
- Bessner, J.; Jacob, T. Understanding the Nitrogen Reduction Reaction Mechanism on CuFeO2 Photocathodes. Chem. Europe 2025, 31, e202500058. [Google Scholar] [CrossRef] [PubMed]
- Li, R.-P.; Yu, S.-M.; Zhao, Z.-Y. Facet engineering for improved carrier separation and transport in CuFeO2 photocathodes. Mater. Chem. Phys. 2024, 311, 128582. [Google Scholar] [CrossRef]
- Danish, M.; Hussain, A.; Shafqat, S.R.; Sandhu, Z.A.; Batoo, R.M.; Ijaz, M.F.; Bhalli, A.H.; Fiaz, M. Multifunctional CuFeO2 Nanocomposites: 3D Series-Metal-Based Materials for Hydrogen Evolution Reaction and Supercapacitor Applications. Ceram. Int. 2025; in press. [Google Scholar] [CrossRef]
- Mao, L.; Mohan, S.; Gupta, S.K.; Mao, Y. Multifunctional delafossite CuFeO2 as water splitting catalyst and rhodamine B sensor. Mater. Chem. Phys. 2022, 278, 125643. [Google Scholar] [CrossRef]
- Zhang, L.; Goodman, B.A.; Xiong, D.K.; Deng, W. Evolution of microstructure, optical, and magnetic properties in MF CuFe1−xSnxO2 (x = 0–0.05). Ceram. Int. 2018, 45, 3007. [Google Scholar] [CrossRef]
- Maouhoubi, A.; Ouzaroual, L.; Toual, Y.; Mouchou, S.; Mezzat, F.; Azouaoui, A.; Ez-Zahraouy, H.; Hourmatallah, A.; Bouslykhane, K.; Benzakour, N. Structural, electronic and magnetic properties of the CuFeO2 multiferroic compound. Arab. J. Chem. 2024, 17, 105437. [Google Scholar] [CrossRef]
- Ye, F.; Ren, Y.; Huang, Q.; Fernandez-Baca, J.A.; Dai, P.; Lynn, J.W.; Kimura, T. Spontaneous spin-lattice coupling in the geometrically frustrated triangular lattice antiferromagnet CuFeO2. Phys. Rev. B 2006, 73, 220404(R). [Google Scholar] [CrossRef]
- Mori, R.; Hachisu, M.; Yamazaki, T.; Ichiyanagi, Y. Magnetic properties of CuFe1−xCrxO2 nanoparticles surrounded by amorphous SiO2. J. Appl. Phys. 2015, 117, 17C756. [Google Scholar] [CrossRef]
- Ye, F.; Dai, H.; Peng, K.; Li, T.; Chen, J.; Chen, Z.; Li, N. Effect of Mn doping on the microstructure and magnetic properties of CuFeO2 ceramics. J. Adv. Ceram. 2020, 9, 444. [Google Scholar] [CrossRef]
- Peng, K.; Wang, M.; Dai, H.; Li, T.; Liu, D.; Chen, Z. The Structural, Optical, and Magnetic Properties of in CuFe0.95M0.05O2 Delafossites (M=transition metal). J. Supercond. Nov. Magn 2021, 34, 1269. [Google Scholar] [CrossRef]
- Peng, K.; Dai, H.; Wang, M.; Li, T.; Liu, D.; Chen, Z.; Cao, X.; Wang, B. Defect characteristics, local electron density, and magnetic properties of rare Earth-doped CuFeO2 ceramics. Ceram. Int. 2020, 46, 28400. [Google Scholar] [CrossRef]
- Chang, Y.-H.; Wang, H.; Siao, T.-F.; Lee, Y.-H.; Bai, S.-Y.; Liao, C.-W.; Zhuang, J.-K.; Chiu, T.-W.; Kuo, C.-H. A new solution route for the synthesis of CuFeO2 and Mg-doped CuFeO2 as catalysts for dye degradation and CO2 conversion. J. Alloys Compd. 2021, 854, 157235. [Google Scholar] [CrossRef]
- Chen, H.-W.; Huang, C.-Y.; Shubcd, G.-J.; Liu, H.-L. Temperature-dependent optical properties of CuFeO2 through the structural phase transition. RSC Adv. 2021, 11, 40173. [Google Scholar] [CrossRef]
- Haiwan Xu, H.; Wu, R.; Zhang, J.; Han, W.; Chen, L.; Liang, X.; Haw, C.Y.; Mazzolini, P.; Bierwagen, O.; Qi, D.-C.; et al. Revealing the Electronic Structure and Optical Properties of CuFeO2 as a p-Type Oxide Semiconductor. ACS Appl. Electr. Mater. 2021, 3, 1834. [Google Scholar] [CrossRef]
- Omeiri, S.; Bellal, B.; Bouguelia, A.; Bessekhouad, Y.; Trari, M. Electrochemical and photoelectrochemical characterization of CuFeO2 single crystal. J. Solid State Electrochem. 2008, 13, 1395. [Google Scholar] [CrossRef]
- Moharam, M.M.; Rashad, M.M.; Elsayed, E.M.; Abou-Shahba, R.M. A facile novel synthesis of delafossite CuFeO2 powders. J. Mater. Sci. Mater. Electron. 2014, 25, 1798. [Google Scholar] [CrossRef]
- Vojkovic, S.; Fernandez, J.; Elgueta, S.; Vega, F.E.; Rojas, S.D.; Wheatley, R.A.; Seifert, B.; Wallentowitz, S.; Cabrera, A.L. Band gap determination in multi-band-gap CuFeO2 delafossite epitaxial thin film by photoconductivity. SN Appl. Sci. 2019, 1, 1322. [Google Scholar] [CrossRef]
- Alkhayatt, A.H.O.; Thahab, S.M.; Zgair, I.A. Structure, surface morphology and optical properties of post-annealed delafossite CuFeO2 thin films. Optik 2016, 127, 3745. [Google Scholar] [CrossRef]
- Yu, R.-S.; Lee, Y.-F.; Lai, Y.-S. Synthesis and Optoelectronic Properties of CuFeO2 Semiconductor Thin Films. ECS J. Solid State Sci. Technol. 2016, 5, P646. [Google Scholar] [CrossRef]
- Xiong, D.; Zhang, Q.; Verma, S.K.; Bao, X.-Q.; Li, H.; Zhao, X. Crystal structural, optical properties and mott-schottky plots of p-type Ca doped CuFeO2 nanoplates. Mater. Res. Bull. 2016, 83, 141. [Google Scholar] [CrossRef]
- Deng, Z.; Fang, K.; Wu, S.; Zhao, Y.; Dong, W.; Shao, J.; Wang, S. Structure and optoelectronic properties of Mg-doped CuFeO2 thin films prepared by sol-gel method. J. Alloys Compd. 2013, 577, 658. [Google Scholar] [CrossRef]
- Deng, Q.; Chen, H.; Wang, G.; Shen, Y.; Liu, F.; Wang, S. Structural, optical and photoelectrochemical properties of p-type Ni doped CuFeO2 by hydrothermal method. Ceram. Int. 2020, 46, 598–603. [Google Scholar] [CrossRef]
- Wheatley, R.A.; Rojas, S.; Oppolzer, C.; Joshi, T.; Borisov, P.; Lederman, D.; Cabrera, A.L. Comparative study of the structural and optical properties of epitaxial CuFeO2 and CuFe1−xGaxO2 delafossite thin films grown by pulsed laser deposition methods. Thin Solid Films 2017, 626, 110. [Google Scholar] [CrossRef]
- Petrenko, O.A.; Lees, M.R.; Balakrishnan, G.; de Brion, S.; Chouteau, G. Revised magnetic properties of CuFeO2-a case of mistaken identity. J. Phys. Condens. Matter 2005, 17, 2741. [Google Scholar] [CrossRef]
- Ribeiro, R.A.P.; de Lazaro, S.R.; Correa, M.A.; Bohn, F.; Longo, E.; Motta, F.V.; Bomio, M.R.D.; Santiago, A.A.G.; Tranquilin, R.L.; Oliveira, M.C. Disclosing the Structural, Electronic, Magnetic, and Morphological Properties of CuMnO2: A Unified Experimental and Theoretical Approach. J. Phys. Chem. C 2020, 124, 5378. [Google Scholar] [CrossRef]
- Apostolov, A.T.; Apostolova, I.N.; Wesselinowa, J.M. Ferroelectricity in the multiferroic delafossite CuFeO2 induced by ion doping or magnetic field. Solid State Commun. 2019, 292, 11. [Google Scholar] [CrossRef]
- Apostolov, A.T.; Apostolova, I.N.; Wesselinowa, J.M. Phonon properties of delafossite multiferroic compound CuFeO2. Comparison with CuCrO2. Mod. Phys. Lett. B 2019, 33, 1950141. [Google Scholar] [CrossRef]
- Tserkovnikov, Y.A. Decoupling of chains of equations for two-time Green’s functions. Theor. Math. Phys. 1971, 7, 511. [Google Scholar] [CrossRef]
- Elkhouni, T.; Amami, M.; Colin, C.V.; Salah, A.B. Structural and magnetoelectric interactions of (Ca, Mg)-doped polycrystalline multiferroic CuFeO2. Mater. Res. Bull. 2014, 53, 151. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).