Design of Ricker Wavelet Neural Networks for Heat and Mass Transport in Magnetohydrodynamic Williamson Nanofluid Boundary-Layer Porous Medium Flow with Multiple Slips
Abstract
1. Introduction
- A novel human-brain-inspired scheme based on Ricker wavelet neural networks was established to solve MHD Williamson nanofluid boundary-layer flow over a stretchable porous surface with multiple slip conditions.
- The MHD-WNF-BL flow problem was solved numerically to evaluate velocity, thermal gradient, and nanofluid concentration using variations in the values of the involved physical parameters based on sundry scenarios.
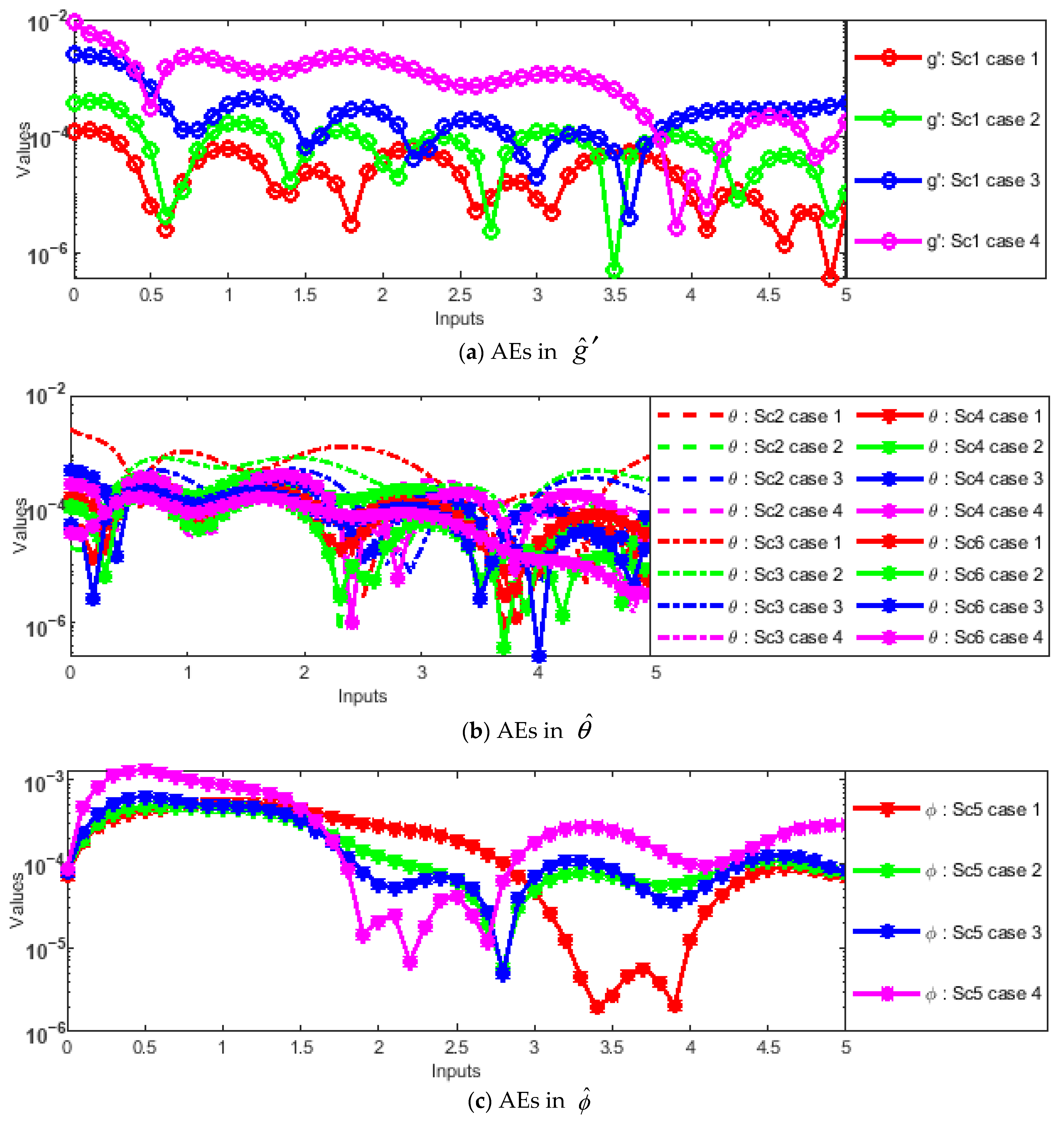
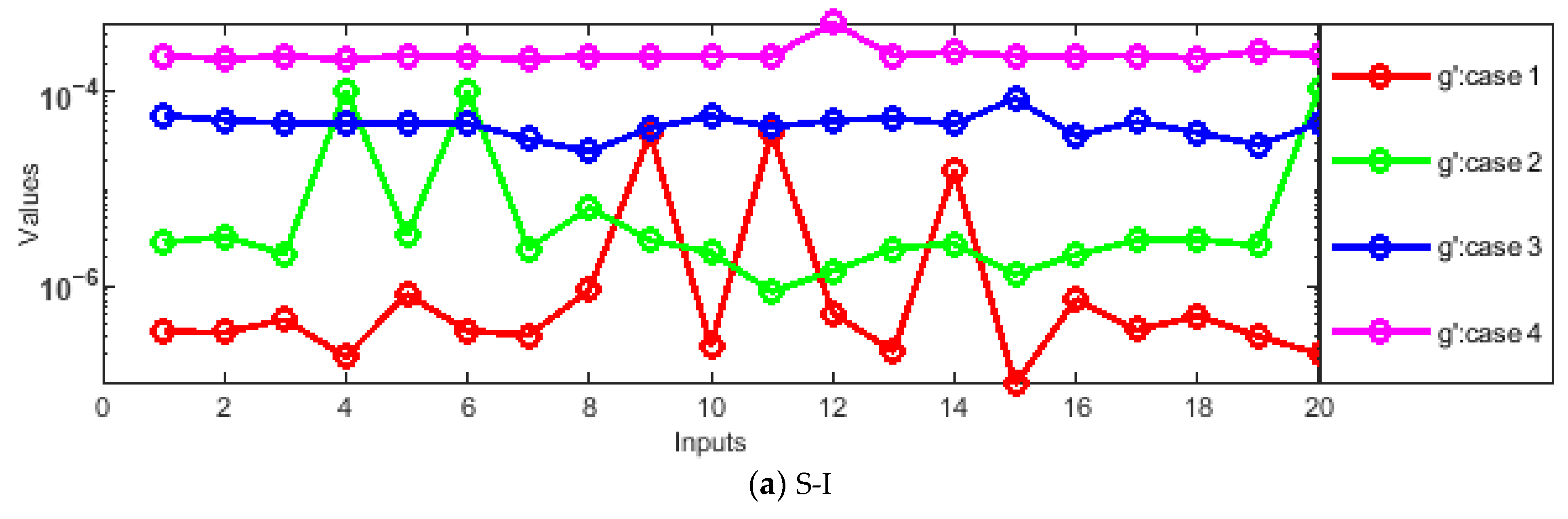
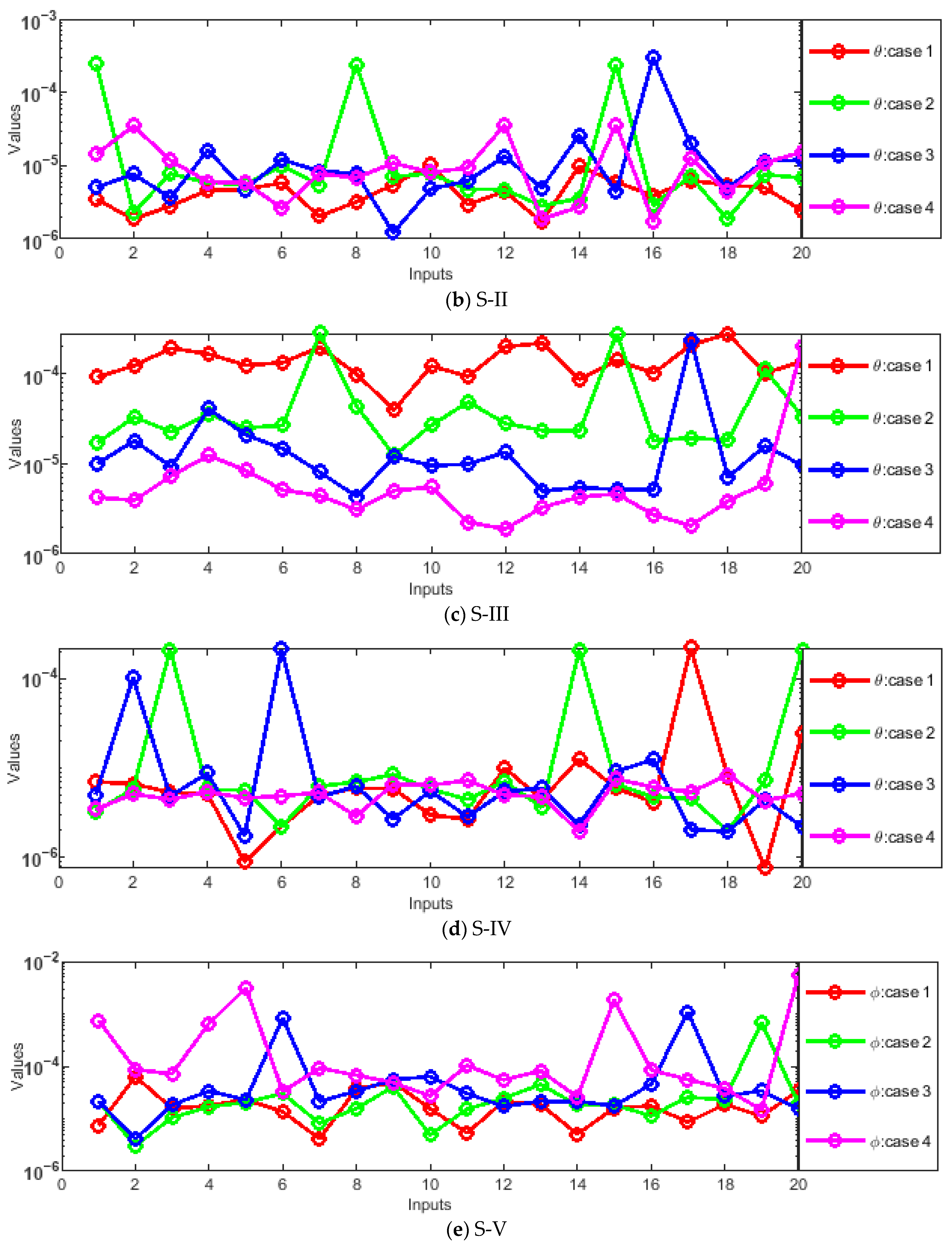
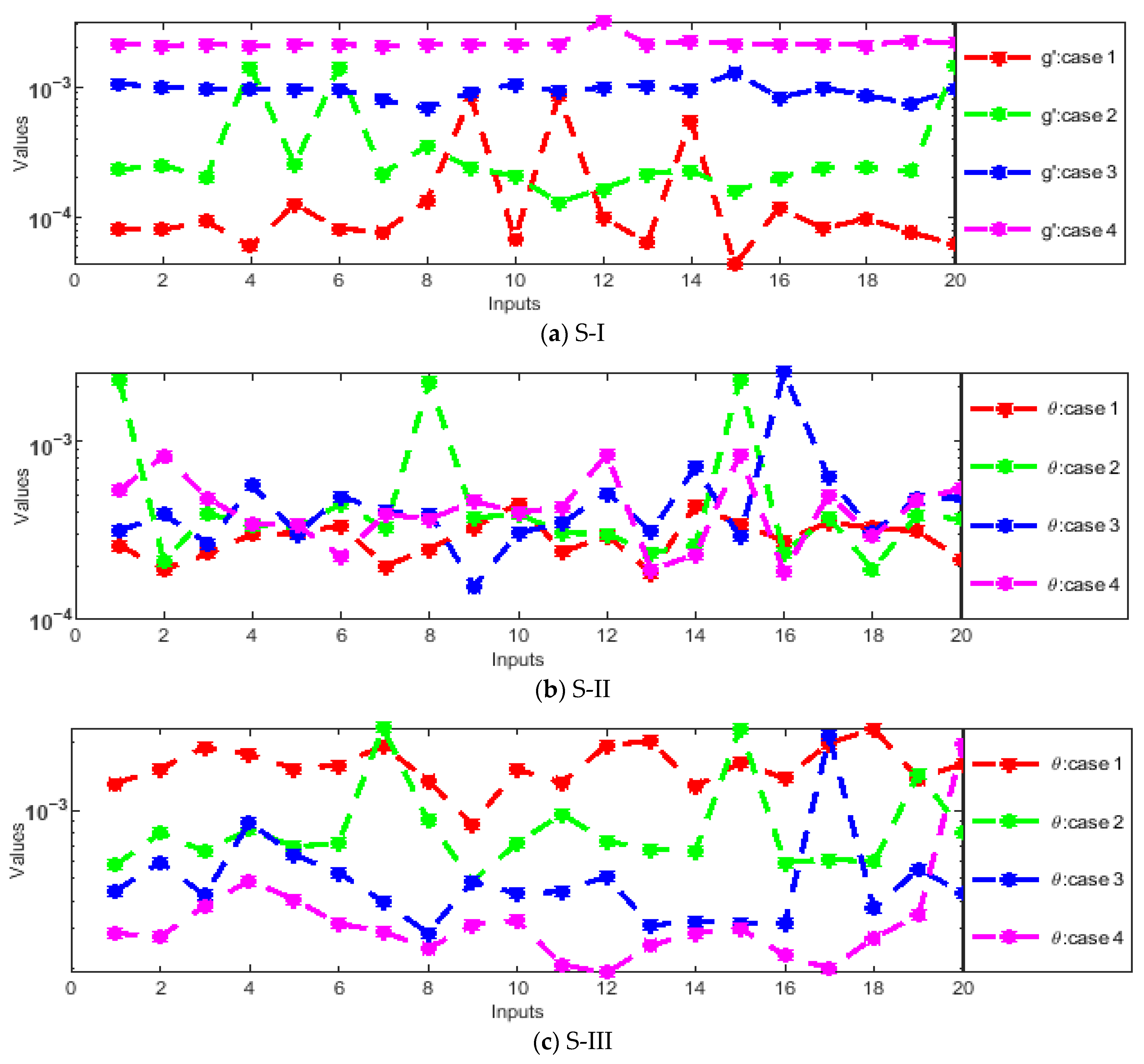
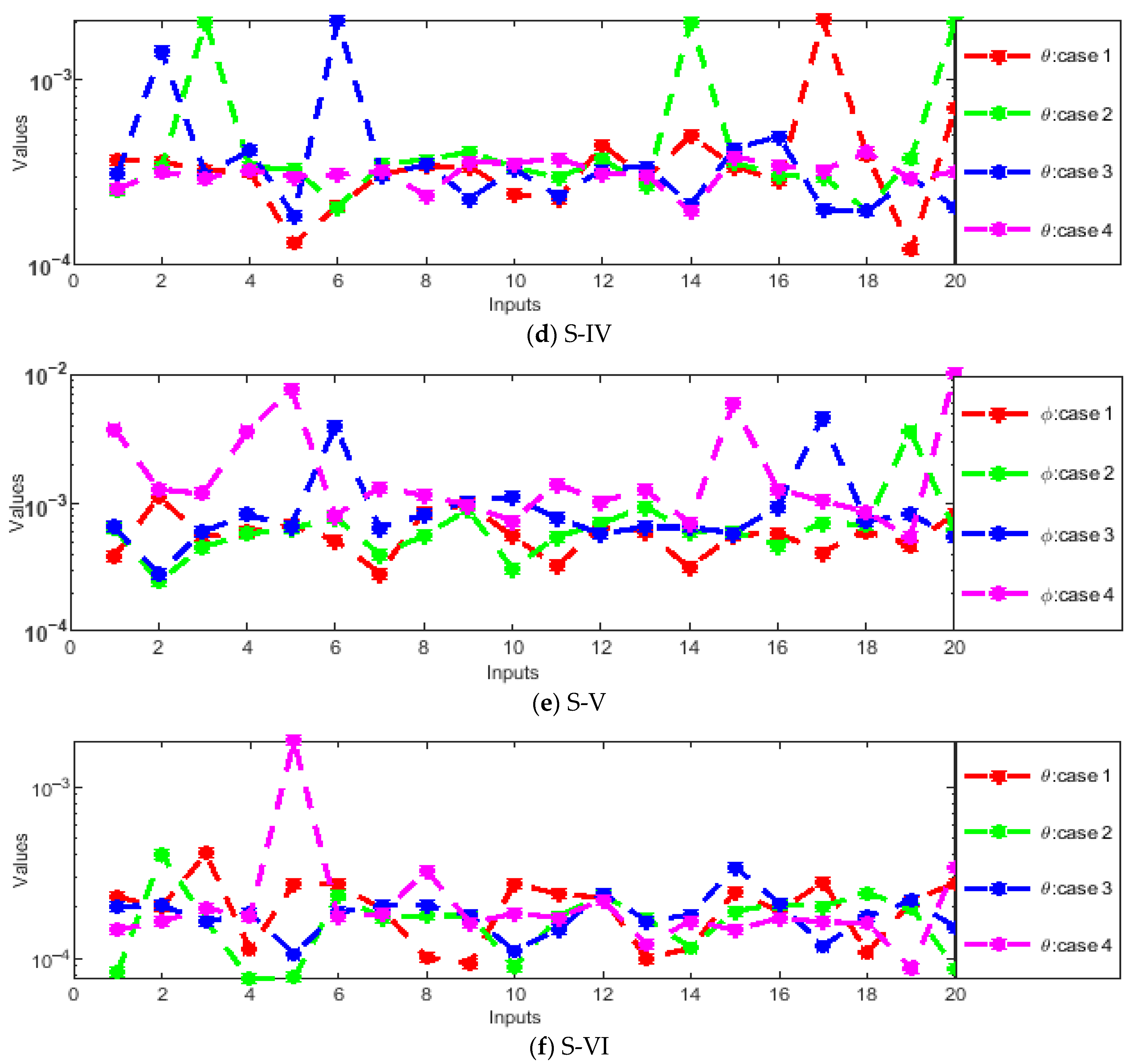
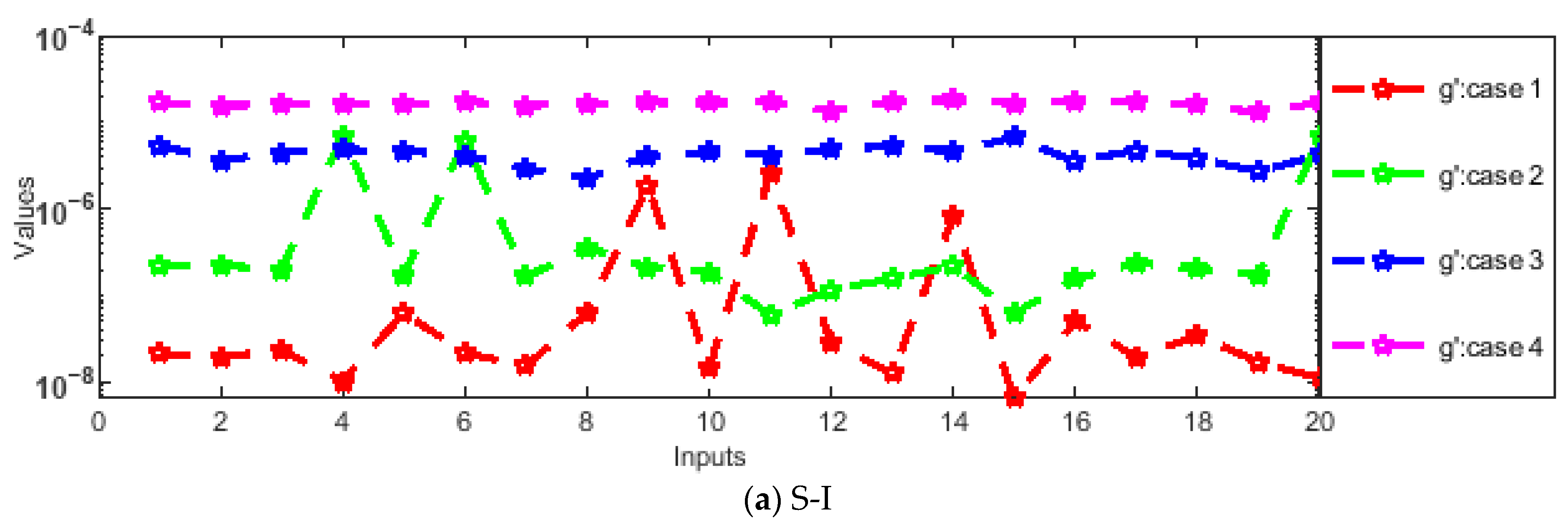
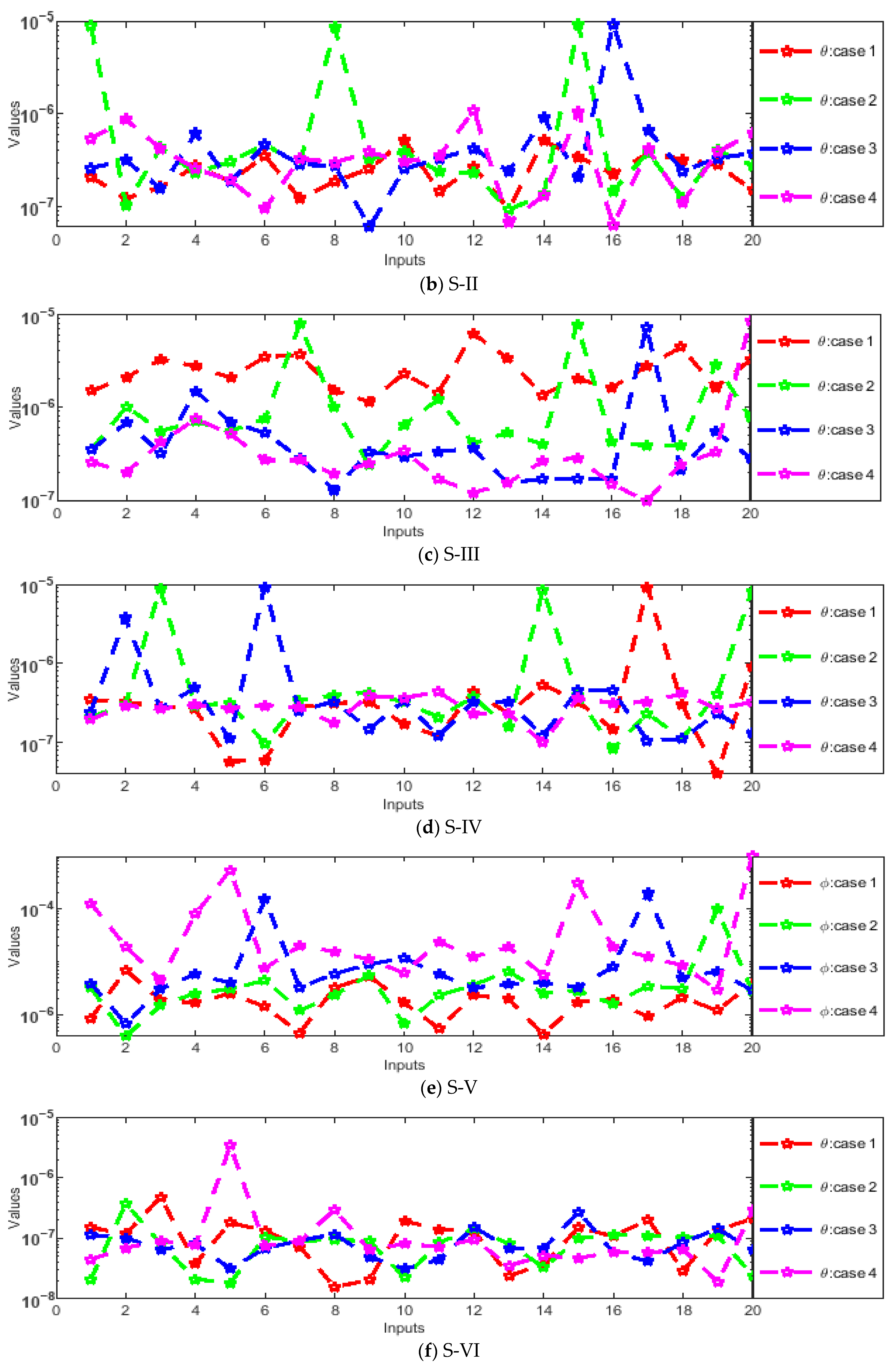
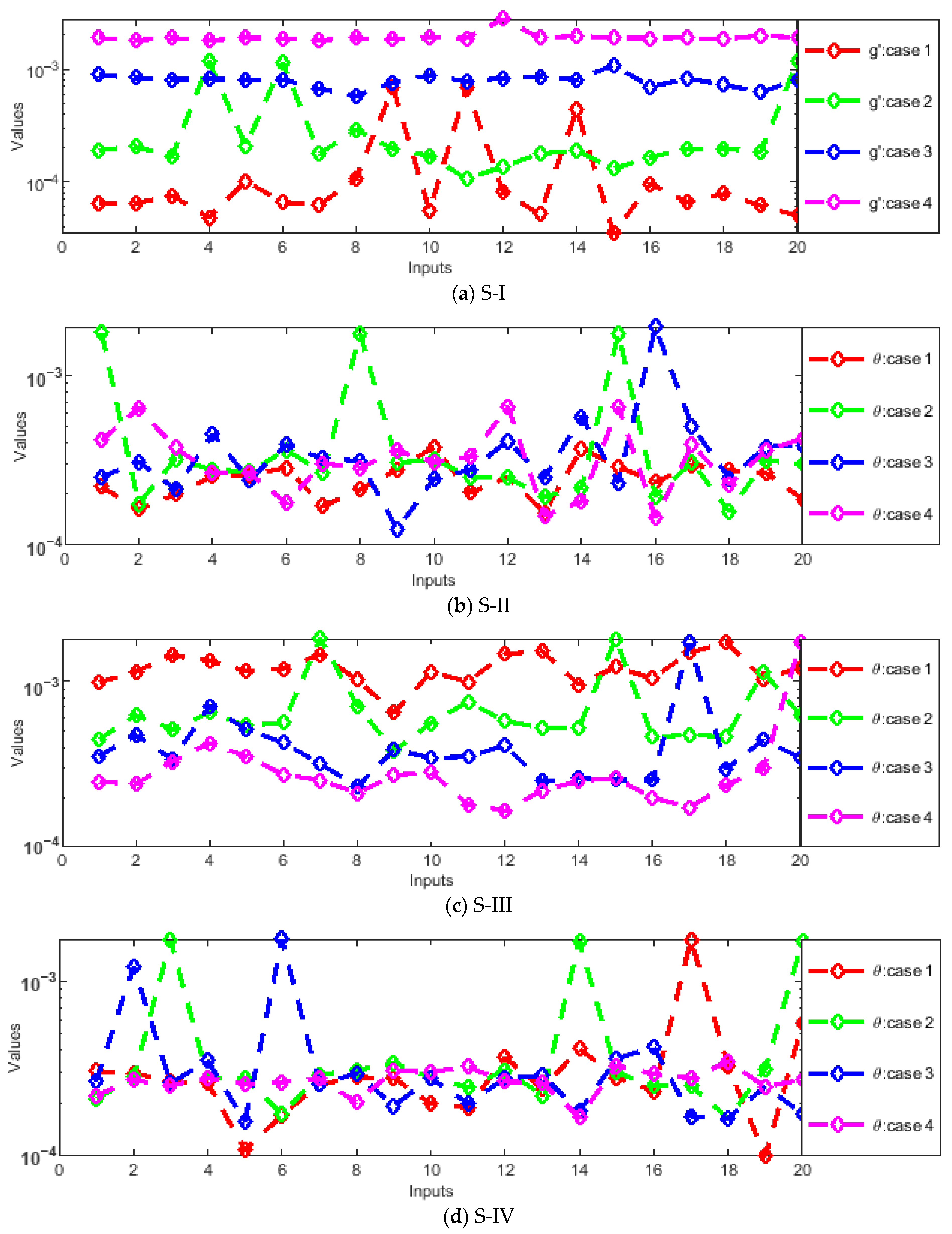
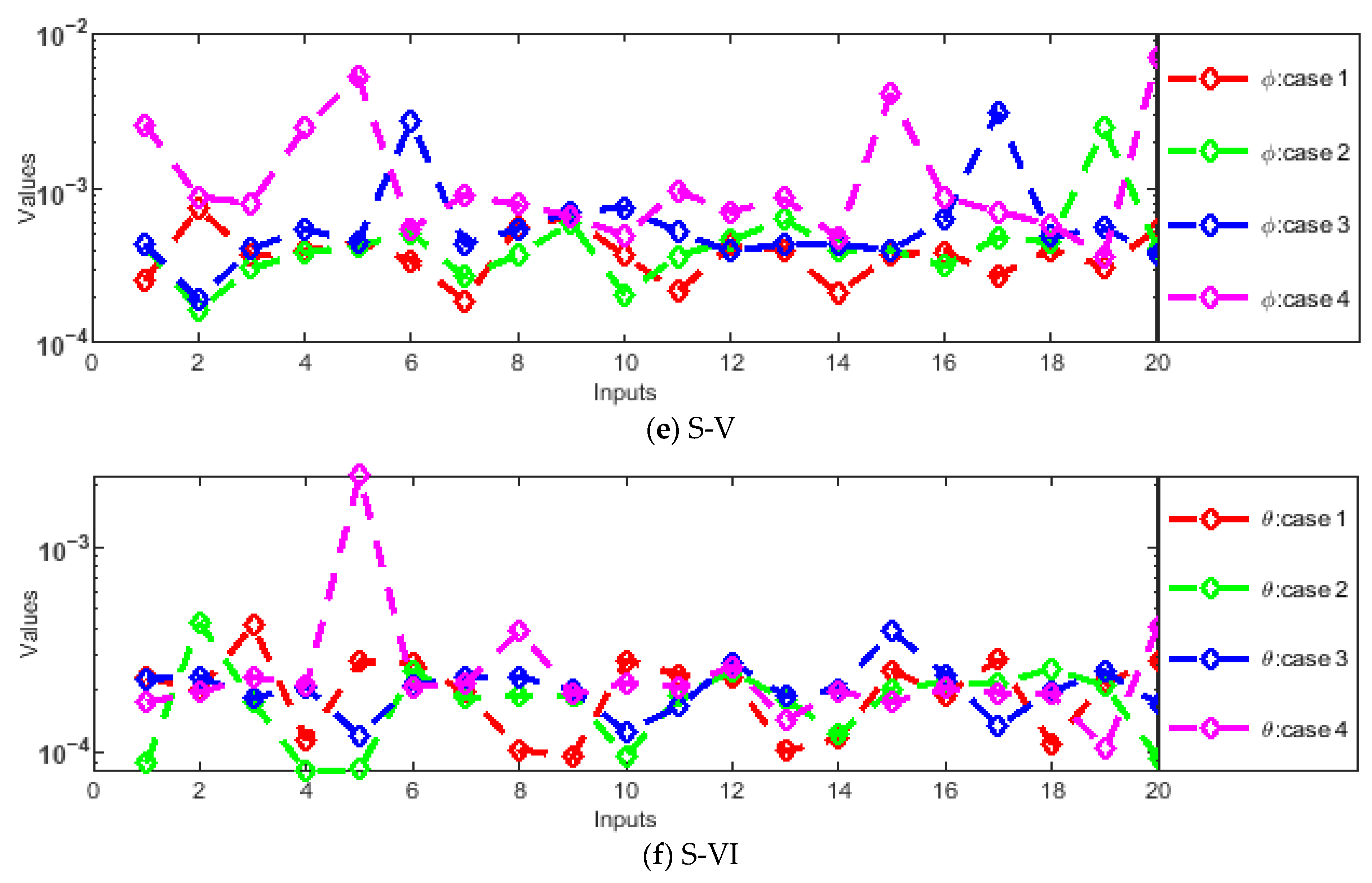
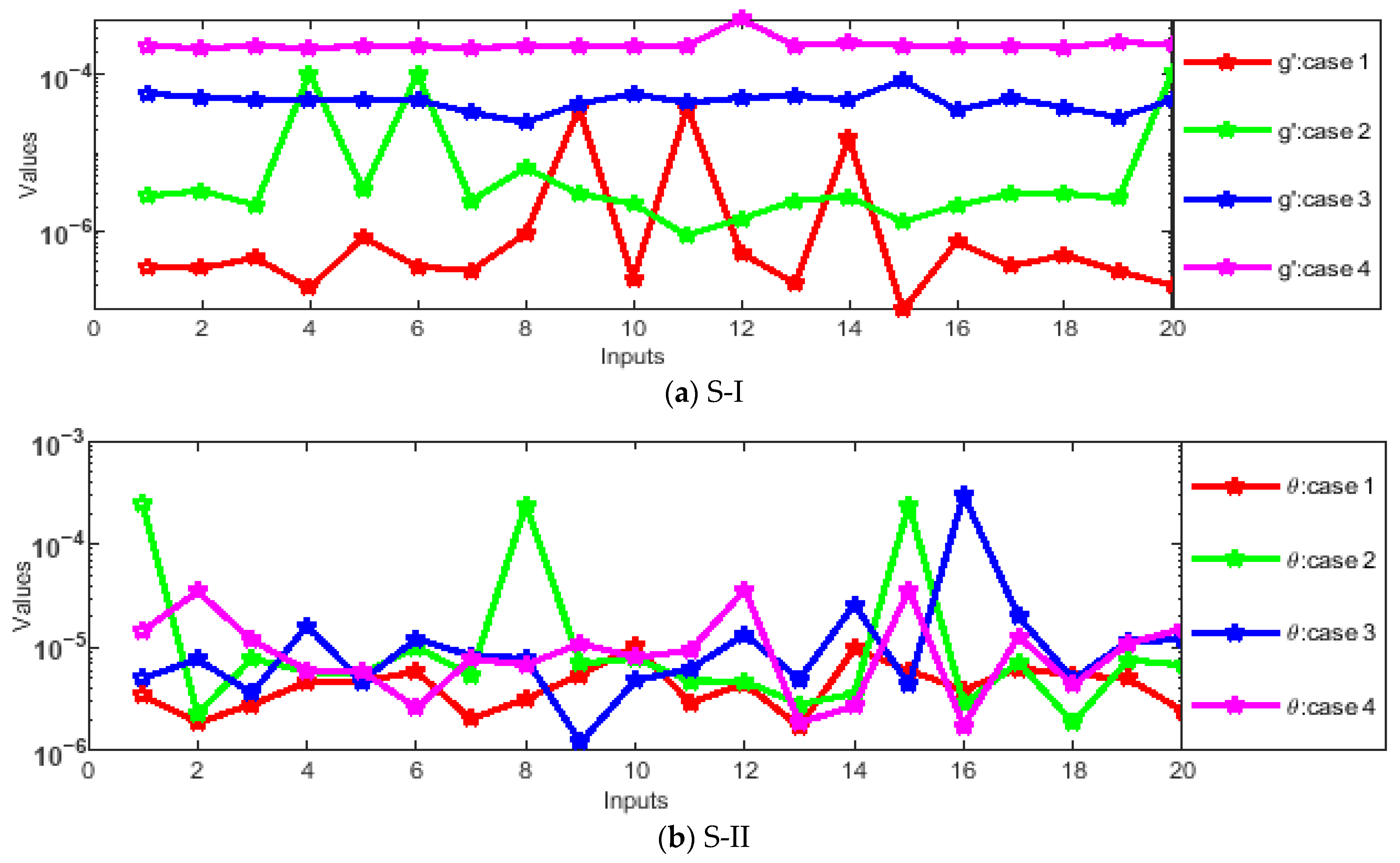
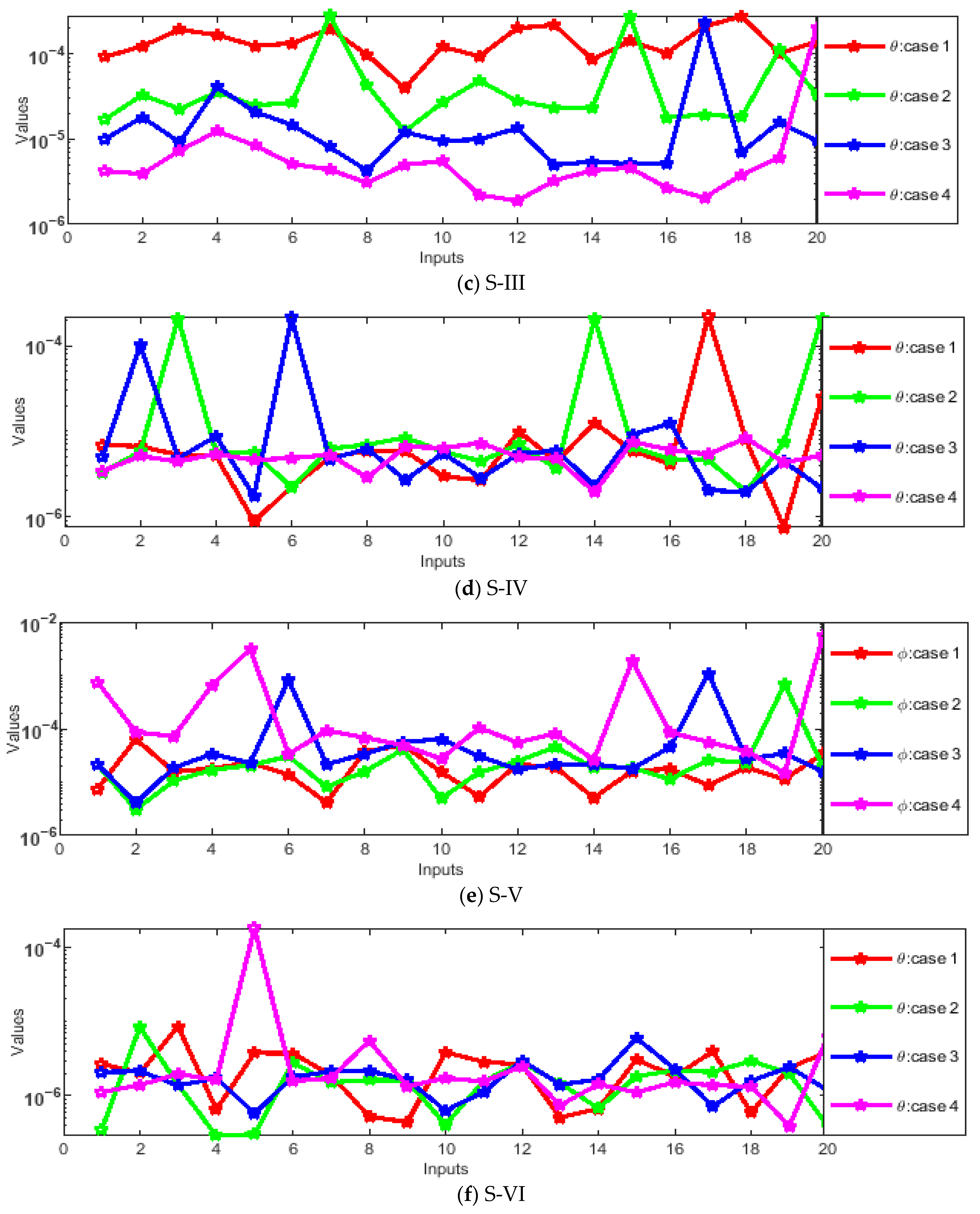
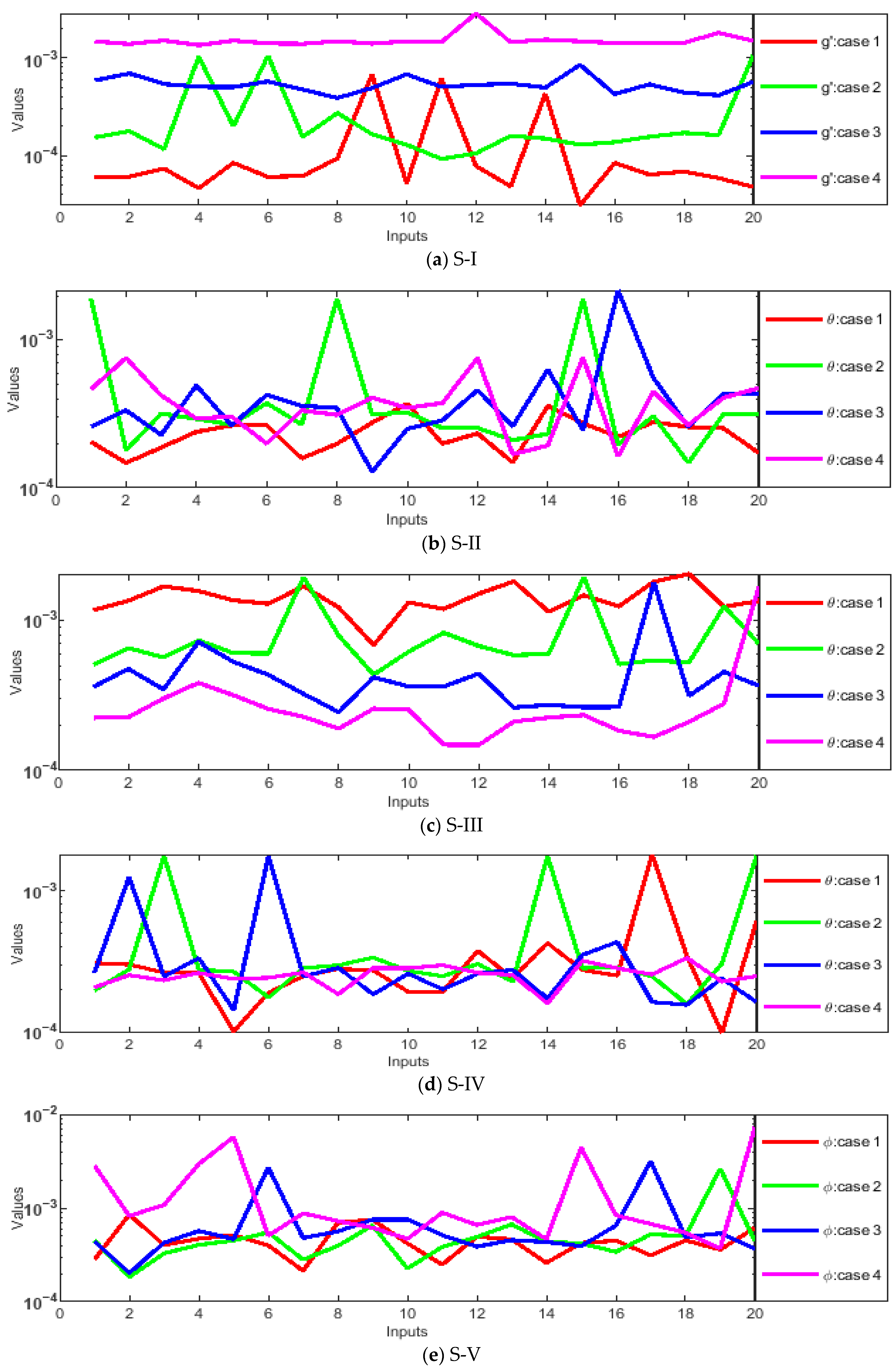
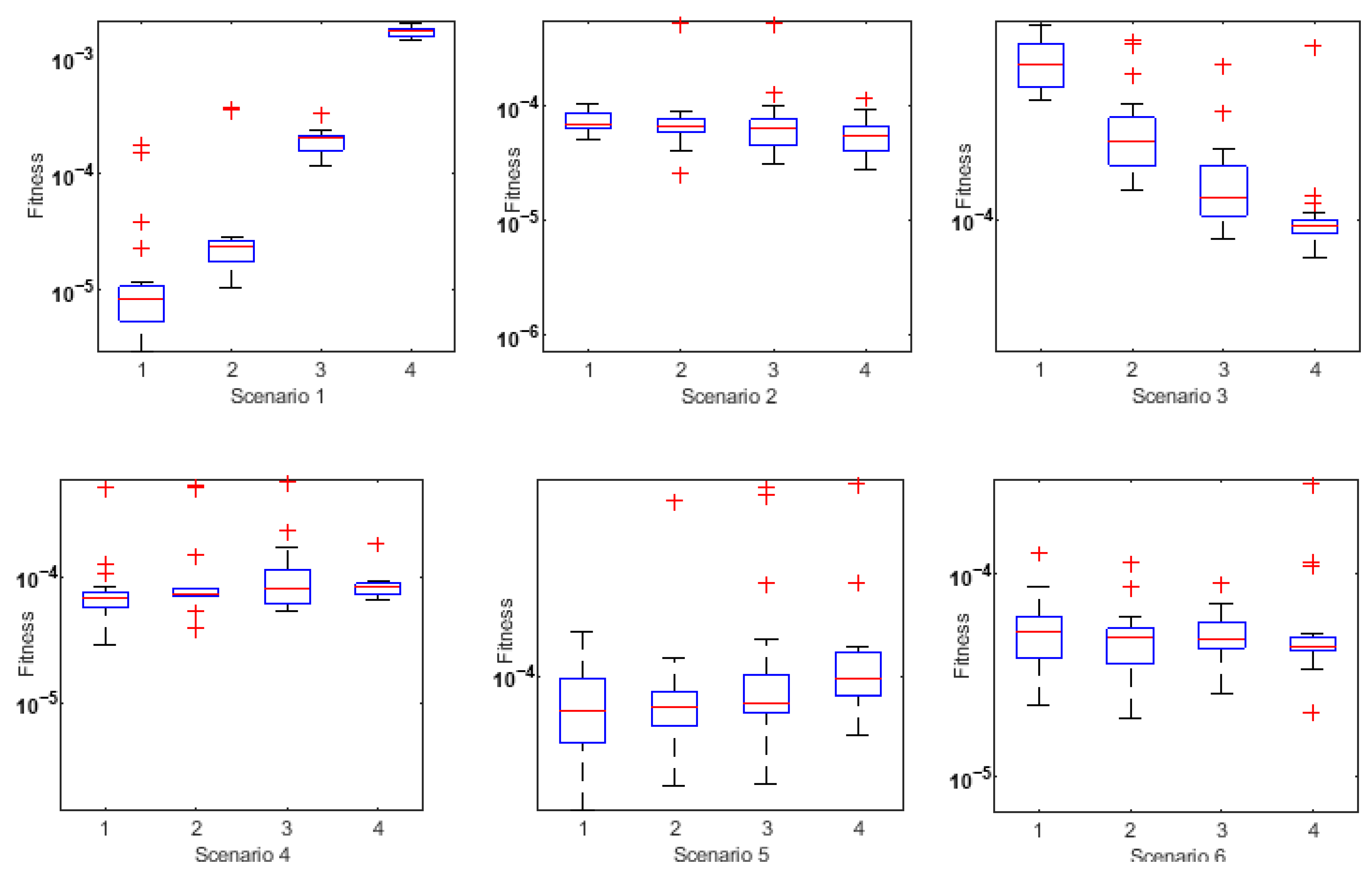
- Absolute errors (AEs) were evaluated through graphs and tables as a result of a comparison of the obtained numerical outcomes with reference solutions.
- The working of the HBI-RWNN solver was examined through various statistical and performance analyses.
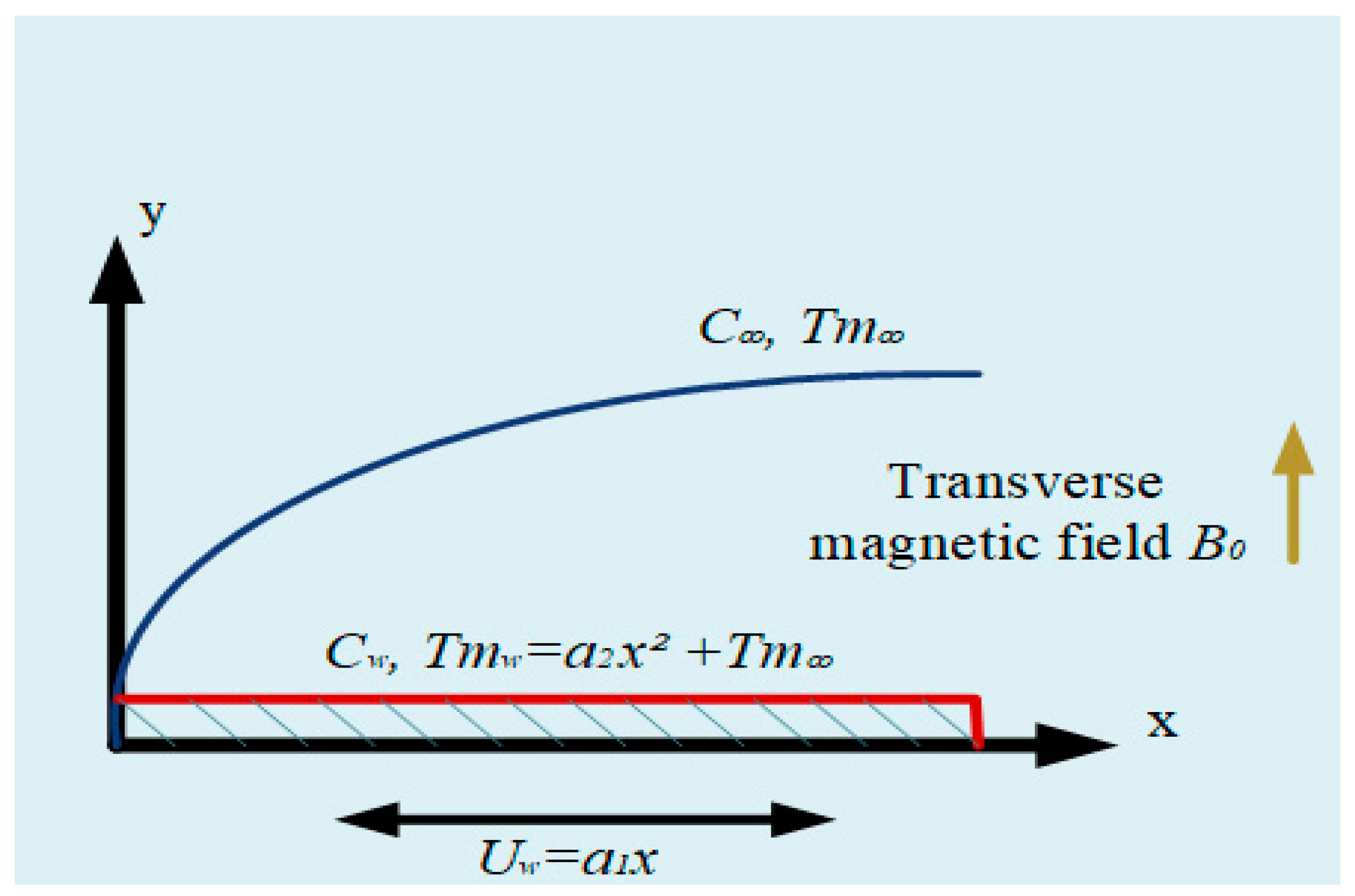
2. Mathematical Modeling
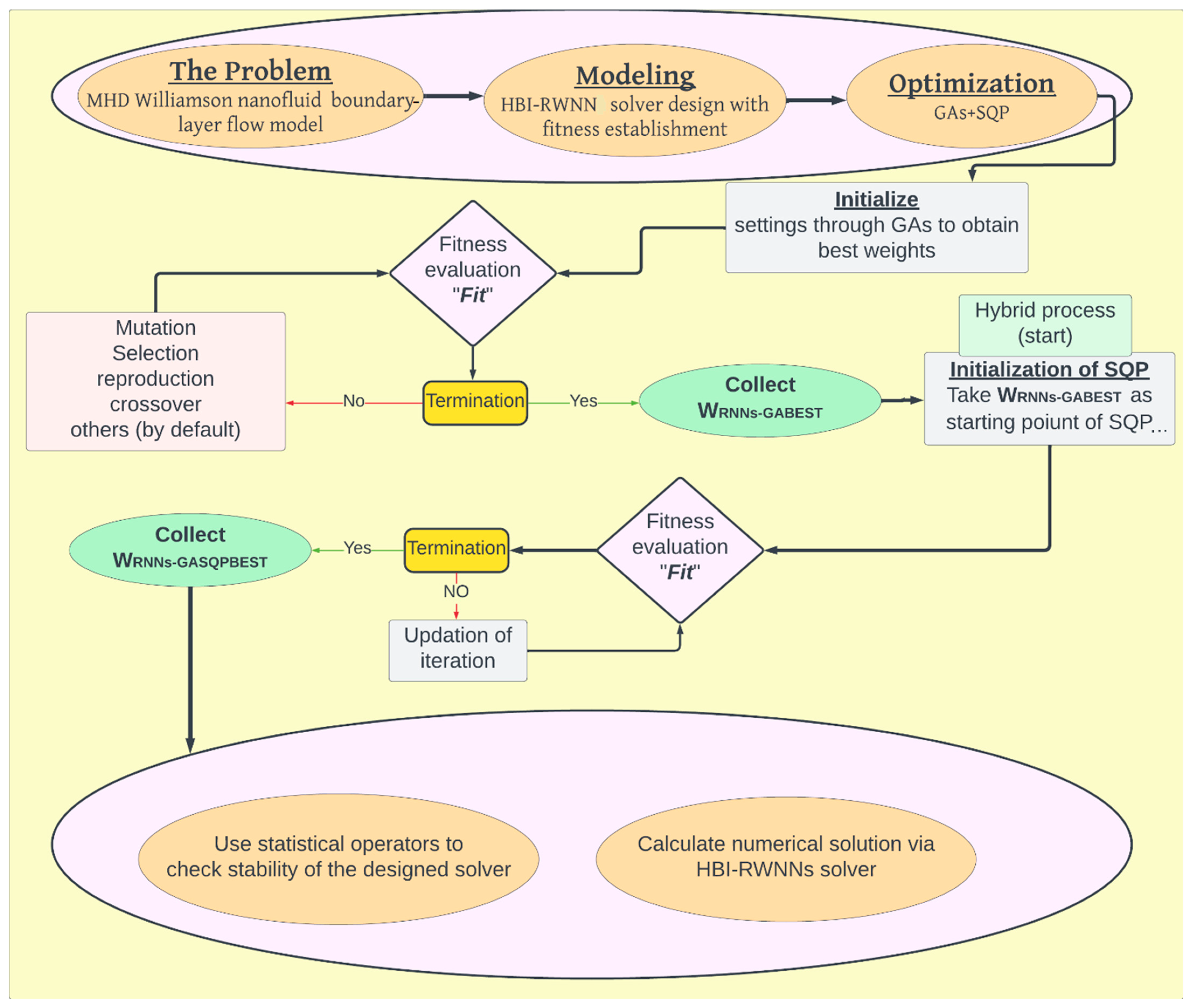
3. Methodology
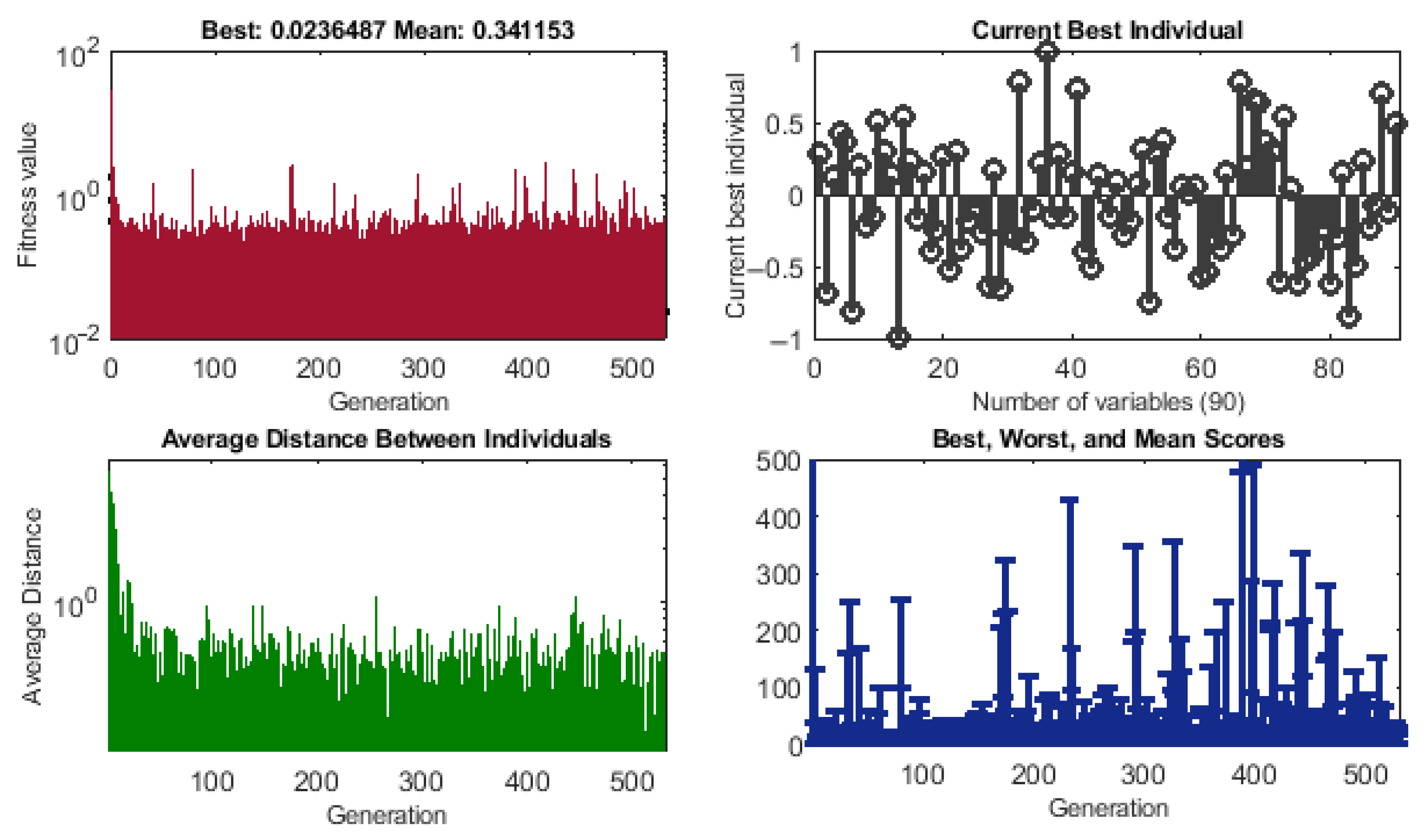
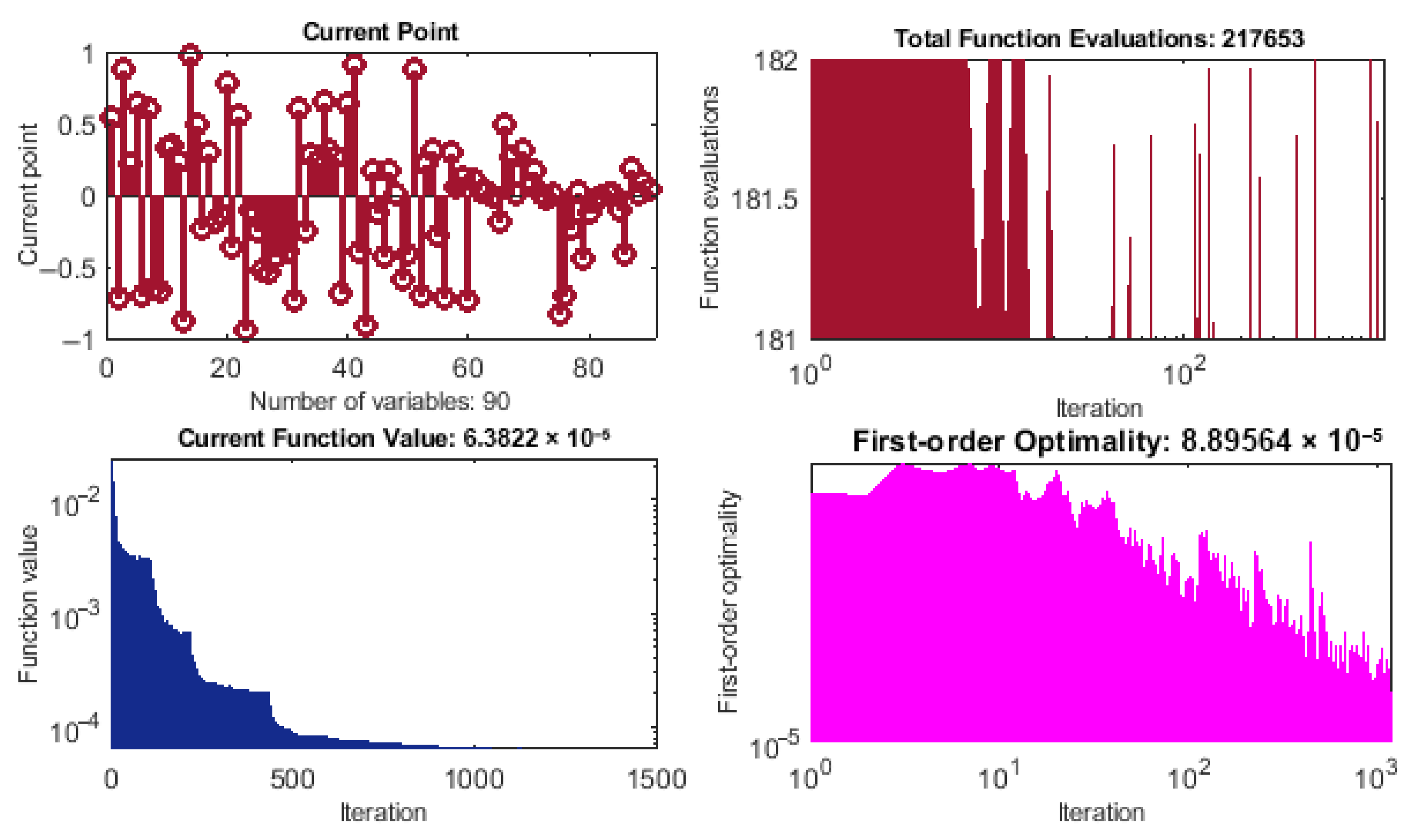
3.1. Learning Procedure
3.2. Performance Metrics
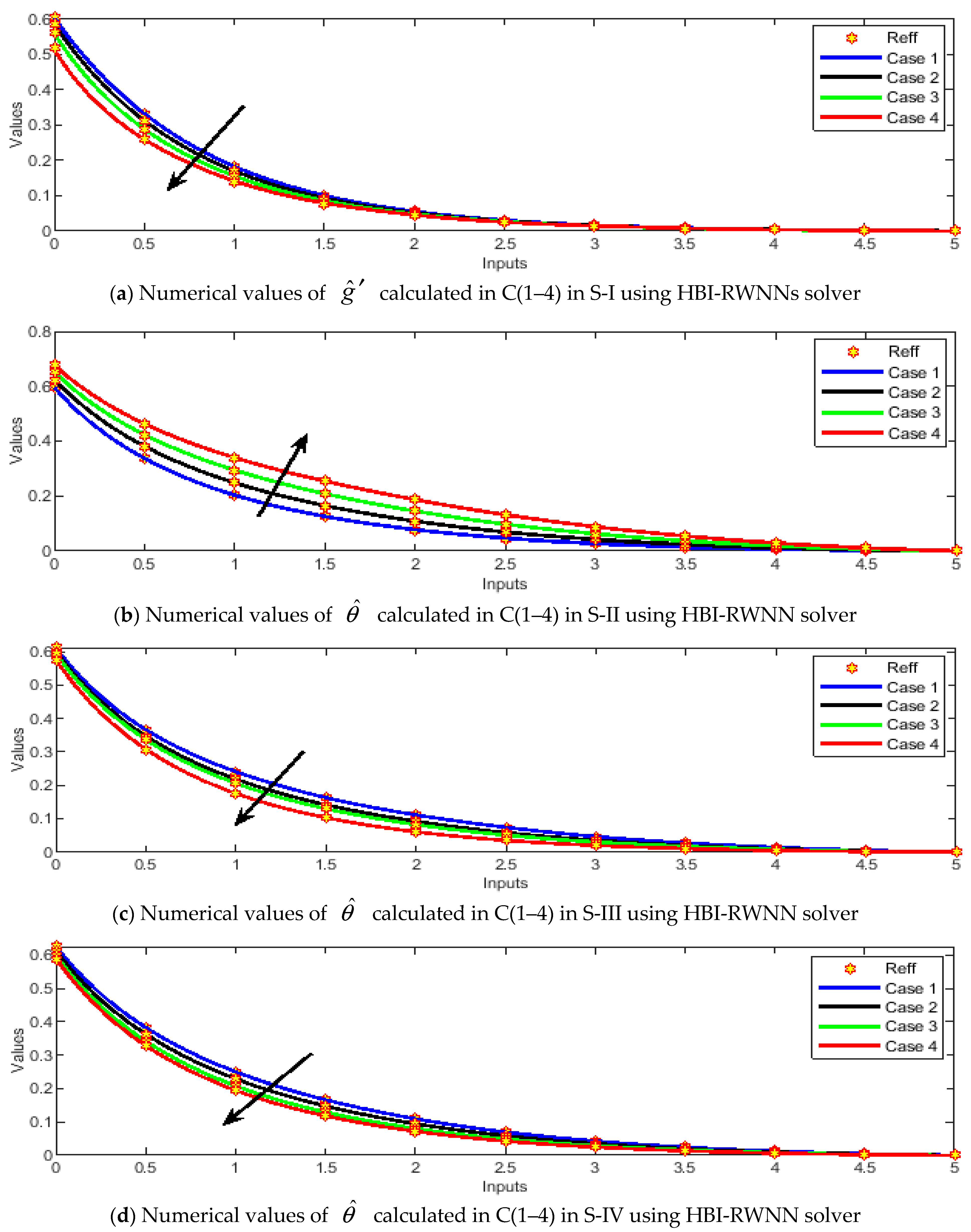
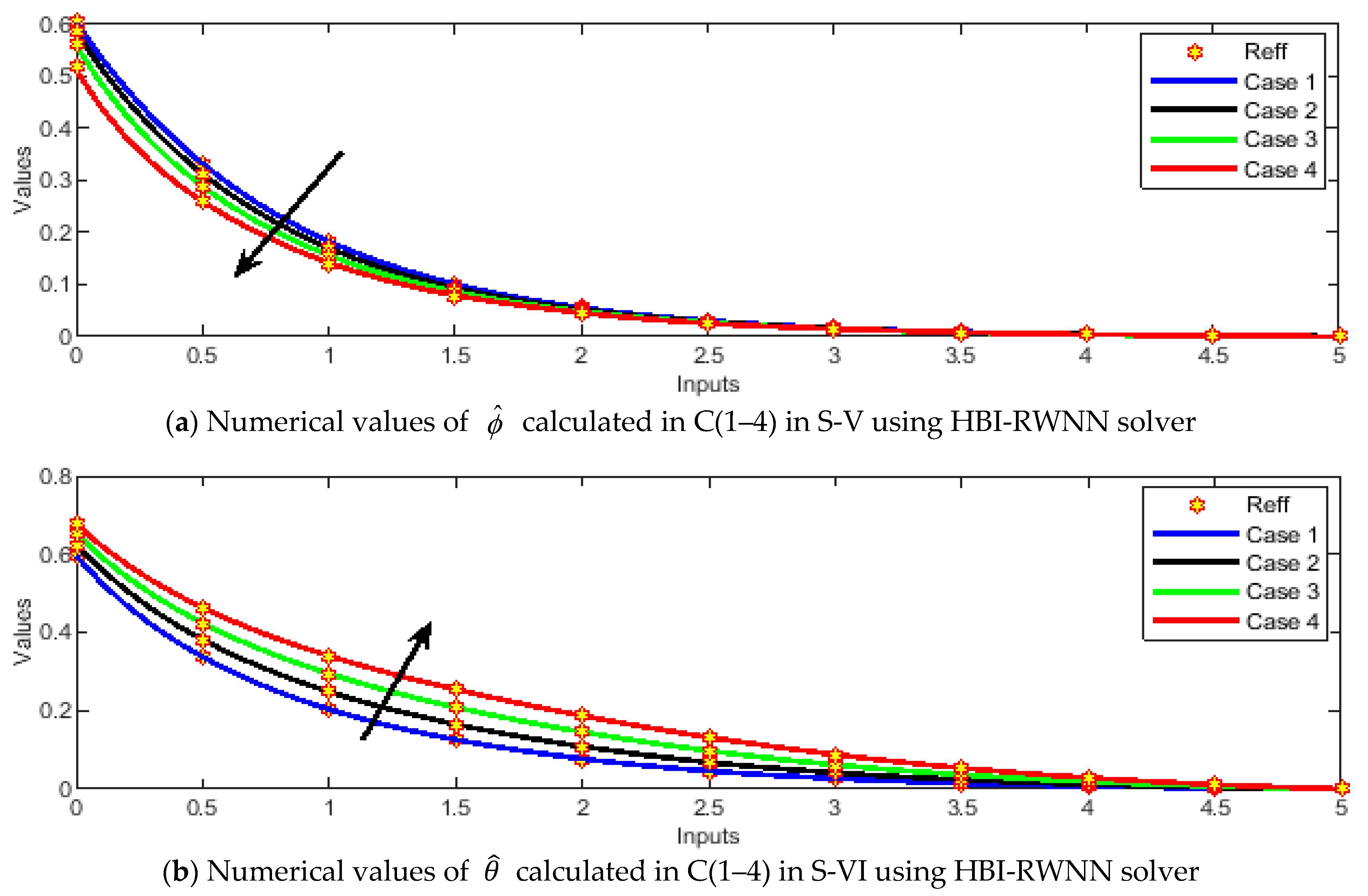
4. Results and Discussion
5. Conclusions
- An increase in the value of Williamson parameter diminishes the nanofluid velocity.
- The consequences of the diffusivity ratio parameter, Lewis number, and thermal slip parameter on the thermal gradient profile are identical, but a reciprocal effect is observed in case of the heat capacity ratio parameter.
- An escalation in the value of the Schmidt parameter reduces the nanofluid concentration.
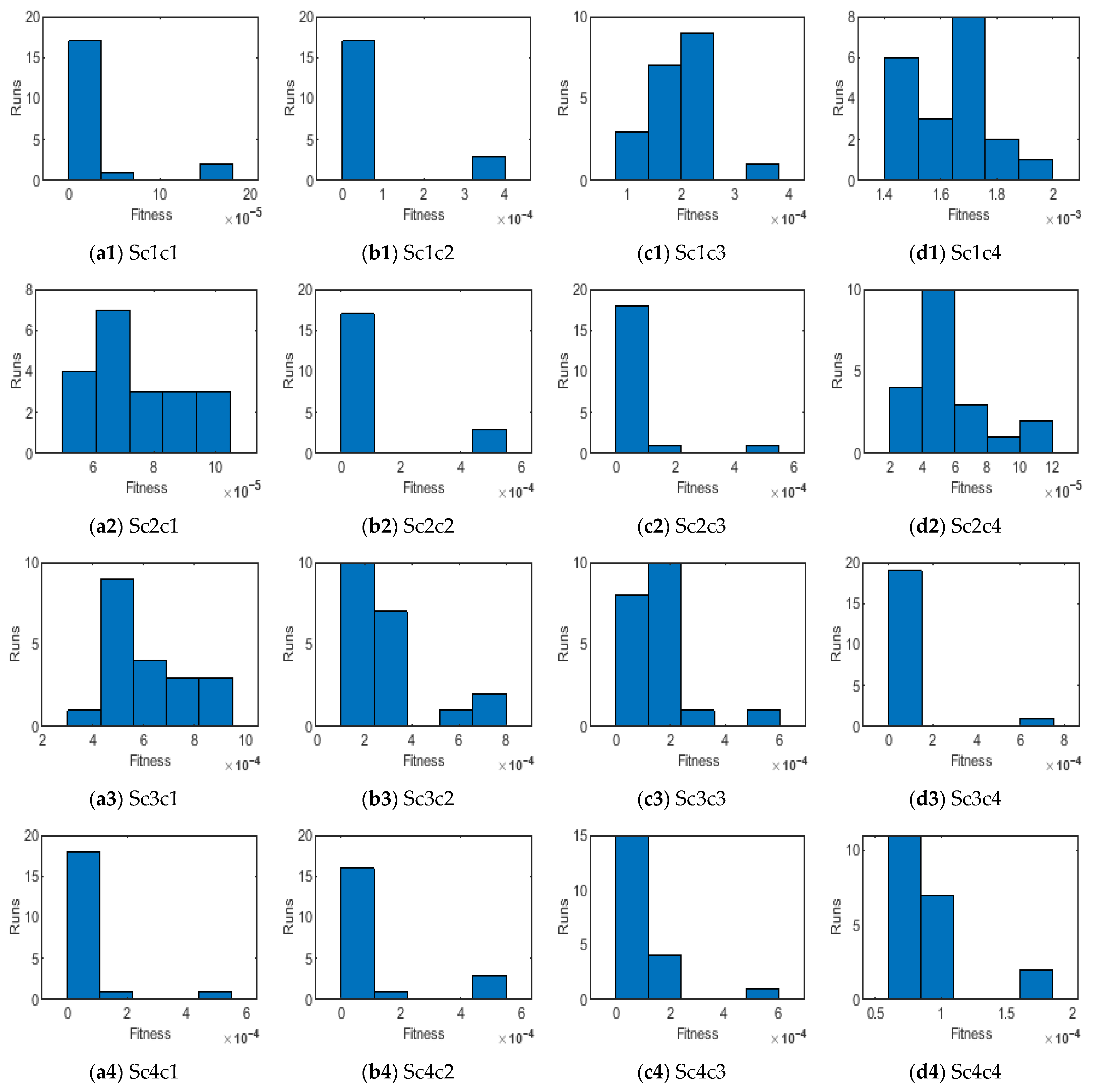
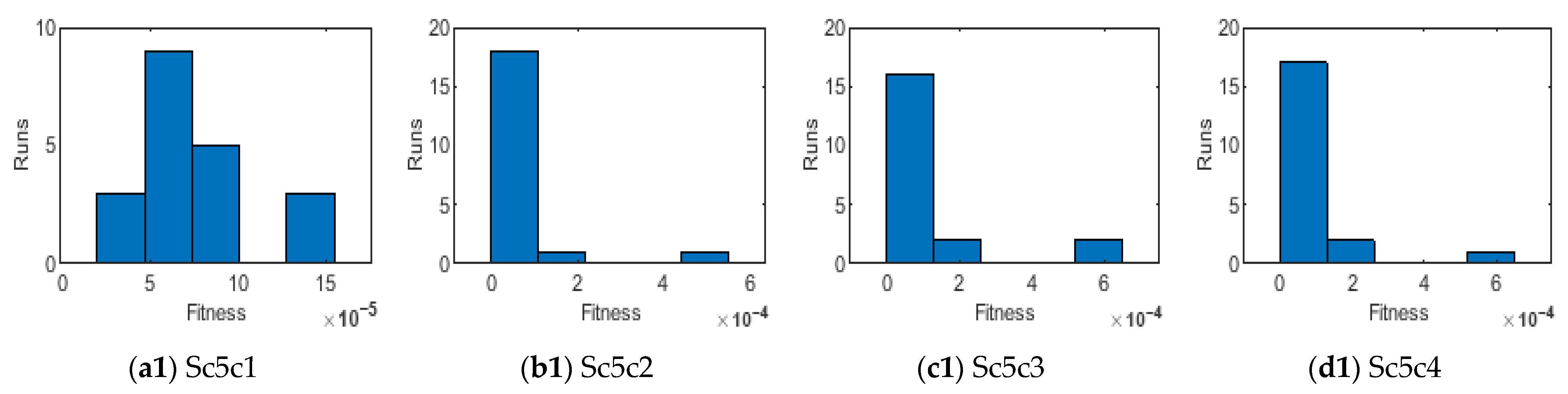
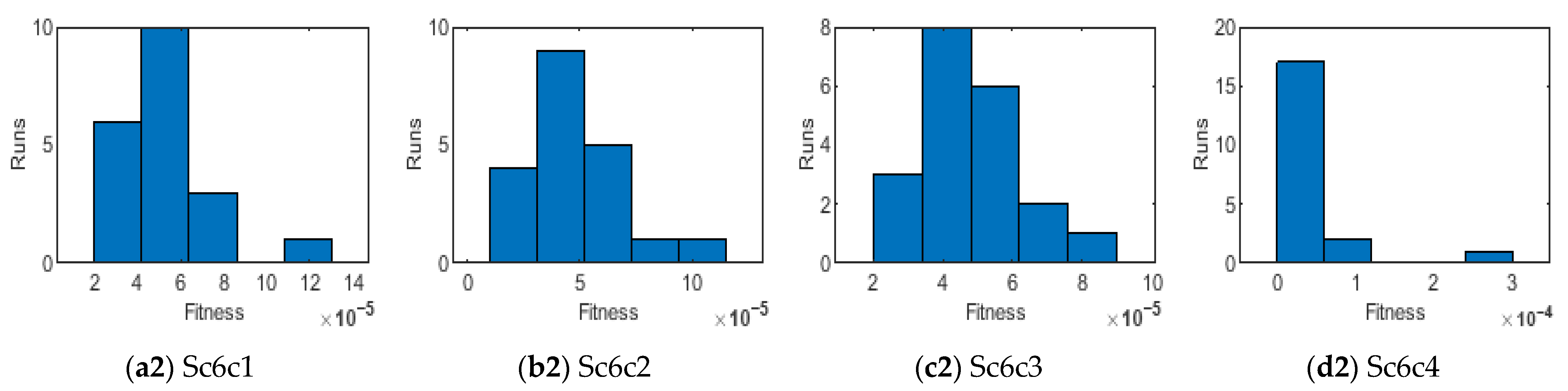
- The designed solver optimized through the hybrid GA-SQP approach achieves exceptionally low AEs, consistently in the order of 10−7 ↔ 10−9, confirming the excellent precision and reliability of the proposed numerical framework.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| v1, v2 | (x, y) components of velocity [ms−1] | a1, a2 | Stretching-rate constants |
| λ | Williamson parameter | Pr | Prandtl number |
| Nc | Heat capacity ratio parameter | Nbt | Diffusivity ratio parameter |
| Le | Lewis number | Sc | Schmidt number |
| M | Magnetic field | K | Permeability parameter |
| R | Radiation parameter | Z1 | Thermal slip factor |
| C | Volume fraction | Tm | Fluid temperature [K] |
| Cp | Specific heat capacity | DT | Thermophoresis diffusion coefficient |
| Stefan–Boltzmann constant | C∞ | Ambient volume fraction [mol m−3] | |
| Time constant | σ | ] | |
| Z2 | Velocity slip parameter | Bo | Induced magnetic field [Tesla] |
| Tmw | Temperature near sheet | αg | Thermal diffusivity [m2 s−1] |
| k2 | Mean absorption coefficient | Cw | Volume fraction at the sheet |
| Uw | Velocity during expansion along x-axis | qr | Radiative heat flux |
| Kinematic viscosity | Dynamic viscosity | ||
| Density of nanofluid [kg m−3] | (ρc)ng | Nanoliquid heat | |
| (ρc)p | Effective heat capacity [JK−1] | k1 | Permeability of the porous medium |
| Z3 | Velocity slip factor | Z4 | Thermal slip parameter |
| Nanoparticles density | Ambient temperature | ||
| DB | Brownian diffusion | Velocity along the sheet | |
| k | Thermal conductivity | Similarity variable |
References
- Masuda, H.; Ebata, A.; Teramae, K. Alteration of thermal conductivity and viscosity of liquid by dispersing ultra-fine particles. Dispersion of Al2O3, SiO2 and TiO2 ultra-fine particles. Netsu Bussei 1993, 7, 227–233. [Google Scholar] [CrossRef]
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; (No. ANL/MSD/CP-84938; CONF-951135-29); Argonne National Lab. (ANL): Argonne, IL, USA, 1995. [Google Scholar]
- Enjavi, Y.; Sedghamiz, M.A.; Rahimpour, M.R. Application of nanofluids in drug delivery and disease treatment. In Nanofluids and Mass Transfer; Elsevier: Amsterdam, The Netherlands, 2022; pp. 449–465. [Google Scholar]
- Buschmann, M.H.; Franzke, U. Improvement of thermosyphon performance by employing nanofluid. Int. J. Refrig. 2014, 40, 416–428. [Google Scholar] [CrossRef]
- Saleem, N.; Ashraf, T.; Daqqa, I.; Munawar, S.; Idrees, N.; Afzal, F.; Afzal, D. Thermal Case Study of Cilia Actuated Transport of Radiated Blood-Based Ternary Nanofluid under the Action of Tilted Magnetic Field. Coatings 2022, 12, 873. [Google Scholar] [CrossRef]
- Zhu, B.; Sun, Y.; Guo, P.; Liu, J. Nano-sized copper oxide enhancing the combustion of aluminum/kerosene-based nanofluid fuel droplets. Combust. Flame 2022, 240, 112028. [Google Scholar]
- Sözen, A.; Özbaş, E.; Menlik, T.; Çakır, M.T.; Gürü, M.; Boran, K. Improving the thermal performance of diffusion absorption refrigeration system with alumina nanofluids: An experimental study. Int. J. Refrig. 2014, 44, 73–80. [Google Scholar] [CrossRef]
- Janocha, M.; Tsotsas, E. Coating layer formation from deposited droplets: A comparison of nanofluid, microfluid and solution. Powder Technol. 2022, 399, 117202. [Google Scholar] [CrossRef]
- Ali, B.; Hussain, S.; Naqvi, S.I.R.; Habib, D.; Abdal, S. Aligned magnetic and bioconvection effects on tangent hyperbolic nanofluid flow across faster/slower stretching wedge with activation energy: Finite element simulation. Int. J. Appl. Comput. Math. 2021, 7, 1–20. [Google Scholar] [CrossRef]
- Khiabani, N.P.; Fakhroueian, Z.; Bahramian, A.; Vatanparast, H. Crystal growth of magnesium oxide nanocompounds for wetting alteration of carbonate surfaces. Chem. Pap. 2019, 73, 2513–2524. [Google Scholar] [CrossRef]
- Ali, B.; Rasool, G.; Hussain, S.; Baleanu, D.; Bano, S. Finite element study of magnetohydrodynamics (MHD) and activation energy in Darcy–Forchheimer rotating flow of Casson Carreau nanofluid. Processes 2020, 8, 1185. [Google Scholar] [CrossRef]
- Khan, K.A.; Javed, M.F.; Ullah, M.A.; Riaz, M.B. Heat and Mass transport analysis for Williamson MHD nanofluid flow over a stretched sheet. Results Phys. 2023, 53, 106873. [Google Scholar] [CrossRef]
- Abbas, A.; Jeelani, M.B.; Alnahdi, A.S.; Ilyas, A. MHD Williamson nanofluid fluid flow and heat transfer past a non-linear stretching sheet implanted in a porous medium: Effects of heat generation and viscous dissipation. Processes 2022, 10, 1221. [Google Scholar] [CrossRef]
- Alqurashi, M.S.; Gul, H.; Ahmad, I.; Majeed, A.H.; Khalifa, H.A.E.W. A study of thermal conductivity enhancement in magnetic blood flow: Applications of medical engineering. Int. J. Heat Fluid Flow 2025, 112, 109719. [Google Scholar] [CrossRef]
- Tarakaramu, N.; Satya Narayana, P.V.; Babu, D.H.; Sarojamma, G.; Makinde, O.D. Joule Heating and Dissipation Effects on Magnetohydrodynamic Couple Stress Nanofluid Flow over a Bidirectional Stretching Surface. Int. J. Heat Technol. 2021, 39, 1–12. [Google Scholar] [CrossRef]
- Hira, F.S.; Rubbab, Q.; Ahmad, I.; Majeed, A.H. Advanced computational modeling of Darcy-Forchheimer effects and nanoparticle-enhanced blood flow in stenosed arteries. Eng. Appl. Artif. Intell. 2025, 152, 110737. [Google Scholar] [CrossRef]
- Ajithkumar, M.; Lakshminarayana, P. A study on bioconvective peristaltic flow of a Casson nanofluid in a porous uniform/non-uniform flexible conduit. ZAMM-J. Appl. Math. Mech./Z. Für Angew. Math. Und Mech. 2024, 104, e202300007. [Google Scholar] [CrossRef]
- Reddy, M.V.; Meenakumari, R.; Ajithkumar, M.; Sucharitha, G.; Lakshminarayana, P.; Nath, J.M. Modeling and simulation of entropy optimization in Darcy–Forchheimer flow of magneto-Ree–Eyring nanofluid with suction/injection and motile microorganisms. Mod. Phys. Lett. B 2025, 36, 2550127. [Google Scholar] [CrossRef]
- Faizan, M.; Ajithkumar, M.; Reddy, M.V.; Jamal, M.A.; Almutairi, B.; Shah, N.A.; Chung, J.D. A theoretical analysis of the ternary hybrid nano-fluid with Williamson fluid model. Ain Shams Eng. J. 2024, 15, 102839. [Google Scholar] [CrossRef]
- Vinodkumar Reddy, M.; Ajithkumar, M.; Zafar, S.S.B.; Faizan, M.; Ali, F.; Lakshminarayana, P. Magnetohydrodynamic stagnation point flow of Williamson hybrid nanofluid via stretching sheet in a porous medium with heat source and chemical reaction. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2024, 09544089241239583. [Google Scholar] [CrossRef]
- Shamshuddin, M.D.; Rajput, G.R.; Jamshed, W.; Shahzad, F.; Salawu, S.O.; Abderrahmane, A.; Patil, V.S. MHD bioconvection microorganism nanofluid driven by a stretchable plate through porous media with an induced heat source. Waves Random Complex Media 2022, 1–25. [Google Scholar] [CrossRef]
- Khan, I.; Weera, W.; Mohamed, A. Heat transfer analysis of Cu and Al2O3 dispersed in ethylene glycol as a base fluid over a stretchable permeable sheet of MHD thin-film flow. Sci. Rep. 2022, 12, 8878. [Google Scholar]
- Alrihieli, H.; Areshi, M.; Alali, E.; Megahed, A.M. MHD dissipative Williamson nanofluid flow with chemical reaction due to a slippery elastic sheet which was contained within a porous medium. Micromachines 2022, 13, 1879. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Khan, Z.; Mohammed, P.O.; Al-Sarairah, E.; Jawad, M.; Jan, R. Heat Transfer of Buoyancy and Radiation on the Free Convection Boundary Layer MHD Flow across a Stretchable Porous Sheet. Energies 2022, 16, 58. [Google Scholar] [CrossRef]
- Biswal, M.M.; Swain, B.K.; Das, M.; Dash, G.C. Heat and mass transfer in MHD stagnation-point flow toward an inclined stretching sheet embedded in a porous medium. Heat Transf. 2022, 51, 4837–4857. [Google Scholar] [CrossRef]
- Sitamahalakshmi, V.; Reddy, G.V.R.; Falodun, B.O. Heat and Mass Transfer Effects on MHD Casson Fluid Flow of Blood in Stretching Permeable Vessel. J. Appl. Nonlinear Dyn. 2023, 12, 87–97. [Google Scholar] [CrossRef]
- Williamson, R.V. The flow of pseudoplastic materials. Ind. Eng. Chem. 1929, 21, 1108–1111. [Google Scholar] [CrossRef]
- Jabeen, K.; Mushtaq, M.; Mushtaq, T.; Muntazir, R.M.A. A numerical study of boundary layer flow of Williamson nanofluid in the presence of viscous dissipation, bioconvection, and activation energy. Numer. Heat Transf. Part A Appl. 2023, 85, 378–399. [Google Scholar] [CrossRef]
- Dyapa, H.; Kishan, N. Numerical simulation of Dufour and Soret impacts on MHD Williamson nanofluid flow through an inclined surface. Heat Transf. 2023, 52, 448–466. [Google Scholar] [CrossRef]
- Pal, D.; Mondal, S.; Vajravelu, K. Analysis of entropy generation and activation energy on double diffusive magnetohydrodynamic Williamson nanofluid flow featuring nonlinear thermal radiation. Int. J. Ambient Energy 2023, 44, 351–362. [Google Scholar] [CrossRef]
- Nayak, M.M.; Mishra, S.R. Fuzzy Parametric Behavior for the Flow of MHD Williamson Nanofluid with Melting Heat Transfer Boundary Condition. Int. J. Appl. Comput. Math. 2023, 9, 18. [Google Scholar] [CrossRef]
- Kairi, R.R.; Roy, S.; Raut, S. Stratified thermosolutal Marangoni bioconvective flow of gyrotactic microorganisms in Williamson nanofluid. Eur. J. Mech.-B/Fluids 2023, 97, 40–52. [Google Scholar] [CrossRef]
- Ahmed, S.E.; Arafa, A.A.; Hussein, S.A. A novel model of non-linear radiative Williamson nanofluid flow along a vertical wavy cone in the presence of gyrotactic microorganisms. Int. J. Model. Simul. 2023, 45, 68–82. [Google Scholar] [CrossRef]
- Patil, P.M.; Benawadi, S.; Muttannavar, V.T. Mixed Bioconvective Flow of Williamson Nanofluid Over a Rough Vertical Cone. Arab. J. Sci. Eng. 2023, 48, 2917–2928. [Google Scholar] [CrossRef]
- Wang, Z.; Shen, Y.; Zhang, D.; Tang, Z.; Li, W. A comparative study of multi-objective optimization with ANN-based VPSA model for CO2 capture from dry flue gas. J. Environ. Chem. Eng. 2022, 10, 108031. [Google Scholar] [CrossRef]
- Shoaib, M.; Tabassum, R.; Raja, M.A.Z.; Nisar, K.S.; Alqahtani, M.S.; Abbas, M. A design of predictive computational network for transmission model of lassa fever in Nigeria. Results Phys. 2022, 39, 105713. [Google Scholar] [CrossRef]
- Ilyas, H.; Raja, M.A.Z.; Ahmad, I.; Shoaib, M. A novel design of Gaussian wavelet neural networks for nonlinear Falkner-Skan systems in fluid dynamics. Chin. J. Phys. 2021, 72, 386–402. [Google Scholar] [CrossRef]
- Raja, M.A.Z.; Mehmood, A.; Ashraf, S.; Awan, K.M.; Shi, P. Design of evolutionary finite difference solver for numerical treatment of computer virus propagation with countermeasures model. Math. Comput. Simul. 2022, 193, 409–430. [Google Scholar] [CrossRef]
- Bilal, H.; Ullah, H.; Fiza, M.; Islam, S.; Raja, M.A.Z.; Shoaib, M.; Khan, I. A Levenberg-Marquardt backpropagation method for unsteady squeezing flow of heat and mass transfer behaviour between parallel plates. Adv. Mech. Eng. 2021, 13, 16878140211040897. [Google Scholar] [CrossRef]
- Cheema, T.N.; Naz, S. Numerical computing with Levenberg–Marquardt backpropagation networks for nonlinear SEIR Ebola virus epidemic model. AIP Adv. 2021, 11, 095205. [Google Scholar] [CrossRef]
- Butt, Z.I.; Ahmad, I.; Shoaib, M.; Hussain, S.I.; Ilyas, H.; Raja, M.A.Z. Stochastic neuro-swarming intelligence paradigm for the analysis of magneto-hydrodynamic prandtl–eyring fluid flow with diffusive magnetic layers effect over an elongated surface. Chin. J. Chem. Eng. 2024, 74, 295–311. [Google Scholar] [CrossRef]
- Yu, X.; Shen, Y.; Guan, Z.; Zhang, D.; Tang, Z.; Li, W. Multi-objective optimization of ANN-based PSA model for hydrogen purification from steam-methane reforming gas. Int. J. Hydrogen Energy 2021, 46, 11740–11755. [Google Scholar] [CrossRef]
- Hussain, S.I.; Ahmad, I.; Yasmeen, N. The remarkable role of hydrogen in conductors with copper and silver nanoparticles by mixed convection using viscosity Reynold’s model. In International Conference on Nonlinear Dynamics and Applications; Springer Nature: Cham, Switzerland, 2023; pp. 49–60. [Google Scholar]
- Butt, Z.I.; Ahmad, I.; Raja, M.A.Z.; Hussain, S.I.; Ilyas, H.; Shoaib, M. MHD slip flow through nanofluids for thermal energy storage in solar collectors using radiation and conductivity effects: A novel design sequential quadratic programming-based neuro-evolutionary approach. Mod. Phys. Lett. B 2024, 37, 2550075. [Google Scholar] [CrossRef]
- Ilyas, H.; Ahmad, I.; Hussain, S.I.; Shoaib, M.; Raja, M.A.Z. Design of evolutionary computational intelligent solver for nonlinear corneal shape model by Mexican Hat and Gaussian wavelet neural networks. Waves Random Complex Media 2024, 1–23. [Google Scholar] [CrossRef]
- Hussain, S.I.; Ahmad, I.; Raja, M.A.Z.; Umer, C.M.Z. A computational convection analysis of SiO2/water and MoS2-SiO2/water based fluidic system in inverted cone. Eng. Rep. 2023, 5, e12660. [Google Scholar] [CrossRef]
- Ahmad, I.; Hussain, S.I.; Ilyas, H.; Raja, M.A.Z.; Afzal, S.; Javed, M. Optimal control of thermoregulation in the human dermal regions investigated through the stochastic integrated techniques. Case Stud. Therm. Eng. 2024, 58, 104381. [Google Scholar] [CrossRef]
- Kho, Y.B.; Hussanan, A.; Mohamed, M.K.A.; Salleh, M.Z. Heat and mass transfer analysis on flow of Williamson nanofluid with thermal and velocity slips: Buongiorno model. Propuls. Power Res. 2019, 8, 243–252. [Google Scholar] [CrossRef]
- Reddy, Y.D.; Mebarek-Oudina, F.; Goud, B.S.; Ismail, A.I. Radiation, velocity and thermal slips effect toward MHD boundary layer flow through heat and mass transport of Williamson nanofluid with porous medium. Arab. J. Sci. Eng. 2022, 47, 16355–16369. [Google Scholar] [CrossRef]
- Reddy, M.V.; Ajithkumar, M.; Lone, S.A.; Ali, F.; Lakshminarayana, P.; Saeed, A. Magneto-Williamson nanofluid flow past a wedge with activation energy: Buongiorno model. Adv. Mech. Eng. 2024, 16, 16878132231223027. [Google Scholar] [CrossRef]
- Reddy, M.V.; Vajravelu, K.; Ajithkumar, M.; Sucharitha, G.; Lakshminarayana, P. Numerical treatment of entropy generation in convective MHD Williamson nanofluid flow with Cattaneo–Christov heat flux and suction/injection. Int. J. Model. Simul. 2024, 1–18. [Google Scholar] [CrossRef]
- Ricker, N. The form and laws of propagation of seismic wavelets. Geophysics 1953, 18, 10–40. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Singh, S.; Ghosh, S.K. A unique artificial intelligence approach and mathematical model to accurately evaluate viscosity and density of several nanofluids from experimental data. Colloids Surf. A Physicochem. Eng. Asp. 2022, 640, 128389. [Google Scholar] [CrossRef]
- Marsalek, R.; Pospisil, J.; Taraba, B. The influence of temperature on the adsorption of CTAB on coals. Colloids Surf. A Physicochem. Eng. Asp. 2011, 383, 80–85. [Google Scholar] [CrossRef]
- Ren, S.; Wang, S.; Dong, Z.; Chen, J.; Li, L. Dynamic behaviors and self-cleaning property of droplet on superhydrophobic coating in uniform DC electric field. Colloids Surf. A Physicochem. Eng. Asp. 2021, 626, 127056. [Google Scholar] [CrossRef]
- Esfe, M.H.; Esmaily, R.; Mahabadi, S.T.; Toghraie, D.; Rahmanian, A.; Fazilati, M.A. Application of artificial intelligence and using optimal ANN to predict the dynamic viscosity of Hybrid nano-lubricant containing Zinc Oxide in Commercial oil. Colloids Surf. A Physicochem. Eng. Asp. 2022, 647, 129115. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S.J. Numerical Optimization; Springer: New York, NY, USA, 1999. [Google Scholar]
- Butt, Z.I.; Ahmad, I.; Hussain, S.I.; Raja, M.A.Z.; Shoaib, M.; Ilyas, H. Intelligent computing paradigm for unsteady magneto nano-polymeric Casson nanofluid with Ohmic dissipation and thermal radiation. Chin. J. Phys. 2024, 88, 212–269. [Google Scholar] [CrossRef]
- Ahmad, I.; Raja, M.A.Z.; Hussain, S.I.; Ilyas, H.; Mohayyuddin, Z. Design of stochastic computational Levenberg Marquardt backpropagation-based technique to investigate temperature distribution of longitudinal moving porous fin. Sci. Rep. 2024, 14, 17359. [Google Scholar] [CrossRef]
- Butt, Z.I.; Ahmad, I.; Hussain, S.I.; Raja, M.A.Z.; Shoaib, M.; Ilyas, H. Inverse multiquadric kernel-based neuro heuristic approach to analyze the unsteady MHD nanofluid flow via permeable elongating surface. ZAMM-J. Appl. Math. Mech./Z. Für Angew. Math. Und Mech. 2024, 104, e202300390. [Google Scholar] [CrossRef]

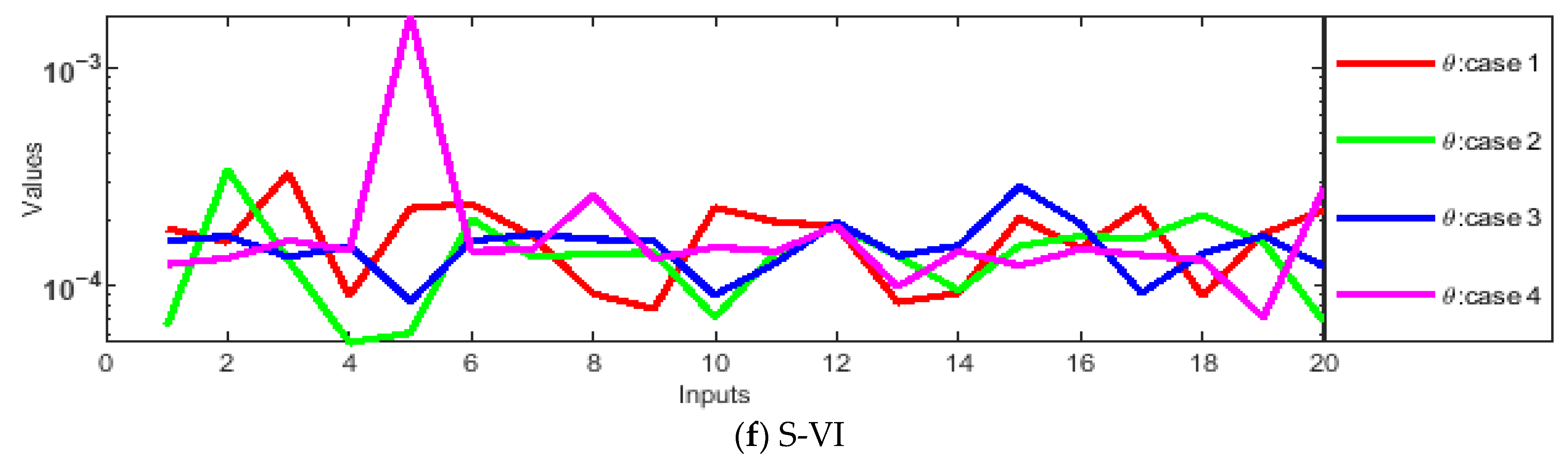
| Cases | Scenarios | |||||
|---|---|---|---|---|---|---|
| S-I | S-II | S-III | S-1V | S-V | S-VI | |
| Nc | Nbt | Le | Sc | |||
| 1. | 0.01 | 3.65 | 0.25 | 1.05 | 3.21 | 0.05 |
| 2. | 0.31 | 5.65 | 0.35 | 1.25 | 4.21 | 0.25 |
| 3. | 0.61 | 7.65 | 0.45 | 1.55 | 5.21 | 0.55 |
| 4. | 0.91 | 9.65 | 1.85 | 1.85 | 6.21 | 0.85 |
| Process for GAs (Start) |
|---|
| Inputs: The chromosomes with the same quantity of identical |
| elements: W = [Wg, Wθ, WΦ] for Wg = [W1g, W2g, W3g], Wθ = [W1θ, W2θ, W3θ] and |
| WΦ = [W1Φ, W2Φ, W3Φ]. |
| Output: WRNNs-GABEST weights obtained via GAs. |
| Initialization: Chromosome formation through the creation of W. |
| Utilization of “gaoptimset” for declarations as well as generations. |
| Fitness calculation: Use Equation (23) to estimate fitness “Fit” W |
| employing population P. |
| Termination: GAs stop working if any one option stated below is achieved: |
|
|
|
| Ranking: Fitness “Fit” is used to rank each W. |
| Reproduction: Reformation of P through the “fitness calculation” |
| step. |
| Storage: Collect WRNNs-GABEST weights as well as fitness “Fit”. |
| Process for GAs (completed) |
| Hybrid Process through SQP (started) |
| Inputs: Take WRNNs-GABEST as a starting point. |
| Output: Collect WRNNs-GASQPBEST. |
| Initialization: Constraints, declarations with other assignments |
| Stopping criteria: GASQP hybrid process terminates if any one of options |
| mentioned below achieved: |
|
|
| Accumulate: WRNNs-GASQPBEST weights stored along the fitness “Fit”. |
| Hybrid process (completed) |
| Data generations |
| HBI-RBNN solver ran twenty times to obtain the best numerical |
| outcomes of MHD-WNF-BL flow problem. |
| Scenario 1 | η | (C-1) | (C-2) | (C-3) | (C-4) |
| 0 | 3.8446 × 10−4 | 1.0050 × 10−3 | 3.3297 × 10−3 | 9.1214 × 10−3 | |
| 0.5 | 2.0773 × 10−4 | 5.7213 × 10−4 | 1.0580 × 10−3 | 2.2657 × 10−4 | |
| 1.0 | 1.6248 × 10−4 | 3.0336 × 10−4 | 3.1709 × 10−4 | 2.1035 × 10−3 | |
| 1.5 | 5.0855 × 10−5 | 6.1123 × 10−5 | 1.9693 × 10−4 | 1.4047 × 10−3 | |
| 2.0 | 1.1975 × 10−4 | 2.4628 × 10−4 | 3.9449 × 10−4 | 2.3183 × 10−3 | |
| 2.5 | 5.8025 × 10−5 | 9.5901 × 10−5 | 2.4098 × 10−4 | 8.4700 × 10−4 | |
| 3.0 | 1.1999 × 10−4 | 2.2566 × 10−4 | 1.0270 × 10−4 | 7.9208 × 10−4 | |
| 3.5 | 7.2501 × 10−5 | 7.1121 × 10−5 | 1.5321 × 10−4 | 1.0269 × 10−3 | |
| 4.0 | 1.2131 × 10−4 | 2.3642 × 10−4 | 3.9321 × 10−4 | 3.8560 × 10−4 | |
| 4.5 | 1.5081 × 10−4 | 2.7370 × 10−4 | 3.8403 × 10−4 | 6.0631 × 10−4 | |
| 5.0 | 1.5266 × 10−4 | 2.3455 × 10−4 | 3.5103 × 10−4 | 6.6130 × 10−4 | |
| Scenario 2 | η | ||||
| 0 | 1.2046 × 10−4 | 2.9140 × 10−4 | 1.6571 × 10−4 | 1.1190 × 10−4 | |
| 0.5 | 4.5802 × 10−4 | 8.0576 × 10−4 | 5.4969 × 10−4 | 3.9657 × 10−4 | |
| 1.0 | 3.1602 × 10−4 | 7.1366 × 10−4 | 5.0445 × 10−4 | 3.7744 × 10−4 | |
| 1.5 | 4.6285 × 10−4 | 8.8757 × 10−4 | 7.2327 × 10−4 | 6.0232 × 10−4 | |
| 2.0 | 4.4825 × 10−4 | 8.7552 × 10−4 | 7.4998 × 10−4 | 6.5574 × 10−4 | |
| 2.5 | 1.4116 × 10−4 | 5.7487 × 10−4 | 5.5163 × 10−4 | 5.3145 × 10−4 | |
| 3.0 | 2.4943 × 10−4 | 5.5947 × 10−4 | 5.8108 × 10−4 | 5.8167 × 10−4 | |
| 3.5 | 1.7556 × 10−4 | 3.7655 × 10−4 | 4.1653 × 10−4 | 4.2284 × 10−4 | |
| 4.0 | 5.3764 × 10−5 | 1.5884 × 10−4 | 1.9176 × 10−4 | 2.0990 × 10−4 | |
| 4.5 | 6.9646 × 10−5 | 1.1158 × 10−4 | 1.4184 × 10−4 | 1.5472 × 10−4 | |
| 5.0 | 3.5327 × 10−5 | 5.6209 × 10−5 | 2.3896 × 10−5 | 4.5895 × 10−5 | |
| Scenario 3 | η | ||||
| 0 | 3.6259 × 10−3 | 1.0148 × 10−3 | 4.7585 × 10−4 | 2.8834 × 10−4 | |
| 0.5 | 6.0176 × 10−4 | 6.9220 × 10−4 | 6.3033 × 10−4 | 6.1176 × 10−4 | |
| 1.0 | 1.7137 × 10−3 | 1.3933 × 10−3 | 8.0702 × 10−4 | 4.5243 × 10−4 | |
| 1.5 | 1.2138 × 10−3 | 1.0209 × 10−3 | 6.2141 × 10−4 | 5.2027 × 10−4 | |
| 2.0 | 1.4580 × 10−3 | 1.2722 × 10−3 | 8.4394 × 10−4 | 5.6733 × 10−4 | |
| 2.5 | 1.6359 × 10−3 | 9.5755 × 10−4 | 5.2769 × 10−4 | 1.6839 × 10−4 | |
| 3.0 | 7.7529 × 10−4 | 4.7207 × 10−4 | 2.5949 × 10−4 | 2.0241 × 10−4 | |
| 3.5 | 5.2878 × 10−4 | 3.0873 × 10−4 | 2.1926 × 10−4 | 2.1333 × 10−4 | |
| 4.0 | 1.2062 × 10−3 | 2.6311 × 10−4 | 1.6837 × 10−4 | 1.4144 × 10−4 | |
| 4.5 | 1.8099 × 10−3 | 5.7342 × 10−4 | 1.7660 × 10−4 | 1.1546 × 10−4 | |
| 5.0 | 2.4708 × 10−3 | 6.8481 × 10−4 | 2.0590 × 10−4 | 5.8698 × 10−5 | |
| Scenario 4 | η | ||||
| 0 | 1.8954 × 10−4 | 3.2330 × 10−4 | 2.9304 × 10−4 | 1.7394 × 10−4 | |
| 0.5 | 5.5086 × 10−4 | 8.1609 × 10−4 | 5.8987 × 10−4 | 4.8000 × 10−4 | |
| 1.0 | 4.6087 × 10−4 | 6.9651 × 10−4 | 4.9099 × 10−4 | 3.4901 × 10−4 | |
| 1.5 | 6.2024 × 10−4 | 8.4176 × 10−4 | 5.9780 × 10−4 | 4.5909 × 10−4 | |
| 2.0 | 6.3282 × 10−4 | 8.2693 × 10−4 | 6.7661 × 10−4 | 5.0497 × 10−4 | |
| 2.5 | 3.4269 × 10−4 | 4.7040 × 10−4 | 2.7228 × 10−4 | 1.3288 × 10−4 | |
| 3.0 | 3.8330 × 10−4 | 4.8066 × 10−4 | 3.0529 × 10−4 | 2.3259 × 10−4 | |
| 3.5 | 2.9232 × 10−4 | 3.4473 × 10−4 | 3.1196 × 10−4 | 2.0651 × 10−4 | |
| 4.0 | 1.0417 × 10−4 | 1.5095 × 10−4 | 1.9463 × 10−4 | 8.7584 × 10−5 | |
| 4.5 | 7.8291 × 10−5 | 1.0541 × 10−4 | 1.2958 × 10−4 | 6.7573 × 10−5 | |
| 5.0 | 4.4607 × 10−5 | 6.7691 × 10−5 | 6.7867 × 10−5 | 5.9711 × 10−5 |
| Scenario 5 | η | ||||
| 0 | 1.1701 × 10−4 | 1.0039 × 10−4 | 9.5489 × 10−5 | 3.3642 × 10−4 | |
| 0.5 | 8.9467 × 10−4 | 1.3697 × 10−3 | 2.2360 × 10−3 | 5.2136 × 10−3 | |
| 1.0 | 1.0949 × 10−3 | 1.4411 × 10−3 | 2.0198 × 10−3 | 4.1335 × 10−3 | |
| 1.5 | 9.2789 × 10−4 | 1.0623 × 10−3 | 1.3583 × 10−3 | 2.6451 × 10−3 | |
| 2.0 | 6.0317 × 10−4 | 5.8218 × 10−4 | 6.0827 × 10−4 | 1.2650 × 10−3 | |
| 2.5 | 4.4400 × 10−4 | 3.6959 × 10−4 | 3.9457 × 10−4 | 8.9253 × 10−4 | |
| 3.0 | 1.9804 × 10−4 | 1.3882 × 10−4 | 1.9556 × 10−4 | 6.7146 × 10−4 | |
| 3.5 | 1.0586 × 10−4 | 7.5692 × 10−5 | 1.2940 × 10−4 | 4.8128 × 10−4 | |
| 4.0 | 8.0747 × 10−5 | 6.7299 × 10−5 | 8.2186 × 10−5 | 4.1204 × 10−4 | |
| 4.5 | 5.6156 × 10−5 | 1.0460 × 10−4 | 9.1240 × 10−5 | 4.3199 × 10−4 | |
| 5.0 | 9.3826 × 10−5 | 1.0299 × 10−4 | 8.2199 × 10−5 | 3.7726 × 10−4 | |
| Scenario 6 | η | ||||
| 0 | 1.3741 × 10−4 | 1.1214 × 10−4 | 1.3242 × 10−4 | 2.5044 × 10−4 | |
| 0.5 | 3.5924 × 10−4 | 3.1423 × 10−4 | 3.2554 × 10−4 | 3.6307 × 10−4 | |
| 1.0 | 2.2704 × 10−4 | 1.9781 × 10−4 | 2.0784 × 10−4 | 2.6413 × 10−4 | |
| 1.5 | 3.2677 × 10−4 | 2.7204 × 10−4 | 2.7551 × 10−4 | 3.7131 × 10−4 | |
| 2.0 | 2.5508 × 10−4 | 2.1246 × 10−4 | 2.0733 × 10−4 | 2.7966 × 10−4 | |
| 2.5 | 1.2889 × 10−4 | 9.6197 × 10−5 | 1.1200 × 10−4 | 1.7712 × 10−4 | |
| 3.0 | 1.7861 × 10−4 | 1.3690 × 10−4 | 1.3346 × 10−4 | 2.1253 × 10−4 | |
| 3.5 | 7.0405 × 10−5 | 5.5480 × 10−5 | 6.6135 × 10−5 | 1.7935 × 10−4 | |
| 4.0 | 3.4260 × 10−5 | 4.8339 × 10−5 | 5.8381 × 10−5 | 1.7202 × 10−4 | |
| 4.5 | 7.2076 × 10−5 | 4.0913 × 10−5 | 8.1231 × 10−5 | 1.2474 × 10−4 | |
| 5.0 | 3.8373 × 10−5 | 3.3374 × 10−5 | 4.3195 × 10−5 | 8.2847 × 10−5 |
| Scenario 1 () | B. V | It# | B. V | It# | B. V | It# | B. V | It# |
|---|---|---|---|---|---|---|---|---|
| (C-1) | (C-2) | (C-3) | (C-4) | |||||
| MAE | 1.7026 × 10−4 | 15 | 1.9737 × 10−4 | 11 | 1.4856 × 10−4 | 8 | 9.1099 × 10−4 | 4 |
| RMSE | 1.7388 × 10−4 | 15 | 2.0099 × 10−4 | 11 | 1.5093 × 10−4 | 8 | 1.0746 × 10−3 | 4 |
| ETIC | 2.5701 × 10−4 | 15 | 2.9707 × 10−4 | 11 | 2.2309 × 10−4 | 8 | 1.5878 × 10−3 | 4 |
| NSEE | 1.5742 × 10−6 | 15 | 2.1033 × 10−6 | 11 | 1.1861 × 10−6 | 8 | 6.0120 × 10−5 | 4 |
| E-VAF | 7.2668 × 10−9 | 15 | 8.4243 × 10−9 | 11 | 4.1561 × 10−9 | 8 | 1.8975 × 10−6 | 19 |
| E-R2 | 1.5742 × 10−6 | 15 | 2.1033 × 10−6 | 11 | 1.1861 × 10−6 | 8 | 6.0120 × 10−5 | 4 |
| Scenario 2 () | ||||||||
| MAE | 1.2287 × 10−4 | 2 | 7.3637 × 10−5 | 18 | 6.2005 × 10−5 | 9 | 6.1234 × 10−4 | 16 |
| RMSE | 1.2837 × 10−4 | 13 | 9.3304 × 10−5 | 18 | 7.7407 × 10−5 | 9 | 8.5668 × 10−4 | 16 |
| ETIC | 1.8974 × 10−4 | 13 | 7.5138 × 10−5 | 18 | 6.2334 × 10−5 | 9 | 6.9084 × 10−4 | 16 |
| NSEE | 8.5795 × 10−7 | 13 | 4.4821 × 10−7 | 18 | 3.0849 × 10−7 | 9 | 3.7785 × 10−5 | 16 |
| E-VAF | 8.0728 × 10−9 | 13 | 2.3445 × 10−8 | 13 | 1.5334 × 10−8 | 9 | 2.5632 × 10−6 | 16 |
| E-R2 | 8.5795 × 10−7 | 13 | 4.4821 × 10−7 | 18 | 3.0849 × 10−7 | 9 | 3.7785 × 10−5 | 16 |
| Scenario 3 () | B. V | It# | B. V | It# | B. V | It# | B. V | It# |
|---|---|---|---|---|---|---|---|---|
| (C-1) | (C-2) | (C-3) | (C-4) | |||||
| MAE | 3.1022 × 10−5 | 9 | 5.8913 × 10−5 | 9 | 3.6979 × 10−5 | 8 | 2.2250 × 10−5 | 12 |
| RMSE | 4.3174 × 10−5 | 9 | 7.6622 × 10−5 | 9 | 4.6419 × 10−5 | 8 | 2.7558 × 10−5 | 12 |
| ETIC | 3.4765 × 10−5 | 9 | 6.1703 × 10−5 | 9 | 3.6034 × 10−5 | 8 | 2.1393 × 10−5 | 12 |
| NSEE | 9.5967 × 10−8 | 9 | 3.0227 × 10−7 | 9 | 1.1020 × 10−7 | 8 | 3.8843 × 10−8 | 12 |
| E-VAF | 6.4384 × 10−9 | 9 | 1.7140 × 10−8 | 9 | 6.7865 × 10−9 | 8 | 2.2794 × 10−9 | 17 |
| E-R2 | 9.5967 × 10−8 | 9 | 3.0227 × 10−7 | 9 | 1.1020 × 10−7 | 8 | 3.8843 × 10−8 | 12 |
| Scenario 4 () | ||||||||
| MAE | 6.6399 × 10−4 | 19 | 2.7485 × 10−5 | 18 | 3.5101 × 10−5 | 5 | 5.3316 × 10−5 | 14 |
| RMSE | 7.3064 × 10−4 | 19 | 3.4620 × 10−5 | 18 | 4.1776 × 10−5 | 5 | 5.6940 × 10−5 | 14 |
| ETIC | 5.6691 × 10−4 | 19 | 2.6876 × 10−5 | 18 | 3.2431 × 10−5 | 5 | 3.6158 × 10−5 | 14 |
| NSEE | 2.7303 × 10−5 | 19 | 6.1301 × 10−8 | 18 | 8.9262 × 10−8 | 5 | 1.6537 × 10−7 | 14 |
| E-VAF | 8.0141 × 10−7 | 19 | 3.8203 × 10−9 | 16 | 4.4239 × 10−9 | 17 | 4.1062 × 10−9 | 14 |
| E-R2 | 2.7303 × 10−5 | 19 | 6.1301 × 10−8 | 18 | 8.9262 × 10−8 | 5 | 1.6537 × 10−7 | 14 |
| Scenario 5 () | ||||||||
| MAE | 1.0474 × 10−4 | 7 | 4.3024 × 10−5 | 2 | 5.5897 × 10−5 | 2 | 4.0007 × 10−5 | 19 |
| RMSE | 1.1837 × 10−4 | 7 | 5.5853 × 10−5 | 2 | 6.7130 × 10−5 | 2 | 5.3986 × 10−5 | 19 |
| ETIC | 7.5165 × 10−5 | 7 | 3.5468 × 10−5 | 2 | 4.2630 × 10−5 | 2 | 3.4283 × 10−5 | 19 |
| NSEE | 7.1472 × 10−7 | 7 | 1.5912 × 10−7 | 2 | 2.2986 × 10−7 | 2 | 1.4866 × 10−7 | 19 |
| E-VAF | 3.1256 × 10−8 | 14 | 1.3037 × 10−8 | 2 | 1.4204 × 10−8 | 2 | 1.3505 × 10−8 | 19 |
| E-R2 | 7.1472 × 10−7 | 7 | 1.5912 × 10−7 | 2 | 2.2986 × 10−7 | 2 | 1.4866 × 10−7 | 19 |
| Scenario 6 () | ||||||||
| MAE | 6.6219 × 10−4 | 9 | 6.7930 × 10−4 | 4 | 3.2799 × 10−4 | 5 | 3.4326 × 10−4 | 19 |
| RMSE | 6.6889 × 10−4 | 9 | 6.8674 × 10−4 | 4 | 3.3080 × 10−4 | 5 | 3.6410 × 10−4 | 19 |
| ETIC | 9.9149 × 10−4 | 9 | 1.0178 × 10−3 | 4 | 4.9044 × 10−4 | 5 | 5.3987 × 10−4 | 19 |
| NSEE | 2.3260 × 10−5 | 9 | 2.4518 × 10−5 | 4 | 5.6888 × 10−6 | 5 | 6.8917 × 10−6 | 19 |
| E-VAF | 5.2098 × 10−8 | 8 | 5.9310 × 10−8 | 5 | 1.0791 × 10−8 | 10 | 8.6019 × 10−8 | 19 |
| E-R2 | 2.3260 × 10−5 | 9 | 2.4518 × 10−5 | 4 | 5.6888 × 10−6 | 5 | 6.8917 × 10−6 | 19 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Butt, Z.I.; Raja, M.A.Z.; Ahmad, I.; Shoaib, M.; Kumar, R.; Hussain, S.I. Design of Ricker Wavelet Neural Networks for Heat and Mass Transport in Magnetohydrodynamic Williamson Nanofluid Boundary-Layer Porous Medium Flow with Multiple Slips. Magnetochemistry 2025, 11, 40. https://doi.org/10.3390/magnetochemistry11050040
Butt ZI, Raja MAZ, Ahmad I, Shoaib M, Kumar R, Hussain SI. Design of Ricker Wavelet Neural Networks for Heat and Mass Transport in Magnetohydrodynamic Williamson Nanofluid Boundary-Layer Porous Medium Flow with Multiple Slips. Magnetochemistry. 2025; 11(5):40. https://doi.org/10.3390/magnetochemistry11050040
Chicago/Turabian StyleButt, Zeeshan Ikram, Muhammad Asif Zahoor Raja, Iftikhar Ahmad, Muhammad Shoaib, Rajesh Kumar, and Syed Ibrar Hussain. 2025. "Design of Ricker Wavelet Neural Networks for Heat and Mass Transport in Magnetohydrodynamic Williamson Nanofluid Boundary-Layer Porous Medium Flow with Multiple Slips" Magnetochemistry 11, no. 5: 40. https://doi.org/10.3390/magnetochemistry11050040
APA StyleButt, Z. I., Raja, M. A. Z., Ahmad, I., Shoaib, M., Kumar, R., & Hussain, S. I. (2025). Design of Ricker Wavelet Neural Networks for Heat and Mass Transport in Magnetohydrodynamic Williamson Nanofluid Boundary-Layer Porous Medium Flow with Multiple Slips. Magnetochemistry, 11(5), 40. https://doi.org/10.3390/magnetochemistry11050040








